Examining slit pore widths within plasma-exfoliated graphitic material utilising Barrett–Joyner–Halenda analysis

Abstract

Plasma-exfoliated multilayer graphitic material (MLG) consists of orderly aligned stacks which contain many partially oxidised graphitic layers. Slit pores are present between successive stacks and their presence allows for improved friability, facile dispersion and accessibility for the intercalation of compounds. Whilst much research exists into the synthesis and application of MLG, there is a lack of quantitative data regarding their porous structures. This report outlines the structure of MLG as well as the application of Barrett–Joyner–Halenda (BJH) analysis to estimate the distance between adjacent stacks of orderly aligned graphitic layers within MLG. It was found that the distance between stacks can vary quite substantially between 2–131 nm within these plasma-derived materials, correlating with the width of meso- and macro-slit pores. Furthermore, t-plot data also suggests that micropores, likely to exist in the form of both slit pores and in-plane pores, are present within the material, hence stack separations may also exhibit distances of <2 nm. Scanning Electron Microscopy (SEM), Atomic Force Microscopy (AFM) and X-ray Diffraction (XRD) were used to assist in this interpretation and to correlate with the BJH analysis. MLG was further analysed using Transmission Electron Microscopy (TEM), Brunauer–Emmett–Teller (BET) and t-plot analysis, X-ray Photoelectron Spectroscopy (XPS) and Raman spectroscopy to gain a comprehensive understanding of the material investigated. The above techniques provided results which were consistent with the BJH porosity analysis, thus establishing it as a straightforward and highly effective method for understanding materials with broad pore distributions such as MLGs.

---

Introduction

Over the years, extensive work has been undertaken to apply porous graphene-based materials in the context of separation membranes, energy storage and sensor technology.¹ Graphene-based materials have been touted as suitable candidates to address limitations of current technologies. These materials possess some outstanding properties. Pristine graphene exhibits a high theoretical Brunauer–Emmett–Teller (BET) specific surface area, high electrical and thermal conductivity, low density, high chemical and thermal stability, high mechanical strength and impermeability to all chemical species including protons.^2–8 It can, however, often be difficult to achieve the theoretical high surface area of graphene (2630 m² g⁻¹) due to the tendency of graphene sheets to aggregate as a result of extensive van der Waals forces.⁸

On the other hand, lesser quality commercial graphene-based materials, which are more readily available, are well known for their thin structures. These provide characteristics which are also desirable to maximise permeance through defects within their structures, for example. As such, many efforts to tailor and tune porosity involve derivatisation. These have been achieved through covalent or non-covalent functionalisation, or structural alteration through defect introduction to overcome this stacking. These strategies thereby provide an enhanced porous network and increased BET surface area.^9,10

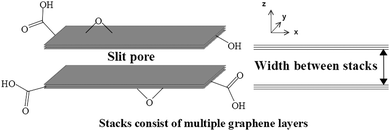
Multi-layer graphitic materials (MLGs), those which are a focus of this investigation, contain a variety of different pore types. Within such materials, there are two main types of pores including in-plane pores and interlayer pores.¹¹ The latter comprise of the spacings between graphene layers or between stacks and commonly makes up “slit pores”. Stacks consists of multiple graphene sheets, ranging in number, forming a substructure within the material. In-plane pores describe holes within the graphitic sheets commonly introduced via various approaches. These include both physical methods such as focused electron beam (FEB) ablation, focused ion beam (FIB) irradiation, ultraviolet (UV)-induced oxidative etching, ion bombardment followed by chemical oxidative etching, oxygen plasma etching, UV light or laser irradiation and chemical methods such as surface-assisted aryl–aryl coupling to fabricate a polyphenylene super-honeycomb network and MnO₂ etching of graphene sheets. These methods have been outlined in a review by Yang and co-workers.¹¹ The combination of slit pores and in-plane pores, as well as composite structures can constitute a variety of interesting 3D porous networks.¹¹ Typically, slit pores exhibit pore widths of sub-nanometre to several nanometres in size which can be widened through the addition of covalently/non-covalently bound external moieties.^9,10,12–20 Furthermore, defective graphene containing ruptured hole edges can serve as a pillaring device for the enlargement of slit pores.⁹

Defective graphitic material can be produced via plasma exfoliation of graphite into fewer layered stacks.²¹ As shown within our previous work, such materials exhibit large slit pores between orderly defined stacks of layers, as indicated through Barrett–Joyner–Halenda (BJH) analysis.²² Within the context of pore analysis during adsorption/desorption experiments, the gaseous adsorbate of choice is very important. The kinetic diameter and shape of the adsorbate govern its ability to penetrate a pore. Nitrogen adsorbate is commonly utilised for BET measurements. It possesses a kinetic diameter of 0.36–0.38 nm.²³ As a result, adsorbing molecules are unable to penetrate any pore beneath this value. In light of this, interlayer slit pores between ordered pristine layers will not be accessed by these molecules, since the interlayer spacing of pristine graphite corresponds to 0.33–0.34 nm.^24,25 As such, spacings between neighbouring stacks govern much of the pore distribution data.

BET and BJH are common and straightforward methods used to analyse the surface area and pore distribution. BET analysis calculates the overall surface area of the micropores, mesopores and macropores within a material, whilst BJH allows analysis of pores between 1.7–300 nm in size. Other techniques such as Density Functional Theory (DFT) and Monte Carlo simulations typically offer more realistic description of the thermodynamic properties of pores.²⁶ On the other hand, although BJH analysis is known to underestimate pores <10 nm, it does provide a practical and straightforward approach for the estimation of many mesopores and macropores.

t-Plot data provides information regarding pores between that of the kinetic diameter of the adsorbate molecule to the upper limit of micropores (2 nm). These techniques are extremely useful for predicting the surface area and porous structures of graphitic materials. Herein, we report a detailed analysis of a plasma-exfoliated material. Whilst our previous work reveals the presence of large slit pores within similar plasma-exfoliated graphitic material via BJH analysis,²² we now demonstrate the application of BJH data to provide actual estimations of the distance between these stacks. It was found that such materials possess large separations between subsequent stacks, thus providing desirable properties including enhanced friability and ease of entry for intercalation compounds.²¹

Results and discussion

Investigating the nature of MLG

The material used for this investigation, denoted hereafter as MLG, was obtained via an industrial collaboration (see Experimental section for further details). Natural flake plasma processing of graphite was carried out using a custom-made multi-electrode dielectric barrier discharge (DBD) plasma reactor. This resulted in flake graphite powders which were exposed to an argon plasma. These powders consisted of exfoliated stacks, which were subsequently treated in an oxygen plasma under similar conditions to introduce surface oxygen-based functionalities. The plasma exfoliation process provided multi-layer stacks of graphitic material with a morphology similar to that outlined in Fig. 1. The material consists of approximately 96.6 atomic% carbon, 3.3 atomic% oxygen and 0.1 atomic% nitrogen functionalities according to X-ray Photoelectron Spectroscopy (XPS) quantitative data (vide infra). Furthermore, the material comprises many orderly aligned, partially oxidised, graphitic layers which aggregate via van der Waals interactions to form stacks. In the dry state, these stacks aggregate forming extensive porous structures in the form of slit pores present between successive stacks. There also may be some degree of pore contribution relating to interparticle pores where adjacent stacks connect or folding of layers takes place. Transmission Electron Microscopy (TEM) and Scanning Electron Microscopy (SEM) imaging carried out on MLG showed that each stack varied quite considerably in dimensions (Fig. 2 and 3, respectively). Additional TEM and SEM images are provided in Fig. S1–S4 (see ESI†). These demonstrate that the stacks generally exhibit lengths of approximately 1–50 μm, although some exceed 200 μm (Fig. S3a, ESI†).

Fig. 1 Diagram outlining the presence of slit pores between successive stacks of MLG.

Fig. 2 Representative TEM images of MLG.

Fig. 3 SEM images of MLG with magnifications of 1730× (left image) and 1040× (right image).

Successive stacks are held at wide spaces from one another. This is due to presence of single-vacancy, double vacancy, complex vacancy and Stone–Wales defects in conjunction with presence of oxygen functionality. These are all introduced during a top-down plasma exfoliation synthesis from raw graphite as outlined above.^21,27–29 The initial argon plasma causes exfoliation of the material through defect introduction. Subsequent oxygen plasma irradiation introduces covalent functionality, resulting in MLG.³⁰ This defective stacked material is exfoliated in comparison to the precursor graphite and partially functionalised with epoxide, hydroxyl, carboxylic acid and carbonyl groups. Again, these are shown in Fig. 1, which also provides a simplified representation of two successive stacks containing multiple layers. This highlights the slit pore occupying the space between stacks and corresponds to the widths between them. It is the nature of the plasma conditions which causes these materials to exhibit such a wide distribution in size and thickness.

Further SEM imaging reveals the presence of thick aggregated structures, which on this particular image possess widths of 313 nm and 152 nm as indicated in Fig. 4. This figure contextualises the presence of stacks within the aggregated structures. These thick aggregates shown in Fig. 4a consist of orderly aligned aggregated stacks (Fig. 4 (right)). Each stack consists of multiple graphitic layers, arranged in a uniform alignment, and held strongly by non-covalent interactions such as π–π bonding. The alignment of these stacks with respect to one another introduces slit pores with width, w, which corresponds to the distance between the stacks. A further SEM image is also shown in Fig. 4b with a Sorbel filter to enhance the observation of individual stacks more clearly.

Fig. 4 SEM images of MLG with and without a Sorbel filter (a) and (b). The schematic on the right of this figure highlights the aggregation of stacks within MLG.

Further analysis of MLG was carried out using Atomic Force Microscopy (AFM) to gain an understanding of the height distribution across overlaying stacks within the various aggregated structures. Fig. 5a depicts a representative example of MLG consisting of multiple aggregated stacks. Magnification of this image shows that these stacks exhibit non-uniform dimensions of several micrometres (Fig. 5b) where some stacks lay flat upon one another, and others protrude from the surface of the material. A two-dimensional (2D) depiction of this figure is displayed in Fig. 5c with a corresponding height scale bar. This highlights that the surface structure deviates in height by 415 nm, indicating the presence of numerous stacked structures. Various height profiles can be estimated by obtaining line profiles across six regions of Fig. 5c, where the AFM tip is scanned directly over one stack and then over the stack directly beneath. These heights provide representative thicknesses of each stack plus its associated slit pore, as outlined in Fig. 5d. Corresponding line profiles are displayed in Fig. 5e and relate to regions 1–6 labelled on Fig. 5c. These show that there is a decrease in height of approximately 22, 83, 32, 26, 27 and 49 nm, respectively. The average decrease in thickness is therefore calculated to be 40 nm, consistent with the average thickness of the stack plus its associated slit pore.

Fig. 5 AFM analysis of MLG depicting: (a) an AFM image of a sample consisting of many aggregated stacks; (b) a magnified image of (a); (c) a two-dimensional top down view of (b); (d) a simplified representation of the AFM tip scanning across one stack of MLG followed by its successive stack directly beneath; and (e) line profiles associated with labels 1–6 in image (c) where the AFM tip scans over one stack followed by its successive stack.

Surface elemental analysis

The surface elemental composition was examined by XPS (see Table 1). The data confirms the presence of carbon, oxygen and nitrogen within the material. Deconvolution of the high-resolution C 1s spectrum (Fig. 6) indicates a total atomic (at) percentage of carbon of 96.7, consisting of seven carbon environments. These are present at binding energies of 284.5, 284.7, 286.5, 288.2, 288.7, 290.8 and 293.9 eV and correspond to the sp², sp³, C–O, C=O, O–C=O, π–π* and π–π* states, respectively. The π–π* satellite structures provide evidence of interplane π bonding within the material.³¹ The data shows that a large proportion of the material comprises of sp² character originating from extensive π-bonding throughout the sheets, as expected for graphitic materials.³² Furthermore, oxygen constitutes a further 3.3 at% of the material in the form of C=O, C–O and O–C=O functional groups, indicating the presence of hydroxyl, carboxy, epoxy and carbonyl functional groups. A trace amount of nitrogen is also present as evidenced by the N 1s state at 399.4 eV, comprising 0.1 at% of the total material. SEM-Energy Dispersive X-ray (EDX) analysis was also conducted on MLG, as shown in Fig. S5 (ESI†). This also reveals the presence of carbon and oxygen within MLG, with trace amounts of silicon.

Table 1 XPS surface elemental composition of MLG

Orbital	Binding energy (eV)	Atomic concentration (%)
sp^2	284.5	76.6
π–π*	290.8	8.0
π–π*	293.9	1.6
C=O	288.2	1.4
C–O	286.5	4.3
sp^3	284.7	3.7
O–C=O	288.7	1.1
Total C	—	96.7
N 1s	399.4	0.1
O 1s	531.9	3.3

---

Fig. 6 Deconvoluted spectra of C 1s orbital within MLG.

Analysis of interlayer spacings and stacking structure using XRD

The X-ray Diffraction (XRD) pattern of MLG was recorded in order to gain an insight into the interlayer spacing between the graphitic layers and the stacking within the material. Copper K_α radiation of wavelength 0.15406 nm was used. The resulting diffraction pattern between 2θ = 10° and 80° is shown in Fig. 7. The figure suggested that the material consists of hexagonal (2H) and rhombohedral (3R) stacking, resulting from an arrangement of layers with ABAB and ABCA stacking sequences, respectively. This coincides with other commercially produced exfoliated graphite materials.³³ Within MLG, a strong diffraction peak characteristic of graphite is shown at 26.6°. This resembles the overlapping (002) 2H and (003) 3R peaks and corresponds to an interlayer spacing of 0.335 nm. Additional evidence of this interlayer spacing is provided by TEM imaging shown in Fig. S2 (ESI†), where the distance between layers was measured to be approximately 0.34 nm. Less prominent peaks are also observed as a four-lined pattern between 42° and 46°. Increased magnification of this four-lined pattern (as shown in the inset of Fig. 7) reveals peaks at 42.5° and 44.6°, which resemble the 2H stacking of the (100) and (101) planes, respectively. The remaining two peaks within the four-lined pattern appear at 43.5° and 46.3° and resemble the 3R (101) and (012) stacking planes. It is observed that these 2H peaks possess a larger intensity than the 3R peaks, suggesting that the majority of the stacking adopts the ABAB orientation. Very small peaks at 54.7° and 77.6° also correspond to graphite 2H (004) and 3R (006), and 2H and 3R (110) planes, respectively. The XRD spectra provides evidence that the stacks of graphitic layers are therefore highly crystalline.

Fig. 7 XRD pattern for MLG in the range between 2θ = 10° and 80° and expanded section in the range between 2θ = 40° and 50°.

In order to gain further insight into the nature of the material, the data obtained from the XRD were used to calculate the dimensions of the graphitic stacks. Full details of these calculations are provided in the ESI.† The Scherrer equation was used to calculate the out-of-plane crystallite size, L_c, and the in-plane crystallite size, L_a.³⁴ The former of these provides an estimation of the thickness of a stack, whilst the latter provides an estimation of the width of a stack as shown in Fig. 8. With this knowledge, the number of graphitic layers within a crystallite, N_c, can be calculated from the interlayer spacing, d_(002)/(003), which is calculated via the Bragg equation.³⁵

Fig. 8 Schematic of the crystalline structure of a seven-layer stack in MLG, displaying the interlayer spacing, d, the out of plane crystallite size, L_c, the in-plane crystallite size, L_a.

The crystallites were found to adopt stacks consisting of numerous graphene layers. The crystallite size (L_c) was calculated to be 35.5 nm, which equates to 106 layers (see Table 2). As such, this material could therefore also be described as graphite nanostructures.³⁶

Table 2 Calculated values of L_c, L_a, N_c and d_(002)/(003) for MLG

Peak position (2θ)	26.6
Interlayer spacing (d(002)) (nm)	0.335
FWHM (radians)	0.22
Crystallite size, Lc (nm)	35.5
In-plane crystallite size, La (nm)	71.8
Number of graphene layers, Nc	106.4

---

Analysis of the graphitic structure using Raman spectroscopy

Raman spectroscopy was conducted on the material to gain an insight into its graphitic structure and the extent of defects throughout the material (Fig. 9). The spectrum incorporates three characteristic peaks, corresponding to the D, G and 2D bands. As expected, the 2D band is broad and heavily upshifted with respect to that of single layer graphene. This suggests the presence of multiple layered stacks consistent with a material synthesised during plasma exfoliation of raw graphite.³⁷ Calculation of the I_2D/I_G ratio gives a value of 0.47, which is significantly lower than that of single layer graphene where the ratio is expected to be between 2 and 3. Thus, the Raman spectrum therefore confirms a multi-layer structure in agreement with the XRD, AFM and SEM analysis outlined above.³⁸ The presence of a D band indicates that defects are also present within the materials as expected. The associated I_D/I_G ratio corresponds to 0.11.

Fig. 9 Raman spectrum of MLG in the region 500 cm⁻¹ to 3000 cm⁻¹.

Surface area and porosity analysis

Nitrogen adsorption–desorption measurements were used to determine the surface area and pore size distribution of MLG utilising Branauer–Emmett–Teller (BET), Barrett–Joyner–Halenda (BJH) and t-plot analyses.³⁹ The results of these analyses are shown in Fig. 10, 11, Table 3 and Fig. S7 (ESI†). The BET results showed that MLG exhibited a Type IIb N₂ adsorption–desorption isotherm typical of materials composed of plate-like particles.⁴⁰ A total surface area of 88.8 m² g⁻¹ was determined to be available to nitrogen adsorbate molecules (Table 3). The large surface area exhibited by this material originates from the presence of a broad distribution of pores, spanning across the microporous, mesoporous and macroporous regions. BJH adsorption cumulative surface area data shows that 66.2 m² g⁻¹ of the total surface area originates from pores between 1.7–300 nm in size, possessing a total cumulative pore volume of 0.172 cm³ g⁻¹. Approximately 74.6% of the overall BET surface area is therefore made up of such pores. The remaining surface area originates from pores above and below the 1.7–300 nm range.

Fig. 10 BET curve of MLG; a magnified perspective focusing on the relative pressures between 0.2 and 0.8 are shown in the inset.

Fig. 11 BJH incremental pore volume as a function of average pore width for MLG.

Table 3 BET and BJH data for MLG

BET surface area (m^2 g^−1)	88.8
t-Plot micropore volume (cm^3 g^−1)	0.0183
BJH adsorption cumulative volume of pores between 1.7–300 nm (cm^3 g^−1)	0.172
BJH adsorption cumulative surface area of pores between 1.7–300 nm (m^2 g^−1)	66.2
% BET surface area made up of pores between 1.7–300 nm	74.6
t-Plot micropore area (m^2 g^−1)	39.7
t-Plot mesopore/macropore surface area (m^2 g^−1)	49.2
% t-plot micropore area compared to total	55.4
BJH adsorption average pore width (4V/A) (nm)	10.4

---

In order to gain more insight into the microporous structure, t-plot analysis was conducted on the material (Fig. S7, ESI†). The data suggested that there is a large contribution of micropore area of 39.7 m² g⁻¹. This represents 44.6% of the total apparent surface area (see Table 3). These types of micropores originate from a contribution of in-plane pores on the graphitic material in addition to small slit micropores between stacks (Fig. 1). It is likely that both types of micropores become introduced during the plasma processing conditions. It has been previously reported that a controlled “destruction” of the graphitic surface is achieved upon the plasma treatment leading to these defect-induced micropores (i.e. pore sizes below 2 nm) within the plane of the sheets.⁴¹ It was not possible to determine the ratio between in-plane pores and slit micropores via this method. Furthermore, these micropores are not visible by SEM imaging due to the associated resolution limit. It is, however, observed that no in-plane pores greater than 2 nm in size are present within MLG during SEM or TEM imaging (using high magnifications up to 398 550 and 50 000×, respectively). As such it is likely that the number of in-plane pores above 2 nm across the material is negligible, and therefore in-plane pores possess dimensions of <2 nm. To confirm this, additional high magnification SEM and TEM images have been provided in the ESI† (see Fig. S2 and S4). It can therefore be concluded that mesopores and macropores originate from slit pores and constitute the remaining 49.2 m² g⁻¹ (55.4%) of the total apparent surface area according to the t-plot method. Thus, we can consider the majority of pores ranging between 2 and 300 nm in size within this material to be slit pores.

Further analysis of the BET data provides information on the nitrogen adsorption–desorption isotherms as shown in Fig. 10. This indicates a steady uptake of N₂ with increasing pressure (P/P₀). A H3 type hysteresis loop is present between the adsorption and desorption branches in the region between 0.45 and 1.0 P/P₀, which is indicative of the presence of slit-like morphologies that are non-rigid in nature and are non-uniform in shape and size.⁴² There is no plateau at high pressures and as such, a type IV isotherm has been ruled out. The curve for the isotherm is consistent with a pseudo-type II (type IIb) isotherm. The absence of a plateau suggests incomplete mesopore filling. This will occur when the size of the pores is too large to be filled and multilayer adsorption continues to proceed to high pressures with no termination.

The presence of a hysteresis loop in the BET data (Fig. 10) arises from the behaviour differences of the adsorbate during adsorption in comparison to desorption. Initially, the adsorption branch increases steeply (<0.001 P/P₀), indicating the presence of micropores within the material. A gradual uptake of adsorbate then occurs up to 0.9 P/P₀, suggesting the presence of mesopores. A sharp uptake is then observed between 0.9–1.0 P/P₀ signifying the presence of macropores.

The behaviour of the nitrogen adsorption and desorption within the material can be rationalised on the basis of a study carried out by Do and co-workers who investigated the adsorption and desorption of simple gases in open end and closed end pores.⁴³ As the pressure increases, the adsorbate covers opposing walls within the slit pores. At the lower contact point, 0.45 P/P₀, the adsorbed layer's state changes from stable to metastable. A metastable adsorbed layer consists of three-regions: the dense adsorbed phase, the mass transfer zone and the gas phase. The mass transfer zone is the region in which the gas molecules exchange between the adsorbed and desorbed phases. If the slit pores are of suitably small size, the mass transfer zones interact forming a bi-convex “liquid-embryo” region. This causes condensation to occur, further adsorbate to be drawn in and subsequently leads to two hemispherical menisci to be formed within the slit pore. A further increase in the pressure from the system leads to saturation and further condensation. In principle, this process should provide a plateau during the adsorption step. This is not observed in this case, however. This is because many of the slit pores within the material are too wide for the mass transfer zones to interact, and hence condensation does not occur below the saturation vapour pressure. As a result, we observe a steep line corresponding to incomplete filling.⁴³ The subsequent reduction in pressure then allows for desorption of the nitrogen molecules via a different thermodynamic process providing the hysteresis curve. In the case of pores in which condensation had occurred, the meniscus increases in their curvature, whilst remaining pinned to the pore mouths.^44,45

The pore size distribution associated with the material was investigated by BJH analysis (Fig. 11). The data reveals a substantially broad range of pore widths spanning between approximately 2 and 131 nm. In contrast, much smaller pore size distributions are found within other exfoliated graphitic materials.^11,46–48 The average pore size, as determined by the BJH analysis, was found to be 10.4 nm (Table 3). Taking into account this average value in conjunction with the crystallite size, L_c (35.5 nm) determined by XRD, it is understood that the thickness of a stack of MLG plus its associated slit pore equates to 45.9 nm. This is consistent with the observations found within the AFM analysis, where the average thickness was estimated to be 40 nm, as outlined above. This demonstrates that BJH analysis can indeed be employed as a technique to estimate the distance between successive stacks. Fig. 12 outlines how these three techniques can be utilised in combination to gain information regarding the stack thicknesses and distance between stacks. Furthermore, SEM imaging also enables the direct measurement of the width between stacks and coincides with data obtained from BJH analysis (vide infra).

Fig. 12 Diagram depicting the stack thickness, the distance between successive stacks and the thickness of a stack plus slit pore on MLG. The corresponding characterisation technique which can be used to estimate these values are shown in bold.

Pores which are much larger in size are also observed within MLG ranging up to 131.2 nm. These relatively large slit pores can be extremely beneficial within various contexts. They improve friability and permit easy dispersion via shear type forces and sonication. Further to this, they provide accessibility for intercalation compounds such as sulfur and molecular hydrogen.²¹

Analysis of the slit porosity using scanning electron microscopy

With a detailed analysis of the porosity carried out, we investigated the slit pores within the MLG materials via SEM imaging. Seven representative SEM images are provided in Fig. 13. These provide evidence of slit pores of various widths as evidenced by the measured distances between the stacks. These pores are observed within the space between two neighbouring stacks. In accordance with the average slit pore determined by BJH analysis, slit pores of 10 nm width were identified within the images as shown in Fig. 13a. The remaining images support the fact that this material contains a range of slit pore sizes. These vary from 9 nm up to 131 nm within the images we obtained for this material. The latter of these equates to the largest slit pores obtained by BJH analysis for MLG, whilst the remaining widths correspond to slit pore widths found within the BJH incremental pore volume plot (Fig. 11). As such, SEM imaging also shows that many of these stacks possess large distances within the range found by the BJH data. Thus, we have therefore provided the first application of BJH to estimate the distance between stacks within MLG materials, also enabling the average slit pore width to be measured.

Fig. 13 SEM images of slit meso- and macro-pores corresponding to widths of (a) 10 nm; (b) 23 nm; (c) 9 nm, 19 nm and 32 nm; (d) 27 and 33 nm; (e) 70 nm; (f) 92 nm; and (g) 131 nm. The distances between representative stacks have been measured and the values are included in the figures. Magnifications of the images correspond to 41 970×, 24 260×, 35 090×, 34 600×, 26 630×, 34 420× and 20 600× for images (a)–(g), respectively.

Conclusions

In summary, we have demonstrated the importance in utilising BJH analysis to quantify the pore distribution within exfoliated graphitic materials. The BJH plot can be used to provide an estimation of the distance between successive stacks within MLG. In this case, we have shown that these vary largely between approximately 2–131 nm in width. These contribute to the majority of the BET surface area. Furthermore, some stacks are likely to possess separation distances of less than 2 nm consistent with slit micropores which contribute to t-plot data. These findings are supported by various other techniques. SEM imaging enabled the direct observation and measurement of many of these slit pores. An average slit pore size of around 10 nm was found by BJH analysis. AFM allowed for the direct height measurement of a stack and its associated slit pore. By summing the crystallite size, L_c, obtained from XRD, and the average slit pore width obtained from BJH analysis, we obtained an average value which is consistent with aforementioned height measurement obtained by AFM. This demonstrates that the three techniques are complementary to each other.

Furthermore, MLG has also been characterised using TEM, XPS and Raman spectroscopy to gain further information regarding the morphology, defects, elemental surface composition and nature of the multi-layer structures.

We have therefore shown for the first time that BJH analysis facilitates facile measurement of the distance between stacks, assisting the interpretation of porous nature of graphitic materials containing slit pores. This is particularly important for building an understanding of those materials with non-uniform porous distributions, such as those synthesised via plasma-exfoliation.

Experimental

General remarks

The plasma-exfoliated multilayer graphitic material (MLG) was provided by Perpetuus Carbon Technologies. This was synthesised via the techniques outlined within the Results and discussion section.

Characterisation methods

Scanning electron microscopy (SEM) images were obtained using a MIRA3 Tescan ×64 SEM instrument. The samples were deposited onto double sided copper tape and gold-coated prior to imaging using a gold sputter coater to enhance the resolution of the images. An electron beam of 20 kV was utilised with a beam intensity of 12 kV. Additional SEM images provided in Fig. S4 (ESI†) were obtained using a field-emission Scanning electron microscope (model 1540XB from Carl Zeiss) using the same preparation and conditions. Transmission electron microscopy (TEM) images were obtained using a Jeol 2100 field emission gun (FEG) TEM with a 200 kV power source. <1 mg of sample was dispersed in ethanol and drop casted onto a 300 mesh Cu grid with holey carbon film. Powder X-ray diffraction (XRD) patterns were collected using a Panalytical X’Pert diffractometer with a copper anode irradiation (l = 1.541 Å) operating at 40 kV and 40 mA. Phase identification was performed by matching experimental patterns against entries in the ICDD standard database. The surface area and porosity characteristics of the materials were analysed using a Micromeritics ASAP 2020 physisorption analyser. Samples were degassed under 0.667 Pa for 720 minutes at 150 °C with a heating rate of 10 °C min⁻¹. The surface area and pore size distribution were measured at 77 K using Brunauer–Emmett–Teller (BET) analysis. A standard sample containing silica–alumina was used to validate surface area and porosity measurements (see ESI† for more details). t-Plot analysis utilised the Harkins Jura thickness equation and Barrett–Joyner–Halenda (BJH) cumulative pore volume methods utilised the Halsey equation with FAAS correction. X-Ray photoelectron spectroscopy (XPS) analysis was performed using a Kratos Axis Ultra-DLD photoelectron spectrometer with a monochromatic aluminium Kα electron source (1486.6 eV). XPS data was analysed using CasaXPS and binding energies were referenced to carbon core level for adventitious carbon at 284.8 eV possessing an uncertainty of 0.2 eV. Curve fitting was carried out using Gaussian and Lorentzian line profiles. Raman Spectroscopy measurements were performed using a Renishaw InVia confocal Raman microscope equipped with an Ar+ visible green laser with emission wavelength of 514 nm laser and magnification ×20, over an extended wavenumber range, 100–3200 cm⁻¹ (static, 625–1900 cm⁻¹). Typical measurements utilised a 5% laser power with 5 accumulations (static, 20 accumulations) at 10 s exposure time (static, 2 s) for each material. Samples were loaded directly onto a slide with no further preparation prior to analysis. Data was extracted from one spot of the sample. Spectra were collected in a reflective mode using a high sensitive charge couple device (CCD) detector. Atomic force microscopy (AFM) analysis was conducted on an AFM XE-100 from Park Systems. Samples were dispersed in chloroform and drop casted onto freshly cleaved mica. Measurements were taken using non-contact mode with NSG30 probes from NT-MDT.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by European Social Fund (ESF) via the Welsh Government through a KESS2 PhD studentship for R. M. It was co-sponsored by Perpetuus Carbon Technologies. The company is also thanked for providing the raw MLG material. We are additionally grateful to Dr Uchechukwu K. Onwukwe, Dr Ashley Howkins and Dr Lorna Anguilano at the Experimental Techniques Centre, Brunel University London, for running TEM analysis. We would also like to thank to Dr Thomas Davies and the Cardiff University EM facility for TEM analysis and Dr Greg Shaw and Dr David Morgan at Cardiff University for Raman, XRD and XPS analysis.

References

1. Y. Tao, Z.-Y. Sui and B.-H. Han, J. Mater. Chem. A, 2020, 8, 6125–6143.
2. K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. L. Stormer, Solid State Commun., 2008, 146, 351–355.
3. R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres and A. K. Geim, Science, 2008, 320, 1308.
4. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907.
5. A. Peigney, C. Laurent, E. Flahaut, R. R. Bacsa and A. Rousset, Carbon, 2001, 39, 507–514.
6. J. S. Bunch, A. M. Van Der Zande, S. S. Verbridge, I. W. Frank, D. M. Tanenbaum, J. M. Parpia, H. G. Craighead and P. L. McEuen, Science, 2007, 315, 490–493.
7. V. Singh, D. Joung, L. Zhai, S. Das, S. I. Khondaker and S. Seal, Prog. Mater. Sci., 2011, 56, 1178–1271.
8. S. Gadipelli and Z. X. Guo, Prog. Mater. Sci., 2015, 69, 1–60.
9. A. Klechikov, G. Mercier, T. Sharifi, I. A. Baburin, G. Seifert and A. V. Talyzin, Chem. Commun., 2015, 51, 15280–15283.
10. I. A. Baburin, A. Klechikov, G. Mercier, A. Talyzin and G. Seifert, Int. J. Hydrogen Energy, 2015, 40, 6594–6599.
11. T. Yang, H. Lin, X. Zheng, K. P. Loh and B. Jia, J. Mater. Chem. A, 2017, 5, 16537–16558.
12. F. Guo, M. Creighton, Y. Chen, R. Hurt and I. Külaots, Carbon, 2014, 66, 476–484.
13. A. Nordenström, A. Iakunkov, J. Sun and A. V. Talyzin, RSC Adv., 2020, 10, 6831–6839.
14. M. Georgakis, G. Stavropoulos and G. P. Sakellaropoulos, Microporous Mesoporous Mater., 2014, 191, 67–73.
15. C. R. Wood, N. T. Skipper and M. J. Gillan, J. Solid State Chem., 2011, 184, 1561–1565.
16. G. Srinivas, A. Lovell, C. A. Howard, N. T. Skipper, M. Ellerby and S. M. Bennington, Synth. Met., 2010, 160, 1631–1635.
17. B. Mi, Science, 2014, 343, 740–742.
18. H. Huang, Z. Song, N. Wei, L. Shi, Y. Mao, Y. Ying, L. Sun, Z. Xu and X. Peng, Nat. Commun., 2013, 4, 2979.
19. G. Mercier, A. Klechikov, M. Hedenström, D. Johnels, I. A. Baburin, G. Seifert, R. Mysyk and A. V. Talyzin, J. Phys. Chem. C, 2015, 119, 27179–27191.
20. R. Kumar, V. M. Suresh, T. K. Maji and C. N. R. Rao, Chem. Commun., 2014, 50, 2015.
21. I. Walters and D. Walters, EU Pat., EP3129323B1, Perpetuus Research & Development Limited, 2019.
22. R. L. McLaren, C. J. Laycock, D. J. Morgan and G. R. Owen, New J. Chem., 2020, 44, 19144–19154.
23. J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504.
24. G. E. Bacon, Acta Crystallogr., 1951, 4, 558–561.
25. G. Çakmak and T. Öztürk, Diamond Relat. Mater., 2019, 96, 134–139.
26. A. V. Neimark, Y. Lin, P. I. Ravikovitch and M. Thommes, Carbon, 2009, 47, 1617–1628.
27. O. Lehtinen, J. Kotakoski, A. V. Krasheninnikov and J. Keinonen, Nanotechnology, 2011, 22, 175306.
28. T. Xu and L. Sun, Defects in Advanced Electronic Materials and Novel Low Dimensional Structures, Elsevier, 2018, vol. 5, pp. 137–160.
29. S. P. Surwade, S. N. Smirnov, I. V. Vlassiouk, R. R. Unocic, G. M. Veith, S. Dai and S. M. Mahurin, Nat. Nanotechnol., 2015, 10, 459–464.
30. C. Chen, B. Liang, A. Ogino, X. Wang and M. Nagatsu, J. Phys. Chem. C, 2009, 113, 7659–7665.
31. A. Theodosiou, B. F. Spencer, J. Counsell and A. N. Jones, Appl. Surf. Sci., 2020, 508, 144764.
32. M. J. Allen, V. C. Tung and R. B. Kaner, Chem. Rev., 2010, 110, 132–145.
33. M. S. Seehra, U. K. Geddam, D. Schwegler-Berry and A. B. Stefaniak, Carbon, 2015, 95, 818–823.
34. A. L. Patterson, Phys. Rev., 1939, 56, 978–982.
35. W. L. Bragg, Proc. Cambridge Philos. Soc., 1913, 17, 43–57.
36. A. Bianco, H.-M. Cheng, T. Enoki, Y. Gogotsi, R. H. Hurt, N. Koratkar, T. Kyotani, M. Monthioux, C. R. Park, J. M. D. Tascon and J. Zhang, Carbon, 2013, 65, 1–6.
37. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
38. V. T. Nguyen, H. D. Le, V. C. Nguyen, T. T. Tam Ngo, D. Q. Le, X. N. Nguyen and N. M. Phan, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2013, 4, 035012.
39. E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380.
40. P. Llewellyn and G. M. F. Rouquerol, J. Rouquerol, K. S. W. Sing, Adsorption by Powders and Porous Solids, Elsevier, 1999.
41. N. Kostoglou, A. Tarat, I. Walters, V. Ryzhkov, C. Tampaxis, G. Charalambopoulou, T. Steriotis, C. Mitterer and C. Rebholz, Microporous Mesoporous Mater., 2016, 225, 482–487.
42. K. S. W. Sing, Pure Appl. Chem., 1985, 57, 603–619.
43. Y. Zeng, L. Prasetyo, S. J. Tan, C. Fan, D. D. Do and D. Nicholson, Chem. Eng. Sci., 2017, 158, 462–479.
44. F. Ancilotto, M. Da Re, S. Grubišić, A. Hernando, P. L. Silvestrelli and F. Toigo, Mol. Phys., 2011, 109, 2787–2796.
45. C. Fan, Y. Zeng, D. D. Do and D. Nicholson, Phys. Chem. Chem. Phys., 2014, 16, 12362.
46. N. Natter, N. Kostoglou, C. Koczwara, C. Tampaxis, T. Steriotis, R. Gupta, O. Paris, C. Rebholz and C. Mitterer, C, 2019, 5, 16.
47. S. Nasir, M. Z. Hussein, Z. Zainal and N. A. Yusof, J. Nanomater., 2019, 2019, 1–13.
48. B. Gurzęda, T. Buchwald, M. Nocuń, A. Bąkowicz and P. Krawczyk, RSC Adv., 2017, 7, 19904–19911.

---

Footnote

† Electronic supplementary information (ESI) available: Containing further spectroscopic and analytical details concerning the characterisation of MLG. See DOI: 10.1039/d1nj01702k

---