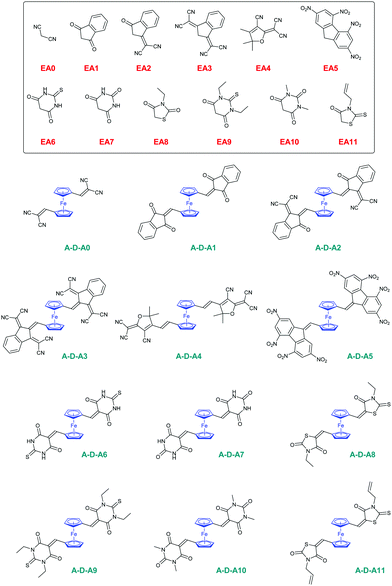
Open Access Article
Open Access ArticleD–A dyads and A–D–A triads based on ferrocene: push–pull dyes with unusual behaviours in solution†
Guillaume
Noirbent
 *a,
Damien
Brunel
*a,
Damien
Brunel
 *a,
Thanh-Tuân
Bui
*a,
Thanh-Tuân
Bui
 b,
Sébastien
Péralta
b,
Sébastien
Péralta
 b,
Pierre-Henri
Aubert
b,
Pierre-Henri
Aubert
 b,
Didier
Gigmes
b,
Didier
Gigmes
 a and
Frédéric
Dumur
a and
Frédéric
Dumur
 *a
*a
aAix Marseille Univ, CNRS, ICR UMR 7273, F-13397 Marseille, France. E-mail: guillaume.noirbent@outlook.fr; damienbru@laposte.net; frederic.dumur@univ-amu.fr
bCY Cergy Paris Université, LPPI, F-95000 Cergy, France
First published on 21st June 2021
Abstract
Ferrocene has been extensively used for the design of chromophores with reversible electrochemical properties. In this work, a series of twelve D–A dyads and twelve symmetrically substituted A–D–A triads have been developed based on twelve different electron acceptors. The photophysical characteristics of the different dyes have been studied using various techniques including UV-visible absorption and photoluminescence spectroscopy. Their electrochemical behaviours have also been determined. To evidence the specificities of the triads relative to those of their donor–acceptor (D–A) dyad analogues, comparison between these two families of dyes (D–A and A–D–A) has been made. The solvatochromic behaviour of the twenty-four dyes has been examined in 22 solvents of different polarities. Parallel to solvatochromism, suppression of the push–pull effect by oxidation of the ferrocene unit using a strong oxidizing agent, i.e. nitrosonium tetrafluoroborate, drastically modified the optical properties of the different dyes. To support the experimental results, theoretical calculations were carried out. Interestingly, in this work, an unprecedented modification of the UV-visible absorption spectra in solution was observed over time for all ferrocene-based push–pull dyes in various solvents. Evidence of this behaviour for ferrocene-based push–pull dyes is unprecedented in the literature.
1. Introduction
During the past few decades, push–pull dyes comprising an electron donor connected to an electron acceptor by means of a conjugated or a non-conjugated spacer have been extensively studied, due to the wide range of applications in which these different chromophores are involved.1 Among the most popular applications, organic photovoltaics (OPVs),2–7 organic field effect transistors (OFETs)8 and non-linear optics (NLO)9–13 can be cited as the most representative ones. However, emerging research fields such as visible light photopolymerization under low light intensity14–23 and the blooming field of 3D-printing requiring dyes absorbing at 405 nm are also worth mentioning.24,25 Compared to their inorganic counterparts, i.e., the pigments that suffer from an incredible insolubility in common organic solvents, organic dyes offer several advantages such as easy tunability of their absorption maxima,26–28 a facile processability due to their remarkable solubility in most of the common organic solvents, and an easy synthetic process, especially, if the Knoevenagel reaction is selected as the reaction used to form the conjugated spacer between the donor and the acceptor. For sub-disciplines29,30 derived from NLO, such as bioimaging, non-linear frequency conversion of laser sources or electro-optic modulators, a fast response time is also required, which can be obtained with organic dyes and metal complexes such as ferrocene.31–35 In numerous applications, organic dyes are often preferred over metal complexes due to the toxicity concerns raised by the use of metal-based dyes. However, non-toxic metals such as iron can be used to create push–pull dyes and one of the most representative complexes in this field is ferrocene.36 This metallocene comprising an iron(II) cation sandwiched between two coplanar cyclopentadienyl cycles can be reversibly oxidized at a moderate potential so that this metallocene is internationally used as a reference for electrochemistry.37 However, its scope of application is not limited to electrochemistry and ferrocene is now extensively used in medicine,38 (photo)polymerization,39,40 enantioselective catalysis,41 for the design of molecular machines,42 metal organic frameworks43 and molecular rectifiers.44 Due to its facile oxidation, ferrocene is also a good candidate for the design of donor–acceptor (D–A) conjugates and numerous dyads have been reported over the years.45–55 Conversely, acceptor–donor–acceptor (A–D–A) triads based on ferrocene have only scarcely been examined in the literature (see Fig. 1).56–61 In particular, the photophysical properties of A–D–A triads based on ferrocene have only been examined in detail in the case of Meldrum's derivatives (UV-visible absorption, fluorescence spectroscopy and spectroelectrochemistry).Ferrocene possesses a low oxidation potential (0.52, 0.44 and 0.43 V vs. SCE in dichloromethane, acetonitrile, or DMF)62 and can be thus oxidized to ferrocenium via a one-electron oxidation process.63 This oxidation can not only be done electrochemically64,65 but also chemically by using oxidizing agents such as nitrosonium tetrafluoroborate66 or iron(III) sulfate.67 One of the main advantages of nitrosonium tetrafluoroborate arises from its excellent solubility in common organic solvents, enabling to carry out the discoloration experiments in dichloromethane. Indeed, when ferrocene is used as an electron donor in push–pull structures, conversion of the electron-donating ferrocene to the electron-deficient ferrocenium can drastically affect the optical properties, as exemplified by A–D–A triads previously reported in the literature and comprising BODIPY and ferrocenes.68 More generally, colour change is observed for all electrochromic devices comprising ferrocene as the electron-donating moiety.69,70
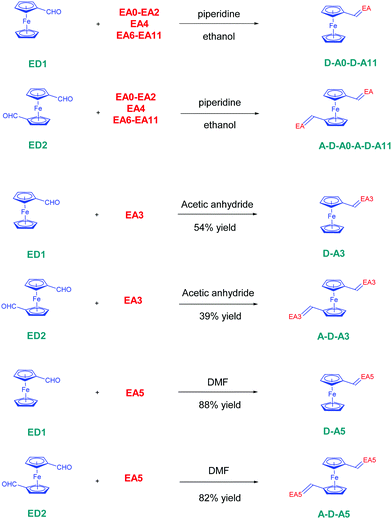
In this work, a series of twelve A–D–A triads comprising ferrocene-1,1′-dicarbaldehyde ED2 as the electron donor have been synthesized and their photophysical properties have been determined (see Fig. 2). To evidence the main differences that exist between the twelve A–D–A triads (A–D–Ax, x = 0–11) and their twelve corresponding D–A dyads (D–Ax, x = 0–11), the latter ones have been synthesized with EA0–EA11 as the electron acceptors and ferrocenecarboxaldehyde ED1 as the donor for comparison (see Fig. 2). Parallel to the different investigations concerning their optical properties and their solvatochromic behaviour in solution, electrochemical measurements were also carried out to characterize the dyads and triads. Finally, by chemical oxidation of ferrocene to ferrocenium, suppression of the electron-donating part in the dyads and triads, and conversion of the electron-donating ferrocene as an electron acceptor (ferrocenium), a dramatic modification of their absorption spectra and colour changes of the solutions were observed. Modulation of the spectra obtained on oxidation has notably been previously examined in the literature, especially to demonstrate “switchable” NLO properties of ferrocene-based push–pull dyes.71 In this work, for several compounds, the use of an excess of chemical oxidant resulted in successive oxidation processes that will be presented in this work. Finally, as one of the most interesting findings of this work, a modification of the optical properties of the ferrocene-based push–pull dyes in solution was demonstrated upon standing for the 24 dyes. This usual behaviour has never been reported in the literature for ferrocene-based dyes, even if numerous dyads and triads comprising ferrocene as the electron donor have been reported in the literature.45–59 This unusual behaviour was investigated using theoretical calculations, UV-visible absorption spectroscopy and cyclic voltammetry.
2. Experimental details
2.1. Materials and instrumentation methods
All reagents and solvents were purchased from Aldrich, Alfa Aesar or TCI Europe and used as received without further purification. Mass spectroscopy was performed at the Spectropole of Aix-Marseille University. ESI mass spectral analysis was recorded using a 3200 QTRAP (Applied Biosystems SCIEX) mass spectrometer. The HRMS mass spectral analysis was performed using a QStar Elite (Applied Biosystems SCIEX) mass spectrometer. Elemental analysis was performed using a Thermo Finnigan EA 1112 elemental analysis apparatus driven by the Eager 300 software. 1H and 13C NMR spectra were determined at room temperature in 5 mm o.d. tubes using a Bruker Avance 400 spectrometer of the Spectropole: 1H (400 MHz) and 13C (100 MHz). The 1H chemical shifts were referenced to the solvent peak CDCl3 (7.26 ppm) and the 13C chemical shifts were referenced to the solvent peak CDCl3 (77 ppm). UV-visible absorption spectra were recorded using a Varian Cary 50 Scan UV visible spectrophotometer, at concentration of 8 × 10−5 M, corresponding to diluted solutions. Fluorescence spectra were recorded using a Jasco FP 6200 spectrometer. The electrochemical properties of the investigated compounds were measured in dichloromethane by cyclic voltammetry, at a scan rate of 100 mV s−1, with tetrabutylammonium perchlorate (0.1 M) as the supporting electrolyte in a standard one-compartment, three-electrode electrochemical cell under an argon stream using a VSP BioLogic potentiostat. The working, pseudo-reference and counter electrodes were platinum disk (Ø = 1 mm), Ag wire, and Au wire gauze, respectively. Ferrocene was used as an internal standard, and the potentials are referred to the reversible formal potential of this compound. Ferrocenecarboxaldehyde72ED1, ferrocene-1,1′-dicarbaldehyde73ED2, D–A5 and A–D–A548 were synthesized as previously reported in the literature, without modification and in similar yields. Computational details: All quantum mechanical calculations were computed using Gaussian Package.74 All geometry optimizations were performed using density functional theory (DFT) with the global hybrid exchange–correlation functional B3LYP75 and all minima on the potential energy surface were verified via a calculation of vibrational frequencies, ensuring no imaginary frequencies were present. The Pople double-zeta basis set with a double set of polarization functions on non-hydrogen atoms (6-3111G(d,p))76 was used throughout. This computational approach was chosen in consistency with previous works, as it provides good agreement with the experimental data. Excited states were probed using time dependent density functional theory (TD-DFT) using the same functional. All transitions (singlet–singlet) were calculated vertically with respect to the singlet ground state geometry. Solvent effects were taken into account by using the implicit polarizable continuum model (PCM).77,78 DCM was chosen in analogy with the experiments. Computed spectra were simulated by convoluting each transition with Gaussian functions – centered on each absorption maximum – using a constant full width at half maximum (FWHM) value of 0.2 eV. The assignment of electronic transitions for λmax has been determined using GaussSum 3.0 software.792.2. Synthesis of the dyes
D–A0: EA0 (0.38 g, 5.79 mmol), mexp = 1.49 g, 98% yield. 1H NMR (CDCl3) δ: 4.33 (s, 5H), 4.85 (s, 2H), 4.98 (s, 2H), 7.72 (s, 1H); 13C NMR (CDCl3) δ: 71.3, 71.9, 74.2, 75.4, 114.5, 115.3, 163.4; HRMS (ESI MS) m/z: theor: 262.0193 found: 262.0195 ([M]+˙ detected).
D–A1: EA1 (0.85 g, 5.79 mmol), mexp = 1.94 g, 98% yield. 1H NMR (CDCl3) δ: 4.23 (s, 5H), 4.84–4.85 (m, 2H), 5.43–5.44 (m, 2H), 7.75–7.79 (m, 2H), 7.88 (s, 1H), 7.93–7.97 (m, 2H); 13C NMR (CDCl3) δ: 70.7, 75.2, 75.3, 76.2, 77.2, 122.6, 122.8, 124.2, 134.5, 134.6, 139.9, 142.3, 149.4, 189.5, 190.5; HRMS (ESI MS) m/z: theor: 342.0343 found: 342.0342 ([M]+˙ detected).
D–A2: EA2 (1.12 g, 5.79 mmol), mexp = 2.20 g, 97% yield. 1H NMR (CDCl3) δ: 4.35 (s, 5H), 5.04 (s, 2H), 5.34 (s, 2H), 7.9–7.78 (m, 2H), 7.86–7.88 (m, 1H), 8.46 (s, 1H), 8.66 (d, 1H, J = 7.0 Hz); 13C NMR (CDCl3) δ: 68.1, 72.0, 76.9, 77.2, 77.7, 115.1, 115.3, 123.3, 123.6, 125.1, 134.2, 134.8, 137.3, 139.4, 149.6, 161.7, 187.2; HRMS (ESI MS) m/z: theor: 390.0456 found: 390.0455 ([M]+˙ detected).
D–A3: EA3 (1.40 g, 5.79 mmol), mexp = 1.1 g, 54% yield. 1H NMR (CDCl3) δ: 8.69–8.63 (m, 1H), 8.45 (s, 1H), 7.86 (dd, J = 6.1, 2.2 Hz, 1H), 7.76–7.69 (m, 2H), 5.35–5.29 (m, 2H), 5.06–5.01 (m, 2H), 4.34 (s, 5H); Anal. calc. for C26H14FeN4: C, 71.2; H, 3.2; N, 12.8; found: C, 71.3; H, 3.3; N, 12.7%; HRMS (ESI MS) m/z: theor: 461.0460 found: 461.0462 ([M + Na]+ detected).
D–A4: EA4 (1.15 g, 5.79 mmol), mexp = 1.86 g, 81% yield. 1H NMR (CDCl3) δ: 7.71 (d, J = 15.9 Hz, 1H), 6.49 (d, J = 15.9 Hz, 1H), 4.83 (s, 2H), 4.71 (s, 2H), 4.24 (s, 5H), 1.74 (s, 6H); 13C NMR (CDCl3) δ: 176.26, 173.28, 151.88, 111.16, 97.16, 79.29, 74.85, 71.22, 70.18, 26.51; HRMS (ESI MS) m/z: theor: 418.0613 found: 418.0611 ([M + Na]+ detected).
D–A5: EA5 (1.42 g, 5.79 mmol), mexp = 2.76 g, 88% yield. 1H NMR (Acetone-d6) δ: 4.45 (s, 5H), 5.08 (t, 2H, J = 1.7 Hz), 5.18 (t, 2H, J = 1.7 Hz), 8.83 (d, 2H, J = 1.9 Hz), 8.96 (s, 1H), 9.47 (d, 1H, J = 1.9 Hz), 9.73 (d, 1H, J = 1.9 Hz); Anal. calc. for C24H14FeN4O8: C, 53.2; H, 2.6; O, 23.6; found: C, 53.3; H, 2.3; O, 23.7%; HRMS (ESI MS) m/z: theor: 565.0053 found: 565.0056 ([M + Na]+ detected).
D–A6: EA6 (0.84 g, 5.79 mmol), mexp = 1.89 g, 96% yield. 1H NMR (CDCl3) δ: 8.48 (s, 1H), 5.36 (s, 2H), 5.10–5.07 (m, 2H), 4.33 (s, 5H); Anal. calc. for C15H12FeN2O2S: C, 52.9; H, 3.6; O, 9.4; found: C, 52.1; H, 3.6; O, 9.5%; HRMS (ESI MS) m/z: theor: 339.9969 found: 340.0002 ([M]+˙ detected).
D–A7: EA7 (0.74 g, 5.79 mmol), mexp = 1.78 g, 95% yield. 1H NMR (CDCl3) δ: 8.47 (s, 1H), 5.34 (s, 2H), 5.00 (s, 2H), 4.30 (s, 5H); Anal. calc. for C15H12FeN2O3: C, 55.6; H, 3.7; O, 14.8; found: C, 55.5; H, 3.6; O, 14.5%; HRMS (ESI MS) m/z: theor: 324.0197 found: 324.0194 ([M]+˙ detected).
D–A8: EA8 (0.84 g, 5.79 mmol), mexp = 1.77 g, 95% yield. 1H NMR (CDCl3) δ: 1.30 (t, 3H, J = 7.1 Hz), 4.17 (q, 2H, J = 7.1 Hz), 4.23 (s, 5H), 4.60 (s, 2H), 4.62 (s, 2H), 7.63 (s, 1H); 13C NMR (CDCl3) δ: 12.3, 39.7, 70.2, 71.0, 72.7, 118.9, 136.1, 142.1, 166.8, 192.9; HRMS (ESI MS) m/z: theor: 324.0197 found: 324.0194 ([M]+˙ detected).
D–A9: EA9 (1.16 g, 5.79 mmol), mexp = 1.12 g, 49% yield. 1H NMR (CDCl3) δ: 8.44 (s, 1H), 5.48–5.22 (m, 2H), 5.13–4.90 (m, 2H), 4.56 (qd, J = 6.9, 1.7 Hz, 4H), 4.29 (s, 5H), 1.31 (td, J = 7.0, 2.8 Hz, 6H). 13C NMR (75 MHz, CDCl3) δ: 179.02, 162.13, 161.43, 159.02, 111.51, 71.29, 44.01, 43.39, 12.58; HRMS (ESI MS) m/z: theor: 419.0487 found: 419.0484 ([M + Na]+ detected).
D–A10: EA10 (0.90 g, 5.79 mmol), mexp = 1.87 g, 92% yield. 1H NMR (CDCl3) δ: 3.36 (s, 3H), 3.39 (s, 3H), 4.27 (s, 5H), 4.89 (t, 2H, J = 1.9 Hz), 5.31 (t, 2H, J = 1.9 Hz), 8.44 (s, 1H); 13C NMR (CDCl3) δ: 28.2, 28.9, 71.0, 76.0, 76.3, 76.8, 110.7, 151.8, 161.0, 161.2, 163.3; HRMS (ESI MS) m/z: theor: 352.0510 found: 352.0513 ([M]+˙ detected).
D–A11: EA11 (1.00 g, 5.79 mmol), mexp = 1.46 g, 68% yield. 1H NMR (CDCl3) δ: 7.64 (s, 1H), 5.94–5.81 (m, 1H), 5.36–5.21 (m, 2H), 4.73 (dt, J = 5.8, 1.4 Hz, 2H), 4.66–4.62 (m, 2H), 4.62–4.57 (m, 2H), 4.30–4.19 (m, 5H); 13C NMR (CDCl3) δ: 192.70, 166.68, 136.51, 129.81, 119.20, 118.63, 77.33, 77.22, 77.01, 76.69, 76.64, 72.84, 71.03, 70.26, 46.39; HRMS (ESI MS) m/z: theor: 391.9837 found: 391.9836 ([M + Na]+ detected).
A–D–A0: EA0 (1.1 g, 16.52 mmol), mexp = 2.1 g, 75% yield. 1H NMR (CDCl3) δ: 7.63 (s, 2H), 5.09 (s, 4H), 4.89 (s, 4H). 13C NMR (CDCl3) δ: 160.58, 113.74, 113.31, 80.13, 75.72, 73.45, 29.69. HRMS (ESI MS) m/z: theor: 356.0593 found: 356.0592 ([M + NH4]+ detected).
A–D–A1: EA1 (2.41 g, 5.79 mmol), mexp = 1.90 g, 66% yield. 1H NMR (CDCl3) δ: 4.77 (s, 4H), 5.45 (s, 4H), 7.36 (s, 2H), 7.57–7.65 (m, 8H); 13C NMR (CDCl3) δ: 76.0, 76.7, 78.4, 122.6, 122.7, 126.3, 134.3, 134.5, 139.5, 141.9, 144.8, 188.7, 189.6; HRMS (ESI MS) m/z: theor: 498.0555 found: 498.0558 ([M]+˙ detected).
A–D–A2: EA2 (3.2 g, 16.52 mmol), mexp = 2 g, 41% yield. Anal. calc. for C36H18FeN4O2: C, 72.7; H, 3.0; O, 5.4; found: C, 72.5; H, 3.3; O, 5.7%; HRMS (ESI MS) m/z: theor: 617.0672 found: 617.0671 ([M + Na]+ detected).
A–D–A3: EA3 (4.0 g, 16.52 mmol), mexp = 0.55 g, 39% yield. Anal. calc. for C42H18FeN8: C, 73.1; H, 2.6; N, 16.2; found: C, 73.3; H, 2.3; O, 16.4%; HRMS (ESI MS) m/z: theor: 797.0052 found: 797.0041 ([M + Ag]+ detected).
A–D–A4: EA4 (3.3 g, 16.52 mmol), mexp = 3 g, 91% yield. Anal. calc. for C34H24FeN6O2: C, 67.6; H, 4.0; O, 5.3; found: C, 67.7; H, 4.3; O, 5.4%; HRMS (ESI MS) m/z: theor: 627.1203 found: 627.1204 ([M + Na]+ detected).
A–D–A5: EA5 (5.72 g, 16.52 mmol), mexp = 12.17 g, 82% yield. Anal. calc. for C38H18FeN8O16: C, 50.8; H, 2.0; O, 28.5; found: C, 50.9; H, 2.1; O, 28.4%; HRMS (ESI MS) m/z: theor: 921.0082 found: 921.0086 ([M + Na]+ detected).
A–D–A6: EA6 (2.12 g, 16.52 mmol), mexp = 3.8 g, 99% yield. Anal. calc. for C20H14FeN4O4S2: C, 48.6; H, 2.8; O, 12.9; found: C, 48.9; H, 2.9; O, 12.8%; HRMS (ESI MS) m/z: theor: 485.0155 found: 485.0156 ([M + Na]+ detected).
A–D–A7: EA7 (2.38 g, 16.52 mmol), mexp = 3.8 g, 93% yield. Anal. calc. for C20H14FeN4O6: C, 52.0; H, 3.0; O, 20.8; found: C, 51.9; H, 3.1; O, 20.6%; HRMS (ESI MS) m/z: theor: 494.9879 found: 494.9877 ([M + Na]+ detected).
A–D–A8: EA8 (2.66 g, 16.52 mmol), mexp = 3.48 g, 80% yield. 1H NMR (CDCl3) δ: 7.38 (s, 2H), 4.62 (m, 8H), 4.12 (d, J = 7.2 Hz, 4H), 1.28 (d, J = 7.1 Hz, 6H); 13C NMR (CDCl3) δ: 192.12, 166.78, 132.95, 121.66, 78.79, 73.84, 72.50, 39.98, 12.37. HRMS (ESI MS) m/z: theor: 550.9650 found: 550.9651 ([M + Na]+ detected).
A–D–A9: EA9 (3.3 g, 16.52 mmol), mexp = 3.6 g, 72% yield. 1H NMR (CDCl3) δ: 8.15 (s, 2H), 5.47 (s, 4H), 4.90–4.79 (m, 4H), 4.48 (q, J = 6.7 Hz, 8H), 1.27 (t, J = 6.6 Hz, 12H); 13C NMR (CDCl3) δ: 178.80, 160.88, 159.71, 158.65, 114.43, 78.75, 77.99, 77.20, 77.16, 44.12, 43.52, 12.48. HRMS (ESI MS) m/z: theor: 629.0951 found: 629.0951 ([M + Na]+ detected).
A–D–A10: EA10 (2.58 g, 16.52 mmol), mexp = 3.86 g, 90% yield. 1H NMR (CDCl3) δ: 8.05 (s, 2H), 5.44 (s, 4H), 4.81 (s, 4H), 3.32 (s, 12H); 13C NMR (CDCl3) δ: 162.58, 160.54, 157.79, 113.03, 78.46, 77.20, 76.60, 28.81, 28.15. HRMS (ESI MS) m/z: theor: 541.0781 found: 541.0779 ([M + Na]+ detected).
A–D–A11: EA11 (2.86 g, 16.52 mmol), mexp = 3.26 g, 72% yield. 1H NMR (CDCl3) δ: 7.41 (s, 2H), 5.86 (ddd, J = 16.3, 11.2, 5.9 Hz, 2H), 5.27 (t, J = 14.8 Hz, 4H), 4.75–4.53 (m, 12H); 13C NMR (CDCl3) δ: 190.75, 165.54, 132.13, 128.78, 120.32, 118.28, 77.60, 72.79, 71.42, 66.90, 45.53; Anal. calc. for C24H20FeN2O3S3: C, 53.7; H, 3.8; O, 8.9; found: C, 53.9; H, 4.1; O, 8.6%; HRMS (ESI MS) m/z: theor: 574.9650 found: 574.9649 ([M + Na]+ detected).
3. Results and discussion
3.1. Synthesis of the different dyes
The twelve D–A dyads D–Ax, x = 0–11 and the twelve triads A–D–Ax, x = 0–11 have been synthesized using a Knoevenagel condensation between the twelve electron acceptors EAx, x = 0–11 and the two ferrocene donors ED1 and ED2. All reactions were carried out using ethanol as the solvent and a catalytic amount of piperidine, excepted for all dyes comprising EA3 and EA5 as the electron acceptors (see Scheme 1). In the case of EA3, as EA3 anion is highly stable and unreactive under basic conditions, D–A3 and A–D–A3 were prepared by refluxing ED1 or ED2 and EA3 in acetic anhydride. The two dyes were obtained in 54 and 39% yields, respectively. Conversely, the methylene group of 2,4,5,7-tetranitro-9H-fluorene (TNF) is highly acidic so that this electron acceptor spontaneously deprotonates in highly polar solvents such as DMF. Consequently, D–A5 and A–D–A5 could be prepared in DMF, at room temperature without using any base. D–A5 and A–D–A5 could be obtained in 88 and 82% yields, respectively. Overall, the different dyes were obtained with reaction yields ranging from 39% for A–D–A3 to 99% for A–D–A6 (see Table 1). Interestingly, for dyes prepared in ethanol, the dyes were obtained as precipitates upon cooling of the ethanolic solutions so that the workup could be reduced to a simple filtration to recover the targeted products in pure form. Similarly, D–A5 and A–D–A5 could be obtained by precipitation from DMF whereas D–A3 and A–D–A3 precipitated from the acetic anhydride solutions.| Compounds | D–A6 | D–A7 | D–A8 | D–A9 | D–A10 | D–A11 |
|---|---|---|---|---|---|---|
| Reaction yields (%) | 96 | 95 | 95 | 49 | 92 | 68 |
| Compounds | A–D–A 6 | A–D–A 7 | A–D–A 8 | A–D–A 9 | A–D–A 10 | A–D–A 11 |
|---|---|---|---|---|---|---|
| Reaction yields (%) | 99 | 93 | 80 | 72 | 90 | 72 |
3.2. Optical properties
| Compounds | λ max (nm) | Epsilon (L mol−1 cm−1) | λ max (ICT1) (nm) | Epsilon (ICT) (L mol−1 cm−1) | ΔE (eV) |
|---|---|---|---|---|---|
| n.s.: not soluble.a Peak detected below 300 nm. | |||||
| D–A0 | 326 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 980 |
531 | 2490 | 2.33 |
| D–A1 | 361 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 070 |
571 | 6000 | 2.17 |
| D–A2 | 319 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
629 | 6720 | 1.97 |
| 413 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
||||
| D–A3 | 318 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
623 | 3000 | 1.98 |
| D–A4 | 424 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890 890 |
630 | 9750 | 1.97 |
| D–A5 | 366 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
607 | 7964 | 2.00 |
| 427 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
||||
| D–A6 | 377 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
583 | 5650 | 2.13 |
| D–A7 | 356 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
565 | 4850 | 2.20 |
| D–A8 | 382 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
542 | 6200 | 2.29 |
| D–A9 | 377 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
583 | 7550 | 2.13 |
| D–A10 | 353 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
558 | 5100 | 2.22 |
| D–A11 | 382 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 150 |
542 | 6200 | 2.29 |
| A–D–A0 | 341 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
445 | 2400 | 2.78 |
| 533 | 2500 | 2.33 | |||
| A–D–A1 | 375 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
572 | 6300 | 2.17 |
| A–D–A2 | 314 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
580 | 4800 | 2.14 |
| A–D–A3 | —a | —a | 632 | 6300 | 1.97 |
| A–D–A4 | 311 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
603 | 1600 | 2.05 |
| 412 | 4800 | ||||
| A–D–A5 | 362 | 7500 | 616 | 1350 | 2.01 |
| 429 | 3400 | ||||
| A–D–A6 | n.s. | n.s. | n.s. | n.s. | n.d. |
| A–D–A7 | n.s. | n.s. | n.s. | n.s. | n.d. |
| A–D–A8 | 364 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
474 | 4750 | 2.62 |
| 393 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
536 | 4300 | 2.31 | |
| A–D–A9 | 309 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
568 | 3100 | 2.18 |
| 395 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||||
| A–D–A10 | 311 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
463 | 2900 | 2.67 |
| 365 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
564 | 2450 | 2.20 | |
| A–D–A11 | 363 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
529 | 4843 | 2.34 |
 | ||
| Fig. 3 UV-visible absorption spectra of D–A dyads D–Ax, x = 0–11 (a and b) and A–D–A triads A–D–Ax, x = 0–11 (c and d) in chloroform. | ||
A stronger absorption band can also be detected in the near-UV-visible range. By finely tuning the electron-accepting ability and by examining twelve electron acceptors (EA0–EA11), positions of the ICT bands could vary from 531 nm for D–A0 exhibiting the weakest electron acceptor to 630 nm for D–A3 comprising the strongest electron acceptor EA3. Interestingly, lower variations of the absorption maxima could be found for the absorption bands located in the near-UV-visible range than for the absorption band at low energy. Based on previous works reported in the literature, this transition was assigned to a transition between an occupied π-orbital consisting of a combination of highest occupied cyclopentadienyl orbital and highest occupied π bridge orbital and the LUMO energy level.82 Considering the specificity of this transition detected at high energy, increase of the electron donating ability of the electron acceptor lowers both the energy levels of the LUMO and the energy level of the degenerated π-orbitals. Consequently, due to the similar variations of these two orbitals the position of this transition remained almost unchanged. Conversely, the HOMO level remains unaffected with increase in the acceptor strength so that a greater variation of the ICT band can be observed with increase in the electron-accepting ability of the acceptors.
Concerning the symmetrically substituted A–D–A triads, positions of the ICT bands varied from 533 nm for A–D–A0 to 632 nm for A–D–A3. These results are consistent with the electron-withdrawing ability of the acceptors, malononitrile EA0 being the weakest acceptor and 2,2′-(1H-indene-1,3(2H)-diylidene)dimalononitrile EA3 being the strongest one. Interestingly, a decrease in the intensity of the charge transfer band was observed while going from D–A dyads to A–D–A triads.
Reduction of the molar extinction coefficients of the A–D–A triads relative to that of their dyad counterparts can be assigned to the fact that, in the case of A–D–A triads, the electron-donating ability of ferrocene is split between the two electron acceptors. On the contrary, the electronic delocalization is unidirectional in the D–A dyads, thus higher molar extinction coefficients can be measured due to the enhanced oscillating strength. However, geometry of D–A and A–D–A complexes have also to be considered to support these differences of molar extinction coefficients. Indeed, when only one cyclopentadienyl ring is functionalized in the case of D–A dyads, the free rotation existing between the two cyclopentadienyl rings of the A–D–A triads can position the two electron-accepting groups in parallel position, antiparallel position, or intermediate situation that can be hardly anticipated.60 As a result of this, the conformational preferences in solution for the different dyes can also contribute to modify their molar extinction coefficients as well as the total dipole moment of the molecules. Noticeably, ICT band with the highest molar extinction coefficient for D–A dyads was determined for D–A4 bearing 2-(3-cyano-4,5,5-trimethylfuran-2(5H)-ylidene)malononitrile (EA4, TCF) (ε = 9750 L mol−1 cm−1) as the acceptor, whereas the highest molar extinction coefficient for the ICT band of the A–D–A triads was measured for A–D–A3 (ε = 6300 L mol−1 cm−1) possessing 2,2′-(1H-indene-1,3(2H)-diylidene)dimalononitrile EA3 as the acceptor. Therefore, it can be concluded that the highest molar extinction coefficients were obtained with the strongest electron acceptors, inducing the highest electronic delocalization. Surprisingly, no clear trend could be established while comparing the maximum absorption of dyads and triads. Indeed, as observed for D–A0, D–A1, D–A5, D–A8 and D–A10, almost no modification of the absorption maxima between dyads and triads was found. This result can be assigned to the weakness of the different electron acceptors used in these dyes so that the presence of one or two electron acceptors does not drastically affect the optical properties. Conversely, a hypsochromic shift was detected for the ICT bands of A–D–A2, A–D–A4, A–D–A9 and A–D–A11 compared to those of their diad analogues. Only A–D–A3 (λmax = 632 nm) showed a red-shifted absorption compared to D–A3 (λmax = 623 nm). These unexpected behaviors detected for A–D–Ax, x = 0–11 can be assigned to the presence of two broad absorption bands in the visible range with positions varying differently from one dye to another.
As shown in Fig. 4, three different situations could be found, affecting the determination of the absorption maxima for the ICT band. Thus, to illustrate this, for A–D–A0, A–D–A9 and A–D–A10, two distinct absorption bands could be detected in the visible range (400–600 nm) so that positions of the two bands could be easily determined. This situation was notably found for dyes prepared with malononitrile EA0, 1,3-diethyl-2-thioxodihydropyrimidine-4,6(1H,5H)-dione EA9 and 1,3-dimethylpyrimidine-2,4,6(1H,3H,5H)-trione EA10. Conversely, for A–D–A2, a broad band extending from 500 to 700 nm could be evidenced, with no real presence of peaks so that the positions of the two bands could not be determined with accuracy. Such absorption spectra were not only found for A–D–A2 comprising 2-(3-oxo-2,3-dihydro-1H-inden-1-ylidene) malononitrile EA2 but also for A–D–A3, A–D–A4, A–D–A6, A–D–A8, A–D–A9 and A–D–A11. In terms of electron-accepting groups, 2,2′-(1H-indene-1,3(2H)-diylidene)dimalononitrile EA3, 2-(3-cyano-4,5,5-trimethylfuran-2(5H)-ylidene)malononitrile EA4, 2-thioxodihydropyrimidine-4,6(1H,5H)-dione EA6, 3-ethyl-thiazolidine-2,4-dione EA8, 1,3-diethyl-2-thioxo-dihydropyrimidine-4,6(1H,5H)-dione EA9 and 3-allyl-2-thioxo-thiazolidin-4-one EA11 drastically differ in their electron-withdrawing abilities. Except for EA8 and EA11, EA2 and EA3, and EA6 and EA9 that are of similar structures, EA4 is the only representative of its category. In particular, if two ICT bands are found with indane-1,3-dione EA2, an overlap of the two bands can be found for EA3 and EA4-based dyes (A–D–A3 and A–D–A4), which can be related to the improvement of the electron-withdrawing ability in EA3 and EA4 compared to EA2. However, as counter-examples, EA8 and EA10 that are rhodanine-based acceptors are weaker acceptors than EA2–EA4. Therefore, no trend between electron-withdrawing ability and coalescence of the two ICT bands can be established. Finally, as observed for A–D–A–1, a coalescence of the bands within a unique absorption band was observed. This behaviour was also found for A–D–A5 and A–D–A7. Here again, A–D–A5 is the strongest electron-acceptor of the series whereas EA7 is of comparable electron-withdrawing ability than EA10. Considering that EA7 and EA10 differ by the alkylation of the barbituric acceptor, once again, no trend between coalescence of the ICT bands or not and electron-withdrawing ability can be established. Considering the difficulty to determine with accuracy the positions of the ICT band of the lowest energy for A–D–A triads, the diversity of situations found for A–D–A0–A–D–A11, only the solvatochromism of the dyads D–Ax, x = 0–11 could be analyzed, due to the presence of a unique ICT band. Optical properties of the twenty-four dyes were also examined theoretically by performing density functional theory (DFT) calculations at the B3LYP/6-311G(d,p) level using the Gaussian09 program. For the different calculations, dichloromethane was selected as the solvent and a polarizable continuum model (PCM) was used to simulate the solvent. A summary of the optical properties is provided in the Table 3. As shown in Fig. 5, a redshift of the absorption spectra of all triads compared to that of dyads was predicted. A severe mismatch between the positions of the ICT bands determined experimentally and theoretically can also be evidenced. Thus, comparison of the absorption maxima for D–A0 showed a difference as high as 100 nm between the experimental and theoretical values (λexp = 531 nm vs. λth = 632 nm). A higher disagreement between the theoretical and experimental values was found for the triads, resulting from the presence of two ICT bands. While examining the main contributions involved in the optical transitions detected at low energy for all dyes (see contributions in ESI†), these absorption bands clearly correspond to an admixture of numerous transitions and transitions occurring between HOMO−2 → LUMO, HOMO−2 → LUMO+1, HOMO−1 → LUMO+1, HOMO → LUMO, and HOMO → LUMO+1 can notably be cited. Additionally, contributions of each transition vary from one dye to another, it can thus support the mismatch existing between the theoretical and the experimental absorption spectra. Finally, examination of the photoluminescence properties of the different dyes revealed that these compounds are not emissive at all.
 | ||
| Fig. 4 Normalized UV-visible absorption spectra of A–D–A triads A–D–A0, A–D–A1, A–D–A2 and A–D–A10 in chloroform. | ||
| Compounds | λ max (nm) | Epsilon (L mol−1 cm−1) | λ max (ICT1) (nm) | Epsilon (ICT) (L mol−1 cm−1) |
|---|---|---|---|---|
| D–A0 | 323 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
632 | 1350 |
| D–A1 | 358 | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
650 | 2400 |
| D–A2 | 417 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
687 | 4000 |
| D–A3 | 438 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
672 | 5000 |
| D–A4 | 429 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
683 | 6200 |
| D–A5 | 401 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
546 | 7700 |
| 831 | 3300 | |||
| D–A6 | 305 (sh) | 4300 | 669 | 2500 |
| 371 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
|||
| D–A7 | 295 (sh) | 6300 | 650 | 1800 |
| 339 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
|||
| D–A8 | 293 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
625 | 2400 |
| 388 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
| D–A9 | 300 | 5450 | 659 | 2800 |
| 374 | 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
|||
| D–A10 | 250 | 7600 | 643 | 1900 |
| 289 | 6400 | |||
| 338 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
|||
| D–A11 | 294 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
623 | 2400 |
| 388 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
|||
| A–D–A0 | 351 | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
712 | 1300 |
| A–D–A1 | 394 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
745 | 2200 |
| A–D–A2 | 450 | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
520 (sh) | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
| A–D–A3 | 492 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
751 | 3600 |
| A–D–A4 | 477 | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
765 | 5400 |
| A–D–A5 | 458(sh) | 8800 | 796 | 6600 |
| 539 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
|||
| A–D–A6 | 439 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
790 | 1700 |
| A–D–A7 | 370 | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
759 | 1150 |
| A–D–A8 | 429 | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
680 | 3200 |
| A–D–A9 | 421 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
777 | 1700 |
| A–D–A10 | 369 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
745 | 1300 |
| A–D–A11 | 428 | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
683 | 3100 |
 | ||
| Fig. 5 Simulated absorption spectra of D–A dyads D–Ax, x = 0–11 and A–D–A triads A–D–Ax, x = 0–11 in dichloromethane. | ||
This result is not surprising considering that ferrocene is commonly used to quench the photoluminescence of fluorescent dyes. In this field, a relevant example of this has recently been reported with a ferrocene–BODIPY dyad so that the photoluminescence of the highly emissive BODIPY could be efficiently quenched by ferrocene, due to photoinduced electron transfer.83 In the present case, presumably, non-radiative pathways win out because (i) oscillator strengths are smaller than those in organic dyes, (ii) Fe leads to greater ISC rates than in typical organics, and perhaps (iii) because of the extra internal conversion pathways associated with rotation around the Cp–Fe–Cp bond.
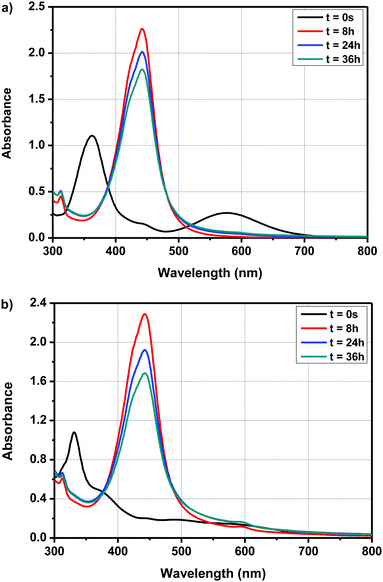
By exciting in this absorption band, a photoinduced electron transfer from ferrocene towards the electron accepting solvent could be demonstrated, enabling the initiation of anionic polymerization. In the present case, due to the electron-withdrawing ability of the different electron acceptors, a red-shift of the CTTS band can be expected and absorption maxima varying between 400 and 500 nm could be determined for dyads D–Ax, x = 0–11 and triads A–D–Ax, x = 0–11, after evolution of their UV-visible absorption spectra. Besides, monitoring of the cyclic voltammograms of A–D–A0 over time in DMSO and by using tetrabutylammonium hexafluorophosphate as the supporting electrolyte revealed that the new product(s) can be more easily oxidized than the initial dye; the oxidation process being detected at lower anodic potentials (see Fig. 8). Therefore, formation of a ferrocenium cation in DMSO cannot be excluded. However, the oxidation of ferrocenium cation should be more difficult than that of ferrocene due to the loss of one electron. To support the electrochemical process detected in solution, the formation of ferrocenium decomposition products can be tentatively proposed. It is noteworthy that the distinction between ICT and CTTS can be easily done for the following reasons. First, even if a solvatochromism is observed, ICT bands are observed at almost the same positions, irrespective of the solvents. This point has been demonstrated in the solvatochromic study. Conversely, since CTTS is a less kinetically favorable process, it can be monitored over time and is not observed immediately after dissolution of the compound. Therefore, positions of the ICT bands given in the solvatochromic study are the correct ones, corroborated by the similarity of values observed in the twenty-three solvents.
Interestingly, while a clear modification of the UV-visible absorption spectra of the push–pull dyes was determined in DMSO, conversely, for ferrocene, no modification of the absorption spectrum was found in DMSO and even in the twenty-two solvents, evidencing a specific activation process originating from the presence of the electron-withdrawing groups in dyads and triads. In light of these results and considering that an interaction between the solvent and the push–pull dyes exists, several hypotheses were examined, notably with A–D–A0 as the model compound. Thus, interactions between ferrocene in the neutral form and DMSO was examined by positioning the DMSO molecule on top or in lateral position with regards to the ferrocene unit. Calculations done with density-functional theory (DFT) using ωb97xd/6-311++g(d,p) as the basis set revealed that similar energies could be determined in the two situations (see Fig. 9).
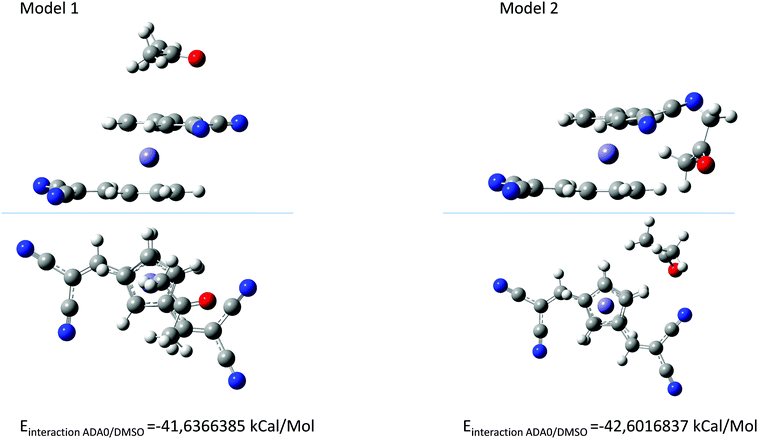 | ||
| Fig. 9 The two possible interactions between A–D–A0 and DMSO with DMSO on top of the ferrocene unit (model 1) and DMSO in the lateral position (model 2). | ||
As shown in Fig. 9, the energy difference between solvent molecules standing on top or in lateral position to the ferrocene group is negligible. Consequently, considering that the energy difference is low, no preferential orientations can be expected. Interestingly, a blue-shift of the theoretical UV-visible absorption spectra compared to that determine for A–D–A0 under vacuum conditions could be determined in these two situations.
Possibility of bimolecular interactions between A–D–A0 molecules was also envisioned. Besides, in this case, a red-shift of the absorption spectra should be observed for the dimers, which is in contradiction with what is experimentally observed (see Fig. 10). Indeed, by theoretical calculations, a maximum absorption around 600 nm is expected, which is not experimentally observed. Besides, from an energy viewpoint, such interactions can theoretically exist. Therefore, based on the different investigations, the formation of a CTTS or the formation of dimers in solutions cannot be proposed as plausible explanations supporting the experimental results. Evolution of the UV-visible absorption spectra over time is also not the result of photoinduced reactions, as similar modifications of the UV-visible absorption spectra over time are detected in the dark and under ambient light.
3.3. Solvatochromism
Solvatochromic behaviors of dyads D–Ax, x = 0–11 and triads A–D–Ax, x = 0–11 were measured at room temperature in 22 common organic solvents ranging from nonpolar to highly polar solvents. A summary of the optical properties is provided in Tables 4 and 5. Intramolecular nature of the charge transfer detected for the dyads D–Ax, x = 0–11 was demonstrated by performing successive dilutions of the solutions and linear correlations between the intensity of the ICT bands and the concentrations could be established. Over the years, numerous empirical polarity scales have been developed to interpret the solvent–solute interaction and the Kamlet–Taft's,92 Dimroth-Reichardt's,93 Lippert–Mataga's,94 Catalan's,95 Kawski-Chamma Viallet's,96 McRae Suppan's97 and Bakhshiev's98 scales are the most widely used. Among the different empirical polarity scales examined, the solvent polarity/polarizability Catalan (SPP) scale and the Kamlet–Taft polarity scale were determined to be highly useful for analyzing the solvatochromic behaviors of dyads D–Ax, x = 0–11.| Compounds | π*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
D–A0 | D–A1 | D–A2 | D–A3 | D–A4 | D–A5 | D–A6 | D–A7 | D–A8 | D–A9 | D–A10 | D–A11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Kamlet and Taft parameters. b Position of the ICT bands are given in nm. c n.s.: not soluble. | |||||||||||||
| Acetone | 0.71 | 524 | 565 | 624 | 612 | 611 | 606 | 565 | 545 | 534 | 571 | 544 | 535 |
| Acetonitrile | 0.75 | 528 | 566 | 617 | 614 | 618 | 598 | 573 | 537 | 536 | 572 | 545 | 538 |
| AcOEt | 0.54 | 523 | 563 | 615 | 607 | 602 | 609 | 566 | 543 | 529 | 567 | 544 | 531 |
| Anisole | 0.73 | 530 | 567 | 617 | 616 | 619 | 619 | 575 | 552 | 536 | 575 | 548 | 539 |
| Chloroform | 0.78 | 533 | 573 | 631 | 619 | 629 | 607 | 585 | 564 | 543 | 581 | 558 | 543 |
| Cyclohexane | 0.00 | 516 | 554 | 613 | 617 | 591 | 643 | n.s.c | n.s.c | 514 | 560 | 538 | 514 |
| 1,2-Dichloroethane | 0.81 | 531 | 569 | 627 | 611 | 627 | 624 | 582 | 558 | 537 | 574 | 550 | 540 |
| Dichloromethane | 0.82 | 530 | 569 | 628 | 620 | 628 | 609 | 584 | 561 | 541 | 578 | 551 | 542 |
| Diethyl carbonate | 0.45 | 523 | 560 | 626 | 608 | 594 | 602 | 565 | 542 | 529 | 567 | 542 | 529 |
| Diethyl ether | 0.27 | 523 | 559 | 617 | 617 | 603 | 613 | 560 | 542 | 524 | 567 | 540 | 526 |
| 1,4-Dioxane | 0.55 | 519 | 562 | 616 | 607 | 596 | 596 | 564 | 544 | 532 | 567 | 543 | 530 |
| Dimethylacetamide | 0.88 | 530 | 572 | 626 | 627 | 619 | 595 | 567 | 544 | 526 | 579 | 547 | 530 |
| DMF | 0.87 | 529 | 571 | 624 | 616 | 622 | 584 | 566 | 545 | 526 | 576 | 546 | 529 |
| DMSO | 1.00 | 531 | 575 | 626 | 620 | 628 | 591 | 572 | 548 | 524 | 579 | 550 | 526 |
| Ethanol | 0.54 | 528 | 569 | 624 | 616 | 625 | 591 | 570 | 553 | 538 | 576 | n.s.c | 536 |
| Heptane | −0.08 | 515 | 554 | 612 | 613 | 585 | n.s.c | n.s.c | n.s.c | 511 | 557 | 538 | 513 |
| Nitrobenzene | 1.01 | 534 | 573 | 639 | 625 | 636 | 605 | 581 | 558 | 543 | 580 | 557 | 545 |
| Pentane | −0.09 | 512 | 551 | 611 | 609 | n.s.c | 605 | n.s.c | n.s.c | 512 | 556 | 534 | 515 |
| THF | 0.58 | 525 | 565 | 620 | 622 | 607 | 609 | 567 | 543 | 531 | 572 | 545 | 533 |
| Toluene | 0.54 | 525 | 565 | 620 | 616 | 602 | 616 | 572 | 551 | 530 | 572 | 545 | 529 |
| Triethylamine | 0.14 | 519 | 558 | n.s.c | n.s.c | 597 | n.s.c | 567 | n.s.c | 519 | n.s.c | 564 | 522 |
| p-Xylene | 0.43 | 522 | 562 | 617 | 618 | 593 | 614 | 570 | 550 | 527 | 574 | 543 | 529 |
| Compounds | π*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
A–D–A 0 | A–D–A 1 | A–D–A2 | A–D–A 3 | A–D–A 4 | A–D–A 5 | A–D–A 6 | A–D–A 7 | A–D–A 8 | A–D–A 9 | A–D–A 10 | A–D–A 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Kamlet and Taft parameters. b Position of the ICT bands are given in nm. c n.s.: not soluble. | |||||||||||||
| Acetone | 0.71 | 437, 525 | 562 | 539 | 631 | 597 | 617 | 608 | 545 | 467, 537 | 487, 572 | 451, 546 | 478, 526 |
| Acetonitrile | 0.75 | 392, 522 | 566 | 429, 532 | 628 | 603 | 614 | 596 | 537 | 473, 538 | 482, 576 | 457, 547 | 492, 516 |
| AcOEt | 0.54 | 438, 525 | 562 | br. band | 626 | 402, 426, 583 | 602 | n.s.c | 543 | 541 | 479, 571 | 454, 558 | 468, 539 |
| Anisole | 0.73 | 442, 534 | 568 | 557, 603 | 637 | n.s.c | 609 | 584, 613 | 552 | 537 | 480, 585 | 458, 556 | 473, 536 |
| Chloroform | 0.78 | 445, 530 | 573 | 580 | 632 | 600 | n.s.c | n.s.c | 564 | 474, 536 | 480, 568 | 459, 557 | 475, 529 |
| Cyclohexane | 0.00 | 429, 521 | 555 | n.s.c | 624 | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | 471, 583 | n.s.c | 522 |
| 1,2-Dichloroethane | 0.81 | 443, 531 | 569 | 557, 624 | 637 | 593, 614 | 620 | n.s.c | 558 | 470, 536 | 484, 565 | 462, 550 | 475, 536 |
| Dichloromethane | 0.82 | 445, 527 | n.s.c | 574 | 637 | 606 | 620 | n.s.c | 561 | 470, 536 | 484, 580 | 460, 554 | 478, 538 |
| Diethyl carbonate | 0.45 | 436, 526 | 562 | 574 | 626 | 580 | 602 | n.s.c | 542 | 530 | 472, 576 | 453, 559 | 463, 536 |
| Diethyl ether | 0.27 | 434, 526 | 559 | n.s.c | 626 | n.s.c | 602 | n.s.c | 542 | 524 | n.s.c | n.s.c | 467, 520 |
| 1,4-Dioxane | 0.55 | 437, 523 | 564 | br. band | 632 | 577 | 596 | 473, 562 | 544 | 537 | 474, 572 | 452, 547 | 475, 536 |
| Dimethylacetamide | 0.88 | 529 | 573 | 544, 650 | 699 | 401, 468, 617 | 624 | 575 | 543 | 493, 522 | 480, 582 | 467, 561 | 439, 545 |
| DMF | 0.87 | 528 | 571 | 441, 521 | 608 | 399, 459, 618 | n.s.c | 570 | 545 | 502, 521 | br. band | 461, 557 | 504, 520 |
| DMSO | 1.00 | 399, 533 | 574 | 440, 535 | 599 | 401, 466, 611 | n.s.c | 580 | 548 | 502, 521 | 491, 580 | 467, 553 | 501, 521 |
| Ethanol | 0.54 | 439, 522 | 575 | 424, 498 | 588 | 398, 449, 611 | 593 | 563 | 553 | 542 | 478, 578 | 474, 553 | 474, 532 |
| Heptane | −0.08 | 428, 520 | 553 | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | 516 |
| Nitrobenzene | 1.01 | 529 | 574 | br. band | 633 | 592, 633 | 642 | n.s.c | 558 | 478, 547 | 486, 586 | 591, 638 | 484, 561 |
| Pentane | −0.09 | 559 | 552 | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | 507 |
| THF | 0.58 | 435, 524 | 564 | 555 | 633 | 594 | 608 | 470, 581 | 543 | 538 | 474, 595 | 452, 544 | 468, 542 |
| Triethylamine | 0.14 | 503 | 559 | n.s.c | 621 | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | n.s.c | 527 |
| Toluene | 0.54 | 441, 529 | 564 | 587 | 630 | 413, 578 | 594 | n.s.c | 551 | 528 | 477, 581 | 454, 558 | 467, 538 |
| p-Xylene | 0.43 | 440, 524 | 563 | 587 | 630 | 418, 598 | 600 | n.s.c | 550 | 516 | 471, 577 | 453, 562 | 471, 536 |
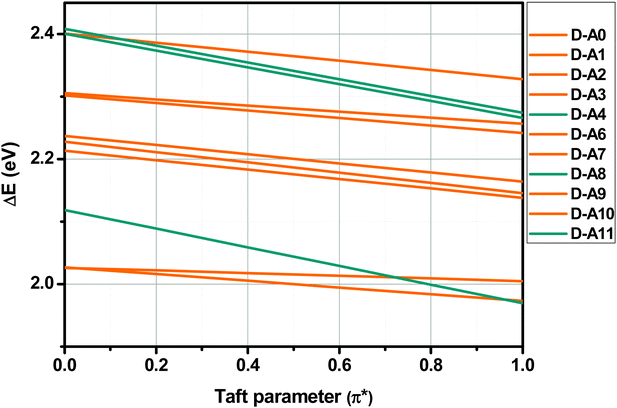
More precisely, in the case of the Kamlet–Taft empirical scale, better linear correlations were obtained while using a multiparameter approach instead of plotting ΔE = f (π*) (see Table S2 and S3 in the ESI†). However, it is noteworthy that the multiparameter approach better interprets the solvatochromic behaviors of D–Ax, x = 0–7 than of D–Ax, x = 8–11. Indeed, for these four dyes, the linear correlations ΔE = f (π*) were more adapted with regards to their larger values for the square of the correlation coefficient (R2). In fact, when using the multiparameter approach, two parameters are considered in addition to the dipolarity/polarizability π*, namely, the hydrogen bond-donating ability α and the hydrogen bond-accepting ability β. These two parameters are of crucial importance in the case of dyes with electron acceptors comprising NH groups such as D–A6 and D–A7. The same holds true for dyes bearing cyano groups such as D–A0, D–A2, D–A3, and D–A4, carbonyl groups such as D–A1, D–A8 and D–A11 or polar groups such as nitro groups. In these different cases, hydrogen bonds can be formed with the precited groups. Conversely, for D–A9 and D–A10, alkylation of the NH groups drastically reduces the sensitivity to the hydrogen-bonding ability of the solvents. Among all dyes, the best correlations were obtained for D–A0, D–A1, D–A8 and D–A11, with R2 > 0.88 (see Fig. 11). While comparing the results obtained with the linear correlations based on the Catalan and the Kamlet–Taft empirical scales, higher R2 values were obtained with the Catalan SPP parameters, indicating that the polarity/polarizability of the solvents governs the solvatochromism of these dyes. These results were confirmed with the multiparameter approach of the Kamlet–Taft polarity scale for which R2 similar to that obtained with the Catalan SPP parameter could be determined. Surprisingly, a positive solvatochromism was found for all dyes except for D–A5 for which a negative solvatochromism was determined (see Fig. 12). This behavior is relatively unusual but is sometimes observed for dyes such as merocyanines.99,100 The pronounced negative solvatochromism observed for D–A5 can be assigned to a highly dipolar electronic ground state and a considerably less dipolar first excited state. With increase in the polarity of the medium, the dipolar ground state was more stabilized than the first excited state so that a hypsochromic shift of the ICT band can be observed.101 The highly polar ground state of D–A5 can be assigned to the exceptional electron-withdrawing ability of TNF; this acceptor is the strongest electron-acceptor reported to date.102 It is noteworthy that D–A5 has previously been examined for its solvatochromic properties according to the literature.103 However, in this work reported in 2001 by Perepichka and coworkers, the authors already mentioned the complexity of the solvatochromism of this TNF-based dye. Indeed, the Kamlet–Taft or the Reichardt parameter were determined not to be satisfactory to investigate the solvatochromic behavior. Notably, the authors evidenced that the four-parameter Koppel–Palm equation was even unable to rationalize the solvatochromic behavior of D–A5.104–106 In the present case and differing from the previous study of Perepichka and coworkers, an acceptable linear correlation was obtained while using the Catalan SPP parameters since a R2 of 0.73 was obtained with this solvent polarity scale. Therefore, it can be concluded that this dye is exceptionally sensitive to the polarity/polarizability of the solvents (taken into account with the Catalan SPP parameter), more than the solvent dipolarity which is primarily considered by the Catalan SdP parameter.
 | ||
| Fig. 11 Linear correlations obtained for D–A0 and D–A1 using the Kamlet–Taft and the Catalan empirical scales. | ||
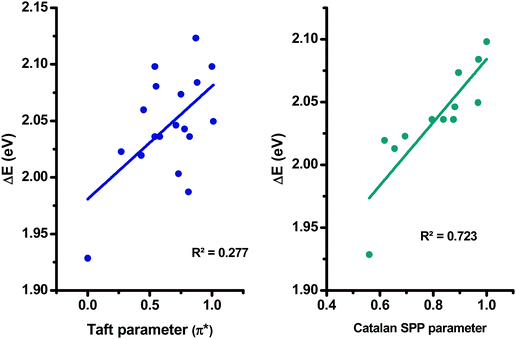 | ||
| Fig. 12 Linear correlations obtained for D–A5 using the Kamlet–Taft and the Catalan empirical scales. | ||
Complexity of the solvatochromism in D–A9 can also arise from the unequal contribution of the nitro groups to the mesomeric forms. Indeed, as shown in Fig. 13, the difference of the conjugation length between the electron-donating ferrocene and the nitro groups can support the presence of several ICT bands for D–A9, but also the unexpected solvatochromic behavior.
 | ||
| Fig. 13 The different mesomeric forms supporting the presence of two ICT bands for the TNF-based dye D–A9. | ||
Finally, sensitivity of the ICT bands of dyads D–Ax, x = 0–11 to solvent polarity was confirmed by examining the slopes obtained by plotting the HOMO–LUMO gaps vs. the Taft parameters. Indeed, a great slope is indicative of a significant charge redistribution upon excitation. In particular, the zwitterionic form is stabilized in highly polar solvents. As shown in Fig. 14, three dyes were more sensitive than the others to solvent polarity, namely, D–A4, D–A8 and D–A11, comprising TCF or rhodanines as the electron acceptors.
3.4. Electrochemical properties
The two series of compounds examined in this work were analyzed by cyclic voltammetry (CV) in order to determine their electrochemical properties in a dilute solution of dichloromethane. A set of four CV curves is shown in Fig. 15 and all CV curves are given in the ESI.† The redox potentials of all dyes relative to the half-wave oxidation potential of the ferrocene/ferrocenium couple are presented in Table 6.| E red | E red | E red | E Ox | E Ox | E HOMO | E LUMO | ΔEET | ΔEopt | |
|---|---|---|---|---|---|---|---|---|---|
| V/Fc | V/Fc | — | — | V/Fc | eV | eV | eV | eV | |
| All potentials were recorded in 0.1M TBAClO4/CH2Cl2. EHOMO (eV) = −4.8 − Eox and ELUMO (eV) = −4.8 − Ered. | |||||||||
| D–A0 | — | −1.36 | — | — | 0.84 | −5.64 | −3.43 | 2.21 | 2.33 |
| D–A1 | — | −1.27 | — | — | 0.72 | −5.52 | −3.52 | 2.00 | 2.17 |
| D–A2 | — | −0.88 | — | — | 0.71 | −5.51 | −3.92 | 1.60 | 1.97 |
| D–A3 | −0.91 | −0.71 | — | — | 0.60 | −5.40 | −4.09 | 1.31 | 1.98 |
| D–A4 | — | −0.86 | — | — | 0.62 | −5.42 | −3.94 | 1.49 | 1.97 |
| D–A5 | −0.68 | −0.49 | — | — | 0.69 | −5.49 | −4.30 | 1.19 | 2.00 |
| D–A6 | — | −1.00 | — | — | 0.80 | −5.60 | −3.79 | 1.81 | 2.13 |
| D–A7 | — | −1.17 | — | — | 0.74 | −5.54 | −3.63 | 1.91 | 2.20 |
| D–A8 | — | −1.33 | −0.62 | −0.30 | 0.74 | −5.55 | −3.46 | 2.08 | 2.29 |
| D–A9 | — | −1.30 | −0.63 | −0.04 | 0.71 | −5.52 | −3.49 | 2.03 | 2.13 |
| D–A10 | — | −1.39 | −0.70 | −0.08 | 0.76 | −5.56 | −3.40 | 2.16 | 2.22 |
| D–A11 | — | −1.29 | −0.56 | −0.23 | 0.75 | −5.55 | −3.50 | 2.05 | 2.29 |
| E red | E red | E red | E Ox | E Ox | E HOMO | E LUMO | ΔEET | ΔEopt | |
|---|---|---|---|---|---|---|---|---|---|
| V/Fc | V/Fc | V/Fc | V/Fc | V/Fc | eV | eV | eV | eV | |
| A–D–A0 | — | — | −1.08 | 1.16 | — | −5.96 | −3.72 | 2.25 | 2.33 |
| A–D–A1 | — | −1.13 | −0.78 | 0.85 | — | −5.65 | −4.02 | 1.62 | 2.17 |
| A–D–A2 | — | −0.93 | −0.63 | 0.74 | 1.03 | −5.54 | −4.17 | 1.37 | 2.14 |
| A–D–A3 | −1.28 | −0.91 | −0.60 | 0.82 | — | −5.62 | −4.20 | 1.42 | 1.97 |
| A–D–A4 | — | — | −0.72 | 0.80 | — | −5.60 | −4.08 | 1.52 | 2.05 |
| A–D–A5 | −1.02 | −0.69 | −0.50 | 0.70 | 0.90 | −5.50 | −4.30 | 1.20 | 2.01 |
| A–D–A6 | n.s | n.s | n.s | n.s | n.s | n.s | n.s | n.s | n.d |
| A–D–A7 | n.s | n.s | n.s | n.s | n.s | n.s | n.s | n.s | n.d |
| A–D–A8 | — | — | −1.16 | 0.51 | 0.97 | −5.31 | −3.64 | 1.67 | 2.31 |
| A–D–A9 | n.s | n.s | n.s | n.s | n.s | n.s | n.s | n.s | 2.18 |
| A–D–A10 | — | — | −1.10 | 0.83 | — | −5.63 | −3.70 | 1.93 | 2.20 |
| A–D–A11 | — | −1.35 | −1.11 | 0.54 | 0.97 | −5.34 | −3.68 | 1.65 | 2.34 |
In this study, the D–Ax, x = 0–11 series has exactly the same electron donor as the A–D–Ax, x = 0–11 series but differs by the number of electron-accepting groups. As anticipated, major differences could be found concerning their electrochemical properties. Notably, oxidation potentials ranging from + 0.84 V to + 0.60 V could be determined for the D–Ax, x = 0–11 series, proving that the oxidation is located on the ferrocene moiety of the push–pull dyes. Indeed, the one-electron oxidation process is detected at low oxidation potentials, comparable to that reported for other push–pull dyes comprising ferrocene as the electron donor.50,105,106 For D–A8–D–A11, additional oxidation and reduction peaks were also detected in the region of −0.5 V to 0 V. These additional peaks were specifically observed for the thio(barbituric) and the rhodanine-based dyes. Considering that the different electron acceptors possess amino group, an oxidation process occurring on the amino group with formation of a radical cation can be tentatively proposed. As another explanation, an oxidation of the vinylic spacer followed by a dimerization reaction can also be proposed. Indeed, such oxidation/dimerization reaction has previously been reported in the literature for organic dyes comprising good electron donating groups.107 For the A–D–Ax, x = 0–11 series, a first one-electron process could be determined at higher oxidation potential than that detected for the dyads. Notably, an oxidation located at + 0.51 V for A–D–A8 to + 1.16 V for A–D–A0 could be thus determined. In some cases, the presence of a second oxidation process could be detected at anodic potentials, notably, at + 0.90 V for A–D–A5 and 1.03 V for A–D–A2. Similarly, the presence of two or even three reduction potentials could be detected for several dyes, especially for the triads as a result of the presence of two electron-accepting groups.
From their redox potentials, energy levels of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) could be estimated using formulas previously reported by Pommerehne et al.108 Values of all HOMO and LUMO energy levels of all molecules are summarized in Table 6. A comparison between the experimental and theoretical values for the HOMO and LUMO energy levels is presented in Fig. 16. In this Figure, a good agreement between the experimental and theoretical results could be evidenced, especially for the D–Ax, x = 0–11 series. Conversely, a greater mismatch was found for the A–D–Ax, x = 0–11 series, especially for the HOMO energy levels. This can be assigned to the fact that the oxidation process is not only affected by the solvent used to perform electrochemistry but also by the fact that the oxidation process can occur on a specific side of the dye rather than on the ferrocene moiety, as exemplified for the thio(barbituric) or the rhodanine derivatives.
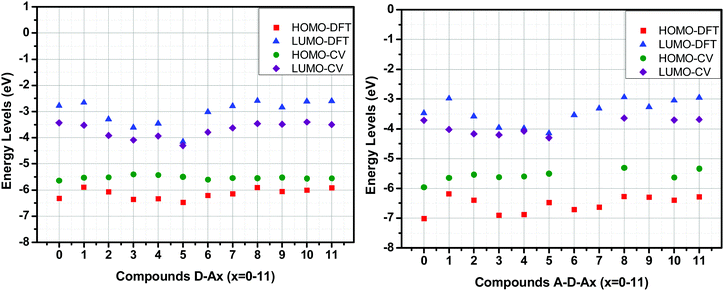 | ||
| Fig. 16 Comparison of frontier orbitals’ energy levels obtained from cyclic voltammetry and DFT calculation. | ||
3.5. Redoxchromic properties
Redoxchromism of the two series of compounds was analyzed by UV-visible spectroscopy at a concentration of 8.0 × 10−5 M for all compounds. For all experiments, five equivalents of nitrosonium tetrafluoroborate (NOBF4) were added to the solutions to oxidize ferrocene while maintaining a reasonable acquisition time. Indeed, while using only one equivalent of oxidant, the reaction proved to be relatively slow. Nitrosonium cation is a strong oxidant that is used in numerous chemical reactions and extensively used in Organic Chemistry to oxidize many organic compounds. Indeed, the oxidation potential E° of the nitrosonium cation is lower than 1.7 V (versus the normal hydrogen electrode).109 By oxidizing ferrocene, suppression of the electron donating moiety was clearly evidenced by a color modification of the different solutions. Thus, conversion of the electron-donating ferrocene as an electron acceptor (ferrocenium) induced the disappearance of the intramolecular charge transfer (ICT) band on the UV-visible absorption spectra of the different dyes.During these analyses, monitoring of the discoloration was performed by recording a spectrum each minute. All spectra are provided in the ESI.† A panel of three representative kinetics is given in Fig. 17. Interestingly, depending on the electron acceptor, different situations could be clearly identified during the chemical oxidation. As anticipated, a decrease in the intensity of the ICT bands could be detected upon the oxidation of ferrocene as can be observed, as exemplified with compound D–A2 (see Fig. 17a). For compounds D–A0, D–A1, D–A3, D–A5, A–D–A0, A–D–A1, A–D–A2, A–D–A3, A–D–A5 and A–D–A9, a similar behavior was observed, with the loss of the ICT band as well as the absorption peaks around 400 nm and 450 nm due to the oxidation of ferrocene to ferrocenium. For the other compounds, a different behavior could be observed, with the appearance during the oxidation process of a new absorption band which eventually decreases after the complete disappearance of the ICT band. This specific behavior can be easily evidenced for D–A4 (see Fig. 17b), with a decrease in the intensity of the charge transfer band at 640 nm for 10 minutes followed by the appearance of a new absorption band at 560 nm, starting to emerge 7 minutes after the suppression of the ICT band and reaching a maximum of intensity after 14 minutes (see Fig. 17c). Finally, a decrease in the band intensity is then observed and a reduction of half of its initial intensity is observed after one hour of reaction (see Fig. 17d). This behavior is detected for several dyes including D–A8, D–A11, A–D–A4, A–D–A8 and A–D–A11. To a lesser extent, this behavior can also be demonstrated for D–A6, D–A7, D–A9, D–A10 and A–D–A10, except that the appearance of the new absorption band is extremely weak. This behavior is found for the same acceptors irrespective of the series (D–A or A–D–A series), which is certainly indicative of the presence of side-reactions on the electron acceptor, subsequent to the oxidation of ferrocene to ferrocenium. Thus, for A–D–A11, this reaction led to the precipitation of a solid in the solution, resulting in the acquisition of noisy absorption spectra during precipitation (see Fig. 17e).
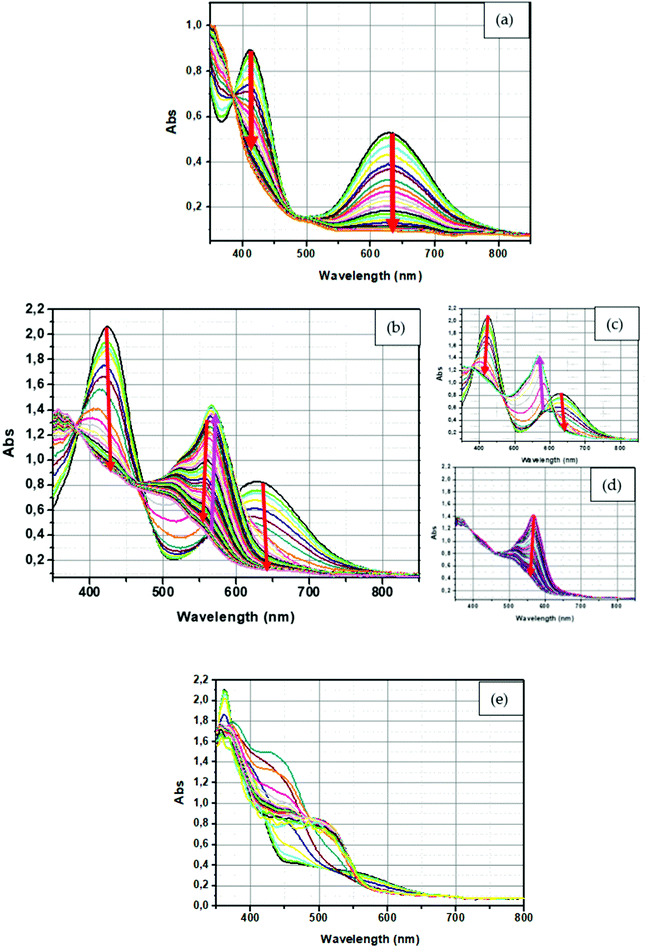 | ||
| Fig. 17 UV-Visible spectrum of (a) D–A2, (b) full spectra of D–A4 (c) during the first minute for D–A4, (d) during the last minute for D–A4 and (e) A–D–A11 in dichloromethane. | ||
 | ||
| Fig. 18 Contour plots of the electronic distribution of the HOMO and LUMO orbitals of D–A0 and D–A2. | ||
For this compound, one possible explanation supporting the formation of this precipitate is the polymerization of A–D–A11 due to the presence of an allyl chain on the electron acceptor. This precipitation is not detected for D–A11, also bearing allyl rhodanine as the acceptor. This can be supported by the fact that, in the case of A–D–A11, the presence of the two allyl groups allow to form extended chains favoring precipitation. Conversely, in the case of D–A11, the presence of a unique polymerizable group per dye only allows the formation of dimers that remain soluble in dichloromethane. From a mechanism viewpoint, several mechanisms can be proposed. Notably, polymerization of A–D–A11 can be induced by an electron transfer reaction between the nitrosonium cation and the allyl function present onto D–A11 and A–D–A11 (see Scheme 2a), inducing the formation of radicals and initiating the polymerization or the dimerization process.110,111 Parallel to this, for D–A8, D–A11, A–D–A8 and A–D–A11, other reactions are possible on the rhodanine acceptors such as the addition of the nitrosonium cation to the thioether function (see Scheme 2b). For these rhodanine-based compounds and also for compounds having an amine function, such as D–A6, D–A7, D–A9, D–A10, A–D–A6, A–D–A7, A–D–A9 and A–D–A10, the nitrosation of the amines is also possible, with the addition of the nitrosonium cation leading to a dealkylation of the tertiary amine (see Scheme 2c). Concerning D–A4 and A–D–A4, the two dyes comprise 2-(3-cyano-4,5,5-trimethylfuran-2(5H)-ylidene) malononitrile (TCF) as the electron acceptor with numerous cyano groups. In this last case, the nitrosonium cation can also add onto the cyano groups of TCF, modifying its electron-withdrawing ability (see Scheme 2d). Finally, another plausible hypothesis, the nitrosonium cation can also add onto the ether function in a similar way to that observed for the thioether functions of rhodanines (see Scheme 2e). In light of the numerous reactions which can occur between the nitrosonium cation and the electron acceptors, it clearly supports the multiple changes detected in the different absorption spectra during the kinetics of discoloration.
 | ||
| Scheme 2 Proposed reaction occurring with the use of nitrosonium cation on the different functions of the electron acceptor part. | ||
3.6. Theoretical investigations
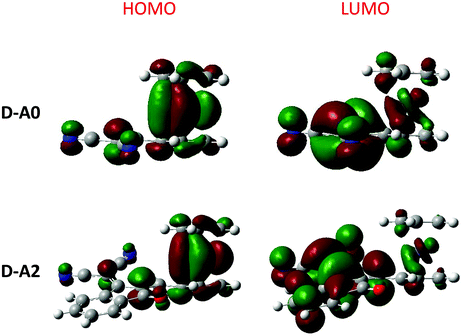
In light of the unexpected optical properties of the triads, electronic distribution of the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) was determined theoretically. DFT calculations were carried out at the B3LYP/6-311G(d,p) level of theory using Gaussian 09 programs. Dichloromethane was used as the solvent and the polarizable continuum model (PCM) was used as the solvent model for the TD-DFT calculations.74–79 More details about the theoretical calculations are given in the ESI.† As shown in Fig. 18, a classical distribution of the molecular orbitals was found for the different dyads, with the HOMO energy level located on the ferrocene moiety and the LUMO energy level on the electron-accepting part. Conversely, an unusual electronic distribution was found for the triads (see Fig. 19). Thus, for A–D–Ax, x = 0–7 and A–D–A10, a classical electronic distribution could be evidenced. On the contrary, for A–D–A8 and A–D–A10, a HOMO−1 and a HOMO level extending on the ferrocene and the rhodanine moiety was determined. More surprisingly, for A–D–A9 which possesses the strongest electron-withdrawing group, no electronic distribution of the ferrocene moiety was found neither for the HOMO nor the HOMO−1 energy levels. In fact, HOMO and HOMO−1 levels located onto the TCF moiety were determined. Only an electronic distribution on HOMO−2 can be found on the ferrocene moiety. By theoretical calculations, the energetic transitions involved in the optical transitions could be determined. Thus, as shown in Table 7, all ICT bands are mainly issued from an admixture of a HOMO → LUMO and a HOMO−1 → LUMO transition. These results are consistent with the aforementioned distributions of the electronic density detected for ferrocene. Indeed, HOMO and HOMO−1 are mainly located on the electron donor. These two orbitals are also the highest occupied orbitals, favorable to an electron transfer towards the LUMO level upon excitation. | ||
| Fig. 19 Contour plots of the electronic distribution of the HOMO and LUMO orbitals of A–D–A0 and A–D–A8 and A–D–A9. | ||
| Compounds | E HOMO (eV) | E LUMO (eV) | λ max (nm) | Transitions |
|---|---|---|---|---|
| D–A0 | −6.326 | −2.773 | 669 | HOMO−1 → LUMO (64%) |
| 632 | HOMO → LUMO (51%) | |||
| 536 | HOMO−2 → LUMO (24%) | |||
| 500 | HOMO → LUMO+1 (62%) | |||
| D–A1 | −5.887 | −2.657 | 689 | HOMO−1 → LUMO (64%) |
| 653 | HOMO → LUMO (54%) | |||
| 506 | HOMO → LUMO+3 (63%) | |||
| D–A2 | −6.071 | −3.291 | 744 | HOMO−1 → LUMO (57%) |
| 688 | HOMO → LUMO (53%) | |||
| 515 | HOMO → LUMO (37%) | |||
| 513 | HOMO → LUMO+3 (45%) | |||
| D–A3 | −6.360 | −3.613 | 746 | HOMO−1 → LUMO+1 (76%) |
| 683 | HOMO → LUMO+1 (67%) | |||
| 597 | HOMO → LUMO (97%) | |||
| 563 | HOMO−1 → LUMO (85%) | |||
| 507 | HOMO → LUMO+3 (48%) | |||
| D–A4 | −6.336 | −3.459 | 736 | HOMO−1 → LUMO (74%) |
| 687 | HOMO → LUMO (62%) | |||
| 553 | HOMO−3 → LUMO (36%) | |||
| 512 | HOMO → LUMO+2 (48%) | |||
| D–A5 | −6.474 | −4.150 | 833 | HOMO−1 → LUMO (47%) |
| 828 | HOMO → LUMO (57%) | |||
| 642 | HOMO → LUMO+4 (29%) | |||
| 629 | HOMO−1 → LUMO+4 (30%) | |||
| 580 | HOMO−2 → LUMO (45%) | |||
| 547 | HOMO−2 → LUMO (40%) | |||
| 536 | HOMO → LUMO+1 (58%) | |||
| 520 | HOMO−1 → LUMO+1 (50%) | |||
| 502 | HOMO → LUMO+2 (85%) | |||
| D–A6 | −6.207 | −3.020 | 727 | HOMO−1 → LUMO (70%) |
| 669 | HOMO → LUMO (60%) | |||
| 503 | HOMO → LUMO+2 (65%) | |||
| 469 | HOMO−1 → LUMO+2 (46%) | |||
| 424 | HOMO−2 → LUMO (95%) | |||
| D–A7 | −6.145 | −2.793 | 699 | HOMO−1 → LUMO (68%) |
| 652 | HOMO → LUMO (56%) | |||
| 546 | HOMO−2 → LUMO (31%) | |||
| 502 | HOMO → LUMO+1 (64%) | |||
| 456 | HOMO+1 → LUMO+1 (45%) | |||
| 430 | HOMO+1 → LUMO+2 (45%) | |||
| D–A8 | −5.908 | −2.586 | 646 | HOMO−1 → LUMO (49%) |
| 627 | HOMO → LUMO (39%) | |||
| 528 | HOMO+1 → LUMO+2 (37%) | |||
| 506 | HOMO → LUMO+2 (52%) | |||
| 450 | HOMO → LUMO (39%) | |||
| 437 | HOMO−1 → LUMO (36%) | |||
| 413 | HOMO−3 → LUMO (94%) | |||
| D–A9 | −6.063 | −2.840 | 712 | HOMO−1 → LUMO (68%) |
| 663 | HOMO → LUMO (57%) | |||
| 550 | HOMO−4 → LUMO (28%) | |||
| 504 | HOMO → LUMO+2 (64%) | |||
| 468 | HOMO−2 → LUMO (89%) | |||
| 465 | HOMO−1 → LUMO+2 (40%) | |||
| 438 | HOMO−1 → LUMO+3 (27%) | |||
| D–A10 | −6.009 | −2.613 | 685 | HOMO−1 → LUMO (65%) |
| 646 | HOMO → LUMO (54%) | |||
| 542 | HOMO−1 → LUMO+1 (27%) | |||
| 502 | HOMO → LUMO+1 (63%) | |||
| 451 | HOMO−1 → LUMO+1 (42%) | |||
| 427 | HOMO−1 → LUMO+2 (27%) | |||
| D–A11 | −5.920 | −2.602 | 647 | HOMO−1 → LUMO (50%) |
| 628 | HOMO → LUMO (39%) | |||
| 528 | HOMO−1 → LUMO+2 (37%) | |||
| 506 | HOMO → LUMO+2 (52%) | |||
| 451 | HOMO → LUMO (39%) | |||
| 438 | HOMO−1 → LUMO (36%) | |||
| 412 | HOMO−3 → LUMO (94%) | |||
| A–D–A0 | 7.015 | −3.465 | 716 | HOMO−1 → LUMO (71%) |
| 684 | HOMO → LUMO (61%) | |||
| 563 | HOMO−3 → LUMO (39%) | |||
| 515 | HOMO → LUMO+2 (46%) | |||
| 447 | HOMO−1 → LUMO+2 (35%) | |||
| 419 | HOMO → LUMO+1 (51%) | |||
| A–D–A1 | −6.185 | −2.983 | 745 | HOMO−1 → LUMO (69%) |
| 711 | HOMO → LUMO (61%) | |||
| 573 | HOMO−3 → LUMO (36%) | |||
| 529 | HOMO → LUMO+5 (38%) | |||
| 467 | HOMO−1 → LUMO+1 (39%) | |||
| 449 | HOMO → LUMO+1 (58%) | |||
| 428 | HOMO−1 → LUMO+1 (47%) | |||
| 415 | HOMO−1 → LUMO (19%) | |||
| A–D–A2 | −6.401 | −3.577 | 828 | HOMO−1 → LUMO (62%) |
| 731 | HOMO → LUMO (55%) | |||
| 596 | HOMO−3 → LUMO (30%) | |||
| 528 | HOMO → LUMO+1 (95%) | |||
| 505 | HOMO → LUMO+5 (63%) | |||
| 503 | HOMO−1 → LUMO+1 (93%) | |||
| 484 | HOMO−1 → LUMO+5 (33%) | |||
| 451 | HOMO−1 → LUMO+2 (34%) | |||
| A–D–A3 | −6.901 | −3.963 | 752 | HOMO−1 → LUMO (57%) |
| 715 | HOMO → LUMO (49%) | |||
| 571 | HOMO−4 → LUMO (21%) | |||
| 562 | HOMO → LUMO+3 (60%) | |||
| 523 | HOMO → LUMO+2 (62%) | |||
| 522 | HOMO → LUMO+1 (70%) | |||
| 512 | HOMO−1 → LUMO+1 (45%) | |||
| 508 | HOMO−1 → LUMO+2 (56%) | |||
| 500 | HOMO−1 → LUMO+3 (48%) | |||
| 482 | HOMO → LUMO+5 (29%) | |||
| A–D–A4 | −6.877 | −3.983 | 767 | HOMO−1 → LUMO (58%) |
| 733 | HOMO → LUMO (59%) | |||
| 578 | HOMO−4 → LUMO (38%) | |||
| 561 | HOMO → LUMO+1 (64%) | |||
| 502 | HOMO−1 → LUMO+1 (55%) | |||
| 484 | HOMO → LUMO+1 (27%) | |||
| 475 | HOMO−2 → LUMO (55%) | |||
| 458 | HOMO−1 → LUMO+4 (32%) | |||
| 436 | HOMO−4 → LUMO+4 (16%) | |||
| A–D–A5 | −6.474 | −4.150 | 804 | HOMO−1 → LUMO (44%) |
| 784 | HOMO → LUMO (44%) | |||
| 677 | HOMO → LUMO+1 (89%) | |||
| 656 | HOMO−1 → LUMO+1 (80%) | |||
| 606 | HOMO−1 → LUMO (31%) | |||
| 600 | HOMO → LUMO (24%) | |||
| 583 | HOMO−4 → LUMO+15 (15%) | |||
| 540 | HOMO−2 → LUMO (83%) | |||
| 538 | HOMO−2 → LUMO+1 (58%) | |||
| 532 | HOMO−2 → LUMO+1 (28%) | |||
| 495 | HOMO−3 → LUMO (27%) | |||
| 484 | HOMO → LUMO+3 (70%) | |||
| 480 | HOMO−3 → LUMO+1 (59%) | |||
| 472 | HOMO−1 → LUMO+3 (55%) | |||
| 471 | HOMO → LUMO+2 (42%) | |||
| 466 | HOMO−1 → LUMO+2 (41%) | |||
| 453 | HOMO−4 → LUMO (15%) | |||
| 447 | HOMO → LUMO+5 (47%) | |||
| 442 | HOMO−1 → LUMO+4 (53%) | |||
| 439 | HOMO → LUMO+4 (19%) | |||
| A–D–A6 | −6.709 | −3.531 | 795 | HOMO−1 → LUMO (74%) |
| 734 | HOMO → LUMO (64%) | |||
| 593 | HOMO−6 → LUMO (43%) | |||
| 526 | HOMO → LUMO+1 (37%) | |||
| 476 | HOMO−1 → LUMO+1 (46%) | |||
| 454 | HOMO → LUMO+1 (56%) | |||
| 445 | HOMO−2 → LUMO (37%) | |||
| 444 | HOMO−3 → LUMO (37%) | |||
| 434 | HOMO−1 → LUMO+1 (41%) | |||
| 415 | HOMO−1 → LUMO (17%) | |||
| A–D–A7 | −6.629 | −3.312 | 766 | HOMO−1 → LUMO (74%) |
| 714 | HOMO → LUMO (64%) | |||
| 582 | HOMO−3 → LUMO (48%) | |||
| 519 | HOMO → LUMO+2 (46%) | |||
| 462 | HOMO−1 → LUMO+2 (35%) | |||
| 436 | HOMO → LUMO+1 (63%) | |||
| 418 | HOMO−1 → LUMO+1 (56%) | |||
| 405 | HOMO−1 → LUMO+3 (22%) | |||
| A–D–A8 | −6.273 | −2.934 | 682 | HOMO−1 → LUMO (43%) |
| 668 | HOMO → LUMO (45%) | |||
| 548 | HOMO−6 → LUMO (27%) | |||
| 522 | HOMO → LUMO+4 (23%) | |||
| 448 | HOMO−1 → LUMO+1 (20%) | |||
| 444 | HOMO → LUMO+1 (59%) | |||
| 427 | HOMO−1 → LUMO (37%) | |||
| 425 | HOMO−1 → LUMO+1 (42%) | |||
| 420 | HOMO−5 → LUMO (41%) | |||
| 419 | HOMO−4 → LUMO (40%) | |||
| A–D–A9 | −6.299 | −3.264 | 780 | HOMO−3 → LUMO (63%) |
| 725 | HOMO → LUMO (62%) | |||
| 586 | HOMO−6 → LUMO (44%) | |||
| 524 | HOMO → LUMO+1 (33%) | |||
| 490 | HOMO−2 → LUMO (59%) | |||
| 489 | HOMO−1 → LUMO (58%) | |||
| 471 | HOMO−3 → LUMO+1 (36%) | |||
| 452 | HOMO → LUMO+1 (59%) | |||
| 432 | HOMO−3 → LUMO+1 (40%) | |||
| 415 | HOMO−3 → LUMO (17%) | |||
| A–D–A10 | −6.392 | −3.049 | 750 | HOMO−1 → LUMO (72%) |
| 705 | HOMO → LUMO (63%) | |||
| 576 | HOMO−3 → LUMO (44%) | |||
| 518 | HOMO → LUMO+2 (46%) | |||
| 458 | HOMO−1 → LUMO+2 (35%) | |||
| 433 | HOMO → LUMO+1 (63%) | |||
| 415 | HOMO−1 → LUMO+1 (59%) | |||
| 404 | HOMO−1 → LUMO+3 (21%) | |||
| A–D–A11 | −6.289 | −2.951 | 684 | HOMO−1 → LUMO (44%) |
| 670 | HOMO → LUMO (46%) | |||
| 549 | HOMO−6 → LUMO (27%) | |||
| 523 | HOMO → LUMO+4 (24%) | |||
| 450 | HOMO−1 → LUMO+1 (21%) | |||
| 446 | HOMO → LUMO+1 (59%) | |||
| 427 | HOMO−1 → LUMO (35%) | |||
| 426 | HOMO−1 → LUMO+1 (41%) | |||
| 422 | HOMO−3 → LUMO (33%) | |||
| 419 | HOMO−5 → LUMO (58%) |
4. Conclusions
To conclude, a series of twenty-four dyes comprising ferrocene as the electron donor have been designed and synthesized. All dyes showed a strong absorption extending over the visible range. Efficient tuning of the absorption maxima could be achieved not only by means of the number of electron acceptors per dye but also by means of the electron-withdrawing ability. Among the most interesting findings, a positive solvatochromism was found for all dyes, except for the triad comprising the tetranitrofluorene acceptor for which the ground state is more polarized than the excited state. Parallel to this, chemical oxidation of ferrocene in the different dyes suppressed the electron donating ability of ferrocene so that a complete color change of the different solutions could be demonstrated. Use of an excess of nitrosonium cation during the chemical oxidation of ferrocene to ferrocenium induced additional reactions onto the electron acceptors subsequent to the oxidation of ferrocene. Among the most surprising findings, a drastic modification of the UV-visible absorption spectra of the 24 dyes could be observed in numerous solvents, and this modification of the UV-visible absorption spectra has never been reported in the literature, even when some of these dyes have been synthesized prior to this work. Although several hypotheses have been examined to support the modification of the absorption spectra over time, isolation and identification of the different reaction products deserve to be investigated in future works. Indeed, although the phenomenon could be clearly evidenced, no clear conclusions could be established concerning the exact origin of these modifications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Aix Marseille University and The Centre National de la Recherche Scientifique (CNRS) for financial support. The Agence Nationale de la Recherche (ANR agency) is acknowledged for its financial support through the PhD grant to the VISICAT project of Guillaume Noirbent (ANR-17-CE08-0054). The Direction Générale de l’Armement (DGA)/Agence Innovation Defense (AID) is acknowledged for its financial support through the PhD grant to Dr Damien Brunel.References
- F. Bures, RSC Adv., 2014, 4, 58826–58851 RSC.
- A. W. Hains, Z. Liang, M. A. Woodhouse and B. A. Gregg, Chem. Rev., 2010, 110, 6689–6735 CrossRef CAS PubMed.
- Y. Wu and W. Zhu, Chem. Soc. Rev., 2013, 42, 2039–2058 RSC.
- J. N. Clifford, E. Martinez-Ferrero, A. Viterisi and E. Palomares, Chem. Soc. Rev., 2011, 40, 1635–1646 RSC.
- C. Duan, K. Zhang, C. Zhong, F. Huang and Y. Cao, Chem. Soc. Rev., 2013, 42, 9071–9104 RSC.
- M. Liang and J. Chen, Chem. Soc. Rev., 2013, 42, 3453–3488 RSC.
- C. Duan, F. Huang and Y. Cao, J. Mater. Chem., 2012, 22, 10416–10434 RSC.
- S. Allard, M. Forster, B. Souharce, H. Thiem and U. Scherf, Angew. Chem., Int. Ed., 2008, 47, 4070–4098 CrossRef CAS PubMed.
- F. Dumur, C. R. Mayer, K. Hoang-Thi, I. Ledoux-Rak, F. Miomandre, G. Clavier, E. Dumas, R. Méallet-Renault, M. Frigoli, J. Zyss and F. Sécheresse, Inorg. Chem., 2009, 48, 8120–8133 CrossRef CAS PubMed.
- J.-M. Raimundo, P. Blanchard, N. Gallego-Planas, N. Mercier, I. Ledoux-Rak, R. Hierle and J. Roncali, J. Org. Chem., 2002, 67, 205–218 CrossRef CAS PubMed.
- B. Jędrzejewska, M. Gordel, J. Szeremeta, P. Krawczyk and M. Samoć, J. Org. Chem., 2015, 80, 9641–9651 CrossRef PubMed.
- W.-J. Shi, P.-C. Lo, A. Singh, I. Ledoux-Rak and D. K. P. Ng, Tetrahedron, 2012, 68, 8712–8718 CrossRef CAS.
- N. Mohammed, A. A. Wiles, M. Belsley, S. S. M. Fernandes, M. Cariello, V. M. Rotello, M. M. M. Raposo and G. Cooke, RSC Adv., 2017, 7, 24462–24469 RSC.
- M.-A. Tehfe, F. Dumur, B. Graff, F. Morlet-Savary, D. Gigmes, J.-P. Fouassier and J. Lalevée, Macromolecules, 2013, 46, 3761–3770 CrossRef CAS.
- M.-A. Tehfe, F. Dumur, B. Graff, F. Morlet-Savary, D. Gigmes, J.-P. Fouassier and J. Lalevée, Polym. Chem., 2013, 4, 3866–3875 RSC.
- H. Mokbel, S. Telitel, F. Dumur, L. Vidal, D.-L. Versace, M.-A. Tehfe, B. Graff, J. Toufaily, J.-P. Fouassier, D. Gigmes, T. Hamieh and J. Lalevée, Polym. Chem., 2013, 4, 5679–5687 RSC.
- P. Xiao, M. Frigoli, F. Dumur, B. Graff, D. Gigmes, J.-P. Fouassier and J. Lalevée, Macromolecules, 2014, 47, 106–112 CrossRef CAS.
- P. Xiao, F. Dumur, B. Graff, L. Vidal, D. Gigmes, J.-P. Fouassier and J. Lalevée, Macromolecules, 2014, 47, 26–34 CrossRef CAS.
- P. Xiao, F. Dumur, M.-A. Tehfe, D. Gigmes, J.-P. Fouassier and J. Lalevée, Macromol. Rapid Commun., 2013, 34, 1452–1458 CrossRef CAS PubMed.
- F. Dumur, D. Gigmes, J.-P. Fouassier and J. Lalevée, Acc. Chem. Res., 2016, 49, 1980–1989 CrossRef CAS PubMed.
- F. Dumur, Eur. Polym. J., 2021, 147, 110328 CrossRef CAS.
- F. Dumur, Eur. Polym. J., 2021, 143, 110178 CrossRef CAS.
- F. Dumur, Eur. Polym. J., 2020, 139, 110026 CrossRef CAS.
- B. Steyrer, P. Neubauer, R. Liska and J. Stampfl, Materials, 2017, 10, 1445 CrossRef PubMed.
- J. Zhang and P. Xiao, Polym. Chem., 2018, 9, 1530–1540 RSC.
- C. Pigot, G. Noirbent, T.-T. Bui, S. Péralta, D. Gigmes, M. Nechab and F. Dumur, Materials, 2019, 12, 1342 CrossRef CAS PubMed.
- F. Dumur, C. R. Mayer, E. Dumas, F. Miomandre, M. Frigoli and F. Sécheresse, Org. Lett., 2008, 10, 321–324 CrossRef CAS PubMed.
- A. Guerlin, F. Dumur, E. Dumas, F. Miomandre, G. Wantz and C. R. Mayer, Org. Lett., 2010, 12, 2382–2385 CrossRef CAS PubMed.
- S. Forget, H. Rabbani-Haghighi, N. Diffalah, A. Siove and S. Chénais, Appl. Phys. Lett., 2011, 98, 131102 CrossRef.
- S. Chénais and S. Forget, Polym. Int., 2011, 61, 390–406 CrossRef.
- P. N. Prasad and D. J. Williams, in Introduction to Nonlinear Optical Effects in Molecules and Polymers, eds. J. Klafter and J. M. Drake, Wiley, New York, 1991, pp. 132–174 Search PubMed.
- H. S. Nalwa and S. Miyata, Nonlinear Optics of Organic Molecules and Polymers, CRC Press, New York, 1997 Search PubMed.
- L. R. Dalton, P. A. Sullivan, D. Bale, B. Olbricht, J. Davies, S. Benight, I. Kosilkin, B. H. Robinson, B. E. Eichinger and A. K. Y. Jen, in Organic Thin Films for Photonic Applications, eds. W. N. Herman, S. R. Flom and S. H. Foulger, American Chemical Society, Washington DC, 2010, ch. 2, vol. 1039, pp. 13–33 Search PubMed.
- T. Verbiest, S. Houbrechts, M. Kauranen, K. Clays and A. Persoons, J. Mater. Chem., 1997, 7, 2175–2189 RSC.
- H. S. Nalwa and S. Miyata, Nonlinear Optics of Organic Molecules and Polymers, CRC Press, New York, 1997 Search PubMed.
- D. Brunel, G. Noirbent and F. Dumur, Dyes Pigm., 2019, 170, 107611 CrossRef CAS.
- R. R. Gagne, C. A. Koval and G. C. Lisensky, Inorg. Chem., 1980, 19, 2854–2855 CrossRef CAS.
- M. Patra and G. Gasser, Nat. Rev. Chem., 2017, 1, 0066 CrossRef CAS.
- P. Garra, D. Brunel, G. Noirbent, B. Graff, F. Morlet-Savary, C. Dietlin, V. F. Sidorkin, F. Dumur, D. Duché, D. Gigmes, J.-P. Fouassier and J. Lalevée, Polym. Chem., 2019, 10, 1431–1441 RSC.
- A. Lai, Z. C. Hern and P. L. Diaconescu, ChemCatChem, 2019, 11, 4210–4218 CrossRef CAS.
- T. Noël and J. Van der Eycken, Green Process. Synth., 2013, 2, 297–309 Search PubMed.
- J. A. Findlay, J. E. Barnsley, K. C. Gordon ID and J. D. Crowley, Molecules, 2018, 23, 2037 CrossRef PubMed.
- Z. Deng, H. Yu, L. Wang, J. Liu and K. J. Shea, J. Mater. Chem. A, 2019, 7, 15975–15980 RSC.
- M. E. Welker, Molecules, 2018, 23, 1551 CrossRef PubMed.
- G. Kelly, F. Darviche, N. Robertson, T. Gelbrich, M. B. Hursthouse, D. A. Thomas and I. R. Butler, Inorg. Chem. Commun., 2005, 8, 874–877 CrossRef CAS.
- P. D. Jarowski, Y.-L. Wu, C. Boudon, J.-P. Gisselbrecht, M. Gross, W. B. Schweizer and F. Diederich, Org. Biomol. Chem., 2009, 7, 1312–1322 RSC.
- T. Shoji, S. Ito, T. Okujima and N. Morita, Chem. – Eur. J., 2013, 19, 5721–5730 CrossRef CAS PubMed.
- T. Mochida and S. Yamazaki, J. Chem. Soc., Dalton Trans., 2002, 3559–3564 RSC.
- A. J. Moore, A. Chesney, M. R. Bryce, A. S. Batsanov, J. F. Kelly, J. A. K. Howard, I. F. Perepichka, D. F. Perepichka, G. Meshulam, G. Berkovic, Z. Kotler, R. Mazor and V. Khodorkovsky, Eur. J. Org. Chem., 2001, 2671–2687 CrossRef CAS.
- D. F. Perepichka, I. F. Perepichka, A. F. Popov, M. R. Bryce, A. S. Batsanov, A. Chesney, J. A. K. Howard and N. I. Sokolov, J. Organomet. Chem., 2001, 637–639, 445–462 CrossRef CAS.
- R. Teimuri-Mofrad, K. Rahimpour and A. Poursadegh, Mater. Chem. Phys., 2017, 200, 384–394 CrossRef CAS.
- I. Janowska, J. Zakrzewski, K. Nakatani, J. A. Delaire, M. Palusiak, M. Walak and H. Scholl, J. Organomet. Chem., 2003, 675, 35–41 CrossRef CAS.
- A. M. Asiri, Appl. Organomet. Chem., 2001, 15, 907–915 CrossRef CAS.
- R. Ziessel, P. Retailleau, K. J. Elliott and A. Harriman, Chem. – Eur. J., 2009, 15, 10369–10374 CrossRef CAS PubMed.
- S. Kaur, M. Kaur, P. Kaur, K. Clays and K. Singh, Coord. Chem. Rev., 2017, 343, 185–219 CrossRef CAS.
- K. Kowalski, Ł. Szczupak, J. Skiba, O. S. Abdel-Rahman, R. F. Winter, R. Czerwieniec and B. Therrien, Organometallics, 2014, 33, 4697–4705 CrossRef CAS.
- L. M. Ombaka, P. G. Ndungu, B. Omondi and V. O. Nyamori, J. Coord. Chem., 2014, 67, 1905–1922 CrossRef CAS.
- A. Ghosh, S. Mishra, S. Giri, S. M. Mobin, A. Bera and S. Chatterjee, Organometallics, 2018, 37, 1999–2002 CrossRef CAS.
- G. Cooke and O. Schulz, Synth. Commun., 1996, 26, 2549–2560 CrossRef CAS.
- J. A. Mata, E. Peris, R. Llusar, S. Uriel, M. P. Cifuentes, M. G. Humphrey, M. Samoc and B. Luther-Davies, Eur. J. Inorg. Chem., 2001, 2113–2122 CrossRef CAS.
- P. Kaur, M. Kaur, G. Depotter, S. Van Cleuvenbergen, I. Asselberghs, K. Clays and K. Singh, J. Mater. Chem., 2012, 22, 10597–10608 RSC.
- D. Bao, B. Millare, W. Xia, B. G. Steyer, A. A. Gerasimenko, A. Ferreira, A. Contreras and V. I. Vullev, J. Phys. Chem. A, 2009, 113, 1259–1267 CrossRef CAS PubMed.
- G. Gritzner, Pure Appl. Chem., 1990, 62, 1839–1858 CAS.
- S. Daniele, M. A. Baldo, P. Ugo and G. A. Mazzocchin, J. Electroanal. Chem., 1990, 295, 95–111 CrossRef CAS.
- K. Nikos and G. Tsierkezos, J. Solution Chem., 2007, 36, 289–302 CrossRef.
- R. M. Nielson, G. E. McManis, L. K. Safford and M. J. Weaver, J. Phys. Chem., 1989, 93, 2152–2157 CrossRef CAS.
- B. S. Aytar, J. P. E. Muller, S. Golan, Y. Kondo, Y. Talmon, N. L. Abbott and D. M. Lynn, J. Colloid Interface Sci., 2012, 387, 56–64 CrossRef CAS PubMed.
- X. Yin, Y. Li, Y. Li, Y. Zhu, X. Tang, H. Zheng and D. Zhu, Tetrahedron, 2009, 65, 8373–8377 CrossRef CAS.
- H. Tahara, K. Uranaka, M. Hirano, T. Ikeda, T. Sagara and H. Murakami, ACS Appl. Mater. Interfaces, 2019, 11, 1–6 CrossRef CAS PubMed.
- B. Gélinas, D. Das and D. Rochefort, ACS Appl. Mater. Interfaces, 2017, 9, 28726–28736 CrossRef PubMed.
- I. Asselberghs, K. Clays, A. Persoons, A. M. McDonagh, M. D. Ward and J. A. McCleverty, Chem. Phys. Lett., 2003, 368, 408–411 CrossRef CAS.
- A. Federman Neto, J. Miller, V. Faria de Andrade, S. Y. Fujimoto, M. M. de Freitas Afonso, F. Costa Archanjo, V. A. Darin, M. L. Andrade e Silva, A. Donizete Lanchote Borges and G. Del Ponte, Z. Anorg. Allg. Chem., 2002, 628, 209–216 CrossRef CAS.
- G. G. A. Balavoine, G. Doisneau and T. Fillebeen-Khan, J. Organomet. Chem., 1991, 412, 381–382 CrossRef CAS.
- M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; J. A. Montgomery, Jr.; T. Vreven; K. N. Kudin; J. C. Burant; J. M. Millam; S. S. Iyengar; J. Tomasi; V. Barone; B. Mennucci; M. Cossi; G. Scalmani; N. Rega; G. A. Petersson; H. Nakatsuji; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; M. Klene; X. Li; J. E. Knox; H. P. Hratchian; J. B. Cross; V. Bakken; C. Adamo; J. Jaramillo; R. Gomperts; R. E. Stratmann; O. Yazyev; A. J. Austin; R. Cammi; C. Pomelli; J. W. Ochterski; P. Y. Ayala; K. Morokuma; G. A. Voth; P. Salvador; J. J. Dannenberg; V. G. Zakrzewski; S. Dapprich; A. D. Daniels; M. C. Strain; O. Farkas; D. K. Malick; A. D. Rabuck; K. Raghavachari; J. B. Foresman; J. V. Ortiz; Q. Cui; A. G. Baboul; S. Clifford; J. Cioslowski; B. B. Stefanov; G. Liu; A. Liashenko; P. Piskorz; I. Komaromi; R. L. Martin; D. J. Fox; T. Keith; M. A. Al-Laham; C. Y. Peng; A. Nanayakkara; M. Challacombe; P. M. W. Gill; B. Johnson; W. Chen; M. W. Wong; C. Gonzalez and J. A. Pople, Gaussian, Inc.Wallingford CT, 2009.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- J. Tomasi, B. Mennucci and E. Cances, THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 9, 839–845 CrossRef PubMed.
- J. C. Calabrese, L.-T. Cheng, J. C. Green, S. R. Marder and W. Tam, J. Am. Chem. Soc., 1991, 113, 7227–7232 CrossRef CAS.
- S. Barlow, H. E. Bunting, C. Ringham, J. C. Green, G. U. Bublitz, S. G. Boxer, J. W. Perry and S. R. Marder, J. Am. Chem. Soc., 1999, 121, 3715–3723 CrossRef CAS.
- Y. Liao, B. E. Eichinger, K. A. Firestone, M. Haller, J. Luo, W. Kaminsky, J. B. Benedict, P. J. Reid, A. K.-Y. Jen, L. R. Dalton and B. H. Robinson, J. Am. Chem. Soc., 2005, 127, 2758–2766 CrossRef CAS PubMed.
- X. Wu, W. Wu, X. Cui, J. Zhao and M. Wu, J. Mater. Chem. C, 2016, 4, 2843–2853 RSC.
- P. Aranyosi, Zs Csepregi, I. Rusznak, L. Töke and A. Vig, Dyes Pigm., 1998, 37, 33–45 CrossRef CAS.
- M. Henary and M. Mojzych, Stability and Reactivity of Polymethine Dyes in Solution, in Heterocyclic Polymethine Dyes, eds. L. Strekowski, Topics in Heterocyclic Chemistry, Springer, Berlin, Heidelberg, 2008, vol 14 Search PubMed.
- S. Oancea and O. Drăghici, Czech J. Food Sci., 2013, 31, 283–291 CrossRef CAS.
- S. Sipahli, V. Mdhanlall and J. J. Mellem, Food Sci. Technol., 2017, 37, 209–215 CrossRef.
- C. T. Sanderson, B. J. Palmer, A. Morgan, M. Murphy, R. A. Dluhy, T. Mize, I. J. Amster and C. Kutal, Macromolecules, 2002, 35, 9648–9652 CrossRef CAS.
- H. Kunkely and A. Vogler, J. Organomet. Chem., 1998, 559, 215–217 CrossRef CAS.
- U. M. Rabie, Spectrochim. Acta, Part A, 2009, 74, 746–752 CrossRef PubMed.
- B. Mallik, Molecules, 2005, 10, 708–727 CrossRef CAS PubMed.
- M. J. Kamlet, J.-L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 8, 2877–2887 CrossRef.
- C. Reichardt, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS.
- E. Lippert, Z. Naturforsch., 1955, 10a, 541–545 CrossRef CAS.
- J. Catalan, J. Org. Chem., 1997, 62, 8231–8234 CrossRef CAS PubMed.
- A. Kawski, Acta Phys. Polon., 1966, 29, 507–518 CAS.
- P. Suppan, J. Chem. Soc. A, 1968, 3125–3133 RSC.
- N. G. Bakshiev, Opt. Spektrosk., 1964, 16, 821–832 Search PubMed.
- S. Cha, M. G. Choi, H. R. Jeon and S.-K. Chang, Sens. Actuators, B, 2011, 157, 14–18 CrossRef CAS.
- C. Reichardt, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS.
- H. Lu and S. C. Rutan, Anal. Chem., 1996, 68, 1381–1386 CrossRef CAS.
- G. Noirbent and F. Dumur, Materials, 2018, 11, 2425 CrossRef PubMed.
- I. A. Koppel and V. A. Palm, in Advances in Linear Free Energy Relationships, eds. N. B. Chapman and J. Shorter, Plenum Press, London, 1972, p. 203 Search PubMed.
- V. A. Palm, Fundamentals of Quantitative Theory of Organic Reactions, Khimiya, Leningrad, 1977, p. 109, in Russian Search PubMed.
- R. Misra, P. Gautam and R. Maragani, Tetrahedron Lett., 2015, 56, 1664–1666 CrossRef CAS.
- I. F. Perepichka, D. F. Perepichka, M. R. Bryce, A. Chesne, A. F. Popov, V. Khodorkovsky, G. Meshulamd and Z. Kotler, Synth. Met., 1999, 102, 1558–1559 CrossRef CAS.
- F. Dumur, C. R. Mayer, E. Dumas, F. Miomandre, M. Frigoli and F. Sécheresse, Org. Lett., 2008, 10, 321–324 CrossRef CAS PubMed.
- J. Pommerehne, H. Vestweber, W. Guss, R. F. Mahrt, H. Bässler, M. Porsch and J. Daub, Adv. Mater., 1995, 7, 551–554 CrossRef CAS.
- Z. V. Todres, Ion-Radical Organic Chemistry: Principles and Applications, 2nd edn, CRC Press, 2008 Search PubMed.
- Y. Zhou, X. Jia, R. Li, Z. Liu, Z. Liu and L. Wu, Tetrahedron Lett., 2005, 46, 8937–8939 CrossRef CAS.
- G. I. Borodkin and V. G. Shubin, Russ. Chem. Rev., 2017, 86, 18–46 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nj01680f |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2021 |