Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bonding, structure, and mechanical stability of 2D materials: the predictive power of the periodic table
Peter
Hess

Institute of Physical Chemistry, INF 253, University of Heidelberg, 69120 Heidelberg, Germany. E-mail: peter.hess@urz.uni-heidelberg.de
First published on 8th September 2021
Abstract
This tutorial review describes the ongoing effort to convert main-group elements of the periodic table and their combinations into stable 2D materials, which is sometimes called modern ‘alchemy’. Theory is successfully approaching this goal, whereas experimental verification is lagging far behind in the synergistic interplay between theory and experiment. The data collected here gives a clear picture of the bonding, structure, and mechanical performance of the main-group elements and their binary compounds. This ranges from group II elements, with two valence electrons, to group VI elements with six valence electrons, which form not only 1D structures but also, owing to their variable oxidation states, low-symmetry 2D networks. Outside of these main groups reviewed here, predominantly ionic bonding may be observed, for example in group II–VII compounds. Besides high-symmetry graphene with its shortest and strongest bonds and outstanding mechanical properties, low-symmetry 2D structures such as various borophene and tellurene phases with intriguing properties are receiving increasing attention. The comprehensive discussion of data also includes bonding and structure of few-layer assemblies, because the electronic properties, e.g., the band gap, of these heterostructures vary with interlayer layer separation and interaction energy. The available data allows the identification of general relationships between bonding, structure, and mechanical stability. This enables the extraction of periodic trends and fundamental rules governing the 2D world, which help to clear up deviating results and to estimate unknown properties. For example, the observed change of the bond length by a factor of two alters the cohesive energy by a factor of four and the extremely sensitive Young's modulus and ultimate strength by more than a factor of 60. Since the stiffness and strength decrease with increasing atom size on going down the columns of the periodic table, it is important to look for suitable allotropes of elements and binaries in the upper rows of the periodic table when mechanical stability and robustness are issues. On the other hand, the heavy compounds are of particular interest because of their low-symmetry structures with exotic electronic properties.
Introduction
The family of two-dimensional (2D) materials is growing rapidly by expanding to more elements of the periodic table and by their characterization being extended predominantly by theoretical studies.1–6 The preparation ranges from straightforward exfoliation of layered materials, such as graphene, with a huge reservoir of weakly bonded layered materials, to entirely synthetic methods, such synthetic 2D monolayers are borophene, silicene, bismuthene, and tellurene.1,6 Besides monolayers this includes bilayers, tri-layers, and few-layer assemblies up to about 10 layers, where a transition to bulk properties is observed.7,8Strong covalent and ionic interatomic bonding in 2D materials and weaker interlayer interaction between monolayers are the focus of this review. Besides the quantum-mechanical concepts of electron sharing, electron transfer, and electron delocalization, phenomenological binding models describe the role played by the three fundamental types of interaction forces, termed covalent, ionic, and metallic bonding. Confining strong chemical bonding to one or a few layers, usually less than five, creates a huge flat molecule without dangling bonds at the surface. Mixing planar sp2 hybridization with tetrahedral sp3 hybrids dramatically extends covalent bonding to quasi-two-dimensional corrugated phases, by introducing buckling and puckering but also chemical reactivity. Besides mechanical constraints, chemical stability under environmental conditions is a crucial requirement, made important by the extremely large surface area exposed to the environment.
Ab initio calculations are the first choice for computing the pristine structure as well as chemical and physical properties of 2D materials.4,9 It is important to note that first-principles calculations have not only predicted the existence of new 2D materials but also helped to find possible routes of synthesis and understand the growth process.9,10 Of the two main approaches, namely, the wave-function-based methods and density functional theory (DFT) calculations, the latter plays the major role. In the latter approach the many-body system of electrons is treated by considering non-interacting electrons moving in an effective potential. To take the exchange and correlation effects in the calculation of electron density into account, the local density approximation (LDA) uses Ceperley–Alder (CA) functionals or Troullier–Martins (TM) pseudopotentials. In most calculations the generalized gradient approximation (GGA) is employed with Perdew–Burke–Ernzerhof (PBE) functionals.4 Large differences may occur between the LDA and GGA approach, especially for few-layer systems, where, besides strong covalent in-plane interaction, weak interlayer forces such as van der Waals and electrostatic interactions must be considered.4 At present, most results are based on the numerical DFT-GGA-PBE approach, which plays a crucial role in our present understanding of 2D materials.
Molecular dynamics (MD) simulations complete the investigation of the atomic structure and mechanical behavior of monolayers because they can deal with system sizes of thousands or even millions of atoms, in comparison with about a hundred atoms usually manageable by DFT calculations. The simulation is based on classical Newtonian dynamics, where potential energy functions, which describe the interaction between atoms, play a critical role. These theoretical methods give access not only to the intrinsic structures of monolayers and few-layer systems but also provide valuable estimates of the thermal or thermodynamic stability of the 2D materials at temperatures above 0 K.4
While the data presented for bonding, structure, and mechanical properties primarily is based on first-principles calculations, we also apply the tight-binding theory of solids that uses the linear combination of atomic orbitals (LCAO). The LCAO approach and hybridization concept can deliver analytical expressions for the coupling parameters and the electronic-state energies.11 Despite the fact that it is less exact than numerical first-principles computations, the simplified bonding model that follows chemical intuition often offers valuable insight and a deeper understanding of the nature of bonding and allows the recognition of chemical relationships within related groups of the periodic table.
Reliable mechanical performance of 2D materials from manufacture to final use is a key requirement for any application.12,13 While calculated intrinsic Young's moduli and ultimate strengths are already available for various monolayers, toughness values that characterize the strength of large-area defective monolayers are available only for graphene. The following work concentrates primarily on calculated mechanical properties such as the intrinsic Young's modulus, Poisson's ratio, ultimate strength, and ultimate strain of both free-standing and surface-bonded monolayers. Most 2D materials exhibit a positive Poisson's ratio between 0 and 0.5, where the material contracts in the transverse direction when stretched in the longitudinal direction. For some low-symmetry monolayers a negative Poisson's ratio or auxetic behavior exists. This means, for example, that the material expands perpendicular to the plane when stretched in the in-plane direction.14 For a rigorous comparison of the 2D mechanical properties of monolayers, 2D units are needed, due to the thickness or volume dependence of the 3D properties.15 These 2D properties can be obtained by transforming 3D units (N m−2) to 2D units (N m−1) using the monolayer thickness or by direct measurement. Unfortunately, reliable measurements of the intrinsic stiffness and ultimate strength, e.g., by indentation, are available only for graphene, while the measurements for other monolayers such as graphene oxide, h-BN, and black P are still preliminary.16 The monolayer thickness can be defined for free-standing layers, whereas in few-layer assemblies the interlayer spacing changes with the strength of interlayer interaction.
Up to now, only a few 2D materials have been prepared in their free-standing form, for example by exfoliation, allowing a direct measurement of their intrinsic properties. It is possible to grow quasi freely suspended monolayers that retain their properties under ultrahigh vacuum (UHV) conditions by molecular beam epitaxy (MBE) on suitable substrates. A buffer layer may stabilize an otherwise unstable monolayer by weak interaction forces. However, often stronger electrostatic and covalent interaction forces dominate the interaction of a monolayer with the substrate and change the structure. Structural analysis is performed by scanning atomic force microscopy (AFM),16 scanning tunneling microscopy (STM), in situ microscopy techniques such as scanning electron microscopy (SEM), low energy electron diffraction (LEED), X-ray diffraction (XRD), X-ray photoelectron spectroscopy (XPS), selected area electron diffraction (SAED), and high resolution transmission electron microscopy (HRTEM), supplemented by energy dispersive X-ray spectroscopy (EDX).17 Atomic steps in layered assemblies are used for the direct measurement of the interlayer spacing by AFM and STM.
The present review of main group elements provides a systematic discussion of covalently bonded elemental group-III monolayers and their isoelectronic group II–IV compounds, elemental and binary group-IV monolayers and their isoelectronic group III–V compounds, elemental and binary group-V monolayers and their isoelectronic group IV–VI compounds, and elemental group-VI monolayers (see Fig. 1). Extension to other groups, for instance to alkaline earth–halogen monolayers, may lead to strong ionic bonding due to the large difference in their electronegativities. Importantly, bonding by long-range Coulomb forces is less effective in 2D than in 3D materials. The relevant bonding information, structural data, and mechanical properties of the predominantly covalently bonded monolayers are presented in 13 tables. The explosive growth of studies on 2D compounds has allowed the identification of general relationships between bonding, structure, and mechanical stability and the extraction of basic rules governing the 2D world down the periodic table.18 These relationships are extracted for main group elements by plots of the cohesive energy, describing the bonding energy of an atom in the 2D solid, versus bond length. To elucidate the intrinsic linear and nonlinear mechanical behavior we plot the Young's modulus and ultimate strength as a function of bond length.
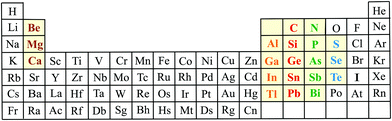 | ||
| Fig. 1 Scheme of the periodic table, highlighting the elements of the columns II, III, IV, V, and VI that form covalently bonded elemental and binary monolayers and isoelectronic mixed monolayers. | ||
Group III elemental monolayers
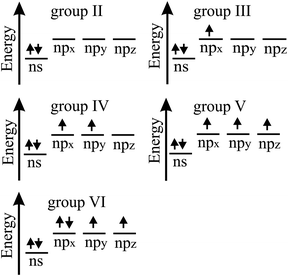
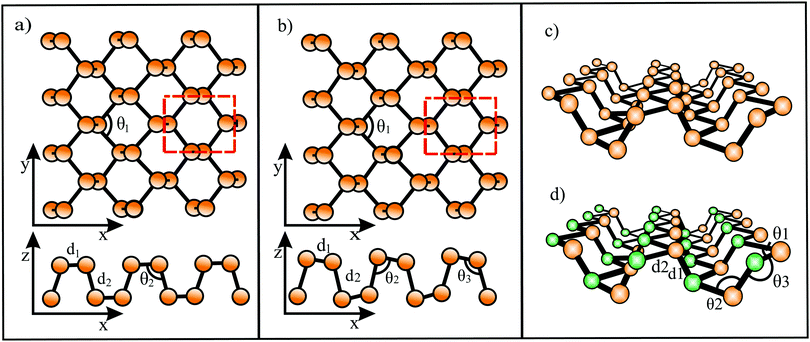
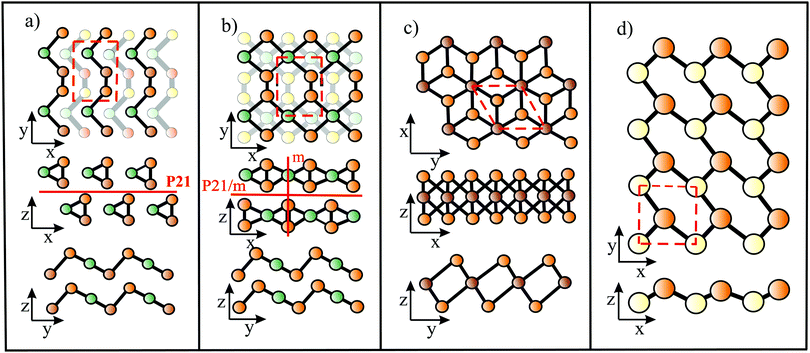
The bonding behavior of elements varies drastically with the main group of the periodic table. The reason for this is that group II elements have two, group III elements three, group IV elements four, group V elements five, and group VI elements six valence electrons in the outer shell (see Fig. 2). It is well known that graphene with its four valence electrons per C atom forms the most stable covalent bonds in the plane, involving eight electrons in the closed outer shell of a noble gas configuration (‘octet rule’). A fundamental question is how the behavior of monolayers changes if the octet rule is not fulfilled and valence electrons are missing or additional electrons are available. For example, trivalent group III atoms cannot form a closed-shell structure by conventional bonding.Since group III atoms have three electrons in their outer valence shell, they can form extended covalent networks by sp2-type hybridization, however, only with electron-deficient bonds, because the 2pz orbital is empty. According to the octet rule for efficient bonding, the missing electron reduces the bond energy and thus the energy of cohesion. The realized bonding type can be elucidated by comparison with the conventional two-center, two-electron bonds of carbon (2c-2e): 1. A single chemical bond is formed when each of two atoms provides an electron, and both share the formed electron pair. 2. Electron configurations with eight atoms in the outer shell possess a lower energy and higher stability (‘octet rule’) due to the stable noble gas configuration. Group III atoms with three valence electrons cannot fulfill these conditions and therefore arrange as delocalized three-centered bonds or multi-centered bonds in σ and π frameworks, where electron pairs are shared at least among three or more atoms.19 This complex bonding behavior gives access to flexible chemistry with a wide variety of allotropes in 2D space. DFT calculations propose a series of dynamically stable 2D structures and a variety of 2D bonding types for borophene, aluminene, gallenene, and indiene, the single layers of boron, aluminium, gallium, and indium.
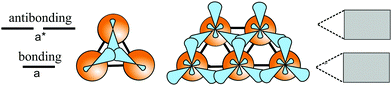
In the following, tight-binding theory is used to treat three-centered bonds by the LCAO ansatz, describing the formation of molecular orbitals, which are combined to produce covalent bonding of an extended 2D network.11,20 The electron configuration and the arrangement of orbitals for three-centered bonding is shown in Fig. 3. Boron is the lightest atom that can develop 2D extended metallic phases by sp2-type hybrids, described by delocalized three-center, two-electron bonds (3c-2e), involving a motif of three shared boron atoms.
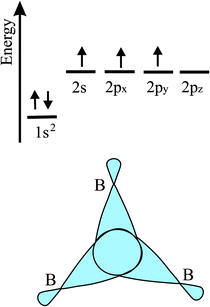 | ||
| Fig. 3 Scheme of the electron configuration of valence electrons and sketch of the corresponding three-center bonding orbitals of boron. | ||
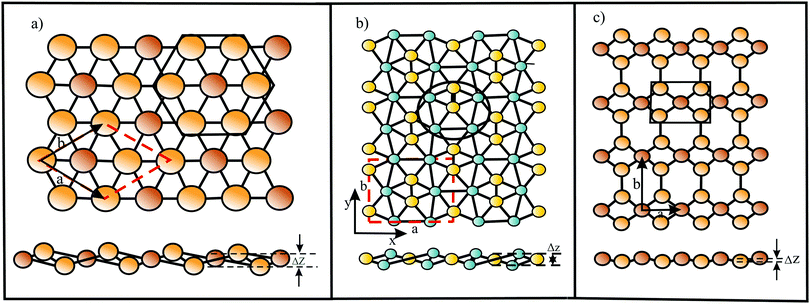
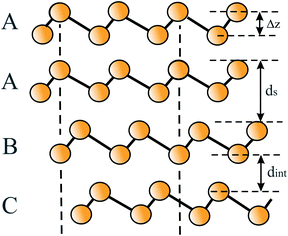
Based on the LCAO method, the electron configuration with promoted electrons can be described by three equivalent atomic orbitals, which form the molecular orbitals of a triangular motif, where three atoms share one pair of electrons.21 In this triangular boron motif, the sp2-like hybrids overlap, yielding one bonding and two anti-bonding orbitals (see Fig. 4). These orbitals broaden into bands by adding more triangles with increasing orbital overlap.21 Two of the three electrons are in the in-plane bonding orbital, but one electron is in an in-plane antibonding orbital and not in the remaining empty 2pz-bonding orbital. Therefore, a planar triangular hybrid prefers to hybridize with a high-energy electron to a σ–π mixture of in-plane and out-of-plane states to gain further stability in a buckled configuration. The fact that a small fraction of electrons occupies bonding π bands and a small fraction of σ states stay unoccupied seems to be the reason for the instability of the planar network.21 This configuration is metallic due to partial occupancy of the σ and π states. However, the freestanding regular triangular borophene sheet with buckling along the armchair direction, called striped δ6-borophene, is dynamically unstable. The cohesive energy and structural data of this polymorph are given in Table 1 and a scheme of the structure is presented in Fig. 5(a).21–23 For corrugated monolayers, Table 1 provides an estimate of the layer thickness dw+Δz by adding the van der Waals diameter dw24 and the corresponding corrugation effect Δz.
| Monolayer | Structure, space group | Cohesive energy, Ec (eV per atom) | Lattice constants a, b (nm) | Bond lengths d1, d2 (nm) | Corrugation distance Δz1, Δz2 (nm) | van der Waals diameter dw,24dw+Δz (nm) |
|---|---|---|---|---|---|---|
| Borophene | Triang., δ6 | −6.0021 | 0.161, 0.28622 | 0.160, 0.18621 | 0.08821 | 0.384,24 0.472 |
| Pmmn 22 | −5.6623 | 0.322, 0.32923 | 0.09122 | |||
| Borophene | Planar, β12 | −6.1522 | 0.293, 0.50722 | 0.165, 0.17025 | 022 | 0.38424 |
| Pmm222 | −5.7123 | 0.292, 0.50623 | ||||
| Borophene | Planar, χ3 | −6.1622 | 0.445, 0.44522 | 0.160, 0.17125 | 022 | 0.38424 |
| Cmmm 2 | ||||||
| −5.7223 | 0.290, 0.44423 | |||||
| Borophene | 4-Layer slab 8-Pmmn26 | −6.3326 | 0.452, 0.32626 | ∼0.17–0.1926 | 0.21826 | 0.384,24 0.602 |
| Borophene | Pucker, acw Pmn2127 | −5.7327 | 0.319, 0.53027 | 0.157–0.22627 | 0.126, 0.20227 | 0.384,24 0.586 |
| Aluminene | Planar | −1.9628 | 0.44928 | 0.25928 | 028 | 0.36824 |
| P6mmm30 | −2.3229 | 0.44629 | 0.25729 | |||
| Aluminene | Buckled | −3.4731 | 0.27531 | 0.275, 0.29231 | 0.24531 | 0.368,24 0.613 |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m131 m131 |
−3.2729 | 0.27229 | 0.29629 | 0.25229 | 0.368,24 0.620 | |
| Aluminene | Triang., Pmmn29 | −2.7629 | 0.268, 0.46529 | 0.26829 | 0.21730 | 0.268,24 0.585 |
| Triang., Pmnm30 | −3.2730 | 0.269, 0.27230 | ||||
| Aluminene | 4-Layer slab 8-Pmmn31 | −3.1631 | 0.674, 0.50331 | 0.258–0.28631 | 0.34431 | 0.368,24 0.712 |
| Gallenene | Quasi planar | 0.787, 0.46532 | 0.266, 0.26732 | 032 | 0.37424 | |
| a100-Ga | 0.250, 0.25133 | 033 | ||||
| Gallenene | Puckered | −2.3234 | 0.474, 0.49232 | 0.27332 | 0.11932 | 0.374,24 0.493 |
| b010-Ga | 0.465, 0.48234 | 0.271, 0.27334 | 0.12734 | 0.374,24 0.501 | ||
| Indiene | Planar | −1.8136 | 0.49636 | 0.28636 | 036 | 0.38624 |
| Indiene | Buckled | −1.8336 | 0.42436 | 0.28936 | 0.15436 | 0.386,24 0.540 |
| Indiene | Pucker, sw | −1.8836 | 0.425, 0.56836 | 0.291, 0.28736 |
Interestingly, besides the unstable striped phase, stable planar borophenes exist. By combining electron donors, provided by the three-center flat triangular regions with a surplus of electrons in an antibonding state, and two-center hexagonal regions, acting as electron acceptors, in the right proportion, boron can form stable polymorphs consisting of hexagonal sites with holes and triangular sites. In Fig. 5(b and c) two such highly symmetric phases, called β12 and χ3 borophene, are displayed. These highly symmetric perfectly flat metallic sheets achieve a high stability of free-standing borophene. The enormous number of possible 2D arrangements of hollow hexagon and triangular sites (variation of boron hexagons with or without a boron atom at the center) makes it possible to tailor lattice properties. The structural and mechanical data of the two phases that have already been synthesized (β12 and χ3 borophene) are given in Tables 1 and 2.21–25 To explain the high stability of the planar phase an aromatic or anti-aromatic character of bonding has been invoked.19
| Monolayer | Structure, space group | Young's modulus (N m−1) Eac, Ezz | Poisson's ratio νac, νzz | Ultimate strength (N m−1) σacσzz | Ultimate strain, εacεzz |
|---|---|---|---|---|---|
| Borophene | Triangular, δ6 | 382, 16325 | −0.0125 | 22.8, 14.025 | 0.11, 0.1525 |
| Pmmn 22 | 399, 16339 | −0.23, 039 | 20.9, 12.239 | 0.087, 0.1439 | |
| Borophene | Planar, β12 | 190, 21025 | 0.1825 | 20.0, 22.425 | 0.20, 0.2125 |
| Pmm222 | 189, 21039 | 0.15, 0.1739 | 16.4, 15.439 | 0.12, 0.1139 | |
| Borophene | Planar, χ3 | 208, 20525 | 0.1125 | 19.9, 20.225 | 0.21, 0.1625 |
| Cmmm 22 | 196, 20839 | 0.11, 0.1239 | |||
| Borophene | 4-Layer slab | 241, 30526 | 0.042, 0.06226 | 21.6, 27.826 | 0.16, 0.1726 |
| 8-Pmmn26 | 248, 32241 | 0.048, 0.06241 | 0.16, 0.1741 | ||
| Aluminene | Planar | 3142 | 0.3142 | 0.26, 0.2442 | |
| Aluminene | Triangular | 3742 | 0.4942 | 0.24, 0.3242 | |
| Gallenene | Puckered | 2534 | 0.2034 | 1134 | 0.3034 |
| Indiene | Planar | 2842 | 0.08542 | 0.3042 | |
| Indiene | Triangular | 2542 | 0.3742 | 0.28, 0.3842 |
Furthermore, complex geometrical structures consisting of several covalently bonded sublayers exist. This includes a borophene phase with the space group 8-Pmmn, consisting of four atomic sublayers (see Fig. 5(d)).26 This hard but flexible material has a large cohesive energy, which is in line with the high values of the other polymorphs. Contrary to the failure mechanism of triangular borophene, which shows elastic instability in the zigzag direction and phonon instability in the stronger armchair direction, the 8-Pmmn structure fails by elastic instability.
In the search for other defect-free polymorphs of borophene, a thermodynamically stable puckered phase with an asymmetric centered-washboard (acw) structure of orthorhombic symmetry has been discovered that, unlike other boron sheets, is a semiconductor (centered because there is another atom at the center of the hexagons).27 According to MD simulations, this semiconducting polymorph is dynamically and thermodynamically stable up to about 800 K. Interestingly, the application of uniaxial or biaxial tensile strain closes the gap and transforms the system back to the metallic state, and the positive Poisson ratio becomes negative.27
For aluminene, besides the planar honeycomb structure of aluminium,28,29 a graphene-like buckled,30 triangular,29 and four-layer 8-Pmmn structure31 have been proposed (see Table 1). Note that some of these phases have not yet been fully characterized and confirmed by other authors and some allotropic modifications may only be stable if the phonon dynamics is stabilized by the strain exerted by monolayer–substrate interaction. For the dynamically and thermodynamically stable four-layer network of 8-Pmmn aluminene, covalent sp3-type bonding seems to be stronger than sp2 bonding, according to an analysis of the electron localization function (ELF).31
In its bulk chemical behavior, α-Ga is known as the only elemental ‘molecular metal’ that favors both covalently bonded dimers and weaker metallic bonding in the plane perpendicular to the average alignment of the Ga–Ga dimers. Monolayers of gallium have been investigated by several authors.32–35 A tight-binding model based on the combination of LCAO and ab initio calculations led to the proposal of the existence of a graphene-like planar a100-gallenene.32 This phase can be derived from bulk α-Ga by extracting a monolayer of Ga from the 100 surface (a100-Ga) and allowing relaxation (see Fig. 6(a)).33 This slightly distorted honeycomb network needs stabilization, for example by strain engineering, due to dynamical instability in its free-standing form. A second phase studied by the tight-binding model is the b010-gallenene monolayer, which resembles a zigzag rhombic lattice.32 This phase can be derived from bulk α-Ga by extracting a monolayer of Ga from the 010 surface (b010-Ga) and allowing relaxation (see Fig. 6(b)).33 The pucker effect originates from mixed hybridization of the in-plane orbitals with the pz orbitals. The Ga–Ga bonds in a100-gallenene are covalent in nature, whereas both metallic and covalent interaction is observed in b010-gallenene. It is important to note that the two gallenene structures exhibit imaginary frequencies, however, they can be stabilized upon application of biaxial strain or by adsorption on a surface. In fact, few-layer assemblies of atomically thin 2D gallenene (∼4 nm) have been successfully exfoliated from the molten phase of α-gallium (∼30 °C) on a silicon substrate, where the substrate stabilizes the dynamically unstable quasi-free-standing layer.33
The investigation of 2D phases of the heavier homologues In and, especially, Tl is still in its infancy. First principles DFT-PBE calculations indicate the existence of two dynamically stable phases of indiene, namely a planar honeycomb phase that behaves like a metal and a buckled graphene-like allotrope, which is an indirect semiconductor that transforms to a metal under compressive and tensile strain.36 In addition, a dynamically unstable puckered structure with a comparable cohesive energy has been described by the authors.
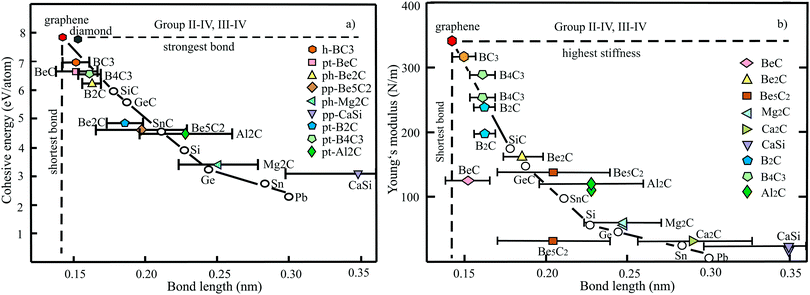
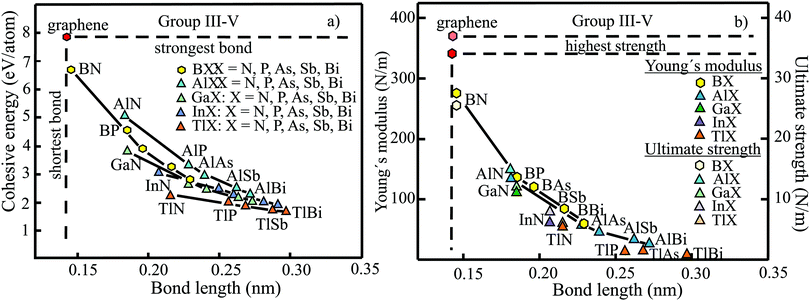
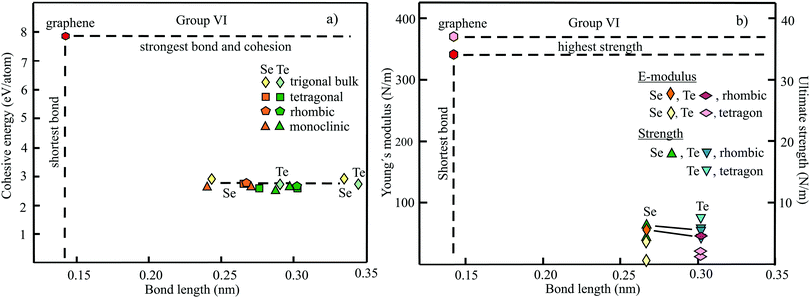
The structure, space group, cohesive energy, lattice constants, bond length, corrugation effect, and monolayer thickness of group III monolayers are presented in Table 1 for the known triangular, planar, 8-Pmmn, and puckered allotropes. To elucidate the nature of the bonding, we plot the cohesive energies as a function of the accurately known bond lengths (see Fig. 7(a)). The cohesive energy describes the interaction of an atom with its surrounding atoms of the 2D network and controls the mechanical stability of the whole network. In the case of corrugated monolayers, usually the largest bond length is employed, designating the bond with lowest critical fracture strength, and for the large differences of some puckered phases the mean value is used. For comparison, graphene is included, which has the largest cohesive energy and shortest bond of any uniform single-atom layer.37,38
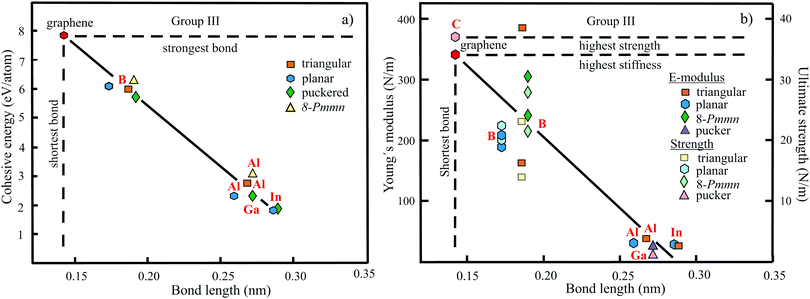 | ||
| Fig. 7 (a) Plot of cohesive energy versus bond length for group III elemental monolayers. (b) Plot of Young's modulus and ultimate strength versus bond length of group III elemental monolayers. | ||
The boron allotropes assemble in a region of short bonds and consequently strong bonding. Note the striking similarity of cohesive energies for the diverse phases. To explain the unusual stability of planar and quasi-planar 2D boron structures, the bonding concepts of aromaticity and anti-aromaticity have been invoked.19 The three heavier group III monolayers cluster in a region with significantly longer bonds and thus much lower cohesive energies. Surprisingly, the atom size, approximated by the van der Waals diameter of B (0.384 nm), Al (0.368 nm), Ga (0.374 nm), and In (0.386 nm), does not increase24 and the corrugation effects are comparable. It is the drastic extension of bond length observed from borophenes (0.16–0.19 nm) to aluminene phases (0.26–0.29 nm) that strongly reduces orbital overlap and leads to the large decrease of bond energy of the homologues of boron. The missing fourth valence electron seems to have a much stronger effect on the stability of the higher homologues than on borophenes.
The structure, Young's modulus, Poisson's ratio, ultimate strength, and ultimate strain of the studied phases of borophene,25,26,39–41 aluminene,42 gallenene,34 and indiene42 are collected in Table 2. The plot of the Young's moduli and ultimate strengths as a function of the bond lengths offers an overview of the mechanical behavior of elemental group III monolayers (see Fig. 7(b)). Note the different scales of the left and right ordinates, which differ by a factor of ten and therefore give direct insight into the applicability of Griffith's rule σ = E/10, where σ is the ultimate strength and E is the Young's modulus. This rule connects the elastic stiffness with the about ten times smaller critical stress or ultimate strength. The intrinsic or ultimate strength is the maximum stress a perfect crystal can withstand at zero temperature, and thus is a measure of the strength of bonding at the ultimate strain. To illustrate the mechanical performance of group III monolayers, we included the outstanding mechanical properties of graphene with the highest Young's modulus of 340 N m−1, confirmed by experiment and theory, and the theoretical mean strength of 37 N m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 for uniaxial tension, in good agreement with 42 N m−1 measured by biaxial indentation using AFM.38
37 for uniaxial tension, in good agreement with 42 N m−1 measured by biaxial indentation using AFM.38
Note that in the armchair direction the Young's modulus of triangular borophene is larger than the stiffness of graphene due to extreme directional bonding. In the zigzag direction, however, a significantly smaller stiffness is calculated and the whole structure becomes dynamically unstable. Altogether, the phases of borophene cover a huge range of stiffnesses and fracture strengths originating from the diversity of accessible 2D structures, which, however, possess comparable cohesive energies. The latter describes the mean reaction energy of the atoms per atom independent of the anisotropy of the structure. Besides the polymorphic behavior, the flexibility of the planar structures is more than twofold higher than graphene's value, which can be explained by delocalized multi-center bonding with well-ordered holes in the planar phases.39
Remarkably, from borophene to aluminene,42 gallenene,34 and indiene,42 concomitant with the observed decrease of the cohesive energy by a factor of about three, the stiffness and strength of all phases decrease drastically by a factor of about ten. This illustrates the severe deterioration of mechanical performance within group III elements, in line with an increase of bond length by a factor of approximately two (see Fig. 7(b)). Thus, besides the higher reactivity, problems with the mechanical in-plane rigidity and strength may appear for the heavier homologues. Amazingly, the strongly anisotropic triangular phase has a negative Poisson ratio (see Table 2). Instead of shrinking along the out-of-plane direction, the ridge-to-ridge distance increases upon application of in-plane strain, due to a much smaller in-plane modulus across the ridges than along the ridges.39 Delocalized multi-center bonding enables structural fluxionality that causes structural phase transitions under tension, for example by inducing atomic rearrangements by bond rotation at small strains. As can be seen in Table 2, the ultimate strains increase substantially, namely by a factor of about three, from borophene to indiene. Surprisingly, β12 borophene exhibits a strain-induced phase transition by atomic rearrangement via bond rotation at a strain of ∼0.12, and then resists loading up to a strain of 0.36.39 A high mechanical toughness with ultimate strains in the range of the latter value is reported for indiene.42
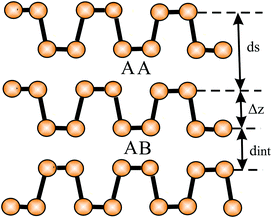
The mechanical properties of few-layer systems (1–4 layers) of metallic triangular borophenes without holes have been studied theoretically.43 The interlayer separations of 0.31 nm (AA stacking) and 0.34 nm (AB stacking) are much smaller than the estimated layer thickness of buckled borophene, taking the corrugation effect into account.43 This points to strong interlayer interaction between the metallic layers. Calculations of the metallic bilayer structure of planar hexagonal aluminene yielded an interlayer separation of 0.270 nm, which is also much smaller than the van der Waals diameter. The small spacing allows interlayer electron transfer, as confirmed by a huge interlayer interaction energy of −519 meV per atom.44 Therefore, aluminene has been recommended as a promising material for electric charge storage and as a nanocapacitor.
In 3D structures the metalloid boron shows neither metallic nor non-metallic behavior, whereas metallic properties are found in its 2D structures. Despite the energetic and dynamic stability suggested by DFT calculations for several allotropes of group-III monolayers, the thermodynamic stability of metallic monolayers remains a fundamental problem. Owing to the absence of electrons occupying π bonds, the stability is significantly reduced. However, close-packed triangular and planar polymorphs with different vacancy patterns have been grown on Ag(111) substrates and identified by STM.22,26 A recent progress report covers the experimental synthesis of metallic and also semiconducting borophene sheets, e.g., on metal substrates by CVD and MBE, and discusses relevant stability issues, which are a prerequisite for practical applications in nanoelectronics and optoelectronics.45
Group II–IV and III–IV monolayers
The distinctive nature of bonding of several group II–IV and III–IV monolayers has been studied theoretically, while experimental verification is still missing. Remarkably, these monolayers show the rule-breaking phenomenon of quasi-planar hypercoordinate chemistry. This is of enormous significance for the development of 2D materials due to the enforced restriction of covalent bonding to two dimensions. Contrary to conventional 3D tetrahedral and planar tricoordinate sp2 bonding of carbon, binary monolayers with Be, Mg, Ca, B, and Al atoms exhibit quasi-planar tetracoordinate (ptC), quasi-planar pentacoordinate (ppC), and quasi-planar hexacoordinate (phC) moieties, deviating from carbon's established tetrahedral bonding and its maximum coordination number of four.46 Reasons for this unusual coordination in the plane are delocalization of electrons of the carbon 2pz orbitals by efficient π-acceptors and the donation of σ electrons to electron-deficient bonding. Moreover, electron transfer is promoted in these compounds by different electronegativities, leading to ionic contributions. The increase of electron density at the C (Si) moiety enforces planarity of the σ bonds. In isolated molecular species besides electronic stabilization of planar hypercoordination mechanical effects such as steric constraints have been studied intensively by theory and by experiments.47The peculiar molecular motifs with unconventional bonding may serve as building blocks for an extension to infinite monolayers (see Fig. 8). To incorporate these generally unstable entities in a monolayer, mechanical interconnects such as non-hexagonal rings can be used to stabilize hypercoordinate bonding in 2D space. This additional structural degree of freedom opens the door to novel although complex structures with unforeseen physico-chemical properties, as well as promising applications. It is well known that elements with multicenter bonding such as boron allow a variety of strong bonding types and various configurations with delocalized charge distribution. The nature of interlinks combining the individual hypercoordinate motifs plays a fundamental role in the stabilization of infinite layers and in the realization of distinct monolayer properties.
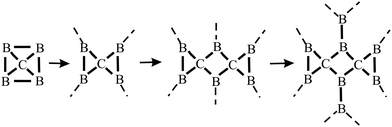 | ||
| Fig. 8 Step-by-step growth of an extended B2C monolayer, containing the hypercoordinated ptC motif, by starting from a hypothetical CB4 molecule. See Fig. 9(c) for the structure of the corresponding extended network. | ||
The necessary information on charge distribution and type of bonding in the extended systems is mainly based on two methods. The interpretation of charge distributions in terms of electron lone pairs, two-center and multicenter bonding are usually examined by the solid state adaptive natural density partitioning (SSAdNDP) method.48 The second method delivering insight into the electron distribution and nature of bonding is ELF.49 The key ELF values of approximately 0, 0.5, and 1 refer to extremely low electron density, fully delocalized electrons, and extremely high density of electrons, respectively.
The theoretical strategies employed to find stable hypercoordinated 2D arrangements of atoms are bottom-up approaches, maintaining the number of valence electrons by isoelectronic substitution, and direct global minimum search. Clearly, 2D materials with the lowest energy configuration of the global minimum on the potential energy surface (PES) have a high chance to be realized experimentally. Quite often, however, additional configurations with a local minimum and quite similar cohesive energies exist. If these monolayers are thermodynamically and dynamically stable, experimental synthesis may be possible, especially if further stabilization takes place by adsorption on a suitable surface.
Global structure search resulted in a minimum energy monolayer of BeC with a complicated structure, containing rings with three, six, and eight atoms.50 In this planar low symmetry structure with ptC moieties the carbon atoms bind four Be atoms. The perfect planarity has been explained by the small-ring mechanical strain and π electron delocalization. Table 3 presents the structure, cohesive energy, lattice constants, bond lengths, Poisson's ratios, and in-plane mechanical moduli of all hypercoordinated compounds considered here. Furthermore, the table gives the sum of the van der Waals radii (dw) of the two constituents and in case of corrugation the van der Waals diameter plus buckling effect (dw+Δz) as an estimate of the layer thickness.15,24 Besides BeC, based on DFT calculations and particle swarm optimization (PSO), global minimum search resulted in quasi-planar phC moieties incorporated in a weakly buckled monolayer of Be2C.51,52 Each C atom binds to six Be atoms, while each Be atom is connected to three C atoms and three Be atoms (see Fig. 9(a)). Symmetric buckling of two adjacent Be atoms of 0.046 nm out of the central C atom plane reduces repulsion between neighboring cations.52 The thermodynamic, dynamic, and thermal stability up to 1500 K have been confirmed for Be2C.
| Monolayer | Planar structure, space group | Cohesive energy, Ec (eV per atom) | Lattice constants a, b (nm) | Bond lengths dCX,SiXdXX, (nm) | Buckling distance Δz (nm) | van der Waals diameter dw, dw+Δz (nm) | Poisson's Ratio νac,a, νzz,b | Young's modulus Eac,a, Ezz,b (N m−1) |
|---|---|---|---|---|---|---|---|---|
| BeC | ptC, AMM250 | −6.6750 | a = b = 0.43550 | 0.138, 0.16650 | 050 | 0.32323 | 14650 | |
| Be2C | phC, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m151 m151 |
−4.8652 | a = b = 0.29952 | 0.173, 0.19852 | 0.09252 | 0.323,24 0,415 | 16252 | |
| Be5C2 | ppC | −4.5853 | 0.892, 0.92153 | 0.170, 0.23953 | 0.21453 | 0.323,24 0.537 | −0.041, −0.1653 | 32.7, 13053 |
| Mg2C | phC, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m155 m155 |
−3.4354 | 0.354,54 0.33555 | 0.223, 0.27155 | 0.17954 | 0.343,24 0.522 | 0.03, −0.02355 | 59.6, 56.855 |
| Ca2C | phC, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
0.39456 | 0.256, 0.32656 | 0.23456 | 0.401,24 0.635 | 0.448, 0.44856 | 72.9, 32.656 | |
| CaSi | ppSi | −3.0757 | 0.933, 0.68657 | 0.297, 0.39857 | 0.07657 | 0.441,24 0.517 | −0.15, −01657 | 21.8, 24.657 |
| B2C | ptC, Pmm270 | −6.4759 | 0.256, 0.34559 | 0.156, 0.16959 | ∼0.008559 | 0.362,24 0.371 | 0.148, 0.12359 | 237, 19759 |
| B4C3 | ptC | −6.5662 | 0.4762 | 0.153, 0.16962 | ∼0.03062 | 0.384,24 0.414 | 252, 28762 | |
| Al2C | ptC | −4.4963 | 0.304, 0.5063 | 0.196, 0.26063 | 063 | 0.35424 | 0.114, 0.10464 | 121, 11064 |
The computationally designed Be5C2 monolayer contains quasi-planar pentacoordinate carbon motifs (quasi-ppC) in a global minimum structure.53 Remarkably, the Be5C2 monolayer contains no classical lone pairs or localized conventional 2c-2e bonds, but only three-, four, and six-center bonds.46 The large buckling effect of 0.214 nm reduces the repulsive interaction between Be atoms. The negative cohesive energy reveals thermodynamic stability, the positive phonon modes dynamic stability, and the high melting point of >1500 K thermal stability. The unit cell contains eight B5C2 units with 72 electrons. The Be5C2 monolayer is a gapless semiconductor with a Dirac-like point in the band structure.
DFT calculations, including electronic structure calculations, revealed that Mg2C monolayers with quasi-planar hexacoordinate C (phC) and hexacoordinate Mg represent a global minimum structure.54,55 The corrugation of the puckered hinge structure is 0.179 nm.54 Owing to the larger Mg atom the bond lengths increase and the cohesive energy decreases to −3.43 eV per atom.54 The monolayer is thermodynamically, dynamically, and, as MD simulations indicate, thermally stable up to 900 K. The strain-tunable band can be tuned from its metallic equilibrium state to a gapless semimetal and narrow semiconductor by modest biaxial tensile strain.54 The monolayers possess the rare intrinsic in-plane negative Poisson's ratio, where responsive strain is observed in the armchair direction if strain is applied in the zigzag direction.55
A structure with quasi-planar hexacoordinate C (phC), as already described for Be2C and Mg2C, is also formed by Ca2C, however, with a larger corrugation of 0.234 nm.56 This monolayer is dynamically, mechanically, and thermally stable up to 700 K.56 According to the long Ca–Ca bonds of 0.326 nm the low cohesive energy and in-plane stiffness is expected. The 2D network shows only small deviations from isotropic mechanical behavior and belongs to the family of MXenes that has received enormous attention for potential use in supercapacitors and batteries.56
Inspired by the bonding of the molecular species Ca4Si22− with a ppSi center as building block, following the 18-electron rule, a CaSi monolayer has been designed by DFT computations (see Fig. 9(b)).57 Stabilization occurs by delocalization of Si 3pz electrons and σ-donation of Ca electrons. In the CaSi layer the Si atom binds with five ligands, namely one Si atom and four Ca atoms (quasi-ppSi). The Ca atoms of this monolayer are buckled with a total buckling distance of 0.076 nm, 0.038 nm on both sides of the central Si layer. The cohesive energy is low, owing to large bond lengths diminishing orbital overlap. The CaSi monolayer is thermodynamically, mechanically, dynamically, and thermally stable up to about 1200 K.57
For B2C first-principles lattice dynamics and electron–phonon coupling calculations predicted a monolayer consisting of a mosaic of hexagons and rhombuses with quasi-ptC moieties, ensuring a preferred 18 valence electron count (see Fig. 9(c)).58 The C layer and B layer are separated by only 0.0032 nm (∼0.0085 nm59).58 Global minimum search on 2D boron-carbon compounds revealed that this thermodynamically and dynamically stable structure has not the lowest-energy configuration, however, a comparable stability.59,60 The possibly metallic network is formed by strong bonds and is dynamically and thermally stable up to about 2000 K.59 Another proposed boron carbide is the B4C3 monolayer derived from quasi-planar hexacoordinated B4C3 clusters61 with tetracoordinate carbon (quasi-ptC).62 This global minimum structure was obtained by DFT computations and swarm-intelligence structure-searching methods. Since the central B atom of each B4C3 motif is situated about 0.03 nm above the hexagonal B3C3 ring, the monolayer is slightly buckled. The strongly bonded thermodynamically stable monolayer is dynamically and thermally stable up to 1600 K.
The Al2C monolayer can be derived from the planar molecular species C2Al62− and follows the already described structure of B2C with tetracoordinate carbon (ptC) and tricoordinate Al atoms with a global minimum structure.63 Better σ-donation due to the larger electronegativity difference between C and Al (∼1.0) than between C and B (∼0.5) completely avoids buckling by delocalized electrons. Note that the size of Al atoms implies much larger bond lengths, resulting in a moderate cohesive energy.64 This semiconducting monolayer is thermodynamically and dynamically stable, and maintains its structural integrity up to 1500 K.
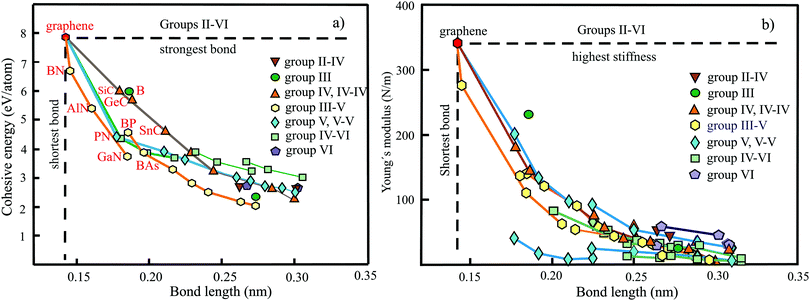
The plot in Fig. 10(a) displays the cohesive binding energies versus the range of bond lengths found in the nonuniform monolayer structures of BeC,50 Be2C,51,52 Be5C2,53 Mg2C54,55 Ca2C,56 CaSi,57 B2C,58–60 B4C3,61,62 and Al2C.63,64 According to the valence-shell electron-pair repulsion (VSEPR) rule, hypercoordinated moieties seem to be energetically unfavorable owing to repulsion of the high density of bonds in the plane. The plot, however, demonstrates surprisingly strong bonding of quasi-planar hypercoordinate structures with their unconventional bonding types. A comparison of planar tetracoordinated structures with the strong 3D tetragonal structure of diamond with a cohesive energy of −7.71 eV per atom (exp. −7.54 eV per atom) and bond length of 0.154 nm supports the statement.65 Obviously, not only stabilization of the molecular moieties achieved by delocalization of lone-pair electrons combined with π-accepting and σ-donating substituents is efficient but also the whole 2D arrangement by inter-motif bonding.
The distinctive inverse dependence of the cohesive energies on the range of calculated bond lengths is consistent with the prediction of tight-binding theory.11 Due to the nonuniform structure the cohesive energy represents a mean value of individual bond energies, which is plotted versus the resulting spread of bond lengths. Notably, the mean values exhibit a characteristic inverse behavior comparable to that of the uniformly bonded group-IV monolayers. According to the tight-binding model the strength of covalent orbital coupling, V (which is the cohesive energy in nonpolar compounds), decreases with increasing bond length as V ∼ 1/d2.20 The binding effect of electrostatic forces is larger for compounds of C (2.55) with Be (1.57) and Al (1.61), and for Si (1.9) with Ca (1.0), whereas it is smaller for C (2.55) and B (2.04) compounds.
In the following the bonding-structure relationship of quasi-planar hypercoordinated compounds is compared with the uniform hexagonal monolayer of graphene, characterized by the smallest bond length of 0.142 nm and the largest cohesive energy. Further, the BC3 monolayer is considered that can be described as a doped graphene with honeycomb structure, where all carbon hexagons are connected by boron atoms.66 The introduction of boron atoms in BC3 monolayers generates B–C bonds of 0.156 nm length, whereas the C–C bonds of the carbon hexagons are still ∼0.142 nm.66 The cohesive energy of graphene of −7.85 eV per atom (see Table 4) decreases to −6.86 eV per atom67 in BC3. The reasons for the decay are the missing valence electrons and the larger atom size of boron. Increasing the boron content, e.g., in hypercoordinated B3C4 and B2C monolayers, reduces the cohesive energy only slightly to −6.56 and −6.47 eV per atom, respectively. While B3C4 contains two different B–C bonds (0.153 nm and 0.159 nm) and one B–B bond (0.169 nm), B2C has one B–C bond (0.156 nm) and one B–B bond (0.169 nm). These observations imply efficient covalent bonding not only within the ptC moieties. The observed behavior can be correlated with the reduction of the mean number of valence electrons per atom.
The large cohesive energy of −6.67 eV per atom for BeC is consistent with the short bonds of 0.138 nm for C–C bonds assigned to carbon triangles and the two bond lengths of 0.160 nm and 0.166 nm for Be–C bonds. The much longer Be–C bonds of 0.173 nm and even longer Be–Be bonds of 0.198 nm in Be2C are responsible for the much smaller cohesive energy of −4.86 eV per atom. While the smaller size of Be atoms improves orbital overlap, the two missing valence electrons per atom reduce the overall binding power. Bonding in Be5C2 compounds fits into the general bonding–structure scheme with −4.58 eV per atom and longer Be–C and Be–Be bonds of 0.170 and 0.239 nm, respectively. The weakest bonds and the largest alteration of bond lengths are observed for Al2C and CaSi monolayers, containing only one or no element of the second period of the periodic table.
To benchmark the bonding–structure relationships of hypercoordinated monolayers with those of the planar sp2-bonded binary group IV carbides SiC, GeC, and SnC, as well as the weakly buckled hexagonal group-IV elements Si, Ge, Sn, and Pb, Fig. 10(a) gives a direct comparison that provides additional insight into the characteristics of hypercoordination. It is well known that the group-IV compounds follow the established octet rule. The used cohesive energy of SiC (−5.97 eV per atom) has been calculated, while those of GeC (−5.57 eV per atom) and SnC (−4.54 eV per atom) are based on the correlation with other group-IV and binary group IV data, because for the two latter compounds much larger and lower values can be found in the literature, as discussed below. As visible in Fig. 10(a), the planar sp2-bonded carbides and weakly buckled group-IV elements show a related inverse behavior, as observed for the mean bond lengths of the hypercoordinated compounds. Only the heaviest elements Sn and Pb show a tendency to lower cohesive energies. Obviously, quasi-planar hypercoordinated motifs can be effectively incorporated into monolayer structures by introducing efficient coordination patterns between the motifs. This conclusion is supported by a comparison of hexagonal siligraphene SiC2 with a binding energy of −6.46 eV per atom68 and silagraphene SiC2 with tetracoordinate silicon (ptSi) motifs at −6.04 eV per atom, containing rings with four and six atoms.69 Of course, when the interconnects do not reflect the steric requirements of the motifs with their specified shapes, the overall stability of the whole network will decrease.
The dependence of the Young's moduli or in-plane stiffnesses on bond lengths is plotted in Fig. 10(b) for the quasi-planar hypercoordinated monolayers (see Table 3). For comparison, the stiffnesses of the hexagonal monolayers of graphene, BC3, binary group IV, and elemental group-IV monolayers are included. By excepting the BeC monolayer, all hypercoordinated monolayers follow roughly the inverse dependence of the stiffness of group-IV monolayers if the range of bond lengths found for each compound is considered. The in-plane stiffness of 146 N m−1 presented for BeC seems not to be consistent with the much lower values, which can be derived from the given elastic constants, nor with the short chemical bonds presented in the publication.54 In any case, the established correlation suggests a much larger in-plane stiffness.
It is important to note the enormous sensitivity of in-plane stiffness on bond length. The stiffness decreases drastically by a factor of about ten for a change of the mean bond length by less than a factor of two. One of the main reasons for this drastic decay is the reduction of orbital overlap by the increasing size of atoms that leads to the loss of planarity in group-IV monolayers and the hypercoordinated compounds. The existence of longer interconnecting bonds between the motifs in the nonuniform 2D networks has an additional influence on the in-plane moduli. In many cases the weaker interconnects reduce the overall mechanical performance to some extent, however, not drastically for the linear in-plane stiffness.
Unfortunately, information on nonlinear mechanical properties such as fracture strength and ultimate strain of monolayers with hypercoordinated motifs is widely missing. This is a fundamental issue, since nonuniform networks with short and long bonds are prone to easier bond rupture. While the linear mechanical behavior of hypercoordinated compounds seems to follow broadly that of regular bonded monolayers, nonlinear properties, such as the ultimate strength, may respond sensitively on the nonuniformity. Since local bond rupture affects the strength of the whole network, the longest bonds with their weaker bond energy will control the overall stability.
Group IV monolayers
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond. This double bond has the shortest bond length and largest bond energy with the highest density of bonding electrons between the two nuclei in a hexagonal network. It is noteworthy that the honeycomb structure used by bees is the optimum way to divide a surface into equal areas with the smallest total perimeter. Interestingly, graphene is labeled as a zero-gap semiconductor (‘semimetal’), because its π valence and π* conduction bands contact at the Dirac points at the Fermi level.70,71 To open a band gap, the in-plane lattice symmetry must be broken. Mechanical deformation is an appealing means to manipulate the electronic structure by strain. However, the strain necessary for opening a sizable band gap in graphene is still controversial.71
C double bond. This double bond has the shortest bond length and largest bond energy with the highest density of bonding electrons between the two nuclei in a hexagonal network. It is noteworthy that the honeycomb structure used by bees is the optimum way to divide a surface into equal areas with the smallest total perimeter. Interestingly, graphene is labeled as a zero-gap semiconductor (‘semimetal’), because its π valence and π* conduction bands contact at the Dirac points at the Fermi level.70,71 To open a band gap, the in-plane lattice symmetry must be broken. Mechanical deformation is an appealing means to manipulate the electronic structure by strain. However, the strain necessary for opening a sizable band gap in graphene is still controversial.71
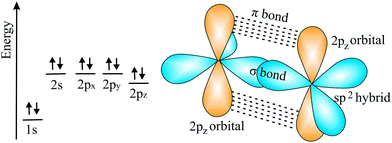 | ||
| Fig. 11 Scheme of electron configuration and the corresponding sp2 hybrids and π orbitals of the carbon double bond. | ||
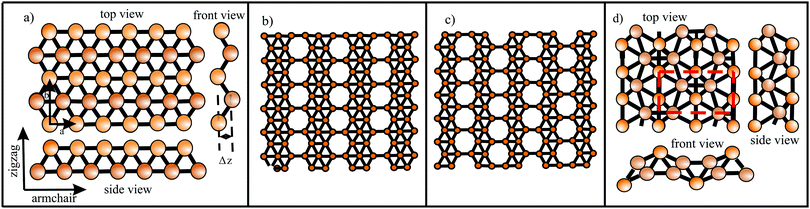
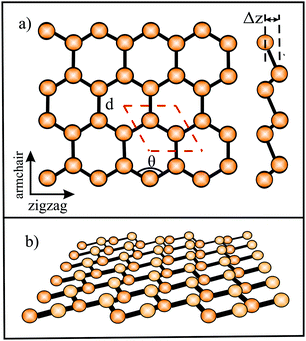
Since Si, Ge, Sn, and Pb belong to the same group as carbon, they have four valence electrons with the electron configuration (ns2np2). However, as known from chemical experience, these elements prefer sp3 hybridization with tetrahedrally bonded atoms. According to DFT calculations, only buckled monolayers are dynamically stable, because buckling allows in this case better interaction of pz–pz orbitals.72 The main reason for buckling is the increasing atom size, which destabilizes π-bonding and stabilizes σ-backbonds. Fig. 12(a) displays the top and side views and Fig. 12(b) a perspective view of a buckled network. For example, the standard van der Waals diameter increases substantially from dw = 0.34 nm to 0.420 nm from carbon to silicon.24 Due to the larger distance between Si atoms, interaction of the pz orbitals is diminished and their mixing with s orbitals creates partial sp3 character, which enhances overlap and thus stability. The smaller difference between 3s and 3p sublevels in comparison to graphene favors this mixing process. Note that in stable low-buckled silicene, σ–π orbital mixing is closer to sp2 than to sp3 hybridization with a small buckling effect of 0.041 nm.73
For the larger Ge atoms, π bonding is further weakened and the contribution of sp3 orbitals and thus buckling increases. This change in the bonding character is clearly visible in the bond angle, which decreases from 120° in graphene to 116.9° in silicene, 112.6° in germanene, and 110.4° in stanene, which is near the bond angle of sp3 hybridization of 109.5°.73 With the further increasing atom size of Sn and Pb, interaction between π orbitals is further reduced and leads to dominant sp3 hybridization in the mixed sp2–sp3 hybrids of plumbene.74 Larger buckling allows a better overlap between σ and π orbitals and stabilizes the network, whereas s–p mixing reduces with increasing atomic number, since in higher homologues s orbitals lower their energy with respect to p orbitals.
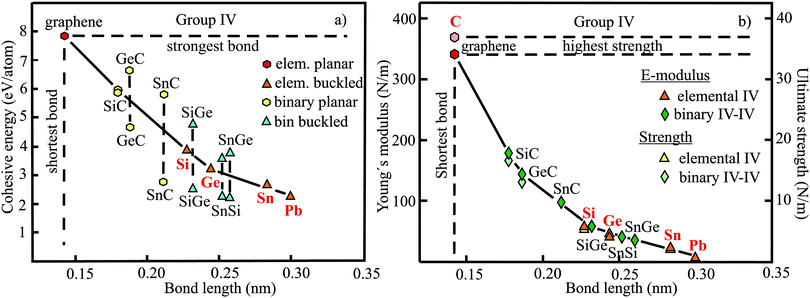
The relevant structural data of graphene,73,75–79 silicene,72,73,75,80–82 germanene,73,75,83–85 stanene,73,75,83,84,86,87 and plumbene74,88–90 are presented in Table 4. In Fig. 13(a) we characterize the bonding behavior of the elemental group IV monolayers by plotting the cohesive energy as a function of the bond length. Graphene is the champion, with the shortest bond and the largest cohesive energy (larger than diamond) and largest dissociation energy of a single C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. A comparison of the bond lengths of graphene (0.142 nm) and diamond (0.154 nm) underlines the high stability of planar sp2 hybridization. However, due to the much longer bonds of the elemental 2D networks of Si, Ge, Sn, and Pb, the cohesive energy decreases dramatically. Note that bonding power is now no longer completely confined to the plane. Remarkably, the bond length of mixed hybridization of silicene, at 0.228 nm, is much larger than that of graphene but still slightly smaller than the bond length of the 3D Si diamond structure (0.235 nm). Continuing down the group, the further increasing influence of sp3 hybrids causes the bond length of germanene to increase to 0.244 nm, agreeing with that of bulk germanium of 0.245 nm. The large increase of bond length from graphene to silicene causes a drastic reduction of the cohesive energy from −7.85 to −3.91 eV per atom.75 This effect slows down for the heavier elements, which show an asymptotic inverse dependence of cohesive energy with modest changes of binding energy at longer bond lengths, similar to the Young's modulus and strength (see Fig. 13(b)).
C bond. A comparison of the bond lengths of graphene (0.142 nm) and diamond (0.154 nm) underlines the high stability of planar sp2 hybridization. However, due to the much longer bonds of the elemental 2D networks of Si, Ge, Sn, and Pb, the cohesive energy decreases dramatically. Note that bonding power is now no longer completely confined to the plane. Remarkably, the bond length of mixed hybridization of silicene, at 0.228 nm, is much larger than that of graphene but still slightly smaller than the bond length of the 3D Si diamond structure (0.235 nm). Continuing down the group, the further increasing influence of sp3 hybrids causes the bond length of germanene to increase to 0.244 nm, agreeing with that of bulk germanium of 0.245 nm. The large increase of bond length from graphene to silicene causes a drastic reduction of the cohesive energy from −7.85 to −3.91 eV per atom.75 This effect slows down for the heavier elements, which show an asymptotic inverse dependence of cohesive energy with modest changes of binding energy at longer bond lengths, similar to the Young's modulus and strength (see Fig. 13(b)).
| Monolayer | Geometry space group | Cohesive energy, Ec (eV per atom) | Lattice constant a (nm) | Bond angle θ (deg.) | Bond length d (nm) | Buckling distance Δz (nm) | van der Waals diameter dw,24dw+Δz (nm) | Interlayer spacing ds (nm) |
|---|---|---|---|---|---|---|---|---|
| Graphene | Planar | −7.8575 | 0.24775 | 12073,75 | 0.14275 | 073 | 0.34,24 | 0.34277 |
| P6/mmm79 | −7.9778 | 0.24673 | 0.14273 | 0.33576 | ||||
| Silicene | Buckled | −4.5780 | 0.38775 | 116.272 | 0.22875 | 0.04675 | 0.42,24 0.466 | 0.24681 |
| P3m181 | −3.9175 | 0.38873 | 116.973 | 0.22773 | 0.04173 | 0.6082 | 0.34082 | |
| Germanene | Buckled | −3.2475 | 0.40675 | 112.673 | 0.24475 | 0.06975 | 0.422,24 0.491 | 0.25583 |
| P3m1 | −2.9385 | 0.40684 | 112.384 | 0.24484 | 0.06984 | |||
| Stanene | Buckled | −3.3187 | 0.46475 | 110.473 | 0.28475 | 0.09575 | 0.434,24 0.529 | 0.29483 |
| P3m186 | −2.7375 | 0.46784 | 111.384 | 0.28384 | 0.08584 | |||
| Plumbene | Buckled | −2.2888 | 0.49374,89 | 0.29989 | 0.09389 | 0.404,24 0.497 | ||
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m174 m174 |
0.49390 | 0.30290 | 0.10190 | |||||
| SiC | Planar | −5.97112 | 0.309112 | 120112 | 0.179112 | 0 | 0.38024 | 0.221116 |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2113 m2113 |
−6.94114 | 0.307115 | 0.177115 | 0.366117 | ||||
| GeC | Planar | −6.62115 | 0.323119 | 120115 | 0.187119 | 0 | 0.38124 | 0.369120 |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 m2 |
−4.65118 | 0.322115 | 0.186115 | |||||
| SnC | Planar | −5.82115 | 0.366122 | 0.211122 | 0.001122 | 0.38724 | ||
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2121 m2121 |
−2.76122 | 0.349121 | 120121 | 0.202121 | 0 | |||
| SiGe | Buckled | −4.81115 | 0.395123 | 114.5115 | 0.232123 | 0.058123 | 0.421,24 0.479 | 0.249123 |
| P3m1 | −2.56123 | 0.396124 | 0.231115 | 0.055115 | ||||
| SnSi | Buckled | −3.61125 | 0.421115 | 113.3115 | 0.252115 | 0.067115 | 0.427,24 0.493 | |
| P3m1126 | −2.28122 | 0.429122 | 0.258122 | 0.073122 | ||||
| SnGe | Buckled | −3.79125 | 0.427115 | 112.3115 | 0.257115 | 0.073115 | 0.428,24 0.501 | |
| P3m1126 | −2.23122 | 0.435122 | 0.263122 | 0.080122 |
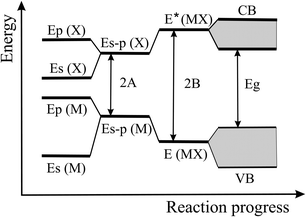
The energy level scheme presented in Fig. 14 illustrates the transition of atomic s and p orbitals to atomic hybrids and bonding orbitals that are responsible for the formation of bands and eventually a band gap in an extended covalently bonded 2D network. Of interest is the bonding–antibonding splitting 2B that results from the energetic stabilization by the bonding orbitals and determines the binding energy.11,20 In nonpolar materials such as elemental monolayers, splitting B is identical with the strength of orbital overlap V, which varies strongly with the bond length as V ∼ 1/d2. Consequently, the energy of covalent bonding declines strongly with the inversely related bond length. In Fig. 13(a) this widely unknown dependence is shown for the cohesive energy of the elemental and binary group IV monolayers.
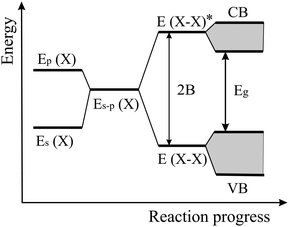 | ||
| Fig. 14 Energy levels of hybridized s and p orbitals, reacting to molecular bonding and antibonding levels with level broadening and band formation of a monolayer. | ||
The mechanical properties of graphene,38,91–94 silicene,95,96 germanene,85,96 stanene,80,96 and plumbene97 are displayed in Table 5. The plot of the Young's moduli and ultimate strengths as a function of bond length offers insight into the linear and nonlinear mechanical behavior of the elemental group IV monolayers (see Fig. 13(b)). This plot reveals a drastic change of mechanical performance from graphene to silicene. The enormous loss of bonding energy from C to Si causes a large decrease of both intrinsic stiffness and ultimate strength, which controls failure. The heavier homologues of Si with their minor increase of atom size experience a much smaller weakening of stiffness and strength, mostly following Griffith's rule. While graphene is the stiffest 2D material, surviving the largest critical stress, these properties weaken enormously down the group, for instance by a factor of about five for buckled silicene. Since mechanical performance declines further from silicene to plumbene, mechanical stability becomes a crucial issue for the heaviest compounds. For example, low stiffness values give rise to rippling and wrinkling of the monolayer structure, with detrimental influence on the electronic properties, and permits easy incorporation of impurities.
| Monolayer | Structure | Young's modulus Eac, Ezz (N m−1) | Poisson's ratio νac, νzz | Ultimate strength σac, σzz (N m−1) | Ultimate strain εac, εzz | Method |
|---|---|---|---|---|---|---|
| Graphene | Planar | 33391 | 0.14-0.2191 | 40, 3792 | 0.3193 | Ab initio |
| 34038 | 0.16538 | 4238 | 0.2538 | Experiment | ||
| Silicene | Low buckled | 62, 5996 | 0.29, 0.3396 | 7.2, 6.096 | 0.18, 0.1996 | DFT-PBE |
| 63, 6095 | 7.1, 5.795 | 0.18, 0.08995 | ||||
| Germanene | Low buckled | 44, 4396 | 0.29, 0.3596 | 4.7, 4.196 | 0.20, 0.2196 | DFT-PBE |
| 42, 3685 | 5.7, 6.085 | 0.16, 0.1885 | ||||
| Stanene | Low buckled | 25, 2496 | 0.36, 0.4296 | 2.6, 2.296 | 0.17, 0.1896 | DFT-PBE |
| 2280 | 0.4080 | 2.6, 2.380 | 0.15, 0.2080 | DFT-GGA | ||
| Plumbene | Buckled | 897 | Ab initio | |||
| SiC | Planar | 160114 | 0.314114 | 16.5, 16.7114 | 0.20, 0.25114 | DFTPBE |
| 173, 180127 | 0.30118 | 17.6, 20.5127 | 0.17, 023127 | |||
| GeC | Planar | 144119 | 0.28119 | 12.7, 12.8119 | 0.18, 019119 | DFT-PBE |
| 140118 | 0.31118 | 13.9, 10.5118 | ||||
| SnC | Planar | 98115 | 0.41115 | DFT-LDA | ||
| SiGe | Buckled | 57,115 59128 | 0.32,115 0.31128 | 1–1.5123 | 0.16123 | PBE, LDA |
| SnSi | Buckled | 40,115 42128 | 0.37,115 0.35128 | DFT-LDA | ||
| SnGe | Buckled | 35,115 33128 | 0.38,115 0.36128 | DFT-LDA |
Graphene is the building block for forming bilayers and few-layer assemblies with new properties up to about ten layers, where the electronic structure approaches the 3D limit of graphite.98 The interlayer interaction energy (sometimes called exfoliation energy) and the stacking order are crucial quantities controlling the stability and the chemical and physical properties of multilayers. The reported interlayer binding energies vary in a large range between −22 and −85 meV per atom for graphite99 and between −18 and −70 meV per atom for AB-stacked bilayers of graphene.100 This large range of values is due to the approximations used in the theoretical treatment of soft layered materials with weak interlayer and strong in-plane forces. Several recent publications have confirmed the early results of a low interlayer interaction energy of about −25 meV per atom101 and interlayer spacing of 0.335 nm76 for graphene.
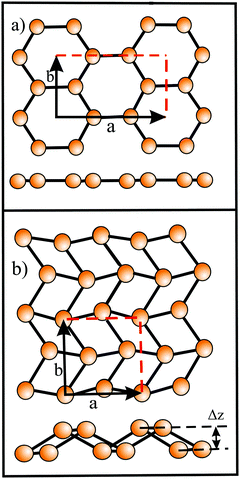
In silicene partial sp3-type bonding intensifies the interlayer interaction between bilayers and multilayers and thus reduces the interlayer separation. The calculated interlayer spacings of bilayers with AA and AB stacking are 0.246 nm and 0.253 nm, respectively (see Fig. 15).81 For free-standing few-layer sheets, interlayer spacings of 0.34 nm were measured by HRTM and SAED in layered silicene sheets.82 Calculations of interlayer separations point to configurations where the spacing of multilayers decreases, because the still existing weak in-plane π bonds are replaced by covalent-type interlayer bonds to further minimize the total energy.102 Similarly, it could be shown theoretically that under external pressure the interlayer spacing of buckled silicene, germanene, and stanene bilayers approaches the intralayer bond length with a flat honeycomb network.83 Interestingly, the dynamically stable and chemically inert flat phases of bilayer germanene and stanene are topologically nontrivial.83
In germanene an even larger contribution of sp3 orbitals to bonding intensifies the interlayer interaction in bi- and multi-layers. Interestingly, under structural optimization the buckled phase converts into the most stable flat bilayer arrangement, with AA stacking, a larger lattice constant, and the same in-plane bond length and interlayer spacing (0.254 nm and 0.255 nm, respectively83,103). This small interlayer spacing is consistent with the large interlayer interaction energy of −300 meV per atom.103 In the flat configuration of bilayer germanene the topological trivial state can be tuned into a 2D topological insulator (TI) by external tensile strain of 6% (Si: >8%).83 Such a strong interlayer interaction with sp3-like inter-layer bonding has also been reported for plumbene.104
In general, the synthesis of 2D materials with the desired perfect structure, domain size, scalability, growth rate, and versatile substrate material is the main challenge in fabricating 2D materials for future applications. The controlled growth of high-quality monolayers and few-layer assemblies of graphene is an active field. An up-to-date overview describes the progress made in the synthesis of graphene and graphene-based materials and specifically covers the practical aspects of this topic.105 A recent report reveals the enormous progress made in growing large-area (>cm2) adlayer-free homogeneous graphene monolayers by using as-received Cu substrates and common chemical vapor deposition (CVD) methods to achieve controlled layer-by-layer growth.106
The preparation of monolayers inevitably leads to defects. Various types of defects have been extensively studied for graphene and are generally categorized as corrugations such as ripples, topological effects such as dislocations or grain boundaries, vacancies, adatoms, and sp3-defects.98 An introduction of disorder such as dislocation alters the bond length and causes re-hybridization of σ and π orbitals and thus may change electronic properties such as the band structure. Point defects such as vacancies function as scattering center for electron waves and reduce the conductivity. While a single vacancy has a negligible effect on the elastic modulus, it may decrease substantially with increasing density of vacancies. The ultimate strength is extremely sensitive to vacancies especially if their separation is small. In polycrystalline graphene the decrease of the grain size from ∼10 nm to ∼2.5 nm leads to a reduction of both Young's modulus and strength, whereas a high density of sp3-defects seems to cause only a minor degradation of the elastic performance.98
The interest in silicene and the heavier elemental group IV monolayers termed Xenes (silicene, germanene, stanene, and plumbene) originates from unique solid-state properties. With increasing sp3 contribution in mixed sp2–sp3 hybridization of heavier Xenes a topologically nontrivial electronic structure develops, originating from larger spin–orbit coupling (SOC). This results in the quantum spin Hall (QSH) effect that is a 2D TI state.83,107 The QSH systems have gapless edge or surface states on the boundary that are topologically protected and immune to geometric perturbations, whereas the bulk is insulating. Since no layered bulk materials exist in nature for silicene (‘silicite’) and its heavier homologues, it is necessary to synthesize these compounds either by exfoliation using a suitable synthetic compound or by CVD or MBE.107 The synthesis of nanosheets of few-layer silicene has been achieved by liquid oxidation and exfoliation of CaSi2.82 A problem originating from mixed sp2–sp3 hybridization states is their reactivity and low environmental stability. Consequently, in practical applications silicene and homologues may require passivation by functionalization or encapsulation.
The synthesis of germanene is possible either chemically (CVD) or by epitaxial growth (MBE) on suitable supporting substrates. As for silicene, the existence of an isolated sheet of germanene has not yet been confirmed. A significant step forward in the direction of 2D topological materials with nontrivial features, including quantum spin/anomalous Hall insulators, has been made recently by the growth of ultraflat stanene on a Cu(111) surface by MBE.108 Remarkably, in this system strong substrate interaction stabilizes the zero-buckling geometry of stanene by stretching the bond. Stanene is a promising material owing to its excellent quantum effects, superconductivity, and thermoelectric properties.86
First compelling evidence for epitaxial growth of a monolayer of planar plumbene by segregation on a Pd1−xPbx(111) surface has been verified by atomic-scale STM images.109 A flat honeycomb plumbene lattice has also been detected by STM on a Fe monolayer deposited on Ir(111), as rationalized by DFT calculations.110 The final goal behind the extensive theoretical and experimental activities is the development of dissipationless transport devices that reduce power consumption and heat production. An up-to-date overview describes the status of synthesis of germanene, stanene, and plumbene.111
Without an element of the second period of the periodic table, the three mixed compounds SiGe, SnSi, and SnGe considered here possess buckled phases. Owing to the increased atom size, the s, px, and py orbitals combine to a variable extent with the pz orbital to form mixed sp2–sp3 orbitals. Three of these orbitals form strong σ bonds with nearest neighbors and the fourth, upward directed orbital can form a weaker bond with neighbors or with an adjacent orbital of another layer. The three compounds exhibit weak polarity, since the electronegativity changes only slightly between Si, Ge, and Sn. According to theory the free-standing monolayers of all three sheets are thermodynamically and dynamically stable.
Table 4 provides the cohesive energies and structural data of the planar group IV carbides SiC,112–117 GeC,115,118–120 and SnC115,121,122 and the buckled monolayers SiGe,115,123,124,128 SnSi,115,122,125,126 and SnGe.115,122,125,126 The dependence of the cohesive energy on bond length of these binary compounds is displayed in Fig. 13(a). One reason for the strong decay of the cohesive energy of the carbides compared with graphene is the increasing size of Si, Ge, and Sn, which gradually reduces efficient π–π bonding. The large scatter of the published cohesive energies, which deviate by more than a factor of two, predicts different inverse behaviors. Bonding energies of binaries consistent with those of elemental monolayers, as observed for SiC, would point to cohesive energies that are roughly the mean of the extreme values presented in Fig. 13(a), resulting in the mean values −5.7 eV per atom for GeC and −4.6 eV per atom for SnC. A similar situation is encountered for the cohesive energies of buckled SiGe, SnSi, and SnGe monolayers. Once again, much larger and smaller cohesive energies were reported than estimated from the cohesion of the two constituents. The assumption of similar bonding behavior of elemental and binary group IV monolayers, despite ionic contributions in the binary compounds, is strongly supported by the similarities of their mechanical properties, as discussed in more detail below.
To explain this finding, we apply the tight-binding model to describe the formation of bonding orbitals in 2D heteronuclear group IV compounds. In polar networks with elements of different electronegativity, the hybrids of the atomic orbitals of atom M and atom X, with an energy difference 2A, hybridize to form the bonding state E (MX) and the antibonding state E* (MX) (see Fig. 16). As mentioned before, the bonding–antibonding splitting 2B delivers the binding energy resulting from the stabilization of the bonding orbitals and the destabilization of the antibonding orbitals. Now, the energy of orbital overlap V depends also on the hybrid polar energy A according to V = (B2 − A2)1/2.11,20 If the polar energy A increases, the covalent energy V decreases, or in other words, with increasing difference of the electronegativities the contribution of covalent orbital overlap diminishes. Consequently, in the polar binary group IV compounds bonding depends on both covalency and ionicity. However, the data points to comparable cohesive energies in elemental and binary monolayers and thus to modest ionic contribution.
Table 5 displays the corresponding mechanical properties of the carbides SiC,114,118,127 GeC,118,119 and SnC115 and the binary monolayers SiGe,115,118,128 SnSi,115,128 and SnGe.115,128 The plot of Young's moduli and ultimate strengths of the planar carbides and buckled compounds versus bond length in Fig. 13(b) shows a joint inverse dependence of elementary and binary compounds and reasonable agreement of the few available critical strength values with Griffith's rule. The inverse decay coinciding for homo- and heteronuclear monolayers owing to related bond lengths supports the assumption of quite similar covalent bonding energies in both cases. The enormous deterioration of mechanical performance from the planar carbides to the buckled elemental and binary monolayers is related to the rising loss of in-plane bonding power.
While the effect of stacking order is relatively small for bilayers of elemental monolayers, the band gap of heteronuclear compounds may change considerably with interlayer separation. For fundamental stacking sequences of SiC, contradictory results can be found in the literature. The strongest interaction of bilayers was found for AA′ stacking, where Si atoms are located over C atoms and vice versa. In this configuration, minimization of the forces reduced the interlayer separation to 0.232 nm, and the planar layers started to buckle.129 Therefore, the authors concluded that no van der Waals bonded layered structure of SiC can exist because it is unstable against interlayer linking similar as in silicene multilayers.129 It seems that the large charge transfer from Si to C and the preference of Si for sp3 hybridization makes bilayers reactive. Calculations concentrating on charge transfer properties and stability predict larger interlayer spacings and interaction energies of 0.324 nm and −156 meV per atom for AB stacking and 0.338 nm and −154 meV per atom for AA stacking (see Fig. 15).116 For AA′ stacking the bond length increases to 0.184 nm and the interlayer separation reduces to 0.221 nm, in agreement with the results described above.116
The increasing focus of attention on silagraphene (SiC) originates from a wide spectrum of optoelectronic properties and highly anisotropic transport properties. Therefore, SiC layers are of particular interest for commercial applications as light-emitting diodes (LEDs) and in photovoltaic devices. Owing to its unusual band structure it is suitable for strain engineering, for instance in highly sensitive sensors.130 While the preparation of free-standing honeycomb SiC monolayers has not been confirmed, few-layer assemblies have been prepared by nano-cleavage exfoliation of nanoflakes in polar solutions and characterized by TEM, XRD, and XPS.130 The authors concluded from the measured step heights, which varied between 0.5 and 1.5 nm for the exfoliated flakes, that some monolayer sheets had been realized.
The optical properties resulting from the capability of direct-to-indirect band gap transitions under in-plane strain make the wide-band-gap material GeC suitable for blue and ultraviolet LEDs, anti-reflection and protection coatings, energy engineering, and applications in photovoltaics.120 Unfortunately, experimental results on the preparation of semiconducting GeC and SnC monolayers and their few-layer assemblies seem not yet to be available.
Group III–V monolayers
The group of III–V monolayers MX (M = B, Al, Ga, In, Tl; X = N, P, As, Sb, Bi) with 25 compounds contains many well-studied monolayers, and some of them have already found applications in electronics and optoelectronics. A recent comprehensive publication presents the structural data and linear elastic properties of these compounds and discusses correlations between related compounds (see Table 6).131 This data agrees well with a previous compilation, where only the Bi and Tl compounds are missing.132 The results are also consistent with former studies, for example on the Ga-compounds GaN, GaP, GaAs, and GaSb133 and the As-compounds BAs, GaAs, and InAs.134| Mono layer | Cohesive energy, Ec (eV per atom) | Lattice constant a (nm) | Bond length d (nm) | Buckling distance Δz (nm) | Bond angle θ (°) | van der Waals diameter dw,24dw+Δz (nm) | Interlayer spacing ds (nm) |
|---|---|---|---|---|---|---|---|
| h-BN | −6.67,131 −7.10136 | 0.251131 | 0.145131 | 0131 | 120131 | 0.34724 | 0.333137,138 |
| h-BP | −4.55,131 −4.99139 | 0.320131 | 0.185131 | 0.0005131 | ∼120131 | 0.37224 | 0.339140 |
| h-BAs | −3.86,131 −4.33136 | 0.339131 | 0.196131 | 0.0012131 | 119.99131 | 0.377,24 0.378 | 0.357141 |
| h-BSb | −3.26,131 −3.73136 | 0.374131 | 0.216131 | 0.0033131 | 119.98131 | 0.398,24 0.401 | |
| h-BBi | −2.81,131 −3.25136 | 0.388131 | 0.229131 | 0.048131 | 115.72131 | 0.399,24 0.447 | |
| h-AlN | −5.08,131 −5.36143 | 0.313131 | 0.181131 | 0131 | 120131 | 0.33924 | 0.213143 |
| h-AlP | −3.36131 | 0.393131 | 0.228131 | 0.018131 | 119.41131 | 0.364,24 0.382 | |
| h-AlAs | −2.96131 | 0.406131 | 0.239131 | 0.046131 | 116.26131 | 0.369,24 0.415 | |
| h-AlSb | −2.51131 | 0.440131 | 0.262131 | 0.062131 | 114.52131 | 0.390,24 0.452 | |
| h-AlBi | −2.28,131 −2.56142 | 0.451131 | 0.272131 | 0.077131 | 112.28131 | 0.391,24 0.468 | |
| h-GaN | −3.80,131 −4.15144 | 0.321131 | 0.185131 | 0131 | 120131 | 0.34224 | 0.247145 |
| h-GaP | −2.77131 | 0.390131 | 0.228131 | 0.038131 | 117.26131 | 0.367,24 0.405 | |
| h-GaAs | −2.46,131 −3.71134 | 0.405131 | 0.241131 | 0.058131 | 114.45131 | 0.372,24 0.430 | |
| h-GaSb | −2.16131 | 0.438131 | 0.263131 | 0.071131 | 112.97131 | 0.393,24 0.464 | |
| h-GaBi | −2.01,131 −2.31142 | 0.452131 | 0.273131 | 0.082131 | 111.94131 | 0.394,24 0.476 | |
| h-InN | −3.03,131 −3.60146 | 0.359131 | 0.207131 | 0131 | 120131 | 0.34824 | 0.240147 |
| h-InP | −2.47131 | 0.422131 | 0.249131 | 0.051131 | 115.97131 | 0.373,24 0.424 | |
| h-InAs | −2.25,131 −3.43134 | 0.436131 | 0.260131 | 0.066131 | 113.89131 | 0.378,24 0.444 | |
| h-InSb | −2.01131 | 0.468131 | 0.281131 | 0.076131 | 112.97131 | 0.399,24 0.475 | |
| h-InBi | −1.89,131 −2.15142 | 0.481131 | 0.291131 | 0.086131 | 111.65131 | 0.400,24 0.486 | |
| h-TlN | −2.20,131 −2.40148 | 0.373131 | 0.215131 | 0.0061131 | 119.92131 | 0.351,24 0.357 | 0.251148 |
| h-TlP | −1.99,131 −2.25148 | 0.432131 | 0.256131 | 0.059131 | 114.82131 | 0.376,24 0.425 | 0.280148 |
| h-TlAs | −1.86,131 −2.14148 | 0.448131 | 0.268131 | 0.069131 | 113.53131 | 0.381,24 0.450 | 0.287148 |
| h-TlSb | −1.71,131 −2.02148 | 0.479131 | 0.287131 | 0.078131 | 112.88131 | 0.402,24 0.480 | 0.303148 |
| h-TlBi | −1.66131 | 0.493131 | 0.297131 | 0.085131 | 112.11131 | 0.403,24 0.488 |
From the planar binary monolayers containing either a boron or nitrogen atom, boron nitride, also called boronitrene, is the best-studied monolayer of the III–V compounds.135 Carbon and BN are isoelectronic because boron and nitrogen are left and right neighbors of carbon in the periodic table. The electronic structure of group III atoms is (ns2np1), with three valence electrons, and that of group V atoms is (ns2np3), with five valence electrons. In the planar hexagonal lattice, the sp2 orbitals form a backbone of three σ bonds in a structure like graphene. This leaves an unoccupied pz orbital in the group III atom and a lone pair of electrons in the group V atom. Owing to the difference in electronegativity between boron and nitrogen, π electrons tend to localize around the nitrogen atoms. The mixed ionic–covalent bonding of planar group III nitrides is characterized by a significant difference of the electronegativities: 3.0 (N), 2.0 (B), 1.5 (Al), 1.8 (Ga), and 1.7 (In). In the large number of III–V monolayers without a second-period element, the buckled configuration is the most stable phase, maintaining the hexagonal symmetry, as discussed for silicene and its heavier homologues.
The main reason for the astonishing similarity of the bonding behavior of III–V monolayers with those of group IV compounds is the identical number of valence electrons. This becomes obvious by the striking relationship between group IV carbides and group III nitrides. Within the errors involved in such calculations, both groups reveal quite a similar dependence of the cohesive energy on bond length. Owing to the small size of carbon and nitrogen atoms, these compounds realize strong planar sp2 hybrids with minor deviations from planarity only for the heaviest compound TlN, as can be seen in Table 6. The monolayer of TlN has a bond angle of 119.9° and a tiny buckling effect of Δz = 0.006 nm. Furthermore, most boron compounds are almost planar, with corrugations of Δz = 0.0005, 0.0012, 0.0033, and 0.048 nm for h-BP, h-BAs, h-BSb, and h-BBi, respectively.131 Consequently, these compounds have shorter bonds and larger cohesive energies than the heavier buckled compounds.
Table 6 contains the cohesive energies and structural data of the groups of related monolayers BX,131,136–142 AlX,131,142,143 GaX,131,134,142,144,145 InX,131,134,142,146,147 and TlX131,148 with X = N, P, As, Sb, and Bi. As revealed in Fig. 17(a), which displays the cohesive energy as a function of bond length, the planar and buckled group III–V monolayers can be divided into five distinct groups of chemically related compounds, each containing one group III element. The group with the strongest bonding is that with the boron compounds BN, BP, BAs, BSb, and BBi, with almost planar monolayers. While the cohesion-bond length plot of the boron group shows the largest decay of bond energy and a pronounced inverse behavior, the dependence changes to a nearly linear modest decay of the thallium group with lowest cohesive energies. For example, the cohesive energy of the planar boron group changes from −6.7 to −2.8 eV per atom, whereas in the buckled thallium group the binding energy varies from −2.2 to −1.7 eV per atom. The pronounced invers decay follows the prediction of the tight-binding model. This has enormous consequences for mechanical stability and performance.
The mechanical properties of the BX,115,118,131,149–152 AlX,115,127,131,143,153,154 GaX,115,127,131,149,154,155 InX,127,131,154,156,157 and TlX131,143,158,159 groups, with X = N, P, As, Sb, and Bi, are compiled in Table 7. In a plot of the Young's modulus and ultimate strength versus bond length, especially the Young's moduli of the BX monolayers, but also the stiffness of other related groups, display a characteristic inverse dependence as a function of bond length (see Fig. 17(b)). Notably, the Young's modulus of graphene can be considered as the upper limit of stiffness. The same is true for the few available strength values, which roughly follow Griffith's rule. The relations revealed by the plot allow a first estimate of largely unknown critical strengths. It is important to note that the characteristic dependence observed for related groups demonstrates a systematic decay of the Young's moduli and ultimate strengths with increasing row number of the incorporated group III element. This is in accordance with the behavior of the cohesive energies discussed above, however, with a huge decrease of stiffness by a factor of 34 from 276 N m−1 for h-BN to 8.1 N m−1 for TlBi. In comparison, the total decrease of the cohesive energy from h-BN to TlBi is only a factor of four. This demonstrates the ultra-sensitivity of mechanical behavior on the cohesive binding energy. Note the enormous alteration of the mechanical properties compared to the modest change of binding energy by a factor of two. The increasing Poisson's ratios indicate less stiffness and more plasticity with increasing row number (see Table 7).
| Monolayer | Structure space group | Young's modulus E (N m−1) | Poisson's ratio ν | Ultimate strength σac, σzz (N m−1) | Ultimate strain εac, εzz |
|---|---|---|---|---|---|
| h-BN |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2149 m2149 |
276,131 270150 | 0.23131 | 23.6, 26.3151 | 0.18, 0.26151 |
| 276,118 279151 | 0.22118 | 26, 28118 | 0.18, 0.29152 | ||
| h-BP | 139,131 135115 | 0.28,131 0.28115 | |||
| h-BAs | 116,131 119115 | 0.28,131 0.29115 | |||
| h-BSb | 84,131 91115 | 0.33,131 0.34115 | |||
| h-BBi | 61131 | 0.30131 | |||
| h-AlN | P63/mmc143 | 113,131 136153 | 0.46,131 | 16.2, 15.9153 | 0.22, 0.27153 |
| 138127 | 037153 | 13, 15127 | 0.18, 0.23127 | ||
| h-AlP | 64,131 58154 | 0.31131 | |||
| h-AlAs | 47,131 46154 | 0.34,131 036154 | |||
| h-AlSb | 33,131 35115 | 0.32,131 0.37115 | |||
| h-AlBi | 27131 | 0.37131 | |||
| h-GaN |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2149 m2149 |
106,131 110115 | 0.45,131 | 11.9, 12.1155 | 0.18, 0.22155 |
| 83, 85127 | 0.48115 | 10,11127 | 0.17, 0.19127 | ||
| h-GaP | 59,131 55154 | 0.31,131 0.34154 | |||
| h-GaAs | 44,131 44154 | 0.33,131 0.34154 | |||
| h-GaSb | 28,131 32154 | 0.39,131 0.35154 | |||
| h-InN | P-6m2156 | 62,131 62157 | 0.58,131 0.59157 | 8.0157 | 0.18, 0.21157 |
| 88, 90127 | 8.4, 9.4127 | 0.16, 0.20127 | |||
| h-InP | 40,131 37154 | 0.38,131 0.42154 | |||
| h-InAs | 31,131 30154 | 0.39,131 0.42154 | |||
| h-InSb | 25,131 22154 | 0.32,131 0.44154 | |||
| h-InBi | 20131 | 0.41131 | |||
| h-TlN | P6/mmm158 | 35159 | 0.69159 | 5.8, 5.7159 | 0.17, 0.21159 |
| −55131 unstable | 0.14131 | 3.8143 | |||
| h-TlP | 14131 | 0.79131 | |||
| h-TlAs | 17131 | 0.58131 | |||
| h-TLSb | −52131 unstable | 0.18131 | |||
| h-TlBi | 8.1131 | 0.73131 |
The main reason for the striking similarity of the interlayer separation of multilayers of boronitrene and graphene was suggested to be that van der Waals forces, rather than electrostatic interaction, are the dominant interaction forces at the interlayer equilibrium distance, while ionic interactions preferentially control the stacking order and interlayer sliding corrugation.160 The experimentally observed AA′ stacking mode (e.g., Al over N and N over Al), is the most stable stacking order not only for BN, with bilayer interaction energies between −26.0 and −38.1 meV per atom,138,160 but also with interlayer interaction energies of −125 meV per atom143 and −292 meV per atom161 for bilayers of AlN, and −142 meV per atom for GaN.144 The low interlayer separations, which vary in the range of 0.21–0.25 nm for AlN, GaN, InN, and TlN, indicate effective electrostatic anion–cation interaction between the layers as the major contribution to strong interlayer interaction (see Table 6). For bilayer honeycomb Tl compounds a p–p band inversion type QSH effect was predicted that is independent of SOP.148
Planar h-BN, with its strong bonding and large band gap, seems to be the best insulator and is particularly attractive as the ultimately thin insulator, barrier, or encapsulant. It is chemically inert and resistant to oxidation up to elevated temperatures and to corrosion. Owing to its high thermal conductivity, it is a useful material for electronic devices and will find use as an ultraviolet (UV) light emitter in optoelectronics. It is useful for far-ultraviolet (FUV) device applications and is of interest as a transparent and flexible material in electronics.135,137,151 Current electronic and photonic device concepts still rely primarily on h-BN exfoliated from small bulk crystallites. In an effort to achieve reproducible and tunable growth of mono- and few-layer systems, different approaches have been investigated, such as CVD on Cu162 or high-temperature plasma-assisted MBE on highly oriented pyrolytic graphite (HOPG) substrates.163 In a recent breakthrough, epitaxial growth of 100 cm2 single crystals of h-BN was accomplished on copper, demonstrating unidirectional alignment and seamless stitching on an annealed industrial copper foil.164 In the meantime, single-crystal h-BN, without undesirable grain boundaries, has been grown on a single-crystal Cu(111) film across a two-inch c-plane sapphire wafer and successfully detached and transferred to a wafer.165
Monolayers of h-AlN show a distinct single absorption peak at ∼6 eV, and therefore they are transparent in the visible region and have promising applications in the UV spectral range. A theoretical analysis revealed that the energetically favored hexagonal phase of up to about 10 monolayers has an indirect band gap.166 Similarly to the onset of interband absorption, the band gaps vary from 2.9 eV for monolayers to ∼3.5 eV for few-layer assemblies, with a transition from an indirect gap to a direct gap of the bulk.166,167 Layered h-AlN bulk assemblies do not exist in nature and single layers of h-AlN are difficult to isolate owing to the strong interlayer interaction. Since the absorption intensity increases with the number of layers, few-layer assemblies are of great interest. Synthesis of the hexagonal form of AlN has been achieved by plasma-assisted MBE on Ag(111) substrates from sub-monolayer to 12 layers.168 A review covering the applications of single-layer and few-layer sheets on different substrates is available.169
The indirect band gap of monolayer h-GaN turns into a direct gap in few-layer h-GaN.170 Furthermore, this wide-band-gap material is a candidate for the fabrication of energy-efficient deep-UV LEDs and it is suitable for biomedical applications and photovoltaics.155 The fundamental band gap of vertical structures varies with the stacking sequence and the number of sheets in the stack.171 Chemical tailoring, on the other hand, shifts the optical activity to the UV region und simultaneously eliminates its instability and generates a direct band gap.172 It is necessary to synthesize monolayers and few-layer assemblies on substrates since layered bulk h-GaN does not exist in nature. The growth of h-GaN sheets on Si(100) substrates and – preferably – on Si(111) substrates with a better crystalline structure, has been achieved by high-temperature pulsed laser deposition (PLD) with intermittent control of the crystalline structure by TEM and SEM.173
Despite many desirable properties of InN the synthesis of mono- or few-layers is still in its infancy. It seems that the formation of 3D structures with strong covalent bonding impedes layer-by layer growth of 2D structures. Based on the narrow band gap, small effective mass, and high electron mobility of InN compared to the lighter group-III nitrides, interest concentrates on potential applications as a field effect transistor, in lasers, solar cells, photodetectors, and in thermoelectric devices.146 The deposition conditions and structural properties of InN films have been studied by the growth of self-standing films using low-temperature electron cyclotron resonance plama-enhanced metal organic CVD (ECR-MOCVD).174
Group V monolayers
| Mono layer | Phase | Cohesive energy, Ec (eV per atom) | Lattice constants a, b (nm) | Bond angles θ1, θ2, θ3 (deg.), θ (deg.) | Bond lengths d1, d2 (nm) | Corrugation effect Δz (nm) | van der Waals diameter dw,24dw+Δz (nm) | Interlayer spacing ds (nm) |
|---|---|---|---|---|---|---|---|---|
| Phosphorene | sw | −3.59,180 −2.57176 | 0.457, 0.333175 | 96.2, 103.8176 | 0.222, 0.226175 | 0.251182 | 0.360,24 0.611 | 0.530179 |
| hb | −3.55,180 −2.32176 | 0.327181 | 93.1176 | 0.226181 | 0.125181 | 0.360,24 0.485 | 0.446183 | |
| Arsenene | sw | −3.13,184 −1.90176 | 0.472, 0.367184 | 94.7, 100.3176 | 0.251, 0.248184 | 0.239184 | 0.370,24 0.609 | 0.554185 |
| hb | −3.13,184 −2.29176 | 0.360184 | 91.9176 | 0.251184 | 0.140184 | 0.370,24 0.511 | 0.465185 | |
| Antimonene | aw | −2.61,186 −1.77176 | 0.474, 0.428188 | 93.8, 97.3176 | 0.291, 0.284188 | 0.282175 | 0.412,24 0.694 | 0.599189 |
| hb | −2.62,187 −1.96176 | 0.408181 | 89.6176 | 0.288181 | 0.166181 | 0.412,24 0.578 | 0.379189 | |
| Bismuthene | aw | −2.42,190 −1.38176 | 0.494, 0.455191 | 92.7, 96.1176 | 0.311, 0.310181 | 0.272175 | 0.414,24 0.686 | |
| hb | −2.41,190 −1.44176 | 0.438191 | 87.8176 | 0.307181 | 0.174181 | 0.414,24 0.588 | ||
| PN | aw | −4.41,192 −3.78176 | 0.416, 0.270194 | 103.2, 97.7, 123.7176 | 0.172, 0.182194 | 0.190194 | 0.335,24 0.525 | 0.636192 |
| hb | −4.09,192 −3.45176 | 0.273194 | 98.8176 | 0.179194 | 0.086194 | 0.335,24 0.421 | 0.576192 | |
| AsN | aw | −3.21176 | 0.418, 0.296194 | 102.3, 95.5, 119.7176 | 0.190, 0.195194 | 0.213194 | 0.340,24 0.553 | |
| hb | −3.38176 | 0.297194 | 98.3176 | 0.196194 | 0.096194 | 0.340,24 0.436 | ||
| SbN | aw | −3.90,195 −3.04176 | 0.419, 0.330194 | 103.5, 91.2, 117.3176 | 0.210, 0.211194 | 0.242194 | 0.361,24 0.503 | 0.590195 |
| hb | −3.59,195 −2.76176 | 0.327194 | 99.5176 | 0.214194 | 0.101194 | 0.361,24 0.462 | 0.332196 | |
| BiN | aw | −2.71176 | 0.362, 0.347197 | 100.5, 86.8, 108.7176 | 0.218, 0.228197 | 0.261197 | 0.362,24 0.623 | |
| hb | −2.38176 | 0.345198 | 100.3176 | 0.225198 | 0.105198 | 0.362,240.467 | ||
| AsP | aw | −3.15,186 −2.32176 | 0.469, 0.350194 | 95.4, 99.6, 103.8176 | 0.238, 0.239194 | 0.235194 | 0.365,24 0.604 | |
| hb | −3.18,187 −2.34176 | 0.346194 | 92.0176 | 0.239194 | 0.132194 | 0.365,24 0.497 | ||
| SbP | aw | −2.97,186 −2.14176 | 0.443, 0.391194 | 96.9, 88.3, 105176 | 0.262, 0.256194 | 0.285194 | 0.386,24 0.671 | 0.334196 |
| hb | −2.96,187 −2.13176 | 0.373194 | 91.6176 | 0.259194 | 0.141194 | 0.386,24 0.527 | ||
| AsSb | aw | −2.77,186 −2,05176 | 0.473, 0.404194 | 95.6, 90.0, 103.9176 | 0.273, 0.267194 | 0.280194 | 0.391,24 0.671 | |
| hb | −2.79,187 −2.07176 | 0.387194 | 91.4176 | 0.270194 | 0.152194 | 0.391,24 0.543 | ||
| BiP | aw | −2.85,186 −1.98176 | 0.433, 0.415199 | 96.7, 90.9, 101.1176 | 0.274, 0.264176 | 0.293199 | 0.387,24 0.680 | 0.606195 |
| hb | −2.79,187 −1.91176 | 0.387187 | 92.2176 | 0.269187 | 0.149176 | 0.387,24 0.536 | 0.342196 | |
| BiAs | aw | −2.69,186 −1.93176 | 0.460, 0.423176 | 96.1, 91.6, 99.7176 | 0.285, 0.277176 | 0.295199 | 0.392,24 0.687 | |
| hb | −2.66,187 −1.90176 | 0.403200 | 91.7176 | 0.27920 | 0.156200 | 0.392,24 0.548 | ||
| BiSb | aw | −2.53,186 −1.78176 | 0.481, 0.446199 | 94.7, 87.0, 102.6176 | 0.304, 0.296176 | 0.335199 | 0.413,24 0.748 | |
| hb | −2.52,197 −1.77176 | 0.424199 | 90.9176 | 0.297201 | 0.169201 | 0.413,24 0.582 |
The pnictogen atoms P, As, Sb, and Bi have an electron configuration (ns2np3) with five valence electrons in the outer shell and therefore need three extra electrons to reach octet stability. Most calculations assume that the s and p orbitals deliver a reasonable description of bonding and that the influence of d orbitals is negligible even for the heavy Bi atom. A planar structure of sp2 hybrids is not stable as a free-standing layer. Thus, sp3-like hybridization of s and p orbitals stabilizes a buckled or puckered configuration, because corrugation allows better overlap of pz–pz orbitals. Fig. 19 shows the electron configuration and atomic orbitals after promotion and hybridization. Accordingly, the monolayer consists of sp3-like hybrids (intermediate between sp2 and sp3) forming three σ backbonds with nearest atoms, which build a pyramid of covalent bonds that provides the rigidity. The lone pair of valence electrons in a pz2-like orbital (not pure p state) primarily interacts with neighboring layers. In the stabilized monolayer structure, the distance between the repulsive lone electron pairs is maximized. Note that threefold-coordinated layered structures can be topologically mapped onto a honeycomb lattice. While the unit cell of the buckled rhombohedral structure contains two atoms, there are four atoms in the unit cell of the puckered orthorhombic structure.
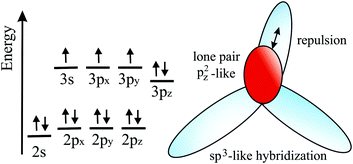 | ||
| Fig. 19 Atomic orbitals of group V atoms with pyramidal sp3-like hybrids and a lone pair of pz2-like electrons. | ||
The strongly folded accordion-like ridged or puckered structure is responsible for the anisotropy, with strongly varying properties parallel to the grooves along the zigzag direction (b direction or y-axis) compared to perpendicular to the grooves in the armchair direction (a direction, x-axis), as visible in Fig. 18(c). Calculations of the cohesive energy indicate that sw-P, sw-As, aw-Sb, and aw-Bi are the energetically most stable puckered phases, together with the hexagonal buckled phases hb-P, hb-As, hb-Sb, and hb-Bi, which exhibit comparable energetic stability.175 For phosphorene, the sw-phase is the most stable monolayer, and for the others, the hb-phase.177 The buckled phase of pnictogens structurally resembles that of silicene and higher homologues, with a buckling effect that increases with row number.
The data collection in Table 8 includes cohesive energies, lattice constants, bond angles, bond lengths, layer thicknesses, and few-layer separations for the elemental monolayers P,175–177,179–183 As,176,184,185 Sb,175,176,181,186–189 Bi,175,176,190,191 and the binary V–V compounds PN,176,192–194 AsN,176,194 SbN,176,194–196 BiN,176,197,198 AsP,176,186,187,194 SbP,176,186,187,194 AsSb,176,186,187,194 BiP,176,186,187,195,196,199 BiAs,176,186,187,199,200 and BiSb.176,186,199,201 In Fig. 20(a) we present a plot of the widely varying cohesive energies versus the longer bond of the puckered phase for the stable sw- or aw-, and the hb-phases of elemental group-V monolayers. Unexpectedly, the independently calculated cohesive energies vary substantially. Most values published for the elemental monolayers belong to two lower almost parallel inverse dependences, one with medium and the other one with much lower energies of cohesion. Note that the included results are based on DFT calculations, treating the exchange–correlation functional by the PBE form of GGA. Unfortunately, a detailed description of the specific approximations used is lacking and the authors do not discuss reasons for the deviations of their results from already existing literature values. A difference stated is that the major study of the small cohesive energies took the SOC effect into account.176 To what extent this explains the observed differences is not clear.
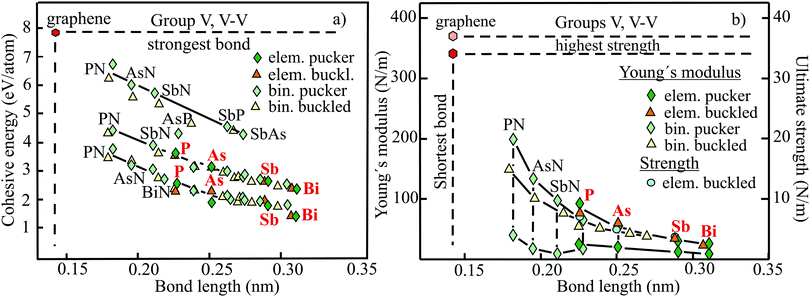 | ||
| Fig. 20 (a) Cohesive energy versus bond length of elemental and binary group V monolayers. (b) Young's moduli and ultimate strengths versus bond length of elemental and binary group V monolayers. | ||
The upper dependence in Fig. 20(a) with the large cohesive energies of binary V–V compounds is not consistent with the much lower values reported for the corresponding elemental monolayers, and therefore these large binding values have not been included in Table 8.193 On the other hand, for each of the two lower nearly parallel dependences with the medium and low cohesive energies the respective authors demand consistent behavior for binaries and elements. This, at least, implies minor influence of polarity on the overall bonding behavior. This conclusion is supported by similar mechanical properties of the elemental and binary monolayers, as will be shown below. To come to a decision between medium and low cohesive energies we make a comparison with the cohesive energy and stiffness of the buckled phase of elemental groups IV monolayers. Since the two elemental groups have similar Young's moduli (those of the group V elements being slightly larger as a comparison of Fig. 20(b) with Fig. 13(b) shows), the assumption that the cohesive energies may also be comparable points to the medium cohesive energies as the more realistic bonding energies.
The mechanical properties reported for the elemental and binary pnictogens P,175,181,182,186,202–205 As,181,184,205,206 Sb,175,181,186,188,189 Bi,175,181,190,191,207 PN,198 AsN,198 SbN,198 BiN,198 AsP,194,208 SbP,194,209 and AsSb194,209 are presented in Table 9. In Fig. 20(b) the available Young's moduli (left) and ultimate strengths (right) of the group V elements are shown versus their bond lengths. Noteworthy is the large anisotropy of the Young's moduli between the armchair and the zigzag direction of the puckered phase, which disappears abruptly for the heavier elements. The reason for the extremely low stiffness in the armchair direction is that tension unfolds and flattens the puckered structure, predominantly involving dihedral angles in the more ductile armchair direction without a significant extension of strong covalent bonds.
| Monolayer | Phase | Space group | Young's modulus Eac, Ezz (N m−1) | Poisson's ratio νac, νzz; νxy, νyx | Ultimate strength σac, σzz (N m−1) | Ultimate strain εac, εzz |
|---|---|---|---|---|---|---|
| Phosphorene | sw | Pmna 186 | 25, 93182 | 0.17, 0.62182 | 4.4, 10182 | 0.30, 0.27182 |
| 22, 56202 | 0.18, 0.70203 | 2.2, 4.5204 | 0.30, 0.16204 | |||
| hb |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1205 m1205 |
75,175 80181 | 0.11175 | 7.1, 6.7181 | 0.16, 0.21181 | |
| Arsenene | sw | Pmna 205 | 20, 55184 | 0.33, 0.91184 | ||
| hb |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1206 m1206 |
58,184 53181 | 0.21184 | 5.2, 4.7181 | 0.17, 0.20181 | |
| Antimonene | aw | Pmn21186 | 12, 29175 | 0.36, 1.20175 | 2.3, 5.8189 | 0.18, 0.32189 |
| hb |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
41,188 33181 | 0.21188 | 3.8, 3.1;181 6.4, 5.8189 | 0.20, 0.21181 | |
| Bismuthene | aw | Pmn21190 | 10, 26191 | 0.26, 0.65191 | ||
| hb |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1190 m1190 |
24,191 30175 | 0.33181 | 4.7207 (100 K) | 0.24, 0.27207 | |
| PN | aw | Pmn21198 | 39, 199198 | 0.11, 0.54198 | ||
| hb | P3m1198 | 149198 | 0.138198 | |||
| AsN | aw | Pmn21 | 18, 133198 | 0.12, 0.91198 | ||
| hb | P3m1 | 102198 | 0.22198 | |||
| SbN | aw | Pmn21 | 7.2, 97198 | 0.06, 0.82198 | ||
| hb | P3m1 | 78198 | 0.21198 | |||
| BiN | aw | Pmn21 | 20, 67198 | 0.11, 0.36198 | ||
| hb | P3m1 | 53198 | 0.28198 | |||
| AsP | hb | P3m1208 | 62,194 52208 | 0.15,194 0.24208 | ||
| SbP | hb | P3m1 | 45194 | 0.19,194 24209 | ||
| AsSb | hb | 39194 | 0.20,194 20209 |
The stiffness of the buckled V–V monolayers is slightly smaller than that of the strong zigzag direction of the puckered phase. In view of the hexagonal structure of hb-P, it is not surprising that the stiffness is isotropic for small strains <0.02 and minor chirality of the ultimate strength and strain is observed only when the hexagonal symmetry is broken by uniaxial strains in the nonlinear part of the stress–strain relationship. The intrinsic strength measures the overall stability of chemical bonding of the 2D network and the values available for phosphorene, arsenene, and antimonene follow Griffith's rule well. Thus, a reasonable first estimate of the ultimate strength for buckled bismuthene of ∼2.5 N m−1 can be extracted from this correlation.
The tunability of electronic properties of few-layer assemblies by changing the interlayer interaction via stacking order and interlayer interaction forces is the main reason for studying the layered systems. This includes indirect-to-direct transitions and the width of the band gap. Usually, the gap increases with decreasing number of layers due to confinement effects. For AB stacking of sw-P bilayers, for example, the layer spacing is around 0.53 nm, which agrees with the van der Waals diameter plus corrugation effect. The interlayer interaction energy of −20 meV per atom equals the van der Waals interaction of bilayer graphene.179 This is also the case for hb-P with ds = 0.446 nm and interlayer interaction of −12.5 meV per atom for AB stacking and comparable values for AA stacking.183 For AB stacking in sw-As, the spacing is 0.554 nm and the interaction increases to −53 meV per atom.185 A comparable behavior is observed for AA stacking of hb-As, with an interaction energy of −30 meV per atom and layer spacing of 0.492 nm.185 While for AB stacking in aw-Sb the layer separation of 0.616 nm is consistent with the interaction of −68 meV per atom, for AA stacking of hb-Sb multilayers the large interaction energy of −124 meV per atom reduces the layer spacing to 0.365 nm.189
Various theoretically predicted monolayer properties of pnictogens, such as large band gap, band gap tuning by strain, thermoelectric and optoelectronic properties, topological phases, high electron mobility, superconductivity, and QSH effect, have aroused the interest of experimentalists. According to theory, both hb-P and sw-P form energetically and dynamically stable free-standing sheets. Epitaxial growth of single monolayers of phosphorene on an Au(111) surface leads to a structure identical with hb-P, as verified by STM and LEED analysis.210 While the sw and hb phases are equally stable, the latter seems to be the preferred phase that grows on a substrate with hexagonal symmetry. A recent review describes in detail the progress made with top-down methods (mechanical, liquid, and electrochemical exfoliation) and bottom-up methods (CVD, MBE) in the fabrication of group V monolayers.211 The quick oxidative degradation of reactive phosphorene, induced by oxygen dissolved in adsorbed water and light exposure, requires effective passivation schemes for synthesis, characterization, and processing.212
Exfoliation of layered bulk grey arsenic, existing in nature, allows the isolation of buckled arsenene monolayers. While the production of few-layer systems of hb-As has been achieved by several methods, such as exfoliation with adhesive tape or ultrasonication, the realization of monolayers is much more demanding.213 Using LEED, STM, and angle-resolved photoemission spectroscopy (ARPES) in combination with DFT calculations for characterization, the formation of a quasi-free-standing buckled honeycomb layer of arsenene on Ag(111) has been confirmed.214 The physicochemical properties of antimonene allotropes resemble those of arsenene. The growth of buckled monolayers of antimonene has been achieved on a 2D layered PdTe2 substrate by MBE.215 The analysis confirmed a weak interaction with the substrate and a high chemical stability in air. Large-area antimonene has been grown on c-plane sapphire by MBE and characterized by XRD and Raman spectra.216 Van der Waals heteroepitaxial deposition allowed the growth of high-quality Sb monolayers with the puckered honeycomb structure.217 A progress report reviews the approaches employed the obtain antimonene and the main characterization techniques used to study this material.218
Interest in monolayers of heavy Bi is based on its strong SOC and the inverted gap. The deposition of supported bismuthene with the MBE method using a SiC(0001) substrate yielded a honeycomb √3 × √3 R30° superstructure of Bi in a planar configuration, owing to the strain effect of the SiC substrate.219 The large band gaps of hexagonal bismuthene, antimonene, and arsenene may offer the possibility of room temperature QHS applications.220 A detailed investigation of the oxidation mechanism and structural stability of 2D pnictogens under oxygen and water exposure comes to the conclusion that the higher stability of antimonene and bismuthene originates from an acceptor role of water, which impedes the formation of acids by the interaction of water molecules and oxygen species.221
Of the large number of phases described in the literature, the buckled (hb or β) and asymmetric washboard structures (aw or α) are the most extensively investigated monolayers due to their stability (see Fig. 18d). Owing to different atom sizes, the binary compounds become asymmetric. This reduces the symmetry of the network, which is no longer centrosymmetric. The compounds discussed here are energetically stable, with a negative cohesive energy, and their free-standing monolayers are dynamically stable, with no soft or imaginary phonon modes. Eventually, MD simulations verified the thermal stability at finite temperatures. Theoretical calculations of structural data such as the bond length are in good agreement, while large deviations exist for the cohesive energies.
Besides the bonding behavior of elemental monolayers, Fig. 20(a) presents the published small, medium, and large cohesive energies of binaries as a function of the longer bond for the most stable sw and aw phases. Generally, we may assume that the stiffness of a particular binary phase lies between those of the two constituents. Some values presented for the cohesive energies of the nitrides PN, AsN, SbN, and AsP are much larger than those of their constituents.193 Of course, the strongest bonding is anticipated for the nitrides, where besides efficient overlap of orbitals owing to the small size of nitrogen atoms, ionic interaction makes the largest contribution to in-plane ionic–covalent bonding. However, we would expect the cohesive energy and bond length of AsP to be located somewhere between the corresponding values of its constituents, As and P. Similarly, the cohesive energies of SbP and SbAs seem to be too large. It is difficult to rationalize why the bonding strength of the AsP monolayer should be much stronger than that of phosphorene with a similar bond length. The same is true for the large cohesive energies of SbP and SbAs. The principle that binary compounds have cohesive energies that correlate with those of the corresponding elemental compounds is clearly followed by the dependences with medium186,187 and small cohesion.176 Like the elements, the binary group IV and binary group V monolayers with medium cohesive energies possess comparable cohesive energies and bond lengths, and thus a similar structural stability.
Besides the mechanical properties of elemental compounds, Fig. 20(b) shows a plot of the available Young's moduli versus bond lengths of binary group V compounds. Noteworthy is the large anisotropy of the Young's moduli between the armchair and the zigzag directions of the puckered nitrides, which again decreases abruptly for the heavier compounds. As can be seen in Fig. 20(b), the strong mechanical performance of binary group V monolayers in the zigzag direction follows the periodic trend of the elements, where graphene defines the upper limit of stiffness. The observed dependences clearly demonstrate correlated cohesive energies of homonuclear and heteronuclear monolayers, despite ionic interaction in the latter case. Unfortunately, calculations of the ultimate strengths and strains are still largely lacking for binary group V sheets.
The fact that the P–N bond is stronger than the P–P bond follows from the better orbital overlap yielding a larger cohesive energy. Therefore, the higher dynamic stability and better oxidation resistance of PN is not surprising.192 PN is a semiconductor with a wide band gap suitable for application as a high-speed transistor, in power electronics, and as an efficient LED. The piezoelectric coefficients, which control mechanical-to-electrical energy conversion, have high values in binary group V monolayers such as PN, owing to their flexible structure and low symmetry.194 The realization of PN monolayers may be possible either as a free-standing sheet or as a monolayer on a suitable substrate. There is evidence from theory that the two configurations considered here are dynamically stable and authors propose potential growth of aw-PN and hb-PN on Ag substrates by CVD with cyclic phosphazene, which contains a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio of P and N, to overcome difficulties with the strong nitrogen triple bond.192 A large separation between PN and the Ag substrate is expected and theoretical STM images suggest a non-planar periodic structure of the adsorbed monolayer. The other binary monolayers are not as well studied as PN.
1 mole ratio of P and N, to overcome difficulties with the strong nitrogen triple bond.192 A large separation between PN and the Ag substrate is expected and theoretical STM images suggest a non-planar periodic structure of the adsorbed monolayer. The other binary monolayers are not as well studied as PN.
Group IV–VI monolayers
The elements of 2D group IV–VI compounds or group IV monochalcogenide monolayers are, as direct neighbors of group V elements, their isoelectronic counterparts, with ten valence electrons in total. For example, SnS, with the electronic configurations Sn (4d105s25p2) and S (3s23p4), is isoelectronic to group V elements with the electronic configuration (ns2np3). Of particular interest are stereochemically active cations with the formal electronic configuration (ns2np0), based on an electron lone pair (ns2), as studied already in detail for bulk crystals of SnX (X = O, S, Se, and Te).222 In the classical picture of ionic bonding in SnS, the Sn (5s2) subshell electrons of the cation Sn2+ with oxidation state two form a chemically inert orbital of lone-pair electrons projecting out on one side of the plane after hybridization. The Sn2+ ion interacts with three S2− ions and, together with the lone-pair electrons of Sn (5s2), sp3-like hybridization with a higher chemical reactivity is achieved. This reactivity causes a stronger interlayer coupling between adjacent layers. DFT calculations delivered evidence that the Sn (5s) and (5p) states may be too far apart for direct coupling and therefore hybridization of Sn (5s) via anion X p states of suitable energy has been postulated, allowing a sterically active asymmetric electron density distribution with nominally filled ns and nominally empty np states of the cation.222 Alternatively, it has been assumed that if the energy gained by s–p hybridization is larger than the energy cost of moving the cation electron from its s to its p state, symmetry will be broken and an asymmetric electron distribution can be generated by the response of the cation's ns and nominally empty np orbitals.223In any case, the structural distortions caused by the lone pair electrons are responsible for the generation of the characteristic orthorhombic structure of the monolayer with strong interlayer interaction and enhanced chemical reactivity. The lone pair of each atom pushes the three covalently bonded atoms towards a tetrahedral coordination. Notwithstanding that a complete molecular understanding is still lacking, the stereo-chemically active lone pair is the source of the structural changes leading to the distinctive elastic, piezoelectric, and optoelectronic properties, and to the anisotropy of thermal expansion.223 Owing to the difference in electronegativity, the bonds of these compounds are polar, with considerable ionic contributions to bonding. Charge transfer occurs from group IV to group VI atoms, with C-containing compounds as an exception. As a result of the different electronegativity and atom size of the constituents, the single-layer structures lack centrosymmetry, and therefore SOC is allowed.
From the geometrical monolayer configurations studied, we consider here the two most stable 2D structures, namely the puckered and buckled phases. In cases where the binding energies of these two phases are comparable, they may even coexist. The aw-phase of the four compounds GeS, GeSe, SnS, and SnSe, with band gaps covering part of the infrared and visible spectrum, has attracted enormous attention.224 These monolayers entail six-membered rings in the so-called chair conformation, with four sublayers (see Fig. 18(d)). The properties of interest are the high flexibility, high carrier mobility, low lattice thermal conductivity, and strong absorbance of visible light, which offer potential applications in optoelectronics, thermoelectrics, piezoelectricity, as photodetectors, and as sensors. Remarkable phenomena related to in-plane strain are giant piezoelectricity and multiferroicity, combining ferroelastic and ferroelectric behavior. Finally, strong SOC opens the door to spintronics. Interestingly, Ge and Sn as well as S and Se have similar electronegativities and comparable, weak bond energies responsible for their surprisingly low stiffness. The unique properties are linked with weak chemical bonding of the puckered structure, which is the minimum energy configuration, except for SiS and SiSe.225
The structural data of group IV–VI monolayers MX, with M = C, Si, Ge, Sn and X = S, Se, Te, has been determined in a comprehensive study by first-principles calculations.225Table 10 contains the cohesive energies and structural data of CS,225 SiS,225–227 GeS,224,225,228 SnS,224,225,229 CSe,225,226,230,231 SiSe,225–227 GeSe,224,225,232 SnSe,224,225,232 CTe,225,226 SiTe,225,233 GeTe,225,226,234 and SnTe.225,234 In a plot of cohesive energies versus the bond lengths of IV–VI monolayers, we group together chemically related compounds, obtained by combining one group IV element with all other group VI elements (see Fig. 21(a)). As can be seen in Table 10, the in-plane bond lengths and those between the sublayers of the puckered structure deviate to some extent. Since longer bonds, with weaker dissociation energy, determine the stability of the network, they are taken in the plot. Based on the results discussed before for other C-containing binaries the planar structure of the carbon group should have the highest energetic stability. According to DFT calculations, however, the puckered and buckled phases have larger cohesive energies than the planar phase, as observed for the other groups.225 Note that the carbon group is clearly separated by shorter bonds from the Si, Ge, and Sn groups, which partially coincide. The puckered structure of the group IV–VI monolayers has the highest energetic stability, closely followed by the buckled phase. Besides the three carbon monochalcogenides (C group) with shorter bonds but only slightly larger cohesion, the other three related groups show a similar bonding behavior in a narrow range of cohesive energies between −3 and −4 eV per atom.
| Mono-layer | Space group | Cohesive energy, Ec (eV per atom) | Lattice constants a, b (nm) | Bond lengths d1, d2 (nm) | Pucker, buckle Δz (nm) | van der Waals diameter dw,24dw+Δz (nm) |
|---|---|---|---|---|---|---|
| CS | Pmn21225 | −4.37225 | 0.280, 0.432225 | 0.176, 0.185225 | ||
| P3m1225 | −4.08225 | 0.284225 | 0.188225 | |||
| SiS | Pmn21226 | −3.91225 | 0.335, 0.477225 | 0.230, 0.234225 | 0.233226 | 0.390,24 0.523 |
| P3m1225 | −3.92,225 −3.95227 | 0.330225,227 | 0.232225,227 | 0.133227 | 0.390,24 0.523 | |
| GeS | Pmn21224 | −3.66,225 −3.76224 | 0.364, 4.49225 | 0.248, 0.242228 | 0.262224 | 0.391,24 0.653 |
| P3m1224 | −3.64,225 −3.74224 | 0.349225 | 0.243225 | 0.136224 | 0.391,24 0.527 | |
| SnS | Pmn21224 | −3.55,225 −3.67224 | 0.405, 0.435225 | 0.273, 0.260225 | 0.285229 | 0.397,24 0.682 |
| P3m1224 | −3.47,225 −3.58224 | 0.376225 | 0.262225 | 0.146224 | 0.397,24 0.543 | |
| CSe | Pmn21226 | −3.84,225 −3.91230 | 0.303, 0.430225 | 0.196, 0.201225 | 0.201226 | 0.360,24 0.561 |
| P3m1231 | −3.64,225 −3.79231 | 0.306225 | 0.206225 | 0.104231 | 0.360,24 0.464 | |
| SiSe | Pmn21226 | −3.53225 | 0.374, 0.440225 | 0.252, 0.245225 | 0.247226 | 0.400,24 0.647 |
| P3m1225 | −3.55,225 −3.60227 | 0.352225 | 0.248225 | 0.142227 | 0.400,24 0.542 | |
| GeSe | Pmn21232 | −3.37,225 −3.88224 | 0.397, 0.430225 | 0.266, 0.254225 | 0.249224 | 0.401,24 0.650 |
| P3m1224 | −3.36,225 −3.85224 | 0.368225 | 0.257225 | 0.141224 | 0.401,24 0.542 | |
| SnSe | Pmn21232 | −3.28,225 −4.57224 | 0.426, 0.445225 | 0.289, 0.273225 | 0.259224 | 0.407,24 0.682 |
| P3m1224 | −3.22,225 −4.56224 | 0.392225 | 0.275225 | 0.153224 | 0.407,24 0.560 | |
| CTe | Pmn21226 | −3.68225 | 0.339, 0.389225 | 0.216, 0.218225 | 0.218226 | 0.376,24 0.594 |
| P3m1225 | −3.43225 | 0.335225 | 0.223225 | |||
| SiTe | Pmn21233 | −3.23,225 −3.30233 | 0.411, 0.430225 | 0.264, 0.277225 | 0.292233 | 0.416,24 0.708 |
| P3m1233 | −3.20,225 −3.27233 | 0.384225 | 0.269225 | 0.153233 | 0.416,24 0.569 | |
| GeTe | Pnma 234 | −3.09225 | 0.424, 0.438225 | 0.274, 0.288225 | 0.288226 | 0.417,24 0.705 |
| P3m1225 | −3.06225 | 0.394225 | 0.277225 | |||
| SnTe | Pmn21225 | −2.99225 | 0.454, 0.458225 | 0.293, 0.316225 | 0.42324 | |
| P3m1225 | −2.93225 | 0.415225 | 0.295225 |
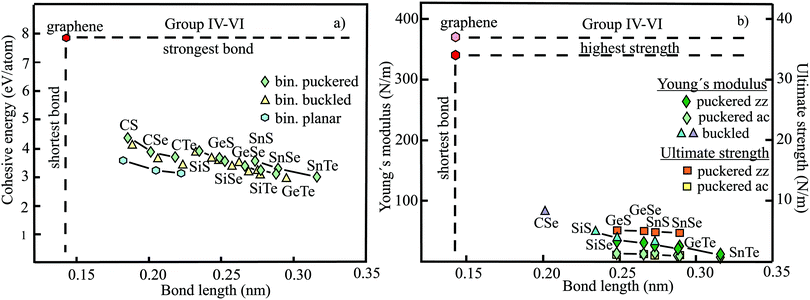 | ||
| Fig. 21 (a) Cohesive energy versus bond lengths of binary group IV–VI monolayers. (b) Young's moduli and ultimate strengths versus bond length of binary group IV–VI monolayers. | ||
The variable contribution of ionicity plays an important role in reducing orbital overlap and thus the bonding strength of group IV–VI monolayers. Since the electronegativities of C (2.55), S (2.58), and Se (2.55) are comparable, a significant charge transfer occurs in the C group only from the Te (2.10) to the C atom. In the other groups, an opposite charge transfer takes place to the chalcogenide atoms, owing to the smaller electronegativities of Si (1.90), Ge (2.01), and Sn (1.96). Since the difference of the electronegativities decreases within each group, electrostatic interactions become less important with increasing atomic number. This may contribute to the characteristic inverse bonding dependence observed for these groups, where the decay of the cohesive energy decreases asymptotically with increasing bond length. The relatively small changes of atom size and electronegativity in the Si, Ge, and Sn groups explain their striking similarity in bonding energy and in their mechanical behavior.
The available linear and nonlinear mechanical properties studied for the compounds CSe,231 SiS,227 SiSe,227 SiTe,227,233 GeS,14,234–236 GeSe,14,234–236 GeTe,234 SnS,14,234–236 SnSe,14,234–236 and SnTe234 are summarized in Table 11. The plot of Young's modulus and strength versus bond length in Fig. 21(b) illustrates the enormous difference to the outstanding mechanical performance of covalently bonded planar graphene, carbides, and nitrides. The calculated Young's moduli and intrinsic strengths disclose a low stiffness and fracture strength of both the puckered and buckled phases. The substantial contribution of far-reaching electrostatic forces reduces orbital overlap and thus the strength of localized covalent bonding. Certainly, the mechanical performance can be a critical problem for any practical application of these compounds. Interestingly, the stiffness and strength of Ge and Sn sulfides and selenides reveal good agreement with Griffith's rule for the armchair direction of the puckered phase, but not for the stronger zigzag direction, where the calculated strengths are much larger than expected.
| Monolayer | Structure, | Young's modulus Eac, Ezz (N m−1) | Poisson's ratio νac, νzz; νzx, νzy | Intrinsic strength σac, σzz (N m−1) | Ultimate strain εac, εzz |
|---|---|---|---|---|---|
| CSe | hb | 86.1, 83.5206 | 0.14, 0.16206 | 5.6, 5.9206 | 0.10, 0.14206 |
| SiS | hb | 51.3202 | 0.13202 | ||
| SiSe | hb | 41.5202 | 0.17202 | ||
| SiTe | aw | 20.8–62.9208 | −0.20 to 0.60208 0.18202,208 | ||
| hb | 34.4202,208 | ||||
| GeS | aw | 15.5, 33.3209 | −0.21, 0.4114 | 1.4, 5.2211 | 0.45, 0.28211 |
| 13.4, 33.4210 | |||||
| GeSe | aw | 12.5, 30.6209 | 0.58, −0.4314 | 1.4, 5.0211 | 0.55, 0.23211 |
| 12.1, 28.4210 | |||||
| GeTe | aw | 12.0, 21.1209 | |||
| SnS | aw | 14.2, 26.0209 | −0.004, 0.40414 | 1.1, 4.7211 | 0.61, 0.23211 |
| 14.1, 26.1210 | |||||
| SnSe | aw | 11.0, 24.9209 | −0.21, 0.3514 | 1.1, 4.5211 | 0.63, 0.22211 |
| 12.5, 24.8210 | |||||
| SnTe | aw | 5.6, 12.9209 |
One reason for the exceptionally small stiffness and strength of these compounds is the contribution of electrostatic forces, which reduces the strength of local covalent bonding. An important consequence of this fact is the superior flexibility of GeS, SnS, and SnSe. Note that this ultrahigh flexibility occurs in the armchair direction, which is the direction with a negative out-of-plane Poisson's ratio under uniaxial strain, as discussed below.236 Based on their high stretchability, these 2D materials can reversibly withstand extreme structural deformations. Under small mechanical strain, several of these semiconductors undergo an indirect-to-direct gap transition.225 Owing to the small elastic stiffness, a large polarization is induced by stress, which leads to piezoelectric coefficients enhanced by one-to-two orders of magnitude.224
Interestingly, the three monolayers aw-GeS, aw-SnS, and aw-SnSe exhibit a negative Poisson's ratio between the armchair (x) direction and the perpendicular out-of-plane (z) direction, whereas for aw-GeSe the auxetic effect appears between the zigzag (y) and the z direction.14,237 The different auxetic behavior of aw-GeSe is attributed to a change in the position of M and X atoms in the four sublayers of the puckered structure and the smaller bending stiffness of the M–X–M bond angle. Recent reviews give a comprehensive description of the enormous progress made by both theory and experiment in understanding this phenomenon.224,238
Optical and electronic properties of 2D materials can be tuned by alloying compounds with little variation of the lattice parameters or by forming few-layer assemblies with variable interaction forces.239 The most stable AA and AB stacking orders of group IV–VI bilayers exhibit covalent-like interaction beyond van der Waals interlayer forces (see Fig. 22). A shortest distance between adjacent layers of dint = 0.279 nm and an interlayer interaction energy of −98 meV per atom were found for AB stacking of aw-GeS.240 Similar stabilities were attained for bilayers with AA, AB, and AC stacking of aw-GeSe. For example, for AA stacking a shortest interlayer distance of 0.30 nm and an interaction energy of −110 meV per atom were obtained.240 For aw-GeSe also lower interlayer interaction energies of −52.3 meV per atom and −48.1 meV per atom have been reported for AA and AB stacking, with dint = 0.303 nm and dint = 0.312 nm, respectively.241 Bilayers of aw-SnS with AB stacking sequence have a shortest distance of adjacent layers of dint = 0.291 nm and a large interlayer interaction energy of −164 meV per atom.240 The interaction energy increases further for bilayers of aw-SnSe to −185 meV per atom with dint = 0.302 nm for AB stacking. These results point to the preferred generation of few-layer assemblies, explaining the difficulties faced in isolating single layers by mechanical exfoliation.240
The present status of preparation methods available for the synthesis of selected group IV monochalcogenides, such as mechanical exfoliation, solution-based methods, CVD, atomic layer deposition, and post-etching methods has been reviewed extensively.224,242 Even in the case of the best developed mechanical exfoliation techniques, it is difficult to control the yield, number of layers, and size of the uniform area of the fabricated nanosheets and nanoflakes. While micrometer-sized GeS sheets have been synthesized by solution-based methods, most studies used CVD techniques, for example for the synthesis of single-crystalline nanoribbons.224 The separation of the already-grown bilayers is difficult owing to the large exfoliation energy.242 By sonication-assisted liquid phase exfoliation of bulk GeSe powders, 4–10 layer stacks of GeSe with lateral sizes >200 nm were obtained in different solvents, as characterized by SAED, HRTEM, and XPS analysis.243 While tape exfoliation and crystal growth lead to few-layer systems, the liquid-phase exfoliation method allowed the production of bilayer SnS nanosheets through size-selective centrifugation.244 The deposition of wafer-scale vertically standing SnS layers of high quality has been realized by sulfur reduction from sputtered SnS2 without post processing.245
Group VI monolayers
The two chalcogenide atoms Se and Te have an electron configuration with six valence electrons in the outer shell, explicitly Se (4s24p4) and Te (5s25p4), and therefore only two extra electrons are needed to reach octet stability. Accordingly, these elements form stable 1D-like chain structures with two covalent bonds. Based on the large separation of the 4s (5s) and 4p (5p) states, the s electrons are treated as core states, which are not directly involved in covalent binding. Thus, the four valence electrons 4p4 (5p4) form two covalent bonds with their direct neighbors arranged in a chain and a lone pair of the remaining p electrons. Since this configuration is threefold degenerate, helical chains with a helical turn of 120° are formed (see Fig. 23). Based on the transition from the nonmetal S to metal Po in group VI, of the two metalloid elements selenium and tellurium the latter is more metallic in nature. This fact is responsible for a stronger delocalization of electrons in the interchain region of tellurene, with an interaction that is sometimes called ‘covalent-like,’ because it is stronger than van der Waals interaction in selenene.
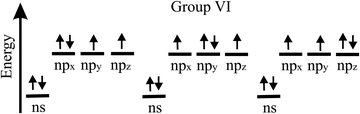 | ||
| Fig. 23 Scheme of degenerate electron configurations of group VI elements with six valence electrons. | ||
The characteristic bonding of bulk Se and Te is displayed in Fig. 24. The helical chains are arranged along the c-axis in a hexagonal pattern of chains and exhibit equilateral triangles in the plane perpendicular to the c-axis. The arrangement of the chains is controlled by the interaction of the lone-pair electrons and interchain van der Waals interaction. Several stable monolayers and few-layer systems can be formally derived by cuts through low index planes, e.g., (0001) and (10−10), by cleaving the bulk either perpendicular or parallel to the chain direction, respectively.
 | ||
| Fig. 24 Bulk structure of Se and Te with helical chains oriented in the z-direction assembled in a hexagonal arrangement. Two low-index crystal planes are indicated to illustrate possible cuts. | ||
One of the most stable (2D) phases is the helical-chain or trigonal phase, which may be considered as a dimension-reduced bulk phase (see Fig. 25(a)). Another stable configuration is the tetragonal phase with mirror-plane and rectangular unit cell that originates from a helix-to-layer transformation process of the trigonal monolayer. It is composed of deformed four-membered and deformed six-membered rings with the coordination number 4 for the central and 3 for the outer atoms, as illustrated in Fig. 25(b). The rhombic phase with 1T-MoS2-like structure is a three-layer structure with coordination number 6 of the central atom and 3 for the atoms in the lower and upper layers, as displayed in Fig. 25(c). Finally, the low-symmetry monoclinic phase forms a chair-like buckled structure as silicene, however, with a square unit cell instead of a hexagonal one (see Fig. 25(d)).
Unfortunately, the currently used nomenclature using Greek letters is not standardized and introduces confusion. Therefore, symmetry elements and space groups are employed here to unambiguously classify individual phases. Note that the rhombic phase, for example, is named α-phase, γ-phase, and T-phase in the literature.246–248 In the following, the thickness direction is defined as the z-direction, and the chain direction is defined as the y-direction for the chain-like and tetragonal phases, whereas for the rhombic phase the y-direction extends along the armchair direction, due to the loss of the original chain structure by reconstruction.247
The space group, cohesive energy, lattice constants, bond length, corrugation, and layer thickness of the trigonal,246,248–250 tetragonal,246,251,252 rhombic,245,248,252–254 and monoclinic224,249 structures of selenene are presented in Table 12, along with the bonding information and structural properties of the trigonal,247,250,255,256 tetragonal,247,255 rhombic,252–255 and monoclinic249 structures of tellurene. This data makes possible a discussion of bonding–structure–performance relationships for these recently discovered 2D materials with novel structures deviating from previous hexagonal 2D materials. In Fig. 26(a) the cohesive energies of the four allotropes of selenene and tellurene are plotted versus bond length, including the short and the longer interchain bond lengths of the trigonal bulk phases. Surprisingly, quite different atomic arrangements of selenene and tellurene have comparable cohesive energies in the narrow range of −2.5 to −2.8 eV per atom. Despite the longer covalent bonds of the tellurenes, the cohesive energies of the polymorphs are only slightly smaller. The anisotropic structure of bulk and few-layer assemblies of helical-chain selenene and tellurene is characterized by two strongly deviating atom spacings. For the trigonal Se bulk structure, the length of covalent intrachain bonds is 0.243 nm and for interchain interaction between neighboring chains it is 0.334 nm with a cohesive energy of −2.88 eV per atom.250 In the case of the trigonal Te bulk structure, the difference of the two bond lengths of 0.290 nm and 0.342 nm is much smaller and the cohesive energy is −2.71 eV per atom.250 For a single layer of the trigonal Te phase, the theoretical bond lengths are 0.278 nm and 0.304 nm.256 In the layered covalently bonded tetragonal and square phases, these large differences in the bond lengths are reduced, and in the layered rhombic phase, the difference reduces to zero, leaving just a single bond length.
| Monolayer, structure | Space group | Cohesive energy, Ec (eV per atom) | Lattice constants a, b (nm) | Bond lengths d1, d2 (nm) | Corrugation, buckling Δz (nm) | van der Waals diameter dw,24dw+Δz (nm) |
|---|---|---|---|---|---|---|
| Selenene | ||||||
| Trigonal chain-like | −2.78249 | 0.413, 0.499248 | 0.240, >0.31249 | 0.176249 | 0.38,24 0.556 | |
| −2.88250 | 0.423, 0.511250 | 0.243, 0.334250 | ||||
| Tetragonal | −2.71251 | 0.499, 0.420251 | 0.265252 | 0.175251 | 0.38,24 0.555 | |
| Rhombic |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1253 m1253 |
−2.72252 | 0.374,248 0.372245 | 0.267,248 0.266252 | 0.311253 | 0.38,24 0.691 |
| Monoclinic | Cm 249 | −2.65249 | 0.365249 | 0.240, 0.271249 | 0.077249 | 0.38,24 0.457 |
| Tellurene | ||||||
| Trigonal chain-like | P2, P21247 | −2.71250 | 0.443, 0.593250 | 0.290, 0.342250 | 0.41224 | |
| −2.79255 | 0.433255 | 0.278, 0.304256 | ||||
| Tetragonal | P2/m, P21/m247 | −2.56255 | 0.417, 0.549255 | 0.275–0.302255 | 0.216255 | 0.412,24 0.628 |
| Rhombic |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1253 m1253 |
−2.62255 | 0.415,255 0.423254 | 0.302,255 0.302252 | 0.367255 | 0.412,24 0.779 |
| Monoclinic | Cm 249 | −2.51249 | 0.408249 | 0.287, 0.305249 | 0.092249 | 0.412,24 0.504 |
The observation of quasi the same cohesive energy for monolayer and bulk phases with widely varying bonding types seems to be a unique performance of the two chalcogenides Se and Te. The increasing metallic character and delocalized interchain interaction of electron lone pairs may be the reason for a comparable cohesion of the Se and Te phases with 1D-like helical chains. In the 2D networks of trigonal, tetragonal, rhombic, and monoclinic monolayers, multivalency of the two elements plays an important role and allows the realization of distinct structures with nearly the same cohesive energy (‘multiple structures with similar cohesion’). This is achieved by varying a pair of bond lengths in the low-symmetry structures in such a way that their mean bond energy approaches that of the single bond of the corresponding high symmetry structure. Of course, this does not imply a similar ultimate strength. However, the comparable cohesive energies make transformation between these phases possible even by thermal energy and by adsorption at surfaces. It seems that the activation barrier of the transition from helix to layer phases can be easily overcome.257 Thus, several stable allotropes may co-exist, especially at higher temperatures. Moreover, helix-to-layer transformations from 1D trigonal to 2D tetragonal phases can be induced by mechanical strain.247
The currently available mechanical properties, which are limited to tetragonal251 and rhombic252–254 selenene as well as trigonal,247 tetragonal,258,259 and rhombic252,258 tellurene, are shown in Table 13. The dependence of the Young's moduli and ultimate strengths on the bond lengths of the tetragonal and rhombic structures of selenene and tellurene is presented in Fig. 26(b). These are two strong layered phases with covalent bonding in both in-plane directions. The Young's moduli of rhombic selenene of 59 N m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252 and rhombic tellurene of 44.5 N m−1
252 and rhombic tellurene of 44.5 N m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252,258 exhibit the largest stiffness. The intrinsic strengths of the rhombic phases mostly follow Griffith's rule. With its smaller stiffness and larger Poisson's ratio, rhombic tellurene is softer and more flexible than rhombic selenene (see Table 13). The maximum stiffnesses of anisotropic tetragonal selenene and tellurene are 31 N m−1
252,258 exhibit the largest stiffness. The intrinsic strengths of the rhombic phases mostly follow Griffith's rule. With its smaller stiffness and larger Poisson's ratio, rhombic tellurene is softer and more flexible than rhombic selenene (see Table 13). The maximum stiffnesses of anisotropic tetragonal selenene and tellurene are 31 N m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 251 and 20.4 N m−1,259 respectively. While for the rhombic phase the ultimate strengths agree with the E/10 rule, this is not the case for tetragonal tellurene. Due to weak interchain forces the stiffness of the trigonal phases is much smaller; for example, for tellurene the stiffness of the monolayer extrapolated from the calculated few-layer values is <10 N m−1.247
251 and 20.4 N m−1,259 respectively. While for the rhombic phase the ultimate strengths agree with the E/10 rule, this is not the case for tetragonal tellurene. Due to weak interchain forces the stiffness of the trigonal phases is much smaller; for example, for tellurene the stiffness of the monolayer extrapolated from the calculated few-layer values is <10 N m−1.247
| Monolayer, structure | Young's modulus Eac, Ezz (N m−1) | Poisson's ratio νac, νzz | Intrinsic strength σac, σzz (N m−1) | Ultimate strain εac, εzz |
|---|---|---|---|---|
| Selenene | ||||
| Tetragonal | 5.4, 31251 | |||
| Rhombic | 59,252 55.1253 | 0.27,252 ∼0.25254 | 4.6, 6.6254 | |
| Tellurene | ||||
| Tetragonal | 11.6, 20.4259 | 0.29, 0.49259 | 4.5, 7.2258 | 0.36, 0.35258 |
| Rhombic | 44.5,252 44.5258 | 0.29,252 0.28258 | 5.2, 5.5258 | 0.26, 0.30258 |
It is worth noting that rhombic selenene with its 1T-MoS2-like structure is about a factor of three softer than the well-studied MoS2 monolayer, with a measured stiffness of 166 N m−1 for biaxial tension and a calculated mean stiffness of 131 N m−1 for uniaxial tension.150 Interestingly, the elastic moduli of the two rhombic phases reach the mechanical performance of their group V neighbors in the periodic table, arsenene and antimonene, which possess a graphene-like network. The reason for the higher modulus of the rhombic phase is that in this 2D network any in-plane strain causes an extension of chemical bonds, while the buckled structure of the tetragonal phase allows stretching in the armchair direction without extending covalent bonds but flattens the structure under low strain conditions.247 As discussed above, the stiffness decreases further for the chain-like-phases.
Despite a crop of interesting first results, up to now the study of few-layer systems has not attracted much attention. For example, 2D ferroelectricity in elemental tellurium multilayers is expected to occur by spontaneous in-plane polarization due to interlayer interaction between the lone pairs of electrons that can be preserved for bilayers above room temperature.260 It is worth mentioning that not only group IV and group V Xenes with honeycomb structure but also group VI selenene and tellurene with square structure are promising topological insulators, hosting nontrivial QSH states. Meanwhile the growth of monolayer tellurene has been achieved by an anisotropic ultrasonication process and evidence of topological insulator behavior has been observed using scanning tunneling spectroscopy (STS) by detecting the insulating interior and the metallic edge states.261
Current interest in selenene and tellurene is based on their favorable properties, such as strong optical absorption, high carrier mobilities, excellent thermoelectric performance, piezoelectricity, high stretchability, and good environmental stability.262,263 While to date detailed studies on interlayer bonding and structure of few-layer assemblies are lacking, such sheets have been attained experimentally. By liquid-phase exfoliation (LPE) 2D Se sheets of the trigonal bulk chain-like structure with 40–120 nm lateral dimension and 3–6 nm thickness could be exfoliated by sonication.264 Physical vapor deposition (PVD) has been employed to grow high-quality Se nanosheets with large size, a minimum thickness of 5 nm, and strong in-plane anisotropy.265 Few-layer assemblies derived from the α-Se and α-Te bulk phase are stable, whereas the trigonal monolayers transform to the tetragonal phase.263
Diverse methods such as LPE and PVD have been applied to deposit tellurene but free-standing single layers have not been realized. Monolayer and few-layer tellurene have been grown by MBE on graphene/SiC substrates266 and HOPG,267 which were analyzed by STM/STS. For ultrathin layers, the cell size was consistent with the predicted rectangular surface cells of the tetragonal phase, whereas for thicker films the detected structure agreed better with the (10–10) surface of the trigonal bulk crystal (α-Te),267 as theoretically predicted.255 For 2D nanoflakes of tellurene a comprehensive review exists, which covers the superior physical properties, synthesis techniques, practical applications, and fabrication of nanodevices.268 A comprehensive review treats the preparation methods, electrical properties, and device applications of group VI materials.269
Summary
The extensive data presented above for chemically related groups of monolayers gives a clear picture of bonding, structure, and resulting mechanical stability of the main group II–VI elements and their binary compounds. As summary, Fig. 27(a) offers an overview of the bonding behavior of the considered columns of the periodic table. This plot shows graphene as a monolayer with limiting properties, such as the largest cohesive energy and the shortest bond. Besides graphene, the strongest compounds belong to the planar structures with a steep decay of cohesive energies versus bond length. These are the homonuclear and heteronuclear compounds with a small atom from the second row of the periodic table (B, C, N). The dependence of the other monolayers with a buckled or puckered structure is characterized by a much faster increase of bond length and an asymptotically decreasing cohesive energy. The plot supports the marked inverse dependence of the binding energy on the bond length for 2D materials, as predicted by tight-binding theory. A coinciding decay of cohesive energies is postulated for elemental and low polarity binary monolayers of group IV and group V elements. Conversely, the elemental monolayers of group IV and group V have larger cohesive energies and bond energies than their isoelectronic counterparts. Generally, an increase of the bond length by a factor of two causes a decrease of the bonding energy by a factor of about four, owing to the strong reduction of orbital overlap. The revealed relationships offer useful guidance for future theoretical and experimental studies.Additionally, Fig. 27(b) displays the Young's moduli of the studied monolayers, as a function of their bond lengths. Interestingly, the stiffness of all related groups follows the same characteristic inverse behavior, at least in the stiffest direction. Note the extremely small Young's moduli of the strongly anisotropic puckered group V compounds in the armchair direction. Only the plane borophene phases and the rhombic configuration of selenene and tellurene deviate slightly from the general dependence. Remarkable is the extreme variation of the Young's modulus from 340 N m−1 to values below 10 N m−1. This demonstrates the enormous sensitivity of stiffness on bond energy that varies by less than a factor of four. Owing to the quite limited data reported for the ultimate strength, this information has not been included in Fig. 27(b) but is given only in the individual plots. At least for some directions the ultimate strength follows Griffith's rule and thus correlates with the stiffness.
Outlook
The extensive results presented here provide an up-to-date picture of calculated intrinsic bonding and mechanical properties of stable elemental and binary 2D materials of main group elements with fully occupied or blocked d orbitals, where only s and p electrons contribute to bonding. The large variation of the configuration of valence electrons dictates the possible types and strengths of bonding. In principle, in-plane bonding forces consist of normally predominant covalent and ionic interaction, where the latter long-range forces are not favorable for binding 2D structures.270 For specific groups conflicting results could be easily recognized and existing gaps were closed using the revealed relationships. Cohesive energies deviating be a factor of two or more have been excluded primarily based on their mechanical behavior. For the heaviest elemental monolayers of strontium, thallium, lead, and bismuth and their binary compounds not only experimental but also theoretical data on mechanical performance is missing. First reasonable estimates can be obtained by extrapolating the presented dependencies of mechanical properties on bond length. Note that for these compounds the low mechanical stability may be a crucial issue.Experimental verification of the extensive theoretical findings is still widely missing. It seems that it is possible to measure intrinsic properties of 2D materials, however, this has been achieved only in a few selected cases. Measurements of the inherent stiffness and ultimate strength, e.g., by AFM nanoindentation, are available for quasi freely suspended graphene, while the results for most other monolayers such as graphene oxide, h-BN, black P, transition metal-dichalcogenides such as MoS2 and WSe2, and MXenes are still preliminary.16,271,272 Besides the problem of preparing a perfect suspended monolayer uncertainties are due to the interpretation of the experimental data by simple mechanical models. Furthermore, it has been shown that ripples on suspended monolayers may have profound effects on the measured in-plane modulus. Notably, the calculated intrinsic properties can serve as a criterion to judge the quality of real defective samples studied experimentally.
An important issue that has not yet found the necessary attention is the change of mechanical properties induced by the ubiquitous interaction of monolayers with substrates during preparation, manipulation, and service. While van der Waals forces may preserve the intrinsic monolayer properties stronger covalent-like and ionic interactions can change the bond length and bonding energy and therefore may modify the fundamental mechanical and electronic properties. Here quantitative data is urgently needed.
Large area samples inevitably contain defects and the effects of prevailing defects have been studied theoretically only for selected 2D materials. While the ultimate strength, already studied in detail, is defined as the maximum stress a material can sustain in the absence of defects, the behavior of defective samples is described by the fracture toughness. Toughness values, which describe the ability of a material containing a crack to resist failure, are rare and seem to be restricted to graphene. Since graphene is brittle, its toughness is not an outstanding property as stiffness and strength.37,273 Its estimated toughness is largely independent of small nanometer defect sizes, whereas for larger defect sizes the experimental values increase as expected for non-ideal micrometer-sized crack paths.37 It is important to note that by intentionally introducing toughening mechanisms, for example, by proper manipulation of grain boundaries or effective use of interacting microdefects fracture resistance could be significantly improved.273
Besides the homonuclear, heteronuclear, and isoelectronic binary compounds considered here, all elements can be mixed in new combinations and stoichiometries, which represents an additional chemical parameter. Already known structures can be used to predict new ones by the method of ‘atomic transmutation’ by changing an element in the periodic table into its neighboring elements while keeping the total number of valence electrons constant. Furthermore, binary structures, consisting of other combination of main group elements such as II–VI, III–VI, IV–V, or V–VI, with stable MX and M2X3 phases, have been studied, thorough characterization, however, often is still missing.274,275 For example, only first results on the structure of three energetically stable phases are available for group III–VII compounds, which are isoelectronic to group V semiconductors.276 Besides different stoichiometries, chemistry allows the grouping of more than two elements to realize a plethora of chemical bonding types and structural arrangements, e.g., in ternary or quaternary 2D materials.277
Besides compounds of main group elements278 transition metal-dichalcogenides (TMDs), with partially empty d orbitals, such as the semiconductors MoS2 and WS2, have already attracted enormous attention.279 Furthermore, layered transition metal oxides (LTMO), layered halide perovskites, and layered double hydroxides (LDHs) belong to emerging 2D materials.280 Analogous to SiC and SiN with excellent mechanical and optical properties the family of MXenes, consisting of 2D transition metal carbides and nitrides, has found increasing interest.271,272 Mostly, MXenes contain functional groups such as fluorine, hydroxyl, and O2 and are endowed with beneficial electronic, magnetic, and optical properties. The extension of this large family to borides is under way.272
Besides monolayers the development of multilayer assemblies with hybrid/hierarchical structures opens innovative avenues to realize presently unknown 2D materials with novel tailored properties.273 Unfortunately, present approaches employed to treat the crucial properties such as the interlayer interaction energy show large deviations due to difficulties of theory treating the simultaneous action of quite different forces such as weak van der Waals interaction and strong covalent bonding. Since interlayer binding forces strongly influence not only the interlayer separation but also the electronic properties of multilayers and heterostructures this is a crucial point. Importantly, the observed deviations of literature values are often larger than a factor of about two found for the calculation of the cohesive binding energy of monolayers. Since the sources of these discrepancies are not understood improved approaches must be developed. Thorough understanding of interlayer interaction will be the key for using heterostructures as building blocks with the perspective of engineering functional materials with high performance, e.g., transistors, sensors, and photocatalysts.281
Conflicts of interest
There are no conflicts to declare.References
- N. Mounet, M. Gibertini, P. Schwaller, A. Merkys, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS PubMed.
- P. Vishnoi, K. Pramoda and C. N. R. Rao, ChemNanoMat, 2019, 5, 1062–1091 CrossRef CAS.
- P. Miró, M. Audiffred and T. Heine, Chem. Soc. Rev., 2014, 43, 6537–6554 RSC.
- B. Liu and K. Zhou, Prog. Mater. Sci., 2019, 100, 99–169 CrossRef CAS.
- S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutiérrez, T. F. Heinz, S. S. Hong, J. Huang, A. F. Ismach, E. Johnston-Halperin, M. Kuno, V. V. Plashnitsa, R. D. Robinson, R. S. Ruoff, S. Salahuddin, J. Shan, L. Shi, M. G. Spencer, M. Terrones, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 2898–2926 CrossRef CAS PubMed.
- A. J. Mannix, B. Kiraly, M. C. Hersam and N. P. Guisinger, Nat. Rev. Chem., 2017, 1, 0014 CrossRef CAS.
- P. Chen, Z. Zhang, X. Duan and X. Duan, Chem. Soc. Rev., 2018, 47, 3129–3151 RSC.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, aac9439 CrossRef CAS PubMed.
- J. Gao, Z. Xu, S. Chen, M. S. Bharathi and Y.-W. Zhang, Adv. Theory Simul., 2018, 1, 1800085 CrossRef.
- A. J. Mannix, Z. Zhang, N. P. Guisinger, B. I. Yakobson and M. C. Hersam, Nat. Nanotechnol., 2018, 13, 444–450 CrossRef CAS PubMed.
- W. A. Harrison, Pure Appl. Chem., 1989, 61, 2161–2169 CAS.
- R. E. Roman, N. M. Pugno and S. W. Cranford, in Advanced Computational Nanomechanics, ed. N. Silvestre, Wiley & Sons, Chichester, UK, 2016 Search PubMed.
- D. Akinwande, C. J. Brennan, J. S. Bunch, P. Egberts, J. R. Felts, H. Gao, R. Huang, J.-S. Kim, T. Li, Y. Li, K. M. Liechti, N. Lu, H. S. Park, E. J. Reed, P. Wang, B. I. Jakobson, T. Zhang, Y.-W. Zhang, Y. Zhou and Y. Zhu, Extreme Mech. Lett., 2017, 13, 42–77 CrossRef.
- B. Liu, M. Niu, J. Fu, Z. Xi, M. Lei and R. Quhe, Phys. Rev. Mater., 2019, 3, 054002 CrossRef CAS.
- P. Hess, Nanoscale Horiz., 2020, 5, 385–399 RSC.
- K. K. Al-Quraishi, Q. He, W. Kaupilla, M. Wang and Y. Yang, Int. J. Smart Nano Mater., 2020, 11, 207–246 CrossRef.
- X. Li, M. Sun, C. Shan, Q. Chen and X. Wei, Adv. Mater. Interfaces, 2018, 5, 1701246 CrossRef.
- P. Hess, Phys. Chem. Chem. Phys., 2018, 20, 7604–7611 RSC.
- A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358 CrossRef CAS PubMed.
- B. Peng, H. Zhang, H. Shao, K. Xu, G. Ni, J. Li, H. Zhu and C. M. Soukoulis, J. Mater. Chem. A, 2018, 6, 2018–2033 RSC.
- H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501 CrossRef PubMed.
- B. Peng, H. Zhang, H. Shao, Z. Ning, Y. Xu, G. Ni, H. Lu, D. W. Zhang and H. Zhu, Mater. Res. Lett., 2017, 5, 399–407 CrossRef CAS.
- X. Wu, J. Dai, Y. Zhao, Z. Zhuo, J. Yang and X. C. Zeng, ACS Nano, 2012, 6, 7443–7453 CrossRef CAS PubMed.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS PubMed.
- B. Mortazavi, O. Rahaman, A. Dianat and T. Rabczuk, Phys. Chem. Chem. Phys., 2016, 18, 27405–27413 RSC.
- J. Yuan, N. Yu, K. Xue and X. Miao, RSC Adv., 2017, 7, 8654–8660 RSC.
- S. Ipek, M. E. Kilic, A. Mogulkoc, S. Cahangirov and E. Durgun, Phys. Rev. B, 2018, 98, 241408(R) CrossRef.
- C. Kamal, A. Chakrabarti and M. Ezawa, New J. Phys., 2015, 17, 083014 CrossRef.
- I. Lukačević, M. V. Pajtler, M. Mužević and S. K. Gupta, J. Mater. Chem. C, 2019, 7, 2666–2675 RSC.
- K. H. Yeoh, T. L. Yoon, Rusi, D. S. Ong and T. L. Lim, Appl. Surf. Sci., 2018, 445, 161–166 CrossRef CAS.
- J. Yuan, N. Yu, K. Xue and X. Miao, Appl. Surf. Sci., 2017, 409, 85–90 CrossRef CAS.
- M. Nakhaee, M. Yagmurcukardes, S. A. Ketabi and F. M. Peeters, Phys. Chem. Chem. Phys., 2019, 21, 15798–15804 RSC.
- V. Kochat, A. Samanta, Y. Zhang, S. Bhowmick, P. Manimunda, S. A. S. Asif, A. S. Stender, R. Vajtai, A. K. Singh, C. S. Tiwary and P. M. Ajayan, Sci. Adv., 2018, 4, e1701373 CrossRef PubMed.
- S. V. Badalov, M. Yagmurcukardes, F. M. Peeters and H. Sahin, J. Phys. Chem. C, 2018, 122, 28302–28309 CrossRef CAS.
- D. Z. Metin, L. Hammerschmidt and N. Gaston, Phys. Chem. Chem. Phys., 2018, 20, 27668–27674 RSC.
- D. Singh, S. K. Gupta, I. Lukačević and Y. Sonvane, RSC Adv., 2016, 6, 8006–8014 RSC.
- P. Hess, J. Appl. Phys., 2016, 120, 124303 CrossRef.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- Z. Zhang, Y. Yang, E. S. Penev and B. I. Jakobson, Adv. Funct. Mater., 2017, 27, 1605059 CrossRef.
- Z.-D. Sha, Q.-X. Pei, K. Zhou, Z. Dong and Y.-W. Zhang, Extreme Mech. Lett., 2018, 19, 39–45 CrossRef.
- Z.-Q. Wang, T.-Y. Lü, H.-Q. Wang, Y. P. Feng and J.-C. Zheng, Front. Phys., 2019, 14, 33403 CrossRef.
- M. Mužević, Doctoral Dissertation, Faculty of Science, University of Zagreb, 2019 Search PubMed.
- H. Zhong, K. Huang, G. Yu and S. Yuan, Phys. Rev. B, 2018, 98, 054104 CrossRef CAS.
- S. Kansara, S. K. Gupta, Y. Sonvane, T. Hussain and R. Ahuja, ACS Appl. Energy Mater., 2018, 1, 3428–3433 CrossRef CAS.
- C. Hou, G. Tai, Z. Wu and J. Hao, ChemPlusChem, 2020, 85, 2186–2196 CrossRef CAS PubMed.
- Y. Wang, Y. Li and Z. Chen, Acc. Chem. Res., 2020, 53, 887–895 CrossRef CAS PubMed.
- L.-M. Yang, E. Ganz, Z. Chen, Z.-X. Wang and P. V. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468–9501 CrossRef CAS PubMed.
- T. R. Galeev, B. D. Dunnington, J. R. Schmidt and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2013, 15, 5022–5029 RSC.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- C.-S. Liu, H.-H. Zhu, X.-J. Ye and X.-H. Yan, Nanoscale, 2017, 9, 5854–5858 RSC.
- G. Sharma and K. C. Bhamu, 2020, arXiv:2003.07400v2.
- Y. Li, Y. Liao and Z. Chen, Angew. Chem., 2014, 126, 7376–7380 CrossRef.
- Y. Wang, F. Li, Y. Li and Z. Chen, Nat. Commun., 2016, 7, 11488 CrossRef CAS PubMed.
- L. Meng, S. Ni, M. Zhou, Y. Zhang, Z. Li and W. Wu, Phys. Chem. Chem. Phys., 2017, 19, 32086–32090 RSC.
- S.-S. Wang, Y. Liu, Z.-M. Yu, X.-L. Sheng, L. Zhu, S. Guan and S. A. Yang, Phys. Rev. Mater., 2018, 2, 104003 CrossRef CAS.
- K. Rajput, V. Kumar, S. Thomas, M. A. Zaeem and D. R. Roy, 2D Mater., 2021, 8, 035015 CrossRef.
- Y. Wang, M. Qiao, Y. Li and Z. Chen, Nanoscale Horiz., 2018, 3, 327–334 RSC.
- J. Dai, Z. Li, J. Yang and J. Hou, Nanoscale, 2012, 4, 3032–3035 RSC.
- X. Wu, Y. Pei and X. C. Zeng, Nano Lett., 2009, 9, 1577–1582 CrossRef CAS PubMed.
- X. Luo, J. Yang, H. Liu, X. Wu, Y. Wang, Y. Ma, S. H. Wei, X. Gong and H. Xiang, J. Am. Chem. Soc., 2011, 133, 16285–16290 CrossRef CAS PubMed.
- K. Exner and P. von Ragué Schleyer, Science, 2000, 290, 1937–1940 CrossRef CAS PubMed.
- H. Chang, K. Tu, X. Zhang, J. Zhao, X. Zhou and H. Zhang, J. Phys. Chem. C, 2019, 123, 25091–25101 CrossRef CAS.
- Y. Li, Y. Liao, P. V. R. Schleyer and Z. Chen, Nanoscale, 2014, 6, 10784–10791 RSC.
- J. Dai, X. Wu, J. Yang and X. C. Zeng, J. Phys. Chem. Lett., 2014, 5, 2058–2065 CrossRef CAS PubMed.
- L. Schimka, J. Harl and G. Kresse, J. Chem. Phys., 2011, 134, 024116 CrossRef PubMed.
- Y. Zhang, Z.-F. Wu, P.-F. Gao, D.-Q. Fang, E.-H. Zhang and S.-L. Zhang, RSC Adv., 2018, 8, 1686–1692 RSC.
- H. Zhang, Y. Liao, G. Yang and X. Zhou, ACS Omega, 2018, 3, 10517–10525 CrossRef CAS PubMed.
- L.-J. Zhou, Y.-F. Zhang and L.-M. Wu, Nano Lett., 2013, 13, 5431–5436 CrossRef CAS PubMed.
- Y. Li, F. Li, Z. Zhou and Z. Chen, J. Am. Chem. Soc., 2011, 133, 900–908 CrossRef CAS PubMed.
- A. K. Geim, Science, 2009, 324, 1530–1534 CrossRef CAS PubMed.
- G. Lu, K. Yu, Z. Wen and J. Chen, Nanoscale, 2013, 5, 1353–1368 RSC.
- J. Zhao, H. Liu, Z. Yu, R. Quhe, S. Zhou, Y. Wang, C. C. Liu, H. Zhong, N. Han, J. Lu, Y. Yao and K. Wu, Prog. Mater. Sci., 2016, 83, 24–151 CrossRef CAS.
- R. John and B. Merlin, Cryst. Struct. Theory Appl., 2016, 5, 43–55 CAS.
- X.-L. Yu, L. Huang and J. Wu, Phys. Rev. B, 2017, 95, 125113 CrossRef.
- J. C. Garcia, D. B. de Lima, L. V. C. Assali and J. F. Justo, J. Phys. Chem. C, 2011, 115, 13242–13246 CrossRef CAS.
- D. D. L. Chung, J. Mater. Sci., 2002, 37, 1475–1489 CrossRef CAS.
- J. D. Bernal, Proc. R. Soc. London, Ser. A, 1924, 106, 749–773 CAS.
- H. Shin, S. Kang, J. Koo, H. Lee and Y. Kwon, J. Chem. Phys., 2014, 140, 114702 CrossRef PubMed.
- L. M. Malard, D. L. Mafra, M. H. D. Guimarães, M. S. C. Mazzoni and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125426 CrossRef.
- H. M. Shodja, F. Ojaghnezhad, A. Etehadieh and M. Tabatabaei, Mech. Mater., 2017, 110, 1–15 CrossRef.
- C. Kamal, A. Banerjee and A. Chakrabarti, CRC Handbook of Chemistry and Physics, Properties of Two-Dimensional Silicon versus Carbon Systems, CRC Press, Boca Raton, FL, 97th edn, ch. 15, 2016, pp. 221–233 Search PubMed.
- J. Liu, Y. Yang, P. Lyu, P. Nachtigall and Y. Xu, Adv. Mater., 2018, 30, 1800838 CrossRef PubMed.
- C. Huang, J. Zhou, H. Wu, K. Deng, P. Jena and E. Kan, J. Phys. Chem. Lett., 2016, 7, 1919–1924 CrossRef CAS PubMed.
- B. Peng, H. Zhang, H. Shao, Y. Xu, G. Ni, R. Zhang and H. Zhu, Phys. Rev. B, 2016, 94, 245420 CrossRef.
- M. R. Arshee, S. Adnan, M. Motalab and P. Bose, RSC Adv., 2019, 9, 34437–34450 RSC.
- J.-K. Lyu, S.-F. Zhang, C.-W. Zhang and P.-J. Wang, Ann. Phys., 2019, 531, 1900017 CrossRef CAS.
- M. J. Cherukara, B. Narayanan, A. Kinaci, K. Sasikumar, S. K. Gray, M. K. Y. Chan and S. K. R. S. Sankaranarayanan, J. Phys. Chem. Lett., 2016, 7, 3752–3759 CrossRef CAS PubMed.
- A. Mahmood and G. Rahman, J. Phys.: Condens. Matter, 2020, 32, 205501 CrossRef CAS PubMed.
- H. Zhao, C.-W. Zhang, W.-X. Ji, R.-W. Zhang, S.-S. Li, S.-S. Yan, B.-M. Zhang, P. Li and P.-J. Wang, Sci. Rep., 2016, 6, 20152 CrossRef CAS PubMed.
- S. Mahmud and Md. K. Alam, RSC Adv., 2019, 9, 42194–42203 RSC.
- G. Cao, Polymers, 2014, 6, 2404–2432 CrossRef.
- T. Zhang, X. Li and H. Gao, Int. J. Fract., 2015, 196, 1–31 CrossRef.
- C. A. Marianetti and H. G. Yevick, Phys. Rev. Lett., 2010, 105, 245502 CrossRef CAS PubMed.
- G. Rajasekaran, P. Narayanan and A. Parashar, Crit. Rev. Solid State Mater. Sci., 2015, 41, 47–71 CrossRef.
- H. Zhao, Phys. Lett. A, 2012, 376, 3546–3550 CrossRef CAS.
- B. Mortazavi, O. Rahaman, M. Makaremi, A. Dianat, G. Cuniberti and T. Rabczuk, Phys. E, 2017, 87, 228–232 CrossRef CAS.
- D. K. Das, J. Sarkar and S. K. Singh, Comput. Mater. Sci., 2018, 151, 196–203 CrossRef CAS.
- G. Yang, L. Li, W. B. Lee and M. C. Ng, Sci. Technol. Adv. Mater., 2018, 19, 613–648 CrossRef CAS PubMed.
- G. Graziano, J. Klimeš, F. Fernandez-Alonso and A. Michaelides, J. Phys.: Condens. Matter, 2012, 24, 424216 CrossRef PubMed.
- T. Gould, S. Lebèque and J. F. Dobson, J. Phys.: Condens. Matter, 2013, 25, 445010 CrossRef PubMed.
- M. C. Schabel and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 7185–7188 CrossRef CAS PubMed.
- J. E. Padilha and R. B. Pontes, J. Phys. Chem. C, 2015, 119, 3818–3825 CrossRef CAS.
- D. K. Sharma, S. Kumar, A. Laref and S. Auluck, Comput. Condens. Matter, 2018, 16, e00314 CrossRef.
- L. Zhang, H. Zhao, W.-X. Ji, C.-W. Zhang, P. Li and P.-J. Wang, Chem. Phys. Lett., 2018, 712, 78–82 CrossRef CAS.
- M. Coroş, F. Pogacean, L. Mageruşan, C. Socaci and S. Pruneanu, Front. Mater. Sci., 2019, 13, 23–32 CrossRef.
- C. Shen, X. Yan, F. Qing, X. Niu, R. Stehle, S. S. Mao, W. Zhang and X. Li, J. Materiomics, 2019, 5, 463–470 CrossRef.
- A. Molle, C. Grazianetti, L. Tao, D. Taneja, Md. H. Alam and D. Akinwande, Chem. Soc. Rev., 2018, 47, 6370–6387 RSC.
- J. Deng, B. Xia, X. Ma, H. Chen, H. Shan, X. Zhai, B. Li, A. Zhao, Y. Xu, W. Duan, S.-C. Zhang, B. Wang and J. G. Hou, Nat. Mater., 2018, 17, 1081–1086 CrossRef CAS PubMed.
- J. Yuhara, B. He, N. Matsunami, M. Nakatake and G. Le Lay, Adv. Mater., 2019, 31, 1901017 CrossRef PubMed.
- G. Bihlmayer, J. Sassmannshausen, A. Kubetzka, S. Blügel, K. von Bergmann and R. Wiesendanger, Phys. Rev. Lett., 2020, 124, 126401 CrossRef CAS PubMed.
- J. Yuhara and G. Le Lay, Jpn. J. Appl. Phys., 2020, 59, SN0801 CrossRef CAS.
- E. Bekaroglu, M. Topsakal, S. Cahangirov and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075433 CrossRef.
- S.-D. Guo and J.-T. Liu, Phys. Chem. Chem. Phys., 2018, 20, 22038–22046 RSC.
- Q. Peng, Mech. Mater., 2020, 148, 103473 CrossRef.
- H. Sahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- A. V. Kalashnikov, A. V. Tuchin, L. A. Bityutskaya and T. V. Kulikova, J. Phys.: Conf. Ser., 2019, 1199, 012009 CrossRef CAS.
- A. Yaghoubi, K. Masenelli-Varlot, O. Boisron, S. Ramesh and P. Melinon, Chem. Mater., 2018, 30, 7234–7244 CrossRef CAS.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- Q. Peng, C. Liang, W. Ji and S. De, Mech. Mater., 2013, 64, 135–141 CrossRef.
- Z. Xu, Y. Li, C. Li and Z. Liu, Appl. Surf. Sci., 2016, 367, 19–25 CrossRef CAS.
- D. M. Hoat, M. Naseri, R. Ponce-Péreze, N. N. Hieu, J. F. Rivas-Silva, T. V. Vu, H. D. Tong and G. H. Cocoletzi, Mater. Res. Express, 2020, 7, 015013 CrossRef CAS.
- M. Fadaie, N. Shahtahmassebi, M. R. Roknabad and O. Gulseren, Comput. Mater. Sci., 2017, 137, 208–214 CrossRef CAS.
- P. Jamdagni, A. Kumar, A. Thakur, R. Pandey and P. K. Ahluwalia, Mater. Res. Express, 2015, 2, 016301 CrossRef CAS.
- W.-Z. Yu, J.-A. Yan and S.-P. Gao, Nanoscale Res. Lett., 2015, 10, 351 CrossRef PubMed.
- Y. Wang and Y. Ding, Appl. Surf. Sci., 2016, 382, 1–9 CrossRef CAS.
- D. D. Sante, A. Stroppa, P. Barone, M.-H. Whangbo and S. Picozzi, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 161401(R) CrossRef.
- M.-Q. Le, J. Comput. Theor. Nanosci., 2014, 11, 1458–1464 CrossRef CAS.
- J. Shi, Y. Gao, X.-L. Wang and S.-N. Yun, Chin. Phys. Lett., 2017, 34, 087701 CrossRef.
- T. Susi, V. Skákalová, A. Mittelberger, P. Kotrusz, M. Hulman, T. J. Pennycook, C. Mangler, J. Kotakoski and J. C. Meyer, Sci. Rep., 2017, 7, 4399 CrossRef PubMed.
- S. S. Lin, J. Phys. Chem. C, 2012, 116, 3951–3955 CrossRef CAS.
- X.-F. Liu, Z.-J. Luo, X. Zhou, J.-M. Wei, Y. Wang, X. Guo, B. Lv and Z. Ding, Chin. Phys. B, 2019, 28, 086105 CrossRef CAS.
- V. O. Özçelik, J. G. Azadani, C. Yang, S. J. Koester and T. Low, Phys. Rev. B, 2016, 94, 035125 CrossRef.
- B. P. Bahuguna, L. K. Saini, R. O. Sharma and B. Tiwari, Phys. E, 2018, 99, 236–243 CrossRef CAS.
- A. Gonzáles-García, W. López-Pérez, J. Rivera-Julio, F. M. Peteers, V. Mendoza-Estrada and R. González-Hernández, Comput. Mater. Sci., 2018, 144, 285–293 CrossRef.
- A. Pakdel, Y. Bando and D. Golberg, Chem. Soc. Rev., 2014, 43, 934–959 RSC.
- H. L. Zhuang and R. G. Hennig, Appl. Phys. Lett., 1012, 101, 153109 CrossRef.
- Y. Shi, C. Hamsen, X. Jia, K. K. Kim, A. Reina, M. Hofmann, A. L. Hsu, K. Zhang, H. Li, Z.-Y. Juang, M. S. Dresselhaus, L.-J. Li and J. Kong, Nano Lett., 2010, 10, 4134–4139 CrossRef CAS PubMed.
- O. Hod and J. Chem, Theory Comput., 2012, 8, 1360–1369 CrossRef CAS PubMed.
- Y. Zhang, J. Kang, F. Zheng, P.-F. Gao, S.-L. Zhang and L.-W. Wang, J. Chem. Phys. Lett., 2019, 10, 6656–6663 CrossRef CAS PubMed.
- X. Chen, C. Tan, Q. Yang, R. Meng, Q. Liang, J. Jiang, X. Sun, D. Q. Yang and T. Ren, Phys. Chem. Chem. Phys., 2016, 18, 16229–16236 RSC.
- J. Zhang, H. Liu, Y. Gao, X. Xia and Z. Huang, Phys. Chem. Chem. Phys., 2019, 21, 20981–20987 RSC.
- R. R. Q. Freitas, R. Rivelino, F. de Brito Mota and C. M. C. de Castilho, J. Phys. Chem. C, 2015, 119, 23599–23606 CrossRef CAS.
- C. Bacaksiz, H. Sahin, H. D. Ozaydin, S. Horzum, R. T. Senger and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 81, 085430 CrossRef.
- D. Kecik, A. Onen, M. Konuk, E. Gürbüz, F. Ersan, S. Cahangirov, E. Aktürk, E. Durgun and S. Ciraci, Appl. Phys. Rev., 2018, 5, 011105 Search PubMed.
- D. Xu, H. He, R. Pandey and S. P. Karna, J. Phys.: Condens. Matter, 2013, 25, 345302 CrossRef PubMed.
- V. Kumar and D. R. Roy, J. Mater. Sci., 2018, 53, 8302–8313 CrossRef CAS.
- M. S. Prete, O. Pulci and F. Bechstadt, Phys. Rev. B, 2018, 98, 235431 CrossRef CAS.
- P. Zhou, L. Xue and L. Z. Sun, J. Mater. Chem. C, 2017, 5, 4268–4274 RSC.
- C.-J. Tong, H. Zhang, Y.-N. Zhang, H. Liu and L.-M. Liu, J. Mater. Chem. A, 2014, 2, 17971–17978 RSC.
- P. Hess, Nanotechnology, 2017, 28, 064002 CrossRef PubMed.
- Q. Peng, W. Ji and S. De, Comput. Mater. Sci., 2012, 56, 11–17 CrossRef CAS.
- J. Wu, B. Wang, Y. Wei, R. Yang and M. Dresselhaus, Mater. Res. Lett., 2013, 1, 200–206 CrossRef CAS.
- Q. Peng, X.-J. Chen, S. Liu and S. De, RSC Adv., 2013, 3, 7083–7092 RSC.
- M. N. Blonsky, H. L. Zhuang, A. K. Singh and R. G. Hennig, ACS Nano, 2015, 9, 9885–9891 CrossRef CAS PubMed.
- Q. Peng, C. Liang, W. Ji and S. De, Appl. Phys. A, 2013, 113, 483–490 CrossRef CAS.
- D. Liang, R. Quhe, Y. Chen, L. Wu, Q. Wang, P. Guan, S. Wang and P. Lu, RSC Adv., 2017, 7, 42455–42461 RSC.
- Q. Peng, X. Sun, H. Wang, Y. Yang, X. Wen, C. Huang, S. Liu and S. De, Appl. Mater. Today, 2017, 7, 169–178 CrossRef.
- X. Li, Y. Dai, Y. Ma, W. Wei, L. Yu and B. Huang, Nano Res., 2015, 8, 2954–2962 CrossRef CAS.
- Q. Peng, C. Liang, W. Ji and S. De, Model. Numer. Simul. Mater. Sci., 2012, 2, 76–84 Search PubMed.
- N. Marom, J. Bernstein, J. Garel, A. Tkatchenko, E. Joselevich, L. Kronik and O. Hod, Phys. Rev. Lett., 2010, 105, 046801 CrossRef PubMed.
- R. B. dos Santos, F. de Brito Mota, R. Rivelino, A. Kakanakova-Georgieva and G. K. Gueorguiev, Nanotechnology, 2016, 27, 145601 CrossRef PubMed.
- A. Azizi, M. A. AlSaud and N. Alem, J. Cryst. Growth, 2018, 496–497, 51–56 CrossRef CAS.
- T. S. Cheng, A. Summerfield and C. J. Mellor, J. Vac. Sci. Technol. B, 2018, 36, 02D103 CrossRef.
- L. Wang, X. Xu, L. Zhang, R. Qiao, M. Wu, Z. Wang, S. Zhang, J. Liang, Z. Zhang, Z. Zhang, W. Chen, X. Xie, J. Zong, Y. Shan, Y. Guo, M. Willinger, H. Wu, Q. Li, W. Wang, P. Gao, S. Wu, Y. Zhang, Y. Jiang, D. Yu, E. Wang, X. Bai, Z.-J. Wang, F. Ding and K. Liu, Nature, 2019, 570, 91–95 CrossRef CAS PubMed.
- T.-A. Chen, C.-P. Chuu, C.-C. Tseng, C.-K. Wen, H.-S. P. Wong, S. Pan, R. Li, T.-A. Chao, W.-C. Chueh, Y. Zhang, Q. Fu, B. I. Yakobson, W.-H. Chang and L.-J. Li, Nature, 2020, 579, 219–223 CrossRef CAS PubMed.
- D. Kecik, C. Bacaksiz, R. T. Senger and E. Durgun, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 165408 CrossRef.
- Y. Cai, Y. Liu, Y. Xie, Y. Zou, C. Gao, Y. Zhao, S. Liu, H. Xu, J. Shi, S. Guo and C. Sun, APL Mater., 2020, 8, 021107 CrossRef CAS.
- P. Tsipas, S. Kassavetis, D. Tsoutsou, E. Xenogiannopoulou, E. Golias, S. A. Giamini, C. Grazianetti, D. Chiappe, A. Molle, M. Fanciulli and A. Dimoulas, Appl. Phys. Lett., 2013, 103, 251605 CrossRef.
- M. Beshkova and R. Yakimova, Vacuum, 2020, 176, 109231 CrossRef CAS.
- A. V. Kolobov, P. Fons, Y. Saito, J. Tominaga, B. Hyot and B. André, Phys. Rev. Mater., 2017, 1, 024003 CrossRef.
- A. Onen, D. Kecik, E. Durgun and S. Ciraci, J. Phys. Chem. C, 2017, 121, 27098–27110 CrossRef CAS.
- H. Shu, X. Niu, X. Ding and Y. Wang, Appl. Surf. Sci., 2019, 479, 475–481 CrossRef CAS.
- W.-K. Wang and M.-C. Jiang, Jpn. J. Appl. Phys., 2016, 55, 095503 CrossRef.
- S. Wang, F. Qin, Y. Bai, D. Zhang and J. Zhang, Coatings, 2020, 10, 1185 CrossRef CAS.
- F. Ersan, D. Kecik, V. O. Özçelik, Y. Kadioglu, O. Ü. Aktürk, E. Durgun, E. Aktürk and S. Ciraci, Appl. Phys. Rev., 2019, 6, 021308 Search PubMed.
- S. Guo, W. Zhou, B. Cai, K. Zhang, S. Zhang and H. Zeng, Nanoscale Horiz., 2019, 4, 1145–1152 RSC.
- S. Zhang, S. Guo, Z. Chen, Y. Wang, H. Gao, J. Gómez-Herrero, P. Ares, F. Zamora, Z. Zhu and H. Zeng, Chem. Soc. Rev., 2018, 47, 982–1021 RSC.
- S. Guo, Y. Zhang, Y. Ge, S. Zhang, H. Zeng and H. Zhang, Adv. Mater., 2019, 31, 1902352 CrossRef PubMed.
- V. Sorkin, Y. Cai, Z. Ong, G. Zhang and Y. W. Zhang, Crit. Rev. Solid State Mater. Sci., 2017, 42, 1–82 CrossRef CAS.
- F. Ersan, E. Aktürk and S. Ciraci, Phys. Rev. B, 2017, 96, 205434 CrossRef.
- G. Liu, Z. Gao and J. Zhou, Phys. E, 2019, 112, 59–65 CrossRef CAS.
- Q. Wei and X. Peng, Appl. Phys. Lett., 2014, 104, 251915 CrossRef.
- Y. Mogulkoc, M. Modarresi, A. Mogulkoc and Y. O. Ciftci, Comput. Mater. Sci., 2016, 124, 23–29 CrossRef CAS.
- D. Kecik, E. Durgun and S. Ciraci, Phys. Rev. B, 2016, 94, 205409 CrossRef.
- Y. Kadioglu, J. A. Santana, H. D. Özaydin, F. Ersan, O. Ü. Aktürk, E. Aktürk and F. A. Reboredo, J. Chem. Phys., 2018, 148, 214706 CrossRef PubMed.
- T. Kocabaş, D. Cakir, O. Gülseren, F. Ay, N. K. Perkgöz and C. Sevik, Nanoscale, 2018, 10, 7803–7812 RSC.
- Y. Nie, M. Rahman, D. Wang, C. Wang and G. Guo, Sci. Rep., 2015, 5, 17980 CrossRef CAS PubMed.
- O. Ü. Aktürk, V. O. Özçelik and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235446 CrossRef.
- G. Wang, R. Pandey and S. P. Karna, ACS Appl. Mater. Interfaces, 2015, 7, 11490–11496 CrossRef CAS PubMed.
- N. A. P. Namari and M. Saito, Jpn. J. Appl. Phys., 2019, 58, 061003 CrossRef CAS.
- E. Aktürk, O. Ü. Aktürk and S. Ciraci, Phys. Rev. B, 2016, 94, 014115 CrossRef.
- S. Ma, C. He, L. Z. Sun, H. Lin, Y. Li and K. W. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 32009–32015 RSC.
- W. Yu, C.-Y. Niu, Z. Zhu, X. Wang and W.-B. Zhang, J. Mater. Chem. C, 2016, 4, 6581–6587 RSC.
- H. Yin, J. Gao, G.-P. Zheng, Y. Wang and Y. Ma, J. Phys. Chem. C, 2017, 121, 25576–25584 CrossRef CAS.
- C. Liu, W. Wan, J. Ma, W. Guo and Y. Yao, Nanoscale, 2018, 10, 7984–7990 RSC.
- Z. Yang, D. Han, G. Chen and S. Chen, Mater. Res. Express, 2018, 5, 035904 CrossRef.
- P. Chen, X.-J. Zhang and B.-G. Liu, ACS Appl. Nano Mater., 2019, 2, 58–63 CrossRef CAS.
- W.-Z. Xiao, G. Xiao, Q.-Y. Rong and L.-L. Wang, Phys. Chem. Chem. Phys., 2018, 20, 22027–22037 RSC.
- W.-Z. Xiao, G. Xiao, Q.-Y. Rong and L.-L. Wang, Mater. Res. Express, 2018, 5, 035903 CrossRef.
- T. Teshome and A. Datta, J. Phys. Chem. C, 2018, 122, 15047–15054 CrossRef CAS.
- W. Yu, C.-Y. Niu, Z. Zhu, X. Cai, L. Zhang, S. Bai, R. Zhao and Y. Jia, RSC Adv., 2017, 7, 27816–27822 RSC.
- J.-W. Jiang and H. S. Park, J. Phys. D: Appl. Phys., 2014, 47, 385304 CrossRef.
- L. Wang, A. Kutana, X. Zou and B. I. Yakobson, Nanoscale, 2015, 7, 9746–9751 RSC.
- N. Liu, J. Hong, R. Pidaparti and X. Wang, Nanoscale, 2016, 8, 5728–5736 RSC.
- J. Ribeiro-Soares, R. M. Almeida, L. G. Cançado, M. S. Dresselhaus and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205421 CrossRef.
- C. Kamal and M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085423 CrossRef.
- E. H. Chowdhury, M. H. Rahman, P. Bose, R. Jayan and M. H. Islam, Phys. Chem. Chem. Phys., 2020, 22, 28238–28255 RSC.
- S.-D. Guo, J. Phys. D: Appl. Phys., 2018, 51, 265307 CrossRef.
- L. Zhu and T. Zhang, J. Nanopart. Res., 2018, 20, 237 CrossRef.
- W. Zhang, H. Enriquez, A. J. Mayne, G. Dujardin and H. Oughaddou, Small, 2018, 14, 1870249 CrossRef.
- P. Juan, T. Zhang, J. Sun, L. Liu, Y. Yao and Y. Wang, J. Semicond., 2020, 41, 081003 CrossRef.
- M. Pica and R. DÁmato, Inorganics, 2020, 8, 29.188 CrossRef.
- M. Pumera and Z. Sofer, Adv. Mater., 2017, 29, 1605299 CrossRef PubMed.
- J. Shah, W. Wang, H. M. Sohail and R. I. G. Uhrberg, 2D Mater, 2020, 7, 025013 CrossRef CAS.
- X. Wu, Y. Shao, H. Liu, Z. Feng, Y.-L. Wang, J.-T. Sun, C. Liu, J.-O. Wang, Z.-L. Liu, S.-Y. Zhu, Y.-Q. Wang, S.-X. Du, Y.-G. Shi, K. Ibrahim and H.-J. Gao, Adv. Mater., 2017, 29, 1605407 CrossRef PubMed.
- M. Gu, C. Li, Y. Ding, K. Zhang, S. Xia, Y. Wang, M.-H. Lu, H. Lu and Y.-F. Chen, Appl. Sci., 2020, 10, 639 CrossRef.
- Z.-Q. Shi, H. Li, Q.-Q. Yuan, Y.-H. Song, Y.-Y. Lv, W. Shi, Z.-Y. Jia, L. Gao, Y.-B. Chen, W. Zhu and S.-C. Li, Adv. Mater., 2019, 31, 1806130 CrossRef PubMed.
- P. Ares, J. J. Palacios, G. Abellán, J. Gómes-Herrero and F. Zamora, Adv. Mater., 2018, 30, 1703771 CrossRef PubMed.
- F. Reis, G. Li, L. Dudy, M. Bauernfeind, S. Glass, W. Hanke, R. Thomale, J. Schäfer and R. Claessen, Science, 2017, 357, 287–290 CrossRef CAS PubMed.
- F. Dominguez, B. Scharf, G. Li, J. Schäfer, R. Claessen, W. Hanke, R. Thomale and E. M. Hankiewicz, Phys. Rev. B, 2018, 98, 161407(R) CrossRef.
- A. A. Kistanov, S. K. Khadiullin, K. Zhou, S. V. Dmitriev and E. A. Korznikova, J. Mater. Chem. C, 2019, 7, 9195–9202 RSC.
- A. Walsh and G. W. Watson, J. Phys. Chem. B, 2005, 109, 18868–18875 CrossRef CAS PubMed.
- Y. Du, H.-C. Ding, L. Sheng, S. Y. Savrasov, X. Wan and C.-G. Duan, J. Phys.: Condens. Matter., 2014, 26, 025503 CrossRef CAS PubMed.
- Z. Hu, Y. Ding, X. Hu, W. Zhou, X. Yu and S. Zhang, Nanotechnology, 2019, 30, 252001 CrossRef CAS PubMed.
- C. Kamal, A. Chakrabarti and M. Ezawa, Phys. Rev. B, 2016, 93, 125428 CrossRef.
- A. Zaharo, A. Purqon, M. Saito, T. Winata and M. Saito, Jpn. J. Appl. Phys., 2020, 59, 071006 CrossRef CAS.
- Y.-L. Zhu, J.-H. Juan, Y.-Q. Song, S. Wang, K.-H. Xue, M. Xu, X.-M. Cheng and X.-S. Miao, J. Mater. Sci., 2019, 54, 11485–11496 CrossRef CAS.
- C. Chowdhury, S. Karmakar and A. Datta, J. Phys. Chem. C, 2017, 121, 7615–7624 CrossRef.
- R. Li, H. Cao and J. Dong, Phys. Lett. A, 2017, 381, 3747–3753 CrossRef CAS.
- Q. Zhang, T. Xin, X. Lu and Y. Wang, Materials, 2018, 11, 431 CrossRef PubMed.
- Q. Zhang, Y. Feng, X. Chen, W. Zhang, L. Wu and Y. Wang, Nanomaterials, 2019, 9, 598 CrossRef CAS PubMed.
- Y. Xu, K. Xu and H. Zhang, Molecules, 2019, 24, 639 CrossRef CAS PubMed.
- Y. Chen, Q. Sun and P. Jena, J. Mater. Chem. C, 2016, 4, 6353–6361 RSC.
- L. Huang, F. Wu and J. Li, J. Chem. Phys., 2016, 144, 114708 CrossRef PubMed.
- G. Qin, Z. Qin, W.-Z. Fang, L.-C. Zhang, S.-Y. Yue, Q.-B. Yan, M. Hu and G. Su, Nanoscale, 2016, 8, 11306–11319 RSC.
- Y. Gao, L. Zhang, G. Yao and H. Wang, J. Appl. Phys., 2019, 125, 082519 CrossRef.
- L.-C. Zhang, G. Qin, W.-Z. Fang, H.-J. Cui, Q.-R. Zheng, Q.-B. Yan and G. Su, Sci. Rep., 2016, 6, 19830 CrossRef CAS PubMed.
- X. Kong, J. Deng, L. Li, X. Ding, J. Sun and J. Z. Liu, Phys. Rev. B, 2018, 98, 184104 CrossRef.
- L. C. Gomes and A. Carvalho, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085406 CrossRef.
- Z.-Y. Li, M.-Y. Liu, Y. Huang, Q.-Y. Chen, C. Cao and Y. He, Phys. Chem. Chem. Phys., 2018, 20, 214–220 RSC.
- Y. Mao, C. Xu, J. Yuan and H. Zhao, Phys. Chem. Chem. Phys., 2018, 20, 6929–6935 RSC.
- K. Chang and S. S. P. Parkin, J. Appl. Phys., 2020, 127, 220902 CrossRef CAS.
- Y. Ye, Q. Guo, X. Liu, C. Liu, J. Wang, Y. Liu and J. Qiu, Chem. Mater., 2017, 29, 8361–8368 CrossRef CAS.
- J. R. Brent, D. J. Lewis, T. Lorenz, E. A. Lewis, N. Savjani, S. J. Haigh, G. Seifert, B. Derby and P. O’Brien, J. Am. Chem. Soc., 2015, 137, 12689–12696 CrossRef CAS PubMed.
- M. Patel, H.-S. Kim and J. Kim, Nanoscale, 2017, 9, 15804 RSC.
- L. Su, X. Fan, C. Wang, Q. Wu, Y. Li, H. Zhang and H. Xie, Nanophotonics, 2020, 9, 1621–1649 CrossRef.
- Y. Xiang, S. Gao, R.-G. Xu, W. Wu and Y. Leng, Nano Energy, 2019, 58, 202–210 CrossRef CAS.
- C. Liu, T. Hu, Y. Wu, H. Gao, Y. Yang and W. Ren, J. Phys.: Condens. Matter, 2019, 31, 235702 CrossRef CAS PubMed.
- L. Xian, A. P. Paz, E. Bianco, P. M. Ajayan and A. Rubio, 2D Mater, 2017, 4, 041003 CrossRef.
- S. Demirci, H. H. Gürel, S. Jahangirov and S. Ciraci, Nanoscale, 2020, 12, 3249–3258 RSC.
- D. Wang, L.-M. Tang, X.-X. Jiang, J.-Y. Tan, M.-D. He, X.-J. Wang and K.-Q. Chen, Adv. Electron. Mater., 2019, 5, 1800475 CrossRef.
- L. Ramírez-Montes, W. López-Pérez, R. González-Hernández and C. Pinilla, Int. J. Quantum Chem., 2020, 120, e26267 CrossRef.
- G. Liu, Z. Gao, G.-L. Li and H. Wang, J. Appl. Phys., 2020, 127, 065103 CrossRef CAS.
- J. Singh, P. Jamdagni, M. Jakhar and A. Kumar, Phys. Chem. Chem. Phys., 2020, 22, 5749–5755 RSC.
- Z. Zhu, X. Cai, S. Yi, J. Chen, Y. Dai, C. Niu, Z. Guo, M. Xie, F. Liu, J.-H. Cho, Y. Jia and Z. Zhang, Phys. Rev. Lett., 2017, 119, 106101 CrossRef PubMed.
- Y. Liu, W. Wu and W. A. Goddard, J. Am. Chem. Soc., 2018, 140, 550–553 CrossRef CAS PubMed.
- D. Liu, X. Lin and D. Tománek, Nano Lett., 2018, 18, 4908 CrossRef CAS PubMed.
- Y. Dong, B. Zeng, X. Zhang, D. Li, J. He and M. Long, J. Appl. Phys., 2019, 125, 064304 CrossRef.
- P. K. Sachdeva, S. Gupta and C. Bera, Nanoscale Adv., 2021, 3, 3279–3287 RSC.
- Y. Wang, C. Xiao, M. Chen., C. Hua, J. Zou, C. Wu, J. Jiang, S. A. Yang, Y. Lu and W. Ji, Mater. Horiz., 2018, 5, 521–528 RSC.
- S. Khatun, A. Banerjee and A. J. Pal, Nanoscale, 2019, 11, 3591 RSC.
- X. Cai, X. Han, C. Zhao, C. Niu and Y. Jia, J. Semicond., 2020, 41, 081002 CrossRef CAS.
- W. Wu, G. Qiu, Y. Wang, R. Wang and P. Ye, Chem. Soc. Rev., 2018, 47, 7203–7212 RSC.
- C. Xing, Z. Xie, Z. Liang, W. Liang, T. Fan., J. S. Ponraj, S. C. Dhanabalan, D. Fan and H. Zhang, Adv. Opt. Mater., 2017, 5, 1700884 CrossRef.
- J. Qin, G. Qiu, J. Jian, H. Zhou, L. Yang, A. Charnas, D. Y. Zemlyanov, C.-Y. Xu, X. Xu, W. Wu, H. Wang and P. D. Ye, ACS Nano, 2017, 11, 10222–10229 CrossRef CAS PubMed.
- X. Huang, J. Guan, B. Liu, S. Xing, W. Wang and J. Guo, J. Nano Lett., 2017, 17, 4619–4623 CrossRef CAS PubMed.
- J. Chen, Y. Dai, Y. Ma, X. Dai, W. Ho and M. Xie, Nanoscale, 2017, 9, 15945–15948 RSC.
- Z. Shi, R. Cao, K. Khan, A. K. Tareen, X. Liu, W. Liang, Y. Zhang, C. Ma, Z. Guo, X. Luo and H. Zhang, Nano-Micro Lett., 2020, 12, 99 CrossRef CAS PubMed.
- Z. Lin, C. Wang and Y. Chai, Small, 2020, 16, 2003319 CrossRef CAS PubMed.
- S.-H. Lin and J.-L. Kuo, Phys. Chem. Chem. Phys., 2014, 16, 20763–20771 RSC.
- X. Zhang and A. Beyer, Nanoscale, 2021, 13, 1443–1484 RSC.
- Y. Gogotsi and B. Anasori, ACS Nano, 2019, 13, 8491–8494 CrossRef CAS PubMed.
- M. A. N. Dewapriya, R. K. N. D. Rajapakse and S. A. Meguid, in Synthesis, Modelling and Characterization of 2D Materials and their Heterostructures, ed. E.-H. Yang, D. Datta, J. Ding and G. Hader, Elsevier, 2020, pp. 9–35 Search PubMed.
- Z. Lu, G. P. Neupane, G. Jia, H. Zhao, D. Qi, Y. Du, Y. Lu and Z. Yin, Adv. Funct. Mater., 2020, 30, 2001127 CrossRef CAS.
- M. Ashton, S. B. Sinnott and R. G. Hennig, Appl. Phys. Lett., 2016, 109, 192103 CrossRef.
- H.-F. Lin, S.-S. Wang, H.-Y. Liu, T.-P. Hou and K.-M. Wu, Phys. E, 2019, 114, 113605 CrossRef CAS.
- W. Gao, Z. Zheng, P. Wen, N. Huo and J. Li, Nanophotonics, 2020, 9, 2147–2168 CAS.
- N. R. Glavin, R. Rao, V. Varshney, E. Bianco, A. Apte, A. Roy, E. Ringe and P. M. Ajayan, Adv. Mater., 2020, 32, 1904302 CrossRef CAS PubMed.
- K. Khan, A. K. Tareen, M. Aslam, R. Wang, Y. Zhang, A. Mahmood, Z. Ouyang, Z. Han and Z. Gou, J. Mater. Chem. C, 2020, 8, 387–440 RSC.
- Y. Liu, B. Shi, Q. Liu and C. Lü, J. Alloys Compd., 2020, 843, 155819 CrossRef CAS.
- A. Di Bartolomeo, Nanomater., 2020, 10, 579 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |