A plasmon-based nanoruler to probe the mechanical properties of synthetic and biogenic nanosized lipid vesicles†
Lucrezia
Caselli
ab,
Andrea
Ridolfi
abc,
Jacopo
Cardellini
ab,
Lewis
Sharpnack
d,
Lucia
Paolini
be,
Marco
Brucale
bc,
Francesco
Valle
 bc,
Costanza
Montis
*ab,
Paolo
Bergese
bc,
Costanza
Montis
*ab,
Paolo
Bergese
 bef and
Debora
Berti
bef and
Debora
Berti
 *ab
*ab
aDepartment of Chemistry, University of Florence, Via della Lastruccia 3, Sesto Fiorentino, Florence 50019, Italy. E-mail: debora.berti@unifi.it; costanza.montis@unifi.it
bConsorzio Sistemi a Grande Interfase, Department of Chemistry, University of Florence, Sesto Fiorentino, Italy
cConsiglio Nazionale delle Ricerche, Istituto per lo Studio dei Materiali Nanostrutturati (CNRISMN), via Gobetti 101, Bologna 40129, Italy
dESRF–The European Synchrotron, Grenoble 38043, France
eDepartment of Molecular and Translational Medicine, University of Brescia, Brescia, Italy
fConsorzio Interuniversitario Nazionale per la Scienza e la Tecnologia dei Materiali, Florence, Italy
First published on 13th April 2021
Abstract
Nanosized lipid vesicles are ubiquitous in living systems (e.g. cellular compartments or extracellular vesicles, EVs) and in formulations for nanomedicine (e.g. liposomes for RNA vaccine formulations). The mechanical properties of such vesicles are crucial in several physicochemical and biological processes, ranging from cellular uptake to stability in aerosols. However, their accurate determination remains challenging and requires sophisticated instruments and data analysis. Here we report the first evidence that the surface plasmon resonance (SPR) of citrated gold nanoparticles (AuNPs) adsorbed on synthetic vesicles is finely sensitive to the vesicles’ mechanical properties. We then leverage this finding to show that the SPR tracking provides quantitative access to the stiffness of vesicles of synthetic and natural origin, such as EVs. The demonstration of this plasmon-based “stiffness nanoruler” paves the way for developing a facile, cost-effective and high-throughput method to assay the mechanical properties of dispersions of vesicles of nanometric size and unknown composition at a collective level.
New conceptsCitrated gold nanoparticles (AuNPs) undergo membrane-templated self-assembly when challenged with nanosized lipid vesicles. We show that the stiffness of the target vesicle finely modulates the extent of AuNPs aggregation, which can be easily monitored by UV-Vis spectrophotometry. Leveraging this discovery, we propose a novel experimental method to assess the mechanical properties of synthetic and natural vesicles. Through a “stiffness index”, S.I., we quantify the extent of AuNPs aggregation and define its functional dependence on the mechanical properties of the vesicles. This method was validated on a set of synthetic lipid vesicles of known stiffness and then tested on a sample of biogenic extracellular vesicles (EVs). The “plasmon-based stiffness nanoruler” is a reproducible, sensitive, high-throughput, and readily accessible method, which overcomes many of the hurdles still hampering an accurate determination of the rigidity of nanovesicles.In addition, it can easily and readily probe the properties of tiny sample amounts, which represents a considerable advantage for biological samples, usually available in low quantities due to purification costs. This new method will advance our understanding of the role of rigidity of nanovesicles in modulating their biological behavior, from the pharmacokinetics of liposomal formulation for drug delivery to the uptake of natural vesicles and viruses. |
Introduction
Membrane-delimited compartments (e.g., cells, organelles and nanosized vesicles of biological origin, such as enveloped viruses1 or extracellular vesicles (EVs)2,3) are among the basic units of living organisms. Importantly, they are also widespread structural motifs in bio-inspired nanomaterials, such as liposomes,4 virosomes5 or polymerosomes.6 The mechanical properties of such membrane compartments regulate the response to external stimuli, which is crucial in a host of biologically-relevant interactions at the nanoscale.7–11 A well-known example is the mechanical response of cells and membrane bound-organelles, which is the key in numerous biological processes (e.g. cell fusion, growth and differentiation, endo- and exocytosis, uptake of nanoparticles or viruses,12–14etc.) and in the onset of pathological cell conditions.15–18 More recent reports have highlighted that the mechanical response of EVs (membrane-delimited nanoparticles secreted by all cell types and essential mediators of cell signalling2,3,19) is a biomarker for malignant conditions of parental cells.20,21 In addition, the nanomechanics of pathogens, including viruses with a lipid envelope (e.g. Moloney murine leukemia virus and HIV22), was recently connected to their infectivity.23 Mechanical properties are also crucial for the interaction of synthetic nanostructures with the biological environment: the deformability of liposomes or polymeric vesicles for drug or vaccine delivery deeply affects their pharmacokinetics in the bloodstream and the internalization route.24Although central in several research areas, the accurate assessment of the mechanical properties of synthetic or natural vesicles still poses a challenge.25,26 Traditional methods, such as shape fluctuation optical analysis,27 micropipette aspiration,28 X-ray scattering29,30 and neutron spin-echo,31 provide insights into biologically-relevant descriptors of the mechanical response of the lipid membrane, such as the bilayer's bending rigidity.27–31 However, these techniques are cost- and/or time-consuming and often yield discrepant results, as pointed out in several reports.25,26,32–34 More recently, techniques that actively probe the mechanical properties at a whole-vesicle level, rather than those of the lipid shell, are gaining the central stage;35 examples include optical tweezers and Atomic Force Microscopy (AFM) operating modes, such as Dynamic Mechanical Analysis, Quantitative Imaging and Lorentz Contact Resonance.20 Most of these methods rely on contact mechanic models for interpreting the measured mechanical properties of the probed objects; however, there is still disagreement on which model is best suited for describing the nanomechanics of a lipid vesicle.36 As a consequence, classical AFM-based force spectroscopy (AFM-FS) indentation experiments still represent a common choice for the nanomechanical analysis of vesicles,37–39 since they allow determining the overall mechanical response of vesicles to applied deformations, i.e. their “stiffness”, in a model-free approach. The measured stiffness includes contributions both from the membrane shell and the enclosed volume, accounting for the mechanical properties of the internal pool, volume variations upon deformation, osmotic imbalance, etc. Unfortunately, all these experimental methods probe a single particle at a time and require sophisticated instruments or/and highly experienced users.35
Here, we propose AuNPs as nanoprobes of the stiffness of membranous nano-objects, with typical submicron sizes. This approach overcomes many limitations of the currently available methods, measurements can be performed with a UV-Vis spectrophotometer and limited data analysis is required. In the following, this communication will (i) explore how the stiffness of liposomes modulates the surface plasmon resonance (SPR) of AuNPs adsorbed on their membrane and (ii) propose this previously unnoticed relationship as the working principle of a new, accessible and robust spectrophotometric method to evaluate the stiffness of both synthetic and natural lipid vesicles of unknown composition.
The SPR of AuNPs is finely sensitive to the chemical environment and the interparticle distance, which underpins their application as nanoscale probes.40 The coupling between the SPR of proximal AuNPs, which results from AuNPs close approach or aggregation, was exploited for the first time by El-Sayed and co-workers as a plasmon ruler41 and is nowadays used in a number of bioanalytical assays.42,43 The CONAN (COlloidal NANoplasmonic) assay is a recent example, where the AuNPs SPR shift upon incubation with EVs is exploited to determine their purity and concentration;44–46 in this latter case, the SPR shift arises from the spontaneous aggregation of AuNPs on the lipid membrane of vesicles (of both synthetic and natural origin, as EVs). This membrane-induced aggregation has been the focus of several recent investigations.47–52 Specifically, the membrane-induced aggregation of AuNPs has been interpreted as on–off mechanism to date,53,54 switchable by the physical state of the membrane: fluid-phase bilayers, characterized by free lipid diffusion and low rigidity, would promote aggregation, resulting in a marked change of AuNPs SPR profile. Conversely, the aggregation of AuNPs would be completely inhibited on tightly packed gel-phase membranes, characterized by a higher rigidity. At variance with the literature, we demonstrate that the SPR shift of AuNPs also interest gel-phase membranes and is rather modulated by the stiffness of the vesicles through a precise functional dependence: this allows defining a “stiffness nanoruler”, able to discriminate vesicles within the same physical state (whether it is gel or fluid) on the basis of their mechanical behaviour. In analogy with the plasmon nanoruler, introduced as distance-sensor,41 this plasmon-based descriptor leverages the unique sensitivity of AuNPs SPR to determine the mechanical properties of lipid vesicles. As a proof-of-principle of applicability to complex natural systems, we tested the assay on EVs, whose stiffness is of prominent relevance in cellular adhesion and uptake55 and a characteristic that distinguish EVs deriving from malignant and non-malignant cells.20,21
Results and discussion
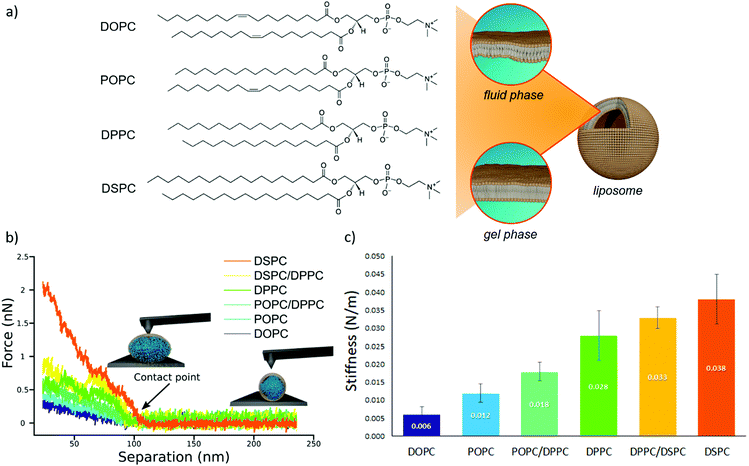
We prepared a library of unilamellar liposomes having a similar average diameter (∼100 nm) and low polidispersity indexes (see ESI† for details on preparation and characterization) from a set of synthetic phosphatidylcholines (PC) differing for length and/or degree of unsaturation of the acyl chains (Fig. 1a). The free-standing bilayers, either in the gel or fluid phase at room temperature (Fig. 1a), display different rigidities.56–59 Given their very similar size distributions and the absence of any osmotic imbalance between the lumen and the external medium, the rigidity of the lipid shells can be considered the sole responsible for the overall stiffnesses of the vesicles.Fig. 1b reports representative AFM-FS force/distance plots of single-vesicle indentation events for each lipid.60,61 The slope of the linear regime occurring immediately after the contact point represents the stiffness of the vesicles; the stiffnesses in Fig. 1c were obtained by averaging the values for multiple vesicles (see ESI† for further details). Taken together, the entire series of stiffness values measured on the selected library of synthetic PC standards can be regarded as a stiffness gauge in which the rigidity monotonically increases from DOPC to DSPC vesicles, in line with the literature.25,62 This set will be used to validate the stiffness plasmon nanoruler.
The vesicles (20 μl of a water dispersion at a 0.35 nM vesicles’ concentration) were then challenged with 100 μl of 6.7 nM water dispersion of negatively charged citrated AuNPs (13 ± 0.6 nm diameter, zeta potential: −36 ± 2 mV), to obtain a final liposomes/AuNPs molar ratio of ∼1/100. The changes in the SPR profile were monitored after 15 minutes of incubation at room temperature (Fig. 2a). These experimental conditions were carefully selected on the basis of our recent investigation on POPC liposomes interacting with citrated AuNPs.52
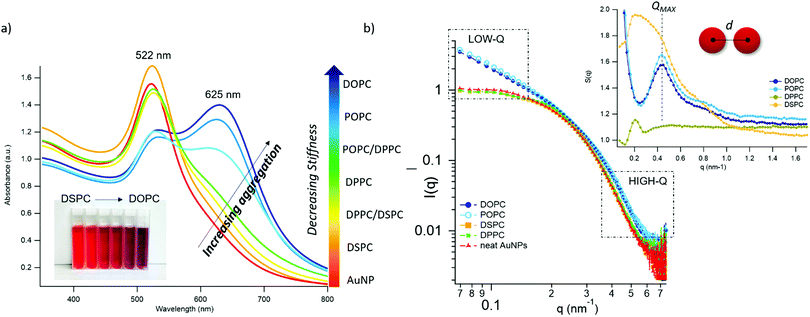 | ||
Fig. 2 AuNPs interaction with lipid bilayers of different stiffness. (a) UV-Vis spectra of AuNPs (6.7 nM) incubated with synthetic vesicles (0.2 nM) (liposomes/AuNPs number ratio 1/100). Inset: Visual appearance of the same samples. (b) SAXS profiles of NPs with and without vesicles (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 vesicles/AuNPs molar ratio). Under these conditions, the scattering from vesicles (subtracted from the scattering of AuNPs-vesicles mixtures) is negligible and the observed signal is only due to AuNPs. The power law dependence at low-q is connected to the presence of AuNPs clusters and to their morphology. The power-lawexponents for DOPC/AuNPs and POPC/AuNPs complexes, i.e. −1.54 and −1.50 respectively (see ESI†), are consistent with an increasing fractal dimension of clusters as the stiffness of vesicles decreases. The absence of such power-law for gel-phase liposomes is related to non-aggregated AuNPs, preserving their original diameter. The right inset is the structure factor (S(q)) vs. q, extracted from the high-q range of vesicles/AuNPs profiles (see ESI†). 8 vesicles/AuNPs molar ratio). Under these conditions, the scattering from vesicles (subtracted from the scattering of AuNPs-vesicles mixtures) is negligible and the observed signal is only due to AuNPs. The power law dependence at low-q is connected to the presence of AuNPs clusters and to their morphology. The power-lawexponents for DOPC/AuNPs and POPC/AuNPs complexes, i.e. −1.54 and −1.50 respectively (see ESI†), are consistent with an increasing fractal dimension of clusters as the stiffness of vesicles decreases. The absence of such power-law for gel-phase liposomes is related to non-aggregated AuNPs, preserving their original diameter. The right inset is the structure factor (S(q)) vs. q, extracted from the high-q range of vesicles/AuNPs profiles (see ESI†). | ||
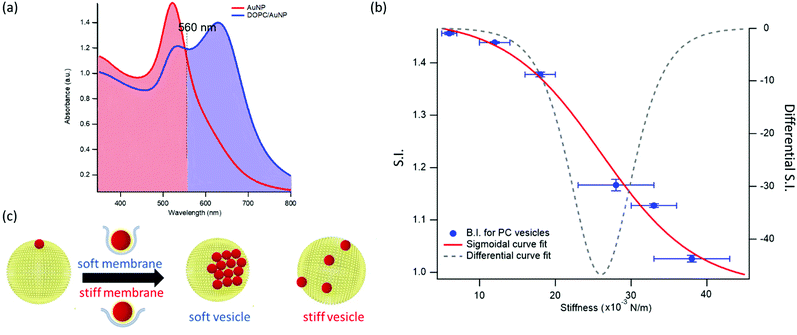
The AuNPs dispersion in the absence of lipid vesicles shows a well-defined SPR peak centred at 522 nm (red curve); upon mixing with liposomes, an immediate colour change is visible to the naked eye (inset, Fig. 2a), which clearly depends on the composition of the target membrane. Going from DSPC to DOPC, we observe colour shifts from red to increasingly dark shades of violet and blue. The variation in the SPR profile gradually increases as the stiffness of vesicles decreases. Specifically, from the stiffest vesicles (DSPC) to the softest ones (DOPC), the progressive emergence of a high-wavelength shoulder can be observed, eventually resulting in a secondary plasmon peak at about 625 nm (see Fig. 2a).
This new spectral feature is the hallmark of the aggregation of AuNPs, whose spatial proximity produces the coupling of the individual AuNPs plasmons.
To get insights into the structure of AuNPs aggregates, we performed Small Angle X-ray Scattering (SAXS) for DOPC, POPC, DPPC and DSPC liposomes challenged with AuNPs (Fig. 2b).
The power-law dependence in the low-q region highlights the presence of AuNPs clusters on fluid-phase bilayers, with a fractal dimension which increases as the stiffness of vesicles decreases (Fig. 2b, inset, and ESI†).63 The spatial correlation between AuNPs was determined from the structure factor S(q), inferred from the high-q region of the scattering profiles (Fig. 2b, inset, and ESI†). The position of the S(q) correlation peaks for fluid-phase liposomes is consistent with AuNP–AuNP center-to-center distances comparable with the particle diameter and decreasing with vesicles’ stiffness (14.5 nm and 14.1 nm for POPC and DOPC, respectively). For liposomes in the gel phase, no low-q upturn of intensity was detected and the positional correlation corresponds to significantly higher AuNP–AuNP distances (i.e., 30.5 nm and 30.2 nm for DSPC and DPPC, respectively), hinting at the presence of multiple AuNPs adsorbed on the same liposomal surface, but not aggregated.
According to recent reports, the aggregation of AuNPs on lecithin vesicles is switched on and off by the membrane phase:53,54 aggregation is inhibited on gel-phase bilayers (e.g. DPPC and DSPC at r.t.) and promoted by fluid-phase membranes (e.g. DOPC and POPC at r.t.), with no differences observed for bilayers in the same phase.53,54 Conversely, the UV-Vis and SAXS data here shown provide additional insights, highlighting that – in these experimental conditions – AuNPs clustering on lipid vesicles is not abruptly switched-on by varying the membrane physical state: the slight – but still evident – differences in the AuNPs SPR induced by vesicles with the same physical state but different rigidities demonstrate that AuNPs aggregation is rather modulated by the membrane rigidity in a “continuous fashion”.
This dependence can be exploited to set-up a UV-Vis spectroscopic assay to probe the mechanical properties of lipid vesicles. With this aim, we analysed the optical spectra to extract a quantitative descriptor. The so-called “stiffness index”, S.I., (see Fig. 3a), accounting for the main variations in the AuNPs SPR profile, was used to build-up an empirical ‘AuNPs spectral response’ vs. ‘vesicles’ stiffness’ scale. The S.I. for each AuNPs/vesicles hybrid is calculated dividing the area subtended by the absorbance spectrum in the 560–800 nm range by the area relative to the total spectral range (350–800 nm). The results are then normalized for the S.I. of neat AuNPs (which is then equal to 1 by definition) to obtain positive integer values of S.I., which gradually increase with increasing AuNPs aggregation extent.
 | ||
| Fig. 3 Quantification of liposomes-induced variation in the AuNPs SPR profile. (a) Visual description of the stiffness index (S.I.); (b) S.I. values (blue spots) with relative errors bars plotted as a function of membrane stiffness. The red curve is the sigmoidal curve fit, while the grey dashed curve is the first derivative of the sigmoidal curve fit with respect to stiffness (see ESI† for details on fitting parameters). (c) Mechanism of interaction between AuNPs and vesicles characterized by different stiffness. The adhesion of an AuNP on a soft membrane is followed by a significant AuNP wrapping by the membrane, resulting into AuNPs aggregation on the vesicle surface. The AuNP docking on a stiffer membrane results in a lower wrapping extent, preventing AuNPs clustering. | ||
Fig. 3b reports the S.I. (blue dots) obtained for the liposome set plotted as a function of vesicles’ stiffness, obtained from AFM-FS measurements (Fig. 1). Each point represents the average value obtained from five independent batches, which highlights a particularly high reproducibility (see Table S5 of ESI† for standard deviations of each vesicles’ batch).
The dependence of the S.I. on stiffness can be expressed by a sigmoidal law, with the following expression:
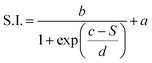 | (1) |
For this set of synthetic vesicles, having superimposable size distributions and a luminal content identical to the external medium, the stiffness differences observed in AFM-FS are only due to a membrane contribution, which results from the different composition of the bilayers. As it is well-established, the mechanical response of a lipid bilayer is mainly controlled by its bending rigidity,25 quantified by the bilayer bending modulus. Therefore, in these experimental conditions, it is the bilayer bending modulus that determines the overall stiffness of the vesicles and in turn the extent of AuNPs aggregation (i.e. the S.I.).
Interestingly, in a recent simulation Lipowsky and co-authors64 report a sigmoidal correlation between the wrapping efficiency of spherical NPs interacting with model membranes and the bilayer bending modulus. This relation holds for fixed NPs radius and membrane-NPs adhesion energy, which perfectly matches our experimental conditions (i.e. NPs of defined size and vesicles with fixed PC headgroups).
This finding is fully in line with a recent report,52 where AuNPs wrapping, modulated by the membrane bending modulus, is recognized as the main driver for the membrane-templated aggregation of AuNPs, through the mechanism sketched in Fig. 3c: briefly, AuNPs adsorb on the vesicle's surface due to Van der Waals attractive interactions and get partially wrapped by the membrane. This wrapping drives a ligand exchange between the membrane lipids and the AuNPs stabilizing agent, i.e. the citrate anion, whose release reduces the interparticle electrostatic energy barrier and leads to the aggregation of AuNPs. Importantly, the extent of AuNPs aggregation is modulated by the wrapping efficiency, which is related to the bending rigidity of the membrane. Our results, reporting the first experimental evidence of a sigmoidal relation between AuNPs aggregation and membrane bending rigidity, reconcile this latter mechanism with the theoretical predictions proposed by Lipowsky et al., who first connected the wrapping ability of a membrane to its bending modulus through a sigmoidal law.
The dependence of the S.I. on the stiffness of vesicles (eqn (1)) allows a quantitative estimate of the mechanical properties of membrane-enclosed compartments of unknown composition. The method here proposed possess high reproducibility and sensitivity. In fact, it is able to robustly discriminate systems with very close stiffnesses (i.e. differences as small as 0.006 N m−1), as POPC and DOPC liposomes, whose mechanical properties are usually not distinguishable with many other techniques.62,65
In addition, the presence of a sigmoidal law, which exhibits the highest variation of S.I. in the central region of the selected set of stiffnesses (see grey dashed curve of Fig. 3b, representing the first derivative of the sigmoidal fit) provides maximum sensitivity in the region where the rigidities of natural membranes usually fall (i.e. 0.02–0.025 N m−166).
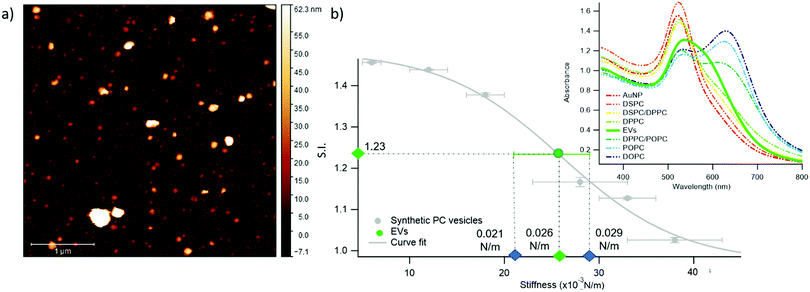
We chose EVs to further validate the method and to provide evidence of its applicability on membranous nanoparticles, which are more challenging both in terms of compositional and structural complexity, as well as in analyte availability. Specifically, we assayed a sample of EVs from the murine cell line TRAMP-C2, with size and z-potential similar to the PC synthetic liposomes (see ESI† for details). The EVs were separated from the cell culture medium and characterized according to international guidelines;67 in particular, we used the protocols described in Paolini et al. (medium EVs),68 to obtain a pure – i.e. not containing exogenous proteins (which would otherwise affect the EVs interaction with AuNPs44,48) – EVs dispersion in water. The morphology of EVs was investigated by liquid imaging AFM (see Fig. 4a), showing the characteristic spherical cap shape of EVs adhered onto a substrate and an average diameter of 74.3 nm (refer to ESI† for further details).
The stiffness of EVs, determined through AFM-FS as previously described for PC liposomes, falls in the middle of the stiffness interval defined by the synthetic standards used for calibration (0.025 ± 0.004 N m−1), in between the values obtained for DPPC and DPPC/POPC liposomes (see Fig. 1c). 20 μl of EVs (0.35 nM) were mixed with 100 μl of AuNPs in the same conditions (AuNPs/vesicles molar ratio, incubation time and temperature) previously employed for synthetic liposomes and the SPR profile change of AuNPs was recorded through UV-Vis spectroscopy (right inset of Fig. 4b).
In full agreement with the AFM analysis, this SPR profile variation, S.I. = 1.23 ± 0.01, is intermediate between the ones of DPPC, S.I. = 1.16 ± 0.01, and DPPC/POPC, S.I.= 1.377 ± 0.005. This result demonstrates that the correlation between AuNPs aggregation and vesicles’ stiffness, observed in liposomes, also holds for the case of far more complex nanosized vesicles of biological origin. More importantly, the value of stiffness estimated from the S.I. of the AuNPs/EVs hybrid according to the calibration trend (i.e., 0.0259 ± 0.0005 N m−1) falls right in the middle of the EVs stiffness range determined through AFM (Fig. 4b): this striking agreement proves the predictive ability of this new optical method, showing that the nanoplasmonic properties of AuNPs can be effectively harnessed to assess the stiffness of membrane-confined objects with high sensitivity.
Conclusions
The determination of the stiffness of synthetic and natural vesicles is particularly challenging. Here, we show that the SPR of AuNPs can be exploited to quantify this property: combining UV-Vis Spectroscopy, Small Angle X-ray Scattering and AFM-based Force Spectroscopy, we prove that AuNPs aggregation, induced by the interaction with lipid membranes and quantified by an empirical index S.I., exhibits a clear dependence on the mechanical properties of synthetic vesicles. This dependence, expressed by a sigmoidal law, can be used to estimate the stiffness of biological membrane compartments, e.g. EVs, of unknown composition and properties. Similarly to the plasmon ruler developed by El-Sayed et al.,41 where the SPR of AuNPs is used to probe their mutual distance, we define a “stiffness nanoruler”, where the plasmon resonance is applied to probe the nanomechanics of a target membrane. The method requires cheap reagents and a standard wet lab facility, while keeping competitive reproducibility and sensitivity. From the sample side, it allows for examination of volumes as small as 15 μl (with a concentration of particles in the 10–8 M range) which is not accessible today to any other method. This allows to minimize the amounts of vesicles required, which is paramount for biological samples, where low amounts of analyte are yearned due to the origin of the samples (e.g. human biological fluids) and/or complex and time-consuming separation protocols. Moreover, differently from other methods – such as AFM and micropipette – which probe the stiffness of single objects, it provides the ensemble-averaged stiffness, i.e. accounting for possible variability across the population, with short-time (few minutes) data acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the European Community through the evFOUNDRY project (H2020-FETopen, ID: 801367) and the BOW project (H2020-EIC-FETPROACT-2019, ID: 952183). We also acknowledge MIUR-Italy (“Progetto Dipartimenti di Eccellenza 2018–2022, ref. B96C1700020008” allocated to Department of Chemistry “Ugo Schiff”) and Ente Cassa di Risparmio di Firenze for the economic support. We thank the SPM@ISMN research facility for support in the AFM experiments. The European Synchrotron Radiation Facility (ESRF) is acknowledged for provision of beam-time.References
- W. Lucas and K. M. David, Encyclopedia of Life Sciences, 2010, pp. 1–7 Search PubMed.
- M. Yáñez-mó and E. Al, J. Extracell. Vesicles, 2015, 14, 27066 CrossRef PubMed.
- G. Raposo and P. D. Stahl, Nat. Rev. Mol. Cell Biol., 2019, 20, 509–510 CrossRef CAS PubMed.
- G. Bozzuto and A. Molinari, Int. J. Nanomed., 2015, 10, 975–999 CrossRef CAS PubMed.
- A. Huckriede, L. Bungener, T. Stegmann, T. Daemen, J. Medema, A. M. Palache and J. Wilschut, Vaccine, 2005, 23, S26 CrossRef.
- X. Zhang and P. Zhang, Curr. Nanosci., 2016, 13, 124–129 CrossRef.
- M. Mendozza, L. Caselli, A. Salvatore, C. Montis and D. Berti, Soft Matter, 2019, 15(44), 8951–8970 RSC.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8(7), 543–557 CrossRef CAS PubMed.
- C. M. Beddoes, C. P. Case and W. H. Briscoe, Adv. Colloid Interface Sci., 2015, 218, 48–68 CrossRef CAS PubMed.
- P. K. K. Nagayama, Particles at Fluid Interfaces and Membranes: Attachment of Colloid Particles, Elsevier Science, 1st edn, 2001 Search PubMed.
- K. L. Chen and G. D. Bothun, Environ. Sci. Technol., 2014, 48, 873–880 CrossRef CAS.
- M. Simunovic, C. Prévost, P. Bassereau and P. Bassereau, Philos. Trans. R. Soc., A, 2016, 374, 20160034 CrossRef PubMed.
- P. B. Canham, J. Theor. Biol., 1970, 26, 61–81 CrossRef CAS.
- E. A. Evans, Biophys. J., 1974, 14, 923–931 CrossRef CAS.
- A. C. Dumitru, M. Poncin, L. Conrard, Y. F. Dufrêne, D. Tyteca and D. Alsteens, Nanoscale Horiz., 2018, 3, 293–304 RSC.
- I. Safeukui, P. A. Buffet, G. Deplaine, S. Perrot, V. Brousse, A. Sauvanet, B. Aussilhou, P. H. David, S. Dokmak, A. Couvelard, D. Cazals-hatem, O. Mercereau-puijalon and N. Mohandas, Blood Adv., 2018, 2, 1–4 Search PubMed.
- C. Alibert, B. Goud and J. Manneville, Biol. Cell., 2017, 109, 167–189 CrossRef PubMed.
- D. Vorselen, S. M. van Dommelen, R. Sorkin, M. C. Piontek, J. Schiller, S. T. Döpp, S. A. A. Kooijmans, B. A. van Oirschot, B. A. Versluijs, M. B. Bierings, R. van Wijk, R. M. Schiffelers, G. J. L. Wuite and W. H. Roos, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- G. Van Niel, G. D. Angelo and G. Raposo, Nat. Rev. Mol. Cell Biol., 2018, 19, 213–228 CrossRef CAS PubMed.
- B. Whitehead, L. P. Wu, M. L. Hvam, H. Aslan, M. Dong, L. DyrskjØt, M. S. Ostenfeld, S. M. Moghimi and K. A. Howard, J. Extracell. Vesicles, 2015, 4, 1–11 Search PubMed.
- L. Paolini, A. Zendrini and A. Radeghieri, Biomarkers Med., 2018, 12(4), 383–391 CrossRef CAS PubMed.
- C. Carrasco, M. Castellanos, P. J. De Pablo and M. G. Mateu, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 4150–4155 CrossRef CAS PubMed.
- W. H. Roos, Semin. Cell Dev. Biol., 2018, 73, 145–152 CrossRef CAS PubMed.
- P. Guo, D. Liu, K. Subramanyam, B. Wang, J. Yang, J. Huang, D. T. Auguste and M. A. Moses, Nat. Commun., 2018, 9(1), 1–9, DOI:10.1038/s41467-017-02588-9.
- J. F. Nagle, M. S. Jablin, S. Tristram-nagle and K. Akabori, Chem. Phys. Lipids, 2015, 185, 3–10 CrossRef CAS PubMed.
- D. Bochicchio and L. Monticelli, The Membrane Bending Modulus in Experiments and Simulations: A Puzzling Picture, Elsevier Inc., 1st edn, 2016, vol. 23 Search PubMed.
- N. Bezlyepkina, R. L. Knorr, R. Lipowsky and R. Dimova, Soft Matter, 2010, 6, 1472–1482 RSC.
- J. R. Henriksen and J. H. Ipsen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 167, 149–167 CrossRef PubMed.
- J. Pan, S. Tristram-nagle and J. F. Nagle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021931 CrossRef PubMed.
- C. Length, G. Fragneto, T. Charitat, E. Bellet-amalric and R. Cubitt, Langmuir, 2003, 19, 7695–7702 CrossRef.
- M. Mell, L. H. Moleiro, Y. Hertle, P. Fouquet, R. Schweins, T. Hellweg and F. Monroy, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 75 CrossRef PubMed.
- D. Marsh, Chem. Phys. Lipids, 2006, 144, 146–159 CrossRef CAS PubMed.
- J. F. Nagle, Faraday Discuss., 2013, 161, 11–29 RSC.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed.
- M. C. Piontek, R. B. Lira and W. H. Roos, Biochim. Biophys. Acta, Gen. Subj., 2019, 129486 Search PubMed.
- M. LeClaire, J. Gimzewski and S. Sharma, Nano Sel., 2021, 2, 1–15 CrossRef.
- D. Vorselen, M. C. Piontek, W. H. Roos and G. J. L. Wuite, Front. Mol. Biosci., 2020, 7, 1–14 CrossRef PubMed.
- S. Li, F. Eghiaian, C. Sieben, A. Herrmann and I. A. T. Schaap, Biophys. J., 2011, 100, 637–645 CrossRef CAS PubMed.
- A. Calò, D. Reguera, G. Oncins, M. A. Persuy, G. Sanz, S. Lobasso, A. Corcelli, E. Pajot-Augy and G. Gomila, Nanoscale, 2014, 6, 2275–2285 RSC.
- V. Amendola, R. Pilot and M. Frasconi, J. Phys.: Condens. Matter, 2017, 29, 203002 CrossRef PubMed.
- P. K. Jain, W. Huang and M. A. El-sayed, Nano Lett., 2007, 7, 2080–2088 CrossRef CAS.
- W. Zhao, M. M. Ali, S. D. Aguirre, M. A. Brook and Y. Li, Anal. Chem., 2008, 80, 8431–8437 CrossRef CAS PubMed.
- C. C. Chang, C. P. Chen, T. H. Wu, C. H. Yang, C. W. Lin and C. Y. Chen, Nanomaterials, 2019, 9, 1–24 Search PubMed.
- D. Maiolo, L. Paolini, G. Di Noto, A. Zendrini, D. Berti, P. Bergese and D. Ricotta, Anal. Chem., 2015, 87(8), 4168–4176 CrossRef CAS PubMed.
- A. Zendrini, L. Paolini, S. Busatto, A. Radeghieri, M. Romano, M. H. M. Wauben, M. J. C. van Herwijnen, P. Nejsum, A. Borup, A. Ridolfi, C. Montis and P. Bergese, Front. Bioeng. Biotechnol., 2020, 7, 452 CrossRef PubMed.
- A. Mallardi, N. Nuzziello, M. Liguori, C. Avolio and G. Palazzo, Colloids Surf., B, 2018, 168, 134–142 CrossRef CAS PubMed.
- A. Ridolfi, L. Caselli, C. Montis, G. Mangiapia, D. Berti, M. Brucale and F. Valle, J. Microsc., 2020, 280(3), 194–203 CrossRef CAS PubMed.
- C. Montis, D. Maiolo, I. Alessandri, P. Bergese and D. Berti, Nanoscale, 2014, 6(12), 6452–6457 RSC.
- C. Montis, V. Generini, G. Boccalini, P. Bergese, D. Bani and D. Berti, J. Colloid Interface Sci., 2018, 516, 284–294 CrossRef CAS PubMed.
- J. Liu, Langmuir, 2016, 32, 4393–4404 CrossRef CAS PubMed.
- F. Wang and J. Liu, Nanoscale, 2015, 7, 15599–15604 RSC.
- C. Montis, L. Caselli, F. Valle, A. Zendrini, F. Carlà, R. Schweins, M. Maccarini, P. Bergese and D. Berti, J. Colloid Interface Sci., 2020, 573, 204–214 CrossRef CAS PubMed.
- K. Sugikawa, T. Kadota, K. Yasuhara and A. Ikeda, Angew. Chem., Int. Ed., 2016, 55, 4059–4063 CrossRef CAS PubMed.
- F. Wang, D. E. Curry and J. Liu, Langmuir, 2015, 31, 13271–13274 CrossRef CAS PubMed.
- R. Sorkin, R. Huisjes, F. Boškovic, D. Vorselen, S. Pignatelli, Y. Ofir-birin, J. K. F. Leal, J. Schiller, D. Mullick, W. H. Roos, G. Bosman, N. Regev-rudzki, R. M. Schiffelers and G. J. L. Wuite, Small, 2018, 1801650, 1–8 Search PubMed.
- J. F. Nagle, J. Pan, S. Tristram-nagle and N. Kuc, Biophys. J., 2008, 94, 117–124 CrossRef PubMed.
- R. Dimova, B. Pouligny and C. Dietrich, Biophys. J., 2000, 79, 340–356 CrossRef CAS.
- C. Lee, W. Lin and J. Wang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 020901 CrossRef CAS PubMed.
- K. R. Mecke and T. Charitat, Langmuir, 2003, 19, 2080–2087 CrossRef CAS.
- U. C. Afm, S. Sharma, H. I. Rasool, V. Palanisamy, C. Mathisen, M. Schmidt, D. T. Wong and J. K. Gimzewski, ACS Nano, 2010, 4, 1921–1926 CrossRef PubMed.
- M. Krieg, G. Fl, D. Alsteens, B. M. Gaub, W. H. Roos, G. J. L. Wuite, H. E. Gaub, C. Gerber and Y. F. Dufr, Nat. Rev. Phys., 2019, 1, 41–57 CrossRef.
- J. F. Nagle, Chem. Phys. Lipids, 2017, 205, 18–24 CrossRef CAS PubMed.
- L. A. Feigin and D. S. Svergun, Structure Anaysis by Small Angle X-Ray and Neutron Scattering, Plenum Press, New York, Princeton, 1987 Search PubMed.
- M. Raatz, R. Lipowsky and T. R. Weikl, Soft Matter, 2014, 10, 3570–3577 RSC.
- G. Niggemann, M. Kummrow, W. Helfrich, G. Niggemann, M. Kummrow, W. H. The and B. Rigidity, J. Phys. II, 1995, 5, 413–425 CrossRef CAS.
- A. Ridolfi, M. Brucale, C. Montis, L. Caselli, L. Paolini, A. Borup, A. T. Boysen, F. Loria, M. J. C. van Herwijnen, M. Kleinjan, P. Nejsum, N. Zarovni, M. H. M. Wauben, D. Berti, P. Bergese and F. Valle, Analytical chemistry, 2020, 92(15), 10274–10282 CrossRef CAS PubMed.
- C. Théry and E. Al, J. Extracell. Vesicles, 2018, 7, 1535750 CrossRef PubMed.
- L. Paolini, S. Federici, G. Consoli, D. Arceri, A. Radeghieri, I. Alessandri and P. Bergese, J. Extracell. Vesicles, 2020, 9(1), 1741174 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nh00012h |
| This journal is © The Royal Society of Chemistry 2021 |