Designing a mechanically driven spin-crossover molecular switch via organic embedding

Abstract

Among spin-crossover complexes, Fe–porphyrin (FeP) stands out for molecular spintronic applications: an intricate, yet favourable balance between ligand fields, charge transfer, and the Coulomb interaction makes FeP highly manipulable, while its planar structure facilitates device integration. Here, we theoretically design a mechanical spin-switch device in which external strain triggers the intrinsic magneto-structural coupling of FeP through a purely organic embedding. Exploiting the chemical compatibility and stretchability of graphene nanoribbon electrodes, we overcome common reliability and reproducibility issues of conventional inorganic setups. The competition between the Coulomb interaction and distortion-induced changes in ligand fields requires methodologies beyond the state-of-the-art: combining density functional theory with many-body techniques, we demonstrate experimentally feasible tensile strain to trigger a low-spin (S = 1) to high-spin (S = 2) crossover. Concomitantly, the current through the device toggles by over an order of magnitude, adding a fully planar mechanical current-switch unit to the panoply of molecular spintronics.

---

The idea of utilising the electrons' spin for information-processing in molecular-scale devices is the foundation for the emerging field of molecular spintronics.^1–4 Elementary molecular devices, including spin-switches,^5–7 spin transistors,^8–11 or spin-valves,¹² exploit reversible control over magnetic states via spin-crossover, magnetic coupling, Kondo resonance, or magnetic anisotropy mechanisms. Among these, the molecular spin-crossover (SCO) is the most robust and versatile mechanism: it can be triggered upon contact with surfaces,^13–15 through external stimuli, e.g., voltage^13,16 or strain,¹⁷ and, importantly, it can operate reliably also at ambient conditions.¹⁸

In standard experimental setups, a functional molecule is contacted between metallic electrodes (typically Au). However, the resulting properties strongly depend on the local atomic configuration of the junction, which is extremely difficult to control. Moreover, high atomic mobility and strong metal-molecule coupling often destroy intrinsic properties of the embedded molecule,^16,19 rendering its functionality unexploitable. To date, ensuring reliability and reproducibility remains a key challenge for device fabrication. A promising route to overcome the above issues is to integrate the magnetic molecule into a more compatible organic environment. In fact, carbon-based architectures have recently been demonstrated to yield highly mechanically stable and atomically precise molecular junctions,^20–24 while at the same time preserving the intrinsic magnetic properties of the contacted molecule. Therefore it is timely to conceptualize functional molecular devices with organic embedding.

Here, we explore the theoretical design of a mechanically-driven SCO device, that consists of a magnetic iron–porphyrin (FeP) molecule covalently bonded to graphene nanoribbon (GNR) electrodes. We identify a strategy to reversibly manipulate the molecular spin state by applying uniaxial strain. Exploiting the stretchability of the GNRs, we can directly engage the Fe–N coupling that controls the competition between ligand-fields and the Coulomb interaction, at the heart of the SCO mechanism.

1 The proposed device

In Fig. 1, we present the device set-up where an FeP molecule is chemically anchored to semi-infinite zigzag-edge graphene nano-ribbon (zGNR) electrodes. The dangling bonds of the edge C atoms of the zGNRs are passivated with H atoms for an enhanced stability and, at the same time, preserving the sp² planar structure.²⁵ The FeP molecule is connected to the electrodes by replacing two H atoms of the pyrrole moiety and two H atoms on the middle of the armchair facet of the GNR with direct C–C bonds, creating a side-sharing hexagon–pentagon interface.

Fig. 1 Unit cell of the molecular device, in which zGNRs are chemically bonded to the FeP bridge. The spin state of the Fe atom is reversibly controlled by strain applied along the x-direction (grey arrows).

We exploit the magneto-structural relationship of the encapsulated FeP molecule^26–29 as the basis for the device functionality. FeP has been demonstrated to realize a spin-crossover (SCO) under various conditions, e.g., through surface adsorption,^29–32 in molecular assembly,³³ or in single-molecule junctions by approaching an STM tip,^34,35 all of which create internal strains in the embedded molecule. However, depending on the surface topology and surface–molecule interactions, outer ligand groups, metal atom coordination and oxidation state, and the nature of external stimuli, the type of magnetic transition, i.e., low-spin (LS) to high-spin (HS) or vice versa, as well as the amount of required strain, vary substantially, often diminishing the propensity for a SCO.^23,36

In fact, the spin-state of the central Fe atom is the result of a delicate interplay of structural distortions in the porphyrin molecule and the Coulomb interaction. We manipulate this balance by mechanical strain, as indicated in Fig. 1, with the objective of inducing a spin-crossover. To effectively include the feedback of a SCO on the atomic structure, we relax the device by taking into account the Coulomb interaction within a static mean-field approximation (DFT + U). With the obtained structures we then go beyond this approximation and include dynamical many-body effects within the Fe-3d multiplet in order to obtain a better description of the electronic and transport properties across the SCO. For technical details, see the ESI.†

Upon atomic relaxation, the free-standing device undergoes a slight out-of-plane buckling due to an internal stress, caused by the mismatch in C–C bond-length at the interface between the hexagon of the zGNR and the C₄N pentagon of the porphyrin ring. Also, the coordination of the central Fe atom becomes asymmetrical and consequently, the D_4h symmetry of the FeN₄ core (present in a free molecule) is lifted, as the Fe–N bonds along (perpendicular to) the zGNR coordination direction are elongated (shortened) to [Fe–N]_x = 2.03 Å ([Fe–N]_y = 1.99 Å).

The uniaxial strain applied to the device is quantified by the relative change in the unit-cell size along the x-direction. The covalent nature of the molecule-zGNR bonds and the high stretchability of zGNRs³⁷ allow a sizeable expansion of the device. A 1% strain is sufficient to release the internal stress caused by the bonding between FeP and the zGNR electrodes and restore planarity, which is retained for higher strains. In Fig. 2(a) we show how the molecule-zGNR contacts and the molecule itself change due to the applied strain, by comparing structures without and with (5%) strain. Strain stretches the C–C bonds at the contacts as well as the longitudinal Fe–N bonds of FeP, which are identified as the softest in the system, by far. As expected, the changes in the Fe–N bond-length is direction-dependent and the [Fe–N]_x distances expand while the [Fe–N]_y distances shrink, see Fig. 2(b) and (c), further enhancing the asymmetry of the active molecule. Between 2% and 2.5% strain, the evolution of interatomic distances is discontinuous as the FeN₄ core suddenly expands in both x- and y-direction. This phenomenon is, as we shall see, the structural signature of the system switching from a LS (S = 1) to a HS (S = 2) ground-state.

Fig. 2 Effects of strain on the structure of the device and the Fe hybridization. (a) Atomic positions for 0% (light) and 5% (dark) strain. The changes in Fe–N bond lengths along the in-plane directions, Δ_x = 0.36 Å and Δ_y = −0.06 Å, are highlighted. (b) Asymmetric expansion of the FeN₄ core; arrows denote the changes with respect to the 0% strain bond-length. (c) Fe–N bonds along the x- and y-direction. (d) Imaginary part of the dynamical hybridization function Δ(ω) of the Fe-d_x²−y² orbital for different strains, with a broadening δ = 0.1 eV.

2 Spin state switching

We now take the perspective of the central Fe-ion, as it carries the magnetic degrees of freedom responsible for the device functionality. More specifically, we quantify how the above structural changes modify the Fe-ligand coupling, by considering the dynamical hybridization function^38–40where denote the Fe-3d orbitals, ε^b_n the energies of the molecular orbitals of the ligands, which include both the porphyrin ring and the zGNR leads, and their coupling. The diagonal component with is the strongest due to the large axial overlap between d_x²−y² and N-2p orbitals. The second strongest contribution comes from the d_yz orbital, whereas the d_xz one is suppressed by the elongation of the [Fe–N]_x distance and together with all other diagonal and off-diagonal components, are already insignificant for the description of the SCO (see Fig. S1 and the corresponding discussion in the ESI†). In the following we focus on the d_x²−y² component of Δ(ω), which is displayed in Fig. 2(d) and denoted as . At 0% strain, is characterized by a broad resonance around ω ∼ −2.0 eV. As a function of strain, it shifts towards higher binding energy and its height decreases, a hallmark of the weakening metal–ligand coupling. A sudden drop between 2% and 2.5% strain reflects again the structural discontinuity connected with the SCO.

In order to reveal the connection between structural and magnetic changes under strain, we now take into account many-body effects in the Fe-3d multiplet embedded into its surrounding via the hybridization function, eqn (1). The latter is restricted to the dominant d_x²−y² and d_yz channels which are treated as bath degrees of freedom. We then solve the ensuing realistic Anderson impurity model that incorporates the full Coulomb tensor⁴¹ with an exact diagonalization (ED) technique (for details, see the ESI†).

In Fig. 3 we show the evolution of the electronic properties under strain. In Fig. 3(a), the spin-transition energy ΔE = E_LS − E_HS, i.e., the energy difference between the lowest-lying many-body states in the LS and HS sectors, displays a discontinuity as a function of mechanical strain. We identify the system to undergo a transition from a LS to a HS state (sign change in ΔE) at the same critical strain (2–2.5%) for which DFT + U accounted for the structural transition. The corresponding electronic configurations are schematically shown in Fig. 3(b) in the basis of the Fe-3d and the two ligand orbitals. The LS and HS states differ for the occupation of the d_xy and d_x²−y² orbitals, and the alignment of spins on different orbitals follows the Hund's rule. The above scenario is confirmed by the discontinuous evolution with strain of the total spin S projected onto the Fe-3d, computed from the operator 〈S²〉 = S(S + 1). We find S_LS ∼ 1.2 (strain ≤2%) and S_HS ∼ 1.9 (strain >2%). Note that the Fe atom is in a paramagnetic state, i.e., 〈S_z〉 = 0. The spin configuration displayed in Fig. 3(b) therefore corresponds to a snapshot in time, as the local moments fluctuate freely—subject only to the constraint of the spin-state S. Concomitant with the spin crossover, the orbital occupation shows a charge transfer from the d_xy to the d_x²−y² orbital. The slight deviation from a pure S_LS = 1 and S_HS = 2 can be mainly attributed to the projection on to the Fe-3d orbitals, as explained previously.⁴² The expectation values of the observables are obtained as a quantum mechanical and thermal average from many-body calculations at T = 300 K, indicating that the SCO survives up to room temperature. The mechanism underlying the SCO is represented schematically by the level diagram in Fig. 3(e), obtained through a static Hartree-like approximation of the many-body simulation (see ESI† for details). The resulting diagram can be understood in terms of the competition between the Coulomb interaction and the ligand field: both in the gas phase and in the device at 0% strain, the anti-bonding orbital with predominant d_x²−y² character lies far above the Fermi level, unoccupied, due to the strong hybridization to the ligands. As the Fe–N bonds soften along the strain direction, the splitting between bonding and anti-bonding orbitals is strongly reduced. At a critical strain, it becomes energetically favorable to promote an electron from the doubly-occupied d_xy to the anti-bonding d_x²−y² orbital, in order to evade the intra-orbital Coulomb repulsion. At the same time, the Hund's exchange couplings within the Fe-3d multiplet suppress inter-orbital double occupations with opposite spins thus stabilizing a HS configuration.⁴¹

Fig. 3 Spin-state switching of FeP in a device. (a) Spin-transition energy. (b) Time-snapshot of the many-body ground state configurations projected onto the Fe-3d and ligand orbitals. (c) Total spin S, and (d) average occupations of the d_x²−y² and d_xy orbitals, as a function of strain. (e) Molecular level-diagrams showing the mechanism of the strain-induced spin-transition.

One can estimate the Coulomb contribution to the spin-transition energy between the electronic configurations in Fig. 3(b). Within a density–density approximation of the Coulomb tensor (see ESI† for an extended discussion) Δ_Coulomb = 2J₁ + 3J₃. The system gains energy in the HS state associated with two exchange interaction parameters: J₁, that couples both the d_xy and d_x²−y² to the d_xz and d_yz orbitals, and J₃, that couples the d_xy and d_x²−y² orbitals. We find Δ_Coulomb ≈ 2.83 eV to be of the same order of magnitude as the ligand field between the d_xz and d_x²−y² orbitals. The competition between these two energy scales, which in the full calculation is represented by ΔE in Fig. 3(a), is the root cause of the SCO in FeP.

3 Electron transport

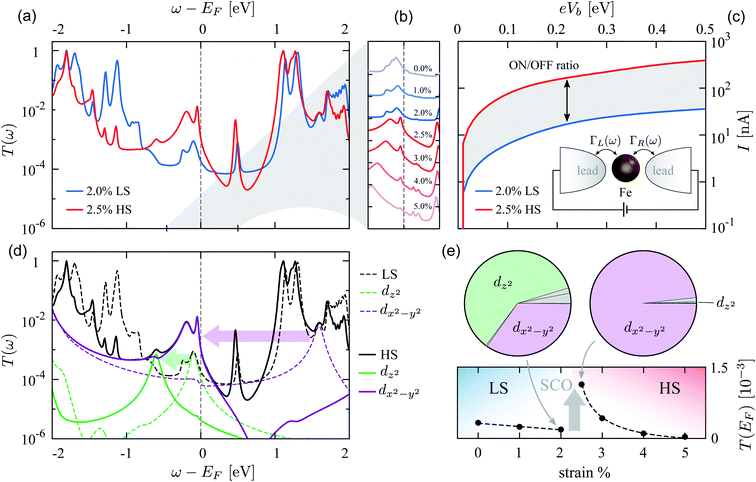
The change of the spin state across the SCO has practical implications, as it drastically changes the charge transport properties through the device. In order to demonstrate that, we map the device onto an effective quantum-dot model. We calculate the Landauer transmission function

T(ω)=Tr[Γ^L(ω)G^†(ω)Γ^R(ω)G(ω)], (2)

that describes the probability of an electron to be transferred coherently through the Fe atom. Here G(ω) denotes the Green's function of the Fe-3d multiplet, which includes the many-body effects stemming from the Coulomb interactions^43–47 while the matrix Γ^α(ω) = ı[Σ^α(ω) − Σ^†α(ω)], describes the coupling to the rest of the device, when the hybridization function is separated into components to the left (L) and the right (R) of the Fe atom as Δ(ω) = Σ^L(ω) + Σ^R(ω) (for details and the applicability of the quantum-dot model, see the ESI†).

The simulated transmission function T(ω) in the LS and HS state is shown in Fig. 4(a) for strains across the SCO, while Fig. 4(b) shows its behavior at low-energy for all strain values. At the Fermi level we identify a significant enhancement of the conductance from about 2 × 10⁻⁴G₀ at 2% strain to values >10⁻³G₀ at 2.5% strain, where G₀ = e²/h is the conductance quantum. This jump is mirrored by an increase in the electric current (per spin) evaluated as

where e is the electron charge, h is the Planck constant, and f_L/R(ω) = f(ω − μ_L/R) is the Fermi-Dirac distribution function of the leads symmetrically displaced by the bias voltage μ_L − μ_R = V_b. The junction displays an approximatively linear transport characteristics and a large ON/OFF ratio I_HS/I_LS > 10, which is remarkably independent on the external bias voltage, as shown in Fig. 4(c). An orbital dependent analysis of the transmission function, reported in Fig. 4(d) and (e) allows us to unambiguously trace back the changes in the transport properties to the SCO. In the LS state, the orbital character of the transmission function is prevalently d_z², with about 30% admixture of d_x²−y² character. In the HS state, the nonbonding d_z² orbital shifts to lower energy and the transmission function is instead dominated by a narrow resonance with d_x²−y² orbital character just below the Fermi level, which appears as a consequence of the partial occupation of the corresponding Fe orbital. As a result, the transmission function at the Fermi level displays a sharp increase as a function of strain at the SCO. Hence, the transport properties allow to discriminate between the two spin states. Similar behavior is observed for switches based on photo-induced molecular isomerization, where the change in the transport properties are ascribed to changes in the chemical configuration.⁴⁸

Fig. 4 (a) Transmission function in the LS and HS state and (b) evolution of the transmission close to E_F across the SCO. (c) I–V characteristics in the LS and HS state, demonstrating the ON/OFF ratio I_HS/I_LS > 10. (d) Transmission function (black lines) and its orbital-resolved contributions from d_x²−y² and d_z² orbitals (color lines), which dominate the charge transport close to E_F. The arrows highlight the redistribution of electronic spectral weight associated to the SCO. (e) Evolution of the transmission at the Fermi level as a function of strain. The pie charts highlight the d_x²−y² and d_z² orbital character in the LS and HS state (color) while all other orbitals are displayed in gray.

4 Conclusions

In summary, we have demonstrated the potential of a molecular spin-switch device, where a mechanically driven spin-crossover results in a bias-independent enhancement of the current through the device by one order of magnitude. This is revealed by realistic simulations that include many-body effects without breaking the spin symmetry of the Fe core. The key advantage of the proposed design is the organic anchoring of the active FeP molecule. The strong covalent bonding to the zGNR electrodes assures a high reliability and reproducibility. The relatively smaller contact-resistance is also expected to enable the proposed device to identify small conductance differences in electrical measurements. Recent technical breakthroughs, such as dash-line lithography²⁰ or on-surface-synthesis^22,49 make it possible to anchor molecules with graphene-nano structures with high atomic-precision. These graphene–molecule–graphene junctions have already shown remarkable functionalities, including magnetism,^21,23,24,49 or rectifying behaviour,⁵⁰ and can be engineered to work in reversible mechanical break-junction setups.⁵¹ These early successes strongly suggest that our proposed device, which couples magnetic and structural degrees of freedom in a fully planar geometry, is experimentally realizable, adding a new building block for organic spintronic devices.

Author contributions

SB designed the project. SB and AV carried out the numerical simulations. All authors discussed the results and contributed to writing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support from the Science Foundation Ireland [19/EPSRC/3605], the Engineering and Physical Sciences Research Council [EP/S030263/1], the European Research Council through Consolidator Grant no. 617196 ‘CORRELMAT’ (SB), and the Austrian Science Fund (FWF) through project ‘LinReTraCe’ P 30213 (JMT, AV) and project P 31631 (AV).

Notes and references

1. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186.
2. A. R. Rocha, V. M. García-suárez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Nat. Mater., 2005, 4, 335.
3. S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355.
4. S. Schmaus, A. Bagrets, Y. Nahas, T. K. Yamada, A. Bork, M. Bowen, E. Beaurepaire, F. Evers and W. Wulfhekel, Nat. Nanotechnol., 2011, 6, 185–189.
5. M. Ormaza, P. Abufager, B. Verlhac, N. Bachellier, M. L. Bocquet, N. Lorente and L. Limot, Nat. Commun., 2017, 8, 1974.
6. K. Bairagi, O. Iasco, A. Bellec, A. Kartsev, D. Li, J. Lagoute, C. Chacon, Y. Girard, S. Rousset, F. Miserque, Y. J. Dappe, A. Smogunov, C. Barreteau, M.-L. Boillot, T. Mallah and V. Repain, Nat. Commun., 2016, 7, 12212.
7. H. Wan, B. Zhou, X. Chen, C. Q. Sun and G. Zhou, J. Phys. Chem. C, 2012, 116, 2570–2574.
8. E. A. Osorio, K. Moth-Poulsen, H. S. J. van der Zant, J. Paaske, P. Hedegård, K. Flensberg, J. Bendix and T. Bjørnholm, Nano Lett., 2010, 10, 105–110.
9. W. Liang, M. P. Shores, M. Bockrath, J. R. Long and H. Park, Nature, 2002, 417, 725.
10. R. Gaudenzi, E. Burzurí, D. Reta, I. d. P. R. Moreira, S. T. Bromley, C. Rovira, J. Veciana and H. S. J. van der Zant, Nano Lett., 2016, 16, 2066–2071.
11. A. S. Zyazin, J. W. G. van den Berg, E. A. Osorio, H. S. J. van der Zant, N. P. Konstantinidis, M. Leijnse, M. R. Wegewijs, F. May, W. Hofstetter, C. Danieli and A. Cornia, Nano Lett., 2010, 10, 3307–3311.
12. M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502.
13. T. G. Gopakumar, F. Matino, H. Naggert, A. Bannwarth, F. Tuczek and R. Berndt, Angew. Chem., Int. Ed., 2012, 51, 6262–6266.
14. M. Bernien, H. Naggert, L. M. Arruda, L. Kipgen, F. Nickel, J. Miguel, C. F. Hermanns, A. Krüger, D. Krüger, E. Schierle, E. Weschke, F. Tuczek and W. Kuch, ACS Nano, 2015, 9, 8960–8966.
15. B. Warner, J. C. Oberg, T. G. Gill, F. El Hallak, C. F. Hirjibehedin, M. Serri, S. Heutz, M.-A. Arrio, P. Sainctavit, M. Mannini, G. Poneti, R. Sessoli and P. Rosa, J. Phys. Chem. Lett., 2013, 4, 1546–1552.
16. T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari, L. Joly, F. Scheurer, G. Rogez, T. K. Yamada, P. Ohresser, E. Beaurepaire and W. Wulfhekel, Nat. Commun., 2012, 3, 938.
17. R. Frisenda, G. D. Harzmann, J. A. Celis Gil, J. M. Thijssen, M. Mayor and H. S. J. van der Zant, Nano Lett., 2016, 16, 4733–4737.
18. F. Prins, M. Monrabal-Capilla, E. A. Osorio, E. Coronado and H. S. J. van der Zant, Adv. Mater., 2011, 23, 1545–1549.
19. C. Jia and X. Guo, Chem. Soc. Rev., 2013, 42, 5642–5660.
20. Y. Cao, S. Dong, S. Liu, L. He, L. Gan, X. Yu, M. L. Steigerwald, X. Wu, Z. Liu and X. Guo, Angew. Chem., Int. Ed., 2012, 51, 12228–12232.
21. C. Jia, B. Ma, N. Xin and X. Guo, Acc. Chem. Res., 2015, 48, 2565–2575.
22. Y. He, M. Garnica, F. Bischoff, J. Ducke, M.-L. Bocquet, M. Batzill, W. Auwärter and J. V. Barth, Nat. Chem., 2017, 9, 33–38.
23. J. Li, N. Friedrich, N. Merino, D. G. de Oteyza, D. Peña, D. Jacob and J. I. Pascual, Nano Lett., 2019, 19, 3288–3294.
24. Y. Li, C. Yang and X. Guo, Acc. Chem. Res., 2020, 53, 159–169.
25. S. Bhandary, O. Eriksson, B. Sanyal and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165405.
26. W. R. Scheidt and C. A. Reed, Chem. Rev., 1981, 81, 543–555.
27. S. Bhandary, M. Schüler, P. Thunström, I. di Marco, B. Brena, O. Eriksson, T. Wehling and B. Sanyal, Phys. Rev. B, 2016, 93, 155158.
28. S. Bhandary, S. Ghosh, H. Herper, H. Wende, O. Eriksson and B. Sanyal, Phys. Rev. Lett., 2011, 107, 257202.
29. S. Bhandary, B. Brena, P. M. Panchmatia, I. Brumboiu, M. Bernien, C. Weis, B. Krumme, C. Etz, W. Kuch, H. Wende, O. Eriksson and B. Sanyal, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 024401.
30. B. Liu, H. Fu, J. Guan, B. Shao, S. Meng, J. Guo and W. Wang, ACS Nano, 2017, 11, 11402–11408.
31. W. Wang, R. Pang, G. Kuang, X. Shi, X. Shang, P. N. Liu and N. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045440.
32. S. Bhandary, O. Eriksson and B. Sanyal, Sci. Rep., 2013, 3, 3405.
33. D. Rolf, C. Lotze, C. Czekelius, B. W. Heinrich and K. J. Franke, J. Phys. Chem. Lett., 2018, 9, 6563–6567.
34. B. W. Heinrich, C. Ehlert, N. Hatter, L. Braun, C. Lotze, P. Saalfrank and K. J. Franke, ACS Nano, 2018, 12, 3172–3177.
35. G. Kuang, Q. Zhang, T. Lin, R. Pang, X. Shi, H. Xu and N. Lin, ACS Nano, 2017, 11, 6295–6300.
36. H. C. Herper, M. Bernien, S. Bhandary, C. F. Hermanns, A. Krüger, J. Miguel, C. Weis, C. Schmitz-Antoniak, B. Krumme, D. Bovenschen, C. Tieg, B. Sanyal, E. Weschke, C. Czekelius, W. Kuch, H. Wende and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 174425.
37. C. Liu, B. Yao, T. Dong, H. Ma, S. Zhang, J. Wang, J. Xu, Y. Shi, K. Chen, L. Gao and L. Yu, npj 2D Mater. Appl., 2019, 3, 23.
38. R. Bulla, T. A. Costi and T. Pruschke, Rev. Mod. Phys., 2008, 80, 395–450.
39. M. Schüler, S. Barthel, T. Wehling, M. Karolak, A. Valli and G. Sangiovanni, Eur. Phys. J.: Spec. Top., 2017, 226, 2615–2640.
40. G. Gandus, A. Valli, D. Passerone and R. Stadler, J. Chem. Phys., 2020, 153, 194103.
41. A. Valli, M. P. Bahlke, A. Kowalski, M. Karolak, C. Herrmann and G. Sangiovanni, Phys. Rev. Res., 2020, 2, 033432.
42. J. Steinbauer, S. Biermann and S. Bhandary, Phys. Rev. B, 2019, 100, 245418.
43. Y. Meir and N. S. Wingreen, Phys. Rev. Lett., 1992, 68, 2512.
44. D. Jacob, J. Phys.: Condens. Matter, 2015, 27, 245606.
45. A. Droghetti and I. Rungger, Phys. Rev. B, 2017, 95, 085131.
46. A. Valli, A. Amaricci, V. Brosco and M. Capone, Nano Lett., 2018, 18, 2158.
47. A. Valli, A. Amaricci, V. Brosco and M. Capone, Phys. Rev. B, 2019, 100, 075118.
48. J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. S. Wee and W. Chen, Chem. Soc. Rev., 2015, 44, 2998–3022.
49. J. Li, N. Merino-Díez, E. Carbonell-Sanromà, M. Vilas-Varela, D. G. de Oteyza, D. Peña, M. Corso and J. I. Pascual, Sci. Adv., 2018, 4, eaaq0582.
50. H. Wan, Y. Xu and G. Zhou, J. Chem. Phys., 2012, 136, 184704.
51. S. Caneva, P. Gehring, V. M. García-Suárez, A. García-Fuente, D. Stefani, I. J. Olavarria-Contreras, J. Ferrer, C. Dekker and H. S. J. van der Zant, Nat. Nanotechnol., 2018, 13, 1126–1131.

---

Footnote

† Electronic supplementary information (ESI) available: Details for ab initio, many-body, and transport calculations; embedding of the Fe-3d multiplet; benchmark against quantum Monte Carlo. See DOI: 10.1039/d1na00407g

---