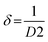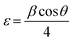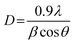Open Access Article
Open Access ArticleAn effective strategy for the development of multiferroic composite nanostructures with enhanced magnetoelectric coupling performance: a perovskite–spinel approach
Preethy
Augustine
 a,
Yerol
Narayana
*a and
Nandakumar
Kalarikkal
b
a,
Yerol
Narayana
*a and
Nandakumar
Kalarikkal
b
aDepartment of Physics, Mangalore University, Mangalagangotri, India. E-mail: narayanay@yahoo.com
bSchool of Pure and Applied Physics, Mahatma Gandhi University, Kottayam, India
First published on 13th July 2021
Abstract
An energy efficient move toward the regulation of magnetization vector solely with E-field by developing multiferroic (MF) magnetoelectric (ME) nanostructures' have opened up vast avenues for novel low power consumption memories and magnetoelectric devices. The present study delineates the development of multiferroic nanocomposites (MF NCs) with perovskite BiFeO3 and spinel NiFe2O4. A simple Pechini one-pot method is employed for the preparation of nanocomposites with different molar concentrations and the modified structural, magnetic, dielectric, and magnetoelectric performance of NCs is carried out at room temperature. The purity in the crystalline phase of BiFeO3 and NiFe2O4 in the NCs are corroborated by XRD and FTIR spectroscopy, which is further substantiated, while EDAX analysis pointed out the elemental composition. The SEM images provide an evidence for the closely compacted and agglomerated grains with some voids in the prepared sample. A well saturated magnetic hysteresis (M–H) loop reveals long range ferromagnetic ordering and the remanence value ascertains the multidomain structure. The dielectric performance and impedance analysis imparts greater knowledge of the dependence of grain and grain boundaries on the resistive and conductive behavior of the composites. The frequency dependence of electric modulus and impedance exhibits a non-Debye type of relaxation process. The P–E hysteresis loops clearly show the lossy behavior of the composites with an increase in the NiFe2O4 concentration. The ME coupling coefficient of the composites evaluated using the dynamic magnetic field method demonstrates the effective coupling interaction between ferroelectric (FE) perovskite BiFeO3 and ferromagnetic (FM) spinel NiFe2O4. Thus, the findings disclose a greater potential for innovative applications in spintronics and information technology.
Introduction
The co-existence and mutual coupling of magnetism and electric polarization in multiferroics enable far-reaching functionalities. It explores the possibility of the design of magnetoelectric devices and non-volatile memories.1,2 Multiferroic nanocomposites has been a topic of an active field of research in recent years because of their multi-functionality at room temperature, device miniaturization, and reduced energy consumption.3 None of the existing single phase multiferroic materials have robust electric and magnetic polarization at room temperature, whereas the cross interaction between the constituent phases in the composites can produce a remarkable ME effect.4 The magneto-electric (ME) coupling property in the material was first envisioned by Curie in 1894.5 This intriguing property brings about an interesting cross coupling effect, i.e., the magnetic (electric) control of electric (magnetic) polarization. The interfacial phenomena of magneto-electric coupling6 provide an alternative route for controlling the ferromagnetism with electric fields. From a technological perspective, it could have tremendous impact on microelectronics, spintronics, sensor technique, magnetic and electric switching, etc., to produce multifunctional miniaturized devices with high efficiency, low power consumption, and low heat dissipation.7–9A perovskite–spinel multiferroic system with interfacial straining effect between ferromagnetic and electric ordering has sparked colossal research on composite nanostructures. Several multiferroic nanocomposites such as BiFeO3/CoFe2O4,10 SrTiO3/NiFe2O4,11 (1 − x)BaTiO3/xNi0.7Zn0.3Fe2O4,12 and BaTiO3/CuFe2O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 have been reported via the perovskite–spinel approach with enhanced values of the magneto-electric coupling coefficient. The ME effect is a multiplicative property of strain-mediated coupling between the ferromagnetic and ferroelectric phases in the material. Pandey et al.14 reported the phase transformation, which introduces strain in the ferroelectric phase, providing a better coupling between two phases in (1 − x)Bi(Ni1/2Ti1/2)O3–PbTiO3/xNi0.6Zn0.4Fe2O4 composites. The low temperature sintering of composites reduces the formation of secondary impurity phases, which will provide a large ME response also observed in the composites. Bangruwa et al.15 discussed about the composites of perovskites and spinel ferrites that give improved ferromagnetic hysteresis loops, good ferroelectric properties, and reduced leakage current.
13 have been reported via the perovskite–spinel approach with enhanced values of the magneto-electric coupling coefficient. The ME effect is a multiplicative property of strain-mediated coupling between the ferromagnetic and ferroelectric phases in the material. Pandey et al.14 reported the phase transformation, which introduces strain in the ferroelectric phase, providing a better coupling between two phases in (1 − x)Bi(Ni1/2Ti1/2)O3–PbTiO3/xNi0.6Zn0.4Fe2O4 composites. The low temperature sintering of composites reduces the formation of secondary impurity phases, which will provide a large ME response also observed in the composites. Bangruwa et al.15 discussed about the composites of perovskites and spinel ferrites that give improved ferromagnetic hysteresis loops, good ferroelectric properties, and reduced leakage current.
Herein, the development of multiferroic nanocomposite of perovskite (ABO3) and spinel ferrite (AB2O4) structures have been focused on to bring out effective ME coupling performance. The perovskite BiFeO3 (BFO) having a rhombohedral structure (R3c space group) stands out as a well-known single phase ME material. It has room temperature spontaneous ferroelectric and antiferromagnetic nature. It exhibits ferroelectric polarization of 100 μC cm−2 and Curie temperature of ∼1103 K due to paired electrons in the outermost 6s orbital of the Bi3+ cation and the material show feeble antiferromagnetic behavior below its Neel temperature (TN ∼ 643 K) due to unpaired d-orbital electronic distribution of the Fe3+ cation.16,17 Though the ME interactions are reported in BiFeO3,18,19 weak ferromagnetic nature,20 poor ferroelectric reliability,21 and weak ME coupling hinders its practical applications. Several studies have been reported wherein the spinel ferrites act as good magnetic materials for device applications because of their greater electrical resistivity and magnetoelasticity than that of the perovskites.22,23 It has a considerable effect on the leakage current of BFO-ferrite composites.15 The inverse spinel structure of soft ferrimagnetic NiFe2O4 (NFO) has a high Neel temperature of 858 K,24 high magnetic permeability, low anisotropy, high magnetostriction coefficient, moderate coercivity, retentivity, and low electrical conductivity.25,26 One of the greatest advantages of NFO is its tunable magnetic and electrical properties due to its low anisotropy.22 In recent decades, it has also been noted that BiFeO3-based nanocomposites, combined with perovskite oxides and spinel ferrites, have provided desirable greater ME response compared to the single phase compound.
However, as per the literature survey, there are no reports on the synthesis of the BiFeO3–NiFe2O4 nanocomposite using the Pechini one-pot method. It is a facile and cost effective method for producing highly pure and homogeneous oxides at reduced temperatures and shorter calcination times than other chemical methods.27,28 In addition to this, this is an introductory work to determine the magnetoelectric coupling performance of the prepared nanocomposites using a lock-in amplifier set up at room temperature. The molar concentration of materials involved in the composites, their grain size, and the resistivity of magnetic and ferroelectric counterparts particularly influence the ME output of the composites. The present study describes the formation of 0–3 type perovskite/spinel ferrite nanocomposites with dielectric and magnetic properties. Further, the detailed study of the magneto-electric coupling coefficient of the BiFeO3–NiFe2O4 (hereafter abbreviated as BFO–NFO) nanocomposite was emphasized to confirm the multiferrocity in the composites.
Experimental details
A simple chemical method called the Pechini one-pot method is used to synthesize the xBiFeO3-(1 − x)NiFe2O4 nanocomposite. A stoichiometric amount of Bi(NO3)3·5H2O, Fe(NO3)3·9H2O, Ni(NO3)2·4H2O, C6H8O7, and ethylene glycol were used for the preparation of the composite in a typical procedure. The ratio of molar concentration of nitrates, Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni:Fe were fixed at 1
Ni:Fe were fixed at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11, 3
11, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13, 5
13, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15, and 7
15, and 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17, which were dissolved in the aqueous solution of citric acid and kept at 70–80 °C with continuous stirring until a homogenous brown clear solution was formed. Then, an appropriate amount of ethylene glycol, CA
17, which were dissolved in the aqueous solution of citric acid and kept at 70–80 °C with continuous stirring until a homogenous brown clear solution was formed. Then, an appropriate amount of ethylene glycol, CA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG = 60
EG = 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, was added to this homogeneous mixture by maintaining the same temperature and stirring until the viscous gel was achieved. Thereafter, the derived gel was kept at 110 °C in a hot air oven for drying and further calcined for 2 h in an air atmosphere at 600 °C. The resultant powder was ground using a pestle mortar and pelletized to a size 8 mm diameter and 1 mm thickness and kept for sintering for 2 h at 700 °C, making a dense sample for electrical and magneto-electric coupling measurements.
40, was added to this homogeneous mixture by maintaining the same temperature and stirring until the viscous gel was achieved. Thereafter, the derived gel was kept at 110 °C in a hot air oven for drying and further calcined for 2 h in an air atmosphere at 600 °C. The resultant powder was ground using a pestle mortar and pelletized to a size 8 mm diameter and 1 mm thickness and kept for sintering for 2 h at 700 °C, making a dense sample for electrical and magneto-electric coupling measurements.
The crystalline nature of the BFO–NFO nanocomposites were examined using Rigaku Miniflex 600 X-ray diffractometer. The 2θ values in the range of 20°–80° were scanned at the rate of 3° min−1. The FT-IR absorption spectra of all the composites were recorded using a ThermoFisher Scientific Fourier Transform Infrared (FT-IR) spectrometer. The SEM images of the samples were captured using a Carl Zeiss Sigma Field Emission Scanning Electron Microscope (FE-SEM). The elemental analysis of the prepared composites was also done using the Energy Dispersive Spectroscopic (EDS) technique. The magnetization measurements were carried out using a Vibrating Sample Magnetometer (VSM) in the field range of 20 kOe ≥ H ≥ −20 kOe. The ferroelectric properties were evaluated by tracing the P–E loop in the field range of −6 kV cm−1 to +6 kV cm−1 at the frequency of 50 Hz. The frequency-dependent dielectric parameters in the range 100 Hz to 2 MHz were measured using an Impedance Analyzer (Agilent E4980). The ME coupling coefficient measurement of the composites were performed at fixed Hac = 10 Oe of frequency 850 Hz collinearly with varying Hdc in the range of 0–5 kOe and at a fixed Hdc of 1 kOe collinearly with varying Hac in the range of 0–80 Oe. A lock-in amplifier set up was used to record the induced ME voltage. All the characterization studies were executed at room temperature.
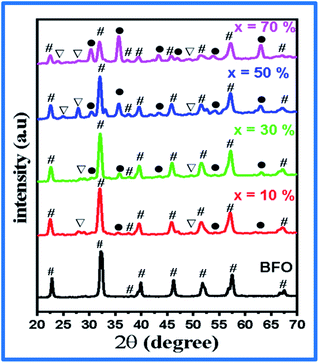
XRD analysis
The XRD pattern of the BFO–NFO nanocomposites in various compositions at x = 10%, 30%, 50% and 70% are depicted in Fig. 1. The peaks appeared at 22.52°, 32.06°, 37.33°, 39.46°, 45.72°, 51.49°, 57.08°, and 67.12° are identified as the reflection planes of (0 1 2), (1 1 0), (1 1 3), (2 0 2), (0 2 4), (1 2 2), (3 0 0), and (2 2 0), respectively, which corresponds to the rhombohedral perovskite structure of BFO (JCPDS #71-2494), as indexed by (#). The rest of the peaks at 30.25°, 35.69°, 43.42°, 47.91°, 54.12°, 57.08°, and 63.01° are identified as the planes of (2 2 0), (3 1 1), (4 0 0), (3 3 1), (4 2 2), (5 1 1), and (4 4 0), respectively, which corresponds to the spinel cubic structure of NFO (JCPDS #89-4927), indexed by (●). There are few minor impurity peaks that correspond to the secondary phases of BFO and NFO, which is indexed by (□) that could be observed at 2θ angles of 24.36°, 27.95°, and 49.02°. It may be due to the evaporation of bismuth during calcination.29 However, the XRD pattern confirmed the presence of both BFO and NFO phases in the composites. The intensity of the NFO peaks increased as the concentration of BFO decreased in the composites.The calculated values of the lattice constants and the cell volume of the BFO and NFO phases in the composites are tabulated in Table 1. It is evident that all the values of lattice parameters match well with the reported values of the individual BFO and NFO phases. However, a small change in the lattice parameters and cell volume of the constituent phases may be due to the compressive strain between them, which is created by lattice distortion.30 Therefore, it is worthwhile to estimate the strain (ε) and dislocation density (δ) using the following relations.31
where β is FWHM and D is the average crystallite size, which is calculated using Scherrer's equation.
| Sample | Density (Dx) (g cm−3) | Crystallite size (D) (nm) | Dislocation density (δ) (Å)2 | Strain (ε) | Surface area (S) m2 g−1 | Lattice constants and cell volume | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| BFO phase | NFO phase | |||||||||
| a (Å) | c (Å) | V (Å)3 | a (Å) | V (Å)3 | ||||||
| BNFO-10 | 1.351 | 9.39 | 0.0113 | 0.3134 | 472.899 | 5.58 | 13.86 | 431.52 | 8.3146 | 574.89 |
| BNFO-30 | 1.653 | 6.45 | 0.0240 | 0.3765 | 562.885 | 5.58 | 13.88 | 432.52 | 8.3083 | 573.51 |
| BNFO-50 | 1.950 | 5.28 | 0.0359 | 0.4246 | 582.731 | 5.58 | 13.89 | 432.79 | 8.3197 | 575.87 |
| BNFO-70 | 2.257 | 4.85 | 0.0425 | 0.4619 | 547.934 | 5.58 | 13.90 | 432.72 | 8.3067 | 573.19 |
Table 1 summarizes all the calculated values of the lattice constants and cell volume, crystallite size (D), dislocation density (δ), strain (ε), and surface area (S). It is clear that there is a reduction in the crystallite size with increasing NFO content in the composites. The crystallite size is reduced because of the lattice distortion caused by the ionic radius difference32 between Bi3+ (1.17 Å) and Ni2+ (0.72 Å). This results in an increase in the dislocation density, which enhances the strain between the BFO and NFO phases, thereby improving the ME effect in the composites.33
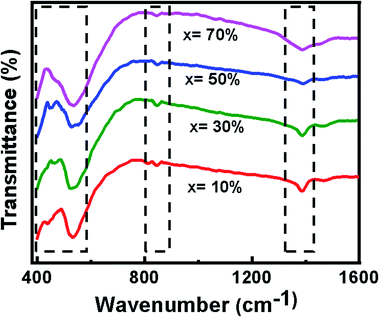
FTIR analysis
The FT-IR spectra of the BFO–NFO nanocomposites, recorded in the wavelength range of 400–1600 cm−1, is displayed in Fig. 2. The absorption peaks exhibited in the range of 400–600 cm−1 are attributed to the intrinsic stretching and bending vibrations of Fe2+ions at tetrahedral (Fetetra ↔ O) and octahedral sites (Feocta ↔ O) of NiFe2O4.25 The peaks observed in the range may also be due to the vibrational mode of the Fe–O6 octahedral, which implies the BFO phase. The peak at wavenumber of 813 cm−1 corresponds to metal–oxygen (Fe–O) stretching frequency mode, which may have resulted from highly crystalline BFO in the composite.34 The peak corresponding to 1362 cm−1 is due to the stretching vibrations of NO3− ions.35FESEM and EDAX analysis
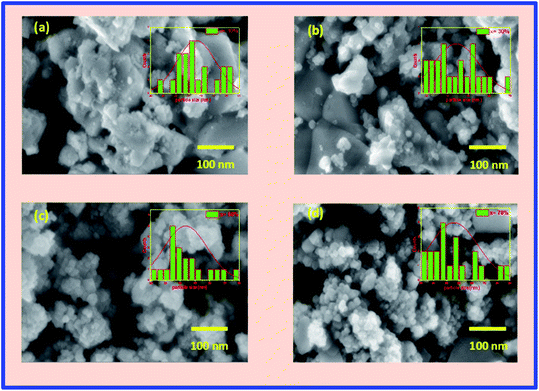
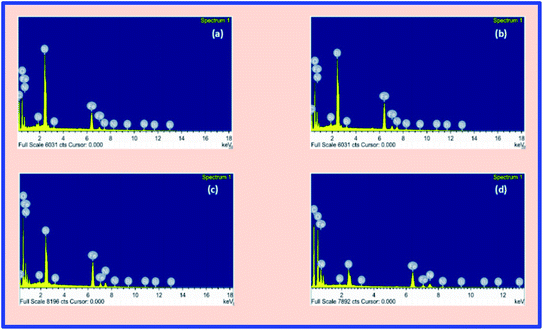
Fig. 3(a–d) represents the FESEM images of the BFO–NFO nanocomposites, which gives information regarding the surface morphology, grain shape, size, and distribution. The images clearly show an inhomogeneous distribution of the grains in the samples with irregular shapes and non-uniform size. An inhomogeneous development of grains may result from the dissimilar growth of individual phases in the composite samples. The grains are completely agglomerated and closely compacted with some voids throughout the samples. However, the larger and smaller grains seen in Fig. 3(a) and (b) indicate that the grain growth of one of the phases is higher than that of the other phase in the composites.15 The reduction in the grain size and its uniform distribution, as the concentration of NFO increases, is due to the magnetic interactions between the grains as well as higher surface to volume ratio of the nanocomposites.36 The grain size distribution histograms are exhibited along with the FESEM images at its top-right corners. The average grain size of the samples was found to be 45, 44, 41, and 38 nm, respectively, for different compositions, using the ImageJ software. The EDX spectra of BFO–NFO nanocomposites in different compositions is depicted in Fig. 4(a–d). The spectra show the incorporation of all the elements, namely, Bi, Ni, Fe, and O, with strong peaks and confirm the stoichiometry of the studied perovskite–spinel ferrite composites.Magnetic properties
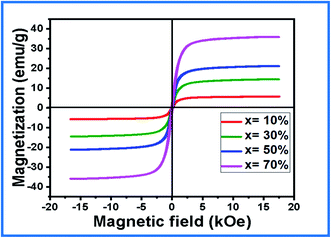
To investigate the ferromagnetic behavior of the (1 − x)BiFeO3–xNiFe2O4 nanocomposites at room temperature, M–H hysteresis loops were plotted within an applied field of −20 kOe ≤ H ≤ 20 kOe, as shown in Fig. 5. A typical ferromagnetic nature is exhibited in the M–H loops for all the composites, which confirms the presence of long-range magnetic ordering in the NFO phase in the composites. The magnetic moment (μ) and magnetic crystalline anisotropy constant (K) were calculated using the following relations.31,37| M = (Ms × W)/5585 |
| K = (Hc × Ms)/0.96 |
| x | M s (emu g−1) | M r (emu g−1) | H c (Oe) | M r/Ms | K | μ (μB) |
|---|---|---|---|---|---|---|
| BFO | 0.12 | 0.01 | 235.52 | 0.0833 | 29.44 | 0.0067 |
| NFO | 30.8 | 12.69 | 93.6 | 0.4120 | 3003 | 1.2926 |
| 10% | 5.7245 | 0.7812 | 165.88 | 0.1365 | 989.15 | 0.0312 |
| 30% | 14.494 | 1.2855 | 123.51 | 0.0887 | 1864.67 | 0.0749 |
| 50% | 21.163 | 1.6169 | 109.44 | 0.0764 | 2412.58 | 0.1035 |
| 70% | 35.996 | 2.1361 | 95.946 | 0.05 | 3597.58 | 0.1661 |
The value of saturation magnetization (Ms) and magnetic moment increases significantly with an increase in the NFO concentration. It is due to the fact that each ferrite grain acts as a center of magnetization and the resultant magnetization is the vector sum of each grain's magnetization.39 There is a strong exchange interaction between the ferromagnetic (NFO) phase and the ferroelectric (BFO) phase. It is because of the increase in the number of magnetic linkages existing between the tetrahedral and octahedral cations of the composites. This also raises the saturation magnetization and magnetic moment in the composites. An increase in the remnant magnetization (Mr) values is observed with an increase in the NFO concentration. It confirms that most of the spins are directed away from the preferred magnetic field, which results in stress and hence the remanent magnetization increases.33 The decrease in the coercivity (Hc) can be attributed to its particle size. Herein, the decrease in the particle size with increasing NFO concentration in the composites contributes to a decrease in the coercivity. The squareness ratio (Mr/Ms) ascertains the domain structure of the composites. The calculated values confirm the multi-domain structure of the composites (Mr/Ms < 0.5). The domain pinning by the ferroelectric phase causes a reduction in the Mr/Ms ratio of the composites. The magnetic crystalline anisotropy (K) increases with an increase in the NFO concentration. This is because of the strong coupling interaction between the ferromagnetic and ferroelectric phase in the composites. The increase in the magnetic anisotropy constant from x = 10–70% shows an inverse relation with the particle size, thereby supporting the FESEM studies.
Dielectric properties
Fig. 6(a) and (b) illustrate the variation in the dielectric constant with respect to frequency, varying from 100 Hz to 2 MHz at room temperature for the BFO–NFO samples with different compositions. It is noted that all the composites have displayed the same dielectric frequency dispersion behavior, wherein the dielectric constant is high at a lower frequency region. The dielectric constant decreases gradually with increasing frequency and remains constant at a higher frequency region. This is a typical characteristic of dielectric materials. The higher values of dielectric constant in the low frequency region is attributed to interfacial and space charge polarization and it can be described on the basis of Maxwell–Wagner polarization mechanism and Koop's theory.40 However, the dielectric constant is high in the low frequency region due to orientation polarization, which is produced from the multi-oxidation state of iron (Fe3+ and Fe2+).41 The hopping of electrons between Fe3+ and Fe2+ can follow the frequency of the applied in the low frequency region. But in the high frequency region, the charge carriers do not respond to the variation in the applied field, which results in the discontinuation of dipolar polarization with an increase in the frequency. Thus, only the ionic and electronic polarization contributes toward the dielectric constant in the high frequency region. Hence, the dielectric constant reduces and becomes independent of the frequency in the high frequency region.33,42 The value of the dielectric constant increases as the concentration of NFO increases in the composites.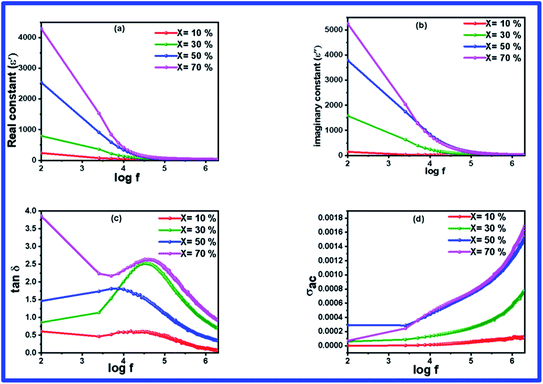 | ||
| Fig. 6 (a–d) Frequency dependent dielectric parameters of (1 − x)BFO–xNFO nanocomposites at x = 10%, 30%, 50%, and 70%. | ||
The frequency-dependent loss tangent of the composites, which is displayed in Fig. 6(c), resembles the result of dielectric constant. The occurrence of dielectric loss in the composites is mainly due to the resistive loss and relaxation loss.39 A loss peak can be found at a frequency of 1 kHz and this relaxation loss is attributed to space charge polarization. In the lower frequency region, the movement of space charges catches up with the frequency of the applied field, resulting in a high loss factor, whereas in the high frequency region, negligible effect of space charges leads to a low value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. Apart from this, there is a significant increase in the loss factor with an increase in the NFO concentration in the BFO–NFO nanocomposites. It can be correlated with resistive losses owing to electron hopping between Fe3+ and Fe2+.
δ. Apart from this, there is a significant increase in the loss factor with an increase in the NFO concentration in the BFO–NFO nanocomposites. It can be correlated with resistive losses owing to electron hopping between Fe3+ and Fe2+.
Fig. 6(d) depicts the variation in the AC conductivity (σac) as a function of frequency in the range of 100 Hz to 2 MHz at room temperature for all the samples with different compositions. There is no change in the conductivity up to a certain frequency and it increases abruptly with an increase in frequency. The frequency-independent conductivity in the low frequency region refers to band conduction, which is equal to the DC conductivity and the frequency-dependent conductivity in the high frequency region owing to small polaron hopping mechanism.43 The conductivity of the composites increases with an increase in the concentration of NFO in the sample and it is due to the presence of charge carriers. This conductivity can be explained on the basis of the hopping of charge carriers between Fe3+/Fe2+ in the composites. The resistive grain boundaries present in the material becomes more active in the low frequency region and reduces the hopping of charge carriers into the grain portion of the material. It reduces the participation of charge carriers in the hopping conduction mechanism. As the frequency of the applied field increases, the charge carriers acquire a certain amount of energy to break the grain boundaries and enter the grain segment.33 Thus, the mobility of charge carriers increases inside the grains, which results in an increase in the conductivity in the high frequency region.
Impedance spectroscopic analysis
Complex impedance spectroscopy is an important metric that is used to understand the relaxation and electrical conductivity of the material. The frequency-dependent real part of the complex impedance (Z′) over a wide range of frequency (100 Hz to 2 MHz) of the BFO–NFO nanocomposite with various compositions is displayed in Fig. 7(a). The plots show that the value of Z′ decreases continuously with an increase in the frequency to a certain limit and then eventually comes to a steady state at higher frequencies. As the frequency increases, the decreasing tendency of Z′ implies the increased conductivity of the samples. The large value of impedance seen in the low frequency region suggests the existence of all kinds of polarization in the region. The plateau at higher frequencies specifies the liberation of space charges at the grain and grain boundary interfaces in the composites under an applied field.44,45 Moreover, the decline of Z′ appears as the concentration of NFO increases in the composites. This is owing to the loss of resistivity and enhanced conductivity of the samples. Fig. 7(b) demonstrates the frequency-dependent imaginary part of impedance, which resembles the behavior of Z′.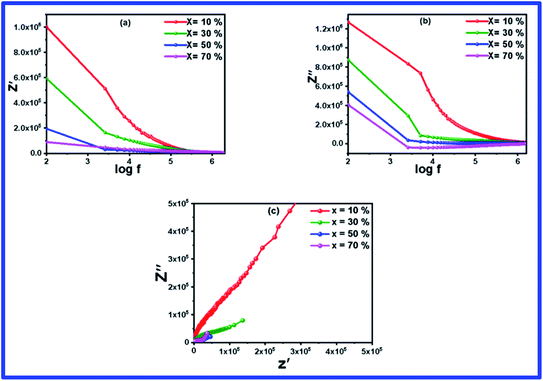 | ||
| Fig. 7 (a–c) Frequency dependent impedance (Z′ & Z′′) spectra and Nyquist plot of (1 − x)BFO–xNFO nanocomposites at x = 10%, 30%, 50%, and 70%. | ||
Fig. 7(c) shows the Nyquist impedance plot of the BFO–NFO nanocomposites evaluated over a wide range of frequencies from 100 Hz to 2 MHz. As stated in Debye's model, dielectric materials possess a single relaxation time, which always produce a semicircle centered on the real (Z′) axis. But all the materials do not generate a perfect semicircle because of the relaxation from the ideal Debye characteristics. In this case, an asymmetric and depressed semicircle appears, which indicates non-Debye relaxation in the materials where there is an existence of dissemination of relaxation times.46 The impedance plot in Fig. 7(c) comprised depressed type of semicircles analogous to the grains and grain boundaries, proposing non-Debye relaxation behavior in the composites. As the concentration of NFO increases in the composites, the radius of the semicircle decreases, which shows decreased resistance and increasing conductivity. It affirms the contribution of resistance from the grain and grain boundaries to the conduction mechanism within the composites.44,47
Electric modulus analysis
Complex modulus spectroscopy is an appropriate technique to determine and comprehend the electrical transport phenomena, i.e., electrode polarization, ion hopping rate, and electrical and space charge relaxation processes of the samples at various frequencies and temperatures.48,49 It is a powerful tool than impedance spectroscopy regarding the distinction between electrode polarization and grain boundary conductivity.50Fig. 8(a) and (b) display the variation of M′ & M′′ with respect to the frequency for different (1 − x)BFO–xNFO nanocomposites at x = 10%, 30%, 50%, and 70%. As observed from Fig. 8(a), the value of M′ becomes closer to zero (except at x = 10%) and coincides with it in the low frequency region, which indicates a small contribution of electrode polarization to M′.51 However, the value of M′ continuously disperses as the frequency increases and reaches its maximum value on further increasing the frequency. It is because of the presence of relaxation processes that spread over the long range frequencies.48 The frequency variation of M′′ for different (1 − x)BFO–xNFO nanocomposites at x = 10%, 30%, 50%, and 70% is shown in Fig. 8(b). The asymmetric peaks observed in the figure indicate non-Debye type relaxation, i.e., the spread of relaxation times with different time constants.51 However, there is a change in the dielectric relaxation process as the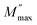 peaks shift toward higher frequencies when the concentration of NFO increases. The peak at low frequencies is ascribed to grain contribution and at high frequencies is attributed to the grain boundaries.2 The frequency at which M′′ is the maximum is known as the relaxation frequency. The charge carriers are mobile at longer distances in the frequency region below
peaks shift toward higher frequencies when the concentration of NFO increases. The peak at low frequencies is ascribed to grain contribution and at high frequencies is attributed to the grain boundaries.2 The frequency at which M′′ is the maximum is known as the relaxation frequency. The charge carriers are mobile at longer distances in the frequency region below 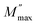 while the movement of charge carriers is confined to potential wells and allowed only for shorter distances in the region above
while the movement of charge carriers is confined to potential wells and allowed only for shorter distances in the region above 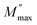 .52Fig. 8(c) shows the complex modulus spectra of M′′ vs. M′ (1 − x)BFO–xNFO nanocomposites with different compositions. The asymmetric semicircular arc substantiates the existence of the electrical relaxation phenomenon in the composites.51
.52Fig. 8(c) shows the complex modulus spectra of M′′ vs. M′ (1 − x)BFO–xNFO nanocomposites with different compositions. The asymmetric semicircular arc substantiates the existence of the electrical relaxation phenomenon in the composites.51
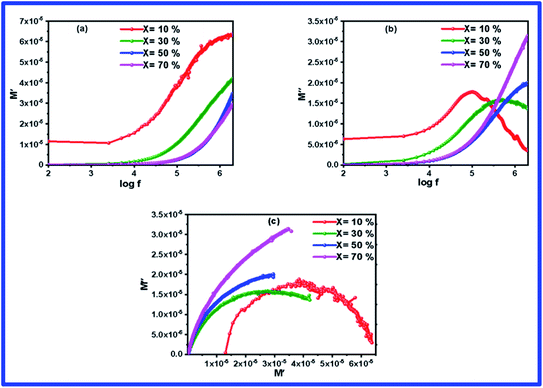 | ||
| Fig. 8 (a–c) Frequency dependence of the electric modulus (M′ & M′′) spectra and complex modulus spectrum (M′ vs. M′′) of the (1 − x)BFO–xNFO nanocomposites at x = 10%, 30%, 50%, and 70%. | ||
Ferroelectric properties
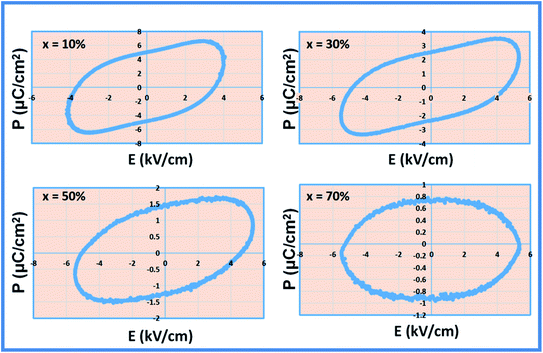
The ferroelectric behavior of the prepared composites at room temperature was examined by recording the P–E hysteresis loops at a frequency of 50 Hz within the electric field range ±6 kV cm−1 and the results are shown in Fig. 9. The composites studied, with the current percentage composition (Table 3), do not show a perfect ferroelectric loop. This is due to the large leakage current associated with it. It shows a banana-shaped leaky loop with polarization not well saturated. This may be due to the oxygen vacancy defects generated during the sintering53 and mixed valence of the magnetic ions (Fe2+ and Fe3+),54 which produces leakage current, prevents obtaining a well saturated P–E loop, and also hinder the switching of the ferroelectric domain.52 The spontaneous and remanent polarizations are observed to be decreased as the concentration of NFO increases and the ferroelectric fraction decreases in the composites. It is indicated by the near circular loop with a large area. The dilution of the FE behavior is very sensitive to the size of the grains and the lattice strain on the BFO–NFO interface. Since the composites have a mixed connectivity, it is difficult to pole larger grains at a lower electric field. During the electric poling of the composite samples, NFO does not respond to this field and hence leads to a decrease in spontaneous polarization.55 Hence, spontaneous polarization decreases with the NFO content, which imparts a guideline for the selection of compositions of phases. The maximum observed saturation polarization (Pm) and remanent polarization (Pr) are 6.59 μC cm−2 and 5.01 μC cm−2, respectively, for the composite at x = 10%. The lowering of polarization values with the distribution of NFO in the BFO matrix at different compositions is listed in Table 3. The fall in the polarization is also attributed to the cubic structure and paraelectric effect56 of spinel ferrite NFO, which is unfavorable for ferroelectric stability.15,36| Sample | Ferroelectric parameters | |
|---|---|---|
| P max (μC cm−2) | P r (μC cm−2) | |
| BFO–NFO (x = 10%) | 6.5874 | 5.0118 |
| BFO–NFO (x = 30%) | 3.4634 | 2.5253 |
| BFO–NFO (x = 50%) | 1.6661 | 1.4544 |
| BFO–NFO (x = 70%) | 0.7161 | 0.6949 |
Magnetoelectric coupling analysis
The magnetoelectric effect is a product property, which occurs due to the simultaneous existence of the electric and magnetic phases in the material. It can be characterized by measuring the coupling interaction of the electric and magnetic order parameters concerning the ME voltage coefficient (αE). For the occurrence of the magnetoelectric phenomenon, it is necessary to have a proper electrical and magnetic poling of the samples. It would enable the dipole reorientations so that the electric and magnetic phases would effectively take part to yield a reasonable polarization, which is measured as the ME output voltage.A conventional measurement method called the dynamic method57 has been employed for measuring the ME output voltage. In this dynamic method, the measurement is carried out at fixed DC magnetic field (Hdc) by varying the AC field (Hac) and by fixing the AC magnetic field (Hac) while varying the DC magnetic field (Hdc). The primary equations, which are required for the estimation of the ME coefficient, are stated by Rivera58 as follows.
If the DC magnetic field H0 is in line with the AC magnetic field h0 at frequency ‘ω’, the effective field is
H = H0 + h0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) sin(ωt) | (1) |
The ME output signal measured using the lock-in amplifier, tuned at the frequency is
| Vout ∝ (αH0 + 2βh0H0) | (2) |
The linear ME coupling coefficient (MECC) 'α' calculated from the ME voltage (Vout), is
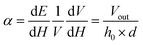 | (3) |
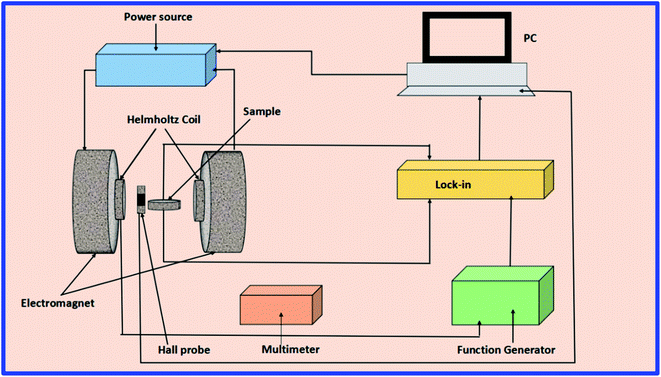
A home-built, lock-in amplifier set up was used for the measurement of Vout experimentally.59 The schematic representation of the ME measurement set up is shown in Fig. 10. The set up consists of an electromagnet to produce varying magnetic fields using the DC power supply. A Hall probe was connected for measuring the DC field. In addition, an AC field is superimposed over the DC field. A Helmholtz coil that is mounted between the pole pieces of an electromagnet generates an AC field with the help of a lock-in amplifier and a function generator. The sample placed at the center of the coil is excited with an AC field. It enables the dipole reorientations within the sample to produce polarization that induces the ME voltage on both the surfaces of the sample through ME coupling. The induced ME voltage is measured in differential units using a lock-in amplifier. The measurement of the pure induced ME signal with a complete reduction of noise is the advantage of this method.
Using the measurement set-up above, the magnetoelectric coupling coefficient (MECC) of the BFO–NFO samples with different compositions at room temperature has been studied. Fig. 11(a) shows the AC measurement of the ME voltage of the composites by varying the AC magnetic field (Hac) of frequency 850 Hz in the range of 0–80 Oe with a constant DC magnetic field of 1 kOe. The ME output voltage grows linearly with varying applied Hac. The linear MECC ‘α’ was determined using eqn (3). The obtained results are reported in Table 4. The maximum observed value of MECC is 11.85 mV cm−1 Oe−1 for the (1 − x)BFO-xNFO sample at x = 10%, which is the ferroelectric rich composition. The MECC decreases substantially for other magnetic phase rich samples (x = 30%, 50%, 70%), which are attributed to the low resistivity of the ferrite phase (NFO) as compared to the ferroelectric phase (BFO) that causes leakage current in the composites. If the concentration of the ferrite phase is high in the composite, it cannot be poled at a high voltage due to its low resistance.60 It reduces the polarization in the composites, which results in poor magnetoelectric coupling. Thus, there is a restriction to the concentration of the ferrite phase while incorporating with the ferroelectric phase to produce a large ME coupling coefficient.
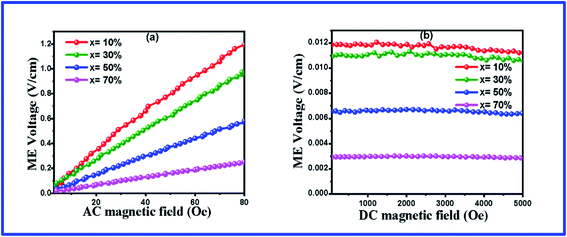 | ||
| Fig. 11 ME coefficient of the (1 − x)BFO–xNFO nanocomposites at x = 10%, 30%, 50%, and 70% (a) under AC bias field and (b) DC bias field. | ||
| Sample | x = 10% | x = 30% | x = 50% | x = 70% |
|---|---|---|---|---|
| α (mV/cmOe) with Hdc | 11.85 | 10.95 | 6.95 | 2.98 |
| α (mV/cmOe) with Hac | 12.10 | 11.13 | 7.15 | 2.89 |
In the DC measurements, the ME voltage was developed across the sample while the DC magnetic field (Hdc) varies in the range of 0–5 kOe with a constant Hac = 10 kOe of frequency 850 Hz, as shown in Fig. 11(b). Herein, the magnetostriction coefficient gets to the saturation state at a certain value of the magnetic field in NFO during magnetic poling, which yields a constant field in the ferroelectric phase (BFO), forcing the ME voltage that appears almost steady throughout the varying field. It is due to the saturated domain wall movement.61 The MECC of all the samples is determined by dividing the ME output voltage by the strength of Hac. The DC measurement values are congruent with the reported results in Table 4. The similar trend of variations of the ME coefficient has been reported earlier in the same type, 0–3 particulate ME composites such as BaTiO3/CoFe2O4,62 BaTiO3/CaFe2O4, BaTiO3/CuFe2O4,13 and Ni0.9Zn0.1Fe2O4/PZT.63 The promising applications of these ME composites include magnetic field sensors, transducers, oscillators, phase shifters, and memory devices.64
In general, magnetoelectric coupling is determined by strain-mediated mechanical coupling between the ferromagnetic and ferroelectric phases in the composite. The phase connectivity and the interface coupling of the constituent phases in the composite is responsible for the strong ME coupling coefficient.65 The ME composites consists of ferromagnetic and ferroelectric substances and the coupling interaction between them will produce a large ME response. The basic principle of this coupling is a product tensor property.66 Thus, the ME effect is a result of the product of the piezoelectric effect of the ferroelectric phase and magnetostriction effect of the ferromagnetic phase.64 The mechanism in detail can be found elsewhere.67 The present BFO–NFO composites have good ferroelectric response and high magnetization, which is essential for the large ME effect. The coupling between the ferroelectric order of BFO and the ferromagnetic order of NFO is attributed to the ME output voltage. Hence, a strong ME effect is reasonable.
Conclusion
The present work has reported a systematic study of the multiferroic properties of the perovskite (BFO)–spinel (NFO) nanocomposites prepared via the simple Pechini one-pot method. The powder X-ray diffraction analysis revealed the presence of individual phases in the composites. Moreover, the crystallite size, lattice constants, cell volume, strain, dislocation density, and surface area are greatly influenced with the incorporation NFO into BFO, thereby enhancing the dielectric, magnetic, and magnetoelectric properties. The FESEM technique evidenced the agglomerated configuration of the grains and its size varied in the range of 38–45 nm. The room temperature magnetic hysteresis curve established the ordered good ferromagnetic nature and increased value of Mr, Ms, K, and μ with an increasing NFO concentration. The electrical conductivity and dielectric performance of the composites are strongly affected by the concentration of NFO. An observed asymmetric and depressed semicircle that indicates non-Debye relaxation in the material was revealed through impedance and electric modulus analyses. The obtained unsaturated and lossy P–E loop disclosed the conducting nature of the nanocomposites. The merging of the perovskite/spinel structured phases in the composite manifests better magnetoelectric performance with improved coupling coefficient. This indicates that these nanocomposites will find applications for ME devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful to CIF, IIT Guwahati for VSM facility and DST Purse Lab, Mangalore University for FESEM characterization.References
- A. Saha and R. Viswanatha, ACS Nano, 2017, 11, 3347–3354 CrossRef CAS PubMed.
- H. Issaoui, A. Benali, M. Bejar, E. Dhahri, B. F. O. Costa, M. P. F. Graca and M. A. Valente, RSC Adv., 2020, 10, 16132–16146 RSC.
- A. R. Abraham, B. Raneesh, T. Woldu, S. Aškrabić, S. Lazović, Z. Dohčević-Mitrović, O. S. Oluwafemi, S. Thomas and N. Kalarikkal, J. Phys. Chem. C, 2017, 121, 4352–4362 CrossRef CAS.
- J. Ma, J. Hu, Z. Li and C. W. Nan, Adv. Mater., 2011, 23, 1062–1087 CrossRef CAS PubMed.
- M. M. Vopson, Crit. Rev. Solid State Mater. Sci., 2015, 40, 223–250 CrossRef CAS.
- N. A. Spaldin, S. W. Cheong and R. Ramesh, Phys. Today, 2010, 63, 38–43 CrossRef.
- Z. Surowiak and D. Bochenek, Arch. Acoust., 2008, 33, 243–260 Search PubMed.
- N. Ortega, A. Kumar, R. S. Katiyar and C. Rinaldi, J. Mater. Sci., 2009, 44, 5127–5142 CrossRef CAS.
- Y. Cheng, B. Peng, Z. Hu, Z. Zhou and M. Liu, Phys. Lett. Sect. A Gen. At. Solid State Phys., 2018, 382, 3018–3025 CAS.
- A. Das, S. De, S. Bandyopadhyay, S. Chatterjee and D. Das, J. Alloys Compd., 2017, 697, 353–360 CrossRef CAS.
- H. Ke, H. Zhang, J. Zhou, D. Jia and Y. Zhou, Ceram. Int., 2019, 45, 8238–8242 CrossRef CAS.
- A. S. Dzunuzovic, M. M. Vijatovic Petrovic, J. D. Bobic, N. I. Ilic, M. Ivanov, R. Grigalaitis, J. Banys and B. D. Stojanovic, Ceram. Int., 2018, 44, 683–694 CrossRef CAS.
- R. M. Thankachan, B. Raneesh, A. Mayeen, S. Karthika, S. Vivek, S. S. Nair, S. Thomas and N. Kalarikkal, J. Alloys Compd., 2018, 731, 288–296 CrossRef CAS.
- R. Pandey, U. Shankar, S. S. Meena and A. K. Singh, Ceram. Int., 2019, 45, 23013–23021 CrossRef CAS.
- J. S. Bangruwa, B. K. Vashisth, N. Singh, N. Singh and V. Verma, J. Alloys Compd., 2018, 739, 319–326 CrossRef CAS.
- T. Zhao, A. Scholl, F. Zavaliche, K. Lee, M. Barry, A. Doran, M. P. Cruz, Y. H. Chu, C. Ederer, N. A. Spaldin, R. R. Das, D. M. Kim, S. H. Baek, C. B. Eom and R. Ramesh, Nat. Mater., 2006, 5, 823–829 CrossRef CAS PubMed.
- S. Dabas, P. Chaudhary, M. Kumar, S. Shankar and O. P. Thakur, J. Mater. Sci.: Mater. Electron., 2019, 30, 2837–2846 CrossRef CAS.
- N. Wang, X. Luo, L. Han, Z. Zhang, R. Zhang and H. Olin, Nano-Micro Lett., 2020, 12, 1–23 CrossRef.
- L. W. Martin, Dalton Trans., 2010, 39, 10813–10826 RSC.
- F. Gao, X. Chen, K. Yin, S. Dong, Z. Ren, F. Yuan, T. Yu, Z. Zou and J. M. Liu, Adv. Mater., 2007, 19, 2889–2892 CrossRef CAS.
- H. Zhang, W. Liu, P. Wu, X. Hai, M. Guo, X. Xi, J. Gao, X. Wang, F. Guo, X. Xu, C. Wang, G. Liu, W. Chu and S. Wang, Nanoscale, 2014, 6, 10831–10838 RSC.
- J. Gu, S. Yang, W. Yang, Y. Qi, G. Zhao and H. Sun, J. Magn. Magn. Mater., 2014, 349, 140–143 CrossRef CAS.
- S. P. Crane, C. Bihler, M. S. Brandt, S. T. B. Goennenwein, M. Gajek and R. Ramesh, J. Magn. Magn. Mater., 2009, 321, L5 CrossRef CAS.
- C. N. Chinnasamy, A. Narayanasamy, N. Ponpandian, R. Justin Joseyphus, B. Jeyadevan, K. Tohji and K. Chattopadhyay, J. Magn. Magn. Mater., 2002, 238, 281–287 CrossRef CAS.
- S. Asiri, M. Sertkol, H. Güngüneş, M. Amir, A. Manikandan, I. Ercan and A. Baykal, J. Inorg. Organomet. Polym. Mater., 2018, 28, 1587–1597 CrossRef CAS.
- T. Bhasin, A. Agarwal, S. Sanghi, R. K. Kotnala, J. Shah, M. Yadav and M. Tuteja, J. Alloys Compd., 2018, 748, 1022–1030 CrossRef CAS.
- L. Dimesso, Handb. Sol-Gel Sci. Technol., 2016, 1–30 Search PubMed.
- W. F. Chen, S. S. Mofarah, D. A. H. Hanaor, P. Koshy, H. K. Chen, Y. Jiang and C. C. Sorrell, Inorg. Chem., 2018, 57, 7279–7289 CrossRef CAS PubMed.
- B. Dhanalakshmi, P. Kollu, B. Parvatheeswara Rao and P. S. V. S. Rao, Ceram. Int., 2016, 42, 2186–2197 CrossRef CAS.
- P. Komalavalli, I. B. Shameem Banu and M. S. Anwar, J. Mater. Sci.: Mater. Electron., 2019, 30, 3411–3417 CrossRef CAS.
- G. M. Nasr, E. Mousa and M. M. Haroun, Egypt. J. Pet., 2019, 28, 361–369 CrossRef.
- A. Das, N. Khamaru, S. Bandyopadhyay and S. Chatterjee, J. Alloys Compd., 2020, 157821 Search PubMed.
- M. ud D. Rather, R. Samad, N. Hassan and B. Want, J. Alloys Compd., 2019, 794, 402–416 CrossRef CAS.
- V. A. Reddy, N. P. Pathak and R. Nath, J. Alloys Compd., 2012, 543, 206–212 CrossRef.
- A. D. Mani and I. Soibam, Ceram. Int., 2018, 44, 2419–2425 CrossRef CAS.
- I. Kaur and N. K. Verma, Mater. Sci. Semicond. Process., 2015, 33, 32–35 CrossRef CAS.
- B. S. Kar, M. N. Goswami and P. C. Jana, J. Alloys Compd., 2020, 157960 Search PubMed.
- S. N. Babu, J. H. Hsu, Y. S. Chen and J. G. Lin, J. Appl. Phys., 2010, 107, 759 CrossRef.
- M. Singh, J. Singh, M. Kumar and S. Kumar, Solid State Sci., 2020, 108, 106380 CrossRef CAS.
- P. K. Jana, S. Sarkar and B. K. Chaudhuri, J. Phys. D: Appl. Phys., 2007, 40, 556–560 CrossRef CAS.
- B. S. Kar, M. N. Goswami and P. C. Jana, J. Alloys Compd., 2021, 861, 157960 CrossRef CAS.
- S. Nath, S. K. Barik, R. N. P. Choudhary and S. K. Barik, Structural, Dielectric and Impedance Characteristics of (Sm0.5Li0.5)(Fe0.5V0.5)O3 Multiferroics, Elsevier B.V., 2017, vol. 381 Search PubMed.
- N. S. Kumar, R. P. Suvarna and K. C. B. Naidu, Mater. Charact., 2020, 166, 110425 CrossRef CAS.
- M. M. Rhaman, M. A. Matin, M. A. Al Mamun, A. Hussain, M. N. Hossain, B. C. Das, M. A. Hakim and M. F. Islam, J. Mater. Sci.: Mater. Electron., 2020, 31, 8727–8736 CrossRef CAS.
- M. K. Das, M. A. Zubair, H. Tanaka and A. K. M. A. Hossain, Mater. Chem. Phys., 2020, 255, 123575 CrossRef CAS.
- D. K. Mahato and T. P. Sinha, J. Electron. Mater., 2017, 46, 107–115 CrossRef CAS.
- K. P. Remya, D. Prabhu, R. J. Joseyphus, A. C. Bose, C. Viswanathan and N. Ponpandian, Mater. Des., 2020, 192, 108694 CrossRef CAS.
- N. Kumar, A. Shukla, N. Kumar, R. N. P. Choudhary and A. Kumar, RSC Adv., 2018, 8, 36939–36950 RSC.
- D. K. Pradhan, R. N. P. Choudhary, C. Rinaldi and R. S. Katiyar, J. Appl. Phys., 2009, 106, 0–10 CrossRef CAS.
- J. H. Joshi, D. K. Kanchan, M. J. Joshi, H. O. Jethva and K. D. Parikh, Mater. Res. Bull., 2017, 93, 63–73 CrossRef CAS.
- S. Pattanayak, B. N. Parida, P. R. Das and R. N. P. Choudhary, Appl. Phys. A: Mater. Sci. Process., 2013, 112, 387–395 CrossRef CAS.
- A. Khalid, S. K. Abbas, G. M. Mustafa, S. Atiq, S. S. Hussain, M. S. Anwar and S. Naseem, Ceram. Int., 2019, 45, 24453–24460 CrossRef CAS.
- V. M. Gaikwad and S. A. Acharya, J. Alloys Compd., 2017, 695, 3689–3703 CrossRef CAS.
- J. F. Scott, J. Phys.: Condens. Matter, 2008, 20, 22–23 Search PubMed.
- R. S. Devan, Y. D. Kolekar and B. K. Chougule, J. Alloys Compd., 2008, 461, 678–683 CrossRef CAS.
- Y. Liu, Y. Wu, D. Li, Y. Zhang, J. Zhang and J. Yang, J. Mater. Sci.: Mater. Electron., 2013, 24, 1900–1904 CrossRef CAS.
- M. Mahesh Kumar, A. Srinivas, S. V. Suryanarayana, G. S. Kumar and T. Bhimasankaram, Bull. Mater. Sci., 1998, 21, 251–255 CrossRef.
- J. Shah and R. K. Kotnala, J. Mater. Chem. A, 2013, 1, 8601–8608 RSC.
- G. V. Duong, R. Groessinger, M. Schoenhart and D. Bueno-Basques, J. Magn. Magn. Mater., 2007, 316, 390–393 CrossRef CAS.
- D. R. Patil, S. A. Lokare, R. S. Devan, S. S. Chougule, Y. D. Kolekar and B. K. Chougule, J. Phys. Chem. Solids, 2007, 68, 1522–1526 CrossRef CAS.
- T. Woldu, B. Raneesh, B. K. Hazra, S. Srinath, P. Saravanan, M. V. R. Reddy and N. Kalarikkal, J. Alloys Compd., 2017, 691, 644–652 CrossRef CAS.
- S. V. Suryanarayana, Bull. Mater. Sci., 1994, 17, 1259–1270 CrossRef CAS.
- S. S. Chougule and B. K. Chougule, J. Alloys Compd., 2008, 456, 441–446 CrossRef CAS.
- C. W. Nan, M. I. Bichurin, S. Dong, D. Viehland and G. Srinivasan, J. Appl. Phys., 2008, 103, 031101 CrossRef.
- J. Chen, Y. Bai, C. Nie and S. Zhao, J. Alloys Compd., 2016, 663, 480–486 CrossRef CAS.
- R. E. Newnham, D. P. Skinner and L. E. Cross, Mater. Res. Bull., 1978, 13, 525–536 CrossRef CAS.
- Y. Bai, H. Zhao, J. Chen, Y. Sun and S. Zhao, Ceram. Int., 2016, 42, 10304–10309 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |