Full parameter space exploration of microphase separation of block copolymer brushes within a single simulation framework

Abstract

Block copolymer brushes where chains are grafted onto the substrate have been of special interest due to their capability to form various self-assembled nanoscale structures. The self-assembled structures depend on complex system variables, including block copolymer composition, segregation strength, grafting density, selectivity of top and bottom surfaces, and solvent quality. In spite of extensive previous efforts on understanding and controlling the microphase separation of diblock copolymer brushes, an individual study focuses only on the subset of the parameter space of system variables. This work systematically explores the full parameter space within a single simulation framework of a coarse-grained model with a generalized Hamiltonian. The topologically unconstrained free surface allowed in the model enables us to investigate brush systems under versatile and more realistic conditions. We show that melt brushes with non-selective surfaces can form previously unexplored structures such as “void” and “curvy” phases at a moderate grafting density; special emphasis is placed on the system's evolution to make such structures. Our simulations demonstrate that the surface selectivity further enriches the phase behavior with a diverse range of phases obtained even at a single composition. We also find out that the phases with a similar morphology from the top view can vary significantly in their internal structures; such variations are discussed when examining the effects of grafting density and surface selectivity. Finally, we studied the influence of exposure to a non-selective solvent on the morphology of block copolymer brushes and compared the topographical variation on the top at varied solvent qualities.

---

Design, System, Application

Functionalized nano-surfaces are at the heart of numerous applications in the fields of microelectronics, biosensing and drug delivery. Multicomponent polymer brushes with a chain end physically constrained to a substrate have emerged as a viable solution to obtain functionalized surfaces due to their ability to microphase separate into diverse nanostructures. However, the success of applying polymer brushes has been limited owing to the precise control of the shape, size, and orientation of the self-assembled structures, which demands comprehensive understanding of the interplay between many system variables. In this work, we use a single simulation framework incorporating important system variables dictating the self-assembly and investigate the microphase separation of diblock copolymer brushes. The inspection of the high-dimensional parameter space of system variables allows us to predict the unexplored phases and significant variations in internal structures, and prove the feasibility of tuning the diverse range of phases at a single polymer composition. Our simulation approach and reported results could provide a guideline in the custom design of brush systems tailored to applications with targeted nano-surfaces.

Introduction

Polymer brushes, in which chain ends are anchored to a substrate, have attracted increasing attention due to their versatility in fabricating functional surfaces for applications in polymer compatibilizers,¹ new adhesive materials,^2,3 colloidal stabilization,^4,5 biomaterials,^6,7 and tailoring adhesion or wettability.^8,9 Multicomponent polymer brushes, including block copolymer (BCP) brushes, have been of particular interest and the subject of theoretical and experimental studies due to their reversible switching surface properties.^10–17 Multicomponent brushes can self-assemble into perpendicularly segregated and laterally homogeneous layers, and alter the species exposed to the top surface in response to changes in the surrounding environment by solvent or pH conditions.^18–21 Lateral phase separation, similar to BCP thin films, enables BCP brushes to access the design of flat or curved surfaces with nanoscale patterns for surface interaction modification, biosensing, cellular manipulation, or electronic and microfluidic devices.^22–25 The precise tuning of the shape and size of the self-assembled structures can provide independent and spatially decoupled surface control in such applications. Smaller nanostructures are achievable by using BCP systems with high segregation strength between blocks; however, the large surface energy difference in such systems often prevents the formation of a laterally varying nanostructure in ungrafted BCP films. Nevertheless, grafted BCPs under asymmetric wetting conditions can still allow lateral phase separation with more versatile morphologies.

The morphologies of BCP brushes are governed by parameter space constructed from system variables including grafting density, block composition, incompatibility among blocks, affinity of blocks with the bottom and top surfaces, solvent quality and selectivity, etc. As it is unfeasible to perform experimental studies to explore such an immense parameter space, numerical simulations provide a valuable tool for establishing a solid theoretical understanding of the morphological dependencies of brushes on the listed system variables. A previous study by Matsen and Griffiths using self-consistent field theory (SCFT) calculations predicted phase diagrams of melt AB diblock copolymer brushes on a flat substrate by controlling the block composition, segregation strength between blocks, and affinity of the grafted block for the air surface.²⁶ In addition to the perpendicularly separated uniform phase, laterally separated periodic patterns as viewed from the top were obtained in a narrow region of the phase diagram, namely the hexagonal phase with an array of untethered blocks, the stripe phase with an alternating sequence of A and B rich domains, and the inverse hexagonal phase with grafted block domains arranged hexagonally. Their calculations also showed that the region of the laterally phase-separated structures was broadened on decreasing the grafting density and increasing the preferentiality of the grafted block with the air surface. However, the obtained results are based on a rigorous assumption that the flat air/polymer surface is valid only at high grafting densities and large air/polymer surface tensions. In addition, the effects of the substrate's affinity with the grafted polymer block were not investigated in their study. Relaxing the assumption of uniform brush thickness and introducing selective affinity of the substrate or the top in a model can produce a more enriched phase behavior. The morphologies of BCP brushes at different solvent qualities have also been studied using SCFT,^26–30 lattice Monte Carlo,^31,32 single-chain-in-mean-field (SCMF),³³ dissipative particle dynamics (DPD),^34,35 hybrid molecular dynamics (MD) with field representation of non-bonded interactions,^36,37 and density functional theory (DFT) simulations.³⁸ Despite such explorations, obtaining a comprehensive understanding of the formation of the morphology in brush systems under different conditions, i.e., melt or exposed to solvent molecules, has been a key challenge.

In this study, by using diffusion Monte Carlo (MC) simulations which adapt a coarse-grained model with a generalized energy functional expressed in terms of density fields expanded up to third order, we conduct a more complete and systematic investigation on morphologies of diblock copolymer brushes (Scheme 1). Previous studies adapting field-theoretical models to studies of polymeric materials at free interfaces place a structural fluid that creates interfacial tension with polymers.³⁹ However, these approaches require significant computational loads for simulating phantom particles in domains of no physical interest. Instead, the generalized virial model, which removes the restriction on the almost uniform density in the simulation box, enables us to explore systems at a low grafting density (σ) and to predict the air/polymer surface that adapts to changes in the structure. The generalized virial model enables us to explore systems at a low grafting density (σ) and by freely adjusting the air/polymer surface. To test the stability of morphologies with lateral phase separation and the possibility of tuning these morphologies, we construct phase diagrams of BCP brushes on neutral and wetting substrates by varying the composition of the grafted A block (f_A) and segregation strength (χN), where χ is the Flory–Huggins parameter and N is the chain length. We predict the existence of void and curved morphologies which were not explored in previous studies, and we investigate their formation induced by the interplay between entropic and enthalpic contributions. The selectivity of the free surface and substrate with both A and B blocks is then studied, reporting the distinct morphologies with lateral phase separation, obtained in the case of systems with a B-preferential substrate and neutral top surface. The effect of grafting density on the phase behavior of BCP brushes is also probed with examinations focused on the arrangement of internal A/B interfaces. Finally, the effect of contact with non-selective solvents of varying qualities, which has been of interest due to its capability to respond to external chemical stimuli^34,40 as well as to tune phase segregation behaviors of BCPs in thin film geometry,^41–43 is considered along with the estimation of the roughness of the brush surface at the top for the predicted morphologies.

Scheme 1 (Left) Major system variables affecting microphase separation of diblock copolymer brushes. (Right) The Hamiltonian equation used in coarse-grained simulations to incorporate the effects of the relevant variables, and the illustration of representative predicted phases.

Methods

In this work, we study the microphase separation of A-b-B diblock copolymers grafted on a flat bottom substrate by performing Monte Carlo (MC) simulations of a coarse-grained model. The model adopted here relies on a particle-based representation of n copolymer chains where each chain is represented by N coarse-grained beads. As has been commonly used, the bonded interactions among beads are derived from harmonic springs attached between adjacent beads in a given chain. The total harmonic potential at a given temperature (T) is then defined aswhere b_k(i) is a vector connecting the ith and (i + 1)th beads in a chain, k_B is the Boltzmann constant and R_e is the end-to-end distance of an ideal chain. Similar to coarse grained models that are widely used in predicting the self-assembly of block copolymers,^44–46 namely, self-consistent field theory and theoretically informed coarse-grained (TICG) models, the non-bonded interactions modelled in this work are expressed as a functional of local densities. However, unlike these models, where the Hamiltonian has a quadratic form in terms of local densities, we use the more generalized approach where interactions also contain a third order term. More specifically, non-bonded interactions among beads are expressed aswhere ϕ_α is the number density of polymer species α in a unit volume R_e³ and integration is performed over the entire volume of a simulation box, V. The density summation within the integral is over all different types of species present in a system. v_αβ and w_αβγ are second and third order virial coefficients, respectively, describing the interaction between species α, β and γ. This generalized Hamiltonian, which contains both repulsive and attractive interactions, allows the coexistence of dense and sparse (or vacuum) regions to enable the prediction of phenomena at the non-flat free surface at the top of the BCP film, without the addition of phantom particles in the air. The above energy functional has been used to analyse a variety of systems including the phase behavior of mixed brushes,^20,47,48 solvent annealing of BCPs,⁴⁹ and simulation of lipid bilayers.⁵⁰

For a two species system (A and B), as is the case in this study, the expanded form of non-bonded interaction can be written as

Virial coefficients v_AA, v_BB, w_AAA and w_BBB are derived from the mean-field state equation of homopolymers to have negligible vapor pressure and finite coarse-grained compressibility of polymer melts. These terms are given bywhere κ_αN (α ∈{A, B}) is the isothermal incompressibility of the A and B blocks and is the average chain density, i.e., the number of chains in a volume of R_e³. The cross-interaction parameter, v_AB, contains the Flory–Huggins parameter, χ, and is defined as

The parameters w_AAB and w_BBA are expressed as arithmetic means of virial coefficients w_AAA and w_BBB and are explicitly written as

To calculate H_nb, the local densities must be inferred from the bead positions. A commonly used “particle-to-mesh” (PM) technique is applied, where we split the simulation box into an M number of cubic grid cells and then estimate the densities of species in these grids. The grid discretization length is defined as ΔL. The implementation details are discussed in the study by Detcheverry et al.⁵¹ The local density for grid cell p, ϕ_α(p) (α ∈{A, B}), is defined as

where the summation above runs over all beads, and t(i) denotes the species of bead i. The delta function here represents that each bead is assigned to its nearest grid cell and contributes to ϕ_α(p).

The interactions of A and B species with the grafting substrate placed at the bottom along the z-direction are included using the one body potential acting on each bead i of type K (K ∈{A, B}) as defined below

where z_i is the vertical distance of the ith bead from the bottom. The potential decays over a short distance d_s = 0.16R_e and the strength of the interaction between the grafting substrate and the species of type K is characterized by the product Λ_KN.

Using the model described above, Monte Carlo (MC) simulations are performed under the NVT ensemble. Simulations are conducted in a simulation box with L_x = 10R_e, L_y = 10R_e and L_z = 3R_e. A periodic boundary condition was applied in the lateral directions, while an impenetrable hard wall boundary condition was used in the z direction. L_z was chosen to be much larger than the brush height of the studied systems, so that the BCP brush films coexist with the empty simulation space forming a free surface. One of the ends of the A block is grafted to a substrate located at z = 0; the grafted ends are uniformly distributed with spacing d in the x and y directions. The spacing d is determined from the grafting density, . The relation between the grafting density (σ) and the average brush thickness (L) is given by σ = L × . For simulations conducted in this work, the values of ΔL = 0.16R_e and N = 128 are used. Under melt conditions, the value of the average chain density 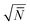is set to 128. Thus, for the system of 0.5R_e brush thickness, a total of 6400 chains and approximately 0.8 million coarse-grained beads are simulated. For every simulation, the observed phases are identified from the morphologies obtained after using sufficiently long MC cycles (>2 million cycles) for equilibration. In each cycle, single bead displacement is performed for all beads on average.

Results

Fig. 1a shows the phase diagram of BCP brushes on a neutral substrate (Λ_AN = Λ_BN = 0) as a function of χN and f_A with grafted A ends at a relatively low grafting density value of 64 (number of grafting ends per unit R_e²). As the chain density is set to 128 (number of chains per unit R_e³), the average film thickness is 0.5R_e. Top views of the observed morphologies are shown in Fig. S1a† with species A and B represented in colors red and blue, respectively. Our phase diagram shows four different phases of uniform, void, stripe and hexagonal phases. The uniform phase of well-mixed (disordered) A and B domains is observed for all values of f_A at lower χN due to the small incompatibility between A and B blocks. The order to disorder transition values of χN are larger than those of non-tethered BCPs; thus, a uniformly well-mixed phase is observed for χN = 20 at which non-tethered symmetric BCPs form a lamellar phase. While the uniform phase at small χN and strongly asymmetric composition corresponds to a homogeneously well-mixed one, in the uniform phase at f_A values of 0.1 and 0.2 upon increasing the value of χN, demixing of A and B occurs and two blocks are vertically layered and homogeneous in the lateral direction. It is notable that A and B interfaces are not in a planar geometry as demonstrated by the gray contour of the A/B interface in tilted view shown for f_A of 0.2 at χN = 100 in Fig. 1b; the minority A block forms semi-cylinders parallel to the substrate. A further increase in f_A as approaching towards symmetric composition results in the formation of voids for a vast range of χN values. Voids are represented by perpendicularly phase separated A and B domains with large dewetted/empty regions; void morphologies are shown in Fig. 1b for f_A values of 0.5 at χN = 50 and 100 as tilted views and in Fig. S1a† as top views. As f_A further increases and the grafted block (A) becomes the majority block, voids disappear, and laterally alternative A and B stripes are observed from the top surface as seen in Fig. S1a.† As depicted in Fig. 1b for a χN value of 100 and f_A = 0.7, A/B interfaces in the stripe phase become non-planar, but the curvature of such interfaces is opposite to f_A = 0.2 with B domains in hemi-cylindrical shapes curved toward the free surface. An increase in the area of A domains on the top upon increasing f_A to 0.8 results in the formation of B dots. Dotted structures tend to hexagonally pack even though a long-range order is not established in our simulations; thus, we labelled it as a hex phase. The possibility of a finite box size effect in our simulation was excluded by confirming the same morphology prediction observed in simulations of a larger lateral box size of 15R_e × 15R_e on varying f_A and χN (Fig. S2†).

Fig. 1 Predicted phase diagram of AB diblock copolymer brushes as a function of the mole fraction of the grafted block f_A and χN when it is grafted at the average brush thickness L = 0.5R_e on substrates of different wettabilities with (a) ΛN = 0 and (c) ΛN = 2. Representative morphologies in tilted view at χN = 50 and 100 with varying f_A are shown in b (ΛN = 0) and d (ΛN = 2). A and B blocks are respectively represented by red and slightly transparent blue, and the interface between A and B blocks is shown by gray.

The obtained phase diagram is now briefly compared with those reported in previous studies. First, our results are compared with SCFT studies by Matsen et al.²⁶ which investigated the system with the same average brush thickness of 0.5R_e as used in our study, however, without allowing topological adjustment at the free top surface. Similar to their studies, stripe, hex and uniform phases are observed at different values of χN and f_A in our work. The void phase occupies a large area of our phase diagram, while SCFT predicts uniform or inverse hex phases for the same conditions of χN and f_A. The envelope of the phase boundary between the uniform and laterally phase separated structures is convex and asymmetric, similar to the SCFT of BCP brushes, but our simulation predicts a wider region of laterally non-uniform morphologies. Void phases, which have an exposed surface with a non-uniform topology, are not observed in our model, when it is modified to have a flat top surface by placing a hard wall on the top of the brushes while keeping the brush thickness value at 0.5R_e; the obtained results closely match with those detailed in the SCFT studies as shown in Fig. S3† for different f_A values at χN = 50. Studies by Wang et al.³³ use a similar model to that applied in this work and they have performed the simulations to obtain the phase behavior of brushes at different solvent qualities of grafted and non-grafted blocks. Their simulations for poor solvent quality for both A and B blocks corresponded to the conditions closely related to our melt brushes and showed the sequence of phase transitions at a relatively low grafting density comparable to the results obtained in our work including the formation of voids. However, the structure of voids has been only briefly described in their work without a clear description on the mechanism of their formation.

To further elucidate the formation of voids, we show the structure evolution as observed in our diffusion MC simulations for f_A = 0.5 and χN = 50 in Fig. 2a–d with representative morphologies and schematic sketches shown at the top and bottom, respectively. The system is quenched from a disordered initial configuration to χN = 50. At the earlier stage, the system forms a uniform phase with perpendicular phase separation and a flat top surface. As depicted in the schematic sketch in Fig. 2a, the chains in the uniform phase are laterally spread out and compressed in the z-direction with an entropic penalty because the brush thickness is only 0.5R_e. The enthalpic cost also arises from the large interfacial area of unfavorable AB contacts in the uniform phase. High entropic and enthalpic costs make the uniform phase unstable and short-lived in our simulations. The uniform phase quickly transits into a structure with a region of thin A domains exposed to the free surface and a thick perpendicularly phase separated region as shown in the schematic sketch in Fig. 2b. The exposed region develops laterally resembling island hole terraced structures commonly observed in non-grafted films. Since there is no favorable interaction between the substrate and A/B blocks, the thickness of bare A domains continues to decrease, eventually dewetting the substrate to form voids (see Fig. 2c). Unlike non-grafted films, the voids cannot endlessly grow, due to the entropic penalty induced by the stretching of grafted A chains and the system eventually equilibrates to a structure with voids that maintain their size (Fig. 2d). The quantitative measurement of void size at the later stage of structure evolution (Fig. S4†) demonstrates that while the number of voids does not change significantly once the voids are initiated, the average size of voids (dewetted regions on the bottom) increases substantially and plateaus at a value of 2.8R_e². It is noticeable that the size of the voids is significantly larger than those in other laterally phase separated structures such as stripes or hexagonal arrays (Fig. S5†), benefiting from the fact that the larger voids can reduce the surface energy of A/B blocks in contact with the top free surface in addition to the decrease in the enthalpic interfacial area. The values of such costs associated with interfacial and surface contacts are respectively related to χN and incompressibility (κ_AN and κ_BN). Large χN and (κ_AN, κ_BN) imply large penalties for A/B interfacial contacts and contacts of A and B with the top surface, respectively. Therefore, increases in χN and (κ_AN, κ_BN) result in the formation of a larger region with voids, as clearly depicted in Fig. S6a and b† at χN = 50 and 100, and Fig. S6a and c† at κ_AN = κ_BN values of 50 and 200 for f_A = 0.5.

Fig. 2 Structure evolution of (a)–(d) the void phase on a substrate of ΛN = 0 and (e)–(h) the curvy phase on a substrate of ΛN = 2. Representative morphologies captured in our diffusion MC simulations (top) and schematic sketches (bottom) are presented. The average brush thickness (L), segregation strength (χN) and mole fraction (f_A) of the systems are set to 0.5R_e, 50 and 0.5, respectively.

We have shown that BCP brushes on a neutral substrate form the void phase over a wide range of f_A and χN conditions. We anticipated that voids can be filled by introducing a substrate with affinity for both A and B blocks, which may result in retaining the phase behavior as observed for the flat top surface system. Thus, simulations are performed for non-zero substrate wettability values of Λ_AN = Λ_BN = 2, and Fig. 1c shows the obtained phase diagram as a function of χN and f_A. As expected, the void phase is no longer observed while the other phases (i.e., stripe, hex and uniform) occur under similar conditions to those on a neutral substrate. Instead of the void phase transiting to inverse hex or uniform phases as observed in SCFT results,²⁶ the void phase in the phase diagram is replaced with laterally phase separated curved domains. We label such structures in the phase diagram as curvy phases. Specifically, as shown in the tilted views in Fig. 1d and the top views shown in Fig. S1b,† laterally phase separated domains adopt different curvatures, including (1) a ring-like structure with an outer shell of A domains around the inner cylindrical B domains and (2) A domains curved in “S”/“C” shapes with enclosed B domains. To understand the origin of such structures, we show their evolution as observed in our MC simulations for the conditions of f_A = 0.5 and χN = 50 in Fig. 2e–h with representative morphologies and schematic sketches shown at the top and bottom, respectively. A uniform phase of perpendicularly layered A/B domains is formed at the initial stage. Similar to the case of the neutral substrate, the system proceeds to increase the brush thickness in perpendicularly separated regions while forming regions of thin A-rich domains exposed to the free surface (see the schematic sketch in Fig. 2e). However, unlike the BCP brushes on the neutral substrate, naked A-rich regions do not evolve to form voids, as there is a favorable interaction between the substrate and A/B blocks; the A block remains in such regions wetting the substrate as shown in Fig. 2f. As naked regions enlarge in size along the lateral direction, stress induced by the stretching of grafted A chains increases. To release the stress, the B block is placed in the middle of the enlarged region, as depicted in Fig. 2g. At this time, the B block wets the substrate, making columns of B-rich domains (Fig. 2g). As shown in the schematic sketch in Fig. 2h, B-rich domains surrounded by A-rich domains eventually develop into curved “S”/“C” shaped structures.

We turn our attention to address the impact of selective surfaces on the self-assembled morphologies. Matsen and Griffiths investigated the effect of preferential wetting of the grafted block toward the flat top surface on the phase diagram of BCP brushes using SCFT²⁶ and compared it with the experimental work by O'Driscoll et al.³⁰ They found that the region of periodic morphologies becomes wider with the shift in phase boundaries. While the bottom surface (i.e. the grafting substrate) was kept neutral in previous studies, here, we focus on the effect of both top and bottom surface selectivity toward the grafted/non-grafted block at the two composition values of f_A = 0.5 and 0.7 for χN = 50. The selective affinity of the grafting substrate and free surface is tuned by individually varying Λ_AN, Λ_BN, κ_AN, and κ_BN while keeping the other values fixed. An increase in Λ_AN (Λ_BN) leads to the selective attraction of the A(B) block with the grafting substrate and a decrease in κ_AN (κ_BN) (i.e., decrease in surface tension) leads to the selective attraction of the A(B) block with the top surface. Fig. 3 shows the top and tilted views of the obtained morphologies at f_A = 0.5 for selective surfaces. In the reference case where both the free surface and bottom substrate are neutral (Λ_AN = Λ_BN = 0 and κ_AN = κ_BN = 200), BCP brushes form a void phase with the equilibrated morphology as shown in Fig. 2d. As shown in Fig. 3a, the voids are filled up with A species and the area where the bare substrate is exposed shrinks in size as we increase the substrate selectivity towards the grafted A block, eventually disappearing at a high Λ_AN value of 8. A more diverse range of phases is observed when the substrate is selective towards the non-grafted B block (Fig. 3b). Upon increasing Λ_BN, the B block condenses into a near-surface layer and the system transits from stripe to hex to uniform phases. The observed laterally phase separated stripe is developed throughout the whole brush due to the enthalpic favorability of the non-grafted B block wetting the substrate. Thus, A/B interfaces are in contact with the grafting substrates as shown in the schematic diagram of Fig. 4a unlike the stripes on a neutral substrate presented in Fig. 4b (f_A = 0.7), which are induced by small values of B fractions with lateral separation only occurring near the top. The hex phase at Λ_BN = 4 also differs from the hex phase on neutral substrates (Fig. 4d) as a layer of B is formed underneath the A domains covering the substrate and partially exposed B domains from that underlayer are seen from the top as hexagonal dots (Fig. 4c). At a large affinity value of Λ_BN = 8, a uniform phase is observed where the graft A blocks cover the top, which is different from the uniform phase presented in Fig. 1 with B at the top. As depicted in Fig. 3c, an increase in the top surface selectivity for the A block upon decreasing κ_AN enlarges the voids and grows into a rather striped shape, thereby reducing the area of B domains in contact with the top surface. The B selective top surface shifts the system from a void phase to a uniform phase. Although the uniform phase has an entropic cost induced due to the brush being confined in a thickness of only 0.5R_e and an enthalpic cost of large A/B contact, such costs are overcome by surface energy being lowered by placing B on the top (Fig. 3d). Fig. S7† shows the top and tilted views of the obtained morphologies for selective surfaces at the asymmetric composition value of f_A = 0.7. When the top and bottom surfaces are neutral, BCP brushes form a stripe pattern with non-grafted minor B components lying on the layer of A blocks similar to parallel cylinders in BCP films, as presented in Fig. 1b. Although the stripe structure prevailed when the A block became preferential to the bottom substrate (Fig. S7a†), we have observed a phase change from stripe to hex with small B clusters (hemispheres) distributed in the continuous A layer when the free surface exhibited a preference for the grafted A block (Fig. S7c†). As B becomes more attractive to the bottom substrate, the B block wets the substrate, and the system transits to the hex phase with B cylinders throughout the film (Fig. S7b†) and then to the uniform phase with graft A blocks on the top (Fig. S7c†). As κ_BN decreases (Fig. S7d†), the upper B blocks of relatively low compressibility cover up the layer of dense A blocks, and at κ_BN = 50, a layered uniform structure is finally formed, even at an asymmetric composition.

Fig. 3 Top and tilted views of morphologies presenting the effects of asymmetric affinity of surfaces on the void phase. With BCP brushes at f_A = 0.5, Λ_AN = Λ_BN = 0 and κ_AN = κ_BN = 200 as a reference, simulations are conducted with increasing preferential wetting on the grafting substrate toward (a) A blocks (increasing Λ_AN from 2 to 8 with fixed Λ_BN = 0) and (b) B blocks (increasing Λ_BN from 2 to 8 with fixed Λ_AN = 0), or increasing preferential wetting on the free surface toward (c) A blocks (decreasing κ_AN from 150 to 50 with fixed κ_BN = 200) and (d) B blocks (decreasing κ_BN from 150 to 50 at κ_AN = 200).

Fig. 4 Tilted views and schematic diagrams of stripe and hexagonal phases formed in symmetric BCP brushes (f_A = 0.5) on B (non-grafted block) selective substrates of (a) Λ_AN = 0 and Λ_BN = 2 and (c) Λ_AN = 0 and Λ_BN = 4. Phases are compared with those observed in asymmetric BCPs of (b) f_A = 0.7 and (d) f_A = 0.8 on a neutral substrate (ΛN = 0).

To this point, we have demonstrated that BCP brushes at a relatively low chain grafting density (σ) result in laterally phase separated structures over a wide region of the phase diagram. At a higher grafting density, steric crowding among chains would increase, thereby inducing vertically stretched chain conformation, and thus resulting in a larger energy penalty for lateral phase separation. We now investigate the effect of grafting density on the phase behavior of BCP brushes. Fig. 5a shows the observed phase diagram of BCP brushes on the wettable substrate (ΛN = 2) with respect to f_A and the average brush thickness, L, which is proportional to the grafting density, σ. L is varied from 0.5R_e to 1.2R_e while χN is fixed at 100. At high grafting densities, the layered uniform structure marked with a black square (perpendicular segregation) exists in a wider interval of f_A than those in the BCP brushes with lower grafting densities. As the grafting density increases, the curvy phases (blue triangle) that were observed at a lower grafting density (L = 0.5R_e) disappear and inverse hexagonal phases (pink hexagon) emerge. The phase boundaries also shift to a larger value of f_A with increasing grafting density. Wang and Muller have reported a similar observation of enhanced stability of perpendicular segregation at a high grafting density in BCP brushes.³³ Matsen and Griffiths also observed that an increase in brush thickness reduces the region of periodic phases in melt BCP brushes.²⁶ Additionally, we found that the internal structures of uniform phases at asymmetric compositions vary depending on the grafting density, as shown in Fig. 5b and c showing the tilted (top) and side (bottom) views of morphologies along with the contour curves of A/B interfaces. For χN = 100 and f_A = 0.2, Fig. 5b shows that the uniform phase with a laterally rippled A/B interface at L = 0.5R_e transits to a uniform phase with an interface consisting of hexagonal arrays of B domains at L = 0.7R_e as the penalty for the chain stretching becomes larger. At an even higher grafting density (L ≥ 0.9R_e), the brush forms a perpendicularly layered morphology with a flat interface. However, such flat A/B interfaces in the uniform phases are destroyed when the brush is under an extremely large grafting density and in a relatively weak segregation strength regime. Fig. 5c shows the results for a very large L = 2.3, 2.5 and 2.7R_e at χN = 30 and f_A = 0.7. To maintain a flat A/B interface with a very large average brush thickness, chains are extremely stretched, which causes an enormous elastic free energy. The system reduces the elastic free energy by retaining some of the chains back to the less stretched conformation, which results in nontrivial A/B interfaces with hexagonally ordered holes of B domains (blue). This was also explained in a previous BCP brush study by Rudov et al.,³⁵ which predicted golf holes, gullies and ridges, and stalactites depending on the composition of the copolymer at an extremely high grafting density.

Fig. 5 (a) Predicted phase diagram of AB diblock copolymer brushes of χN = 100 on the wettable substrate of ΛN = 2, with respect to the mole fraction of the grafted A block, f_A, and average brush thickness, L. (b) Tilted view of the uniform phase (perpendicularly layered A and B domains represented by transparent red and blue) and its A/B interface (gray contour) at f_A = 0.2 and χN = 100. As the grafting density increases, i.e., the average brush thickness L, the rippled A/B interface at L = 0.5R_e transits to the one with hexagonal arrays of dimples at L = 0.7R_e and a planar interface at L = 0.9R_e. (c) Tilted (top) and side (bottom) views of the morphology along with contour curves of the A/B interface for a very large L = 2.3, 2.5 and 2.7R_e at χN = 30 and f_A = 0.7. As the grafting density increases to an extremely large value (L = 2.7R_e), the planar interface transits to hexagonal arrays of golf hole structures.

Solvent quality is another parameter that directly affects the extent of stretching present among chains which then could alter the phase behavior of BCP brushes. Hence, we study the morphologies in different solvents on a wettable substrate of ΛN = 2 with the brush thickness of L = 0.5R_e and χN = 50. Four different solvents, which are labeled S1 to S4 in the order of increasing solvent quality, are investigated, and the results are presented along with those for melt BCP brushes (S0). The detailed parameters used for the S0–S4 conditions in our implicit solvent model are listed in Table 1 and marked in the colormap of Fig. S8† showing the averaged size of a single chain on the (v_αα, w_ααα) parameter space referring to Park et al.³⁶ For each solvent, the types of observed phases are shown in Fig. 6a at f_A values ranging from 0.2 and 0.8; the top views of the phases are shown in Fig. S9a.† The roughness of the top surface of the phases is also measured by estimating the standard deviation s of the brush height in the lateral dimensions. Local polymer densities for cubic grid cells with a size of (0.16R_e)³ defined in eqn (9) are used to measure the brush height at each lateral position as the z-location where the local polymer density drops below half of the average density value. Fig. 6b shows the measured roughness (3s) along with the tilted views of the representative morphologies at selected f_A values for S0–S4. Finally, at an f_A value of 0.7, we show the laterally averaged density profiles as a function of distance z from the grafting substrate for S0, S2 and S4 in Fig. S9b.†

Table 1 Second- and third-order model parameters (v_αα, v_AB, w_ααα) for simulations of BCP brushes in implicit solvents. The averaged radius of gyration relative to the size of an ideal chain <R_g>/R_g,ideal under the given model parameter is also listed. The values used in S0 are the same as those of the melt conditions, and the solvent quality becomes better as moving from S0 to S4

	v αα	v AB	w ααα	<Rg>/Rg,ideal
S0	−3.17	−2.7813	0.01849	0.951
S1	−2.75	−2.3594	0.01699	1.095
S2	−2.50	−2.1094	0.01609	1.220
S3	−2.25	−1.8594	0.01520	1.370
S4	−2.00	−1.6094	0.01430	1.558

---

Fig. 6 (a) Phase diagram of BCP brushes with varying compositions of f_A from 0.2 to 0.8 grafted on the wettable substrate (ΛN = 2) and exposed to a non-selective solvent with various qualities from S0 (melt) to S4. In the melt brush system, the average brush thickness is L = 0.5R_e and χN is set to 50. (b) Variation in the roughness of free surfaces when BCP brushes of f_A = 0.2, 0.5 and 0.7 are exposed to different solvents, S0–S4. The representative morphologies in S0, S2 and S4 are presented as well.

Chains stretch vertically further as the solvent quality is enhanced, thereby increasing the brush thickness as depicted in the broader density profile in Fig. S9b.† The vertically stretched chain conformations increase the entropic penalty to form laterally phase separated structures. Thus, the phase boundary in f_A for lateral phase separation is shifted to a higher value upon increasing the solvent quality (Fig. 6a). The stretching of chains also results in flatness of the top surface of the observed phases resulting in a decrease in the 3s value as the system moves from S0 to S4 (Fig. 6b). At f_A = 0.2, the type of phase for all the solvents is the same as the one for melt conditions, i.e., a uniform phase, denoted in Fig. 6a as a black square. However, around symmetric compositions, the curvy phase under melt conditions (S0) disappears when the system is placed in a good solvent. Instead, the morphology with circular A domains exposed at the top, which tends to be packed hexagonally, is recognized and labeled as inverse hex (pink hexagon). As depicted in Fig. 6b, the roughness of the top surface for f_A = 0.5 is much larger than those of the other cases due to the type of observed phase. In the curvy phase, the thickness varies sharply with a step edge of A/B domains near the laterally phase separated curved domains. However, 3s is reduced significantly in S4 as these curved domains are removed. Similar to the results for symmetric composition, the types of phases also change for large f_A values upon varying the solvent quality. The stripe and hexagonal phases observed in S1 at f_A = 0.7 and 0.8 transit to inverse hexagonal and stripe phases with reduced 3s in S4, respectively.

Conclusions

Diblock copolymers grafted on planar substrates are studied using a combination of Monte Carlo simulations and a coarse-grained model with a generalized Hamiltonian, which allows for topological adjustment at a free surface. We systematically investigate the dependence of the phase behavior of the BCP brushes on various system variables. We construct the phase diagram for various values of block composition f_A and χN and have noted new morphologies and several differences in comparison with previous studies. BCP brushes grafted on a neutral substrate (ΛN = 0) at a moderately low grafting density phase separate into uniform, void, stripe, and hexagonal arrays. The uniform phase at an elevated χN consists of layered A and B domains, but the A/B interface has a non-planar geometry. Voids, a mixed morphology with large-sized circular dewetting areas and perpendicularly separated A and B layers are observed in a wide range of f_A values. When the substrate is attractive to both blocks, regions with voids in the phase diagram are replaced with new types of laterally phase separated structures that are curved in nature, adopting either a ring-like structure with an outer shell of A domains around the inner cylindrical B domains or “S”/“C” shaped A domains with B domains enclosed within. The phase behavior is further enriched by introducing the selective top/bottom surfaces. By tuning the top and bottom surface affinities towards A/B blocks, the void, hex, stripe, and uniform phases with either A or B covering the top are obtained even at a single composition. This implies that a diverse range of phases can be obtained from a single system of the same χN and f_A. We have also shown that phases with a similar morphology from the top view can have significantly different internal structures. Specifically, stripe and hex structures in symmetric BCP brushes on a non-grafted B block attractive substrate contain A/B lines and a hexagonal array of circular B domains throughout the film. These are in contrast to the stripe and hex phases on a neutral substrate seen at asymmetric compositions where the periodic domains are separated from the substrate by a continuous layer of A. These variations in internal structures have a direct application in the field of nanopatterning, e.g., etching out one of the blocks can result in the formation of patterns with or without a periodic topography. The effect of grafting density on the phase behavior of BCP brushes is also probed, focusing on the topology of internal A/B interfaces. The non-planar A/B interface in the uniform phase at a moderate grafting density becomes flat at a high grafting density. However, at an extremely high grafting density, the flat interface breaks up and forms golf hole structures, thereby reducing the excessive elastic free energy caused by highly stretched chains. Finally, we demonstrated that good non-selective solvents increase chain stretching in the vertical direction and reduce the roughness of the brush surface, thus presenting similar effects on the morphology as the grafting density increases.

One of the future directions is to expand our exploratory study for diblock polymers grafted on curved substrates, in particular, for cylindrical/spherical substrates. The grafted films coated on a curved substrate are useful in synthesizing colloids with environmentally responsive surface patterns which then have biomedical applications, e.g., targeted drug delivery and medical imaging. Naturally, chains will be more sterically crowded near the surface of the sphere/cylinder due to the curvature, which will result in extended chain conformations. Thus, the phase behavior of BCP brushes is expected to be significantly altered compared to that on a flat substrate.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S.-M. H., V. T. and T.-Y. K. gratefully acknowledge the support from the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (Grant No. 2021R1A2C1008861 and 2018R1D1A1A02044073). M. K. acknowledges the support from Inha University (Grant No. INHA-65348).

References

1. X. Chen and S. P. Armes, Adv. Mater., 2003, 15, 1558–1562.
2. M. Husemann, D. Mecerreyes, C. J. Hawker, J. L. Hedrick, R. Shah and N. L. Abbott, Angew. Chem., Int. Ed., 1999, 38, 647–649.
3. B. Zhao and W. J. Brittain, Prog. Polym. Sci., 2000, 25, 677–710.
4. D. H. Napper, Polymeric stabilization of colloidal dispersions, Academic Press, 1983.
5. P. Pincus, Macromolecules, 1991, 24, 2912–2919.
6. T. L. Fox, S. Tang, G. Zhang, J. M. Horton, B. Zhao, L. Zhu and P. L. Stewart, Macromol. Chem. Phys., 2016, 217, 1767–1776.
7. Y. Fu, Y. Yang, S. Xiao, L. Zhang, L. Huang, F. Chen, P. Fan, M. Zhong, J. Tan and J. Yang, Prog. Org. Coat., 2019, 130, 75–82.
8. L. Léger, E. Raphaël and H. Hervet, Polymers in confined environments, 1999, pp. 185–225.
9. P. Mansky, Y. Liu, E. Huang, T. Russell and C. Hawker, Science, 1997, 275, 1458–1460.
10. M. Motornov, R. Sheparovych, E. Katz and S. Minko, ACS Nano, 2008, 2, 41–52.
11. D. Julthongpiput, Y.-H. Lin, J. Teng, E. R. Zubarev and V. V. Tsukruk, Langmuir, 2003, 19, 7832–7836.
12. S. Minko, J. Macromol. Sci., Polym. Rev., 2006, 46, 397–420.
13. T. Chen, R. Ferris, J. Zhang, R. Ducker and S. Zauscher, Prog. Polym. Sci., 2010, 35, 94–112.
14. S. Edmondson, V. L. Osborne and W. T. Huck, Chem. Soc. Rev., 2004, 33, 14–22.
15. B. Zhao and W. J. Brittain, J. Am. Chem. Soc., 1999, 121, 3557–3558.
16. P. Uhlmann, H. Merlitz, J. U. Sommer and M. Stamm, Macromol. Rapid Commun., 2009, 30, 732–740.
17. A. Sidorenko, S. Minko, K. Schenk-Meuser, H. Duschner and M. Stamm, Langmuir, 1999, 15, 8349–8355.
18. M. A. C. Stuart, W. T. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk and M. Urban, Nat. Mater., 2010, 9, 101–113.
19. S. Kumar, Y. L. Dory, M. Lepage and Y. Zhao, Macromolecules, 2011, 44, 7385–7393.
20. J. Wang and M. Muller, J. Phys. Chem. B, 2009, 113, 11384–11402.
21. M. Müller and G. D. Smith, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 934–958.
22. M. Kim, E. Han, D. P. Sweat and P. Gopalan, Soft Matter, 2013, 9, 6135–6141.
23. Q. Yu, Y. Zhang, H. Chen, F. Zhou, Z. Wu, H. Huang and J. L. Brash, Langmuir, 2010, 26, 8582–8588.
24. M. Y. Paik, Y. Xu, A. Rastogi, M. Tanaka, Y. Yi and C. K. Ober, Nano Lett., 2010, 10, 3873–3879.
25. E. Han, M. Kim and P. Gopalan, ACS Nano, 2012, 6, 1823–1829.
26. M. W. Matsen and G. H. Griffiths, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 29, 219–227.
27. E. B. Zhulina, C. Singh and A. C. Balazs, Macromolecules, 1996, 29, 6338–6348.
28. E. B. Zhulina, C. Singh and A. C. Balazs, Macromolecules, 1996, 29, 8254–8259.
29. P. Ferreira and L. Leibler, J. Chem. Phys., 1996, 105, 9362–9370.
30. B. M. O'driscoll, G. H. Griffiths, M. W. Matsen, S. Perrier, V. Ladmiral and I. W. Hamley, Macromolecules, 2010, 43, 8177–8184.
31. Y. Yin, P. Sun, B. Li, T. Chen, Q. Jin, D. Ding and A.-C. Shi, Macromolecules, 2007, 40, 5161–5170.
32. R. Jiang, B. Li, Z. Wang, Y. Yin and A.-C. Shi, Macromolecules, 2012, 45, 4920–4931.
33. J. Wang and M. Muller, Macromolecules, 2009, 42, 2251–2264.
34. O. Guskova and C. Seidel, Macromolecules, 2011, 44, 671–682.
35. A. A. Rudov, P. G. Khalatur and I. I. Potemkin, Macromolecules, 2012, 45, 4870–4875.
36. J. Park, A. Ramírez-Hernández, V. Thapar and S.-M. Hur, Polymer, 2021, 13, 953.
37. K. Sparnacci, R. Chiarcos, V. Gianotti, M. Laus, T. J. Giammaria, M. Perego, G. Munao, G. Milano, A. De Nicola and M. Haese, ACS Appl. Mater. Interfaces, 2020, 12, 7777–7787.
38. K. Gong, B. D. Marshall and W. G. Chapman, J. Chem. Phys., 2012, 137, 154904.
39. H. Morita, T. Kawakatsu and M. Doi, Macromolecules, 2001, 34, 8777–8783.
40. C. Xu, T. Wu, C. M. Drain, J. D. Batteas, M. J. Fasolka and K. L. Beers, Macromolecules, 2006, 39, 3359–3364.
41. C. Sinturel, M. Vayer, M. Morris and M. A. Hillmyer, Macromolecules, 2013, 46, 5399–5415.
42. J. K. Bosworth, M. Y. Paik, R. Ruiz, E. L. Schwartz, J. Q. Huang, A. W. Ko, D.-M. Smilgies, C. T. Black and C. K. Ober, ACS Nano, 2008, 2, 1396–1402.
43. J. Choi, J. Huh, K. R. Carter and T. P. Russell, ACS Nano, 2016, 10, 7915–7925.
44. F. A. Detcheverry, D. Q. Pike, P. F. Nealey, M. Müller and J. J. de Pablo, Phys. Rev. Lett., 2009, 102, 197801.
45. F. A. Detcheverry, D. Q. Pike, U. Nagpal, P. F. Nealey and J. J. de Pablo, Soft Matter, 2009, 5, 4858–4865.
46. F. A. Detcheverry, G. Liu, P. F. Nealey and J. J. de Pablo, Macromolecules, 2010, 43, 3446–3454.
47. M. Müller, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 030802.
48. W. Wei, T.-Y. Kim, A. Balamurugan, J. Sun, R. Chen, A. Ghosh, F. Rodolakis, J. L. McChesney, A. Lakkham and P. G. Evans, ACS Macro Lett., 2019, 8, 1086–1090.
49. S.-M. Hur, G. S. Khaira, A. Ramírez-Hernández, M. Müller, P. F. Nealey and J. J. de Pablo, ACS Macro Lett., 2015, 4, 11–15.
50. M. Hömberg and M. Müller, J. Chem. Phys., 2010, 132, 04B609.
51. F. A. Detcheverry, H. Kang, K. C. Daoulas, M. Müller, P. F. Nealey and J. J. De Pablo, Macromolecules, 2008, 41, 4989–5001.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1me00126d

---