Design of non-transition-metal-doped nanoribbon catalysis to achieve efficient nitrogen fixation

Abstract

The high percentage of N₂ in the air can provide an abundant nitrogen source for the ammonia industry. However, the nitrogen fixation process still faces great challenges due to the stable nitrogen–nitrogen triple bonds. Recently, single-atom catalysts (SACs) have arguably become the most promising frontier in the synthetic ammonia industry due to their high activity, selectivity and stability. In particular, metal-free catalysis has attracted great attention due to its low-cost and environmentally friendly features. Herein, we investigate a series of nitrogen-reduction reaction (NRR) electrocatalysts as graphene nanoribbons (GNRs) embedded with 16 kinds of non-transition metal single-atom catalysts (non-TMSACs) using density functional theory (DFT) computations. The stability of this system is first confirmed by AIMD simulations and formation energies. Among all the candidates, Si anchored on the GNR system achieves a limiting potential as low as −0.45 V and the binding energy for NNH also serves as a good descriptor for the onset potential. The electronic structure reveals that this design satisfies an “acceptance–donation” interaction scenario, which is also confirmed by the crystal orbital Hamilton population (COHP) and the spatial charge distribution. This study not only proposes an effective catalysis approach for the NRR, but also emphasizes the origin of electronic structures, which may provide guidance for future NRR catalyst designs.

---

1. Introduction

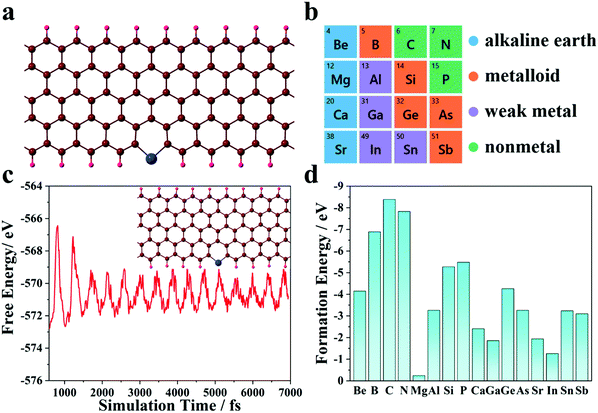
Nitrogen fixation, the process of converting atmospheric nitrogen (N₂) into ammonia (NH₃), is considered an important process in industry. Furthermore, half of the nitrogen needed by the biological world comes from nitrogen fertilizers, and these nitrogen fertilizers are all made from synthetic ammonia.^1–3 Previously, ammonia has been synthesized by the Haber–Bosch process, which needs high temperatures (300–500 °C) and high pressures (150–200 atm) and consumes about 2% of the world's energy supply.^4–8 Therefore, it is significant to design a sustainable, environmentally friendly and alternative process that can fix nitrogen under ambient conditions.

The electrochemical catalytic reaction has become an eco-friendly and sustainable alternative to the artificial nitrogen-reduction reaction at ambient temperature and pressure. Amongst available catalysts, single-atom catalysts (SACs), which display high selectivity, high activity and low cost, have attracted much attention in recent years. When a single atom acts as a catalytically active site, the activity will increase with decreasing particle size and reach a constant value until atomic dispersion is achieved.⁹ However, these single atoms in SACs exhibit a high surface energy due to their atomic dispersion and are easily aggregated into particles.¹⁰ Therefore, in order to stabilize these single atoms, it is necessary to establish a strong interaction between these single atoms and the loading matrix. These interactions not only stabilize the atoms, but also have a great influence on their electronic structures and catalytic properties.^11,12 Hitherto, most reported SACs employ transition metals as single atoms, while defect-rich nitrides/sulfides/oxides or metal–organic frameworks (MOFs) often serve as support materials for anchoring these SACs.^12–17 Wu et al.¹⁸ have systematically investigated the potential electrocatalytic performance of single transition metal atoms (e.g., Pd, Ag, Rh, Cu, Ti, Mo, Mn, Zn, Fe, Co, Ru, and Pt) embedded in a defective boron phosphide (TMs/BP) monolayer with a phosphorus monovacancy for ambient NH₃ production. Among them, Mo/BP exhibits the best catalytic performance for ambient reduction of N₂ through typical enzymatic and consecutive reaction pathways with an activation barrier value of 0.68 eV, indicating that Mo/BP is an efficient catalyst for N₂ fixation. However, transition metal-based SACs face several problems during the manufacturing process, such as high cost and easy atom aggregation. Therefore, it is of great significance to investigate the new type of SAC¹⁹ that uses non-transition metal elements, which not only shows the advantage of low-cost and environmentally friendly features but also avoids poisoning and crossover effects.^20–32 As research has progressed, many metal-free catalysts have been reported. Ma et al.³³ synthesized nitrogen-doped hollow carbon nanoparticles (N-HCNPs) and obtained an excellent electrocatalytic performance for the oxygen-reduction reaction. Zheng et al. discovered that graphitic–carbon nitride supported by nitrogen-doped graphene (g-C₃N₄@NG) can serve as a non-metallic electrocatalyst with an unexpected HER activity.³⁴ Thus, metal-free catalysis is promising for application in the NRR system.

Recently, graphene nanoribbons (GNRs) have been widely used as various electrocatalysts in catalytic reactions such as the oxygen-evolution reaction (OER), the oxygen-reduction reaction (ORR),³⁵ and in lithium–sulfur electrocatalysis.³⁶ Therefore, graphene ribbons can serve as an excellent loading substrate for non-transition metal SACs. A series of experimental and computational studies have also demonstrated the feasibility of edge-doped SAC@GNRs.^37–43 Shi et al.^44,45 first reviewed the progress of research on the applications of multiscale computational methods in energy materials, including first-principles calculations, molecular dynamics, phase field simulation, finite element analysis and machine learning in 2016. Yi et al.⁴⁶ first synthesized the Pr-N dominated highly oriented pyrolytic graphite (N-HOPG) with a nitrogen content from 0.74% to 2.73%, which demonstrates excellent ORR activity. Raman and positron annihilation (PA) measurements demonstrated that specific carbon defect types (edged pentagon) could be selectively created via controllable nitrogen doping. Yang et al.⁴⁷ used nanoporous carbon as the substrate material and investigated the non-metallic elements of the chalcogen/oxygen group (e.g., O, S, Se, and Te) as dopants in carbon catalysts to tune their NRR activity theoretically and experimentally. Hou et al.36 modeled a series of edge-doped graphene nanoribbons (GNRs) and evaluated their binding behaviors for both polar lithium polysulfide and non-polar elemental sulfur. Thus, it can be observed that heteroatom-doped graphene nanoribbons (GNRs) are feasible experimentally and theoretically.

Hence, in this paper, a series of heteroatom-doped GNRs are modeled by applying first-principles calculations, and their catalytic effects on the NRR are systematically studied. The electronic structure reveals that this design satisfies an “acceptance–donation” interaction scenario, and a low limiting potential of −0.45V is obtained with the Si-doped GNR system. By meticulously analyzing the configuration, binding energy, charge transfer, and deformation charge density, a set of principle rules and a linearity curve correlating the binding energy with NNH to the onset potential are plotted. This finding not only opens a new route for NH₃ production using single-atom catalysts under ambient conditions but also reveals the electronic origins, providing theoretical guidance on the catalytic effect by non-transition metals for future NRR catalyst designs.

2. Computational methods

The spin-polarized density functional theory (DFT) method is employed for all calculations using the Vienna ab initio Simulation Package (VASP).^48,49 The projector-augmented wave pseudopotential is utilized to treat the ion–electron interaction,^50,51 while the Perdew–Burke–Ernzerhof revised for solids (PBEsol) exchange correlation functional of the generalized gradient approximation (GGA), which is confirmed to describe the adsorption of small molecules on solid surfaces accurately,⁵² is adopted for describing the electron interactions.⁵³ The kinetic energy cut-off value for the plane wave expansion is set at 550 eV and the reciprocal space is sampled using 4 × 2 × 2 k points for fully relaxed geometry optimization until the maximal residual force is less than 0.01 eV Å⁻¹.⁵⁴ In the vertical direction, two vacuum layers are introduced. We employ ab initio molecular dynamics (AIMD)^55,56 simulations to confirm the thermodynamic stabilities under ambient conditions (300 K). The NVT ensemble is used with the Nosé mass parameter set to 0.5 to control the temperature oscillations.

The formation energy of a vacancy is calculated by:

E_form = E_slab@SAC − (E_slab + E_SAC),

where E_slab@SAC, E_slab, E_SAC are the energies of the SAC@GNR system, the nanoribbon with a vacancy system, and the single-atom catalyst, respectively.^36,57

We employ the computational hydrogen electrode model proposed by Nørskov et al. to simulate the electrocatalytic NRR performance.⁵⁸ The change in the Gibbs free energy (ΔG) can be calculated as follows:

ΔG = ΔE + ΔE_ZPE − TΔS + eU,

where ΔE is the electronic energy difference directly obtained using DFT calculations, ΔE_ZPE is the change in the zero-point energy, T is room temperature (298.15 K) and ΔS is the entropy variance. The zero-point vibrational energy (ZPE) and the vibrational entropy of the adsorbed groups are obtained after frequency calculations. U is the applied electrode potential that can offset ΔG to the value of zero.

3. Result and discussion

3.1 Structure and stability of the SAC@GNR system

Non-metallic atoms can tailor the electronic structures and coordinate with the graphene nanoribbon substrate to serve as the electron reservoir. Here, 16 kinds of non-transition metal element with higher chemical activities are considered as the single atom to screen a superior SAC, as shown in Fig. 1b (atomic configuration is shown in Fig. 1a). The formation energies are calculated to investigate the stabilities of SACs (Fig. 1d). The results show that all the candidates are thermodynamically stable. We further perform AIMD simulations to confirm the stability of the best catalytic system, and Fig. 1c shows the time-dependent free energy evolution of the Si@GNR system. The curve shows equal amplitude vibration features, while the detachment of the SAC is not observed (an illustration is shown in the inset to Fig. 1c) during the whole simulation time, thus demonstrating that the GNR substrate can act as an effective anchor for SACs.

Fig. 1 (a) Atomic configuration of the SAC@GNR system. (b) Sixteen kinds of SAC considered for screening. (c) Ab initio molecular dynamics (AIMD) simulations for the Si@GNR system. (d) Formation energy for 16 kinds of SAC@GNR systems.

3.2 NRR processes and electrochemical performance

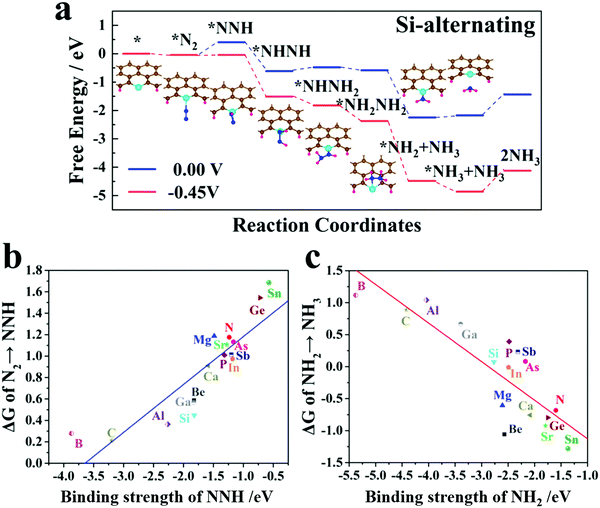
After identifying the stable SAC geometry, we further evaluate the electrocatalytic performance of the SAC@GNR system for the reduction of N₂ to NH₃. The hydrogenation process can follow three typical reaction mechanisms: distal, alternating and enzymatic.^59,60 For the distal mechanism, the N₂ molecule is first adsorbed in the end-on pattern and the proton–electron pairs (H⁺ + e⁻) attack the distal N atom to produce the first NH₃. Then, hydrogen attacks the other N atom to produce the second NH₃ molecule. By contrast, for the alternating mechanism, the N₂ molecule is still adsorbed in the end-on pattern and two N atoms are hydrogenated by the proton–electron pairs alternately. The second NH₃ molecule will be released just after the first one. For the enzymatic mechanism, the N₂ molecule will start from a side-on adsorbed configuration and proceed via an alternative hydrogenation process. Since in SAC@GNR system, the N₂ molecule cannot be adsorbed stably in the side-on pattern, we consider only the distal and alternating hydrogenation mechanisms.

Table S1 (ESI†) shows the limiting potential, the corresponding potential-determining step (PDS) and the hydrogenation mechanism for the 16 kinds of SAC@GNR system. It is found that, for most SAC@GNR systems, the limiting potential is around −1 V and most PDSs concentrate on the *N₂ → *NNH step. For a few systems (e.g., B, C, Al, and Ga), their PDSs concentrate on the *NH₂ → *NH₃ step. The alternating mechanism is suitable for all the SAC@GNR systems except for N@GNR. Furthermore, for some systems (e.g., C, Ge, and As), both hydrogenation mechanisms are applicable. Among them, the Si-doped GNR system can induce the lowest limiting potential. With a potential of −0.45 V, the N₂ adsorbed on the Si-doped GNR catalytic system performed the alternating mechanism to yield two NH₃ molecules overall (structures for the hydrogenation process and the pathway are illustrated in Fig. 2a, and the other 15 candidates are displayed in the ESI†). Compared with other traditional BN-,⁶¹ BP-⁶² and g-C₃N₄- based^63,64 single-atom catalysts, SAC@GNR exhibits a competitive catalytic activity. This is mainly because the intrinsic edge sites of graphene have a high chemical activity.^37–43 After the electronic structure of the GNR has been adjusted by single atoms, these active sites exhibit a better catalytic performance.^35,36

Fig. 2 (a) Free energy evolution process for the Si@GNR system. (b) Scaling relations between the onset potential and the binding strength of the single NNH molecule. (c) Scaling relations between the onset potential and the binding strength of the single NH₂ molecule.

From Table S1 (ESI†), it can be clearly observed that the *N₂ → *NNH step plays the decisive role as the PDS for most SAC candidates. Therefore, it is important to study the interaction of PDS molecules with the matrix. Herein, we extract the PDS structures of all the SAC@GNR systems and compute the binding strength of NNH, which can serve as a rational descriptor for evaluating the catalytic effect. There is a clear linear relationship between the onset potential and the binding energy of *NNH (Fig. 2b). This shows that B@GNR, C@GNR, Al@GNR, Si@GNR and Ga@GNR systems induce a relatively high adsorption energy for NNH among all of the systems we studied, which can effectively reduce the potential for the *N₂ → *NNH step and thus result in a lower onset potential. For the other systems, due to the weak adsorption of NNH molecules, the energy of the NNH*SAC@GNR structure increases, resulting in a higher energy cost for the *N₂ → *NNH process. As a result, this step becomes the PDS. Thus, it can be concluded that in the initial stage of the nitrogen-reduction reaction, SAC@GNR systems should perform the intense adsorption of small molecules to ensure that the hydrogenation process can proceed smoothly at a low onset potential. Table S1 (ESI†) also shows that for some systems, *NH₂ → *NH₃ becomes the PDS instead of *N₂ → *NNH, e.g., the B@GNR, C@GNR, Al@GNR, and Ga@GNR systems, which have a low onset potential for the *N₂ → *NNH process. This demonstrates that in the late stage of the nitrogen-reduction reaction, i.e., the process of ammonia release the strong adsorption of small molecules will inversely affect the NRR. Fig. 2c shows the linear relationship between the onset potential and the binding energy of *NH₂. It can be observed that the onset potentials of the *NH₂ → *NH₃ process are very high for the B@GNR, C@GNR, Al@GNR, and Ga@GNR systems. It is interesting that the energy required for the *NH₂ → *NH₃ process is negative in the systems that have a weak adsorption of small molecules. This means that this step can proceed spontaneously. Overall, it can be concluded that interactions that are either too intense or too weak are not conducive to nitrogen fixation reactions. Only an intermediate binding strength is beneficial for the NRR. In a comprehensive comparison, the Si@GNR system has a strong adsorption of the NNH molecule to ensure that the *N₂ → *NNH process proceeds smoothly, while the adsorption of NH₂ is weak to guarantee the normal release of ammonia in the late stage of the NRR.

3.3 Electronic structure origins of the rate-determining step

Since the PDS is an aspect that restrains the electrochemical performance and the PDSs of most SAC@GNR systems focus on the *N₂ → *NNH process, the electronic structures of N₂*SAC@GNR and NNH*SAC@GNR are further investigated to examine whether or not this design can achieve an effective electronic interaction. In order to investigate the effect of this interaction on the N–N bond, we apply the Bader charge for each system to calculate the charge redistribution between the matrix and the adsorbed molecule. The crystal orbital Hamilton population (COHP) is also applied to reveal how much the N–N bond is weakened.^65,66 The results demonstrate that there is an explicit linear relationship between the amount of charges received by the N₂ and the integrated COHP (ICOHP) of the N–N bond after N₂ adsorbed on the SAC substrate, as shown in Fig. S16 (ESI†). For SAC@GNR systems, the majority of catalytic systems (left bottom in Fig. S16, ESI†) have little influence on weakening the N–N bond of the N₂ molecule, resulting in similar values of ICOHP to that of the intrinsic nitrogen–nitrogen triple bond. Thus, the relatively weak ability of N₂ adsorption leads to a high onset potential at this stage, and the first hydrogenation step becomes the PDS for these systems, as discussed in Section 3.2. For the SAC@GNRs based on the C, B or Al atom (upper right in Fig. S16, ESI†), the strong binding interaction with nitrogen makes the first hydrogenation step much easier. However, these systems also have an intense adsorption of the *NH₂ molecule, inducing a relatively harder ammonia desorption in the late stage of the NRR, as also discussed in Section 3.2. Therefore, the PDS concentrates on the *NH₂ → *NH₃ process for these systems.

Since most SAC candidates do not exhibit the remarkable ability of N₂ molecule adsorption, the interaction of the NNH molecule becomes more significant. It is found that the Si@GNR system has an excellent adsorption effect on NNH molecules and has the lowest limiting potential of −0.45V among all the SAC@GNR systems. Herein, we take Si as the typical system and compare it with other systems. In order to investigate the effect of this interaction on the NNH molecule, the PDOS and crystal orbital Hamilton population (COHP) of the NNH*Si@GNR structure are plotted in Fig. 3a and b, respectively (the PDOS for the other SAC@GNR systems is shown in Fig. S18–S21, ESI†). The spatial charge distribution in these energy intervals is further shown (Fig. 3c). The results indicate that compared with other systems, the Si states overlap with the electronic state packets of N₂ in many energy-level ranges. In particular, the Si atom can bond with the N atom strongly even at a deep energy level, such as −20 to −22 eV. This is also confirmed by the bonding peaks in the COHP (Fig. 3b and 4b). However, SAC atoms in other systems that have a higher onset potential for the *N₂ → *NNH process do not exhibit this hybridization, e.g., the Sb@GNR system, where the COHP indicates that the Sb atom cannot bond with N atoms at a lower energy level (Fig. S22, ESI†). The integrated crystal orbital Hamilton population (ICOHP) of all the SAC@GNR systems is plotted to reflect the bonding relationship between the SAC and N atoms after the NNH molecules are adsorbed in each system (Fig. S23, ESI†). It can be clearly observed that for the elements of the same main group, which have the same valence electron, with the increase of the atomic period, the ICOHP of the SAC–N bond shows an increasing trend, indicating that the bond energy between the SAC and N atoms becomes weaker. These systems with the weak bonding ability of the SAC and N atoms all have a high onset potential for the *N₂ → *NNH process (upper right in Fig. S23, ESI†).

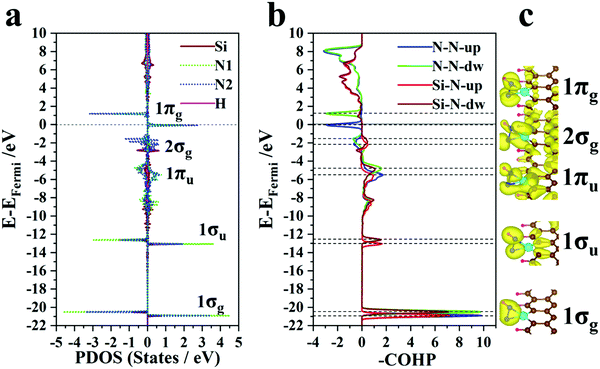Fig. 3 (a) Partial density of states (PDOS) for the NNH*Si@GNR structure. (b) Crystal orbital Hamilton population (COHP) for NNH*Si@GNR. (c) Spatial charge distribution for NNH*Si@GNR.

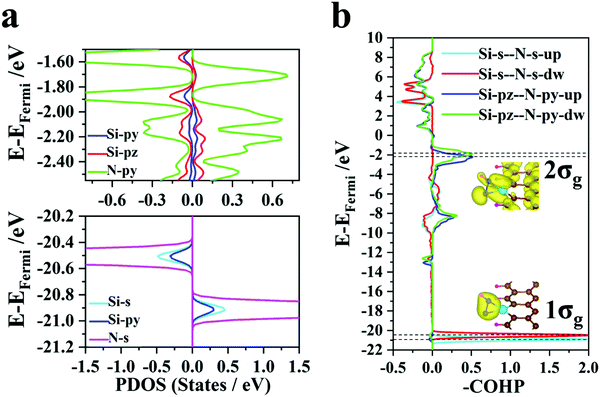Fig. 4 (a) Partial density of states (PDOS) for Si and N atoms. (b) COHP for Si and N atoms. The insets show the spatial charge distributions of the 1σ_g and 2σ_g molecular orbits.

Unlike transition metal (TM) atoms, which rely on d electrons for the catalysis process, non-transition metal atoms take advantage of p electrons to regulate the electronic structures of the SAC@GNR systems. The partial density of states (Fig. 4a) shows that the s and p_y orbitals of the Si atom hybridize with the s orbitals of two N atoms at the −20 to −22 eV energy level. The spatial charge distribution characteristics (illustrated in Fig. 4b) also indicate that the 1σ_g orbit stems from s-orbital hybridization. Near the Fermi level (−1 to −3 eV), the p_y and p_z orbitals of the Si atom hybridize with the p_y orbitals of two N atoms and form the bonding 2σ_g states, which are again validated by the COHP evolution and the spatial charge distribution. Therefore, the strong interaction between the Si and N atoms can effectively weaken the original N–N triple bond. The density of electronic states (Fig. 3a) demonstrates that the electrons of the N atoms donated from the matrix fill up 1π_g anti-bonding orbits and lower the energy level to the Fermi level, which is also validated by the COHP evolution (Fig. 3c). Due to this infusion of electrons from the SAC to the N atoms, the anti-bonding states of N₂ are filled near the Fermi level, thus destabilizing the small molecule and weakening the N–N binding strength. Thus, this suitable multiple orbital interaction scenario can be viewed as an ideal “acceptance–donation” mechanism, which makes it conducive to the further progress of hydrogenation. Thus, for the Si@GNR system, which shows the best NRR performance (−0.45 V), compared with the other NRR catalysts, the COHP and DOS demonstrate that the Si atom can bond well with nitrogen–hydrogen intermediate groups in the whole NRR process and have a moderate adsorption with the intermediate molecule to ensure the smooth progress of the hydrogenation reaction.

The hydrogen-evolution reaction (HER) is the major competitive reaction that consumes protons and electrons,^67,68 which even overcome the NRR process for pure transitional metals.⁶⁹ We further simulate the HER performance here. A common three-step evolution process, with the initial H⁺ state, intermediate H*, and 1/2 H₂, was adopted.^70–72 Fig. S24 (ESI†) compares the overall NRR and HER performance of SAC@GNR systems, where the dashed line denotes represents the same overpotential of NRR and HER. For SAC@GNR systems, most candidate systems exhibit a superior HER performance compared with the NRR process. Since the N₂ molecules have an intrinsic stable chemical activity, these substrates (e.g., As, In, Sn, Sb, etc.) cannot effectively weaken the N–N bond when N₂ molecules are absorbed, which causes the high limiting potential and concentrates the PDS in the *N₂ → *NNH process. However, these systems have a moderate adsorption of a single H atom, which cause a superior HER performance. In summary, the SAC@GNR systems that we screened with an excellent NRR catalytic ability (e.g., Si@GNR, Be@GNR, and Ga@GNR) also showed a competitive NRR performance compared with the HER process.

4. Conclusion

In summary, we systematically investigated the electrocatalytic NRR performance for 16 kinds of SAC embedded in the edge of graphene nanoribbons (GNRs). The formation energy and AIMD simulation results demonstrate that the GNR is a reliable matrix that can effectively anchor non-metallic atoms. Then, the electrocatalytic performance was assessed for two kinds of hydrogenation mechanism, such as distal and alternating hydrogenation mechanisms. Based on these, two linear relationship curves were plotted. There is a distinct linear relationship between the amount of charges received by N₂ and the ICOHP of the N–N bond after N₂ adsorption. For the PDS, the binding energy of NNH also serves as an effective descriptor for the onset potential. Finally, we investigated the electronic structures of the Si-doped GNR system, which has the lowest limiting potential of −0.45V. Through analysis of the PDS, combining molecular orbital theory and an “acceptance–donation” mechanism, the excellent NRR performance of the Si-doped GNR system was confirmed. This study not only investigates the NRR electrocatalytic performance of a novel catalytic system as a non-TMSAC@GNR but also emphasizes the significance of orbital hybridization and the “acceptance–donation” mechanism, which can further serve as theoretical guidance for future NRR catalyst design.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

Q. F. Z. was supported by the Beijing Natural Science Foundation (2192029), the National Key Research and Development Program of China (2017YFB0702100), the National Natural Science Foundation of China (11404017), the Technology Foundation for Selected Overseas Chinese Scholars, and the Ministry of Human Resources and Social Security of China. D. L. was supported by the ERDF in the IT4Innovations national supercomputing center - path to exascale project (CZ.02.1.01/0.0/0.0/16_013/0001791) within the OPRDE and the project e-INFRA CZ (ID:90140) by the Ministry of Education, Youth and Sports of the Czech Republic. J. L. Q. was supported by the Academic Excellence Foundation of BUAA for PhD Students.

References

1. J. Deng, J. A. Iñiguez and C. Liu, Joule, 2018, 2, 846–856.
2. S. L. Foster, S. I. P. Bakovic and R. D. Duda, Nat. Catal., 2018, 1, 490–500.
3. M. A. Shipman and M. D. Symes, Catal. Today, 2016, 286, 57–68.
4. J. M. Mcenaney, A. R. Singh and J. A. Schwalbe, Energy Environ. Sci., 2017, 10, 1621–1630.
5. Y. Tanabe and Y. Nishibayashi, Coord. Chem. Rev., 2013, 257, 2551–2564.
6. S. Licht, B. Cui and B. Wang, Science, 2014, 345, 637–640.
7. T. Oshikiri, K. Ueno and H. Misawa, Angew. Chem., Int. Ed., 2016, 128, 4010–4014.
8. M. Kitano, Y. Inoue and Y. Yamazaki, Nat. Chem., 2012, 4, 934–940.
9. X. Zhang, H. Shi and B. Q. Xu, Angew. Chem., Int. Ed., 2005, 44, 7132–7135.
10. W. Shengjie, L. Ang and L. J. Cheng, Nat. Nanotechnol., 2018, 13, 856–861.
11. A. Q. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81.
12. Z. P. Chen, E. Vorobyeva, S. Mitchell, E. Fako, M. A. Ortuno, N. Lopez, S. M. Collins, P. A. Midgley, S. Richard and G. Vile, Nat. Nanotechnol., 2018, 13, 702–707.
13. J. J. Shan, M. W. Li, L. F. Allard and S. Lee, Nature, 2017, 551, 605–608.
14. P. X. Liu, Y. Zhao, R. X. Qin, S. G. Mo and G. X. Chen, Science, 2016, 352, 797–801.
15. G. Liu, A. W. Robertson and M. J. Li, Nat. Chem., 2017, 9, 810–816.
16. S. Yang, J. Kim, Y. J. Tak, A. Soon and H. Lee, Angew. Chem., Int. Ed., 2016, 55, 2058–2062.
17. Z. Xiao, K. Du, W. Meng, J. Wang and Y. Yanfa, J. Am. Chem. Soc., 2017, 139, 6054.
18. Z. Liu, T. Huang, H. Chang, F. Wang, J. Wen, H. Sun and W. Yuping, Energy Environ. Mater., 2021, 4, 255–262.
19. C. X. Ling and Q. Li, J. Am. Chem. Soc., 2018, 140, 14161–14168.
20. L. Qu, Y. Liu and J. B. Baek, ACS Nano, 2010, 4, 1321–1326.
21. G. C. Welch, R. R. S. Juan and J. D. Masuda, Science, 2006, 314, 1124–1126.
22. Z. Yang, Z. Yao and G. Li, ACS Nano, 2012, 6, 205–211.
23. J. Liu, Y. Liu and N. Liu, Science, 2015, 347, 970–974.
24. X. Wang, K. Maeda and A. Thomas, Nat. Mater., 2009, 8, 76–80.
25. J. Zhu, Y. Wei, W. Chen and Z. Zhao, Chem. Commun., 2010, 46, 6965–6967.
26. Y. Xu, M. Kraft and R. Xu, Chem. Soc. Rev., 2016, 3039–3052.
27. G. Gao, Y. Jiao and F. Ma, J. Catal., 2015, 332, 149–155.
28. L. Dai, Y. Xue and L. Qu, Chem. Rev., 2015, 115, 4823–4892.
29. S. Chen, J. Bi and Y. Zhao, Adv. Mater., 2012, 24, 5646.
30. S. Yang, X. Feng, X. Wang and K. Müllen, Angew. Chem., 2011, 123, 5451–5455.
31. K. Gong, F. Du and Z. Xia, Science, 2009, 323, 760–764.
32. Y. Zheng, Y. Jiao and J. Chen, J. Am. Chem. Soc., 2011, 133, 20116–20119.
33. G. Ma, R. Jia and J. Zhao, J. Phys. Chem. C, 2011, 115, 25148–25154.
34. Y. Zheng, Y. Jiao, Y. H. Zhu, L. H. Li, Y. Han, Y. Chen, A. Du, M. Jaroniec and S. Z. Qiao, Nat. Commun., 2014, 5, 3783.
35. Y. Jia, L. Zhang and L. Zhuang, Nat. Catal., 2019, 688–695.
36. T. Z. Hou, X. Chen and H. J. Peng, Small, 2016, 12, 3283–3291.
37. Z. Yun, C. Penghui, G. Xu, W. Bo, L. Heng, W. Hao, L. Huakun and D. Shixue, Adv. Funct. Mater., 2016, 26, 7754–7765.
38. A. Z. Khosousi, L. Zhao and L. Palova, J. Am. Chem. Soc., 2014, 136, 1391–1397.
39. F. C. Sodi, G. Csányi and S. Piscanec, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 77, 165427.
40. N. Gorjizadeh, A. A. Farajian and K. Esfarjani, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 155427–155429.
41. V. A. Rigo, T. B. Martins and A. J. R. D. Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 75435.
42. E. Cruzsilva, Z. M. Barnett and B. G. Sumpter, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 23–28.
43. T. B. Martins, R. H. Miwa and A. J. R. D. Silva, Phys. Rev. Lett., 2007, 98, 304–308.
44. S. Shi, J. Gao, Y. Liu, Y. Zhao, Q. Wu, W. Ju, C. Ouyang and R. Xiao, Chin. Phys. B, 2016, 25, 018212.
45. B. Deng, D. Wang, Z. Jiang, J. Jiang, S. Shi, Z. Jiang and M. Liu, Carbon, 2018, 138, 169–178.
46. Y. Jia, L. Zhang and L. Zhuang, Nat. Catal., 2019, 19, 2974.
47. T. Ling, Y. Yang and L. Zhang, Angew. Chem., Int. Ed., 2020, 59.
48. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 1–50.
49. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
50. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
51. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
52. J. P. Perdew and A. Ruzsinszky, Phys. Rev. Lett., 2008, 100, 136406.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
55. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
56. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
57. J. Qu, J. Xiao and H. T. Chen, Chin. J. Catal., 2021, 42, 288–296.
58. J. K. Noerskov, T. Bligaard and A. Logadottir, Chem. Inf., 2005, 36, 12154.
59. J. Zhao and Z. Chen, J. Am. Chem. Soc., 2017, 12480–12487.
60. C. Ling, X. Niu and Q. Li, J. Am. Chem. Soc., 2018, 140, 14161–14168.
61. Z. Ma, Z. Cui, C. Xiao, W. Dai, Y. Lv, Q. Li and R. Sa, Nanoscale, 2020, 12, 1541–1550.
62. K. Liu, J. Fu, L. Zhu, X. Zhang and M. Liu, Nanoscale, 2020, 12, 8.
63. Z. Chen, J. Zhao and C. R. Cabrera, Small Methods, 2019, 3, 6.
64. K. Chu, Q. Q. Li, Y. P. Liu, J. Wang and Y. H. Cheng, Appl. Catal., B, 2020, 267, 118693.
65. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
66. S. Maintz, V. L. Deringer and L. Andrei, J. Comput. Chem., 2016, 37, 1030–1035.
67. C. Choi, S. Back, N. Kim, J. Lim, Y. Kim and Y. Jung, ACS Catal., 2018, 8, 7517–7525.
68. W. Schmickler and S. Trasatti, J. Electrochem. Soc., 2006, 153(12), L31–L32.
69. J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8, 2180–2186.
70. Y. Zhao, C. Chang, F. Teng, Y. Zhao, G. Chen, R. Shi, G. Waterhouse, W. Huang and T. Zhang, Adv. Energy Mater., 2017, 7(18), 17000051.
71. Q. Zheng, J. H. Lee, X. Shen, X. Chen and J. K. Kim, Mater. Today, 2020, 39, 158–179.
72. J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5(11), 909–913.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00518a

---