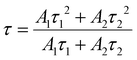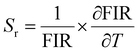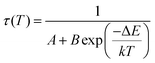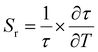DOI:
10.1039/D0MA00471E
(Paper)
Mater. Adv., 2021,
2, 1328-1342
Distortion induced structural characteristics of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb and Lu) double perovskites and their multifunctional optical properties for lighting and ratiometric temperature sensing†
Received
1st July 2020
, Accepted 8th December 2020
First published on 10th December 2020
Abstract
Group theoretical predictions obtained from Raman and IR spectra emphasize the structures of B-site ordered double perovskites Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) with ubiquitous BO6 or B′O6 octahedral tilting are monoclinic (P21/n), which was further confirmed via the Rietveld refinement of XRD patterns. The wide band gaps of these compounds were consistent with their ability to absorb UV radiation and hence their potential to act as photoluminescent host materials. Photoluminescence spectra of Eu3+-activated Ba2Y2/3TeO6, irrespective of substitution at A- or B-sites, yielded a dominant magnetic dipole transition at 592 nm and a less intense electric dipole transition at 610 nm when excited at 276 nm suggested the preference of Eu3+ ions to occupy Y3+ sites. The thermal activation energy of the Ba2Y2/3TeO6:Eu3+ phosphor was 0.15 eV and its relative sensitivity in the temperature range 300–500 K was estimated to have a maximum of 0.18% K−1 at 300 K for FIR measurements, which is better than its decay lifetime counterpart. The red shift and the peak broadening of the high-energy Raman modes at elevated temperatures of Ba2Y2/3TeO6:Eu3+ are due to enhanced B-site octahedral distortions and are correlated with the thermal quenching of Eu3+ emission. Temperature-dependent lifetimes in the range 80–500 K imply intensification of non-radiative relaxation within the limit. Furthermore, the phosphorescence lifetime, color parameters, and JuddOfelt parameters are explained in detail. The multifunctional optical properties of this phosphor can thus be utilized for technological applications, such as solid-state lighting and ratiometric optical thermometry.
Introduction
Among the different structural families of ceramic compounds, perovskites (ABX3) form the most often encountered materials since they are well known for their technological applications owing to their physical and chemical properties.1 The ideal cubic perovskite structure has a twelve-coordinated A-site cation, a six-coordinated B-site cation and an anion. The perovskite family can be extended by substituting cations at either A- or B-sites to form complex perovskites or double perovskites with the general formulae A2BB′X6, AA′BB′X6 and AA′B2X6, where the anion site is usually occupied by oxygen.1–4 Cationic substitution may cause expansion/contraction or tilting of the BX6 octahedra in order to compensate for the mismatch in ionic radii of the cations and hence, the symmetry of these compounds reduces to tetragonal, monoclinic, trigonal, etc. Amongst the quaternary perovskites, the B-site ordered A2BB′O6 arouse particular attention among researchers and have been extensively studied for their intriguing structure-dependent properties. Double perovskites with cationic substitution in the B-sites usually adopt 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rock salt ordering, where B and B′ cations alternate in all three dimensions. The possibility of different cations at the B-site allows novel combinations of elements, including transition metals, lanthanides, actinides and some main group elements. The cation substitution may cause structural alterations, which result in symmetry changes from aristotype cubic (Fm
1 rock salt ordering, where B and B′ cations alternate in all three dimensions. The possibility of different cations at the B-site allows novel combinations of elements, including transition metals, lanthanides, actinides and some main group elements. The cation substitution may cause structural alterations, which result in symmetry changes from aristotype cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to hettotypes such as tetragonal (I4/m), rhombohedral (R
m) to hettotypes such as tetragonal (I4/m), rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) or monoclinic (P21/n or I2/m). Moreover, the B-site ordered double perovskites exhibit interesting magnetic, optical, and dielectric as well as superconducting properties.5–11
) or monoclinic (P21/n or I2/m). Moreover, the B-site ordered double perovskites exhibit interesting magnetic, optical, and dielectric as well as superconducting properties.5–11
Extensive reviews have been carried out on B-site ordered double perovskites, exploring their structural and physical properties.1–3 Several types of inter-lanthanide perovskites showing remarkable physical properties, for example magnetic and optical properties, which can be attributed to the deep-lying 4f electrons of the rare earth ions, were discovered in the 1960s.12,13 These perovskites also have potential applications in the field of solid oxide fuel cells when doped with bivalent ions. In addition, perovskites containing lanthanides have been probed for their properties and applications.13 Later, in 2017, Kong and Cava14 reported the crystal structure and magnetic properties of the double perovskites Ba2R2/3TeO6 (R = Y, La, Pr, …, Lu). The crystal structure was reported to be cubic. However, our group15 re-examined the crystal symmetry of five of these double perovskites Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu) using Raman spectroscopy and Rietveld refinement of the XRD patterns and found that the most likely space group is P21/n with monoclinic symmetry. Moreover, their optical properties were also investigated, and a red-emitting phosphor Ba2La2/3TeO6:Eu3+ was also developed in anticipation of using it in white light emitting diodes.
Phosphor-converted white light emitting diodes (WLEDs) are considered to be the next generation of lighting sources.16–21 However, the deficient emission in the red spectral region results in a low color rendering index (CRI) for these WLEDs. In order to improve the performance of WLEDs, highly efficient and stable red phosphors are usually incorporated.22–34 Phosphor-converted red emitting LEDs have been a breakthrough in plant cultivation research, since red and far red light serve important functions in photosynthesis as well as in photomorphogenesis.35 Optical thermometry based on rare earth ion doped oxides is a promising method to gather large-scale imaging and contactless measurement of temperature compared to other conventional thermometers.36 Recently, optical thermometry has become a major research interest owing to its fast response time, contactless measurement, high precision and accuracy, high signal yield, etc. Optical temperature sensing is based on measuring the change in emission intensity against temperature when interacting with physical systems. There are several parameters of luminescence, such as intensity, spectrum bandwidth, spectral shift and lifetime, that can be used to calculate the temperature change, among which measuring the fluorescence intensity ratio (FIR) is the most favourable technique.36 Trivalent rare earth ion doped systems are used for optical thermometric applications due to the abundant 4f energy levels of these ions. Among the different rare earth ions, Eu3+ ions, owing to their thermally coupled energy levels (TCLs) 5D1 and 5D0, are also used for optical thermometry applications.37 Therefore, it is essential to synthesize and characterize novel red phosphors that can be used in various technological applications.
Rare earth doped red phosphors require a suitable host matrix that has good absorbance in the near UV region and excellent thermal and chemical stability. Double perovskites are among such host materials for luminescent centers or so-called activator ions. Red phosphors based on rare earth substituted complex perovskites are widely reported for lighting applications.38–47 In addition, several double perovskite phosphors, Gd2ZnTiO6:Pr3+, Y2MgTiO6:Mn4+, LiLaMgWO6:Er3+, etc., have been explored for their temperature-sensing potential.45–47
In the present work, we successfully synthesized Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) double perovskites and their crystal structure is examined by XRD, Raman and FTIR spectroscopy with B-site substitution of rare earth ions. The previously reported Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu) show no symmetry variation when the B-site is substituted with La3+ to Eu3+. However, the total number of modes in the Raman spectra decrease from 21 to 16 when the B-site changes from La3+ to Eu3+. In addition to this, the tilting or distortion of the BO6 and B′O6 octahedra also reduces and the B–O–B′ (B = La, Pr, Nd, Sm, Eu; B′ = Te) bond angle approaches 180° with B-site variation.15 This gives an intuition of a possible change in symmetry for Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) from monoclinic to cubic when the B-site undergoes substitution from Gd3+ to Lu3+. The photoluminescence properties of both A- and B-site substituted Ba2Y2/3TeO6:Eu3+, temperature-dependent luminescence, optical thermometric parameters, photoluminescence decay curves and Judd–Ofelt theory are discussed in detail. This is carried out on the assumption that, unlike Ba2La2/3TeO6:Eu3+ which was previously reported, Ba2Y2/3TeO6:Eu3+ shows enhanced luminescence performance as yttrium-based host matrices like Y2O2S:Eu2+ have been established as potential red phosphors that can be excited using ultraviolet (UV) radiation due to their wide band gap characteristics (4.6–4.8 eV) and hence utilized in the field of light emitting diode applications.
Materials and methods
Synthesis procedure
Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) double perovskites were synthesized via a solid-state ceramic route. BaCO3 (Sigma Aldrich, ≥99%), Y2O3 (Alfa Aesar, 99.99%), Gd2O3 (Sigma Aldrich, 99.9%), Tb4O7 (Sigma Aldrich, 99.9%), Dy2O3 (Aldrich, 99.9%), Ho2O3 (Sigma Aldrich, ≥99.9%), Er2O3 (Alfa Aesar, 99.9%), Tm2O3 (Alfa Aesar, 99.997%), Yb2O3 (Alfa Aesar, 99.9%), Lu2O3 (Alfa Aesar, 99.9%), and TeO2 (Sigma Aldrich, ≥99%) were the starting materials used. Stoichiometric amounts of the powders were weighed and mixed together in acetone medium by ball milling with ceria-stabilized zirconia balls for 18 h. The slurries of Ba2Gd2/3TeO6 and Ba2Dy2/3TeO6 were calcined at 1000 °C for 20 h and those of Ba2Y2/3TeO6, Ba2Tb2/3TeO6, Ba2Ho2/3TeO6, and both A- and B-site substituted Ba2Y2/3TeO6:Eu3+ (2.5, 5, 7.5, 10, 12.5, 15, 17.5 and 20 mol%) were calcined at 1200 °C for 20 h whereas Ba2Er2/3TeO6, Ba2Tm2/3TeO6, Ba2Yb2/3TeO6 and Ba2Lu2/3TeO6 were calcined at 1300 °C for 20 h. A slow heating rate (1 °C min−1) was applied to oxidize Te4+ to Te6+.
Characterization techniques
X-ray diffractograms were collected using a Bruker D8 Advance diffractometer (40 kV, 40 mA) equipped with a Cu-Kα source (λ = 1.5406 Å), a nickel filter and a Lynx eye position sensitive detector. Topas 4.2 software was used to perform the Rietveld refinement of the XRD patterns. A Chebychev polynomial was used to fit the background. Cell parameters, atomic coordinates, occupancy and isotropic temperature factors were refined. An Ametek EDAX – Octane Plus system was used to carry out EDS analysis. Room temperature micro Raman scattering spectra were recorded using a LABRAM HR-800 Raman spectrometer with a 633 nm He–Ne laser (5 mW) with a resolution of 1 cm−1. The FTIR spectra of the samples in the far-IR and mid-IR range were recorded by the ATR method in vacuum using a JASCO FTIR 6800 spectrometer. In the mid-IR region (400–1000 cm−1), a Ge-KBr beam splitter and triglycerine sulfate (TGS) detector and in the far-IR region (50–630 cm−1), a Myla beam splitter and a polyethylene triglycerine sulfate (PE-TGS) detector were used. The diffuse reflectance spectra were obtained in the range 190–900 nm using a JASCO V-750 UV-Vis spectrophotometer. A Fluorolog spectrofluorometer with a 450 W xenon lamp was used to record the photoluminescence excitation (PLE) and emission (PL) spectra (slit width 1 nm, integration time 0.5 s). The temperature-dependent photoluminescence and lifetime measurements were collected using a cryostat designed by Oxford Instruments attached with a FLS 1000 spectrophotometer from Edinburgh Instruments in a temperature range of 80–500 K. Decay curves were recorded with a flash lamp frequency of 25 Hz with a time range of 40 ms and maximum peak counts of 10 000. Temperature-dependent Raman spectra were recorded using a Horiba Jobin Yvon LABRAM HR-evolution Raman spectrometer with a 785 nm high-power single-frequency diode laser (90 mW). Quantum yield was measured with the aid of a Quanta-φ integrating sphere set-up associated with a Fluorolog spectrofluorometer using a 450 W xenon lamp.
Results and discussion
XRD patterns of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu)
X-ray diffraction technique was used to analyse the crystallinity and phase purity of all the calcined powders. Fig. 1a shows the XRD patterns of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) indexed with pseudocubic lattice planes. XRD patterns of Ba2Gd2/3TeO6 and Ba2Lu2/3TeO6 are shown separately in Fig. S1 and S2 (ESI†). For double perovskites, if the charge difference is ≥2 and the size difference is greater than 0.1 Å, then the most favourable ordering among the B-site cations is rocksalt ordering. For Ba2R2/3TeO6, the charge difference between R3+ and Te6+ is +3 and the size difference is greater than 0.1 Å, denoting a possible rocksalt ordering of B-site cations. The characteristic R point 111 reflection around 2θ ≈ 18° also indicates the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rocksalt ordering of these compounds. The splitting of reflections at 440 planes in Ba2Lu2/3TeO6 and Ba2Gd2/3TeO6 shown in Fig. 1b and c points to the existence of a possible octahedral distortion and hence a lower symmetry instead of the aristotype cubic (Fm
1 rocksalt ordering of these compounds. The splitting of reflections at 440 planes in Ba2Lu2/3TeO6 and Ba2Gd2/3TeO6 shown in Fig. 1b and c points to the existence of a possible octahedral distortion and hence a lower symmetry instead of the aristotype cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure. Another parameter that defines the extent of distortion is the tolerance factor, which is equal to one for an ideal cubic structure and is less than/greater than unity for lower symmetries. A tolerance factor that deviates from unity also suggests the structural variation of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) from cubic (Fm
m) structure. Another parameter that defines the extent of distortion is the tolerance factor, which is equal to one for an ideal cubic structure and is less than/greater than unity for lower symmetries. A tolerance factor that deviates from unity also suggests the structural variation of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) from cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure. The tolerance factor is determined by considering the effective size of vacancies the same as that of the B-site cations (R3+) and varies from 0.9904 to 1.0085 when the B-site is substituted with Gd3+ to Lu3+. This implies a cubic symmetry for these double perovskites since the tolerance factor lies within the limits defined for a cubic structure. In addition to this, our earlier report suggests some evidence for an increase in symmetry when going from La3+ to Eu3+ in the B-site of Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm, Eu). The tolerance factors are given in Table S3 (ESI†). Interestingly, the tolerance factor exceeds as well as falls short of unity, when the B-site is occupied by R3+ ions (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). However, these striking values of the tolerance factor may be due to the assumption of taking the effective size of vacancies (concentration ≈33%) and lanthanide ions to be the same. There is a possibility that the effective size of vacancies gets larger along with lanthanide contraction and hence compensates for the reduction in ionic size, which is the reason for obtaining a tolerance factor greater than one. Nonetheless, the tolerance factor is only a rough estimate since it varies in accordance with the value of ionic radii taken for determining it and in this case the tolerance factor suggests the possibility of a structural transition to cubic when Ba2R2/3TeO6 is substituted from Gd3+ to Lu3+. In summary, we are expecting a symmetry change from XRD analysis which could be more easily identifiable from vibrational spectroscopic techniques such Raman and IR spectroscopy.
m) structure. The tolerance factor is determined by considering the effective size of vacancies the same as that of the B-site cations (R3+) and varies from 0.9904 to 1.0085 when the B-site is substituted with Gd3+ to Lu3+. This implies a cubic symmetry for these double perovskites since the tolerance factor lies within the limits defined for a cubic structure. In addition to this, our earlier report suggests some evidence for an increase in symmetry when going from La3+ to Eu3+ in the B-site of Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm, Eu). The tolerance factors are given in Table S3 (ESI†). Interestingly, the tolerance factor exceeds as well as falls short of unity, when the B-site is occupied by R3+ ions (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). However, these striking values of the tolerance factor may be due to the assumption of taking the effective size of vacancies (concentration ≈33%) and lanthanide ions to be the same. There is a possibility that the effective size of vacancies gets larger along with lanthanide contraction and hence compensates for the reduction in ionic size, which is the reason for obtaining a tolerance factor greater than one. Nonetheless, the tolerance factor is only a rough estimate since it varies in accordance with the value of ionic radii taken for determining it and in this case the tolerance factor suggests the possibility of a structural transition to cubic when Ba2R2/3TeO6 is substituted from Gd3+ to Lu3+. In summary, we are expecting a symmetry change from XRD analysis which could be more easily identifiable from vibrational spectroscopic techniques such Raman and IR spectroscopy.
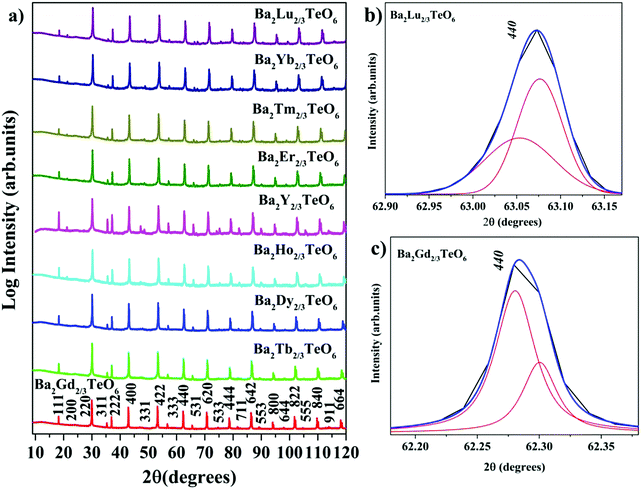 |
| | Fig. 1 (a) The combined XRD patterns of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). (b) The splitting of the 440 planes of Ba2Lu2/3TeO6 and (c) Ba2Gd2/3TeO6. | |
Energy dispersive X-ray spectra (EDS) of five samples were recorded to identify the elemental composition. The EDS of Ba2Gd2/3TeO6 and their elemental mappings are shown in Fig. 2a and b. The EDS and elemental mappings of Ba2Dy2/3TeO6, Ba2Y2/3TeO6, Ba2Er2/3TeO6, Ba2Lu2/3TeO6 are shown in Fig. S4 to S7 (ESI†).
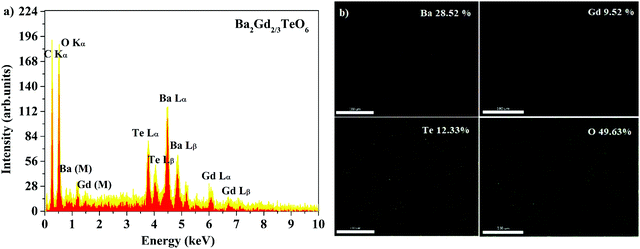 |
| | Fig. 2 (a) The EDS spectrum and (b) elemental mapping of Ba2Gd2/3TeO6. | |
The EDS indicate that Ba2R2/3TeO6 (R = Gd, Dy, Y, Er, Lu) have an elemental composition of Ba, Te, O, and the rare earths Gd, Dy, Y, Er and Lu. The obvious adventitious carbon peak is due to surface contamination. Elemental mapping shows that all the elements are distributed uniformly in the compounds. Table S8 (ESI†) gives the atomic percentage of elements obtained from EDS.
Raman and infrared spectra of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu)
The room-temperature Raman spectra shown in Fig. 3a exhibit similar spectral profiles imply same symmetry for Ba2R2/3TeO6. For an ideal double perovskite with aristotype cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, four Raman active modes are possible. However, more than four modes are observed in the Raman spectra of Ba2R2/3TeO6 similar to Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu) evidently point to a lower symmetry for these double perovskites. The exact number of modes is determined by deconvoluting the spectra using the Lorentzian function and the bands obtained are assigned in Table 1. The deconvoluted Raman spectra of Ba2Lu2/3TeO6 and Ba2Gd2/3TeO6 are shown in Fig. 3b and c, respectively, and those of Ba2R2/3TeO6 (R = Y, Tb, Dy, Ho, Er, Tm, Yb) are shown in Fig. S9–S15 (ESI†). The total number of Raman modes for all these double perovskites varies from 12 to 15 in the range 100–1000 cm−1 and are lower than previously reported Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu). Eventhough, we expected a gradual decrease in the number of modes with lanthanide contraction of rare earth ions, as shown in Table 1, they do not follow a trend. For example, in Ba2Gd2/3TeO6, the number of Raman modes is 15 and decreases to 12 for Ba2Ho2/3TeO6. Again, for Ba2Y2/3TeO6, the number of modes increases to 15. This might be due to the presence of sparse amount of impurities that could not be identified from the XRD patterns. Though XRD patterns signify the phase purity of all the compounds, Raman spectroscopy is able to find very small traces of impurities which do not even affect the crystallography of these compounds, since this technique is more sensitive than XRD. The addition of impurities lighter or heavier than the host atoms gives rise to new vibrational modes of higher or lower frequencies, respectively, in the Raman and IR spectra.
m symmetry, four Raman active modes are possible. However, more than four modes are observed in the Raman spectra of Ba2R2/3TeO6 similar to Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu) evidently point to a lower symmetry for these double perovskites. The exact number of modes is determined by deconvoluting the spectra using the Lorentzian function and the bands obtained are assigned in Table 1. The deconvoluted Raman spectra of Ba2Lu2/3TeO6 and Ba2Gd2/3TeO6 are shown in Fig. 3b and c, respectively, and those of Ba2R2/3TeO6 (R = Y, Tb, Dy, Ho, Er, Tm, Yb) are shown in Fig. S9–S15 (ESI†). The total number of Raman modes for all these double perovskites varies from 12 to 15 in the range 100–1000 cm−1 and are lower than previously reported Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu). Eventhough, we expected a gradual decrease in the number of modes with lanthanide contraction of rare earth ions, as shown in Table 1, they do not follow a trend. For example, in Ba2Gd2/3TeO6, the number of Raman modes is 15 and decreases to 12 for Ba2Ho2/3TeO6. Again, for Ba2Y2/3TeO6, the number of modes increases to 15. This might be due to the presence of sparse amount of impurities that could not be identified from the XRD patterns. Though XRD patterns signify the phase purity of all the compounds, Raman spectroscopy is able to find very small traces of impurities which do not even affect the crystallography of these compounds, since this technique is more sensitive than XRD. The addition of impurities lighter or heavier than the host atoms gives rise to new vibrational modes of higher or lower frequencies, respectively, in the Raman and IR spectra.
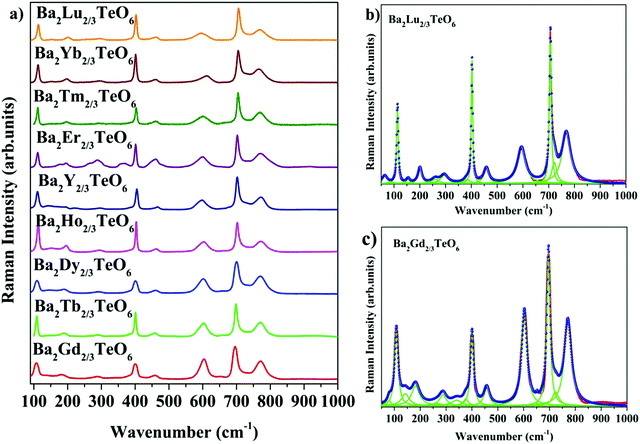 |
| | Fig. 3 (a) Room-temperature Raman spectra of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). Deconvoluted Raman spectra of (b) Ba2Lu2/3TeO6 and (c) Ba2Gd2/3TeO6. | |
Table 1 Raman modes of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu)
| Compound |
Internal |
External |
|
ν
1 (cm−1) |
ν
2 (cm−1) |
ν
5 (cm−1) |
T or L (cm−1) |
| Ba2Gd2/3TeO6 |
771 |
603 |
377 |
80 |
|
|
651 |
400 |
106 |
|
|
696 |
457 |
142 |
|
|
723 |
|
182 |
|
|
|
|
261 |
|
|
|
|
288 |
|
|
|
|
341 |
|
|
|
|
|
|
|
|
|
|
|
|
| Ba2Tb2/3TeO6 |
770 |
602 |
384 |
109 |
|
|
657 |
401 |
149 |
|
|
698 |
457 |
183 |
|
|
715 |
|
192 |
|
|
|
|
|
268 |
|
|
|
|
|
290 |
|
|
|
|
|
339 |
|
|
|
|
|
|
| Ba2Dy2/3TeO6 |
770 |
600 |
377 |
72 |
|
|
700 |
401 |
109 |
|
|
724 |
460 |
141 |
|
|
|
|
161 |
|
|
|
|
190 |
|
|
|
|
237 |
|
|
|
|
290 |
|
|
|
|
|
|
| Ba2Ho2/3TeO6 |
772 |
602 |
387 |
69 |
|
|
702 |
403 |
113 |
|
|
718 |
460 |
155 |
|
|
|
|
|
155 |
|
|
|
|
|
|
| Ba2Y2/3TeO6 |
771 |
596 |
384 |
79 |
|
|
702 |
405 |
111 |
|
|
725 |
465 |
144 |
|
|
|
|
171 |
|
|
|
|
|
194 |
|
|
|
|
|
225 |
|
|
|
|
|
272 |
|
|
|
|
|
295 |
|
|
|
|
|
|
| Ba2Er2/3TeO6 |
772 |
598 |
366 |
65 |
|
|
|
401 |
|
|
|
|
458 |
|
|
|
|
703 |
|
111 |
|
|
|
|
|
176 |
|
|
|
718 |
481 |
196 |
|
|
|
|
|
265 |
|
|
|
|
|
289 |
| Ba2Tm2/3TeO6 |
769 |
600 |
388 |
111 |
|
|
705 |
403 |
158 |
|
|
|
713 |
460 |
196 |
|
|
|
|
|
264 |
|
|
|
|
|
296 |
| Ba2Yb2/3TeO6 |
766 |
607 |
373 |
64 |
|
|
706 |
401 |
|
|
|
726 |
458 |
|
|
|
|
|
|
|
|
|
|
|
|
112 |
|
|
|
|
|
156 |
|
|
|
|
|
196 |
|
|
|
|
|
266 |
|
|
|
|
|
295 |
| Ba2Lu2/3TeO6 |
768 |
595 |
383 |
64 |
|
|
|
707 |
402 |
|
|
|
|
722 |
458 |
295 |
|
|
|
|
|
|
|
|
|
|
|
113 |
|
|
|
|
|
155 |
|
|
|
|
|
201 |
|
|
|
|
|
260 |
|
|
|
|
|
29 |
The ν1 modes due to the symmetric oxygen stretching vibrations are located in the region 750–800 cm−1 and the ν2 modes due to the asymmetric oxygen stretching vibrations of the octahedra are located in the region 550–740 cm−1, whereas the vibrational bands due to the oxygen bending motion of the octahedra are observed in the region 350–510 cm−1. The low-energy external modes in the range 100–350 cm−1 are due to translational and liberational modes, which are sensitive to lowering of symmetry due to octahedral tilting. Octahedral distortions are evident from the presence of low-energy modes. For modes above 650 cm−1, a significant shift to the longer wavenumber region (Fig. S16, ESI†) is noticed with a decrease in the ionic radii of the B-site cation from Gd3+ to Lu3+. As the unit cell gets contracted with the substitution of less massive ions, the ionic bonds become stronger and thus more energy is needed for the vibrations of the molecules.
Based on group theoretical calculations, there are 12 different space groups possible for double perovskites with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 B-site ordering combined with octahedral tilting. For Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu), there are more than four modes and hence, among the 12 space groups, the possible symmetries for Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) are P42/n, P4/mnc and I4/m (tetragonal) and C2/c and P21/n (monoclinic). Group theory predicts nine Raman active modes for tetragonal (I4/m) and P42/n has 35 Raman active modes, among which 17 are low-energy lattice modes.
1 B-site ordering combined with octahedral tilting. For Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu), there are more than four modes and hence, among the 12 space groups, the possible symmetries for Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) are P42/n, P4/mnc and I4/m (tetragonal) and C2/c and P21/n (monoclinic). Group theory predicts nine Raman active modes for tetragonal (I4/m) and P42/n has 35 Raman active modes, among which 17 are low-energy lattice modes.
In addition, this space group is ascribed to double perovskites with Jahn–Teller ions like Mn3+, Ni3+ or Cu3+ as in the case of Sr2MnWO648 and Sr2MnMoO6.49 The space groups P4/mnc has 14 Raman active modes and C2/c has 27 Raman active modes. However, these space groups can be ruled out since the Rietveld refinement parameters are not reliable compared to the space group P21/n. Thus, in accordance with the previously reported evidences and confirmation of the symmetry of Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu), the most likely symmetry of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) is found to be monoclinic (P21/n). The monoclinic (P21/n) symmetry is a combination of in-phase and anti-phase tilting of the BO6 and B'O6 octahedra around the 001 axes of the ideal cubic structure. The irreducible representation of P21/n space group is given by
| | | Γ = T(3Ag + 3Bg) + L(3Ag + 3Bg) + ν1(Ag + Bg) + ν2(2Ag + 2Bg) + ν5(3Ag + 3Bg) | (1) |
Thus, there are 24 Raman active modes possible for a double perovskite that crystallizes in monoclinic (
P2
1/
n) symmetry. The absence of other bands predicted by group theory might be due to the polycrystallinity of the compounds, the weak bands which could not be identified among the background noise and some modes may fall outside the range of the spectrum.
The IR transmittance spectra obtained using the ATR method are shown in Fig. 4. The spectra look almost identical and their visual inspection shows six well-defined modes. A careful inspection of the IR spectra indicates the presence of additional bands and the exact number of modes can only be identified by fitting the IR reflectivity spectra. However, group theory predicts 33 infrared active modes for a monoclinic structure belonging to the P21/n space group. Strong vibration coupling exists between the BO6 and B′O6 octahedral moieties. The six-coordinated octahedral units with a charge difference of +3 consist of B–O and B′–O bonds which are stronger than the twelve coordinated A–O bonds. This simple argument proves that the isolated octahedral groupings will dominate the vibrations in infrared as well as in Raman spectroscopy. Among the 6 well-defined modes, two modes around 340 cm−1 and 605 cm−1 are dominant, which can be assigned to the deformational modes and the antisymmetric stretching vibrations of the BO6 octahedral moieties, respectively. All vibrational modes located in the ranges 150–175 cm−1, 180–220 cm−1, 325–350 cm−1, 450–500 cm−1, 592–610 cm−1 and 660–680 cm−1 essentially come from the vibrations of RO6 and TeO6 octahedra. Similar to Raman spectra, the modes above 590 cm−1 show a spectral shift towards the high wavenumber region with lanthanide contraction.
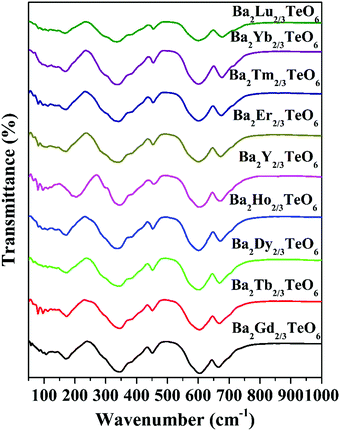 |
| | Fig. 4 FTIR spectra of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). | |
The translational symmetry elements, such as glide planes and screw axes, give rise to systematic absences/extinctions of some (hkl) reflections in the XRD patterns. The systematic absences of (hkl) reflections, such as (h0l) with h + l = 2n + 1 and (0k0) with k = 2n + 1, in the XRD patterns implies the monoclinic symmetry (P21/n) of the crystals. The presence of the (330) reflection for atomic displacement and (204) and (404) reflections for in-phase tilting also suggest monoclinic symmetry. The refined XRD patterns of Ba2Gd2/3TeO6 and Ba2Lu2/3TeO6 are shown in Fig. 5a and b. The Rietveld refinement parameters of Ba2Gd2/3TeO6 and Ba2Lu2/3TeO6 are given in Table 2. From the refined results, β is close to 90°, suggesting the possibility of a structural transition to orthorhombic along with the lanthanide contraction. Among the 12 different space groups predicted by Howard, only pnnn belongs to orthorhombic. Very few reports have been published about ordered double perovskites with octahedral tilting belonging to the space group pnnn. This space group does not permit the splitting of (hhh) reflections which we could not observe in XRD patterns of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) and hence rule out orthorhombic structure. However, in general for compounds crystallizing in P21/n symmetry, the value of β is larger than 90° if the size of at least one cation in the B-site is larger such as the rare earth ions in this case. These large cations can afford the distortions caused by the neighboring octahedral environment better than smaller cations with higher charges. Thus, it is plausible to conclude that the structure of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) double perovskites with a larger difference in ionic radii could be a distinct monoclinic unit cell rather than orthorhombic. To sum up, the monoclinic crystal structure derived from Raman and IR spectra is confirmed from the Rietveld refinement of the XRD patterns. The refined XRD patterns and parameters of Ba2R2/3TeO6 (R = Y, Tb, Dy, Ho, Er, Tm, Yb) are given in Fig. S17–S23 and Table S24 (ESI†). Lattice parameters as well as unit cell volume are decreased along with lanthanide contraction of the rare earth ions.
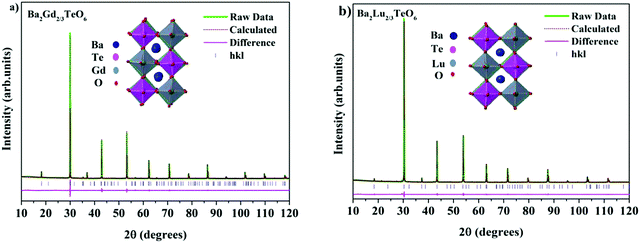 |
| | Fig. 5 The Rietveld refinement of the XRD patterns of (a) Ba2Gd2/3TeO6 and (b) Ba2Lu2/3TeO6. The insets show the crystal structures of Ba2Gd2/3TeO6 and Ba2Lu2/3TeO6. | |
Table 2 Refined crystallographic parameters of Ba2R2/3TeO6 (R = Gd and Lu)
| Ba2Gd2/3TeO6 |
|
a = 5.9538(9) Å |
b = 5.9905(2) Å |
c = 8.4658(3) Å |
β = 90.0129° |
|
R
exp = 1.95% |
R
wp = 4.99% |
R
p = 3.76% |
GOF = 2.56 |
| Ion |
Wyckoff site |
x
|
y
|
z
|
Occupancy |
B
eq (Å2) |
| Ba |
4e |
0.487(4) |
0.546(2) |
0.254(7) |
1 |
0.85(1) |
| Gd |
2d |
0.5 |
0 |
0 |
0.667 |
0.40(5) |
| Te |
2c |
0 |
0.5 |
0 |
1 |
0.40(5) |
| O1 |
4e |
0.215(5) |
0.251(5) |
0.018(1) |
1 |
0.98(8) |
| O2 |
4e |
0.200(5) |
0.771(1) |
0.004(5) |
1 |
0.98(2) |
| O3 |
4e |
0.534(2) |
0.016(6) |
0.264(3) |
1 |
0.97(3) |
| Ba2Lu2/3TeO6 |
|
a = 5.8894(5) Å |
b = 5.8998(6) Å |
c = 8.3329(7) Å |
β = 90.0105° |
|
R
exp = 2.12% |
R
wp = 5.42% |
R
p = 4.01% |
GOF = 2.56 |
| Ion |
Wyckoff site |
x
|
y
|
z
|
Occupancy |
B
eq (Å2) |
| Ba |
4e |
0.497(6) |
0.507(2) |
0.256(9) |
1 |
0.99(6) |
| Lu |
2d |
0.5 |
0. |
0 |
0.667 |
0.65(3) |
| Te |
2c |
0 |
0.5 |
0 |
1 |
0.65(2) |
| O1 |
4e |
0.215(5) |
0.251(4) |
0.008(3) |
1 |
0.85(5) |
| O2 |
4e |
0.200(5) |
0.771(6) |
0.001(7) |
1 |
0.90(5) |
| O3 |
4e |
0.494(3) |
0.016(6) |
0.264(3) |
1 |
0.82(5) |
In this system, Ba2+ and O2− occupy the Wyckoff position 4e, R3+ and Te6+ occupy the Wyckoff positions 2d and 2c respectively. Occupancy is fixed at unity except for R3+ which has only 2/3rd occupancy of the atomic site. The satisfactory R factors, Rwp, RP, Rexp and goodness of fit confirm the P21/n space group of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). Selected bond distances of Ba2Gd2/3TeO6 and Ba2Lu2/3TeO6 are shown in Table 3 and bond distances of Ba2R2/3TeO6 (R = Y, Tb, Dy, Ho, Er, Tm, Yb) are shown in Table S25 (ESI†). The expected reduction of bond distances with lanthanide contraction of B-site cations, is an indication of the magnitude of distortion. The average Gd–O and Te–O bond lengths of Ba2Gd2/3TeO6 are less than the previously reported Eu–O and Te–O bond lengths of Ba2Eu2/3TeO6. Octahedra get tilted in order to accommodate the changes caused by the smaller ions and the average bond angle shifts from 167° for Gd–O–Te to 170° for Lu–O–Te from 165° for Eu–O–Te denotes minimization in distortion with lanthanide contraction of B-site cations.
Table 3 Selected bond distances of Ba2Gd2/3TeO6 and Ba2Lu2/3TeO6
| Bond |
Bond length (Å) |
Bond |
Bond length (Å) |
| Gd–O1 |
2.272 |
Lu–O1 |
2.239 |
| Gd–O2 |
2.248 |
Lu–O2 |
2.239 |
| Gd–O3 |
2.249 |
Lu–O3 |
2.205 |
| Te–O1 |
1.971 |
Te–O1 |
1.941 |
| Te–O2 |
2.018 |
Te–O2 |
1.991 |
| Te–O3 |
2.008 |
Te–O3 |
1.967 |
Diffuse reflectance spectra of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu)
The optical band gaps of all the synthesized compounds are determined using diffuse reflectance spectroscopy (DRS) in order to discover their potential to act as host materials for luminescence centers. The band gaps are determined using the Kubelka–Munk method for direct band transition using the expression50| | | [F(R∞)hν]2 ∝ (hν − Eg) | (2) |
where F(R∞) is the Kubelka–Munk function, hν is the energy in eV and Eg is the optical band gap. Similar to Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu), all the compounds exhibit a direct band transition. Fig. 6 shows the diffuse reflectance spectra (Kubelka–Munk method) of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). The obtained band gaps are shown in the inset to Fig. 6 and the values remain almost constant. In Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu), the hybridization of Ba2+ 5p, R3+ 4f, Te6+ 4d and O2− 2p states contribute to the formation of valence and conduction bands. In all these compounds, only the B-site cations, i.e. the rare earth ions, vary and their empty 4f orbitals are involved in bonding. In addition, the band gap energies (Eg) of covalent solids are related to the electronegativity difference between the elements. Across a period, the electronegativity increases, which in turn increases the orbital overlap, resulting in larger band gaps, as in the case of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu).51
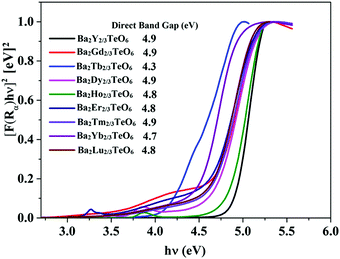 |
| | Fig. 6 DRS of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). The inset shows the band gaps of Ba2R2/3TeO6. | |
Photoluminescence spectra of Ba2Y2/3TeO6:x%Eu3+ (x = 2.5, 5, 7.5 10, 12.5, 15, 17.5 and 20)
In order to further analyze the optical properties of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu), Eu3+ ions are substituted in the B-site of Ba2Y2/3TeO6 for eight different concentrations in accordance with the stoichiometry Ba2Y2/3−xEuxTeO6 (x = 0.025, 0.05, 0.075, 0.1, 0.125, 0.15, 0.175 and 0.2). Their XRD patterns do not show the presence of any additional phases and the combined graph is shown in Fig. S26 (ESI†). Eu3+ ions are substituted at the B-site of the host lattice i.e., the Y3+ site. The ionic radius of Y3+ in six coordination is 0.9 Å and that of Eu3+ in six coordination is 0.947 Å. This means Eu3+ ions replace Y3+ ions with smaller ionic radii and hence there is a possibility of unit cell expansion with Eu3+ concentration. The leftward shift of monoclinic 112 reflection around 2θ ≈ 30° indicates the enhancement in cell volume with the addition of Eu3+ ions. The shift in XRD peaks is depicted in Fig. S27 (ESI†) and a table of lattice parameters is shown in Table S28 (ESI†). Rietveld refinement of the XRD pattern of Ba2Y2/3TeO6:10% Eu3+ with optimal concentration fitted using the monoclinic (P21/n) space group is shown in Fig. 7 and the refinement parameters are given in Table S29 (ESI†). In order to confirm the occupancy of activator ions in the Y3+ site and check the possibility of the crystallographic site swapping to the Ba2+ site, Eu3+ ions are distributed at different occupancies in both A- and B-sites in accordance with their stoichiometry, which results in poor refinement parameters. However, it is reported that such swapping cannot be detected directly from XRD at lower concentrations; only the Rietveld refinement of XRD patterns of higher concentrations will give a feasible result.52 On the other hand, the relative intensity of electric and magnetic dipole transitions obtained from photoluminescence spectroscopy is a probe to detect any crystallographic off-centering of the Eu3+ ions.
The EDS of Ba2Y2/3TeO6:10%Eu3+ have an elemental composition of Ba, Te, O, and the rare earths Y and Eu. The elemental mapping shown in Fig. S30 (ESI†) exhibits a uniform distribution of elements in the phosphor. Table S8 (ESI†) gives the atomic percentage of elements obtained from EDS. DRS of Ba2Y2/3TeO6:x%Eu3+ (x = 5, 10, 15 mol%) and their Kubelka–Munk plots for finding the optical band gap are shown in Fig. S31(a) and (b) (ESI†). The reflectance spectra present absorption peaks at 394 nm and 464 nm corresponding to the characteristic f–f transitions of the Eu3+ ions. As the Eu3+ concentration increases, the band gap reduces from 4.9 eV of the host Ba2Y2/3TeO6 to 4.3 eV of Ba2Y2/3TeO6:15%Eu3+ possibly due to the rise in density of the 4f band gap states within the forbidden band with Eu3+ content.
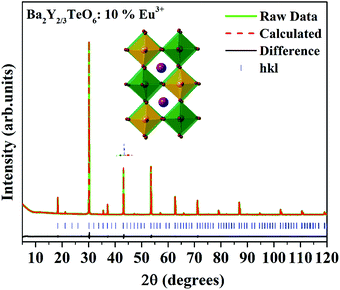 |
| | Fig. 7 The Rietveld refinement of the XRD pattern of Ba2Y2/3TeO6:10%Eu3+. The inset shows the crystal structure of Ba2Y2/3TeO6. | |
The band gap energy of 4.9 eV of Ba2Y2/3TeO6 which corresponds to the wavelength of absorption in the UV region suggests the ability of this material to act as a host material for luminescent centres. Fig. 8a and b show the photoluminescence excitation (PLE) spectra of Ba2Y2/3TeO6:Eu3+ and the emission spectra (PL) of Ba2Y2/3TeO6:x% Eu3+ (x = 2.5, 5, 7.5 10, 12.5, 15, 17.5 and 20). The photoluminescence excitation spectrum monitored at 592 nm presents a broad band ranging from 230 to 340 nm attributed to the charge transfer states of EuO6 groups and the narrow peaks at 362, 382, 394 and 464 nm can be assigned to 7F0–5D4, 7F0–5G2,3, 7F0–5L6 and 7F0–5D2 transitions, respectively, which correspond to the characteristic f–f electronic transitions in the Eu3+ ions. The luminescence spectra present emissions at 592 (5D0–7F1), 610 (5D0–7F2), 635 (5D0–7F3) and 710 (5D0–7F4) nm in which the magnetic dipole transition (5D0–7F1) is the most intense. The emission spectrum with high spectral resolution in the 570–590 nm spectral region is also shown in Fig. S32 (ESI†). The peak at 582 nm corresponds to the 5D0–7F0 transition of the Eu3+ ions. The energy level diagram of Ba2Y2/3TeO6:Eu3+ is shown in Fig. S33 (ESI†). When excited at 276 nm, ligand-to-metal charge transition occurs from the O2− 2p orbitals from the valence band to the empty 4f orbitals of Eu3+. The absorbed energy is transferred to Eu3+ ions and the electrons from the highest energy levels relaxes non-radiatively to the 5D0 state. From there, electrons further transit to 7FJ ground levels giving visible emission. It can be seen that the photoluminescence emission intensity increases with Eu3+ ions concentration but decreases when Eu3+ concentration reaches 12.5 mol%. As the doping concentration increases, the electric multipolar interactions between Eu3+ causes energy migration among them. This non-radiative energy transfer among the activator ions increases with doping concentration and correspondingly the emission intensity decreases. The critical distance (Rc) of energy transfer among the activator ions can be determined using the equation:53
| |  | (3) |
where
V is the volume of the unit cell,
xc is the concentration of the activator ions beyond which quenching happens and
N is the number of Y
3+ ions in the unit cell. Substituting the values for
V,
N and
xc as 295 Å
3, 6 and 0.1 respectively, the critical distance is estimated to be 9.79 Å. The value of
Rc greater than 4 Å implies electric multipolar interaction among the activator ions. Based on Dexter’s theory, if the interaction among the activator ions is multipolar, then it can be quantitatively explained using the equation
54| | 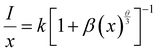 | (4) |
where
I is the luminescence intensity,
x is the activator ion concentration after quenching,
k and
β are constants for the different types of interactions for the same system and
θ represents the type of interaction between the activator ions. The value of
θ = 3, 6, 8 and 10 imply exchange interaction, electric dipole–dipole (D–D), electric dipole–quadrupole (D–Q) and electric quadrupole–quadrupole (Q–Q) interactions respectively. Ba
2Y
2/3TeO:
x% Eu
3+ (
x = 10, 12.5, 15, 17.5 and 20) phosphors are selected and Fig. S34 (ESI
†) represents the plots of ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x vs.
x vs. ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
(
I/
x) at different emissions of 592, 610 and 635 nm. The slopes of linear fittings of the plots are −
θ/3 and they are −1.65 (592 nm), −1.65 (610 nm) and −1.51 (635 nm). Hence
θ can be estimated to be 4.95 for 592 and 610 nm and 4.53 for 635 nm. The
θ values are close to 6 and thus the type of interaction among the activator ions is electric dipole–dipole in nature.
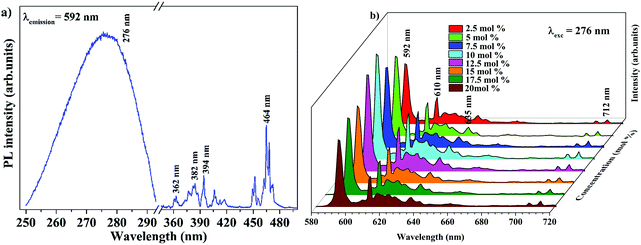 |
| | Fig. 8 (a) PLE of Ba2Y2/3TeO6:10%Eu3+ and (b) PL emission spectra of Ba2Y2/3TeO6:x%Eu3+ (x = 2.5, 5, 7.5 10, 12.5, 15, 17.5, and 20). | |
The relative intensity of the electric (610 nm) and magnetic (592 nm) dipole transition is a strong probe to determine the site symmetry of activator ions. Thus, hypersensitivity or the strong influence of the ligand field on the activator ions and hence on the emission intensity gives an idea about the site symmetry in which the ions remain. The dominant magnetic dipole transition in the PL spectra indicates that Eu3+ ions occupy a site with an inversion center or B-site. However, the emission at 610 nm denotes the occupancy of some of the Eu3+ ions in a non-center of symmetric environment or A-site of the lattice. Further, to investigate the photoluminescence properties of A-site substituted Ba2Y2/3TeO6, two different concentrations, a concentration lower than optimal concentration (5 mol%) and optimal concentration (10 mol%) for B-site substituted Ba2Y2/3TeO6:Eu3+, are substituted in the A-site of the lattice. The combined XRD patterns of A-site substituted Ba2Y2/3TeO6 are shown in Fig. S35 (ESI†). The XRD patterns show an indistinct additional impurity phase around 2θ ≈ 30°. Interestingly the same luminescence spectrum is observed with more intense magnetic transitions as well as electric dipole transitions. The fluorescence intensity ratio between the electric (5D0–7F2) and magnetic dipole (5D0–7F1) transitions defined as the asymmetry ratio, is a measure of the distortion of Eu3+ ions from the symmetric environment of the host matrix. We expected a slightly larger asymmetry ratios for A-site substituted Ba2Y2/3TeO6:Eu3+, since in that case the probability of occurrence of electric dipole transitions is greater. Here the asymmetry ratio for Ba1.85Y2/3Eu0.1TeO6, Ba1.925Y2/3Eu0.05TeO6, Ba2Y0.567Eu0.1TeO6 and Ba2Y0.517Eu0.05TeO6 are obtained as 0.46, which implies Eu3+ ions prefer to occupy B-site rather than A-site even if the substitution is done on the A-site. This is in contradiction to the photoluminescence behavior of other double perovskites, which show a dominant electric dipole transition when the Eu3+ ions are substituted in an asymmetric site. Fig. 9 shows a comparison of PL spectra of A- and B-site substituted Ba2Y2/3TeO6:Eu3+. Raman spectra of A- and B-site substituted Ba2Y2/3TeO6:Eu3+ are shown in Fig. S36 (ESI†). The Raman spectrum does not exhibit any considerable changes in the low-energy lattice modes when Eu3+ is substituted in the A-site, which further confirms the above result.
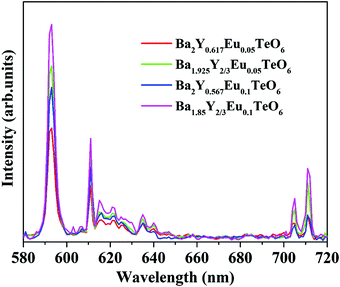 |
| | Fig. 9 A comparison of the PL spectra of A- and B-site substituted Ba2Y2/3TeO6:Eu3+. | |
Temperature-dependent photoluminescence
Temperature-dependent photoluminescence spectra of Ba2Y2/3TeO6:10%Eu3+ in the range 80–500 K are shown in Fig. 10a. Below 300 K, the emission intensity almost maintains a steady value with no remarkable variation. However, above 300 K, the intensity of photoluminescence shows an appreciable change with rise in temperature. It is essential to probe the thermal stability of phosphors above room temperature, because temperature can influence the color stability and emission intensity, which is a major concern during fabrication of LEDs since they usually work above room temperature.
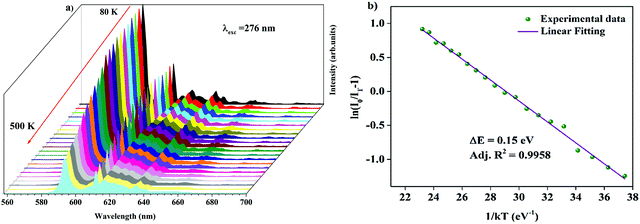 |
| | Fig. 10 (a) Temperature-dependent photoluminescence spectra of Ba2Y2/3TeO6:10%Eu3+. (b) The Arrhenius plot of the temperature dependence in the range of 300–500 K of the PL emission intensity of Ba2Y2/3TeO6:10%Eu3+. | |
At 480 K, the maximum intensity reaches 41% of the emission intensity at room temperature. Thermal quenching is attained at 400 K and the effect can be better understood by determining the thermal activation energy. The thermal activation energy, ΔE is determined from the Arrhenius equation
| | 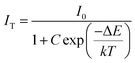 | (5) |
where
I0 is the original intensity,
IT is the intensity at a temperature
T,
C is a constant,
k is the Boltzmann constant (8.617 × 10
−5 eV K
−1) and Δ
E is the activation energy. A plot of 1/
kT vs. ln(
I0/
IT − 1) is given in
Fig. 10b and the activation energy, Δ
E is obtained as 0.15 eV. The exact mechanism of thermal quenching is given in Fig. S37 (ESI
†). Thermal activation energy is defined as the energy required by the electrons to cross the
5D
0 excited state to the Eu–O CTS and a larger value of Δ
E indicates good thermal stability of the phosphor. A lower activation energy indicates faster degradation of emission intensity of the phosphor. Generally, as temperature increases, phonon-assisted non-radiative transitions become significant and will suppress the luminescence intensity. However, in case of tellurate glasses, the phonon energy is very low, in the range of 800–900 cm
−1, which suggests that Eu
3+ in tellurate host materials are less affected by phonon-assisted non-radiative transitions.
55 Hence, we expect Ba
2Y
2/3TeO
6 activated with Eu
3+ ions to exhibit exceptional photoluminescence behaviour and to be a potential candidate for solid-state lighting device applications. Even though its spectral characteristics are good enough for LED applications, unlike other tellurate phosphors, its thermal activation energy is slightly low. Thermal activation energies of various double perovskite tellurates are shown in
Table 4.
Table 4 An overview of the activation energies and quantum yields of tellurate double perovskite phosphors and commercial red phosphors
| Red phosphor |
Activation energy (eV) |
Quantum yield (%) |
Ref. |
| Sr2Si5N8:Eu2+ |
0.42 |
80 |
56
|
| Y2O3:Eu3+ |
— |
9.6 |
57
|
| Y2O2S:Eu3+ |
— |
4.2 |
58
|
| LiSrBiTeO6:Eu3+ |
0.29 |
— |
28
|
| Sr2MgTeO6:Eu3+ |
0.27 |
— |
29
|
| NaMgGdTeO6:Mn4+ |
0.25 |
41.19 |
30
|
| NaMgLaTeO6:Mn4+ |
0.25 |
57 |
31
|
| NaLaCaTeO6:Mn4+ |
0.179 |
92.2 |
32
|
| Sr2MgTeO6:Sm3+ |
0.34 |
— |
33
|
| LiLaMgTeO6:Mn4+ |
0.46 |
— |
34
|
| Ba2Y2/3TeO6:Eu3+ |
0.15 |
24 |
This work |
Temperature-dependent Raman spectra of Ba2Y2/3TeO6:10%Eu3+
In order to analyze the dependence of thermal quenching of Eu3+ ions on the structural changes in the host matrix, the temperature-dependent Raman spectra of Ba2Y2/3TeO6:10% Eu3+ are recorded in a temperature range of 93 K to 873 K. The spectral profile of the Raman spectra of phosphor show no evidence for phase transitions above or below room temperature. Fig. S38 (ESI†) shows the temperature-dependent Raman spectra of Ba2Y2/3TeO6:10% Eu3+. The Raman bands around 730–820 cm−1 above room temperature corresponding to the symmetric stretching vibrations of the B-site octahedral cations are shown in Fig. S39 (ESI†). The band near 770 cm−1 at room temperature undergoes a red shift and broadens at elevated temperature, which implies that more vibrations occur even at low energies. The distortion of a B-site octahedra as well as tilting get enhanced at higher temperatures. Hence, distortions also affect the B-site Eu3+ ions, which further results in faster degradation of the Eu3+ emission due to the thermally stimulated non-radiative energy transfer from Eu3+ to the distortion defects.59 In brief, the peak broadening and red shift above room temperature occur due to the temperature effects. The peak position as well as FWHM values are plotted in Fig. 11.
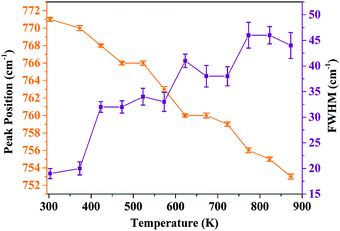 |
| | Fig. 11 Peak position and FWHM (cm−1) of the symmetric stretching vibrations of the B-site octahedron above room temperature (peak around 770 cm−1 at room temperature). | |
Temperature-dependent PL decay curves
The temperature-dependent PL lifetime decay curves in the range 80–500 K are obtained by exciting the phosphor Ba2Y2/3TeO6:10%Eu3+ using 276 nm with λem = 592 nm. Fig. 12a and b show the low-temperature and high-temperature behavior of the decay curves, respectively. The decay curves are well fitted using a double exponential function given by| | I(t) = A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2 exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) + I0 exp(−t/τ2) + I0 | (6) |
where I0 is the emission intensity at time t = 0 ms and I(t) is the intensity at t = t ms. A1 and A2 are both constants, and τ1 and τ2 are the decay components. The average lifetimes at various temperatures can be determined using the fitting parameters obtained from eqn (6) and substituted in the following equation| | 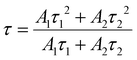 | (7) |
The lifetime falls off from 4.826 ± 0.259 ms at 80 K to 2.906 ± 0.139 ms at 500 K due to the intensification of non-radiative relaxation rate with a rise in temperature, which in turn decreases the decay rate. Usually, the 5D0 measured lifetimes of Eu3+ are dominated by non-radiative relaxation mechanisms, such as multiphonon emission, direct or indirect phonon assisted energy transfer to the impurity traps or crossover to a low-lying ligand to the metal CT state.60 Even though non-radiative relaxations are predominant at low temperatures, their effects become more evident at high temperatures in the form of a rapid decrease in lifetime. Fig. S 40 (ESI†) shows the decay curves of Ba2Y2/3TeO6:x%Eu3+ (x = 5, 10, 12.5, 15 and 20). Lifetimes are estimated as 3.937 ± 0.286, 3.784 ± 0.218, 3.770 ± 0.242, 3.511 ± 0.170 and 2.935 ± 0.066 ms, respectively, for x = 5, 10, 12.5, 15 and 20 mol%. The lifetime is found to decrease with concentration, due to the faster decay rates. The rate of increase of non-radiative transitions among the activator ions allows faster decay and hence a shortening of the lifetime. The room-temperature quantum yield of Ba2Y2/3TeO6:10% Eu3+ is 24%. The quantum yields of different tellurate red phosphors are shown in Table 4. Even though the quantum yield of Ba2Y2/3TeO6:Eu3+ is comparatively lower than that of other tellurates, it is much better than those of commercially available Y3+-based red phosphors used in WLED applications, as shown in Table 4. Chromaticity coordinates obtained as (0.615, 0.384) imply that the phosphor exhibits an orange-red color, as shown in the inset of Fig. 12b. The chromaticity coordinates are close to those of commercial red phosphor Sr2Si5N8:Eu2+ (0.62, 0.37). Correlated color temperature (CCT) is calculated using the McCamy method.61| | | CCT = −449n3 + 3525n2 − 6823.3n + 5520.33 | (8) |
where n = (x − xe)/(y − ye). (x, y) are the chromaticity coordinates and (xe, ye) are (0.3320, 0.1858), the coordinates corresponding to the epicenter of convergence of the isotemperature lines of the CIE 1931 chromaticity diagram. CCT is calculated as 1657 K, which indicates warmer yellow-red light.
 |
| | Fig. 12 (a) Low-temperature and (b) high-temperature decay profiles of Ba2Y2/3TeO6:10%Eu3+. The inset shows the chromaticity diagram of Ba2Y2/3TeO6:10%Eu3+. | |
Optical thermometric properties of Ba2Y2/3TeO6:10%Eu3+
Optical thermometers using various phosphors explore certain parameters of luminescence like the fluorescence intensity ratio (FIR), lifetime, spectral bandwidth, etc. for calculating temperature sensitivity. The intensity ratio, 5D0–7F1/5D0–7F2, and the emission lifetimes of Eu3+ ions in the temperature range 300–500 K are used to probe the sensitivity of the Ba2Y2/3TeO6:10%Eu3+ phosphor. Hou et al.37 proposed a new temperature-sensing formula for evaluating the FIR of Eu3+-doped Ba2TiGe2O8, which is equivalent to the general fluorescence intensity ratio formula FIR = B × exp(−ΔE/kBT). The new FIR is the ratio of 5D0–7F1 and 5D0–7F2 transitions. A plot of temperature vs. FIR is shown in Fig. S41 (ESI†). The relative sensitivity is defined as| | 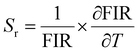 | (9) |
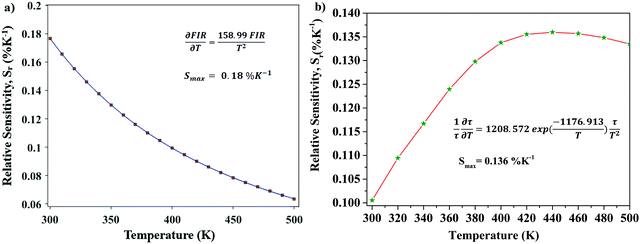
The relative sensitivity of the Ba2Y2/3TeO6:10%Eu3+ phosphor is determined using the TeSen calculator, developed by Kaczmarek et al.62 for determining thermometric parameters in ratiometric optical thermometry. A plot of temperature vs. relative sensitivity obtained from FIR is given in Fig. 13a. The maximum relative sensor sensitivity is 0.18% K−1 at 300 K and it reduces to 0.06% K−1 at 500 K. The dependence of lifetime on temperature can be fitted using the Struck and Fonger model given by63
| | 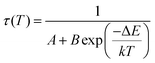 | (10) |
where
τ(
T) is the lifetime at temperature
T,
A is a constant,
B is the frequency factor,
k is the Boltzmann constant and Δ
E is the thermal activation energy. Temperature
vs. lifetime data was plotted and is shown in Fig. S42 (ESI
†). The relative sensitivity,
Sr is therefore given by
| | 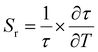 | (11) |
A plot of temperature
vs. relative sensitivity obtained from lifetime is given in
Fig. 13b. The maximum sensitivity is 0.136% K
−1 at 500 K and it reduces to 0.100% K
−1 at 300 K. From a comparison of both results, the temperature sensor sensitivity for FIR is better than the lifetime measurement. A comparison of relative sensitivities of different phosphors is tabulated in
Table 5 and the relative sensitivity of Ba
2Y
2/3TeO
6:10% Eu
3+ indicates the ability of this phosphor to be used for temperature-sensing applications in the range 300–500 K. Thus, Ba
2Y
2/3TeO
6:Eu
3+ phosphor can be used in non-contact optical thermometers.
 |
| | Fig. 13 (a) A plot of temperature vs. relative sensitivity obtained from FIR, and (b) a plot of lifetime vs. relative sensitivity of Ba2Y2/3TeO6:10%Eu3+. | |
Table 5 A comparison of the sensitivity values of various double perovskite phosphors
| Phosphor |
Temperature range (K) |
Relative sensitivity (Sr) % K−1 |
| Ba2Y2/3TeO6:Eu3+ |
303–483 |
0.18 [present work] |
| Ba2La2/3TeO6:Eu3+ |
315–483 |
0.2115 |
| Gd2ZnTiO6:Pr3+ |
293–433 |
1.6745 |
| Y2MgTiO6:Mn4+ |
10–513 |
0.1446 |
| LiLaMgWO6:Er3+ |
303–483 |
2.2447 |
Judd–Ofelt analysis
Further analysis of the site symmetry modifications of Eu3+ ions are investigated by determining the Judd–Ofelt intensity parameters Ωλ (λ = 2, 4).64–69 The Ω2 parameter is an indicator of site asymmetry, whereas the Ω4 parameter is sensitive to macroscopic properties, such as rigidity of the host materials, viscosity and dielectric constant. In this work, the intensity parameters were calculated from the emission spectrum, taking the 5D0–7F1 transition as the reference. The Judd–Ofelt intensity parameters and radiative parameters are presented in Table 6. The low value of the J–O parameter Ω2 suggests that most of the Eu3+ ions occupy a site with inversion symmetry, which is in good agreement with the PL spectrum. In addition, the 5D0–7F1 transition contributes almost 71% of the total radiative transition. The phosphor has a maximum internal quantum efficiency of 42.86%, which suggests the potential application of these phosphors in various technological applications, including WLEDs and optical thermometers. A detailed explanation of the Judd–Ofelt analysis is given in the ESI.†
Table 6 Judd–Ofelt intensity parameters and radiative parameters obtained from the emission spectrum and lifetime data
|
Judd–Ofelt intensity parameters
|
|
Ω
2 (×10−20 cm2) |
0.26 ± 10−4 |
|
Ω
4 (×10−20 cm2) |
0.04 ± 10−4 |
|
|
|
Radiative parameters
|
| Radiative transition rate, AR (s−1) |
113.28 ± 6.52 |
| Non-radiative transition rate, ANR (s−1) |
150.98 ± 8.69 |
| Total transition rate, AT (s−1) |
264.27 ± 15.22 |
| Measured lifetime, τobs (ms) |
3.784 ± 0.218 |
| Calculated radiative lifetime, τrad (ms) |
8.82 ± 0.51 |
| Quantum efficiency, η (%) |
42.86 ± 0.72 |
| Branching ratio of 5D0–7F1 transition, β01 (%) |
71.58 ± 4.89 |
| Branching ratio of 5D0–7F2 transition, β02 (%) |
17.38 ± 4.89 |
| Branching ratio of 5D0–7F4 transition, β04 (%) |
11.03 ± 4.89 |
Conclusions
In summary, Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) were synthesized via a solid-state ceramic route, and their crystal structures and optical properties were investigated for the first time. Even though we expected a structural transition from monoclinic to cubic when the B-site ions varied from Gd3+ to Lu3+, Raman and IR spectra presented more than four modes which contradicts our assumption. The Raman spectra were deconvoluted using the Lorentzian function and the space group was identified as P21/n, which was further confirmed by the Rietveld refinement of the XRD patterns. The optical band gaps suggested that the compounds can act as host materials for luminescence centers, and their photoluminescence properties were broadly investigated via substituting Eu3+ in the B-site of Ba2Y2/3TeO6. The luminescence spectra implied the presence of Eu3+ ions at both A- and B-sites but they were mostly present at the B-sites. Eu3+ ions substituted at the A-site of Ba2Y2/3TeO6 exhibited similar PL spectra with an asymmetry ratio almost equal to that of B-site-substituted Ba2Y2/3TeO6. The thermal activation energy and the color parameters indicated the potential application of the phosphor in the field of solid-state lighting. Temperature-dependent Raman spectra of the phosphor with an optimal concentration suggested the dependence of structural distortions at elevated temperatures on thermal quenching. The lifetime decreases from 4.826 ± 0.259 ms at 80 K to 2.906 ± 0.139 ms at 500 K due to the intensification of non-radiative relaxation rate with a rise in temperature. Additionally, the phosphor shows a relative temperature sensitivity of 0.18% K−1 at 300 K for FIR measurements, which is better than for lifetime measurements, and hence it could also find applications in ratiometric optical temperature sensing. The PL spectrum and J–O parameters together suggest the occupation of symmetric B-sites by the majority of Eu3+ ions in the host lattice. In brief, Ba2Y2/3TeO6:Eu3+ is the first double perovskite phosphor with defects that shows distinct photoluminescence behavior as well as temperature-sensing potential. The substitution of Eu3+ ions as well other rare-earth ions into Ba2R2/3TeO6 (R = Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) double perovskites might provide better photoluminescence properties.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
SCL is grateful for a DST-INSPIRE fellowship. The authors acknowledge DST SERB for financial support (YSS/000868/2014). The authors also acknowledge CLIF, University of Kerala, and Department of Optoelectronics, University of Kerala, for their experimental support.
References
- S. Vasala and M. Karppinen, Prog. Solid State Chem., 2015, 43, 1–36 CrossRef CAS.
- C. Moure and O. Pena, Prog. Solid State Chem., 2015, 43, 123–148 CrossRef CAS.
- M. T. Anderson, K. B. Greenwood, G. A. Taylor and K. R. Poeppelmeier, Prog. Solid State Chem., 1993, 22, 197–233 CrossRef CAS.
- M. C. Knapp and P. M. Woodward, J. Solid State Chem., 2006, 179, 1076–1085 CrossRef CAS.
- J.-H. Park and P. M. Woodward, Int. J. Inorg. Mater., 2000, 2, 153–166 CrossRef CAS.
- A. Dias, G. Subodh, M. T. Sebastian, M. M. Lage and R. L. Moreira, Chem. Mater., 2008, 20, 4347–4355 CrossRef CAS.
- N. Panda, B. N. Parida, R. Padhee and R. N. P. Choudhary, J. Electron. Mater., 2015, 44, 4275–4282 CrossRef CAS.
- E. S. Madruga, Y. Sun, A. M. Arevalo-Lopez and J. P. Attfield, Chem. Commun., 2019, 55, 2605–2608 RSC.
- R. Yu, A. Fan, T. Li, M. Yuan and J. Wang, Mater. Chem. Phys., 2017, 196, 75–81 CrossRef CAS.
- K. N. Nandha and A. Nag, Chem. Commun., 2018, 54, 5205–5208 RSC.
- R. J. Cava, B. Batlogg, J. J. Krajewski, R. Farrow, L. W. Rupp, A. E. White, K. Short, W. F. Peck and T. Kometani, Nature, 1988, 332, 814–816 CrossRef CAS.
- J. Su, Z. Yang, X. Lu, J. Zhang, L. Gu, C. Lu, Q. Li, J. Liu and J. Zhu, ACS Appl. Mater. Interfaces, 2015, 7, 13260–13265 CrossRef CAS PubMed.
- C. Artinini, J. Eur. Ceram. Soc., 2016, 37, 1–14 Search PubMed.
- T. Kong and R. J. Cava, Mater. Res. Express, 2017, 4, 106101 CrossRef.
- S. C. Lal, V. Lalan and G. Subodh, Inorg. Chem., 2018, 57, 6226–6236 CrossRef CAS PubMed.
- C. Feldmann, T. Jüstel, C. R. Ronda and P. J. Schmidt, Adv. Funct. Mater., 2003, 13, 511–516 CrossRef CAS.
- M. Shang, C. Li and J. Lin, Chem. Soc. Rev., 2014, 43, 1372–1386 RSC.
- J. Meyer and F. Tappe, Adv. Opt. Mater., 2015, 3, 424–430 CrossRef CAS.
- P. Pust, P. J. Schmidt and W. Schnick, Nat. Mater., 2015, 14, 454–458 CrossRef CAS PubMed.
- S. Li, X. Wei, K. Deng, X. Tian, Y. Qin, Y. Chen and M. Yin, Curr. Appl. Phys., 2013, 13, 1288–1291 CrossRef.
- L. Li, W. Chang, W. Chen, Z. Feng, C. Zhao, P. Jiang, Y. Wang, X. Zhou and A. Suchocki, Ceram. Int., 2017, 43, 2720–2729 CrossRef CAS.
- S. Wang, Q. Sun, B. Devakumar, J. Liang, L. Sun and X. Huang, J. Alloys Compd., 2019, 804, 93–99 CrossRef CAS.
- Q. Sun, S. Wang, B. Devakumar, L. Sun, J. Liang, T. Sakthivel, S. J. Dhoble and X. Huang, J. Alloys Compd., 2019, 804, 230–236 CrossRef CAS.
- Z. Zhang, L. Sun, B. Devakumar, G. Annadurai, J. Liang, S. Wang, Q. Sun and X. Huang, J. Lumin., 2020, 222, 117173 CrossRef CAS.
- X. Huang, Q. Sun and B. Devakumar, J. Lumin., 2020, 225, 117373 CrossRef CAS.
- J. Liang, B. Devakumar, L. Sun, G. Annadurai, S. Wang, Q. Sun and X. Huang, J. Lumin., 2019, 214, 116605 CrossRef CAS.
- Z. Zhang, L. Sun, B. Devakumar, J. Liang, S. Wang, Q. Sun, S. J. Dhoble and X. Huang, J. Lumin., 2020, 221, 117105 CrossRef CAS.
- J. He, Z. Gao, S. Liu, J. H. Jeong, R. Yu and B. Deng, J. Lumin., 2018, 202, 7–12 CrossRef CAS.
- J. Liang, S. Zhao, X. Yuan and Z. Li, Opt. Laser Technol., 2018, 101, 451–456 CrossRef CAS.
- K. Li, H. Lian and R. V. Deun, J. Lumin., 2018, 198, 155–162 CrossRef CAS.
- K. Li, H. Lian, R. V. Deun and M. G. Brik, Dyes Pigm., 2019, 162, 214–221 CrossRef CAS.
- K. Li and R. V. Deun, Chem. Commun., 2019, 55, 10697–10700 RSC.
- L. Zhao, P. Xu, F. Fan, J. Yu, Y. Shang, Y. Li, L. Huang and R. Yu, J. Lumin., 2019, 207, 520–525 CrossRef CAS.
- L. Li, G. Tian, W. Chang, Y. Yan, F. Ling, S. Jiang, G. Xiang and X. Zhou, J. Alloys Compd., 2020, 832, 154905 CrossRef CAS.
- Y. Ren, R. Cao, T. Chen, L. Su, X. Cheng, T. Chen, S. Guo and X. Yu, J. Lumin., 2019, 209, 1–7 CrossRef CAS.
- X. Wang, Q. Liu, Y. Bu, C.-S. Liu, T. Liu and X. Yan, RSC Adv., 2015, 5, 86219–86236 RSC.
- B. Hou, M. Jia, P. Li, G. Liu, Z. Sun and Z. Fu, Inorg. Chem., 2019, 58, 7939–7946 CrossRef PubMed.
- S. C. Lal, A. Rajan and G. Subodh, Mater. Today: Proc., 2017, 4, 4396–4402 Search PubMed.
- R. Yu, C. Wang, J. Chen, Y. Wu, H. Li and H. Ma, ECS J. Solid State Sci. Technol., 2014, 3, 33–37 CrossRef.
- D. Gu, K. Du, L. Qin and H. J. Seo, Mater. Lett., 2016, 177, 64–67 CrossRef CAS.
- Y. Yang, L. Wang, P. Huang, Q. Shi, Y. Tian and C. Cui, Polyhedron, 2014, 129, 65–70 CrossRef.
- W. Xie, Y. W. Mo, C. W. Zou, F. W. Kang and G. H. Sun, Inorg. Chem. Front., 2018, 5, 1076–1084 RSC.
- J. Luo, M. Hu, G. Niu and J. Tang, ACS Appl. Mater. Interfaces, 2019, 11, 31575–31584 CrossRef CAS PubMed.
- G. Zhou, X. Jiang, J. Zhao, M. S. Molokeev, Z. Lin, Q. Liu and Z. Xia, ACS Appl. Mater. Interfaces, 2018, 10, 24648–24655 CrossRef CAS PubMed.
- Y. Gao, Y. Cheng, T. Hu, Z. Ji, H. Lin, J. Xu and Y. Wang, J. Mater. Chem. C, 2018, 6, 11178–11183 RSC.
- P. Cai, L. Qin, C. Chen, J. Wang, S. Bi, S.-I. Kim, Y. Huang and H. J. Seo, Inorg. Chem., 2018, 57, 3073–3081 CrossRef CAS PubMed.
- W. Ran, H. M. Noh, S. H. Park, B. R. Lu, J. H. Kim, J. H. Jeong, J. Shi and G. Liu, RSC Adv., 2019, 9, 7189–7195 RSC.
- A. K. Azad, S. Ivanov, S. G. Eriksson, H. Rundlof, J. Eriksen, R. Mathieu and P. Svedlindh, J. Magn. Magn. Mater., 2001, 237, 124–134 CrossRef CAS.
- A. K. Azad, S. G. Eriksson, S. A. Ivanov, R. Mathieu, P. Svedlindh, J. Eriksen and H. Rundlof, J. Alloys Compd., 2004, 364, 77–82 CrossRef CAS.
- A. E. Morales, E. S. Mora and U. Pal, Rev. Mex. Fis. S, 2007, 53, 18–22 CAS.
-
P. A. Cox, Instant notes in Inorganic Chemistry, Taylor & Francis, London, 2nd edn, 2004, ch. D7, pp. 125–126 Search PubMed.
- R. Phatak, S. K. Gupta, K. Krishnan, S. K. Sali, S. V. Godbole and A. Das, Dalton Trans., 2014, 43, 3306–3312 RSC.
- G. Blasse, Philips Res. Rep., 1969, 24, 131–144 CAS.
- L. G. Van Uitert and L. F. Johnson, J. Chem. Phys., 1966, 44, 3514–3522 CrossRef CAS.
- H. Cankaya and A. Sennaroglu, Appl. Phys. B: Lasers Opt., 2010, 99, 121–125 CrossRef CAS.
- R.-J. Xie, N. Hirosaki, T. Suehiro, F.-F. Xu and M. Mitomo, Chem. Mater., 2006, 18, 5578–5583 CrossRef CAS.
- S. Som, S. Das, S. Dutta, H. G. Visser, M. K. Pandey, P. Kumar, R. K. Dubey and S. K. Sharma, RSC Adv., 2015, 5, 70887–70898 RSC.
- S. Som, P. Mitra, V. Kumar, V. Kumar, J. Terblans, H. C. Swart and S. K. Sharma, Dalton Trans., 2014, 43, 9860–9871 RSC.
- C. Wang, S. Ye and Q. Zhang, Opt. Mater., 2015, 75, 337–346 CrossRef.
- M. T. Berry, P. S. May and H. Xu, J. Phys. Chem., 1996, 100, 9216–9222 CrossRef CAS.
- C. S. McCamy, Color Res. Appl., 1991, 17, 142–144 CrossRef.
- A. M. Kaczmarek, R. V. Deun and M. K. Kaczmarek, Sens. Actuators, B, 2018, 273, 696–702 CrossRef CAS.
- J. Zhou, R. Lei, H. Wang, Y. Hua, D. Li, Q. Yang, D. Deng and S. Xu, Nanophotonics, 2019, 8, 2347–2358 CAS.
- W. F. Krupke, Phys. Rev., 1966, 145, 325–337 CrossRef CAS.
- B. R. Judd, Phys. Rev., 1962, 127, 750–761 CrossRef CAS.
- G. S. Ofelt, J. Chem. Phys., 1962, 37, 511–520 CrossRef CAS.
- M. P. Hehlen, M. G. Brik and K. W. Kramer, J. Lumin., 2013, 136, 221–239 CrossRef CAS.
-
B. M. Walsh, Advances in Spectroscopy for Lasers and Sensing conference proceedings, 2005, ch. 21, pp. 403–433 Search PubMed.
- J. D. L. Dutra, T. D. Bispo and R. O. Freire, J. Comput. Chem., 2014, 35, 772–775 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00471e |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rock salt ordering, where B and B′ cations alternate in all three dimensions. The possibility of different cations at the B-site allows novel combinations of elements, including transition metals, lanthanides, actinides and some main group elements. The cation substitution may cause structural alterations, which result in symmetry changes from aristotype cubic (Fm
1 rock salt ordering, where B and B′ cations alternate in all three dimensions. The possibility of different cations at the B-site allows novel combinations of elements, including transition metals, lanthanides, actinides and some main group elements. The cation substitution may cause structural alterations, which result in symmetry changes from aristotype cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to hettotypes such as tetragonal (I4/m), rhombohedral (R
m) to hettotypes such as tetragonal (I4/m), rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) or monoclinic (P21/n or I2/m). Moreover, the B-site ordered double perovskites exhibit interesting magnetic, optical, and dielectric as well as superconducting properties.5–11
) or monoclinic (P21/n or I2/m). Moreover, the B-site ordered double perovskites exhibit interesting magnetic, optical, and dielectric as well as superconducting properties.5–11
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rocksalt ordering of these compounds. The splitting of reflections at 440 planes in Ba2Lu2/3TeO6 and Ba2Gd2/3TeO6 shown in Fig. 1b and c points to the existence of a possible octahedral distortion and hence a lower symmetry instead of the aristotype cubic (Fm
1 rocksalt ordering of these compounds. The splitting of reflections at 440 planes in Ba2Lu2/3TeO6 and Ba2Gd2/3TeO6 shown in Fig. 1b and c points to the existence of a possible octahedral distortion and hence a lower symmetry instead of the aristotype cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure. Another parameter that defines the extent of distortion is the tolerance factor, which is equal to one for an ideal cubic structure and is less than/greater than unity for lower symmetries. A tolerance factor that deviates from unity also suggests the structural variation of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) from cubic (Fm
m) structure. Another parameter that defines the extent of distortion is the tolerance factor, which is equal to one for an ideal cubic structure and is less than/greater than unity for lower symmetries. A tolerance factor that deviates from unity also suggests the structural variation of Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) from cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure. The tolerance factor is determined by considering the effective size of vacancies the same as that of the B-site cations (R3+) and varies from 0.9904 to 1.0085 when the B-site is substituted with Gd3+ to Lu3+. This implies a cubic symmetry for these double perovskites since the tolerance factor lies within the limits defined for a cubic structure. In addition to this, our earlier report suggests some evidence for an increase in symmetry when going from La3+ to Eu3+ in the B-site of Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm, Eu). The tolerance factors are given in Table S3 (ESI†). Interestingly, the tolerance factor exceeds as well as falls short of unity, when the B-site is occupied by R3+ ions (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). However, these striking values of the tolerance factor may be due to the assumption of taking the effective size of vacancies (concentration ≈33%) and lanthanide ions to be the same. There is a possibility that the effective size of vacancies gets larger along with lanthanide contraction and hence compensates for the reduction in ionic size, which is the reason for obtaining a tolerance factor greater than one. Nonetheless, the tolerance factor is only a rough estimate since it varies in accordance with the value of ionic radii taken for determining it and in this case the tolerance factor suggests the possibility of a structural transition to cubic when Ba2R2/3TeO6 is substituted from Gd3+ to Lu3+. In summary, we are expecting a symmetry change from XRD analysis which could be more easily identifiable from vibrational spectroscopic techniques such Raman and IR spectroscopy.
m) structure. The tolerance factor is determined by considering the effective size of vacancies the same as that of the B-site cations (R3+) and varies from 0.9904 to 1.0085 when the B-site is substituted with Gd3+ to Lu3+. This implies a cubic symmetry for these double perovskites since the tolerance factor lies within the limits defined for a cubic structure. In addition to this, our earlier report suggests some evidence for an increase in symmetry when going from La3+ to Eu3+ in the B-site of Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm, Eu). The tolerance factors are given in Table S3 (ESI†). Interestingly, the tolerance factor exceeds as well as falls short of unity, when the B-site is occupied by R3+ ions (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu). However, these striking values of the tolerance factor may be due to the assumption of taking the effective size of vacancies (concentration ≈33%) and lanthanide ions to be the same. There is a possibility that the effective size of vacancies gets larger along with lanthanide contraction and hence compensates for the reduction in ionic size, which is the reason for obtaining a tolerance factor greater than one. Nonetheless, the tolerance factor is only a rough estimate since it varies in accordance with the value of ionic radii taken for determining it and in this case the tolerance factor suggests the possibility of a structural transition to cubic when Ba2R2/3TeO6 is substituted from Gd3+ to Lu3+. In summary, we are expecting a symmetry change from XRD analysis which could be more easily identifiable from vibrational spectroscopic techniques such Raman and IR spectroscopy.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, four Raman active modes are possible. However, more than four modes are observed in the Raman spectra of Ba2R2/3TeO6 similar to Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu) evidently point to a lower symmetry for these double perovskites. The exact number of modes is determined by deconvoluting the spectra using the Lorentzian function and the bands obtained are assigned in Table 1. The deconvoluted Raman spectra of Ba2Lu2/3TeO6 and Ba2Gd2/3TeO6 are shown in Fig. 3b and c, respectively, and those of Ba2R2/3TeO6 (R = Y, Tb, Dy, Ho, Er, Tm, Yb) are shown in Fig. S9–S15 (ESI†). The total number of Raman modes for all these double perovskites varies from 12 to 15 in the range 100–1000 cm−1 and are lower than previously reported Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu). Eventhough, we expected a gradual decrease in the number of modes with lanthanide contraction of rare earth ions, as shown in Table 1, they do not follow a trend. For example, in Ba2Gd2/3TeO6, the number of Raman modes is 15 and decreases to 12 for Ba2Ho2/3TeO6. Again, for Ba2Y2/3TeO6, the number of modes increases to 15. This might be due to the presence of sparse amount of impurities that could not be identified from the XRD patterns. Though XRD patterns signify the phase purity of all the compounds, Raman spectroscopy is able to find very small traces of impurities which do not even affect the crystallography of these compounds, since this technique is more sensitive than XRD. The addition of impurities lighter or heavier than the host atoms gives rise to new vibrational modes of higher or lower frequencies, respectively, in the Raman and IR spectra.
m symmetry, four Raman active modes are possible. However, more than four modes are observed in the Raman spectra of Ba2R2/3TeO6 similar to Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu) evidently point to a lower symmetry for these double perovskites. The exact number of modes is determined by deconvoluting the spectra using the Lorentzian function and the bands obtained are assigned in Table 1. The deconvoluted Raman spectra of Ba2Lu2/3TeO6 and Ba2Gd2/3TeO6 are shown in Fig. 3b and c, respectively, and those of Ba2R2/3TeO6 (R = Y, Tb, Dy, Ho, Er, Tm, Yb) are shown in Fig. S9–S15 (ESI†). The total number of Raman modes for all these double perovskites varies from 12 to 15 in the range 100–1000 cm−1 and are lower than previously reported Ba2Ln2/3TeO6 (Ln = La, Pr, Nd, Sm and Eu). Eventhough, we expected a gradual decrease in the number of modes with lanthanide contraction of rare earth ions, as shown in Table 1, they do not follow a trend. For example, in Ba2Gd2/3TeO6, the number of Raman modes is 15 and decreases to 12 for Ba2Ho2/3TeO6. Again, for Ba2Y2/3TeO6, the number of modes increases to 15. This might be due to the presence of sparse amount of impurities that could not be identified from the XRD patterns. Though XRD patterns signify the phase purity of all the compounds, Raman spectroscopy is able to find very small traces of impurities which do not even affect the crystallography of these compounds, since this technique is more sensitive than XRD. The addition of impurities lighter or heavier than the host atoms gives rise to new vibrational modes of higher or lower frequencies, respectively, in the Raman and IR spectra.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 B-site ordering combined with octahedral tilting. For Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu), there are more than four modes and hence, among the 12 space groups, the possible symmetries for Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) are P42/n, P4/mnc and I4/m (tetragonal) and C2/c and P21/n (monoclinic). Group theory predicts nine Raman active modes for tetragonal (I4/m) and P42/n has 35 Raman active modes, among which 17 are low-energy lattice modes.
1 B-site ordering combined with octahedral tilting. For Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu), there are more than four modes and hence, among the 12 space groups, the possible symmetries for Ba2R2/3TeO6 (R = Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) are P42/n, P4/mnc and I4/m (tetragonal) and C2/c and P21/n (monoclinic). Group theory predicts nine Raman active modes for tetragonal (I4/m) and P42/n has 35 Raman active modes, among which 17 are low-energy lattice modes.



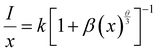
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x vs. ln
x vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (I/x) at different emissions of 592, 610 and 635 nm. The slopes of linear fittings of the plots are −θ/3 and they are −1.65 (592 nm), −1.65 (610 nm) and −1.51 (635 nm). Hence θ can be estimated to be 4.95 for 592 and 610 nm and 4.53 for 635 nm. The θ values are close to 6 and thus the type of interaction among the activator ions is electric dipole–dipole in nature.
(I/x) at different emissions of 592, 610 and 635 nm. The slopes of linear fittings of the plots are −θ/3 and they are −1.65 (592 nm), −1.65 (610 nm) and −1.51 (635 nm). Hence θ can be estimated to be 4.95 for 592 and 610 nm and 4.53 for 635 nm. The θ values are close to 6 and thus the type of interaction among the activator ions is electric dipole–dipole in nature.

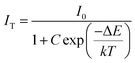

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2
exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) + I0
exp(−t/τ2) + I0