3D magnetically controlled spatiotemporal probing and actuation of collagen networks from a single cell perspective

Abstract

Cells continuously sense and react to mechanical cues from their surrounding matrix, which consists of a fibrous network of biopolymers that influences their fate and behavior. Several powerful methods employing magnetic control have been developed to assess the micromechanical properties within extracellular matrix (ECM) models hosting cells. However, many of these are limited to in-plane sensing and actuation, which does not allow the matrix to be probed within its full 3D context. Moreover, little attention has been given to factors specific to the model ECM systems that can profoundly influence the cells contained there. Here we present methods to spatiotemporally probe and manipulate extracellular matrix networks at the scale relevant to cells using magnetic microprobes (μRods). Our techniques leverage 3D magnetic field generation, physical modeling, and image analysis to examine and apply mechanical stimuli to fibrous collagen matrices. We determined shear moduli ranging between hundreds of Pa to tens of kPa and modeled the effects of proximity to rigid surfaces and local fiber densification. We analyzed the spatial extent and dynamics of matrix deformation produced in response to magnetic torques on the order of 10 pNm, deflecting fibers over an area spanning tens of micrometers. Finally, we demonstrate 3D actuation and pose extraction of fluorescently labelled μRods.

---

Introduction

Mechanical forces are known to influence cell fate and behavior, and are crucial for physiological regulation of the human body during development and homeostasis.^1–4 Residing within tissues, cells perceive the mechanics of their surroundings by sensing imposed stimuli (e.g., compression or tension) and actively probing the extracellular matrix (ECM), the complex biomolecular fiber network that surrounds them.^5–8 Accordingly, efforts have been made in biomedical research to develop 3D cell culture model systems and lab-on-a-chip microfluidic devices that more accurately recapitulate physiologically relevant mechanical features and offer opportunities for targeted mechanical actuation.^9,10

Collagen is a biomolecule frequently employed to create 3D ECM-mimicking environments in vitro. As a major constituent of the native ECM, it provides tensile strength and structural support while offering attachment sites to embedded cells.^6,11 When reconstituted in vitro, it forms a fibrous network that exhibits local heterogeneity, with regions of high fiber density alongside porous cavities reaching several micrometers in diameter.^12,13 It has been suggested that such disordered fibrous networks result in a broad distribution of effective local stiffnesses, implying that neighboring cells embedded in collagen can experience a diverse biomechanical landscape within the same tissue environment.¹⁴ Moreover, within these in vitro models, factors such as proximity to rigid surfaces or local densification of collagen fibers further contribute to the variability of the mechanical environment that cells experience.

Incorporating capabilities for combined mechanical actuation and probing of biomimetic 3D cell culture models requires several considerations: First, the scale dependence of mechanical interaction is particularly relevant for the mechanical properties of collagen hydrogels.^15–19 Second, the sites of measurement and actuation within the hydrogel volume should ideally preserve the 3D context of the surrounding network. This more effectively approximates the perspective of embedded cells than techniques that only probe the surface. Third, the control system should not impede detailed, real time, high resolution observation of the cells and their surrounding matrix. Fourth, the applicable forces and torques should resemble those applied by cells.

Several experimental techniques have been used to assess the mechanical properties of 3D hydrogel networks.^20,21 Macroscale approaches include stretch,²² compression,²³ or shear rheology^24,25 and report bulk continuum properties of interrogated materials, yet fail to resolve local stiffness heterogeneity inherent to fiber networks.¹⁹ On a smaller scale, atomic force microscopy,^26–28 traction force microscopy,²⁹ and both optical³⁰ and magnetic tweezers³¹ have been used to measure mechanical properties of biomaterials with micro- and nanometer resolution. In particular, magnetic tweezers offer unimpeded wireless actuation and sensing capabilities within intact models of 3D ECM networks.^32,33 These efforts have primarily focused on in-plane measurements leveraging magnetic particles, most frequently spherical magnetic beads with dimensions on the scale of a few micrometers. Traits including viscoelasticity,³¹ stiffness,³⁴ anisotropy, and cell-induced forces²⁹ have been assessed with high temporal and spatial resolution. However, assessing influences on mechanical properties specific to reconstituted model ECM systems, along with 3D actuation and sensing, are crucial for understanding the single cell perspective and applying micromechanical stimuli within these matrices.^19,35–37

Here, we adapted techniques originally developed for microscale material characterization to probe, manipulate, and study collagen hydrogel networks suitable for hosting cells. To do this, we used image analysis to extract deflection versus time data for rod-shaped magnetic microprobes (μRods) entrapped in collagen hydrogels as they responded to a precisely controlled rotating magnetic field. We then used a magnetic model accounting for individual μRod variation to infer their rotational stiffness functions. A finite element model describing large angular deflections of μRods within linear elastic media translated rotational stiffness into an effective shear modulus.

This approach allowed for the resolution of microscale heterogeneity within intact hydrogel volumes, as well as allowing the study of extrinsic influences such as boundary proximity and local densification. We find effective microscale shear moduli spanning a range of three orders of magnitude (100 s of Pa to 10s of kPa) within an individual, macroscopically homogenous collagen hydrogel sample. These values are smaller than those measured for individual collagen fibers at the nanoscale (32 MPa to 2 GPa),^{16–18,38,39} yet larger than the shear moduli of collagen hydrogels as measured by bulk rheology (10s of Pa).^15,40 While the scale of measurement partly accounts for this discrepancy, our modelling indicates that local densification of the network, a phenomenon experienced by both cells and μRods alike, is also an important determining factor.

To characterize the effect of magnetically controlled μRod deflection on the surrounding fiber network, we analyzed the range and velocity of matrix fiber deformation. 3D image processing, when combined with an electromagnetic manipulation system enabling μRod rotation in 3D, allows for the extraction of mechanical information in any direction. Finally, we demonstrate that, in addition to mechanical characterization, magnetic μRods are suitable for applying controlled matrix deformation in systems that incorporate living components. By integrating human dermal fibroblasts into a μRod-enriched 3D collagen matrix, we confirm the compatibility of our system with incubation and live imaging of a cell culture model.

Results

Magnetically controlled μRods reveal heterogeneity in local stiffness at the microscale

We sought to examine the mechanics of 3D tissue model environments at the scale of cells using magnetic μRods embedded in hydrogels, polymerized inside polydimethyl-siloxane (PDMS) devices. For this purpose, μRods were synthesized by template-assisted electrodeposition of a metallic Co–Ni alloy to form high aspect ratio structures with a mean length of 5.9 μm and a mean diameter of 1.3 μm (Fig. S1a†), dimensions comparable to many mammalian cell types. Vibrating sample magnetometry (VSM) on dispersed samples confirmed their ferromagnetic properties (Fig. S1b†), and a Co to Ni ratio of approximately 38 : 62 was determined by energy-dispersive X-ray spectroscopy (EDX) (Fig. S1c†). By applying torques via rotating uniform magnetic fields, μRods were wirelessly actuated within 3D collagen I hydrogels while observing their deflection by optical microscopy (Fig. 1a).

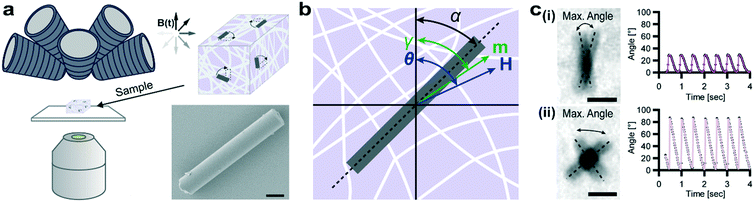Fig. 1 Rod-shaped cobalt–nickel microparticles for magnetic probing and actuation. (a) Schematic overview of the experimental setup. An eight-coil electromagnet (top left) allows for untethered 3D control of embedded Co–Ni microparticles (μRods) observed via optical microscopy (objective lens, bottom left). μRod deflection in response to a rotating magnetic field B(t) is extracted. Bottom right: Scanning electron micrograph of a single μRod. Scale bar: 1 μm. (b) Schematic representation of quantities defined for modelling network-embedded μRod response to applied rotating magnetic fields (see text for details). (c) Selected examples of bright-field image overlays of deflection extrema (noted by dashed lines) for μRods embedded in a 2.0 mg mL⁻¹ collagen matrix during exposure to an in-plane (XY) rotating magnetic field of 73 mT at 1 Hz. Scale bars: 5 μm. Corresponding plots for (i) and (ii) show μRod deflection over time overlaid with best fits provided by our model. A representative image sequence is provided as Video S1.†

We used the deflection data gathered from μRods across a field of view to probe effective micromechanical properties within volumetric hydrogel samples. To interpret these deflections, we developed a magnetic model describing the response of μRod orientation to magnetic manipulation. Briefly, a magnetized object will be twisted by a torque on its magnetic moment (m, oriented at an angle γ) toward alignment with a uniform externally applied magnetic field (H, oriented at an angle θ) (Fig. 1b, ESI† section 1). Detected physical deflections away from elastic equilibrium, described by the angle α, are the result of magnetic shape anisotropy, which couples magnetic and mechanical response and sets an upper limit on the applied torque. Based on composition and geometry, the estimated mean upper limit of available torque for our μRods was 9.9 pNm (±3.3 pNm s.d.). We determined local shear moduli within collagen I hydrogel matrices by monitoring the deflection of embedded μRods during exposure to precisely controlled rotating magnetic fields (Fig. 1b). Surface functionalization allowed for direct attachment of the μRods to the surrounding collagen fibers (see Fig. S2†) and optical transparency of the investigated hydrogels facilitated measurement of μRod size and orientation.

Automated image analysis enabled μRod recognition, measurement of dimensions, filtering suitable candidates for analysis, and extraction of deflection (ESI† section 2, text S2.1). We used our model to fit this deflection data, incorporating field parameters and μRod dimensions. At each instant, the model considers the total energy of a μRod to be the sum of three contributions: potential energy arising from deformation of the elastic matrix, the energy of its moment in the field, and the magnetic anisotropy of the μRod, which couples the previous two terms. This total energy can be written as follows:

where k₂, k₄, and k₆ are rotational stiffness terms of order 2, 4 and 6. These quantities are determined by both the mechanical properties of the surrounding matrix and the geometry of the investigated μRod. M_s is the magnetization of the material comprising the μRod, V is its volume, μ₀ is the permeability of free space, and N_z is the demagnetizing factor calculated for the μRod based on its observed aspect ratio. Because the storage component of shear modulus is much larger than the loss component at the relevant strain rates, damping was neglected, and it was assumed that the μRod approaches equilibrium at each instant. The minimal energy state of the system varies in time, yielding a predicted displacement versus time curve. In one scenario considered by the model, the magnetic moment is constrained to a local energy minimum, whereas in another scenario, it can easily switch magnetization directions to reach the global energy minimum at each instant. Both scenarios are reflected in the data, and the apparent periodicity of the deflection curve dictates which minimization method is most appropriate. After the rotational stiffness coefficients k₂, k₄, and k₆ have been fitted, the corresponding effective shear modulus G is estimated in Pa using k₂ and observed dimensions of the μRod under study, based on a numerical interpolation function describing the results of a finite element model for large angular displacements of μRods in linear elastic media. Collagen is well understood to behave nonlinearly, especially in networks with high connectivity subjected to large deformations,⁴¹ a fact reflected by the nonzero fitted values of k₄ and k₆ in our modelling. The true shear modulus is a function of strain, and by considering k₂ and using a finite element model of a linear medium, we restrict our discussion to “effective shear modulus”. Additional details of the physical model and its application to our datasets can be found in Fig. S3 and ESI† section 1. The examples shown in Fig. 1c exhibit steady-state deflection behavior upon repeated in-plane actuation, with Fig. 1c(i) demonstrating a higher rotational stiffness and Fig. 1c(ii) demonstrating a lower rotational stiffness. Both curves are superimposed with the fits produced by the model. 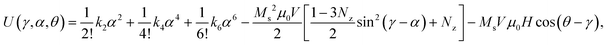The data for these plots was extracted from Video S1.†

Effective shear moduli are influenced by scale of measurement, local densification, and boundary effects

After observing local variation in deflection reflective of micromechanical heterogeneity, we tested whether our method can also distinguish variation in global stiffness values of collagen I hydrogels with increasing concentration.⁴² We applied our approach to determine effective shear moduli for concentrations of collagen ranging from 0.5 to 2.0 mg mL⁻¹ (Fig. 2). For microscale analysis, samples incorporating μRods were subjected to an in-plane (XY) rotating magnetic field of 73 mT at 1 Hz. For each concentration, we analyzed three fields of view to extract effective shear moduli, summarized in Fig. 2a and S4.† Corresponding measurements of bulk shear moduli are shown in Fig. S5.†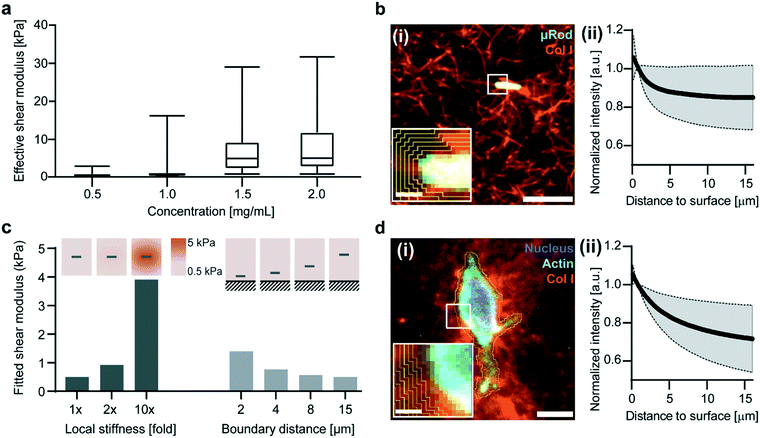

Fig. 2 Embedded μRods probe local stiffness of a surrounding collagen matrix and are influenced by local densification and proximity of boundaries. (a) Effective shear moduli experienced by μRods in collagen matrices of varying concentration, based on observed deflection caused by a 1 Hz in-plane rotating magnetic field of 73 mT. Three fields of view were analyzed for each collagen concentration, ranging from 0.5 to 2.0 mg mL⁻¹. (b) Merged micrograph (i) of a 0.5 mg mL⁻¹ TAMRA-labeled collagen matrix (confocal fluorescence) encapsulating a μRod (brightfield, false color). Scale bar: 10 μm. Inset shows an example of regions of integration used to quantify fluorescence intensity as a function of distance from the μRod. Scale bar 1 μm. (ii) Fluorescence intensity (collagen fiber density) versus distance from μRod surface, normalized to intensity at 1.6 μm. (n = 19, shaded region represents s.d.). (c) Results from finite element model detailed in ESI† section 1 for a linear elastic matrix with a shear modulus of 500 Pa. Local densification and proximity to a rigid boundary are found to increase extracted effective shear moduli. (d) Merged confocal fluorescence micrograph (i) of a fibroblast cultured in 0.5 mg mL⁻¹ collagen matrix for 3 days, stained for nucleus and actin cytoskeleton. Scale bar: 10 μm. Inset shows example of integration regions analogous to (b). Scale bar: 1 μm. (ii) Fluorescence intensity (collagen fiber density) versus distance from fibroblast surface, normalized to intensity at 1.6 μm (n = 17, shaded region represents s.d.).

Overall, our data show a trend of shear moduli increasing with collagen concentration. The average microscale effective shear modulus for 0.5 mg mL⁻¹ collagen was 0.8 kPa and increased consistently with concentration to 9.5 kPa at 2.0 mg mL⁻¹ (Fig. 2a). By contrast, the shear moduli determined through bulk measurements ranged from 5.7 Pa at 0.5 mg mL⁻¹ to 54.8 Pa at 2.0 mg mL⁻¹ (Fig. S5a†).

Previous literature indicates that the scale of measurement can partly explain this discrepancy, especially given the comparability of the dimensions of the μRods to the characteristic length scale of the collagen I networks studied here.^14–19 Using our finite element model, we studied whether extrinsic factors could also contribute to the higher apparent rotational stiffness observed. By correlating fluorescence intensity with local concentration of TAMRA-labelled collagen, we studied the drop-off in intensity at the periphery of the μRods (Fig. 2b), finding that the collagen is approximately 15% denser at the surface of the μRod. Increased collagen density is correlated with increasing stiffness. The finite element model was adapted accordingly to include elastic moduli that varied with distance from the surface of the μRods, dropping off at a characteristic length scale matching the one observed here. We found that the fitted rotational stiffness increased by a factor bounded by the fold increase in elastic modulus set at the surface of the μRod. For smaller increases in elastic modulus at the surface, as in the 2× case, this limit is approached more closely (Fig. 2c, right). In addition, we studied the influence of a nearby rigid wall on the deflection of μRods, finding that it contributes mainly to higher order stiffness terms and is most pronounced for μRods that are close to the wall and embedded in softer media (Fig. 2c, left). Both factors tend to systematically increase values determined for effective shear modulus. This reflects relevant aspects of the mechanical environment experienced directly by cells in a 3D ECM model.⁴³ In fact, densification was even more pronounced for fibroblasts that had been cultured in identical collagen I hydrogels for 3 days, which exhibited an approximately 28% increase of collagen density at their surfaces (Fig. 2d).

μRods sense matrix softening during enzymatic degradation

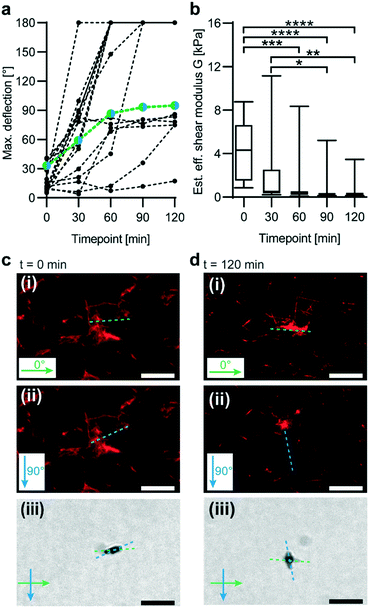
We next tested whether our magnetic probing technique can reveal changes in microscale stiffness as a function of time. In vivo, collagen is a frequent target of enzyme remodelling processes.⁴⁴ Thus, we conducted an experiment in which a fluorescently labelled collagen I matrix was subjected to enzymatic degradation by collagenase (Fig. 3). Effective microscale shear moduli were then tested in 30 min intervals at five different time points via magnetic in-plane actuation of embedded μRods. A decrease in effective shear moduli was determined through analysis of μRod deflection during collagenase incubation (Fig. 3a and b). With an initial mean effective shear modulus of 4.2 kPa, a consistent decrease was observed, reaching 0.5 kPa after 120 min. The mean effective shear modulus decreased most rapidly during the first 30 min of collagenase incubation.

Fig. 3 Analysis of enzymatic degradation of a collagen I matrix. (a) Angular deflections observed for embedded μRods during collagenase incubation. Values are indicated for each identified μRod in intervals of 30 minutes. Green and blue datapoints indicate values extracted from the μRod displayed below (in c and d). (n = 17). (b) Mean and SD of effective shear moduli monitored during enzymatic degradation corresponding to the μRod deflection values presented in (a). A Friedman test and ANOVA analysis was performed to test significance. If not otherwise indicated: ns; **** indicates p < 0.0001; *** indicates p = 0.0003; ** indicates p = 0.0052; * indicates 0.0341. (n = 17). (c) Confocal fluorescence micrographs of TAMRA-labeled collagen hydrogel (0.5 mg mL⁻¹) embedding a magnetic μRod before (i) and after (ii) 90° in-plane rotation of a magnetic field (55 mT) at t = 0 min (immediately after collagenase addition). Dashed lines show μRod pose extracted from the respective bright field micrographs. (iii) Bright-field micrograph overlay of the μRod before and after magnetic field rotation at t = 0 min, green arrow: 0° field orientation, green dashed line: corresponding μRod orientation, blue arrow: 90° field orientation, blue dashed line: corresponding μRod orientation). (d) Confocal fluorescence micrographs of the collagen network after 120 min of incubation with collagenase before (i) and after (ii) 90° magnetic field rotation. Dashed lines show μRod orientation. (iii) Bright-field micrograph overlay of the collagen-embedded μRod before and after magnetic field rotation at t = 120 min (green arrow: 0° field orientation, green dashed line: corresponding μRod orientation, blue arrow: 90° field orientation, blue dashed line: corresponding μRod orientation). All scale bars: 10 μm.

μRods enable analysis of local collagen I network deformation

In addition to local mechanical probing, μRods are capable of applying mechanical actuation to cells either directly or via their embedding matrix. Thus, we were interested in the spatial extent of μRod deflection on the surrounding fiber network under exposure to a rotating magnetic field. To study this, we used fluorescently labelled TAMRA-collagen, which was found to avoid introducing structural artifacts (Fig. S7†) and allowed for fiber detection during cyclic actuation (Fig. S8†). Deformation was quantified with fiber tracking analysis using the Horn–Schunck method.⁴⁵ Briefly, a thresholding algorithm was applied to fluorescence images at each time point, and optical flow was calculated between frames. These results were filtered to isolate direct motion of the collagen surrounding the μRod, while ignoring deflection of the μRod itself. Next, by applying automated thresholding with Otsu’s method,⁴⁶ sets of adjacent pixels with high magnitude of movement were grouped together. Deflection velocity arrows were then generated at the weighted centroid of these high movement regions with a magnitude and orientation according to the mean of all the pixels belonging to the region. An area of influence (AOI) was defined based on these regions, describing the spatial extent of collagen fiber displacement (Fig. 4). Details regarding the tracking algorithm are provided in ESI† section 2 text S2.2. and S2.4. This method allowed us to monitor the propagation of local microscale deformation within the surrounding network during cyclic actuation.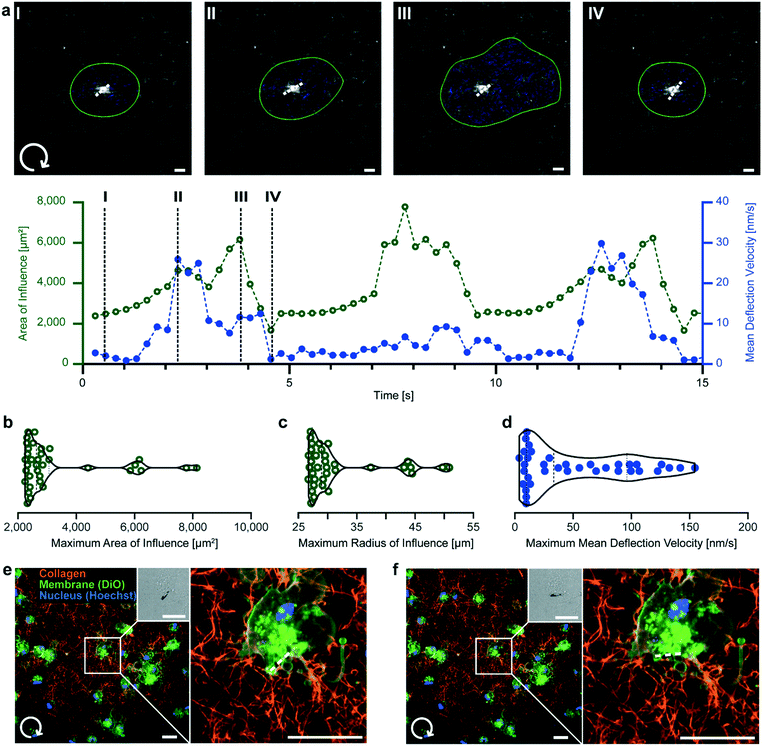

Fig. 4 μRod deformation of the local collagen network. (a) Clockwise μRod deflection over time at 73 mT and 0.1 Hz. Top: Confocal fluorescence micrographs of 0.5 mg mL⁻¹ TAMRA-labelled collagen hydrogels under μRod deflection superimposed with detected area of influence (green outline) and mean deflection velocity (blue arrows). μRod position and orientation extracted from the respective bright field micrographs is marked by the white dashed line (see Fig. S8†). Bottom: area of influence and mean deflection velocity plotted over time. Black dashed lines indicate the timepoints I–IV corresponding to the images. (b) Violin plots of maximum radius, (c) area of influence, and (d) maximum mean deflection velocity. Values calculated from local maxima detected for each sample (n = 11). (e and f) Clockwise deflection at 109 mT of a μRod incorporated in a 0.5 mg mL⁻¹ TAMRA-labeled collagen matrix containing human foreskin fibroblasts. Initial position (e) and deflected position (f). Insets: Brightfield images of a representative μRod. All scale bars: 10 μm.

Consistent with global energy minimization during magnetic actuation, the AOI and mean deflection velocity were periodic in time, passing through two mechanical equilibrium states. As the μRod rotated, it deformed the matrix, increasing the AOI (Fig. 4a, I–II). The AOI decreased again after the μRod had approached its maximal deflection angle, slowed, and subsequently stopped rotating. When the μRod then rotated back in the opposite direction, the AOI grew (Fig. 4a, III), slowing again and reaching a local minimum (Fig. 4a, IV). Our assessment of the deformation caused by μRods to their surrounding network indicated that the region affected by a single deflecting μRod spanned a radius several times its length (Fig. 4b and c). The mean fiber deflection velocity reached two notable local maxima in the vicinity of magnetic reversal and motion through mechanical equilibrium during actuation (Fig. 4a and d). The instantaneous mean deflection velocity likely reaches higher values than indicated during μRod relaxation (Fig. 4a, III and IV), but due to limitations in the flow tracking algorithm, this was not detectable. The full actuation is provided in Video S2† and superimposed with the results of the optical flow analysis in Video S3.† With the system's capability to exert torques on the order of cell contractile moments estimated to range between single to tens of pNm^47–49 we show that μRods produce spatial extents of deformation comparable to cells, which have been shown to affect areas spanning several times their body length.^50–52

To combine μRod actuation with standard cell culture models, we cultured human dermal foreskin fibroblasts (HFF cells) with μRods inside a collagen I hydrogel. After three days of culture, we magnetically actuated the sample and imaged the HFF cells before and after μRod deflection (Fig. 4e and f). We observed stable integration of the cells into the matrix in the presence of μRods over three days of co-culture and tested cell viability with an MTT assay (Fig. S9†). Magnetic deflection locally deformed the matrix without any adverse effect on cell attachment. Bright-field insets show the change of μRod orientation during the course of in-plane magnetic field rotation (Fig. 4e and f).

3D actuation and pose extraction of μRods

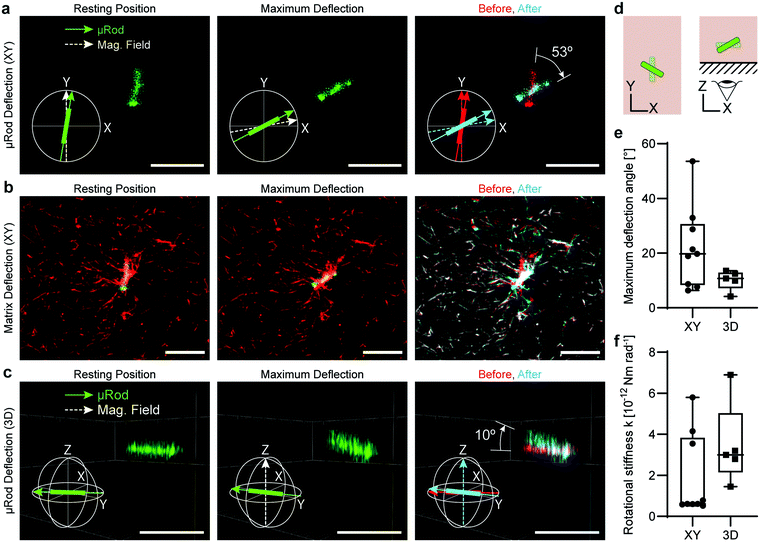
Finally, we deflected the μRods out of the XY-plane to show the potential of our system for 3D volumetric mechanical measurements and actuation. To assess deflection in 3D, we acquired confocal Z-stacks of fluorescently labelled μRods embedded in a TAMRA-collagen matrix. We rotated the magnetic field to apply a torque on the μRods that produced an angular displacement away from the XY-plane (Fig. 5).

Fig. 5 Actuation of μRods in 3D. (a) In-plane actuation of a CF-488A-labeled μRod in a TAMRA-labeled collagen matrix. A fluorescent μRod is imaged in its initial resting position (left) and after maximum clockwise deflection under 73 mT (center). Compasses indicate magnetic field orientation (white dashed arrows) and μRod position (green arrow). Right: Overlay of the initial (red) and maximum deflection (cyan) positions with extracted maximum deflection angle. (b) Confocal fluorescence image of the corresponding CF-488A-labeled μRod (green) and TAMRA-labeled collagen matrix (red) from (a) (left and center) and a false-colored overlay of the resting and maximum deflection positions of the TAMRA-collagen matrix (right). Red indicates the initial resting position of the collagen matrix, cyan indicates the maximum deflection position of the collagen matrix, and white indicates overlap. (c) Out-of-plane actuation of a CF-488A-labeled μRod in a collagen matrix. Left: Side view of a CF-488A-μRod in a collagen matrix in the initial resting position. Center: Actuation of a CF488A-μRod upward and out of the X–Y plane. Compasses indicate magnetic field orientation (white dashed arrows) and μRod position (green arrow). Right: Overlay of the initial (red) and maximum deflection (cyan) positions with extracted maximum deflection angle. (d) Schematic for illustration of in plane (XY, left) and out-of-plane (XZ, right) deflection of μRods. (e) Box and whisker plots of extracted maximum deflection angles for in-plane (XY) and out-of-plane (3D) actuation. (n = 9 for XY, n = 5 for 3D). (f) Extracted rotational stiffness calculated from μRod maximum deflection angles for in-plane (XY) and out-of-plane (3D) actuation displayed in (e). The selected μRods were near the glass coverslip, explaining the higher stiffness observed for out-of-plane deflections. All scale bars: 10 μm.

First, μRod deflection in the XY-plane was investigated by aligning the magnetic field with the initial resting position of μRods (Fig. 5a, left). The μRods were then brought to their maximum deflection (Fig. 5a, center) by rotating the magnetic field clockwise. Z-stacks were acquired and analyzed in MATLAB to extract μRod poses as 3D vectors (ESI† section 2 text S2.3). These vectors were then compared, and the maximum deflection angle was calculated (Fig. 5a, right). μRod deflection in the XY-plane was analyzed, revealing a range of maximum deflection angles from approximately 5° to 55°.

We visualized deformation of the TAMRA-labelled collagen matrix by comparing the collagen I network structure in the initial resting position (Fig. 5b, left) to the maximally deflected position (Fig. 5b, center). These images were false-colored and overlaid to highlight the change in collagen I structure during μRod deflection, with red indicating the initial resting position, cyan indicating the maximally deflected position, and white indicating overlap of the superimposed images (Fig. 5b, right). As expected, matrix deformation is most pronounced in proximity to the μRod.

Finally, we actuated the fluorescent μRods out of the XY-plane. Again, we aligned the magnetic field with the initial equilibrium position (Fig. 5c, left) within the XY-plane. We next brought the μRods to their maximum deflection points by rotating the magnetic field out of plane by +90° and −90° (Fig. 5c, center), extracting poses as 3D vectors (Fig. 5c, right). A schematic display of these two actuation strategies is depicted in Fig. 5d. We compared the extracted vectors to calculate the maximum deflection angle (Fig. 5e). In total, the 3D deflections of five μRods were analyzed and exhibited a range of maximum deflection angles between approx. 5° and 15°, as displayed in Fig. 5e. The mean rotational stiffness k found for out-of-plane deflections was 3.5 × 10⁻¹² Nm rad⁻¹, approximately 85% higher than for deflections in the XY-plane, which had a mean of 1.9 × 10⁻¹² Nm rad⁻¹ (Fig. 5f). This difference likely reflects the stronger influence of the cover glass boundary on out-of-plane deflection, a factor that would also be relevant for cells embedded in the matrix and close to the boundary.

Discussion and conclusion

Mechanical forces are key regulators of cellular function and help govern their behavior in both health and disease. In addition to recapitulating salient features of the ECM, biomolecular hydrogels provide opportunities to study the mechanical interplay of cells with fiber networks. Here, we have demonstrated the potential of embedded Co–Ni μRods for the measurement of mechanical properties and application of mechanical stimuli in 3D at a scale relevant to cells. Although magnetic manipulation of embedded microstructures is widespread, a combination of 3D magnetic actuation capabilities, physical modelling, and advanced image analysis allowed us to gain insight into aspects that have been previously unexplored.

Simultaneously observing the deflections of multiple μRods within a single sample permitted us to extract a range of values for the effective shear modulus within a macroscopically homogenous hydrogel volume (Fig. 1c and 2a). The resulting spread in values for effective shear modulus corresponds with intrinsic microscopic heterogeneity, inherent to biopolymer networks such as collagen.^34,36 Extrinsic factors that may be present in ECM model systems also play a role. We modelled the influence of proximity to rigid boundaries and local densification effects, showing that both factors systematically increase rotational stiffness functions (Fig. 2c and 5).

These effects are relevant to cells in devices that incorporate 3D ECM models. The densification observed at the surface of the μRods, likely attributable to their chemical functionalization (Fig. S2†), was similar to the densification observed at the surface of HFF cells (Fig. 2b and d), which attach to and reconfigure surrounding biopolymer networks.^53,54 Similarly, the presence of a rigid boundary occurs for cells embedded in devices.

Using our system, we were able to demonstrate temporal monitoring of matrix degradation driven by enzymatic cleavage and to gain insight into the length scales and dynamical deformation of fiber networks by individual μRods. This was accomplished by extracting the velocity of displacement of collagen fibers, which defined an observed area of influence that evolved during a cycle of magnetic actuation. The magnetic torques applied to produce this deformation were in a similar range to cell contractile moments.^47,48 High-resolution volumetric imaging, combined with out-of-plane field generation, allowed us to probe collagen-network mechanics in 3D. Together these capabilities show that collagen networks enriched with μRods may serve as a useful in vitro platform.

While the physical model we developed fits the extracted deflection data well, it also bears inherent approximations and limitations. For one, it assumes a uniform magnetization of the μRod, an assumption that is well motivated at sufficiently high fields and greatly simplifies the model, but neglects internal effects of the demagnetizing field and other micromagnetic considerations that are more relevant for weaker or more rapidly varying applied fields. From a mechanical standpoint, ignoring damping at higher actuation frequencies will eventually introduce error. Converting rotational stiffness functions that include higher order terms to effective shear modulus required simplifying assumptions such as assuming a value for Poisson’s ratio and only retaining the k₂ term, which dominates at small displacements. A consideration that may be of interest in the future is to examine deflection that is non-collinear with the expected direction of displacement. In the most general case, spatial asymmetry of surrounding mechanical properties or irregularities in the attachment to the fiber network may cause deflections in unexpected directions. Indicating the relevance of these effects, Fig. 1c illustrates that the rotational center of μRods did not always perfectly coincide with their geometric center.

The finite element model used to fit rotational stiffness was based on a linear elastic matrix, whereas real hydrogels are inherently nonlinear. Because only second order rotational stiffness was used for fitting, this is a justifiable approach. Nevertheless, future work could also consider an expanded interpolation space spanning nonlinear elastic properties of the matrix and use fitted higher order stiffness terms to extract effective shear modulus as an explicit function of displacement. Additional case-specific parameters such as local fiber concentration, connectivity, and fiber alignment might also contribute to a refined approach that better accounts for these factors’ local influence.

Our investigation of 3D actuation showed what is possible, but several factors make this mode more challenging in practice than in-plane actuation. One issue is the time required to collect spatial information in the Z-direction, which limits temporal resolution for detecting actuation events. Analyzed μRods must also be optically accessible, a requirement limiting the thickness of the investigated volume of the ECM model. Thus, it introduces a constraint placing accessible μRods closer to rigid surfaces, thereby increasing the influence of edge effects. For instance, the proximity of the μRods analyzed in Fig. 5 to the glass coverslip is likely contributing to the measured difference in rotational stiffness for in-plane and out-of-plane actuation, while a certain level of stiffness anisotropy might be inherent to the matrix architecture.

In conclusion, enriching volumetric ECM models with magnetic μRods is a promising approach to mechanically probe and manipulate reconstituted cell environments with microscale resolution in a 3D manner. Future extensions of these techniques could offer tools for addressing emerging experimental questions and are compatible with investigations on lab-on-a-chip devices. ECM models of greater complexity could be developed that incorporate additional morphological features or biomolecular constituents (e.g., peptidoglycans). As a platform enabling biological experiments, embedded μRods may allow either precise application of mechanical stimuli or observation of mechanical alterations induced by cells on their surrounding matrix networks. This tool offers insight into the mechanical landscape created by the surrounding fibrous ECM, experienced from the perspective of the cell, as revealed by microscale magnetic proxies.

Experimental

Magnetic μRod synthesis

Cobalt–nickel (Co–Ni) magnetic μRods were synthesized by template-assisted restrictive electrodeposition. Track-etched polycarbonate membranes served as cathodic templates with a pore size of 1.2 μm and a thickness of 24 μm (IsoporeTM Membrane Filters, Merck RTTP02500). As a conductive base layer, membranes were sputtered with a uniform 650 nm gold layer. Co–Ni deposition via pulse electrodeposition was performed with a custom setup using previously described methods.⁵⁵ The current was cycled in 4 ms pulses with a density of 50 to 100 mA cm⁻² followed by 10 ms of rest repeated for 6 min at a working voltage of 2.2 V. Table S1† specifies the composition of the electrolyte solution. μRods were released from the template by etching the conductive gold layer and subsequent washes in dichloromethane (DCM) and isopropanol. μRods were stored in ethanol. Ultrasonication was used to disperse the μRods immediately prior to use.

ND-PEG-NHS production for surface functionalization of magnetic μRods.

NHS-functionalized μRods were prepared using nitrodopamine (ND) – polyethylene glycol (PEG) – succinimidyl carbonate (NHS) (Creative PEGWorks, Cat. No. PSB-9014). ND–PEG–NHS was prepared by adapting a protocol from Aghanejad et al.⁵⁶ For a schematic overview, see Fig. S2a.† Briefly, 500 mg of 5000 M_W NHS–PEG–NHS (0.1 mmol) was dissolved in 5 mL DCM. 20 mg of ND (0.1 mmol) was dissolved in 5 mL DCM, added to the NHS–PEG–NHS solution, and incubated under N₂ flow at 25 °C overnight. Next, the reaction mix was gravity filtered using cellulose filter paper to remove insoluble compounds, and the filtrate was precipitated using 100 mL diethyl ether (10 : 1 ratio). The precipitate was centrifuged for 10 min at 4500 rpm (1924 g), and the pellet was dried first under N₂ flow and then under vacuum overnight. The ND-PEG-NHS stock was stored under N₂ at −20 °C.

μRod functionalization

μRods were functionalized with NHS groups to allow for direct attachment to the collagen hydrogel matrices through NHS amidation. This resulted in good dispersion and incorporation of the μRods into the fibrous hydrogel structure. First, μRods suspended in ethanol were centrifuged for 5 min at 15 000 rpm (21 382 g) and re-suspended in 0.1 M triethylammonium acetate (TEA). Next, 1 mg of ND–PEG–NHS was dissolved in 1 mL of 0.1 M TEA and then mixed with the μRods. After 2 hours of incubation on a shaker table under gentle agitation, the μRods were washed 4 times by centrifugation for 5 min at 15 000 rpm (21 382 g), followed by resuspension in 0.1 M TEA, vortexing, and repeating the centrifugation. The washed μRods were finally re-suspended in 20 μL of 0.1 M TEA. Fluorescent μRods were prepared using a mixture of pre-labeled ND–PEG–CF488 and unlabeled ND–PEG–NHS. Briefly, pre-labeled ND–PEG–CF488 was prepared by mixing nitrodopamine, NHS–PEG–NHS, and CF488 amine in a 1 : 1 : 1 molar ratio in 0.1 M TEA buffer for 24 hours (Fig. S2b†). This stock was protected from light and stored at 4 °C. μRods were then functionalized with 20% ND–PEG–CF488 and 80% ND–PEG–NHS in 0.1 M TEA for 2 hours (Fig. S2c†).

Vibrating sample magnetometer analysis

Magnetic properties of a 100 μL suspension of CoNi μRods were measured via vibrating sample magnetometry (EZ-VSM, Microsense). The sample was placed in NMR tubes shortened to 1 cm, capped, and affixed to a custom modified glass sample rod with vacuum grease. The diamagnetic signal from the sample holder was subtracted by a linear fit of the saturated sample.

Scanning electron microscopy

For imaging via scanning electron microscopy (SEM), μRods were dispersed in isopropanol, pipetted on platinum-coated Si wafers and left to dry. SEM images were acquired using a Zeiss Ultra 55 scanning electron microscope (maintained by FIRST – Center for Micro-and Nanoscience, Zurich, Switzerland).

Energy-dispersive X-ray spectroscopy

Energy-dispersive X-ray spectroscopy (EDX) analysis was performed using an Ultim® Max Silicon Drift Detector (Oxford Instruments) mounted on a Zeiss Ultra 55 SEM unit (maintained by FIRST – Center for Micro-and Nanoscience, Zurich, Switzerland). Samples were prepared according to the protocol described for SEM analysis. For each μRod, spectra were acquired in sets of three technical replicates at three different locations on the particle surface. Elemental identification and atomic percent calculations were performed automatically using the AztecLive software (Oxford Instruments). Voigt peak fitting and deconvolution were performed using MATLAB.⁵⁷ The background was subtracted, and individual peaks were automatically identified (r² = 0.995).

PDMS pool preparation

Polydimethylsiloxane (PDMS) polymer (SYLGARD^TM 184 Silicone Elastomer kit, Dow Corning #01673921) was mixed according to manufacturer instructions. After degassing for 1 h, the polymer was poured onto a silicon wafer at a thickness of 4 mm, and cured for 4 h or overnight at 80 °C. Ring-shaped sample chambers with inner diameters ranging from 6 mm to 14 mm were prepared with punches. PDMS rings were directly bonded to glass coverslips following oxygen plasma treatment.

Collagen hydrogel preparation

Collagen hydrogels were prepared from rat-tail collagen-I (Corning, 354 249). The collagen stock was mixed with water, 10× PBS, and 0.5 M NaOH, according to manufacturer instructions. The sample was briefly vortexed and then incubated at 37 °C to gel. For fluorescently labeled collagen-I hydrogels, 10% of the collagen was substituted by labeled collagen, prepared via the protocol specified below.

Fluorescent labeling of collagen

Fluorescently labelled collagen was prepared from rat-tail collagen-I (Corning, 354 249). A 5(6)-TAMRA N-succinimidyl ester (Chemodex, C0027) stock solution was first re-suspended in dimethyl sulfoxide (DMSO) to a concentration of 10 mg mL⁻¹, vortexed thoroughly, protected from light and stored at −20 °C. 2 mL of concentrated collagen was placed inside a 3 mL 3500 MWCO Slide-a-Lyzer Dialysis Cassette (ThermoFisher, 66 330) and dialyzed overnight against 2 L of aqueous labeling buffer (0.25 M NaHCO₃, 0.4 M NaCl, pH 9.5) at 4 °C. All subsequent steps were protected from light. The dialysis cassette was removed from the labeling buffer, and 100 μL of TAMRA stock was then mixed with 900 μL of labeling buffer, injected into the dialysis cassette, placed on a shaker table for overnight incubation at 4 °C. The dialysis cassette was then placed in 1 L of 0.5 M acetic acid at pH 4 and dialyzed overnight at 4 °C. This was followed by two subsequent overnight dialysis washes in 0.02 M acetic acid at pH 4 and 4 °C. The TAMRA-labelled collagen was then removed from the dialysis cassette and stored at 4 °C. To exclude artifacts introduced by fluorescent labelling of collagen hydrogels, TAMRA-labelled collagen hydrogels were compared to unstained collagen samples via CT fire analysis for structural characterization (Fig. S7†).

Rheological analysis of hydrogels

Rheological measurements were performed using an Anton Paar MCR 302 Modular Compact Rheometer with a water-cooled Peltier plate and a parallel plate geometry (20 mm diameter, Part No. 45950). The hydrogel precursor solution was pipetted onto the rheometer plate directly after thorough mixing of all components, the geometry was lowered to measurement height, and the hydrogel was left to polymerize at 37 °C for 20 min. The polymerized sample's shear modulus was monitored at constant temperature via a frequency sweep performed under 0.1% strain and a frequency range between 1.0–10.0 Hz.

Cell culture

Normal human dermal fibroblasts derived from foreskin (HFF cells, Promocells, Heidelberg, Germany) were maintained in complete medium (MEM Alpha w L-glutamine w/o ribonucleosides w/o deoxyribonucleosides, Biowest L0476) supplemented with 10% fetal bovine serum (FBS, Biowest S1810) and 1% penicillin/streptomycin (10 000 U mL⁻¹, Thermo Scientific, 15 140 122) (in T75 flasks) in a standard incubator with 5% CO₂ at 37 °C. Cells were passaged at 70–80% confluence. For detachment, cells were washed once with Doublecco’s phosphate buffered saline (DPBS) (Gibco®) prior to a 3 min incubation with 0.25% trypsin-EDTA (1×) (Gibco®). Subsequent neutralization of the trypsin-EDTA with complete medium was followed by direct reseeding of the cells into a cell culture flask containing pre-warmed complete medium or centrifugation for up-concentration of the cell suspension.

MTT cell viability test

HFF cells were seeded in 96-well plates at a density of 1 × 10⁴ cells per well. After 1 day of culture, cells had reached a confluency of 70–80% and were supplemented with 200 μL of fresh medium, containing two different concentrations of ND–PEG–NHS–functionalized μRods, dispersed in 3 μL of 0.1 M triethylammonium acetate buffer (low μRod conc.: same conditions as used for 3D cell culture samples, see below; high μRod conc.: 10-fold concentration low μRod conc.). Control samples with no treatment and 3 μL of TEA buffer only were prepared in parallel. After 1, 2, and 3 days of co-incubation, cell viability was tested via CyQUANT MTT Cell Viability Assay (Thermo Fisher Scientific, V13154) according to the manufacturer’s instructions. After 10 minutes of incubation at 37 °C and 5% CO₂, and gentle agitation, absorbance was measured at 540 nm with a multimode microplate reader (Spark, Tekan, Switzerland). Background signal from media control was subtracted from final values.

Fluorescent labelling of cells

Cells were fluorescently labelled with Hoechst (Hoechst 33342, 10 mg mL⁻¹ solution in water, Invitrogen) and 3,3′-dioctadecyloxacarbocyanine perchlorate (DiO, D4292-20 mg, Sigma-Fine Chemicals). Prior to staining, cells were seeded into a T25 flask with an anticipated confluence of 60% on the following day. After one day of incubation, the medium was aspirated, cells were washed once with DPBS, and subsequently incubated with 5 μg mL⁻¹ DiO in fresh medium under standard incubating conditions. After 30 min, Hoechst was added to a final concentration of 1 : 1000, and the cells were returned to the incubator for 15 min. Next, cells were washed once with DPBS, detached by incubation with 0.25% trypsin-EDTA (1×) (Gibco®) for 3 min at 37 °C prior to the addition of fresh complete medium and centrifugation for 3 min at 150 g. Excess medium was removed, and the cells re-suspended in fresh complete medium to the desired concentration.

Preparation of 3D cell culture samples

TAMRA-collagen was prepared as described above to a final concentration of 0.5 mg mL⁻¹ using complete medium instead of PBS for increased cell compatibility. 5 μL of fluorescently labeled cell suspension (passage 9) at a concentration of 9.7 × 10⁶ cells mL⁻¹ was added per 200 μL volume of final collagen mix and briefly vortexed. For co-incubation of μRods and cells, 3 μL of functionalized μRods dispersed in TEA buffer were added per 200 μL of final sample volume. The sample was vortexed, and 200 μL was transferred to UV-sterilized PDMS pools. Samples were incubated in a humidified chamber in a standard incubator (5% CO₂ at 37 °C) for 3 days prior to imaging.

Imaging

Bright-field and fluorescence images were acquired using a Nikon Eclipse Ti2 microscope equipped with a Yokogawa CSU-W1 Confocal Scanner Unit and a Hamamatsu C13440-20CU ORCA Flash 4.0 V3 Digital CMOS camera. Microscope operation and image acquisition were performed using Nikon NIS-Elements Advanced Research 5.02 (Build 1266) software. Experiments were recorded with either a Nikon CFI Plan Apochromat λ 20× or 40× long working distance objective, resulting in an effective pixel size of 0.33 μm or 0.16 μm, respectively. Deconvolution of image stacks was performed using the Huygens Remote Manager v3.5 (Scientific Volume Imaging BL, Netherlands). Image data was processed and analyzed using Nikon NIS-Elements software (Advanced Research 5.02, Build 1266; Elements Viewer 4, Version 4.5, Build 1125; FIJI, Imaris v9.2, and MATLAB R2019a).

Second harmonic generation (SHG) imaging was performed on a Leica SP8 MP (Multiphoton) equipped with Mai Tai XF (Spectra-Physics, tunable from 720–950 nm) and InSight DeepSee (Spectra-Physics, tunable from 950–1300 nm) lasers, Leica Hybrid detectors (HyD SP GaAsP), a 40× 1.1NA Water HC PL IRAPO CORR objective, and Leica LAS AF SP8 Version 4.0 software.

Fiber density analysis

Quantification of fiber density surrounding μRods or cells embedded in fluorescently labelled collagen matrices was performed using FIJI. Briefly, acquired image stacks were Z-projected, converted to 8-bit and μRod or cell outlines, respectively, were identified using the “analyze particle” function. Bands with one pixel increment were created around the defined outlines and the mean grey value of the fluorescent collagen signal was extracted for each band. Mean grey values were normalized to the average of the first 10 bands directly surrounding the innermost outline.

Image-based tracking analysis

Tracking analysis of collagen fiber actuation and μRod actuation in 2D and 3D is documented in Table S2 and ESI† section 2.

Magnetic manipulation setup

The applied electromagnetic control system consisted of eight electromagnets arranged in a hemispherical manner, generating a homogenous magnetic field workspace of 1 cm3 (MFG-100-i, Magnebotix AG).⁵⁸ To achieve higher field magnitudes, conical core extensions were employed to focus the magnetic field to a spherical working volume of 1 mm radius. Documentation of the specific configuration of the magnetic field generator and calibration data can be found in Fig. S10.† The system was integrated into an inverted microscope, in which the sample was placed above the lens and below the electromagnetic field generator.

Collagenase experiments

TAMRA-labeled collagen hydrogels were monitored at 30 min intervals over 120 min starting immediately after addition of 200 μL of collagenase (1 mg mL⁻¹ in DPBS, CellSystems) to a PDMS pool containing TAMRA-labeled collagen (0.5 mg mL⁻¹) that had been prepared as described above. Rotational magnetic actuation at a field magnitude of 55mT at a frequency of 1.0 Hz was applied. At each time point, bright-field and confocal fluorescence data were acquired before, during, and after actuation. Three separate TAMRA-collagen hydrogel samples were tested, with a total count of 17 analyzed μRods.

Long-term actuation of collagen hydrogels

Magnetic μRods embedded within a 0.5 mg mL⁻¹ collagen hydrogel were constantly actuated with a 1.0 Hz rotating magnetic field of 55 mT magnitude. Starting at the beginning of continuous rotational magnetic actuation, an 8 seconds-long bright-field image sequence was acquired in intervals of 10 min and analyzed for the recorded μRod’s angle of deflection over time. Three different locations were imaged, each region presenting 5 to 8 detected μRods.

Author contributions

S. S. conceived the idea and initiated the study. S. S., V. H., A. H., D. O. A., T. V. and L. S. designed the experiments. D. O. A., T. V., L. S. and N. M. collected and analyzed the data. L. S. developed algorithms for data analysis and image post processing and M. G. C. and N. M. developed the physical model of the mechanics and analyzed data, S. S. advised. D. O. A., M. G. C., T. V. and S. S. wrote the manuscript. D. O. A. and T. V. prepared the figures. S. S. supervised the study. All authors read and edited the manuscript.

Conflicts of interest

S. S. is co-founder and member of the board of Magnebotix AG. All authors declare no conflict of interest.

Acknowledgements

The authors thank Dr. Salvador Pané i Vidal and Siyu Deng for training and advice on synthesis of μRods, Prof. Dr. André Studart for providing access to the rheometer. We thank Pietro Ronchetti for support in calibrating the system with core extensions. Further, the authors acknowledge Dr. Andrea De Micheli for critical reading of the manuscript. Use of the cleanroom facilities at the FIRST Center for Micro and Nanoscience, ETH Zurich is gratefully acknowledged. M. G. C. was supported by an ETH Zurich Postdoctoral Fellowship (18-1 FEL-53). V. H. acknowledges the Swiss National Foundation Postdoctoral Fellowship (P2EZP2_187980).

References

1. A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689.
2. S. Hopyan, Dev. Biol., 2017, 429, 429–433.
3. P. A. Janmey and R. T. Miller, J. Cell Sci., 2011, 124, 9–18.
4. D. Lu and G. S. Kassab, J. R. Soc., Interface, 2011, 8, 1379–1385.
5. K. A. Jansen, P. Atherton and C. Ballestrem, Semin. Cell Dev. Biol., 2017, 71, 75–83.
6. M. Barczyk, S. Carracedo and D. Gullberg, Cell Tissue Res., 2010, 339, 269–280.
7. M. A. Schwartz, Cold Spring Harbor Perspect. Biol., 2010, 2(12), a005066.
8. C. G. Galbraith, K. M. Yamada and J. A. Galbraith, Science, 2007, 315, 992–995.
9. D. Huh, G. A. Hamilton and D. E. Ingber, Trends Cell Biol., 2011, 21, 745–754.
10. W. J. Polacheck, R. Li, S. G. M. Uzel and R. D. Kamm, Lab Chip, 2013, 13, 2252–2267.
11. K. Henriksen and M. A. Karsdal, Type I Collagen, in Biochemistry of Collagens, Laminins and Elastin: Structure, Function and Biomarkers, ed. M. A. Karsdal, Academic Press, San Diego, USA, 1st edn, 2016, pp. 1–11.
12. Y. L. Yang, S. Motte and L. J. Kaufman, Biomaterials, 2010, 31, 5678–5688.
13. N. R. Lang, S. Münster, C. Metzner, P. Krauss, S. Schürmann, J. Lange, K. E. Aifantis, O. Friedrich and B. Fabry, Biophys. J., 2013, 105, 1967–1975.
14. F. Beroz, L. M. Jawerth, S. Münster, D. A. Weitz, C. P. Broedersz and N. S. Wingreen, Nat. Commun., 2017, 8, 16096.
15. Y. L. Yang, L. M. Leone and L. J. Kaufman, Biophys. J., 2009, 97, 2051–2060.
16. P. Dutov, O. Antipova, S. Varma, J. P. R. O. Orgel and J. D. Schieber, PLoS One, 2016, 11, e0145711.
17. J. S. Graham, A. N. Vomund, C. L. Phillips and M. Grandbois, Exp. Cell Res., 2004, 299, 335–342.
18. J. A. J. Van Der Rijt, K. O. Van Der Werf, M. L. Bennink, P. J. Dijkstra and J. Feijen, Macromol. Biosci., 2006, 6, 697–702.
19. C. A. R. Jones, M. Cibula, J. Feng, E. A. Krnacik, D. H. McIntyre, H. Levine and B. Sun, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E5117–E5122.
20. E. M. Ahmed, J. Advert. Res., 2015, 6, 105–121.
21. M. Ahearne, Y. Yang and K. Liu, Tissue Eng., 2008, 4, 1–16.
22. H. Sanz-Fraile, S. Amoros, I. Mendizabal, C. Galvez-Monton, C. Prat-Vidal, A. Bayes-Genis, D. Navajas, R. Farre and J. Otero, Tissue Eng., Part A, 2020, 26, 358–370.
23. G. A. Busby, M. H. Grant, S. P. MacKay and P. E. Riches, J. Biomech., 2013, 46, 837–840.
24. D. R. Picout and S. B. Ross-Murphy, Sci. World J., 2003, 3, 105–121.
25. T. Cox and C. Madsen, Bio-Protoc., 2017, 7(1), 1–8.
26. M. Plodinec and R. Y. H. Lim, Methods Mol. Biol., 2015, 1293, 231–246.
27. S. Van Helvert and P. Friedl, ACS Appl. Mater. Interfaces, 2016, 8, 21946–21955.
28. I. Jorba, J. J. Uriarte, N. Campillo, R. Farré and D. Navajas, J. Cell. Physiol., 2017, 232, 19–26.
29. R. W. Style, R. Boltyanskiy, G. K. German, C. Hyland, C. W. MacMinn, A. F. Mertz, L. A. Wilen, Y. Xu and E. R. Dufresne, Soft Matter, 2014, 10, 4047–4055.
30. K. Lehmann, M. Shayegan, G. A. Blab and N. R. Forde, Front. Mol. Biosci., 2020, 7(259), 1–7.
31. C. Aermes, A. Hayn, T. Fischer and C. T. Mierke, Sci. Rep., 2020, 10, 13453.
32. C. P. Moerland, L. J. Van IJzendoorn and M. W. J. Prins, Lab Chip, 2019, 19, 919–933.
33. D. Dasgupta, D. Pally, D. K. Saini, R. Bhat and A. Ghosh, Angew. Chem., Int. Ed., 2020, 59(52), 23690–23696.
34. L. Y. Leung, D. Tian, C. P. Brangwynne, D. A. Weitz and D. J. Tschumperlin, FASEB J., 2007, 21, 2064–2073.
35. M. A. Kotlarchyk, E. L. Botvinick and A. J. Putnam, J. Phys.: Condens. Matter, 2010, 22, 194121.
36. U. Chippada, B. Yurke, P. C. Georges and N. A. Langrana, J. Biomech. Eng., 2009, 131, 021014.
37. D. Mohammed, M. Versaevel, C. Bruyère, L. Alaimo, M. Luciano, E. Vercruysse, A. Procès and S. Gabriele, Front. Bioeng. Biotechnol., 2019, 7, 162.
38. Z. L. Shen, H. Kahn, R. Ballarini and S. J. Eppell, Biophys. J., 2011, 100, 3008–3015.
39. A. J. Heim, W. G. Matthews and T. J. Koob, Appl. Phys. Lett., 2006, 89, 181902.
40. R. C. Arevalo, J. S. Urbach and D. L. Blair, Biophys. J., 2010, 99, L65–L67.
41. A. Sharma, A. J. Licup, K. A. Jansen, R. Rens, M. Sheinman, G. H. Koenderink and F. C. MacKintosh, Nat. Phys., 2016, 12, 584–587.
42. V. Perez-Puyana, A. Romero and A. Guerrero, J. Biomed. Mater. Res., Part A, 2016, 104, 1462–1468.
43. A. Buxboim, K. Rajagopal, A. E. X. Brown and D. E. Discher, J. Phys.: Condens. Matter, 2010, 22, 1–10.
44. R. Ala-Aho and V. M. Kähäri, Biochimie, 2005, 87, 273–286.
45. J. L. Barron, D. J. Fleet, S. S. Beauchemin and T. A. Burkitt, in Proceedings 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1992, pp. 236–242.
46. N. Otsu, IEEE Trans. Syst. Man Cybern. Syst, 1979, 9(1), 62–66.
47. A. R. Yoon, I. Stasinopoulos, J. H. Kim, H. M. Yong, O. Kilic, D. Wirtz, Z. M. Bhujwalla and S. S. An, Cancer Biol. Ther., 2015, 16, 430–437.
48. S. S. An, J. Kim, K. Ahn, X. Trepat, K. J. Drake, S. Kumar, G. Ling, C. Purington, T. Rangasamy, T. W. Kensler, W. Mitzner, J. J. Fredberg and S. Biswal, Biochem. Biophys. Res. Commun., 2009, 382, 697–703.
49. T. Pompe, S. Glorius, T. Bischoff, I. Uhlmann, M. Kaufmann, S. Brenner and C. Werner, Biophys. J., 2009, 97, 2154–2163.
50. P. Pakshir, M. Alizadehgiashi, B. Wong, N. M. Coelho, X. Chen, Z. Gong, V. B. Shenoy, C. McCulloch and B. Hinz, Nat. Commun., 2019, 10, 1–10.
51. J. Steinwachs, C. Metzner, K. Skodzek, N. Lang, I. Thievessen, C. Mark, S. Münster, K. E. Aifantis and B. Fabry, Nat. Methods, 2016, 13, 171–176.
52. M. S. Hall, F. Alisafaei, E. Ban, X. Feng, C.-Y. Hui, V. B. Shenoy and M. Wu, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14043–14048.
53. X. Ma, M. E. Schickel, M. D. Stevenson, A. L. Sarang-Sieminski, K. J. Gooch, S. N. Ghadiali and R. T. Hart, Biophys. J., 2013, 104, 1410–1418.
54. A.-M. Pena, D. Fagot, C. Olive, J.-F. Michelet, J.-B. Galey, F. Leroy, E. Beaurepaire, J.-L. Martin, A. Colonna and M.-C. Schanne-Klein, J. Biomed. Opt., 2010, 15(5), 056018.
55. S. Schuerle, I. A. Vizcarra, J. Moeller, M. S. Sakar, B. Özkale, A. M. H. Lindo, F. Mushtaq, I. Schoen, S. Pané, V. Vogel and B. J. Nelson, Sci. Robot., 2017, 2(2), eaah6094.
56. A. Aghanejad, H. Babamiri, K. Adibkia, J. Barar and Y. Omidi, BioImpacts, 2018, 8, 117–127.
57. Maxim, Peak fitting to either Voigt or LogNormal line shapes, https://www.mathworks.com/matlabcentral/fileexchange/52321-peak-fitting-to-either-voigt-or-lognormal-line-shapes, MATLAB Central File Exchange. Retrieved March 30, 2020.
58. S. Schuerle, S. Erni, M. Flink, B. E. Kratochvil and B. J. Nelson, IEEE Trans. Magn., 2013, 49, 321–330.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1lc00657f

---