Planar hydrodynamic traps and buried channels for bead and cell trapping and releasing

Abstract

We present a novel concept for the controlled trapping and releasing of beads and cells in a PDMS microfluidic channel without obstacles present around the particle or in the channel. The trapping principle relies on a two-level microfluidic configuration: a top main PDMS channel interconnected to a buried glass microchannel using round vias. As the fluidic resistances rule the way the liquid flows inside the channels, particles located in the streamlines passing inside the buried level are immobilized by the round via with a smaller diameter, leaving the object motionless in the upper PDMS channel. The particle is maintained by the difference of pressure established across its interface and acts as an infinite fluidic resistance, virtually cancelling the subsequent buried fluidic path. The pressure is controlled at the outlet of the buried path and three modes of operation of a trap are defined: idle, trapping and releasing. The pressure conditions for each mode are defined based on the hydraulic–electrical circuit equivalence. The trapping of polystyrene beads in a compact array of 522 parallel traps controlled by a single pressure was demonstrated with a trapping efficiency of 94%. Pressure conditions necessary to safely trap cells in holes of different diameters were determined and demonstrated in an array of 25 traps, establishing the design and operation rules for the use of planar hydrodynamic traps for biological assays.

---

Microfluidics is very popular for its ability to manipulate objects in the micron range at the single particle resolution.¹ Beads and cells can be manipulated in microfluidic devices using different forces, such as dielectrophoresis,^2,3 optics,^4,5 acoustics,^6,7 hydrodynamics^8,9 or magnetics.¹⁰ Among these, hydrodynamic trapping is the most convenient way of handling a large number of particles with single object resolution.¹¹ In particular, large arrays of parallel single cell hydrodynamic traps in microfluidic chips are popular as they reveal single cell behavior among a population when subjected to various stimuli or when brought into contact with another cell type.^12–14 Similarly, manipulation of beads in microfluidic channels has applications in the biomedical field among others for performing ultrasensitive immunoassays on beads¹⁵ and capturing cells¹⁶ or extracellular vesicles.¹⁷ Hydrodynamic trapping consists in placing an obstacle smaller than the particle dimension in its flow path. The force maintaining the particle against the obstacle is derived from the shear stress coming from the leaks around the cell, and/or from the difference of pressure built at the interface of the trapped particle. One very popular type of hydrodynamic trap, here named the pachinko array, consists of dense arrays with obstacles placed so that the particles have a large probability of encountering one when flowed in the devices.^8,18 Another popular hydrodynamic trapping principle, here named the serpentine array, relies on splitting a channel into two flow paths, with the lowest resistance path comprising a restriction. The first particle arriving in the channel will be dragged to the restriction, increasing its flow resistance. Once the first restriction path is blocked, the following particle follows the bypass channel and is trapped in the next restriction.^19,20 Both types of hydrodynamic trapping principles are adapted to beads and cells and require the presence of the material around the trapped particle, and unless coupled with pneumatic soft valve actuation, they cannot be dynamically controlled.^21–23 Massive immobilization of single cells can be achieved using single wells,²⁴ micropore arrays sandwiched between two microfluidic PDMS channels,²⁵ or micropore arrays combined with dielectrophoresis.²⁶ However, these methods use non standard materials that are non compatible with further microfabrication processing and lack controllability in both design and operation.

We thus propose a hydrodynamic trapping principle that overcomes the problem of space congestion and its resulting low trap density intrinsic to the presented well-known hydrodynamic traps. This novel trapping principle relies on two superimposed levels of microchannels, connected by round traps smaller than the particle of interest. As the hydrodynamic flow resistance rules the way the liquid flows in the channels, particles lying in the streamlines passing inside the vias will be stopped due to their size and will generate an infinite fluidic resistance, virtually cancelling the lower hydrodynamic path. Once a particle is trapped, it is immobilized in the top channel without any material surrounding it, free for interactions with other particles or for biological assays.

These planar hydrodynamic traps can be dynamically switched between different modes of operation by simply tuning the pressure at the outlet of the microfluidic buried level, controlling the magnitude and direction of the flow inside the buried channel layer. We propose three modes of operations for the trapping and releasing of beads and cells with their respective design criteria. The process for the microfabrication of the buried level of microchannels and the micron-sized vias using standard materials and processes is presented, together with the bonding of a top channel made of a PDMS replica. The final chip is totally transparent and compatible with widely used inverted microscopes.

The trapping and releasing of beads and cells are then investigated theoretically and experimentally, and demonstrate good trapping efficiency in compact arrays composed of a large number of traps. To our knowledge, this is the first demonstration of the controlled planar trapping and releasing of beads and cells in microfluidic channels.

1 Experimental

1.1 Fabrication

The top layer channels are made by PDMS casting, a well documented method that is widely used for fabricating microfluidic devices. The microfluidic traps and lower (buried) fluidic channels are manufactured using another microfabrication process presented in 1994 by Kaplan et al.,²⁷ in which channels are obtained by opening small access holes in a thin structural layer for the subsequent selective under-etching of the substrate. The access holes are then closed by the deposition of a layer, sealing the channel.

1.1.1 Process flow. As illustrated in Fig. 1a, the buried level and the vias are fabricated by first sputtering 500 nm of Al₂O₃ (SPIDER 600, Pfeiffer) on top of a 4 inch fused silica substrate. The small access holes of 1 μm diameter and vias of chosen diameter are patterned on a photoresist (AZ ECI 3007, MicroChemicals) by direct laser writing (MLA150, Heidelberg Instruments) that was developed (ACS200, Süss) and the pattern is transferred to the structural layer using ion beam etching (Nexus IBE350, Veeco) (step 1a). The photoresist is stripped and the wafer is exposed to hydrofluoric acid (HF) in the vapor phase (uEtch, SPTS), which selectively etches fused silica, until the desired depth of the buried channel is reached, which was set to 5 μm in this study (step 1b). The distance between two neighbouring access holes is set so that the under-etched holes coalesce and create a continuous channel. The access holes are then sealed using a deposition of 2.5 μm of low temperature silicon oxide (LTO, Centrotherm furnace) (step 1c).

Fig. 1 (a) Process flow for the fabrication of two levels of channels with micron-sized fluidic vias. 1a) Al₂O₃ is sputtered on a fused silica substrate and access holes and microfluidic vias are etched in the Al₂O₃ film. 1b) Fused silica is selectively etched using HF in the vapor phase. The under-etched neighbouring access holes coalesce to create a channel. 1c) Silicon dioxide is deposited to close the access holes and bury the fused silica channels, leaving the microfluidic vias open. 2) Fabrication of the top microfluidic layer using PDMS casting. 3) The PDMS layer is aligned and permanently bonded to the fused silica substrate to form two superimposed levels of microfluidic channels connected by micron-sized vias in a totally transparent chip. (b) Bright-field picture of a buried channel connecting a single trap in the main PDMS channel on the left to the PDMS control channel on the right. An orange filter is added where the PDMS is bonded to the glass. The top inset shows an SEM picture of a trap and the bottom inset shows the equivalent electric circuit where P_in is the inlet pressure, R_in is the resistance of the main PDMS channel upstream of the trap, R_out is the resistance of the main PDMS channel downstream of the trap, R_h is the resistance of a trap, R_bc is the resistance of the buried channel and P_c is the pressure imposed to the control channel.

The top layer fabrication, alignment and bonding were previously precisely described.²⁸ Shortly, PDMS is molded on a DRIE-etched silicon substrate, cured and punched (steps 2). The PDMS is then aligned and permanently bonded to the bottom substrate using a mask aligner (MJB4, Süss) (step 3). The height of the PDMS channel was set to 30 μm. The inset of Fig. 1b shows an SEM picture of a trap fabricated using this process.

1.1.2 Design rules. To obtain a trap of diameter d after the 2.5 μm LTO deposition, we found that a diameter of d + 2 μm should be designed and etched in the Al₂O₃ layer. The final deposition of LTO induces a gradient of stress that deforms the membrane which would break during the dicing step for dimensions above 200 μm. To overcome that problem, regions without access holes were designed periodically on the membrane, leaving the substrate protected below those regions and creating pillars that sustain the membrane. Using this design, membranes with dimensions of 300 × 400 μm² were successfully fabricated. The depth of the channel is defined by the etching time and is uniform across the wafer. Its width however is determined by the design of the access holes and can be chosen arbitrarily. The minimum width however is restricted to twice that of the depth due to the isotropic nature of the etching. The distance between two neighboring access holes should be larger than the depth of the isotropic etch of the fused silica to obtain a continuous channel. This distance was chosen to be equal to the etch depth, 5 μm, in this study, to ensure the minimum topography of the buried channel. In order to avoid deformation under the difference of pressure, the distance between the main and the control channels should be equal or larger than the height of the PDMS channel.

1.2 Materials

5 μm diameter polystyrene beads were purchased from Sigma-Aldrich and suspended in deionized water containing 0.1% TWEEN 20 (Sigma-Aldrich) at a concentration of 5 × 10⁵ beads per ml.

1.3 Cell culture and preparation

The semi-adherent cell line Colo205 (ATCC) was cultured in RPMI 1640 supplemented with 10% FBS and 1% penicillin–streptomycin at 37 °C in a 5% CO₂ atmosphere. Cell staining was performed by incubating the adherent part of the cell population for 1 h in RPMI with 1 μM calcein AM (Calbiochem). The supernatant was removed and the cells were washed with PBS, detached using trypsin and centrifuged at 1200 rpm for 2 minutes. The cells were resuspended in PBS containing 1 mM EDTA and 1% BSA and passed through a 40 μm cell strainer for the experiment. All the reagents are from Gibco unless specified.

The distribution in the cell diameter was measured using an image analysis method on 260 cells. The mean diameter was 16.9 μm with a standard deviation of 3.1 μm.

1.4 Experimental set-up

The PDMS chip was degassed in a desiccator for 30 minutes prior to the experiment to avoid formation of bubbles, and primed with Pierce™ protein-free (PBS) blocking buffer for 1 h to prevent proteins from adhering to the surfaces. The cells or beads were placed in a chromatography vial connected to the punched PDMS with 360 μm outer diameter tubing for tight sealing. Pressure was applied to the vial using Fluigent Flow-EZ pressure controllers. The chip was mounted on the stage of a Leica DMI3000 B inverted microscope and observed using a uEye (IDS) camera.

2 Results

2.1 Principle of operation

Fig. 1b shows a brightfield view of a buried channel and trap connecting two PDMS channels. An orange filter is superimposed to the image and indicates the regions where the PDMS is bonded to the substrate. The control channel on the right is short and wide in order to minimize its fluidic resistance and is connected to the pressure control P_c, while beads or cells flow in the left PDMS channel from the top to the bottom under the effect of the inlet pressure P_in. The top inset shows an SEM picture of a trap, whose diameter is smaller than the dimension of the particle to be trapped. P_c is the control pressure, P_in is the inlet pressure, Q_in is the flow upstream of the trap and Q_bc is the flow inside the buried channel. The chip presented here can be operated in four different modes as presented in Fig. 2a.

Fig. 2 (a) Scheme showing the different modes of operation. Idle mode: P_c is set to obtain a still flow in the buried channel and the flow in the main channel behaves as if no trap was present. Trapping mode, empty: some of the main channel fluid is directed toward the buried path. The particles lying in the streamlines going to the buried path are deviated towards the trap. Trapping mode, full: a particle is trapped and there is no fluid flow in the buried channel. The particle is immobilized by the difference of pressure at its interface ΔP_p. Release mode: The control pressure P_c is increased to reverse the flow in the buried path, and the trapped particle is pushed away from the trap. (b) Brightfield pictures showing a sequence of trapping and releasing of a Colo205 cell in a single trap.

In order to model the behaviour of the chip, we assumed a non-compressible Newtonian fluid and used the Hagen–Poiseuille law ΔP = R_hydQ,²⁹ where ΔP is the difference of pressure across a channel with fluidic resistance R_hyd in which a flow Q is present, and used the electric–hydraulic circuit equivalence³⁰ to model the behaviour of the chip. The equivalent circuit is shown in the bottom inset of Fig. 1b where R_in is the resistance of the PDMS channel upstream of the trap, R_out is the resistance of the PDMS channel downstream of the trap, R_h is the resistance of a trap, R_bc is the resistance of the buried channel, P_in is the inlet pressure and P_c is the control pressure. We used these values to determine the conditions to operate in each of the four modes that are illustrated in Fig. 2a:

Idle mode. In the idle mode, P_c is set such that there is no flow in the buried channel (Q_bc = 0). The particles behave as if no trap or buried path was present.

Trapping mode, empty. To trap a particle, the control pressure is set to a value smaller than the idle control pressure (P_c < P_c,idle), resulting in a net flow in the buried channel from the main channel towards the control channel (Q_bc > 0). The particles in the flow lines passing inside the buried path are directed towards the trap.

Trapping mode, full. A particle is trapped, sealing the buried path and stopping the flow in the buried channel (Q_bc = 0). The main channel behaves as in the idle mode and a pressure difference across the trapped particle ΔP_p maintains it in the trap:

Release mode. To release a trapped particle, the control pressure is larger than the idle control pressure (P_c > P_c,idle), resulting in a net flow in the buried channel from the control channel towards the main channel (Q_bc < 0). The particle is pushed away from the trap.

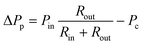2.2 Characterization of single cell trapping

Although polystyrene beads are rigid and can withstand large pressures, special consideration must be taken when trapping cells with this novel kind of hydrodynamic traps. Indeed, cells are deformable bodies whose shapes are impacted by the difference of pressure built across them.³¹ When immobilizing cells in traps similar to the one presented in Fig. 1b, one must adapt the pressures and trap dimensions such that the cells stay intact.

In this study, we consider the cell membrane integrity as a gauge of success, such that the cells can be used for a subsequent assay on the cell membrane on the chip. Cells were immobilized in traps of 3, 5, 7, and 9 μm in diameter using a chip with a single trap and control pressure channel, to find the critical ΔP_p where the membrane fails. For the visualization of membrane failure, the cell cytosol was loaded with fluorescent calcein as it is a small molecule with no covalent binding to cell compounds that quickly diffuses in case of membrane rupture. To avoid fluorophore bleaching, the cells were imaged every minute up to 15 minutes. This time threshold was chosen by overestimating the maximum time the filling of an array could take.

ΔP_p was controlled by setting P_c to a negative value and setting P_in to zero, thus stopping the flow in the main channel. The different outcomes that could be observed after 15 minutes are shown in Fig. 3b. Intact cells could either have a round appearance and no visible deformation, or have a protrusion visible in the buried channel. Membrane failure was identified as dye leaking in the buried channel, or as an engulfed cell that could be found inside the buried channel or in the control PDMS channel.

Fig. 3 (a) Graph representing the percentage of intact cells after 15 minutes for different trap diameters and different pressure gradients at the interface of the trapped cells ΔP_p. The number of experiments is N ≥ 5 for each condition. (b) Fluorescence pictures of the different cell outcomes when trapped. (i) The cell is intact without any visible deformation. (ii) The cell is intact and a protrusion inside the buried channel is visible. (iii) The membrane is ruptured and the fluorescent dye diffuses in the buried channel. (iv) The cell passed through the trap and is found inside the buried channel or in the PDMS control channel. (c) The minimum pressure with less than 50% intact cells after 15 minutes of trapping as a function of the trap diameter is represented in red. The blue area corresponds to the fit of eqn (3) for a range of cell diameters of 13.8–20 μm. The inset shows the range of membrane tension at rupture extracted from the fit measured in this work compared to the range of vesicle membrane tension at rupture from the literature.

The graph in Fig. 3a shows the percentage of intact cells after 15 minutes, as a function of the trap diameter and the pressure difference across the trapped cells ΔP_p. A pressure threshold under which the cells did not suffer any membrane rupture or engulfment was found for each trap diameter. The minimum pressure with a percentage of intact cells lower than 50% is represented as a function of trap diameter in red in Fig. 3c, indicating that the cells resist higher pressures in smaller traps. Previous studies on vesicle and cell deformation in pipettes indicate that the tension τ of a spherical membrane of radius R_v can be determined via the difference of pressure ΔP_p between the inside and outside of the pipette and the radius of curvature R_p in the pipette.^32–34

Since the vertical configuration of the planar traps makes the direct measurement of the radius of curvature R_p technically demanding, we used the radius of the trap as an estimate. We measured the distribution of the cell radius using image analysis methods, which was found to be 8.4 μm with a standard deviation of 1.5 μm as an estimate of R_v. We highlighted the region resulting from the fitting of eqn (3) to our experimental data using these estimates in blue in Fig. 3c: we observed a good accordance of the predicted trend with the measurement results. Moreover, the range of tension at rupture resulting from the fitting is shown in the inset of Fig. 3c. We obtain higher values for the fitted rupture tension compared to values obtained for lipid vesicles,^32,35 which is coherent with the presence of cholesterol in the cell membrane and the presence of cytoskeleton inside the cell, which are both expected to contribute to increase the rupture tension of the cell membrane.

2.3 Hydrodynamic trapping of beads in large arrays

We demonstrate here the trapping of 5 μm polystyrene beads in an array composed of 522 parallel traps arranged in an equilateral triangle tiling pattern spaced by 9 μm. Fig. 4a shows a brightfield picture of an array of 522 traps used for this study, partially filled with beads and connected by a buried channel to a control PDMS channel on the right. The triangles visible on the membrane are the regions where no access holes or traps were designed to prevent under-etch and mechanically support the membrane. An orange filter is superimposed to the image where the PDMS is bonded to the substrate, and the inset shows an SEM picture of the 2 μm diameter traps. We made the choice of operating the chip at constant pressure in order to avoid the need to use complex feedback control systems. Supplementary file S1† shows a video of the filling of the arrays with 5 μm diameter beads at an inlet pressure of P_in = 40 mbar and a control pressure P_c = 0 mbar.

Fig. 4 (a) Bright-field picture of an array of 522 traps partially filled with polystyrene beads, connected by a buried channel to a control channel on the right. An orange filter highlights the regions where the PDMS is bonded to the substrate. The inset shows an SEM picture of the 2 μm traps. (b) Graph showing the experimentally measured evolution of the fraction of lost beads as a function of the filling percentage of the array for different inlet pressures P_in and pressure ratios P_c/P_in. The inset shows a colormap of the experimentally measured order of the filling of the array.

Fig. 4b shows the experimentally measured fraction of lost beads, defined as , as a function of the percentage of filled traps for different pressures P_in and pressure ratios P_c/P_in, measured while filling the arrays. Using these measurements, the trapping efficiency, here defined as η = 1 − LF, at 98% filling was measured and was found to be constant for experiments with the same pressure ratio and different inlet pressures. The trapping efficiency at 98% filling percentage and its standard deviation for a pressure ratio P_c/P_in = 0.2 were respectively 70.4% and 1.1%, whereas for a pressure ratio of P_c/P_in = 0, the trapping efficiency and its standard deviation were 94.4% and 2.7%. By adapting the circuit in Fig. 2 and replacing the resistance of a single trap of resistance R_h by n traps in parallel of the total resistance R_h/n, the ratio of the inlet flow going in the buried channel is calculated as follows:

This equation indicates that the flow ratio decreases as the array is being filled with particles, explaining the increasing lost fraction as the filling percentage of the array increases as shown in Fig. 4b. This also shows that the flow ratio can be controlled dynamically by the pressure ratio only, decreasing when the latter increases. A constant trapping efficiency for equivalent pressure ratios hence indicates the dependency of the trapping efficiency on the ratio of the inlet flow going inside the traps, similar to other trapping mechanisms.^36,37 The geometry also plays a role in the lost fraction as can be seen from the inset of Fig. 4b: the center-top part is the first to be filled whereas the borders are the last and most difficult to be filled, following the particle distribution in the channel. We can also notice that the centerline of the trapped bead distribution is offset from the center of the channel towards the control channel. This comes from the increased resistance created by the channel under the membrane favoring the filling of the traps close to the control channel. An array geometry for improved efficiency would thus contain more traps in the center of the PDMS channel with a bias towards the control channel, following the curve shape formed by the trapped bead distribution as shown in Fig. 4b. The time needed to reach the 98% filling percentage increases with a reduction of the inlet pressure because of the lower flow rate, and increases with a larger pressure ratio P_c/P_in, which indicates that for an efficient and fast filling, a small pressure ratio and large inlet pressure should be used.

Furthermore, if the only criteria are fast and efficient filling, the resistances can be tailored for that application with a small inlet and buried channel resistances, R_in and R_bc, together with large outlet resistance R_out. This combination will increase the flow ratio Q_bc/Q_in, improve the trapping efficiency and reduce the filling time. In order to achieve 100% trapping efficiency, the downstream path should be of infinite resistance R_out = ∞. To that end, the downstream path could either not exist and be designed as a dead-end, which would remove the possibility of flowing subsequent analytes over the array and the releasing in a channel path different than the inlet, or be blocked with a valve that could be switched off once the array is totally filled.

98% of the beads could be released from the array and brought to the outlet channel by increasing the control pressure together with the inlet pressure.

2.4 Hydrodynamic trapping of cells in the arrays

The design used for the trapping of cells was modified to allow the passage of flowing cells around the immobilized ones, and the triangular tiling pattern forces the contact between the trapped and flowing cells. The distance between two traps was thus set to 50 μm. During the filling of an array of traps with cells, the already immobilized cells are subjected to a pressure gradient ΔP_p that varies with 1/n, with n being the number of remaining free traps as follows:ΔP_p thus increases significantly as the last free traps are filled to reach the maximum pressure, defined by eqn (2), once the array is totally filled. We determined the maximum pressure a cell can withstand for 15 minutes as shown in Fig. 3a and found that the maximum trapping efficiency is achieved at P_c = 0, which determines the working inlet pressure to fill an array with cells: . Once the array is totally filled, the control pressure P_c can be increased to minimize ΔP_p while maintaining the trapped cells intact and flowing additional material on top of the trapped cells, as illustrated in supplementary file S3.†

Fig. 5 shows the fluorescence picture of the successful trapping of 24 Colo205 cells stained with calcein AM in a compact array of 25 traps. Supplementary file S2† shows the trapping of the Colo205 cells in the array using an inlet pressure of P_in = 40 mbar and a control pressure of P_c = 0 mbar. We chose traps with a diameter of 5 μm to allow working at reasonable pressures without compromising the successful filling of the array because of debris clogging the traps, which was the case with the 3 μm diameter traps. The inlet pressure was set to 40 mbar in a chip with R_in = R_out such that the maximum pressure the cells were subjected to was 20 mbar, below the threshold pressure corresponding to that of the trap diameter, while working at a pressure ratio of P_c/P_in = 0 for a maximum trapping efficiency. The trapping efficiency η was 88.4% at 92% filling percentage and η = 68.6% at 96% filling percentage. 88% of the cells could be released from the array and brought to the outlet channel by increasing the control pressure together with the inlet pressure.

Fig. 5 Fluorescence picture showing the successful trapping of the 24 Colo205 cells stained with calcein AM in an array of 25 traps. The pressures are set so that the difference of pressure ΔP_p endured by the cells is always under the pressure threshold for membrane rupture.

3 Discussion

This novel type of hydrodynamic traps differs significantly from the typical traps found in the literature. It resolves the problem of space cluttering around the trapped object while allowing a dynamic control over the trapping state. We compare here different characteristics of the array of planar hydrodynamic traps with the two common types of hydrodynamic trapping arrays presented in the introduction in the case of particle trapping: the pachinko and the serpentine arrays.

Scalability and density of traps

An interesting parameter to compare is the scalability of the array, or how many traps the system can handle. Each trap of the serpentine and pachinko trapping principles is independent of each other and relies on local flow lines. Once the geometry of one trap is optimized, they can theoretically be scaled indefinitely. Both types can be optimized for density,^18,38 however the pachinko arrays are more dense and can accommodate more traps per unit surface because the serpentine arrays require the presence of a space-consuming bypass channel. In contrast, the planar hydrodynamic traps proposed here are interdependent when used in an array: eqn (4) applied to a single trap shows that the flow passing in each trap depends on the percentage of filled traps of an array. It was also shown that the traps close to the border opposite to the control pressure channel were more difficult to fill due to the additional resistance under the membrane. To scale up the planar traps and limit interdependency, the array should be divided into separate parts controlled by independent control channels and filled sequentially: while the first part of the array is being filled, the other parts can be operated in idle mode and so forth until all parts are filled. This comes to the cost of increasing the complexity of the control. However, the density of the traps can be higher than that for the other two mechanisms since there is no material around the trap and more particles can be observed in a defined field of view.

Addressability and multiplexing

We suggested using independent control channels for different parts of an array to allow scalability, and this property can be exploited to multiplex and capture different species in the different parts of the channel. The possibility of running the chip in the idle mode and the possibility of multiplexing are also available using the serpentine array only when coupled with side pneumatic valve actuation.²¹

Compliance with the particle size

A limitation of the serpentine and pachinko trapping methods comes from the fact that the single-particle trapping efficiency depends on the height of the channel. Although the height has to be larger than the size of the particle to avoid clogging for any type of trapping, a height larger than twice that of the particle causes multiple particles to stack in a single trap in the pachinko and serpentine arrays. In contrast, the height of the main channel is not limited in the case of coplanar traps, as proved by the trapping of beads of 5 μm diameter in a channel of 30 μm height.

Trapping efficiency and filling percentage

Due to its deterministic trapping property, the serpentine trapping can reach 100% trapping efficiency and filling percentage. The pachinko array was shown to have a filling percentage up to >99%¹⁸ but no reported trapping efficiency was found for beads. In comparison, the planar hydrodynamic traps have both good trapping efficiency and filling percentage with respective values of 94% and 98%.

Space availability and complexity of fabrication

The planar hydrodynamic traps have the advantage of having the space around the trapped particle completely available for the interaction with another particle, which can be manipulated with different forces, such as hydrodynamics, optical tweezers, dielectrophoresis, or others³⁹ as the microfabrication process with standard materials and processes allows an additional layer to be easily added to fabricate microelectrodes aligned to the buried and PDMS channels. Supplementary file S3† shows the flow of subsequent cells around the ones trapped in the array, demonstrating the potential of this technology for studying in flow cell–cell interaction. This space could also be used to place electrodes for the impedance measurement of the particle for example. However, this possibility comes to the cost of an increased complexity of fabrication: while the serpentine and pachinko devices can be fabricated by a single PDMS casting step, the planar hydrodynamic traps require an extra photolithography step for the fabrication of the buried channels.

4 Conclusions

We presented novel hydrodynamic traps that enable the trapping of beads and cells in flow with no material surrounding the trapped particles. The traps can be dynamically operated in different modes thanks to the presence of a pressure control channel and are able to trap and release particles, but also stand in an idle mode. We studied the resistance to pressure difference of cells trapped in holes of different diameters and fitted the result using a theoretical model from pipette assays to extract the tension at rupture of the cell membrane. We proposed a model to understand the properties of this type and showed that this technology could be used for the trapping and releasing of beads and cells in compact arrays, opening new possibilities in the field of biological assays. We believe that the presented fabrication method for multi-level microfluidic channels connected by vias compatible with electrode fabrication can open new possibilities in different fields of study such as microfluidic filtering, impedance measurements, on-chip patch clamping, flow focusing, microfluidic mixing and droplet microfluidics, among others.

Author contributions

Conceptualization: C. L., J. C., A. B. and P. R.; Investigation: C. L. and K. U.; Data Curation: C. L., K. U. and D. M.; Writing original draft: C. L.; Editing: C. L., K. U., J. C., D. M., A. B. and P. R.; Supervision: A. B. and P. R.

Conflicts of interest

The authors declare that they have no conflict of interest.

Acknowledgements

We would like to deeply thank Margaux Duchamp for her precious help in the laboratory and for the discussion. This work was possible thanks to the outstanding platform for micro and nanofabrication of EPFL: the Center for MicroNanoTechnology (CMi). This work was supported by the French Agence Nationale de la Recherche and the Swiss National Science Foundation through the CoDiCell project (contract “ANR-17-CE33-0009” and “No. 00021E_175592/1”, respectively).

References

1. P. Shinde, L. Mohan, A. Kumar, K. Dey, A. Maddi, A. Patananan, F.-G. Tseng, H.-Y. Chang, M. Nagai and T. Santra, Int. J. Mol. Sci., 2018, 19, 3143.
2. N. Mittal, A. Rosenthal and J. Voldman, Lab Chip, 2007, 7, 1146.
3. M. Kim, J. Lee, K. Nam, I. Park, M. Son, H. Ko, S. Lee, D. Yoon, W.-J. Chang and S. Lee, Sensors, 2017, 17, 2272.
4. P. Polimeno, A. Magazzù, M. A. Iatì, F. Patti, R. Saija, C. D. Esposti Boschi, M. G. Donato, P. G. Gucciardi, P. H. Jones, G. Volpe and O. M. Maragò, J. Quant. Spectrosc. Radiat. Transfer, 2018, 218, 131–150.
5. X. Wang, S. Chen, M. Kong, Z. Wang, K. D. Costa, R. A. Li and D. Sun, Lab Chip, 2011, 11, 3656.
6. D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Nat. Commun., 2015, 6, 8686.
7. X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11105–11109.
8. D. Di Carlo, N. Aghdam and L. P. Lee, Anal. Chem., 2006, 78(14), 4925–4930.
9. M. Nagai, K. Oohara, K. Kato, T. Kawashima and T. Shibata, Biomed. Microdevices, 2015, 17, 41.
10. N.-T. Huang, Y.-J. Hwong and R. L. Lai, Microfluid. Nanofluid., 2018, 22, 16.
11. L. Pang, J. Ding, X.-X. Liu, H. Yuan, Y. Ge, J. Fan and S.-K. Fan, TrAC, Trends Anal. Chem., 2020, 129, 115940.
12. B. Dura, S. K. Dougan, M. Barisa, M. M. Hoehl, C. T. Lo, H. L. Ploegh and J. Voldman, Nat. Commun., 2015, 6, 5940.
13. B. Dura, M. M. Servos, R. M. Barry, H. L. Ploegh, S. K. Dougan and J. Voldman, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E3599–E3608.
14. M. Duchamp, T. Dahoun, C. Vaillier, M. Arnaud, S. Bobisse, G. Coukos, A. Harari and P. Renaud, RSC Adv., 2019, 9, 41066–41073.
15. I. F. Pinto, R. R. G. Soares, M. E.-L. Mäkinen, V. Chotteau and A. Russom, ACS Sens., 2021, 6(3), 842–851.
16. A.-E. Saliba, L. Saias, E. Psychari, N. Minc, D. Simon, F.-C. Bidard, C. Mathiot, J.-Y. Pierga, V. Fraisier and J. E. A. Salamero, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14524–14529.
17. M. Tayebi, Y. Zhou, P. Tripathi, R. Chandramohanadas and Y. Ai, Anal. Chem., 2020, 92, 10733–10742.
18. X. Xu, P. Sarder, Z. Li and A. Nehorai, Biomicrofluidics, 2013, 7, 014112.
19. W.-H. Tan and S. Takeuchi, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 1146–1151.
20. J. Chung, Y.-J. Kim and E. Yoon, Appl. Phys. Lett., 2011, 98, 123701.
21. H. Kim and J. Kim, Microfluid. Nanofluid., 2013, 16, 623–633.
22. H. S. Kim, T. P. Devarenne and A. Han, Lab Chip, 2015, 15, 2467–2475.
23. L. Pang, W. Liu, C. Tian, J. Xu, T. Li, S.-W. Chen and J. Wang, Lab Chip, 2016, 16, 4612–4620.
24. C.-H. Lin, Y.-H. Hsiao, H.-C. Chang, C.-F. Yeh, C.-K. He, E. M. Salm, C. Chen, I.-M. Chiu and C.-H. Hsu, Lab Chip, 2015, 15, 2928–2938.
25. Y. Tang, J. Shi, S. Li, L. Wang, Y. E. Cayre and Y. Chen, Sci. Rep., 2014, 4, 6052.
26. Y. Kimura, M. Gel, B. Techaumnat, H. Oana, H. Kotera and M. Washizu, Electrophoresis, 2011, 32, 2496–2501.
27. W. Kaplan, H. Elderstig and C. Veider, A novel fabrication method of capillary tubes on quartz for chemical analysis applications, Proceedings IEEE Micro Electro Mechanical Systems An Investigation of Micro Structures, Sensors, Actuators, Machines and Robotic Systems, 1994, pp. 63–68,  DOI:10.1109/MEMSYS.1994.555599.
28. J. Cottet, C. Vaillier, F. Buret, M. Frénéa-Robin and P. Renaud, Biomicrofluidics, 2017, 11, 064111.
29. H. Bruus, Theoretical microfluidics, Oxford Univ. Press, 2011.
30. K. W. Oh, K. Lee, B. Ahn and E. P. Furlani, Lab Chip, 2012, 12, 515–545.
31. C. Lim, E. Zhou and S. Quek, J. Biomech., 2006, 39, 195–216.
32. R. Kwok and E. Evans, Biophys. J., 1981, 35, 637–652.
33. S. C. W. Tan, T. Yang, Y. Gong and K. Liao, J. Biomech., 2011, 44, 1361–1366.
34. P. Sens and J. Plastino, J. Phys.: Condens. Matter, 2015, 27, 273103.
35. S. U. Alam Shibly, C. Ghatak, M. A. Sayem Karal, M. Moniruzzaman and M. Yamazaki, Biophys. J., 2016, 111, 2190–2201.
36. A. Sohrabi Kashani and M. Packirisamy, Sci. Rep., 2019, 9, 5511.
37. S. Kobel, A. Valero, J. Latt, P. Renaud and M. Lutolf, Lab Chip, 2010, 10, 857.
38. D. Jin, B. Deng, J. X. Li, W. Cai, L. Tu, J. Chen, Q. Wu and W. H. Wang, Biomicrofluidics, 2015, 9, 014101.
39. M. Arnaud, M. Duchamp, S. Bobisse, P. Renaud, G. Coukos and A. Harari, Curr. Opin. Biotechnol., 2020, 65, 52–59.

---

Footnotes

† Supplementary files are available externally at DOI: 10.5281/zenodo.5483561

‡ Present address: Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA.

---