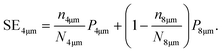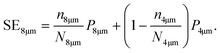Efficient flowless separation of mixed microbead populations on periodic ferromagnetic surface structures

Abstract

The simultaneous separational control of motion of individual objects is vital to achieve high efficiency separation for biological analytes in biomedical applications. Here, we show the selective and directed movement of different populations of microbeads depending on their size in a flowless environment by means of a hexagonally structured soft-magnetic microchip platform. By adjusting strength and asymmetry of a modulated in-plane magnetic field, discrete and switchable movement patterns of two different types of beads above a magnetic surface structure are achieved. Starting from a heterogeneous mixture of bead populations and depending on the type of field sequences, directional forward transport of one type of beads is achieved, while the other bead population is immobilized. Despite significant size and magnetic content distributions within each population of microbeads, high separation efficiencies are demonstrated. The selection and movement processes are supported by full-scale magnetofluidic numerical simulations. The magnetic platform allowing multidirectional and selective microbead movement can greatly contribute to the progress of functional lab-on-chip and future diagnostics devices.

---

Introduction

Magnetic microbeads are being utilized to handle biomaterials in microfluidic environments for diagnostics and lab-on-chip applications.^1,2 Labelled to the biological analytes such as proteins, DNAs and circulating tumour cells, microbeads enable the isolation of target analytes in complex biological samples under externally applied magnetic fields.

Magnetically patterned microchip surfaces are employed for the handling and sensing of magnetic bead-biological cell conjugates at a single cell level.^3,4 Utilizing various magnetic platforms, populations of microbeads are manipulated to perform numerous analytical operations.^5–7 One type of particles are selectively transported across a chip during the immobile response of the other type.^8–12 Multiple particles are simultaneously separated to different directions^12,13 and collected at various locations⁶ on a chip. A coexistent control over the motion of multiple type particles is crucial for the efficient separation of target biomolecular entities. Yet, the non-reproducible motion of particles and the undesired motion of immobilized particles may result directly in a reduced separation efficiency of the devices.^9,12,13 The particle separation on a magnetic surface is dependent on the mutual magnetic interaction between immobile and moving particles. Furthermore, geometric and magnetic irregularities in the manipulation system may affect the paths of particle motion, causing inefficient separation of mixed particle populations. To understand the influence of magnetic irregularities, the paths of moving particles are investigated through numerical simulations and experiments for single beads.^14–16 The separation efficiency of magnetic beads is often not stated^{8,9,11–13,17} or it is significant lower⁶ than for flow-based magnetic systems.^18,19 Therefore, the separation of mixed magnetic beads is considered an obstacle to the commercial adaptation of magnetic chip technology.⁴ The non-uniform magnetic response of particle movement patterns,²⁰ magnetic field related inappropriate control parameters,¹⁴ and improper size of magnetic particles^14,20 are the presumed reasons of inefficient particle separation. By optimizing the geometric parameters such as shape, size and distance of periodic magnetic patterns together with the size of the microbeads, the simultaneous separation of different type beads has been realized.^6,9–13,21 Achieving high separation efficiency is further impeded due to the existing heterogeneity of microbead population properties, determined as Gaussian property distributions.^6,8,17,21 Yet, high efficiency microbead separation was reported in ref. 21.

Despite the benefits of single cell analyses on magnetically patterned chips, flow-based magnetic technology is the preferred option to obtain rapid analyses.^{3,4,19,22–25} In flow-based systems the results of analyses rely on ensemble averaging, which limits the access to single analytes. On the other hand, the process throughput of flow-less systems is lower than for flow-based devices.³ To improve device performance, flow-less magnetic platforms are often combined with flow cytometry.^21,26 However, the commercialization of such platforms has not been realized so far. Existing magnetic chip technology has shown the simultaneous manipulation of about 10⁵ microbeads.³ A magnetic surface based device capable of handling more than 10⁷ microbeads is envisioned to fill the gap between laboratory and commercial device technology.³

Magnetic patterns in closely spaced arrangements increase the surface site density on chips for positioning and separation of large populations of microbeads to compete with the high-throughput of flow-based devices.³ A fundamental requirement for the selective manipulation of complete populations is the reproducibility of the movement paths for different beads at the single bead level.^9,14

A magnetic microchip enabling the selectable sorting of bead populations should provide an ideal platform for handling the multiple analytes from complex biological samples. A lab-on-chip tool should provide nearly entire control over single cells and their populations, enabling good separation efficiency.

In this work, we present the controlled and independent movement of two types of microbeads across a surface of a hexagonally arranged soft magnetic triangular thin film element array. The work is based on our initial work for the simultaneous two-way separation for single beads.¹² There, we could show that changes in the stray magnetic field landscapes slightly alter the equilibrium bead positions, by which the emergence and direction of bead motion with the application of alternating magnetic field sequences is defined.

Here, we show and explain the selectable movement and, as a result, the separation of microbeads at their population level. Proper combinations of in-plane magnetic field strengths and directions permit the directional and selective motion of a single population of beads, while keeping the other type of beads immobile. Quasi square wave modulated external magnetic fields sequences move the bead ensembles selectively along the same magnetic micro-corridors of hexagonal potential energy landscapes across the chip surface. Mobility and immobility are interchangeable with variations of magnetic field angle and amplitude. By this, a high separation efficiency is demonstrated based on a nearly complete immobilization of one type of beads with the directed motion of the other type of beads. Two alternative magnetic field sequences enable the selective separation of the two different populations of microbeads. The selectable motion of both small and large beads agrees with the simulated bead motion characteristics.

Methods

Ferromagnetic surface

The ferromagnetic surface for bead manipulation was prepared as a Ta (5 nm)/Ni₈₁Fe₁₉ (50 nm)/TaN (3 nm) layer on an oxidized silicon wafer by sputter deposition. The covering of ferromagnetic structures with TaN protects the Ni₈₁Fe₁₉ layer from corrosion by the aqueous medium. The magnetic surface was patterned by standard photolithography and selective ion beam etching, resulting in an array of micrometre sized equilateral ferromagnetic triangles. The patterned wafer was diced into pieces of 10 mm × 10 mm for single Si chips. The soft magnetic Ni₈₁Fe₁₉ has a saturation polarization J_s = 1.0 T. Typical values of uniaxial anisotropies of the material are very low at a value of K_u = 200 J m⁻³.

Magnetic force microscopy

Magnetic force microscopy (MFM) above the magnetic surface was performed with a modified commercial imaging system (Nanosurf LensAFM).²⁷ The customized MFM system allows the application of in-plane magnetic fields with varying angle and amplitude. The imaging of the magnetic structures was performed in phase contrast mode with a medium magnetic moment hard magnetic tip at a distance of 500 nm above the sample surface.

Microbead solution

The device experiments are performed with superparamagnetic polystyrene-based microbeads (micromer-M) with different diameters, which were purchased from micromod Partikeltechnologie GmbH, Rostock, Germany.²⁸ Monodispersed superparamagnetic particles of magnetite are embedded at the shell of the spherical beads. To ensure the encapsulation of magnetite the beads are coated with an additional polymer layer. In order to investigate the movement of individual microspheres on the ferromagnetic structures, the stock suspension of the particles was diluted in distilled water to a microbead concentration of 5 × 10⁻⁶ mg ml⁻¹. Surface adhesion of microbeads to the microfluidic chip was avoided by reducing the surface tension of the aqueous solution with an addition of 0.02 ± 0.01% Triton X-100 to the microbeads' suspension, facilitating smooth movement of the microbeads. Superparamagnetic beads with a diameter of Ø_MB = 4 μm and Ø_MB = 8 μm beads were used in the experiments.

Microfluidic cell

A paraffin-polyethylene sealing film (Parafilm M) was used to form a closed microfluidic cell on top of a single Si substrate chip. The well of the cell is 400 μm deep and has a diameter of 7 mm. A transparent microscope cover glass was used to seal the cell. This allows the direct optical observation of the microbeads' motion.

Simulations

The magnetisation configuration of the triangular ferromagnetic array structure was numerically evaluated for the experimentally applied external magnetic field amplitudes and angles by micromagnetic calculations using MuMax3.²⁹ A cell size of 17.8 nm × 20.5 nm × 12.5 nm was employed for the calculations of the micromagnetic configurations, covering a triangle magnetic element in the centre and a quarter of a triangle in each corner to comprise a unit cell for the hexagonal element arrangement. The influence of a low uniaxial magnetic anisotropy was neglected for the calculations, as the applied magnetic fields are much higher than the anisotropy field. A stiffness constant of A = 1.3 × 10⁻¹¹ J m⁻¹ (ref. 30) is used for the calculations. Periodic boundary conditions are applied for the two different field configurations. The magnetization data was averaged over the film thickness. The expected MFM response in 500 nm height was computed using MuMax3's built-in MFM function.²⁹

To quantitatively compute the trajectory of the different sized microbeads across the array of triangular magnetic elements, we used the algorithm described in ref. 31. It takes the magnetic forces between the superparamagnetic microbeads and the micromagnetic state of the parent structure, as well as the hydrodynamic drag forces, into account. Surface friction was neglected in accordance with a lifting of the bead above the surface during movement. For this, the micromagnetic data imported from MuMax3 was arranged in the magnetic chip layout and averaged by a factor of four prior to the potential calculation. The potential grid used was 120 × 120 with cell dimensions of 300 nm × 175 nm. In the shown microfluidic simulations we used a volume susceptibility χ_v = 0.065 for particles with Ø_MB = 4 μm and χ_v = 0.035 for the Ø_MB = 8 μm beads, the ratio of which nearly corresponding to the size difference. We applied moving periodic boundary conditions to accommodate for the particle moving across numerous repeating magnetic structures. For the alternating field configurations, a switching time of t_s = 2 ms between the different field angles is assumed in the simulations with a temporal resolution of Δt = 10⁻⁴ s. The value agrees with the temporal magnetic field measurements of the complementary real-world experiments. The equation of bead motion is calculated for time steps of a maximum of Δt_max = 7 × 10⁻⁴ s. The viscosity of the aqueous medium is set to the room temperature value of viscosity of water η = 9.547 × 10⁻⁴ Pa s.

Imaging and data analysis

An optical polarization microscope was employed to track the movement of beads. The microscope is routinely used for magnetic domain observation³² and is therefore equipped with a two-axis in-plane electromagnet with soft-magnetic laminated yokes to generate the varying magnetic in-plane fields. Two bipolar power supplies are used for the control of the two-axis magnet. The electromagnet allows for applying individual and computer-controlled in-plane magnetic vector fields along different axes with varying amplitudes of up to H_ext ≈ 200 kA m⁻¹. The magnetic field switching times are in the order of t_s = 2 ms, limited by switching speed of the soft-magnetic laminated yokes. The magnet is centred to the microscope objective and the field of view. Magnetic field homogeneity within a 1 mm × 1 mm region is better than 0.6%. The field of view for the microscopic observation is below 1 mm × 1 mm for the presented experiments. Magnetic field homogeneity over a 10 mm × 10 mm area is better than 8%.

The amplitudes and angles of the magnetic field were recorded for all image frames. A digital CCD camera was utilized to record the images with a frame rate of 15 Hz. The spatial–temporal position of the moving microbeads was tracked using the image processing package ImageJ.³³ Using this, the spatial x- and y-coordinates of the centre of the microsphere are obtained for all individual image frames. From this the path of microbead motion is determined.

Results

Hexagonal ferromagnetic surface

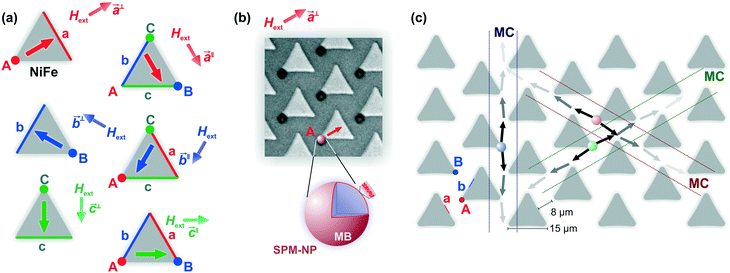
Discrete Ni₈₁Fe₁₉ triangular patterns in a 2D hexagonal arrangement provide the micromagnetic surface for the free and selectable lateral movement of microbeads along trisymmetric magnetic pathways. The general design of the pattern and the in principle multiple applicable corridors of motion are reported in ref. 12. The overall arrangement is shown in Fig. 1. Using in-plane sequences of a time-varying external magnetic field H_ext the identical corners A–C and the opposite edges a–c of the triangular magnetic elements are magnetically polarized differently (Fig. 1a). We use such a scheme for the positioning of superparamagnetic microbeads (Fig. 1b). Applying magnetic field sequences, microbeads become movable along the corresponding directions as shown in Fig. 1c. This enables the movement of microbeads along certain microcorridors (MC) down to the single particle level. The corresponding possible fundamental directions of motion are indicated as black arrows.

Fig. 1 (a) Schematic top view of a hexagonally patterned discrete Ni₈₁Fe₁₉ triangular structures on a chip. The main directions of the applied field H_ext with the field along (||) or perpendicular (⊥) to one of the sides of the triangle are sketched. The parallel and perpendicular orientation of the applied magnetic field are assigned as a⃑^∥, a⃑^⊥ and b⃑^∥, b⃑^⊥ relative to the edges a and b (c equivalent). (b) Optical micrograph of an ensemble of superparamagnetic (SPM) microbeads adhering to the triangular ferromagnetic elements and an applied magnetic field, as indicated. A sketch of the microbeads with embedded superparamagnetic nanoparticles (SPM-NP) is shown. (c) Sketch of a single triangular ferromagnetic Ni₈₁Fe₁₉ elements with H_ext switching its direction between edges a and b to move the beads in vertical direction along a vertical microchannel (MC). For the vertical movement of microbeads, the closely spaced adhesion sites are exemplary highlighted. Depending on the alternating configuration of the magnetic field, microbeads are consecutively and selectively collected at specific element corners and the microbeads are thereby moved across the chip surface along different microchannels. The thickness of the Ni₈₁Fe₁₉ patterned film is 50 nm. Dimension and distance of the equilateral triangular structures are indicated.

The selective movement of different microbeads relies on the exact orientation and sequence of the applied magnetic field. Aligning the magnetic field H_ext with its directions switching between normal to the edges a and b, along a⃑^⊥ and b⃑^⊥, polarizes the edges and the opposite corners A and B of the magnetic triangles (Fig. 1a, left). The highlighted vertices A and B and the opposite edges a and b provide a closely spaced adhesion network, generating a magnetic pathway for the vertical movement of microbeads. Parallel orientations of the applied field are assigned as a⃑^∥ and b⃑^∥ and lead to magnetic poles at two edges and two corners for each applied field direction (Fig. 1a, right).

Selective transport of different microbeads

The overall selective separation of a mixture of microbeads by the sole and directed transport of one size of beads on the periodic magnetic element array is shown. Separation is accomplished by the simultaneous locking of the other size of beads. Motion and immobility of the two types of beads can be inverted. This is achieved by altering the applied magnetic field sequences in terms of field strength and field orientation. We thus enable a multimodal manipulation of different bead populations and the efficient separation of different types of beads. Because of the structural periodicity of the magnetic triangular micropatterns, microbeads are trapped at different positions, depending on their size and interactive volume.

The achievable movement depends on the bead diameter to stray magnetic field periodicity, defined by the magnetic array pattern.¹¹ Larger diameter beads may interact with the stray field gradients of adjacent magnetic elements, whereas smaller diameter beads mainly interact with the stray field gradients of a single magnetic element. On the other hand, the bead diameter dependent drag force adds a dynamic component to the bead motion.

Once positioned, the beads can be moved selectively across the chip surface by an applied proper bi-modal magnetic field sequence, the elements and the achievement of which are demonstrated next.

Selective forward movement of smaller sized beads

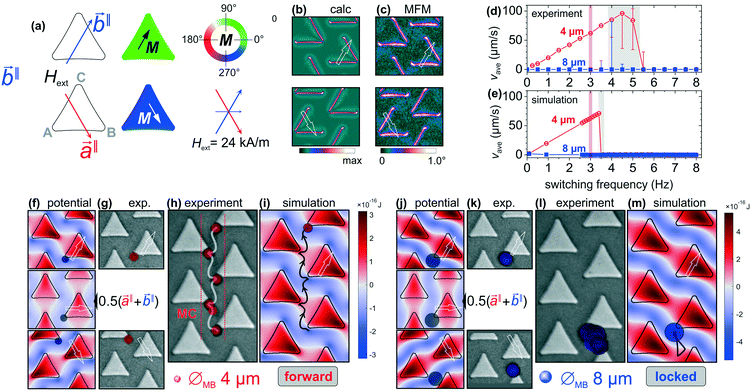
Here we prove the selective movement of smaller beads under conditions where the positions of larger beads are maintained. Orienting the applied field along one edge of the triangles results in magnetic polarization at the other two edges and related corners (Fig. 1a), forming a specific stray magnetic field gradient landscape. An overview on the magnetic and potential landscape together with exemplary results for the selective forward movement of beads with a diameter Ø_MB = 4 μm together with the simultaneous locked motion of a Ø_MB = 8 μm bead is presented in Fig. 2. The applied magnetic field is switched with a fixed field amplitude of H_ext = 24 kA m⁻¹ alternatively between the two directions b⃑^∥ and a⃑^∥.

Fig. 2 Forward motion of a Ø_MB = 4 μm bead with a simultaneous locked motion of a Ø_MB = 8 μm bead for alternating switching applied magnetic field amplitudes of H_ext = 24 kA m⁻¹. The frequency of switching is 3 Hz. (a) Field conditions with H_ext along b⃑^∥ and a⃑^∥ and the corresponding calculated states of magnetization of the Ni₈₁Fe₁₉ elements. (b) Calculated out-of-plane stray field gradients under the two conditions of magnetic field application and (c) corresponding magnetic force microscopy (MFM) images obtained under the same experimental conditions. The main magnetization directions are indicated. (d) Experimental and (e) simulated average movement velocity v_aveversus field switching frequency f_swit. The chosen stable frequency for the experiments (f_swit = 3 Hz) and the regime of incomplete bead motion are indicated. (f) Simulated potential landscapes and equilibrium positions for the Ø_MB = 4 μm bead at the magnetic field states b⃑^∥ and a⃑^∥. The central image displays the potential state during field switching [0.5·(a⃑^∥ + b⃑^∥)]. (g) Optical images of a Ø_MB = 4 μm bead in its equilibrium positions under the two magnetic field conditions. (h) Experimental path of upward tip-to-tip microbead motion for the applied field alternatively changing between b⃑^∥ and a⃑^∥. The recorded positions of the mobile bead are highlighted. (i) Corresponding simulated path of bead motion for a Ø_MB = 4 μm bead. The calculated path of motion along a vertical microcorridor is superimposed in (h). (j) Magnetic potential landscape and (k) optical micrographs show the equilibrium positions of Ø_MB = 8 μm beads with the two different magnetic field conditions. (l) Experimental and (m) simulated path of the locked bead motion.

Fig. 2a shows the corresponding results of micromagnetic calculations with magnetically polarized triangles with the sites of higher (corners) and lower (edges) magnitudes of magnetic field gradients. The stray magnetic field gradients at the corners and edges of the magnetic triangles are determined for the two principle directions of the applied magnetic field (Fig. 2b). Comparing the results of micromagnetic simulations with the MFM data (Fig. 2c) confirms the validity of the micromagnetic simulations, forming the base for the simulations of bead motion. Changing the field direction from b⃑^∥ to a⃑^∥ leads to a quasi-inversion of the corresponding field gradient landscape and energy potential landscape.

The motion behaviour of the different sized microbeads with frequency is analysed by experiments (Fig. 2d) and simulations (Fig. 2e). Despite differences in the critical frequency, a sufficient match between simulations and experiments is obtained. Especially the simulations provide insight in the motion path of the beads. For the further experiments, the field switching frequency was chosen at f_swit = 3 Hz in accordance with the presented results. This frequency is well below the critical frequency of the moving smaller beads. No motion over the probed frequency range was detected for the larger beads.

Fig. 2f shows the calculated magnetic potential energy landscapes together with the experimentally obtained positions of a Ø_MB = 4 μm diameter bead becoming positioned slightly below corner A and B for both field directions along b⃑^∥ and a⃑^∥. For the intermediate switching field condition (0.5·(a⃑^∥ + b⃑^∥)) and with the bead still below A, the potential landscape reveals a potential landscape favouring the initial movement of the bead away from corner A (centre image in Fig. 2f). The experimentally obtained positions of bead resting are displayed in Fig. 2g. The bead positions agree with the potential minima from the simulation. The experimental moving response of a bead with alternating field conditions is shown in Fig. 2h (see also ESI† Movie S1), where the tracked bead positions and the simulated path of motion in forward direction across the chip surface are indicated. By switching the magnetic field between b⃑^∥ to a⃑^∥, the microbead moves first away from one corner of higher field gradient (A) and then forward to the next corner of higher field gradient (B) and vice versa. This is agreement with the change of the potential landscape sketched in Fig. 2f. Therefore, for continuously changing field vectors between b⃑^∥ and a⃑^∥ the bead is moved in a forward (upward) direction with continuous flipping the magnetic potential landscape. Fig. 2i shows the simulated trajectory of the bead together with the potential energy landscape with the field along b⃑^∥ for the same conditions as in the experiment (see also ESI† Movie S2). The modelled data matches well the experimental response probed with lower sampling (frame) rate at identical applied field parameters. The results display a curved bead motion, not to be identified from the lower frame rate imaging.

For the same magnetic field conditions the locked motion of the larger Ø_MB = 8 μm bead is realized. The immobilization is a result of the beads' larger interactive volume on top of the closely spaced magnetic field gradients of the magnetic elements. For the initial field state b⃑^∥, the shifted position of the larger bead is indicated at corner A as seen from the calculated field gradient maps in Fig. 2j. The trapped position of the larger bead is determined by the corner A with the additional contribution form the adjacent edge gradient of the same triangle. This causes a large asymmetric shift in bead position around the corner. This effect of the field gradients from the neighbouring element adds to the shifted position of the bead. After switching the field direction from b⃑^∥ to a⃑^∥, the beads equilibrium position is towards the nearest higher field gradient at the top corner B of the neighbouring element. The optical images in Fig. 2k show the corresponding equilibrium positions of the bead before and after the switching of applied magnetic field which agrees with the simulation results. During the continuous field switching between b⃑^∥ and a⃑^∥ the bead is locked between the close positions (Fig. 2l, see also ESI† Movie S3). Modelling with equivalent applied parameters confirms the results (Fig. 2m, see also ESI† Movie S4). The larger bead moves in a triangular fashion and remains with the alternating field application.

Control experiments confirm no dependence of the motion of larger Ø_MB = 8 μm beads on the sense of directional switching of the applied field, i.e. between b⃑^∥ and now -a⃑^∥. In contrast, the motion response of smaller beads is determined by the signs of the applied switching fields. When the field sequence is altered from its initial state to b⃑^∥ and -a⃑^∥, the direction of bead motion changes accordingly. This consequently causes its trapping at the top corner of the adjacent pattern. Thus, altering the field directions along ±a⃑^∥, ±b⃑^∥ and ±c⃑^∥ different microcorridors and moving directions are realized on the trisymmetric magnetic pattern.

Selective forward movement of a larger bead

Here we show the selective movement of larger beads, where now the smaller beads' positions are kept. The stable position of the beads at a corner of the triangle and the change of their position with respect to the adjacent elements is controllable by adjusting the magnitude of the stray magnetic field gradient by varying the strength and the direction of the applied magnetic field. Using the size of bead as a control parameter, we now show that the characteristics of microbead motion can be inverted, so that the selectivity of bead movement and immobility is precisely the opposite with a modified sequence of alternating magnetic fields.

Exploiting the larger effective volume of bigger size beads, the weaker magnetic field gradients are employed to now enable the directional motion of larger beads. At the same time, smaller beads stay immobile on the magnetic surface due to the mutual effects of the weaker magnetic field gradients and the lower interactive volume of the beads.

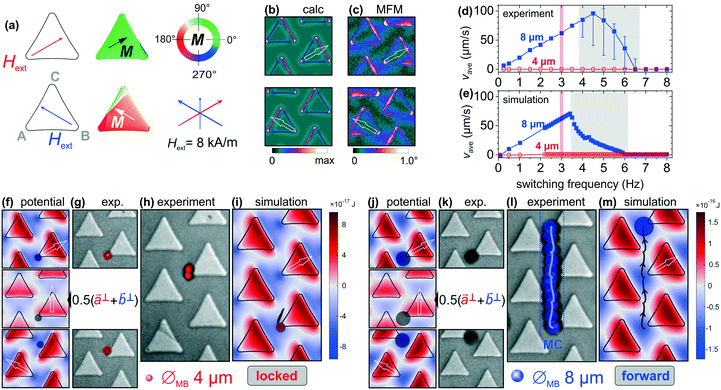
Shown in Fig. 3 are the exemplary results for the immobile motion of a Ø_MB = 4 μm bead with the simultaneous forward motion of a Ø_MB = 8 μm bead at the applied magnetic field switching with a lower amplitude (H_ext = 8 kA m⁻¹). As a result, weaker magnetic field gradients develop that are revealed both by micromagnetic calculations and MFM measurements as shown in Fig. 3b and c.

Fig. 3 Forward motion of a Ø_MB = 8 μm bead with a simultaneous locked motion of a Ø_MB = 4 μm bead for alternating switching applied magnetic field amplitudes of H_ext = 8 kA m⁻¹. The frequency of switching is 3 Hz. (a) Field conditions with H_ext along b⃑^⊥ and a⃑^⊥ and the calculated distribution of magnetization. (b) Calculated out-of-plane stray field gradients under the two conditions of magnetic field application and (c) corresponding MFM images obtained under the same experimental conditions. (d) Experimental and (e) simulated average movement velocity v_aveversus field switching frequency f_swit. (f) Simulated potential landscapes and equilibrium positions for the smaller bead with H_ext at b⃑^⊥ and a⃑^⊥ and at the switching of fields. The central image displays the potential state during field switching [0.5·(a⃑^⊥ + b⃑^⊥)]. (g) Optical images of a Ø_MB = 4 μm bead in its equilibrium positions under the two magnetic field conditions. (h) Experimental locked microbead motion for the alternate applied fields. The recorded bead positions are highlighted. (i) Simulated path of locked Ø_MB = 4 μm bead. (j) Magnetic potential landscape and (k) optical micrographs show the equilibrium positions of Ø_MB = 8 μm beads with the two different magnetic field conditions. (l) Experimental and (m) simulated path of bead motion. The calculated path of upward motion along a vertical microcorridor is superimposed in (j).

The motion behaviour with frequency for experiments and simulations are shown in Fig. 3d and e. The main experimental characteristics are reproduced by the simulations. Stable conditions are again obtained for a field switching frequency of f_swit = 3 Hz. No motion over the probed frequency range was detected for the smaller beads.

The initial position of the smaller bead is determined at the point of higher field gradient at the corner A with the application of field perpendicular to the opposite edge a of the triangle. Changing the field direction from a⃑^⊥ to b⃑^⊥ does not facilitate the motion of the smaller bead towards the next site of higher field gradient (corner B). The bead's immobility is due to the insufficient magnetic force from the edge b of the triangle. During the immobile response of the bead, only a slight lateral displacement in its initial position is determined by the calculated (Fig. 3f) and experimental (Fig. 3g) bead positioning. For the magnetic fields switching between a⃑^⊥ and b⃑^⊥, a continuous immobility of the bead is retraced in the tracked positions in Fig. 3h (see also ESI† Movie S5). Fig. 3i shows the simulated response of the smaller bead, matching well with the experiments (see also ESI† Movie S6). Using the low field amplitude sequence, the smaller bead is now made immobile.

The higher interactive volume of the larger Ø_MB = 8 μm beads now allows for their movement and thereby selective separation under the same applied field conditions. The symmetrically applied magnetic fields, with their orientations along the magnetic array edges, position the bead symmetrically between the patterns. The numerically calculated and experimentally determined matching positions of a Ø_MB = 8 μm bead before and after the magnetic field switching are displayed in Fig. 3j and k. The calculated transitional field condition is shown in Fig. 3j. The biased forward motion of the bead relies on inverting the field gradient landscape. At switching the field position from a⃑^⊥ to b⃑^⊥, the bead is first drawn toward the left (see centre potential map in Fig. 3j) and then after the switching attracted upward through the edge gradient until it reaches the corner B of the next triangle. The situation with changing the field from a⃑^⊥ to b⃑^⊥results in a net upward movement of the bead as indicated in Fig. 3l. Fig. 3m shows the calculated trace of the forward motion of a Ø_MB = 8 μm bead with alternatingly changing the directions of magnetic fields (see also ESI† Movie S7). The agreeing simulated path of bead motion for the same applied parameters is added in Fig. 3j (see also ESI† Movie S8). Naturally, varying the field along two of the ±a⃑^⊥, ±b⃑^⊥, and ±c⃑^⊥ directions other microcorridors and moving directions can be enabled on the magnetic array pattern.

Separation of individual bead populations from a mixture

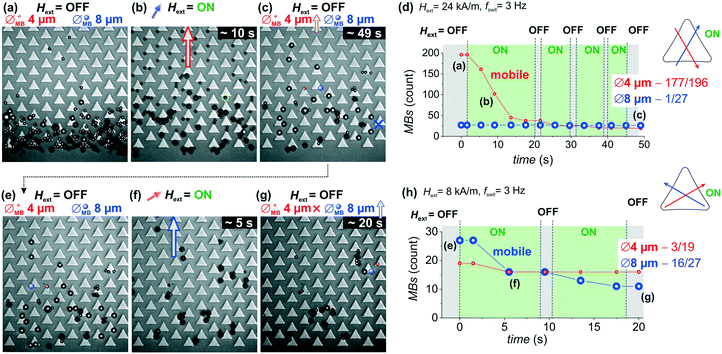
At this point we segregate beads from a mixture of differently sized microbeads using the beforehand determined conditions of magnetic field applications. An example of experimental demonstration of the separation and selective movement of Ø_MB = 4 μm beads and Ø_MB = 8 μm beads is provided in Fig. 4. Shown in Fig. 4a is a mixture of partly clustered microbead populations, collected at the magnetic boundary on the magnetic matrix chip surface (bottom in Fig. 4a) before the application of external magnetic fields. With the applied magnetic field changing its direction between b⃑^∥ and a⃑^∥with a fixed field amplitude and switching frequency (H_ext = 24 kA m⁻¹, f_swit = 3 Hz) the smaller beads move selectively forward, while keeping the larger beads around the initial position (compare to Fig. 2). Fig. 4b shows the trapped positions of beads for the magnetic field along b^∥ during the forward separation of smaller beads. The original bead clusters at the magnetic boundary have dissolved. During the tip-to-tip forward motion of the smaller Ø_MB = 4 μm beads the larger Ø_MB = 8 μm beads alternate between the top and side corners of two adjacent structures, mostly remaining in place. A separation of Ø_MB = 4 μm beads is achieved within approx. 50 seconds, e.g. 300 sequences, of alternating magnetic field application (Fig. 4c), while the Ø_MB = 8 μm beads stay within the field of view. For the complete process, see ESI† Movie S9.

Fig. 4 Selective separation of Ø_MB = 4 μm and Ø_MB = 8 μm beads. (a) Field of view with the mixed populations of microbeads collected at the magnetic boundary at the bottom before the application of alternating magnetic fields. (b) The trapped positions of both types of beads are shown for the field state b⃑^∥ during the separation process. The applied magnetic field changing its direction between b⃑^∥ and a⃑^∥ moves the smaller beads forward while it keeps the larger beads locked. The upward direction of smaller bead motion is indicated with a red arrow. (c) The locked Ø_MB = 8 μm beads remain after almost complete separation of Ø_MB = 4 μm beads. (d) Microbeads count inside the field of view versus time depicts the separation of Ø_MB = 4 μm beads as their reducing number with the constant number of locked Ø_MB = 8 μm beads. The fractions of beads moved out the field of view are indicated. (e) Remaining population of Ø_MB = 8 μm beads and a few Ø_MB = 4 μm beads, after their selective separation. (f) The trapped positions of both types of beads are shown for the field state a⃑^⊥ during the subsequent separation process. The applied magnetic field, now switching between a⃑^⊥ and b⃑^⊥, now moves the larger beads forward, while the smaller beads become immobilized. (g) The Ø_MB = 4 μm beads are left behind after the selective separation of Ø_MB = 8 μm beads. (h) Microbeads count versus time depicts the separation of Ø_MB = 8 μm beads as their reducing number against and the constant (low) number of immobilized Ø_MB = 4 μm beads. Switching the applied field status to ON and OFF repeatedly is to check the slipping motion of locked Ø_MB = 8 μm and Ø_MB = 4 μm beads, respectively. The applied magnetic field conditions are indicated.

The quantitative representation of the separation process is given in Fig. 4d. Shown are microbead counts within the field of observation versus the time required to complete the separation process. The smaller beads start moving forward from the mixture of bead populations as soon as the switching magnetic field is applied (H_ext = ON). Already above 50% of the beads leave the field of view after 10 seconds of alternating field application. From 196 smaller beads in this example, 19 single beads remain within the field of view after 50 seconds. Throughout the separation process almost all the larger beads remain immobile and stay in the field of view, which is shown as a constant number on the microbeads count in Fig. 4d (only 1 out of 27 beads moved out of the field of view). To check the tendency of a possibly occurring unwanted slipping motion of locked larger beads, the applied magnetic field is changed to an ON and OFF status during the separation process. A few locked beads are displaced from their initial positions and only one bead slipping sideward from the area of observation was found.

Immobility of smaller beads is related to the possible emergence of their trapping at the opposite magnetic potential of the patterns with higher switching frequency of the magnetic field. An example of this is evidenced by a yellow encircled bead position in Fig. 4b.

Quantitative numbers of the separation efficiencies of microbeads²¹ with Ø_MB = 4 μm (SE_4μm) are obtained using

P_4μm and P_8μm are the percentages of the bead sizes with 4 μm, respectively 8 μm, in the original mixture. N_4μm and N_8μm are the number of total beads present in the initial mixture on the area of observation, and n_4μm and n_8μm are the number of separated beads. The first terms define the separation of the desired beads, while second terms address the behavior of the undesired beads.

For the data in plotted in Fig. 4d we obtain a separation efficiency of SE_4μm = 0.91. Totaling counts of beads from six independent experiments results in an overall efficiency of SE_4μm = 0.86 (see ESI† for details). Here the microbeads of different sizes are already separated with high efficiency. The obtained numbers are similar to the quantities obtained by flow cytometry reported in ref. 21.

Now we demonstrate the subsequent movement of the remaining larger diameter beads from the resultant mixture of differently sized microbeads with reversed separation characteristics. This is achieved by reducing the strength of applied magnetic field together with its reorientation to the triangular magnetic elements. The motion behaviour of both types of particles is now inverted. Starting from the first separation process, the previously locked larger beads are now transported across the magnetic chip with a simultaneous immobilization of the residual smaller beads. For the process, see ESI† Movie S10.

Fig. 4e shows the subsequently obtained ensemble of larger Ø_MB = 8 μm beads along with a few remaining smaller Ø_MB = 4 μm beads. At this time, we change the applied magnetic field to switching between a⃑^⊥ and b⃑^⊥ with a lower magnetic field amplitude of H_ext = 8 kA m⁻¹. With the same switching frequency of f_swit = 3 Hz the larger beads are now selectively moved forward. Concurrently, the smaller beads are immobilized at their original positions. Fig. 4f shows the trapped positions of both type of beads for the field state a⃑^⊥, where the larger beads are in the forward direction and the smaller beads are being immobilized. Most of the larger beads move forward across the chip within the first 5 seconds of the subsequent magnetic field application. The micrograph in Fig. 4g shows that sixteen of the nineteen immobilized Ø_MB = 4 μm beads are still present on the chip surface within the field of view after the achieved selective separation from Ø_MB = 8 μm beads.

The microbead count versus time behaviour shown in Fig. 4h illustrates the directed separation of Ø_MB = 8 μm beads. Their number is constantly reducing in time, while three of the immobilized Ø_MB = 4 μm beads slip out of the field of view in the first 6 s. From a total 27 free moving Ø_MB = 8 μm beads 11 beads are still present after 20 s. Reason for the lower efficiency of separation is the blockage of their motion path by the residual immobilized smaller particles and particle agglomerates along the upward magnetic microcorridors.

Analogous to the first case, quantitative numbers of the total separation efficiencies of microbeads with Ø_MB = 8 μm diameter (SE_8μm) are obtained using

For the data plotted in Fig. 4h we obtain a separation efficiency of SE_8μm = 0.70. Summing the total counts of beads from again six independent experiments results in an overall efficiency of SE_8μm = 0.70 (see ESI† for details).

Conclusions

We have modelled and shown the independent movement along a single direction and, as a result, efficient separation of microbead populations at a single bead level. A hexagonal arrangement of soft magnetic thin film triangular patterns enables the programmable and individual manipulation of different sized microbeads on a microchip along variable directional paths. Experimental and simulated characteristics of separational bead motion are in agreement. Modelling reveals the exact motion path. Using discerning sequences of externally applied magnetic fields, large numbers of beads are selectively transported along the magnetic pathways on the magnetic array chip surface.

Utilizing a combination of geometric (shape, size and distribution of magnetic patterns and diameters of beads) and magnetic (amplitude and direction of applied magnetic field) control parameters, the alternative separation of two bead populations is realized. An almost complete immobilization of one type of beads is demonstrated during the separating movement of the other type of beads.

Magnetic pattern array surfaces can enable the efficient separation of target biological entities from a biological sample for future lab-on-chip applications and in vitro diagnostics. The method is scalable and the requirements for magnetic field applications are straightforward. It is envisioned that the general scheme of flexible and field programmable magnetic surfaces for bead separation demonstrated here can be further extended to other magnetic surface designs and magnetic field sequences, offering manifold separation possibilities in comparison to the demonstrated two-fold separation scheme. With added periodicities of magnetic features, the separation of more than two sizes is envisioned. Applications of similar schemes to flow cells for selectively influencing the motion paths of dissimilar particles appear feasible. Magnetic array surfaces provide a platform with manifold possibilities for the incorporation in lab-on-chip applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge funding through the Deutsche Forschungsgemeinschaft grant DFG MC 9/13-1 and DFG MC 9/13-2.

Notes and references

1. P. Li, D. Kilinc, Y. F. Ran and G. U. Lee, Lab Chip, 2013, 13, 4400–4408.
2. B.-I. Haukanes and C. Kvam, Nat. Biotechnol., 1993, 11, 60–63.
3. S. Rampini, P. Li and G. U. Lee, Lab Chip, 2016, 327, 1072–1074.
4. B. Lim, P. Vavassori, R. Sooryakumar and C. Kim, J. Phys. D: Appl. Phys., 2017, 50, 033002.
5. L. Chang, M. Howdyshell, W. C. Liao, C. L. Chiang, D. Gallego-Perez, Z. Yang, W. Lu, J. C. Byrd, N. Muthusamy, L. J. Lee and R. Sooryakumar, Small, 2015, 11, 1818–1828.
6. C. Murray, E. Pao, P. Tseng, S. Aftab, R. Kulkarni, M. Rettig and D. Di Carlo, Small, 2016, 12, 1891–1899.
7. B. Lim, S. R. Torati, K. W. Kim, X. Hu, V. Reddy and C. G. Kim, NPG Asia Mater., 2017, 9, e369.
8. B. B. Yellen, R. M. Erb, H. S. Son, R. Hewlin, Jr., H. Shang and G. U. Lee, Lab Chip, 2007, 7, 1681–1688.
9. P. Tierno, A. Soba, T. H. Johansen and F. Sagús, Appl. Phys. Lett., 2008, 93, 10–13.
10. M. Donolato, B. T. Dalslet and M. F. Hansen, Biomicrofluidics, 2012, 6, 24110.
11. M. Ouk and G. S. D. Beach, J. Magn. Magn. Mater., 2017, 444, 218–226.
12. U. Sajjad, E. Lage and J. McCord, Adv. Mater. Interfaces, 2018, 5, 1801201.
13. F. Martinez-Pedrero, H. Massana-Cid, T. Ziegler, T. H. Johansen, A. V. Straube and P. Tierno, Phys. Chem. Chem. Phys., 2016, 18, 26353–26357.
14. M. A. Tahir, L. Gao, L. N. Virgin and B. B. Yellen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 1–8.
15. L. Gao, M. A. Tahir, L. N. Virgin and B. B. Yellen, Lab Chip, 2011, 11, 4214–4220.
16. U. Sajjad, R. Bahne Holländer, F. Klingbeil and J. McCord, J. Phys. D: Appl. Phys., 2017, 50, 135003.
17. E. Rapoport and G. S. D. Beach, Sci. Rep., 2017, 7, 10139.
18. F. Del Giudice, H. Madadi, M. M. Villone, G. D'Avino, A. M. Cusano, R. Vecchione, M. Ventre, P. L. Maffettone and P. A. Netti, Lab Chip, 2015, 15, 1912–1922.
19. J. Gómez-Pastora, X. Xue, I. H. Karampelas, E. Bringas, E. P. Furlani and I. Ortiz, Sep. Purif. Technol., 2017, 172, 16–31.
20. Y. Ouyang, M. A. Tahir, D. J. Lichtenwalner and B. B. Yellen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041407.
21. P. Li, D. Kilinc, Y. F. Ran and G. U. Lee, Lab Chip, 2013, 13, 4400–4408.
22. N. Pamme and C. Wilhelm, Lab Chip, 2006, 6, 974–980.
23. N. M. Karabacak, P. S. Spuhler, F. Fachin, E. J. Lim, V. Pai, E. Ozkumur, J. M. Martel, N. Kojic, K. Smith, P. I. Chen, J. Yang, H. Hwang, B. Morgan, J. Trautwein, T. A. Barber, S. L. Stott, S. Maheswaran, R. Kapur, D. A. Haber and M. Toner, Nat. Protoc., 2014, 9, 694–710.
24. B. D. Plouffe, S. K. Murthy and L. H. Lewis, Rep. Prog. Phys., 2014, 78, 016601.
25. C. Fields, P. Li, J. J. O'Mahony and G. U. Lee, Biotechnol. Bioeng., 2016, 113, 11–25.
26. J. J. Chalmers, T. Byvank, B. L. Miller, W.-J. Chang, A. Bharde, G. Vieira, A. Chen, R. Bashir and R. Sooryakumar, Lab Chip, 2013, 13, 1172.
27. D. Rugar, H. J. Mamin, P. Guethner, S. E. Lambert, J. E. Stern, I. McFadyen and T. Yogi, J. Appl. Phys., 1990, 68, 1169.
28. micromer-M, www.micromod.de.
29. A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, AIP Adv., 2014, 4, 107133.
30. R. D. McMichael and M. J. Donahue, IEEE Trans. Magn., 1997, 33, 4167–4169.
31. F. Klingbeil, F. Block, U. Sajjad, R. B. Holländer, S. Deshpande and J. McCord, Sci. Rep., 2020, 10, 1–12.
32. J. McCord, J. Phys. D: Appl. Phys., 2015, 48, 333001.
33. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1lc00161b

---