Closed-loop feedback control of microfluidic cell manipulation via deep-learning integrated sensor networks†
Abstract
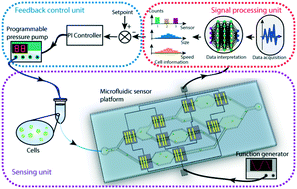
Microfluidic technologies have long enabled the manipulation of flow-driven cells en masse under a variety of force fields with the goal of characterizing them or discriminating the pathogenic ones. On the other hand, a microfluidic platform is typically designed to function under optimized conditions, which rarely account for specimen heterogeneity and internal/external perturbations. In this work, we demonstrate a proof-of-principle adaptive microfluidic system that consists of an integrated network of distributed electrical sensors for on-chip tracking of cells and closed-loop feedback control that modulates chip parameters based on the sensor data. In our system, cell flow speed is measured at multiple locations throughout the device, the data is interpreted in real-time via deep learning-based algorithms, and a proportional-integral feedback controller updates a programmable pressure pump to maintain a desired cell flow speed. We validate the adaptive microfluidic system with both static and dynamic targets and also observe a fast convergence of the system under continuous external perturbations. With an ability to sustain optimal processing conditions in unsupervised settings, adaptive microfluidic systems would be less prone to artifacts and could eventually serve as reliable standardized biomedical tests at the point of care.
- This article is part of the themed collection: Lab on a Chip HOT Articles 2021


 Please wait while we load your content...
Please wait while we load your content...