Fiber optic hydrogen sensor based on a Fabry–Perot interferometer with a fiber Bragg grating and a nanofilm

Abstract

Hydrogen is widely used in industrial production and clinical medicine, and as fuel. Hydrogen becomes explosive when the hydrogen–air mixture ranges from 4 to 76 vol%; thus, a rapid hydrogen concentration measurement is particularly important in practical applications. We present a novel fiber optic hydrogen sensor with fast response fabricated from a graphene–Au–Pd sandwich nanofilm and an ultrashort fiber Bragg grating. The response time is only 4.3 s at a 3.5 vol% hydrogen concentration. When the measured hydrogen concentration was increased from 0 to 4.5 vol%, the optical resonance dip in the sensor near 1550 nm shifted by 290 pm. In addition, the sensor has an insertion loss of only −2.22 dB, a spectral contrast of 10.8 dB, and a spectral finesse of 5. Such a flexible, fast-response sensor is expected to be used in the development of hydrogen sensors with low power consumption.

---

1. Introduction

Greenhouse gases emitted in the process of worldwide industrialization have caused irreversible impacts.^1,2 Hydrogen is considered one of the most promising clean energy sources to replace fossil fuels. Hydrogen releases energy and produces water without greenhouse gas emission during combustion. Detecting hydrogen concentration is crucial in many applications. Examples include detecting leakage of stored hydrogen, monitoring hydrogen production from hydrogen generators,³ detection of hydrogen in oil transformers for fault diagnosis,^4–6 and hydrogen detection in fuel cell rooms in electric vessels.⁷ Because a hydrogen–air mixture of 4 to 76 vol% is explosive, the response at 4 vol% is an extremely important index for determining the performance of hydrogen sensors.⁸ Although hydrogen sensors with electrical readout have low detection limits,^9,10 they usually cannot be used for detection of hydrogen concentrations greater than 4 vol% due to the risk of local explosions caused by electric sparks.

In the past few decades, a variety of methods have been applied for optical hydrogen sensors to improve the performances of those sensors. Among them, surface plasmon resonance (SPR) has attracted a great amount of attention in optical detection.^11–15 After Liu et al. experimentally demonstrated a surface plasmon resonance (SPR) sensor with perfect absorption in the SPR structure,¹⁶ many hydrogen sensors that use perfect absorption and SPR have been proposed.^17–21 Such optical hydrogen sensors with perfect absorption provide low insertion loss and high spectral contrast, which contribute to their high sensitivity and low detection limit. However, these sensors need bulky optical setups to ensure that the input and readout signals are properly coupled to optical detectors. In contrast, an optical fiber hydrogen sensor, such as that based on an interferometer,^22–25 a fiber Bragg grating (FBG),^26,27 a long period fiber grating^28,29 and a fiber evanescent field structure,^30–32 does not need additional optical alignment. Xiong et al. prepared a polymer micro-scale cantilever at the end of a single mode fiber (SMF) to form a Fabry–Perot interferometer (FPI) and deposited a 120 nm thick palladium (Pd) film on the cantilever to detect hydrogen. Pd undergoes reversible lattice expansion from a metal to a metal hydride (PdH_x) when exposed to hydrogen. After a period of exposure to a certain concentration of hydrogen, the Pd film reaches adsorption equilibrium and no longer expands. The extent of lattice expansion is highly dependent on the hydrogen concentration, making Pd suitable for hydrogen sensing.^33,34 However, because the reflectivity of the fiber end facet is approximately 3.5%, this kind of optical fiber FPI has the inherent disadvantages of high insertion loss and low spectral finesse. Finesse is a parameter of an optical cavity that is as important as the insertion loss and contrast; it can be calculated using F = FSR/FWHM, where FWHM is the full width half maximum of a resonance dip in the FPI, and FSR is the free spectral range of the resonance dip. In general, optical cavity sensors with high finesse have higher sensitivity and resolution than those with low finesse, as mentioned in previous reports.^35–39

A novel probe-type FPI-based fiber optic hydrogen sensor with a graphene–Au–Pd sandwich structure film and an FBG is proposed and experimentally demonstrated in this study. The FPI is formed by covering the hollow cavity at the fiber tip with the graphene–Au–Pd film (the thickness of the graphene–Au–Pd film is ∼128 nm and the thickness of the Pd film is ∼13 nm), and an FBG is inscribed into the SMF core using line-by-line femtosecond (fs) laser etching. The FPI-based fiber optic hydrogen sensors fabricated by the fabrication method proposed in this paper have the spectral characteristics of low insertion loss, high finesse, and high contrast. The hydrogen sensing characteristics of the proposed hydrogen sensor are studied in this paper.

2. Sensor fabrication

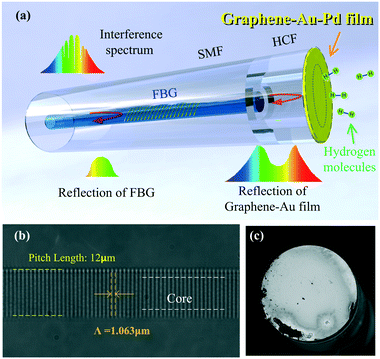
Fig. 1(a) illustrates the schematic of the proposed hydrogen sensor. Taking sample-1 as an example, the sensor is fabricated as follows.

Fig. 1 (a) Schematic of the probe-type FPI-based fiber optic hydrogen sensor with a graphene–Au–Pd sandwich structure film and an FBG. (b) Enlarged microscopy image of the FBG inscribed using line-by-line etching. (c) Scanning electron microscopy (SEM) image of the graphene–Au–Pd film covered on the fiber end facet.

In the first fabrication step, a section of a hollow core fiber (HCF, 75 μm internal diameter) was spliced to an SMF end facet with a commercial fusion splicer. The HCF had a well-cleaved end facet and a short length of ∼31 μm. The short hollow cavity length and cleaved end of the HCF can effectively reduce the divergence losses and thus the insertion loss of the sensor.

In the second step, a multilayer graphene film (6Carbon Technology, 6–8 layers, approximately 2 nm thick) was transferred to the end of the HCF with a wet transfer technique. The details on this procedure are described in ref. 40.

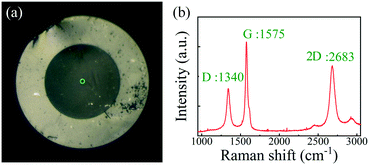
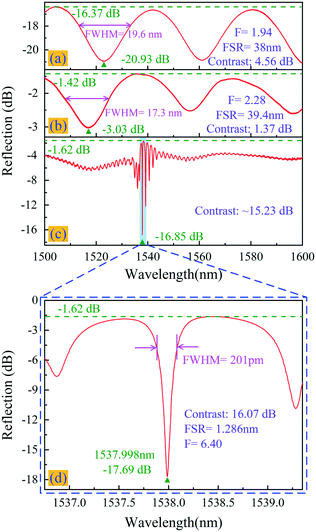
Fig. 2(a) shows the microscopy image of the graphene-covered end facet of the fiber tip. Fig. 2(b) shows the obtained Raman spectrum of the transferred graphene film (the area marked by the green circle in Fig. 2(a) was illuminated with a 532 nm laser). The reflection from the two surfaces of the SMF end facet and the graphene film forms an FPI with low reflectivity, and the reflection spectrum was measured using a circulator, a broadband light source (BBS), and an optical spectrum analyzer (OSA, Yokogawa, AQ6317C) with a 0.02 nm resolution; the results are shown in Fig. 3(a). The FPI has low reflection, a high insertion loss of −16.37 dB, and a low contrast of 4.56 dB.

Fig. 2 (a) Multilayer graphene-covered fiber-tip end facet, where the green circle shows the selected area for Raman spectroscopy. (b) Raman spectrum from the suspended multilayer graphene (6–8 layers) measured using a 532 nm laser.

Fig. 3 Reflection spectra after (a) the graphene was transferred to the end facet of the fiber-tip, (b) Au and Pd were successively deposited on the graphene, and (c) an ultrashort line-by-line FBG was inscribed in the SMF core close to the fiber tip. (d) Enlarged view of the blue area in (c).

In the third step, a layer of Au film and Pd film were successively deposited onto the graphene on the tip of the sensor via magnetron sputtering. The Au–Pd film was used to ensure that the sensor had higher reflectivity, and the Pd film exhibited reversible expansion via adsorption of hydrogen.

While the sensor was being coated, a glass slide was placed adjacent to the sensor and coated with an Au–Pd film of the same thickness to allow its thickness to be measured (see Fig. 4(a)). A small area of the glass slide was covered, which was denoted as A1. Then, a layer of gold film with the same thickness as the sensor was coated on the slide except for A1. Part of the coated area was covered, which was denoted as A2. The remaining area was denoted as A3, and a Pd film with the same thickness as the sensor was coated on A3. The thicknesses of coatings A2 and A3 were measured with a surface profilometer (BRUKER, DEKTAK XT) with a vertical resolution of 0.1 nm, and the results are shown in Fig. 4(b) and (c), respectively. The Au film thickness was measured to be ∼113 nm, and that of the Pd film was ∼13 nm.

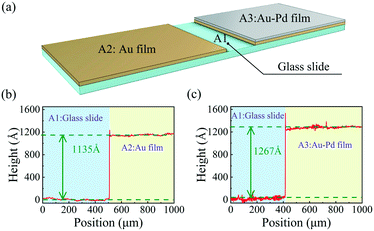Fig. 4 (a) Schematic diagram of the glass slide used to measure the thicknesses of the Au and Au–Pd films; (b) and (c) height profiles of the Au and Au–Pd films, respectively.

The reflection spectrum of sample-1 (after coating graphene with the Au–Pd film) is shown in Fig. 3(b). The high reflectivity of the Au–Pd film reflector provided a much lower insertion loss of −1.42 dB in sample-1, compared to an insertion loss of −16.37 dB without the Au–Pd film. The loss of −1.42 dB was caused by beam divergence and the subsequent escape, as well as the absorption in the graphene–Au–Pd film. However, because much more light was reflected from the graphene–Au–Pd film than from the SMF end facet, the spectral fringe contrast in sample-1 was only approximately 1.37 dB.

In the final step, an ultrashort line-by-line FBG with a pitch of 1.063 nm and ∼250 μm length was inscribed in the SMF core close to the fiber tip using a 1.7 mW fs laser (514 nm wavelength, 290 fs pulse width, and 200 kHz repetition rate); the beam was focused with a 100× oil objective (NA = 1.34). The Bragg resonant wavelength λ of the mth order FBG can be calculated using the following formula:⁴¹

mλ = 2n_effΛ

where n_eff is the effective refractive index of the SMF core, and Λ is the grating pitch. Fig. 1(b) shows an enlarged partial view of the inscribed FBG, revealing that the FBG has a pitch of 1.063 μm, corresponding to a second order Bragg resonant wavelength of 1538 nm. The reflection spectrum of sample-1 after this step is shown in Fig. 3(c).

The FBG, as a semi-transparent reflector, reflects a certain bandwidth of light centered at the Bragg resonant wavelength. It also interferes with light reflected from the graphene–Au–Pd film forming an FPI. As the grating pitch is increased, the Bragg reflection intensity also gradually increases. When the Bragg reflection intensity is almost equal to the graphene–Au–Pd film reflection intensity, the interference fringe contrast is large. After the final step process, the high resolution (1.5 pm) reflection spectrum of sample-1 was measured using a circulator, a computer (PC), a tunable laser (Agilent Technologies, 81940A), and a power meter (Agilent Technologies, N7744A). Sample-1 exhibits a high spectrum contrast of 16.07 dB (equivalent to 68.9–1.7% of the incident light intensity), a finesse of 6.4, and a low insertion loss of −1.62 dB, as shown in Fig. 3(d). Due to the high reflectivity of the Au–Pd film and the semi-transparent FBG, the fiber optic FPI has a much lower insertion loss, a higher contrast, and a higher finesse than other fiber optic FPIs prepared from graphene,⁴² silica^43–45 or polymers.⁴⁶ The finesse and insertion loss of the sensor based on the optical cavity is limited by the loss mechanisms that allow light to leak out of the cavity.⁴⁷ The main escape routes are through the FBG and hollow cavity, as well as via the absorption in the graphene–Au–Pd film.⁴⁸

3. Hydrogen concentration sensing and discussion

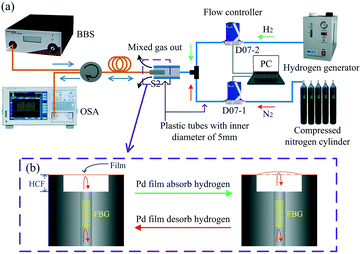
The response of the sensor was measured at different hydrogen concentrations. The experimental setup is shown in Fig. 5. For the hydrogen concentration measurements, nitrogen and hydrogen were provided from a compressed nitrogen cylinder and hydrogen generator, respectively. The volume ratio of nitrogen and hydrogen gases was controlled with two gas mass flow controllers (Seven Star, D07) and a PC, and the gases were mixed using a T-shaped three-way plastic tube (5 mm internal diameter) to obtain different hydrogen concentration values. The full control range of two Seven Star D07 series mass flow controllers is 500 SCCM (standard cubic centimeters per minute) and 30 SCCM, respectively, and the control error is less than ±1%. The D07–1 with a full range of 500 SCCM was used for nitrogen flow control and the D07–2 with 30 SCCM was used for hydrogen flow control, and the error between the actual and set hydrogen concentration of mixed gas is less than ±5%. The sensor was fixed in the vertical channel of the T-shaped three-way plastic tube to detect the changes in the hydrogen gas concentration. During this experiment, the total gas flow was set to 500 SCCM.

Fig. 5 (a) Experimental setup for characterizing the sensor response to hydrogen; (b) schematic diagram of how the expansion of the Pd film cause the graphene–Au–Pd film to arch outward and return to its original position.

Here, the sensing mechanism of hydrogen detection is as follows: the suspended graphene–Au–Pd film deforms due to the Pd lattice expansion caused by hydrogen adsorption, and the axial displacement of the film can be resolved by measuring a shift in the resonance dip in the fiber optic FPI. The extent of film deformation is highly dependent on the hydrogen concentration.^33,34 Therefore, the hydrogen concentration can be detected by reading the dip change. The schematic diagram of the hydrogen-induced outward arching and recovery of the film is shown in Fig. 5(b). In addition, the effect of the possibility of gas entering the cavity on the sensor results can be ignored, because the difference of the refractive indexes of nitrogen and hydrogen is small, and is in the order of 10⁻⁴.^49,50

Fig. 6(a) shows the spectrum of sample-2, which was created using the fabrication method described above. Sample-2 has a free spectral range (FSR) of approximately 0.7 nm, a 10.8 dB contrast, a −2.2 dB insertion loss, and a resonant wavelength dip at 1550.03 nm (Λ = 1.071 μm). Fig. 6(b) shows the evolution of the reflection spectra of sample-2 as the hydrogen gas concentration increased from 0 to 4.5 vol% at room temperature. Each measurement was carried out for 5 min to ensure that adsorption equilibrium was reached. The dip at 1550.03 nm moves toward longer wavelengths as the hydrogen gas concentration increased, which is due to elongation of the FPI cavity length caused by the hydrogen-induced outward arching of the graphene–Au–Pd film. The total shift in the dip wavelength near 1550 nm was approximately 290 pm. The adsorption of hydrogen by the Pd film belongs to the dissociation adsorption of the Langmuir theory.^51,52 Therefore, the data of hydrogen adsorption equilibrium concentration vs. wavelength shift can be fitted with a sigmoidal curve. Fig. 7 shows the Boltzmann fitting of the experimental data.

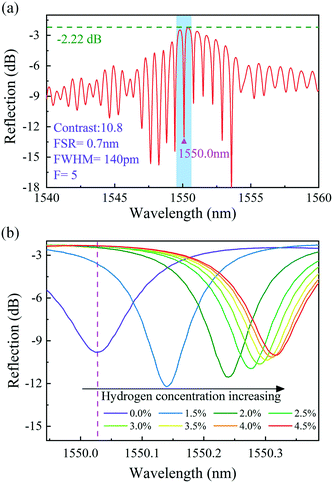Fig. 6 (a) Reflection spectrum of sample-2. (b) Enlarged view of the blue area in (a) and the changes in the reflection spectra of sample-2 with different hydrogen concentrations.

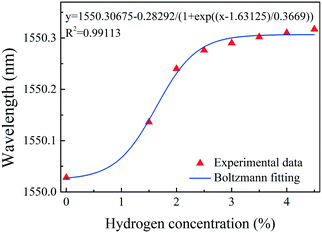Fig. 7 Dip wavelength shift in sample-2 after exposure to various concentrations of hydrogen. The blue line shows the Boltzmann fitting of the experimental data.

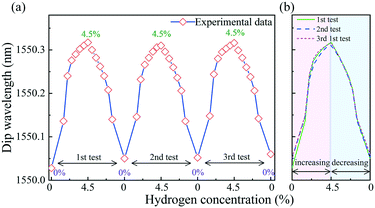
To investigate the reproducibility of the hydrogen sensor, the hydrogen concentration was cycled between 0 and 4.5 vol%, where the sensor was held at each concentration value for 2 min. As shown in Fig. 8, in the three repeatability tests of increasing hydrogen concentration, the resonance wavelengths redshifted by 290 pm, 260 pm, and 270 pm, respectively. The desorption processes on the sensor show hysteresis. The blueshift in the resonance dip is different from the redshift in the cycle test with the hydrogen concentration increasing and then decreasing. However, in the increasing hydrogen concentration test, the drift trend was similar for all 3 cycles.

Fig. 8 The reproducibility data of sample-2 as the hydrogen concentration increase was cycled between 0 and 4.5 vol% for three cycles. Three cycle data (a) arranged beside each other and (b) overlapping each other.

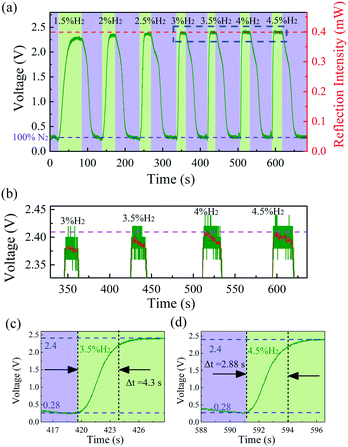
An experimental setup was used to measure the response time of the hydrogen sensor. A tunable laser was used as a source of light with an output set to 0.7 mW at 1550.03 nm, which is located at a minimum in the reflection spectrum. For clarity, the detecting laser is highlighted with a pink dashed line in Fig. 6(b). The detecting laser enters the sensor through the circulator, and the reflected light was received by a photodetector (PD). The PD converts the light intensity into a voltage that is fed to an oscilloscope. When the sensor was exposed to hydrogen, the dip wavelength redshifted and the reflected laser intensity increased, resulting in a higher voltage.

Fig. 9(a) shows the voltage measured with the oscilloscope in the time domain at different hydrogen concentrations. The sensor response time is defined as the time interval for the sensor to reach 90% of its steady state response. Due to the high finesse (= 5) of sample-2, the 1550.03 nm laser intensity reflected from the sensor was likely saturated when the hydrogen concentration reached 4 vol%, even though the adsorption of hydrogen by the Pd film has not yet reached saturation, as shown in Fig. 9(b), which is the enlarged view of the blue dashed box in Fig. 9(a). For clarity, a red line was used in Fig. 9(b) to show the result of smoothing the data. Note that the saturation of reflected 1550.03 nm laser intensity does not mean that the Pd film adsorption of hydrogen already reached saturation. The sensor was able to detect 4.5 vol% hydrogen in the wavelength drift dominated hydrogen detection, as shown in Fig. 6(b). In other words, there may be a deviation between the measured response time and the actual response time at concentrations of 4 vol% and 4.5 vol%. Therefore, it is objective to define the fastest response time of the sensor using the approximately 4.3 s response time at 3.5 vol% hydrogen concentration.

Fig. 9 (a) Temporal response test results from sample-2 for various hydrogen concentrations. (b) Enlarged view of the blue dashed box in Fig. 9(a); the red line was obtained by smoothing the experimental data. (c) and (d) Enlarged views of the temporal response at 3.5 and 4.5 vol% hydrogen, respectively.

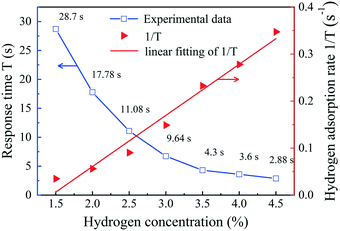
The response time vs. hydrogen concentration in sample-2 is plotted in Fig. 10. The response time is the longest when the concentration of hydrogen is 1.5 vol%, which is 28.7 s. The response time measured at 4.5 vol% hydrogen concentration is the shortest, reaching 2.88 s, although this is slightly shorter than the actual response time. Here, we defined the inverse of the response time (T) as the initial hydrogen adsorption rate (1/T). The results show that the concentration of hydrogen is inversely proportional to the response time and has a linear relationship with the initial hydrogen adsorption rate. The response time behavior of the sensor is consistent with the sensing behavior of devices constructed from decorated Pd, which can be described using the Langmuir adsorption theory.^53,54

Fig. 10 Response time of sample-2 for different hydrogen concentrations. The red squares are experimental data. The green triangles are the inverse of the response time, which has a linear correlation to the concentration of hydrogen.

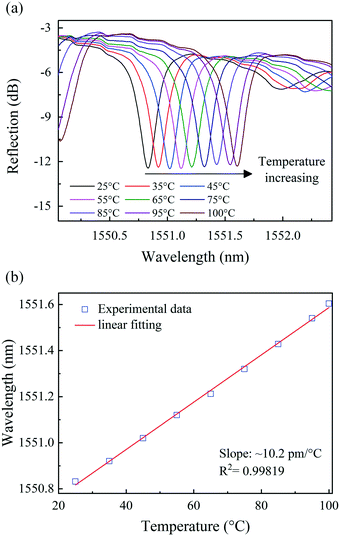
The influence of temperature was investigated by placing sample-3 in a thermostat and gradually increasing the temperature from 25 to 100 °C in 10 °C increments and holding the sample at each temperature for 2 min at atmospheric pressure. Sample-3 was fabricated by the method previously proposed, and has a finesse of 5.4, a spectral contrast of 9.05 dB and an insertion loss of −3.4 dB. The reflection spectrum evolution of sample-3 with temperature change is shown in Fig. 11(a). The correlation plots are shown in Fig. 11(b), and the slope of the linear fit gives a temperature sensitivity of ∼10.2 pm °C⁻¹ with a correlation factor of R² ∼ 0.99819 showing a good linearity of wavelength changes with increasing temperature. The temperature sensitivity is consistent with the previously reported temperature response of an FBG, which is mainly affected by the temperature on the FBG, i.e., the photo-thermal effect.⁵⁵

Fig. 11 (a) Changes in the reflection spectrum of sample-3 at different temperatures. (b) Extracted linear relationship between the dip wavelength in the reflection spectrum and the ambient temperature.

4. Conclusions

In conclusion, a fiber optic FPI-based hydrogen sensor with low loss and fast response was fabricated using a graphene–Au–Pd sandwich nano film and FBG. This sensor exhibited a high spectral contrast of 10.8 dB, a high spectral finesse of 5, and a low insertion loss of only −2.22 dB. The external hydrogen concentration can be resolved by monitoring the resonance dip changes in the reflection spectrum. Experimental results show that the optical resonant dip of the sensor exhibited a nonlinear redshift of 290 pm near 1550 nm as the hydrogen concentration was varied from 0 to 4.5 vol%. The sensor has a response time of 4.3 s at a hydrogen concentration of 3.5%. In addition, the proposed hydrogen sensor exhibits a linear temperature sensitivity of ∼10.2 pm °C⁻¹ from 25 to 100 °C.

Author contributions

J. L. and S. Liu jointly conceptualized and fabricated the devices, built the experimental setup, and carried out the experiments. P. C., S. Lu, and Q. Z. provided help for the experiment. J. L. wrote the original draft. P. C., Y. C., B. D., and J. T. helped to analyse the data. S. Liu edited the manuscript. Y. W., C. L. and J. H. helped to edit the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge financial support by the National Natural Science Foundation of China (NSFC) (61905165, 61905164, and 61805155), the Natural Science Foundation of Guangdong Province (2018KQNCX219), and the Science and Technology Innovation Commission of Shenzhen (JCYJ20170818143853289). We would furthermore like to thank Kaiming Yang, Zhengyong Li, Cong Xiong, and Zhongyuan Sun for useful discussions.

References

1. M. Meinshausen, N. Meinshausen, W. Hare, S. C. B. Raper, K. Frieler, R. Knutti, D. J. Frame and M. R. Allen, Nature, 2009, 458, 1158–1162.
2. S. Solomon, G.-K. Plattner, R. Knutti and P. Friedlingstein, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1704–1709.
3. M. A. Modestino, M. Dumortier, S. M. H. Hashemi, S. Haussener, C. Moser and D. Psaltis, Lab Chip, 2015, 15, 2287–2296.
4. J. Bodzenta, B. Burak, Z. Gacek, W. P. Jakubik, S. Kochowski and M. Urbanczyk, Sens. Actuators, B, 2002, 87, 82–87.
5. V. V. Kondalkar, J. Park and K. Lee, Sens. Actuators, B, 2021, 326, 128989.
6. X. Gui, Q. Zhou, S. Peng, L. Xu and W. Zeng, Appl. Surf. Sci., 2020, 533, 147509.
7. L. E. Klebanoff, J. W. Pratt and C. B. LaFleur, Int. J. Hydrogen Energy, 2017, 42, 757–774.
8. M. Matuschek, D. P. Singh, H.-H. Jeong, M. Nesterov, T. Weiss, P. Fischer, F. Neubrech and N. Liu, Small, 2018, 14, 1702990.
9. D. Khan, H. Li, D. Gajula, F. Bayram and G. Koley, ACS Sens., 2020, 5, 3124–3132.
10. U. T. Nakate, R. Ahmad, P. Patil, Y. Wang, K. S. Bhat, T. Mahmoudi, Y. T. Yu, E.-K. Suh and Y.-B. Hahn, J. Alloys Compd., 2019, 797, 456–464.
11. A. Tittl, X. Yin, H. Giessen, X.-D. Tian, Z.-Q. Tian, C. Kremers, D. N. Chigrin and N. Liu, Nano Lett., 2013, 13, 1816–1821.
12. C. Perrotton, R. J. Westerwaal, N. Javahiraly, M. Slaman, H. Schreuders, B. Dam and P. Meyrueis, Opt. Express, 2013, 21, 382–390.
13. N. Liu, M. L. Tang, M. Hentschel, H. Giessen and A. P. Alivisatos, Nat. Mater., 2011, 10, 631–636.
14. V. N. Konopsky, D. V. Basmanov, E. V. Alieva, D. I. Dolgy, E. D. Olshansky, S. K. Sekatskii and G. Dietler, New J. Phys., 2009, 11, 063049.
15. N. Strohfeldt, A. Tittl and H. Giessen, Opt. Mater. Express, 2013, 3, 194–204.
16. N. Liu, M. Mesch, T. Weiss, M. Hentschel and H. Giessen, Nano Lett., 2010, 10, 2342–2348.
17. A. Tittl, P. Mai, R. Taubert, D. Dregely, N. Liu and H. Giessen, Nano Lett., 2011, 11, 4366–4369.
18. M. Serhatlioglu, S. Ayas, N. Biyikli, A. Dana and M. E. Solmaz, Opt. Lett., 2016, 41, 1724–1727.
19. A. Tittl, H. Giessen and N. Liu, Nanophotonics, 2014, 3, 157–180.
20. S. Bagheri, N. Strohfeldt, F. Sterl, A. Berrier, A. Tittl and H. Giessen, ACS Sens., 2016, 1, 1148–1154.
21. E. Herkert, F. Sterl, N. Strohfeldt, R. Walter and H. Giessen, ACS Sens., 2020, 5, 978–983.
22. J. Ma, Y. Zhou, X. Bai, K. Chen and B.-O. Guan, Nanoscale, 2019, 11, 15821–15827.
23. C. Xiong, J. Zhou, C. Liao, M. Zhu, Y. Wang, S. Liu, C. Li, Y. Zhang, Y. Zhao, Z. Gan, L. Venturelli, S. Kasas, X. Zhang, G. Dietler and Y. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 33163–33172.
24. M. Wang, D. N. Wang, M. Yang, J. Cheng and J. Li, Sens. Actuators, B, 2014, 202, 893–896.
25. B. Wu, C. Zhao, B. Xu and Y. Li, Sens. Actuators, B, 2018, 255, 3011–3016.
26. G. Wang, S. Yang, J. Dai, Y. Dai, T. Zou, J. Roths and M. Yang, Sensors, 2019, 19, 4775.
27. J. Dai, M. Yang, Y. Chen, K. Cao, H. Liao and P. Zhang, Opt. Express, 2011, 19, 6141–6148.
28. X. T. Wei, T. Wei, H. Xiao and Y. S. Lin, Sens. Actuators, B, 2011, 152, 214–219.
29. C. Caucheteur, M. Debliquy, D. Lahem and P. Megret, Opt. Express, 2008, 16, 16854–16859.
30. Z. L. Poole, P. R. Ohodnicki, A. Yan, Y. Lin and K. P. Chen, ACS Sens., 2017, 2, 87–91.
31. Y. Qi, Y. Zhao, H. Bao, W. Jin and H. L. Ho, Optica, 2019, 6, 570–576.
32. K. Schroeder, W. Ecke and R. Willsch, Opt. Laser Eng., 2009, 47, 1018–1022.
33. T. C. Narayan, A. Baldi, A. L. Koh, R. Sinclair and J. A. Dionne, Nat. Mater., 2016, 15, 768–774.
34. R. Griessen, N. Strohfeldt and H. Giessen, Nat. Mater., 2016, 15, 311–317.
35. O. Arcizet, P. F. Cohadon, T. Briant, M. Pinard, A. Heidmann, J. M. Mackowski, C. Michel, L. Pinard, O. Francais and L. Rousseau, Phys. Rev. Lett., 2006, 97, 133601.
36. G. Gagliardi, M. Salza, S. Avino, P. Ferraro and P. De Natale, Science, 2012, 335, 286.
37. M. Ding, M. Komanec, D. Suslov, D. Dousek, S. Zvanovec, E. R. N. Fokoua, T. D. Bradley, F. Poletti, D. J. Richardson and R. Slavik, J. Lightwave Technol., 2020, 38, 2423–2427.
38. M. Li, W. H. P. Pernice, C. Xiong, T. Baehr-Jones, M. Hochberg and H. X. Tang, Nature, 2008, 456, 480–484.
39. Y. Tan, W. Jin, F. Yang, Y. Qi, C. Zhang, Y. Lin and H. L. Ho, J. Lightwave Technol., 2017, 35, 2887–2893.
40. J. Ma, W. Jin, H. L. Ho and J. Y. Dai, Opt. Lett., 2012, 37, 2493–2495.
41. J. Luo, S. Liu, Y. Zhao, Y. Chen, K. Yang, K. Guo, J. He, C. Liao and Y. Wang, Opt. Lett., 2020, 45, 507–510.
42. B. C. Zheng, S. C. Yan, J. H. Chen, G. X. Cui, F. Xu and Y. Q. Lu, Laser Photonics Rev., 2015, 9, 517–522.
43. M. Haque, K. K. C. Lee, S. Ho, L. A. Fernandes and P. R. Herman, Lab Chip, 2014, 14, 3817–3829.
44. S. Liu, Y. Wang, C. Liao, Y. Wang, J. He, C. Fu, K. Yang, Z. Bai and F. Zhang, Sci. Rep., 2017, 7, 1–9.
45. N. Gaber, M. Malak, F. Marty, D. E. Angelescu, E. Richalot and T. Bourouina, Lab Chip, 2014, 14, 2259–2265.
46. M. Li, Y. Liu, R. Gao, Y. Li, X. Zhao and S. Qu, Sens. Actuators, B, 2016, 233, 496–501.
47. S. Zaitsev, A. K. Pandey, O. Shtempluck and E. Buks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 046605.
48. R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres and A. K. Geim, Science, 2008, 320, 1308.
49. K. Li, N. Zhang, N. M. Y. Zhang, G. Liu, T. Zhang and L. Wei, Opt. Lett., 2018, 43, 679–682.
50. L. Jiang, L. Zhao, S. Wang, J. Yang and H. Xiao, Opt. Express, 2011, 19, 17591–17598.
51. H. Swenson and N. P. Stadie, Langmuir, 2019, 35, 5409–5426.
52. H. Rauscher, Surf. Sci. Rep., 2001, 42, 207–328.
53. Y. Sun and H. H. Wang, Adv. Mater., 2007, 19, 2818–2823.
54. S. F. Yu, U. Welp, L. Z. Hua, A. Rydh, W. K. Kwok and H. H. Wang, Chem. Mater., 2005, 17, 3445–3450.
55. C. Liao, L. Xu, C. Wang, D. N. Wang, Y. Wang, Q. Wang, K. Yang, Z. Li, X. Zhong, J. Zhou and Y. Liu, Opt. Lett., 2013, 38, 4473–4476.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1lc00012h

---