Integration of capillary–hydrodynamic logic circuitries for built-in control over multiple droplets in microfluidic networks

Abstract

Here, we show the successful implementation of advanced sequential logic in droplet microfluidics, whose principles rely on capillary wells establishing stationary states, where droplets can communicate remotely via pressure impulses, influencing each other and switching the device states. All logic operations perform spontaneously due to the utilization of nothing more than capillary–hydrodynamic interactions, inherent for the confined biphasic flow. Our approach offers integration feasibility allowing to encode unprecedentedly long algorithms, e.g., 1000-droplet counting. This work has the potential for the advancement of liquid computers and thereby could participate in the development of the next generation of portable microfluidic systems with embedded control, enabling applications from single-cell analysis and biochemical assays to materials science.

---

Introduction

The implementation of the idea of liquid computer¹ would be revolutionary for microfluidics, not because microfluidics seeks computational capabilities, but because it would enable the encoding of a variety of algorithms (laboratory procedures) into the structure of the device.

In terms of miniaturization and complexity of performed tasks, microfluidics is often compared to microelectronics.² The promising vision is that the miniaturization and increase of operational throughput, so fruitful in computer engineering, would be implemented in control over small liquid volumes, thus opening a new era for sample processing and analysis techniques. However, one of the remaining problems in microfluidics is the implementation of the fundamental concept of electronics: the control embedded in integrated circuits. In microelectronics, the most fundamental level is constituted by base modules, where both input and output are of the same nature—they are electric signals. Thus, different elements can be combined directly with each other into hierarchical self-regulated circuitries. Despite their incredible complexity, electronic architectures, e.g., microprocessors, are completely autonomous; besides the input data and energy supply, they do not require any additional control.

In microfluidics, in contrast, liquids are usually operated by valves, electrodes, pumps, etc. that are centrally controlled by a computer.^3–5 This requires the microchannels to be designed to be connectable with the electromechanical regulatory system, the intricacy of which usually increases with the complexity of the laboratory task.⁶

In the article, we focus on two-phase flows in microchannels, where droplets can be formed and used as tiny laboratory beakers. Microfluidics has developed manipulation techniques for droplets enabling such operations such as splitting, merging and positioning.^4,5,7,8 The combinatorial sequences of base operations allow for the implementation of any laboratory procedure. The precision, low consumption of reagents, and automation capabilities render this technology increasingly attractive for biological and chemical experimentations.^8–10

Droplets are predominantly manipulated by computer-controlled external actuators.^4,5 An intriguing alternative is an idea of a liquid computer¹ with droplets as digital entities self-regulating via coupling capillary and hydrodynamic interactions in specially designed geometries.

Thus far, some alternative strategies of the embedded control devices for both single-phase flow^11–14 and droplets^4,15–23 have been proposed. In the case of droplets, the system that is probably the closest to computer technology is the system presented by Katsikis et al.,²⁰ where automated tasks were performed on ferromagnetic droplets activated by a rotating external magnetic field. Actually, droplets in microfluidics do not require any additional force to be self-regulated, which is important for a variety of applications, where droplets can not be ferromagnetic. The intriguing aspect of confined, biphasic microflows is that the surface tension is relatively large and introduces non-linearity into Stokes flows, opening the perspectives for purely hydrodynamic built-in control. Prior examples exploiting this approach encompass cascades of consecutive dissolution encoded by the use of hydrodynamic traps.^17–19 However, without logic elements, the coding capabilities of such systems are insufficient for the programming of arbitrary algorithms. Although single logic operations were shown in pressure-regulated flows of droplets over a decade ago,^15,16,24 their further integration has proved difficult, inhibiting the creation of systems with nontrivial functionalities. Advanced built-in control remains one of the most important and open problems of microfluidics, hampering the development of autonomous and portable devices in line with the lab-on-a-chip concept.

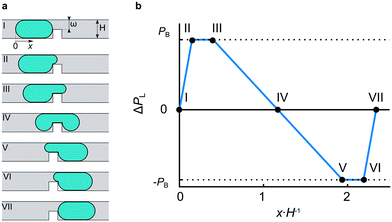
Here, we address this issue and propose a droplet logic platform enabling the building of sequential logic units with multiple internal states. We use water droplets that do not wet the channel walls, surrounded by oil as the continuous phase (CP) that wets the channel walls. Droplets larger than the channel cross-section are squashed between walls. This peculiar environment limits the height of droplets to dimensions where capillarity dominates over gravity, rendering the latter negligible. Thus, the capillarity, minimizing the surface area, forms elongated plug-shaped droplets with rounded ends.²⁵ The interface curvature introduces the capillary pressure difference P_L, sustained across the interface and described by the Young–Laplace equation, which for a droplet confined by the rectangular channel of width W and height H and the surface tension γ can be estimated as P_L = γ(2H⁻¹ − 2W⁻¹). Here, we assume the shape of the droplet's end to be prescribed by circles spanned between opposite walls of radii W/2 and H/2, respectively.

The dependence of P_L on the local dimensions of the duct implies that the transfer of a droplet to the more constricted region increases the pressure inside the droplet. Thus, a change of the channel lumen can be used to establish a capillary well for the droplet.²⁶

A convenient way to introduce such a barrier for droplets is to provide obstacles that locally decrease the height of the channel from H to ω (Fig. 1a). In crossing the obstacle, a droplet penetrates the narrow slit, developing there the protrusion with curvature radii ω/2 and W/2 (Fig. 1a). Hence, the breakthrough pressure P_B, defined as a difference of P_L between the front and the back of a droplet, is:

P_B = γ(2ω⁻¹ − 2W⁻¹) − γ(2H⁻¹ − 2W⁻¹) = 2γ(ω⁻¹ − H⁻¹)

The droplet crossing the obstacle raises the pressure behind it to P_B (Fig. 1b), generating the pressure impulse, which propagates in the network, carrying the information about the droplet travelling through the barrier. However, until the pressure drop acting across the droplet reaches P_B, the droplet cannot cross the barrier. Such a situation can occur in microfluidic networks distributing the flow of CP between parallel structures, where a droplet can be effectively immobilized at the capillary barrier while the entire stream of CP flows around through bypasses.^18,23,26

Fig. 1 The evolution of a droplet shape when crossing a barrier in a channel. (a) Schematic side view of the channel with a barrier. H and ω – the height of the channel and the slit above the obstacle, respectively. (I–VII) Consecutive shapes of a droplet during its travel across the barrier from left to right. (b) Difference of Laplace pressure between the front and the back of a droplet (estimated from curvatures) as a function of the position of a droplet x relative to the obstacle and normalized by H. The roman numbers (I–VII) correspond to the pictures in (a).

In this work, we exploit both these advantages of the use of obstacles—the generation of a pressure impulse and droplet trapping. We design microfluidic structures with stationary droplets assigned to logic states, where pressure impulses are used for remote communication and for triggering the device's embedded logic operations for the sequential switching of states. We present this idea starting from the experimental analysis of a simple example of a two-state flip-flop device. Then, we develop the multi-state decimal ring-counter. Finally, we demonstrate the feasibility of the integration of such devices with the example of the three-fold decimal counter counting 1000 droplets.

Results and discussion

Bimodal loop

First, let us consider a simple loop, which bifurcates the incoming flow between two branches and then merges them into one output. Simple laminar hydrodynamics explains that the pressure drop Δp in a channel is proportional to the flow rate Q with the linear relation Δp = RQ (ref. 27 and 28) introducing the resistance R proportional to the length of the channel and inversely proportional to the square of the cross-sectional area.²⁷ Analysis of the loop as two parallel resistors implies that the incoming stream distributes between branches with the ratio of flow rates inversely proportional to the ratio of the resistances of the branches (see methods). Therefore, in the case of an asymmetric loop, the flow through the branch of lower resistance is the faster one. While such a single-phase flow is steady, groups of flowing droplets distribute between branches of the loop in a highly dynamic way, disclosing complex periodic or chaotic behaviour.^21,29 The reason is that the feedback mechanism was introduced by the droplets, which prefer the channel of the higher flow rate while also lowering the flow through the channel they resided in.²⁹

Here, we present the construction of a loop, where the flow of droplets is deterministic, reproducible, and exhibits the functionality of a simple finite state machine. Our design (Fig. 2a) comprises two unequal branches with obstacles (Fig. 2b) in each of them (for practical reasons, the dimensions of these obstacles vary slightly – see methods). As we can expect, the first droplet entering the loop travels to the shorter and faster branch until it reaches the obstacle there (Fig. 2c). In the series of trials, we set the constant input flow rate Q_in sufficiently low to keep the first droplet immobilized in such a configuration (see methods). Therefore, even if the short branch is blocked by the droplet (Q_short = 0), directing the whole flow to the longer branch (Q_long = Q_in), the generated pressure drop does not exceed the breakthrough pressure of the obstacle, Q_inR_long < P_B. Here, Q_short and Q_long are the flow rates in the short and the long branch of the loop, respectively, and R_long is the resistance of the long branch.

Fig. 2 Bimodal loop. (a) Schematic view of the bimodal loop. (b) 3D view of an obstacle fabricated by milling. (c–g) Experimental micrographs of the flow of two consecutive droplets through the bimodal loop (see Movie S1†). Black dots – positions of the measurements of droplet-presence-signals; S_in (in the inlet), S_st (at the state), S_tr (at the trigger), and S_out (in the outlet). The signals were obtained by the analysis of the brightness of pixels (see methods), where two values, 0 and 1, are assigned to the absence and the presence of a droplet, respectively. (h) Timing diagrams presenting all signals together during the flow of the two droplets as a function of time. Droplets in motion occupy a given position for a relatively short time, thus marking narrow peaks in time-diagrams. The spikes in S_in indicate consecutive droplets entering the system and can be seen as a digital clock-signal. Soon after the peak of the first droplet in S_in, the ‘state’ signal S_st assumes value 1, and the droplet is immobilized at this position. After the next peak of S_in indicating the entrance of the second droplet, the peak of S_tr appears with the delay proportional to the distance between input and trigger positions. Simultaneously, with the S_tr-peak, the S_st assumes value 0, and the first droplet leaves the static state position. Then, two peaks of S_out appear, indicating the release of both droplets from the device. After that, the device resets to its ground state (without droplets). (i) The repeatability of the process – timing diagrams for the sequence of 10 droplets as functions of dimensionless time τ, where τ = (time − t₁ + Δt)/Δt: t₁ is the time of the appearance of the first droplet and Δt is the mean delay interval between droplets (see (h)). The rounded down value of dimensionless time τ corresponds to the total number of droplets, which have been introduced to the device so far. For the convenience, we will use the dimensionless time τ in the subsequent analysis in this article. After the first pair of droplets, the next third and fourth droplets entering the system reproduce the identical sequence. Thus, the process is reproduced for each consecutive pair of droplets. For the reference, the rectangle shows the part of the timing diagram for the first two droplets equivalent to the whole time-diagram showed in (h). The mean time interval between two consecutive droplets entering the loop was Δt = 17.2 s, equivalent to the frequency of operations which is equal to 0.058 Hz.

Such an altered flow of CP moves the second droplet to the long branch. Hereby, the second droplet ‘knows’ about the first droplet occupying the short branch and ‘decides’ adequately (Fig. 2d). When the second droplet reaches the obstacle in the long branch (Fig. 2e), both channels become obstructed, and the incoming flow of the CP builds up the pressure behind droplets, exceeding breakthrough pressure and allowing both droplets to cross the obstacles simultaneously (Fig. 2e). In this way, the first droplet, previously immobilized in the short branch, is now released (Fig. 2f), and then both droplets leave the loop, resetting the state of the device to the initial condition (Fig. 2g). Each consecutive pair of droplets repeats the above sequence.

The presented system exhibits the functionality of the so-called flip-flop sequential logic unit with two internal states defining different functionalities of obstacles: the presence of a droplet at the state-obstacle in the short channel indicates the excited state, while the other trigger-obstacle initiates a reset to the ground state without any droplet in the loop.

We conducted the quantitative investigation of the device operation via the analysis of the selected pixels' brightness in consecutive frames of the movie recorded during the experiments (see methods). Thanks to that, we retrieved the time-dependent digital signals, which assume only values of 0 or 1, corresponding to a droplet's absence or presence at a given point, respectively (see methods for more details). The signals from the selected points of the device put together in the form of timing diagrams (Fig. 2h and i) show the device's repetitive operation.

Decimal counter

In the considered above bi-modal loop, the first droplet enters the branch of lower resistance. As we showed in our previous work,³⁰ a modified junction with a slit can fix the custom direction of a droplet regardless of the resistances of the branches. Such a solution provides a higher degree of control, allowing the direction of the first droplet to the long branch and swapping functionalities between loop-branches. Thus, we can put the trigger-obstacle in the short branch, while the state-obstacle is in the long branch (see Note S1 and Movie S2†).

In the next example (Fig. 3), we use such a modified junction (Fig. 3b) to place 9 subsequent state-obstacles in the long branch (Fig. 3a); hence, accounting for the empty loop as the 0-state, the device exhibits ten states (Fig. 3h). The first droplet entering such a refashioned loop halts at the first obstacle in the long branch assigned to the first state (Fig. 3c). As in the bi-modal loop, the next droplet chooses the opposite, empty branch—in this case, the shorter one (Fig. 3d)—and after touching the trigger-obstacle, it releases the state-droplet from the first state (Fig. 3e). The state-droplet keeps moving until it meets the next obstacle (Fig. 3f), then sets the second state (Fig. 3g). Each subsequent droplet moves the state-droplet one obstacle forward so that its current position corresponds to the count of all droplets that have been introduced to the loop thus far (Fig. 3h and see Movie S3†). After the 10th droplet, the state-droplet leaves the loop, resetting it to the ground state, and the sequence starts from the beginning (Fig. 3i).

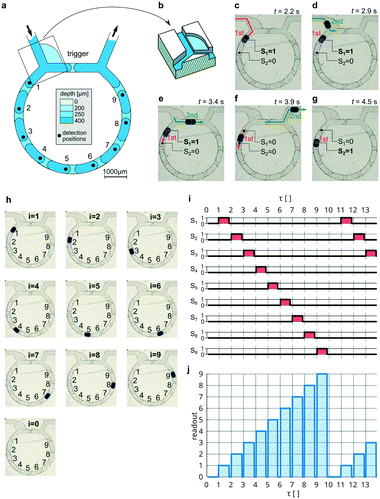Fig. 3 The decimal counter. (a) The schematic top view of the counter with a trigger-barrier in the short branch and 9 state-barriers in the longer branch. (b) 3D view of the special junction with a slit used to direct the first droplet to the longer branch.²⁷ (c–g) Experimental micrographs of the flow of two subsequent droplets introduced to the counter (see Movie S3†). (h) The position of the indicator-droplet assigned to the state number i corresponding to the occupied state position. The empty device is assigned to i = 0. (i) Signals of the presence of a droplet S_i from all 9 positions measured continuously during the introduction of the series of 13 consecutive droplets. The presence of the state-droplet at each i-th position was analysed by the use of brightness analysis of pixels and assigned to the digital signal S_i (see methods). (j) The readout of the current count. Due to the orthogonality of signals S_i, the instantaneous vector of 9 signal values can be transformed into one value of the readout (see methods). The value of the readout (from 0 to 9) indicates the currently active state and equals the result of the counting. The mean time interval between two consecutive droplets entering the counter was Δt = 2.7 s, equivalent to counting 0.37 droplets per second.

Permutations

In addition to the obvious analogy to the 10-modulo ring-counter, the device performs a transformation by rearranging the initial droplet sequence. Indeed, all droplets from the second to 10th one leave the system before the first droplet. Thus, the device performs the circular shift permutation σ(i) = (i + 1) modulo 10, transforming the sequence (1 2 3 4 5 6 7 8 9 10) into (2 3 4 5 6 7 8 9 10 1).

In order to increase the spectrum of permutations available, we can use the serial combinations of the ring-counters utilizing the fact that more complex permutation can be decomposed into a series of base permutations, e.g., in computational science, the Heap's³¹ algorithm is used for the efficient generation of all possible permutations. The target permutation is decomposed into the series of operations, wherein the single step, only a single pair of elements interchanges.

The application of modified Heap's algorithm allows the achievement of wide spectrum of permutations by combining different circular shift permutations in a series, e.g., permutation transforming the sequence (1 2 3 4 5 6) into (6 5 4 3 2 1), as presented in Fig. 4 and Movie S4.†

Fig. 4 Microfluidic system performing permutation of the set (1 2 3 4 5 6) into (6 5 4 3 2 1). (a and b) Schemes of the microfluidic loops performing base permutations. (a) ‘SWAP’ permutation: (1 2) into (2 1). (b) ‘ROTATE’ permutation: (1 2 3) into (2 3 1). (c) The scheme of the permutation-device consisting of base permutation-loops, ‘SWAP’ and ‘ROTATE’, connected in series. (d) The photo of the fabricated device used in Movie S4.† The single permutation of six droplets was completed within about 100 s.

Three-fold decimal counter

The advanced finite state machines in microelectronics utilize the integration of multiple elements in cascades so that the number of all available states is the multiplication of states of all connected components. For example, n bimodal loops create a binary counter comprising 2ⁿ states (see Note S2 and Movie S5†).

To integrate the decimal counters in a series, we augmented the previous design with two separate outlets: the excess-output and the signal-output channels (Fig. 5a, Note S3 and Movie S6†). Two corresponding inlets ensure the compatibility for connections of subsequent units. Such a construction separates the trigger droplets from the state droplets. Droplets that have passed through the trigger branch are directed to the excess-output (Fig. 5b). Thus, the excess collector channel receives trigger-droplets from all antecedent counters. The state-droplet leaving a counter enters the signal-inlet of a subsequent counter, thus transmitting the information about each count of 10 to the next counter (Fig. 5c). We integrated three such modules, obtaining a 3-fold decimal counter (Fig. 5b). In such a system, the first so-called 1×-counter counts units, and after the enumeration of each 10 droplets, it sends the signal-droplet to the next 10×-counter, which counts tens. Consequently, the third 100×-counter receives a signal from the 10×-counter and enumerates hundreds of droplets. The running result of the count can be directly read out from the positions of the droplets in the counters (Fig. 5d and e). The experiments showed that the 3-fold counter works without errors, correctly processing every 1000 droplets (Fig. 5f and Movie S7†).

Fig. 5 The 3-fold cascade decimal counter. (a) The schematic top view of the single counting-module. (b) Photo of the whole device (taken after the counting of three droplets) with highlighted droplet generation unit (DGU) and three counting-modules. The black dotted line shows the trajectory of trigger-droplets, which travel via the excess output into the excess-collector channel of the subsequent clock-module. (c) The mechanism of the signal transfer between subsequent counting-modules. The 10th droplet triggers the release of the state-droplet from the 1×-counter. The state droplet travels through the signal channel to the 10× counter and stops at the first state position initiating the count of tens. The 11th droplet enters the empty 1×-counter and initiates the next unit's counting sequence. (d and e) Micro-graphs showing examples of the instantaneous positions of droplets for 125 and 568 counted droplets, respectively. (f) The readout from all counters together. We obtained the readout for each counting-module separately, as described in methods. The top – the sequence of 1050 droplets. The middle – magnification for the range from 100 to 205 droplets. The bottom – magnification for droplets from 120 to 132. The visible delay between signals from different counters is caused by the time the signal-droplet needs to travel between subsequent modules. The mean time interval between two consecutive droplets entering the counter was Δt = 0.91 s, equivalent to counting 1.1 droplets per second.

Conclusions

In the article, we aimed to restore, and substantially advance, the original idea of purely hydrodynamic-regulated droplet logic,¹⁵ whose beauty consists in the utilization of nothing more than the interactions inherent for the confined biphasic flow.

The examples of systems that we demonstrated here showed that the large-scale integration of microfluidic logic circuitries is feasible and can facilitate the device's embedded encoding of the arbitrary analytical algorithm executed on multiple beaker-like droplets. The exploration of this field is promising for the development of lab-on-a-chip devices inter alia for medical diagnosis and biochemical analysis.

In terms of the speed of operation, the presented devices, performing about 1 operation per second, may look modest, especially when compared with high-throughput automated systems, e.g., for droplet sorting or cells counting. Indeed, the maximal flow-rate and the efficiency are limited in order to satisfy demanding conditions imposed by capillary well's concept. However, the presented technology is attractive for the applications demanding embedded control and high accuracy of the combinatorial algorithms more than the high throughput.

The implementation of advanced assays in portable devices is one of the main motivations stimulating the development of microfluidics. Modern analytical methods like digital PCR or screening rely on the processing of multiple independent compartments of the sample.⁹ Thanks to the use of droplets as tiny beakers, microfluidic techniques offer the minimization of the volume of single compartments, capacity for the processing of a large number of aliquots, and precise manipulation techniques, which can be applied to every droplet individually.³²

The development of microfluidic methods must account for seemingly contradictory market-related demands – the optimization of the compactness, portability, and ease of use on the one hand, versus the increasing complexity of laboratory algorithms on the other hand.

Thus, the integrated fluidic logic in microfluidics appears as an attractive solution, offering both the passive regulation in place of mechanical activators and the encoding of advanced procedures in the architecture of the device.

We showed that our logic platform enables a variety of concepts of microelectronics to be applied to droplet microfluidics. Besides the examples presented in the article, we can mention some other modules that can emerge via further modifications and combinations of already known structures, e.g., an adjusted version of the bimodal device can work as a set/reset flip-flop for the synchronization of droplets from two different sources (see Note S4 and Movie S8†). Another solution can distribute droplets from a single channel to several parallel ducts in ordered combination (e.g., see Note S5 and Movie S9†). Such a joint or a split of outputs is well-known in electronics as a multiplexer and demultiplexer, respectively. They allow for the implementation of droplet buses in microfluidic devices similar to the data bus in computer processors.

In this preliminary research, we focused on the presentation of the feasibility of the large scale integration, providing the principles of the design and fabrication of logic circuitries. The advantage of the presented platform is that its elements can be connected (in series or in parallel) with other microfluidic modules.

In the next step, we envision the combination of logic structures with hydrodynamic traps,¹⁸ which can process the content of droplets thanks to the operations like merging and splitting of droplets. This set of functions is enough to mix the content of two droplets and divide it into even parts again. In this way, two droplets align the concentrations of reagents or interchange the populations of bacteria or cells.

As we showed in the previous work,¹⁸ the iterative repetition of this procedure to the series of droplets dissolves the reagent from the first droplet gradually in droplets containing the buffer, finally resulting in the array of droplets with descending concentrations. Such an operation can be seen and described as a numerical low-pass filter processing the initial vector of concentrations represented by a series of input droplets. The logic operations can facilitate both the setting of the custom input vector of droplets and the realization of more complex procedures represented by other numerical filters.

The examples presented in the article allow for the synchronization of droplets from different sources and their permutations. Hence, two kinds of droplets (with and without the reagent) can be independently generated and then arranged in the desired order so that the application of the filter would result in the custom shape of the output signal of concentration distributions, e.g., sinus, saw-tooth, triangular, etc. The output stream of droplets can be permutated and processed again by the use of droplet to droplet interchange. Such an iterative approach allows for the realization of more advanced algorithms improving the dynamical range of the concentration control.

The microfluidic hardware with built-in algorithms manipulating the concentration of reagents in droplets and interchanging the microbial populations can advance the application and development of biological assays utilizing statistical analysis of numerous sample divisions. Thus, we envision that integrated logic circuitries are a promising field of exploration as a potential direction of future microfluidics evolution.

Materials and methods

Device fabrication

All the presented devices were fabricated by the milling of channels, obstacles, and slits in a plate of polycarbonate (Macrolon, Bayer, Germany) using a CNC milling machine (Ergwind, Poland) with a reproducibility of the positioning of 5 μm. The chips with channels were bonded to flat slabs of polycarbonate using a hot press at 135 °C for 10 minutes. No further channel modifications were applied.

The height and width of the square cross-section of regular channels were 400 μm. In the course of numerous trials, for the more reliable performance of the logic systems, the dimensions of obstacles in the long and the short branch of the loop were varied. We fabricated the obstacle in the short branch with a width of 100 μm (measured along the central axis of the channel) and a height of 200 μm (depth of the gap above – ω = 200 μm), while the obstacle in the long branch had a width of 150 μm and height of 150 μm (depth of the gap above – ω = 250 μm). Varying dimensions allow for the compensation of the contrast of resistances between branches, thus improving the robustness of the microfluidic logic systems. The height of all other slits in the modified junctions or those connecting channels was 200 μm.

Liquids and flow control

To feed our systems with liquids, we used Nemesis pumps (Cetoni GmbH, Germany) with glass syringes connected to the inlets of the devices via PE-60 tubing (Beckton-Dickinson, USA). In all experiments, we used two syringe pumps for independent injection of two immiscible liquids. The outlet channel was connected through the tubing to the waste container.

We used hexadecane (Sigma Aldrich Co.) with the addition of 1.3% Span 80 (Sigma Aldrich Co.) as the CP and Milli-Q water as the droplet phase (DP). The DP was coloured by methylene blue to increase the contrast between liquids for the better visualization of droplets and for image analysis improvement. The viscosity of the CP was estimated via the measurement of the time within which the fixed volume of the liquid flows through the calibrated capillary under a known pressure drop. The viscosity of liquids (at 22 °C) was 3.6 mPa s for CP and 0.95 mPa s for DP. The interfacial tension was measured by means of a pending droplet method and for our set of liquids was 4.8 mN m⁻¹ (at 22 °C).

Distribution of flows in a loop-like channels

The simple loop bifurcates the incoming flow Q_in between two streams, Q₁ and Q₂, in the two branches and then merges them into one output, Q_out = Q_in. Analysing the single-phase flow of CP, we use the linear Ohm-like²⁸ relation Δp = RQ, relating pressure drop Δp to flow rate Q. R = αμ_CLA⁻² is a hydraulic resistance, where α is a geometrical factor,²⁷μ_C is the dynamic viscosity of CP, and L and A are the length and cross-sectional area of the channel, respectively. Considering the loop as a parallel circuit of two resistors, we obtain the splitting ratio Q₁/Q₂ = R₂/R₁ = L₂/L₁, implying that the flow through the shorter branch (with lower resistance) is the faster one.

The breakthrough pressure estimation

We estimated the breakthrough pressure experimentally for both dimensions of the obstacles used in this paper. For this purpose, we fabricated two loop devices (for each geometry of the obstacle) with only one obstacle in the short branch. After placing one droplet at the obstacle, we increased the flow rate of CP until the droplet was removed from the loop. In this way, in the series of trials, we estimated the critical flow rate Q_crit, which demarcates the transition between immobilization and passing-through modes.

Then, the values of breakthrough pressure were calculated using the relation P_B = R_long × Q_crit. Here, we assume that the whole flow is through the long branch only and R_long = αμ_CLA⁻², where α = 28.4 is the geometrical coefficient of the square-shape cross-section of the channel, μ_C is the viscosity of CP, L = 6.9 mm is the length of the long branch, and A = H × W = (400 μm)² is the cross-sectional area. The values of breakthrough pressure, estimated in the above-described way, are 7.78 ± 0.37 Pa and 12.59 ± 0.37 Pa for the obstacles of the slit depth ω which is equal to 250 μm and 200 μm, respectively.

Droplet generation

Droplets were produced in the block-and-brake type T-junction generator,³³ which produces droplets of similar size regardless of the ratio of rates of flow of both phases³⁴ (see Note S6†). This solution ensures the appropriate size of droplets required for the correct performance of microfluidic logic units. The other factor that needed to be adjusted was the frequency of droplets, which could not be too high. Stationary flows of both phases yielded a constant frequency of mono-dispersed droplet generation.

Image acquisition

The sequences of droplets flowing through the investigated microfluidic devices were observed by the use of a stereoscope (Huvitz HSZ-645TR) equipped with a CCD camera (IDS UI-3274LE-C-HQ) to record movies during the experiments. The recorded movies were stored for evidence and further analysis.

Measurement of the signal of the presence of droplets

The presence or absence of a droplet at a given point of the microfluidic network can be assigned to the signal, which assumes Boolean values. We obtained time-dependent signals from experiments via analysis of the light intensity of selected pixels in the recorded movies. Due to the enhanced contrast between both liquid phases, the value of intensity fluctuates between two well-distinguishable levels. Applying an appropriate threshold (average of extreme values) yields a digital signal assuming only values of 0 or 1, indicating the absence or presence of a droplet, respectively.

The readout of the droplet counting

All signals S_i(t) from the decimal counter (see Fig. 3i) are orthogonal (〈S_i(t)|S_j(t)〉 = δ_ij), which means that only one state can be active at one time, so the product of signals from different state positions is 0. This feature can be used for the transformation of the vector of the 9 signal values into only one value of the readout: . Such a transformation yields the number from 0 to 9, indicating the currently active state. The readout equals the modulo-10 counting of droplets.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The project operated within the First Team grant (POIR.04.04.00-00-3FEF/17-00) of the Foundation for Polish Science co-financed by the EU under the Smart Growth Operational Programme. D. Z. acknowledges support within the Preludium grant (UMO-2018/29/N/ST3/01711) of the National Science Centre, Poland.

Notes and references

1. A. Adamatzky, Philos. Trans. R. Soc., B, 2019, 374, 20180372.
2. G. M. Whitesides, Nature, 2006, 442, 368–373.
3. D. Mark, S. Haeberle, G. Roth, F. von Stetten and R. Zengerle, Chem. Soc. Rev., 2010, 39, 1153–1182.
4. A. M. Pit, M. H. G. Duits and F. Mugele, Micromachines, 2015, 6, 1768–1793.
5. P. Zhu and L. Wang, Lab Chip, 2016, 17, 34–75.
6. R. Gómez-Sjöberg, A. A. Leyrat, D. M. Pirone, C. S. Chen and S. R. Quake, Anal. Chem., 2007, 79, 8557–8563.
7. S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220.
8. L. Shang, Y. Cheng and Y. Zhao, Chem. Rev., 2017, 117, 7964–8040.
9. T. S. Kaminski and P. Garstecki, Chem. Soc. Rev., 2017, 46, 6210–6226.
10. O. Scheler, W. Postek and P. Garstecki, Curr. Opin. Biotechnol., 2019, 55, 60–67.
11. B. Mosadegh, C.-H. Kuo, Y.-C. Tung, Y. Torisawa, T. Bersano-Begey, H. Tavana and S. Takayama, Nat. Phys., 2010, 6, 433–437.
12. S.-J. Kim, D. Lai, J. Y. Park, R. Yokokawa and S. Takayama, Small, 2012, 8, 2925–2934.
13. P. N. Duncan, S. Ahrar and E. E. Hui, Lab Chip, 2015, 15, 1360–1365.
14. D. J. Case, Y. Liu, I. Z. Kiss, J.-R. Angilella and A. E. Motter, Nature, 2019, 574, 647–652.
15. M. Prakash and N. Gershenfeld, Science, 2007, 315, 832–835.
16. L. F. Cheow, L. Yobas and D.-L. Kwong, Appl. Phys. Lett., 2007, 90, 054107.
17. X. Niu, F. Gielen, J. B. Edel and A. J. deMello, Nat. Chem., 2011, 3, 437–442.
18. P. M. Korczyk, L. Derzsi, S. Jakieła and P. Garstecki, Lab Chip, 2013, 13, 4096–4102.
19. S. S. Bithi and S. A. Vanapalli, Sci. Rep., 2017, 7, 41707.
20. G. Katsikis, J. S. Cybulski and M. Prakash, Nat. Phys., 2015, 11, 588–596.
21. M. J. Fuerstman, P. Garstecki and G. M. Whitesides, Science, 2007, 315, 828–832.
22. M. Zagnoni and J. M. Cooper, Lab Chip, 2010, 10, 3069–3073.
23. P. Abbyad, R. Dangla, A. Alexandrou and C. N. Baroud, Lab Chip, 2011, 11, 813–821.
24. M. W. Toepke, V. V. Abhyankar and D. J. Beebe, Lab Chip, 2007, 7, 1449–1453.
25. C. N. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032–2045.
26. R. Dangla, S. Lee and C. N. Baroud, Phys. Rev. Lett., 2011, 107, 124501.
27. N. A. Mortensen, F. Okkels and H. Bruus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 057301.
28. K. W. Oh, K. Lee, B. Ahn and E. P. Furlani, Lab Chip, 2012, 12, 515–545.
29. O. Cybulski, P. Garstecki and B. A. Grzybowski, Nat. Phys., 2019, 15, 706–713.
30. D. Zaremba, S. Blonski, M. J. Marijnissen and P. M. Korczyk, Microfluid. Nanofluid., 2019, 23, 55.
31. B. R. Heap, Comput. J., 1963, 6, 293–298.
32. S. Jakiela, T. S. Kaminski, O. Cybulski, D. B. Weibel and P. Garstecki, Angew. Chem., Int. Ed., 2013, 52, 8908–8911.
33. V. van Steijn, P. M. Korczyk, L. Derzsi, A. R. Abate, D. A. Weitz and P. Garstecki, Biomicrofluidics, 2013, 7, 024108.
34. P. M. Korczyk, V. van Steijn, S. Blonski, D. Zaremba, D. A. Beattie and P. Garstecki, Nat. Commun., 2019, 10, 2528.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary notes, supplementary movies and list of supplementary movies. See DOI: 10.1039/d0lc00900h

---