Open Access Article
Open Access ArticleMulti-element analysis of minerals using laser ablation inductively coupled plasma time of flight mass spectrometry and geochemical data visualization using t-distributed stochastic neighbor embedding: case study on emeralds†
Hao A. O.
Wang
 *a and
Michael S.
Krzemnicki
*a and
Michael S.
Krzemnicki
 ab
ab
aSwiss Gemmological Institute SSEF, CH-4051, Basel, Switzerland
bDepartment of Environmental Sciences, Mineralogy and Petrology, University of Basel, CH-4056, Basel, Switzerland. E-mail: hao.wang@ssef.ch; michael.krzemnicki@ssef.ch
First published on 18th January 2021
Abstract
In recent years, multi-element chemical analysis has been applied to a broad range of solid samples in mineralogy, geology, environmental science, biology and beyond. In this study, we present a quantification method for the multi-element composition of minerals and a statistical method to investigate chemical similarity among samples. We obtain almost the entire elemental composition simultaneously using laser ablation inductively coupled plasma time-of-flight mass spectrometry (LA-ICP-TOF-MS). A novel concept of “first measure, then determine” which elements are of interest is introduced for multi-element analysis of geological samples. This case study focuses on major, minor and trace element analysis of emerald, a highly relevant mineral in the gemstone trade. In total, 168 samples were analyzed without a priori knowledge of their geographic provenance. They were grouped/clustered solely based on similarities in multi-element concentrations using non-linear unsupervised dimension reduction algorithm t-distributed stochastic neighbor embedding (t-SNE). A comparison with a PCA plot reveals that the application of t-SNE results in better cluster separation. The clusters in the t-SNE plot coincide with the geographic provenance of these emeralds, probably due to unique elemental fingerprints within the geological setting in each provenance. Based on our results, we consider LA-ICP-TOF-MS multi-element data acquisition in combination with t-SNE data visualization a powerful and promising tool in mineralogy and geology. Not only for provenance studies, but when combined with further sample characteristics (e.g. spectroscopic features, host rock composition, geochronology, inclusions) it may assist in understanding the geological formation and setting of minerals within their host-rock and their deposits.
Introduction
Multi-element analysis of minerals is fundamental in geochemistry to characterize minerals and rocks and to understand their formation and transformation during geological processes. In the past decades, laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) has proven to be a versatile and powerful method in geosciences, as it provides high sensitivity for the detection of almost all elements in the periodic table. This has led to numerous applications ranging from elemental characterization of rocks/minerals,1 solid and fluid inclusions,2in situ geochronological dating,3 analysis of artefacts of cultural heritage,4 to provenance or traceability studies of ore minerals5 and gemstones6,7 to name a few.Among available mass separation methods in LA-ICP-MS, quadrupole mass spectrometer (Q-MS) is by far the most popular one used in geoscience to date. This robust and cost-effective instrument routinely detects elemental information based on a peak-hopping mode, namely the signal is measured on one mass to charge ratio (m/Q) before hopping to the next one. A drawback of this sequential mass separation is that users are required to setup a list of isotopes of interest before measurement. This means, a priori knowledge about elemental content of the sample must be presumed. The limitations of this approach are evident when analyzing samples containing trace and ultra-trace elements which occur only rarely and occasionally (e.g. in a narrow growth zone) or samples with unknown solid/fluid inclusions. Furthermore, once the isotope selection is set and ablation is completed using Q-MS, it is not possible to quantify elements whose isotopes were originally excluded from the list without re-ablating the sample.
A solution to overcome these drawbacks is to apply full mass spectrum acquisition, such as time-of-flight mass spectrometry (TOF-MS) as presented in this study. TOF-MS was first coupled to ICP in the 1990s8–10 and applied in the early 2000s.11 But only in the last decade, has LA-ICP-TOF-MS gained more attention,12,13 especially in 2D and 3D chemical imaging applications in geology14,15 and biology,16 thanks to improved data acquisition speed, signal to noise ratio and limits of detection.17 In addition, the simultaneous acquisition of full mass spectra using LA-ICP-TOF-MS enables a novel paradigm for multi-elemental analysis based on the principle “first measure, then determine” which elements are of interest. As a consequence, there is no need to establish a list of elements of interest prior to analysis as with Q-MS. This is particularly helpful in cases where unexpected trace elements are present in a mineral matrix.
If more detailed composition information (expected and unexpected) can be obtained from an unknown sample, then it can be compared with that of reference samples from a database in a more accurate and confident manner. This widely applied approach is based on the assumption that samples of similar elemental concentration form in similar geological environments and conditions, and may thus originate from the same geographic provenance. In provenance and traceability studies of minerals, the elemental composition of interested samples are often compared with reference samples using bivariate plots, tri-plots, or 3D-scatter plots.18 Although routinely used, it is common to encounter data overlaps in such plots visualizing reference samples from various geographic provenances. This is especially the case when only a few elements are used for the plotting.19 Consequently, the provenance of an analyzed sample cannot be accurately determined, if its data plots within such overlapping zones of references from different provenances.
LA-ICP-MS analysis of minerals intrinsically produce a high-dimensional dataset (multi-element concentration). Since direct visualization of such a dataset is challenging, one would need to compare multiple bivariate-plots for a comprehensive data analysis. Alternatively, statistical dimension reduction is often applied on the original high-dimensional dataset. A common method is the principle component analysis (PCA). It linearly combines multi-element concentrations (dimensions) to a reduced number of principle components (PCs), which maximize sample variances. Hence, this method is often chosen due to its ability to extract major features and to minimize data noise.20 However, PCA or similar linear methods, which project low dimensional space (PCs), are often not suitable to reveal true sample relationships in original high dimensional space.21
Among many non-linear methods for dimension reduction,22 we applied t-distributed stochastic neighbor embedding (t-SNE) in this study, as it has proven to be a versatile method for a non-linear transformation from high to low dimensional space to visualize sample relationships.21 The t-SNE algorithm is popular and is so far mainly applied to biological studies, for example, in the field of genomics23 and single cell analysis24 using mass cytometry.12 Not only can cell sub-populations or phenotypes (subgroups) within the dataset be visualized and interpreted, there is also a great potential for this method to be used in geochemistry. Inspired by previous biological applications, we further developed this method for minerals and gemstones.
As a case study, we have chose gem quality emeralds from various deposits worldwide. The geographic provenance of an emerald is a major value factor in the gem trade and therefore reliable provenance determination on such gemstones is requested by the trade and offered as a service by specialized gemological laboratories. In this work, we obtained high dimensional datasets (without a pre-defined list of isotopes, hence without a priori knowledge) using LA-ICP-TOF-MS as well as precise and accurate element quantification procedures. We compare the capability of non-linear t-SNE and linear PCA methods separating mineral datasets into various subgroups. Similar to PCA, the t-SNE is an unsupervised machine learning method, which works without the necessity of labelling the dataset (in contrast to supervised machine learning). The color of a data point is added after the reduction process. Consequently, groups of data points in our study are solely dependent on the elemental similarities of analyzed emeralds and without a priori information, such as geographic provenance determined using conventional gem testing methods.
Experimental
Samples and standards
Emerald is the green variety of beryl Be3Al2(SiO3)6, owing its appealing green color mainly to traces of Cr. For this study, we measured 168 rough and faceted gem quality emerald samples from deposits in Afghanistan, Brazil (several regions), Colombia, Ethiopia, Tanzania and Zambia (Table S-1†). Specifically, the analyzed emerald samples from Brazil originate from Itabira and Nova Era regions in the state of Minas Gerais, Carnaíba region in the state of Bahia, and St. Terezinha region in the state of Goiás. Some samples were only referenced to as Brazil but still included in this study.The samples consist of our in-house collection samples (the SSEF and Prof. Henry A. Hänni collections, which cover decades of collecting history) and client samples, which were tested in the gem lab and a reliable and confident provenance information can be deduced. Both are considered equally in the following multi-element analyses. Ablation was performed on polished areas of the gemstones that were homogeneous in appearance and were deemed inclusion-free.
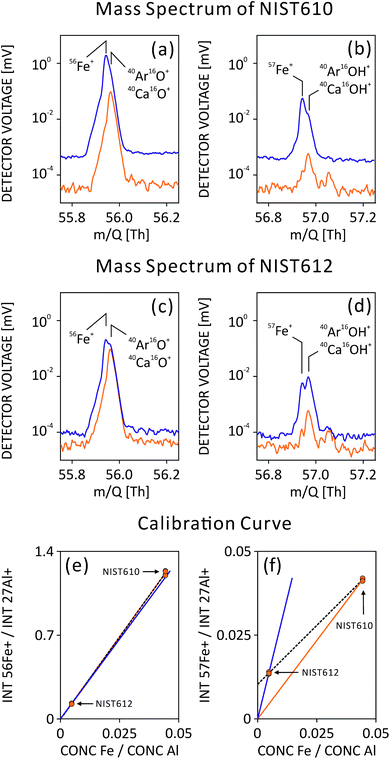
For LA-ICP-MS quantitative analysis of solid samples, a matrix-matched standard is preferred. However, such a standard may not contain more than several quantified elements and is often hard to obtain or even inexistent, as in our case. We thus selected NIST standard reference material (SRM) 610 in combination with 612 for external calibration, mainly due to its coverage of nearly all elements in the periodic table.25,26 It allowed us to quantify most elements of the periodic table including rarely occurring and unexpected elements in emerald. However, it is known that non-matrix matched SRMs may have some drawbacks.27 For example, most emeralds contain only traces or a non-detectable amount of Ca, whereas Ca is a major component in NIST SRMs (NIST612, Ca ∼8.5 wt%; NIST610, Ca ∼8.15 wt%). Consequently, mass interferences based on Ca molecules may affect the quantification of other elements in Ca-free samples, e.g.40Ca16O+ interferes with 56Fe+, hence challenging accurate Fe quantification. Due to similar matrices, both NIST612 and NIST610 were applied as external standards to create a linear calibration curve (dual-SRM calibration) in order to partially reduce/cancel matrix effect (see details below).
LA-ICP-TOF-MS setup
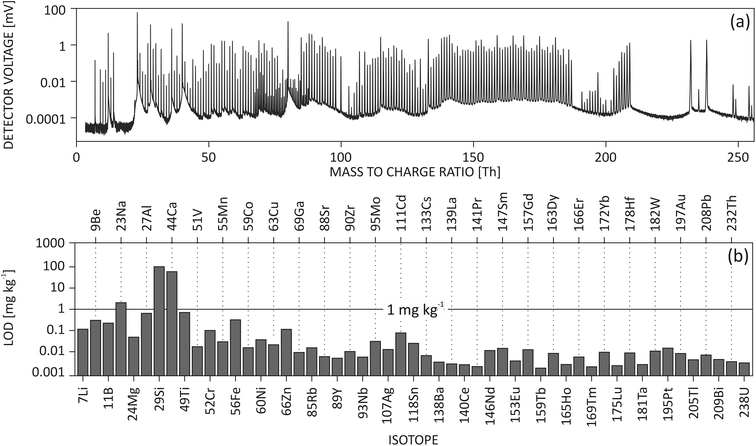
Trace element analysis was performed using an ArF excimer laser ablation unit equipped with a TwoVol2 ablation chamber (NWR193UC, ESI, USA) coupled to a commercial ICP-TOF-MS unit (icpTOF, TOFWERK AG, Switzerland). Hole drilling mode was applied for both SRMs and samples. Ablation spot diameter was 75 μm on NIST SRMs and 100 μm on emeralds. All spots were ablated 600 shots at 20 Hz. Additional five pre-cleaning laser shots were performed at the beginning of each measurement. The instrument was tuned daily for maximum sensitivity on light, middle and heavy masses from m/Q = 7 to 238 Thomson (Th, from 7Li+ to 238U+, Fig. 1) simultaneously, while keeping the oxide rate of thorium ThO+/Th+ < 0.6%, and 238U+/232Th+ close to 1.17 The influence of doubly charged species on neighboring singly charged ions was monitored using 138Ba2+calculated/69Ga+ (<3–4%). Signal of 138Ba2+calculated was estimated from 137Ba2+ and natural abundance of Ba isotopes. Single Ion Signal (SIS) was measured to report accurate intensity in counts per second (cps). Both NIST612 and NIST610 were measured twice before and after the measurements of gemstone samples. Internal standard of 29Si+ was used for emerald measurement, while for cross-quantification of NIST610 and NIST612, internal standard of 27Al+ was used. Table S-2† lists further details of the instrumental operating parameters.Post mass spectrum processing
Raw data were saved in HDF5 files by TofDaq acquisition software (version 1.2.97). Mass calibration was performed using 12C+, 23Na+, 40Ar2+ and 127I+ calibration peaks. Full mass spectrum was saved for each data point. Artifacts correction, such as the baseline correction in the mass spectrum, is not available in TofDaq. Hence, in this study, post mass spectrum correction was done using in-house script developed in MATLAB 2018a (MathWorks). The following steps were performed: (1) from the transient signal, 27 s background and 24 s ablation signal were selected; (2) outlier in transient signal was determined to be any data point (>6 cps) that deviated out of 3 standard deviations with respect to a second order polynomial baseline fitted into the background and ablation signal; (3) net mass spectrum was obtained by subtracting the averaged mass spectrum of the background from the averaged spectrum of the ablation signal; (4) linearly fitted baseline correction was done for a mass window of 0.5 Th centered at the target m/Q (0.25 Th on each side of the center mass position and 5 data points on each end of the window are used to anchor and draw the baseline), instead of applying a baseline fitting curve over the full mass spectrum; (5) the isotope peak was integrated in the baseline corrected spectrum and converted to intensity in cps using SIS factor; (6) interference correction due to doubly charged ions was applied to selected isotopes, such as 69Ga+ signal (interfered by 138Ba2+), which was mathematically corrected using the 137Ba2+ signal and natural abundance of Ba isotopes. Baseline correction is necessary as it minimizes the apparent signal intrusion into neighboring m/Qs (Fig. S-1†). The described baseline correction procedure is computationally efficient and it is a close approximation of true baseline due to the low abundance sensitivity of the TOF-MS.28 The last step is critical in order to correct for matrix effects, as for example NIST612 and NIST610 contain 50–500 mg kg−1 Ba, while Ba in emerald is not detectable. And such a correction is only feasible when doubly charged isotopes appear at half masses due to sufficient mass resolving power.Dual-SRM calibration
NIST610 SRM is often used as an external calibration standard and quantification procedures are done following Longerich et al.29 However, isotopes such as 56Fe+ and 57Fe+ may be interfered by Ca-polyatomic ions, which cannot be resolved by our TOF-MS and could lead to inaccurate results. Calcium is present at high concentrations in NIST610 (up to 8.15 wt%, and similarly in NIST612), whereas in emerald it is present only in trace amounts. Since our TOF-MS's mass resolving power (MRP) is not sufficient to fully separate interferences from the analyte, a dual-SRM calibration can be applied for trace element quantification (similar as solution analysis, where multiple standards are used to generate a calibration curve).30 When compared to the gas background, ablation mass spectra showed interferences of 40Ca16O+ and 40Ar16O+ on 56Fe+ as well as 40Ca16OH+ and 40Ar16OH+ on 57Fe+ (Fig. 2(a)–(d)). In the current setup, a more pronounced influence of the interference on the 57Fe+ concentration accuracy was observed compared to that of 56Fe+, as can be seen from the calibration curve (Fig. 2(e) and (f)). Although similar influences are caused by 40Ca16O+ and 40Ca16OH+, the pronounced effect on 57Fe+ can be attributed to its low natural abundance. Here, we make an approximation that NIST612 and NIST610 have the same amount of Ca influence on Fe isotopes due to similar Ca content and that they are matrix-matched. The slopes of the Fe calibration curves are hence not affected by Ca, only the intercepts indicate the net Ca contribution when there is no Fe in the sample. Therefore, the slopes calculated from the calibration curves are used for quantification of Fe isotopes assuming an intercept at zero.Limit of detection
Limit of detection (LOD) indicates the figure of merit of the experimental setup. It is a combined factor of sensitivity, gas blank signal intensity and number of data points measured. In this study, LOD calculations follow the method described in Pettke et al.31 LODs may vary from one measurement to another. The presence of one element may be solely due to a better LOD, and it is difficult to compare with another measurement with a higher LOD. Trace element compositions are often heterogeneous among minerals from various geological settings. If element concentrations are below the LOD, the result is missing, and the dataset is not complete. In order to fill in these missing values, concentrations below LOD can be substituted by zero, a mean value,32 a minimum value in the dataset,33 or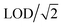 ,34 and the influence on statistical results using various methods were compared in literature.35
,34 and the influence on statistical results using various methods were compared in literature.35
Sporadically occurring trace elements in minerals or gemstones may hold characteristic information about their geological formation and geographic provenance. For our case study on gem quality emeralds from various deposits, we developed a novel method to replace element concentrations below LOD in order to use them for our statistical data evaluation and visualization. First, stable instrument performance was required over the time period of measurements. Then LOD histograms of various isotopes in emeralds were fitted to a log-normal function. The selection of log-normal distribution is due to its similar shape comparing to a LOD histogram as well as its range covering positive real number (same as LOD). Finally, trace elements below LOD were replaced by random concentration values generated from fitted distributions. By this, a complete concentration table could be achieved for all emerald samples and elements included in this study.
Data visualization using t-SNE
Elements used in t-SNE calculation were chosen based on their occurrence frequency in the dataset, meaning an element is selected when its concentration is above LOD in more than a certain percentage of measurements. The empirical threshold can be different for different mineral species. In our study on gem quality emeralds, we selected only elements that are observed in at least 80% of the measurements for t-SNE calculation. An in-house developed script in MATLAB 2018a performs dimension reduction using t-SNE algorithm. Calculation parameters include: standardized Euclidean distance for distance calculation; two dimensions for embedded space; 35 for perplexity, which is an estimate of the number of surrounding data points; and exact optimization for the Kullback–Leibler divergence.36 The algorithm converged within 1500 iterations. Afterwards, scatter plots in 2D were constructed using the dataset from embedded space. In this case study, the original dataset involves elemental concentrations only. Independently-determined geographic provenance information, either deduced by gemologists using routine gemological techniques or given by reliable sources, can be overlaid on top of the scatter plot for data point labeling (colors and symbols). Closely grouped data points indicate that they are more similar in chemical composition to each other. As a comparison, the same dataset has been analyzed using PCA (MATLAB 2018a), and the resulted first two principle components were plotted and labelled with provenance information.Results & discussion
Full mass spectrum
LA-ICP-TOF-MS acquires a full mass spectrum covering almost all elements from the periodic table, as shown in Fig. 1(a). In a typical mass spectrum of NIST610, the lightest ion (on the far left) is 7Li+ and the heaviest molecular ion (on the far right) is 238U16OH+. Although it is possible to tune the instrument to measure 6Li+, it would result in a large sensitivity loss in the heavy mass range. Therefore, 6Li+ is not included in routine measurements. Higher peak density around m/Q = 60–80 Th is due to the presence of both singly charged isotopes and doubly charged isotopes of Ba and lanthanides appearing at both unit and half masses (Fig. S-2†).By acquiring the full mass spectrum simultaneously, LA-ICP-TOF-MS has changed the paradigm of LA analysis. Instead of defining in advance which elements to measure, TOF users are capable of conducting the experiment first and then selecting isotopes of interest. This can be advantageous, as less a priori knowledge about the sample is needed before analysis, for example, when analyzing unknown inclusions, or rarely occurring trace elements in minerals. In addition, full mass acquisition allows to re-analyze raw data and add additional isotopes of interest without re-ablating the sample.
Mass resolving power and mass interference
Isotopes of a specific element to be quantified may be changed or corrected in the post-data processing, in case (unforeseen) mass interferences occur. In order to better prepare for such scenarios, ICP-TOF-MS measures from a sample not only its full mass spectrum, but also with moderate mass resolving power (MRP).In case of gemstone provenance studies, gallium (Ga) is an important element for provenance determination of Al-bearing minerals (e.g. Al-oxides and Al-bearing silicates), therefore its accurate quantification is required. However, often both Ga isotopes (m/Q = 69 and 71 Th) are interfered by doubly charged ions of, e.g. Ba and lanthanides, which induce inaccurate Ga quantification. These inaccuracies are mainly due to different concentrations of interference content in the sample and the external calibration standard. Benefiting from a moderate MRP (∼2000 for 69Ga+) of ICP-TOF-MS, half masses can easily be resolved from neighboring unit masses, as seen in NIST610 mass spectrum in Fig. S-2.† A clear separation of half m/Q (137Ba2+, 68.5 Th) from unit m/Q (69Ga+ and 138Ba2+, 69 Th) allows mathematical interference correction for 69Ga+ signal detected in NIST610 using a signal intensity of 137Ba2+ and natural abundance of Ba isotopes. After subtracting the 138Ba2+ interference, Ga quantification accuracy in Ba-free minerals (e.g. emerald) using non-matrix-matched NIST610 SRM can be improved.
Limit of detection
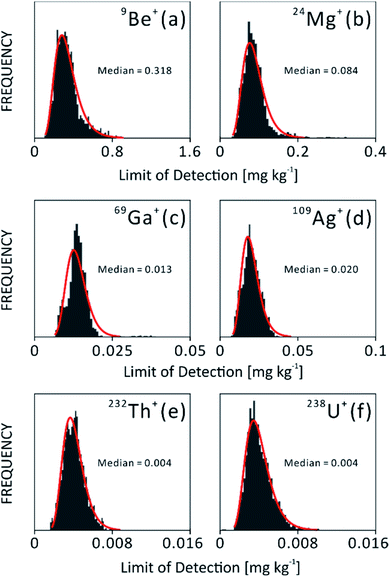
The limits of detection of light to heavy elements from NIST610 are shown in Fig. 1(b). Light elements have lower sensitivity and result in a few hundred μg kg−1 LOD. On the other hand, single digit μg kg−1 LODs can be routinely achieved for heavy elements due to higher sensitivity and lower background noise.Limit of detection is a useful figure of merit to monitor the performance of an analytical system over a long period of time. In this study, LODs of different isotopes tested in NIST610 were monitored during one year of experiments. In Fig. 3, histograms of selected LODs indicate the stability of instrument over the year of operation. Isotopes have showed narrow distribution allowing the comparison and statistical analysis of chemical results measured at different times. Such distribution also reflects the stability of instrument performance during a long time period. However, histograms of Be and Mg in Fig. 3(a) and (b) are not fitted well with log-normal distribution at the right tailing part, which could be due to different behaviors of light and heavy ions. In histograms of Ga and Ag in Fig. 3(c) and (d), a secondary peak can be seen on the left tailing of the fitting, which may be related to difference instrument settings and tunings applied during the one year of instrument operation.
Case study on emeralds from various deposits
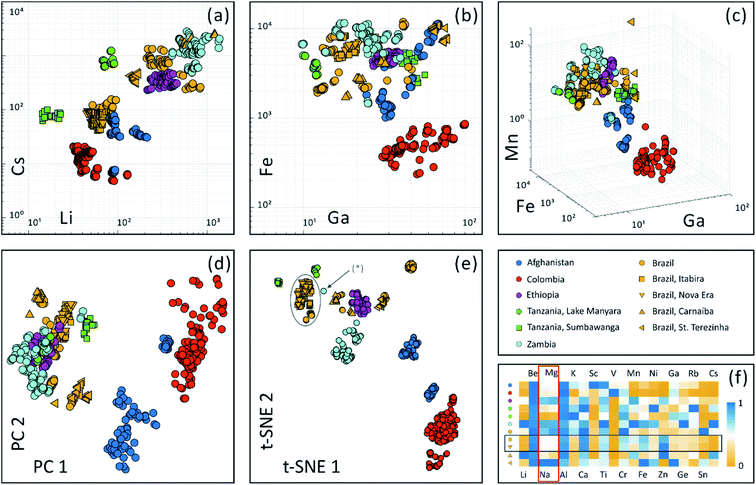
Trace element concentration of reference samples from a database is usually plotted in bivariate or 3D scatter plots to visualize their elemental similarity. For example, Fig. 4 display bivariate plots of (a) Li–Cs and (b) Ga–Fe as well as a 3D scatter plot (c) Ga–Fe–Mn using our in-house emerald database of the Swiss Gemmological Institute SSEF. This dataset consists of multi-element information of more than 700 analyses on 168 emerald samples.High dimensional dataset of twenty selected elements (occurrence frequency threshold is 80% and excluding internal standard Si) is projected onto a two dimensional space using linear PCA and non-linear t-SNE algorithms, as illustrated in Fig. 4(d) and (e). These two unsupervised analyses labeled geographic provenance in various colors after the calculation process. It is apparent that the t-SNE algorithm achieves a better differentiation of origins compared to PCA.
Both PCA and t-SNE algorithms separated these samples into subgroups. First, a subgroup with Colombian emeralds sits far away compared to emeralds from other origins. This may be in accordance with their hydrothermal formation in veins in black shales and limestones in Colombia, while most other origins belong to ‘schist’ type deposits (typical for those in Brazil, Ethiopia, Tanzania and Zambia), where emeralds are mostly found in metamorphic biotite schists.37,38 Emeralds from Afghanistan are related to hydrothermal veins cross cutting metasedimentary rocks39 and are plotted in a separate group, with a small subgroup of Afghani samples discovered only very recently. Further studies are necessary to verify the geological setting and formation specifically of this new Afghani finding.40 Second, PCA analysis is limited in separating ‘schist’ type samples (e.g. Brazil, Ethiopia, Tanzania and Zambia) into more detailed subgroups. In contrast, t-SNE has successfully distinguished ‘schist’ type emerald samples into subgroups in Fig. 4(e). As illustrated in the plot, not only were geographic provenances distinguished, but also different emerald deposits within countries can be separated. The Brazilian samples from St. Terezinha and Carnaíba can be separated with this method. In contrast to this, emeralds from the two locations Itabira and Nova Era in Brazil are strongly overlapping (indicated by grey oval). This is because they are geographically close to each other (only about 20 km distance, Fig. S-3†),41 and share a similar geological environment.
The chemical similarity of Itabira and Nova Era emeralds can be confirmed additionally when comparing median concentrations of the 20 most frequently occurring elements, as shown in ESI Table S-3† and Fig. 4(f). For each element, median concentrations from 11 origins were normalized to the max median concentration of all locations. Normalized median values of all elements are displayed within a range of 0 to 1. The rows of yellow square (Itabira, Brazil) and yellow triangle facing down (Nova Era, Brazil) are in apparent correlation (indicated by a horizontal box). Interestingly, Na composition correlates with Mg across all origins (indicated by a vertical box) and similar correlation is observed between 23Na+ and all 24Mg+, 25Mg+ and 26Mg+ isotopes. Since a baseline correction eliminates the possibility of intruding a high signal into neighboring m/Qs (as shown in Fig. S-1†), such an observation is a real effect from the sample. The reason for the correlation can be explained by elemental substitution in the crystal structure. When Mg2+ substitutes Al3+ (Y-site) in the beryl lattice, the charge difference is balanced by adding Na+ into the channel structure of beryl.42
Due to limited analytical capabilities, lack of characteristic features, measuring on inclusions, or mistakes in labelling (of collection samples), outliers may occur. They can fall into two categories: (i) those overlapping with other groups (not observed in this study): thorough investigation of the similarity to the overlapped group helps to determine whether the outlier is a mislabel or a real geological outlier (such as caused by chemical heterogeneity), which creates special attention when another sample falls into the same group; (ii) those that stand alone and are not close to other groups (e.g. outlier labeled (*) in Fig. 4(e)): special attention should be given to whether they are from a yet-unknown provenance, or if the trace element results may contain contributions from inclusions.
Emeralds often contain a large number of chemical impurities, partly due to its specific crystal structure offering several potential substitution sites, but also due to the large range of chemical elements available in the geological environment during emerald formation.42 For this visualization, twenty elements were selected with occurrence frequency above 80%, meaning these elements are above the limit of detection in more than 80% of the analyses. Other elements were omitted in order to avoid randomness added on to the t-SNE plot, due to more random concentration values of less frequently occurring elements (Fig. S-4†). As an outlook, independent threshold adjustment on each element should be further studied to investigate clustering quality. Furthermore, when more samples (e.g. from new emerald mines) are going to be analyzed, additional elements which were not used in this calculation may be included in the future. This dynamic element selection scheme can be realized if the original dataset contains as many elements as possible. ICP-TOF-MS, which acquires almost all elements from mineral samples, will reveal its strength in this respect.
Conclusions
We characterized a new LA-ICP-TOF-MS setup and developed a method to perform multi-element analysis of minerals. The full mass spectrum of the ICP-TOF-MS, which acquires almost all elements in the periodic table, from Li to U, allows comprehensive investigation of samples with limited or without a priori information about elemental composition. This advantage is helpful for studying elements which occur infrequently. Such information provides additional characteristic patterns of minerals from different geological/geographic provenances. Given the mass resolving power of ICP-TOF-MS, some common interferences, such as doubly charged ions of Ba and lanthanides, can be corrected. Moreover, artifacts due to non-matrix matched standards can be (partially) eliminated using a dual-SRM calibration method. Other mass spectrum correction methods, such as baseline correction, are required for TOF data in order to improve precision and accuracy of trace element analysis.In this study, we analyzed 168 emerald samples using LA-ICP-TOF-MS in an industrial case study that covers samples available in the emerald trade. The performance of projecting high dimensional datasets onto low dimension spaces was compared between linear PCA and non-linear t-SNE. Both algorithms consider multi-element datasets as a whole without provenance information (unsupervised). We found that non-linear dimension reduction by t-SNE is better at maintaining intrinsic structure from the original high dimensional space and embedding such information onto low dimensional datasets for visualization. Therefore, the t-SNE method excels in distinguishing within-group similarities from between-group similarities. The separation of subgroups achieved with t-SNE is in agreement with geological origins which are determined through careful collection onsite or independently by experienced gemologists using routine gemological testing methods. Hence, in the context of traceability services, this statistical approach provides further evidence for geographic provenance determination. More investigations are needed to generalize common microscopic, physical and chemical properties that group samples together. These microscopic and spectroscopic characterizations of a mineral (gemstone) will add new dimensions to the dataset, besides multi-element composition.
Based on the successful application of t-SNE for data visualization of emeralds from different geographic and geological origins, we are convinced that the methodology described in this study may be applied to process high dimensional datasets in other scientific fields, such as geology, archaeology, forensics and biology, as well as in 2D or 3D chemical imaging.
Author contributions
HAOW and MSK contribute to the conceptualization and supervision of this project. Both authors contribute in preparing the manuscript. MSK conducted the gemmological determination of provenance for emerald samples. HAOW designed analysis protocol, conducted the experiment and developed MATLAB scripts for post data processing, t-SNE calculation and multi-element data visualisation. HAOW and MSK validate the data and investigate the results.Conflicts of interest
The authors declare no conflict of interest. This work was conducted at the Swiss Gemmological Institute SSEF, which is a gem testing laboratory and part of the Swiss Foundation of Gemstone Research, a non-profit organization in Switzerland.Acknowledgements
We acknowledge fruitful discussions on ICP-TOF-MS with Dr Olga Borovinskaya, Dr Martin Rittner and Dr Martin Tanner at TOFWERK AG, Thun, Switzerland, as well as on t-SNE with Dr Xiaokang Lun and Dr Vito Zanotelli at University of Zurich. We also would like to thank the Board of the Swiss Foundation of Gemstone Research (SSEF) for their support in this project of the SSEF laboratory. Many worldwide gemstone dealers and the Swiss Association of Gemstone Dealers (ASNP) are appreciated for their generous gemstone and financial donations. Thanks also to the entire SSEF team for their support and discussions, especially Susanne Büche, Ramon Schmid and Judith Braun, for helping with part of the LA-ICP-TOF-MS measurements, all gemologists at SSEF for careful geographic provenance determination, Dr Alexander Gundlach-Graham, Dr Laurent E. Cartier and Dr Tashia Dzikowski for commenting on the manuscript.References
- B. Paul, J. D. Woodhead, C. Paton, J. M. Hergt, J. Hellstrom and C. A. Norris, Towards a Method for Quantitative LA-ICP-MS Imaging of Multi-Phase Assemblages: Mineral Identification and Analysis Correction Procedures, Geostand. Geoanal. Res., 2014, 38, 253–263 CrossRef.
- Z. Zajacz, W. E. Halter, T. Pettke and M. Guillong, Determination of Fluid/Melt Partition Coefficients by LA-ICPMS Analysis of Co-Existing Fluid and Silicate Melt Inclusions: Controls on Element Partitioning, Geochim. Cosmochim. Acta, 2008, 72, 2169–2197 CrossRef CAS.
- P. W. Reiners, R. W. Carlson, K. M. Cooper, D. E. Granger, N. M. McLean and B. Schoene, Geochronology and Thermochronology, 2017 Search PubMed.
- R. Kovacs, S. Schlosser, S. P. Staub, A. Schmiderer, E. Pernicka and D. Günther, Characterization of Calibration Materials for Trace Element Analysis and Fingerprint Studies of Gold Using LA-ICP-MS, J. Anal. At. Spectrom., 2009, 24, 476–483 RSC.
- H.-E. Gäbler, W. Schink, S. Goldmann, A. Bahr and T. Gawronski, Analytical Fingerprint of Wolframite Ore Concentrates, J. Forensic Sci., 2017, 62, 881–888 CrossRef.
- F. Sutherland, K. Zaw, S. Meffre, T.-F. Yui and K. Thu, Advances in Trace Element “Fingerprinting” of Gem Corundum, Ruby and Sapphire, Mogok Area, Myanmar, Minerals, 2014, 5, 61–79 CrossRef.
- H. A. O. Wang, M. S. Krzemnicki, J.-P. Chalain, P. Lefèvre, W. Zhou and L. Cartier, Simultaneous High Sensitivity Trace-Element and Isotopic Analysis of Gemstones Using Laser Ablation Inductively Coupled Plasma Time-of-Flight Mass Spectrometry, J. Gemmol., 2016, 35, 212–223 CrossRef.
- D. P. Myers and G. M. Hieftje, Preliminary Design Considerations and Characteristics of an Inductively Coupled Plasma-Time-of-Flight Mass Spectrometer, Microchem. J., 1993, 48, 259–277 CrossRef CAS.
- D. P. Myers, G. Li, P. Yang and G. M. Hieftje, An Inductively Coupled Plasma-Time-of-Flight Mass Spectrometer for Elemental Analysis. Part I: Optimization and Characteristics, J. Am. Soc. Mass Spectrom., 1994, 5, 1008–1016 CrossRef CAS.
- D. Myers, G. Li, P. Mahoney and G. Hieftje, An Inductively Coupled Plasma-Time-of-Flight Mass Spectrometer for Elemental Analysis. Part III: Analytical Performance, J. Am. Soc. Mass Spectrom., 1995, 6, 411–427 CrossRef CAS.
- A. Kindness, Two-Dimensional Mapping of Copper and Zinc in Liver Sections by Laser Ablation-Inductively Coupled Plasma Mass Spectrometry, Clin. Chem., 2003, 49, 1916–1923 CrossRef CAS.
- V. I. Baranov, X. Lou, D. R. Bandura, A. Antonov, O. I. Ornatsky, J. E. Dick, R. Kinach, S. Pavlov, S. Vorobiev and S. D. Tanner, Mass Cytometry: Technique for Real Time Single Cell Multitarget Immunoassay Based on Inductively Coupled Plasma Time-of-Flight Mass Spectrometry, Anal. Chem., 2009, 81, 6813–6822 CrossRef.
- O. Borovinskaya, B. Hattendorf, M. Tanner, S. Gschwind and D. Günther, A Prototype of a New Inductively Coupled Plasma Time-of-Flight Mass Spectrometer Providing Temporally Resolved, Multi-Element Detection of Short Signals Generated by Single Particles and Droplets, J. Anal. At. Spectrom., 2013, 28, 226–233 RSC.
- A. Gundlach-Graham, M. Burger, S. Allner, G. Schwarz, H. A. O. Wang, L. Gyr, D. Grolimund, B. Hattendorf and D. Günther, High-Speed, High-Resolution, Multielemental Laser Ablation-Inductively Coupled Plasma-Time-of-Flight Mass Spectrometry Imaging: Part I. Instrumentation and Two-Dimensional Imaging of Geological Samples, Anal. Chem., 2015, 87, 8250–8258 CrossRef CAS.
- M. Burger, A. Gundlach-Graham, S. Allner, G. Schwarz, H. A. O. Wang, L. Gyr, S. Burgener, B. Hattendorf, D. Grolimund and D. Günther, High-Speed, High-Resolution, Multielemental LA-ICP-TOFMS Imaging: Part II. Critical Evaluation of Quantitative Three-Dimensional Imaging of Major, Minor, and Trace Elements in Geological Samples, Anal. Chem., 2015, 87, 8259–8267 CrossRef CAS.
- C. Giesen, H. A. O. Wang, D. Schapiro, N. Zivanovic, A. Jacobs, B. Hattendorf, P. J. Schüffler, D. Grolimund, J. M. Buhmann, S. Brandt, Z. Varga, P. J. Wild, D. Günther and B. Bodenmiller, Highly Multiplexed Imaging of Tumor Tissues with Subcellular Resolution by Mass Cytometry, Nat. Methods, 2014, 11, 417–422 CrossRef CAS.
- M. Burger, G. Schwarz, A. Gundlach-Graham, D. Käser, B. Hattendorf and D. Günther, Capabilities of Laser Ablation Inductively Coupled Plasma Time-of-Flight Mass Spectrometry, J. Anal. At. Spectrom., 2017, 32, 1946–1959, 10.1039/C7JA00236J.
- H. R. Rollinson, Using Geochemical Data: Evaluation, Presentation, Interpretation, Routledge, 2014 Search PubMed.
- S. Saeseaw, N. D. Renfro, A. C. Palke, Z. Sun and S. F. McClure, Geographic Origin Determination of Emerald, Gems Gemol., 2019, 4, 614–646, DOI:10.5741/GEMS.55.4.614.
- J. N. Miller and J. C. Miller, Statistics and Chemometrics for Analytical Chemistry, Person, 6th edn, 2010 Search PubMed.
- L. J. P. Van Der Maaten and G. E. Hinton, Visualizing High-Dimensional Data Using t-SNE, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- G. E. Hinton and S. T. Roweis, Stochastic Neighbor Embedding, in Advances in Neural Information Processing Systems, The MIT Press, 2002, pp. 833–840 Search PubMed.
- A. Platzer, Visualization of SNPs with T-SNE, PLoS One, 2013, 8(2) DOI:10.1371/journal.pone.0056883.
- E. A. D. Amir, K. L. Davis, M. D. Tadmor, E. F. Simonds, J. H. Levine, S. C. Bendall, D. K. Shenfeld, S. Krishnaswamy, G. P. Nolan and D. Pe'Er, ViSNE Enables Visualization of High Dimensional Single-Cell Data and Reveals Phenotypic Heterogeneity of Leukemia, Nat. Biotechnol., 2013, 31, 545–552 CrossRef CAS.
- A. Abduriyim and H. Kitawaki, Applications of Laser Ablation—Inductively Coupled Plasma-Mass Spectrometry (LA-ICP-MS) to Gemology, Gems Gemol., 2006, 42, 98–118 CrossRef CAS.
- K. P. Jochum, U. Weis, B. Stoll, D. Kuzmin, Q. Yang, I. Raczek, D. E. Jacob, A. Stracke, K. Birbaum, D. A. Frick, D. Günther and J. Enzweiler, Determination of Reference Values for NIST SRM 610-617 Glasses Following ISO Guidelines, Geostand. Geoanal. Res., 2011, 35, 397–429 CrossRef CAS.
- S. Zhang, M. He, Z. Yin, E. Zhu, W. Hang and B. Huang, Elemental Fractionation and Matrix Effects in Laser Sampling Based Spectrometry, J. Anal. At. Spectrom., 2016, 31, 358–382 RSC.
- L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, Characterization of a New ICP-TOFMS Instrument with Continuous and Discrete Introduction of Solutions, J. Anal. At. Spectrom., 2017, 32, 548–561 RSC.
- H. P. Longerich, S. E. Jackson and D. Günther, Inter-Laboratory Note. Laser Ablation Inductively Coupled Plasma Mass Spectrometric Transient Signal Data Acquisition and Analyte Concentration Calculation, J. Anal. At. Spectrom., 2004, 11, 899–904 RSC.
- Y. Liu, Z. Hu, S. Gao, D. Günther, J. Xu, C. Gao and H. Chen, In Situ Analysis of Major and Trace Elements of Anhydrous Minerals by LA-ICP-MS without Applying an Internal Standard, Chem. Geol., 2008, 257, 34–43 CrossRef CAS.
- T. Pettke, F. Oberli, A. Audétat, M. Guillong, A. C. Simon, J. J. Hanley and L. M. Klemm, Recent Developments in Element Concentration and Isotope Ratio Analysis of Individual Fluid Inclusions by Laser Ablation Single and Multiple Collector ICP-MS, Ore Geol. Rev., 2012, 44, 10–38 CrossRef.
- G. Rugg and M. Petre, A Gentle Guide to Research Methods, Mc Graw Hill, 2007, p. 228 Search PubMed.
- J. Xia, N. Psychogios, N. Young and D. S. Wishart, MetaboAnalyst: A Web Server for Metabolomic Data Analysis and Interpretation, Nucleic Acids Res., 2009, 37(suppl_2), W652–W660, DOI:10.1093/nar/gkp356.
- C. W. Croghan and P. P. Egeghy, Methods of Dealing With Values Below the Limit of Detection Using SAS, proceeding in Southern SAS User Group, 2003, 5 Search PubMed.
- P. Gromski, Y. Xu, H. Kotze, E. Correa, D. Ellis, E. Armitage, M. Turner and R. Goodacre, Influence of Missing Values Substitutes on Multivariate Analysis of Metabolomics Data, Metabolites, 2014, 4, 433–452 CrossRef.
- S. Kullback and R. A. Leibler, On Information and Sufficiency, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
- W. A. Deer, R. A. Howie and J. Zussman, Rock-Forming Minerals, 2nd edn, 1992 Search PubMed.
- L. A. Groat, G. Giuliani, D. D. Marshall and D. Turner, Emerald Deposits and Occurrences: A Review, Ore Geol. Rev., 2008, 34, 87–112 CrossRef.
- G. Bowersox, L. W. Snee, E. E. Foord and R. R. Seal, Emeralds of the Panjshir Valley, Afghanistan, Gems Gemol., 1991, 27, 26–39 CrossRef.
- M. S. Krzemnicki, New Emeralds From Afghanistan, Facette, 2018, 12–13 Search PubMed.
- H. Jordt-Evangelista, C. Lana, C. E. R. Delgado and D. J. Viana, Age of the emerald mineralization from the Itabira-Nova Era District, Minas Gerais, Brazil, based on LA-ICP-MS geochronology of cogenetic titanite, Braz. J. Geol., 2016, 46, 427–437 CrossRef.
- L. Groat, G. Giuliani, D. Marshall and D. Turner, Emerald, in Geology of Gem Deposits, 2014, p. 135 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00484g |
| This journal is © The Royal Society of Chemistry 2021 |