Towards understanding of delignification of grassy and woody biomass in cholinium-based ionic liquids

Abstract

The molecular level details of dissolution of lignin in certain ionic liquids (ILs), such as cholinium-based ILs, are a relatively underexplored area and several key details to comprehend the dissolution mechanism are yet to be discovered. To understand, answer, and connect the missing links in the delignification mechanism during biomass pretreatment using cholinium-based ILs we employ COnductor like Screening MOdel for Real Solvents (COSMO-RS) and molecular dynamics (MD) simulations to evaluate the interactions between lignin-like model compounds and the anion and cation of several cholinium-based ILs. Initially, lignin dissolution was studied for cholinium-based ILs containing five different carboxylate anions ([For], [Ace], [But], [Hex], and [Oct]) and were compared with lysinate as the anion. The microscopic properties such as interaction energies, activity coefficient, radial and spatial distribution functions (RDF/SDF), and hydrogen bonds and their dynamics were assessed to characterize lignin dissolution in these ILs and were validated with experimental data. Among the anions studied, both octanoate and lysinate containing ILs demonstrated better lignin dissolution; lysinate being the best. The simulation data suggested that [Ch][Lys] has higher affinity for ether linkages of lignin (e.g., β-O-4) than for C–C linkages, which explains the higher delignification of hardwood and grassy biomasses (60–80% C–O–C linkages) in [Ch][Lys].

---

1. Introduction

Lignin, one of the major constituents of the lignocellulosic biomass along with cellulose and hemicellulose, is the most-abundant bio-renewable source for aromatics on earth.^1,2 It is a complex heterogeneous biopolymer composed of three major phenylpropane units, namely p-coumaryl, coniferyl, and sinapyl. These phenylpropane monomers are strongly bonded together by C–O–C ether (carbon–oxygen: β-O-4, α-O-4, and 4-O-5) and C–C interunit (β–β, β-5, β-1, and 5–5) bonds.^3–5 β-O-4 bonds are the most abundant ether linkage in lignin, representing about 40–65% of all inter-subunit bonds. Additionally, lignin accommodates various functional groups, such as methoxy, phenolics, aliphatic hydroxy, cyclic and noncyclic ethers, and carbonyl groups, which affects its polarity and reactivity.^3,6 The H-bonds between neighboring O-containing groups and π–π interactions between aromatic moieties further complicates the lignin structure and enhances its recalcitrance to facile deconstruction.^7–9 Nevertheless, the utilization of lignin as a feedstock for the production of hydrocarbons and chemicals offers a significant opportunity for enhancing the overall operational efficiency, carbon conversion rate, economic viability, and sustainability of biorefinery processes.² But, due to the recalcitrance, heterogeneity, strong interactions, and hydrophobicity of lignin, fractionation of lignin remains a major challenge for biorefineries.¹⁰ Hence, suitable solvents to enable lignin removal, solubility and accessibility to enzymatic depolymerization of both sugar and lignin polymers is required.

Over the past few decades, certain ionic liquids (IL), which are organic salts with a melting temperature lower than 100 °C (ref. 11–13) have emerged as potent solvents and have opened new opportunities for efficient biomass processing.^14–17 IL-based pretreatment offers several advantages, including reduction of biomass particle size, reduction of cellulose crystallinity, and selective extraction of lignin from biomass, thus enhancing fermentable sugars release.^14,18,19 There is an extensive literature available on the dissolution and reduction of the crystallinity of cellulose in ILs using both experimental and computational techniques.^{11,12,15,17,20} Compared to cellulose, very limited work has been performed to understand the influence of the structure and chemical properties of ILs on lignin dissolution.^7,21,22 Previous studies used solubility parameters such as Hildebrand and Hansen solubility parameters (HSP),^23,24 continuum solvation model,^24–26 and the quantum chemical (QC) calculations^7,27 to understand biomass delignification at the molecular level. For instance, Balaji et al.(2012)²⁴ and Casas et al. (2012,2013)^25,26 screened various ILs based on solubility parameters and thermodynamic properties (e.g. excess enthalpy and activity coefficient) predicted using COnductor like Screening MOdel for Real Solvents (COSMO-RS) model. These studies concluded that smaller differences between the solubility parameter values of lignin and those of the solvent, the lower the activity coefficient and exothermic behavior of excess enthalpy positively correlated with lignin dissolution in any given IL.^24–26 Later, Zhang et al. (2017)⁷ and Ji et al. (2012)²⁸ performed QC calculations on IL–lignin systems and deduced that stronger H-bonding interactions between lignin and imidazolium-based IL mixtures drive lignin dissolution. Further, Zhu et al. (2017) studied the dissolution behavior of lignin (veratrylglycerol-β-guaiacyl ether) in 1-allyl-3-methylimidazolium chloride ([Amim]Cl) by both QC and molecular dynamics (MD) simulations²⁹ and showed that chloride anions form strong hydrogen bonds with lignin, while the cation [Amim]⁺ interacts with lignin via weaker π–π stacking and van der Waals interactions. In the literature, imidazolium-based cations are the most studied ILs for lignin dissolution by both computational and experimental.^7,21,27,28

Recently, cholinium-based ILs have gained much attention as efficient biomass pretreatment solvents, because they, in generalized terms, can efficiently solubilize lignin, are less expensive, and are more biocompatible with biorefinery-relevant enzymes and microorganisms when compared with majority of the imidazolium-based ILs.^30–32 Hou et al. (2012) studied the dissolution of lignin and efficacy of biomass pretreatment in 28 cholinium-based ILs and reported that anions with basic group(s) (e.g.: lysinate [Lys]⁻) are effective ILs for biomass delignification and significantly enhanced enzymatic hydrolysis rate.¹⁹ In a later study, Sun et al. (2014) investigated the pretreatment of switchgrass in imidazolium and cholinium-based cations with lysinate and acetate anions (ILs: [Emim][Lys], [Emim][Ace], [Ch][Lys], and [Ch][Ace]) both experimentally and computationally.³¹ It has been reported that [Lys]⁻-based ILs achieved higher delignification (70–87%) efficacy and enhanced glucose yields up to 96% compared to [Ace]⁻-based ILs irrespective of the cation.³¹ The strength of interaction energies between lignin and ILs were predicted in the following order: [Ch][Ace] > [Emim][Ace] > [Ch][Lys] > [Emim][Lys], which is contrary to experimental delignification values. Dutta et al. (2018) studied delignification of three different lignocellulosic biomasses, namely switchgrass (grass), eucalyptus (hardwood), and pine (softwood) in [Ch][Lys] IL. Surprisingly, the removal of lignin in grass (74%) and hardwood (70%) biomasses were much higher than the softwood (21%).³² Based on these studies, the lower removal of lignin in softwood biomass remains questionable. These discrepancies indicate that many key details have not been considered while predicting the dissolution of lignin from biomass in cholinium-based ILs and are yet to be addressed. Hence, a systematic study with promising ILs (e.g. [Ch][Lys] and [Ch][Ace]) is needed and is the focus of the present work.

We used MD simulations and COSMO-RS calculations to reveal the mechanism of lignin dissolution in cholinium-based ILs. The calculations were performed on cholinium-based ILs containing carboxylate anions, including formate [For]⁻, acetate [Ace]⁻, butyrate [But]⁻, hexanoate [Hex]⁻, and octanoate [Oct]⁻ to comprehend the effect of different alkyl chain lengths on lignin dissolution. We intended to develop this key understanding by answering the following questions: (1) what is the dissolution mechanism of lignin in cholinium-carboxylate anions? (2) what are the critical factors that influence lignin dissolution in cholinium lysinate ([Ch][Lys]) compared to carboxylate IL? and (3) what are the dissolution mechanisms in [Ch][Lys] for common lignin moieties linked via different bond types? Microscopic properties such as activity coefficient, interaction energies, contact probability, radial and spatial distribution functions, H-bonds and their dynamics, and ionic pair dynamic analysis were evaluated to address these questions and assess the molecular level details of lignin dissolution in cholinium-based ionic liquids.

2. Computational details

2.1. Molecular dynamics simulations

The chemical structures of lignin dimers, cation (cholinium, [Ch]⁺), and anions ([For]⁻, [Ace]⁻, [But]⁻, [Hex]⁻, [Oct]⁻, and [Lys]⁻) were created using Avogadro³³ and are depicted in Fig. 1. Here, lignin-like model dimers with 4-O-5, β-O-4, and 5–5 linkages were used as lignin structures for all the MD simulations. The molecular geometries of all the investigated molecules were optimized using Gaussian09 with energies calculated at the B3LYP level of theory and 6-311+G(d,p) basis set.^7,34,35 To study the microscopic interactions between lignin and cholinium-based ILs ([Ch][For], [Ch][Ace], [Ch][But], [Ch][Hex], [Ch][Oct], and [Ch][Lys]), molecular dynamics simulations were carried out using NAMD.³⁶ For all the investigated molecules, CHARMM36 force field parameters were employed. The force field parameters for lignin were taken from Vermaas et al. (2019)³⁷ and parameters for cholinium, formate, butyrate, hexanoate, octanoate, and lysinate, the force field parameters were developed using the CGENFF tool.^38,39 The force field parameters developed for ILs were further validated by measuring their densities, and the deviation between predicted and experimental densities is less than 3% (Table S1†).

Fig. 1 Chemical structures of investigated lignin and IL molecules. The color scheme used for different atoms is C (ash), O (red), N (blue), and H (white), respectively.

All MD simulations were performed at constant temperature (363.15 K) and pressure (1 atm) using Langevin thermostat and Nose–Hoover Langevin barostat.^40,41 Temperature was controlled using a damping coefficient of 1 ps⁻¹ for Langevin dynamics and a damping factor of 50 fs was used for pressure control with an oscillation period of 100 fs.^15,42 A 1 fs of time step was used to integrate the equations of motion, and the SHAKE algorithm was implemented to constrain all the bonds involving hydrogen atoms with a tolerance of 10⁻⁵.⁴³ The Particle Mesh Ewald (PME) method was adopted to treat long-range electrostatic interactions with an accuracy of 10⁻⁶ (PME tolerance) at a cut-off distance of 12 Å.⁴⁴ The initial configuration of lignin and ionic pairs (cation + anion) were prepared using PACKMOL⁴⁵ in a cubic box containing 300 molecules of IL and 30 molecules of lignin. Two random initial configurations were prepared as starting geometries.

Initially, the potential energy of the simulated systems was minimized for 1 ns. After energy minimization, the molecular system was heated using a heating schedule of 0.001 K/step over 0.5 ns until the system reached the target simulation temperature. At the target temperature, the system was equilibrated for 8 ns under the NPT (isothermal–isobaric) ensemble to converge the system to its experimental condition. Hereafter, the production phase was run for 60 ns under the constant NVT (canonical) ensemble. The MD production run trajectory was analyzed to measure the RMSD of the lignin to confirm the simulation run time and fluctuations in the lignin structure. From the RMSD curves, the molecular positions of lignin changed sharply during the initial part of the simulation (<20 ns) after which steady-state diffusion of lignin molecule occurs (see Fig. S1†), which confirmed the system was in an equilibrium state after ∼20 ns and about 60 ns of the production run is sufficient to study the diffusion and interactions of ILs with the lignin-like dimers. At every 5 ps, the production data was saved for analysis of radial distribution functions (RDF) and non-bonded interaction energy calculations. MD simulation trajectories were visualized and analyzed with the Visual Molecular Dynamics (VMD) and TRAVIS packages.^46–48 The non-bonded interaction energies and the number of hydrogen bonds between lignin and ILs were calculated per mole of lignin. Similarly, the interaction energy between the [Ch]⁺ and [Anions]⁻ was calculated per mol of IL. Tables S2 and S3† report the summary of MD simulations.

2.2. COSMO-RS calculations

The COSMO-RS calculations have been performed to predict the logarithmic activity coefficient (ln(γ)) of lignin in the investigated ILs. The activity coefficient is often used as a quantitative descriptor for the solvation power of a solvent.^15,26,49,50 Based on the assumptions devised in the solid–liquid equilibrium (SLE), the reciprocal of the activity coefficient describes the solvency of a solute in the solvent (i.e., lower ln(γ) value, higher solubility).^34,49,51 After optimizing the geometries of the investigated molecules, the COSMO file was generated using BVP86/TZVP/DGA1 level of theory and basis set.^51,52 The generated COSMO files were then used as an input in the COSMOtherm (version 19.0.4, COSMOlogic, Leverkusen, Germany) package with BP_TZVP_19 parametrization.^53,54 The activity coefficient of component i was calculated according to the following expression.⁵⁵where, μ_i is the chemical potential of the mixture, μ⁰_i is the chemical potential of the pure component i, R is the real gas contact and T is the absolute temperature. Additional details on the methodology of COSMO-RS calculations in predicting activity coefficients are provided in the COSMOtherm's user Manual.⁵³

3. Experimental procedure

3.1. Biomass pretreatment

All pretreatment reactions were conducted in duplicate. 2 mm sorghum samples and IL were mixed in a 1 : 4 ratio (w/w) to afford a biomass loading of 20 wt% in a 15 mL capped glass pressure tube and pretreated for 3 h in an oil bath heated at 140 °C. After pretreatment, samples were removed from the oil bath and allowed to cool. 10 mL DI water–ethanol (1 : 1 v/v) was slowly added to the biomass-IL slurry and mixed well. The mixture was transferred to 50 mL Falcon tubes and centrifuged at high speed (4000 rpm) to separate solids and remove any residual IL (washing steps repeated another four times). The ethanol-water washed solid was freeze-dried to obtain dried pretreated biomass for further analysis.

3.2. Compositional analysis – lignin

All compositional analysis experiments were conducted in duplicate. Acetyl bromide-based lignin assay method was employed to determine the lignin content in IL pretreated sorghum samples as reported previously.⁵⁶ 10 mg alcohol insoluble biomass residues were weighed in a 2 mL screw cap tubes vial. 1 mL 25% (v/v) acetyl bromide in glacial acetic acid was added to the vials containing biomass samples (Caution: must be operated in fume hood). The vials were sealed and incubated at 50 °C for 2 h with a rotational motion. After 2 h of incubation, vials were cooled in an ice bath for about 5 minutes before centrifuging the samples at 14 000 rpm for 5 minutes. The UV absorbance (at 280 nm) was measured by diluting 6 μL of supernatant with 60 μL master solution (obtained by mixing 48 μL acetic acid, 9.5 μL 2 M NaOH and 1.7 μL 0.5 M hydroxylamine hydrochloride) and 200 μL glacial acetic acid.

The lignin concentration was measured by calibration curve method. In a 2 mL screw cap tubes vial, 10 mg alkaline lignin was treated with 1 mL 25% (v/v) acetyl bromide in glacial acetic acid and incubated at 50 °C for 2 h with a rotational motion. After 2 h of incubation, vials were cooled in an ice bath for about 5 minutes before centrifuging the samples at 14 000 rpm for 5 minutes. Standard samples were prepared by diluting 1, 2, 4, and 6 μL of supernatant with 60 μL master solution and 200 μL glacial acetic acid. UV absorbance was measured at 280 nm and compared against blank (60 μL master solution and 200 μL glacial acetic acid).

4. Results and discussion

4.1. Dissolution mechanism of lignin in cholinium-carboxylate anions

4.1.1. Non-bonded interaction energies. Molecular dynamics simulations are a prevailing computational tool for investigating the interactions among molecules in binary solutions and were used here to measure non-bonded interaction energies between lignin-dimer and cholinium carboxylate-based ILs to understand the effect of carboxylate anions ([For]⁻, [Ace]⁻, [But]⁻, [Hex]⁻, and [Oct]⁻) on lignin dissolution. The electrostatic interactions have been reported to govern the dissolution mechanism of cellulose and hemicellulose in ILs.^12,15,57 We speculate that both electrostatic and van der Waals interactions play important roles in the dissolution of lignin in cholinium carboxylate-based ILs due to the significant presence of both hydrophilic and hydrophobic sites on lignin.^58,59

Non-bonded interaction energies between the lignin 4-O-5 compound and five [Ch][carboxylate] ILs were calculated as the summation of van der Waals (E_vdW) and electrostatic (E_elec) interactions and are depicted in Fig. 2. The electrostatic interactions between the 4-O-5 lignin compound and the IL are stronger (more negative) than the vdW interactions signifying that electrostatic interactions are the governing parameter for lignin–IL interactions. It is important to mention that we decompose the total interaction energy into ion (cation and anion)–lignin pairs to get deeper insights into each ion on the lignin dissolution. As the alkyl chain length of anion increases from formate (−54.3 kcal mol⁻¹) to octanoate (−33.1 kcal mol⁻¹), the strength of the electrostatic interactions between lignin and anion decreases. This fact can be explained by the polarity of the anions. The anions with shorter alkyl chain lengths have higher polarity than hexanoate and octanoate, thus leading to stronger electrostatic interactions. In contrary to electrostatic interactions, a longer alkyl chain of anions ([Hex]⁻ and [Oct]⁻) results in more favorable vdW interactions with lignin than the anions with shorter alkyl chain (i.e., [For]⁻, [Ace]⁻, and [But]⁻). On the other hand, the electrostatic interaction energy values between lignin and the cation decreased (or became more favorable) with increasing alkyl chain length of the anion. These stronger electrostatic interactions are due to lower occupancy of hexanoate and octanoate anions around the lignin molecule (see section 4.1.2. coordination numbers). In addition, the stronger electrostatic interactions can also be explained based on the fact that the interaction between cation and anion weakens with increase in alkyl chain length (see Table S3†), and thus the cation is more available to interact with lignin. Hence, the cholinium cation is seen to possess stronger interactions with lignin in hexanoate and octanoate-based ILs. While the vdW interactions between lignin and cation are higher for shorter alkyl chain anions than they are for longer chain length anions.

Fig. 2 Electrostatic (a) and van der Waals (b) interaction energies between the lignin–cation and lignin–anions for different lignin–IL systems at 363.15 K.

Hou et al. (2012)¹⁹ reported experimental dissolution of lignin in [Ch][carboxylate] ILs. They observed that [Ch][Oct] and [Ch][Hex] had higher lignin dissolution capability as compared to [Ch][For], [Ch][Ace], and [Ch][But].³⁰ These experimental findings are in line with our simulation data in which the [Oct]⁻ and [Hex]⁻ anions had significant electrostatic and vdW interactions (see Fig. 2) with lignin, explaining how it leads to higher dissolution of lignin. In addition to interaction energies, the ionization of lignin in ILs can be expressed by dissociation constants (pK_a). The pK_a range of carboxylate-anions are 4.27 to 5.19 (see Table S4†), so only lignin protons with a pK_a < 5.2 will be significantly deprotonated by carboxylate-anions. Taking the pK_a-distribution of acidic protons in lignin into account, carboxylate-anions can deprotonate carboxylic acid protons (pK_a ∼ 2–5) but not the phenolic protons (pK_a ∼ 7–10), which reveals the reduced total charge density and lowers the solubility of lignin. The pK_a of [Ch][Oct] (5.19) and [Ch][Hex] (5.09) are higher than the [Ch][For] (4.27), [Ch][Ace] (4.76), and [Ch][But] (4.91) ILs. The commercial tool, ChemAxon was used for the prediction of pK_a values.⁶⁰

4.1.2. Radial distribution functions and coordination numbers. To further examine the microscopic interactions and structural arrangements radial distribution functions (RDF) for lignin–anions and lignin–cation were evaluated. The radial distribution functions, RDF (g(r)) measure the probability of finding a molecule at a distance of ‘r’ from the reference molecule and thus are an important tool in understanding the structural interactions of lignin with explicit atoms of ILs. In our case, RDFs were plotted between the oxygen of hydrogen bond donors of lignin molecule with oxygen hydrogen bond acceptor atoms of the anion and nitrogen hydrogen bond acceptor atoms of the cation ([Ch]⁺) (Fig. 3). The first and largest solvation shell (full width of the first maxima) of RDF peak between lignin and anions was attained at a distance of 2.60 Å, indicating that anions form regular and definite coordination spheres around lignin moiety at a distance of 2.60 Å and the RDF plot is primarily dominated by the first coordination shell. The secondary solvation shells are less ordered than the first solvation shell (Fig. 3a). It is interesting to note that the RDF peak height g(r) of lignin–octanoate (∼10) implying that the contact probability between lignin and octanoate molecules are almost 10 times greater in their first solvation shell (3.45 Å), which is larger than the other investigated anions. In the case of lignin–cation RDFs, the cation approaches the lignin moiety at a distance of 3.85 Å in all the cases (Fig. 3b), indicating that the cation is well ordered around the lignin molecule at 3.85 Å, which may leads to weaker interactions with lignin. This is further confirmed by the interaction energies between lignin and cation, where the cation has shown weaker interactions with lignin than anion. For the octanoate-based system, the higher g(r) value of 3.4 was obtained for lignin-[Ch]⁺ (Fig. 3b), implying that [Ch][Oct] showed greater influence on lignin solubility. The effect of anions is further established by the secondary features in the RDF plots between lignin and cation (highlighted as gray bar in Fig. 3b). It is important to highlight that flat secondary features indicate limited interactions as observed for the cation in formate-IL. On the other hand, the cation in octanoate-IL had modulations showing a second and third well-ordered shell of cation around lignin. An increased number of interactions of a common cation as a function of anion is speculated as the decreased cation–anion interaction. From these findings, it is confirmed that lignin solubility predominantly depends on and can thus be manipulated by the choice of the anion.

Fig. 3 Radial distribution function (RDF) plot between the O atom of lignin 4-O-5 linkage with (a) O1 atom of anions and (b) N1 atom of cation ([Ch]⁺) for different lignin–IL systems (see Fig. 1 for atom notations).

In addition to the RDF, the coordination number, which provides an estimate of how many IL molecules interact with lignin in their solvation/coordination shell, was calculated from the height and width of the RDFs and density of the system.⁶¹Fig. 4 reports the coordination numbers for lignin–anion and lignin–cation systems. The lignin molecule is surrounded by one to two anions (3.45 Å) and two to three cations (6.5 Å) in their first solvation shell (full width of the first maxima). As the distance (r) between lignin and ions increases, the presence of shorter alkyl chain length anions becomes greater than the cations around the lignin molecule (Fig. 4); therefore, the interaction between lignin and the anion is stronger than it is for lignin and the cation. However, in the case of hexanoate and octanoate-based systems, the presence of cations is higher than the anions around the lignin molecule due to the bulky structures of hexanoate and octanoate anions.

Fig. 4 Coordination numbers (CN) plot between the lignin 4-O-5 linkage- (a) anions and (b) cation ([Ch]⁺) for different lignin–IL systems.

4.1.3. Hydrogen bonds and lifetimes. Owing to a higher number of anions surrounding the lignin molecule, it is expected that the shorter alkyl chain length anions form a greater number of hydrogen bonds with the lignin. Fig. 5a reports the average number of hydrogen bonds per lignin molecule between lignin and anions as a function of simulation time. The hydrogen bonds are calculated using a hydrogen bond measurement tool in VMD,⁴⁶ in which the criterion for the distance between acceptor and donor was set to 3.5 Å, and the cutoff angle for the donor-H⋯acceptor triplet was set at 30°. In this analysis, formate and acetate (shorter alkyl chain length) anions had a marginally higher number of hydrogen bonds (O–H⋯O) with lignin than hexanoate and octanoate; however, the solubility of lignin has been reported to be higher in [Ch][Oct] and [Ch][Hex] ILs.³⁰ This peculiarity was elucidated by measuring the dynamics of hydrogen bonds (i.e., HB lifetimes) using the hydrogen-bond autocorrelation function approach, in which the integral of the autocorrelation function provides an estimate of HB lifetimes. Diffusion and orientation of entities are primarily responsible for HB making and breaking processes, which results in decay of the autocorrelation function of hydrogen bonds. The autocorrelation function, C_HB(t), was calculated according to Luzar and Chandler's definition of intermittent hydrogen bond autocorrelation function.^62,63

Fig. 5 (a) average number of hydrogen bonds per lignin molecule and (b) HB autocorrelation function (lifetime) of lignin/anion h-bond for different lignin–IL systems as a function of simulation time. The parentless in Fig. 5a are the average number of H-bonds per lignin molecule calculated over all the frames.

If the hydrogen bonds are allowed to break and reform, HB lifetimes can be calculated by defining the hydrogen bond population operator h(t) and h(0), which is defined as 1 when HB is present and zero in the absence of HB. The product of both h(0)h(t) in eqn (2) is equal to 1 for the presence of HB at both times 0 and t and is equal to zero otherwise. These HB autocorrelation functions were obtained using the TRAVIS package.^63,64

Fig. 5b shows the HB autocorrelation functions of lignin with anions as a function of simulation time. The decay of the autocorrelation functions for octanoate is the slowest among the anions and had the longest lifetime of 9122.02 ps, while formate and acetate had the faster HB decay and shortest HB lifetimes of 2457.35 and 2077.53 ps, respectively. The HB lifetimes between lignin and anions are decreasing with a decrease in the alkyl chain length of the anions, which in turn means that the self-diffusivity of shorter alkyl chain anions are faster. From the above observation, it was clear that octanoate and hexanoate show the strongest O–H⋯O hydrogen bond lifetimes among all studied ILs. From the RDF plots, it was also evident that octanoate forms a solvation shell around and in close proximity (∼2.5 Å) to lignin, which is likely due to making hydrogen bonds with lignin as confirmed by the HB autocorrelation functions and long HB lifetimes. Thus, the longer HB lifetimes between lignin and octanoate is also one of the critical parameters in achieving higher lignin solubility.

Further, the experimental lignin solubility is correlated with the COSMO-RS predicted logarithmic activity coefficient (ln(γ)) and anion contact probability.^15,26,49 [Ch][Oct] has shown lower ln(γ) of lignin than other ILs, which implies higher solubility of lignin in [Ch][Oct]. Also, the contact probability of octanoate and hexanoate anions with lignin is higher than the shorter alkyl chain length anions, thus results in higher solubility of lignin (Fig. S2†). Overall, the significant electrostatic and vdW interactions, higher contact probability of anion, longer HB lifetime, and lower ln(γ) values indicate a higher lignin solubility in [Ch][Oct] (Fig. 6). A higher lignin removal (thus lignin solubility) was observed with [Ch][Oct] (∼52%) when compared to [Ch][Ace] (∼45%) after the pretreatment of lignocellulosic biomass (sorghum) with these ILs⁶⁵ validating our current computational observations.

Fig. 6 Correlation between theoretical (MD and COSMO-RS) parameters and experimental lignin solubility data.

4.2. Dissolution mechanism of lignin in cholinium lysinate

Recent studies demonstrated that cholinium lysinate [Ch][Lys] is an effective biomass solvent for lignin removal and higher sugar yields.^31,32 To clearly understand the dissolution mechanism of lignin in [Ch][Lys], MD simulations were performed and interaction energies, RDFs, HB connection matrix, and HB lifetimes were evaluated. Fig. 7 compares the electrostatic and vdW interaction energies between lignin in [Ch][Lys] and lignin in [Ch][Oct]. From Fig. 7a, it can be seen that the electrostatic interactions between the lignin 4-O-5 compound and lysinate (−39.7 kcal mol⁻¹) is stronger than that between lignin and octanoate (−33.1 kcal mol⁻¹), whereas the vdW interactions were relatively similar (20.2–22.5 kcal mol⁻¹). The stronger electrostatic interactions between lignin and lysinate are due to lysinate having greater polarity than octanoate. On the other hand, the lignin–cation interactions are within the range of −20.65 to −26.3 kcal mol⁻¹, while the lignin–anion contributions are significantly higher (−55.6 to −59.9 kcal mol⁻¹). This is additional evidence in support of our claim that the anion is of central importance for lignin solubility. Overall, the total interaction energies between lignin-[Ch][Lys] and lignin-[Ch][Oct] were similar. It is also interesting to point out that the cross-interaction between anion and cations in [Ch][Lys] is −285.02 kcal mol⁻¹, which is relatively weaker than [Ch][Oct] (−288.23 kcal mol⁻¹) (Table S3†). Additionally, the interaction energies and corresponding lignin dissolution ability of lysinate (basic) and acetate (acidic)-containing ILs have been reported to be similar.³¹ A tabulated summary of this data has been included as Table S5 in the ESI.†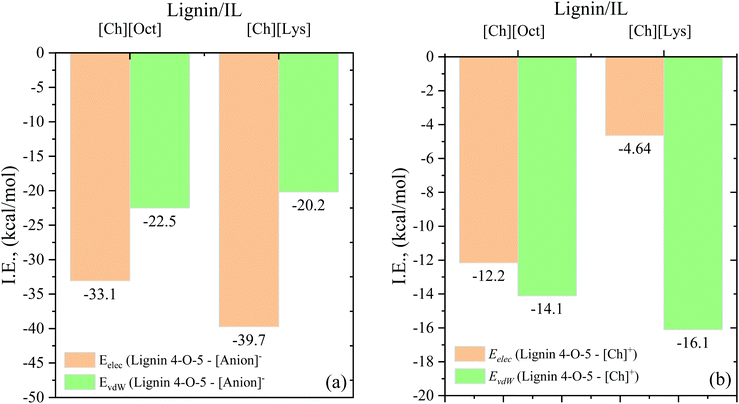

Fig. 7 Interaction energies between the (a) lignin–anion and (b) lignin–cation [Ch]⁺ in the different lignin–IL systems at 363.15 K.

Further, to visualize the HB patterns between the hydrogen bond donors and acceptors of lignin and [Ch][Lys], an HB connection matrix was calculated using TRAVIS and plotted with the rows of the matrix on the left-hand side corresponding to hydrogen bond acceptors of all the molecules in the system and the columns corresponding to the hydrogen bond donors (Fig. 8). This data shows, for example, that hydroxyl groups of lignin form hydrogen bonds with both acceptor (anion) and donor (cation) atoms of ILs. For each HB matrix, TRAVIS internally computes the RDF and extracts the height of the first maxima of RDF peak (g(r)) and the distance, thereby resulting in the hydrogen bond matrix. Both distance and height of the first RDF maximum are encoded in color (right-hand side of Fig. 8). A closer observation from the matrix, the anion ([Oct]⁻ and [Lys]⁻) forms strong hydrogen bonds with lignin (O1,2⋯H20–22) and cation (O1,2⋯H3). Lysinate forms multiple and strong hydrogen bonds (O1,2⋯H20–22 and N1,2⋯ H20–22) with lignin than [Oct]⁻. However, the first maximum height of the N1,2⋯ H20–22 (lignin-[Lys]) is lower than O1,2⋯H20–22, implying that lower HB lifetime of N1,2⋯ H20–22. On the other hand, cation forms multiple and weaker hydrogen bonds with lignin. One weaker intramolecular hydrogen bond visible in [Lys]⁻ and [Ch]⁺, but there is no evidence of intramolecular hydrogen bond within the lignin molecule.

Fig. 8 Connection matrix analysis of lignin dissolved in (a) [Ch][Oct] and (b) [Ch][Lys]. Rows represent hydrogen bond acceptors, and columns stand for hydrogen bond donors. The color in each square represents both the intensity and distance of the first maximum in the corresponding RDF (for color scale, see the right-hand side). If the hydrogen bond exists, the square of the matrix is filled with a color according to the color scale, otherwise, the square is simply filled with a black cross. The red color indicates a hydrogen bond with a lower distance and maximum RDF height (i.e., strong hydrogen bond with longer lifetime), whereas blue color indicates a hydrogen bond with a smaller distance and lower height (i.e., strong hydrogen bond with lesser lifetime). On the other hand, the yellow color corresponds to a hydrogen bond with a higher RDF peak, but the distance is larger, indicating a very weak hydrogen bond.

Further, the radial distribution functions (RDFs) were evaluated to examine the structural arrangements and confirm the HB connection matrix. The RDF plots between the oxygen atom of lignin with the O1 atom of anion and N1 of the cation ([Ch]⁺) are depicted in Fig. 9. The first RDF peak occurs at a distance of 2.65 Å with a g(r) value of 7/10 for [Lys]⁻/[Oct]⁻ systems. The g(r) values demonstrate that the contact probability between lignin and lysinate anion are seen to be 7 times in their first solvation shell (3.45 Å), which is lower than the lignin–octanoate. Whereas in the case of lignin–cation RDFs, the cation approaches the lignin moiety at a distance of 3.85 Å indicating cation is well ordered around the lignin moiety at a distance of 3.85 Å and possibly that it forms an ordered salvation shell. The higher contact probability between lignin and anions are further evaluated by computing the dynamics of hydrogen bond (i.e., HB autocorrelation function). The decay of HB autocorrelation functions of lysinate (O–H⋯O and O–H⋯N) is faster and shows the lowest HB lifetime (Fig. 10). For lysinate-based system, the HB lifetime of O–H⋯O is higher than O–H⋯N bond, which is in good agreement with our HB connection matrix analysis (Fig. 8 and 10).

Fig. 9 Radial distribution function (RDF) plot between the O atom of lignin 4-O-5 linkage with (a) O1 atom of Anions and (b) N1 atom of Cation ([Ch]⁺) for different Lignin–IL systems (see Fig. 1 for atom notations).

Fig. 10 HB autocorrelation function (lifetime) of lignin/anion h-bond for different lignin–IL systems as a function of simulation time.

Based on the interaction energies (with anion) and HB matrix, [Ch][Lys] stands out as a better solvent, while the RDF and HB lifetimes suggests [Ch][Oct] would be a better solvent for lignin removal. In order to reveal the underlying hypothesis, the biomass pretreatment experiments were performed and seen that highest lignin removal was achieved with [Ch][Lys] (77% vs. 52% with [Ch][Oct]). In this case, the interaction energies and multiple hydrogen bond networks dominates the lignin solubility. In fact, a small change in the strength of a HB donor or acceptors leads to large effects. These results can be further correlated with the dissociation constant (pK_a) and viscosity of ILs. It is worthy to highlight that the pK_a values of lignin protons lie in the range of 1–5 (carboxylic protons) and 6–11 (phenolic protons).⁶⁶ This implies that all lignin protons would be deprotonated (hence enhancing the solubility of lignin) in the presence of a chemical with pK_a values greater than 11. Also, in contrast to octanoate (pK_a ∼ 4.89), the pK_a's of lysinate are 2.74 (COOH), 9.44 (α-NH₃⁺), and 10.29 (ε-NH₃⁺). Lysinate-based ILs are therefore able to deprotonate the protons of lignin with a pK_a value up to10.3, which implies the deprotonation of almost all the available carboxylic and phenolic protons of lignin, leading to a maximum charge density and higher delignification. The higher removal of lignin in [Ch][Lys] may also be due to the lower viscosity of [Ch][Lys], because a decreased viscosity has been shown to enhance the mass transfer of IL in the dissolution of solutes.⁵⁷ The solvents with lower viscosity are easier to handle but still believed that the basicity and polarity of the solvent is a better indicator of their ability to dissolve (biopolymers).⁵⁷ Therefore, [Ch][Lys] is seen to have a greater hydrogen bond basicity and lower viscosity, thus, [Ch][Lys] results in higher lignin dissolution than [Ch][Oct]. The factors that influence lignin dissolution in an IL have been tabulated as Table S6 in the ESI.†

4.3. Interaction between [Ch][Lys] and different linkages of lignin

Lignin is an asymmetrical, cross–linked, and a polyphenolic polymer which is interlinked by two major categories of chemical bonds i.e., ether (β-O-4, α-O-4, and 4-O-5) and carbon–carbon (5–5, β–β, β-5, and β-1) linkages. Depending on the biomass source, the major linkages in lignin namely β-O-4, 5–5, and 4-O-5 can be present up to 45–50%, 19–22%, and 4–10%, respectively.^10,67 Therefore, in this section, we discuss the dissolution mechanism of lignin-like dimers with different linkage compounds such as β-O-4, 5–5, and 4-O-5 in [Ch][Lys] using MD simulations.

The non-bonded interaction energies, RDFs, SDFs, HB network, and lifetimes of ionic pairs and HB are calculated from MD simulations. Fig. 11 gives the interaction energies between the major linkages in lignin (with lignin-dimers as model compounds) and [Ch][Lys]. The non-bonded interaction energies between the lignin β-O-4 linked dimer and [Ch][Lys] is stronger (−94.08 kcal mol⁻¹) than the other two investigated dimers (−80.6 kcal mol⁻¹; Fig. 11). The higher interaction energies between lignin β-O-4 and [Ch][Lys] is due to the higher polarity and reactivity of β-O-4 linked compound (Fig. 12a). Further, the radial distribution functions (RDFs) of lignin linkage compounds and lysinate were computed and reported in Fig. S3.† The first solvation shell of RDF peak was obtained at 2.65 Å with a g(r) value of 7 indicating that lysinate has shown similar contact probability with all the lignin linkages. In order to better understand the RDF plots, spatial distribution functions (SDFs) for the chemical neighborhood of lignin linkage compounds and IL molecules are obtained by the TRAVIS.⁴⁸ The isovalues employed for the SDFs corresponding to the lignin–lysinate and lignin–cholinium systems are 4 and 0.25 particle per nm³, respectively. As can be seen from Fig. 12(a–c), lignin linkages are surrounded by lysinate anion. Clearly, the ether linkage compounds containing lignin moieties namely β-O-4 and 4-O-5 are heavily surrounded by the lysinate anion compared to C–C linkage bearing moiety (5–5). Amongst the β-O-4 and 4-O-5 linked compounds, lysinate anions exhibited a higher affinity for β-O-4 linked compound, which helps explain the observed higher electrostatic interactions (see Fig. 11). Not only the anion but the cation also demonstrated stronger interactions towards the ether (β-O-4) linkage. N⁺-site of the cation engulfed the surface of lignin β-O-4 compound resulting in stronger vdW and cation-π interactions (visualized from the MD simulations) between lignin β-O-4 compound and cholinium cation (see Fig. 12d and S4†). Nevertheless, based on these results, the dissolution of lignin in [Ch][Lys] can be correlated to the higher interactions of constituent ions with ether linked compounds of lignin than C–C linked compound. This could be further extended to explain the 5 times higher removal of hardwood lignin (32%) than the softwood lignin (6.4%) in [Ch][Lys] (under similar conditions; 140 °C and 3 h) as the number of C–C linkages goes from 16–30% in hardwoods to 24–50% in softwoods.⁶⁸ In addition, a similar observation was also reported by Dutta et al. (2018) during their study on the pretreatment of different biomasses (grass, hardwood, and softwood) using [Ch][Lys].³² The removal of lignin was reported to be up to ∼74% for hardwood and grassy biomass, whereas 21% of lignin removal was seen for softwood biomass at similar pretreatment conditions. The higher removal of lignin from hardwood and grassy biomasses in [Ch][Lys] is due to the presence of larger amounts of ether linkages 60–80%.^10,67 and the data here shows these linkages are highly solvated by [Ch][Lys] when compared to C–C linkages.

Fig. 11 Interaction energies between the lignin linkages and [Ch][Lys].

Fig. 12 SDF plots of (a) β-O-4, (b) 4-O-5, and (c) 5–5 linkage of lignin surrounded by the lysinate anion at an isovalue of 3.5 nm⁻³ in lignin/[Ch][Lys] system, (d) β-O-4, (e) 4-O-5, and (f) 5–5 linkages of lignin around the choline cation at an isovalue of 0.25 particle per nm³ in lignin/[Ch][Lys] system. The color scheme used for different atoms is C (cyan), O (red), N (blue), and H (white), respectively.

In addition to the RDF and SDFs, the dynamics of hydrogen bond (HB) and ionic pairs (IP) were calculated to further understand their role in lignin dissolution by lignin-[Ch][Lys] (Fig. 13). From Fig. 13, the decay of HB autocorrelation function of lignin β-O-4 compound is slower than it is for 5–5 and 4-O-5 linkage compounds which results in longer HB lifetimes between the lignin β-O-4 linked compound and lysinate. On the other hand, the decay of the IP autocorrelation functions of lignin β-O-4 and 4-O-5 linked compounds are faster than 5–5 linked compound (Fig. 13b), which results in stronger interaction between [Ch]⁺ and [Lys]⁻ for lignin 5–5 linkage-based system. The stronger interaction between [Ch]⁺ and [Lys]⁻ results in lower solubility of lignin with the 5–5 linked compound. Besides HB and IP lifetimes, the hydrogen bond network topology for lignin and [Ch][Lys] was obtained and is shown in Fig. 14. For the projection of hydrogen bonding topology of the mixture, we use a modern visualization technique called ‘Sankey diagram’ (see Fig. 14), which is created by TRAVIS.⁴⁷ In this analysis, three hydrogen bond donors (lignin H, [Lys]⁻ H, and [Ch]⁺ H) and four hydrogen bond acceptors (lignin O, [Lys]⁻ O and N, and [Ch]⁺ O) represent the lignin-[Ch][Lys] hydrogen bond topology. The numbers in Fig. 14 signify the average hydrogen bond count per donor/acceptor, and the connection widths are directly proportional to the number of hydrogen bonds for the connected groups. Lignin forms multiple hydrogen bonds with lysinate and cholinium, however, as per the bar width, the strength of lignin–lysinate H-bond is much stronger than the lignin–cholinium. Overall, based on the interaction energies, SDFs, hydrogen bond topology, and HB/IP lifetimes results, [Ch][Lys] has shown higher dissolution capability of lignin due to the solvation of major ether (e.g., β-O-4) linkages. Further, the structural conformation of lignin β-O-4 linkage is evaluated as a function of interaction energies between lignin–anion and lignin–cation and reported in ESI.†

Fig. 13 (a) HB autocorrelation function (lifetime) of lignin/anion h-bond (b) IP autocorrelation function (lifetime) of IL for different IL–Lignin linkages systems as a function of simulation time.

Fig. 14 Circular Sankey diagram depicting the hydrogen bonding topology of lignin dissolution in [Ch][Lys]. Number corresponds to the average hydrogen bond count per donor/acceptor. The H-bond cutoff distance (acceptor–donor) is 3.5 Å.

5. Conclusions

In summary, we were able to throw light on the dissolution mechanism of lignin in various cholinium-based ionic liquids using molecular dynamics and COSMO-RS simulations. First, the dissolution of lignin was carried out in five different cholinium-carboxylate anions ([For], [Ace], [But], [Hex], and [Oct]). The vdW interaction energies between lignin and anion were found to be more effective in lignin dissolution than electrostatic interactions. The interactions of lignin–anion were predicted to be stronger than lignin–cation interaction, suggesting anion plays a vital role in the lignin dissolution. The stronger vdW interactions, lower activity coefficient, and higher HB lifetimes between lignin and [Ch][Oct] results in higher dissolution capability of lignin. From the RDFs, it was noticed that the contact probability between lignin and octanoate were ∼10 times higher than other carboxylate anions in their first solvation shell (3.45 Å). Second, the dissolution of lignin was performed in [Ch][Lys] and the results were compared with [Ch][Oct]. From both experimental and computational approaches, [Ch][Lys] was found to be a potential solvent for lignin due to the stronger interactions, formation of multiple hydrogen bonds, higher dissociation constant, and lower viscosity of [Ch][Lys]. Finally, MD simulations have also been employed to obtain additional insights on the different linkages of lignin (β-O-4, 5–5, and 4-O-5) in [Ch][Lys]. Results from this analysis confirms the lignin with ether linkage has shown higher solvation capability by the virtue of stronger interactions and higher HB lifetimes with lysinate anion and also shown π–π-interactions with cholinium cation leading to the higher delignification of grass and hardwood biomasses in [Ch][Lys]. The results presented in this study provide fundamental insights into the dissolution of lignin in cholinium-based ILs and opens a path for the design of new IL to improve the biomass delignification efficacy and enhance the release of fermentable sugars. We foresee this study as an example to compute the dissolution mechanism of lignin or any other (bio)polymer in a chosen IL system.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was part of the DOE Joint BioEnergy Institute (http://www.jbei.org) supported by the U. S. Department of Energy, Office of Science, Office of Biological and Environmental Research, through contract DE-AC02-05CH11231 between Lawrence Berkeley National Laboratory and the U. S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes.

References

1. I. Cesarino, P. Araújo, A. P. Domingues Júnior and P. Mazzafera, Braz. J. Bot., 2012, 35, 303–311.
2. W. G. Glasser, Front. Chem., 2019, 7, 565.
3. Z.-H. Liu and J. S. Yuan, in Lignin Valorization, 2018, pp. 314–332.
4. C. Xu and F. Ferdosian, in Conversion of Lignin into Bio-Based Chemicals and Materials, Springer, 2017, pp. 13–33.
5. R. Vanholme, B. Demedts, K. Morreel, J. Ralph and W. Boerjan, Plant Physiol., 2010, 153, 895–905.
6. Z. Fang and R. L. Smith Jr., Production of biofuels and chemicals from lignin, Springer, 2016.
7. Y. Zhang, H. He, K. Dong, M. Fan and S. Zhang, RSC Adv., 2017, 7, 12670–12681.
8. B. G. Janesko, Phys. Chem. Chem. Phys., 2011, 13, 11393–11401.
9. X. Qiu, Q. Kong, M. Zhou and D. Yang, J. Phys. Chem. B, 2010, 114, 15857–15861.
10. L. Longe, G. Garnier and K. Saito, in Production of Biofuels and Chemicals from Lignin, Springer, 2016, pp. 147–179.
11. M. Mohan, C. Balaji, V. V. Goud and T. Banerjee, J. Solution Chem., 2015, 44, 538–557.
12. M. Mohan, T. Banerjee and V. V. Goud, ChemistrySelect, 2016, 1, 4823–4832.
13. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576.
14. M. Mohan, N. N. Deshavath, T. Banerjee, V. V. Goud and V. V. Dasu, Ind. Eng. Chem. Res., 2018, 57, 10105–10117.
15. M. Mohan, P. Viswanath, T. Banerjee and V. V. Goud, Mol. Phys., 2018, 116, 2108–2128.
16. R. P. Swatloski, S. K. Spear, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2002, 124, 4974–4975.
17. Y. Li, J. Wang, X. Liu and S. Zhang, Chem. Sci., 2018, 9, 4027–4043.
18. S. H. Lee, T. V. Doherty, R. J. Linhardt and J. S. Dordick, Biotechnol. Bioeng., 2009, 102, 1368–1376.
19. X. D. Hou, T. J. Smith, N. Li and M. H. Zong, Biotechnol. Bioeng., 2012, 109, 2484–2493.
20. M. Brehm, M. Pulst, J. r. Kressler and D. Sebastiani, J. Phys. Chem. B, 2019, 123, 3994–4003.
21. D. Fu, G. Mazza and Y. Tamaki, J. Agric. Food Chem., 2010, 58, 2915–2922.
22. M. M. Hossain and L. Aldous, Aust. J. Chem., 2012, 65, 1465–1477.
23. T. T.-m. Kwok, J. R. Bright, M. J. Realff and A. S. Bommarius, BioResources, 2019, 14, 5988–6003.
24. C. Balaji, T. Banerjee and V. V. Goud, J. Solution Chem., 2012, 41, 1610–1630.
25. A. Casas, J. Palomar, M. V. Alonso, M. Oliet, S. Omar and F. Rodriguez, Ind. Crops Prod., 2012, 37, 155–163.
26. A. Casas, S. Omar, J. Palomar, M. Oliet, M. V. Alonso and F. Rodriguez, RSC Adv., 2013, 3, 3453–3460.
27. Z. Ju, W. Xiao, X. Yao, X. Tan, B. A. Simmons, K. L. Sale and N. Sun, Phys. Chem. Chem. Phys., 2020, 22, 2878–2886.
28. W. Ji, Z. Ding, J. Liu, Q. Song, X. Xia, H. Gao, H. Wang and W. Gu, Energy Fuels, 2012, 26, 6393–6403.
29. Y. Zhu, J. Yan, C. Liu and D. Zhang, Biopolymers, 2017, 107, e23022.
30. X. D. Hou, J. Xu, N. Li and M. H. Zong, Biotechnol. Bioeng., 2015, 112, 65–73.
31. N. Sun, R. Parthasarathi, A. M. Socha, J. Shi, S. Zhang, V. Stavila, K. L. Sale, B. A. Simmons and S. Singh, Green Chem., 2014, 16, 2546–2557.
32. T. Dutta, G. Papa, E. Wang, J. Sun, N. G. Isern, J. R. Cort, B. A. Simmons and S. Singh, ACS Sustainable Chem. Eng., 2018, 6, 3079–3090.
33. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
34. M. Mohan, T. Banerjee and V. V. Goud, ACS Omega, 2018, 3, 7358–7370.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, 2009.
36. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
37. J. V. Vermaas, L. Petridis, J. Ralph, M. F. Crowley and G. T. Beckham, Green Chem., 2019, 21, 109–122.
38. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, J. Comput. Chem., 2010, 31, 671–690.
39. W. Yu, X. He, K. Vanommeslaeghe and A. D. MacKerell Jr., J. Comput. Chem., 2012, 33, 2451–2468.
40. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621.
41. G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189.
42. G. Stirnemann, D. Giganti, J. M. Fernandez and B. Berne, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3847–3852.
43. M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, New York, 1987.
44. S. W. Deleeuw, J. W. Perram and E. R. Smith, Proc. R. Soc. London, Ser. A, 1983, 388, 177–193.
45. L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164.
46. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
47. M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105.
48. M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023.
49. J. Kahlen, K. Masuch and K. Leonhard, Green Chem., 2010, 12, 2172–2181.
50. Y.-R. Liu, K. Thomsen, Y. Nie, S.-J. Zhang and A. S. Meyer, Green Chem., 2016, 18, 6246–6254.
51. M. Mohan, V. V. Goud and T. Banerjee, Fluid Phase Equilib., 2015, 395, 33–43.
52. M. Mohan, T. Banerjee and V. V. Goud, J. Chem. Eng. Data, 2016, 61, 2923–2932.
53. F. Eckert and A. Klamt, COSMOtherm, version C3.0 release 19.0.1, COSMOlogic GmbH & Co KG, Leverkusen, Germany, 2019.
54. F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385.
55. K. A. Kurnia, S. o. P. Pinho and J. o. A. Coutinho, Ind. Eng. Chem. Res., 2014, 53, 12466–12475.
56. R. S. Fukushima, M. S. Kerley, M. H. Ramos, J. H. Porter and R. L. Kallenbach, Anim. Feed Sci. Technol., 2015, 201, 25–37.
57. J.-M. Andanson, E. Bordes, J. Devémy, F. Leroux, A. A. Pádua and M. F. C. Gomes, Green Chem., 2014, 16, 2528–2538.
58. H. Wu, F. Chen, Q. Feng and X. Yue, BioResources, 2012, 7, 2742–2751.
59. M. K. Konduri, F. Kong and P. Fatehi, Eur. Polym. J., 2015, 70, 371–383.
60. ChemAxon, Chemicalize. https://chemicalize.com/app/calculation, (accessed 21 July 2020).
61. M. L. Batista, H. Passos, B. J. Henriques, E. J. Maginn, S. P. Pinho, M. G. Freire, J. R. Gomes and J. A. Coutinho, Phys. Chem. Chem. Phys., 2016, 18, 18958–18970.
62. A. Luzar and D. Chandler, Phys. Rev. Lett., 1996, 76, 928.
63. S. Gehrke, M. von Domaros, R. Clark, O. Hollóczki, M. Brehm, T. Welton, A. Luzar and B. Kirchner, Faraday Discuss., 2017, 206, 219–245.
64. J. Lentz and S. H. Garofalini, Phys. Chem. Chem. Phys., 2019, 21, 12265–12278.
65. A. Yao, H. Choudhary, M. Mohan, A. Rodriguez, H. Magurudeniya, J. G. Pelton, A. George, B. A. Simmons and J. M. Gladden, ACS Sustainable Chem. Eng., 2021, 9, 4371–4376.
66. P. K. Mishra and A. Ekielski, Nanomaterials, 2019, 9, 243.
67. B. Saha, I. Klein, T. Parsell and M. M. Abu-Omar, in Reaction Pathways and Mechanisms in Thermocatalytic Biomass Conversion II, Springer, 2016, pp. 119–129.
68. Q. Mei, X. Shen, H. Liu and B. Han, Chin. Chem. Lett., 2019, 30, 15–24.

---

Footnote

† Electronic supplementary information (ESI) available: The summary of lignin–IL MD simulations, RMSD, MD predicted interaction energies between anion and cation in lignin–IL system, dissociation constants (pK_a) of lignin dimers and ILs, COSMO-RS predicted contact probabilities of lignin-anions, and the structural confirmation of lignin in [Ch][Lys]. See DOI: 10.1039/d1gc01622a

---