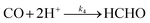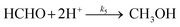Open Access Article
Open Access ArticleA mathematical analysis of carbon fixing materials that grow, reinforce, and self-heal from atmospheric carbon dioxide†
Dorsa
Parviz‡
,
Daniel J.
Lundberg‡
,
Seonyeong
Kwak
 ,
Hyunah
Kim
and
Michael S.
Strano
,
Hyunah
Kim
and
Michael S.
Strano
 *
*
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA. E-mail: strano@mit.edu
First published on 28th May 2021
Abstract
Carbon fixing materials are a new class of self-healing, self-reinforcing materials we have introduced that utilize ambient CO2 to chemically add to an ever extending carbon backbone. This class of materials can utilize biological or non-biological photocatalysts and support a wide range of potential backbone chemistries. However, there is no analysis to date that describes their fundamental limits in terms of chemical kinetics and mass transfer. In this computational study, we employ a reaction engineering, and materials science analysis to answer basic questions about the maximum growth rate, photocatalytic requirements and limits of applicable materials. Our proposed mathematical framework envelops three main functions required for carbon fixing materials: (1) adsorption of CO2 from air, (2) photocatalytic reduction of CO2 into selected monomers, and (3) polymerization of CO2-derived monomers. First, by performing a Damköhler number analysis, we derive criteria for the cross over from kinetic control to mass transfer limited growth, setting upper limits on performance of a potential photocatalyst. Next, we analyze photocatalytic reduction of CO2 to single carbon products, using known catalytic pathways and kinetic data. We identify formaldehyde as a C1 intermediate having unique potential for incorporation into the material backbone of carbon fixing materials. As an example, we find that a diamond-shaped reaction network graph for CO2 reduction, passing through CO and HCOOH intermediates, accurately describes kinetic data for cobalt-promoted TiO2 nanoparticles at room temperature and 1 atm CO2. Finally, as an applied case study, we consider and analyze the example of a carbon fixing poly(oxymethylene) system with embedded catalyst promoting the photocatalytic reduction of CO2 to formaldehyde. The latter then trimerizes to a trioxane monomer which subsequently polymerizes to polyoxymethylene. This reaction engineering analysis introduces benchmarks for carbon fixing materials with respect to achievable rates of photocatalysis, adsorption, and polymerization. These results should prove valuable for the design, evaluation, and benchmarking of this emergent and new class of environmentally sustainable materials.
1. Introduction
Industrial polymer production worldwide exceeds 350 million tons per annum and is mostly derived from petroleum sources. Moreover, consumer and industrial products are most commonly designed for short term usage lifetimes and to be disposable, generating 4600 million tons of cumulative landfill waste since 1950.1 The urgency surrounding issues of climate change and environmental protection have motivated the search for alternative materials and circular carbon solutions to replace those with substantial carbon footprints. Carbon fixing materials are a new class of self-healing, self-reinforcing materials recently introduced by our laboratory as a concept and prototype example.2 These materials are designed to utilize ambient CO2 to chemically add to an ever extending carbon-based backbone, granting unique benefits. Such materials are carbon negative as their service lifetime persists, providing an attractive alternative to petroleum derived polymers. Microcracks formation and propagation can be restricted in carbon fixing materials, because the presence of active adsorbents and photocatalysts in their structure enables continuous CO2 reduction and monomer polymerization on the defective sites, giving rise to their self-healing behavior. The continual addition of carbon mass can potentially offset the micro-cracks and degradation that impart typical polymers with short lifetimes that ultimately swell landfill volumes. The design of such carbon fixing materials currently lacks an analysis of key synthetic constraints. These include performance criteria and limits for polymer growth imposed by kinetic versus mass transfer limitations on carbon adsorption and conversion within the material. An integrated framework that provides understanding of the limits on CO2 adsorption, kinetics governing the photocatalytic reduction of CO2, and polymerization of intermediates is the centerpiece in design and engineering of carbon fixing materials. We address this integrated analysis in this work and provide a general roadmap for interfacing and improving these components to maximize the polymer growth rate over time.As an example carbon fixing material, we recently coupled extracted chloroplast with a secondary polymerization chemistry to produce self-healing polymeric materials only by using atmospheric CO2 and light as energy source.2 Among the three major sugars exported from chloroplasts (glucose, maltose, and triose phosphate), glucose is often used for glycopolymer synthesis since it is easily converted to gluconolactone by glucose oxidase. In our carbon fixing, the exported glucose was converted by glucose oxidase to gluconolactone, which subsequently reacted with primary amine-functionalized acrylamide monomers, 3-aminopropyl methacrylamide, to form a polymer matrix. We have enhanced glucose export from the isolated chloroplasts to gain quantifiable molecules for building of a self-growing material. In the presence of light and exposure to atmospheric carbon dioxide for 18 hours at room temperature, the formation of hydrogel-like material was observed around the chloroplast membrane. This design achieves an average growth rate of 60 μm3 per h per chloroplast under ambient CO2 and illumination over 18 h, thickening with a shear modulus of 3 kPa. This material can demonstrate self-repair using the exported glucose from chloroplasts and chemical crosslinking. However, a plant-based carbon fixing may be inefficient as a large portion of the design volume is dedicated to functions other than carbon fixation such as biosynthesis. On the other hand, a plant-based system may suffer from short lifetime of the extracted chloroplast. Hence, a more chemically robust, efficient, and long-lasting carbon fixing may be realized by replacing the chloroplast with an inorganic photocatalyst that allows for the use of a range of CO2 reduction products (formaldehyde, formic acid, methanol) in production of a polymeric material.
There have been attempts in the literature to create polymers from carbon dioxide to facilitate the transition from fossil-based to CO2-sourced plastics. Thus far, these efforts have been focused on the catalytic conversion of CO2 to four classes of polymers including polycarbonates, polyurethanes, polyureas, and polyesters can be synthesized from CO2.3 These polymers may be synthesized either by direct co-polymerization of CO2 with co-monomers or by the synthesis of CO2-sourced monomers including cyclic carbonates, carbamates, urea, and lactones, followed by their copolymerization with other compounds.4–9 These CO2-sourced monomers can be obtained via various pathways among which the CO2 reactions with epoxides to yield carbonates, with primary amines and amino alcohols to produce carbamates, with ammonia to generate urea, and with butadiene to form lactone intermediates are the most studied ones.3,10–12 These synthetic processes commonly require high energy input; thus, are often performed at elevated temperatures in presence of noble metal catalysts. These processes have not been adapted and evaluated at temperatures near ambient and atmospheric pressures of CO2, making it unclear as to whether they apply as carbon fixing strategies. They also need co-reactants and tend towards expensive and non-earth abundant catalysts. In all carbon reduction strategies, the energy budget must be carefully examined.
Since the first demonstration of CO2 reduction on several semiconductors upon illumination by Inoue et al.,13 researchers have investigated various families of materials for their potential application in harvesting light energy for CO2 photocatalytic reduction.14 In this process, the photocatalyst absorbs light energy, separates the photogenerated charges and transfers them to the CO2 and other reactants adsorbed on the photocatalysts active site.14–16 Commonly, a semiconductor with a band gap capable of absorbing light in UV and visible range and band edges properly positioned to provide sufficient overpotential for CO2 reduction is the main component of this photocatalytic process. TiO2 and ZnO, meeting all the theoretical requirements for a high-efficiency photocatalyst, have been vastly studied for their performance in the CO2 reduction.17,18 Often, a metal co-catalyst such as Pt, Pd, Ni, Co, and Cu or metal oxides such as RuO2 is added to the semiconductor to avoid the electron–hole recombination and facilitate the charge transfer to CO2 on the surface.19 Additionally, photosensitizer may be added to enhance the light absorption.16 In recent years, the efforts have been focused on developing nanostructures and hybrids of various semiconductors and co-catalysts for improved performance in CO2 reduction.20,21 Despite of all the efforts in this field, the practical application of these systems is challenged by the low energy conversion efficiency (due to fast electron–hole recombination), low product yield (few tens of μmol per g catalyst per h), poor selectivity of the products, and the lack of control over the competing H2 production reaction. Fortunately, inspired by the emergent need for renewable energy sources and limiting of the atmospheric CO2 level, current efforts are focused on discovery and development of novel efficient photocatalyst to overcome these challenges.
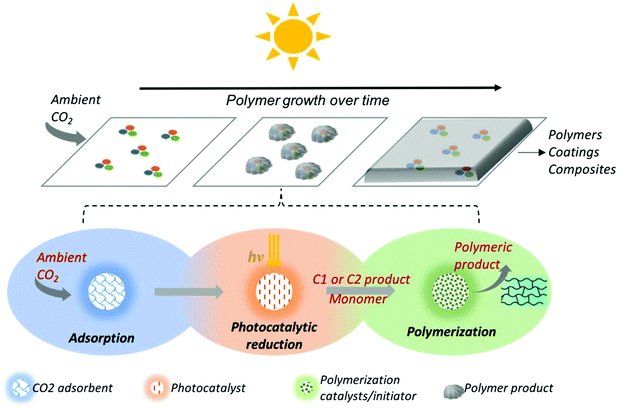
In this work, we envision the carbon fixing material as a compartmental composite that enables the atmospheric CO2 adsorption, its photocatalytic reduction to intermediates, and further polymerization of the selected intermediate to yield a self-healing composite as shown in Fig. 1. We introduce a general theoretical framework that captures the overall effect of multiple interconnected processes on CO2 fixation and polymer growth rates and allows one to evaluate and benchmark any design for a carbon fixing material. Using this platform, any combination of CO2 adsorbent, photocatalyst, and polymerization pathway may be investigated for an estimation of optimum growth rate and inherent limitations of the designed system. Identifying the rate limiting process within the designed carbon fixing material, either CO2 adsorption or CO2 photocatalytic conversion or polymerization, guides the engineering of these constituents—either independently or in conjunction. As a case study, we apply this framework to a representative pathway of CO2 fixation to polyoxymethylene (POM) through formaldehyde as the CO2-sourced monomer. The full chemical pathway consists of CO2 adsorption and three chemical conversions. For each step, we propose a reaction mechanism based on experimental data reported in the literature, obtain the optimum rate constants, and integrate the individual steps into a single kinetic model to represent an idealized one-pot reaction system converting CO2 to POM. Mapping the polymer growth with respect to improvements in photocatalytic activity and CO2 adsorption kinetics provides a roadmap to direct the design and engineering of a desired carbon fixing material toward technologically feasible adsorbents-photocatalysts hybrids with polymer growth rates comparable to those of plants.
2. Simultaneous adsorption and photocatalytic conversion of CO2
The success of any carbon fixing material is tied to the rate at which it is able to gain mass for growth, self-reinforcement, and repair. The rate at which a carbon fixing material is able to adsorb CO2 from the atmosphere sets an upper limit on its ultimate growth rate. Therefore, the analysis of any carbon fixing material begins with the analysis of CO2 adsorption and coupling it with later reduction and polymerization.Consider a carbon fixing material containing a material CO2 adsorbent at a mass loading of ma (gads). The adsorbent has a maximum capacity of CO2 adsorption defined as qe (mol CO2 per gads) with the current amount of CO2 adsorbed given as q (mol CO2 per gads). In the simplest cases, the adsorption process is modeled as a pseudo-first order process with a rate constant of adsorption kads (time−1):22
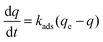 | (1) |
The total amount of adsorbed CO2 is given by the product maq, and a governing equation on the amount of CO2 adsorbed in the material is written as:
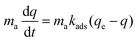 | (2) |
This adsorbent is interfaced with some photocatalyst capable of CO2 conversion, present at a mass loading of mc (g-cat). The photocatalytic conversion of CO2 within the composite is approximated to be pseudo-first order, with a rate of conversion proportional to the amount of adsorbed CO2. At saturation of the adsorbent, the photocatalytic rate of CO2 conversion is kc,sat (mol CO2 per gcat per time)—conversion is taken as proportional to the total amount of adsorbed CO2: q/qe. This consumption rate is added to the governing equation for CO2 within the composite construct.
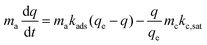 | (3) |
The above differential equation is solved analytically for the value of adsorbed CO2 at steady state, given as qss.
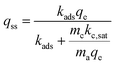 | (4) |
The rate—at steady state—that the carbon fixing material converts CO2 is given as rCO2 (mol CO2 per time).
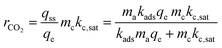 | (5) |
A Damköhler number for the system, defined as the rate of reaction to the rate of adsorption, is presented, where α represents the ratio of mass loading of catalyst to adsorbent.
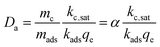 | (6) |
This non-dimensional value is introduced into eqn (5) as:
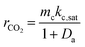 | (7) |
The steady-state consumption rate of CO2 is then normalized by mckc,sat, the maximum catalytic rate of CO2 conversion within the saturated system, yielding a simplified non-dimensional expression:
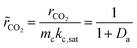 | (8) |
This equation can be used to estimate the upper limit of any carbon fixing material capacity to capture and convert CO2. The Damköhler number presents a description of the carbon fixing material as either being limited by rate of adsorption or rate of catalysis. In the limit of large Damköhler number, where catalysis is much faster than adsorption (mckc,sat ≫ madskadsqe), the rate of CO2 conversion within the system approaches madskadsqe, the fastest rate at which the system can adsorb CO2. In the limit of small Damköhler number (madskadsqe ≫ mckc,sat) adsorption is much faster than catalysis and the rate of CO2 conversion approaches mckc,sat and the adsorbent is always saturated with CO2.
The presented adsorption-reaction analysis informs the inherent limitation within any designed carbon fixing material given a selection of CO2 adsorbent and photocatalyst. This is illustrated in Fig. 2, where for a variety of possible carbon fixing material comprised of various CO2 adsorbents materials, where the rate at which they are able to convert CO2 is presented as a function of activity of a hypothetical photocatalysts which they are in combination with. The ratio of adsorbent to catalyst mass is taken as unity, and the results are normalized per total mass of adsorbent and catalyst present.
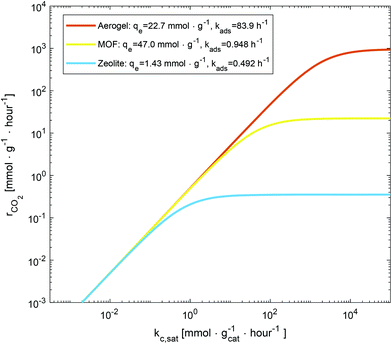 | ||
| Fig. 2 The transition from chemical reaction to mass transfer limitations for three commonly utilized CO2 adsorbents: zeolite,69 amine-functionalized aerogel,70 and amine-functionalized metal–organic framework.71 The estimated rate of CO2 conversion in a coupled adsorbent/photocatalyst systems is plotted versus surface rate constant for CO2 reduction. Zeolite,69 amine-functionalized aerogel,70 and amine-functionalized metal–organic framework71 with different adsorption capacity and rate of CO2 adsorption are assumedly interfaced with a range of photocatalytic activity to indicate two different regimes of CO2 conversion: (i) reaction-limited regime in which the conversion rate is determined by the photocatalyst activity, and (ii) the adsorption-limited regime in which the conversion rate increases with adsorption capacity and adsorption rate. In (i) for a given adsorbent the value of rCO2 is dependent on kc,sat whereas in (ii) the value of rCO2 becomes constant with increasing kc,sat. | ||
Given CO2 photocatalysts with increasingly large activity, the cross-over between carbon fixing materials which are catalytically limited and those that are adsorption limited is illustrated in Fig. 2. At low Damköhler number and low kc,sat, regardless of adsorbent, the CO2 conversion rate collapses to the same curve representing mckc,sat. As catalytic rate increases, the rate of carbon conversion of the different adsorbent systems diverges, the systems become limited by adsorption and those with the highest absorption rate and capacity allow the system to convert larger amounts of CO2.
3. Chemical kinetic analysis of photocatalytic CO2 reduction
The photocatalytic reduction of CO2 consists of a series of deoxygenation and hydrogenation reactions occurring through multiple electron and proton transfer steps. These reaction lead to formation of a variety of products depending on the specific reaction pathway and the number of electrons transferred to CO2 and the intermediates. Carbon monoxide, formic acid, formaldehyde, methanol, methane, ethane and ethane have been reported as the major products in many experiments, while some other compounds including ethanol and higher alcohols, acetaldehydes, oxalic acid, and higher hydrocarbons have been observed in fewer systems.15 Obviously, the photocatalytic CO2 reduction follows a complicated mechanism in which multiple parallel and branched pathways can be activated and depending on the reaction conditions and the catalyst structure become dominant. Table S1† lists some of the feasible pathways and corresponding steps, suggested in the literature based on theoretical calculations and/or experimentally observed intermediated and products. Most studies, performed on titanium dioxide (TiO2) as a benchmark photocatalyst, consider reduced models consisting of a subset of these reactions.The formaldehyde or fast hydrogenation pathway is a subset of the CO2 reduction pathway that proceeds:
| CO2 → HCOOH → HCHO → CH3OH → CH4 | (RF) |
While this pathway is thermodynamically feasible, kinetic models based on this mechanism often fail to explain the production of methanol as an intermediate species.23 An alternatively proposed carbene pathway proceeds as:
| CO2 → CO → C˙ → CH3˙ → CH3OH/CH4 | (RC) |
This pathway better explains observed concentration profiles of methanol and methane but does not describe the presence of formates.24,25
A reduced model for CO2 photocatalytic reduction
Titanium dioxide (TiO2) represents a benchmark photocatalyst for the process of CO2 photocatalytic reduction. For this semiconductor may take on one or multiple crystalline phases (anatase, brookite, and rutile), many pathways have been proposed due to the wide range of experimentally observed intermediates and products. We consider the kinetic data for the photocatalytic reduction of CO2 on TiO2-supported cobalt phthalocyanine nanoparticles reported by Liu et al. and presented in Fig. 3a.26 This dataset was chosen as it reports on all prominent intermediates products of the reaction, including carbon monoxide, formic acid, formaldehyde, methanol, and methane. Additionally, the high yield of formates reported make this dataset of particular interest for the proposed overall pathway toward POM. The experimental system under investigation was saturated with 1 atm of CO2 in the presence of 25 g of nanoparticles in 100 mL 0.15 M aqueous sodium hydroxide solution, and irradiated with a 500 W tungsten–halogen lamp. The system was stirred during the reaction and the concentration of products were measured after six hours, ten hours, and then at ten hour-intervals thereafter until 50 hours of total reaction time was reached.26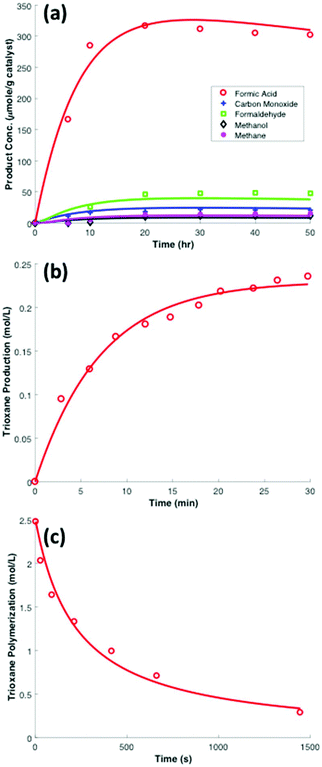 | ||
| Fig. 3 Experimental chemical kinetic data and comparison to the mathematical model in this work represented by (a) eqn (9)–(14), based on the reduced chemical network of (R1)–(R6) for the photocatalytic reduction of CO2 to carbon monoxide, formic acid, formaldehyde, methanol, and methane over cobalt/phthalocyanine promoted TiO2 at room temperature under 1 atm of CO2. Kinetic parameters for the model curves are presented in Table 1. Experimental data was obtained from Liu et al.,26 (b) conversion of formaldehyde to trioxane in aqueous solution at room temperature in presence of sulfuric acid presented in this work by eqn (15)–(19) based on the reduced reaction network of (R7)–(R10) (experimental data obtained from Yin et al.),72 and (c) trioxane polymerization to polyoxymethylene (POM) at 30 °C in presence of BF3 as initiator presented in this work by eqn (20) based on the chemical reaction of (R11) (experimental data obtained from Shieh et al.).56 | ||
Various thermodynamically feasible reaction networks including carbene and formaldehyde pathways, with and without reversible reactions, were fitted against the experimental data.27 To develop the kinetic model for each network surface reactions were considered the rate-limiting steps, assuming no limitations in mass transfer to/from catalyst surface and no limitation in electron transfer from bulk of catalyst to the reactants. Additionally, adsorption/desorption of reagents, intermediates, and products were assumed to happen fast. Since CO2 and hydrogen evolution (water oxidation reaction) data was not reported in this study, we refrained from using a surface Langmuir–Hinshelwood model that will include a variable proton concentration profile over time and instead used bulk product concentration in the first order rate expressions to avoid overfitting the data and over parameterizing the kinetic model. Also, we assumed abundant proton is provided in the system through the water oxidation reaction such that its concentration can be considered constant. Lastly, the concentration of CO2 in the liquid phase was calculated using Henry's law. The detail of the data fitting can be found in the ESI.†
Hence, we find that the following series–parallel reaction network describes the Liu et al. data very accurately. Here, the initial reduction of CO2 bifurcates into the formaldehyde and carbene pathways, passing though formic acid (HCOOH) and carbon monoxide (CO) intermediates respectively, converging at the desired formaldehyde. The series of reactions ((R1)–(R6)) are shown to fit the kinetic data of Liu et al. with the least square error (Fig. 3a). The details of kinetic model fitting can be found in ESI.†
 | (R1) |
 | (R2) |
 | (R3) |
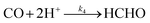 | (R4) |
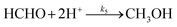 | (R5) |
 | (R6) |
Reactions (R1) through (R6) have the following mass action net rates:
| d[CO2]/dt = −k1[CO2] − k2[CO2] | (9) |
| d[HCOOH]/dt = k1[CO2] − k3[HCOOH] | (10) |
| d[CO]/dt = k2[CO2] − k4[CO] | (11) |
| d[HCHO]/dt = k3[HCOOH] + k4[CO] − k5[HCHO] | (12) |
| d[CH3OH]/dt = k5[HCHO] − k6[CH3OH] | (13) |
| d[CH4]/dt = k6[CH3OH] | (14) |
The series of irreversible reaction steps each proceed through two electron transfers along with protons. These two-electron transfer steps have been the subject of extensive theoretical studies for the CO2 reduction pathway and have been shown to have a lower energy barrier than single-electron transfers.28,29 Recently, DFT studies have shown that reduction of CO2 to carbon monoxide and formic acid, and then subsequent reduction of these products to formaldehyde has a lower energy barrier as compared to the well-established formaldehyde and carbene pathways.27 This new proposed mechanism accurately fits the high formic acid and formaldehyde concentrations observed, while explaining the low methanol and methane concentrations.
The calculated rate constants at 298 K and their confidence intervals for the developed reaction mechanism are presented in Table 1. The obtained rate constants for the formation of the conversion of formic acid to formaldehyde, formaldehyde to methanol, and methanol to methane are in agreement with those reported by Peng et al. for the photoelectrochemical reduction of CO2 on a TiO2 surface.73 The initial reduction of CO2 to either formic acid or carbon monoxide is the rate-limiting step in its photocatalytic reduction—having rate constants at least three orders of magnitude smaller than all other reaction steps. It is emphasized that the reduction of formaldehyde is comparably fast, and upon production is quickly consumed to yield methanol. Local sensitivity analysis with respects to k1–k6 around their optimal value was performed and normalized sensitivity indices are presented in Fig. S1.† The most influential parameter proves to be k1, affecting all products except CO thorough the reaction duration. k2 has high impact on the CO concentration, yet shows negligible effect on other products. Due to the linear dependence of the product concentrations on the rate constants, each product is considerably dependent on its consumption reaction rate constant and reaches a steady behavior over time, while the rest of the products are either not impacted by other rate constants or gradually become insensitive.
The dominant mechanism operative during photocatalytic CO2 reduction depends on specific catalytic architecture.14,17 Catalyst structure and morphology (type and availability of active sites, mode of adsorption of reactants on the surface, size and position of the semiconductor bandgap) and reaction conditions (light source, temperature, feed composition, pH, presence or absence of hole scavengers) dictate the chemical reaction mechanism(s), where reactions seemingly proceed through different, sometimes competing, pathways that yield a variety of products.15 Although the sensitivity analysis indicates the robustness of the proposed model to explain the experimental data used here, one must remember the reaction mechanism and their corresponding rate constants may alter when the reduction reaction is carried on a different catalytic surface and under different experimental conditions. Additionally, it is important to obtain experimental data with more exhaustive quantification of possible chemical species produced during CO2 photoreduction, with higher accuracy and repeatability before generalizing specific pathways as main routes of CO2 photoreduction.
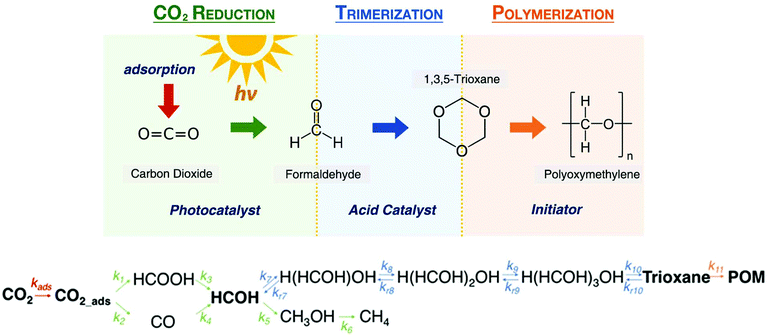
4. A case study: from CO2 to polyoxymethylene within a carbon fixing material
Here, we present one possible complete chemical route towards the production of a carbon fixing material including: (i) CO2 adsorption, (ii) CO2 photocatalytic reduction, and (iii) polymerization mechanism. The modeling and analysis of the designed system is to serve as a case study into the modular engineering of carbon fixing materials. Within the analysis, any of the three constituent parts may easily be substituted, allowing the conceptual analysis of many potential carbon fixing material. Through this analysis the current limitations of potential carbon fixing material are identified. These limitations then serve as guides—conceptually and experimentally—for the development of improved carbon fixing materials.Adsorption of CO2
Direct carbon capture at atmospheric pressure (400 ppm of CO2) can yield effective concentrations as high as 7 mmol per g per adsorbent,30 effectively concentrating this reagent two to three orders of magnitude more over the bulk concentration of CO2 in aqueous solution in equilibrium with 400 ppm CO2 (∼10−5 mol L−1). Successful interfacing of MOF adsorbents with the TiO2 surface has been reported, leading to higher adsorption capacity as well as an increase in active catalytic sites.31 Interfacing of TiO2 with zeolites also enhances photocatalytic activity as measured by the rate of degradation of organic waste products; directly attributed to an increase in reagent concentration near the surface.32 Integrated photocatalytic adsorbents, also used for the degradation of organic pollutants, have been shown to broadly enhance the effectiveness of TiO2 photocatalysts33,34 Other potential engineering routes include interfacing polymer-based CO2 adsorbents to the photocatalytic surface, or usage of amine-containing 2D nanosheets such as functionalized reduced graphene oxide that has been shown to enhance CO2 reduction rate.35The use of aqueous solutions of amine-containing molecules to capture CO2 is an established practice industrially.36 Here, an aqueous solution of monoethanolamine (MEA) is presented as a benchmark CO2 adsorbent for a carbon fixing material system. Such amines are commonly interfaced with photocatalysts such as TiO2 to enhance CO2 uptake and conversion rates.37,38 Here we estimate values for such a system's CO2 adsorption capacity and adsorption rate based on experimental data, and define the system such that the maximum adsorption capacity when exposed to ambient concentrations of CO2 equals that of the work from which the photocatalytic reduction kinetics were taken (equivalent to an aqueous solution saturated with CO2 under one atmosphere of the gas). The capacity of the amine is taken as 0.2 moles of CO2 per mole of MEA, as estimated from experimental data presented by Jou et al. for 30 mass percent aqueous solutions of MEA exposed to ambient partial pressures of CO2 (400 ppm of one atmosphere).39 An MEA concentration of 0.175 molar is then used. Taking into account the mass of water and MEA as the full adsorbent, the system has an adsorbent capacity per total mass, qe, of 0.035 mmol CO2 per gram of adsorbent. The rate, kads, at which this system is capable of adsorption is taken as 7.62 × 10−4 s−1 or 2.74 h−1, obtained from the fit of the pseudo-first order model of adsorption (eqn (1)) to experimental results presented by Yoo et al.40 for the adsorption of CO2 by basic, aqueous solutions as seen in Fig. S2.† This adsorbent and the capacity specified are taken as an example of realistic CO2 adsorbent capacities and rates of adsorption. These values represent what is reasonable to obtain with such adsorbent systems.
Photocatalytic reduction of CO2
Carbon fixing materials, as envisioned, necessarily rely on photocatalytic CO2 reduction. Therefore, our analysis should include a chemical kinetic evaluation of current and future reaction pathways involving carbon dioxide conversion to chemically relevant monomers. In this case study, we focus on our analysis on formaldehyde production as the monomer for POM, but our approach extends to other C1 carbons in the CO2 reduction pathway. We use the kinetic model developed in section 3 based on photocatalytic reaction (R1)–(R6) and the corresponding rate expressions of eqn (9)–(14). Using the rate constants obtained from this reduced kinetic model, we proceed to evaluate the kinetics and growth rate of POM next.Polymerization
Carbon fixing synthetic approaches can be designed around a broad range of functional polymers. In this case study, we consider the polymerization of formaldehyde obtained from CO2 reduction to polyoxymethylene (POM). POM is a high value, engineering plastic widely used in the automotive and electronics industry for its unique chemical stability and mechanical properties. A self-healing and densifying POM composite generated from atmospheric CO2 would bring new opportunities for the production of protective coatings and structural composites. The synthesis of this polymer can be achieved through the (a) trimerization of formaldehyde to trioxane, and (b) trioxane's subsequent polymerization to high molecular weight POM.41,42 Thus, two independent chemical reaction schemes are presented here, representing these two processes.| HCHO + H2O ⇌ HO(CH2O)H | (R7) |
| 2HO(CH2O)H ⇌ HO(CH2O)2H | (R8) |
| HO(CH2O)H + HO(CH2O)2 ⇌ HO(CH2O)3H | (R9) |
| HO(CH2O)3H ⇌ (CH2O)3 + H2O | (R10) |
For a well-mixed reaction system, neglecting volume expansion at constant density, we can utilize the following mass action rates for the reactant, intermediates, and product, assuming excess aqueous solvent.
| d[HCHO]/dt = −k7[HCHO] + kr7[HO(CH2O)H] | (15) |
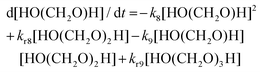 | (16) |
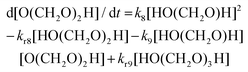 | (17) |
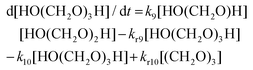 | (18) |
| d[(CH2O)3]/dt = k10[HO(CH2O)3H] − kr10[(CH2O3)] | (19) |
We use these mass action rates to fit the experimental data reported by Yin et al. to estimate the rate constants of the reversible cyclization reactions (Fig. 3b).48 The rate constants for (R7)–(R9) were directly calculated from the kinetic and equilibrium data reported by the Winkelman et al., Ott et al., and Kuhnert et al.49–51 The rate constants at the room temperature were obtained using the energy barrier estimated for cyclization reaction by Kua et al.52 The reversible rate constants of reaction (7)–(9) at 371 K were calculated by extrapolating the rate constants reported by Winkelman et al. at 293–333 K (R7) and Ott et al. at 293–323 ((R8) and (R9)), the forward reaction rate constants were calculated using the reverse rate constants and the equilibrium constants reported by Winkelman et al. and Kuhnert et al. at 371 K. The rate constants for the cyclization reaction (R10) were obtained by fitting experimental data of trioxane formation reported by Yin et al. at 371 K to the above kinetic model. Full details of these calculations can be found in the ESI.† The rate-limiting step in the conversion of formaldehyde to trioxane is proposed to be the cyclization reaction (R10), having a rate constant that is three to four orders of magnitude smaller than both the hydration (R7) and the oligomerization ((R8) and (R9)) (Table 1). While poly(oxymethylene) glycol oligomers have been experimentally observed at lower temperatures, formation of the trioxane has only been reported at higher temperatures, confirming the cyclization reaction as the bottleneck in formation of trioxane.46 At room temperature, this cyclization reaction (R10) imposes a kinetic barrier as slow as that of CO2 conversion to formic acid and carbon monoxide—similarly affecting the kinetics of the overall pathway toward POM production.
Here, we only take the growth phase of the reaction into consideration for the overall CO2 to POM pathway, as this slower phase dictates the overall rate of production of the final polymer. Shieh et al. reported kinetic data on polymerization of trioxane at 30 °C using BF3 as initiator in an organic solvent (Fig. 3c).56 They proposed a kinetic model that emphasizes on the crystallization and depolymerization steps, however, their rate constants depended on the initial trioxane concentration. To obtain rate constant that is independent of initial concentration, we used overall reaction (R11) as the kinetic model explaining the growth phase:
| (CH2O)3 + (CH2O)3,n → (CH2O)3,n+1 | (R11) |
| d[(CH2O)3]/dt = −k11[I][(CH2O)3]2 | (20) |
Our proposed rate expression reflects the kinetics of the chain growth in the cationic polymerization process. Total polymer production, regardless of molecular weight is output. This cationic polymerization mechanism has second-order dependence in trioxane concentration and first-order dependence in initiator concentration (I). Commonly the concentration of initiator is kept at two to three orders of magnitude lower than trioxane concentration to assure formation of high molecular weight chains. While the rate constant of this reaction (R11) at 30 °C (Table 1) is four orders of magnitude larger than the trioxane cyclization reaction (R10), the polymerization reaction proceeds more slowly at lower trioxane concentrations due to the effectively cubed dependence on trioxane concentration.
The data of vapor–liquid equilibria of formaldehyde aqueous mixtures confirms the stability of formaldehyde in solution with minimal mass loss from liquid phase. Formaldehyde oligomerization reactions rates are multiple orders of magnitude higher than the formaldehyde production reaction rates, guaranteeing the continuous conversion of formaldehyde upon production in the solution with minimal mass loss.51,57–59 For the catalytic conversion of CO2, the initial reduction of CO2 to either formic acid or carbon monoxide is the rate-limiting step, having rate constants two to three orders of magnitude smaller than all other photocatalytic reaction steps. The subsequent reaction of photocatalytically produced formaldehyde is fast, and the hydration of formaldehyde will outcompete its subsequent reduction to methanol. Thus, for this system all photocatalytically converted CO2 will ultimately be incorporated into the polymer. Concerning the polymerization kinetics, the trimerization of formaldehyde to trioxane is kinetically limited by ring-closing of the trimer (R10), because formaldehyde hydration, dimerization, and trimerization ((R7)–(R9)) are comparatively rapid with k7–k9 being four to five orders of magnitude higher than k10.
With the rate-limiting steps identified, a simplified reaction network can be developed facilitating the analysis of carbon fixing materials. In this simplified scheme, the photocatalytic reduction of CO2 to formic acid and carbon monoxide is combined into a single step which directly produces formaldehyde. Formaldehyde is converted with perfect selectivity to the trimer H(HCHO)3OH, which then reacts to produce trioxane and ultimately POM.
Analysis of the carbon fixing material begins with discussion of the competition between the rate of adsorption and rate of photocatalytic conversion of CO2. To obtain a representative value for kc,sat of the system, the rate of reactions (R1) and (R2) are calculated for the system interfaced with amine adsorbent. As these rates are proportional to the dissolved CO2 concentration, kc,sat is taken as the effective rate of CO2 conversion in the presence of the saturated CO2 concentration. As calculated in (i), the aqueous amine adsorbent system provides a saturated CO2 concentration of 0.035 molar. kc,sat for the designed system is then calculated as:
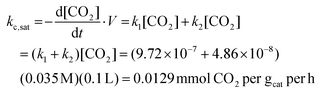 | (21) |
The rate of adsorption and capacity of the amine solution are taken as previously calculated, 2.74 per hour and 0.035 mmol gads−1, respectively. The mass-ratio of catalyst to adsorbent is taken to be the same as the concentration within the experimental photocatalytic system analyzed, 25 g of photocatalyst per 100 mL of aqueous solution, to give an approximate mass ratio of catalyst to adsorbent mater (here taken as the whole aqueous solution mass), of one-forth. The Damköhler number for this carbon fixing material is:
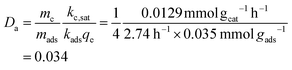 | (22) |
The carbon fixing material adsorbent-catalysis system here is strongly limited by its catalytic activity. The steady-state rate of CO2 conversion with the carbon fixing material is 0.312 mmol h−1 calculated following eqn (5). Normalized per total mass of the carbon fixing material including aqueous amine adsorbent and photocatalyst this value is 2.5 μmol h−1 g−1. Because the system is catalytically limited, the rate of CO2 photocatalytic conversion is approximately to instantly reach the rate of kc,sat. This fast saturation assumption is reasonable given that CO2 rapidly partitions between the atmosphere and the aqueous solution.60
As the hydration of formaldehyde, and subsequent reaction to become H(HCHO)3OH are rapid compared to the rate at which CO2 is converted, the production rate of formaldehyde, and formation rate of H(HCHO)3OH are taken to be identical and equal to this value of rCO2. Mass action rate expressions for the reactions of H(HCHO)3OH conversion to trioxane, and trioxane polymerization to POM are then:
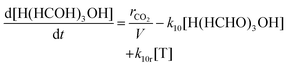 | (23) |
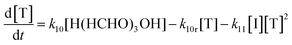 | (24) |
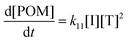 | (25) |
Here the square bracketed term represents a concentration of formaldehyde per reaction volume V, which is introduced to normalize the conversion rate of CO2, rCO2, as a rate per volume. The reaction volume within which the formaldehyde is produced and subsequently reacts is a design parameter for the carbon fixing material, and is taken as identical across all reaction steps, regardless of required aqueous or organic phase.
With all physical and chemical parameters of the carbon fixing material defined, the above three coupled differential equations are solved numerically to calculate the rate at which the designed carbon fixing material produces POM.
5. General insights for carbon fixing materials from case study analysis
The polymer growth rate is a parameter that affects the utility and possible applications of any carbon fixing material. The production rate of POM over time is shown in Fig. 5, normalized per sum of the mass of adsorbent and photocatalyst. A steady state POM growth rate of ∼0.08 mg h−1 gcat−1 can be achieved for the model pathway developed in section 4. It is noted that in the absence of the adsorbent material, the proposed carbon fixing material would convert a negligible amount of CO2 (<10−10 mg h−1 gcat−1). Hence, interface of the catalytic system with some CO2 adsorbent is necessary to achieve a non-negligible POM growth rate. Furthermore, nearly all of the CO2 converted to formaldehyde is ultimately incorporated into the POM product due to the fast rate of formaldehyde hydration and polymerization reactions. Because of this, improvements to the kinetics of polymerization have do not alter the POM steady-state growth rate and only affect the time to arrive at steady-state growth; regardless of polymerization kinetics, the POM potential for growth will always be defined by either adsorption or catalytic activity. This may not be the case for other polymers grown by atmospheric CO2 fixation through different polymerization pathways.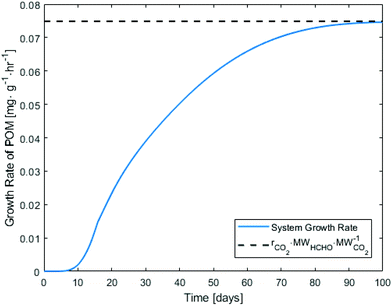 | ||
| Fig. 5 Simulated growth rate of POM over time under 400 ppm CO2 pressure at room temperature calculated using eqn (23)–(25) assuming the CO2 reduction to CO and HCHO as the main rate limiting steps in the overall pathway network. | ||
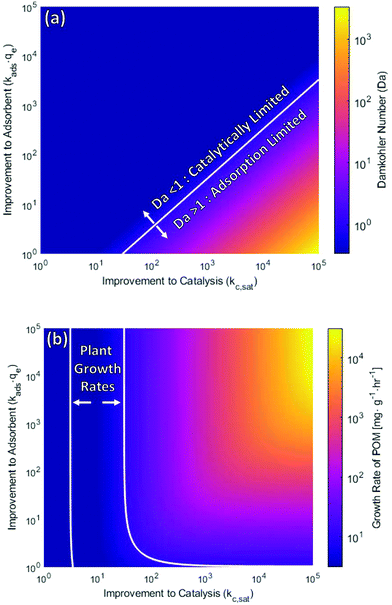
Creating a carbon fixing material that grows faster than the case study presented here requires improvements to the photocatalytic system and possibly the adsorbent. Using the tools introduced in this work, the parameter space can be explored as the rate of catalytic reduction (given as improvements to kc,sat), or adsorption (given as improvements to the product kads·qe). The Damköhler number of these systems, as well as their maximum growth rate, is presented in Fig. 6a. In the current POM example explored in this work, the system is catalytically limited. Hence, its interface with a more effective adsorbent produces a carbon fixing material only negligibly better. The catalytic limitation needs to be overcome first before adsorption capacity can impact the overall growth rate. Quantitatively, we observe that the increase must be at least an order of magnitude before the system Damköhler number reaches unity where the crossover to mass transfer limitation occurs.
To analyze potential growth rates achievable through carbon fixation, rates can be benchmarked against that of living plants—a natural carbon fixing material also capable of growth, self-repair and reinforcement through use of the same chemical feedstocks. While maximum growth rates of plants vary by stage of growth and species, a representative range is taken as growth between 1 and 10 mg of mass gained per hour per gram of dry plant mass (mg h−1 gplant−1).61,62–64 This range brackets at an upper limit the rapid growth of invasive and weedy species such as Artemisia vulgaris with a relative growth rate of greater than 9.4 mg h−1 gplant−1, and the more moderate growth of mature woody deciduous trees such as Fagus sylvatica at less than one mg h−1 gplant−1. This range of growth rates is marked in Fig. 6b.
To reach the lower bound of growth rate that rivals that of living plant systems, photocatalytic activity of the proposed case needs only be increased by nearly a factor of three. To reach the upper bound of 10 mg g−1 h−1 without an improved adsorbent the catalytic activity need be improved over four orders of magnitude. However, if an adsorbent ten times more active than the aqueous amine solution explored in this work is incorporated, improvements to catalytic activity need only be improved 36 times to reach this upper bound of plant growth rate. This highlights the interplay between adsorption and catalytic conversion within such systems, where one must quantify the inherent limitations (defined by the Damköhler number) in order to achieve the largest improvement to growth rate by the most reasonable and experimentally feasible improvements to adsorbent or the catalyst.
The time to reach the steady state growth rate is a function of the polymerization kinetics as conversion rate of CO2. For a range of improved systems with faster polymerization rates and CO2 conversion rates, the time to reach 95% of the systems steady state growth rate is shown in Fig. S3.† For the case study explored in this work, this time is nearly two months. Increasing the polymerization rate and the rate of CO2 conversion will always improve the time for the system to reach steady state growth—yielding a faster growing system overall.
6. Future outlook for carbon fixing materials
A material system that can convert ambient CO2 into a strong and self-healing material would greatly benefit the construction industry, where lightweight precursors would be able to be shipped and upon arrive would grow and densify into the desired structural material and self-healing protective coatings. Gradual degradation of conventional protective coatings is associated with high cost of maintenance, repair, and reapplying coatings. Application of self-healing CFM coatings allows for growth of additional coating layer over time. Depending on the relative rate of growth to degradation, the CFM coating lifetime can be extended marginally or drastically (Fig. S4†). This would be especially beneficial in applications where it is exceedingly dangerous and costly to reapply a coating, such as offshore wind turbines or oil rigs.65,66 An accurate techno-economic assessment of carbon fixing materials requires designing a prototype product with well-defined geometry for a targeted application. Yet, the potential economic benefit of a self-repairing coating is reflected in Fig. S5,† where the lifetime of different types of conventional coatings is presumable extended by multiple factors upon applying self-healing CFM. The economic impact is particularly evident for off-shore wind applications, where coatings can cost thousands of dollars per square meter to repair and reapply, with maintenance accounting for over half the upkeep cost of these installations.67,68To avoid additional energy input to the carbon fixing materials and solely relying on solar energy for reduction of CO2, ideally, the carbon fixing network of reactions are engineered to run at room temperature. This is vital for CO2 photocatalytic reduction as the dominant pathways and rate constants of competing reactions may be adversely affected at higher temperatures by the increased electron–hole recombination in the photocatalyst. On the other hand, the kinetics of polymerization reactions may be accelerated at higher temperature. For example, in this case study, the rate constants of formaldehyde conversion to 1,3,5-trioxane (k7–k10) will increase by two to three orders of magnitude at temperatures above 60 °C. Therefore, depending on the chemistry of carbon fixing material, minimal energy input to raise the polymerization kinetics may be advantageous and can be included in the analysis of the pathways.
Our performance calculation for the presented chemical route to a carbon fixing material can help guide the research and development of these composite materials. Our compartmental approach in developing overall kinetic models may be used to evaluate growth via alternative chemical pathways. However, adopting this general theoretical framework must be accompanied by some experimental considerations. Major considerations include the following: the study of CO2 adsorbents under low partial pressure of CO2 and excess nitrogen, where the adsorption selectivity of CO2 over nitrogen may limit capacity; the quantification of probable intermediate species and complete C1 products monitoring during photocatalytic reduction of CO2 with high accuracy and repeatability; the long-timescale study of photocatalytic activity; and finally evaluating the relative monomer production rate to consumption rate at room temperature and in presence of atmospheric CO2. Detailed discussion of each point can be found in the ESI.† For realization of CFM in lab, further design parameters such as morphology of each compartment, efficient interfacing of the compartments, concentrating the intermediates, and directional growth of the product must be thoroughly analyzed and optimized. In other words, the timescale and chemical reaction conditions for carbon fixing materials in the environment can vary significantly from those used for the experimental study of CO2 adsorbents and photocatalyst in the laboratory or used in industry. Many experimental and chemical approaches to successful CO2 photoreduction may not be directly applicable for incorporation into carbon fixing material, providing an opportunity to discover catalysts under previously unexplored conditions with alternative catalyst/adsorbent morphologies and interfaces.
7. Summary
The work introduces a series of new analytical tools by which one can describe the fundamental limits of growth for what we call carbon fixing materials – a new class that can convert atmospheric CO2 into high-strength, high-stability polymer systems which grow and self-repair using only energy input from sunlight. The two distinct limits of chemical kinetic limitations and mass transfer limitations are discussed. We employ a reaction engineering, and materials science analysis to answer basic questions about the maximum growth rate, photocatalytic requirements and limits of applicable materials. A Damköhler analysis is used to derive criteria for the cross over from kinetic control to mass transfer limited growth, setting upper limits on performance of a potential photocatalyst that may be used for carbon fixation. Another tool introduced is a reduced model that describes the photocatalytic reduction of CO2 to single carbon products, validated using known catalytic pathways and kinetic data. In this work, we show that formaldehyde as a C1 intermediate has unique potential for incorporation into the material backbone of carbon fixing materials. A diamond-shaped reaction network graph for CO2 reduction, passing through CO and HCOOH intermediates, accurately describes kinetic data for Co promoted TiO2 nanoparticles at room temperature and 1 atm CO2 and used to analyze the example of a carbon fixing poly(oxymethylene) system with embedded catalyst promoting the photocatalytic reduction of CO2 to formaldehyde. The latter then trimerizes to a trioxane monomer which subsequently polymerizes to polyoxymethylene. This reaction engineering analysis introduces benchmarks for carbon fixing materials with respect to achievable rates of photocatalysis, mass transport and polymerization. These results should prove valuable for the design, evaluation and benchmarking of this emergent, new class of environmentally sustainable materials.Author contributions
D. P. performed the kinetic modeling and relevant calculations of photocatalytic reduction, formaldehyde trimerization, trioxane polymerization, overall CO2 to POM conversion, and interfacing with CO2 adsorbents for growth rate analysis of the case study carbon fixing material. D. J. L. developed the simultaneous adsorption and reaction of CO2 analysis, and performed the growth rate analysis of the case study carbon fixing material system. S. K. assisted in developing proposed chemical pathway from CO2 to POM. H. K. prepared the schematic in Table of Contents, Fig. 4 and Table S1.† M.S. S. developed the concept of the carbon fixing material and supervised the whole project.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work, including concept development, model reaction and literature analysis, and chemical kinetic investigation, was supported by the US Department of Energy, Office of Science, DE-FG02-08ER46488. D. Lundberg is grateful for support via a National Science Foundation Graduate Fellowship, used to support specifically the simultaneous adsorption and reaction of CO2 analysis and the growth rate analysis in this work. Also, we like to thank Dr Mohammad Mirzadeh of MIT and Dr Jonathan Raftery of Honeywell UOP for their valuable comments and many useful inputs.References
- R. Geyer, J. R. Jambeck and K. L. Law, Production, use, and fate of all plastics ever made, Sci. Adv., 2017, 3(7), e1700782 CrossRef.
- S. Y. Kwak, J. P. Giraldo, T. T. S. Lew, M. H. Wong, P. Liu, Y. J. Yang, V. B. Koman, M. K. McGee, B. D. Olsen and M. S. Strano, Polymethacrylamide and Carbon Composites that Grow, Strengthen, and Self-Repair using Ambient Carbon Dioxide Fixation, Adv. Mater., 2018, 30(46), 1804037 CrossRef.
- B. Grignard, S. Gennen, C. Jerome, A. W. Kleij and C. Detrembleur, Advances in the use of CO2 as a renewable feedstock for the synthesis of polymers, Chem. Soc. Rev., 2019, 48(16), 4466–4514 RSC.
- G. L. Gregory, G. Kociok-Kohn and A. Buchard, Polymers from sugars and CO2: ring-opening polymerisation and copolymerisation of cyclic carbonates derived from 2-deoxy-D-ribose, Polym. Chem., 2017, 8(13), 2093–2104 RSC.
- E. M. Lopez-Vidal, G. L. Gregory, G. Kociok-Kohn and A. Buchard, Polymers from sugars and CS2: synthesis and ring-opening polymerisation of sulfur-containing monomers derived from 2-deoxy-D-ribose and D-xylose, Polym. Chem., 2018, 9(13), 1577–1582 RSC.
- X. F. Xiang, L. Guo, X. Wu, X. X. Ma and Y. S. Xia, Urea formation from carbon dioxide and ammonia at atmospheric pressure, Environ. Chem. Lett., 2012, 10(3), 295–300 CrossRef CAS.
- P. Braunstein, D. Matt and D. Nobel, Carbon-dioxide activation and catalytic lactone synthesis by telomerization of butadiene and CO2, J. Am. Chem. Soc., 1988, 110(10), 3207–3212 CrossRef CAS.
- R. Nakano, S. Ito and K. Nozaki, Copolymerization of carbon dioxide and butadiene via a lactone intermediate, Nat. Chem., 2014, 6(4), 325–331 CrossRef CAS.
- R. H. Heyn, I. Jacobs and R. H. Carr, Synthesis of Aromatic Carbamates from CO2: Implications for the Polyurethane Industry, Adv. Inorg. Chem., 2014, 66, 83–115 CrossRef CAS.
- F. Barzagli, F. Mani and M. Peruzzini, From greenhouse gas to feedstock: formation of ammonium carbamate from CO2 and NH3 in organic solvents and its catalytic conversion into urea under mild conditions, Green Chem., 2011, 13(5), 1267–1274 RSC.
- A. J. Kamphuis, F. Picchioni and P. P. Pescarmona, CO2-fixation into cyclic and polymeric carbonates: principles and applications, Green Chem., 2019, 21(3), 406–448 RSC.
- F. Auriemma, C. De Rosa, M. R. Di Caprio, R. Di Girolamo and G. W. Coates, Crystallization of Alternating Limonene Oxide/Carbon Dioxide Copolymers: Determination of the Crystal Structure of Stereocomplex Poly(limonene carbonate), Macromolecules, 2015, 48(8), 2534–2550 CrossRef CAS.
- T. Inoue, A. Fujishima, S. Konishi and K. Honda, Photoelectrocatalytic reduction of carbon-dioxide in aqueous suspensions of semiconductor powders, Nature, 1979, 277(5698), 637–638 CrossRef CAS.
- J. L. White, M. F. Baruch, J. E. Pander, Y. Hu, I. C. Fortmeyer, J. E. Park, T. Zhang, K. Liao, J. Gu, Y. Yan, T. W. Shaw, E. Abelev and A. B. Bocarsly, Light-Driven Heterogeneous Reduction of Carbon Dioxide: Photocatalysts and Photoelectrodes, Chem. Rev., 2015, 115(23), 12888–12935 CrossRef CAS PubMed.
- S. N. Habisreutinger, L. Schmidt-Mende and J. K. Stolarczyk, Photocatalytic Reduction of CO2 on TiO2 and Other Semiconductors, Angew. Chem., Int. Ed., 2013, 52(29), 7372–7408 CrossRef CAS PubMed.
- M. Mikkelsen, M. Jorgensen and F. C. Krebs, The teraton challenge. A review of fixation and transformation of carbon dioxide, Energy Environ. Sci., 2010, 3(1), 43–81 RSC.
- W. G. Tu, Y. Zhou and Z. G. Zou, Photocatalytic Conversion of CO2 into Renewable Hydrocarbon Fuels: State-of-the-Art Accomplishment, Challenges, and Prospects, Adv. Mater., 2014, 26(27), 4607–4626 CrossRef CAS PubMed.
- A. Dhakshinamoorthy, S. Navalon, A. Corma and H. Garcia, Photocatalytic CO2 reduction by TiO2 and related titanium containing solids, Energy Environ. Sci., 2012, 5(11), 9217–9233 RSC.
- P. V. Kamat, Manipulation of Charge Transfer Across Semiconductor Interface. A Criterion That Cannot Be Ignored in Photocatalyst Design, J. Phys. Chem. Lett., 2012, 3(5), 663–672 CrossRef CAS PubMed.
- A. Kubacka, M. Fernandez-Garcia and G. Colon, Advanced Nanoarchitectures for Solar Photocatalytic Applications, Chem. Rev., 2012, 112(3), 1555–1614 CrossRef CAS PubMed.
- H. L. Zhou, Y. Q. Qu, T. Zeid and X. F. Duan, Towards highly efficient photocatalysts using semiconductor nanoarchitectures, Energy Environ. Sci., 2012, 5(5), 6732–6743 RSC.
- S. Jribi, T. Miyazaki, B. B. Saha, A. Pal, M. M. Younes, S. Koyama and A. Maalej, Equilibrium and kinetics of CO2 adsorption onto activated carbon, Int. J. Heat Mass Transfer, 2017, 108, 1941–1946 CrossRef CAS.
- K. Koci, L. Obalova and O. Solcova, Kinetic study of photocatalytic reduction of CO2 over TIO2, Chem. Process Eng., 2010, 31(3), 395–407 CAS.
- N. M. Dimitrijevic, I. A. Shkrob, D. J. Gosztola and T. Rajh, Dynamics of Interfacial Charge Transfer to Formic Acid, Formaldehyde, and Methanol on the Surface of TiO2 Nanoparticles and Its Role in Methane Production, J. Phys. Chem. C, 2012, 116(1), 878–885 CrossRef CAS.
- S. S. Tan, L. Zou and E. Hu, Kinetic modelling for photosynthesis of hydrogen and methane through catalytic reduction of carbon dioxide with water vapour, Catal. Today, 2008, 131(1–4), 125–129 CrossRef CAS.
- S. H. Liu, Z. H. Zhao and Z. Z. Wang, Photocatalytic reduction of carbon dioxide using sol-gel derived titania-supported CoPc catalysts, Photochem. Photobiol. Sci., 2007, 6(6), 695–700 CrossRef CAS PubMed.
- Y. F. Ji and Y. Luo, Theoretical Study on the Mechanism of Photoreduction of CO2 to CH4 on the Anatase TiO2(101) Surface, ACS Catal., 2016, 6(3), 2018–2025 CrossRef CAS.
- J. Rasko and F. Solymosi, Infrared spectroscopic study of the photoinduced activation of CO2 on TIO2 and RH/TIO2 catalysts, J. Phys. Chem., 1994, 98(29), 7147–7152 CrossRef CAS.
- P. Usubharatana, D. McMartin, A. Veawab and P. Tontiwachwuthikul, Photocatalytic process for CO2 emission reduction from industrial flue gas streams, Ind. Eng. Chem. Res., 2006, 45(8), 2558–2568 CrossRef CAS.
- E. S. Sanz-Perez, C. R. Murdock, S. A. Didas and C. W. Jones, Direct Capture of CO2 from Ambient Air, Chem. Rev., 2016, 116(19), 11840–11876 CrossRef CAS PubMed.
- A. Crake, K. C. Christoforidis, A. Kafizas, S. Zafeiratos and C. Petit, CO2 capture and photocatalytic reduction using bifunctional TiO2/MOF nanocomposites under UV-vis irradiation, Appl. Catal., B, 2017, 210, 131–140 CrossRef CAS.
- M. Noorjahan, V. D. Kumari, M. Subrahmanyam and P. Boule, A novel and efficient photocatalyst: TiO2-HZSM-5 combinate thin film, Appl. Catal., B, 2004, 47(3), 209–213 CrossRef CAS.
- N. Yahya, F. Aziz, N. A. Jamaludin, M. A. Mutalib, A. F. Ismail, W. N. W. Salleh, J. Jaafar, N. Yusof and N. A. Ludin, A review of integrated photocatalyst adsorbents for wastewater treatment, J. Environ. Chem. Eng., 2018, 6(6), 7411–7425 CrossRef CAS.
- T. Torimoto, S. Ito, S. Kuwabata and H. Yoneyama, Effects of adsorbents used as supports for titanium dioxide loading on photocatalytic degradation of propyzamide, Environ. Sci. Technol., 1996, 30(4), 1275–1281 CrossRef CAS.
- K. M. Cho, K. H. Kim, K. Park, C. Kim, S. Kim, A. Al-Saggaf, I. Gereige and H. T. Jung, Amine-Functionalized Graphene/CdS Composite for Photocatalytic Reduction of CO2, ACS Catal., 2017, 7(10), 7064–7069 CrossRef CAS.
- B. Dutcher, M. Fan and A. G. Russell, Amine-Based CO2 Capture Technology Development from the Beginning of 2013-A Review, ACS Appl. Mater. Interfaces, 2015, 7(4), 2137–2148 CrossRef CAS PubMed.
- M. Ota, Y. Hirota, Y. Uchida and N. Nishiyama, CO2 Adsorption Property of Amine-Modified Amorphous TiO2 Nanoparticles with a High Surface Area, Colloids Interfaces, 2018, 2(3), 25 CrossRef CAS.
- Y. Liao, S.-W. Cao, Y. Yuan, Q. Gu, Z. Zhang and C. Xue, Efficient CO2 capture and photoreduction by amine-functionalized TiO2, Chem. – Eur. J., 2014, 20(33), 10220–10222 CrossRef CAS PubMed.
- F. Y. Jou, A. E. Mather and F. D. Otto, The solubility of CO2 IN A 30-mass-percent monoethanolamine solution, Can. J. Chem. Eng., 1995, 73(1), 140–147 CrossRef CAS.
- M. Yoo, S.-J. Han and J.-H. Wee, Carbon dioxide capture capacity of sodium hydroxide aqueous solution, J. Environ. Manage., 2013, 114, 512–519 CrossRef CAS.
- K. Weissermel, E. Fischer, K. Gutweiler, H. D. Hermann and H. Cherdron, Polymerization of trioxane, Angew. Chem., Int. Ed. Engl., 1967, 6(6), 526–533 CrossRef CAS.
- J. K. Fink, Polymerization and Manufacture of Polyoxymethylene, in Polyoxymethylene Handbook: Structure, Properties, Applications and Their Nanocomposites, 2014, pp. 21–51 Search PubMed.
- J. F. Walker and A. F. Chadwick, Trioxane as a source of formaldehyde, Ind. Eng. Chem., 1947, 39(8), 974–977 CrossRef CAS.
- J. Masamoto, K. Hamanaka, K. Yoshida, H. Nagahara, K. Kagawa, T. Iwaisako and H. Komaki, Synthesis of trioxane using heteropolyacids as catalyst, Angew. Chem., Int. Ed., 2000, 39(12), 2102–2104 CrossRef CAS.
- T. Grutzner, H. Hasse, N. Lang, M. Siegert and E. Strofer, Development of a new industrial process for trioxane production, Chem. Eng. Sci., 2007, 62(18–20), 5613–5620 CrossRef.
- M. Maiwald, T. Grutzner, E. Strofer and H. Hasse, Quantitative NMR spectroscopy of complex technical mixtures using a virtual reference: chemical equilibria and reaction kinetics of formaldehyde-water-1,3,5-trioxane, Anal. Bioanal. Chem., 2006, 385(5), 910–917 CrossRef CAS.
- X. M. Zhang, Y. F. Hu and W. T. Ma, A model for the reaction kinetics of main and side reactions during the industrial production of trioxane, and its applications, J. Chem. Technol. Biotechnol., 2018, 93(8), 2111–2117 CrossRef CAS.
- L. Y. Yin, Y. F. Hu, X. M. Zhang, J. G. Qi and W. T. Ma, The salt effect on the yields of trioxane in reaction solution and in distillate, RSC Adv., 2015, 5(47), 37697–37702 RSC.
- J. G. M. Winkelman, M. Ottens and A. Beenackers, The kinetics of the dehydration of methylene glycol, Chem. Eng. Sci., 2000, 55(11), 2065–2071 CrossRef CAS.
- M. Ott, H. H. Fischer, M. Maiwald, K. Albert and H. Hasse, Kinetics of oligomerization reactions in formaldehyde solutions: NMR experiments up to 373 K and thermodynamically consistent model, Chem. Eng. Process., 2005, 44(6), 653–660 CrossRef CAS.
- C. Kuhnert, M. Albert, S. Breyer, I. Hahnenstein, H. Hasse and G. Maurer, Phase equilibrium in formaldehyde containing multicomponent mixtures: Experimental results for fluid phase equilibria of (formaldehyde plus (water or methanol) plus methylal)) and (formaldehyde plus water plus methanol plus methylal) and comparison with predictions, Ind. Eng. Chem. Res., 2006, 45(14), 5155–5164 CrossRef CAS.
- J. Kua, J. E. Avila, C. G. Lee and W. D. Smith, Mapping the Kinetic and Thermodynamic Landscape of Formaldehyde Oligomerization under Neutral Conditions, J. Phys. Chem. A, 2013, 117(47), 12658–12667 CrossRef CAS PubMed.
- M. Hoffmann, C. Bizzarri, W. Leitner and T. E. Muller, Reaction pathways at the initial steps of trioxane polymerisation, Catal. Sci. Technol., 2018, 8(21), 5594–5603 RSC.
- W. Kern and V. Jaacks, Some kinetic effects in the polymerization of 1,3,5-trioxane, J. Polym. Sci., 1960, 48(150), 399–404 CrossRef CAS.
- T. Higashimura, T. Miki and S. Okamura, Kinetic studies of solution polymerization of trioxane catalyzed by BF3.O(C2H5)2 .3. Effect of monomer concentration, Bull. Chem. Soc. Jpn., 1966, 39(1), 31–36 CrossRef CAS.
- Y. T. Shieh and S. A. Chen, Kinetics and mechanism of the cationic polymerization of trioxane. I. Crystallization during polymerization, J. Polym. Sci., Part A: Polym. Chem., 1999, 37(4), 483–492 CrossRef CAS.
- H. Hasse and G. Maurer, Vapor-liquid-equilibrium of formaldehyde-containing mixtures at temperatures below 320-K, Fluid Phase Equilib., 1991, 64, 185–199 CrossRef CAS.
- M. Detcheberry, P. Destrac, X. M. Meyer and J. S. Condoret, Phase equilibria of aqueous solutions of formaldehyde and methanol: Improved approach using UNIQUAC coupled to chemical equilibria, Fluid Phase Equilib., 2015, 392, 84–94 CrossRef CAS.
- N. Schmitz, A. Friebel, E. von Harbou, J. Burger and H. Hasse, Liquid-liquid equilibrium in binary and ternary mixtures containing formaldehyde, water, methanol, methylal, and poly(oxymethylene) dimethyl ethers, Fluid Phase Equilib., 2016, 425, 127–135 CrossRef CAS.
- M. J. Mitchell, O. E. Jensen, K. A. Cliffe and M. M. Maroto-Valer, A model of carbon dioxide dissolution and mineral carbonation kinetics, Proc. R. Soc. A, 2010, 466(2117), 1265–1290 CrossRef CAS.
- D. Bruhn, J. W. Leverenz and H. Saxe, Effects of tree size and temperature on relative growth rate and its components of Fagus sylvatica seedlings exposed to two partial pressures of atmospheric CO2, New Phytol., 2000, 146(3), 415–425 CrossRef.
- R. Hunt and J. H. C. Cornelissen, Components of relative growth rate and their interrelations in 59 temperate plant species, New Phytol., 1997, 135(3), 395–417 CrossRef.
- Y. Peng, K. J. Niklas and S. Sun, The relationship between relative growth rate and whole-plant C:N:P stoichiometry in plant seedlings grown under nutrient-enriched conditions, J. Plant Ecol., 2011, 4(3), 147–156 CrossRef.
- J. S. Almeida-Cortez, B. Shipley and J. T. Arnason, Do plant species with high relative growth rates have poorer chemical defences?, Funct. Ecol., 1999, 13(6), 819–827 CrossRef.
- P. Cavassi and M. Cornago, The cost of corrosion in the oil \& gas industry, J. Prot. Coat. Linings, 1999, 16(5), 30–40 Search PubMed.
- G. Krause and S. M. Stead, Governance and offshore aquaculture in multi-resource use settings, 2017, pp. 149–162 Search PubMed.
- M. Ohle, Long-lasting rust protection for offshore wind turbines, 2016, pp. 1–3 Search PubMed.
- L. Isaksen, Corrosion protection and the cost of failure, INTSOK Navigating Deepwater Opportunities and Challenges, 2014, (February), 1–26 Search PubMed.
- V. K. Singh and E. A. Kumar, Comparative Studies on CO2 Adsorption Isotherms by Solid Adsorbents, Mater. Today: Proc., 2018, 5(11), 23033–23042 Search PubMed.
- W. J. Xie, M. Q. Yu and R. Wang, CO2 Capture Behaviors of Amine-Modified Resorcinol-Based Carbon Aerogels Adsorbents, Aerosol Air Qual. Res., 2017, 17(11), 2715–2725 CrossRef CAS.
- A. Rehman, S. Farrukh, A. Hussain, X. F. Fan and E. Pervaiz, Adsorption of CO2 on amine-functionalized green metal-organic framework: an interaction between amine and CO2 molecules, Environ. Sci. Pollut. Res., 2019, 26, 36214–36225 CrossRef CAS PubMed.
- L. Y. Yin, Y. F. Hu and H. Y. Wang, The remarkable effect of organic salts on 1,3,5-trioxane synthesis, Pet. Sci., 2016, 13(4), 770–775 CrossRef CAS.
- Y. P. Peng, Y. T. Yeh, S. I. Shah and C. P. Huang, Concurrent photoelectrochemical reduction of CO2 and oxidation of methyl orange using nitrogen-doped TiO2, Appl. Catal., B, 2012, 123, 414–423 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1gc00965f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |