Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of micro-aeration on the mechanical behaviour of chocolates and implications for oral processing
D.
Bikos
 *a,
G.
Samaras
a,
P.
Cann
a,
M.
Masen
a,
Y.
Hardalupas
a,
C.
Hartmann
b,
J.
Vieira
c and
M. N.
Charalambides
*a
*a,
G.
Samaras
a,
P.
Cann
a,
M.
Masen
a,
Y.
Hardalupas
a,
C.
Hartmann
b,
J.
Vieira
c and
M. N.
Charalambides
*a
aDepartment of Mechanical Engineering, Imperial College London, UK. E-mail: d.bikos17@imperial.ac.uk; m.charalambides@imperial.ac.uk
bNestlé Research, Lausanne, UK
cNestlé Product Technology Centre, York, UK
First published on 5th May 2021
Abstract
Aeration in foods has been widely utilised in the food industry to develop novel foods with enhanced sensorial characteristics. Specifically, aeration at the micron-sized scale has a significant impact on the microstructure where micro-bubbles interact with the other microstructural features in chocolates. This study aims to determine the effect of micro-aeration on the mechanical properties of chocolate products, which are directly correlated with textural attributes such as hardness and crumbliness. Uniaxial compression tests were performed to determine the mechanical properties such as Poisson's ratio, Young's modulus and macroscopic yield strength together with fracture tests to estimate the fracture toughness. In vivo mastication tests were also conducted to investigate the link between the fracture properties and fragmentation during the first two chewing cycles. The uniaxial stress–strain data were used to calibrate a viscoplastic constitutive law. The results showed that micro-aeration significantly affects mechanical properties such as Young's modulus, yield and fracture stresses, as well as fracture toughness. In addition, it enhances the brittle nature of the chocolate, as evidenced by lower fracture stress but also lower fracture toughness leading to higher fragmentation, in agreement with observations in the in vivo mastication tests. As evidenced by the XRT images and the stress–strain measurements micro-aeration hinders the re-arrangement of the microscopic features inside the chocolate during the material's deformation. The work provides a new insight of the role of bubbles on the bulk behaviour of complex multiphase materials, such as chocolates, and defines the mechanical properties which are important input parameters for the development of oral processing simulations.
1. Introduction
The increasing demand for foods with reduced sugar,1,2 fat3–5 and salt content6,7 has led the food industry to consider possible replacements whilst aiming to maintain the desirable sensorial and textural characteristics of the foods. The option of gas inclusion into food networks has been widely utilised and is associated with positive consumer experience, while at the same time can lead to a reduction of the energy density of the food product.8–10 Aeration in food systems can lead to changes in the mouthfeel, may enhance satiety in the case of porous liquids,8,11 and even improve the food product stability.12 Based on this, aeration has been widely adopted in numerous food systems, such as milk, cakes, bread and chocolates9,13–15 producing novel and complex food structures aiming to improve the food design and the consumer experience.In the chocolate industry, aeration in chocolates is being practised, as part of a growing effort to replace health sensitive nutrients, such as sugars and fats, with gas, leading to the design of new products with enhanced mouthfeel.16,17 This concept lies in the fact that without reducing the volume fraction of the ingredients, the original sensorial perception of the chocolate is retained or even enhanced which is extensively discussed for a variety of food materials by Minor et al.18 The consequent reduction of the mass fraction of the ingredients additionally addresses the reduction of the calorific value of the product, leading to optimised, healthier products.11
Various manufacturing techniques, such as gas injection and the use of vacuum chambers, and types of gases, CO2 and N2, have been employed to create a range of bubbly structures with different bubble sizes.17,19 In chocolate, based on the gas selection, different bubble sizes can be formed in the chocolate matrix varying from tens of microns up to several millimetres19 contributing to changes in the material's structure as well as in textural perception.17 The size of the bubble strongly affects the mouthfeel outcome. Bubbles of millimetre size, which are visible to the unaided eye, could increase the brittleness of the material, while the micro-bubbles, could potentially attribute to a smoother mouthfeel.17
Micro-bubbles dispersed into a chocolate network greatly influence the material microstructure and the dispersion characteristics of the solid particles found in the chocolate.20 The size of these micro-bubbles is of similar scale with the rest of the ingredients found in chocolate. Chocolates are a suspension of solid particles, such as sugar, cocoa, and milk powder in the case of the milk chocolate in a continuous fat network of cocoa butter.21,22 Aeration in this multiphase microstructure could lead to structural changes in the chocolate and consequently to changes in the chocolate texture in terms of the eating experience and the mouthfeel sensations.17,23
It has been well established that the microstructure of chocolate significantly impacts the macroscopic rheological behaviour of the material22,24,25 and textural attributes such as hardness and firmness.25 In general, the macroscopic behaviour of a solid food product can be characterised by material properties such as Young's modulus,26 yield and fracture stress. These properties are responsible for the bulk response of the food material during the first bite, where large deformations and complex loading phenomena are observed.27 These properties, together with the fracture characteristics of the material will determine the textural characteristics of the food material during consumption.28–30
However, compared to the number of reported rheological studies of melted (liquid) chocolate, there are limited studies available in the literature investigating in depth the mechanics of chocolates at solid-state.31–34 From these, only Svanberg et al.34 measured the mechanical properties such as elastic modulus using a newly proposed experimental method. No studies according to the authors’ knowledge used systematic mechanical protocols to determine the mechanical properties of either aerated or non-aerated chocolates, such as the Young's modulus, Poisson's ratio, yield stress and fracture toughness. As a result, currently there are no calibrated constitutive laws in the literature, based on such rigorous experimental data. Such constitutive laws are required to predict fracture in events such as the first bite. Furthermore, even though many researchers in the past highlighted the viscoelastic behaviour of the chocolate when the chocolate is molten,22,35 no investigation on the rate-dependency of the mechanical properties has been conducted so far when the chocolate is in its solid state. When the investigation moves towards micro-aeration and its effect on mechanical properties of chocolates but also oral processing, there are no studies available in the literature tackling this multidisciplinary problem.
Evaluating accurately the bulk and fracture properties of the food product will assist the prediction of the food's mechanical response inside the oral cavity and the initiation of fracture when the material model will be used in conjunction with a damage criterion.36 The bulk properties are best evaluated through a series of mechanical test protocols under different modes of deformation, such as uniaxial/biaxial compression and tension or shear.36–38 However, no damage model was introduced in this work, which was focused on the mechanical characterisation and the calibration of the constitutive model.
This study investigates the bulk behaviour of three milk chocolate products with typical compositions (two aerated at 10% and 15% by volume and one non-aerated) under a mechanical action simulating the oral conditions. Uniaxial compression tests and fracture tests are performed on all chocolate products to highlight the effect of aeration on the mechanical and fracture properties respectively. In vivo mastication tests on aerated and non-aerated commercial chocolates (one aerated of 12% porosity and a non-aerated chocolate) are also conducted, to highlight the effect of the respective mechanical response on the oral process. In addition, the extracted stress–strain data and mechanical properties from the uniaxial compression tests, both from the monotonic and the loading–unloading tests, are utilised to calibrate a viscoplastic constitutive model, such that it can be readily used in future computational models simulating the oral conditions. This study attempts to link both the mechanical and fracture properties with the mastication conditions and with the food structure, which is closely related to textural attributes such as food hardness, crumbliness and grittiness.
2. Materials and methods
2.1. Materials
Three types of milk chocolate, two aerated chocolates with 10% and 15% by volume gas (also referred throughout the text as porosity) and a non-aerated chocolate, consisting of 44 wt% sugar particles, 27 wt% cocoa fat, 10 wt% whole milk powder and 6 wt% non-fat cocoa solids were provided by Nestlé Product Technology Centre (NPTC) in York. The chocolate mass was produced by the standardised manufacturing steps of mixing, refining and conching. Specifically, the cocoa liquor, the cocoa butter, the skimmed milk powder and milk fat were mixed together and refined employing a three-roll refiner to a target particle size of 33 μm. This particle size represented the Dv,90 (90% of the particles by volume are finer than this threshold) and measured by a Malvern Mastersizer 3000. The chocolate flakes were then conched on a 60 kg Frisse conching machine at 60 °C for ten hours to reduce the viscosity levels and enhance the final flavour of the chocolate product. After the completion of the conching, sunflower lecithin was added to the chocolate mixture, which acts as an emulsifier, to reach suitable viscosity levels and the conching step was repeated for another two hours. The chocolate mass was then tested for its viscosity and yield values at a temperature of 40 °C with a Haake VT550 viscometer to examine the quality of the chocolate mass. The outcome showed a viscosity value of 7.21 Pa s and yield stress of 8.31 Pa at shear rates of 40 s−1 and 5 s−1 respectively.24,39The non-aerated chocolate is produced using conventional/standardised manufacturing process, whilst the micro-aeration is achieved by dispersing nitrogen gas (N2) in the tempered chocolate suspension followed by depositing the micro-aerated mixture into the mould. This will result in the formation of micro-bubbles due to the pressure drop when the gas leaves the nozzle. The porosity was evaluated during manufacturing by measuring the mass of non-aerated and micro-aerated chocolate samples of the same volume. In both manufacturing processes of the non-aerated and the aerated materials, a vibration step was performed on the moulded samples to prevent the formation of larger air bubbles. However, it is worth noting that the vibration step for the micro-aerated chocolate was performed for a shorter period of time to avoid the release of the micro-bubbles from the mixture. Therefore, a few large bubbles (>100 μm) might be trapped in the chocolate mixture which is not associated with the micro-aeration process.
The geometries, which were provided by Nestlé, were cylindrical samples of 20 mm diameter and 20 mm height (Fig. 1a) and rectangular beams of 80 mm length L, 15 mm width W and 8 mm thickness B (Fig. 1e). The cylindrical samples were used for uniaxial compression tests due to the desired diameter to height ratio, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is required for these tests to reduce the effect of friction at the sample/loading platen interfaces on the measurement outcome.29,37 The rectangular beams were used for single-edge notched bending tests to evaluate the fracture toughness of the chocolate material.
1, which is required for these tests to reduce the effect of friction at the sample/loading platen interfaces on the measurement outcome.29,37 The rectangular beams were used for single-edge notched bending tests to evaluate the fracture toughness of the chocolate material.
In addition, two types of commercial chocolate samples (Fig. 1h and i), one non-aerated and one aerated with a 12% porosity and a rectangular shape of 90 mm length L, 14 mm width W and 8 mm thickness B were utilised for in vivo mastication tests in order to bridge the gap between in vivo studies and mechanical protocols. These commercial chocolates followed the same manufacturing procedure and had the same composition as the samples provided by NPTC to ensure that the in vivo experiments and the experiments using the mechanical protocols are directly comparable. These commercial chocolates were used in the in vivo studies instead of the chocolate samples provided by the NPTC, due to the fact that the latter chocolates were produced in a pilot plant which does not follow the required industrial safety procedures for human consumption.
2.2. Investigation of the microstructure
The samples were pre-cracked along all faces with a razor blade followed by a tap with a plastic mallet to produce a flat naturally fractured surface. This process was performed to ensure flat fractured surfaces on the samples and consequently to assist the accuracy of the measurements used from the microscopic investigation.The microstructure of all types of chocolates was investigated through scanning electron microscopy (SEM). A Hitachi S-3400 SEM was used at variable pressure mode and at relatively low accelerating voltages of 5 kV and 10 kV to prevent the samples from melting. Three different regions, which included at least fifty bubbles, and five chocolate samples were inspected through SEM to describe a statistically representative bubble size distribution. The acquired 2D images were further processed via the open-source software ImageJ [v1.52 National Institutes of Health]40 to calculate the bubble size distribution of the aerated chocolate. A manual tool available on ImageJ was used to select the surface area covered by the bubbles and measure the corresponding area in mm2. This process was performed in the maximum available magnification to minimise possible errors. The 2D area was then converted to an equivalent diameter (a diameter which corresponds to the same area). The 2D bubble size distribution was finally converted into a 3D size distribution based on the methodology described by Sahagian and Proussevitch.41 This approach takes into account any random cut plane and any shape of particles to convert the 2D size distribution into a 3D and therefore to correct any errors associated with the naturally fractured 2D surfaces.
A Carl Zeiss Xradia Versa 520 micro-scanning tomography system was utilised to scan only the chocolate samples with no aeration and aeration of 15% porosity due to the high cost of the XRT experiments. For these tests, chocolate samples of 5 mm diameter and 5 mm height, under an accelerating voltage of 40 kV and a current of 76 μA were used. An optical lens with 4× magnification was used between the sensor and the sample to increase the raw image resolution. The raw stack of images was used to reconstruct the 3D volume geometry of the chocolate microstructure of four hundred bubbles using the software Avizo [v6.5.0 Thermo Fisher Scientific].42 The raw XRT data were generated in the form of a volume file. Overall, close to 500 images were stacked from an initial image size of 1984 × 2028 pixels and pixel size of 1.7 μm to ensure that all the voids/bubbles can be identified. The pixel size of 1.7 μm ensures that any bubble with a diameter of 4 μm and higher can be recognised in the XRT images. This resolution was found to be adequate since no bubbles were reported with sizes less than 10 μm from the SEM images. The stack of images was then further processed in Avizo for 3D reconstruction. Segmentation was first employed on one image to isolate the gas bubbles from the chocolate microstructure. The same settings for segmentation were automatically processed through all stack of images to create the 3D volume of the voids. The volume of bubbles was statistically processed within the available tools in Avizo to visualise the size distribution of the bubbles, classify the bubbles according to their sizes and compute the porosity of the micro-aerated material. The reconstruction of the 3D geometry was performed once since it proved a challenging and time-consuming task and the bubble size distribution of the aerated chocolate of 15% porosity was compared with the results extracted from the SEM images.
The 2D XRT raw data were further processed with ImageJ to investigate the interface region between the gas bubble and the chocolate matrix. Initially, the contrast of the image was adjusted to highlight the regions in the vicinity to the gas bubble and chocolate matrix interface, followed by a threshold process to distinguish the higher density surfaces which are shown in white colour.
2.3. Mechanical tests – uniaxial compression
Uniaxial compression tests (see Fig. 1c) were performed on a 5584 universal Instron testing instrument with a 2 kN load cell capacity (maximum loads observed during the compression tests reached approximately 950 N) at a room temperature of 20 °C and 50% humidity. The axial and lateral expansion of the chocolate samples were both measured via digital instruments and by optical means from video recordings of the compression tests. For the former technique the axial expansion was measured by the Instron instrument while the lateral expansion was monitored with the use of a micrometer which was positioned in the middle of the sample. For the latter technique, the video recordings, using a Logitech HD Pro Webcam C920 as shown in Fig. 1c, label 2, were synchronised with the instrumental readings and images from the video recordings were collected at different time intervals within the linear regime of the material. The two techniques agreed well, however, only the results from the imaging method are shown in this study because it led to data with a lower scatter. The lateral and axial contraction were then converted to transverse and axial strains, respectively, using eqn (1) and the ratio of these two strains is the estimation of the Poisson's ratio. This procedure was repeated three times for each sample and each type of chocolate to account for any variations through the batch. As it will be shown in section 3.2, based on the measurements of the lateral and axial expansions taken from the video images, we assume perfect incompressibility in all samples, i.e. Poisson's ratio of v = 0.5.The data from the uniaxial compression tests were used to determine the values of true (Cauchy) stress and true (Hencky) strain data through the given relationship:
 | (1) |
 | (2) |
| HA = H0A0 | (3) |
Compression tests were performed under monotonically increasing applied strain, up to ultimate fracture (∼ε = 0.15) at four constant true strain rates, 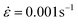 , 0.01 s−1, 0.1 s−1 and 1 s−1 with each condition repeated five times. These rates were chosen as they are relevant to the strain rates during mastication, which ranges from 0.1 s−1 up to 2.5 s−1, as reported by ref. 43–47. In order to minimise the barrelling of the specimens in the compression tests, 0.2 mm thick PTFE sheets (labelled 3 in Fig. 1c) were attached to both metallic compression plates to minimise the interfacial friction between the sample and the steel plates.37 Thin PTFE sheets were chosen due to the fact that they have lower surface energy compared to steel and consequently lower surface adhesion,48 which is related to friction.
, 0.01 s−1, 0.1 s−1 and 1 s−1 with each condition repeated five times. These rates were chosen as they are relevant to the strain rates during mastication, which ranges from 0.1 s−1 up to 2.5 s−1, as reported by ref. 43–47. In order to minimise the barrelling of the specimens in the compression tests, 0.2 mm thick PTFE sheets (labelled 3 in Fig. 1c) were attached to both metallic compression plates to minimise the interfacial friction between the sample and the steel plates.37 Thin PTFE sheets were chosen due to the fact that they have lower surface energy compared to steel and consequently lower surface adhesion,48 which is related to friction.
Loading and unloading tests in compression mode were undertaken on all chocolate products to highlight any inelastic effects. For the non-aerated specimen, an initial strain up to three strain thresholds of 0.015, 0.025, 0.045 was applied followed by a strain removal until the sample returned to zero force position (unloading stage). For the case of the aerated specimens with 10% and 15% porosity, two strain levels were applied of 0.01, 0.025 and 0.04, 0.025 respectively, during the loading stage, and then the specimens returned to zero force position. The procedure was repeated three times for each condition and each type of chocolate, with the strain rate during the loading and unloading stage remaining constant for all tests at 0.01 s−1.
2.4. Mechanical tests – single edge notched bending (SENB)
Single edge notched bending tests were conducted according to the ASTM standard D5045-9949 on rectangular beams of 80 mm length, 15 mm width 8 mm thickness to compute the fracture toughness, Gc, of the chocolate product. The chocolate samples were loaded in a three-point bending setup on a 5543 Instron testing instrument with a load cell capacity of 100 N (maximum load observed approximately 20 N) and testing conditions of 20 °C temperature and 50% humidity. The length span, see ‘Lspan’ in Fig. 1d, and the notch depth, see a in Fig. 1f and g, were chosen to be 60 mm and 7 mm respectively, which is aligned with the requirements of the ASTM protocol to ensure plane strain conditions. Force displacement data were recorded at three constant crosshead speeds of 0.02 mm/s, 0.2 mm/s and 2 mm/s. Four repeats were used for each testing speed for all chocolate materials.The stress intensity factor assuming plane strain conditions for the SENB test was computed from:
 | (4) |
Assuming linear elastic behaviour, the critical energy release rate, known as fracture toughness Gc, can be evaluated from eqn (5):
 | (5) |
Combining the fracture toughness Gc and the stress intensity factor KQ, which was extracted from the SENB tests, into eqn (6), the Young's modulus of the material, E, can be calculated and compared to the value obtained from the uniaxial compression tests:
 | (6) |
The SENB test configuration is shown in Fig. 2a. During some of these tests, crack initiation was observed prior to the maximum load for some repeats. In this case, according to ASTM standard D5045-99, the load corresponding to the point of crack initiation is defined as the point of intersection of the 5% compliance curve and the material's load–displacement (P–d) response, as shown in Fig. 2b (see black arrow). In addition, a correction to the energy U was performed in order to account for possible indentation of the loading pin and the supports into the sample and eliminate any machine compliance, see Fig. 2c. In all cases, PQ is considered as the load leading to the crack initiation which was also verified from the video images obtained during the tests and synchronised with the P–d response.
 | ||
| Fig. 2 SENB experimental setup. Images show: (a) the pre-notched chocolate sample placed on the three-point bending rig according to the ASTM standards,49 (b) typical load–displacement curve extracted from the SENB test on the non-aerated chocolate at 2 mm s−1 speed and compliance curves C and C5% for determination of load at crack initiation, which is pointed with the black arrow,49 (c) a compliance test which was employed to eliminate any effects of indentation into the chocolate and the machine compliance. | ||
2.5. In vivo mastication tests
The two commercial chocolates with rectangular shapes, see Fig. 1h and i, were cut into specimens of 10 mm length L and 14 mm width W (Fig. 1j). The total 2D area from these rectangular geometries was converted into a diameter which corresponds to the same total 2D area, equivalent diameter. The equivalent diameter for this geometry was found to be 14 mm. This size, which corresponds to 1.5 g, was found to be comparable to the ones used by Lucas, Luke50 and within the ranges of the mouthful size based on.51–53 The samples were inserted into plastic thin sealed bags of 0.02 mm thickness to prevent interactions between the chocolate specimen and saliva. These dry mastication conditions were employed in order to reduce the scatter in the data which would obscure the underlying physics of the mastication process. After each mastication step, the sealed bags were collected and inspected in terms of local melting, failure of the plastic bag and any form of interaction between the chocolate sample and the plastic sealed bag. The mastication procedure covered the first two chewing cycles to avoid melting of the chocolate sample, but also to minimise agglomeration phenomena of the fragments which are observed after the first couple of chewing cycles.52 This process was repeated up to two times for both chocolate products.The chocolate sample within the plastic sealed bag was placed directly onto the molar teeth for all mastication tests. A mastication cycle started once the chocolate sample was in contact with the molar teeth and ended once contact between the two opposed molar teeth was achieved. Then the plastic bags were collected and further processed. No specific instructions were given regarding the chewing speed or the chewing force, instead the volunteers were instructed to bite into the samples as they would naturally.
Five volunteers were instructed to chew the commercial chocolate samples naturally for two cycles and the chocolate fragments were further processed by imaging techniques.52 In this study, the in vivo mastication tests were coupled with the instrumental mechanical experiments in order to study the implications of the changes in mechanical behaviour on oral processing and specifically the first bite stage, as a result of micro-aeration. Therefore, these tests were limited to five volunteers to focus only on the difference of fragmentation performance between the two chocolate materials without considering physiological mastication parameters such as chewing speed, jaw kinematics, chewing force and saliva production which may vary significantly from person to person.
After completion of the mastication process, the chewed plastic bags were collected and processed via visual techniques using the open-source software ImageJ [v1.52 National Institutes of Health].40 The full-colour images obtained from the optical camera were fed into ImageJ to remove the background and then calculate the 2D area covered by the fragments. Initially, an automatic contrast tool was employed to enhance the background, make the edges of the fragments distinct, and assist the segmentation process. Before the images are processed through the threshold tool, they had to be binarised into black and white (8-bit format). Only then, became possible to distinguish the background from the area covered by the fragments through the threshold process. The threshold was adjusted manually to produce an accurate representation of the derived photo especially at the edges of the fragments. The surface area covered by the fragments was then converted to an equivalent diameter, which corresponds to the same area to the one computed from the software. Based on these diameters the size distribution was computed and averaged across the five subjects and the two replicates for each subject. Similarly to the process of computing the size distribution of bubbles presented in section 2.1, the conversion of the 2D to the 3D size distribution of the fragments was employed41 assuming that all fragments had a cubic shape, i.e. aspect ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. However, the difference between the corrected and the original distribution found to be less than 1% and therefore the original distribution was considered to be sufficiently accurate. This procedure was repeated for the two chewing cycles and for both the non-aerated and aerated chocolate of 12% porosity.
1. However, the difference between the corrected and the original distribution found to be less than 1% and therefore the original distribution was considered to be sufficiently accurate. This procedure was repeated for the two chewing cycles and for both the non-aerated and aerated chocolate of 12% porosity.
3. Experimental results
3.1. Microscopic investigation
Fig. 3a, b, and c show the microstructure of the cross-sectional fractured surface of the non-aerated sample, and the 15% and 10% aerated chocolate samples respectively, through the scanning electron microscope (SEM). In all types of chocolate, the sugar particles (see dashed arrow in Fig. 3a and c) are distinctly visible as crystals and range from sizes of 10 μm to 40 μm, which is in agreement with values found in the literature reporting average values of 20 μm.25,54,55 However, it is hard to identify the cocoa and milk particles in these SEM images, which is mainly used to illustrate possible changes in the morphology of the chocolate microstructure. Inspection of microstructure through SEM in conjunction with X-ray spectroscopy assists the investigation of the crystallisation type inside the chocolate matrix.56,57 However, no X-ray spectroscopy work has been conducted in the present study.Fig. 3d and e show the microstructure of the non-aerated and aerated chocolate with 15% porosity, respectively, in the form of binary images, which were processed from XRT images. In both images, the whiter regions denote particles with a higher density. Comparing the two images, it is clear that agglomeration of the dense particles/regions are observed at the interface of the gas bubble and the chocolate matrix, as indicated by the red arrows. This phenomenon could be explained either by the migration of hard particles such as sugar and fat crystals to the interface of the gas bubble or the presence of gas bubbles in the chocolate matrix affecting the crystallisation during the manufacturing process. The matrix concentration by the migration of particles has been reported before for oil–water suspensions by ref. 58 and 59. Based on Hagan's study,59 the surfactants found inside latex paints can migrate to the particle's surface in the polymer matrix and develop a distinct third phase. However, no other studies have reported similar phenomena to oil–gas interfaces or any other porous material.
The size distributions of the bubbles along with the representation of the 3D volume of the aerated chocolate from X-ray tomography (XRT) images are shown in Fig. 4. The average bubble size distribution measured from 2D SEM images of five chocolate samples was corrected according to Sahagian, Proussevitch41 and agreed very well with the 3D reconstructed geometry generated from XRT images as shown in Fig. 4a. It needs to be noted that the size distributions of the bubbles from the chocolates of 10% and 15% porosity were found to be similar and within the experimental scatter as shown in Fig. 4a. The generated 3D volume, which was selected for this analysis, is presented in Fig. 4b together with the 3D reconstructed geometry of the gas bubbles, see Fig. 4c. Based on this image, the porosity and the bubble size distribution of the material were evaluated. The results showed a porosity value of 14.4%, which is found to be close to the data provided by NPTC obtained during the manufacturing of the chocolate.
Based on Fig. 4a, the mean bubble size of 38 μm and 45 μm was found from the 2D SEM images and 3D volumes extracted from the XRT images respectively. These values are similar to the other microstructural features found in the chocolates such as the sugar particles, the cocoa solids, and the milk powder25,55,60 who reported particle sizes for these features to lie between 10 μm and 35 μm. However, bigger bubbles of 100 μm or more, which are shown both in Fig. 3b and the graph of Fig. 4a, are believed to be air bubbles that were trapped in the chocolate mixture during the manufacturing process and they are not associated with the micro-aeration method.
3.2. Mechanical tests – uniaxial compression
Fig. 5 shows the averaged measured values of the axial strain versus the transverse strain for all types of chocolates at a constant strain rate of 0.1 s−1 combined with the theoretical values of Poisson's ratio for 0.4, 0.45, and 0.5 (dashed line). Although there is variability between the measurements due to the relatively small strains in the initial linear region of the stress–strain curve observed in all chocolates, Fig. 5 depicts that all chocolate materials can be assumed to be almost incompressible (v = 0.5) which was found to be true for other food materials, such as cheese products, potato, butter, food gels, and dough.61–67 A maximum difference of 5% is observed between the Poisson's ratio measurements of the two types of chocolates, which is within the experimental scatter. However, the average measurements of the Poisson's ratio decrease slightly, by up to 3% for porous chocolate. A similar trend was reported by ref. 68 and 69 for porous ceramics and it was found that the Poisson's ratio shows a weaker dependency on the porosity compared to the other elastic properties. An extensive investigation of the effect of porosity on the Poisson's ratio on closed-cell Aluminium foams has been performed by Kováčik J et al.70 who also reported a similar trend. Similarly, no significant dependence of the Poisson's ratio with porosity was reported by Zerhouni et al.71 on 3D printed plastic materials.The stress–strain plots during uniaxial compression for the non-aerated chocolate and the aerated chocolates with 10% and 15% porosity at strain rates of 0.001 s−1, 0.01 s−1 0.1 s−1 and 1 s−1 are summarised in Fig. 6. All chocolate samples exhibited a small variation, less than 5%, in their mechanical response over the five repeats for all testing rates. Therefore, the error bars are very small and not shown in Fig. 6a, c, and e. Higher stress–strain plots are observed in the case of the non-aerated chocolate for all testing speeds where a maximum 50% difference is observed compared to the aerated chocolates with both porosity levels. A significant dependence of the stress–strain response for all types of chocolates on strain rate is observed. This was accompanied by different fracture behaviours depending on strain rate, as will be discussed in more detail shortly. Specifically, as evidenced in Fig. 6a, c, and e, a significant strain hardening effect was observed in the case of the non-aerated chocolate and this effect was found to decrease with strain rate but also with increasing porosity; in the case of the 15% porosity, an elastic-perfectly-plastic behaviour was shown at lower rates. At higher rates, failure before pronounced macroscopic plasticity was observed for both aerated materials.
In metals and polymers, strain hardening is associated by the movement of the microscopic features, once yielding is reached, which strengthens the material as the plastic deformation is being increased.72 Similarly, for chocolates, an analogous microscopic movement of the chocolate ingredients such as sugar and fat crystals within the continuous fat matrix, potentially strengthens the material during increasing plastic deformation. Based on Fig. 6, these hardening effects are diminishing with porosity implying that the presence of the bubbles seems to interfere with this microscopic movement.
The larger red dots in the stress–strain plots of Fig. 6 denote the points where macroscopic fracture was observed while the red arrows indicate the onset of the shear band formation. This is also confirmed by the images extracted from video recordings during the tests at a rate of 0.1 s−1, as shown in Fig. 6b, d, and f for the non-aerated and the aerated chocolate with 10% and 15% porosity respectively. In all cases, white lines aligned at 45° were observed and the crack is propagating through these paths implying a shear failure mechanism. Based on Fig. 6, these bands are firstly shown after the onset of non-linearity in the σ–ε curve (see Fig. 6a, c and d) and keep forming until macro-cracks initiate.
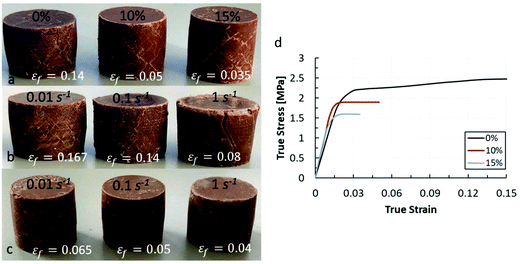
The shear band formation between the different types of chocolates and different strain rates is summarised in Fig. 7. In Fig. 7a, the shear band formation of the non-aerated, and the aerated chocolate with 10% and 15% at 0.1 s−1 under fracture strains of 0.14, 0.05, and 0.035 respectively is shown. Fig. 7b shows the shear band formation of the non-aerated sample for three strain rates of 0.01 s−1 0.1 s−1 and 1 s−1 after it was subjected to fracture strains of 0.167, 0.14, and 0.08 respectively. The shear band formation for the 10% aerated chocolate under different strain rates is shown in Fig. 7c.
Based on Fig. 6a, c, e, and 7a, in cases where the plastic region of σ–ε curve is larger, more shear bands are formed. Specifically, a larger number of shear bands is formed in the non-aerated chocolates compared to the aerated chocolates for the same strain rate, e.g. at 0.1 s−1, as shown in Fig. 7a. Keeping the material the same, a larger number of shear bands is apparent at slower strain rates due to the larger plastic region, Fig. 7b. This was found to be true for all three types of chocolates regardless of porosity (see Fig. 7c, in the case of 10% porosity). The formation of shear bands is followed by initiation of macroscopic cracks at these regions at lower strain rates while at higher rates macroscopic cracks are shown prior the formation of shear bands or at least the formation of many shear bands as opposed to lower rates. The formation of shear bands, as shown in Fig. 6, can act as indication of initiation of material's macroscopic plasticity.
In Fig. 7d, the typical stress–strain behaviour at a constant strain rate of 0.1 s−1 is shown for the non-aerated and the aerated chocolates with 10% and 15% porosity. The graph illustrates a stiffer bulk stress–strain relationship for the aerated chocolates compared to the non-aerated product at a strain rate of 0.1 s−1, which was also observed at all testing speeds. Specifically, an average increase of 38% and 51% was observed between the non-aerated chocolate and the aerated chocolates with 10% and 15% porosity level respectively. This difference was also captured by the computation of the compressive moduli for all chocolate materials from the monotonic compression tests, as summarised in Fig. 8a in the form of a bar chart.
This enhancement in stiffness was unexpected compared to the results found in the literature for porous materials.73–76 Based on these studies, the Young's modulus indicates decreasing trends as a function of porosity. The fact that the elastic modulus was observed to increase with porosity, implies that the chocolate matrix of the porous material may not be identical to the non-aerated chocolate. Based on the XRT images of Fig. 3d and e, it is argued that micro-aeration alters the microstructure of the chocolate matrix as evidenced in the regions close to the bubble's interface, which could potentially be responsible for such differences. In this figure, the white regions indicate features of higher density but unknown composition. These features could be agglomerated solid particles, such as sugar particles, cocoa solids or fat crystals with a different form of crystallisation.
Moreover, material properties such as the macroscopic yield stress and the compressive strength decrease, as expected, in relation to the porosity as shown in Fig. 8b. Specifically, for all testing speeds an average difference of 18% is observed between the yield stress values of the non-aerated chocolate and the aerated chocolate with 10% porosity. This difference increases to 27% when the yield stress of the non-aerated chocolate is compared to the yield stress of the aerated chocolate with 15% porosity. Similar decreasing trends are observed for the compressive strength values.
Fig. 9 summarises the stress–strain plots extracted from the loading–unloading tests. For the non-aerated, Fig. 9a, three strain levels of 0.015, 0.025, 0.045 are shown, whilst for the aerated chocolate with 10% and 15% porosity two strain levels of 0.01, 0.025 (Fig. 9b) and 0.04, 0.025 (Fig. 9c) are shown, respectively. The Young's modulus as computed from the linear unloading part of the curve in each case is summarised in Fig. 9d for all strain levels.
Comparing the slopes of the loading and unloading part of the curve in Fig. 9a, a significant difference is observed. Specifically, when the Young's modulus values from the monotonic tests (see Fig. 8a) are compared to Young's modulus computed from the loading–unloading tests based on the slope of unloading region of the curve (see Fig. 9a), for the non-aerated chocolate a difference up to 350% difference is observed, providing indications of the presence of permanent inelastic effects from the early stages of the compression test. The Young's modulus from the monotonic tests is found to be 100 MPa (see Fig. 8a or dotted bars in Fig. 9d) whilst the slope of the unloading path from loading–unloading tests is approximately 440 MPa as shown in Fig. 9d. These indications were observed for all three maximum applied strains.
This gradient difference between the values of Young's modulus from the loading and unloading paths is less pronounced for the porous chocolates, where maximum differences of 230% and 170% are observed in the cases of 10% and 15% porosity respectively, see Fig. 9b and c. Specifically, the unloading path exhibits a Young's modulus of approximately 380 MPa and 340 MPa for 10% and 15% chocolates, as shown in Fig. 9d. It is evident that viscoelastic effects are present for all chocolates and that, as the porosity increases, the response is closer to viscoplasticity, i.e. the gradient of the unloading path becomes closer to the gradient of the loading path. It seems that these inelastic effects are present from earlier stages of the material's deformation are diminishing with increasing porosity. In addition, based on the modulus values of Fig. 9d, a decreasing trend is observed with porosity, as would be expected.73–76
For all tested chocolate materials, when small elastic strains of 0.015, 0.01 and 0.004 were applied to the 0%, 10% and 15% chocolates respectively (see Fig. 9a–c) and then removed, the loading and unloading paths do not coincide as would be expected for linear elastic materials. Even when time was allowed after completion of the experiments, the tested samples did not return to their original state implying significant permanent deformations (see red stars in Fig. 9a–c). This implies that significant inelastic strains are experienced in these materials, even though the samples were loaded to well within the initial linear region of the stress–strain curve. It seems that the work to deform the material is not totally recoverable even when the applied strain lies within the linear region.
Based on Gonzalez-Gutierrez and Scanlon,63 who studied the mechanical characterisation of fat based materials, this inelastic deformation from the early loading stages of the compression test is caused due to the complex response of the fat crystals during the compression action, where structural plastic rearrangement occurred.63 Therefore, it is suggested that the material's elasticity is determined from the unloading process measuring the degree of the deformation which is recovered.77 Similar findings were reported by other studies which investigated the mechanical properties of bone materials.78,79 Based on these studies, not all energy applied on a system during a mechanical test is recoverable and in materials with high energy dissipation, such as bio-materials, only the unloading portion of the mechanical work is directly associated with the elasticity of the material. Such materials show inelastic effects (micro-crack evolution) from the start of the deformation and it is not clear which part of the deformation is recoverable. Hence, the true Young's modulus of the material should be computed from the unloading part of the stress–strain curve. Furthermore, based on Hellmich and Katti,80 in soft biological materials such as soft tissues, the loading part of the curve is not usually identical to the part of the curve corresponding to unloading. This is attributed to the fact that there is a rearrangement of microscopic features in these materials during loading, altering the microstructure of the material and producing a different stiffness when the material is unloaded. However, in this study, the presence of bubbles in the chocolate suspension seems to be hindering this possible microstructural rearrangement. As evidenced by the XRT images of Fig. 3d and e, it is argued that these denser regions close to the bubble's interface is evidence that this region acts as a barrier to this microstructural re-arrangement.
3.3. Mechanical tests – single edge notched bending (SENB)
Fig. 10a, c, and e show the typical load–deflection response for all three chocolate materials under three different testing speeds of 0.02 mm s−1, 0.2 mm s−1, and 2 mm s−1. The load–deflection data from these tests showed significantly higher scatter amongst the repeats compared to the monotonic and loading–unloading tests. Specifically, a maximum difference of 12% is observed amongst the repeats in the case of the non-aerated chocolate, whilst the repeats for the 10% and 15% chocolate samples showed a variation of 17% and 18% respectively, as shown in Fig. 10a, c, and e. These variations are caused by the fact that the length and sharpness of the notch cannot be controlled sufficiently precisely. In addition, SENB tests are far more sensitive to material heterogeneities, particularly in the vicinity to the crack tip, compared to the uniaxial compression tests presented in the previous section. However, when the fracture properties were computed, a smaller scatter was observed compared to the scatter in the P–d curves.Based on all three curves shown in Fig. 10, the load increases non-linearly, up to a maximum load followed by a smooth drop to zero load, implying complete fracture of the surfaces. This gradual drop of the load also suggests a stable crack growth for all three chocolate materials. The arrows in plots of Fig. 10a, c and e indicate the crack initiation of each chocolate material for each testing speed, which was observed visually from video images recorded during the experiments as shown in Fig. 10b, d, and f. It is also important to note that the separation of the cracked surfaces was not observed at the end of the tests for all chocolate materials and testing speeds. The cracked surfaces remained in contact, implying the presence of an adhesion force that holds the two surfaces together even when the samples returned to the zero-force position.
Different crack propagation patterns were observed between the three types of materials. A straight sharp crack was present in the case of the non-aerated material (see Fig. 10b) whilst a tortuous crack path was observed in the case of the two aerated materials (see Fig. 10d and f). This is probably due to the fact that the cracks are propagating within the imperfections of the material's microstructure; in the case of the porous material, the numerous bubbles dispersed into the fat network act as flaws, creating scattered micro-cracking, which could lead to the observed, more tortuous crack propagation.
The energy release rate Gc of the three chocolate samples was computed based on eqn (5) and summarised in Fig. 11 as a function of chocolate porosity. The energy U is calculated from the area under the load–deflection curve up to the loading point where crack initiation was observed visually from the video images during the SENB tests. A significant rate dependency of the fracture toughness is observed for all chocolate materials, which is consistent with the compression tests.
 | ||
| Fig. 11 (a) Summary of the fracture toughness measurements as a function of the testing speed for 0%, 10% and 15% porosity chocolates, (b) Young's modulus values extracted from eqn (6) for all three chocolate materials in relation to the crosshead speed. | ||
As expected, the Gc values for soft materials such as chocolate, are relatively low and range between 8–12 J m−2, 5.5–10 J m−2 and 4–8 J m−2 for the 0%, 10% and 15% porosity respectively. It seems that the porosity has also noticeable impact on the fracture toughness, enhancing the brittle nature of the material, i.e. the fracture toughness decreases. According to Bucknall and Narkis et al.81,82 who developed an analytical model to predict the fracture toughness of foams as a function of porosity, the pore will not contribute to the total deformation of the material and a crack will propagate through the smallest possible cross-section of the material's matrix.83
The Gc values for the three chocolates are relatively close to other food materials, such as cheese,29 carrot and apple84 and frozen meat.85 Based on Berthaume,86 who performed an extensive review of the fracture mechanics of several food materials, and Lucas et al. and Vincent,84,87 who evaluated material parameters such as the elastic modulus and fracture toughness of different food products, these fracture parameters can be related to textural attributes such as food hardness, chewiness and brittleness.
Combining the fracture toughness and the stress intensity values extracted from the SENB tests into eqn (6), the Young's modulus of the three chocolate materials can be expressed as a function of crosshead speed, as shown in Fig. 11b. Comparing the values of Young's modulus, E, extracted from the monotonic compression tests (see Fig. 8a) and the one extracted from eqn (6), an average difference of 350% is observed. Specifically based on Fig. 11b, average values of 450 MPa, 400 MPa and 350 MPa are calculated for 0%, 10% and 15% porosity respectively. According to ASTM standard D5045-99, possible discrepancies might be observed between the E extracted from compression tests and the modulus taken from eqn (6). However, it is mentioned that no differences higher than 15% should be expected. Comparing the values of the Young's modulus from eqn (6) and the one computed from the loading–unloading tests the maximum differences lie within 5% error in all chocolate materials. This acts as an additional and independent confirmation about the modulus of the chocolates should be measured from the slopes of the unloading part of the curves, as opposed to the slope of the monotonic loading part.
3.4. In vivo mastication tests
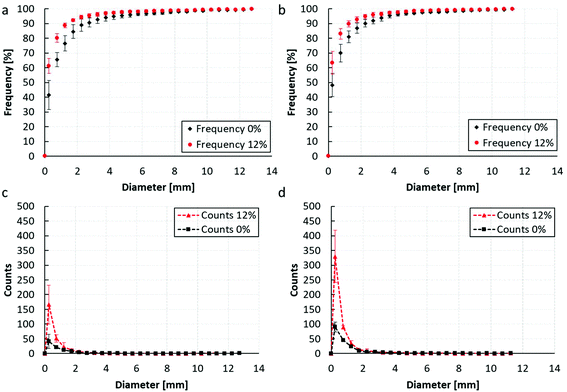
Typical results of the mastication action from one subject for the two types of commercial chocolates with 0% and 12% porosity after the first and the second chewing cycle are shown in Fig. 12a together with their binary images in Fig. 12b. Based on these images, it is clear that the chocolate breaks rapidly into small fragments during the initial stages of the mastication, implying a brittle behaviour, i.e. multiple small fragments generated from bigger ones. The relatively high fragmentation of both chocolate materials was a consequence of the material response observed during the uniaxial compression tests. During these tests, several microcracks are produced when the chocolate deformed within the plastic region. These microcracks are expected to extend and produce new macroscopic cracks and fragments as the deformation by the molar teeth increases.The averaged cumulative equivalent diameter distributions from all five volunteers obtained from the two commercial chocolates are summarised in Fig. 13a for the first chewing cycle and in Fig. 13b for the second chewing cycle. During the first bite over 76% of the non-aerated fragments are smaller than 1.25 mm, compared to the corresponding value of 88% for the aerated fragments. It is important to highlight that amongst all subjects, a clear difference between the fragmentation in the two types of chocolates was observed. As evidenced by the results of Fig. 13, the aerated chocolate breaks into multiple smaller fragments during the first chewing cycle thus exhibiting a higher fragmentation. Specifically, based on Fig. 13c, an average number of 280 and 95 fragments in the first chewing cycle are produced in the case of the aerated and the non-aerated chocolate. These values are increased to 500 and 195 during the second chewing cycle, as shown in Fig. 13d. Based on Fig. 13a and c, the main difference is located at the smaller fragment sizes of approximately 1.5 mm where approximately 250 and 75 fragments are of size 1.5 mm or less in the case of the aerated and non-aerated material respectively.
This difference in fragmentation between the two chocolate products is aligned with the response measured from the mechanical and fracture tests presented in sections 3.2 and 3.3 respectively, where a decrease of the fracture strains and the fracture toughness values was observed with increasing porosity. Based on both in vivo and instrumental tests, aeration enhances the brittle nature of the chocolate material, i.e. lower fracture toughness, leading to higher rates of fragmentation from the first bite onwards. Similar conclusions were reported by ref. 52 where a link between the mechanical properties of two cereal products and the difference in their rate of fragmentation was observed. Based on that study, the fragmentation is also correlated to textural properties such as crispiness and food structure.
4. Constitutive model
4.1. Two-layer viscoplastic model
Based on the experimental results of section 3.2, all three chocolates showed a clear rate-dependency in the plastic region implying viscoplastic behaviour, and also time-dependent effects which were captured by the loading–unloading tests. The two-layer viscoplastic model, employed here, finds wide applicability in materials with significant time and rate-dependent responses which was firstly introduced by ref. 88 and 89. This constitutive model has the advantage to capture all these effects, taking at the same time into account the elastic, plastic and viscous strains experienced during deformation. In the one-dimensional idealisation, this model can be represented as a parallel connection of an elastic-plastic and an elastic-viscous layer as shown in Fig. 14. In the three-dimensional formulation, the two-layer viscoplastic model is combined with the Von Mises yield criterion.90 | ||
| Fig. 14 1D representation of the two-layer viscoplastic model in the form of an mechanical analog consisting of springs, dashpots and sliding elements.92,93 | ||
The elastic-plastic layer defines the time-independent behaviour of the material and is based on the Von Mises yield condition. The elastic-plastic element consists of an elastic component described by an elastic modulus Eep in series with a plastic component represented by a parallel combination of a sliding element to model the yield stress σyo and a spring H′ representing the strain hardening effect in the plastic region which is activated when the yield stress is reached. The elastic-plastic stress data, based on the configuration of Fig. 14, can be computed based on whether the yield point has been exceeded assuming isotropic hardening conditions and it is described by the following equations:
| σep = εEep when εEep ≤ σyo | (7) |
 | (8) |
In contrast, the elastic-viscous layer is represented by a Maxwell element, a linear combination of a spring and a dashpot and describes the time-dependent response of the material. This layer is based on a generalised viscous power law model (generalised Norton power law rule) whilst any viscous or creep model could be implemented. The elastic component of the elastic-viscous layer is represented by the elastic modulus, Eev, connected in series with a viscous component modelled by a dashpot with the following parameters: A, which is a power-law multiplier, n and m are power-law order parameters. These two parts of the elastic-viscous layer is responsible for the time-dependent behaviour of the material which means the rate dependency observed after yielding is due to the action of the elastic-viscous layer. The viscous parameters A, m, and n, are known as the Norton Hoff rate parameters91,92 and must obey the following constraints: A,n > 0 and −1 ≤ m ≤ 0. The elastic-viscous stress can be computed by the given generalised equation, see eqn (9):91–93
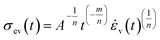 | (9) |
From eqn (9), the following relationship can be obtained:
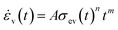 | (10) |
 is the strain rate of the dashpot in the elastic-viscous layer.
is the strain rate of the dashpot in the elastic-viscous layer.
The two-layer viscoplastic model considers the deviatoric stresses through the von Mises equivalent stresses, σeq, from the following relationship:90
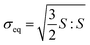 | (11) |
The elastic part of each of the two layers contributes to the ratio, f, which determines the contribution of the elastic viscous modulus, Eev, to the total elastic modulus Einstant describing the instantaneous response, which is the summation of the Eev and Eep:
 | (12) |
The elastic part of the two layers was assumed to be isotropic for all chocolates. Based on the isotropic assumption, the Poisson's ratio of the two layers is the same and equal to the one of the instantaneous elastic response.
Based on the configuration of Fig. 14, the elastic-plastic and elastic-viscous layers can be assumed to be independent and the following equations can be adopted:
| σ(t) = σev(t) + σep | (13) |
| ε(t) = εev(t) = εep | (14) |
Combining eqn (7)–(9) and substituting in eqn (13), the total stress, σ(t), can be derived as:
 | (15) |
 | (16) |
In both eqn (14) and (15), the viscous strain rate of the dashpot element,  , is an unknown, which makes the calibration of the constitutive model challenging. A simplification suggested by Kang et al. and Simulia91,92 is to assume steady-state conditions for the elastic-viscous system, m = 0, which will simplify the computation of the final stress values. The latter simplification is valid for relatively low strain rates and in materials with no or limited time-dependency. However, assuming such steady-state conditions in this study would compromise the accuracy of the results, due to the fact that during the oral process moderate to high strain rates are experienced43,94 and that the chocolate exhibits significant time-dependency effects. However, according to Skamniotis93 who employed the two-layer viscoplastic model to calibrate the same model using experimental data on pet foods, an explicit numerical integration can be used using a relatively small time increment (<0.01 s) to compute the viscous strain rate,
, is an unknown, which makes the calibration of the constitutive model challenging. A simplification suggested by Kang et al. and Simulia91,92 is to assume steady-state conditions for the elastic-viscous system, m = 0, which will simplify the computation of the final stress values. The latter simplification is valid for relatively low strain rates and in materials with no or limited time-dependency. However, assuming such steady-state conditions in this study would compromise the accuracy of the results, due to the fact that during the oral process moderate to high strain rates are experienced43,94 and that the chocolate exhibits significant time-dependency effects. However, according to Skamniotis93 who employed the two-layer viscoplastic model to calibrate the same model using experimental data on pet foods, an explicit numerical integration can be used using a relatively small time increment (<0.01 s) to compute the viscous strain rate,  , of the dashpot element and overcome the need for this simplification (m = 0). The numerical integration scheme is briefly described below.
, of the dashpot element and overcome the need for this simplification (m = 0). The numerical integration scheme is briefly described below.
In order to quantify the viscous strain rate of the dashpot,  , the decomposition of the total strain rate of the elastic-viscous layer,
, the decomposition of the total strain rate of the elastic-viscous layer, 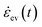 , needs to be employed according to the configuration of Fig. 14, as shown in below:
, needs to be employed according to the configuration of Fig. 14, as shown in below:
 | (17) |
 ,
,  are the total strain rate, the viscous strain rate of the dashpot and elastic strain rate in the spring Eev respectively all in the elastic-viscous layer.
are the total strain rate, the viscous strain rate of the dashpot and elastic strain rate in the spring Eev respectively all in the elastic-viscous layer.
It is worth noting here that according to eqn (14), the total strain of the elastic-viscous layer, εev(t), is equal to the total applied strain, ε(t). Integrating numerically eqn (17) and combining it with eqn (10), the expression below for the total strain, εev,e(t), in the elastic-viscous layer is derived:
| εiev,e(t) − εi−1ev,e(t) = Δε(t) − ΔtAσi−1ev(t)ntm | (18) |
The calibration process starts at t = 0 assuming that the strains are also zero. Based on eqn (18) the strains of the spring in the elastic-viscous layer, εev,e(t), can be computed. In combination with eqn (17) the viscous strain rate of the dashpot, 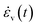 , can be found and consequently the total stress experienced by the system, σ(t), employing eqn (15) or (16) depending on whether yielding has initiated. Alternatively, once the εev,e(t) has been calculated, the stress in the elastic viscous layer can be found (based on the configuration of Fig. 14) as the product of the modulus in the spring Eev and the elastic strain εev,e(t) in the elastic-viscous layer. The total stress is then computed again from eqn (15) or (16).
, can be found and consequently the total stress experienced by the system, σ(t), employing eqn (15) or (16) depending on whether yielding has initiated. Alternatively, once the εev,e(t) has been calculated, the stress in the elastic viscous layer can be found (based on the configuration of Fig. 14) as the product of the modulus in the spring Eev and the elastic strain εev,e(t) in the elastic-viscous layer. The total stress is then computed again from eqn (15) or (16).
4.2. Numerical results
Two scenarios were investigated to calibrate the viscoplastic model, viscoplastic model 1 and viscoplastic model 2. In both cases, the aforementioned methodology and eqn (15) and (16) were implemented on an MS-excel spreadsheet and the MS-excel solver function was employed to calibrate the material constants f, A, n, m, H′ and σyo.In the first scenario, i.e. viscoplastic model 1, the material parameters were calibrated according to the stress–strain data from the monotonic compression tests. An instantaneous modulus (Eev + Eep) of 100 MPa, 120 MPa and 130 MPa was selected for the 0%, 10% and 15% porosity respectively which are the average values of Young's modulus between all rates extracted from the monotonic uniaxial compression tests, as shown in Fig. 8a. The hardening modulus H′ was computed as the gradient defined by two data points corresponding to two stress values. These stress values represent the onset of plastic deformation which is also depicted as the static yield stress σyo,s,92 and the stress σyo,m, which corresponds to the maximum strain observed in the monotonic tests at the rate of 0.001 s−1 where the strain hardening effect was more pronounced. The maximum strain values for the 0%, 10% and 15% chocolate were found to be 0.2, 0.07 and 0.05 respectively, as shown in Fig. 6. The stress values σyo,s and σyo,m were calibrated to match the slope of the experimental curves in the plastic region. In addition, the material parameter m showed only a small sensitivity to the final stress–strain response when a relatively small value was selected (<10−2). Therefore, it was kept constant at 0.01 through all three types of chocolate materials. The material constants of the two-layer viscoplastic model 1 required to fit the experimental data are summarised in Table 1.
| Material | E instant (MPa) | σ yo,s (MPa) | σ yo,m (MPa) | A (MPa−n s−1−m) | n | m | f |
|---|---|---|---|---|---|---|---|
| 0% | 100 | 0.8 | 1.8 | 0.04 | 4 | −0.01 | 0.57 |
| 10% | 120 | 0.6 | 0.8 | 0.04 | 4 | −0.01 | 0.58 |
| 15% | 130 | 0.4 | 0.4 | 0.005 | 6 | −0.01 | 0.6 |
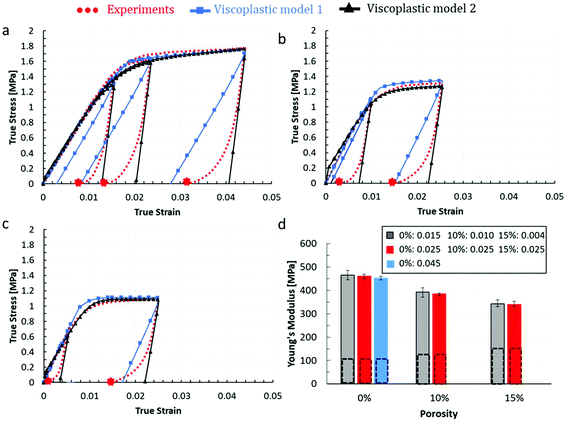
The first model of the calibrated viscoplastic model for all three chocolate materials with material parameters shown in Table 1 is summarised in Fig. 6a, b and c together with the monotonic experimental results. Although a relatively accurate fitting with a discrepancy less than 5% is observed for all strain rates and all chocolate materials, less accurate predictions are observed in the non-aerated chocolate in the initial part of the σ–ε curve where the material behaviour is idealised to a rate-independent elastic response. This assumption seems to be violated for the slowest strain rate of 0.001 s−1. In addition, the model exhibits weaker predictions (see Fig. 9) of the unloading response for all three chocolates due to the significant difference between the slope of the curves in these two regions (loading–unloading) implying inelastic effects since the onset of the deformation.
Based on Luczynski KW et al.,78 the true Young's modulus value should be computed in the unloading part of the curve due to the direct link of this region of the curve to elasticity. In addition, further validation to this statement is achieved when the chocolate materials are deformed in the initial linear region and the unloading response is recorded, as shown in section 3.2. In this case, the unloading response did not coincide with the loading response showing significant inelastic effects. This is true for all strain rates and materials. Based on these observations a second scenario, viscoplastic model 2, was investigated to calibrate the viscoplastic model, the viscoplastic model 2.
In this model, the material constants were calibrated based on the assumption that inelastic effects are dominant since the start of the material deformation. Therefore, a sufficiently small linear elastic region was selected to support this assumption, which corresponded to the arbitrarily chosen yield stress values of 0.05 MPa, 0.15 MPa and 0.1 MPa for the chocolates of 0%, 10% and 15% porosity respectively. The instantaneous modulus (Eev + Eep) in this small elastic region was selected to match the slope of the unloading part of the curve. Specifically, moduli of 450 MPa, 380 MPa and 330 MPa for the chocolates of 0%, 10% and 15% porosity respectively were selected, similar to the values presented in Fig. 9d. The material constants of the viscoplastic model 2 are summarised in Table 2.
| Material | E instant (MPa) | σ yo,s (MPa) | σ yo,m (MPa) | A (MPa−n s−1−m) | n | m | f |
|---|---|---|---|---|---|---|---|
| 0% | 450 | 0.05 | 1 | 0.003 | 5 | −0.2 | 0.2 |
| 10% | 380 | 0.15 | 0.35 | 0.008 | 5 | −0.05 | 0.25 |
| 15% | 330 | 0.1 | 0.1 | 0.0007 | 6 | −0.01 | 0.3 |
The stress-plots generated from the viscoplastic model 2 are shown in Fig. 6 and 7 together with the monotonic compression tests and the loading–unloading tests, respectively. Both stress–strain plots from the monotonic and loading–unloading tests are predicted accurately from the viscoplastic model 2 where an average 11% difference between the viscoplastic model and the experiments is observed for all strain rates and all chocolate materials. Viscoplastic model 2 exhibits more accurate predictions compared to viscoplastic model 1 especially in the regions during unloading, as shown in Fig. 9. No significant discrepancies in the initial linear region were observed between the experimental data and the predictions from the viscoplastic model 2, even though significant higher Einstant was used, due to the assumption of a relatively small elastic region. This can be easily identified from Tables 1 and 2, where a yield stress of 0.8 MPa and 0.05 MPa was selected for the viscoplastic model 1 and 2 respectively. These findings gave further confidence regarding the initial assumption of model 2.
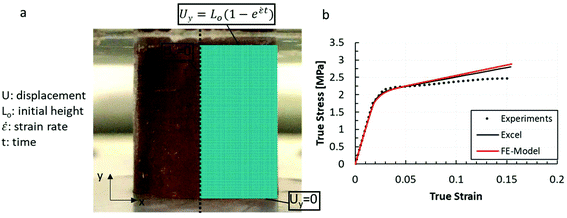
The explicit calibration methodology from MS-excel solver described previously was further confirmed with a Finite Element Modelling (FEM) using the commercially available software Abaqus.92 An axisymmetric model as shown in Fig. 15a with a radius of 10 mm and a height of 20 mm was used and compared with the experimental results. A 4-node axisymmetric linear, reduced integration element was employed for this model and the boundary conditions included restriction of the bottom surface in the direction of the compression and symmetric boundary condition for the vertical axis of symmetry. The top surface was displaced in the y-direction, see Fig. 15a, such as that the strain rate remains constant at 0.1 s−1 throughout the simulation similar to the experiments. A Poisson's ratio of 0.49 was selected in all chocolate materials which was aligned with the experimental values shown in section 3.2. Based on Fig. 15b, both the simulations using the viscoplastic model 1 and the results from the explicit integration are aligned with the experimental response of the non-aerated chocolate at the strain rate of 0.1 s−1. This was found to be true for all speeds, all chocolate materials, and for both viscoplastic models 1 and 2.
The results in this section showed that all chocolate materials investigated in this study exhibit a good agreement between the experimental data from both the monotonic and loading–unloading tests and the two investigated viscoplastic models. According to the authors’ knowledge, no such material model has been used before in the literature for complex multiphase materials such as chocolates. The calibrated parameters in this model can be used in conjunction with a damage criterion to assist the prediction of the progressive breakdown during the first bite and link the outcome with in vivo but also in vitro mastication tests. This will advance the knowledge regarding key aspects of the oral breakdown in a time and cost-effective way without relying solely on costly in vivo studies, which also exhibit significant sensitivities to the human oral physiology.
5. Discussion
The results from the mechanical tests showed that micro-aeration creates weaker structures which lead to a reduction of the overall stresses for the same strains and lower values of fracture toughness compared to the reference, non-aerated chocolate. The material properties and specifically the Young's modulus, the fracture stresses, fracture strains, and the fracture toughness decrease as a function of porosity. It is believed that the presence of the bubbles in the chocolate matrix creates local stress concentrations at the vicinity of the chocolate matrix and the bubble interface, promoting fracture at lower strains, as evident by the results of this work.The reduction of the chocolate stiffness and fracture stresses could potentially influence the hardness perception of the chocolate. It is well established in the literature that the Young's modulus and the fracture stress are directly linked with the hardness perception of food materials.95–98 Food materials which are sensed as hard require higher forces, more chewing cycles and higher chewing rates.53,97 For materials with high rate dependency such as chocolates, the perception of hardness or softness could be enhanced even more. For instance, in the case of the non-aerated chocolate, which showed higher fracture stresses and higher values of stiffness (Young's modulus) compared to the aerated products, higher chewing rates will be used compared to the aerated chocolate. This means the difference in fracture stresses would be even higher because there would be a comparison in stresses between two different strain rates for the two chocolate products. Specifically, in this case, the difference in hardness perception could increase by 38% between the non-aerated chocolate and the 10% aerated chocolate when the fracture stress of the non-aerated chocolate at a strain rate of 1 s−1 (3.04 MPa) is compared to the one of the aerated chocolate at 0.1 s−1 (1.89 MPa).
Based on the results shown in Fig. 6, decreasing trends of the level of strain hardening with increasing porosity were observed and this is also believed to affect the hardness perception. In the case of the non-aerated chocolate, as the material undergoes plastic deformation, higher fracture forces are required to be applied by the teeth due to the strengthening mechanism. This increase of the stresses while the chocolate undergoes plastic deformation will ultimately affect hardness and the associated textural perception. This is less pronounced in the aerated materials, where no or only slight increase of forces are required once plastic deformation is initiated, leading to a potentially softer textural perception.
Moreover, according to Chen,53 hardness perception is not a sensorial attribute only perceived during the first bite, as many researchers have reported in the past. Instead, hardness is believed to be perceived throughout the mastication process and determines the mastication pattern.99 This means when a food is perceived as hard, higher forces, higher chewing rates and higher number of chews are experienced to successfully fragment the food product and as the food product breaks down, lower forces are needed to be applied affecting mastication parameters such as the jaw movements and chewing speed. Hence, a dynamic change of hardness perception with time is observed. This means for materials with higher scores of hardness perception such as the non-aerated chocolate, the duration of the mastication step and consequently oral residence time will be potentially increased compared to the two aerated chocolates. Therefore, the initial perception (hardness) at the beginning of the oral process will determine the sensorial attributes perceived at the subsequent steps of oral processing.
Apart from the clear impact of aeration on the mechanical properties and the fragmentation, which can be directly correlated with the oral processing, aeration affects textural attributes such as crumbliness as well as hardness as discussed above.17 Based on Haedelt J et al.,17 hardness is defined as the bite resistance while crumbliness constitutes the degree of fragmentation. Haedelt J et al.17 reported that aeration is inversely proportional to the chocolate's hardness and proportional to crumbliness. Based on the same study, the degree of fragmentation is inversely proportional to fracture toughness, a statement that is also supported by the findings presented in Fig. 11 and 13. These links between aeration and crumbliness reported by this study17 are confirmed in this work by quantifying the effect of aeration on material properties such as compressive strength and the fracture toughness.
The review by Devezeaux de Lavergne M100et al. discusses the relationship between fracture properties and fracture energy with textural properties such as crumbliness, fracturability, cohesiveness and adhesiveness. Based on this review, low values of fracture stress/strain and fracture toughness can lead to brittle products with high fragmentation. This effect was also evident by the in vivo mastication tests as shown in Fig. 13. In addition, the rate dependency of the fracture toughness could be also correlated to textural attributes such as hardness and smoothness. Carvalho-da-silva et al.45 investigated the textural attributes of two chocolates with similar compositions and melting characteristics with subjects of different chewing preferences. Based on this study, textural attributes such as hardness and smoothness were perceived differently among subjects with different chewing rates. A similar argument was proposed by Meullenet et al.44 where the chewing speed was associated with the food's mechanical properties and finally to texture. Specifically, different chewing speeds can attribute different perception of texture such as food hardness but also promote different degree of fragmentation.
On the other hand, the speed of fragmentation will influence the melting behaviour of the chocolate and consequently the oral residence time, with smaller fragments accelerating the oral processing time.101 This rapid increase of fragmentation between the two types of chocolate, which is suggested from both the lower fracture toughness (see Fig. 11) and the cumulative distributions of Fig. 13, could potentially reduce melting time of the material during oral processing because the surface area of the material increases strongly during mastication, exposing more surfaces to the oral temperature. A reduced melting time could potentially accelerate and affect the thin film formation and its tribological behaviour,102 therefore expediting the oral process affecting the consumer experience and the flavour intensity.101 This hypothesis is also supported by Haedelt J et al.,17 who showed a negative correlation between aeration and melting time. This not only means that the chocolate will melt rapidly but more importantly a higher number of solid particles such as the sugar particles and the cocoa particles are in contact with the oral surfaces leading to an enhancement of flavour intensity (cocoa, milky perception) and possibly taste (sweetness).103
6. Conclusions
This study investigates the mechanics of the first bite of aerated and non-aerated chocolate as governed by the mechanical properties of the materials. Similar to every material and, more importantly, to complex multiphase materials such as chocolates, it is crucial to accurately characterise these properties towards the simulation of the conditions to which the materials will be exposed to in service. In the case of chocolate, this translates to the oral mastication conditions. The effect of the aeration of the chocolate on the mechanical response and the oral process was determined.The mechanical properties and specifically the Young's modulus, macroscopic yield stress and the fracture toughness, are greatly influenced by aeration. An unexpected increase of Young's modulus with increasing porosity is observed when the modulus is measured from the initial linear region of the monotonic uniaxial compression tests. This is attributed to the fact that small microscopic plastic deformation occurs from the early stages of the test due to re-arrangement of the microscopic features inside the chocolate. As evidenced by the XRT images and the stress–strain measurements micro-aeration hinders this microscopic re-arrangement during material's deformation. The Young's modulus for all chocolate materials should be measured from the loading–unloading experiments quoting the slope of the unloading part of curve. The material properties such as the yield stress and the fracture toughness decrease in the presence of porosity, thus enhancing the brittle nature of the material. This effect correlates well with the rate of fragmentation based on the in vivo mastication tests and could potentially be associated with a change in textural attributes such as hardness and crumbliness but also with the melting time and smoothness.100 The latter could be also linked with aroma release.
The two-layer viscoplastic model has been successfully applied to chocolate systems and has been calibrated based on monotonic and loading–unloading compression tests. The model parameters can be used in future simulations of the first bite conditions and can be linked to in vivo and in vitro mastication tests and consequently to texture. This can provide a powerful tool towards the design of novel food products with enhanced and controlled sensorial attributes.
Author contributions
D. Bikos: conception of the idea, investigation, formal analysis, writing the original draft, writing, review, and editing of the revised manuscript. M. N. Charalambides: conception of the idea, writing the original draft, writing, review, and editing of the revised manuscript, project administration, supervision and funding acquisition. G. Samaras, Y. Hardalupas, P. Cann, M. Masen, J. Vieira, C. Hartmann: validation, review and editing the manuscript.Conflicts of interest
The authors would like to declare that they have no competing financial interest or personal relationships personal relationships that could have influenced the work reported in this paper.Acknowledgements
The authors thank the Engineering and Physical Sciences Research Council (EPSRC) for the Ph.D. studentship via the Centre for Doctoral Training – Theory and Simulation of Materials (CDT-TSM) and Nestlé PTC York for funding the project and providing the materials for testing. The authors would like also to acknowledge Brett Clark, the Natural History Museum for performing the X-ray scanning tests and Dr Ruth Brooker for invaluable technical guidance during experiments.References
- E. Gallagher, C. M. O’Brien, A. G. M. Scannell and E. K. Arendt, Evaluation of sugar replacers in short dough biscuit production, J. Food Eng., 2003, 56, 261–263 CrossRef.
- J. Gao, M. A. Brennan, S. L. Mason and C. S. Brennan, Effect of sugar replacement with stevianna and inulin on the texture and predictive glycaemic response of muffins, Int. J. Food Sci. Technol., 2016, 51, 1979–1987 CrossRef CAS.
- C. M. O’Brien, A. Mueller, A. G. M. Scannell and E. K. Arendt, Evaluation of the effects of fat replacers on the quality of wheat bread, J. Food Eng., 2003, 56, 265–267 CrossRef.
- D. J. McMahon, M. C. Alleyne, R. L. Fife and C. J. Oberg, Use of Fat Replacers in Low Fat Mozzarella Cheese, J. Dairy Sci., 1996, 79, 1911–1921 CrossRef CAS.
- O. Sandoval-Castilla, C. Lobato-Calleros, E. Aguirre-Mandujano and E. J. Vernon-Carter, Microstructure and texture of yogurt as influenced by fat replacers, Int. Dairy J., 2004, 14, 151–159 CrossRef CAS.
- D. A. Omana, G. Plastow and M. Betti, The use of β-glucan as a partial salt replacer in high pressure processed chicken breast meat, Food Chem., 2011, 129, 768–776 CrossRef CAS PubMed.
- A. Tamm, T. Bolumar, B. Bajovic and S. Toepfl, Salt (NaCl) reduction in cooked ham by a combined approach of high pressure treatment and the salt replacer KCl, Innovative Food Sci. Emerging Technol., 2016, 36, 294–302 CrossRef CAS.
- S. M. Melnikov, S. D. Stoyanov, E. M. R. Kovacs, L. Arnaudov, P. De Groot and E. A. H. Schuring, et al., Sustained hunger suppression from stable liquid food foams, Obesity, 2014, 22(10), 2131–2136 CrossRef CAS PubMed.
- G. M. Campbell and E. Mougeot, Creation and characterisation of aerated food products, Trends Food Sci. Technol., 1999, 10(9), 283–296 CrossRef CAS.
- J. C. Arboleya, M. García-Quiroga, D. Lasa, O. Oliva and A. Luis-Aduriz, Effect of highly aerated food on expected satiety, Int. J. Gastron Food Sci., 2014, 2(1), 14–21, DOI:10.1016/j.ijgfs.2013.12.002.
- J. Kokini and G. Van Aken, Discussion session on food emulsions and foams, Food Hydrocolloids, 2006, 20(4), 438–445 CrossRef CAS.
- C. K. Lau and E. Dickinson, Instability and structural change in an aerated system containing egg albumen and invert sugar, Food Hydrocolloids, 2005, 19, 111–121 CrossRef CAS.
- T. Huppertz, Foaming properties of milk: A review of the influence of composition and processing, Int. J. Dairy Technol., 2010, 63, 477–488 CrossRef.
- T. M. Ho, T. H. A. Le, A. Yan, B. R. Bhandari and N. Bansal, Foaming properties and foam structure of milk during storage, Food Res. Int., 2019, 116, 379–386 CrossRef CAS PubMed.
- L. Trinh, T. Lowe, G. M. Campbell, P. J. Withers and P. J. Martin, Bread dough aeration dynamics during pressure step-change mixing: Studies by X-ray tomography, dough density and population balance modelling, Chem. Eng. Sci., 2013, 101, 470–477 CrossRef CAS.
- J. Haedelt, L. D. Pyle, S. T. Beckett and K. Niranjan, Vaccum-induced Bubble Formation in Liquid-tempered chocolate, Food Eng. Phys. Prop., 2005, 70(2), 160–164 Search PubMed.
- J. Haedelt, S. T. Beckett and K. Niranjan, Bubble-included chocolate: Relating structure with sensory response, J. Food Sci., 2007, 72(3), E138–E142 CrossRef CAS PubMed.
- M. Minor, M. H. Vingerhoeds, F. D. Zoet, R. De Wijk and G. A. Van Aken, Preparation and sensory perception of fat-free foams - Effect of matrix properties and level of aeration, Int. J. Food Sci. Technol., 2009, 44(4), 735–747 CrossRef CAS.
- P. Frisullo, F. Licciardello, G. Muratore and M. A. Del Nobile, Microstructural characterization of multiphase chocolate using X-Ray microtomography, J. Food Sci., 2010, 75(7), E469–E476 CrossRef CAS PubMed.
- E. Jakubczyk and K. Niranjan, Transient development of whipped cream properties, J. Food Eng., 2006, 77(1), 79–83 CrossRef.
- E. V. Gonçalves and S. C. da Silva Lannes, Reologia de chocolate, Cienc. Tecnol. Aliment., 2010, 30(4), 845–851 CrossRef.
- V. Glicerina, F. Balestra, M. Dalla and S. Romani, Rheological, textural and calorimetric modifications of dark chocolate during process, J. Food Eng., 2013, 119(1), 173–179, DOI:10.1016/j.jfoodeng.2013.05.012.
- T. A. M. Rovers, G. Sala, L. Evander and M. B. Meinders, Potential Of Microbubbles As Fat Replacer : Effect On Rheological, Tribological And Sensorial Properties Of Model Food Systems, J. Texture Stud., 2016, 47, 220–230 CrossRef.
- S. T. Beckett, L. Info, M. Records and R. S. C. Read, Science of Chocolate, in The Science of Chocolate, 2008, 103–124 p Search PubMed.
- E. O. Afoakwa, A. Paterson, M. Fowler and J. Vieira, Microstructure and mechanical properties related to particle size distribution and composition in dark chocolate, Int. J. Food Sci. Technol., 2009, 44(1), 111–119 CrossRef CAS.
- L. Chaunier, G. Della Valle and D. Lourdin, Relationships between texture, mechanical properties and structure of cornflakes, Food Res. Int., 2007, 40(4), 493–503 CrossRef.
- B. Le Révérend, F. Saucy, M. Moser and C. Loret, Adaptation of mastication mechanics and eating behaviour to small differences in food texture, Physiol. Behav., 2016, 165, 136–145, DOI:10.1016/j.physbeh.2016.07.010.
- S. M. Goh, M. N. Charalambides and J. G. Williams, On the mechanics of wire cutting of cheese, Eng. Fract. Mech., 2005, 72(6 SPEC. ISS.), 931–946 CrossRef.
- M. N. Charalambides, J. G. Williams and S. Chakrabarti, A study of the influence of ageing on the mechanical properties of Cheddar cheese, J. Mater. Sci., 1995, 30, 3959–3967 CrossRef CAS.
- I. K. Mohammed, M. N. Charalambides, J. G. Williams and J. Rasburn, Modelling deformation and fracture in confectionery wafers, Procedia Food Sci., 2011, 1, 499–504 CrossRef http://dx.doi.org/10.1016/j.profoo.2011.09.076%0Ahttp://linkinghub.elsevier.com/retrieve/pii/S2211601X11000770 .
- B. J. Diak, Strength by chocolate, Int. J. Eng. Educ., 2006, 22(5), 925–936 Search PubMed.
- L. Severa, Deformation and fracture properties of dark chocolate, Acta Univ. Agric. Silvic. Mendelianae Brun., 2008, 56(2), 115–121 CrossRef.
- L. B. Parsons and R. Goodall, Testing the fracture behaviour of chocolate, Phys. Educ., 2011, 46(1), 50–56 CrossRef.
- L. Svanberg, L. Ahrné, N. Lorén and E. Windhab, A method to assess changes in mechanical properties of chocolate confectionery systems subjected to moisture and fat migration during storage, J. Texture Stud., 2012, 43(2), 106–114 CrossRef.
- N. Baldino, D. Gabriele and M. Migliori, The influence of formulation and cooling rate on the rheological properties of chocolate, Eur. Food Res. Technol., 2010, 821–828 CrossRef CAS.
- C. G. Skamniotis, M. Elliott and M. N. Charalambides, On modeling the large strain fracture behaviour of soft viscous foods, Phys. Fluids, 2017, 29(12) DOI:10.1063/1.4993754.
- M. N. Charalambides, S. M. Goh, L. Wanigasooriya, J. G. Williams and W. Xiao, Effect of friction on uniaxial compression of bread dough, J. Mater. Sci., 2005, 40(13), 3375–3381 CrossRef CAS.
- S. M. Goh, M. N. Charalambides and J. G. Williams, Large strain time dependent behavior of cheese, J. Rheol., 2003, 47(3), 701–716 CrossRef CAS . Available from: http://sor.scitation.org/doi/10.1122/1.1562153.
- International Confectionery Association, Viscosity of Cocoa and Chocolate products, Analytical Methods 46, Bruxelles, Belgium, 2000. Available from: http://www.caobisco.com/page.asp?p=220 Search PubMed.
- W. Rasband, ImageJ, U S Natl Institutes Heal Bethesda, Maryland, USA, 2017; http:////imagej.nih.gov/ij/ Search PubMed.
- D. L. Sahagian and A. A. Proussevitch, 3D particle size distributions from 2D observations: Stereology for natural applications, J. Volcanol. Geotherm. Res., 1998, 84(3–4), 173–196 CrossRef CAS.
- FEI, Avizo User's Guide, Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB), Germany, 2015 Search PubMed.
- A. Sánchez-Ayala, A. Farias-Neto, N. H. Campanha and R. C. M. Rodrigues Garcia, Relationship between chewing rate and masticatory performance, Cranio, 2013, 31(2), 118–122 CrossRef PubMed.
- J. F. Meullenet, M. L. Finney and M. Gaud, Measurement of biting velocities, and predetermined and individual crosshead speed instrumental imitative tests for predicting cheese hardness, J. Texture Stud., 2002, 33(1), 45–58 CrossRef.
- A. M. Carvalho-da-silva, I. Van Damme, B. Wolf and J. Hort, Characterisation of chocolate eating behaviour, Physiol. Behav., 2011, 104(5), 929–933, DOI:10.1016/j.physbeh.2011.06.001.
- S. Panda, J. Chen and O. Benjamin, Development of model mouth for food oral processing studies: Present challenges and scopes, Innovative Food Sci. Emerging Technol., 2020, 66, 102524 CrossRef.
- P. Morell, A. Tárrega, E. A. Foegeding and S. Fiszman, Impact of composition and texture of protein-added yogurts on oral activity, Food Funct., 2018, 9(10), 5443–5454 RSC.
- E. L. Keijbets, J. Chen, E. Dickinson and J. Vieira, Surface energy investigation of chocolate adhesion to solid mould materials, J. Food Eng., 2009, 92, 217–225 CrossRef.
- ASTM, Standard Test Methods for Plane-Strain Fracture Toughness and Strain Energy Release Rate of Plastic Materials, ASTM, 2014. Available from: file:///C:/Users/Matt/Documents/University/FourthYear/FractureandFailure/D5045.19517.pdf Search PubMed.
- P. W. Lucas and D. A. Luke, Methods for analysing the breakdown of food in human mastication, Arch. Oral Biol., 1983, 28(9), 813–819 CrossRef CAS.
- P. W. Lucas and D. A. Luke, Optimum mouthful for food comminution in human mastication, Arch. Oral Biol., 1984, 29(3), 205–210 CrossRef CAS.
- C. Yven, S. Guessasma, L. Chaunier, G. Della Valle and C. Salles, The role of mechanical properties of brittle airy foods on the masticatory performance, J. Food Eng., 2010, 101(1), 85–91, DOI:10.1016/j.jfoodeng.2010.06.012.
- J. Chen, Food oral processing-A review, Food Hydrocolloids, 2009, 23(1), 1–25 CrossRef CAS.
- V. Glicerina, F. Balestra, M. Dalla Rosa and S. Romani, Microstructural and rheological characteristics of dark, milk and white chocolate: A comparative study, J. Food Eng., 2016, 169, 165–171 CrossRef.
- S. K. Reinke, F. Wilde, S. Kozhar, F. Beckmann, J. Vieira and S. Heinrich, et al., Synchrotron X-Ray microtomography reveals interior microstructure of multicomponent food materials such as chocolate, J. Food Eng., 2016, 174, 37–46 CrossRef.
- B. J. James and B. G. Smith, Surface structure and composition of fresh and bloomed chocolate analysed using X-ray photoelectron spectroscopy, cryo-scanning electron microscopy and environmental scanning electron microscopy, LWT–Food Sci. Technol., 2009, 42, 929–937 CrossRef CAS.
- T. S. Skelhon, P. K. A. Olsson, A. R. Morgan and S. A. F. Bon, High internal phase agar hydrogel dispersions in cocoa butter and chocolate as a route towards reducing fat content, Food Funct., 2013, 4(9), 1314–1321 RSC.
- E. W. S. Hagan, The Viscoelastic Properties of Latex Artist Paints, Imperial College London, 2009 Search PubMed.
- E. W. S. Hagan, M. N. Charalambides, C. T. Young, T. J. S. Learner and S. Hackney, Tensile properties of latex paint films with TiO2 pigment, Mech. Time-Depend. Mater., 2009, 13(2), 149–161 CrossRef CAS.
- E. O. Afoakwa, A. Paterson, M. Fowler and J. Vieira, Characterization of melting properties in dark chocolates from varying particle size distribution and composition using differential scanning calorimetry, Food Res. Int., 2008, 41(7), 751–757 CrossRef CAS.
- J. R. Hammerle and W. F. McCLURE, The Determination of Poisson'S Ratio By Compression Tests of Cylindrical Specimens, J. Texture Stud., 1971, 2(1), 31–49 CrossRef CAS PubMed.
- G. E. Timbers, L. M. Staley and E. Watson, Some Mechanical And Rheological Properties Of The Netted Gem Potato, Can. Agric. Eng., 1966, 15–18 Search PubMed.
- J. Gonzalez-Gutierrez and M. G. Scanlon, Rheology and Mechanical Properties of Fats, in Structure-Function Analysis of Edible Fats, 2012, 119–168 p Search PubMed.
- M. A. P. Mohammed, E. Tarleton, M. N. Charalambides and J. G. Williams, Mechanical characterization and micromechanical modeling of bread dough, J. Rheol., 2013, 57(1), 249–272 CrossRef CAS.
- A. Anand, Texture-Related Mechanical Properties of Foods, University of Manitoba, 2001 Search PubMed.
- H. Luyten, The rheological and fracture properties of Gouda cheese, 1988 Search PubMed.
- C. G. Skamniotis, C. H. Edwards, S. Bakalis, G. Frost and M. N. Charalambides, Eulerian-Lagrangian finite element modelling of food flow-fracture in the stomach to engineer digestion, Innovative Food Sci. Emerging Technol., 2020, 102510 CrossRef CAS.
- A. P. Roberts and E. J. Garboczi, Elastic properties of model porous ceramics, J. Am. Ceram. Soc., 2000, 83, 3041–3048 CrossRef CAS.
- H. N. Yoshimura, A. L. Molisani, N. E. Narita, P. F. Cesar and H. Goldenstein, Porosity dependence of elastic constants in aluminum nitride ceramics, Mater. Res., 2007, 10, 127–133 CrossRef CAS.
- J. Kováčik, L. Marsavina and E. Linul, Poisson’s ratio of closed-cell aluminium foams, Materials, 2018, 11(10), 1904 CrossRef PubMed.
- O. Zerhouni, M. G. Tarantino and K. Danas, Numerically-aided 3D printed random isotropic porous materials approaching the Hashin-Shtrikman bounds, Composites, Part B, 2019, 156, 344–354 CrossRef CAS.
- E. P. Degarmo, J. T. Black and R. A. Kohser, Materials and Processes in Manufacturing, 9th edn, 2003, vol. 32. Available from: https://books.google.co.uk/books/about/Materials_and_processes_in_manufacturing.html?id=depTAAAAMAAJ&pgis=1 Search PubMed.
- J. C. Wang, Young's modulus of porous materials - Part 1 Theoretical derivation of modulus-porosity correlation, J. Mater. Sci., 1984, 19(3), 801–808 CrossRef CAS.
- J. Kováčik, Correlation between Young’s modulus and porosity in porous materials, J. Mater. Sci. Lett., 1999, 18, 1007–1010 CrossRef.
- H. Nakajima, Fabrication, properties and application of porous metals with directional pores, Prog. Mater. Sci., 2007, 52(7), 1091–1173 CrossRef CAS.
- M. I. El Ghezal, Y. Maalej and I. Doghri, Micromechanical models for porous and cellular materials in linear elasticity and viscoelasticity, Comput. Mater. Sci., 2013, 70(December), 51–70 CrossRef.
- S. M. Goh and M. G. Scanlon, Indentation of lipid-based particle gels: An experimental, theoretical and numerical study, Acta Mater., 2007, 55(11), 3857–3866 CrossRef CAS.
- K. W. Luczynski, A. Steiger-Thirsfeld, J. Bernardi, J. Eberhardsteiner and C. Hellmich, Extracellular bone matrix exhibits hardening elastoplasticity and more than double cortical strength: Evidence from homogeneous compression of non-tapered single micron-sized pillars welded to a rigid substrate, J. Mech. Behav. Biomed. Mater., 2015, 52, 51–62 CrossRef PubMed.
- S. Zhao, M. Arnold, R. L. Abel, J. P. Cobb, S. Ma and U. Hansen, et al., Standardizing Compression Testing for Measuring the Stiffness of Human Bone, Bone Jt. Res., 2018, 7(8), 524–538 CrossRef CAS PubMed.
- C. Hellmich and D. Katti, Multiscale mechanics of biological, bioinspired, and biomedical materials, MRS Bull., 2015, 40(4), 309–313 CrossRef.
- C. B. Bucknall, Fracture And Failure Of Multiphase Polymers And Polymer Composites, Adv. Polym. Sci., 1978, 27, 121–148 CrossRef CAS.
- M. Narkis, I. Bercovich, L. Nicolais and C. Migliaresi, Cell cracking in open cell rigid polymeric foams, Polymer, 1978, 19(9), 1103–1105 CrossRef CAS.
- O. A. Stapountzi, Alumina Trihydrate Filled, Imperial College London, 2008 Search PubMed.
- J. F. V. Vincent, Application of fracture mechanics to the texture of food, Eng. Failure Anal., 2004, 11(5), 695–704 CrossRef.
- B. J. Dobraszczy, A. G. Atkins, G. Jeronimidis and P. P. Purslow, Fracture toughness of frozen meat, Meat Sci., 1987, 21(1), 25–49 CrossRef CAS PubMed.
- M. A. Berthaume, Food mechanical properties and dietary ecology, Am. J. Phys. Anthropol., 2016, 159, 79–104 CrossRef PubMed.
- P. W. Lucas, J. F. Prinz, K. R. Agrawal and I. C. Bruce, Food Physics and Oral Physiology, Food Qual. Prefer., 2002, 13, 203–213 CrossRef.
- J. Kichenin, Comportement thermomécanique du polyéthylène. Application aux structures gazières, École polytechnique, Palaiseau, Essonne, 1992 Search PubMed.
- J. Kichenin, K. Dang Van and K. Boytard, Finite-element simulation of a new two-dissipative mechanisms model for bulk medium-density polyethylene, J. Mater. Sci., 1996, 31(6), 1653–1661 CrossRef CAS.
- S. Berezvai and A. Kossa, Performance of a parallel viscoelastic-viscoplastic model for a microcellular thermoplastic foam on wide temperature range, Polym. Test., 2020, 84, 106395, DOI:10.1016/j.polymertesting.2020.106395.
- J. J. Kang, A. A. Becker and W. Sun, Determination of elastic and viscoplastic material properties obtained from indentation tests using a combined finite element analysis and optimization approach, Proc. Inst. Mech. Eng., Part L, 2015, 229(3), 175–188 Search PubMed.
- Simulia, Abaqus 6.11 Theory Manual, DS SIMULIA Corp., Providence, RI, USA, 2017 Search PubMed.
- C. G. Skamniotis, Characterising and modelling fracture in functional pet foods, 2017 Search PubMed.
- A. M. Carvalho-da-silva, I. Van Damme, W. Taylor and B. Wolf, Oral processing of two milk chocolate samples, R. Soc. Chem., 2013, 4, 461–469 CAS.
- E. H. J. Kim, V. K. Corrigan, A. J. Wilson, I. R. Waters, D. I. Hedderley and M. P. Morgenstern, Fundamental fracture properties associated with sensory hardness of brittle solid foods, J. Texture Stud., 2012, 43(1), 49–62 CrossRef.
- J. F. V. Vincent, D. E. J. Saunders and P. Beyts, The use of critical stress intensity factor to quantify “hardness” and “crunchiness” objectively, J. Texture Stud., 2002, 33(2), 149–159 CrossRef.
- T. Witt and J. R. Stokes, Physics of food structure breakdown and bolus formation during oral processing of hard and soft solids, Curr. Opin. Food Sci., 2015, 3, 110–117, DOI:10.1016/j.cofs.2015.06.011.
- Y. Pascua, H. Koç and E. A. Foegeding, Food structure: Roles of mechanical properties and oral processing in determining sensory texture of soft materials, Curr. Opin. Colloid Interface Sci., 2013, 18(4), 324–333, DOI:10.1016/j.cocis.2013.03.009.
- H. Koç, C. J. Vinyard, G. K. Essick and E. A. Foegeding, Food Oral Processing: Conversion of Food Structure to Textural Perception, Annu. Rev. Food Sci. Technol., 2013, 4(1), 237–266 CrossRef PubMed . Available from: http://www.annualreviews.org/doi/10.1146/annurev-food-030212-182637.
- M. Devezeaux de Lavergne, F. Van de Velde and M. Stieger, Bolus matters: the influence of food oral breakdown on dynamic texture perception, Food Funct., 2017, 8(2), 464–480 RSC.
- G. R. Ziegler, G. Mongia and R. Hollender, The role of particle size distribution of suspended solids in defining the sensory properties of milk chocolate, Int. J. Food Prop., 2001, 4(2), 353–370 CrossRef.
- G. Samaras, D. Bikos, J. Vieira, C. Hartmann, M. Charalambides, Y. Hardalupas, M. Masen and P. Cann, et al., Measurement of molten chocolate friction under simulated tongue-palate kinematics: Effect of cocoa solids content and aeration, Curr. Res. Food Sci., 2020, 3, 304–313 CrossRef PubMed.
- M. A. Peyron and A. Woda, An update about artificial mastication, Curr. Opin. Food Sci., 2016, 9, 21–28, DOI:10.1016/j.cofs.2016.03.006.
| This journal is © The Royal Society of Chemistry 2021 |