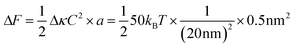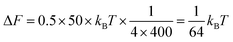Open Access Article
Open Access ArticleCommon principles of surface deformation in biology
Aurélien
Roux
 *ab
*ab
aDepartment of Biochemistry, University of Geneva, CH-1211 Geneva, Switzerland. E-mail: aurelien.roux@unige.ch
bNational Center of Competence in Research Chemical Biology, University of Geneva, CH-1211 Geneva, Switzerland
First published on 16th July 2021
Abstract
Living organisms, whether they are cells or multicellular organisms, are separated from their environment by an interface. For example, cells are delimited by lipid bilayers while embryos or individuals are delimited by epithelia, ectoderms or epiderms. These biological interfaces, while being different in nature and composition, and at very different scales, share common properties: they are surfaces, their thickness being very small compared to their size. They are materials of chemical composition or cell type that is unique and different from the core of the material they envelop. They are visco-elastic sheets, meaning that components can flow in the plane of the surface. The shape of cells and of embryos is inherently dictated by the shape of their envelope, and because these interfaces have common properties, we explore in this commentary article the different mechanisms that remodel these different biological surfaces, and their common principles.
Introduction
All living units are separated from their environment by a surface, which is unique in that it materializes as a sheet of visco-elastic material. For example, cells are delimited by lipid membranes; and multi-cellular organisms, at least the vast majority of them, by a cell monolayer that protects them from the environment – epiderms, ectoderms, epithelia, or endothelia are common examples. While being at very different scales, and very different in their nature, these envelopes share common properties and have functions essential to life: first, they are diffusion barriers, with selective permeability – while plasma membranes are impermeable to most water solutes because of their hydrophobic core, they are still permeable to partially hydrophobic molecules, and transmembrane transporters and channels control molecules through them. Cell monolayers that protect multicellular organisms are known to be strong osmotic barriers, even reducing water efflux to avoid air-living organisms from drying out. Second, they are visco-elastic surfaces, which means that they can deform by changing their area and curvature elastically over short time scales, and viscously over longer times. This is essential because all living units have the property of changing their shape and size – cells grow and divide during cycles, and during early development many organs are formed by deforming the ectoderm of the embryo. Also, during the life of multicellular organisms, growth of new parts in plants, or muscle-driven movements in animals, will require their envelope to smoothly adapt to the new shape. Yet, this shape is given by the visco-elastic surface, which conserves the living units integrity.The common visco-elastic nature of living surfaces makes us wonder, do these surfaces share common mechanisms of shape acquisition? Of course, while comparing very different biological structures in order to find common properties, one should not forget about their differences: lipid membranes are composed of amphiphilic molecules which spontaneously assemble into bilayers of three to five nanometers; while cell monolayers are usually composed of polarized cells spreading from one side to the other over tens of microns. Thus, while lipid bilayers are basically non-active materials, cell monolayers are intrinsically active – they can proliferate, generate internal forces, and composing units (cells) can actively change their shape with time. On the other hand, lipids in bilayers form non-polarized structures, at least if the compositions of the two leaflets are the same, they are subject to Brownian motion, and cannot multiply themselves. Some of these intrinsic properties can however be changed in the cellular context, where the activity of proteins can create asymmetry in the leaflet composition, or change the number of lipids, or their chemical nature. Another crucial difference between lipid bilayers and cell monolayers is the time scale at which they acquire their shape: while lipid bilayers can change shape in seconds, or even faster, cell monolayers require at least several hours if not days for the same transformation. Also, the characteristic visco-elastic time of lipid bilayers and cell monolayers – the threshold time of deformation application below which the surface responds elastically, and above which it responds viscously – is very different, a few tens of milliseconds for lipid membranes compared to a few tens of minutes for cell monolayers.
In this review, while comparing examples taken from the literature, I discuss principles by which living surfaces deform. While detailed mechanisms are clearly different, their mechanistic principles are usually similar.
A – Curvature of surfaces is coupled to the asymmetric shapes of the basic components
Because living surfaces have a given thickness, the spontaneous (at equilibrium, or minimal energy) shape of these surfaces is usually coupled to the shapes of their components. Numerous examples in the literature couple the curvature of lipid membranes to lipid shapes, and cell monolayer shapes to cell shapes. However, the specific fluid properties of the surface can make this coupling weaker.1 Lipid vs. cell shapes and spontaneous curvature of lipid membranes vs. epithelia
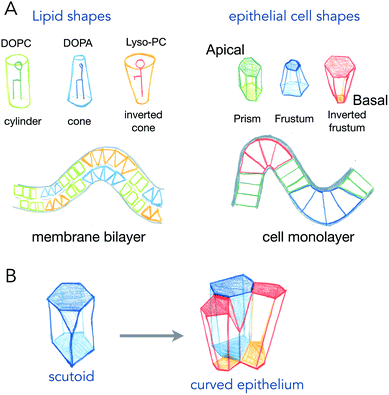
Phospholipids, the main components of lipid membranes have two chemically different parts: the hydrophilic headgroup and the hydrophobic acyl chains. The steric hindrance of the head, and the length and number of acyls can modify the overall shape of the lipids from being cylindrical to being conical or an inverted shape (see Fig. 1). These shapes, of course, from very simple geometrical arguments, are more adapted to different curvatures: cylinders like phosphatidyl-choline will adapt better to flat bilayers, while inverted cone shapes like phosphatidic acid will adapt better to concave leaflets, and conical lysolipids to convex leaflets. In the 70s, Israelachvili et al. detailed how the spontaneous curvature of lipid self-assembled structures is coupled to the shape of the lipids.2 The spontaneous curvature of lipids calculated from their chemical structure and molecular properties is a rather predictive parameter of the formation of micelles, inverted micelles or bilayers.While the situation in mixed lipid composition bilayers with low curvature may be quite different (see discussion point 1.2 in the article2), the same reasoning, coupling cell shape to curvature of the epithelium for example, has been made for cell monolayers (Fig. 1). The most common example is the one of intestinal villi, where cells in crypts have a smaller apical area, and cells at the tip of villis have a larger apical area. The exact area difference between apical and basal sides of the cells not only depends on the curvature, but also on the thickness of the cells. This is best represented in the recent example where epithelial cells were grown on wavy substrates, and where the thickness of the cells dramatically changed from concave to convex structures.3 As it will be discussed further in active process curving cell monolayers (see Section 2), these observations support that several shape transitions with varying apical-basal area difference and cell thickness, are required to generate the proper shape of organs.4
An interesting case is the one of anisotropic curvatures, such as in cylinders: in one direction (along the cylinder axis) the curvature is null, while being constant and high in the perpendicular axis. Many epithelial or endothelial structures have such anisotropic curvatures, at least in branched conductive networks such as lungs or secretory organs. In these situations, the easiest way to accommodate cell shape with curvature is to create anisotropic cell shapes, which are more conical in the direction of highest curvature in the plane of the cell monolayer. But recently, several reports show that the anisotropy may arise in the number of neighbors for cells (see Fig. 1B). As cells will extend more on the basal side in the direction of curvature, and much less in the apical side, the number of neighbors may change to accommodate the anisotropic curvature. These cell shapes, equivalent to a T1 transition in the normal direction, are called scutoids, and have been shown to represent a fairly high percentage of cell shapes in tubular organ structures.5 However, they do not represent a minimal energy shape, and their dynamics (whether they are stable shapes or transitory shapes between two or more stable shapes) is not known.
Interestingly, lipids spontaneously form different types of micelles, with isotropic shapes (spheres) or anisotropic shapes (tubules). At least, the anisotropy of curvature should also be linked in this case to an anisotropy in the specific spontaneous curvature of lipids. In this case a certain degree of order, or persistent orientation of the lipids should allow to propagate the anisotropy over large distances. But the link between anisotropy in the chemical structure, order and the final curvature anisotropy in the lipid assembly, is not well characterized to my knowledge.
2 Brownian motion and diffusion counteract lipid shape coupling to the curvature
In self-assembled structures of lipids such as micelles, the curvature of the structure is very high, and close to the specific spontaneous curvature of the lipid that composed it. However, in cellular membranes, the overall structure is a bilayer with curvature more than ten times the size of the lipids (1.5 nm), and the composition mixed hundreds of different types of lipids. In this context, whether the shape of lipids inserted in the bilayer is a strong determinant of the spontaneous curvature of the membrane is still debated. Moreover, the bilayer nature of the lipid membrane means the contribution of spontaneous curvature of the lipids in one leaflet is compensated by the ones in the opposite leaflet, as long as the two leaflets have the same composition. A counter effect could be linked to lipid diffusion, as lipids favorable to convex curvature may diffuse and accumulate in the convex leaflet, while ones preferring concave curvature may accumulate in the opposite leaflet, in the same place. Overall, the curvature of the membrane would be zero, but the local concentration of curvature sensitive lipids may enhance curvature changes locally.However, most probably, Brownian motion and diffusion strongly interfere with these effects. A simple calculation (see Box 1) shows that the energy gain of localizing a single lipid molecule to an area that matches its curvature better, is much lower than kT, meaning that this curvature sorting of single lipid molecules is overruled by Brownian motion.
Box 1: Estimate of energy gain for curvature sorting of lipidsOne can estimate the gain of energy ΔF upon curvature-dependent lipid sorting, in the extreme case of a difference of bending rigidity Δκ between the soft and stiff phase of 50kBT, for a membrane curvature C of 1/20 nm and an area per lipid a ≈ 0.5 nm2:Due to the very small size of lipid molecules, the gain of energy per lipid is then much smaller than kBT, which means that at room temperature, entropic motion counteracts lipid sorting by curvature. Increasing a through lipid nanoclustering will increase the energy gain, thereby making lipid nanoclusters more sensitive to curvature then single lipids. Adapted from ref. 1. |
As a matter of fact, curvature sorting of lipids strongly depends on the capacity of lipids to form more viscous domains, and to be close to a phase separation.6,7
All these counteracting processes that reduce the coupling of lipid shapes to curvature in lipid bilayers are, by nature, absent in cell monolayers. Thus, the coupling between cell shape and curvature is much stronger in a cell monolayer, and physiological curvatures of cell monolayers are close to the thickness of cells in the tissue (microns to tens of microns). Moreover, and contrary to lipids, cells can actively change their shape, dynamically changing the shapes of cell monolayers. But, as we will discuss in the following, proteins involved in lipid membrane remodeling have evolved to use similar principles for deforming membranes than cells use to induce curvature of cell monolayers.
B – Dynamic change of surface shape by shape changes in the basic components
While the shape and curvature of surfaces may correlate with the shape of their constituents, active changes of a constituent’s shape can drive deformation of living surfaces. In the following, I try to find similar principles to examples of mechanisms found at different scales and on different biological systems.1 Apical constriction and head group compaction
The most well understood principle of cell monolayer deformation is called apical constriction. In a polarized epithelium, in which cells have a contractile acto-myosin ring on the apical side, activation of contractility in a group of cells results in their apical area reduction, forcing the cells to adopt a conical shape bending the epithelium (Fig. 2). This mechanism was first proposed a century ago, by pioneer studies of gastrulation of sea anemones.8,9 A large pool of data has confirmed this mechanism as essential for triggering epithelium folding in many morphogenetic events.4 It is also one of the most beautiful examples in which single cell mechanics and geometries can directly explain the shape of simple tissues, like the sea anemone embryo. There are, however, several theoretical descriptions that can generate the same shapes as the ones experimentally observed.10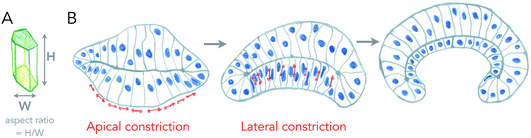 | ||
| Fig. 2 Changes of cell aspect ratio enhance invagination. (A) Definition of cell aspect ratio. (B) Sequence of apical constriction followed by cell aspect ratio change (lateral constriction) helps a tissue to reverse its curvature (adapted from ref. 4). | ||
Interestingly, parallels can be drawn between apical constriction, and some lipid membrane remodeling mechanisms driven by proteins. The most obvious one is the mechanism by which the Shiga toxin forms its own membrane carrier to enter cells by toxin-induced endocytosis.11,12 In this mechanism, the pentameric beta domain of the Shiga toxin binds 15 Gb3 molecules, a ganglioside, by their headgroups. The binding induces a reduction of the specific lipid headgroup volume, condensing the 15 lipids on the side to which the toxin binds. This condensation leads to membrane curvature, by transforming cylindrical lipids into inverted cone-shaped lipids, allowing the formation of membrane buds that accumulate the toxin. Not surprisingly this mechanism was found in other lipid binding molecules, such as lectins,13 and requires a high affinity for the lipids, and high valency in order to cluster enough lipids together to compensate for entropic dissipation.
Importantly, in lipid membranes, the reverse mechanism of apical constriction, which consists of area expansion to induce curvature in the opposite direction, is a very common mechanism used by membrane traffic proteins. For example, amphipathic helices found in coat proteins can insert in between lipid headgroups to generate a cone-shaped insertion.14 When clustered together by polymerization of the coat, the membrane will deform locally. It is important to notice that in this mechanism, there are two effects causing curvature that are at play. The first one is the wedge-like effect, pushing the headgroups away from each other, and forcing conical insertions locally. The second one is to create an area difference between the 2 leaflets, by increasing the number of constituents in one of the two leaflets.15 While the first effect is local and can be very strong (high curvature induced for a very low number of proteins binding to the membrane), the second effect is global, and requires a substantial increase of the number of lipids/proteins in one leaflet to obtain low curvatures.16 Thus, the wedge-like effect is often considered to be the dominant effect in curvature induced by a protein inserting into the membrane.
All the mechanisms that cause curvature by generating an area difference between the two sides of the surface strongly depend on the thickness of the surface, as the thicker they are, the less area difference is required for creating the same curvature. Thus, mechanisms that can change the thickness of the surface, locally or globally, may help curvature acquisition.
2 Mechanisms of surface thickness changes associated with curvature
Cell monolayers display a large variety of thickness, usually linked to the cell aspect ratio of specific cell lines (ratio between height and width of cells, see Fig. 2A). Cell shortening during apical constriction further promotes invagination.4 Importantly, changes in lateral tension of cells may also cause invagination, by locally changing the aspect ratio of cells, and if cells remain attached to a flat surface.17 Thus, cells found in monolayers have multiple ways to change their shape locally or globally in order to induce a specific curvature of the entire tissue, all of which are based on localizing acto-myosin contractility in cells, that can redistribute in cells in order to change tissue shape with time. One of the best examples of this is the growth of the fish eye cup, which requires reorganization of the actin cytoskeleton in the neuroepithelium, to change the aspect ratio of cells while they proliferate, in order to keep the overall general proportions of the eye.18Similar principles of thickness change in lipid bilayers seem a priori excluded. Furthermore, as discussed above, since typical radii of curvatures in lipid bilayers are usually more than ten times larger than their thickness, changing the thickness may not strongly affect curvatures induced by other means. However, two processes may strongly interfere with membrane thickness and susceptibility of the membrane to curving. First, phase transition, as lipids in the liquid-disordered state are less packed than in ordered phases, and thus membrane phase transitions to more ordered states increase their thickness, but also their bending rigidity as rigidity increases with order. Another important aspect is the lack of saturation in lipid acyl chains. Besides strongly affecting the order, reducing melting temperatures dramatically, it also makes the membrane more deformable, as lipid acyl chains with poly-unsaturations can form conformations that change thickness necessary for bending.19 All the dynamic processes of curvature generation discussed above result from internal and local stresses within the surface. But can external, or global stresses shape living surfaces?
C – Global and external forces involved in surface shaping
Surfaces can be deformed by applying global or local forces externally to the surface. In the following I review known mechanisms of surface deformation by external forces.1 Global: buckling of surface through growth under confinement
Growth can generate internal stresses, in particular when growth is confined. For surfaces, growth means area expansion, which can lead to folding when surfaces grow in confined volumes. In this situation, the surface is buckling, forming local folds from global compressive stresses. This is a very general and simple, force driven mechanism of deformation, which relies on the elastic properties of surfaces.Buckling of surfaces was proposed as a folding mechanism of cell monolayers a century ago, by the same pioneers that discovered apical constriction.8,20 Indeed, many of the shapes observed in developing cell monolayers are reproduced by theory and simulations of buckling surfaces.10 However, it turns out to be difficult to show that biological shapes are indeed generated by buckling, as other mechanisms such as apical constriction can generate similar shapes, and measuring global forces within epithelia remains technically challenging. My team recently used an artificial system (see Fig. 3A), in which epithelial cells growing in elastic hollow spheres formed a cell monolayer that spontaneously buckled while growing. Combining theory and global pressure measurements (obtained from the elastic deformations of the spherical shell), we could show that the shapes obtained were generated from buckling.21
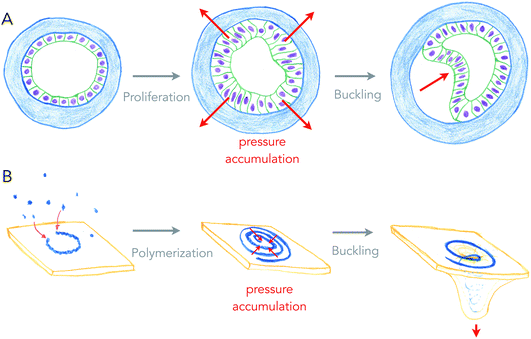 | ||
| Fig. 3 Buckling of an epithelium and of a lipid membrane by growth-generated pressure accumulation. (A) Proliferation of epithelial cells under spherical confinement (elastic, hollow shell) generates pressure within the epithelium that causes inward buckling (from ref. 21). (B) Elongation of a curved ESCRT-III filament into a spiral accumulates elastic pressure, causing its buckling into a tubular shape, deforming the membrane beneath (from ref. 27). | ||
Is buckling a mechanism by which lipid membranes can be deformed? Theoretically, rapid changes of membrane area by large fluxes of lipids can induce curvature instabilities.22 Another buckling instability was proposed for the deformation of lipid membranes by growing circular cytoskeletal filaments,23 in order to explain the beautiful membrane protrusions emerging from the center of filamentous spirals formed by ESCRT-III assemblies in cells.24,25 ESCRT-III polymers are thought to be the most evolutionary ancient membrane remodeling machinery, as they are the only ones present in archaea, and the only ones to work on virtually all cell membrane organelles.26 In the ESCRT-III buckling mechanism (see Fig. 3B), filaments of ESCRT-III protein initially grow with a preferred radius of curvature of about 35 nm on the surface of the membrane.27 When about to reach the closed ring state, it can continue growing further into a flat spiral if the tips do not anneal. While growing as a spiral, the ESCRT-III filament accumulates elastic energy because filament turns inside the spiral are at a lower radius than their preferred one, and filament turns outside have a larger radius than their preferred one. In this situation, filament elastic stress can be released by buckling, transforming a flat spiral into a helical filament, in which most turns are at their preferred radius of curvature. Buckling of the ESCRT-III spiral will be in competition with the deformation of the membrane, but conditions in which buckling instability can deform the membrane constitute a fairly large area of the parameter space.23 But most mechanical properties of the ESCRT-III filaments are compatible with this mechanism, even though the trigger for buckling may come from the addition of secondary subunits.28–30
So what is common to buckling an epithelium and buckling of the membrane by the ECSRT-III? First, growth is the source of compressive stresses in both cases: proliferation of cells in one case, addition of subunits to the polymer in the other case. Second, the confinement permits accumulation of the stress, and is provided by the elastic shell or the structure of the spirals, making a sort of auto-confinement in the ESCRT-III case. And finally, the shape of protrusion, only dictated by the mechanics of surfaces, are very similar. In physiological cases of cell tissue morphogenesis, confinement may be generated by fast growing domains of cells within slowly growing tissues.31
2 Local: local forces applied by external elements
Surface deformations can be generated by local forces applied by external elements. This situation is often seen in membrane traffic, in which protein coats, made of polymerized multi-protein complexes that have a given shape, force the membrane to adopt this shape. This mechanism is called scaffolding, and the best known examples are spherical coats in the form of clathrin and COPs.32 But many other coats, from dynamin-like proteins to BAR domain proteins tubulate membranes by making helical cylindrical polymers.Scaffolding is rather unknown to epithelium folding during morphogenesis. One putative example though, is the formation of the eye cup, the precursor of the eye lens, which is pinched by a growing and folding neuroepithelium that will become the retina. Whether forces generated by the growing retina participate in the folding of the eye cup, which finally separates from the ectoderm, is not known, but the current model proposes that it is simultaneous folding through polarized constriction of the two epithelia (neuroepithelium and ectoderm), coordinated by morphogen gradients, that causes the formation of the eye cup.33 Thus, while the structure of the eye cup is seemingly similar to a spherical bud generated by membrane coats, the mechanism may be totally different.
Conclusion
New mechanisms of membrane remodeling or of epithelium morphogenesis are still being discovered, or proposed. Recent theoretical work has proposed membrane remodeling through nematic order of chiral molecules that can create gradients of stresses within the plane of the lipid membrane.34 Recently, we showed that gradients of active stresses organized by topological defects in cell monolayers can concentrate stresses to form cell protrusions.35 The future will say if among these two possibilities, common principles can be found.Conflicts of interest
There are no conflicts to declare.References
-
B. Sorre, PhD thesis, Université Paris-Diderot, 2010
.
- J. N. Israelachvili, S. Marcelja and R. G. Horn, Q. Rev. Biophys., 1980, 13, 121–200 CrossRef CAS PubMed
.
- M. Luciano, S.-L. Xue, W. H. De Vos, L. R. Morata, M. Surin, F. Lafont, E. Hannezo and S. Gabriele, Nat. Phys., 2021 DOI:10.1038/s41567-021-01374-1
.
- T. Lecuit, P. F. Lenne and E. Munro, Annu. Rev. Cell Dev. Biol., 2011, 27, 157–184 CrossRef CAS PubMed
.
- P. Gomez-Galvez, P. Vicente-Munuera, A. Tagua, C. Forja, A. M. Castro, M. Letran, A. Valencia-Exposito, C. Grima, M. Bermudez-Gallardo, O. Serrano-Perez-Higueras, F. Cavodeassi, S. Sotillos, M. D. Martin-Bermudo, A. Marquez, J. Buceta and L. M. Escudero, Nat. Commun., 2018, 9, 2960 CrossRef PubMed
.
- A. Roux, D. Cuvelier, P. Nassoy, J. Prost, P. Bassereau and B. Goud, EMBO J., 2005, 24, 1537–1545 CrossRef CAS PubMed
.
- B. Sorre, A. Callan-Jones, J. B. Manneville, P. Nassoy, J. F. Joanny, J. Prost, B. Goud and P. Bassereau, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5622–5626 CrossRef CAS PubMed
.
- L. Rhumbler, Arch. Entwicklungsmech. Org., 1902, 14, 401–476 CrossRef
.
- N. Rashevsky, Bull. Math. Biophys., 1940, 2, 169–175 CrossRef
.
- M. Rauzi, A. Hocevar Brezavscek, P. Ziherl and M. Leptin, Biophys. J., 2013, 105, 3–10 CrossRef CAS PubMed
.
- W. Romer, L. Berland, V. Chambon, K. Gaus, B. Windschiegl, D. Tenza, M. R. Aly, V. Fraisier, J. C. Florent, D. Perrais, C. Lamaze, G. Raposo, C. Steinem, P. Sens, P. Bassereau and L. Johannes, Nature, 2007, 450, 670–675 CrossRef PubMed
.
- W. Romer, L. L. Pontani, B. Sorre, C. Rentero, L. Berland, V. Chambon, C. Lamaze, P. Bassereau, C. Sykes, K. Gaus and L. Johannes, Cell, 2010, 140, 540–553 CrossRef CAS PubMed
.
- R. Lakshminarayan, C. Wunder, U. Becken, M. T. Howes, C. Benzing, S. Arumugam, S. Sales, N. Ariotti, V. Chambon, C. Lamaze, D. Loew, A. Shevchenko, K. Gaus, R. G. Parton and L. Johannes, Nat. Cell Biol., 2014, 16, 595–606 CrossRef CAS PubMed
.
- B. Antonny, Curr. Opin. Cell Biol., 2006, 18, 386–394 CrossRef CAS PubMed
.
- M. P. Sheetz and S. J. Singer, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 4457–4461 CrossRef CAS PubMed
.
- M. M. Kozlov, F. Campelo, N. Liska, L. V. Chernomordik, S. J. Marrink and H. T. McMahon, Curr. Opin. Cell Biol., 2014, 29, 53–60 CrossRef CAS PubMed
.
- C. Bielmeier, S. Alt, V. Weichselberger, M. La Fortezza, H. Harz, F. Julicher, G. Salbreux and A. K. Classen, Curr. Biol., 2016, 26, 563–574 CrossRef CAS PubMed
.
- M. Matejcic, G. Salbreux and C. Norden, PLoS Biol., 2018, 16, e2006018 CrossRef PubMed
.
- B. Antonny, S. Vanni, H. Shindou and T. Ferreira, Trends Cell Biol., 2015, 25, 427–436 CrossRef CAS PubMed
.
- N. Rashevsky, Bull. Math. Biophys., 1940, 2, 109–121 CrossRef
.
- A. Trushko, I. Di Meglio, A. Merzouki, C. Blanch-Mercader, S. Abuhattum, J. Guck, K. Alessandri, P. Nassoy, K. Kruse, B. Chopard and A. Roux, Dev. Cell, 2020, 54, 655–668 CrossRef CAS PubMed
.
- J. Solon, J. Pécréaux, P. Girard, M. Fauré, J. Prost and P. Bassereau, Phys. Rev. Lett., 2006, 97, 1–4 CrossRef PubMed
.
- M. Lenz, D. J. Crow and J. F. Joanny, Phys. Rev. Lett., 2009, 103, 038101 CrossRef PubMed
.
- P. I. Hanson, R. Roth, Y. Lin and J. E. Heuser, J. Cell Biol., 2008, 180, 389–402 CrossRef CAS PubMed
.
- A. G. Cashikar, S. Shim, R. Roth, M. R. Maldazys, J. E. Heuser and P. I. Hanson, eLife, 2014, 3, e02184 CrossRef PubMed
.
- M. Vietri, M. Radulovic and H. Stenmark, Nat. Rev. Mol. Cell Biol., 2020, 21, 25–42 CrossRef CAS PubMed
.
- N. Chiaruttini, L. Redondo-Morata, A. Colom, F. Humbert, M. Lenz, S. Scheuring and A. Roux, Cell, 2015, 163, 866–879 CrossRef CAS PubMed
.
- A. Bertin, N. de Franceschi, E. de la Mora, S. Maity, M. Alqabandi, N. Miguet, A. di Cicco, W. H. Roos, S. Mangenot, W. Weissenhorn and P. Bassereau, Nat. Commun., 2020, 11, 2663 CrossRef CAS PubMed
.
- J. Moser von Filseck, L. Barberi, N. Talledge, I. E. Johnson, A. Frost, M. Lenz and A. Roux, Nat. Commun., 2020, 11, 1516 CrossRef CAS PubMed
.
- A. K. Pfitzner, V. Mercier, X. Jiang, J. Moser von Filseck, B. Baum, A. Saric and A. Roux, Cell, 2020, 182, 1140–1155 CrossRef CAS PubMed
.
- M. Tozluoglu, M. Duda, N. J. Kirkland, R. Barrientos, J. J. Burden, J. J. Munoz and Y. Mao, Dev. Cell, 2019, 51, 299–312 CrossRef CAS PubMed
.
- T. Kirchhausen, Nat. Rev. Mol. Cell Biol., 2000, 1, 187–198 CrossRef CAS PubMed
.
- S. Fuhrmann, Curr. Top. Dev. Biol., 2010, 93, 61–84 Search PubMed
.
- R. C. Sarasij and M. Rao, Phys. Rev. Lett., 2002, 88, 088101 CrossRef PubMed
.
- P. Guillamat, C. Blanch-Mercader, K. Kruse and A. Roux, Integer topological defects organize stresses driving tissue morphogenesis, Nat. Mater., 2021 Search PubMed
, in press.
| This journal is © The Royal Society of Chemistry 2021 |