Time-resolved pump–probe spectroscopy with spectral domain ghost imaging

Abstract

An atomic-level picture of molecular and bulk processes, such as chemical bonding and charge transfer, necessitates an understanding of the dynamical evolution of these systems. On the ultrafast timescales associated with nuclear and electronic motion, the temporal behaviour of a system is often interrogated in a ‘pump–probe’ scheme. Here, an initial ‘pump’ pulse triggers dynamics through photoexcitation, and after a carefully controlled delay a ‘probe’ pulse initiates projection of the instantaneous state of the evolving system onto an informative measurable quantity, such as electron binding energy. In this paper, we apply spectral ghost imaging to a pump–probe time-resolved experiment at an X-ray free-electron laser (XFEL) facility, where the observable is spectral absorption in the X-ray regime. By exploiting the correlation present in the shot-to-shot fluctuations in the incoming X-ray pulses and measured electron kinetic energies, we show that spectral ghost imaging can be applied to time-resolved pump–probe measurements. In the experiment presented, interpretation of the measurement is simplified because spectral ghost imaging separates the overlapping contributions to the photoelectron spectrum from the pump and probe pulse.

---

1 Introduction

Chemical changes can take place on timescales as fast as femtoseconds (10⁻¹⁵ s), and the motion of the electrons which may drive these changes, for example in the case of electronic photoexcitation, is faster still, with valence electronic states typically evolving over tens to hundreds of attoseconds (10⁻¹⁸ s). These timescales far exceed the temporal resolution of the fastest cameras, time-resolving sensors, and electrical circuits. However, modern laser technology enables the routine production of isolated light pulses on the femtosecond¹ and attosecond² timescales, providing the requisite tools to probe molecular change on its natural timescale. Time-resolved measurement of the dynamical evolution of a system can be obtained in a so-called ‘pump–probe’ scheme. Here, two ultrafast laser pulses are created and sent into the sample under interrogation. The first pump pulse photoexcites the system and initiates the dynamical process to be probed. The second probe pulse is sent into the sample after a controlled delay, τ, later. The probe pulse captures a quasi-instantaneous snapshot of the dynamical evolution of the system, by projecting onto a physically measurable quantity such as fluorescence, nuclear position (e.g. via a diffraction pattern) or electron binding energy.^3,4 It is possible with current technology to control the delay with attosecond precision by changing the path lengths taken by the pulses. By scanning the delay between the pump and probe pulses, the temporal evolution of the system in response to the probe pulse is mapped out.

The implementation of these experiments can be very challenging. Pump–probe measurements require overlapping two ultrafast laser pulses in space and time, and achieving sufficient selectivity in both pump and probe steps to provide access to the dynamics of interest. Because the number of photoexcitation mechanisms available to the system at both the pump and probe interaction can be very large, the observable of interest is often obscured by contamination arising from competing processes. For example, in a photoelectron detection scheme, the spectrum can often be congested by photoelectrons produced by e.g. direct ionization by the pump pulse or photoionization of molecules which did not interact with the probe pulse.

The sudden photoionisation of molecules is a frontier problem in photo-physics and photo-chemistry as it lies at the heart of critical phenomena such as radiation damage in biomolecules and charge migration,^5–8 and the implications of the latter process for charge transfer. Moreover, quantitative measurements of the electronic state dynamics, and the coupled electronic-nuclear state evolution, are vital to test advanced quantum chemistry theoretical methods, e.g. semiclassical (i.e. with classical nuclear dynamics)^9,10 and fully quantum approaches.¹¹ This is especially true for the case where the cationic state lies in the inner valence energy region and where breakdown of the molecular orbital picture occurs,¹² and so advanced theoretical methods for electron dynamics that accurately account for electron–electron correlation, such as algebraic diagramatic construction (ADC),¹³ are vital.

In this work, we perform a pump–probe measurement of suddenly photoionised isopropanol using two X-ray pulses generated by an X-ray free-electron laser (XFEL). The pump pulse suddenly ionizes the system, producing a superposition of cationic states which undergoes rapid charge motion. The probe pulse interrogates the electronic structure of the non-stationary cationic superposition by measuring the transient X-ray absorption spectrum of the sample. We present an analysis of the experimental measurement using spectral domain ghost imaging,^14,15 extending the technique to time-resolved measurements. We demonstrate the general utility of such an approach in time-resolved pump–probe measurements by separating the overlapping spectral features generated by the pump and probe pulses in the recorded photoelectron spectrum. We calculate the sample response resolved in incoming photon energy, electron kinetic energy, and time delay. Our analysis scheme identifies a resonant transient signal in the X-ray absorption spectrum of pumped isopropanol, paving the way for time-resolved pump–probe measurements to exploit the improved spectral resolution afforded by spectral ghost imaging.

For cationic states in the inner valence region, electronic correlation results in strong configuration interaction between ϕ_i (one electron hole) and ϕ^a_ij (two electron holes, one excited bound electron) configurations, leading to what is often termed the breakdown of the molecular orbital picture of ionization.¹⁶ In other words, the states produced are no longer well characterized by a particular 1-hole configuration in the ionized orbital. We have identified from our ADC(2) calculations¹⁷ that the state populated by the pump step can show a break-down of the molecular orbital picture and undergo frustrated Coster–Kronig dynamics. We have also performed calculations on some outer valence states in the isopropanol molecule that can be well described by the molecular orbital picture. We treat the photoionization dynamics in isopropanol within the sudden approximation¹⁸ using an ab initio theoretical method (ADC(2)x)¹³ that sufficiently captures the electron correlation physics. In our measurements, the transient absorption approach suggested by Cooper¹⁹ probes the time-dependent hole survival probability in each case.

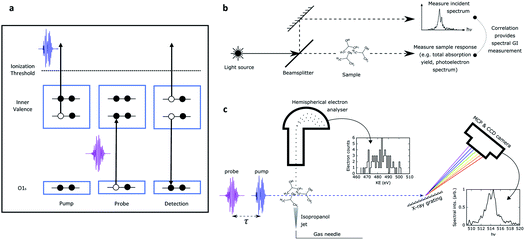
A schematic of the experiment is shown in Fig. 1, panel (a). A non-resonant short pump pulse (∼ 5 fs duration), tuned below the oxygen K-edge, produces a non-stationary superposition of cationic states through photoionisation from the valence region of the molecule. The ultrafast motion of the cationic states is probed by transient absorption. A probe pulse, delayed with respect to the pump pulse, is tuned to be resonant between the oxygen 1s orbital and a particular inner or outer valence hole state. Interaction with the probe pulse thus creates a 1s core vacancy at the oxygen site through a dipole allowed interaction promoting the core electron to the inner valence hole. The probability to promote the electron from the oxygen 1s orbital to the hole is sensitive to the overlap of the hole with the 1s orbital, thus providing a site-specific probe of local hole density. The resulting Auger electron emission from the decay of the core excited cation is the signal used for detecting the time dependent valence hole state survival probability. In our experiment we used a probe pulse photon energy that spanned the range from 513 to 520 eV, and so targeted the hole states 6a, 7a and 8a. These hole states display a range of behaviours spanning from significant molecular orbital picture breakdown (6a) to a metastable Koopmans-like state (8a).

Fig. 1 (a) Experimental methodology for probing hole dynamics in isopropanol. A pump pulse at 502 eV ionizes the molecule, generating inner valence hole (IVH) states. The time delayed probe resonantly interacts with these states via O 1s–IVH transitions, filling the photoexcited hole. This is followed by Auger decay of the core excited cation releasing high energy electrons. (b) General schematic for spectral domain ghost imaging. The incoming source is split into two arms on a shot-to-shot basis. One arm (‘pixellated’ measurement) provides a reference measurement of the incoming spectrum. The second arm (‘bucket’ measurement) passes through the sample, and the sample response (such as total photoproduct yield or photoelectron spectrum) is measured. The correlation in the shot-to-shot fluctuations of these two measurements provides the spectral response of the system. (c) Implementation of spectral domain ghost imaging in our experiment. The SASE X-ray pulse passes through a dilute gaseous sample of isopropanol. The ‘bucket measurement’ is the photoelectron spectrum, measured by a hemispherical analyser. The ‘pixellated measurement’ is performed by a downstream X-ray spectrometer. Photon depletion through the sample is negligible so the downstream spectral measurement is a faithful measurement of the incoming photon spectrum.

The measurement presented was performed at the Linac Coherent Light Source (LCLS) X-ray free-electron laser (XFEL) facility. The XFEL was operated in the so called “fresh-slice” mode,^20,21 producing two X-ray pulses of ∼5 fs duration, controllable delay, and with slightly offset (∼10 eV separation) photon energy. Like all self-amplified spontaneous emission (SASE) modes of XFEL operation, these pulses show considerable shot-to-shot variation in parameters, especially in the photon spectrum and pulse energies of both the pump and probe pulses. This greatly complicates the determination of the desired time-dependent signal. In a recently submitted manuscript¹⁷ we employ extensive binning of the data to enable artefact-free comparison of pump–probe spectra measured at different time delays. This revealed a very fast decay of the 6a state driven by a frustrated Coster–Kronig process²² (few femtosecond lifetime, consistent with our calculations), and a somewhat slower decay (∼10 fs lifetime) for the 7a state that is in the region near the onset of the breakdown of the molecular orbital picture. The down-selection inherent in the binning procedure, however, leads to relatively poor statistics even from a data set comprising millions of shots. The down-selection on the data also precludes us from understanding the dependence of the measured signal on key parameters. For instance, we are unable to access the dependence on the pump pulse energy, which may reveal saturation effects and the role of other channels, as the reduction in the available data leads to statistics that appear too poor. Moreover, the spectral resolution of the measurement was compromised by the source. Although the single-shot X-ray spectrum was recorded and used to determine the spectral dependence of the pump–probe signal, the achievable spectral resolution was limited by the fundamental bandwidth of the source.

Here we present an alternative approach to the analysis of this dataset set which utilises a novel correlation-based method. The technique is an implementation of spectral domain ghost imaging, which has been termed ‘spooktroscopy’. This is the first application of this method to analyse time-dependent data and offers the possibility for additional insights that go beyond the conventional binning analysis. In general, spooktroscopy offers improved spectral resolution in X-ray absorption¹⁴ and X-ray photoelectron spectroscopy²³ measurements. As well as correcting for the loss in resolution due to natural spectral jitter inherent to SASE operation, spooktroscopy has been shown to provide spectral resolution below the bandwidth of the incoming source. This is particularly important for measurements in the attosecond regime, where the bandwidth required to support sub-femtosecond pulses surpasses the required resolution for a meaningful spectral measurement. The technique is also ‘normalisation-free’; the dependence on the signal of the spectral intensity of the probe is naturally accounted for by the correlation method, meaning it is insensitive to fluctuations or drift in the spectral intensity of the probe.

2 Methods

2.1 Experimental setup

Soft X-ray pump and probe pulses were generated using the fresh-slide mode of LCLS.²⁰ A magnetic chicane is used to control the pump–probe delay between −15 to +25 fs. Using an electron beam energy of 3.96 GeV we could produce two pulses, one (the pump) around 502 eV, the other (the probe) at around the target resonances, between 514 eV and 519 eV. We targeted ionization of the 6a, 7a and 8a molecular orbitals and probed the hole formed by photoionization using a probe tuned resonantly to the transition from the 1a orbital located on the oxygen atom to the 6a, 7a or 8a orbitals which have transition energies near 514 eV, 516 eV and 519 eV, respectively (see ref. 1). The interaction with the probe leaves the molecule in a core-excited configuration (1a⁻¹) that will undergo rapid Auger decay producing high energy electrons. The yield of Auger electrons gives a precise measurement of the total X-ray absorption.²⁴ This must be detected on a strong background of photoemission which includes the various photoelectron channels.

Both pulses were focused to a spot size of ∼2 μm diameter using a pair of Kirkpatrick–Baez mirrors. The isopropanol sample was prepared at 298 K and introduced into the focus of the X-rays with a 50 μm diameter gas needle with careful monitoring of the constancy of the partial pressure through the experiment. The emitted photo- and Auger electrons were measured using a hemispherical electron analyzer (Scienta) with an energy resolution of ∼0.1 eV over the range of electron energies 470–510 eV (the region of interest). The incident X-ray spectrum of the pump and probe pulses were recorded for every shot using a downstream X-ray spectrometer. The spectrometer was an adapted version of the instrument described in ref. 25 with a 1200 l mm⁻¹ grating operated in the Rowland geometry imaging a mechanical slit onto a microchannel plate coupled to a phosphor screen.

The general principle of spectral domain ghost imaging is illustrated in Fig. 1, panel (b). For each laser shot, the incoming source is split into two arms: one provides a reference spectral measurement, and the other passes through the sample and the sample response is measured. The reference arm is often referred to as the ‘pixellated measurement’ and the measurement of the sample arm as the ‘bucket measurement’. Typically in ghost imaging experiments, the bucket measurement is a one-dimensional (1-D) vector where each number represents the total number of particle yield for each shot. We implemented the 1-D spectral domain ghost imaging method in ref. 14 to reconstruct the resonant oxygen absorption in nitric oxide molecules. In that example, the bucket is the total number of resonant oxygen Auger electrons, which is linear to the absorption feature. In the current work, we take full advantage of the energy resolved electron spectrum, and expand the analysis to two dimensions. In this way, the bucket measurement becomes a 2-D matrix. This analysis approach has been applied to single X-ray pulse photoionization spectroscopy.¹⁵

Fig. 1, panel (c) shows the measurement we performed. The probing SASE pulse illuminates a dilute gaseous sample of isopropanol molecules, following the pump pulse after a delay, τ. The bucket measurement is a spectrally-resolved measurement of the resultant photoelectrons, recorded by a hemispherical electron analyser. The pixellated measurement is performed by a downstream photon spectrometer. The photon depletion through the sample is negligible (∼10⁻¹⁰), so the downstream X-ray spectrum is a good measurement of the incoming spectrum.

2.2 Analysis

The key for ghost imaging to work is the shot-to-shot variation in the incident illuminating source. This variation results in fluctuations in both the reference measurement and the bucket measurement, from which we can extract correlations of the signal from the background and the noise. With stable sources, researchers often employ shaping techniques such as spatial light modulators to introduce external variation to the system.^23,26 In contrast, SASE XFELs have inherent variation since the X-ray pulse builds up from noise. Spectral domain ghost imaging with XFELs takes full advantage of this inherent variation and moves the focus of spectroscopy measurements from control of a noisy source to measurement of the source properties. One further advantage of spectral domain ghost imaging, as opposed to a more conventional raster scan method,²⁴ is that the spectral resolution is limited only by the measured variation in the incident beam, instead of by the spectral bandwidth of the X-ray pulse. This latter point is particularly important for attosecond experiments, since attosecond pulses necessarily have large spectral bandwidth. In our previous demonstration,¹⁴ we showed that with spectral domain ghost imaging we can achieve sub-bandwidth resolution by exploiting the variation from SASE pulses.

The underlying assumption in our implementation of spectral domain ghost imaging is that the electron yield is linear to the X-ray pulse spectral intensity. Then we can write this expression to describe the problem,

b = Ax, (1)

where b stands for the bucket or photoemission measurement, A stands for the reference measurement, and x stands for the unknown spectral response of the target we hope to retrieve.

There are various established methods to solve x, given A and b. For example, one can take the pseudo-inverse ((A^TA)⁻¹) of A to arrive at the solution, but this method is often extremely sensitive to noise. To better handle noise in the measurement, we apply regularization on x based on prior knowledge of the target, which we assume to be smooth, sparse, and nonnegative. These assumptions can be implemented by optimizing the expression,

‖Ax − b‖²₂ + λ₁‖x‖₁ + Ind₊(x) + λ₂‖Lx‖²₂, (2)

where the λ’s are referred to as “hyperparameters”, whose values describe the relative importance of the different regularisation terms. The second term in eqn (2) will minimise the L₁ norm (or the sum of the absolute values of the vector entries) to impose sparsity. In the third term, the Ind₊ is the indicator function, which is 0 when the argument is non-negative and infinity otherwise. The final term in eqn (2) will minimise the L₂ norm (or the sum of absolute value squared of the vector entries) of the second derivative of x, which imposes smoothness. The second derivative operator is represented by the Laplacian matrix L. This regularization scheme can be implemented in the numerical optimization method: alternating direction method of multipliers (ADMM).²⁷

3 Results

3.1 Resolving spectral response in electron kinetic energy

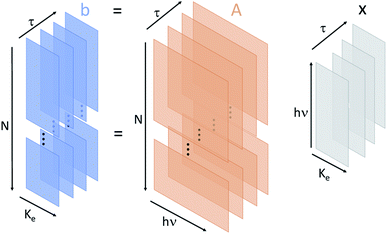
The full-dimensional structure of the dataset analyzed in this paper is shown in Fig. 2. Each XFEL shot is resolved in three separate dimensions: incident X-ray photon energy, electron kinetic energy, and pump–probe delay. We do not have sufficient statistics in the full dataset to enable a full three-dimensional reconstruction of the sample response using spectral domain ghost imaging.¹⁵ However, we are able to extract information from the data by selecting different dimensions for the spectral response function x which we reconstruct. We perform a simple binning of the shots in the dataset along the dimension which we do not resolve in x.

Fig. 2 Schematic representation of the data structures used in this work. The matrix b represents the number of electrons recorded in the measurement as a function of kinetic energy (K_e), shot number (N), and pump–probe delay (τ). The A matrix is the measured X-ray photon spectrum for each shot and delay as a function of X-ray photon energy (hν). Then x is the unknown sample response as a function of K_e, hν, and τ. In our analysis we regularize in the minimization procedure across two of the variables, either K_e and hν, or hν and τ.

First, we determine the spectral response of our sample resolved in electron kinetic energy and incoming photon energy. We measure the electron kinetic energy spectrum with 0.42 eV wide bins, and the X-ray photon energy spectrum with 0.79 eV resolution. This corresponds to 119 bins in electron kinetic energy (i.e. p = 119) and 40 bins in the incident photon energy (i.e. m = 40). This particular binning was chosen in order to resolve fine structure in the target response function without excessively consuming computational power. Therefore, b in eqn (1) is an n_τ × p matrix where each of the n_τ-rows is a separate measurement of the electron kinetic energy spectrum with p electron energy bins. A is an n_τ × m matrix where each of the n_τ-rows is a measurement of the X-ray spectrum of the incident pulse with m photon energy pixels. Then, x is an unknown matrix of size m × p that describes the system response as a function of the electron kinetic energy and the photon energy.

Our data consists of 15 different pump–probe delay values. For each delay point, we group the laser shots into 5 bins determined by the pump pulse energy measured in the photon spectrometer. In other words, we divide the entire data set into 15 × 5 = 75 subsets and obtain 75 copies of eqn (2) with respective b and A. Note that n_τ represents the number of shots for each delay point and each pump pulse energy bin. When averaged over delay points, there are 6870, 16 147, 22 951, 20 527, and 11 112 shots in each pump pulse energy bin (sorted from lowest to highest). We apply ADMM to determine x at each delay point and pump pulse energy bin. Varying the delay between the pump and the probe pulse introduced an energy shift in the photon spectrometer calibration. We correct this effect by converting the photoelectron kinetic energy axis of the 2-D reconstruction into binding energy axis. Then we sum the 2-D reconstruction over photon energy to obtain a 1D reconstruction as a function of binding energy. The photon energy calibration is found by maximizing the overlap between the reconstruction with a previous measurement on X-ray photoelectron spectroscopy with isopropanol molecules with a monochromatized X-ray source.²⁸

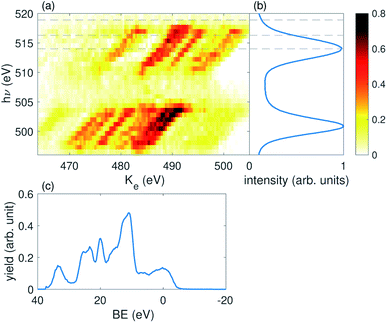
We perform this reconstruction for each of the individual 75 sets of independent shots defined above. From the ADMM optimization procedure we reconstruct x(K_e, hν; τ, I_pu), which is a function of electron kinetic energy (K_e) and incident photon energy (hν). We obtain a different spectral response for each of the pump energy (I_pu) and pump–probe delay (τ) bins. A representative reconstruction of x for τ = 0 and one pump pulse energy bin is shown in Fig. 3 panel (a). Panel (b) of Fig. 3 shows the average X-ray spectrum recorded in the X-ray photon spectrometer. The pulse centered near 513 eV is the probe pulse and the pulse centered near 502 eV is the pump. Most of the electrons measured in the experiment result from outer- or inner-valence photoionization. The energy of these photoelectrons will be given by the expression: K_e = hν − BE, where BE is the binding energy (or ionization potential) resulting in a particular ionic state. This dispersion relation is clearly reproduced in the reconstructed electron spectra in panel (a). Moreover, the ghost imaging analysis is able to cleanly separate overlapping features in the electron kinetic energy spectrum resulting from either the pump or the probe pulse, as shown by the clear dispersive lines in panel (a). This is a remarkable result given the substantial overlap of the different photoelectron features in kinetic energy, and presents a general solution to the problem of overlapping signal in multi-pulse measurements such as pump–probe experiments. In panel (c) of Fig. 3 we convert kinetic energy to binding energy, using the above expression, and sum over the pump photon range to obtain the 1-D result.

Fig. 3 (a) A representative example of the 2D reconstruction using spectral ghost imaging. This reconstruction is with delay τ = 0 fs, and the third pump pulse energy bin. (b) Is the averaged photon spectrum. The three dashed lines across (a) and (b) indicate the energies of the 6a, 7a, and 8a states. (c) 1D spectrum obtained by converting the horizontal axis in (a) to binding energy and then summing over pump photon energy range.

3.2 Resolving spectral response in pump–probe delay – I

It is instructive to interrogate the spectral response of the sample at a delay point when the inner valence hole is expected to be well localized on the oxygen site of the system, compared with a delay point where the hole is expected to have significantly delocalized. Such a differential measurement should highlight the signal resulting from the filling of the transient hole due to promotion of an oxygen 1s electron to the inner valence hole.

To investigate the residual signal, we define a differential signal:

S(K_e,hν; I_pu, τ) = ∫dK_e[x(K_e,hν; τ, I_pu) − x(K_e,hν; τ, I_r)], (3)

where I_r is a reference pump pulse energy bin. In previous work, using a similar dataset, we showed that in order to produce a quality reconstruction of the photoelectron spectrum, we require at least 10 000 shots.¹⁵ Since the lowest pump energy bin contains fewer than 10 000 shots, we discard this bin and treat the second lowest pulse energy bin as the reference. The subsequent pump pulse energy bins have a value of 1.2I_r, 1.4I_r, and 1.7I_r. The differential signal is plotted in Fig. 4. The differential signal is averaged across all delay points between ±9 fs. The FWHM duration of each X-ray pulse is ∼7 fs.¹⁷ Here we have zoomed into the photon energy region which represents the photoelectron spectrum from the probe pulse. The primary feature of the time-dependent signal is a faint increase in the electron yield near hν ∼ 516 eV. This signal initially increases with pump pulse energy, but decreases for the highest pump energy bin, suggesting the pump pulse energy is approaching the overpumping regime in the experiment.

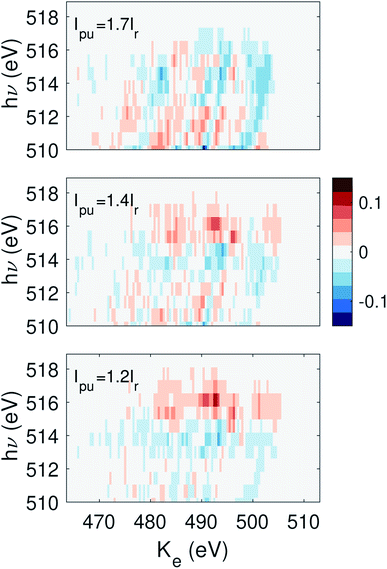Fig. 4 The signal as defined in eqn (3) summed over delay τ from −9 to 9 fs, where the second pump energy bin is chosen as the reference. The photon energy range shown here corresponds to the region constrained by the dashed lines in Fig. 3 panel (a).

3.3 Resolving spectral response in pump–probe delay – II

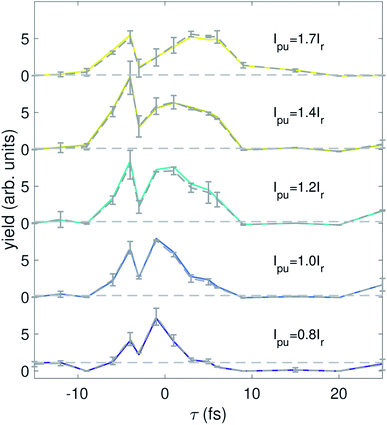
We are also able to adapt our implementation of spectral domain ghost imaging to refine the analysis of the pump–probe delay dependence of our signal. To best exploit the available statistics for the time-domain analysis of the electron spectrum, we now replace the electron kinetic energy dimension of b and x with the pump–probe delay. To do so, we integrate the electron kinetic energy spectrum at each shot between 473.6–503.1 eV to calculate a single electron yield for each shot, and construct b as an n × q matrix where n is the total number of shots across all delay points for one pulse energy bin, and q is number of time delay points sampled across the whole experiment. Each row of b has only one non-zero element, where the i^th element (i corresponds to the pump–probe delay for the given shot) is the total integrated electron yield at that shot. The matrix A becomes a n × p dimension matrix, where each row represents the photon energy spectrum at each of the n shots across all pump–probe delays for each pump pulse energy bin. Now, x becomes an m × q matrix which describes the photon-energy dependence of the integrated electron signal across each of the different delay points, x(hν, τ; I_pu). By ordering the q axis with ascending order in pump–probe delay, our ADMM-based implementation of spectral domain ghost imaging allows us to regularize x according to known properties of the temporal behaviour of the system. For example, the final term in eqn (2) enforces smoothness of the temporal evolution of localized hole density.

Fig. 5 shows the solution x(hν, τ; I_pu) summed over the photon energy region corresponding to the differential signal in Fig. 4 (515–520 eV, which covers the absorption features for the 6a, 7a, and 8a states). The error bars shown in Fig. 5 are derived from 4 times the standard deviation of 30 iterations of bootstrapping analysis. Bootstrapping analysis indicates the convergence of the reconstruction. The signal shows a clear peak centered near τ = −2 fs at lower pump pulse energy and gradually migrates to later delays at higher pump pulse energy. This peak also initially increases with pump pulse energy but then seems to decrease in the highest pump pulse energy bin. This behavior is consistent with our observations of overpumping in Fig. 4.

Fig. 5 The solution x(hν, τ; I_pu) integrated over photon energy from 515 to 520 eV for each pump pulse energy. The dashed curves and the errorbars are the average and four standard deviations from the bootstrapping analysis over 30 iterations. The horizontal dashed lines are calculated by averaging the first two delay points, used as a visual aide to show signal variation as a function of delay.

We have performed theoretical calculations of sudden ionization of isopropanol in a frozen nuclei approximation, which includes zero-point motion of the molecule (to be published elsewhere). These simulations show that the hole-survival probability¹⁹ lifetime for initial states corresponding to ionization of the 6a molecular orbital is around 2 fs, for the 7a orbital the lifetime is around 9 fs, and an initial states corresponding to an 8a orbital vacancy is approximately static within the femtosecond range that we are interested in. In the result shown in Fig. 5 we analyze the photon energy range that encompasses all of these superposition states, and the delay-dependent signal displays a lifetime of a few femtoseconds, consistent with these calculations. Further work is needed to quantify the lifetime for each initial hole-state from the spooktroscopy result, combined with modeling of the X-ray absorption features of the superposition states.

4 Discussion and conclusion

In this work we have applied spectral domain ghost imaging, or spooktroscopy, to an X-ray pump–probe experiment. We demonstrate the ability of correlation based techniques to separate overlapping signals arising from the pump and probe pulses. This is of high value given the congested nature of the photoelectron emission signals, which is typical of X-ray experiments. Moreover, we believe this approach can find general application for pump–probe experiments performed across all photon-energy ranges and not solely for X-ray spectroscopy. In particular, it works well with X-ray sources that are inherently stochastic, such as an XFEL.

By selecting the dimensions for which we reconstruct the transfer matrix x across our multi-dimensional dataset, we are able to answer different questions about our sample. Reconstructing the transfer matrix between incident spectral intensity and kinetic energy-resolved photoelectron yield, by summing our data across delay points, we identify the resonant feature which is the observable of our pump–probe measurement. Identification of this feature allows us to integrate over the relevant kinetic energy range and thus reconstruct the transfer matrix between incident spectral intensity and delay-dependent partial photoelectron yield. This provides a direct time-resolved measurement of the strength of the O 1s → π* transition following interaction with a pump pulse, which maps to the localization of the inner valence hole on the oxygen atom of isopropanol. As illustrated in Fig. 2, our data can be fully described by a 3-D transfer matrix relating time delay, kinetic energy of photoelectrons and incoming spectral intensity. Although in this work we retrieve only two-dimensional cuts of this full 3-D matrix, the scope of future work with improved statistics will be reconstruction of the full three- or higher-dimensional x matrix describing the data. Moreover, in both transfer matrices a pump pulse intensity dependent behaviour, not accessible to that conventional anlysis, can be identified. As this method, like all correlation-based methods, is dependent upon the quantity of data available, we can anticipate huge improvement as we move to higher data rate experiments. For instance, whilst in the present experiment, with a 120 Hz XFEL, our data was obtained from around 10⁶ XFEL shots across all the delays over a 6 h period, in future experiments with higher repetition rate XFELs, greater than 10⁹ shots will be readily available in the same beam access period.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under contract No. DE-AC02-76SF00515. The authors acknowledge the invaluable support of the technical and scientific staff of the LCLS at the SLAC National Accelerator Laboratory. JPM, OA, BC, TD, DG acknowledge funding from EPSRC through grants EP/I032517/1, EP/N018680/1 and EP/R019509/1, and ERC Advanced Grant ASTEX (2012-17). JPC was supported by the U.S. Department of Energy Office of Science, Basic Energy Science Division. We gratefully acknowledge the contribution of the LR25 beamtime collaboration to the development of the experiment, data collection and the initial analysis.

Notes and references

1. F. Krausz, M. E. Fermann, T. Brabec, P. F. Curley, M. Hofer, M. H. Ober, C. Spielmann, E. Wintner and A. Schmidt, IEEE J. Quantum Electron., 1992, 28, 2097–2122.
2. M. Hentschel, R. Kienberger, C. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinzmann, M. Drescher and F. Krausz, Nature, 2001, 414, 509–513.
3. A. H. Zewail, Femtochemistry: Ultrafast Dynamics of the Chemical Bond: Volume I, World Scientific, 1994, pp. 3–22.
4. A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1758.
5. F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios and P. Decleva, et al. , Science, 2014, 346, 336–339.
6. E. Perfetto, A. Trabattoni, F. Calegari, M. Nisoli, A. Marini and G. Stefanucci, J. Phys. Chem. Lett., 2020, 11, 891–899.
7. V. May and O. Kühn, Charge and energy transfer dynamics in molecular systems, John Wiley & Sons, 2008.
8. H. J. Wörner, C. A. Arrell, N. Banerji, A. Cannizzo, M. Chergui, A. K. Das, P. Hamm, U. Keller, P. M. Kraus and E. Liberatore, et al. , Struct. Dyn., 2017, 4, 061508.
9. G. Worth, M. Robb and B. Lasorne, Mol. Phys., 2008, 106, 2077–2091.
10. M. Vacher, D. Mendive-Tapia, M. J. Bearpark and M. A. Robb, J. Chem. Phys., 2015, 142, 094105.
11. A. J. Jenkins, K. E. Spinlove, M. Vacher, G. A. Worth and M. A. Robb, J. Chem. Phys., 2018, 149, 094108.
12. A. I. Kuleff and L. S. Cederbaum, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124002.
13. A. Trofimov and J. Schirmer, J. Chem. Phys., 2005, 123, 144115.
14. T. Driver, S. Li, E. G. Champenois, J. Duris, D. Ratner, T. J. Lane, P. Rosenberger, A. Al-Haddad, V. Averbukh and T. Barnard, et al. , Phys. Chem. Chem. Phys., 2020, 22, 2704–2712.
15. S. Li, T. Driver, A. Al-Haddad and E. t. Champenois, J. Phys. B: At., Mol. Opt. Phys., 2020 DOI:10.1088/1361-6455/abcdf1.
16. L. S. Cederbaum, W. Domcke, J. Schirmer and W. V. Niessen, in Correlation Effects in the Ionization of Molecules: Breakdown of the Molecular Orbital Picture, John Wiley Sons, Ltd, 2007, pp. 115–159.
17. T. Barillot, O. Alexander, B. Cooper, T. Driver, D. Garratt and S. Li, et al. , Phys. Rev. X, 2020 , submitted.
18. T. Åberg, Phys. Rev., 1967, 156, 35–41.
19. B. Cooper, P. Kolorenč, L. J. Frasinski, V. Averbukh and J. P. Marangos, Faraday Discuss., 2014, 171, 93–111.
20. A. A. Lutman, T. J. Maxwell, J. P. MacArthur, M. W. Guetg, N. Berrah, R. N. Coffee, Y. Ding, Z. Huang, A. Marinelli and S. Moeller, et al. , Nat. Photonics, 2016, 10, 745.
21. A. A. Lutman, M. W. Guetg, T. J. Maxwell, J. P. MacArthur, Y. Ding, C. Emma, J. Krzywinski, A. Marinelli and Z. Huang, Phys. Rev. Lett., 2018, 120, 264801.
22. D. Coster and R. D. L. Kronig, Physica, 1935, 2, 13–24.
23. S. Li, F. Cropp, K. Kabra, T. Lane, G. Wetzstein, P. Musumeci and D. Ratner, Phys. Rev. Lett., 2018, 121, 114801.
24. T. Wolf, R. H. Myhre, J. Cryan, S. Coriani, R. Squibb, A. Battistoni, N. Berrah, C. Bostedt, P. Bucksbaum and G. Coslovich, et al. , Nat. Commun., 2017, 8, 1–7.
25. J. Nordgren, G. Bray, S. Cramm, R. Nyholm, J.-E. Rubensson and N. Wassdahl, Rev. Sci. Instrum., 1989, 60, 1690–1696.
26. J. H. Shapiro, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 061802.
27. S. Boyd, N. Parikh, E. Chu, B. Peleato and J. Eckstein, Found. Trends Mach. Learn., 2011, 3, 1–122.
28. D. Nordfors, A. Nilsson, S. Svensson, U. Gelius and H. Ågren, et al. , J. Electron Spectrosc. Relat. Phenom., 1991, 56, 117–164.

---