Determination of excited state molecular structures from time-resolved gas-phase X-ray scattering
Haiwang
Yong
 a,
Andrés
Moreno Carrascosa
a,
Lingyu
Ma
a,
Andrés
Moreno Carrascosa
a,
Lingyu
Ma
 a,
Brian
Stankus
b,
Michael P.
Minitti
a,
Brian
Stankus
b,
Michael P.
Minitti
 c,
Adam
Kirrander
c,
Adam
Kirrander
 ad and
Peter M.
Weber
ad and
Peter M.
Weber
 *a
*a
aBrown University, Department of Chemistry, Providence, Rhode Island 02912, USA. E-mail: peter_weber@brown.edu
bDepartment of Chemistry and Biochemistry, Western Connecticut State University, Danbury, Connecticut 06810, USA
cSLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
dEaStCHEM School of Chemistry and Centre for Science at Extreme Conditions, University of Edinburgh, David Brewster Road, Edinburgh EH9 3FJ, UK
First published on 18th November 2020
Abstract
We present a comprehensive investigation of a recently introduced method to determine transient structures of molecules in excited electronic states with sub-ångstrom resolution from time-resolved gas-phase scattering signals. The method, which is examined using time-resolved X-ray scattering data measured on the molecule N-methylmorpholine (NMM) at the Linac Coherent Light Source (LCLS), compares the experimentally measured scattering patterns against the simulated patterns corresponding to a large pool of molecular structures to determine the full set of structural parameters. In addition, we examine the influence of vibrational state distributions and find the effect negligible within the current experimental detection limits, despite that the molecules have a comparatively high internal vibrational energy. The excited state structures determined using three structure pools generated using three different computational methods are in good agreement, demonstrating that the procedure is largely independent of the computational chemistry method employed as long as the pool is sufficiently expansive in the vicinity of the sought structure and dense enough to yield good matches to the experimental patterns.
1. Introduction
The determination of ground-state molecular structures using static gas-phase X-ray and electron scattering is foundational for modern chemistry.1–5 The recent emergence of ultrafast pulsed X-ray free-electron lasers6,7 and mega-electron-volt radio frequency (RF) electron guns8 has opened the opportunity to determine transient molecular structures in excited states. As an important application of these ultrabright and ultrashort pulses, time-resolved gas-phase scattering experiments can track electronic9,10 and nuclear motions of molecules11–15 in excited states during photochemical reactions. The scattering patterns reflect the structures of the molecules and can in principle be directly transformed to yield molecular structures16,17 and even the electron density.18 Yet the limited range of the observed scattering momentum transfer and rotational averaging coupled with the intrinsic structural complexity of non-linear polyatomic molecules make the determination of accurate excited state structures challenging. We recently introduced an analysis approach that is capable of determining transient molecular structures in excited states with sub-ångstrom resolution from time-resolved X-ray scattering signals.14 An important question that we explore here is how the excited state structures so determined might depend on the computational methods used to create the required structure pools. We find that the excited state structures depend minimally on the computational method and thus are largely of experimental nature.For static ground state structures, a least-squares refinement of structural parameters such as interatomic distances or characteristic torsional angles is traditionally employed to determine molecular structures from scattering data.3 Based on an assumed structure, a matrix of interatomic distances Rij is created. To simulate the scattering signal the Independent Atom Model (IAM) is often invoked, which, for X-ray scattering, is written as,1
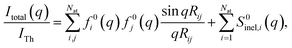 | (1) |
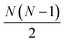 interatomic distances while only 3N − 6 geometrical parameters are needed to describe a molecular structure. Multiple solutions could occur when there are correlations among the parameters chosen for refinement, making the approach difficult to implement for complicated polyatomic molecules in excited electronic states.
interatomic distances while only 3N − 6 geometrical parameters are needed to describe a molecular structure. Multiple solutions could occur when there are correlations among the parameters chosen for refinement, making the approach difficult to implement for complicated polyatomic molecules in excited electronic states.
To circumvent this complexity, alternative approaches compare the experimental patterns with high-level theoretical simulations11,13 or restrict the studied systems to relatively simple models.15,21 We have recently introduced a novel structure determination method and applied it to a vibrating polyatomic molecule in an excited electronic state.14 The method yields precise molecular structures by matching the experimental X-ray scattering patterns against a large set of simulated patterns calculated from a pool of potential structures created from molecular dynamics simulations. Excited state molecular structures were obtained even in a complicated molecular system with 21 non-hydrogenic interatomic distances. Since then, additional evaluations and improvements have been made, resulting in a robust structure determination method without a need to reference to high level ab initio methods. In this article we provide a detailed description of the structure determination method. We introduce two additional methods for creating pools of potential structures that reduce the computational cost compared to molecular dynamics (MD) sampling. The excited state structures determined with the three different pools agree well with each other, suggesting that the procedure itself is independent of the quantum chemistry methods employed and could work for any pool that contains sufficiently dense structures that embody the correct structure.
2. Concepts
2.1 Time-resolved gas-phase X-ray scattering
Optical excitation of tertiary amines, which typically are pyramidal in the ground electronic state, leads to Rydberg states with a nearly planar geometry.22–24 As time-resolved photoionization spectra have shown, excitation with an ultrafast pulsed laser launches a coherent wavepacket in the amine inversion direction that can persist for several oscillations before dephasing into a bath of low frequency modes.25–27 X-ray scattering experiments on N-methylmorpholine (NMM) using the Linac Coherent Light Source (LCLS) X-ray free-electron laser revealed the corresponding structural evolution.14 For the present investigation we adopt the experimental signals at long delay times (2.6–3.9 ps), which reflect the excited-state structure of N-methylmorpholine (NMM) in the 3s Rydberg state.The experimental implementation has been described in detail previously.28,29 The ensemble of free NMM molecules was excited by a 200 nm laser pulse and then probed with a 9.5 keV X-ray pulse generated by the LCLS. The scattering patterns were measured on a 2.3-megapixel Cornell-SLAC Pixel Array Detector (CSPAD)30 at various delay times between the pump and probe pulses. The 2-dimensional scattering patterns can be decomposed into an isotropic component and anisotropic component.31 The anisotropic part reflects a second order Legendre polynomial that arises from the polarized nature of the laser beam. Our analysis here focuses on the isotropic, rotationally averaged component that contains all the intrinsic molecular properties in the molecular frame. An additional analysis of the anisotropic component that reveals the initially excited electronic state has been described elsewhere.32
The signal measured in the time-resolved X-ray scattering experiment is expressed as a percent difference, written as11,33
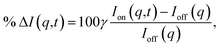 | (2) |
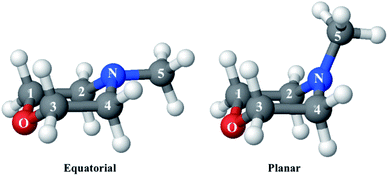
Since the reference scattering signal corresponds to the molecules in the ground state, the percent difference scattering patterns measure the excited state molecular structures in reference to the ground state. Considering that the change of the scattering patterns can be measured quite accurately29 and that the ground-state structure is usually well known,3,5 accurate excited state molecular structures can thus be derived. In the present study, the ground-state structure of NMM (see equatorial structure in Fig. 1) is taken from previous studies.14
2.2 Structure determination analysis
Our knowledge of ground state molecular structures is based on X-ray and electron diffraction investigations that started with the emergence of electron diffraction in the 1930s.34–36 A molecular structure is deemed to be determined when a comparison of an experimental pattern with a computed pattern yields satisfactory agreement. The process of refining a structure consists of adjusting the structure of the molecule until agreement is achieved.3 Compared to this traditional least-squares refinement of structural parameters, the structure determination method introduced in this article (illustrated in Fig. 2) has three main advantages. First, it inherently overcomes the problem of correlation among different structural parameters of the molecule since the scattering patterns used to compare with experiments are directly computed from 3D structures instead of a subset of independently adjustable structural parameters.37 Second, the method utilizes a large number of trial structures that are sufficiently comprehensive and dense to include a structure that is close to the ‘right’ one, while reducing the space of all possible atom arrangements by restricting their positions to those that conform with fundamental chemistry concepts. This prevents the analysis from converging to a structure that is physically or chemically impossible.37 Third, the analysis does not need to restrain the molecular symmetry or manually define independent structural parameters, making it applicable to relatively large polyatomic molecular systems.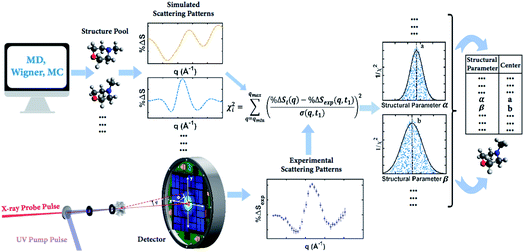 | ||
| Fig. 2 Concept of the method for determining molecular structures in excited electronic states from experimental scattering patterns. | ||
The goal of the structure pool is to provide many structures that are close to the correct target structure. Yet the purpose of sampling many structures is to displace their geometries so as to provide the opportunity to find unexpected structures. As the shape of the cationic state potential surface of the molecule is similar to that of the Rydberg states, the ion structure of NMM is likely quite similar to the structure in the 3s state. We thus use the optimized structure of NMM in its ion ground state as an initial structure and displace the geometries starting from there. Specifically, to sample the structure pool for NMM in 3s, we calculated the optimized ionic ground state structure of NMM (see planar structure in Fig. 1). We found its vibrational normal modes at the UMP2/6-311++g** level using the electronic structure package Molpro.38 A pool of one million geometries is sampled from a quantum Wigner distribution39 at 1000 K using SHARC40 based on the calculated vibrational normal modes of NMM in the ionic ground state. This provides a large variety of perturbed structures that most certainly includes the structure of the molecule in the 3s state. We use a 1000 K scaling temperature to make sure the displaced geometries are expansive enough to include target structures. For the sake of convenience we call this pool the Wigner pool in the following discussions.
A third approach derives a sample pool with even less dependence on theory and with more randomness. A Monte Carlo (MC) based approach randomly creates chemically viable structures by making use of the vibrational normal modes in the molecule. In this procedure, each of the normal modes is represented as a Gaussian distribution in Cartesian coordinates with the displacement of the atoms depending on their mass and the vibrational frequency of the mode. By randomly exciting each of the normal modes we create a grid of displacements in Cartesian coordinates. A random value for each displacement is chosen in every normal mode and then all displacements are applied to the original molecular structure. This procedure not only guarantees the randomness of the method but also generates new molecular structures that are chemically sound. A pool of one million structures is generated using this routine based on the calculated ionic ground state structure of NMM and its vibrational normal modes as described above. The accuracy in the calculation of the vibrational normal modes does not affect the mapping procedure or the posterior analysis as the generated structure pool is randomized and any probabilistic distributions are reproduced within the structure pool. In the following sections we call this structure pool the MC pool.
In the present simulation, the small mass of the hydrogen atoms often produces a distortion in the final structure as their displacements can be unrealistic for large excitations. Considering that X-ray signals are not sensitive towards the positions of hydrogen atoms41 and that C–H bond lengths are well known and are quite stiff, one may choose to clamp the C–H bond lengths of all sampled geometries at 1.09 Å. While constraining the bond length, the direction of the C–H bond vectors remains free to adjust. This clamping greatly reduces the number of degrees of freedom to be considered in the structure analysis. Results using the structure pools with and without clamped C–H bond lengths are compared in the Result and discussion section.
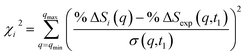 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔSi(q) is the computed percent difference pattern for structure i in the pool, %
ΔSi(q) is the computed percent difference pattern for structure i in the pool, %![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔSexp(q,t1) is the experimental percent difference scattering pattern %
ΔSexp(q,t1) is the experimental percent difference scattering pattern %![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔI(q,t) divided by the excitation fraction γ at delay time t1, and σ(q,t1) represents the experimental uncertainty of %
ΔI(q,t) divided by the excitation fraction γ at delay time t1, and σ(q,t1) represents the experimental uncertainty of %![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔSexp(q,t1), calculated as the statistical counting noise. Using eqn (3), each structure in the pool is associated with a specific χi2 value, which is a representation of how well the structure’s scattering pattern agrees with the experimentally measured pattern.
ΔSexp(q,t1), calculated as the statistical counting noise. Using eqn (3), each structure in the pool is associated with a specific χi2 value, which is a representation of how well the structure’s scattering pattern agrees with the experimentally measured pattern.
It is tempting to identify the structure with the lowest χ2 as the best result. But even with a large number of structures in the pool, it is very unlikely that the exactly ‘right’ structure is included. As a result, the structure with the lowest χ2 is not necessarily the correct structure, but may rather be an artifact from the sampling. To determine the best structure, the inverse of the χi2 values, i.e. 1/χi2, are plotted against molecular structure parameters such as the interatomic distances, bond angles or torsional angles, for all structures. By looking at the complete distributions instead of just picking the lowest χi2 structure, the artifact from the sampling is largely overcome. Given the randomness inherent in the generation of the structure pools, it is not surprising that for any value of a structure parameter, there are many structures that give poor fits, i.e. high values of χi2 as sketched in Fig. 2 for structural parameter α and β. Those poor fits fall beneath the envelope of the overall distribution. Retaining only the best-fitting structure for each value of the structure parameter, the envelope of the distribution assumes a normal or skewed normal distribution.14
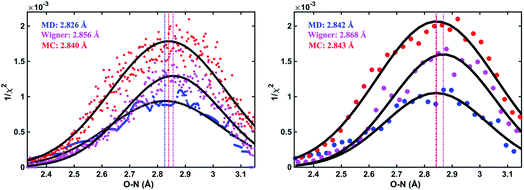
As an illustration, Fig. 3 plots the 1/χi2 values as a function of the O–N interatomic distance for the 3s excited state of NMM when using three different structure pools. To select the structure with the best fit for each value of the structure parameter, it is necessary to choose a bin size for the chosen interatomic distance. Fig. 3 shows the result for two different bin widths: 0.1% and 1% of the distance of the ground state structure for each selected structural parameter, respectively. For example, the O–N distance of the ground-state structure is 2.818 Å. Thus 0.1% bin corresponds to a bin size of 0.003 Å while 1% bin has a bin size of 0.028 Å in the O–N coordinate as shown in Fig. 3. For each structure bin, one best fitting structure is plotted so that there are more points in the plot with the smaller bin size. These data points, which are essentially the envelope of all structures, are then fitted with Gaussian functions and the maxima of the fitted curves are extracted as the determined value for the structural parameters of interest. As expected, the best structural parameters so determined depend slightly on the chosen bin widths.
To characterize the similarity between two selected structures while considering all relevant interatomic distances, we define the mean absolute percent deviation (MAPD) as41
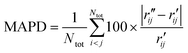 | (4) |
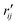 and
and 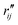 are the interatomic distances between atoms i and j for two different selected structures, respectively. In the case of NMM, we consider all interatomic distances between the seven non-hydrogenic atoms so that Ntot = 21. For the two bin sizes used in Fig. 3, we find that the MAPD (with the determined structural parameters using 1% bin as
are the interatomic distances between atoms i and j for two different selected structures, respectively. In the case of NMM, we consider all interatomic distances between the seven non-hydrogenic atoms so that Ntot = 21. For the two bin sizes used in Fig. 3, we find that the MAPD (with the determined structural parameters using 1% bin as 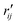 and the determined structural parameters using 0.1% bin as
and the determined structural parameters using 0.1% bin as 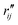 ) is only about 0.6%. This is much smaller than the previously reported experimental uncertainty of ∼1.0% (averaged relative standard deviation over 21 distances) of the excited-state structure determined from many time points.14 We therefore consider the 1% bin size sufficient for the subsequent analysis as it reduces the computational complexity of the procedure without sacrificing accuracy. It nevertheless is important to emphasize that the bin size and the fitting function must be carefully chosen to ensure that the envelopes of the 1/χi2 error plots are well captured.
) is only about 0.6%. This is much smaller than the previously reported experimental uncertainty of ∼1.0% (averaged relative standard deviation over 21 distances) of the excited-state structure determined from many time points.14 We therefore consider the 1% bin size sufficient for the subsequent analysis as it reduces the computational complexity of the procedure without sacrificing accuracy. It nevertheless is important to emphasize that the bin size and the fitting function must be carefully chosen to ensure that the envelopes of the 1/χi2 error plots are well captured.
Conceptually, the plot of 1/χi2 is a surface in a multi-dimensional space, as it depends on the 3N − 6 dimensions for a non-linear molecule with N atoms. The best-fitting structure should be the extremal point on this surface. Because it is impractical to analyze such a multi-dimensional surface we reduce this to a series of one-dimensional fits. Fig. 3 can be viewed as a one-dimensional projection to a specific structural parameter of the multi-dimensional surface. We note that a list of determined structural parameters does not necessarily correspond to a physically possible structure because there may be correlations between structural parameters.37 One could examine this effect by characterizing the similarity between the representative structures in the pool and the list of experimentally determined best-fitting structural parameters, as explained in detail in Section 3. We find that the correlations between structural parameters are largely preserved during our analysis, benefiting from the fact that each 1/χi2 value shown in the plot is calculated from a 3D geometrical structure.
As has been introduced previously, the theoretical percent difference scattering signal between a molecule in an excited state versus the ground state can be written as9
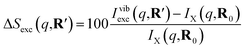 | (5) |
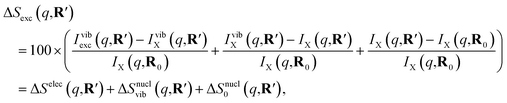 | (6) |
The IAM expression, eqn (1), can adequately describe the ΔSnucl0(q,R′) term but ignores the effect of electronic excitation and nuclear vibrations. Previous studies have established that the ΔSelec(q,R′) term for electronic excitation to a Rydberg state is nearly independent of the molecular geometry, suggesting that the time-evolving scattering signal can be approximated as arising mainly from nuclear structural dynamics with the electronic contribution as a correction term.9,14 In this study, we use the electronic contribution of the near-planar structure (R′) in the 3s state calculated previously from the state-averaged complete active-space self-consistent field method (SA5-CASSCF(2,5)/6-311++G(d,p)) as the electronic scattering correction factor.14
Next we address the effect of nuclear vibrations. Using a Boltzmann distribution, the IAM formula in eqn (1) is traditionally modified for harmonically vibrating molecules as3
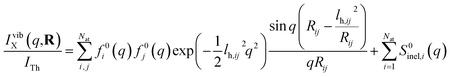 | (7) |
To explore the importance of the vibrational term, we use eqn (6) and (7) to examine a special case where the nuclear vibrations are thermalized to all degrees of freedom. The excitation and subsequent electronic relaxation of NMM with 200 nm inserts ∼1.50 eV of excess kinetic energy into the vibrational manifold,25 which corresponds to 990 K of vibrational temperature if thermalized harmonic vibrations are assumed. To model this situation, we created ensembles of structures from quantum Wigner distributions at T0 = 0 K and T′ = 1000 K using SHARC software, and extracted the corresponding lh,ij for all interatomic distances. Eqn (7) is then used to calculate IvibX(q,R′), IX(q,R′) and IX(q,R0), where R′ is the ionic near-planar structure of NMM optimized at the UMP2/6-311++g** level of theory. The vibrational term ΔSnuclvib(q,R′) is then calculated using eqn (6), yielding the result shown in Fig. 4.
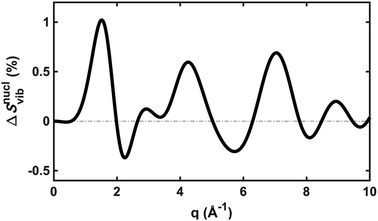 | ||
| Fig. 4 The vibrational correction term, ΔSnuclvib(q,R′), for NMM in the 3s Rydberg state, assuming a vibrational temperature of 1000 K. | ||
Although the details of the calculated vibrational term might not be accurate due to the intrinsic shortcomings of eqn (7), it nevertheless provides a fair estimate of the magnitude of the effect. The change in the percent difference scattering patterns due to vibrations is less than 1%, corresponding to a change in the experimental scattering signal of less than 0.06% given the excitation fraction of the present experiment. This is approaching the current experimental detection limit of ∼0.05%.14 Because the experiment is not able to uncover this effect, we don’t include this factor in the further analysis. Looking forward to upcoming improvements in the instrument design and the ongoing development of robust methods for data analysis, the effects of vibrational distributions may become observable. Eqn (6) offers an approach to treat such effects as an additive correction term. This will be adequate as long as the vibrational term ΔSnuclvib(q,R′) remains independent of the nuclear structure R′.
3. Results and discussion
In a prior publication, the original MD pool (without clamping C–H bond lengths) was first used to determine the excited-state structure of NMM from the experimental patterns at long delay times (2.6–3.9 ps, totally 25 time points).14 These experimental difference scattering signals converge to an essentially constant value. Viewing each time point as an independent measurement of the equilibrium structure of NMM in the 3s state, the standard deviation associated with these repeated measurements is a measure of the precision of the structure determination. The present analysis builds on that by clamping the C–H bond lengths of all structures in the pools, an approximation that is rational because X-ray scattering is only weakly sensitive to the positions of hydrogen atoms.41 Of course, the calculation of the scattering patterns includes all hydrogen atoms. Clamping the C–H bond lengths greatly reduces the dimensionality of the conformational space, which leads to a better agreement between the calculated scattering patterns and the experimental results. We also introduce two additional randomized structure pools to determine excited structures, demonstrating that the structure analysis method is robust vis-à-vis the computational method chosen to create the structure pool.The structure determination analysis is performed independently for each of the 25 time points and then averaged to obtain the structural parameters. Experimental signals at three representative delay times are shown in Fig. 5, along with the calculated scattering patterns using the interatomic distances optimized from the respective data. The excellent agreement between calculated and experimental scattering patterns indicates that the experimentally determined distances are rather accurate. The remaining small discrepancies could originate from the vibrational effects that the current analysis ignores, or from uncertainties in the calculated electronic correction term.
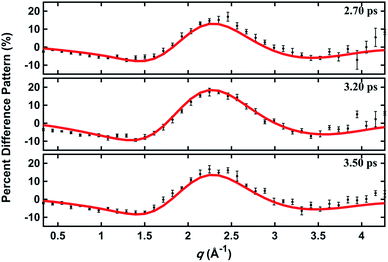 | ||
| Fig. 5 Experimental and calculated percent difference scattering patterns at several representative delay time points. The experimental results (black dots) are adopted from ref. 14 with 3σ error bars and scaled to 100% excitation. Calculated scattering patterns (red lines) are computed using the structural parameters determined with the present method, using the Wigner pool and a computed electronic correction term as described in the text. | ||
To investigate how the structure pool might affect the outcome we followed all the analysis steps separately for the three different structure pools with clamped C–H distances, giving rise to three sets of interatomic distances as listed in Table 1. The table also lists the precision of the measurement for each set of determined distances, i.e. how reproducible the results are over the measurement of the 25 independent time points. Although our method does not constrain the molecular symmetry, the results show that those bond lengths that should be symmetrically equivalent (grouped in the same cells) are determined to be equal within the stated uncertainties.
| Experimental 3s Rydberg state | Calculated ion ground state (Å) | |||||||
|---|---|---|---|---|---|---|---|---|
| MD | Wigner | MC | SD (Å) | |||||
| Interatomic distances (Å) | Precision (Å) | Interatomic distances (Å) | Precision (Å) | Interatomic distances (Å) | Precision (Å) | |||
| O–N | 2.862 | 0.026 | 2.892 | 0.026 | 2.890 | 0.027 | 0.017 | 2.762 |
| O–C1 | 1.370 | 0.015 | 1.283 | 0.064 | 1.341 | 0.013 | 0.044 | 1.401 |
| O–C3 | 1.376 | 0.012 | 1.349 | 0.010 | 1.329 | 0.012 | 0.024 | |
| O–C2 | 2.479 | 0.032 | 2.476 | 0.014 | 2.505 | 0.023 | 0.016 | 2.425 |
| O–C4 | 2.476 | 0.017 | 2.503 | 0.022 | 2.509 | 0.017 | 0.018 | |
| O–C5 | 4.156 | 0.054 | 4.142 | 0.036 | 4.130 | 0.038 | 0.013 | 4.015 |
| N–C1 | 2.496 | 0.026 | 2.494 | 0.019 | 2.519 | 0.019 | 0.014 | 2.433 |
| N–C3 | 2.469 | 0.021 | 2.502 | 0.019 | 2.521 | 0.016 | 0.026 | |
| N–C2 | 1.449 | 0.016 | 1.434 | 0.015 | 1.414 | 0.015 | 0.018 | 1.439 |
| N–C4 | 1.440 | 0.024 | 1.439 | 0.010 | 1.418 | 0.013 | 0.012 | |
| N–C5 | 1.438 | 0.015 | 1.429 | 0.012 | 1.467 | 0.020 | 0.020 | 1.454 |
| C1–C2 | 1.584 | 0.021 | 1.601 | 0.008 | 1.655 | 0.021 | 0.037 | 1.580 |
| C3–C4 | 1.571 | 0.010 | 1.634 | 0.017 | 1.658 | 0.023 | 0.045 | |
| C1–C4 | 2.819 | 0.016 | 2.819 | 0.018 | 2.818 | 0.018 | 0.001 | 2.864 |
| C2–C3 | 2.823 | 0.032 | 2.819 | 0.015 | 2.827 | 0.017 | 0.004 | |
| C1–C3 | 2.316 | 0.017 | 2.234 | 0.015 | 2.224 | 0.014 | 0.051 | 2.345 |
| C2–C4 | 2.424 | 0.026 | 2.388 | 0.017 | 2.335 | 0.021 | 0.044 | 2.433 |
| C5–C2 | 2.524 | 0.017 | 2.514 | 0.020 | 2.520 | 0.027 | 0.005 | 2.525 |
| C5–C4 | 2.512 | 0.039 | 2.511 | 0.019 | 2.501 | 0.025 | 0.006 | |
| C5–C1 | 3.667 | 0.051 | 3.604 | 0.037 | 3.600 | 0.028 | 0.038 | 3.493 |
| C5–C3 | 3.629 | 0.035 | 3.632 | 0.037 | 3.600 | 0.036 | 0.018 | |
Because the calculation of structures of polyatomic molecules in Rydberg excited electronic states is problematic,27,32 we do not have theoretical results that can be used as absolute benchmarks. In Table 1, we include the interatomic distances calculated for the electronic ground state of the NMM cation for a qualitative comparison. Even though the structure of NMM in the molecular Rydberg state is not identical to the structure in the ion state, they are probably fairly similar. That said, the dependence of the Rydberg state binding energy on the vibrational motions of the 3s-excited molecule observed in the photoelectron spectra indicates that at least in some coordinates there are substantial differences between the 3s and the ion structures.25 In light of this caveat, the good agreement between the experimental and the calculated results suggests a good accuracy of the structure analysis method.
Importantly, the results of the analysis using three different structure pools are very close to each other, as indicated by the small standard deviations (SD) shown in Table 1. Averaged over all 21 interatomic distances, the standard deviations are only 1.1% of the respective atom–atom distances. Thus we conclude that the structures determined using three very different structure pools are in good agreement with each other. This illustrates that the presented structure analysis method is largely independent of how the structure pool is created. Any structure pool must, however, contain a sufficiently expansive and dense pool of chemically viable structures in the vicinity of the sought structure. Since the standard deviations reported here are calculated from independent analyses of the same set of experimental data using the three different structure pools, they validate the structure determination as a largely experimental method.
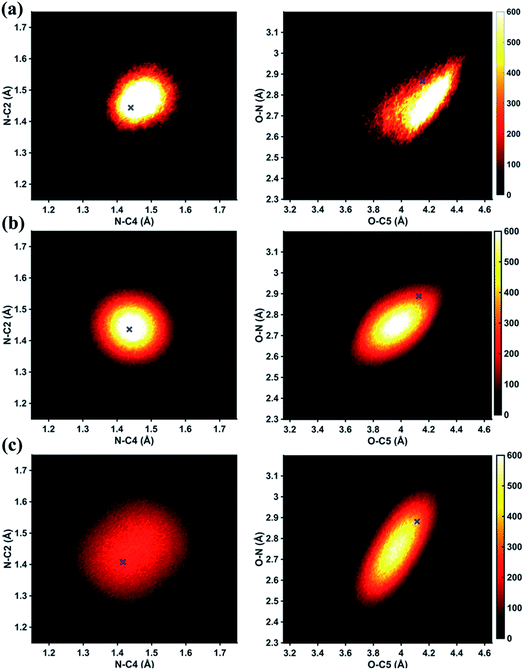
In Fig. 6 we examine the performances of the three structure pools using several different metrics. In Fig. 6a we see that the scattering patterns calculated from structure pools with clamped C–H bond lengths agree better with the experimental results than those calculated from the original, un-clamped structure pools. This is consistent across all structure pools and possibly caused by the large number of O–H, N–H, C–H and H–H distances, which means that the dimensionality of the full structure space is vastly larger when the C–H distances are not clamped. Considering that the C–H bond lengths are well known to be near 1.09 Å, clamping the C–H bond lengths proves to be a simple but effective way to reduce the dimensionality of the structure space, which increases the density in the remaining space. Furthermore, although the deviations of all three pools in Fig. 6a are all rather small, the Wigner pool appears to yield the best fits. This might be due to a better balance between expansiveness and denseness of the Wigner pool compared to the dense but overly localized MD pool, and the expansive but too sparse MC pool, as illustrated in the phase space density plots for three pools in Fig. 7.
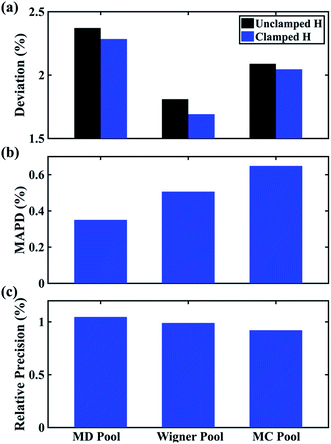 | ||
Fig. 6 Comparison of structure analysis results using three different structure pools. (a) The scattering pattern deviations calculated as 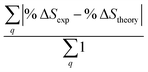 and averaged over all 25 time points, where % and averaged over all 25 time points, where %![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔSexp is the experimental scattering pattern at each time point (black dots in Fig. 5) and % ΔSexp is the experimental scattering pattern at each time point (black dots in Fig. 5) and %![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔStheory is the corresponding calculated pattern (red curve in Fig. 5). Black and blue bars: results when using structural pools before (black) and after (blue) clamping the C–H bond lengths, respectively. (b) Mean absolute percent deviation calculated by eqn (4) with the determined structural parameters as ΔStheory is the corresponding calculated pattern (red curve in Fig. 5). Black and blue bars: results when using structural pools before (black) and after (blue) clamping the C–H bond lengths, respectively. (b) Mean absolute percent deviation calculated by eqn (4) with the determined structural parameters as 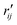 and distances of representative structure as and distances of representative structure as 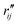 . (c) Averaged relative experimental precision over 21 interatomic distances as reported in Table 1 for analyses using the individual structure pools. . (c) Averaged relative experimental precision over 21 interatomic distances as reported in Table 1 for analyses using the individual structure pools. | ||
Fig. 6b explores how the sparseness of the sampled conformation space affects the structure determination analysis. The structural parameters reported in Table 1 are the optimal values of the individual one-dimensional 1/χ2 error distributions. The question is how close these best-fitting structural parameters are to a real geometrical structure that exists in the structure pool. We note that, a priori, a list of bond distances and angles must not necessarily imply a physically possible structure. Our analysis picks the structure that most closely approximates the bond distance table. To select that representative structure, we find the structure in the pool that has the smallest MAPD (see eqn (4)) across all 21 non-hydrogenic interatomic distances. As shown in Fig. 6b, the three representative structures from the different pools are very close to their corresponding determined structural parameters, with MAPD deviations of only 0.3–0.6%. This is well within ∼1.0% of the experimental precision, see Table 1, indicating that the uncertainty arising from examining one-dimensional projections rather than a multi-dimensional surface is negligible. The MD pool exhibits the smallest MAPD value, 0.35%, suggesting that it has the highest density near the optimal structures. This is consistent with the phase space densities shown in Fig. 7, where the MD shows the largest density around the determined structural parameters using that pool (blue cross). On the other hand, the MC pool shows a very sparse density in some particular coordinates such as N–C bonds, leading to the largest MAPD of 0.65%.
To further investigate the local density around the determined structure, we selected the 100 structures with the smallest MAPD from the structure pool and calculated their average MAPD. We define an indicator of local density, Γ, by dividing the averaged relative experimental precision of 1.0% by the averaged MAPD over the 100 nearest structures. The Γ of MD, Wigner and MC are calculated to be 0.92, 0.65 and 0.55, respectively. A larger value of Γ means that those selected structures are much closer to the determined structure, indicating a larger local density around the determined structure. This is again consistent with the results in Fig. 6b and 7. A careful inspection of the determined structural parameters in Table 1 shows that the results from the MC pool contribute the most to the SD values. Specifically, the C1–C2 and C3–C4 bond lengths are longer than usual. This could be caused by the relatively low local density of the MC pool, leading to less accurate results compared to the other two structure pools. This again emphasizes the importance of the local density near the sought structure. Since the results of the MC pool start to show minor deviations due to the sparseness, we estimate that the Γ should be larger than 0.6 to assure the accuracy of the determined structures.
Fig. 6c plots the precision of the measurements with the different structure pools, which are largely independent of the chosen structure pools. As explained previously, since these precisions are calculated from the standard deviations over 25 independent time point measurements, they mostly reflect the precision of the experiment itself regardless of the chosen structure analysis method.
4. Conclusions
We examine a novel method to determine excited-state structures from time-resolved gas-phase X-ray scattering measurements. The method should be equally applicable to time-resolved gas-phase electron scattering experiments as long as the representation of percent difference signals is used.41 Examining three structure pools created using three different computational methods, we show that the resulting structures deviate very little from each other, with only a 1.1% standard deviation. A sufficiently expansive and densely sampled structure pool is essential for the quality of the structure analysis, suggesting that the structure pool should be carefully examined when using the method. The choice of the method to create a structure pool is partially a matter of convenience and should depend on the experiment at hand. For an equilibrium excited-state structure that is near the minimum of a potential surface, the Wigner and MC pools are most effective. For example, we have recently used the Wigner pool to determine the charge-localized and charge-delocalized structures of N,N′-dimethylpiperazine (DMP) in the 3s Rydberg state,44 demonstrating the method’s applicability to other molecular systems. If the molecular system involves a coherent molecular motion through a significant part of the potential energy surface, the MD pool is a better choice as it samples structures across a larger section of the potential surface(s).Looking ahead, we plan to develop the method further to determine the vibrational distributions. One possible option could be to include them as additive factors as discussed in Section 2.2.3. It also seems possible to explore the information contained in the width of the error distributions illustrated in Fig. 3. So far, we have considered only the maxima of the distributions. Moreover, the current method applies to the experimental pattern that measures only one single classical structure. An extension of the method to cases where the experimental pattern measures multiple structures in different channels simultaneously still requires further development. Ultimately, we hope the structure determination method introduced here could be applied to determine both nuclear and electronic structures of the molecule in the excited state from time-resolved gas-phase scattering experiments.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award No. DE-SC0017995 and DE-SC0020276, and by the National Science Foundation, Award Number CHE-1953839. The work was further supported by the Carnegie Trust for the Universities of Scotland under research grant CRG050414 (A. K.) and the Royal Society of Edinburgh under Sabbatical Fellowship 58507 (A. K.).References
- B. E. Warren, X-ray Diffraction, Courier Corporation, 1969 Search PubMed.
- D. A. Kohl and L. S. Bartell, J. Chem. Phys., 1969, 51, 2891 CrossRef CAS.
- I. Hargittai and M. Hargittai, Stereochemical Applications of Gas-Phase Electron Diffraction, VCH, Weinheim, 1988 Search PubMed.
- T. S. Koritsanszky, Chem. Rev., 2001, 101, 1583 CrossRef CAS.
- E. Prince, International Tables for Crystallography, Volume C: Mathematical, Physical and Chemical Tables, Springer, Dordrecht, The Netherlands, 3rd edn, 2006 Search PubMed.
- P. Emma, R. Akre, J. Arthur, R. Bionta, C. Bostedt, J. Bozek, A. Brachmann, P. Bucksbaum, R. Coffee, F.-J. Decker, Y. Ding, D. Dowell, S. Edstrom, A. Fisher, J. Frisch, S. Gilevich, J. Hastings, G. Hays, Ph. Hering, Z. Huang, R. Iverson, H. Loos, M. Messerschmidt, A. Miahnahri, S. Moeller, H.-D. Nuhn, G. Pile, D. Ratner, J. Rzepiela, D. Schultz, T. Smith, P. Stefan, H. Tompkins, J. Turner, J. Welch, W. White, J. Wu, G. Yocky and J. Galayda, Nat. Photonics, 2010, 4, 641–647 CrossRef CAS.
- W. Decking, et al. , Nat. Photonics, 2020, 14, 391–397 CrossRef CAS.
- S. P. Weathersby, G. Brown, M. Centurion, T. F. Chase, R. Coffee, J. Corbett, J. P. Eichner, J. C. Frisch, A. R. Fry, M. Gühr, N. Hartmann, C. Hast, R. Hettel, R. K. Jobe, E. N. Jongewaard, J. R. Lewandowski, R. K. Li, A. M. Lindenberg, I. Makasyuk, J. E. May, D. McCormick, M. N. Nguyen, A. H. Reid, X. Shen, K. Sokolowski-Tinten, T. Vecchione, S. L. Vetter, J. Wu, J. Yang, H. A. Dürr and X. J. Wang, Rev. Sci. Instrum., 2015, 86, 073702 CrossRef CAS.
- H. Yong, N. Zotev, J. M. Ruddock, B. Stankus, M. Simmermacher, A. M. Carrascosa, W. Du, N. Goff, Y. Chang, D. Bellshaw, M. Liang, S. Carbajo, J. E. Koglin, J. S. Robinson, S. Boutet, M. P. Minitti, A. Kirrander and P. M. Weber, Nat. Commun., 2020, 11, 2157 CrossRef CAS.
- J. Yang, X. Zhu, J. P. F. Nunes, J. K. Yu, R. M. Parrish, T. J. A. Wolf, M. Centurion, M. Gühr, R. Li, Y. Liu, B. Moore, M. Niebuhr, S. Park, X. Shen, S. Weathersby, T. Weinacht, T. J. Martinez and X. Wang, Science, 2020, 368, 885–889 CrossRef CAS.
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. S. Robinson, D. Ratner, T. J. Lane, D. Zhu, J. M. Glownia, M. Kozina, H. T. Lemke, M. Sikorski, Y. Feng, S. Nelson, K. Saita, B. Stankus, T. Northey, J. B. Hastings and P. M. Weber, Phys. Rev. Lett., 2015, 114, 255501 CrossRef CAS.
- J. Yang, X. Zhu, T. J. A. Wolf, Z. Li, J. P. F. Nunes, R. Coffee, J. P. Cryan, M. Gühr, K. Hegazy, T. F. Heinz, K. Jobe, R. Li, X. Shen, T. Veccione, S. Weathersby, K. J. Wilkin, C. Yoneda, Q. Zheng, T. J. Martinez, M. Centurion and X. Wang, Science, 2018, 361, 64 CrossRef CAS.
- T. J. A. Wolf, D. M. Sanchez, J. Yang, R. M. Parrish, J. P. F. Nunes, M. Centurion, R. Coffee, J. P. Cryan, M. Gühr, K. Hegazy, A. Kirrander, R. K. Li, J. Ruddock, X. Shen, T. Vecchione, S. P. Weathersby, P. M. Weber, K. Wilkin, H. Yong, Q. Zheng, X. J. Wang, M. P. Minitti and T. J. Martinez, Nat. Chem., 2019, 11, 504 CrossRef CAS.
- B. Stankus, H. Yong, N. Zotev, J. Ruddock, D. Bellshaw, T. J. Lane, M. Liang, S. Boutet, E. Carbajo, J. S. Robinson, W. Du, N. Goff, Y. Chang, J. E. Koglin, M. P. Minitti, A. Kirrander and P. M. Weber, Nat. Chem., 2019, 11, 716 CrossRef CAS.
- M. R. Ware, J. M. Glownia, N. Al-Sayyad, J. T. O’Neal and P. H. Bucksbaum, Phys. Rev. A, 2019, 100, 033413 CrossRef CAS.
- J. Cao and K. R. Wilson, J. Phys. Chem. A, 1998, 102, 9523–9530 CrossRef CAS.
- J. Yang, V. Makhija, V. Kumarappan and M. Centurion, Struct. Dyn., 2014, 1, 044101 CrossRef.
- T. Bredtmann, M. Ivanov and G. Dixit, Nat. Commun., 2014, 5, 5589 CrossRef CAS.
- T. Northey, A. M. Carrascosa, S. Schäfer and A. Kirrander, J. Chem. Phys., 2016, 145, 154304 CrossRef.
- T. Northey, N. Zotev and A. Kirrander, J. Chem. Theory Comput., 2014, 10, 4911–4920 CrossRef CAS.
- J. Yang, M. Guehr, X. Shen, R. Li, T. Vecchione, R. Coffee, J. Corbett, A. Fry, N. Hartmann, C. Hast, K. Hegazy, K. Jobe, I. Makasyuk, J. Robinson, M. S. Robinson, S. Vetter, S. Weathersby, C. Yoneda, X. Wang and M. Centurion, Phys. Rev. Lett., 2016, 117, 153002 CrossRef.
- J. L. Gosselin, M. P. Minitti, F. M. Rudakov, T. I. Sølling and P. M. Weber, J. Phys. Chem. A, 2006, 110, 4251–4255 CrossRef CAS.
- J. D. Cardoza, F. M. Rudakov and P. M. Weber, J. Phys. Chem. A, 2008, 112, 10736–10743 CrossRef CAS.
- S. Deb, B. A. Bayes, M. P. Minitti and P. M. Weber, J. Phys. Chem. A, 2011, 115, 1804–1809 CrossRef CAS.
- Y. Zhang, S. Deb, H. Jónsson and P. M. Weber, J. Phys. Chem. Lett., 2017, 8, 3740–3744 CrossRef CAS.
- Y. Zhang, H. Jonsson and P. M. Weber, Phys. Chem. Chem. Phys., 2017, 19, 26403 RSC.
- R. Dsouza, X. Cheng, Z. Li, R. J. D. Miller and M. A. Kochman, J. Phys. Chem. A, 2018, 122, 9688–9700 CrossRef CAS.
- J. M. Budarz, M. P. Minitti, D. V. Cofer-Shabica, B. Stankus, A. Kirrander, J. B. Hastings and P. M. Weber, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 034001 CrossRef.
- B. Stankus, H. Yong, J. Ruddock, L. Ma, A. M. Carrascosa, N. Goff, S. Boutet, X. Xu, N. Zotev, A. Kirrander, M. P. Minitti and P. M. Weber, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 234004 CrossRef.
- H. T. Philipp, M. Hromalik, M. Tate, L. Koerner and S. M. Gruner, Nucl. Instrum. Methods Phys. Res., Sect. A, 2011, 649, 67 CrossRef CAS.
- U. Lorenz, K. B. Møller and N. E. Henriksen, New J. Phys., 2010, 12, 113022 CrossRef.
- H. Yong, N. Zotev, B. Stankus, J. M. Ruddock, D. Bellshaw, S. Boutet, T. J. Lane, M. Liang, S. Carbajo, J. S. Robinson, W. Du, N. Goff, Y. Chang, J. E. Koglin, M. D. J. Waters, T. I. Solling, M. P. Minitti, A. Kirrander and P. M. Weber, J. Phys. Chem. Lett., 2018, 9, 6556 CrossRef CAS.
- R. C. Dudek and P. M. Weber, J. Phys. Chem. A, 2001, 105, 4167–4171 CrossRef CAS.
- H. Mark and R. Wierl, Z. Phys., 1930, 60, 741 CrossRef CAS.
- R. W. James, Phys. Z., 1932, 33, 737 CAS.
- R. W. Dornte, J. Chem. Phys., 1933, 1, 566 CrossRef CAS.
- H. Yong, J. M. Ruddock, B. Stankus, L. Ma, W. Du, N. Goff, Y. Chang, N. Zotev, D. Bellshaw, S. Boutet, S. Carbajo, J. E. Koglin, M. Liang, J. S. Robinson, A. Kirrander, M. P. Minitti and P. M. Weber, J. Chem. Phys., 2019, 151, 084301 CrossRef.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- J. P. Dahl and M. Springborg, J. Chem. Phys., 1988, 88, 4535–4547 CrossRef CAS.
- S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1400 Search PubMed.
- L. Ma, H. Yong, J. D. Geiser, A. M. Carrascosa, N. Goff and P. M. Weber, Struct. Dyn., 2020, 7, 034102 CrossRef CAS.
- A. M. Carrascosa, H. Yong, D. L. Crittenden, P. M. Weber and A. Kirrander, J. Chem. Theory Comput., 2019, 15, 2836–2846 CrossRef.
- N. Zotev, A. M. Carrascosa, M. Simmermacher and A. Kirrander, J. Chem. Theory Comput., 2020, 16, 2594–2605 CrossRef CAS.
- H. Yong, X. Xu, J. M. Ruddock, B. Stankus, A. M. Carrascosa, N. Zotev, D. Bellshaw, W. Du, N. Goff, Y. Chang, S. Boutet, S. Carbajo, J. E. Koglin, M. Liang, J. S. Robinson, A. Kirrander, M. P. Minitti and P. M. Weber, Ultrafast X-Ray Scattering Offers a Structural View of Excited State Charge Transfer, 2020, submitted.
| This journal is © The Royal Society of Chemistry 2021 |