Open Access Article
Open Access ArticleQuantum electronic coherences by attosecond transient absorption spectroscopy: ab initio B-spline RCS-ADC study
M.
Ruberti
 *
*
Department of Physics, Imperial College London, Prince Consort Road, London SW7 2AZ, UK. E-mail: m.ruberti11@imperial.ac.uk; Tel: +44 (0)20 7589 47728
First published on 8th December 2020
Abstract
Here I present a fully ab initio time-resolved study of X-ray attosecond transient absorption spectroscopy (ATAS) in a prototypical polyatomic molecule, pyrazine, and demonstrate the possibility of retrieving the many-electron quantum ionic coherences arising in attosecond molecular photoionisation and pre-determining the subsequent charge-directed photochemical reactivity. Advanced first-principles many-electron simulations are performed, within a hybrid XUV pump/X-ray probe setup, to describe the interaction of pyrazine with both XUV pump and X-ray probe pulses, and study the triggered correlated many-electron dynamics. The calculations are carried out by means of the recently-developed ab initio method for many-electron dynamics in polyatomic molecules, the time-dependent (TD) B-spline Restricted Correlation Space-Algebraic Diagrammatic Construction (RCS-ADC). RCS-ADC simulates molecular ionisation from first principles, combining the accurate description of electron correlation of quantum chemistry with the full account of the continuum dynamics of the photoelectron. Complete theoretical characterisation of the atto-ionised many-electron state and photo-induced attosecond charge dynamics is achieved by calculating the reduced ionic density matrix (R-IDM) of the bipartite ion–photoelectron system, with full inclusion of the correlated shakeup states. Deviations from the sudden approximation picture of photoionisation, in the low-photon-energy limit, are presented. The effect of the multi-channel interaction between the parent-ion and the emitted photoelectron on the onset of the quantum electronic coherences is analysed. Moreover, I show how the Schmidt decomposition of the R-IDM unravels the many-electron dynamics triggered by the pump, allowing for the identification of the key channels involved. Finally, I calculate the X-ray attosecond transient absorption spectra of XUV-ionised pyrazine. The results unveil the mapping of the ATAS measurement onto the quantum electronic coherences, and related non-zero R-IDM matrix elements, produced upon ionisation by the XUV pump laser pulse.
1 Introduction
Triggering, imaging and ultimately achieving control of many-electron dynamics on its intrinsic time-scale in molecular systems are at the heart of modern attosecond science, with the fundamental important goal of unveiling the role played by quantum-coherent electronic motion in driving and determining the photo-induced physical and chemical change of matter. In particular, as a result of the interaction with a pulse of ionising laser radiation, the molecular many-electron quantum system breaks up as the emitted photoelectron drifts away from the parent-ion. In a traditional synchrotron photoionisation experiment, the resulting population of the series of ionised states occurs incoherently. Indeed, the application of narrow-bandwidth synchrotron radiation to an atom or a molecule, for the best resolution of the cationic eigenstates (e.g. through photoelectron spectra), results in each given ionised eigenstate being coupled to its own outgoing photoelectron wave of corresponding energy. The total N-electron wavefunction of the neutral (ion + photoelectron) system is thus completely entangled and cannot be represented as a separable product of ionic and free-electron states. Creation of ionic state coherence requires, on the contrary, short-pulse, broadband sources, e.g. in the XUV to X-ray range, of the kind that have only become available in the last two decades with the advent of high-order harmonic generation (HHG)-based attosecond lasers,1 as well as X-ray free electron lasers (XFELs).2 Ionisation of finite many-electron systems by these new generation attosecond laser sources creates a partially-entangled state of the ionised electron and parent-ion sub-systems, where the emerging ionic system is characterised by a density matrix and a partially-coherent superposition of ionic eigenstates is populated. This drives an ultrafast charge dynamics in the molecular ion, where (in several biomolecules) the positive charge is predicted to migrate (hole-migration) across the molecular backbone on a time-scale from a few femtoseconds (fs) down to hundreds of attoseconds (as).3–6 On longer time scales, this purely electronic coherent dynamics eventually undergoes decoherence due to the coupling to the nuclear motion (environment) degree of freedom,7–11 which leads to its final localisation.The study of the coherent many-electron dynamics upon photoionisation is a central topic in attosecond science. Since molecular bonds are more likely to break where the hole is localised, direct access to the ultrafast charge redistribution underpinned by electronic coherence in the ion could be ultimately exploited to control photoionisation-induced charge-directed reactivity on unprecedented ultrafast (attosecond) time-scales, steering the reaction dynamics at a very early stage of its quantum evolution by acting only on the electronic degrees of freedom, i.e. before the nuclei start to move and the de-phasing of electronic coherences occurs. This represents a unique opportunity, which was previously unavailable on the much longer (femto/pico-second) time-scales intrinsic to nuclear dynamics, to find new ways of controlling photochemical reactions by acting on the quantum electronic coherences, rather than just on the populations. Moreover, since the ultrafast charge redistribution underpinned by electronic coherences in the ion initiates all photochemical change,12,13 and as a result also pre-determines radiation damage, the study of quantum electronic coherence and entanglement in photoionisation deepens our understanding of the basic processes leading to photosynthesis, radiation damage, mutation and, more generally, the alteration of molecular biological functions.
To this end, the goal should be to develop quantum protocols, based on attosecond measurement techniques, for the tomographic reconstruction of the attosecond ionised quantum states. Indeed, the existence of long-enough lived quantum electronic coherences would not only make their experimental observation possible, but could also enable quantum state tomography of the ionic density matrix emerging from a molecular attosecond ionisation event. In this direction, the recent spectacular advances in ultrafast light-source technology have opened up the possibility of unprecedented direct experimental access to electronic quantum coherences through cutting-edge attosecond pump–probe spectroscopy techniques.14,15
However, in order to reach these goals, a crucial role is played by the development of a comprehensive theoretical understanding, based on an accurate theoretical modelling of the ultrafast molecular ionisation process and the role of the measurement, which can strongly support and guide attosecond experiments and their interpretation. The present theoretical picture lacks a full understanding of the level of entanglement produced in the photoionisation process and the consequent role of measurement in the observation of the ensuing dynamics. Moreover, in spite of the fact that predicting the quantum ionic coherences arising in photoionisation is essential for modelling attosecond hole migration,14 until very recently the density matrix characterising the ionic state emerging from attosecond ionisation could not be predicted theoretically or characterised experimentally, except for 2-level atomic cases.16 This is because predicting the ionic coherence in attosecond molecular ionisation represents a major theoretical challenge, where the multi-channel and multi-centre many-electron problem, in the presence of a laser field, must be solved with an accurate description of the photoelectron and parent-ion.
With the availability of the new B-spline restricted correlation space (RCS)-ADC many-body theoretical approach,17,18 complete theoretical characterisation of the attosecond ionised states in molecular systems has become possible.18 This has opened up the possibility of calculating, in a fully ab initio fashion and including the correlated ionic shakeup states, the reduced ionic density matrix (R-IDM) of the bipartite ion–photoelectron system produced by molecular attosecond ionisation. It also allows us to fully capture the onset of the quantum electronic coherences in the ionic system, generated during the laser-induced dynamics, as well as the ion–photoelectron entanglement. The B-spline restricted correlation space (RCS)-ADC method for many-electron dynamics allows one to model ionisation of much larger molecular systems than previously possible within the standard B-spline ADC method,25–28 at the same or higher level of accuracy. It successfully combines the full description of the photoelectron continuum states (described in terms of a multi-centre B-spline basis set) with a realistic quantum chemistry approach to the modelling of electron correlation. Moreover, the new method goes beyond the previous theoretical studies where the ionisation step (and the photoelectron degree of freedom) was either completely neglected,3–5,8–11,19,20 or modelled without taking into account important electron correlation effects such as interchannel couplings and ionic shakeup.14,21–24 RCS-ADC is based on the separation of the orbital space into correlation and ionisation spaces and naturally bridges the gap between standard ADC multi-configurational ab initio techniques and closed-coupling schemes based on the limited number of essential, physically relevant, ionic states, combining the key advantages of both.
In this article, I apply the B-spline RCS-ADC method to describe, in a fully ab initio fashion, a complete attosecond pump–attosecond probe experiment in a prototypical polyatomic molecule, i.e. pyrazine. In particular, I present a time-resolved study of X-ray attosecond transient absorption spectroscopy (ATAS) in pyrazine and demonstrate the possibility of retrieving the many-electron quantum ionic coherences arising in attosecond photoionisation and pre-determining the subsequent charge-directed reactivity. Advanced first-principles many-electron simulations are performed, within a hybrid XUV/X-ray pump–probe setup, to describe the interaction of pyrazine with both the XUV pump and X-ray probe pulses. First, during the pump step, I calculate the density matrix of the bipartite ion–photoelectron system, from which I extract a R-IDM fully including the correlated shakeup ionic states. I perform a Schmidt decomposition of the R-IDM in order to analyse the coherent ionic states emerging from the ionisation event. As a result, the pump-triggered charge dynamics and predominant timescales for many-electron motion are identified and mapped onto the quantum coherences between the populated ionic eigenstates. In addition, I analyse the effects of the residual interaction between the emitted photoelectron and the parent-ion on the quantum coherent many-electron dynamics, as well as its deviations from the predictions of the sudden approximation, in the low-photon-energy regime, i.e. close to the ionisation thresholds of the many-body system. In this way, this work provides a complete theoretical characterisation of the atto-ionised many-electron state and photo-induced charge dynamics.
Second, I study how this dynamics is reflected in the actual pump–probe signal by calculating the X-ray transient absorption spectra of XUV-ionised pyrazine. The ab initio simulation of the ATAS measurement is performed by solving the von Neumann equations for the characterised R-IDM prepared by the pump interacting with the X-ray probe field. The results of the simulation show how the ATAS measurement observables can be mapped onto the quantum electronic coherences corresponding to the non-zero R-IDM matrix elements, and related charge dynamics, produced upon ionisation by the pump laser pulse. The chemically site-specific information is obtained by using X-ray photon energies able to resonantly excite the ionic system to the nitrogen and carbon K-edges. The results presented here extend the work reported in a recent theoretical study on the simulation of pump–probe experiments in CO228 to a larger molecular system and, at the same time, at a higher level of accuracy in the description of electron correlation. Furthermore, it represents an important step further with respect to previous reports where the calculations were restricted to describing the electron dynamics following the ionisation induced by the pump pulse, but ignored the effect of the probe pulse and the role of the attosecond measurement.18,29 The calculations are performed within the frozen-nuclei approximation and focus only on the electronic degree of freedom, which is a valid approach for the first few femtoseconds after ionisation.7,11,13 On longer time-scales, these calculations provide a frozen-nuclei benchmark to which the experimental results can be compared, in order to identify the effects of nuclear motion.
2 Theoretical methods
In this section, I summarise the main features of the B-spline RCS-ADC method and its time-dependent implementation, and briefly describe the basic equations that allow one to extract the reduced ionic density matrix from the full N-electron wavefunction as well as the key quantities employed to describe the evolution of quantum electronic coherences and the hole-density in the molecular cation. Finally, I discuss the modelling of the interaction between the ionised system, created in the pump step, and the X-ray probe pulse.2.1 Description of the pump step: time-dependent B-spline RCS-ADC
Within B-spline RCS-ADC, the single-electron orbitals are expanded in a multicentre B-spline basis set,17,33 designed to accurately describe both bound and ionised states of the neutral molecule. The resulting Hartree–Fock (HF) virtual orbital space (VS)17 (ϕa) is subsequently partitioned into two orthonormal subspaces: the (restricted) correlation space (RCS) (χα), designed to accurately describe the localised short-range correlation of the system, and its orthonormal complement, the ionisation space (IS) (ψμ), which describes the long-range part of the photoelectron wavefunction and complements the RCS in order to represent the electronic wavefunction over the entire spatial region. Here and in what follows, the α, β, … and μ, ν… indices refer to the virtual space (unoccupied) RCS and IS orbitals, respectively, whereas i, j, k, …, indicate the occupied HF orbitals. Within the time-dependent (TD) B-spline restricted correlation space (RCS)-ADC(n) approach to molecular ionisation dynamics, the 3D time-dependent Schrödinger equation (TDSE) for an N-electron polyatomic molecule interacting with an ultrashort laser pulse,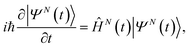 | (1) |
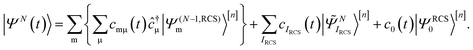 | (2) |
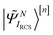 indicates the excited intermediate states of the nth-order ADC(n) scheme, built using the single-particle RCS. The ansatz of eqn (2) includes a full description of electron correlation effects, such as shakeup processes, breakdown of the molecular orbital picture and doubly-excited autoionising resonances, as well as inter-channel couplings in the continuum, which play an essential role both during the ionisation event and in the post-ionisation charge dynamics. Within the method of the ADC(n) hierarchy used in this work, i.e. ADC(2)-extended (ADC(2)x),17 the excited N-electron intermediate states span the configuration space consisting of 1h1p (|
indicates the excited intermediate states of the nth-order ADC(n) scheme, built using the single-particle RCS. The ansatz of eqn (2) includes a full description of electron correlation effects, such as shakeup processes, breakdown of the molecular orbital picture and doubly-excited autoionising resonances, as well as inter-channel couplings in the continuum, which play an essential role both during the ionisation event and in the post-ionisation charge dynamics. Within the method of the ADC(n) hierarchy used in this work, i.e. ADC(2)-extended (ADC(2)x),17 the excited N-electron intermediate states span the configuration space consisting of 1h1p (|![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) Niα〉[n]) and 2h2p (|
Niα〉[n]) and 2h2p (|![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) Nαβij〉[n]) excitation classes built on top of the RCS correlated ground state |ΨRCS0〉[n].17 The first term on the left-hand side of eqn (2) describes the IS configuration states of B-spline RCS-ADC, which take the form of ionisation-channel-specific product-states and read as17
Nαβij〉[n]) excitation classes built on top of the RCS correlated ground state |ΨRCS0〉[n].17 The first term on the left-hand side of eqn (2) describes the IS configuration states of B-spline RCS-ADC, which take the form of ionisation-channel-specific product-states and read as17|![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) Nμ,n〉 = ĉ†μ|ΨN−1,RCSn〉, Nμ,n〉 = ĉ†μ|ΨN−1,RCSn〉, | (3) |
| ĤN−1RCS-ADC(n)|ΨN−1,RCSn〉 = Inp|ΨN−1,RCSn〉, | (4) |
![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) N−1i〉) and 2h1p (|
N−1i〉) and 2h1p (|![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) N−1αij〉) configurations derived from the RCS perturbation theoretically corrected HF ground state of the neutral molecule17
N−1αij〉) configurations derived from the RCS perturbation theoretically corrected HF ground state of the neutral molecule17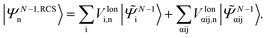 | (5) |
A complex absorbing potential (CAP) of the form Ŵ = η(r − rCAP)2, r ≥ rCAP is used to eliminate wave packet reflection effects from the radial grid boundaries. With the addition of the CAP term, the total time-dependent Hamiltonian of eqn (1) reads as
ĤN(t) = ĤNRCS-ADC(n) + ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) NRCS-ADC(n)EPump(t) − iŴ, NRCS-ADC(n)EPump(t) − iŴ, | (6) |
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) NRCS-ADC(n) are the representation of the shifted field-free RCS-ADC Hamiltonian
NRCS-ADC(n) are the representation of the shifted field-free RCS-ADC Hamiltonian 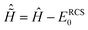 and the dipole operator
and the dipole operator ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) , respectively, in the space of RCS-ADC intermediate states (see eqn (2)). These matrices contain the conventional ADC(n) matrices computed within the RCS-based excitation space and augmented with the blocks corresponding to the ĉ†μ|ΨN−1,RCSn〉 product-states, which describe ionisation and interaction in the continuum.17,18 The time propagation of the unknown coefficients of the neutral many-electron wavefunction (see eqn (2)) is performed by means of the Arnoldi/Lanczos algorithm.18 During the simulation of the pump step, I have included in the expansion of the many-electron wavefunction (eqn (2)) only the open ionisation channels |ΨN−1,RCSn,Pump-ionised〉, i.e. the ones that are energetically accessible by the pump-pulse ionisation, which are characterised by an (ionisation) spectral intensity value (see ref. 17 and 18) greater than 1%. All the remaining ionic channels have been kept frozen. Doing so guarantees that all the ADC(2)x ionic states that can be effectively populated in the (mainly single-photon) ionisation of pyrazine by the broadband XUV pulse used in this work, and consequently play the main role in the ensuing many-electron dynamics taking place in the molecular cation, are accounted for.18 The contribution of ionic states with a smaller spectral-intensity value, as well as of deeper core-ionisation channels, was found to be negligible.
, respectively, in the space of RCS-ADC intermediate states (see eqn (2)). These matrices contain the conventional ADC(n) matrices computed within the RCS-based excitation space and augmented with the blocks corresponding to the ĉ†μ|ΨN−1,RCSn〉 product-states, which describe ionisation and interaction in the continuum.17,18 The time propagation of the unknown coefficients of the neutral many-electron wavefunction (see eqn (2)) is performed by means of the Arnoldi/Lanczos algorithm.18 During the simulation of the pump step, I have included in the expansion of the many-electron wavefunction (eqn (2)) only the open ionisation channels |ΨN−1,RCSn,Pump-ionised〉, i.e. the ones that are energetically accessible by the pump-pulse ionisation, which are characterised by an (ionisation) spectral intensity value (see ref. 17 and 18) greater than 1%. All the remaining ionic channels have been kept frozen. Doing so guarantees that all the ADC(2)x ionic states that can be effectively populated in the (mainly single-photon) ionisation of pyrazine by the broadband XUV pulse used in this work, and consequently play the main role in the ensuing many-electron dynamics taking place in the molecular cation, are accounted for.18 The contribution of ionic states with a smaller spectral-intensity value, as well as of deeper core-ionisation channels, was found to be negligible.
2.2 Pump-triggered ionic density matrix and charge dynamics
The pump-triggered coherent electron dynamics is obtained by calculating the time-dependent R-IDM ρR-IDM(t) of the molecular ion emerging from the attosecond pump-ionisation step. This is achieved by tracing out the unobserved photoelectron degree of freedom from the total time-dependent density matrix of the N-electron system![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) R-IDM(t) = Trμ[|ΨN(t)〉〈ΨN(t)|]. Doing so, and using the many-electron states of eqn (3) within the TD RCS-ADC(n) frameworks, yields the following expression in the basis of ADC(n) ionic eigenstates
R-IDM(t) = Trμ[|ΨN(t)〉〈ΨN(t)|]. Doing so, and using the many-electron states of eqn (3) within the TD RCS-ADC(n) frameworks, yields the following expression in the basis of ADC(n) ionic eigenstates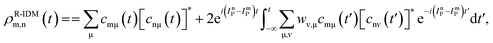 | (7) |
The R-IDM fully describes the ionic state prepared by attosecond molecular ionisation; its diagonal elements correspond to the TD population of the different ionic eigenstates, Pn(t) = |ρn,n(t)|, while the off-diagonal ones, ρm,n, are related to the degrees of coherence, 0 ≤ Gm,n ≤ 1, between any pair of populated ionic channels m and n
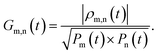 | (8) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) i:
i: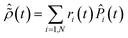 | (9) |
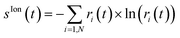 , respectively. Indeed, a pure ionic state yields Tr[ρ2] = Tr[ρ] and S(ρ) = 0, while, for mixed states, the higher the rank of the density matrix, i.e. the number of pure states involved in the purification of the density matrix for which ri ≠ 0, the greater the value of the entropy and Tr[ρ2] ≤ Tr[ρ]. Moreover, both quantities have the advantage of being representation-independent and they are especially convenient when several cationic states are considered.
, respectively. Indeed, a pure ionic state yields Tr[ρ2] = Tr[ρ] and S(ρ) = 0, while, for mixed states, the higher the rank of the density matrix, i.e. the number of pure states involved in the purification of the density matrix for which ri ≠ 0, the greater the value of the entropy and Tr[ρ2] ≤ Tr[ρ]. Moreover, both quantities have the advantage of being representation-independent and they are especially convenient when several cationic states are considered.
The time evolution of the hole-density ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) (r,t) created upon removal of one electron by the pump pulse is calculated in the RCS as
(r,t) created upon removal of one electron by the pump pulse is calculated in the RCS as 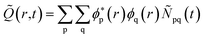 , where the hole-density matrix Ñpq(t)17 depends on the R-IDM and reads as
, where the hole-density matrix Ñpq(t)17 depends on the R-IDM and reads as
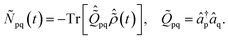 | (10) |
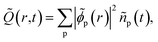 | (11) |
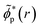 , and their respective hole-occupation numbers, ñp(t). The latter describe what fraction of the created hole-charge is, at each instant of time t, in the natural charge orbitals
, and their respective hole-occupation numbers, ñp(t). The latter describe what fraction of the created hole-charge is, at each instant of time t, in the natural charge orbitals ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) p(r), which are themselves time-dependent linear combinations of the RCS orbital basis ϕp(r).
p(r), which are themselves time-dependent linear combinations of the RCS orbital basis ϕp(r).
2.3 Description of the probe step: solving the RCS-ADC von Neumann equations
In this work, I explicitly simulate the interaction of the pump-ionised system with the probe pulse. This is achieved by calculating the time-delay dependence of the probe-induced absorption spectra of the pump-ionised pyrazine cation, and allows one to obtain a realistic description of the attosecond observables. The simulated pump–probe scheme assumes non-overlapping pump and probe pulses, with the X-ray probe following the XUV pump. This choice does not limit the use of the scheme proposed in the present work, nor does it affect the results of the simulations, since both the XUV pump and X-ray probe pulses considered here are of ultrashort (almost instantaneous) duration. The case of overlapping pump and probe, more relevant for longer pulses, would simply require one to treat equally the simultaneous interaction of the molecular system with both the pump and probe pulses, by means of eqn (1) and (2). The latter scheme, more demanding from the computational point of view but equally tackleable by the presented TD RCS-ADC machinery, will be considered in future work. The time-dependent description of the cation–probe interaction is performed by solving the time-dependent von Neumann equations for the characterised ionic density matrix interacting with the probe laser field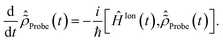 | (12) |
ĤIon(t) = ĤN−1RCS-ADC(n) + ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) N−1RCS-ADC(n)EX(t), N−1RCS-ADC(n)EX(t), | (13) |
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) N−1RCS-ADC(n) are the representation of the shifted field-free ionic Hamiltonian
N−1RCS-ADC(n) are the representation of the shifted field-free ionic Hamiltonian 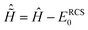 and the dipole operator
and the dipole operator ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) , respectively, in the (N − 1)-electron configuration space spanned by all the ionic states of eqn (5), |ΨN−1,RCSn〉, built within the single-particle RCS. The ionic density matrix
, respectively, in the (N − 1)-electron configuration space spanned by all the ionic states of eqn (5), |ΨN−1,RCSn〉, built within the single-particle RCS. The ionic density matrix 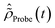 is thus constructed on the full electronic spectrum of the ionic subsystem, including both its low-energy bound excitations, i.e. the valence-ionised states populated by the pump pulse |ΨN−1n,Pump-ionised〉, as well as the initially unoccupied C(1s) and N(1s) core-ionised states |ΨN−1n,Core〉, which were kept frozen in the pump step simulation. The continuum of the valence-doubly-ionised states is not included in the simulation. This approximation assumes the direct photoionisation contribution to the cross-section, where the X-ray probe pulse directly populates the continuum of the valence-doubly-ionised states of the molecular dication, to be negligible with respect to the contribution of the excitation to the metastable core-singly-ionised resonances. The natural Auger decay of the C(1s) and N(1s) core-ionised states (labelled by index m) is modelled (semi-empirically) in the solution of the TD von Neumann equations for the R-IDM (eqn (12)) by adding the extra non-Hermitian diagonal terms
is thus constructed on the full electronic spectrum of the ionic subsystem, including both its low-energy bound excitations, i.e. the valence-ionised states populated by the pump pulse |ΨN−1n,Pump-ionised〉, as well as the initially unoccupied C(1s) and N(1s) core-ionised states |ΨN−1n,Core〉, which were kept frozen in the pump step simulation. The continuum of the valence-doubly-ionised states is not included in the simulation. This approximation assumes the direct photoionisation contribution to the cross-section, where the X-ray probe pulse directly populates the continuum of the valence-doubly-ionised states of the molecular dication, to be negligible with respect to the contribution of the excitation to the metastable core-singly-ionised resonances. The natural Auger decay of the C(1s) and N(1s) core-ionised states (labelled by index m) is modelled (semi-empirically) in the solution of the TD von Neumann equations for the R-IDM (eqn (12)) by adding the extra non-Hermitian diagonal terms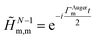 | (14) |
The initial condition used to solve eqn (12) is 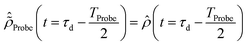 , where
, where 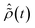 is the R-IDM as calculated in eqn (7), τd > 0 is the pump–probe time-delay and TProbe is the time-duration of the X-ray probe pulse. Note that, prior to the arrival of the probe pulse
is the R-IDM as calculated in eqn (7), τd > 0 is the pump–probe time-delay and TProbe is the time-duration of the X-ray probe pulse. Note that, prior to the arrival of the probe pulse 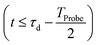 , the time-dependence of the R-IDM is given by
, the time-dependence of the R-IDM is given by 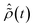 , which is in general different from the free-evolution solution of eqn (12) in the same time interval
, which is in general different from the free-evolution solution of eqn (12) in the same time interval 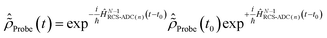 because of the residual interaction between the parent-ion sub-system and the photoelectron “bath” after the pump ionisation event. On the contrary, this interaction is neglected at later times
because of the residual interaction between the parent-ion sub-system and the photoelectron “bath” after the pump ionisation event. On the contrary, this interaction is neglected at later times 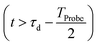 , where the time evolution of the R-IDM interacting with the X-ray probe pulse is given by the solution of eqn (12)
, where the time evolution of the R-IDM interacting with the X-ray probe pulse is given by the solution of eqn (12)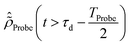 . The validity of this approximation requires the effect of the interaction with the X-ray probe pulse to dominate over the residual interaction with the emitted photoelectron and to mainly govern the many-electron dynamics of interest in the cation. This is confirmed, for values of the pump–probe time-delay τd approximately >1 fs, by the results presented in Section 3. The frequency-dependent absorption cross-section σ(ω;τd)30 is calculated from the expectation value of the molecular electric dipole moment,
. The validity of this approximation requires the effect of the interaction with the X-ray probe pulse to dominate over the residual interaction with the emitted photoelectron and to mainly govern the many-electron dynamics of interest in the cation. This is confirmed, for values of the pump–probe time-delay τd approximately >1 fs, by the results presented in Section 3. The frequency-dependent absorption cross-section σ(ω;τd)30 is calculated from the expectation value of the molecular electric dipole moment, 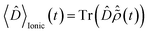 , and the incident X-ray probe field EX(t) as
, and the incident X-ray probe field EX(t) as
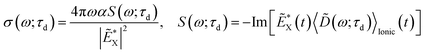 | (15) |
3 Results and discussion
In this section, the general formalism of Section 2 is applied to describe a complete attosecond pump–attosecond probe experiment in the C4H4N2 molecule. Pump ionisation is described by directly propagating the initial ground state of the neutral molecule with the full many-body B-spline RCS-ADC(2)x Hamiltonian. The electronic state of the emerging ionic system is fully characterised by computing the R-IDM. The multicentre B-spline basis17,33 used here is characterised by a radial box radius rOCEmax = 120 a.u., and a linear grid in the centre-of-mass expansion,17 with step size h = 0.8 a.u. and maximum value of the orbital angular momentum lmax = 12. The RCS is built from the virtual orbitals of an HF calculation performed in the cc-pVDZ GTO basis set. The number of open ionic channels included in the TD B-spline RCS-ADC(2)x calculation (see eqn (2)) and the highest value (among the different symmetry spaces) of the Hamiltonian matrix dimension are NIonic = 56 and HRCS-ADC(2)xMaxDim = 169![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700, respectively. The values of the CAP parameters used in this calculation are η = 4 × 10−3 and rCAP = 70 a.u.
700, respectively. The values of the CAP parameters used in this calculation are η = 4 × 10−3 and rCAP = 70 a.u.
The ab initio simulation of the pump step has been performed using a linearly polarised low-photon-energy XUV pulse, characterised by a Gaussian temporal envelope, a central frequency ℏωPump = 25 eV, a peak intensity IPump = 6 × 1011 W cm−2 and a time duration TPump ∼ 500 as at full width at half maximum (fwhm). The latter value corresponds to a few-cycle pulse with a broad, e.g. ≈7.5 eV fwhm, spectral-energy bandwidth. Results for the pump-triggered dynamics are presented for one specific orientation of the laser polarisation direction with respect to the molecular frame, namely the one parallel to the C–C bonds (and the N–N axis, z-direction). Convergence of the results has been achieved by using a Δt = 5 time-step and a K = 40 Krylov-space dimension in the Arnoldi/Lanczos time propagation.
3.1 Simulation of the XUV pump ionisation step
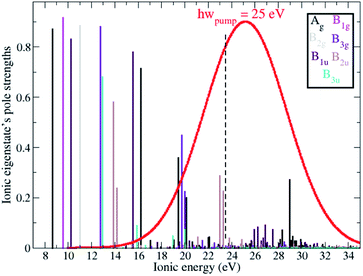
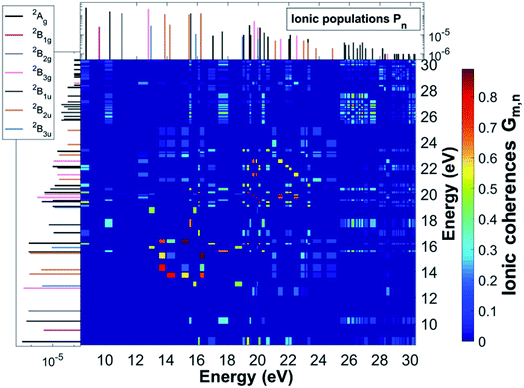
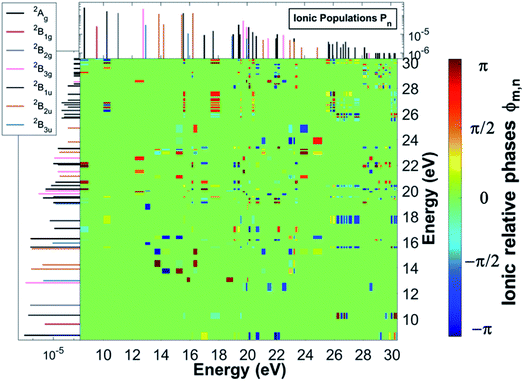
Ionisation of a molecular system by an ultrashort laser pulse such as the one used in the present work, whose spectral intensity envelope profile is shown in Fig. 1, can in principle simultaneously populate, either coherently or incoherently, a high number of ionisation channels in both the outer-valence and inner-valence energy regions of the ionic electronic spectrum. This can be seen in Fig. 1, which shows the relative spectral-intensities of all the energetically-accessible ADC(2)x ionic states of the C4H4N2 molecule, calculated using the cc-pVDZ basis set. The ADC(2)x valence shell spectrum of photoionized pyrazine shown in Fig. 1 is in very good agreement with previously reported experimental results obtained by means of photoelectron spectroscopy and using synchrotron radiation (see ref. 34 and references therein). In this previous work,34 where the photoionized spectrum of pyrazine has been studied both experimentally and theoretically, the structure observed in the experimental photoelectron spectra (recorded at photon energies ranging from 20 to 90 eV), was interpreted with the aid of vertical ionization energies, and partial cross-sections, calculated with various theoretical methods ranging from TDDFT to configuration interaction. In particular, the results of ref. 34 have enabled the identification and characterisation of the principal bands due to single-hole states as well as the realisation that the inner-valence ionization region is strongly affected by many-body effects, such as electron correlation, and formation of numerous satellite states. This is confirmed and quantified here in the calculated spectrum in Fig. 1, where each line represents an ionic eigenstate and is located at the corresponding ionisation energy. The values of the spectral intensities reflect the contribution of the 1h configurations to the ionic states. The complete neglect of electron correlation, such as that characterising the Koopmans approximation level,35 would give a series of lines with a height of 1 for each occupied molecular orbital. On the contrary, within the second order ADC(2)x scheme of the ionic ADC(n) hierarchy, the description of the cation includes all the ionic 2h1p configurations, which allow one to describe the shakeup process, where the removal of an electron from a particular orbital is accompanied by the excitation of another electron to an initially unoccupied orbital. Thus, electron correlation in the description of the ionic system manifests itself as a decrease in the spectral-intensity line height in individual ionic states (with the “missing” part reflecting the contribution of 2h1p configurations) and the appearance of additional (satellite) lines in the spectrum. As can be seen in Fig. 1, the ADC(2)x spectrum of the pyrazine cation can be divided approximately into three regions. In what follows, the standard D2h symmetry notation is used. The outer-valence region, which in the case of pyrazine extends up to ≈13 eV, contains Koopmans mainly-1h states, namely, as the ionisation potential (IP) increases, 12Ag, 12B1g, 12B1u, 12B2g, 12B3g and 12B3u, corresponding to the removal of one electron from the HOMO down to the HOMO−5 molecular orbital. As we go to higher energies, ionic states with strong shakeup character and satellite structures start to appear, where the 1h content for the 4ag, 5ag, 2b3g, 3b2u and 4b2u molecular orbitals is more equally shared between two or a few more ionic states. In this region two principal (mainly-1h) lines are also present, corresponding to the 22B1u and 22Ag ionic excited states with IP equal to 15.6 eV and 16.25 eV, respectively. Finally, for larger ionic energies up to the double ionisation potential (DIP) (≈30 eV), the molecular orbital picture of ionisation starts to break down,36 as it is here that ionisation from the inner-valence 3ag, 3b1u and 2b2u orbitals occurs, which is characterised by the population of many ionic eigenstates with relatively low 1h weight.As a result of this rich electronic structure and the high density of states in the electronic spectrum of the molecular cation, the broad bandwidth of the laser pulse can, in principle, create quantum coherence between multiple pairs of ionic many-electron states. Fig. 2 shows the TD RCS-ADC(2)x calculated final (at about 40 fs after ionisation) degree of coherence Gm,n between each pair of ionic eigenstates populated by the XUV pump pulse. The final stationary populations Pn(∞) of the RCS-ADC(2)x states of the pyrazine cation are also shown in the vertical and horizontal side panels of Fig. 2. In the calculations presented here, all the ionic time-dependent populations Pn(t) have converged to their final stationary value at ∼2 fs after ionisation. The relative phases Φm,n between the partially coherently populated eigenstates of energies Em and En are shown in Fig. 3. The Φm,n relative phases are extracted from the phases of the off-diagonal matrix elements of the R-IDM and read as Φm,n = arg|ρm,n(t)e+i(Em−En)t|. Note that the hermiticity of the density matrix  implies that Φm,n = −Φn,m. The Pn, Gm,n and Φm,n quantities represent a complete set of information for the description of the ionic state, which is fully characterised by its density matrix, prepared by ionisation in the pump step. In Fig. 2, it is possible to identify islands of strong coherence close to the diagonal (the highest degree of generated coherence being 0.9), mainly for ionic states with ionisation potential up to 23 eV. In general, a robust degree of coherence is produced between pairs of states with an energy gap up to approximately the value of the pump–pulse bandwidth, while for larger energy separations, the coherence rapidly decays to very low (<0.2) values. Furthermore, the potentially very high number of energetically-allowed coherences is reduced by the high symmetry of the molecule. Indeed, when ionisation occurs by one-photon absorption from the ground-state of the molecule, as is mainly the case with the pump pulse parameters used in this work, a degree of quantum coherence different from zero is possible only between ionic eigenstates of the same molecular point group symmetry. This is because the ionic density matrix is calculated by tracing the full N-electron neutral wavefunction over all the spatial-symmetry quantum numbers of the photoelectron, implying a measurement set-up where the direction of the emitted photoelectron is either not measured or integrated out in the analysis of the experimental data.
implies that Φm,n = −Φn,m. The Pn, Gm,n and Φm,n quantities represent a complete set of information for the description of the ionic state, which is fully characterised by its density matrix, prepared by ionisation in the pump step. In Fig. 2, it is possible to identify islands of strong coherence close to the diagonal (the highest degree of generated coherence being 0.9), mainly for ionic states with ionisation potential up to 23 eV. In general, a robust degree of coherence is produced between pairs of states with an energy gap up to approximately the value of the pump–pulse bandwidth, while for larger energy separations, the coherence rapidly decays to very low (<0.2) values. Furthermore, the potentially very high number of energetically-allowed coherences is reduced by the high symmetry of the molecule. Indeed, when ionisation occurs by one-photon absorption from the ground-state of the molecule, as is mainly the case with the pump pulse parameters used in this work, a degree of quantum coherence different from zero is possible only between ionic eigenstates of the same molecular point group symmetry. This is because the ionic density matrix is calculated by tracing the full N-electron neutral wavefunction over all the spatial-symmetry quantum numbers of the photoelectron, implying a measurement set-up where the direction of the emitted photoelectron is either not measured or integrated out in the analysis of the experimental data.
The charge dynamics triggered by the partially-coherent population of ionic eigenstate pairs upon XUV pump ionisation is analysed in Fig. 4, which shows the B-spline RCS-ADC(2)x calculated time evolution, as well as its Fourier-transform, of the hole-occupation numbers ñp(t) (positive eigenvalues of the hole-density matrix, see eqn (11)) for the most contributing natural charge orbitals. Fig. 4 also provides a snapshot of the difference between the pyrazine hole-densities at times t2 and t1 as indicated in the upper panel (a). Note that the two times correspond to the minimum and maximum positions in the hole-occupation number evolution for the natural charge orbitals, showing a ∼5.5 fs period oscillation. The dominant frequencies of the charge dynamics are highlighted in panel b. As it is possible to see in Fig. 4, the emerging charge dynamics in the pyrazine cation is characterised by two predominant timescales; a main, relatively slow one with period ∼5.5 fs, and a faster one, with period ∼500 as. The former dynamics is driven exclusively by electron correlation, i.e. by the coherence between the main ionic state characterised by 1h 3b2u content at 16.2 eV and its satellite at 15.45 eV. On the contrary, the faster timescale is a result of the partially-coherent superposition of the ground (8.7 eV) and first excited (16.25 eV) ionic states of Ag symmetry, mainly representing ionisation from the two different 6ag and 5ag molecular orbitals, respectively. Therefore, in spite of the multitude of channels involved in pump ionisation, the theoretical analysis presented here makes it possible to disentangle the triggered dynamics and attribute it to a few specific, coherently-populated, ionic channels. In terms of charge redistribution across the molecular backbone, the periodic ∼5.5 fs oscillation mode originating from electronic correlation consists of hole-density fluctuations that occur both off-plane and in-plane along the pyrazine skeleton, between the molecular (C–C and C–N) bonds and the carbon and nitrogen atomic centres. The 500 as charge dynamics consists of anti-phase oscillations of the hole-density around the nitrogen and carbon atoms, as can be seen, in Section 3.2, from the spatially-resolved information that can be obtained from the energy-integrated ATAS spectra. In the present work, molecular ionisation is modelled beyond the sudden approximation (SA)3 by fully describing the details of the interaction with the laser pulse as well as the residual interaction between the ionised electron and the remaining ionic core. Therefore, it is interesting to compare the full TD B-spline RCS-ADC(2)x results with those obtained using the SA ansatz.3 This is done in Fig. 4, where the hole-occupation numbers ñp(t) calculated within the SA framework are also shown. The results demonstrate that, in the low-photon-energy limit, the deviations from the sudden approximation results are strong and more pronounced with respect to those present at higher photon energies.18 The pronounced deviations visible in Fig. 4 can be explained by both the different values of the degrees of coherence, which are assumed maximal in the sudden approximation ansatz, and, predominantly, the differences in the amplitudes, i.e. populations and phases, of the created ionic wavepacket. This is due to the fact that, in the low-photon-energy limit, the ionisation partial cross-sections of the various open channels (and respective transition dipole matrix elements in the continuum) usually present a strong non-monotonous energy dependence, which is more pronounced than at higher photon energies. This feature, as well as the specific laser pulse parameters and polarisation, is completely neglected within the sudden approximation and causes the relative ionic-state populations to differ considerably from the spectral intensity values in Fig. 1. The correct description of the ionisation amplitudes, which also define the relative phases imprinted in the ionic wavepacket (see Fig. 3) and thus the characteristics of the prepared many-electron system, is necessary for the accurate simulation and interpretation of ionisation experiments. Therefore, for pulses characterised by photon energies close to the ionisation thresholds of the system, a quantitative description of the induced many-electron dynamics requires modelling of the ionisation step beyond the sudden approximation, including an explicit time-dependent description of the process and, in addition to the correlated motion of the bound electrons, the molecular electronic continua.
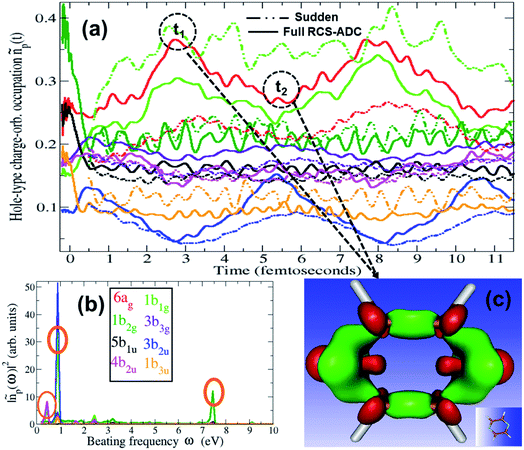 | ||
| Fig. 4 (a) Time-dependent hole-occupation numbers ñp(t) (eqn (11)) of the hole-type natural charge orbitals most contributing to the ultrafast charge dynamics emerging from the pump step ionisation of the C4H4N2 molecule, calculated using the full TD B-spline RCS-ADC(2)x theoretical method (full lines) and the sudden approximation ansatz (dashed lines). The natural charge orbitals with positive occupation number correspond to the removal of one electron from one of the occupied orbitals in the HF ground state, with different coloured lines describing the fraction of the removed bound electron from the HOMO (1b1g) (green curve), HOMO−1 (6ag) (red curve), HOMO−2 (1b2g) (dark green curve), HOMO−3 (5b1u) (black curve), HOMO−5 (1b3u) (orange curve), HOMO−6 (4b2u) (magenta curve), HOMO−8 (3b2u) (blue curve) and HOMO−10 (3b3g) (purple curve) occupied HF orbitals. (b) Fourier-transform of the TD B-spline RCS-ADC(2)x results in (a); the dominant frequencies are highlighted with circles. (c) Charge density representing the difference between the pyrazine hole-densities at times t2 and t1 as indicated in (a); the red and green isosurfaces enclose negative and positive charge densities, respectively. | ||
Moreover, when ionisation happens at photon energies close to the various ionisation thresholds of the molecular system, it is possible to expect a fraction of slow photoelectrons to be produced, which will then be interacting in close proximity with the parent-ion for relatively long times compared to the natural bound-electron timescales. It is therefore interesting to investigate, in the present case of XUV pump ionisation, the effect of the residual inter-channel interaction between the parent-ion and the photoelectron “bath” on the quantum ionic coherence, the ion–photoelectron entanglement and, ultimately, on the ionic charge dynamics while the emitted photoelectron is moving away from the molecular region. In Fig. 5, the full TD RCS-ADC(2)x result for the pump-induced charge dynamics in pyrazine is compared to that obtained by neglecting the inter-channel ion–photoelectron interaction at times t > 170 as after the ionisation event. The results show a quantitative deviation between the two results, demonstrating that, for low-photon-energy pulses, the effect of the interaction with the slower photoelectron on the ionic coherences is stronger than that calculated in ref. 18, where higher photon energies (60–80 eV) were considered. The differences in charge dynamics, when neglecting the residual ion–photoelectron interaction at t > 170 as, are due to the fact that, as can be seen in panel (d) of Fig. 5, the driving quantum electronic coherences keep changing in an appreciable way for longer times. The main coherences responsible for the charge dynamics, G1Ag,2Ag(t) and G3B2u,4B2u(t), become effectively stationary at t ∼ 1 fs after ionisation, whereas the values of other coherences either drop or oscillate for times up to ∼2 fs. At times t > 2 fs after the XUV pump ionisation event, the values of the relevant coherences show an effectively negligible variation, which explains why the charge dynamics computed with the full TD B-spline RCS-ADC(2)x method does not experience any effective damping. The very small residual variation at t > 2 fs reflects the fact that, in agreement with the results presented in ref. 21, the fraction of photoelectrons with “infinitely”-low kinetic energy, that can remain close to the parent-ion for longer times, is effectively negligible. Moreover, this result confirms the validity of using eqn (12), which neglects the residual ion–photoelectron interaction, to describe the interaction of the pump-ionised system with the probe pulse at time-delays τd > 2 fs. The time evolution of all the individual coherences is reflected in that of the purity Tr[ρ2](t) (shown in panel (b)), which shows a fast decay over the first fs after ionisation (with consistent increase in the ion–photoelectron entanglement as measured by the von Neumann entropy s(t)) and a further, slower and relatively smaller decay which persists for the entire time-range of the simulation.
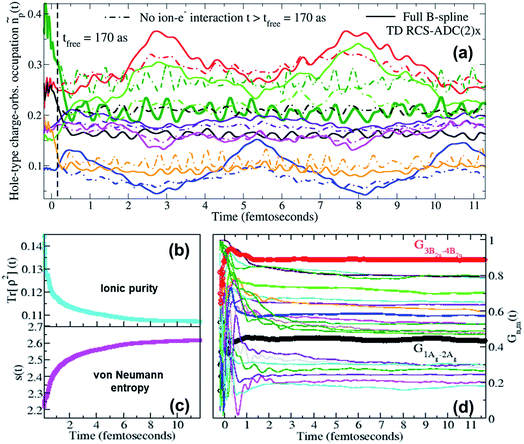 | ||
| Fig. 5 (a) Time-dependent hole-occupation numbers ñp(t) (eqn (11)) of the “occupied” natural charge orbitals triggered by attosecond ionisation of the C4H4N2 molecule in the pump step; full lines: full TD RCS-ADC(2)x results; dashed lines: results obtained by switching off the residual interaction between the parent-ion and the photoelectron at tfree = 170 as after ionisation. Time evolution of (b) the purity Tr[ρ2](t) and (c) the von Neumann entropy of entanglement s(t) of the bipartite ion–photoelectron system after pump ionisation of the C4H4N2 molecule. (d) Time evolution, upon ionisation by the pump laser pulse, of the degrees of coherence Gm,n(t) of the pairs of ionic states mostly contributing to the density-matrix purification (see Fig. 6); the time evolution of the G1Ag,2Ag(t) (black curve) and G3B2u,4B2u(t) (red curve) coherences, mostly contributing to the pump-triggered charge dynamics, are highlighted. | ||
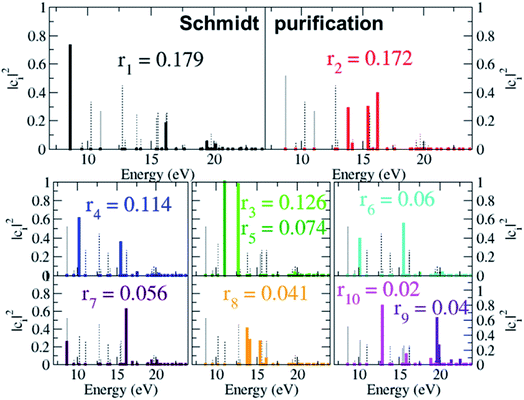
As already mentioned, the results presented in Fig. 4 and 5 have revealed that, despite the high number of open ionisation channels (see Fig. 1) and triggered ionic coherences (see Fig. 2 and 3), the charge dynamics in the pyrazine cation can be effectively traced back to a few quantum electronic coherences, in particular G1Ag,2Ag(t) and G3B2u,4B2u(t), by which it is mainly driven. The question is then: can the description of the full state of the ionic system, i.e. the density matrix, also be simplified and reduced to a few key, physically-relevant, ionic eigenstates? The key theoretical tool that allows us to answer this question is the Schmidt decomposition, i.e. the purification of the ionic density matrix (see eqn (9)). Diagonalization of the ionic density matrix emerging from XUV pump ionisation of pyrazine yields a few pure-state channels with weight greater than 0.1, i.e. whose contributions, more than 10%, dominate the Schmidt decomposition, while the majority of the resulting pure-state channels have negligible contributions (weight rn ≤ 0.01). Therefore, the answer to the above question is affirmative. This is shown in Fig. 6, which shows the weights rn and expansion coefficients |cni|2, in the basis of ionic eigenstates i, of the 10 pure states that contribute most to the purification. Each pure-state channel is a coherent superposition of the ionic eigenstates with a non-zero coefficient |cni|2. In particular, the two coherences G1Ag,2Ag(t) and G3B2u,4B2u(t) arise in the two principal channels with weights r1 and r2, respectively. The r4 channel consists of a coherent superposition of the 1B1u and 2B1u ionic eigenstates, while the r3 and r5 channels in Fig. 6 mainly coincide with the 1B3g and 1B2g ionic eigenstates, respectively. Finally, the coherently-populated ionic eigenstates contributing to the pure-state channels of weight r1, r2 and r3 are the same as those characterising the lower-weighted r6, r7 and r8 pure-state channels shown in Fig. 6. The theoretical simulation presented here therefore shows that the state of the ionic system prepared by XUV pump ionisation of pyrazine can be approximated by a reduced, limited number of physically-relevant pure-state channels, to which the triggered many-electron dynamics can be ascribed, and further allows one to identify and characterise them.
3.2 Simulation of the X-ray probe step: ATAS of pump-ionised pyrazine
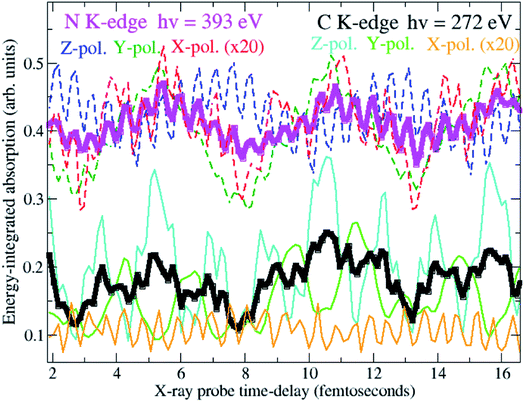
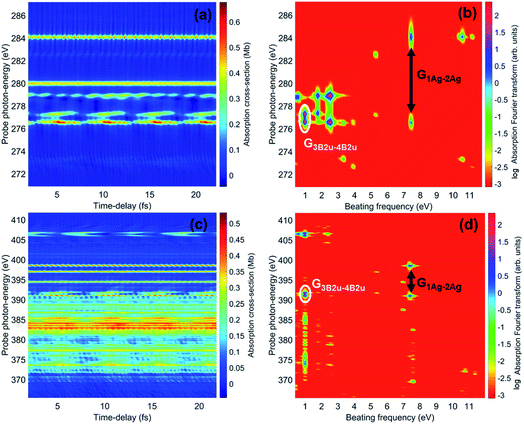
Here I present the results of the TD-ADC simulation of the X-ray ATAS attosecond measurements on the fully characterised ionised state prepared by the XUV pump pulse. The ATAS technique16,30,37–43 is based on the use of a spectrally broadband attosecond probe pulse, with central photon energies suitable for the excitation of an electron from a core shell to the valence shell, which is spectrally dispersed and analysed after being transmitted through the sample under investigation. The spectral decomposition of the measured signal gives information about the different energy level populations within the probed ionic system. Moreover, information on the coherent dynamics of the system can be retrieved by varying the time-delay between the ultrashort pump and probe pulses. This allows one to monitor the valence electron dynamics with both high temporal and high spectral resolution. Atomic spatial resolution is also made possible by the strong atomic localisation of the core orbitals involved in the dynamics as well as the element-specificity of the core-ionised state’s energies.37,44,45 The simulations presented here allow one to shed light on the effects of the strong resonant X-ray probe pulse on the system’s dynamics, model the anticipated experimental pump–probe signals and directly calculate the attosecond measurement’s observable. The purpose of this is to provide answers to the two following questions: (i) can attosecond transient absorption spectroscopy be used successfully in an experiment to evidence and trace the various quantum electronic coherences that can be triggered in attosecond ionisation of a polyatomic molecule? (ii) Is the X-ray probe pulse, under the likely conditions of a real experiment where the pulse intensities are high enough to give measurable signals, “soft” enough not to significantly perturb the relevant many-electron dynamics it has excited in the outer- and inner-valence energy regions, and, at the same time, sensitive enough to capture it?To answer these questions, the density matrix of XUV-ionised pyrazine interacting with the X-ray probe pulse is time-propagated here by solving the TD von Neumann equation in eqn (12). This is done for the three independent linear-polarisation directions of the probe field relative to the molecular frame, namely perpendicular to the molecular plane (x-direction), and along (z-direction) and perpendicular to (y-direction) the C–C bond of the fixed-in-space C4H4N2 molecule. In what follows I focus on orientation-averaged cross-sections for unaligned molecules. The size of the ionic ADC matrices is ∼4000, making the TD Hamiltonian matrix amenable to full diagonalization. Therefore, in this work, the equations of motion (eqn (12)) discussed in the previous section are solved by fully diagonalizing the time-dependent ionic Hamiltonian at each time-step. The calculation is performed for 160 values of the pump–probe delay, ranging from 1 to approximately 22 fs. The time-delay sampling used is 140 as, which is in principle small enough to allow for every coherent oscillation triggered by the pump pulse bandwidth to be resolved. The simulations are carried out for two different Gaussian probe pulses with photon energy centred at 272 eV and 393 eV, i.e. at the average transition-energy between the valence-ionised states of pyrazine and the C(1s) and N(1s) core-ionised states, respectively. Since the C(1s) to valence transitions and the N(1s) to valence transitions are energetically well separated, ATAS allows one to study valence coherent many-electron dynamics in pyrazine with atomic spatial resolution. Moreover, extremely high time-resolution is achieved by using ultrashort pulses of fwhm duration TCProbe = 150 as (C(1s) pulse) and TNProbe = 120 as (N(1s) pulse), corresponding to bandwidths ≥30 eV. The intensity of the probe fields is 5 × 1014 W cm−2. The latter is in fact a relatively low intensity compared to the much higher intensities achievable in X-ray FEL experiments, and presents the advantage of operating in the linear interaction regime. I also assume a uniform intensity distribution over the ionised sample and thus do not perform spatial averaging over the pulse. Fig. 7 shows the time-delay dependent absorption cross-section integrated over selected spectral regions, i.e. the C K-edge and N K-edge energy windows centred at 272 eV and 393 eV, respectively. Results are shown both for the orientation-averaged cross-section and for the three independent linear-polarisation directions of the probe pulse relative to the molecular frame. The orientation-averaged absorption signals, energy-integrated over the carbon and nitrogen windows, reflect the time-evolution of the partial hole-density45 around the C and N atomic centres, respectively, whereas the polarisation-dependent signals are sensitive to the local oscillations of the atomic partial charge along the specific directions. The results show that the charge dynamics takes place at both the carbon and nitrogen atomic centres of the C4H4N2 ring. In particular, it is noticeable that the fast ∼500 as period oscillation characterises both the carbon- and the nitrogen-window curves, but with opposite phases, reflecting a charge dynamics which involves an oscillation of the hole-density between the C and N centres. On the contrary, the two C- and N-window curves show an in-phase ∼5.5 fs oscillation. This indicates that the related charge dynamics (shown in Fig. 4) corresponds to an in-phase oscillatory evolution of the hole-density around the C and N atomic centres.
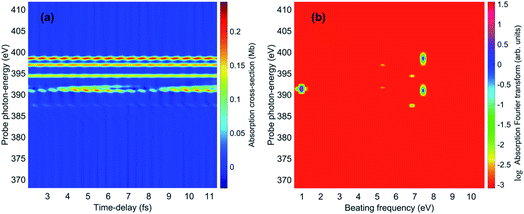
The spectrally-resolved transient absorption spectra at the carbon and nitrogen K-edges are shown in Fig. 8 together with their Fourier-transforms along the time-delay axis, which reveal the quantum electronic beatings resolved by the ATAS measurements. The absorption’s interference pattern, characterised by a rapidly oscillating signal as a function of the pump–probe time-delay, is a result of the electronic beatings within the pump-ionised wavepacket. In particular, the peaks associated with the main core-ionised final states of 1h character and which reflect the predominant quantum beatings governing the charge dynamics of the ionic system are marked in Fig. 8. The time-resolved spectrum in the nitrogen window presents a richer structure compared with that of the carbon-window, with the corresponding time-dependent absorption extending over broader spectral-energy ranges with respect to the very well-defined spectral lines visible in the carbon-window energy range. This is due to the presence of final core-ionised states of mainly 2h1p character in the energy region around the N(1s) K-edge. These states are absent in the vicinity of the C(1s) K-edge, i.e. the carbon-window energy range is predominantly characterised by the main core-ionised states with C(1s) 1h content greater than 0.9. As a consequence, the ATAS spectrum in the carbon-window effectively probes only the 1h content of the valence-ionised initial states. This is demonstrated in Fig. 9, which shows the spectrally-resolved transient absorption spectrum at the nitrogen K-edge, together with its Fourier-transform along the time-delay axis, calculated by neglecting the final core-ionised states of 2h1p character. The 2h1p states describe shakeup resonances in the core-ionised spectrum, as well as providing a very approximate model (based on the discrete set of GTO basis functions forming the RCS) of the double ionisation continuum for dicationic states with a hole in the core orbitals. Thus, their inclusion not only allows one to probe the 2h1p content of the initial pump-ionised channels in the valence energy region, but also gives rise to a background signal that models further ionisation directly from the core orbitals ([|i〉|ai;j〉] → |ai;core〉). The latter transitions include possible single-photon laser-enabled Auger decay (sp-LEAD) transitions46,47 from the initial superposition of states directly to the final |i;core〉 dicationic states. These results demonstrate that, when spectrally resolved, the time-resolved absorbance is sensitive to the different excitation classes participating in the coherent many-electron dynamics and thus provides highly-detailed insight into the correlated many-electron dynamics of a polyatomic molecule such as pyrazine. In particular, as shown in Fig. 10 for the carbon-window, it becomes possible to unveil the mapping between the spectrally-resolved frequency beatings observable in the Fourier-transformed absorption spectrum, and the predominant pump-triggered quantum electronic coherences as given by the ionic-density-matrix purification procedure (see Fig. 6). As can be seen in Fig. 10, by using a short-enough laser pulse and sampling the time-delay with sufficient temporal resolution, down to the attosecond regime, it is possible to resolve all the interference patterns that arise from the main quantum beatings in the system under investigation. The ionic coherences unveiled by the ATAS measurement are in fact the ones which characterise the principal, dominating pure-state channels of the ionic system shown in Fig. 6. This also shows that the X-ray probe pulse used in this work allows the retrieval of the quantum electronic coherences without substantially perturbing the dynamics induced by the pump pulse, e.g. without introducing new coherences. Achieving the necessary temporal resolution in the X-ray regime, by using pulses of attosecond duration with controlled time-delay, has recently become possible both in lab-scale experiments, where HHG sources are used to produce attosecond pulses in the water energy window,48–51 as well as at X-ray FEL facilities such as the Linac Coherent Light Source (LCLS) at Stanford where, following the successful development of the X-ray laser-enhanced attosecond pulse generation (XLEAP) set-up at the LCLS-II machine, recent experiments have demonstrated the production of high-power, isolated sub-femtosecond pulses in the soft X-ray regime.52 Thus, by using appropriate pulses capable of retrieving the calculated ionic coherences Gm,n, the use of the ATAS technique, combined with advanced theoretical simulations of the kind presented above, allows one to unveil the mapping of the measurement results onto the non-zero off-diagonal matrix elements of the ionic density matrix ρm,n, related to the coherences by eqn (8).
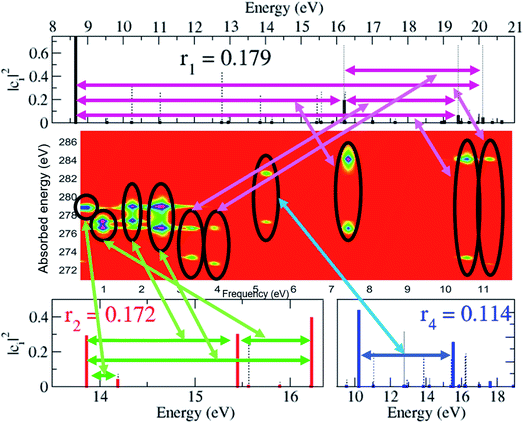 | ||
| Fig. 10 Map between the measurement observable, i.e. the spectrally-resolved frequency beatings detectable in the carbon K-edge transient absorption spectrum, and the predominant pump-triggered quantum electronic coherences as obtained by the ionic-density-matrix purification procedure; the relevant pairs of coherently-populated ionic eigenstates for the pure-state channels of weight r1, and r2 and r4 are indicated by the horizontal arrows on the upper and lower panels, respectively. These pairs coincide with the ones characterising the lower-weighted r6, r7 and r8 pure-state channels shown in Fig. 6. Since the r3 and r5 channels in Fig. 6 mainly coincide with the 1B3g and 1B2g ionic eigenstates, respectively, no correspondent, appreciable, quantum beatings are detected at the presented resolution. | ||
Moreover, the analysis in Section 3.1 demonstrated that the physical observables can be described well within a limited Hilbert space of reduced dimensionality, consisting of the physically-relevant pure-state channels. Under these conditions, the results in Fig. 10 offer the exciting prospect of performing quantum state reconstruction of the ionic density matrix in a molecular system by generalising the same techniques already successfully used to treat an atomic 2-level case16 to systems described by a few additional states. The extent to which this result is affected by also explicitly taking into account the nuclear degrees of freedom remains to be seen, and will mainly depend on the timescales of the resulting decoherence, i.e. whether the electronic coherences live long enough before they are damped as a result of the chemical change that they pre-determine,53,54 and the spatial delocalisation of the ground-state nuclear wavefunction.55 Nevertheless, the importance of these results is in the fact that they demonstrate, by means of advanced ab initio calculations, that the ATAS technique, combined with the use of sub-fs X-ray pulses of the kind that have become available at X-ray FELs,52 is perfectly suitable for imaging the complex many-electron dynamics which emerges from attosecond ionisation of polyatomic molecules, including correlation-driven charge dynamics, and retrieving the quantum electronic coherences that are not completely washed out by the dephasing effect of nuclear motion.
4 Conclusions
Here I have presented a fully ab initio time-resolved study of X-ray attosecond transient absorption spectroscopy (ATAS) in the prototypical polyatomic molecule pyrazine and demonstrated the possibility of retrieving the many-electron quantum ionic coherences arising in attosecond photoionisation and pre-determining the subsequent charge-directed reactivity. The simulation of the complete XUV/X-ray attosecond pump–attosecond probe experiment proposed here has been performed by means of the TD B-spline RCS-ADC ab initio method, with full inclusion of both the outer- and inner-valence molecular ionisation channels. The latter has been extended here to describe the probe step. In particular, the ionic state and related charge dynamics emerging from the XUV pump ionisation have been fully characterised. Strong deviations from the sudden approximation results for ionisation have been demonstrated in the low-photon-energy limit. The relevant time-scales over which the ion–photoelectron multi-channel interaction affects the coherent electron dynamics have been identified. Furthermore, I have shown that the state of the ionic system prepared by XUV pump ionisation of pyrazine can be approximated by a reduced, limited number of physically-relevant pure-state channels, to which the overall many-electron dynamics as well as the ATAS measurement’s observables can be traced back. Therefore, the first-principles theoretical analysis of attosecond experiments presented here allows one to unravel the complex many-electron dynamics triggered by the laser pulses, to identify and characterise the key coherent channels involved, and to map the ATAS measurement observables onto all the main quantum electronic coherences. This work represents a crucial advance in the theory and computational modelling of attosecond pump–probe spectroscopy. It paves the way to achieving quantum state tomography in attosecond photoionisation, unravelling the interpretation of experimental observations in polyatomic molecules in terms of quantum electronic coherences, and ultimately to controlling charge-directed photo-chemical reactivity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the EPSRC/DSTL MURI grant EP/N018680/1.References
- F. Krausz and M. Ivanov, Rev. Mod. Phys., 2009, 81, 163 CrossRef.
- B. W. J. McNeil and N. R. Thompson, Nat. Photonics, 2010, 4, 814 CrossRef CAS.
- L. S. Cederbaum and J. Zobeley, Chem. Phys. Lett., 1999, 307, 205–210 CrossRef CAS.
- J. Breidbach and L. S. Cederbaum, J. Chem. Phys., 2003, 118, 3983–3996 CrossRef CAS.
- A. I. Kuleff, S. Lünnemann and L. S. Cederbaum, Chem. Phys., 2013, 414, 100 CrossRef CAS.
- A. I. Kuleff, N. V. Kryzhevoi, M. Pernpointner and L. S. Cederbaum, Phys. Rev. Lett., 2016, 117, 093002 CrossRef.
- D. Mendive-Tapia, M. Vacher, M. J. Bearpark and M. A. Robb, J. Chem. Phys., 2013, 139, 044110 CrossRef.
- V. Despre, A. Marciniak, V. Loriot, M. C. E. Galbraith, A. Rouzee, M. J. J. Vrakking, F. Lepine and A. I. Kuleff, J. Phys. Chem. Lett., 2015, 6, 426–431 CrossRef CAS.
- M. Vacher, M. J. Bearpark, M. A. Robb and J. P. Malhado, Phys. Rev. Lett., 2017, 118, 083001 CrossRef.
- C. Arnold, O. Vendrell and R. Santra, Phys. Rev. A, 2017, 95, 033425 CrossRef.
- V. Despre, N. V. Golubev and A. I. Kuleff, Phys. Rev. Lett., 2018, 121, 203002 CrossRef CAS.
- E. Romero, R. Augulis, V. I. Novoderezhkin, M. Ferretti, J. Thieme, D. Zigmantas and R. van Grondelle, Nat. Phys., 2014, 10, 676 Search PubMed.
- M. Nisoli, F. Calegari, A. Palacios, P. Decleva and F. Martin, Chem. Rev., 2017, 117, 10760 CrossRef CAS.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martin and M. Nisoli, Science, 2014, 346, 336–339 CrossRef CAS.
- P. M. Kraus, B. Mignolet, D. Baykusheva, A. Rupenyan, L. Horný, E. F. Penka, G. Grassi, O. I. Tolstikhin, J. Schneider, F. Jensen, L. B. Madsen, A. D. Bandrauk, F. Remacle and H. J. Worner, Science, 2015, 350, 790–795 CrossRef CAS.
- E. Goulielmakis, Z. Loh, A. Wirth, R. Santra, N. Rohringer, V. S. Yakovlev, S. Zherebtsov, T. Pfeifer, A. M. Azzeer, M. F. Kling, S. R. Leone and F. Krausz, Nature, 2010, 466, 739–743 CrossRef CAS.
- M. Ruberti, J. Chem. Theory Comput., 2019, 15, 3635 CrossRef CAS.
- M. Ruberti, Phys. Chem. Chem. Phys., 2019, 21, 17584 RSC.
- F. Remacle and R. D. Levine, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6793–6798 CrossRef CAS.
- A. Bruner, S. Hernandez, F. Mauger, P. M. Abanador, D. J. LaMaster, M. B. Gaarde, K. J. Schafer and K. Lopata, J. Phys. Chem. Lett., 2017, 8, 3991–3996 CrossRef CAS.
- M. Lara-Astiaso, D. Ayuso, I. Tavernelli, P. Decleva, A. Palacios and F. Martin, Faraday Discuss., 2016, 194, 41–59 RSC.
- D. Ayuso, A. Palacios, P. Decleva and F. Martin, Phys. Chem. Chem. Phys., 2017, 19, 19767–19776 RSC.
- E. Plesiat, M. Lara-Astiaso, P. Decleva, A. Palacios and F. Martin, Chem.–Eur. J., 2018, 24, 12061–12070 CrossRef CAS.
- M. Lara-Astiaso, M. Galli, A. Trabattoni, A. Palacios, D. Ayuso, F. Frassetto, L. Poletto, S. De Camillis, J. Greenwood, P. Decleva, I. Tavernelli, F. Calegari, M. Nisoli and F. Martin, J. Phys. Chem. Lett., 2018, 9(16), 4570–4577 CrossRef CAS.
- M. Ruberti, V. Averbukh and P. Decleva, J. Chem. Phys., 2014, 141, 164126 CrossRef CAS.
- M. Ruberti, P. Decleva and V. Averbukh, Phys. Chem. Chem. Phys., 2018, 20, 8311–8325 RSC.
- V. Averbukh and M. Ruberti, in Attosecond Molecular Dynamics, ed. M. J. J. Vrakking and F. Lepine, RSC Theoretical and Computational Chemistry Series, 2018, pp. 68–102 Search PubMed.
- M. Ruberti, P. Decleva and V. Averbukh, J. Chem. Theory Comput., 2018, 14, 4991–5000 CrossRef CAS.
- E. Perfetto, D. Sangalli, A. Marini and G. Stefanucci, J. Phys. Chem. Lett., 2018, 9, 1353–1358 CrossRef CAS.
- E. R. Simpson, A. Sanchez-Gonzalez, D. R. Austin, Z. Diveki, S. E. E. Hutchinson, T. Siegel, M. Ruberti, V. Averbukh, L. Miseikis, C. S. Struber, L. Chipperfield and J. P. Marangos, New J. Phys., 2016, 18, 083032 CrossRef.
- M. O. Krause and J. H. Oliver, J. Phys. Chem. Ref. Data, 1979, 8, 329 CrossRef CAS.
- N. Saito, A. Hempelmann, F. Heiser, O. Hemmers, K. Wieliczek, J. Viefhaus and U. Becker, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 61, 022709 CrossRef.
- D. Toffoli, M. Stener, G. Fronzoni and P. Decleva, Chem. Phys., 2002, 276, 25 CrossRef CAS.
- D. M. P. Holland, A. W. Potts, L. Karlsson, M. Stener and P. Decleva, Chem. Phys., 2011, 390, 25–35 CrossRef CAS.
- A. Szabo and N. S. Ostlund, Modern quantum chemistry: Introduction to advanced electronic structure theory, Dover Publications, Mineola, N.Y., 1996 Search PubMed.
- L. S. Cederbaum, J. Schirmer, W. Domcke and W. von Niessen, J. Phys. B: At. Mol. Phys., 1977, 10, L549 CrossRef CAS.
- A. D. Dutoi, K. Gokhberg and L. S. Cederbaum, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 013419 CrossRef.
- H. Wang, M. Chini, S. Chen, C.-H. Zhang, F. He, Y. Cheng, Y. Wu, U. Thumm and Z. Chang, Phys. Rev. Lett., 2010, 105, 143002 CrossRef.
- M. Holler, F. Schapper, L. Gallmann and U. Keller, Phys. Rev. Lett., 2011, 106, 123601 CrossRef CAS.
- R. Santra, V. S. Yakovlev, T. Pfeifer and Z.-H. Loh, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 033405 CrossRef.
- K. Ramasesha, S. R. Leone and D. M. Neumark, Annu. Rev. Phys. Chem., 2016, 67, 41 CrossRef CAS.
- M. Chini, X. Wang, Y. Cheng, Y. Wu, D. Zhao, D. A. Telnov, S.-I. Chu and Z. Chang, Sci. Rep., 2013, 3, 1105 CrossRef.
- C. Ott, A. Kaldun, L. Argenti, P. Raith, K. Meyer, M. Laux, Y. Zhang, A. Blattermann, S. Hagstotz, T. Ding, R. Heck, J. Madronero, F. Martin and T. Pfeifer, Nature, 2014, 516, 374 CrossRef CAS.
- A. D. Dutoi and L. S. Cederbaum, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 023414 CrossRef.
- M. Hollstein, R. Santra and D. Pfannkuche, Phys. Rev. A, 2017, 95, 053411 CrossRef.
- B. Cooper and V. Averbukh, Phys. Rev. Lett., 2013, 111, 083004 CrossRef.
- D. You, K. Ueda, M. Ruberti, K. L Ishikawa, P. A. Carpeggiani, T. Csizmadia, L. G. Olda, N. G. Harshitha, G. Sansone, P. K. Maroju, K. Kooser, C. Callegari, M. Di Fraia, O. Plekan, L. Giannessi, E. Allaria, G. De Ninno, M. Trovo, L. Badano, B. Diviacco, D. Gauthier, N. Mirian, G. Penco, P. R. Ribic, S. Spampinati, C. Spezzani, S. Di Mitri, G. Gaio and K. C. Prince, New J. Phys., 2019, 21, 113036 CrossRef CAS.
- J. Li, X. Ren, Y. Yin, K. Zhao, A. Chew, Y. Cheng, E. Cunningham, Y. Wang, S. Hu, Y. Wu, M. Chini and Z. Chang, Nat. Commun., 2017, 8, 186 CrossRef.
- S. L. Cousin, N. Di Palo, B. Buades, S. M. Teichmann, M. Reduzzi, M. Devetta, A. Kheifets, G. Sansone and J. Biegert, Phys. Rev. X, 2017, 7, 041030 Search PubMed.
- T. Gaumnitz, A. Jain, Y. Pertot, M. Huppert, I. Jordan, F. Ardana-Lamas and H. J. Wörner, Opt. Express, 2017, 25, 27506 CrossRef CAS.
- A. S. Johnson, D. R. Austin, D. A. Wood, C. Brahms, A. Gregory, K. B. Holzner, S. Jarosch, E. W. Larsen, S. Parker, C. S. Strüber, P. Ye, J. W. G. Tisch and J. P. Marangos, Sci. Adv., 2018, 4, eaar3761 CrossRef.
- J. Duris, S. Li, T. Driver, E. G. Champenois, J. P. MacArthur, A. A. Lutman, Z. Zhang, P. Rosenberger, J. W. Aldrich, R. Coffee, G. Coslovich, F.-J. Decker, J. M. Glownia, G. Hartmann, W. Helml, A. Kamalov, J. Knurr, J. Krzywinski, M.-F. Lin, J. P. Marangos, M. Nantel, A. Natan, J. T. O’Neal, N. Shivaram, P. Walter, A. L. Wang, J. J. Welch, T. J. A. Wolf, J. Z. Xu, M. F. Kling, P. H. Bucksbaum, A. Zholents, Z. Huang, J. P. Cryan and A. Marinelli, Nat. Photonics, 2020, 14, 30–36 CrossRef CAS.
- M. Vacher, F. E. A. Albertani, A. J. Jenkins, I. Polyak, M. J. Bearpark and M. A. Robb, Faraday Discuss., 2016, 194, 95–115 RSC.
- I. Polyak, A. J. Jenkins, M. Vacher, M. E. F. Bouduban, M. J. Bearpark and M. A. Robb, Mol. Phys., 2018, 116, 2474–2489 CrossRef CAS.
- M. Vacher, L. Steinberg, A. J. Jenkins, M. J. Bearpark and M. A. Robb, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 040502 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |