Fates and spatial variations of accumulation mode particles in a multi-zone indoor environment during the HOMEChem campaign

Abstract

Studying the indoor dynamics that impact particles is crucial in order to understand indoor air chemistry and assess overall human exposure to particles. This work investigates spatial gradients in particle concentration, caused by indoor transport and loss mechanisms. We conducted a variety of cooking experiments during the House Observations of Microbial and Environmental Chemistry (HOMEChem) campaign in June 2018 that allowed us to probe these mechanisms. We measured size-resolved (0.06–1 μm and 0.13–3 μm) particle number concentrations from cooking experiments using optical instruments at four locations throughout the house simultaneously. The particle number concentration in the kitchen was 40 ± 10% and 70 ± 10% higher than the concentrations in the living room and the bedroom, respectively. There was a minor size dependence, with larger differences in the smaller sizes of the accumulation mode (0.1–2.5 μm) than the larger end of the range. Dilution accounts for the majority of these concentration differences. Surface deposition was the dominant fate of particles within a zone, with observed deposition velocities ranging from 0.1 to 0.6 m h⁻¹.

---

Environmental significance

Aerosol lifetimes and concentrations indoors play a critical role in both indoor air quality and chemistry. Using data from the House Observations of Microbial and Environmental Chemistry (HOMEChem) campaign we analyzed the processes controlling aerosol lifetimes and spatial variations in aerosol size and concentration, providing new insight into the importance of various mechanisms controlling deposition and aerosol transport in indoor environments. Traditionally considered physical processes controlling aerosol lifetime within a room, such as deposition and exfiltration, are shown to be too slow to account for the large spatial variations observed, and alternative mechanisms are addressed. These results can be used to improve both modeled aerosol process as well as aerosol chemistry and exposure in indoor environments.

1. Introduction

Annually, ambient air pollution accounts for approximately 3.7–4.8 million deaths globally.¹ One important pollutant that contributes to air quality is particulate matter. Particles have been shown to have a significant impact on health, and are a major cause of cardiovascular and respiratory disease.^2–4 Particles present in the built environment contribute substantially to overall exposure,⁵ as people spend more time indoors than outside. In the US alone, people spend an average of 80–90% of their time indoors.⁶ The impact of particles on human health is a function of their concentration, size, and composition, which are influenced by emission sources, a variety of dynamic processes (e.g. deposition, coagulation, and gas-to-particle partitioning), and building mechanics (e.g. natural and mechanical ventilation, infiltration air exchange, filtration, envelope penetration, and interzonal transport).^7–11 In order to better understand the full effect of indoor environments (relative to outdoor environments) on human exposure to particles, a quantitative description of the sources and sinks, including transport and deposition, of indoor particles is essential.

Indoor sources of particles include gas stoves,¹² printers,^13,14 3D printers,^15,16 cigarette smoke,¹⁷ and human activity¹⁸ which have been well quantified elsewhere. Cooking is a dominant source of particle indoors and mainly contributes to ultrafine (<100 nm) and fine (100 nm to 2.5 μm) mode particles.^12,19,20 After emission, particles can deposit onto surfaces in the building and ventilation system, coagulate to form fewer but larger particles, and undergo gas–particle partitioning where particles are transformed when individual compounds evaporate off or condense onto particles.⁷ In addition, particles can be transported from room to room within indoor environments and potentially outdoors.⁷ Transport away from particle sources induces spatial gradients within buildings, which are influenced by building mechanics, environmental conditions such as temperature and humidity, and size-dependent particle losses.

While several models have been proposed for predicting particle spatial gradients,^21–25 there have been few comprehensive measurements of these gradients in occupied houses. The first studies to explore spatial variation indoors focused on overall concentration differences between rooms (zones) within a building. Ju and Spengler (1981) measured 24 h averages of respirable particles in four homes in Boston, MA, and observed significant zonal differences in half the homes.²⁶ Multi-zone experiments done by Miller and Nazaroff (2001) on environmental tobacco smoke using time- and size-resolved measurements in a two-room facility observed a 14–97% drop in particle mass concentration across zones after emission events.²⁷ The magnitude of this difference was dependent on ventilation and zone segregation conditions: increasing ventilation resulted in a 57–83% difference while segregating the two zones resulted in a 97% difference in particle mass. Other studies have since expanded on these observations including zonal differences in trace gas species.^28–30 However, most previous research on multi-zone systems has utilized simple two-zone environments, unoccupied houses, or has been limited in the number of size-resolved measurement points. Quantifying indoor spatial gradients of particles, both in terms of concentration and size, is necessary to accurately characterize and minimize human exposure to indoor particle sources and gain insight into particle chemistry occurring throughout an indoor environment.

The objective of this work was to critically analyze particle gradients observed in a test house during cooking events using several optical particle measurements. In order to fully characterize the fates of accumulation mode particles indoors, we looked at particle production during cooking, particle transportation through the house, and major loss mechanisms between and within different zones. Data presented here were collected as part of the House Observations of Microbial and Environmental Chemistry (HOMEChem) study, a month-long indoor chemistry campaign conducted in the UTest House at the University of Texas at Austin.³¹

2. Methods

2.1 Experimental overview

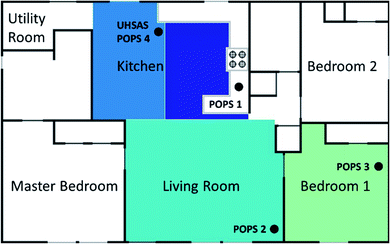
The HOMEChem campaign took place from 1 to 30 June 2018.³¹ HOMEChem included a comprehensive suite of chemical and physical measurements that monitored both particle and gas-phase species during cooking, cleaning, and occupancy activities. The campaign utilized the UTest house at the University of Texas at Austin (Austin, TX, USA); a 3-bedroom, 2-bath house with a total house volume of 250 m³ and a total floor area of 111 m². This analysis separated the house into three main zones: the kitchen, living room and bedroom (Fig. 1).

Fig. 1 Floor plan of the UTest house. Black dots and labels indicate instrument sampling positions. Colors for the different zones on this plot indicate how the data in this paper will be organized, with the darkest color being the measurement closest to the source (kitchen) and the lightest color being the furthest from the sources (bedroom 1). The kitchen is considered a single zone in this analysis but has two colors to represent the two different instruments and sampling points within the zone.

The outdoor air-change rate (ACR) of the house was maintained at 0.5 ± 0.1 h⁻¹ by positively pressurizing the house relative to the outdoor environment when both of the two doors and all nine windows were closed. This minimized variations in temperature and humidity around the house. During the campaign, the electric air handling unit with overhead air diffusers was operated continuously with a recirculation flow rate of 8 h⁻¹ (2000 m³ h⁻¹). Filters on the outdoor air supply and internal ducts were removed during the campaign, to ensure results were not affected by the filter conditions,^9,10 and no stove exhaust hood was used during the study. The air conditioning (AC) system was set to 25 °C throughout the campaign, except during designated venting periods. The AC system also provided dehumidification when cooling. Indoor temperature was 25 ± 2 °C and indoor relative humidity was 57 ± 6% on experimental days. Outdoor temperature and relative humidity were 29 ± 4 °C and 71 ± 17% respectively throughout the campaign. Further details about the ventilation system employed during the campaign are described elsewhere.³¹

In order to investigate interzonal transport and deposition of particles indoors the cooking experiments from the HOMEChem campaign were investigated. Cooking experiments during HOMEChem included a total of sixteen vegetable stir-fry experiments, six breakfast experiments, three chili experiments, ten toast experiments, and two full typical U.S. Thanksgiving meals. Further details of the campaign set-up and experimental schedule are described elsewhere.³¹

2.2 Instrumentation

Size-resolved particle concentrations were measured using an Ultra-High Sensitivity Aerosol Spectrometer (UHSAS, model UHSAS-G; DMT Inc., Longmont, CO),³² which was calibrated regularly throughout the campaign using NIST standard polystyrene latex spheres (60–900 nm mobility diameter). We ran daily filters on the UHSAS to monitor instrument background and ensure that there were no internal leaks. The UHSAS was set to have 1 second resolution and count particles in 99 size bins between 0.06 and 1 μm by directing a solid-state laser (1054 nm) at the sample air flow and quantifying the resulting particle size-dependent scatter. Indoor air was sampled through an 8 m copper sampling line (ID: 6.35 mm) and outdoor air was sampled through a separate 4.8 m copper line (ID: 6.35 mm). Both lines connected to a 1.5 m segment of stainless-steel tubing (ID: 6.35 mm) attached to the valve switching system that included a HEPA bypass system for running blanks and a Nafion dryer (MD700, Perma Pure LLC, Lakewood, NJ) which all normal sampling ran through. The UHSAS sampled at 50 mL min⁻¹ off the line, which had a total flow of ∼ 6 L min⁻¹ (Re ≈ 1300; residence time of 3 s in the main line). Line losses calculated using the method described by Weiden et al. (2009) were negligible for the measured size range (<5%).³³ Throughout the campaign the UHSAS typically switched at regular intervals between indoor (25 min) and outdoor sampling (5 min).

We simultaneously measured particle size distributions in four locations within the test house using four Portable Optical Particle Spectrometers (POPS; Handix Scientific LLC, Boulder, CO).³⁴ These instruments measure particles ranging from 0.13 to 3 μm using a 405 nm laser diode, and collected a size distribution every second. Both the UHSAS and the POPS correlate light scatter to particle size following Mie theory. The four POPS were placed in the kitchen, living room, and one of the three bedrooms of the test house (Fig. 1), as well as in an external trailer to monitor outdoor conditions. The POPS had a 1.0 cm long stainless-steel inlet nozzle (ID: 0.81 mm) as an inlet housed in a stainless-steel tube (ID: 1.75 mm). The flow rate through the inlet was set to 180 mL min⁻¹. Particles were not actively dried like the UHSAS line was with the Nafion dryer, but sample flow was mixed with a filtered sheath flow which likely reduced the RH near particles.

Optical instruments have limitations on the magnitude of particle concentrations they can measure and can be biased because of differences in the composition of particles used for calibration and the particles measured. To address these limitations, we preformed saturation analysis and compared the optical measurements to a scanning mobility particle sizer (SMPS, TSI Inc., Shoreview, MN) that was present during the campaign. The intercomparisons of the optical instruments with the SMPS show good agreement between the average measured distributions in the size ranges used for analysis, validating the use of these instruments for the size dependent analysis presented here. Total concentration was underestimated compared to the SMPS indicating that further corrections would need to be applied (i.e. refractive index, saturation, etc.) if this data was being used to characterize cooking emissions, however, that is outside the scope of this work. Data presented herein utilizes the full size range of all instruments except during instances where total concentrations are compared across the two instruments. Additionally, periods where saturation had a significant effect on the UHSAS measurements – saturation was not observed in the POPS measurements – were removed from the analysis. In cases of saturation, only data for the unaffected size bins of the UHSAS are presented. A detailed description of all instrument intercomparisons, saturation analysis, and data treatment, can be found in the ESI (Section S1†).

2.3 Calculation of deposition velocity

We derived the rate of deposition from the total particle concentration loss rate after the termination of cooking events using the general method described by Thatcher and Layton (1995).³⁵ However, in these measurements we omit the initial decay period from the calculation of the particle loss rate to account for the impact of dilution. The initial decay period ends when the house becomes well-mixed, at which point we assume exfiltration – controlled by the ACR of the house – and deposition are the major sinks of particles. Deposition within the ductwork was neglected because of the small size of the particles and the high recirculation rate. We assume particle removal by filtration within the recirculation ducts was zero due to the absence of filters. However, the impact of recirculation on turbulence characteristics and deposition is poorly understood and may warrant future study. The house was assumed to be well-mixed at the point when POPS concentration data from around the house converged on each other. We determine loss rate due to deposition loss as well as loss due to exfiltration using a linear fit to the natural log of the decay for the period after the cooking event had been terminated – the stove was turned off – and the house had achieved a well-mixed state. The deposition loss rate (λ_d) was calculated: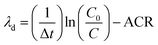where Δt is the time change between the initial and final concentration, C₀ is the initial concentration (particles per cm³) at the start of the decay period when the house was well-mixed, C is the concentration (particles per cm³) at the end of the decay. Deposition velocity, ν_d (m h⁻¹)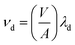, was derived using an approximate volume (V, m³) to area (A, m²) ratio:

We derived the volume-to-surface-area ratio to be 0.47 from the room geometry of bedroom 1 where a POPS was located. It was the only zone monitored that had well-defined boundaries that could be used to constrain this ratio. Using this geometry, the surface-area-to-volume ratio was determined to be 2.1, consistent with the findings of Manuja et al. (2019) who found this ratio to be 2.0 ± 0.2 for bedrooms when the contents of the room were not considered and 3.0 ± 0.4 when the contents were included.³⁶ While bedroom 1 was unfurnished, we acknowledge that additional objects or people could alter these ratios and this is discussed in the deposition modeling section. The application of the bedroom's volume-to-surface-area ratio to all the measurements is justified by the fact that the observed trend in deposition loss rate was consistent across the different zones of the house and the zones were similarly unfurnished.

2.4 Deposition models

Two models were compared to the experimentally determined deposition velocities. The first was the indoor deposition model developed by Lai and Nazaroff (2000).³⁷ This model estimates total deposition using the surface-area-to-volume ratio of the indoor space and the deposition velocities for different indoor surfaces (i.e. floors, ceilings, and walls) (Section S2†).

The second model used was an outdoor resistance model developed by Emerson et al. (2020), which is a modification of the Zhang et al. (2001) model (Section S3†).^38,39 This model was originally designed to apply to outdoor environments, such as forests or grasslands, and breaks down deposition into contributions from Brownian diffusion, gravitational settling, impaction, and interception to total deposition velocity. The land use category and seasonal select category for a needleleaf forest in the midsummer were used to represent the indoor environment. These parameters determine the characteristic radius of the collectors (2 mm) and the roughness length (0.8 m). An air speed typical for an indoor environment (v = 0.1 m s⁻¹) was applied, and the measurement height (z_r) was set to the UHSAS inlet height (∼1.5 meters). Other model parameters are described in the ESI (Section S3†).

For both models a particle density of 1 g cm⁻³ was used based on evidence described in Patel et al. (2020) suggesting this as an appropriate density for cooking particles. Friction velocities (u_*), which are velocity measurements representing the shear stress between flows, ranging from 0.01 to 0.03 m s⁻¹ are considered reasonable for an indoor environment. Several friction velocities were applied to both models, ranging from 0.01 to 1 m s⁻¹, in order to determine the best fits to the data.

2.5 Spatial gradient and dilution calculations

The concentration gradient was calculated using the average size-dependent concentrations for the cooking event during the cooking period – defined by an experimental log as the time when the stove was turned on to the time the stove was turned off. The percent difference was calculated as the change in the other zones compared to the kitchen values. Time off-sets between when enhancement was observed in the different zones was not used shift the data. The size-dependent percent differences for all the cooking events were averaged and we present the median for all the cooking events.

We assumed each zone to be well-mixed. The measured kitchen particle concentration was taken to be representative of the entire kitchen volume (∼40 m³). The kitchen particle concentration was diluted into the adjoining spaces: the utility room (∼9 m³) and living room (∼52 m³). This method was also used to estimate the particle concentration in the bedroom by diluting the measured living room particle concentration into its adjoining spaces: the master bedroom (∼36 m³) and bedroom 1 (∼28 m³). These calculations do not include the volume from closed spaces (i.e. bathrooms and closet spaces) and the hallway space in the dilution volume. These spaces can be neglected since their collective volume only produced a 3–5% change in the predicted distribution when included. This method neglects the impact of dilution and repartitioning of semi-volatile particles.

3. Results and discussion

Cooking particles were used to investigate interzonal transport and deposition indoors; however, the results herein are not differentiated by the cooking method. Analysis of different cooking sources indoors is outside the scope of this work but is well documented by Patel et al. (2020). Background conditions, such as particle concentration and indoor-to-outdoor concentration ratios, as well as some source observations, are described in the ESI (Sections S4 and S5†).

3.1 Sinks for indoor particles

Accumulation mode particles throughout the house had loss rates ranging from 0.66 to 1.95 h⁻¹, which encompass the losses due to surface deposition and exfiltration. Concentration decay was size-dependent with the slowest decay corresponding to particles around 200 nm. Loss rates did not vary substantially for accumulation mode particles across cooking type or between zones. This indicates that in the context of this work, cooking data from our measured size range can be treated similarly regardless of cooking method when determining major sinks for particles indoors (Section S6†). We evaluate possible sinks for accumulation mode particles using direct observations and theoretical calculations. We evaluate different sink contributions to the net loss and explore the factors controlling these sinks.

Deposition is one of the dominant processes that drives particle loss indoors. The deposition trends observed during the cooking emission experiments were size dependent with particles around 200 nm in the accumulation mode depositing least efficiently due to less influence from the mechanisms driving deposition (Fig. S13†).⁴⁰ These data are consistent with previous studies that examined size-resolved deposition indoors for accumulation mode particles.^41–45 Deposition measurements made by Tian et al. (2020) for deposition of supermicron particles during the HOMEChem campaign seamed together well with our observations and are used here to present a more meaningful analysis of the mechanisms controlling deposition.⁴⁶

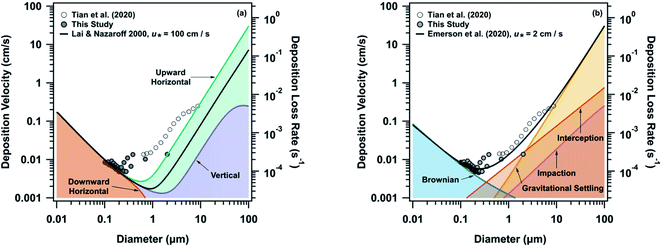
In order to understand the intricacies of deposition of particles in indoor environments, we probed different mechanisms controlling deposition using two models. First, the widely-used indoor deposition model developed by Lai & Nazaroff (2000) is useful for understanding the particle contribution to deposited films on surfaces.³⁷ However, this model did not accurately capture the observed deposition at HOMEChem (Fig. 2a). In order to better constrain this model, we investigated the impact of both the friction velocity term and the surface-area-to-volume ratio. A friction velocity (u_*) of 1 cm s⁻¹ resulted in a 98.7 ± 0.5% underestimation of deposition. The model only agreed with deposition velocities measured for particles less than 200 nm, when a u_* of 100 cm s⁻¹ was used (Fig. S15†). Large u_* values have previously been used with this model to enable reasonable fits with observed data,⁴¹ although most literature suggests that reasonable u_* values for indoor environments are in the range of 1–3 cm s⁻¹.³⁷ Even with the larger u_* the model underrepresented deposition rates by up to 82% (10 ± 20% on average) in the accumulation mode and 86 ± 6% on average in the coarse mode (Fig. S14†). In order to constrain the surface-area-to-volume ratio used in the model, the ratio was varied according to Manuja et al. (2019).³⁶ Based on this analysis, the surface-area-to-volume ratio could be used to fine tune the model approximation; however, modifying this ratio did not significantly change the agreement between the model and observed deposition rates (Fig. S16†). This analysis also agrees with the findings of Thatcher et al. (2002) (Fig. S17†), where even in a more realistic fully furnished room the Lai and Nazaroff (2000) model underrepresented particle deposition for particles smaller than 0.5 μm by an order of magnitude.⁴³

Fig. 2 Size-dependent deposition for accumulation mode aerosols from this study and coarse mode particles from Tian et al. (2020) observed for cooking aerosols during HOMEChem. The measured deposition is compared to (a) the indoor model developed by Lai and Nazaroff (2000) and (b) the outdoor model developed by Emerson et al. (2020). In both plots deposition velocity is displayed on the left axis and deposition loss rate is displayed on right axis. The data from this study, both POPS and UHSAS data, are represented by the filled data points.

The second model we used (Fig. 2b) was the outdoor resistance model of Emerson et al. (2020), which is based on the framework of Slinn and Zhang.^39,47 The Emerson model places emphasis on interception as an efficient collector of aerosols, and is thus appropriate for deposition to irregular, non-horizontal surfaces. The outdoor model agreed well with the measured deposition velocities, with an average difference of 10 ± 9% in the accumulation mode and 30 ± 10% in the coarse mode (Fig. S14†). The model was also able to accurately reproduce the minimum (around 200 nm) in the observed deposition trend, in contrast to Lai and Nazaroff (2000). Tian et al. (2020) provide deposition rates for supermicron cooking particles at HOMEChem. Impaction and interception likely affect particles larger than 10 μm, which is at the limit of most indoor deposition measurements. Further measurements are thus needed to characterize the processes driving deposition of larger particles indoors. However, the close agreement of the Emerson model and the HOMEChem deposition measurements suggests that this resistance-based approach may be a useful alternative to the established Lai and Nazaroff approach in indoor settings.

Our model comparisons indicate that interception is playing a larger role in indoor deposition than currently accounted for and that current indoor models are likely underestimating particle loss rates even when elevated u_* values are used. The agreement between our observed indoor deposition rates and the outdoor Emerson et al. (2020) model shows that incorporation of interception terms, as well as an increased emphasis on the physical processes controlling particle deposition could led to improvements in indoor deposition models. This conclusion is consistent with previous literature: Thatcher et al. (1996) showed from experiments measuring deposition rates of fluorescent particles onto surfaces in a small chamber that deposition models did not consider all of the physical processes influencing particle deposition, additionally Lai (2005) added interception terms to the widely-used Lai and Nazaroff (2000) model to improve model-measurement comparisons over an array of surfaces.^48,49

The significance of underestimating particle deposition with the current indoor models is clearly illustrated through particle lifetime calculations. Using the Emerson et al. (2020) model, deposition loss rate for 100 nm, 1 μm, and 10 μm particles are estimated to be 0.0001 s⁻¹, 0.001 s⁻¹, and 0.01 s⁻¹ respectively. Using these rates, the lifetimes of these particle sizes with respect to deposition are approximately 3 hours, 17 minutes, and 2 minutes, respectively. However, when the same estimation is done using the Lai and Nazaroff (2000) model – with a u_* value of 2 cm s⁻¹, as used in the Emerson et al. (2020) model to obtain the best fit to the data – the lifetimes for the same sized particles become 74 hours, 20 hours, and 14 minutes, respectively. This elevation of lifetime with respect to deposition is highly problematic for determining what controls particle lifetime indoors. If we compare these rates with the particle lifetime from exfiltration, which is approximately 2 hours (based off an average ACR of 0.5 h⁻¹ for the house), we see that the Lai and Nazaroff (2000) model predicts that exfiltration will control the lifetime of all accumulation mode aerosols when in actuality the lifetime of larger accumulation mode and coarse mode particles are determined by their deposition rate. Both models suggest that lifetimes of smaller accumulation mode particles are impacted more by the ventilation of the house. Of course, lowering the ventilation rate will enhance the relative importance of deposition. These discrepancies are particularly relevant when considering the effectiveness of ventilation in controlling particle lifetime – Bond et al. (2020) suggest that these discrepancies in predicted indoor deposition rate may be substantial enough to impact recommendations for different mitigation techniques for reducing exhaled respiratory aerosol exposure.⁵⁰

Coagulation is a second order process, dependent on concentration and is therefore important in areas of high concentrations, however, initial analysis of the size distribution over the course of typical cooking events did not indicate evidence of coagulation within the measured size range (Fig. S18†). In order to strengthen these observations and rule out the impact of coagulation on accumulation mode particles, we calculated coagulation rates based on an average particle distribution during cooking from the UHSAS, which included the median diameters and average associated concentrations (Table S11†).⁵¹ These calculations indicate that over the course of an hour coagulation would only lower particle number concentration by 1–6%, thereby ruling out coagulation as a major sink for accumulation mode particles during typical cooking events (Fig. S19†). This result was the same when concentrations of larger particles from a POPS were included in the calculations. However, during Thanksgiving experiments, the peak particle concentration was about four times higher than the concentration of the other cooking events. The elevated particle concentrations lasted longer due to the sustained nature of the cooking events. Visual analysis of particle size distribution evolution during Thanksgiving indicates that coagulation is occurring (Fig. S18†), and the theoretical calculations indicate that coagulation could account for a 1–12% decrease in particle concentration (Fig. S19†). The recirculation time (2000 m³ h⁻¹) is on average 30 times and 20 times greater than the calculated coagulation rate for typical cooking (0.03–10 particles per cm³ per h) and Thanksgiving (0.002–30 particles per cm³ per h) events respectively. These data indicate that when indoor mechanics – like an enhanced rate of air recirculation in the house – are impacting particles by rapidly mixing particles through the space, particle concentration needs to be highly elevated for a period that greatly exceeds the air residence time of the house before coagulation occurs in the accumulation mode.

3.2 Transport and spatial variation of particles

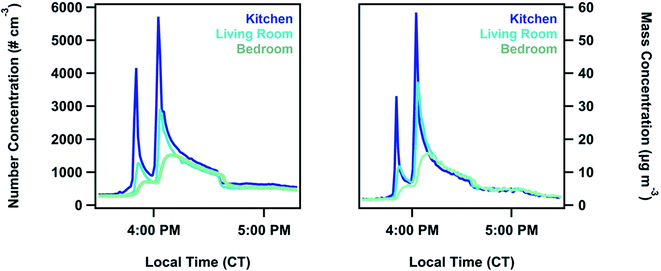
Size distribution characteristics have been previously observed in multi-zone environments;^27,30 however, processes that control the changes in magnitude and shape of particle size distributions between zones have not been thoroughly explored. In this work, we analyzed different zonal distributions to determine which size-dependent physical processes contribute to the development of a spatial gradient.

During all cooking events, a significant concentration gradient was observed throughout the house (Fig. 3). This gradient persisted until the end of the cooking event. Between the kitchen and the living room there was, on average, a 40 ± 10% decrease in the total particle number concentration, integrated over the entire cooking event (30 ± 20% for surface area, and 30 ± 20% in mass). Number concentration in the bedroom was, on average, 70 ± 10% lower (60 ± 10% for surface area, 50 ± 20% in mass) than what was measured in the kitchen. The spikes in the concentration during events had a slight time offset between zones, with 0.7 ± 0.1 minutes between kitchen and living room signal peaks and 2.4 ± 0.9 minutes between the kitchen and the bedroom peaks.

Fig. 3 Time series of a typical stir-fry cooking event, with data from the POPS in all three rooms monitored during the experiments. The left panel shows number concentration and the right panel shows mass concentration (using an assumed density of 1.0 g cm⁻³) over the course of the stir-fry.

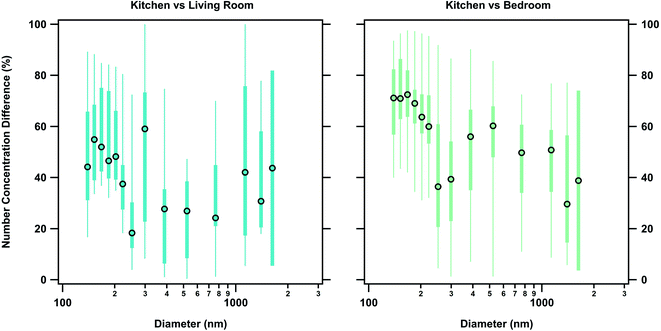
We observed a particle size dependence in the concentration gradient. Percent differences were calculated as a function of size using the POPS data. Accumulation mode particles between 130–250 nm generally had a higher percent difference compared to 250 nm to 3 μm particles (Fig. 4, Tables S12 and S13†). This size dependence explains the small changes in percent differences for total concentration measurements in number, area, and volume space for the measured size range. Higher percent differences between the zones for the particles bellow 250 nm indicate that a loss mechanism favoring the removal of these particles is contributing to spatial variation. One possibility for this removal mechanism is the entrapment of smaller particles in eddies created by the air flow through the house. Due to their smaller inertia and relaxation times, accumulation mode particles become trapped in the circulating flows of the house and are therefore not transported as easily as coarse particles are between zones. This mechanism has been proposed by multi-zone models but not directly observed before this work.^52,53

Fig. 4 Size-dependent percent changes in aerosol number concentration between the kitchen and the other zones. The lower and upper bounds of the boxes represent the second and third quartiles, respectively, and the center point indicates the median of the data. The lower and upper tails mark the minimum and maximums of the data. Smaller accumulation mode particles (>250 nm) had larger concentration differences between the kitchen and living room (left) and the kitchen and the bedroom (right) than the larger particles (<250 nm) in the mode.

3.3 Impact of sinks on spatial variation

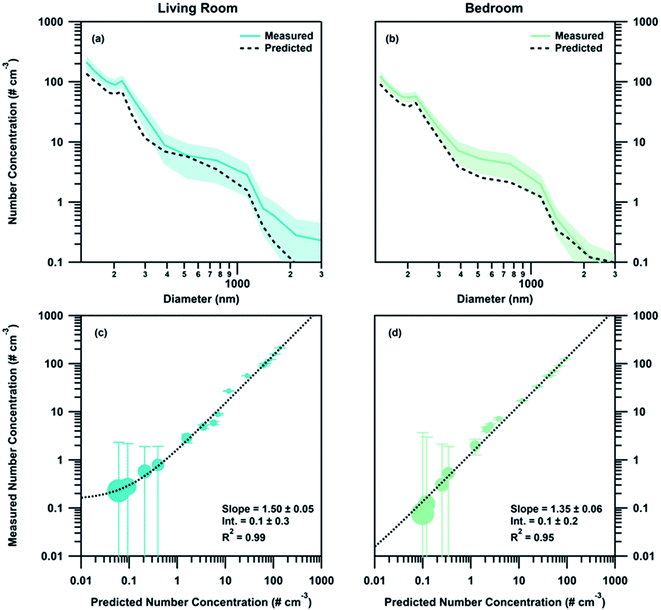
While deposition and exfiltration are the dominant sinks for particles within a given zone, their estimated contribution to the measured loss rates are too slow to account for the magnitude of the particle concentration differences between zones for the measured size range during HOMEChem. Using the observed time offset (0.7 ± 0.1 minutes and 2.4 ± 0.9 minutes for the living room and bedroom respectively) between particle appearance in the different zones and the observed deposition and exfiltration rates, we calculated the contribution of each of these sinks to the gradient observed. Application of estimated losses from deposition and exfiltration to the measured particle concentration in the kitchen resulted in a 0.009 ± 0.006% loss between the kitchen and the living room and a 0.03 ± 0.02% loss between the kitchen and the bedroom. This change is negligible compared to the observed losses between the zones, therefore ruling out deposition and exfiltration as mechanisms that contribute significantly to the development of concentration gradients indoors. The minor impact of deposition on these concentration gradients is also evidenced by the fact that 130–250 nm accumulation mode particles had higher percent differences than the 250 nm to 3 μm particles. If the observed particle concentration gradient was driven by deposition losses, there would be larger differences in the concentrations of 250 nm to 3 μm particles due to their larger deposition rates. For example, a 1 μm and 200 nm particle had observed deposition rates of approximately 0.7 ± 0.2 h⁻¹ and 0.3 ± 0.2 h⁻¹ respectively. If the gradient was driven by deposition alone, then larger accumulation mode particles would have approximately two times the loss of the smaller particles.

Dilution, via transport through the house, accounts for the bulk concentration change between zones. Calculated diluted distributions using the overall zone volumes compared well with the measured distributions although underestimated the concentration (slope of 1.50 ± 0.05, R² = 0.99 for the living room comparison and slope of 1.35 ± 0.06, R² = 0.95 for the bedroom comparison) (Fig. 5). The high associated error in larger size bins (produced by the low counts recorded for those particles) was accounted for when comparing the measured and calculated distributions. Agreement between measured concentrations and dilution calculations indicate that the loss between zones can be approximated using a simple dilution calculation when the internal recirculation rate of the indoor environment is high. Increased flow through the recirculation system (equivalent to 8 house volume exchanges h⁻¹) did not contribute significantly to the observed gradient; when applied to the observed kitchen measurements it produced a 0.07 ± 0.04% change between the kitchen and living room and 0.2 ± 0.1% change between the kitchen and bedroom.

Fig. 5 Average particle distribution for an entire stir-fry cooking event compared to the diluted source measurement: (a) kitchen to living room and (b) the living room to bedroom. The shaded regions represent the standard deviation of the measurement. Direct comparison between the diluted approximation to the measured distribution in (c) the living room and (d) the bedroom, with the error bars representing the error of the measurement. Marker size in the bottom panels is representative of particle size.

4. Conclusions

Significant spatial differences in particle concentration persist indoors throughout emission periods. Deposition and dilution are the most important factors controlling particle concentration within a zone. Larger differences in the accumulation mode particles between 130–250 nm compared to 250 nm to 3 μm particles between zones during cooking indicate that there is an additional loss process that favors smaller particles. This additional loss could be a result of indoor air flow trapping smaller particles as they are transported, which has been speculated in multi-zone models – but not directly observed before our work.^52,53 Additionally, the deposition observations herein show that widely-used indoor models are inadequate for predicting particle deposition indoors, typically leading to an underestimate in particle loss rates for the accumulation mode. Incorporating interception terms into existing models improve model-measurement comparisons for this study, and may similarly improve the observed model-measurement discrepancies in previous studies.⁴⁹ Understanding and accurately modeling deposition processes is crucial for understanding particle lifetimes indoors, which determine how long particles, including those containing disease causing agents, persist in indoor environments. Characterizing deposition indoors is therefore necessary in establishing particle impact on human health and determining mitigation strategies.

However, these findings extend beyond understanding indoor particle dynamics and have implications for surface chemistry, gas uptake onto particles, and exposure assessments. Particle deposition impacts surface reservoirs indoors, which control multiphase surface chemistry.⁵⁴ Observed airborne gradients in particle concentration imply differences in particle loadings on surfaces, which would in turn modulate surface chemistry in different zones. Particle concentration and composition both influence gas-phase uptake onto particles.^55,56 Observed gradients indicate that this concentration-dependent partitioning process will occur differently throughout the house during cooking periods. For example, the uptake coefficient of dinitrogen pentoxide (N₂O₅) – which has been detected in indoor environments during cooking⁵⁷ – is inversely proportional to the available particle surface area.⁵⁸ Using our observed percent differences in particle surface area between zones, we estimate that N₂O₅ uptake could increase by 40% between the kitchen and the living room. However, this process is also complicated by the high surface-to-volume ratios of indoor environments, where particle surface area in the kitchen, living room, and bedroom only accounts for maximum of 0.06%, 0.04%, and 0.02% of the total available surface area, respectively. This would be especially true in fully furnished, more realistic environments. Thus, further analysis of indoor spatial variations in particle and gas species concentrations are needed to fully characterize the impacts of spatial gradients on partitioning processes.

Finally, these observed spatial gradients have significant implications for exposure assessment to individuals. Particle concentration indoors not only determines an individual's exposure to particulate matter, but can also dictate exposure to lower volatility gas-phase species like diethylhexyl phthalate (DEHP),^56,59 a common indoor phthalate found in building materials.⁶⁰ Particle phase DEHP correlates with increased particle concentration indoors, a process attributed to surface-to-gas-to-particle exchanges.^56,59 Transport of particles therefore provide a mechanism to move pollutants through homes. Our observations suggest this partitioning processes and subsequent exposures may have strong spatial gradients in the indoor environment.

Conflicts of interest

The authors have no conflict to declare.

Acknowledgements

Funding provided by the Alfred P. Sloan Foundation (G-2017-9944; G-2019-12442). We thank the entire HOMEChem science team, including Drs Atila Novoselac and Steve Bourne for operating the UTest house.

References

1. A. J. Cohen, M. Brauer, R. Burnett, H. R. Anderson, J. Frostad, K. Estep, K. Balakrishnan, B. Brunekreef, L. Dandona, R. Dandona, V. Feigin, G. Freedman, B. Hubbell, A. Jobling, H. Kan, L. Knibbs, Y. Liu, R. Martin, L. Morawska, C. A. Pope, H. Shin, K. Straif, G. Shaddick, M. Thomas, R. van Dingenen, A. van Donkelaar, T. Vos, C. J. L. Murray and M. H. Forouzanfar, Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: an analysis of data from the Global Burden of Diseases Study 2015, Lancet, 2017, 389, 1907–1918.
2. C. A. Pope, III and D. W. Dockery, Health Effects of Fine Particulate Air Pollution: Lines that Connect, J. Air Waste Manage. Assoc., 2006, 56, 709–742.
3. D. W. Dockery and C. A. Pope, III, Acute Respiratory Effects of Particulate Air Pollution, Annu. Rev. Public Health, 1994, 15, 107–132.
4. D. Brook Robert, S. Rajagopalan, C. A. Pope, R. Brook Jeffrey, A. Bhatnagar, V. Diez-Roux Ana, F. Holguin, Y. Hong, V. Luepker Russell, A. Mittleman Murray, A. Peters, D. Siscovick, C. Smith Sidney, L. Whitsel and D. Kaufman Joel, Particulate Matter Air Pollution and Cardiovascular Disease, Circulation, 2010, 121, 2331–2378.
5. P. Azimi and B. Stephens, A framework for estimating the US mortality burden of fine particulate matter exposure attributable to indoor and outdoor microenvironments, J. Exposure Sci. Environ. Epidemiol., 2020, 30, 271–284.
6. N. E. Klepeis, W. C. Nelson, W. R. Ott, J. P. Robinson, A. M. Tsang, P. Switzer, J. V. Behar, S. C. Hern and W. H. Engelmann, The National Human Activity Pattern Survey (NHAPS): a resource for assessing exposure to environmental pollutants, J. Exposure Sci. Environ. Epidemiol., 2001, 11, 231–252.
7. W. W. Nazaroff, Indoor particle dynamics, Indoor Air, 2004, 14, 175–183.
8. W. J. Riley, T. E. McKone, A. C. K. Lai and W. W. Nazaroff, Indoor Particulate Matter of Outdoor Origin:  Importance of Size-Dependent Removal Mechanisms, Environ. Sci. Technol., 2002, 36, 200–207.
9. C. Howard-Reed, L. A. Wallace and S. J. Emmerich, Effect of ventilation systems and air filters on decay rates of particles produced by indoor sources in an occupied townhouse, Atmos. Environ., 2003, 37, 5295–5306.
10. L. A. Wallace, S. J. Emmerich and C. Howard-Reed, Effect of central fans and in-duct filters on deposition rates of ultrafine and fine particles in an occupied townhouse, Atmos. Environ., 2004, 38, 405–413.
11. L. Wallace, W. Kindzierski, J. Kearney, M. MacNeill, M.-È. Héroux and A. J. Wheeler, Fine and Ultrafine Particle Decay Rates in Multiple Homes, Environ. Sci. Technol., 2013, 47, 12929–12937.
12. L. A. Wallace, S. J. Emmerich and C. Howard-Reed, Source Strengths of Ultrafine and Fine Particles Due to Cooking with a Gas Stove, Environ. Sci. Technol., 2004, 38, 2304–2311.
13. C. He, L. Morawska and L. Taplin, Particle Emission Characteristics of Office Printers, Environ. Sci. Technol., 2007, 41, 6039–6045.
14. T. Schripp, M. Wensing, E. Uhde, T. Salthammer, C. He and L. Morawska, Evaluation of Ultrafine Particle Emissions from Laser Printers Using Emission Test Chambers, Environ. Sci. Technol., 2008, 42, 4338–4343.
15. Y. Kim, C. Yoon, S. Ham, J. Park, S. Kim, O. Kwon and P.-J. Tsai, Emissions of Nanoparticles and Gaseous Material from 3D Printer Operation, Environ. Sci. Technol., 2015, 49, 12044–12053.
16. P. Azimi, D. Zhao, C. Pouzet, N. E. Crain and B. Stephens, Emissions of Ultrafine Particles and Volatile Organic Compounds from Commercially Available Desktop Three-Dimensional Printers with Multiple Filaments, Environ. Sci. Technol., 2016, 50, 1260–1268.
17. N. E. Klepeis, M. G. Apte, L. A. Gundel, R. G. Sextro and W. W. Nazaroff, Determining Size-Specific Emission Factors for Environmental Tobacco Smoke Particles, Aerosol Sci. Technol., 2003, 37, 780–790.
18. A. R. Ferro, R. J. Kopperud and L. M. Hildemann, Source Strengths for Indoor Human Activities that Resuspend Particulate Matter, Environ. Sci. Technol., 2004, 38, 1759–1764.
19. E. Abt, H. H. Suh, P. Catalano and P. Koutrakis, Relative Contribution of Outdoor and Indoor Particle Sources to Indoor Concentrations, Environ. Sci. Technol., 2000, 34, 3579–3587.
20. S. Patel, S. Sankhyan, E. K. Boedicker, P. F. DeCarlo, D. K. Farmer, A. H. Goldstein, E. F. Katz, W. W. Nazaroff, Y. Tian, J. Vanhanen and M. E. Vance, Indoor Particulate Matter during HOMEChem: Concentrations, Size Distributions, and Exposures, Environ. Sci. Technol., 2020, 54, 7107–7116.
21. A. C. K. Lai, K. Wang and F. Z. Chen, Experimental and numerical study on particle distribution in a two-zone chamber, Atmos. Environ., 2008, 42, 1717–1726.
22. W. Lu and A. T. Howarth, Numerical analysis of indoor aerosol particle deposition and distribution in two-zone ventilation system, Build. Environ., 1996, 31, 41–50.
23. K. C. Chung, Three-dimensional analysis of airflow and contaminant particle transport in a partitioned enclosure, Build. Environ., 1998, 34, 7–17.
24. B. Zhao, Y. Zhang, X. Li, X. Yang and D. Huang, Comparison of indoor aerosol particle concentration and deposition in different ventilated rooms by numerical method, Build. Environ., 2004, 39, 1–8.
25. H.-M. Kao, T.-J. Chang, Y.-F. Hsieh, C.-H. Wang and C.-I. Hsieh, Comparison of airflow and particulate matter transport in multi-room buildings for different natural ventilation patterns, Energy Build., 2009, 41, 966–974.
26. C. Ju and J. D. Spengler, Room-to-Room Variations in Concentration of Respirable Particles in Residences, Environ. Sci. Technol., 1981, 15, 592–596.
27. S. L. Miller and W. W. Nazaroff, Environmental tobacco smoke particles in multizone indoor environments, Atmos. Environ., 2001, 35, 2053–2067.
28. M. Tang, N. Zhu, K. Kinney and A. Novoselac, Transport of indoor aerosols to hidden interior spaces, Aerosol Sci. Technol., 2020, 54, 94–110.
29. B. C. Singer, R. Z. Pass, W. W. Delp, D. M. Lorenzetti and R. L. Maddalena, Pollutant concentrations and emission rates from natural gas cooking burners without and with range hood exhaust in nine California homes, Build. Environ., 2017, 122, 215–229.
30. B. Mølgaard, J. Ondráček, P. Št'ávová, L. Džumbová, M. Barták, T. Hussein and J. Smolík, Migration of aerosol particles inside a two-zone apartment with natural ventilation: a multi-zone validation of the multi-compartment and size-resolved indoor aerosol model, Indoor Built Environ., 2014, 23, 742–756.
31. D. K. Farmer, M. E. Vance, J. P. D. Abbatt, A. Abeleira, M. R. Alves, C. Arata, E. Boedicker, S. Bourne, F. Cardoso-Saldaña, R. Corsi, P. F. DeCarlo, A. H. Goldstein, V. H. Grassian, L. H. Ruiz, J. L. Jimenez, T. F. Kahan, E. F. Katz, J. M. Mattila, W. W. Nazaroff, A. Novoselac, R. E. O'Brien, V. W. Or, S. Patel, S. Sankhyan, P. S. Stevens, Y. Tian, M. Wade, C. Wang, S. Zhou and Y. Zhou, Overview of HOMEChem: House Observations of Microbial and Environmental Chemistry, Environ. Sci.: Processes Impacts, 2019, 21, 1280–1300.
32. Y. Cai, D. C. Montague, W. Mooiweer-Bryan and T. Deshler, Performance characteristics of the ultra high sensitivity aerosol spectrometer for particles between 55 and 800 nm: laboratory and field studies, J. Aerosol Sci., 2008, 39, 759–769.
33. S.-L. von der Weiden, F. Drewnick and S. Borrmann, Particle loss calculator – a new software tool for the assessment of the performance of aerosol inlet systems, Atmos. Meas. Tech., 2009, 2, 479–494.
34. R. S. Gao, H. Telg, R. J. McLaughlin, S. J. Ciciora, L. A. Watts, M. S. Richardson, J. P. Schwarz, A. E. Perring, T. D. Thornberry, A. W. Rollins, M. Z. Markovic, T. S. Bates, J. E. Johnson and D. W. Fahey, A light-weight, high-sensitivity particle spectrometer for PM2.5 aerosol measurements, Aerosol Sci. Technol., 2016, 50, 88–99.
35. T. L. Thatcher and D. W. Layton, Deposition, resuspension, and penetration of particles within a residence, Atmos. Environ., 1995, 29, 1487–1497.
36. A. Manuja, J. Ritchie, K. Buch, Y. Wu, C. M. A. Eichler, J. C. Little and L. C. Marr, Total surface area in indoor environments, Environ. Sci.: Processes Impacts, 2019, 21, 1384–1392.
37. A. C. K. Lai and W. W. Nazaroff, Modeling Indoor Particle Deposition from Turbulent Flow onto Smooth Surfaces, J. Aerosol Sci., 2000, 31, 463–476.
38. E. W. Emerson, A. L. Hodshire, H. M. DeBolt, K. R. Bilsback, J. R. Pierce, G. R. McMeeking and D. K. Farmer, Revisiting particle dry deposition and its role in radiative effect estimates, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(42), 26076–26082.
39. L. Zhang, S. Gong, J. Padro and L. Barrie, A size-segregated particle dry deposition scheme for an atmospheric aerosol module, Atmos. Environ., 2001, 35, 549–560.
40. W. C. Hinds, Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles, John Wiley & Sons, Inc., New York, NY, 2nd edn, 1999.
41. T. Hussein, T. Glytsos, J. Ondráček, P. Dohányosová, V. Ždímal, K. Hämeri, M. Lazaridis, J. Smolík and M. Kulmala, Particle size characterization and emission rates during indoor activities in a house, Atmos. Environ., 2006, 40, 4285–4307.
42. C. He, L. Morawska and D. Gilbert, Particle deposition rates in residential houses, Atmos. Environ., 2005, 39, 3891–3899.
43. T. L. Thatcher, A. C. K. Lai, R. Moreno-Jackson, R. G. Sextro and W. W. Nazaroff, Effects of room furnishings and air speed on particle deposition rates indoors, Atmos. Environ., 2002, 36, 1811–1819.
44. A. F. Vette, A. W. Rea, P. A. Lawless, C. E. Rodes, G. Evans, V. R. Highsmith and L. Sheldon, Characterization of Indoor-Outdoor Aerosol Concentration Relationships during the Fresno PM Exposure Studies, Aerosol Sci. Technol., 2001, 34, 118–126.
45. W.-C. Lee, J. M. Wolfson, P. J. Catalano, S. N. Rudnick and P. Koutrakis, Size-Resolved Deposition Rates for Ultrafine and Submicrometer Particles in a Residential Housing Unit, Environ. Sci. Technol., 2014, 48, 10282–10290.
46. Y. Tian, C. Arata, E. Boedicker, D. M. Lunderberg, S. Patel, S.t Sankhyan, K. Kristensen, P. K. Misztal, D. K. Farmer, M. Vance, A. Novoselac, W. W. Nazaroff and A. H. Goldstein, Indoor emissions of total and fluorescent supermicron particles during HOMEChem, Indoor Air, 2020, 31(1), 88–98.
47. W. G. N. Slinn, Predictions for particle deposition to vegetative canopies, Atmos. Environ., 1967, 1982(16), 1785–1794.
48. T. L. Thatcher, W. A. Fairchild and W. W. Nazaroff, Particle Deposition from Natural Convection Enclosure Flow Onto Smooth Surfaces, Aerosol Sci. Technol., 1996, 25, 359–374.
49. A. C. K. Lai, Modeling indoor coarse particle deposition onto smooth and rough vertical surfaces, Atmos. Environ., 2005, 39, 3823–3830.
50. T. C. Bond, A. Bosco-Lauth, D. K. Farmer, P. W. Francisco, J. R. Pierce, K. M. Fedak, J. M. Ham, S. H. Jathar and S. VandeWoude, Quantifying proximity, confinement, and interventions in disease outbreaks: a decision support framework for air-transported pathogens, Environ. Sci. Technol., 2021, 55(5), 2890–2898.
51. J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, John Wiley & Sons, Inc., New York, NY, 3rd edn, 1998.
52. T.-J. Chang and T.-S. Hu, Transport mechanisms of airborne particulate matters in partitioned indoor environment, Build. Environ., 2008, 43, 886–895.
53. T.-J. Chang, H.-M. Kao and Y.-F. Hsieh, Numerical Study of the Effect of Ventilation Pattern on Coarse, Fine, and Very Fine Particulate Matter Removal in Partitioned Indoor Environment, J. Air Waste Manage. Assoc., 2007, 57, 179–189.
54. J. P. D. Abbatt and C. Wang, The atmospheric chemistry of indoor environments, Environ. Sci.: Processes Impacts, 2020, 22, 25–48.
55. D. B. Collins, C. Wang and J. P. D. Abbatt, Selective Uptake of Third-Hand Tobacco Smoke Components to Inorganic and Organic Aerosol Particles, Environ. Sci. Technol., 2018, 52, 13195–13201.
56. D. M. Lunderberg, K. Kristensen, Y. Tian, C. Arata, P. K. Misztal, Y. Liu, N. Kreisberg, E. F. Katz, P. F. DeCarlo, S. Patel, M. E. Vance, W. W. Nazaroff and A. H. Goldstein, Surface Emissions Modulate Indoor SVOC Concentrations through Volatility-Dependent Partitioning, Environ. Sci. Technol., 2020, 54, 6751–6760.
57. C. Arata, K. J. Zarzana, P. K. Misztal, Y. Liu, S. S. Brown, W. W. Nazaroff and A. H. Goldstein, Measurement of NO₃ and N₂O₅ in a Residential Kitchen, Environ. Sci. Technol. Lett., 2018, 5, 595–599.
58. S. S. Brown, W. P. Dubé, H. Fuchs, T. B. Ryerson, A. G. Wollny, C. A. Brock, R. Bahreini, A. M. Middlebrook, J. A. Neuman, E. Atlas, J. M. Roberts, H. D. Osthoff, M. Trainer, F. C. Fehsenfeld and A. R. Ravishankara, Reactive uptake coefficients for N₂O₅ determined from aircraft measurements during the second Texas air quality study: comparison to current model parameterizations, J. Geophys. Res.: Atmos., 2009, 114, D00F10.
59. D. M. Lunderberg, K. Kristensen, Y. Liu, P. K. Misztal, Y. Tian, C. Arata, R. Wernis, N. Kreisberg, W. W. Nazaroff and A. H. Goldstein, Characterizing Airborne Phthalate Concentrations and Dynamics in a Normally Occupied Residence, Environ. Sci. Technol., 2019, 53, 7337–7346.
60. S. Shi, J. Cao, Y. Zhang and B. Zhao, Emissions of Phthalates from Indoor Flat Materials in Chinese Residences, Environ. Sci. Technol., 2018, 52, 13166–13173.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1em00087j

---