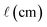Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Factors affecting the mixed-layer concentrations of singlet oxygen in sunlit lakes†
Sarah B.
Partanen
 a,
Jennifer N.
Apell
a,
Jennifer N.
Apell
 *ab,
Jianming
Lin
*ab,
Jianming
Lin
 c and
Kristopher
McNeill
c and
Kristopher
McNeill
 *a
*a
aInstitute of Biogeochemistry and Pollutant Dynamics (IBP), Department of Environmental Systems Science, ETH Zurich, 8092 Zurich, Switzerland. E-mail: japell@nyu.edu; kristopher.mcneill@env.ethz.ch
bDepartment of Civil and Urban Engineering, New York University Tandon School of Engineering, 6 MetroTech Center, Brooklyn, NY 11201, USA
cFirmenich Incorporated, P.O. Box 5880, Princeton, New Jersey 08543, USA
First published on 23rd June 2021
Abstract
The steady-state concentration of singlet oxygen within a lake ([1O2]SS) is an important parameter that can affect the environmental half-life of pollutants and environmental fate modelling. However, values of [1O2]SS are often determined for the near-surface of a lake, and these values typically do not represent the average over the epilimnia of lakes. In this work, the environmental and physical factors that have the largest impact on [1O2]SS within lake epilimnia were identified. It was found that the depth of the epilimnion has the largest impact on depth-averaged [1O2]SS, with a factor of 8.8 decrease in [1O2]SS when epilimnion depth increases from 2 m to 20 m. The next most important factors are the wavelength-dependent singlet oxygen quantum yield relationship and the latitude of the lake, causing variations in [1O2]SS by factors of 3.2 and 2.5 respectively, over ranges of representative values. For a set of representative parameters, the depth-averaged value of [1O2]SS within an average epilimnion depth of 9.0 m was found to be 5.8 × 10−16 M and the near-surface value of [1O2]SS was found to be 1.9 × 10−14 M. We recommend a range of 6 × 10−17 to 5 × 10−15 M as being more representative of [1O2]SS values within the epilimnia of lakes globally and potentially more useful for estimating pollutant lifetimes than those calculated using [1O2]SS values that correspond to near-surface, summer midday values. This work advances our understanding of [1O2]SS inter-lake variability in the environment, and provides estimates of [1O2]SS for practitioners and researchers to assess environmental half-lives of pollutants due to reaction with singlet oxygen.
Environmental significanceReaction with singlet oxygen has been shown to be an important degradation pathway for several aqueous organic pollutants, and the environmental half-life for this reaction pathway strongly depends on the steady-state concentration of singlet oxygen ([1O2]SS). While [1O2]SS have been measured for many surface waters, reported values are often representative of near-surface conditions, and are not representative of [1O2]SS averaged over the epilimnia of lakes. This work shows that average [1O2]SS in lake epilimnia can be up to two orders of magnitude lower than what is typically measured at the near-surface. The epilimnion depth was found to have the greatest impact on the depth-averaged [1O2]SS, whereas the dissolved organic carbon concentration was found to have a limited impact. Using depth-averaged [1O2]SS values allows for more accurate predictions of pollutant half-lives within lakes due to reaction with singlet oxygen. |
Introduction
Photochemical processes in surface waters such as lakes and rivers are important pathways for the degradation of some organic contaminants.1–4 While some photodegradable compounds react following the direct absorption of photons, others, such as the pesticide fludioxonil5 and the pharmaceutical cimetidine,6 are mainly attenuated via indirect photochemical processes. Indirect photochemistry is distinguished by the formation of photochemically produced reactive intermediates (PPRI), often through absorption of light by the chromophoric fraction of dissolved organic matter (CDOM).7–9 One PPRI of importance is singlet oxygen (1O2), a reactive oxygen species that selectively reacts with functional groups such as cyclic dienes, heterocycles, and reduced sulfur-containing compounds.6,10,11While the processes by which 1O2 is formed and quenched in surface waters are relatively well understood,11–131O2 steady-state concentrations ([1O2]SS) in the natural environment are less well defined. This is partly due to the variability caused by environmental conditions such as latitude, epilimnion depth, and the dissolved organic carbon (DOC) concentration in a water body. There is also added uncertainty due to limited experimental data characterizing parameters such as the wavelength-dependent 1O2 quantum yields (ΦΔ,λ), the fraction of total absorbance that is attributable to CDOM (fa,CDOM), and the fraction of light that is backscattered (fbackscatter) out of the water column. Understanding how these factors affect [1O2]SS would help constrain possible values of [1O2]SS, which in turn can be used to more accurately quantify the role of 1O2 in pollutant degradation and biogeochemical processes in the natural environment.
Typically, 1O2 in natural waters is investigated by taking a surface water sample from the field and conducting laboratory measurements to determine the quantum yield and the [1O2]SS.13–16 Singlet oxygen quantum yield measurements require accurate characterization of the incident light, making these results independent of the light source when performed correctly.17 In contrast, measurements of [1O2]SS do not require light source characterization, so values reported by different researchers or at different times may not be comparable. Additionally, laboratory measurement conditions are not generally representative of conditions in the environment. Specifically, laboratory light sources often do not replicate the solar spectrum, and the irradiance is usually substantially higher in these systems. In some cases, laboratory light spectra are designed to mimic solar noon or “sunny summer day” solar irradiance spectra,18–20 but even these spectra are not representative of the sunlight received by a water body over an entire day or year. Similarly, natural water samples examined in the laboratory tend to be more representative of surface conditions.13,18,21–23 Half-lives based on ideal conditions (summer, midday, near-surface) are overly rosy with respect to the importance of reaction with 1O2. A step toward more realistic values would be to instead use [1O2]SS values that are averaged over the epilimnion (mixed layer) of a lake.
Modelling photochemical processes can generate more environmentally relevant results compared to measuring samples in the laboratory because a range of values representing diverse geographical locations and surface waters can be more easily simulated.24,25 However, current models have important limitations such as (1) using only a representative value instead of a range of values that capture uncertainty or variability for some input parameters, (2) focusing only on direct photolysis, or (3) having low ease of use.24,26,27 Additionally, a systematic sensitivity analysis of the parameters affecting 1O2 formation and quenching in natural surface waters has not been addressed.
In this work the variability of [1O2]SS in a wide range of theoretical surface waters was investigated by examining the effect on [1O2]SS due to epilimnion depth, incident irradiance, singlet oxygen quantum yield, dissolved organic carbon concentration, and fraction of absorbance attributable to CDOM. Which parameters introduce the most uncertainty and variability into predictions of [1O2]SS has also been explored. Using the predicted [1O2]SS values, a range of potential environmental half-lives of organic contaminants due to reaction with 1O2 was estimated. The [1O2]SS values reported here are valuable for practitioners wishing to estimate the environmental half-lives of specific chemical compounds in diverse surface waters as well as for researchers interested in the environmental variability of singlet oxygen.
Methods
Governing equations for estimating [1O2]SS
The average [1O2]SS within the epilimnion of a lake was estimated based on the following relationships: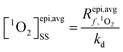 | (1) |
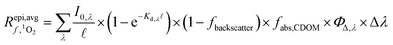 | (2) |
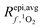 is the average rate of formation of 1O2 throughout the epilimnion (M s−1), kd is the deactivation rate constant for 1O2 in water (s−1), I0,λ is the incident irradiance (mmol photons cm−2 s−1 nm−1),
is the average rate of formation of 1O2 throughout the epilimnion (M s−1), kd is the deactivation rate constant for 1O2 in water (s−1), I0,λ is the incident irradiance (mmol photons cm−2 s−1 nm−1), 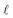 is the epilimnion depth (cm), Kd,λ is the diffuse attenuation coefficient (cm−1), fbackscatter is the fraction of light that is backscattered out of the water column, fabs,CDOM is the fraction of the total absorbance that is attributable to absorbance by CDOM, ΦΔ,λ is the wavelength-dependent singlet oxygen quantum yield, and Δλ is the wavelength interval for the summation, here 1 nm. In this work we use [1O2]epi,avgSS to refer to the singlet oxygen steady-state concentration averaged over the epilimnion depth of a lake, and [1O2]SS to refer to singlet oxygen steady-state concentrations in general.
is the epilimnion depth (cm), Kd,λ is the diffuse attenuation coefficient (cm−1), fbackscatter is the fraction of light that is backscattered out of the water column, fabs,CDOM is the fraction of the total absorbance that is attributable to absorbance by CDOM, ΦΔ,λ is the wavelength-dependent singlet oxygen quantum yield, and Δλ is the wavelength interval for the summation, here 1 nm. In this work we use [1O2]epi,avgSS to refer to the singlet oxygen steady-state concentration averaged over the epilimnion depth of a lake, and [1O2]SS to refer to singlet oxygen steady-state concentrations in general.
Eqn (2) can be conceptualized as comprising five separate terms; the first term describes the amount of light entering the water body, the second term describes the fraction of that light that is attenuated in the water column by all processes, the third term is the fraction of light that is not removed from the water column by backscattering (i.e. the fraction of light remaining after backscattering occurs), the fourth term is the fraction of the total light absorbance that is absorbance by CDOM, and the fifth term describes the efficiency at which singlet oxygen is produced from the photons absorbed by CDOM. Eqn (2) can also be used to calculate near-surface concentrations by setting 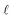 to a shallow depth (1 cm in this work). With the exception of
to a shallow depth (1 cm in this work). With the exception of 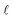 at the near-surface, the parameters that govern the terms in eqn (2) are not set values, rather they vary depending on environmental factors. Note that incident irradiance, the diffuse attenuation coefficient, and singlet oxygen quantum yields are all functions of wavelength, represented by a subscript λ in eqn (2). When subsequently referring to these variables in the text, the λ has been omitted for brevity. While fbackscatter and fabs,CDOM are also functions of wavelength, the wavelength dependence of these parameters is not as well understood. For this reason, single values of fbackscatter and fabs,CDOM are used here. Some of the parameters in eqn (2) also depend either implicitly or explicitly on other factors including wavelength (λ, nm), latitude (°N or °S), dissolved organic carbon concentration (DOC, mgC L−1), and temporal factors such as season or time of day. Additionally, many of the parameters are interdependent. For example, light in the water column is attenuated as a function of both depth and wavelength, and the rate of attenuation depends on the DOC concentration in the water body. Finally, the only quenching process for 1O2 considered in eqn (1) is 1O2 deactivation by water (kd, s−1). While other 1O2 sinks exist such as reaction with pollutants, previous work has found that in most natural waters the effect of other 1O2 quenchers is negligible compared to physical deactivation by water.11 The value of kd was recently updated for 1O2 deactivation in water, and the updated value of (2.76 ± 0.02) × 105 s−1 measured at 20 °C has been used here.28kd is weakly temperature dependent,28 but for temperatures ranging from 5 to 30 °C, subsequent calculated values of [1O2]SS vary by less than 5%.
at the near-surface, the parameters that govern the terms in eqn (2) are not set values, rather they vary depending on environmental factors. Note that incident irradiance, the diffuse attenuation coefficient, and singlet oxygen quantum yields are all functions of wavelength, represented by a subscript λ in eqn (2). When subsequently referring to these variables in the text, the λ has been omitted for brevity. While fbackscatter and fabs,CDOM are also functions of wavelength, the wavelength dependence of these parameters is not as well understood. For this reason, single values of fbackscatter and fabs,CDOM are used here. Some of the parameters in eqn (2) also depend either implicitly or explicitly on other factors including wavelength (λ, nm), latitude (°N or °S), dissolved organic carbon concentration (DOC, mgC L−1), and temporal factors such as season or time of day. Additionally, many of the parameters are interdependent. For example, light in the water column is attenuated as a function of both depth and wavelength, and the rate of attenuation depends on the DOC concentration in the water body. Finally, the only quenching process for 1O2 considered in eqn (1) is 1O2 deactivation by water (kd, s−1). While other 1O2 sinks exist such as reaction with pollutants, previous work has found that in most natural waters the effect of other 1O2 quenchers is negligible compared to physical deactivation by water.11 The value of kd was recently updated for 1O2 deactivation in water, and the updated value of (2.76 ± 0.02) × 105 s−1 measured at 20 °C has been used here.28kd is weakly temperature dependent,28 but for temperatures ranging from 5 to 30 °C, subsequent calculated values of [1O2]SS vary by less than 5%.
A form of eqn (2) has been used by researchers over the past 30 years.7,29 However, for filtered laboratory samples, decadic absorbance has typically been used in place of diffuse attenuation coefficients, and assumptions are made that negate the need for the fbackscatter and fabs,CDOM terms (eqn S9†). When decadic absorbance is used in eqn (2) instead of the diffuse attenuation coefficient, the first two terms are often referred to as the rate of light absorbance, and are derived from the physics of light absorption.30 The form of eqn (2) used here accounts for light scattering and for components other than CDOM that absorb light in the water column. As such, we believe it better represents the rate of formation of 1O2 in the environment.
In this work the variability of [1O2]SS within epilimnia and at the near-surface of representative lakes was examined. Variability in [1O2]epi,avgSS was explored by defining a range of possible values as well as a “representative case” for epilimnion depth, latitude, DOC concentration, singlet oxygen quantum yield, backscattering fraction, and fraction of total absorbance attributable to CDOM (Table 1 and Fig. 1). Note that setting values for latitude and DOC also sets the I0 values and Kd values, respectively. The confidence column in Table 1 gives a qualitative assessment of the data available (both quantity and quality) for each of the parameters, and will be discussed in the following sections. To investigate which parameter had the largest effect on [1O2]epi,avgSS, each parameter was varied individually over the range of possible values, while the remaining parameters were held constant at their representative value.
| [1O2]SS,epi,avg (10−16 M) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Latitude (° N) | ||||||||
| Epilimnion depth (m) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 2 | 32 | 31 | 29 | 27 | 23 | 20 | 16 | 13 |
| 3 | 22 | 22 | 20 | 19 | 16 | 14 | 11 | 8.8 |
| 4 | 17 | 17 | 16 | 14 | 13 | 10 | 8.4 | 6.8 |
| 5 | 14 | 14 | 13 | 12 | 10 | 8.5 | 6.8 | 5.5 |
| 6 | 12 | 11 | 11 | 9.8 | 8.6 | 7.2 | 5.8 | 4.6 |
| 7 | 10 | 9.8 | 9.3 | 8.5 | 7.4 | 6.2 | 5 | 4 |
| 8 | 8.8 | 8.6 | 8.2 | 7.5 | 6.5 | 5.5 | 4.4 | 3.5 |
| 9 | 7.9 | 7.7 | 7.3 | 6.7 | 5.8 | 4.9 | 3.9 | 3.1 |
| 10 | 7.1 | 7 | 6.6 | 6 | 5.3 | 4.4 | 3.5 | 2.8 |
| 11 | 6.5 | 6.3 | 6 | 5.5 | 4.8 | 4 | 3.2 | 2.6 |
| 12 | 5.9 | 5.8 | 5.5 | 5 | 4.4 | 3.7 | 3 | 2.4 |
| 13 | 5.5 | 5.4 | 5.1 | 4.7 | 4.1 | 3.4 | 2.7 | 2.2 |
| 14 | 5.1 | 5 | 4.7 | 4.3 | 3.8 | 3.2 | 2.5 | 2 |
| 15 | 4.8 | 4.7 | 4.4 | 4.1 | 3.5 | 3 | 2.4 | 1.9 |
| 16 | 4.5 | 4.4 | 4.2 | 3.8 | 3.3 | 2.8 | 2.2 | 1.8 |
| 17 | 4.2 | 4.1 | 3.9 | 3.6 | 3.1 | 2.6 | 2.1 | 1.7 |
| 18 | 4 | 3.9 | 3.7 | 3.4 | 3 | 2.5 | 2 | 1.6 |
| 19 | 3.8 | 3.7 | 3.5 | 3.2 | 2.8 | 2.3 | 1.9 | 1.5 |
| 20 | 3.6 | 3.5 | 3.3 | 3.1 | 2.7 | 2.2 | 1.8 | 1.4 |
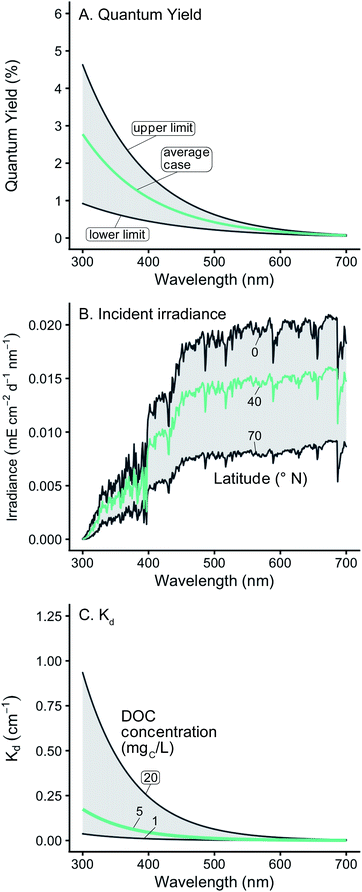 | ||
| Fig. 1 (A) Range of wavelength-dependent 1O2 quantum yields used. The shaded area represents the envelope that includes all the experimental data found in Partanen et al.,31 and the green line represents the average of the two bounds. (B) Range of incident solar irradiance spectra used. The green line shows a representative case of 40° N. (C) Range of modeled diffuse attenuation coefficients (Kd) used. The green line shows a representative case of modelled Kd values using 5 mgC L−1. | ||
Data sources
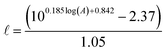 | (3) |
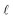 is the epilimnion depth in m, and A is the lake area in km2.
is the epilimnion depth in m, and A is the lake area in km2.
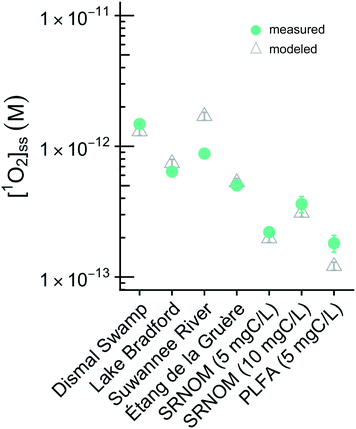
Using this empirical relationship, it is possible to calculate a theoretical epilimnion depth that is greater than the maximum depth of the lake. This occurred for 13% of the lakes in the Global Lakes Database. We assumed a lake to be fully mixed if its theoretical epilimnion depth was greater than the maximum lake depth. In these cases the maximum lake depth was used in place of the epilimnion depth. Summary plots and statistics for the 573 lakes are available in the ESI (Fig. S1 and Table S1†). Briefly, the average epilimnion depth is 9 m, and 96% of lakes have an epilimnion depth that falls between 2 and 20 m.
Note that the delta symbol in the notation for 1O2 quantum yield (ΦΔ) comes from the term symbol for the lowest energy singlet excited state of molecular oxygen (i.e.1Δg). The delta symbol has become a shorthand in the literature for 1O2 (1Δg).
| Kd = exp(−0.01347λ + 5.36(DOC)0.157) | (4) |
For fbackscatter, a range of single values (not wavelength-dependent) were investigated,36–40 and a representative value of 0.03 was chosen for analysis. Whether fbackscatter is wavelength-dependent is somewhat controversial, though recent research suggests that the fraction decreases with increasing wavelength.37,41 However, very little wavelength-dependent fbackscatter data exists in the literature, especially in the UV region.
f a,CDOM is most often measured over photosynthetically active radiation wavelengths (400–700 nm)42–46 or at 440 nm,47–50 with only a few measurements made within the UV region.51–53 As with fbackscatter, wavelength-dependent information for fa,CDOM is sparse. The value used for fa,CDOM has a large impact on [1O2]epi,avgSS (Fig. S11†), but since this parameter is not well characterized for a variety of lake types, an average value for measurements in the UV range (0.7) was used throughout this work.
Environmental half-life calculations
The estimated ranges of values for [1O2]epi,avgSS were used to calculate half-lives (t1/2) of chemical compounds in the epilimnia of lakes due to reaction with 1O2 using eqn (5):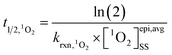 | (5) |
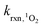 is the bimolecular rate constant of a compound reacting with 1O2 (M−1 s−1).
is the bimolecular rate constant of a compound reacting with 1O2 (M−1 s−1).
Relating test tube [1O2]SS to surface [1O2]SS
Values of [1O2]SS determined for natural water samples in test tubes in the laboratory (referred to as the “test tube case”) can be similar to environmental near-surface [1O2]SS values because the depth in both cases is very shallow (i.e., 1 cm), though in order for this equivalency to hold, the incident irradiance in both the laboratory and the near-surface environment must be the same. Test tube measurements are important because near-surface values of [1O2]SS represent the conditions described in testing guidelines such as the one published by the US EPA54 and are also representative of most of the literature values of [1O2]SS.13,18,21–23Test tube [1O2]SS values for seven surface waters and organic matter isolates were experimentally determined in a Rayonet photoreactor using furfuryl alcohol as a probe molecule for 1O2. Experimental details can be found in the ESI.† Values of [1O2]SS for these seven samples were then independently estimated using eqn (1) and S9,† where the irradiance parameter is the spectral output of the lamps used in the laboratory (Fig. S15†), the absorbance spectra of the water samples were measured by a UV-vis spectrophotometer (Fig. S13†), and  is equal to the average pathlength of the test tube (i.e., 1 cm). ΦΔ values for the samples are from Partanen et al.31 (Table S5†), and were independently measured using the 1O2 phosphorescence method, rather than through steady-state photolysis. The experimentally determined [1O2]SS values were then compared with the independently calculated values. In this analysis eqn S9† was used instead of eqn (2) because experimentally determined absorbance spectra for the samples were available, and because the samples were filtered, meaning that the impact of particulates was assumed to be negligible. Details on the collection and characterization of these samples can be found in the ESI.†
is equal to the average pathlength of the test tube (i.e., 1 cm). ΦΔ values for the samples are from Partanen et al.31 (Table S5†), and were independently measured using the 1O2 phosphorescence method, rather than through steady-state photolysis. The experimentally determined [1O2]SS values were then compared with the independently calculated values. In this analysis eqn S9† was used instead of eqn (2) because experimentally determined absorbance spectra for the samples were available, and because the samples were filtered, meaning that the impact of particulates was assumed to be negligible. Details on the collection and characterization of these samples can be found in the ESI.†
For the test tube case, differences between values of [1O2]SS calculated using eqn 1 and S9,† and values of [1O2]SS measured in the laboratory range from 5 to 64% (Fig. 2). The experimental values are between 1.8 × 10−13 (±2.7 × 10−14) and 1.5 × 10−12 (±1.0 × 10−13) M, whereas values calculated using eqn 1 and S9† range from 1.2 × 10−13 (±8.5 × 10−15) to 1.7 × 10−12 (±1.2 × 10−13) M.
Reference ΦΔ values for the seven samples were measured independently in previous work using the 1O2 phosphorescence method,31 and were subsequently used in calculations of [1O2]SS. These values were used so that the calculated values of [1O2]SS would not rely on ΦΔ values determined from the steady-state photolysis experiments performed for the test-tube case. However, it is also possible to calculate ΦΔ values from the steady-state photolyses used to experimentally determine [1O2]SS values (see the ESI† for details). The difference between ΦΔ values determined using steady-state photolysis and the reference ΦΔ values from Partanen et al. for each of the samples closely tracks the difference between experimentally measured and calculated [1O2]SS values, indicating that this parameter is the source of much of the variability. There are many potential sources of error when measuring ΦΔ values,55 and it is likely experimental error that leads to the difference between experimentally measured ΦΔ values and reference ΦΔ values in this analysis, rather than an incorrect [1O2]SS estimation framework. Overall, our approach estimates [1O2]SS values that are in good agreement with experimentally measured [1O2]SS values for the test-tube case.
Results and discussion
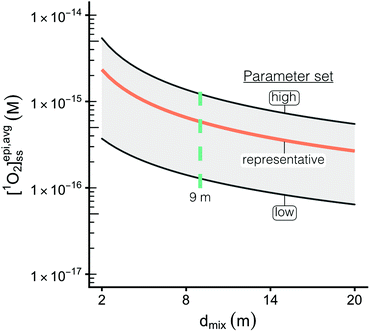
For a given epilimnion depth, the [1O2]epi,avgSS can vary by over an order of magnitude depending on the set of input parameters (ΦΔ relationship, latitude, and DOC concentration) (Fig. 3). Similarly, varying epilimnion depth from 2–20 m (accounting for 96% of lakes within the Global Lakes Database32) causes a decrease in [1O2]epi,avgSS by a factor of 8.8 (Table 3). The ΦΔ relationship used and the latitude of the lake have the next largest impacts (Table 3, Fig. 4A and B). Finally, while DOC concentrations have a substantial effect on near-surface [1O2]SS, at epilimnion depths below 2 m increasing the DOC concentration from 1–20 mgC L−1 has only a small effect on [1O2]epi,avgSS (Table 3 and Fig. 4C). Data tables of [1O2]epi,avgSS for a range of epilimnion depths and latitudes and for three sets of input parameters can be found in Tables 2 and S6.† The results shown in Table 3, Fig. 3 and 4 will be discussed in the following sections.The range of [1O2]SS values often quoted in the literature is 10−14 to 10−12 M.7,13,56 This range explicitly refers to the top layer (<1 cm) of a sunlit lake under ideal conditions (noon, summer day), and not to the epilimnion or to less ideal conditions. We propose using a range of 6 × 10−17 to 5 × 10−15 M to represent values of [1O2]SS within the mixed layer of lakes. This range represents the top left-most point (epilimnion depth = 2 m, DOC = 20 mgC L−1, Latitude = 0°, upper limit of modelled ΦΔ relationships) to bottom right-most point (epilimnion depth = 20 m, DOC = 1 mgC L−1, Latitude = 70°N, lower limit of modelled ΦΔrelationships) of Fig. 3.
Epilimnion depth and lake depth
The epilimnion depth has a large impact on depth-averaged values of [1O2]SS within a lake, causing variation of close to a factor of 9 over epilimnion depths between 2 and 20 m. The reason for the large variability in [1O2]epi,avgSS is because once all of the photons entering the water column are absorbed (Fig. S7†), no additional 1O2 can be produced. Therefore, as the epilimnion depth increases, the same amount of 1O2 is diluted over a larger volume of water. While many [1O2]SS values reported in the literature are valid for the near-surface of lakes, the average epilimnion depth within the Global Lakes Database is 9 m. Because the two scenarios substantially differ in terms of [1O2]SS, it is important to ensure that values for the near-surface are not conflated with depth-averaged values.It is also important to note that the equation representing the rate of formation of 1O2 differs depending on whether the rate is being calculated for a specific lake depth or is averaged over the epilimnion depth. Eqn (1) and (2) presented above are used to calculate an average concentration of 1O2 within the epilimnion of a lake, whereas eqn (6) below is used to calculate the rate of formation of 1O2 at a given depth (i.e., assuming no mixing).
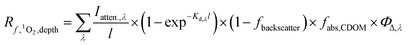 | (6) |
| Iatten.,λ = I0,λ × exp−Kd,λd | (7) |
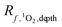 is the rate of formation of 1O2 in a water body at a given depth (M s−1), Iatten.,λ is the attenuated irradiance (mmol photons cm−2 s−1 nm−1), l is the pathlength (1 cm intervals were used in this work), d is the depth of interest (cm) at which the attenuated irradiance is being calculated, and Kd,λ, fbackscatter, fabs,CDOM, ΦΔ,λ, and I0,λ are defined above.
is the rate of formation of 1O2 in a water body at a given depth (M s−1), Iatten.,λ is the attenuated irradiance (mmol photons cm−2 s−1 nm−1), l is the pathlength (1 cm intervals were used in this work), d is the depth of interest (cm) at which the attenuated irradiance is being calculated, and Kd,λ, fbackscatter, fabs,CDOM, ΦΔ,λ, and I0,λ are defined above.
There are two main differences between eqn (2) and (6). First, when calculating 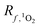 at a particular depth, the attenuation of light due to the overlying water column must be taken into account using eqn (7), where d is the depth at which the attenuated irradiance is being calculated. Second, in eqn (1),
at a particular depth, the attenuation of light due to the overlying water column must be taken into account using eqn (7), where d is the depth at which the attenuated irradiance is being calculated. Second, in eqn (1), 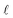 is the epilimnion depth, whereas in eqn (6)Rf is being calculated within subsequent thin layers of water, so l is a constant value. Note that where water bodies are not considered well-mixed, such as below the epilimnion where vertical mixing is slow, the [1O2]SS varies as a function of depth (i.e., according to equation (6)). A graphical representation of the difference between [1O2]SS as a function of the depth of a water body and [1O2]epi,avgSS as a function of well-mixed epilimnion depth can be seen in Fig. S2.†
is the epilimnion depth, whereas in eqn (6)Rf is being calculated within subsequent thin layers of water, so l is a constant value. Note that where water bodies are not considered well-mixed, such as below the epilimnion where vertical mixing is slow, the [1O2]SS varies as a function of depth (i.e., according to equation (6)). A graphical representation of the difference between [1O2]SS as a function of the depth of a water body and [1O2]epi,avgSS as a function of well-mixed epilimnion depth can be seen in Fig. S2.†
The calculated [1O2]epi,avgSS values are only applicable to the epilimnia of lakes and do not apply to the hypolimnia of the lakes. Therefore, calculated lifetimes of 1O2-reactive compounds are also only valid for the epilimnion. If such a compound is not present within the epilimnion (e.g. introduced into the lake via groundwater infiltration), then it is not possible to estimate the pollutant lifetime based on the [1O2]epi,avgSS values presented here.
Quantum yield relationships
The particular ΦΔ relationship used in calculations of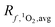 impacts values of [1O2]epi,avgSS by a factor of 3.2 (Fig. 4A) between the upper and lower limits of the modelled ΦΔ relationship (see Table 1 and Fig. 1A), but unlike epilimnion depth and latitude, this variability is in part due to limited experimental data rather than innate environmental variability. The range of ΦΔ values used here was modelled based on experimentally determined wavelength-dependent relationships of ΦΔ that we believe are currently the best available data31 (Fig. S3†). However, much remains unknown about the wavelength dependence of ΦΔ, and more information could reduce the uncertainty in this parameter. Specifically, having the ability to correlate a wavelength-dependent ΦΔ relationship to different types of water bodies would help to reduce the variability attributable to this parameter. In addition, the available wavelength-dependent experimental data only includes organic matter from lakes and rivers, and does not include other types of organic matter such as effluent organic matter or marine organic matter. Since these types of organic matter are known to have different single-value ΦΔ compared to lake or river organic matter,21,57 they may also have different wavelength-dependent ΦΔ relationships.
impacts values of [1O2]epi,avgSS by a factor of 3.2 (Fig. 4A) between the upper and lower limits of the modelled ΦΔ relationship (see Table 1 and Fig. 1A), but unlike epilimnion depth and latitude, this variability is in part due to limited experimental data rather than innate environmental variability. The range of ΦΔ values used here was modelled based on experimentally determined wavelength-dependent relationships of ΦΔ that we believe are currently the best available data31 (Fig. S3†). However, much remains unknown about the wavelength dependence of ΦΔ, and more information could reduce the uncertainty in this parameter. Specifically, having the ability to correlate a wavelength-dependent ΦΔ relationship to different types of water bodies would help to reduce the variability attributable to this parameter. In addition, the available wavelength-dependent experimental data only includes organic matter from lakes and rivers, and does not include other types of organic matter such as effluent organic matter or marine organic matter. Since these types of organic matter are known to have different single-value ΦΔ compared to lake or river organic matter,21,57 they may also have different wavelength-dependent ΦΔ relationships.
Values of ΦΔ are also known to increase with increasing oxygen concentration within the range of 0.96–9.3 mgO2 L−1.58 Since the oxygen concentration within surface waters varies both seasonally and diurnally as a nonlinear function of temperature and phytoplankton activity,59 one would expect ΦΔ values within lakes to be higher when the oxygen saturation is higher. ΦΔ values will mainly be affected when water temperatures are above 19 °C, as below 19 °C ΦΔ has been found to be constant with respect to [O2].59 While it is clear that ΦΔ can vary as a function of [O2], we believe that the range of values for ΦΔ used here capture this variability.
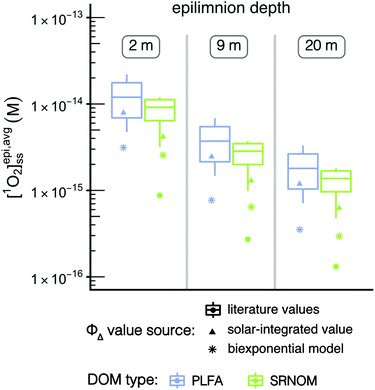
Since it is common to simplify the ΦΔ,λ relationship to a single value across the wavelength range being studied, the impact of using single values for ΦΔ on the calculated values of [1O2]epi,avgSS was explored. Two different sources of single values for ΦΔ were investigated: (1) solar-integrated ΦΔ values and (2) the range of ΦΔ values available from the literature. Solar-integrated ΦΔ values for SRNOM (1.0%) and PLFA (1.9%) were taken from Partanen et al.31 and were calculated by integrating the wavelength-dependent ΦΔ relationships for these isolates over the entire solar spectrum. The range of ΦΔ values obtained from the literature were 0.21–2.89% for SRNOM (n = 15) and 1.14–5.29% for PLFA (n = 10).17 These literature values were measured using a solar simulator or xenon lamp to represent solar irradiance. [1O2]epi,avgSS values were calculated from the single values for ΦΔ, and were compared to [1O2]epi,avgSS values calculated using biexponential models of wavelength-dependent ΦΔ data for SRNOM and PLFA (Fig. S4†).
Values of [1O2]epi,avgSS calculated with wavelength-dependent ΦΔ relationships are consistently lower than any single ΦΔ value (Fig. 5, stars compared to box plots and triangles). Of the non-wavelength-dependent ΦΔ values used for PLFA and SRNOM, the [1O2]epi,avgSS values calculated using solar-integrated ΦΔ values (triangles) are below the median of those calculated using the range of values reported in the literature (boxplots). Note that outliers in the boxplots are represented by dots. This analysis shows that if a non-wavelength-dependent value for ΦΔ is used in calculations of [1O2]epi,avgSS, it generally results in higher estimations of [1O2]epi,avgSS at any epilimnion depth, although there is one outlier literature ΦΔ value that would predict lower [1O2]epi,avgSS. This reinforces the need for more complete experimental data on ΦΔ wavelength-dependent relationships.
Latitude and other factors affecting incident irradiance
Variability in incident irradiance comes from multiple sources, some of which are more straightforward to account for than others. Latitude is the largest source of variability in the incident irradiance but is accounted for in the reference irradiance spectra. The reference spectra themselves also have some uncertainty, as they tend to overestimate the values measured by spectroradiometers.34 The calculated [1O2]epi,avgSS in a lake with an average epilimnion depth (9 m) was found to vary by a factor of 2.5 depending on whether calculations of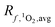 use incident irradiance spectra from the equator or from above the Arctic circle (Fig. 4B). In contrast, reflectance of light from the surface of a water body decreases the number of photons entering the water column by 4.5 to 15% for latitudes between 0 and 70° N (Table S2 and Fig. S5; † details on the reflectance calculations can also be found in the ESI†).
use incident irradiance spectra from the equator or from above the Arctic circle (Fig. 4B). In contrast, reflectance of light from the surface of a water body decreases the number of photons entering the water column by 4.5 to 15% for latitudes between 0 and 70° N (Table S2 and Fig. S5; † details on the reflectance calculations can also be found in the ESI†).
The season also impacts the incident irradiance, and in this work average annual irradiance spectra were used, as this likely gives a more accurate representation of the amount of 1O2 in the water column on timescales relevant to pollutant lifetimes. These annual average spectra were calculated by averaging day-averaged spectra from the solstices and equinoxes. When estimating environmental concentrations of PPRIs such as 1O2, it is common to use a summer irradiance spectrum (either day-averaged or solar noon) as the input for incident irradiance,18–20 but these irradiance spectra represent a “best-case scenario” in terms of the number of photons entering the water body. Using sunny summer day or June 21st solar noon spectra results in [1O2]epi,avgSS values that are higher by a factor of 1.5 and 4.4, respectively, when compared to using average annual irradiance spectra (Fig. S6†).
Another factor that can impact incident irradiance is the effect of clouds, which depends on the extent of cloud cover, the type of cloud, and seasonal and location variability. Some progress has been made in developing empirical models that relate the ratio of measured irradiance under cloudy conditions and the estimated irradiance under cloudless conditions60 to the fraction of cloud coverage.61–63 However, not all of these models capture the impact of different types of clouds and many require location-specific information. Cloud cover will impact the incident irradiance entering a lake or river, but because the impact is so location specific, it is not accounted for in the calculations of [1O2]epi,avgSS presented here.
Overall, reflectance off the water surface, cloud cover, and using average annual irradiance instead of summer day or solar noon values decrease the incident irradiance, leading to lower [1O2]epi,avgSS values in the epilimnia of lakes. The proper magnitude of this decrease must await future studies that give better estimates of these effects on the incident irradiance entering a surface water.
DOC concentration has a limited impact on depth-averaged [1O2]epi,avgSS
Changes in the DOC concentration in a lake have an impact on the modelled diffuse attenuation coefficients used in this work (Fig. 1C), but [1O2]epi,avgSS changes by only 14% over a range of 1 to 20 mgC L−1 at an epilimnion depth of 9 m (Fig. 4C). Once all the photons entering a water body are absorbed, the change in [1O2]epi,avgSS over a range of DOC concentrations decreases as epilimnion depth increases due to the increase in dilution volume. Thus, for a 20 m epilimnion, the change in [1O2]epi,avgSS is only 6% over the same DOC range. The extreme case occurs at the near-surface of lakes, where DOC concentration has a large impact on [1O2]SS. This special case is discussed in the section “Estimations of [1O2]SS at the near-surface of lakes” below.DOC concentration has such a limited effect on [1O2]epi,avgSS within the epilimnion of lakes because once all the photons entering the water column are absorbed by DOM, increasing the DOC has no further effect on 1O2 production. The depth at which the majority of photons are absorbed in the water column depends on the DOC concentration and on the wavelength of light (see Fig. S7†), but light at all but the longest wavelengths (>500 nm) is completely attenuated by 4 m, even for lakes containing only 1 mgC L−1. Therefore, for most lakes, the same number of photons are absorbed in the epilimnion irrespective of the DOC concentration within the lake, and thus for the epilimnion of stratified lakes or for shallow well mixed lakes, the [1O2]epi,avgSS is not greatly impacted by DOC concentration.
Diffuse attenuation coefficients and absorbance spectra
In this work, modelled diffuse attenuation coefficients (Kd) were used to represent the absorbance and scattering of light in the water column (Fig. 1C).35Kd is theoretically better for modelling [1O2]epi,avgSS in real surface waters compared to decadic absorbance because it takes into account all light attenuation processes within the water column. However, to accurately calculate [1O2]epi,avgSS using Kd values, both the backscattering fraction and the fraction of total light absorbance that is specific to CDOM must also be known.The Kd relationship used in this work (eqn (4)) is a function of DOC concentration, and was developed using data from lakes in a variety of different locations and spanning a wide range of DOC concentrations.35 As such, we believe it provides a reasonable estimate of Kd values within lakes, though researchers have found that Kd values measured in surface waters using radiometers sometimes deviate from Kd values modelled based on DOC concentrations.44,64–66 These differences have been attributed to attenuation caused by scattering or absorbance by particulate components, which are not explicitly accounted for in attenuation models that use DOC as the only input parameter. Scattering and particle absorbance can account for anywhere from 20 to ∼70% of light attenuation depending on factors such as turbidity and presence of algal blooms.35,44,64,65 Most data used to develop Kd relationships is specific to a certain lake type or location, meaning that relationships developed for high-turbidity lakes will be different than those developed for clear, low DOC waters. Thus, if site-specific Kd values are known, estimates of [1O2]epi,avgSS could be improved for a given waterbody.
Measured decadic absorbance spectra of filtered water samples are most often used in laboratory measurements of [1O2]SS, so the impact of using measured absorbance instead of modelled Kd values in calculations of [1O2]epi,avgSS was investigated (Fig. S9†). The [1O2]epi,avgSS calculated using absorbance spectra measured in the lab was found to be a factor of 1.5 higher than that calculated using modelled Kd values, for an epilimnion depth of 9 m and a DOC concentration of 5 mgC L−1. Note that the equations for calculating the rate of formation of 1O2 are different if one is using a base e attenuation/absorption coefficient (e.g., Kd) or a base 10 coefficient (e.g., α) (see eqn S9†). The difference in the equation for rate of formation of 1O2 is due to the fact that filtered water samples are most often used in laboratory measurements of [1O2]SS, leading to assumptions that all of the absorbance in the sample is due to CDOM and that there is no particle scattering. While eqn S9† may be valid for laboratory measurements, it does not capture the complexity of light attenuation processes within the water column. As such, we believe that using Kd values instead of decadic absorbance provides more accurate estimates for [1O2]epi,avgSS.
In some photochemistry models, absorbance spectra are estimated using DOC values when measured absorbance spectra are not available.24 We investigated the use of modelled absorbance spectra in place of measured absorbance spectra and found that in general, the modelled absorbance relationships used in the APEX model do not well represent the absorbance spectra from 7 samples of surface waters from Switzerland and the U.S. and one organic matter isolate (Fig. S8 and S10†). While this does not have a large impact on depth-averaged [1O2]epi,avgSS, as discussed above, it would have a significant effect on near-surface estimates. Experimentally obtained absorbance spectra can also be used as an input parameter, but while these spectra are more accurate for a single water body, the results may not be generalizable to other lakes. We believe that using modelled Kd values in calculations of [1O2]SS gives results that are more representative of environmental systems by accounting for light scattering and absorbance by other water constituents as well as absorbance by CDOM and that they are the most generalizable to lakes globally.
f backscatter and fabs,CDOM
The Kd term used in eqn (2) accounts for all light attenuation, including absorbance by water, CDOM, phytoplankton, and non-algal particles, as well as light scattering.42 Since we assume that only light absorbance by CDOM leads to the formation of 1O2, the fraction of light backscattered out of the water column (fbackscatter) and the fraction of total absorbance attributable to CDOM (fabs,CDOM) must be taken into account.Values for fbackscatter are typically measured in marine environments, though some values exist for lakes. Literature values range from 0.005–0.07, depending on the type of water body.36–40 While there is some debate about the importance or even the existance of the wavelength-dependence of fbackscatter, variability due to different types of water bodies is likely larger than variability due to wavelength.36,37 Varying fbackscatter between 0.005 and 0.07 has a limited impact on [1O2]epi,avgSS (Fig. S11†). More data on fbackscatter in lakes, especially over UV wavelengths, could result in a more accurate value or the development of a wavelength-dependent relationship for fbackscatter. However, the variability in other parameters such as ΦΔ and fabs,CDOM has a much greater impact on [1O2]epi,avgSS, and should therefore be the focus of future data collection efforts.
The range of values for fabs,CDOM (0.3–0.9) is much greater than for fbackscatter,42–53 leading to a large impact on [1O2]epi,avgSS (Fig. S11†). However, the values in this range are not equally realistic for the environments considered in this work. Firstly, fabs,CDOM is wavelength-dependent and is higher in the UV range than in the visible range,53 but most fabs,CDOM values are measured for visible wavelengths. Additionally, in coastal and marine environments, CDOM absorbance, and therefore it's fractional importance to total absorbance, is low.42 For these reasons, a fabs,CDOM value that represents an average of the available data collected within the UV range (0.7) was used, but we note that there is a large uncertainty in this value.
Estimated [1O2]SS at the near-surface of lakes
While predictions of [1O2]epi,avgSS within the epilimnia of lakes are broadly applicable to modelling pollutant fate in the environment, the behavior of [1O2]SS at the near-surface of a water body is sufficiently different to warrant a separate discussion. Specifically, the near-surface of a water body (defined here as having a 1 cm epilimnion) and shallow water bodies (defined here as having a 1 m epilimnion) have particular relevance in engineered environments such as waste stabilization ponds, constructed wetlands, and mesocosm experiments.67–69 In addition, the near-surface condition is relevant in pollutant fate and transport regulations54 and also represents the bulk of the literature values for [1O2]SS. Near-surface literature values for [1O2]SS range from 4.8 × 10−15 to 5.6 × 10−12 M and vary as a function of water source and light source (Fig. S12 and Table S4†).13,18,21,70–79 This range of literature values is in agreement with the ranges of estimated [1O2]SS values at the near-surface and in shallow water bodies (Fig. 6 and Table 4) and with the estimated near-surface [1O2]SS value of 1.9 × 10−14 M obtained for the representative case (5.0 mgC L−1, 40° N, average ΦΔ as a function of wavelength relationship).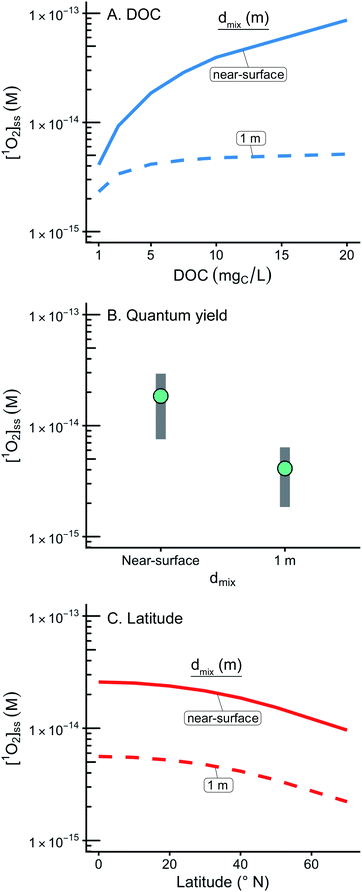 | ||
| Fig. 6 Impact of variable input parameters on [1O2]SS at the near surface (defined as having a 1 cm epilimnion depth) and within a 1 m epilimnion. In panels A, B, and C, one parameter is varied, while the rest of the parameters are held constant at their “representative case” values (see Table 1). (A) Range of possible [1O2]SS values for DOC concentrations ranging from 1 to 20 mgC L−1. (B) Range of possible [1O2]SS values for a range of modelled ΦΔ relationships. Green points represent the average case. (C) Range of possible [1O2]SS values for latitudes ranging from the equator to 70°N. | ||
At the near-surface, calculated [1O2]SS concentrations are one to two orders of magnitude higher than those calculated within an average (9 m) epilimnion. These significantly higher [1O2]SS values occur because the incident irradiance has not been attenuated nor has the 1O2 formed at the surface been diluted within the epilimnion. The difference in [1O2]SS values also manifests in the differing importance of the DOC concentration. For epilimnion depths of 9 m, changing DOC concentrations from 1–20 mgC L−1 results in a 14% difference in [1O2]epi,avgSS whereas at the near-surface the same change in DOC concentration results in an increase in [1O2]SS by over a factor of 20.
Estimated pollutant half-lives
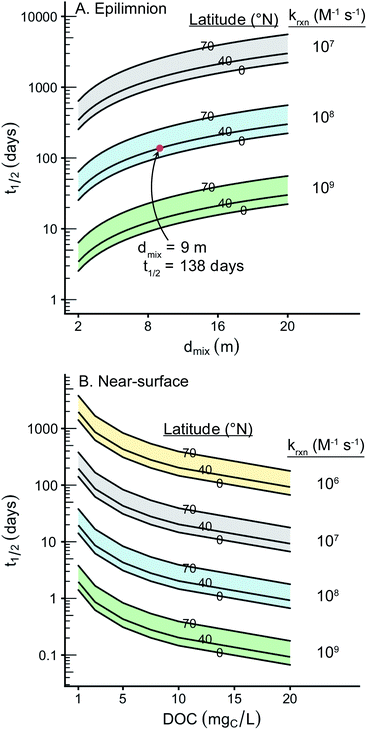
Pollutant half-lives within the epilimnia and at the near-surface of lakes were calculated using the estimated values of [1O2]SS and bimolecular rate constants of 106 to 109 M−1 s−1 (Fig. 7). This analysis shows that for lakes with epilimnia between 2 and 20 m the bimolecular rate constant of the pollutant of interest defines the timescale of the pollutant's half-life (Table S7†). For compounds that have very slow bimolecular rate constants such as sulfamethoxazole (2 (±1) × 104 M−1 s−1),80 reaction with 1O2 will also be very slow, even at the near-surface (i.e., t1/2 ≈ 40 years). For compounds with bimolecular rate constants on the order of 107 M−1 s−1, reaction with singlet oxygen leads to half-lives on the order of years for most lakes with epilimnia greater than 2 m.For compounds that react quickly with 1O2, such as cimetidine (2.2 (±0.2) × 108 M−1 s−1 at a pH of 8.2),6 reaction with 1O2 results in half-lives of less than a week at the near-surface of a representative lake. When considering a representative lake with an average epilimnion depth (dmix = 9 m), the half-life is approximately 4.5 months. In lakes with an epilimnion deeper than 9 m or at more polar latitudes, the predicted half-life can be a year or more.
Limitations and applications of the estimates presented here
It is important to note that we have not focused on estimating the [1O2]epi,avgSS in any one particular lake. Rather, by using ranges of values for the input parameters that impact [1O2]epi,avgSS, a deeper understanding of the [1O2]epi,avgSS values that are possible within the epilimnia of a variety of lakes is presented. This approach requires some simplifying assumptions. Specifically, lakes have been treated as a simplified box model. This means that changes in mixed depth and [1O2]epi,avgSS due to seasonal lake turnover or due to seasonal changes such as ice cover are not incorporated. As the focus of this work is on improving the estimate of environmentally representative values for [1O2]epi,avgSS rather than on modelling pollutant dynamics, the half-life estimates presented here are most relevant for pollutants whose residence time within a lake is on the order of days to months. These half-lives offer an estimate of how pollutant lifetimes are impacted by factors such as epilimnion depth, latitude, singlet oxygen quantum yield, and pollutant bimolecular rate constant.Some of the parameters considered in this work, such as Kd and fa,CDOM, are likely to co-vary, and interactions between such parameters have not explicitly been accounted for in this work. Similarly, not all combinations of parameters are equally probable. This would lead to either a narrower range of predicted [1O2]SS values or different regimes of values depending on sets of parameters valid for a specific environment or lake type. By not excluding any combination of parameters, we provide a wide range of possible values of [1O2]SS in this work, which we expect to narrow as future work provides better values for the parameters.
In previous sections additional limitations regarding other simplifications in our system have been noted, including the difficulty in estimating the impacts of cloud cover on the irradiance incident to a lake, the broad range of possible wavelength-dependent ΦΔ values for different types of DOM, and the lack of generalizable data for the fraction of light attenuation due to absorbance by CDOM. The impact of including many of these factors would be to decrease the [1O2]epi,avgSS, though by how much is currently unknown.
The equations used here could be adapted to a specific lake if experimental data on the ΦΔ and absorption coefficient of the DOM in that lake as well as information on lake dynamics were known. The framework presented here provides a basis for more environmentally representative values of [1O2]epi,avgSS that can be used by researchers and practitioners to estimate indirect photodegradation rates in lakes.
A similar approach could in principle be used to estimate the concentrations of other PPRIs, such as hydroxyl radicals (OH˙) or triplet excited state CDOM, in sunlit lakes. However, the formation and quenching processes for other PPRIs are more complicated than those of 1O2 and in many cases are less well understood. To take OH˙ as an example, while there is evidence that CDOM is the main source of OH˙ in surface waters, other sources include nitrate and nitrite.81,82 The main scavenger of OH˙ in surface waters is CDOM, but in seawater bromide is the most important scavenger, while in some freshwaters carbonate and bicarbonate might also be relevant sinks.81,83 For each of these pathways the range of concentrations of these constituents in surface waters must be estimated, as well as the quantum yield of formation of OH˙ from the relevant sources. The more complicated dynamics of OH˙ formation and quenching increase the uncertainty of the resulting steady-state concentration such that the range of values obtained is not useful for predictions of pollutant half-lives. That being said, [OH˙]SS is generally known to be around two orders of magnitude lower than [1O2]SS in sunlit surface waters. Thus, as a first approximation, one could estimate depth-averaged values of [OH˙]SS to be 6 × 10−19 to 5 × 10−17 M, similar to previous depth-averaged estimates.84,85
Conclusions
In this work the variability of singlet oxygen steady-state concentrations within the epilimnia as well as at the near-surface of lakes has been investigated. The depth of the epilimnion is the environmental factor that most impacts the mixed-layer [1O2]epi,avgSS, while DOC concentration has a very limited effect. This contrasts the situation at the near-surface, where the DOC concentration is a dominant factor affecting [1O2]SS.Near-surface [1O2]SS values and epilimnion-averaged [1O2]epi,avgSS values differ by approximately two orders of magnitude. For estimating environmental half-lives of 1O2-reactive compounds in sunlit lakes, we suggest using a range of 6 × 10−17 to 5 × 10−15 M for depth-averaged values of [1O2]SS. We believe that this range of [1O2]epi,avgSS values provides a more complete picture of 1O2 in the mixed layer of surface waters, and using these values will provide more realistic estimates of environmental half-lives of pollutants in surface waters. Our results show that for the half-life of a pollutant reacting with 1O2 to be less than one year in a representative lake, the pollutant must have a bimolecular rate constant of at least 108 M−1 s−1.
This work also highlights the need for more data on parameters such as wavelength-dependent ΦΔ relationships and fraction of absorbance in surface waters that is due to CDOM. Variability in both of these parameters leads to a large variation in possible [1O2]epi,avgSS values. In the case of ΦΔ, though there are many single values available in the literature, their use in calculations of 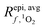 leads to overestimations in [1O2]epi,avgSS. For fabs,CDOM, many of the available literature values are for visible wavelengths and marine environments, limiting their applicability to photochemical generation of 1O2 in surface waters. A more complete understanding of the distribution of these two parameters within surface waters globally would lead to less variability and more confident predictions of [1O2]epi,avgSS within the epilimnia of lakes.
leads to overestimations in [1O2]epi,avgSS. For fabs,CDOM, many of the available literature values are for visible wavelengths and marine environments, limiting their applicability to photochemical generation of 1O2 in surface waters. A more complete understanding of the distribution of these two parameters within surface waters globally would lead to less variability and more confident predictions of [1O2]epi,avgSS within the epilimnia of lakes.
Finally, this work has implications for practitioners and researchers designing engineered systems that rely on photodegradation as a treatment mechanism. Our work shows that once all the photons entering a system have been absorbed, increasing the depth leads to lower [1O2]epi,avgSS values. Similarly, for shallow ponds (i.e. ≤1 m deep), increasing the DOC concentration can lead to large increases in [1O2]SS. The data provided in Tables 2 and S5† can help researchers optimize engineered systems to maximize the production of 1O2 within the system.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We gratefully acknowledge financial support for this work from the Swiss National Science Foundation (Grant Number 200020_188565), and from Firmenich Incorporated. We thank Dr Vivian Lin for collecting the Great Dismal Swamp water, and Dr Paul Erickson for collecting the Suwannee River water. We also thank Céline Jenni for work in the field and laboratory, and Sophie Bogler for work in the laboratory.References
- E. M. L. Janssen, E. Marron and K. McNeill, Aquatic Photochemical Kinetics of Benzotriazole and Structurally Related Compounds, Environ. Sci.: Processes Impacts, 2015, 17(5), 939–946, 10.1039/C5EM00045A.
- A. Bianco, D. Fabbri, M. Minella, M. Brigante, G. Mailhot, V. Maurino, C. Minero and D. Vione, New Insights into the Environmental Photochemistry of 5-Chloro-2-(2,4-Dichlorophenoxy)Phenol (Triclosan): Reconsidering the Importance of Indirect Photoreactions, Water Res., 2015, 72, 271–280, DOI:10.1016/j.watres.2014.07.036.
- C. A. Davis, P. R. Erickson, K. McNeill and E. M.-L. Janssen, Environmental Photochemistry of Fenamate NSAIDs and Their Radical Intermediates, Environ. Sci.: Processes Impacts, 2017, 19(5), 656–665, 10.1039/C7EM00079K.
- G. Ruggeri, G. Ghigo, V. Maurino, C. Minero and D. Vione, Photochemical Transformation of Ibuprofen into Harmful 4-Isobutylacetophenone: Pathways, Kinetics, and Significance for Surface Waters, Water Res., 2013, 47(16), 6109–6121, DOI:10.1016/j.watres.2013.07.031.
- J. N. Apell, N. C. Pflug and K. McNeill, Photodegradation of Fludioxonil and Other Pyrroles: The Importance of Indirect Photodegradation for Understanding Environmental Fate and Photoproduct Formation, Environ. Sci. Technol., 2019, 53(19), 11240–11250, DOI:10.1021/acs.est.9b03948.
- D. E. Latch, B. L. Stender, J. L. Packer, W. A. Arnold and K. McNeill, Photochemical Fate of Pharmaceuticals in the Environment: Cimetidine and Ranitidine, Environ. Sci. Technol., 2003, 37(15), 3342–3350, DOI:10.1021/es0340782.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Indirect Photolysis: Reactions with Photooxidants in Natural Waters and in the Atmosphere, in Environmental Organic Chemistry, John Wiley & Sons, Ltd, 2005, pp. 655–686, DOI:10.1002/0471649643.ch16.
- K. McNeill and S. Canonica, Triplet State Dissolved Organic Matter in Aquatic Photochemistry: Reaction Mechanisms, Substrate Scope, and Photophysical Properties, Environ. Sci.: Processes Impacts, 2016, 18(11), 1381–1399, 10.1039/C6EM00408C.
- P. P. Vaughan and N. V. Blough, Photochemical Formation of Hydroxyl Radical by Constituents of Natural Waters, Environ. Sci. Technol., 1998, 32(19), 2947–2953, DOI:10.1021/es9710417.
- A. L. Boreen, W. A. Arnold and K. McNeill, Triplet-Sensitized Photodegradation of Sulfa Drugs Containing Six-Membered Heterocyclic Groups: Identification of an SO2 Extrusion Photoproduct, Environ. Sci. Technol., 2005, 39(10), 3630–3638, DOI:10.1021/es048331p.
- D. E. Latch, Chapter 8: The Role of Singlet Oxygen in Surface Water Photochemistry, in Surface Water Photochemistry, 2015, pp. 139–165, 10.1039/9781782622154-00139.
- R. G. Zepp, N. L. Wolfe, G. L. Baughman and R. C. Hollis, Singlet Oxygen in Natural Waters, Nature, 1977, 267(5610), 421–423, DOI:10.1038/267421a0.
- W. R. Haag and J. Hoigné, Singlet Oxygen in Surface Waters. 3. Photochemical Formation and Steady-State Concentrations in Various Types of Waters, Environ. Sci. Technol., 1986, 20(4), 341–348, DOI:10.1021/es00146a005.
- A. C. Maizel, J. Li and C. K. Remucal, Relationships Between Dissolved Organic Matter Composition and Photochemistry in Lakes of Diverse Trophic Status, Environ. Sci. Technol., 2017, 51(17), 9624–9632, DOI:10.1021/acs.est.7b01270.
- L. C. Bodhipaksha, C. M. Sharpless, Y.-P. Chin and A. A. MacKay, Role of Effluent Organic Matter in the Photochemical Degradation of Compounds of Wastewater Origin, Water Res., 2017, 110, 170–179, DOI:10.1016/j.watres.2016.12.016.
- A. Marchisio, M. Minella, V. Maurino, C. Minero and D. Vione, Photogeneration of Reactive Transient Species upon Irradiation of Natural Water Samples: Formation Quantum Yields in Different Spectral Intervals, and Implications for the Photochemistry of Surface Waters, Water Res., 2015, 73, 145–156, DOI:10.1016/j.watres.2015.01.016.
- R. Ossola, O. M. Jönsson, K. Moor and K. McNeill, Singlet Oxygen Quantum Yields in Environmental Waters, Chem. Rev., 2021, 121(7), 4100–4146, DOI:10.1021/acs.chemrev.0c00781.
- D. Vione, D. Bagnus, V. Maurino and C. Minero, Quantification of Singlet Oxygen and Hydroxyl Radicals upon UV Irradiation of Surface Water, Environ. Chem. Lett., 2010, 8(2), 193–198, DOI:10.1007/s10311-009-0208-z.
- C. Minero, S. Chiron, G. Falletti, V. Maurino, E. Pelizzetti, R. Ajassa, M. E. Carlotti and D. Vione, Photochemincal Processes Involving Nitrite in Surface Water Samples, Aquat. Sci., 2007, 69(1), 71–85, DOI:10.1007/s00027-007-0881-6.
- S. Bahnmüller, U. von Gunten and S. Canonica, Sunlight-Induced Transformation of Sulfadiazine and Sulfamethoxazole in Surface Waters and Wastewater Effluents, Water Res., 2014, 57, 183–192, DOI:10.1016/j.watres.2014.03.019.
- F. a. Housari, D. Vione, S. Chiron and S. Barbati, Reactive Photoinduced Species in Estuarine Waters. Characterization of Hydroxyl Radical, Singlet Oxygen and Dissolved Organic Matter Triplet State in Natural Oxidation Processes, Photochem. Photobiol. Sci., 2010, 9(1), 78–86, 10.1039/B9PP00030E.
- C. Shao, W. J. Cooper, D. R. S. Lean, W. J. Cooper and D. R. S. Lean, Singlet Oxygen Formation in Lake Waters from Mid-Latitudes, https://www.taylorfrancis.com/, accessed 2019-10-11, DOI:10.1201/9781351069847-18.
- S. A. Timko, C. Romera-Castillo, R. Jaffé and W. J. Cooper, Photo-Reactivity of Natural Dissolved Organic Matter from Fresh to Marine Waters in the Florida Everglades, USA, Environ. Sci.: Processes Impacts, 2014, 16(4), 866–878, 10.1039/C3EM00591G.
- M. Bodrato and D. Vione, APEX (Aqueous Photochemistry of Environmentally Occurring Xenobiotics): A Free Software Tool to Predict the Kinetics of Photochemical Processes in Surface Waters, Environ. Sci.: Processes Impacts, 2014, 16(4), 732–740, 10.1039/C3EM00541K.
- US EPA, O. GCSOLAR, https://www.epa.gov/ceam/gcsolar, accessed 2020-07-22.
- D. A. Vione, Critical View of the Application of the APEX Software (Aqueous Photochemistry of Environmentally-Occurring Xenobiotics) to Predict Photoreaction Kinetics in Surface Freshwaters, Molecules, 2019, 25(9), 1–34 Search PubMed.
- R. G. Zepp and D. M. Cline, Rates of Direct Photolysis in Aquatic Environment, Environ. Sci. Technol., 1977, 11(4), 359–366, DOI:10.1021/es60127a013.
- E. Appiani, R. Ossola, D. E. Latch, P. R. Erickson and K. McNeill, Aqueous Singlet Oxygen Reaction Kinetics of Furfuryl Alcohol: Effect of Temperature, PH, and Salt Content, Environ. Sci.: Processes Impacts, 2017, 19(4), 507–516, 10.1039/C6EM00646A.
- J. Hoigné, B. C. Faust, W. R. Haag, F. E. Scully and R. G. Zepp, Aquatic Humic Substances as Sources and Sinks of Photochemically Produced Transient Reactants, in Aquatic Humic Substances; Advances in Chemistry, American Chemical Society, 1988, vol. 219, pp. 363–381, DOI:10.1021/ba-1988-0219.ch023.
- H. Shaw and S. Toby, Light Absorption in Photochemistry, J. Chem. Educ., 1966, 43(8), 408, DOI:10.1021/ed043p408.
- S. B. Partanen, P. R. Erickson, D. E. Latch, K. J. Moor and K. McNeill, Dissolved Organic Matter Singlet Oxygen Quantum Yields: Evaluation Using Time-Resolved Singlet Oxygen Phosphorescence, Environ. Sci. Technol., 2020, 54(6), 3316–3324, DOI:10.1021/acs.est.9b07246.
- B. Qin, J. Zhou, J. J. Elser, W. S. Gardner, J. Deng and J. D. Brookes, Water Depth Underpins the Relative Roles and Fates of Nitrogen and Phosphorus in Lakes, Environ. Sci. Technol., 2020, 54(6), 3191–3198, DOI:10.1021/acs.est.9b05858.
- M. Hanna, Evaluation of Models Predicting Mixing Depth, Can. J. Fish. Aquat. Sci., 1990, 47(5), 940–947, DOI:10.1139/f90-108.
- J. N. Apell and K. McNeill, Updated and Validated Solar Irradiance Reference Spectra for Estimating Environmental Photodegradation Rates, Environ. Sci.: Processes Impacts, 2019, 21(3), 427–437, 10.1039/C8EM00478A.
- D. P. Morris, H. Zagarese, C. E. Williamson, E. G. Balseiro, B. R. Hargreaves, B. Modenutti, R. Moeller and C. Queimalinos, The Attenuation of Solar UV Radiation in Lakes and the Role of Dissolved Organic Carbon, Limnol. Oceanogr., 1995, 40(8), 1381–1391, DOI:10.4319/lo.1995.40.8.1381.
- S. W. Effler, F. Peng, D. M. O'Donnell and C. Strait, The Backscattering Coefficient and Its Components in the Great Lakes: A Review and Synthesis, J. Great Lakes Res., 2013, 39, 108–122, DOI:10.1016/j.jglr.2013.02.002.
- H. Lyu, Q. Wang, C. Wu, L. Zhu, Y. Li and J. Huang, Variations in Optical Scattering and Backscattering by Organic and Inorganic Particulates in Chinese Lakes of Taihu, Chaohu and Dianchi, Chinese Geographical Science, 2015, 25(1), 26–38, DOI:10.1007/s11769-014-0689-y.
- E. Boss, W. S. Pegau, M. Lee, M. Twardowski, E. Shybanov, G. Korotaev and F. Baratange, Particulate Backscattering Ratio at LEO 15 and Its Use to Study Particle Composition and Distribution, J. Geophys. Res.: Oceans, 2004, 109(C1) DOI:10.1029/2002JC001514.
- H. Loisel, X. Mériaux, J.-F. Berthon and A. Poteau, Investigation of the Optical Backscattering to Scattering Ratio of Marine Particles in Relation to Their Biogeochemical Composition in the Eastern English Channel and Southern North Sea, Limnol. Oceanogr., 2007, 52(2), 739–752, DOI:10.4319/lo.2007.52.2.0739.
- W. A. Snyder, R. A. Arnone, C. O. Davis, W. Goode, R. W. Gould, S. Ladner, G. Lamela, W. J. Rhea, R. Stavn, M. Sydor and A. Weidemann, Optical Scattering and Backscattering by Organic and Inorganic Particulates in U.S. Coastal Waters, Appl. Opt., 2008, 47(5), 666–677, DOI:10.1364/AO.47.000666.
- D. McKee, M. Chami, I. Brown, V. S. Calzado, D. Doxaran and A. Cunningham, Role of Measurement Uncertainties in Observed Variability in the Spectral Backscattering Ratio: A Case Study in Mineral-Rich Coastal Waters, Appl. Opt., 2009, 48(24), 4663–4675, DOI:10.1364/AO.48.004663.
- J. T. O. Kirk, Light and Photosynthesis in Aquatic Ecosystems, Cambridge University Press, Cambridge, 3rd edn, 2010, DOI:10.1017/CBO9781139168212.
- D. Mckee, A. Cunningham and K. J. Jones, Optical and Hydrographic Consequences of Freshwater Run-off during Spring Phytoplankton Growth in a Scottish Fjord, J. Plankton Res., 2002, 24(11), 1163–1171, DOI:10.1093/plankt/24.11.1163.
- C. Belzile, W. F. Vincent and M. Kumagai, Contribution of Absorption and Scattering to the Attenuation of UV and Photosynthetically Available Radiation in Lake Biwa, Limnol. Oceanogr., 2002, 47(1), 95–107, DOI:10.4319/lo.2002.47.1.0095.
- J.-E. Thrane, D. O. Hessen and T. Andersen, The Absorption of Light in Lakes: Negative Impact of Dissolved Organic Carbon on Primary Productivity, Ecosystems, 2014, 17(6), 1040–1052, DOI:10.1007/s10021-014-9776-2.
- S. Watanabe, I. Laurion, S. Markager and W. F. Vincent, Abiotic Control of Underwater Light in a Drinking Water Reservoir: Photon Budget Analysis and Implications for Water Quality Monitoring, Water Resour. Res., 2015, 51(8), 6290–6310, DOI:10.1002/2014WR015617.
- S. W. Effler, M. Perkins, F. Peng, C. Strait, A. D. Weidemann and M. T. Auer, Light-Absorbing Components in Lake Superior, J. Great Lakes Res., 2010, 36(4), 656–665, DOI:10.1016/j.jglr.2010.08.001.
- M. G. Perkins, S. W. Effler and C. Strait, Light Absorption Components in Onondaga Lake, New York, U.S.A., Fundam. Appl. Limnol., 2010, 209–223, DOI:10.1127/1863-9135/2010/0176-0209.
- M. Perkins, S. W. Gail Effler, C. Strait and L. Zhang, Light Absorbing Components in the Finger Lakes of New York, Fundam. Appl. Limnol., 2009, 305–320, DOI:10.1127/1863-9135/2009/0173-0305.
- R. Ma, J. Tang, J. Dai, Y. Zhang and Q. Song, Absorption and Scattering Properties of Water Body in Taihu Lake, China: Absorption, International Journal of Remote Sensing, 2006, 27(19), 4277–4304, DOI:10.1080/01431160600851835.
- M. Zhang, Y. Zhou, Y. Zhang, K. Shi, C. Jiang and Y. Zhang, Attenuation of UVR and PAR in a Clear and Deep Lake: Spatial Distribution and Affecting Factors, Limnologica, 2020, 84, 125798, DOI:10.1016/j.limno.2020.125798.
- R. M. Cory, T. W. Davis, G. J. Dick, T. Johengen, V. J. Denef, M. A. Berry, S. E. Page, S. B. Watson, K. Yuhas and G. W. Kling, Seasonal Dynamics in Dissolved Organic Matter, Hydrogen Peroxide, and Cyanobacterial Blooms in Lake Erie, Frontiers in Marine Science, 2016, 3, 54, DOI:10.3389/fmars.2016.00054.
- J. H. Jerome and R. P. Bukata, Tracking the Propagation of Solar Ultraviolet Radiation: Dispersal of Ultraviolet Photons in Inland Waters, J. Great Lakes Res., 1998, 24(3), 666–680, DOI:10.1016/S0380-1330(98)70853-6.
- US EPA, Fate, Transport and Transformation Test Guidelines: OPPTS 835.5270 - Indirect Photolysis Screening Test, United States Environmental Protection Agenc January, 1998 Search PubMed.
- R. Ossola, O. M. Jönsson, K. Moor and K. McNeill, Singlet Oxygen Quantum Yields in Environmental Waters, Chem. Rev., 2021, 121(7), 4100–4146, DOI:10.1021/acs.chemrev.0c00781.
- B. Sulzberger, S. Canonica, T. Egli, W. Giger, J. Klausen and U. von Gunten, Oxidative Transformations of Contaminants in Natural and in Technical Systems, CHIMIA International Journal for Chemistry, 1997, 51(12), 900–907 CAS.
- M. O'Connor, S. R. Helal, D. E. Latch and W. A. Arnold, Quantifying Photo-Production of Triplet Excited States and Singlet Oxygen from Effluent Organic Matter, Water Res., 2019, 156, 23–33, DOI:10.1016/j.watres.2019.03.002.
- C. M. Sharpless, Lifetimes of Triplet Dissolved Natural Organic Matter (DOM) and the Effect of NaBH4 Reduction on Singlet Oxygen Quantum Yields: Implications for DOM Photophysics, Environ. Sci. Technol., 2012, 46(8), 4466–4473, DOI:10.1021/es300217h.
- R. G. Wetzel, 9 - OXYGEN, in Limnology, ed. R. G. Wetzel, Academic Press, San Diego, 3rd edn, 2001, pp. 151–168, DOI:10.1016/B978-0-08-057439-4.50013-7.
- J. Calbó, D. Pagès and J.-A. González, Empirical Studies of Cloud Effects on UV Radiation: A Review, Rev. Geophys., 2005, 43(2) DOI:10.1029/2004RG000155.
- F. Kasten and G. Czeplak, Solar and Terrestrial Radiation Dependent on the Amount and Type of Cloud, Sol. Energy, 1980, 24(2), 177–189, DOI:10.1016/0038-092X(80)90391-6.
- T. Muneer and M. S. Gul, Evaluation of Sunshine and Cloud Cover Based Models for Generating Solar Radiation Data, Energy Convers. Manage., 2000, 41(5), 461–482, DOI:10.1016/S0196-8904(99)00108-9.
- J. C. Lam and D. H. W. Li, Correlation Analysis of Solar Radiation and Cloud Cover, Int. J. Ambient Energy, 1998, 19(4), 187–198, DOI:10.1080/01430750.1998.9675305.
- R. E. H. Smith, C. D. Allen and M. N. Charlton, Dissolved Organic Matter and Ultraviolet Radiation Penetration in the Laurentian Great Lakes and Tributary Waters, J. Great Lakes Res., 2004, 30(3), 367–380, DOI:10.1016/S0380-1330(04)70354-8.
- K. C. Rose, D. P. Hamilton, C. E. Williamson, C. G. McBride, J. M. Fischer, M. H. Olson, J. E. Saros, M. G. Allan and N. Cabrol, Light Attenuation Characteristics of Glacially-Fed Lakes: Transparency of Glacially-Fed Lakes, J. Geophys. Res.: Biogeosci., 2014, 119(7), 1446–1457, DOI:10.1002/2014JG002674.
- I. Laurion, M. Ventura, J. Catalan, R. Psenner and R. Sommaruga, Attenuation of Ultraviolet Radiation in Mountain Lakes: Factors Controlling the among- and within-Lake Variability, Limnol. Oceanogr., 2000, 45(6), 1274–1288, DOI:10.4319/lo.2000.45.6.1274.
- J. Wenk, M. T. Nguyen and K. L. Nelson, Natural Photosensitizers in Constructed Unit Process Wetlands: Photochemical Characterization and Inactivation of Pathogen Indicator Organisms, Environ. Sci. Technol., 2019, 53(13), 7724–7735, DOI:10.1021/acs.est.9b01180.
- A. Sardana, B. Cottrell, D. Soulsby and T. N. Aziz, Dissolved Organic Matter Processing and Photoreactivity in a Wastewater Treatment Constructed Wetland, Sci. Total Environ., 2019, 648, 923–934, DOI:10.1016/j.scitotenv.2018.08.138.
- D.-P. Häder, Does Enhanced Solar UV-B Radiation Affect Marine Primary Producers in Their Natural Habitats?, Photochem. Photobiol., 2011, 87(2), 263–266, DOI:10.1111/j.1751-1097.2011.00888.x.
- T. Zeng and W. A. Arnold, Pesticide Photolysis in Prairie Potholes: Probing Photosensitized Processes, Environ. Sci. Technol., 2013, 47(13), 6735–6745, DOI:10.1021/es3030808.
- Y. Li, X. Qiao, C. Zhou, Y. Zhang, Z. Fu and J. Chen, Photochemical Transformation of Sunscreen Agent Benzophenone-3 and Its Metabolite in Surface Freshwater and Seawater, Chemosphere, 2016, 153, 494–499, DOI:10.1016/j.chemosphere.2016.03.080.
- A. J. McCabe and W. A. Arnold, Seasonal and Spatial Variabilities in the Water Chemistry of Prairie Pothole Wetlands Influence the Photoproduction of Reactive Intermediates, Chemosphere, 2016, 155, 640–647, DOI:10.1016/j.chemosphere.2016.04.078.
- S. Mostafa and F. L. Rosario-Ortiz, Singlet Oxygen Formation from Wastewater Organic Matter, Environ. Sci. Technol., 2013, 47(15), 8179–8186, DOI:10.1021/es401814s.
- A. C. Maizel and C. K. Remucal, The Effect of Probe Choice and Solution Conditions on the Apparent Photoreactivity of Dissolved Organic Matter, Environ. Sci.: Processes Impacts, 2017, 19(8), 1040–1050, 10.1039/c7em00235a.
- D. Zhang, S. Yan and W. Song, Photochemically Induced Formation of Reactive Oxygen Species (ROS) from Effluent Organic Matter, Environ. Sci. Technol., 2014, 48(21), 12645–12653, DOI:10.1021/es5028663.
- B. M. Peterson, A. M. McNally, R. M. Cory, J. D. Thoemke, J. B. Cotner and K. McNeill, Spatial and Temporal Distribution of Singlet Oxygen in Lake Superior, Environ. Sci. Technol., 2012, 46(13), 7222–7229, DOI:10.1021/es301105e.
- N. M. Scully, W. F. Vincent, D. R. S. Lean and W. Cooper, J. Implications of Ozone Depletion for Surface-Water Photochemistry: Sensitivity of Clear Lakes, Aquat. Sci., 1997, 59(3), 260–274, DOI:10.1007/BF02523277.
- J. Wasswa, C. T. Driscoll and T. Zeng, Photochemical Characterization of Surface Waters from Lakes in the Adirondack Region of New York, Environ. Sci. Technol., 2020, 54(17), 10654–10667, DOI:10.1021/acs.est.0c02811.
- Y. Chen, R. M. Hozalski, L. G. Olmanson, B. P. Page, J. C. Finlay, P. L. Brezonik and W. A. Arnold, Prediction of Photochemically Produced Reactive Intermediates in Surface Waters via Satellite Remote Sensing, Environ. Sci. Technol., 2020, 54(11), 6671–6681, DOI:10.1021/acs.est.0c00344.
- A. L. Boreen, W. A. Arnold and K. McNeill, Photochemical Fate of Sulfa Drugs in the Aquatic Environment: Sulfa Drugs Containing Five-Membered Heterocyclic Groups, Environ. Sci. Technol., 2004, 38(14), 3933–3940, DOI:10.1021/es0353053.
- D. Vione, M. Minella, V. Maurino and C. Minero, Indirect Photochemistry in Sunlit Surface Waters: Photoinduced Production of Reactive Transient Species, Chem.–Eur. J., 2014, 20(34), 10590–10606, DOI:10.1002/chem.201400413.
- D. Vione, G. Falletti, V. Maurino, C. Minero, E. Pelizzetti, M. Malandrino, R. Ajassa, R.-I. Olariu and C. Arsene, Sources and Sinks of Hydroxyl Radicals upon Irradiation of Natural Water Samples, Environ. Sci. Technol., 2006, 40(12), 3775–3781, DOI:10.1021/es052206b.
- C. M. Glover and F. L. Rosario-Ortiz, Impact of Halides on the Photoproduction of Reactive Intermediates from Organic Matter, Environ. Sci. Technol., 2013, 47(24), 13949–13956, DOI:10.1021/es4026886.
- P. L. Brezonik and J. Fulkerson-Brekken, Nitrate-Induced Photolysis in Natural Waters: Controls on Concentrations of Hydroxyl Radical Photo-Intermediates by Natural Scavenging Agents, Environ. Sci. Technol., 1998, 32(19), 3004–3010, DOI:10.1021/es9802908.
- R. G. Zepp, J. Hoigné and H. Bader, Nitrate-Induced Photooxidation of Trace Organic Chemicals in Water, Environ. Sci. Technol., 1987, 21(5), 443–450, DOI:10.1021/es00159a004.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1em00062d |
| This journal is © The Royal Society of Chemistry 2021 |