Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Wasted photons: photogeneration yield and charge carrier collection efficiency of hematite photoanodes for photoelectrochemical water splitting†
Yifat
Piekner
 a,
David S.
Ellis
a,
David S.
Ellis
 b,
Daniel A.
Grave
b,
Daniel A.
Grave
 bc,
Anton
Tsyganok
bc,
Anton
Tsyganok
 b and
Avner
Rothschild
b and
Avner
Rothschild
 *ab
*ab
aThe Nancy & Stephen Grand Technion Energy Program (GTEP), Technion – Israel Institute of Technology, Haifa 3200002, Israel. E-mail: avnerrot@technion.ac.il
bDepartment of Materials Science and Engineering, Technion – Israel Institute of Technology, Haifa 3200002, Israel
cDepartment of Materials Engineering and Ilse Katz Institute for Nanoscale Science and Technology, Ben Gurion University of the Negev, Be’er Sheva 8410501, Israel
First published on 15th July 2021
Abstract
Hematite (α-Fe2O3) is a leading photoanode candidate for photoelectrochemical water splitting. Despite extensive research efforts, the champion hematite photoanodes reported to date have achieved less than half of the maximal photocurrent predicted by its bandgap energy. Here we show that this underachievement arises, to a large extent, because of unproductive optical excitations that give rise to localized electronic transitions that do not generate electron–hole pairs. A comprehensive method for extraction of the photogeneration yield spectrum, the wavelength-dependent fraction of absorbed photons that generate electron–hole pairs, and the spatial charge carrier collection efficiency is presented, and applied for a thin (32 nm) film hematite photoanode. Its photogeneration yield is less than unity across the entire absorption range, limiting the maximal photocurrent that may be attained in an ideal hematite photoanode to about half of the theoretical limit predicted without accounting for this effect.
Broader contextAt the heart of solar cells is a semiconductor photoabsorber: a material capable of absorbing photons and generating electrons and holes that contribute to the photocurrent. But where commercial photovoltaic cells use silicon for that purpose, photoelectrochemical water splitting cells for solar energy conversion to green hydrogen must rely on other materials that are suitable for operation in aqueous electrolytes. An apparently promising material for that purpose is hematite, an abundant form of iron oxide (α-Fe2O3). It is cheap, nontoxic, stable in alkaline electrolytes, and it absorbs visible light such that it could generate, theoretically, photocurrents as high as 12.6 mA cm−2. Alas, for half a century hematite has been frustrating scientists who have been able to obtain from it less than half of the theoretical photocurrent limit. This work shows why this is the case, and presents an analytical way of assessing the actual limit that might be obtained from hematite, as a case-study for other correlated electron materials. To this end, a comprehensive method is introduced to extract both the spatial profile of the charge carrier collection efficiency and the photogeneration yield spectrum, defined as the wavelength-dependent fraction of absorbed photons that generate electron–hole pairs. |
Introduction
Photovoltaic and photocatalytic materials have been extensively studied since Edmond Becquerel discovered the photovoltaic effect in 1839.1 One of the fundamental material properties that controls their photoconversion efficiency is the bandgap energy, which determines the fraction of the solar spectrum that can be absorbed in a semiconductor photoabsorber.2 In conventional semiconductors, such as Si, absorption of photons with energy above the bandgap energy generates electron–hole pairs that can be separated and collected at opposite contacts, thereby contributing to the photocurrent. However, in many nonconventional semiconductors with correlated electrons, which typically have coordination complexes of transition metals surrounded by oxygen or other ligands, some of the absorbed photons excite localized electronic transitions that do not contribute to electron–hole generation, such as ligand field d–d transitions.3–5 For such materials, the wavelength-dependent photogeneration yield is defined as the ratio between the contributing light absorption that generate electron–hole pairs and the overall absorption comprising both contributing and non-contributing optical transitions.6 The photogeneration yield spectrum, ξ(λ), is an intrinsic material property that significantly influences the photoconversion efficiency of these materials, as reported in hematite (α-Fe2O3) photoanodes for photoelectrochemical water splitting.6,7 A similar effect was recently reported in organic photovoltaic materials.8 Finding a way to measure the ξ(λ) spectrum is an open challenge that would advance understanding of the fundamental limitations of correlated electron materials in photovoltaic and photocatalytic applications.The photogeneration yield can be extracted, in principle, from quantum efficiency and optical measurements.6 The external quantum efficiency (EQE) spectrum, which is also known as the incident photon to electron conversion efficiency (IPCE) spectrum, is routinely measured for photovoltaic and photoelectrochemical devices.9,10 It can be expressed by the following integral over the photoabsorber thickness d:
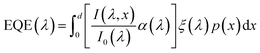 | (1) |
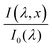 is the wavelength-dependent photon flux at distance x from the surface normalized by the incident flux at the surface (x = 0), α(λ) is the absorption coefficient (aka attenuation coefficient), and p(x) is the spatial-dependent charge carrier collection efficiency. For brevity, we define
is the wavelength-dependent photon flux at distance x from the surface normalized by the incident flux at the surface (x = 0), α(λ) is the absorption coefficient (aka attenuation coefficient), and p(x) is the spatial-dependent charge carrier collection efficiency. For brevity, we define 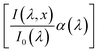 as aPA(λ,x) which describes the incremental absorptance in the photoabsorber layer:
as aPA(λ,x) which describes the incremental absorptance in the photoabsorber layer: 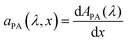 , where APA(λ) is the absorptance within the photoabsorber layer. aPA(λ,x) gathers all the terms in the integrand that can be obtained by independent measurements: the incident photon flux, I0(λ), can be directly measured with a spectrophotometer; the absorption coefficient, α(λ), can be obtained from spectroscopic ellipsometry measurements; and the photon flux inside the photoabsorber, I(λ,x), can be calculated by optical modeling (e.g., by the transfer-matrix method) that can be verified against spectrophotometric transmission and reflection measurements. The EQE spectrum is directly measured, but since both p(x) and ξ(λ) are unknown, this ill-posed inverse problem cannot be solved using traditional numerical solution methods of the Fredholm integral equation of the first kind.11 Hence, extracting both p(x) and ξ(λ) is a nontrivial numerical challenge that requires a priori assumptions and can lead to uncertain results, as discussed elsewhere.6
, where APA(λ) is the absorptance within the photoabsorber layer. aPA(λ,x) gathers all the terms in the integrand that can be obtained by independent measurements: the incident photon flux, I0(λ), can be directly measured with a spectrophotometer; the absorption coefficient, α(λ), can be obtained from spectroscopic ellipsometry measurements; and the photon flux inside the photoabsorber, I(λ,x), can be calculated by optical modeling (e.g., by the transfer-matrix method) that can be verified against spectrophotometric transmission and reflection measurements. The EQE spectrum is directly measured, but since both p(x) and ξ(λ) are unknown, this ill-posed inverse problem cannot be solved using traditional numerical solution methods of the Fredholm integral equation of the first kind.11 Hence, extracting both p(x) and ξ(λ) is a nontrivial numerical challenge that requires a priori assumptions and can lead to uncertain results, as discussed elsewhere.6
The numerical challenge can be circumvented by analyzing ultrathin (typically below ∼10 nm) films wherein the spatial variations in I(λ,x) and p(x) can be ignored, allowing these functions to be replaced by their spatially averaged values, Ī(λ) and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) . In this case, eqn (1) can be expressed as a product of averages and explicitly solved for ξ(λ), as we recently presented elsewhere:7
. In this case, eqn (1) can be expressed as a product of averages and explicitly solved for ξ(λ), as we recently presented elsewhere:7
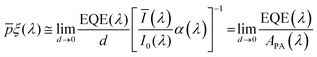 | (2) |
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) product directly from EQE and optical measurements, without any a priori assumptions regarding the p(x) profile. However, it only applies to ultrathin (<10 nm for hematite) films that, due to the quantum size effect,12–15 may not fully represent bulk hematite. Another issue is that this approximation yields the
ξ(λ) product directly from EQE and optical measurements, without any a priori assumptions regarding the p(x) profile. However, it only applies to ultrathin (<10 nm for hematite) films that, due to the quantum size effect,12–15 may not fully represent bulk hematite. Another issue is that this approximation yields the ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) product rather than fully separating ξ(λ) and p(x), meaning that the extracted ξ(λ) spectrum is scaled by a generally unknown factor (0 ≤
ξ(λ) product rather than fully separating ξ(λ) and p(x), meaning that the extracted ξ(λ) spectrum is scaled by a generally unknown factor (0 ≤ ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ≤ 1) leaving uncertainty in the magnitude of ξ(λ). Furthermore, it reveals nothing about the spatial properties of p(x) in thicker hematite layers, such as the minority charge carrier diffusion length. The ultrathin film approximation was applied to TiO2, BiVO4 and α-Fe2O3 (hematite) photoanodes for water photo-oxidation in photoelectrochemical cells for solar water splitting.7 The TiO2 and BiVO4 photoanodes were found to display a minor effect, with near unity photogeneration yield throughout most of the absorption range (above the bandgap energy). In contrast, the hematite photoanode displayed non-trivial behavior with
≤ 1) leaving uncertainty in the magnitude of ξ(λ). Furthermore, it reveals nothing about the spatial properties of p(x) in thicker hematite layers, such as the minority charge carrier diffusion length. The ultrathin film approximation was applied to TiO2, BiVO4 and α-Fe2O3 (hematite) photoanodes for water photo-oxidation in photoelectrochemical cells for solar water splitting.7 The TiO2 and BiVO4 photoanodes were found to display a minor effect, with near unity photogeneration yield throughout most of the absorption range (above the bandgap energy). In contrast, the hematite photoanode displayed non-trivial behavior with ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) values ranging between ∼40% and ∼20% in the wavelength range of 350 to 590 nm. The
ξ(λ) values ranging between ∼40% and ∼20% in the wavelength range of 350 to 590 nm. The ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) spectra of the ultrathin BiVO4 and hematite photoanodes presented similarly shaped profiles as the
ξ(λ) spectra of the ultrathin BiVO4 and hematite photoanodes presented similarly shaped profiles as the 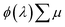 spectra obtained from time-resolved microwave conductivity (TRMC) measurements of their thick film counterparts,7 where ϕ(λ) is the quantum yield spectra and
spectra obtained from time-resolved microwave conductivity (TRMC) measurements of their thick film counterparts,7 where ϕ(λ) is the quantum yield spectra and 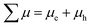 is the sum of the electron and hole mobilities. The results showed that the photogeneration yield significantly limits hematite performance to between ∼30% and ∼70% of the maximal photocurrent potential, depending on the value
is the sum of the electron and hole mobilities. The results showed that the photogeneration yield significantly limits hematite performance to between ∼30% and ∼70% of the maximal photocurrent potential, depending on the value ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) that was unknown in that work. As both the ultrathin film approximation and the TRMC methods find the photogeneration yield and quantum yield spectra, respectively, only up to a factor, the challenge still remains to extract their absolute values separately and independently of the charge carrier collection efficiency or charge carrier mobility. To this end, this work presents a rigorous analysis that extracts both the ξ(λ) spectrum and p(x) profile of thin film hematite photoanodes. The analysis is applied to a 32 nm thick hematite film that is more closely representative of bulk hematite than the ultrathin (7 nm) film that was analyzed previously.7
that was unknown in that work. As both the ultrathin film approximation and the TRMC methods find the photogeneration yield and quantum yield spectra, respectively, only up to a factor, the challenge still remains to extract their absolute values separately and independently of the charge carrier collection efficiency or charge carrier mobility. To this end, this work presents a rigorous analysis that extracts both the ξ(λ) spectrum and p(x) profile of thin film hematite photoanodes. The analysis is applied to a 32 nm thick hematite film that is more closely representative of bulk hematite than the ultrathin (7 nm) film that was analyzed previously.7
Due to its visible light absorption, stability in alkaline solutions,16 nontoxicity and abundance, hematite (α-Fe2O3) has been widely examined as a photoanode for water photo-oxidation in photoelectrochemical cells for solar water splitting.17 With a bandgap energy of 2.1 eV, hematite photoanodes have been commonly cited for their potential to reach a photocurrent density of 12.6 mA cm−2 under standard sunlight illumination (AM1.5G),17 if all photons with energy above 2.1 eV were to generate electrons and holes that contribute to the photocurrent without any optical and recombination losses. In practice, however, hematite photoanodes reach substantially lower photocurrents, with the highest reported records reaching less than half of the theoretical limit.18–20 For comparison, the champion BiVO4 photoanode reaches 90% of its theoretical photocurrent limit.21 The low internal quantum efficiency (IQE) of hematite photoanodes has been attributed to fast charge carrier recombination that limits their charge carrier collection efficiency.17,22 Extensive efforts to overcome this barrier using nanostructuring19,20 or light trapping in ultrathin films18,23 approaches to reduce the hole transport length to the surface have yielded only partial success, suggesting that there might be an elusive factor that limits the photocurrent in addition to recombination. Indeed, several studies suggested that the striking difference between the photocurrent action and light absorption spectra in hematite photoanodes may be attributed, in part, to optical excitations that result in localized electronic transitions such as ligand field d–d transitions that do not contribute to electron–hole generation,24–26 whereas others argued that polaronic charge carrier dynamics is responsible for this discrepancy.27 However, the majority of studies on hematite photoanodes attribute their low IQE to charge carrier recombination in the bulk and at the surface,17,22 whereas only few studies address the effect of low photogeneration yield on the photocurrent.6,7,25–28 While the physical origin of hematite's low photogeneration yield is still under investigation,29 it is important to have a reliable way to extract ξ(λ) from empirical measurements with a minimum of a priori assumptions.
In this work we introduce a general method that applies to thin and thick films, regardless of their thickness. Our method involves minimal a priori assumptions regarding the spatial dependence of the charge carrier collection efficiency p(x), that are supported by classical semiconductor junction physics.30,31 It extracts p(x) and ξ(λ) from optical and photoelectrochemical EQE measurements in a stepwise algorithm that converges to the correct solution, using complementary measurements in order to reduce the number of free parameters, as demonstrated in the following. Using the extracted ξ(λ) and α(λ) spectra, we calculate the contributing and non-contributing components of the absorption coefficient (α), and resolve the individual optical excitations that give rise to extended and localized electronic transitions, respectively. Finally, we estimate the photocurrent limit of hematite photoanodes based on the photogeneration yield spectrum we extract in this study, and show that it chops about half of the familiar 12.6 mA cm−2 limit that overlooks non-contributing absorption.
Results and discussion
Methodology
Eqn (1) has a likeness to the Fredholm integral equation of the first kind, which itself presents a formidable challenge to solve.11 However, the only unknown to deal with in the classical Fredholm problem would be the equivalent of eqn (1)'s p(x). This is not the case for our situation, however, since we have an additional unknown along the λ dimension in the form of ξ(λ). Therefore, additional information is required to solve the equation. To this end, a reasonable approximation of the form of the charge carrier collection efficiency, p(x), is provided by consideration of the physics of charge carrier transport in homogeneous semiconductors. The exponential decay of the steady-state concentration of injected minority charge carriers along the length of a semiconductor is well known in semiconductor textbooks.32 In light of the reciprocity theorem for charge carrier collection,33,34 which essentially states that the collection probability p(x) of a charge carrier at distance x to the surface has the same spatial profile as would be the steady-state concentration profile for the reverse case, i.e., injection from the surface, it is reasonable that, assuming a uniform segment of material, p(x) should be an exponentially decaying function. This is also supported by empirical observations using electron beam-induced current (EBIC) measurements to directly measure the charge carrier spatial distribution across semiconductor junctions under illumination.35 Therefore, we begin by using a simplified p(x) function with only two unknown parameters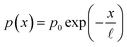 | (3) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is the collection length of the photo-generated minority charge carriers (holes in our case), and p0 is the charge carrier collection efficiency at the surface (x = 0). The latter can be measured by different techniques36 to reduce the number of free parameters.
is the collection length of the photo-generated minority charge carriers (holes in our case), and p0 is the charge carrier collection efficiency at the surface (x = 0). The latter can be measured by different techniques36 to reduce the number of free parameters.
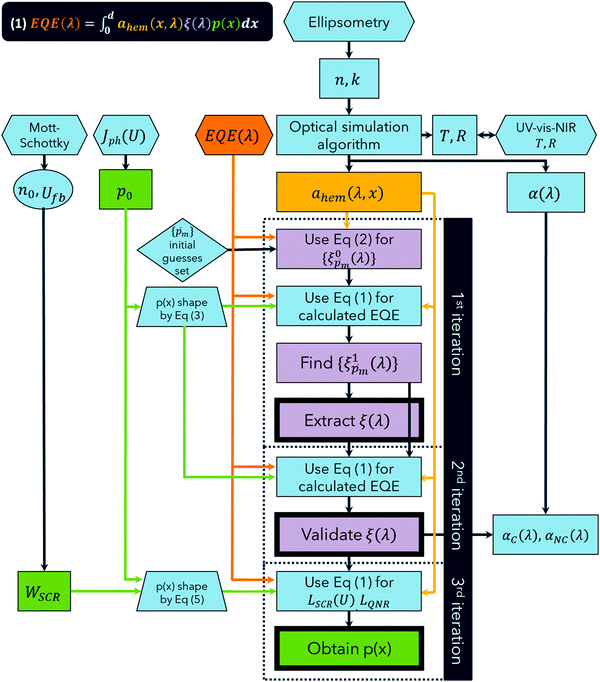
For the core experimental data required to solve eqn (1), we measured the EQE spectra,10 and used spectroscopic ellipsometry37 to calculate the incremental absorptance in the hematite layer, ahem(λ,x), the equivalent of aPA(λ,x) in eqn (1). Fig. 1 presents a flow chart describing our algorithm to extract ξ(λ) and p(x) by repeated applications of eqn (1), in three stepwise iterations. In every iteration, the calculated ahem(λ,x) spectrum and multiple ξ(λ) guesses (or the final ξ(λ) spectrum in the last iteration) were substituted into eqn (1), and the fitting parameters of p(x) were tuned by the Levenberg–Marquardt method38,39 to generate the EQE spectra that best fit the measured spectra. To reduce the number of fitting parameters and increase the confidence level in the analysis, some of the physical parameters that shape p(x) were constrained by complementary capacitance–voltage (Mott–Schottky),40 and photocurrent voltammetry measurements with and without hole scavenger.41 As described below in more detail, our first iteration extracts the ξ(λ) spectrum, the second validates it, and the third one extracts the final p(x) profile.
The first step in the process is spectroscopic ellipsometry measurements to find the complex refractive indices (n and k) of the hematite and ITO layers and of the glass substrate comprising the photoanode. To confirm the complex refractive indices obtained, the total transmittance (T) and reflectance (R) spectra of the photoanode were calculated using the transfer-matrix method,23 and compared with UV-vis-NIR spectrophotometry measurements. Using the complex refractive indices, we calculated ahem(x,λ) which was later inserted to eqn (1) for every subsequent iteration. Next, we measured EQE spectra with front, and then back, monochromatic illumination at different potentials. Analyzing EQE spectra measured for both front and the back illuminations increases the confidence in the extracted ξ(λ) spectrum, because it provides a set of two alternative ahem(λ,x) profiles to apply to eqn (1), with the other variables remaining unchanged. While probing with the monochromatic light, a stationary light bias was at all times applied to the front of the sample by a high-power white LED (more than a hundred times more intense than the monochromatic probe beam), to simulate approximate sunlight conditions. It is this white-light bias, along with the applied potential, which determines the steady-state charge carrier concentration and energy band bending profiles within the sample, and therefore the p(x) profile is not expected to change by the front and back illuminations of the weak monochromatic probe beam. Thus, observed differences between the EQE spectra measured at different potentials are attributed to the potential-dependence of p(x), while seeking the ξ(λ) solution that does not depend on the applied potential, as we confirmed previously.7
To approximate the initial guess of the ξ(λ) spectrum for the first iteration, we used the ultrathin film approximation presented in eqn (2), which ignores spatial variations but otherwise comes directly from our EQE and optical measurements. Since eqn (2) only calculates the ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) product, leaving uncertainty in the magnitude of ξ(λ), we applied eqn (2) assuming 21 different values of
ξ(λ) product, leaving uncertainty in the magnitude of ξ(λ), we applied eqn (2) assuming 21 different values of ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (
(![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m, where m is an index between 1 to 21) covering the full range of possible physical values to generate 21 alternative initial guess spectra, marked as
m, where m is an index between 1 to 21) covering the full range of possible physical values to generate 21 alternative initial guess spectra, marked as 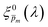 . In the first iteration, each of these spectra was inserted into eqn (1) and its respective EQE spectrum was calculated assuming the simplified p(x) function from eqn (3). The pre-exponential factor in eqn (3) describing the charge carrier collection efficiency at the surface, p0 ≡ p(x = 0), was determined empirically from the ratio between the photocurrent voltammograms (Jph(U)) measured without and with the hole scavenger H2O2, since this ratio yields the charge transfer efficiency at the surface (x = 0) at a given potential.41 Next, the ratios between the measured and calculated EQE spectra were then applied as a (wavelength-dependent) correction factor to the respective
. In the first iteration, each of these spectra was inserted into eqn (1) and its respective EQE spectrum was calculated assuming the simplified p(x) function from eqn (3). The pre-exponential factor in eqn (3) describing the charge carrier collection efficiency at the surface, p0 ≡ p(x = 0), was determined empirically from the ratio between the photocurrent voltammograms (Jph(U)) measured without and with the hole scavenger H2O2, since this ratio yields the charge transfer efficiency at the surface (x = 0) at a given potential.41 Next, the ratios between the measured and calculated EQE spectra were then applied as a (wavelength-dependent) correction factor to the respective 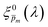 spectra according to
spectra according to
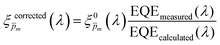 | (4) |
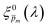 spectrum. Averaging the sixfold corrected spectra
spectrum. Averaging the sixfold corrected spectra 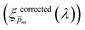 led to a new set of 21 averaged spectra, marked as
led to a new set of 21 averaged spectra, marked as 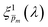 . Since the photogeneration yield should be independent of both p(x) (which was modified by the applied potential) and ahem(λ,x) (which was modified by back vs. front illumination),6,7 we calculated the standard deviation (σ) between the sixfold corrected spectra for each of the 21
. Since the photogeneration yield should be independent of both p(x) (which was modified by the applied potential) and ahem(λ,x) (which was modified by back vs. front illumination),6,7 we calculated the standard deviation (σ) between the sixfold corrected spectra for each of the 21 ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m initial guesses and selected a subset of
m initial guesses and selected a subset of 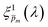 spectra that corresponded to the least deviation of the respective
spectra that corresponded to the least deviation of the respective  spectra for different measurement conditions. The selected
spectra for different measurement conditions. The selected 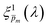 spectra were then averaged to obtain the final ξ(λ) spectrum, which remained unaltered during subsequent iterations. To validate our selection of the
spectra were then averaged to obtain the final ξ(λ) spectrum, which remained unaltered during subsequent iterations. To validate our selection of the 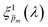 spectra that compounded the final ξ(λ) spectrum, in the second iteration we inserted all the 21
spectra that compounded the final ξ(λ) spectrum, in the second iteration we inserted all the 21 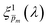 spectra obtained in the first iteration back into eqn (1) to produce a set of calculated EQE spectra, and verified that the selected spectra produce calculated EQE spectra that match well the measured EQE spectra.
spectra obtained in the first iteration back into eqn (1) to produce a set of calculated EQE spectra, and verified that the selected spectra produce calculated EQE spectra that match well the measured EQE spectra.
In the third and last iteration, we refine p(x) by replacing the original p(x) function of eqn (3), which assumed a uniform segment of material, with a more complex model comprising two distinct segments, which correspond to the space charge (depletion) region near the surface and the quasi-neutral region adjacent to it:
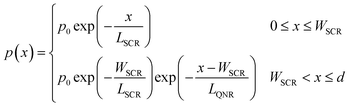 | (5) |
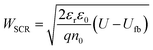 where εr = 33 is the relative dielectric constant of hematite,44ε0 is the vacuum permittivity, q is the elementary charge, n0 is the equilibrium charge carrier concentration, U is the applied potential and Ufb is the flat-band potential. n0 and Ufb were determined empirically by Mott–Schottky analysis of capacitance–voltage measurements,40 leaving only two fitting parameters, LSCR and LQNR, to be obtained by fitting the calculated and measured EQE spectra using the previously obtained ξ(λ) spectrum.
where εr = 33 is the relative dielectric constant of hematite,44ε0 is the vacuum permittivity, q is the elementary charge, n0 is the equilibrium charge carrier concentration, U is the applied potential and Ufb is the flat-band potential. n0 and Ufb were determined empirically by Mott–Schottky analysis of capacitance–voltage measurements,40 leaving only two fitting parameters, LSCR and LQNR, to be obtained by fitting the calculated and measured EQE spectra using the previously obtained ξ(λ) spectrum.
Finally, we multiplied the absorption coefficient α(λ) by ξ(λ) to express the contributing component of the absorption coefficient that generates electrons and holes, αC(λ), and by 1 − ξ(λ) to express the non-contributing component, αNC(λ). The contributing and non-contributing components of the absorption coefficient spectra were then decomposed to resolve their constituent Gaussian peaks with characteristic energies that were compared to optical transitions reported in the literature.45
The above analysis was applied to study a thin (32 nm) film hematite photoanode, and the extracted ξ(λ) spectrum was compared with the ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) spectrum reported in ref. 7 for an ultrathin (7 nm) film hematite photoanode. Additional measurements were carried out to resolve the ξ(λ) spectrum of the ultrathin sample from its
ξ(λ) spectrum reported in ref. 7 for an ultrathin (7 nm) film hematite photoanode. Additional measurements were carried out to resolve the ξ(λ) spectrum of the ultrathin sample from its ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) product, in order to allow direct comparison with the ξ(λ) spectrum of the thin (32 nm) film photoanode investigated in this work. This was done to corroborate the consistency of our approach and to examine whether the quantum size effect17,18 influences the photogeneration yield.
ξ(λ) product, in order to allow direct comparison with the ξ(λ) spectrum of the thin (32 nm) film photoanode investigated in this work. This was done to corroborate the consistency of our approach and to examine whether the quantum size effect17,18 influences the photogeneration yield.
Optical measurements and simulations
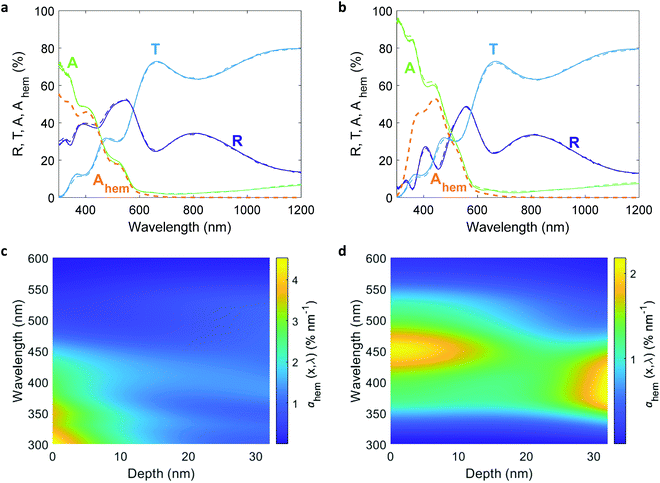
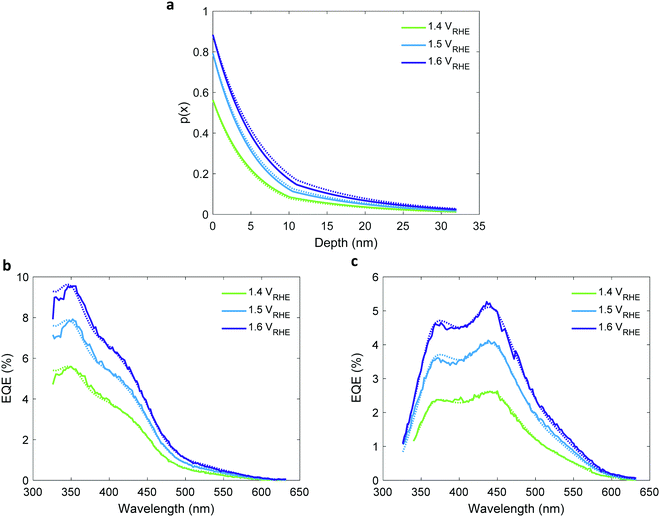
The comprehensive analysis outlined in the above section was applied to study a 32 nm thick Sn-doped (1 cation%) hematite film deposited by pulsed laser deposition (PLD) on a glass substrate (Eagle glass, Corning) coated with a 269 nm thick indium tin oxide (ITO) layer (deposited by PLD) for current collection. Material characterizations of this photoanode are presented in the ESI† (Fig. S1–S6). We used PLD to obtain smooth and uniform planar layers that diminish scattering and support accurate ellipsometry analysis of the complex refractive indices of the hematite and ITO layers. Ellipsometry analysis is often complicated by correlations between different parameters which may result in different optical models that fit the measured spectra.46 To verify that the chosen model describes the optics of the sample accurately, we calculated the transmittance and reflectance spectra of the optical stack comprising the photoanode using the optical parameters of the individual layers that were obtained by spectroscopic ellipsometry and the optical modeling algorithm reported elsewhere,23 and compared them to the empirical spectra measured by UV-vis-NIR spectrophotometry. The results are presented in Fig. 2(a) and (b), showing excellent agreement between the calculated and measured spectra for both front and back illuminations. More information about the ellipsometry modeling, including the optical parameters of all the layers, are presented in the ESI† (Fig. S5–S7). Following the optical model validation, the next step was to replace the air medium in front of the photoanode with a water medium and calculate the absorbed photon flux within the hematite layer under the same conditions as in the EQE measurements. Fig. 2(c) and (d) present maps that show the incremental absorptance, ahem(λ,x), within the hematite layer at different wavelengths and depths, calculated for front and back illuminations through water, respectively.EQE measurements
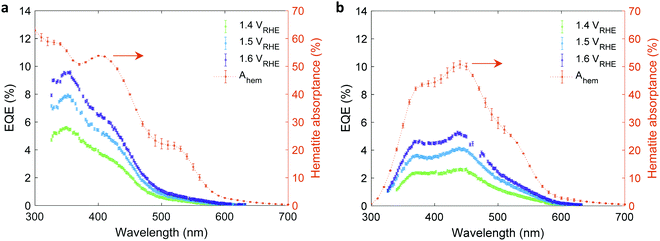
The EQE spectra of the 32 nm thick film hematite photoanode were measured under light bias using a white-light LED calibrated to 100 mW cm−2, as described in the experimental procedures section. The photoelectrochemical (PEC) “cappuccino” cell47 and the LED were rotated by 180° with respect to the monochromator to obtain front and back monochromatic probe light illuminations riding on the white-light bias in front of the PEC cell. Since the LED intensity was higher by 2–3 orders of magnitude (depending on the wavelength) than that of the monochromatic probe light, it is safe to assume that physical properties such as WSCR, LSCR and LQNR that characterize the spatial collection efficiency (eqn (5)) were unaffected by the position of the weak monochromatic probe light. Fig. 3 shows the measured EQE spectra at applied potentials of 1.4, 1.5 and 1.6 V vs. the reversible hydrogen electrode (RHE) scale (VRHE), well above the photocurrent onset potential (1.2 VRHE, see Fig. 4(a)). The calculated absorptance in the 32 nm thick hematite layer is overlaid on the EQE spectra. Direct comparison between front and back illuminations is presented in Fig. S8 (ESI†). The discrepancy between the wavelength-dependent profiles of the absorptance and EQE spectra cannot be resolved by considering spatial charge carrier collection effects alone,6 indicating that the wavelength-dependent photogeneration yield plays a critical role in shaping the EQE spectra.Complementary measurements
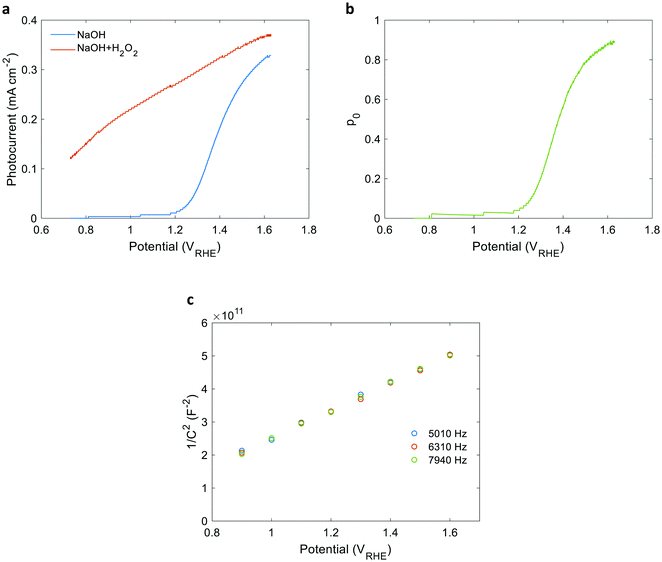
Linear sweep voltammetry measurements of the 32 nm thick film hematite photoanode were carried out in dark and under white-light LED illumination calibrated to 100 mW cm−2 in a “cappuccino” cell47 with 1 M NaOH aqueous electrolytes with and without 0.5 M H2O2 serving as a sacrificial hole scavenger. The respective photocurrent voltammograms (Jph(U)) are presented in Fig. 4(a). Additional dark, light and chopped light voltammograms are presented in Fig. S9 (ESI†). The potential-dependent charge carrier collection efficiency at the surface (p0) curve presented in Fig. 4(b) was obtained by plotting the ratio between the photocurrent measured without and with H2O2 as a function of the applied potential, as reported elsewhere.41 This analysis holds when the flux of holes reaching the surface remains unchanged by the presence of the hole scavenger agent (H2O2). This prerequisite was verified by intensity modulated photocurrent spectroscopy (IMPS) measurements36,48 with and without H2O2, as detailed in Fig. S11 and S12 and Table S1 in the ESI.† Since the intensity of the white-light bias was much higher than that of the monochromatic probe light, both front and back EQE measurements shared the same p(x) profile, and therefore the same p0 values were used for both cases. To verify the consistency of our EQE measurements with the photocurrent voltammetry measurements, the front and back EQE spectra from Fig. 3(a) and (b), respectively, were integrated over the spectrum of the white-light LED and converted to photocurrent values by multiplying with the elementary charge (q). The values obtained are overlaid in Fig. S13 (ESI†) on the photocurrent voltammograms measured in front and back illuminations, showing good agreement that supports the consistency of our EQE measurements. Fig. 4(c) presents Mott–Schottky plots of capacitance – potential measurements taken in dark at different frequencies between 5 and 8 kHz that probe the capacitance of the space charge (depletion) region, as reported elsewhere.49 The results trace a linear curve, as expected, where the slope yields an equilibrium charge carrier concentration (n0) of (3.60 ± 0.05) × 1019 cm−3, and the intercept yields a flat-band potential (Ufb) of 0.40 ± 0.02 VRHE. Using these values, the space-charge region width (WSCR) was calculated to be 10.1, 10.5 and 11.0 nm at 1.4, 1.5 and 1.6 VRHE, respectively, as detailed in the ESI† (Tables S2 and S3). Obtaining these parameters from independent measurements reduces the number of unknown variables of p(x) and increases the confidence level in the analysis.ξ(λ) and p(x) extraction
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . First, the
. First, the ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) product calculated by eqn (2) was divided by selected
ξ(λ) product calculated by eqn (2) was divided by selected ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) values to generate initial guess ξ(λ) spectra. Towards this end, we selected a set of 21 reasonable
values to generate initial guess ξ(λ) spectra. Towards this end, we selected a set of 21 reasonable ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) values between 0.1 and 0.3 with 0.01 increments, denoted as
values between 0.1 and 0.3 with 0.01 increments, denoted as ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m. This range was selected because lower values than 0.1 resulted in unphysical photogeneration yield values greater than 1 (see Fig. S15, ESI†), whereas larger values than 0.3 resulted in considerable misfits between the calculated and measured EQE spectra (see Fig. S16, ESI†). For every
m. This range was selected because lower values than 0.1 resulted in unphysical photogeneration yield values greater than 1 (see Fig. S15, ESI†), whereas larger values than 0.3 resulted in considerable misfits between the calculated and measured EQE spectra (see Fig. S16, ESI†). For every ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m value in this range we calculated the corresponding initial guess spectrum,
m value in this range we calculated the corresponding initial guess spectrum, 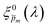 , by solving eqn (2). Next, for each of the 21
, by solving eqn (2). Next, for each of the 21 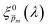 spectra, we tuned, using the Levenberg–Marquardt method,38,39 the fitting parameter
spectra, we tuned, using the Levenberg–Marquardt method,38,39 the fitting parameter ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) in the simplified p(x) function (eqn (3)) so as to generate calculated EQE spectra (by solving eqn (1)) that best fit the measured EQE spectra. The agreement between the calculated and measured EQE spectra was not satisfactory, as demonstrated in Fig. S17a and b (ESI†). This is not surprising because the ultrathin film approximation (eqn (2)) does not apply for our photoanode with a 32 nm thick hematite film, which previous analysis determined to be too thick to neglect spatial variations in p(x) and I(λ,x).7 Although the initial guess spectra obtained by eqn (2) are not precise in our case, they were found to serve well enough as approximate initial guesses that ultimately lead to effective convergence of our solution algorithm (outlined in Fig. 1). Yet, further tuning was in order.
in the simplified p(x) function (eqn (3)) so as to generate calculated EQE spectra (by solving eqn (1)) that best fit the measured EQE spectra. The agreement between the calculated and measured EQE spectra was not satisfactory, as demonstrated in Fig. S17a and b (ESI†). This is not surprising because the ultrathin film approximation (eqn (2)) does not apply for our photoanode with a 32 nm thick hematite film, which previous analysis determined to be too thick to neglect spatial variations in p(x) and I(λ,x).7 Although the initial guess spectra obtained by eqn (2) are not precise in our case, they were found to serve well enough as approximate initial guesses that ultimately lead to effective convergence of our solution algorithm (outlined in Fig. 1). Yet, further tuning was in order.
Next, each of the alternative 21 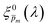 initial guesses was multiplied by the ratio between the measured and calculated EQE spectra obtained for the respective conditions, according to eqn (4). This resulted in sixfold corrected spectra,
initial guesses was multiplied by the ratio between the measured and calculated EQE spectra obtained for the respective conditions, according to eqn (4). This resulted in sixfold corrected spectra,  , for each
, for each 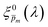 spectrum, since the EQE spectra were measured at three potentials under front and back illuminations. Averaging the corrected spectra for each
spectrum, since the EQE spectra were measured at three potentials under front and back illuminations. Averaging the corrected spectra for each 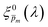 spectrum yielded a new set of 21 spectra denoted as
spectrum yielded a new set of 21 spectra denoted as 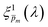 . Out of this set of possible solutions, we needed to find the physical solution that corresponds to the photogeneration yield spectrum of our photoanode. Since the photogeneration yield is invariant to the applied potential and probe illumination direction,6,7 our selection criterion was minimal deviations for different potentials and illumination conditions. Thus, to select the physical
. Out of this set of possible solutions, we needed to find the physical solution that corresponds to the photogeneration yield spectrum of our photoanode. Since the photogeneration yield is invariant to the applied potential and probe illumination direction,6,7 our selection criterion was minimal deviations for different potentials and illumination conditions. Thus, to select the physical 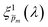 spectra, we calculated the wavelength-dependent standard deviation (σ
spectra, we calculated the wavelength-dependent standard deviation (σ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m(λ)) of the sixfold corrected spectra for every
m(λ)) of the sixfold corrected spectra for every 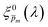 spectrum, normalized it by the respective
spectrum, normalized it by the respective 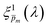 value (at the same wavelength), and averaged this ratio along the wavelength range to obtain the average normalized deviation
value (at the same wavelength), and averaged this ratio along the wavelength range to obtain the average normalized deviation 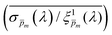 for each of the 21
for each of the 21 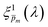 solutions. Fig. 5a plots the
solutions. Fig. 5a plots the 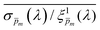 values against the respective
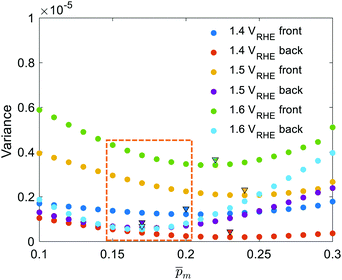
values against the respective ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m values. This plot displays a concave (“bathtub”) shape with a minimum at
m values. This plot displays a concave (“bathtub”) shape with a minimum at ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m = 0.17. The lowest solutions around this point, between
m = 0.17. The lowest solutions around this point, between ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m = 0.15 and 0.20 (marked by a frame in Fig. 5a), are within less than 5% of the minimum point, therefore we consider them as the “best” solutions. The sixfold corrected spectra,
m = 0.15 and 0.20 (marked by a frame in Fig. 5a), are within less than 5% of the minimum point, therefore we consider them as the “best” solutions. The sixfold corrected spectra,  , that correspond to each of the framed points in Fig. 5a are presented in Fig. S19 (ESI†). They demonstrate good agreement with each other, indicating satisfactory compliance with our selection criterion. The subset of
, that correspond to each of the framed points in Fig. 5a are presented in Fig. S19 (ESI†). They demonstrate good agreement with each other, indicating satisfactory compliance with our selection criterion. The subset of  solutions that correspond to the framed points in Fig. 5a were selected as the “best” solutions, and their mean, standard deviation and range values are shown in Fig. 5(b) by the blue dots, error bars and blue shaded area, respectively.
solutions that correspond to the framed points in Fig. 5a were selected as the “best” solutions, and their mean, standard deviation and range values are shown in Fig. 5(b) by the blue dots, error bars and blue shaded area, respectively.
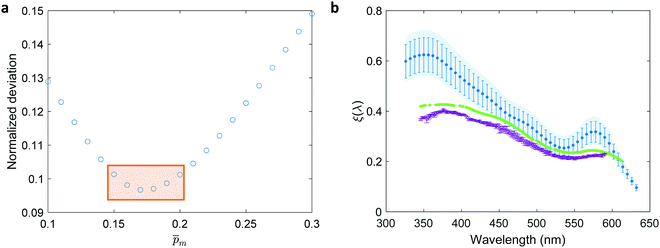 | ||
Fig. 5 The photogeneration yield spectrum, ξ(λ), of a 32 nm thick film hematite photoanode. (a) The wavelength-averaged normalized deviation of the sixfold  spectra vs the respective spectra vs the respective ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m values. The lowest six points (framed by the orange box) are within 5% of the minimum, therefore they were selected as the “best” solutions. (b) The mean value (blue dots), standard deviation (blue error bars) and range (blue shaded area) of the selected m values. The lowest six points (framed by the orange box) are within 5% of the minimum, therefore they were selected as the “best” solutions. (b) The mean value (blue dots), standard deviation (blue error bars) and range (blue shaded area) of the selected  solutions that compound the ξ(λ) spectrum extracted by this analysis. Overlaid on this figure are the ξ(λ) (green) and solutions that compound the ξ(λ) spectrum extracted by this analysis. Overlaid on this figure are the ξ(λ) (green) and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) (purple) spectra of the ultrathin (7 nm) film hematite photoanode examined in ref. 7. The former was extracted in this work using the same approach as for the 32 nm thick film hematite photoanode, whereas the latter was reproduced from Fig. 1c in ref. 7. ξ(λ) (purple) spectra of the ultrathin (7 nm) film hematite photoanode examined in ref. 7. The former was extracted in this work using the same approach as for the 32 nm thick film hematite photoanode, whereas the latter was reproduced from Fig. 1c in ref. 7. | ||
Overlaid on the ξ(λ) spectrum of the 32 nm thick film hematite photoanode studied in this work (blue) is the ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ξ(λ) spectrum of the ultrathin (7 nm) film hematite photoanode from ref. 7 (purple). The latter was further resolved into its
ξ(λ) spectrum of the ultrathin (7 nm) film hematite photoanode from ref. 7 (purple). The latter was further resolved into its ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) and ξ(λ) components using the algorithm presented in Fig. 1, as described in the ESI† (Fig. S20 and S21). The extracted p(x) profile of the ultrathin film photoanode is nearly flat (see Fig. S21(a), ESI†), meeting one of the prerequisites for applying the ultrathin film approximation (eqn (2)). The other one, namely, a (nearly) constant light intensity spatial profile, was verified in ref. 7. The spatial collection efficiency was found to be ∼90% throughout the 7 nm thick hematite layer, indicating that the photocurrent in this ultrathin film is not limited by charge carrier recombination but rather by low light absorptance and low photogeneration yield. Whereas the absorptance can be enhanced by sophisticated optical designs such as the resonant light trapping architecture,18,23 the photogeneration yield is an intrinsic property of the photoabsorber material that is more difficult to manipulate. The fair agreement in the ξ(λ) spectra of the thin (32 nm) and ultrathin (7 nm) films in large parts of the wavelength range supports the consistency of our approach. The differences at wavelengths below 440 nm and around 575 nm may be attributed to the quantum size effect14,15 that blue shifts the absorption peaks positioned at 400 and 520 nm (see Fig. S6(b), ESI†), thereby altering the photogeneration yield in the adjacent wavelengths.
and ξ(λ) components using the algorithm presented in Fig. 1, as described in the ESI† (Fig. S20 and S21). The extracted p(x) profile of the ultrathin film photoanode is nearly flat (see Fig. S21(a), ESI†), meeting one of the prerequisites for applying the ultrathin film approximation (eqn (2)). The other one, namely, a (nearly) constant light intensity spatial profile, was verified in ref. 7. The spatial collection efficiency was found to be ∼90% throughout the 7 nm thick hematite layer, indicating that the photocurrent in this ultrathin film is not limited by charge carrier recombination but rather by low light absorptance and low photogeneration yield. Whereas the absorptance can be enhanced by sophisticated optical designs such as the resonant light trapping architecture,18,23 the photogeneration yield is an intrinsic property of the photoabsorber material that is more difficult to manipulate. The fair agreement in the ξ(λ) spectra of the thin (32 nm) and ultrathin (7 nm) films in large parts of the wavelength range supports the consistency of our approach. The differences at wavelengths below 440 nm and around 575 nm may be attributed to the quantum size effect14,15 that blue shifts the absorption peaks positioned at 400 and 520 nm (see Fig. S6(b), ESI†), thereby altering the photogeneration yield in the adjacent wavelengths.
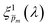 solutions that comprise the photogeneration yield spectrum presented in Fig. 5(b) according to their compliance with a physical selection criterion that seeks invariant ξ(λ) solutions for different applied potentials and illumination directions. In the second iteration, we verify that the selected
solutions that comprise the photogeneration yield spectrum presented in Fig. 5(b) according to their compliance with a physical selection criterion that seeks invariant ξ(λ) solutions for different applied potentials and illumination directions. In the second iteration, we verify that the selected 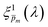 solutions also yield good agreement with minimal variance between the calculated and measured EQE spectra. Towards this end, instead of the less-accurate
solutions also yield good agreement with minimal variance between the calculated and measured EQE spectra. Towards this end, instead of the less-accurate 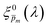 initial guess spectra that were used in the first iteration, each of the 21 refined
initial guess spectra that were used in the first iteration, each of the 21 refined 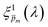 spectra obtained in the first iteration were inserted into eqn (1) and the EQE spectra were recalculated by adjusting the
spectra obtained in the first iteration were inserted into eqn (1) and the EQE spectra were recalculated by adjusting the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) parameter in the simplified p(x) function (eqn (3)), as we did in the first iteration. The agreement between the measured and recalculated EQE spectra improved in the second iteration, as demonstrated in Fig. S17 (ESI†), although the
parameter in the simplified p(x) function (eqn (3)), as we did in the first iteration. The agreement between the measured and recalculated EQE spectra improved in the second iteration, as demonstrated in Fig. S17 (ESI†), although the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) values obtained in both iterations were close to each other, as shown in Fig. S18 (ESI†). The variance between the measured and recalculated EQE spectra are plotted against the respective
values obtained in both iterations were close to each other, as shown in Fig. S18 (ESI†). The variance between the measured and recalculated EQE spectra are plotted against the respective ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m values in Fig. 6. These plots yield six concave “bathtub” curves, one for each of the EQE measurement conditions. Three of the minimum points are within the selected (framed) range (0.15 ≤
m values in Fig. 6. These plots yield six concave “bathtub” curves, one for each of the EQE measurement conditions. Three of the minimum points are within the selected (framed) range (0.15 ≤ ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) m ≤ 0.2) in Fig. 5a (also shown in Fig. 6), and the other three are very close to the values in this range. This result shows that the selected
m ≤ 0.2) in Fig. 5a (also shown in Fig. 6), and the other three are very close to the values in this range. This result shows that the selected 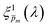 spectra are not only the most physically sound ones, but they also yield the best (or nearly the best) fitting between the calculated and measured EQE spectra.
spectra are not only the most physically sound ones, but they also yield the best (or nearly the best) fitting between the calculated and measured EQE spectra.
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) values obtained in the first and second iterations were found to increase with increasing potentials, as shown in Fig. S18 and Table S4 in the ESI.† This trend is seemingly in disagreement with classical semiconductor physics that predicts constant (i.e., potential-independent) diffusion length.32 This suggests that the simplified mathematical expression by which p(x) was calculated (eqn (3)) does not fully suffice to give an accurate description of the underlying physics. Therefore, in the third iteration it was replaced with the more complex expression in eqn (5) that accounts for two distinct segments that contribute to the photocurrent: the potential-dependent space-charge region (SCR) near the surface, and the potential-independent quasi-neutral region (QNR) adjacent to it.30 Then, by solving eqn (1) again using the ξ(λ) spectrum obtained in the first iteration, p0 obtained by photocurrent voltammetry measurements with and without H2O2, and the WSCR obtained by Mott–Schottky analysis, we found the unknown parameters in eqn (5), LQNR and LSCR, and obtained refined EQE spectra that best fitted the measured EQE spectra. Hence, we obtained the two-region charge carrier collection efficiency (p(x)) profiles presented in Fig. 7(a). In the quasi-neutral region, we obtained a potential-independent and illumination direction independent diffusion length (LQNR) of 11.6 ± 0.7 nm, whereas in the space charge region the diffusion length (LSCR) was found to increase with increasing potentials, as presented in Table 1. This behavior may be reasoned by the lower electron concentration in this region with increased reverse bias (i.e., higher potential), which leads to less recombination and, hence, longer lifetime and larger diffusion length of the minority charge carriers (holes). The LSCR values are nearly the same for front and back illuminations, consistent with our physical model. The calculated EQE spectra agree with the measured spectra very well, as shown in Fig. 7(b) and Fig. 7(c) for front and back illuminations, respectively. The agreement is slightly better using eqn (5) instead of eqn (3), as shown in Table S5 (ESI†). The small discrepancies between the measured and calculated EQE spectra at short wavelengths and between the front and back p(x) profiles may have resulted from small inaccuracies in the calculated hematite absorptance spectrum (Ahem), or unaccounted contribution from the ITO layer. The third iteration concludes the extraction of the ξ(λ) spectrum and p(x) profile. In the following section we use the extracted ξ(λ) spectrum (from Fig. 5b) to resolve contributing and non-contributing optical transitions.
values obtained in the first and second iterations were found to increase with increasing potentials, as shown in Fig. S18 and Table S4 in the ESI.† This trend is seemingly in disagreement with classical semiconductor physics that predicts constant (i.e., potential-independent) diffusion length.32 This suggests that the simplified mathematical expression by which p(x) was calculated (eqn (3)) does not fully suffice to give an accurate description of the underlying physics. Therefore, in the third iteration it was replaced with the more complex expression in eqn (5) that accounts for two distinct segments that contribute to the photocurrent: the potential-dependent space-charge region (SCR) near the surface, and the potential-independent quasi-neutral region (QNR) adjacent to it.30 Then, by solving eqn (1) again using the ξ(λ) spectrum obtained in the first iteration, p0 obtained by photocurrent voltammetry measurements with and without H2O2, and the WSCR obtained by Mott–Schottky analysis, we found the unknown parameters in eqn (5), LQNR and LSCR, and obtained refined EQE spectra that best fitted the measured EQE spectra. Hence, we obtained the two-region charge carrier collection efficiency (p(x)) profiles presented in Fig. 7(a). In the quasi-neutral region, we obtained a potential-independent and illumination direction independent diffusion length (LQNR) of 11.6 ± 0.7 nm, whereas in the space charge region the diffusion length (LSCR) was found to increase with increasing potentials, as presented in Table 1. This behavior may be reasoned by the lower electron concentration in this region with increased reverse bias (i.e., higher potential), which leads to less recombination and, hence, longer lifetime and larger diffusion length of the minority charge carriers (holes). The LSCR values are nearly the same for front and back illuminations, consistent with our physical model. The calculated EQE spectra agree with the measured spectra very well, as shown in Fig. 7(b) and Fig. 7(c) for front and back illuminations, respectively. The agreement is slightly better using eqn (5) instead of eqn (3), as shown in Table S5 (ESI†). The small discrepancies between the measured and calculated EQE spectra at short wavelengths and between the front and back p(x) profiles may have resulted from small inaccuracies in the calculated hematite absorptance spectrum (Ahem), or unaccounted contribution from the ITO layer. The third iteration concludes the extraction of the ξ(λ) spectrum and p(x) profile. In the following section we use the extracted ξ(λ) spectrum (from Fig. 5b) to resolve contributing and non-contributing optical transitions.
| Potential (VRHE) | W SCR (nm) | L SCR (nm) | L QNR (nm) | |
|---|---|---|---|---|
| Front | Back | |||
| 1.4 | 10.1 | 5.4 ± 0.1 | 5.1 ± 0.1 | 11.6 ± 0.7 |
| 1.5 | 10.5 | 5.4 ± 0.1 | 5.7 ± 0.1 | |
| 1.6 | 11.0 | 6.1 ± 0.1 | 6.7 ± 0.1 | |
Contributing and non-contributing optical transitions
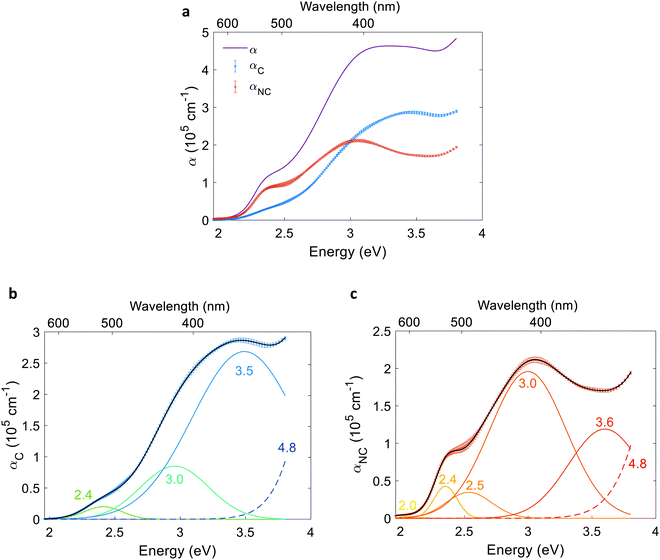
To resolve the contributing and non-contributing optical excitations that generate electron–hole pairs or lead to localized electronic transitions, respectively, we first define the contributing component of the absorption coefficient as the product of the absorption coefficient spectrum and the photogeneration yield spectrum: αC(λ) = α(λ)ξ(λ). The non-contributing component is defined as: αNC(λ) = α(λ)(1 − ξ(λ)). The contributing and non-contributing components are presented in Fig. 8(a). Next, the αC and αNC spectra were fitted with the minimal number of Gaussians required to yield good agreement. The resolved Gaussians of the contributing and non-contributing components are presented in Fig. 8(b) and (c), respectively. Tails of high energy peaks outside our measurement range are evident in both components (marked by a dashed line). Due to lack of sufficient information to resolve these peaks, we fixed the center energy of the high-energy tails at 4.8 eV based on a study by Marusak et al. that reports the absorption coefficient of hematite in the 200–1100 nm wavelength range,45 while resolving their width and intensity with limited confidence. The resolved energies are summarized in Table S6 in the ESI.†Given the complex electronic structure of hematite,3,50–52 there might be more optical transitions than the number of Gaussians resolved in Fig. 8. But since fitting the contributing and non-contributing spectra with more oscillators than the minimum number required to trace the spectra results in multiple non-unique solutions that are sensitive to the initial guess (for example, compare Fig. S24 with S23, ESI†), the additional features cannot be resolved with a satisfactory level of confidence. Notably, all the peaks in Fig. 8(b) were evident, within a margin of 0.1 eV, in all of the alternative fittings (see examples in Fig. S24, ESI†).
Performance limitations
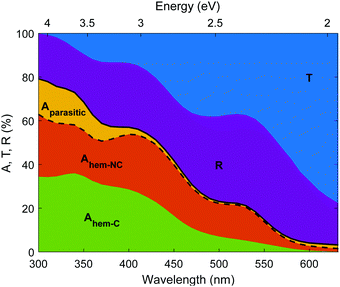
The photogeneration yield unveils the real photoconversion potential of hematite photoanodes. As presented in Fig. 9, only a small portion of the incident photons generate electron–hole pairs that may be separated and ultimately contribute to the photocurrent. In our photoanode, most of the incident photons are transmitted through the thin (32 nm thick) hematite layer, or reflected from the photoanode. Out of the remaining photons that are absorbed in the photoanode, some photons are absorbed in segments of the photoanode that are not photocatalytic (Aparasitic), whereas the photons absorbed in the hematite layer (Ahem) are split between contributing and non-contributing components (Ahem-C and Ahem-NC, respectively). Since the EQE spectra were measured between 326 and 632 nm (see Fig. 3), we linearly extrapolated ξ(λ) to 300 nm to reach the beginning of the AM1.5G sunlight spectrum. Interestingly, some contributing absorption is evident at energies below the familiar absorption edge of hematite (590 nm) that corresponds to a bandgap energy of 2.1 eV. The absorptance values are small for wavelengths above 590 nm, but there are plenty of photons in the solar spectrum with wavelengths between 590 and 632 nm that may contribute to the photocurrent, especially for thick (≥1 μm) hematite layers, as shown in Fig. S25 (ESI†). Considering only photons below the familiar absorption edge (590 nm) results in underestimating the maximal photocurrent (Table S7, ESI†) by up to 11% of the maximal photocurrent calculated using the full spectral range (Table 2).| Thickness | Theoretical photocurrent limit (mA cm−2) | Maximal photocurrent limit considering only contributing photons (mA cm−2) | ||
|---|---|---|---|---|
| Minimum (ξ10.20(λ)) | Mean (ξ(λ)) | Maximum (ξ10.15(λ)) | ||
| 32 nm | 5.0 | 1.8 | 2.1 | 2.5 |
| 100 nm | 8.8 | 3.0 | 3.5 | 4.1 |
| 1 μm | 13.4 | 4.1 | 4.8 | 5.6 |
| 10 μm | 15.4 | 4.4 | 5.2 | 6.1 |
| 100 μm | 15.4 | 4.4 | 5.2 | 6.1 |
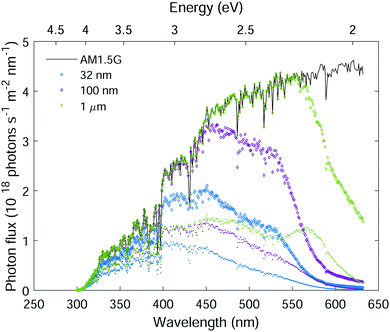
The low photogeneration yield of hematite severely diminishes its photoconversion efficiency. In light of this effect, we estimate the maximal photocurrent that may be obtained under standard sunlight illumination (AM1.5G) considering the ξ(λ) spectrum presented in Fig. 5(b). Fig. 10 plots the AM1.5G photon flux spectrum (black curve), the absorbed photon flux spectra for planar hematite layers of different thicknesses (color diamond markers), and the contributing part of the absorbed photon flux (color point markers). The absorbed photon flux was calculated using the Beer–Lambert law, Iabs(λ,d) = I0(λ){1 − exp[−α(λ)d]}, where the incident photon flux I0(λ) was taken as the AM1.5G photon flux standard,53α(λ) is the absorption coefficient spectrum from Fig. 8(a), and d is the hematite layer thickness as indicated in the legend. This calculation ignores trivial optical losses such as scattering and reflection, therefore it represents the maximal absorption in hematite layers of thickness d. The contributing absorbed photon flux, IC(λ,d), was obtained by multiplying Iabs(λ,d) by ξ(λ), taking the ξ(λ) spectrum from Fig. 5(b), linearly extrapolated to 300 nm.
To estimate the theoretical photocurrent limit that may be obtained in ideal hematite photoanodes (in a single-junction photoelectrochemical cell) with perfect photogeneration (ξ(λ) = 1) without trivial optical losses (reflection and parasitic absorption) and without charge carrier recombination losses (p(x) = 1), we multiply the integrated absorbed photon flux, 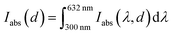 , by the elementary charge, q. The maximal photocurrent that can be obtained in real hematite with the photogeneration yield spectrum extracted in this work (Fig. 5(b)), but no other losses, was calculated similarly by integrating IC(λ,d) between 300 and 632 nm and multiplying by q. The results obtained using the minimum, maximum and mean ξ(λ) spectra from Fig. 5(b) are presented in Table 2. According to these calculations, the maximal photocurrent limit in thick (≥10 μm) hematite layers is expected to reach 4.4 to 6.1 mA cm−2, which is less than 40% of the theoretical limit obtained by considering all photons in this wavelength range. This shows the deleterious effect of non-contributing absorption in hematite, suggesting that future efforts should aim at reducing the photogeneration loss, while enhancing the contributing optical excitations that ultimately generate mobile electrons and holes.
, by the elementary charge, q. The maximal photocurrent that can be obtained in real hematite with the photogeneration yield spectrum extracted in this work (Fig. 5(b)), but no other losses, was calculated similarly by integrating IC(λ,d) between 300 and 632 nm and multiplying by q. The results obtained using the minimum, maximum and mean ξ(λ) spectra from Fig. 5(b) are presented in Table 2. According to these calculations, the maximal photocurrent limit in thick (≥10 μm) hematite layers is expected to reach 4.4 to 6.1 mA cm−2, which is less than 40% of the theoretical limit obtained by considering all photons in this wavelength range. This shows the deleterious effect of non-contributing absorption in hematite, suggesting that future efforts should aim at reducing the photogeneration loss, while enhancing the contributing optical excitations that ultimately generate mobile electrons and holes.
Conclusions
A rigorous method for extracting the photogeneration yield spectrum and the charge carrier collection efficiency profile of planar photoelectrodes for photoelectrochemical water splitting was presented and applied for a 32 nm thick film hematite photoanode. The photogeneration yield of this photoanode is significantly less than unity across the entire absorption range (up to 632 nm), especially at high wavelengths. Therefore, it limits the maximal photocurrent that can be reached with an ideal hematite photoanode without trivial optical (e.g., reflection and transmission) and charge carrier recombination losses to about half of the theoretical limit that ignores non-contributing light absorption. The photogeneration yield spectrum can be multiplied by the absorption coefficient spectrum to resolve contributing and non-contributing optical transitions, shedding light into light–matter interaction in correlated electron martials such as hematite where photons may be absorbed to excite both extended and localized electronic transitions. We hope that this work will inspire further research into the effect of non-contributing light absorption in photocatalytic and photovoltaic materials with correlated electrons that often give rise to non-trivial physical phenomena that may affect their properties and performance.Experimental procedures
The hematite and ITO layers were deposited on eagle glass substrate (Eagle XG glass substrates, Corning) by pulsed laser deposition (PLD) using a turn-key PLD workstation (PLD/MBE 2100, PVD Products, USA) equipped with a KrF pulsed excimer laser beam (λ = 248 nm, COMPex PRO 102 Excimer Laser, Lambda Physik/Coherent). The hematite layer was deposited from a 1% (cation based) Sn-doped Fe2O3 target which was prepared by a solid-state route as described elsewhere.23 The ITO layer was deposited from a commercial target (purity 99.99%, In2O3/SnO2 ratio of 90/10, ACI Alloys). These layers were deposited at a set-point temperature of 500 °C and in oxygen pressures of 25 and 10 mTorr, respectively, in a similar manner to that reported previously.7 Topography mapping was conducted by atomic force microscopy (AFM, MFP-3D Infinity AFM, Asylum Research, Oxford instruments) in tapping mode using a height sensor. Scanning electron microscopy (SEM) images were recorded by an in-lens detector in a Zeiss Ultra-Plus FEG-SEM at an accelerating voltage of 3 kV. Grazing incidence X-ray diffraction (GIXRD) analysis was performed using a Rigaku SmartLab X-ray diffractometer. X-ray diffractograms were acquired in parallel beam configuration at an incident beam angle of 1° with a Cu Kα radiation source (λ = 0.15406 nm) in the 2θ range of 20–80° at a scan rate of 0.01° s−1. The sample transmission and reflection spectra were measured by a Cary 5000 series UV-vis-NIR spectrophotometer (Agilent Technologies) using a Universal Measurement Accessory (UMA) at the minimal possible incident angle (5.1°) which is the closest to the normal illumination in the EQE setup. The optical parameters (complex refractive index) of all the layers were obtained by spectroscopic ellipsometry (VASE Ellipsometer, J. A. Woollam). The optical modeling was performed using the optical modeling algorithm that we presented elsewhere.23 The absorption coefficient, α(λ), was calculated according to: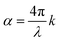 where k is the imaginary part of the complex refractive index:
where k is the imaginary part of the complex refractive index: ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) = n + ik. The photocurrent was measured by linear sweep voltammetry using a potentiostat (CompacStat; Ivium Technologies) under illumination intensity of the order of one sun (100 mW cm−2) provided by a high-power white-light LED (Mightex Systems, 6500K “glacial white” spectrum, 300 mW maximum radiant flux). The spectrum of the LED is shown in Fig. S14 (ESI†). Dark and light voltammograms were measured as a function of the applied potential using a three-electrode setup with an Hg/HgO in 1 M NaOH reference electrode (ALS Co., Ltd) and a Pt wire counter electrode (ALS Co., Ltd) in a photoelectrochemical “cappuccino” cell.47 The potential was scanned anodically at a scan rate of 10 mV s−1. The measurements were carried out in both 1 M NaOH solution (in deionized water, without any sacrificial reagents) and in 1 M NaOH + 0.5 M H2O2 aqueous solution. Mott–Schottky capacitance – potential measurements were measured in the same “cappuccino cell” using the same potentiostat. The capacitance was measured in alkaline aqueous electrolyte solution (1 M NaOH in deionized water) with no sacrificial agents, in the dark. The EQE (aka IPCE) measurements were carried out in a modified Quantum Efficiency measurement system (Oriel QE-PV-SI, Newport Inc.) which included a 1 kW Xenon lamp coupled to a Cornerstone 260 monochromator operated at ∼2 nm wavelength resolution. The wavelength-dependent photocurrent was measured in three-electrode mode using a potentiostat (Zennium, Zahner Electrik) in 1 M NaOH aqueous solution. The photocurrent was normalized by the incident light intensity using a wavelength-calibrated optical power meter with a high-performance UV-enhanced Si-photodiode sensor (Newport 1918-C power meter). The white-light bias was provided by the same high-power white-light LED used for voltammetry. Rotating the “cappuccino cell” (and the sample in it) 180° in respect to the incident monochromatic probe light allowed us to measure both “front” and “back” EQE. In both cases the LED was positioned to shine in front of the hematite surface in similar conditions to produce approximately the same photocurrent when illuminated solely with the LED. This indicated same spatial collection efficiency for front and back illumination for each measured potential, since the monochromatic probe beam intensity is at least two order of magnitudes (depends on the wavelength) lower than the white-light bias intensity, and hence should not affect the spatial collection efficiency. The measurement procedure for front and back probe illumination EQE measurements is presented in detail elsewhere.7 The IMPS spectra in the ESI,† were obtained from PEIS and IMVS measurements because of superior data quality as described elsewhere.48 The measurements were carried out in 1 M NaOH and 1 M NaOH + 0.5 M H2O2 aqueous solutions using a Zahner CIMPS system with a white-light LED (LSW-2, 4300 K) that provided continuous light bias at two intensities for each potential, 50 and 100 mW cm−2. The spectrum of this LED is also shown in Fig. S14 (ESI†). For PEIS measurements an AC signal of 10 mV was superimposed on the DC bias component. For IMVS measurements an AC perturbation of 20 mV was performed on the light source power supply, operating under 0.8 V or 1.6 V DC voltage, dependent on light intensity. For both PEIS and IMVS measurements, the frequency was scanned form 10 kHz to 300 mHz.
= n + ik. The photocurrent was measured by linear sweep voltammetry using a potentiostat (CompacStat; Ivium Technologies) under illumination intensity of the order of one sun (100 mW cm−2) provided by a high-power white-light LED (Mightex Systems, 6500K “glacial white” spectrum, 300 mW maximum radiant flux). The spectrum of the LED is shown in Fig. S14 (ESI†). Dark and light voltammograms were measured as a function of the applied potential using a three-electrode setup with an Hg/HgO in 1 M NaOH reference electrode (ALS Co., Ltd) and a Pt wire counter electrode (ALS Co., Ltd) in a photoelectrochemical “cappuccino” cell.47 The potential was scanned anodically at a scan rate of 10 mV s−1. The measurements were carried out in both 1 M NaOH solution (in deionized water, without any sacrificial reagents) and in 1 M NaOH + 0.5 M H2O2 aqueous solution. Mott–Schottky capacitance – potential measurements were measured in the same “cappuccino cell” using the same potentiostat. The capacitance was measured in alkaline aqueous electrolyte solution (1 M NaOH in deionized water) with no sacrificial agents, in the dark. The EQE (aka IPCE) measurements were carried out in a modified Quantum Efficiency measurement system (Oriel QE-PV-SI, Newport Inc.) which included a 1 kW Xenon lamp coupled to a Cornerstone 260 monochromator operated at ∼2 nm wavelength resolution. The wavelength-dependent photocurrent was measured in three-electrode mode using a potentiostat (Zennium, Zahner Electrik) in 1 M NaOH aqueous solution. The photocurrent was normalized by the incident light intensity using a wavelength-calibrated optical power meter with a high-performance UV-enhanced Si-photodiode sensor (Newport 1918-C power meter). The white-light bias was provided by the same high-power white-light LED used for voltammetry. Rotating the “cappuccino cell” (and the sample in it) 180° in respect to the incident monochromatic probe light allowed us to measure both “front” and “back” EQE. In both cases the LED was positioned to shine in front of the hematite surface in similar conditions to produce approximately the same photocurrent when illuminated solely with the LED. This indicated same spatial collection efficiency for front and back illumination for each measured potential, since the monochromatic probe beam intensity is at least two order of magnitudes (depends on the wavelength) lower than the white-light bias intensity, and hence should not affect the spatial collection efficiency. The measurement procedure for front and back probe illumination EQE measurements is presented in detail elsewhere.7 The IMPS spectra in the ESI,† were obtained from PEIS and IMVS measurements because of superior data quality as described elsewhere.48 The measurements were carried out in 1 M NaOH and 1 M NaOH + 0.5 M H2O2 aqueous solutions using a Zahner CIMPS system with a white-light LED (LSW-2, 4300 K) that provided continuous light bias at two intensities for each potential, 50 and 100 mW cm−2. The spectrum of this LED is also shown in Fig. S14 (ESI†). For PEIS measurements an AC signal of 10 mV was superimposed on the DC bias component. For IMVS measurements an AC perturbation of 20 mV was performed on the light source power supply, operating under 0.8 V or 1.6 V DC voltage, dependent on light intensity. For both PEIS and IMVS measurements, the frequency was scanned form 10 kHz to 300 mHz.
Contributions
Y. P. developed the methodology with the help of D. S. E. and D. A. G. D. A. G. conceived the idea of using spatial collection efficiency analysis to identify contributing and non-contributing excitations. Y. P. fabricated the sample, characterized its optical behavior and topography, performed the ellipsometry analysis, modeled the optical performance, performed the data analysis and wrote the first draft of the manuscript. D. S. E. and Y. P. measured the sample photoelectrochemical performance. D. S. E. and D. A. G carried out the GIXRD measurements. A. T. performed the IMPS analysis. A. R. supervised the project. All authors contributed to the scientific discussion and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge Dr Hen Dotan for early discussions on this subject, Dr Guy Ankonina for assisting on technical matters in the Technion's Photovoltaics Laboratory, Dr Cecile Saguy for advising with the AFM measurements, and Netta Gal for recording the SEM images. The research leading to these results has received funding from the PAT Center of Research Excellence supported by the Israel Science Foundation (Grant No. 1867/17). The EQE and optical measurements were carried out at the Technion's Photovoltaics Laboratory (HTRL), supported by the Russell Berrie Nanotechnology Institute (RBNI), the Nancy and Stephen Grand Technion Energy Program (GTEP) and the Adelis Foundation. Y. P. acknowledges support by the Grand Technion Energy Program (GTEP), and the Levi Eshkol scholarship from the Ministry of Science and Technology of Israel (Grant No. 3-14501). D. A. G. acknowledges support from the Center for Absorption in Science at the Ministry of Aliyah and Immigrant Absorption in Israel. A. R. acknowledges the support of the L. Shirley Tark Chair in Science.References
- E. Becquerel, Mémoire sur les effets électriques produits sous l’influence des rayons solaires, C. R. Hebd. Seances Acad. Sci., 1839, 9, 561–567 Search PubMed
.
- W. Shockley and H. J. Queisser, Detailed balance limit of efficiency of p-n junction solar cells, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS
.
- D. M. Sherman and T. D. Waite, Electronic spectra of Fe3+ oxides and oxide hydroxides in the near IR to near UV, Am. Mineral., 1985, 70, 1262–1269 CAS
.
- J. A. Tossell, D. J. Vaughan and K. H. Johnson, The Electronic structure of Rutile,Wustite,a nd Hematite from Molecular Orrbital calculations, Am. Mineral., 1974, 59, 319–334 CAS
.
-
B. Fromme, d–d Excitations on Transition-Metal Oxides, Springer Tracts in Modern Physics, Springer, vol. 170, 2001 Search PubMed
.
- G. Segev,
et al., The Spatial Collection Efficiency of Charge Carriers in Photovoltaic and Photoelectrochemical Cells, Joule, 2018, 2, 210–224 CrossRef CAS
.
- D. A. Grave, D. S. Ellis, Y. Piekner, M. Kölbach, H. Dotan, A. Kay, P. Schnell, R. van de Krol, F. F. Abdi, D. Friedrich and A. Rothschild, Extraction of mobile charge carrier photogeneration yield spectrum of metal oxide photoanodes for solar water splitting, Nat. Mater., 2021, 20, 833–840 CrossRef CAS PubMed
.
- K. Ding, X. Huang, Y. Li and S. R. Forrest, Photogeneration and the bulk quantum efficiency of organic photovoltaics, Energy Environ. Sci., 2021, 14, 1584–1593 RSC
.
-
P. Würfel and U. Würfel, Physics of solar cells: from basic principles to advanced concepts, John Wiley & Sons, 2016 Search PubMed
.
- Z. Chen, et al., Incident Photon-to-Current Efficiency and Photocurrent Spectroscopy, Photoelectrochemical Water Splitting, Springer, New York, 2013, pp. 87–97 Search PubMed.
- D. Yuan and X. Zhang, An overview of numerical methods for the first kind Fredholm integral equation, SN Appl. Sci., 2019, 1, 1178 CrossRef
.
- L. E. Brus, Electron-electron and electron-hole interactions in small semiconductor crystallites: The size dependence of the lowest excited electronic state, J. Chem. Phys., 1984, 80, 4403–4409 CrossRef CAS
.
- A. I. Ekimov, A. L. Efros and A. A. Onushchenko, Quantum size effect in semiconductor microcrystals, Solid State Commun., 1985, 56, 921–924 CrossRef CAS
.
- I. V. Chernyshova, S. Ponnurangam and P. Somasundaran, On the origin of an unusual dependence of (bio)chemical reactivity of ferric hydroxides on nanoparticle size, Phys. Chem. Chem. Phys., 2010, 12, 14045–14056 RSC
.
- M. Fondell, T. J. Jacobsson, M. Boman and T. Edvinsson, Optical quantum confinement in low dimensional hematite, J. Mater. Chem. A, 2014, 2, 3352–3363 RSC
.
- P. Dias, A. Vilanova, T. Lopes, L. Andrade and A. Mendes, Extremely stable bare hematite photoanode for solar water splitting, Nano Energy, 2016, 23, 70–79 CrossRef CAS
.
- K. Sivula, F. Le Formal and M. Grätzel, Solar water splitting: Progress using hematite (α-Fe2O3) photoelectrodes, ChemSusChem, 2011, 4, 432–449 CrossRef CAS PubMed
.
- H. Dotan,
et al., Resonant light trapping in ultrathin films for water splitting, Nat. Mater., 2012, 12, 158–164 CrossRef PubMed
.
- S. C. Warren,
et al., Identifying champion nanostructures for solar water-splitting, Nat. Mater., 2013, 12, 842–849 CrossRef CAS PubMed
.
- X. Guo, L. Wang and Y. Tan, Hematite nanorods Co-doped with Ru cations with different valence states as high performance photoanodes for water splitting, Nano Energy, 2015, 16, 320–328 CrossRef CAS
.
- Y. Pihosh,
et al., Photocatalytic generation of hydrogen by core-shell WO3/BiVO4 nanorods with ultimate water splitting efficiency, Sci. Rep., 2015, 5, 11141 CrossRef PubMed
.
- Y. Lin, G. Yuan, S. Sheehan, S. Zhou and D. Wang, Hematite-based solar water splitting: Challenges and opportunities, Energy Environ. Sci., 2011, 4, 4862–4869 RSC
.
- Y. Piekner,
et al., Implementing strong interference in ultrathin film top absorbers for tandem solar cells, ACS Photonics, 2018, 5, 5068–5078 CrossRef CAS
.
- H. H. Kung, H. S. Jarrett, A. W. Sleight and A. Ferretti, Semiconducting oxide anodes in photoassisted electrolysis of water, J. Appl. Phys., 1977, 48, 2463–2469 CrossRef CAS
.
- J. H. Kennedy and K. W. Frese, Photooxidation of Water at α-Fe2O3 Electrodes, J. Electrochem. Soc., 1978, 125, 709–714 CrossRef CAS
.
- D. Hayes,
et al., Electronic and nuclear contributions to time-resolved optical and X-ray absorption spectra of hematite and insights into photoelectrochemical performance, Energy Environ. Sci., 2016, 9, 3754–3769 RSC
.
- L. M. Carneiro,
et al., Excitation-wavelength-dependent small polaron trapping of photoexcited carriers in α-Fe2O3, Nat. Mater., 2017, 16, 819–825 CrossRef CAS
.
- A. Braun,
et al., Direct observation of two electron holes in a hematite photoanode during photoelectrochemical water splitting, J. Phys. Chem. C, 2012, 116, 16870–16875 CrossRef CAS
.
- D. A. Grave, N. Yatom, D. S. Ellis, M. C. Toroker and A. Rothschild, The “rust” challenge: On the correlations between electronic structure, excited state dynamics, and photoelectrochemical performance of hematite photoanodes for solar water splitting, Adv. Mater., 2018, 30, 1706577 CrossRef
.
- W. W. Gärtner, Depletion-layer photoeffects in semiconductors, Phys. Rev., 1959, 116, 84–87 CrossRef
.
- J. Reichman, Collection efficiency of low-mobility solar cells, Appl. Phys. Lett., 1981, 38, 251–253 CrossRef CAS
.
-
D. K. Ferry, Semiconductor Transport, CRC Press, London, 2000 Search PubMed
.
- C. Donolato, A reciprocity theorem for charge collection, Appl. Phys. Lett., 1985, 46, 270–272 CrossRef
.
- K. Toprasertpong, A. Delamarre, Y. Nakano, J. F. Guillemoles and M. Sugiyama, Generalized reciprocity relations in solar cells with voltage-dependent carrier collection: Application to p-i-n junction devices, Phys. Rev. Appl., 2019, 11, 024029 CrossRef CAS
.
- D. Abou-Ras and T. Kirchartz, Electron-beam-induced current measurements of thin-film solar cells, ACS Appl. Energy Mater., 2019, 2, 6127–6139 CrossRef CAS
.
- D. Klotz, D. A. Grave and A. Rothschild, Accurate determination of the charge transfer efficiency of photoanodes for solar water splitting, Phys. Chem. Chem. Phys., 2017, 19, 20383–20392 RSC
.
- J. A. Woollam,
et al., Overview of variable-angle spectroscopic ellipsometry (VASE): I. Basic theory and typical applications, Opt. Metrol. A Crit. Rev., 1999, 10294, 1029402 Search PubMed
.
- K. Levenberg, A method for the solution of certain non-linear problems in least squares, Q. Appl. Math., 1944, 2, 164–168 CrossRef
.
- D. W. Marquardt, An algorithm for least-squares estimation of nonlinear parameters, J. Soc. Ind. Appl. Math., 1963, 11, 431–441 CrossRef
.
-
Z. Chen, et al., Flat-Band Potential Techniques, Photoelectrochemical Water Splitting, Springer, New York, 2013, pp. 63–85 Search PubMed
.
- H. Dotan, K. Sivula, M. Grätzel, A. Rothschild and S. C. Warren, Probing the photoelectrochemical properties of hematite (α-Fe2O3) electrodes using hydrogen peroxide as a hole scavenger, Energy Environ. Sci., 2011, 4, 958–964 RSC
.
- C. Leendertz, A. M. Teodoreanu, L. Korte and B. Rech, The influence of space charge regions on effective charge carrier lifetime in thin films and resulting opportunities for materials characterization, J. Appl. Phys., 2013, 113, 044510 CrossRef
.
- T. Kirchartz, J. Bisquert, I. Mora-Sero and G. Garcia-Belmonte, Classification of solar cells according to mechanisms of charge separation and charge collection, Phys. Chem. Chem. Phys., 2015, 17, 4007–4014 RSC
.
- R. A. Lunt, A. J. Jackson and A. Walsh, Dielectric response of Fe2O3 crystals and thin films, Chem. Phys. Lett., 2013, 586, 67–69 CrossRef CAS
.
- L. A. Marusak, R. Messier and W. B. White, Optical absorption spectrum of hematite, α-Fe2O3 near IR to UV, J. Phys. Chem. Solids, 1980, 41, 981–984 CrossRef CAS
.
- J. N. Hilfiker,
et al., Survey of methods to characterize thin absorbing films with spectroscopic ellipsometry, Thin Solid Films, 2008, 516(218), 737 Search PubMed
.
- T. Lopes, L. Andrade, H. A. Ribeiro and A. Mendes, Characterization of photoelectrochemical cells for water splitting by electrochemical impedance spectroscopy, Int. J. Hydrogen Energy, 2010, 35, 11601–11608 CrossRef CAS
.
- D. Klotz, D. S. Ellis, H. Dotan and A. Rothschild, Empirical in operando analysis of the charge carrier dynamics in hematite photoanodes by, Phys. Chem. Chem. Phys., 2016, 18, 23438–23457 RSC
.
- A. Kay, D. A. Grave, D. S. Ellis, H. Dotan and A. Rothschild, Heterogeneous doping to improve the performance of thin-film hematite photoanodes for solar water splitting, ACS Energy Lett., 2016, 1, 827–833 CrossRef CAS
.
- S. Piccinin, The band structure and optical absorption of hematite (α-Fe2O3): A first-principles GW-BSE study, Phys. Chem. Chem. Phys., 2019, 21, 2957–2967 RSC
.
- N. Snir and M. C. Toroker, The operando optical spectrum of hematite during water splitting through a GW-BSE calculation, J. Chem. Theory Comput., 2020, 16, 4857–4864 CrossRef CAS PubMed
.
- P. Liao and E. A. Carter, Optical excitations in hematite (α-Fe2O3) via embedded cluster models: A CASPT2 study, J. Phys. Chem. C, 2011, 115, 20795–20805 CrossRef CAS
.
- Reference Solar Spectral Irradiance: “Air Mass 1.5: Terrestrial Global 37 Deg South Facing Tilt”. Spectrum wownloaded from: https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee01772a |
| This journal is © The Royal Society of Chemistry 2021 |