Multi-length scale microstructural design of lithium-ion battery electrodes for improved discharge rate performance

Abstract

Fast discharge capability of automotive batteries not only affects the acceleration and climbing performance of electric vehicles, but also the accessible driving range under complex driving cycles. Understanding the intricate physical and chemical processes across multiple length-scales is critical to assist the strategic design of electrodes for improved rate performance. Here, we correlate the discharge rate performance of Ni-rich LiNi_1−x−yCo_xMn_yO₂ (NMC) cathodes to the electrode architectures, ranging from the crystallographic orientations, surface morphology and cracks at single particle level, to the factors that affect the dominance of the solid and liquid-state transport (SST and LST) at electrode level. A random orientation of the primary particles is found to incur an increase of the SST resistance by a factor of 2.35 at 5C and a heterogeneous intra-particle lithiation. Internal cracks significantly restrict the accessibility to the active material. Double-layered particles are proved to be a more promising candidate than single-crystal particles. At electrode level, the SST-dominance depth is quantified for the first time to guide the microstructural tuning and rational operating windows are proposed for electrodes of various architectures. The reaction front is observed to shuttle across the electrode depth to mitigate the polarization, which can provide valuable insights into the battery management development. Finally, by comparing the performance of single crystal and polycrystalline NMC811 electrodes, it is suggested that electrode thickness and porosity are more critical in the former for enhanced discharge rate performance, in contrast to polycrystalline electrodes, in which a gradient particle fraction and size distribution are recommended.

---

Broader context

Electrified transportation is regarded as a global strategy to mitigate the air pollution and promote low-carbon economy. More than 10 million electric vehicles hit the roads all over the world in 2020 despite the Covid pandemic. Breakthroughs in the design and manufacturing of the next-generation automotive lithium-ion batteries can further improve the market penetration of electric vehicles. Ni-rich layered transition metal oxide materials such as NMC are promising cathodes due to their high energy density. However, they are susceptible to substantial capacity under-utilization due to the polarization arising from transport dynamics both at the particle and electrode level, which could deteriorate due to defects and microstructural degradation over long-term cycling. This study aims to elucidate the multi-length scale microstructural design strategies for both single crystal and polycrystalline NMC electrodes, assisted by a combined microstructure-resolved 3D model and electrochemical tests to improve the discharge rate performance. These insights are easily transferrable to other battery chemistries such as sodium-ion battery and solid-state batteries. The knowledge of spatial dynamics during lithiation is also conducive to the development of advanced driving cycles and battery management systems (BMS) for the electric vehicles.

1. Introduction

Lithium-ion batteries (LiBs) have undergone rapid advancements in the last three decades since their first appearance on the market, and now play a critical role in automotive electrification due to their superior power and energy densities. Despite the recent growth, the driving range, rate capabilities and cost are recognized as predominant factors limiting further market penetration of electric vehicles (EVs).¹ While a concerted effort has been made on the breakthrough of LiB technologies to target an energy density of 500 W h kg⁻¹ with a charging time of less than 10 minutes, fast discharge capability of automotive batteries, which not only heavily affects the acceleration and climbing performance, but also the driving range under complex driving cycles,² has become another challenge to be addressed. It is predominantly determined by cathodes due to the low electronic conductivity³ and Li⁺ ion transport resistance in both the liquid and solid phase,⁴ particularly in Ni-rich NMC electrodes.

However, the optimal electrode design for energy and power-oriented cells differs significantly and often leads to trade-offs.⁵ For instance, thicker electrodes, low porosity and heavy calendering are common material design strategies for high energy density cells, which inevitably suffer from large polarization due to the poor percolation and high tortuosity of the pore network,^6,7 consequently sacrificing the rate capability of the cell.⁸ Accordingly, researchers have been exploring either advanced electrode architectures, such as gradient porosity/pore size^9,10 and directional pore phase architectures,¹¹ or innovational flexible 1D batteries with hybrid electrodes to overcome this challenge.¹² Despite the remarkable performance improvement of these designs, the scalability, cost and structural integrity remain of concern for large-scale electrode manufacturing and commercialization. Although Ni-rich NMC electrodes can mitigate the microstructure limitation, they are known to suffer from capacity loss due to the chemical and mechanical degradation mechanisms such as Ni²⁺/Li⁺ disordering,¹³ surface reconstruction¹⁴ and particle cracking¹⁵ at high cutoff voltage or long-term cycling.

Apart from the liquid-state transport (LST) of Li⁺ ions, the solid-state transport (SST) resistance of the intercalated lithium is another main factor that restricts the rate capability, particularly for electrodes composed of large particles that have longer solid-state diffusion paths.¹⁶ This results in a large concentration gradient, and therefore higher polarization, from the surface to the core of the active material particle and an electrochemical shielding effect due to surface saturation of the intercalated lithium. As a consequence, the nominal capacity is underutilized, particularly at high C-rates,¹⁷ while at the anode safety can be compromised by lithium dendrite formation. Another disadvantage of large-particle electrodes is the slow reaction kinetics due to the low specific reaction area. Thus, nanostructured electrodes have been proposed to tackle these issues;^18–20 however the large surface area requires more conductive carbon and binder additives to maintain the good electronic percolation and adhesion of the electrode, undermining the volumetric energy density. Furthermore, large surface area leads to low coulombic efficiency and severe electrolyte decomposition.^21,22 Tailoring the ratio between small and large particles is a simple but effective solution. However, an electrode with a mixture of small and large particles could lead to uneven distribution of state-of-lithiation, reactivity,⁹ heat generation²³ and aging. While large particles are more susceptible to mechanical failure during long-term cycling,¹⁵ small particles introduce faster chemical degradation and a lower onset temperature of thermal runaway.²⁴ Thus, a sensible mixture ratio (i.e., particle size distribution, PSD) is critical to improve the electrochemical performance while maintaining good durability and safety. However, this is often achieved by manipulating the PSD ratio of D30, D50 and D90 (‘D90’ represents the particle size that is larger than 90% of the particles in the electrode) of the electrode based on empirical optimization and ‘know-how’ in manufacturing processes. The rational design criteria for high performance electrodes remain either largely unknown, or a closely guarded industrial secret, and consequently this information is sparse in the literature.

LST and SST are two complementary transport mechanisms that govern the performance of a cell, depending on the operating conditions and microstructural design of the electrode. In general, LST is rate determining for energy-oriented cells that are heavily calendered or fabricated with thick electrodes, but for power-oriented cells with high porosity or low mass loading (i.e., thin electrodes), SST often outweighs LST in determining the rate performance. However, it should be noted that the polarization associated with SST in thick electrodes is more severe compared to thinner electrodes due to the increased capacity and thus the higher current density at the same C-rate. Moreover, the locally high current density in the vicinity of the separator, which is more significant in thick electrodes, can exacerbate the local polarization due to the SST resistance. Accordingly, electrodes fabricated with a gradient particle size across the thickness direction have been investigated.^9,25,26 Nonetheless, understanding of the competition between the two rate-limiting mechanisms for different electrode designs under different conditions is scarce but would provide valuable input to rationalizing electrode manufacturing for next-generation automotive LiBs.

In addition to the electrode level, the architecture at the particle length-scale also significantly affects the discharge rate performance in high energy density LiBs. In poly-crystalline materials, the random arrangement of crystallographic orientations of the primary particles within the secondary particles and the presence of internal defects (e.g., cracks and voids) are closely linked to anisotropic deformation, heterogeneous lithiation and high mass transport resistance that undermine the electrochemical performance at the particle level and lead to early degradation. Kim et al.²⁷ developed LiNi_1−x−yCo_xMn_yO₂ (NMC) particles with a gradient concentration distribution of transition metals and radially-aligned primary particles that showed a marked reduction in grain boundary crack propagation. Heterogeneous stress/strain between primary particles can also be alleviated. This design is believed to exhibit faster SST due to the mitigated intra-particle anisotropy. However, few studies have managed to quantify the impact of intra-particle architecture and cracking on the rate capability, which is necessary to guide the microstructural design. Moreover, the surface roughness of the secondary particles, as a consequence of the random orientation of the primary particles at the outer surface, has also been reported to facilitate the power performance²⁸ due to more active reaction sites and therefore lower effective charge transfer current density, but is rarely quantified.

This work aims to elucidate the strategies of multi-length scale electrode microstructural design by unravelling the interplay of electrochemical performance with the microstructure characteristics ranging from primary particles up to the electrode level, assisted by a combined microstructure-resolved 3D model and electrochemical tests. The impact of the crystallographic arrangement of primary particles, cracks and surface roughness on the discharge rate performance is evaluated. The efficacy of advanced particle structures is examined. At the electrode level, the competition between SST and LST is highlighted for a variety of different electrode designs. Building on these insights, a practical mixture ratio of small/large particles (i.e., PSD) is proposed. This study also identifies for the first time a spatial self-balancing mechanism that highlights the utility of gradient electrode design. Finally, the rate performance of single crystal (SC) and polycrystalline (PC) NMC811 electrodes is compared to provide new insights into the microstructural design and optimization of electrodes for next-generation automotive LiBs.

2. Experimental

2.1 Materials

SC and PC NMC811 electrodes manufactured by Li-FUN Technology Corp. Ltd (China) were used in this study. The mass loading of the active material is 95.5% (SC) and 96.4% (PC), corresponding to areal loadings of 16.7 mg cm⁻² and 18 mg cm⁻², respectively. Both types of electrodes were calendered to a density of 3.3 g cm⁻³. The aluminium current collector was 15 μm thick. These two types of electrodes were assembled into coin cells (half-cells) as the positive electrode (15 mm diameter), with lithium metal as the negative electrode (16 mm diameter), and Celgard 2325 (19 mm) as the separator. 80 μL of 1 M LiPF₆ in ethylene carbonate (EC)/ethyl methyl carbonate (EMC) (3 : 7 v/v) + 1 wt% vinylene carbonate (VC, Soulbrain, USA) was used as the electrolyte.

2.2 Electrochemical performance tests

Prior to the rate capability test, the assembled cells underwent a formation step composed of constant current–constant voltage (CC–CV) charge at C/10 (C/40 cut-off) and CC discharge at C/10 from 4.2 V to 2.8 V for two cycles on BCS battery cyclers (Biologic, France). The capacity of these two types of cells was measured to be 4.4 mA h (2.49 mA h cm⁻², SC) and 4.9 mA h (2.77 mA h cm⁻², PC), respectively. GITT²⁹ was conducted to measure the OCV of NMC811 vs. Li/Li⁺ for each type of electrode (Fig. S7, ESI†). The first measurement point started from 4.2 V. The cell was discharged at C/10 for 15 min (2.5% state of charge, SOC), followed by a relaxation step, then discharged for 45 mins CC (C/10, 7.5% SOC), followed by a relaxation step before starting the next measurement point (i.e., step size is 10% SOC). All the relaxation periods were set to be 4 hours relaxation to ensure equilibrium condition. This discharge/relaxation + pulse/relaxation cycle was repeated until reaching the cut-off voltage of 2.8 V. The solid-state diffusion coefficient was also measured by analysing the GITT curve according to the previously developed methodology.³⁰

2.3 X-ray nano-computed tomography for NMC811 electrodes and a single secondary particle

The SC and PC NMC811 electrodes were firstly cut by a handheld punch to extract 1 mm disks, which were subsequently mounted onto the tip of a pin by epoxy, followed by laser milling³¹ to reduce the sample diameter to approx. 70 μm for improved transmission and contrast. The prepared electrode pillars were then scanned using a Zeiss Xradia Ultra 810 X-ray microscope (Carl Zeiss, CA, USA),³² which provides a quasi-monochromatic parallel beam with an energy of 5.4 keV. 1201 projections at an exposure time of 60 seconds per frame were taken sequentially over 180° rotation. The scans were captured with camera binning 2, achieving a voxel size of 126 nm and a field of view of 64 × 64 μm². A standard filtered back-projection algorithm³³ was used for the 3D reconstruction, which was then imported into the commercial software package Avizo V9.5 (Avizo, Thermo Fisher Scientific, Waltham, Massachusetts, U.S.) for post-reconstruction analysis. The internal cracks in Fig. 1j were visualized by extracting the boundaries of neighbouring primary particles, followed by image processing to control the length of the crack to obtain the target crack density. In the single particle simulation, surface cracks were removed for Case Study 1 (Fig. 2e–h) and Case Study 2 (Fig. 2f–i) using the morphological operation method ‘closing’;³⁴ the smooth surface in Case Study 2 was achieved by applying a smoothing filter on the particle domain.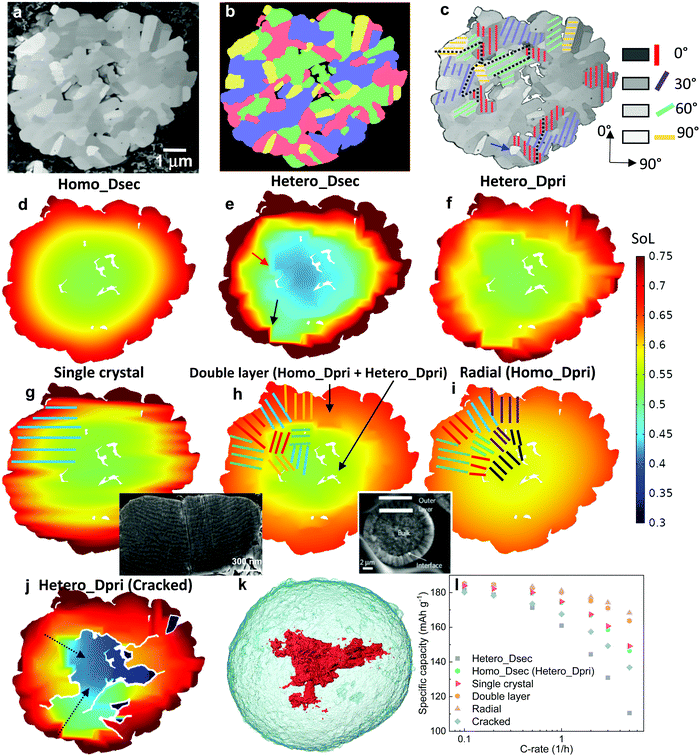

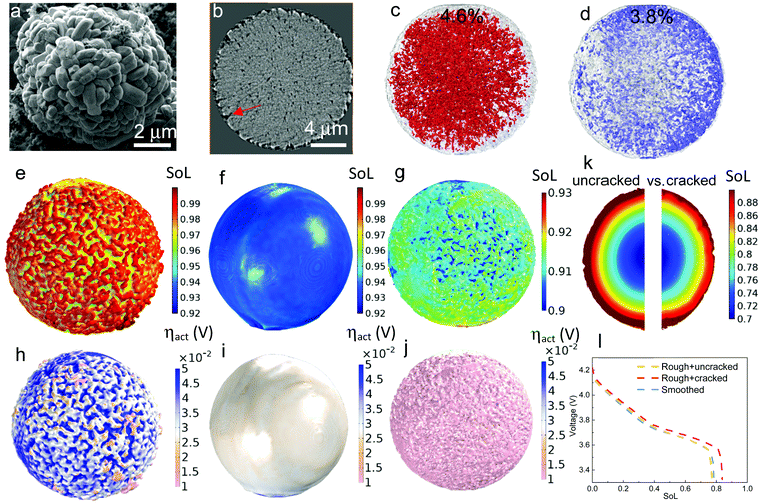
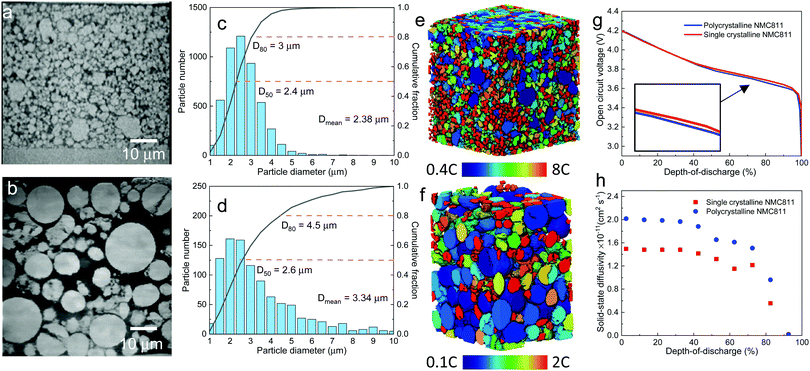
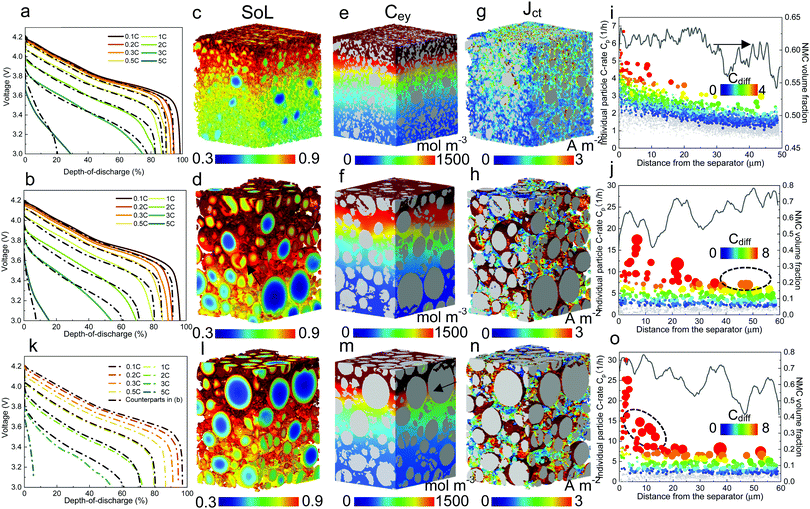
Fig. 1 The dependence of discharge rate performance on the microstructural heterogeneity within a single secondary NMC particle. (a) SEM image showing the random arrangement of primary particles, which are (b) classified into four groups (denoted by different colours) according to their grayscale values; (c) a monotonic change of the crystallographic orientation associated with the greyscale is defined for primary particles of each group, with the dotted lines schematically showing the tortuous SST pathway; (d) a particle level electrochemical simulation using a solid-state diffusion coefficient Dsec measured by the GITT experiment, homogenizing the effect of intra-particle orientation; (e) a single particle simulation accounting for the intra-particle heterogeneity by assigning orientation-dependent diffusivity of each primary particle; (f) the particle shows identical performance as (d) when using a primary particle diffusion coefficient Dpri that is 3.05 times larger than Dsec; (g) SoL simulated on an SC NMC particle. The inset shows the planar structure on the cross section. More SEM images can be found in Fig. S3 (ESI†); (h) simulated performance with a double-layered structure (the inset is reproduced with permission⁴³) and (i) radially-aligned primary particles; (j) the effect of internal cracks on capacity loss and lithiation heterogeneity; (k) 3D visualization of an internal crack in an NMC secondary particle after long-term cycling; (l) comparison of the rated capacity for different cases. The colourmap in (d)–(j) shows the lithium concentration distribution at 60% state-of-lithiation (SoL) at 5C.

Fig. 2 The dependence of discharge rate performance on the surface morphology of a 16 μm secondary NMC particle. (a) SEM image showing the surface roughness due to the random arrangement of primary particles; (b) a cross-sectional slice showing the surface roughness and cracks of the secondary particle scanned by X-ray nano-CT; (c) internal voids (red) and (d) surface cracks (purple) shown within the particle (semi-transparent); (e)–(g) and (h)–(j) show SoL and activation overpotential distribution respectively at 80% DoD simulated at 1C accounting for the surface roughness, neglecting the surface roughness and accounting for both surface roughness and cracks; (k) cross-sectional view to compare the SoL with (right) and without (left) surface cracks; (i) comparison of the discharge curves for each case.

2.4 Physics-based microstructure-resolved model

Electrochemical simulations were performed on 4 types of data in this study: (1) 2D secondary particle cross section; (2) 3D secondary particle (nano-CT); (3) 3D electrodes of different particle size (generated by open-source Python code Porespy³⁵); (4) 3D electrodes of SC and PC electrode (nano-CT). Except for the first case, in which the secondary particle was divided into four subgroups of the primary particles according to the greyscale value, all the 3D geometries were first segmented to binary data (solid particle and everything else) using the marker-based watershed method,³⁶ and were then imported to the commercial software Simpleware ScanIp for adaptive meshing. The carbon-binder domain (CBD) was lumped into the non-solid domain (NSD) with the pore phase, with the effective mass transport parameters (i.e., porosity and tortuosity) assigned based on the microstructure-resolved CFD modelling (Fig. S11, ESI†). The generalized Poisson–Nernst–Planck (gPNP) mathematical model,³⁷ a derivative of the Newman battery model,³⁸ was implemented in COMSOL Multiphysics V5.5 by assigning partial differential governing equations (PDEs) to solve for potential in the electron-conducting (NMC and CBD) and ion-conducting (pore) phases, lithium concentration in NMC (Fick's law) and electrolyte salt concentration in the pore phase (concentrated solution theory).^37,39 The Butler–Volmer equation was used for the reaction kinetics and the exchange current density was expressed as a function of the concentration of the reactants in the electrolyte and active material. The detailed mathematical description of the model, parameters and boundary conditions are presented in the ESI.†

3. Results and discussion

3.1 Crystalline orientation and internal defects in secondary particles

Fig. 1a shows the SEM image of a cross section of a representative PC secondary NMC particle (more secondary particles like this can be seen in Fig. S1, ESI†), in which randomly arranged primary particles are observed, identifiable by distinct grayscale contrast that is associated with the crystallographic orientation of these particles relative to the inspection plane. In addition, internal voids left over from the powder sintering process are evident. The primary particles may be classified into four groups (Fig. 1b), with each group representing an in-plane crystallographic orientation (i.e., 0°, 30°, 60° and 90°, Fig. 1c), according to their grayscale values. Although the assumed brightness vs. orientation relationship could be reversed, this makes only a trivial difference due to the high randomness of the primary particle arrangement, as will be proved later. The coloured solid lines schematically indicate the transition metal planes in the layered crystal structure (the c-axis aligns in the normal direction). Note that the greyscale intensity of the primary particle is associated with the backscattered electrons that are primarily dependent on the out-of-plane angle of c-axis, thus the 3D crystallography can be simplified to 2D in this study by neglecting the in-plane angle, which is interchangeable with the other depending on the cutting plane for observation. In the later part of the study, the 3D solid-state diffusion will be compared with the simplified 2D case here. 3D EBSD is the planned future work in order to reconstruct the full orientation map for individual primary particles. The SST resistance induced by the internal heterogeneity of the crystallographic orientations is schematically illustrated in Fig. 1c, as the intercalated lithium preferentially diffuses along the layered plane as indicated by the black dotted lines.

To evaluate the impact of primary particle arrangement, two types of single-particle lithiation (5C discharge) simulation are performed (see model details in the ESI†). The first model homogenizes the internal microstructure by adopting a volume-averaged diffusion coefficient in the NMC622 secondary particles Dsec (Homo_Dsec, Fig. 1d) measured by the Galvanostatic Intermittent Titration Technique (GITT) from a previous study¹⁷ (concentration-dependent). The second model accounts for the intra-particle heterogeneity (Hetero_Dsec, Fig. 1e) by assigning different orthogonal diffusion coefficients for each primary particle according to its group, so that Dsec is oriented in the vertical direction for the red primary particles (i.e., crystalline diffusion coefficient Dy = Dsec) and zero in the horizontal direction (Dx = 0), and vice versa for the yellow primary particles. For the purple particles, Dy = Dsec·cos(30°) and Dx = Dsec·cos (60°), and vice versa for the green particles. Results at 60% state-of-lithiation (SoL) are compared. It is shown that the homogenized model (Fig. 1d) predicts a much smoother concentration gradient compared to the heterogeneous one (Fig. 1e), in which a strongly non-uniform lithium concentration is observed. It is noted that neighbouring primary particles of large-angle crystallographic orientation (i.e., the red/yellow primary particle interface indicated by the black arrow and purple/yellow by the red arrow) render a sharp concentration gradient at the particle boundaries. Large SST resistance associated with restricted diffusion paths resulting from crystalline heterogeneity leads to capacity underutilization. The SoL distribution simulated using the reversed brightness vs. orientation relationship as defined in Fig. 1c is shown in Fig. S2 (ESI†), which is macroscopically similar to Fig. 1e, and identical in terms of rated capacity. This is not surprising as the primary particle arrangement is fairly random so that the final result is independent of the hypothesis of the brightness vs. orientation relationship. However, a localized difference between the two cases is observed; for instance, a narrow and elongated low concentration zone in Fig. S2 (ESI†) (indicated by the black arrow) aligned parallel to the c-axis of the primary particle at this position (i.e., large diffusion resistance). This low concentration zone also initiates from the interface of the red/yellow primary particles. A sharp concentration gradient between neighbouring primary particles is not favourable for structural integrity due to stress accumulation and cracking over long-term cycling.^15,40–42

Since Dsec measured by GITT is a mean-field parameter with intra-particle heterogeneity inherently accounted for, Homo_Dsec in Fig. 1d represents the real SoL in operation whereas Hetero_Dsec in Fig. 1e apparently underestimates the SST rate; in other words, the crystalline diffusion coefficient of the primary particle Dpri, must be much larger than Dsec to produce an identical SoL pattern to that in Fig. 1d. This ratio is found to be Dpri = 3.05·Dsec and the associated SoL map predicted by the corrected Dpri is shown in Fig. 1f, meaning that the intra-particle heterogeneity yields a tortuosity of 3.05 for solid-state diffusion. The third row of Fig. 1 compares three different arrangements of primary particles: Fig. 1g shows the SoL distribution simulated on an SC NMC particle, i.e., the lithium transport pathway is along the planar orientation (illustrated by the schematic). The inset is a FIB-SEM image displaying the planar structure on the cross section of the SC NMC particle (more SEM images shown in Fig. S3, ESI†). Comparing with Fig. 1f, the SC particle does not provide significant improvement of lithium transport capability, primarily arising from the restricted diffusion (along the planar direction) in comparison to the PC design where lithium diffuses inward from the entire periphery. Note that the SC NMC particles are normally much smaller than the PC particles, and therefore offer faster SST, whereas the comparison here solely highlights the transport affected by the crystal orientations given the same particle size. Apart from SC design, gradient secondary particles, either chemically or structurally, have aroused wide attention. Recently, researchers managed to fabricate secondary particles with a double-layered structure, in which the outer layer (approx. one-third of the radius) is composed of side-by-side aligned primary particles (inset in Fig. 1h)⁴³ accompanied by a concentration gradient of Ni and Mn from the outer surface to the core to suppress chemical degradation at the electrode/electrolyte interface. The benefit of this design in facilitating SST is evidenced by a smoothed concentration gradient at the outer layer (i.e., a decreased transport resistance) in Fig. 1h, compared to the original arrangement (Fig. 1g). The alleviation of concentration saturation at the electrode/electrolyte interface is critical for fast reaction kinetics and thus low polarization. A secondary particle with fully radially-aligned primary particles is also added for comparison; the SST resistance is trivial and good lithiation homogeneity is obtained (Fig. 1i).

Internal defects, either originating from the material synthesis process or formed due to heterogeneous stress/strain after aggressive or long-term cycling, particularly in the PC secondary particles,⁴⁴ also play an important role in the particle performance. Fig. 1j shows a simulation of the same secondary particle with internal cracks initiating from internal defects (i.e., voids), with the crack density being manipulated (more details in Experimental section 2.3) to be quantitatively consistent with the image of the cracked NMC particle after cycling (Fig. 1k, 3D crack rendered in red). The cracks partially reduce the percolating network, and as a consequence the core of the secondary particle can only be lithiated via the restricted transport pathways (indicated by the black dashed arrows), rendering a much higher tortuosity, which is found to be 1.65 times larger than for the non-cracked electrode in this case (Fig. 1f). Moreover, internal cracks (not connected to the electrolyte bulk) create shielded ‘islands’ that are inaccessible to lithium flux, as can be seen in Fig. 1j. These factors lead to an underutilization of the cell capacity. Fig. 1l compares the rated capacity for the simulated particles in Fig. 1d–j. The arrangement of radially-aligned primary particles provides the optimal rate performance, exhibiting a drastic improvement compared to the as-synthesized NMC particle (green). The SC particle (red) shows similar performance compared to the same-sized PC secondary particle. The influence of internal heterogeneity is highlighted by comparing the case of Fig. 1e (dark grey) with the green plot. This adverse effect is even more impactful than structural degradation due to cracking (blue), as evidenced by the aforementioned increase of the tortuosity (3.05 vs. 1.65). Note that the double-layer arrangement (orange) shows trivial disparity compared to the radially-aligned particle design, indicating that the outer layer plays a dominant role in determining the overall rate performance and should be the main focus for structural optimization.

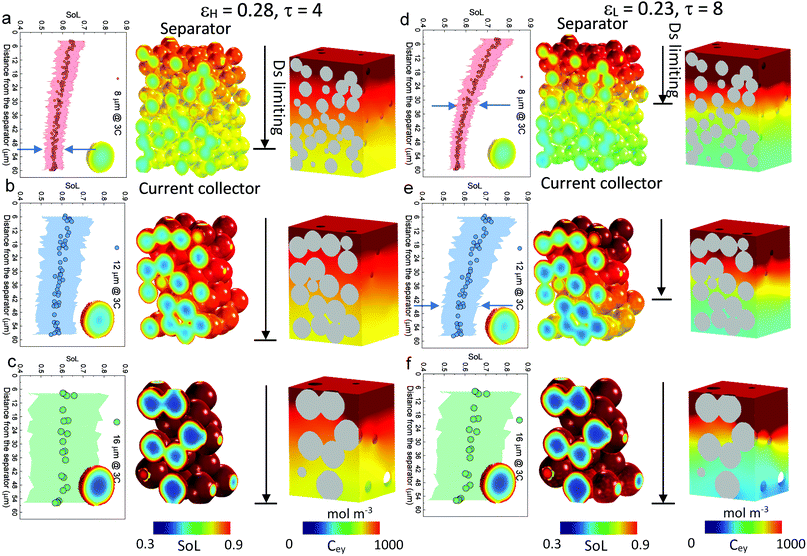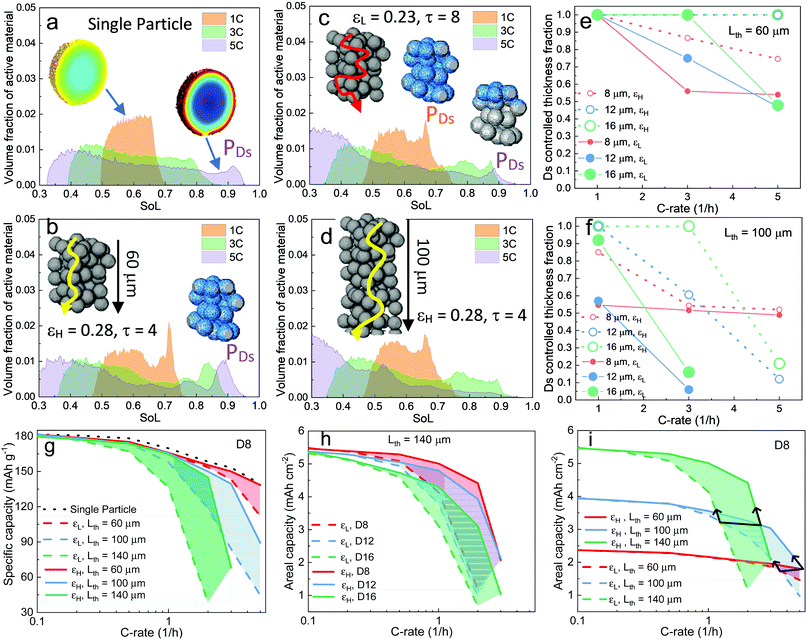
Fig. 3 Electrochemical simulation (3C discharge, half cell NMC vs. Li anode) in (a) D8 (b) D12 and (c) D16 at high porosity (ε_H) and (d) D8 (e) D12 and (f) D16 at low porosity (ε_L), respectively. The average SoL and its standard deviation within each particle are plotted alongside each electrode at 60% DoD. The inset in each plot presents the single-particle simulation, regarded as a reference to determine the Ds limiting region. Ds varies with SoL, as shown in Fig. S8 (ESI†).

3.2 Surface roughness and cracks in secondary particles

Apart from the intra-particle heterogeneity, surface roughness and surface cracks are the other characteristic features that could affect the reaction kinetics and diffusion dynamics at the particle level. The former arises from the random arrangement of the primary particles at the secondary particle surface while the latter are defects from the sintering process of NMC precursor. Fig. 2a and b show the morphology of surface roughness under SEM and X-ray nano-computed tomography (Nano-CT) respectively. The internal voids and surface cracks (indicated by a red arrow in Fig. 2b) obtained from the 3D reconstruction are visualized in Fig. 2c and d, with each taking up 4.6% and 3.8% volume fraction of the secondary particle, respectively. To evaluate the impact of surface roughness and surface cracks on the particle performance, three different types of discharge (lithiation) simulation are conducted on a 16 μm diameter particle: Fig. 2e–g compare the SoL at 80% depth-of-discharge (DoD) at 1C when (1) accounting for surface roughness (Fig. 2e); (2) neglecting surface roughness (Fig. 2f); (3) accounting for both surface roughness and surface cracks (Fig. 2g, details of the model setup is introduced in Experimental section 2.3), whereas Fig. 2h–j compare the activation overpotential η_act for each case. Simulations show a higher degree of lithiation of the surface ridges compared to the valleys (Fig. 2e); as a consequence, the ridges are saturated with lithium where the reaction kinetics and thermodynamics (i.e., lower equilibrium potential) are slower and the charge transfer mostly takes place at the valleys, leading to a lowered effective reaction area and thus a higher activation overpotential (Fig. 2h). In comparison, the particle with a smoothed surface exhibits a uniform lithiation state and less surface saturation (Fig. 2f), which suppresses the heterogeneous surface reactivity and the activation overpotential (Fig. 2i). This poses a question over whether high surface roughness and therefore higher specific reaction area (1.12 μm⁻¹, compared to the smoothed particle 0.82 μm⁻¹) is advantageous for the performance, since the active reaction area is not necessarily higher due to the early saturation of the surface ridges, in addition to the potential risk of uneven aging and mechanical degradation due to the disparity of SoL between the primary particles at the ridge and valley.

The surface-cracked particle shows the lowest SST resistance, evidenced by a significantly lower surface concentration and concentration gradient than the other two cases (Fig. 2g), which are more visible from the cross-sectional view in Fig. 2k (left: uncracked vs. right: cracked). This is because the penetration of surface cracks provides a shorter diffusion path and more lithiation sites from the newly generated surfaces so that lithiation can take place both in the radial and hoop direction. The overpotential at the surface is accordingly lower (Fig. 2j) due to the improved reaction kinetics. The discharge curves of the three cases are compared in Fig. 2I, which displays an insignificant difference between the smoothed particle and the rough but uncracked particle. This is in contrast to the rough and surface-cracked particle, which shows a remarkable performance improvement as long as the surface cracks do not propagate deeper into the secondary particle to amalgamate with internal cracks. This highlights that SST outweighs reaction kinetics in determining the electrochemical performance at the particle level, which is corroborated by the comparison of maximum accessible C-rate for reaction kinetics vs. SST in Fig. S4 (ESI†) under a variety of conditions such as different particle size, SoL and electrolyte concentration. It is noted that surface cracks are not prevalent in fresh electrodes based on the SEM observation (Fig. S5, ESI†), but may be formed during fast or long-term cycling and heavy calendering, leading to exacerbated side reactions and electrolyte decomposition at the cathode/electrolyte interface.

3.3 Competition between solid-state and liquid-state transport in governing rate performance

Scaling up from a single secondary particle to the electrode level, PSD and porosity ε (and the associated tortuosity, τ) are the primary material design parameters that significantly influence the discharge rate performance of the cell by tailoring the SST and LST capability for different energy applications. Understanding the competition between these two mechanisms for different microstructures is critical to optimize the energy and power performance of the battery. Here we examine the SST in three electrodes (generated by Porespy³⁵) composed of monodisperse secondary particles, 8 μm (D8), 12 μm (D12) and 16 μm (D16), and different porosities (ε_H = 0.28 and ε_L = 0.23 for high and low porosity respectively) in Fig. 3, where D8 and D16 correspond to the average (7.5 μm) and upper limit of the particle diameter (16 μm) in commercial NMC622 electrodes (Fig. S6, ESI†). Note that the volume fractions of NMC particles are consistent (0.43, corresponding to 90 wt% NMC and an areal capacity of 1.5 mA h cm⁻²) between each electrode, and the porosity is defined as the ratio of the pore volume in the non-solid phase (lumped pore + carbon binder domain) to the electrode volume. The results of the performance simulation at two porosities are presented in Fig. 3a–c and d–f, respectively (discharged at 3C, shown at 60% DoD). Compared to ε_H, ε_L demonstrates a more preferential lithiation in the vicinity of the separator (at the top in Fig. 3), particularly when the particle size is small (D8), which indicates a dominant role of LST. As the particle size increases, LST becomes outweighed by SST in determining the rate capability, evidenced by a less significant gradient of SoL across the thickness as well as a high intra-particle concentration gradient. This competition between the SST and LST limitation is not obvious in ε_H due to the high porosity and thus a mild electrolyte concentration (C_ey) gradient. 3D simulation results shown here are compared with those generated using a pseudo2D (P2D) method,⁴⁵ which is less computationally expensive (Fig. S7, ESI†). It is found that the average SoL predicted by the P2D model is within the scatter of the predictions for the individual particles of the 3D model. Macroscopically the SoL distribution within the particles is identical along the thickness direction, but the line profile of the single particle shows a higher SoL in the P2D prediction, possibly because the NMC particles in the P2D model are homogenized across the whole simulation domain, free from the contact and overlap effect which could alter the internal lithiation.

The SoL of each secondary particle and its standard deviation (STD, the shaded zone) are linked to the SST resistance, which is dependent on the nominal solid-state diffusion coefficient, Ds. The SoL and its STD are plotted alongside the SoL map for each electrode in Fig. 3. Apart from the aforementioned larger gradient of SoL in the through-thickness direction, ε_L electrodes exhibit a larger in-plane STD of SoL in the proximity of the separator, particularly for D8 and D12 electrodes, due to the gradient of C_ey that imposes a higher local current density at the separator. Moreover, the STD becomes narrower towards the current collector for these two types of electrodes, suggesting a decreasing impact of the SST resistance. In contrast, an insignificant difference in STD between the separator and current collector is observed for D16 as a consequence of the dominance of SST over LST so that the electrode thickness and porosity are less important. This phenomenon is quantified by conducting single-particle simulations that rule out the influence of the LST (shown as insets in each plot). These simulations are regarded as benchmarks to assess the depth of the electrode that is dynamically limited by SST (Ds limiting), by identifying the same STD as that of the single particle across the depth of the electrode (indicated by arrows on the plots). Thus, within the Ds limiting depth, the SST is the limiting resistance, while LST resistance dominates the remainder of the electrode. It is found that the Ds limiting depth increases as the particle size becomes larger for both types of electrodes but decreases with the reduction of porosity. For instance, in the D8, ε_H electrode, 83% of the electrode depth is primarily governed by SST and this becomes 100% with larger particle size, in contrast to 55% (D8) and 75% (D12) for ε_L. This finding is consistent with the general design rules that smaller particles and higher porosity favour SST and LST respectively, but provides much needed quantification of the trade-offs inherent to microstructure optimization.

The histogram distribution of SoL for the active material particles can provide additional insights into the relative importance of SST and LST. Fig. 4a shows the result of a single-particle (D16) simulation, with the x-axis displaying the range of SoL in the particle and y-axis the corresponding volume fraction of the active material particle at each SoL. The SoL distribution is observed to be more uniform at 1C discharge, denoted by a narrow peak, in sharp contrast to the 3C and 5C cases, where the SoL distribution expands significantly. A peak (P_Ds) appears at the high end of SoL under 5C discharge, attributed to the saturation of lithium at the particle surfaces. Fig. 4b presents the result of the D16 electrode simulation with ε_H, in which a higher P_Ds is observed even at 1C, suggesting a more dominant role of SST. This is attributed to a higher current density in the electrode in contrast to the single particle. The inset displays the region (blue) corresponding to the voxels under P_Ds at 5C. The full coverage along the thickness direction is consistent with the previous measurement of the SST limiting zone (i.e., Ds limiting) in Fig. 3. In comparison, Fig. 4c for the ε_L electrode demonstrates a less significant influence of SST compared to LST, evidenced by the closer peaks and the height of P_Ds, relative to the ε_H electrode. Notably, P_Ds originally covers the whole thickness of the electrode at 1C, but fades towards the separator region (shown by the insets), indicating a shift of the limiting mechanism from SST to LST. The effect of electrode thickness is also investigated on a 100 μm thick electrode (Fig. 4d). It shows a similar SoL distribution to those in Fig. 4c at 1C and 3C, but no P_Ds is visible at 5C, due to a more dominant role of LST in the thicker electrode. The complete histogram distribution of different electrodes with varied particle sizes is shown in Fig. S9 (ESI†).

Fig. 4 Analysis of the competition between LST and SST in determining the discharge rate performance of the cell. Histogram distribution of (a) single particle (b) ε_H (c) ε_L and (d) thicker electrode (L_th = 100 μm). Results at 60% DoD are shown. The insets in (a) represent the SoL distribution at the corresponding C-rates; insets in (b)–(d) with diffusion trajectory, schematically highlight the electrode thickness as control parameters; the insets with blue surface display the voxels under the area of peak P_Ds, which represents the surface saturation of the particles; (e) and (f) quantify the SST limiting region for electrodes of different particle sizes and porosities, at L_th = 60 μm and L_th = 100 μm, respectively; (g)–(i) capacity comparison of different electrode designs as a function of C-rate.

Fig. 4e and f summarize the SST limiting zone in electrodes fabricated with different particle sizes, porosities and thicknesses (L_th). The dominance of SST generally increases with larger particle size and higher porosity, but decays with increasing electrode thickness. A sharper decrease of the SST limiting zone is observed in thicker electrodes at the same porosity. Note that the plot for D8 at ε = 0.23 (ε_L) in the thin electrode (L_th = 60 μm) is almost identical to that at ε = 0.28 (ε_H) in the thick electrode (L_th = 100 μm), suggesting an equivalent LST impact on the two electrodes. Moreover, the SST limiting zone reaches a plateau (approx. 0.52) only for the D8 electrode as the C_ey builds up as a function of the C-rate, which is speculated to be a consequence of reaction front propagation and will be investigated in the later section. Fig. 4g compares the effect of porosity and thickness on the gravimetric capacity of the D8 electrode. At the thickness of 60 μm, the performance of high porosity D8 shows a negligible difference compared with that of the single-particle (dotted black line), indicating a negligible LST resistance. The increase of the shaded area in thicker electrodes indicates an increasingly dominant role of porosity, which is substantiated by the superior gravimetric capacity of the high porosity (0.28) 140 μm electrode compared to the low porosity (0.23) 100 μm electrode. This also implies that porosity is more important than electrode thickness in determining LST limitations. Fig. 4h compares the areal capacity of electrodes composed of different particle sizes and porosities in the 140 μm thick electrode. It is worth recalling that all the electrodes have nominally the same volumetric fraction of active material, and thus approach the same theoretical areal capacity as the C-rate approaches zero. It is observed that none of the ε_L electrodes retain 80% of the total capacity beyond 1C. Electrodes with large particles exhibit a faster capacity drop. Note that the shaded area for D8 is larger than that for D16, indicating that porosity is more influential in electrodes that are LST-limited, in good agreement with the analysis in Fig. 3. Fig. 4i compares the areal capacity of D8 electrodes with different porosities and thicknesses while keeping the volume fraction of the NMC particles constant. As thicker electrodes demonstrate a faster capacity drop and LST resistance increase at low porosity, the 100 μm electrode provides less capacity than the 60 μm electrode beyond 3.5C for ε_L and 5C for ε_H; and these become 1.3C and 2.8C when the 140 μm electrode is compared to the 100 μm one. These findings suggest a practical operating window of maximum current for each microstructural design to fully exploit the active materials (outlined by the black arrows).

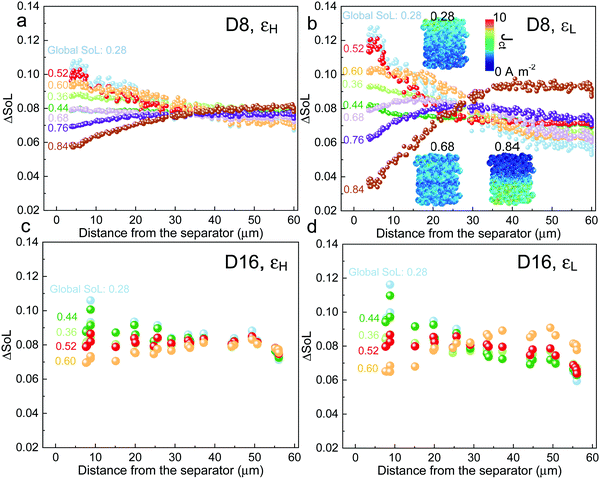
The spatial dynamics of the electrochemical reaction are heavily dependent on the competing dominance between LST and SST, which is further investigated in Fig. 5. The figure reports the differential SoL (ΔSoL, i.e., the difference between maximum and minimum SoL) of each NMC particle at incremental lithiation time steps at 3C, for D8 and D16 at low and high porosities, respectively. At the initial stage of discharge in D8, the particles close to the separator are lithiated faster than the particles near the current collector for both cases due to the C_ey gradient as discussed above. As the discharge continues until SoL = 0.44, the non-uniform lithiation rate is mitigated (i.e., ΔSoL decreases) for both ε_H and ε_L electrodes, as a consequence of the propagation of the reaction front, which is a self-balancing mechanism; particles lithiated faster in the vicinity of the separator suffer from larger polarization attributed to the slow SST and thus the reaction front propagates deeper into the electrode where the reaction energy barrier is lower, which helps to reduce the SoL gradient across the electrode thickness. This is followed by a repeated rise of ΔSoL at SoL = 0.52, indicating that the C_ey regains dominance in determining reaction kinetics. However, ΔSoL quickly drops again for the same reason and does not rise until the end of discharge due to the surface saturation as well as the faster drop of Ds as a function of SoL for the particles close to the separator.

Fig. 5 Spatial dynamics of the charge transfer process analyzed in terms of the differential SoL (ΔSoL) of each particle across the thickness of the electrode at different discharge time steps at 3C. Insets in (b) represent the distribution of charge transfer current density J_ct at global SoL of 0.28, 0.68 and 0.84.

The insets in Fig. 5b show the distribution of the charge transfer current density (J_ct) at global SoL = 0.28, 0.68 and 0.84. They clearly demonstrate the spatial transition of the reaction kinetics, which shifts from the separator side to the current collector side from SoL = 0.28 to SoL = 0.84. This explains the plateau of the SST limited region observed in D8 (Fig. 4e and f). Note that this self-balancing phenomenon is more significant in ε_L, as the LST is more severe and thus the C_ey is larger. D16 electrodes exhibit a similar trend of self-balancing, however, the second rise of the curve appears earlier (SoL = 0.44) than for D8 (SoL = 0.52), suggesting a faster SoL homogenization process across the electrode, since LST is less limiting, as expected for the electrodes with larger PSD. This knowledge can provide valuable insights into the development of BMS for rational fast discharging protocols for electrodes of different geometries in order to mitigate polarization and early degradation.

3.4 Electrode design building on the insights of governing mechanism and spatial dynamics

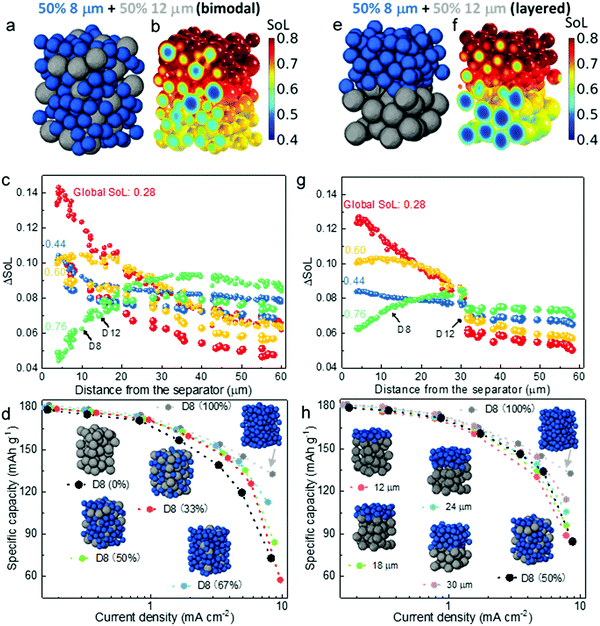
The obtained knowledge of the dominant limiting mechanism of the discharge rate performance as a function of particle size and thickness, together with the interpreted spatial dynamics, are anticipated to guide the optimization of electrode design and engineering in the battery manufacturing industry. Although electrodes with small particles provide much better rate capability, in most commercial battery electrodes a mixture of different sized active material particles (i.e. optimized PSD) is the normal practice, not only to increase the packing density but, more importantly, to suppress side reactions,⁴⁶ degradation^47,48 and self-discharge, while mitigating safety concerns^49,50 (e.g. increasing the onset temperature of thermal runaway) arising from the large specific reaction area associated with the small particles. Fig. 6a shows a 60 μm thick ε_L electrode consisting of bimodal particles with 50% volume fraction (generated by Porespy³⁵). The SoL distribution corresponding to 3C (i.e., 4.5 mA h cm⁻²) discharge at 60% DoD is presented alongside (Fig. 6b). A distinct difference in SoL is observed between the small particles (D8) and the larger ones (D12). Moreover, small particles play an important role in shielding the larger ones from lithium saturation at the surface, thereby reducing the overpotential, as can be evaluated by comparing Fig. 6b and 3e. Fig. 6c plots the differential SoL at different states of discharge. A similar self-balancing phenomenon is found in the bimodal electrode. Note that there is a large difference of ΔSoL between D8 and D12 particles, which is most prominent at the initial stage of discharge, meaning that the smaller particles lithiate much faster than the larger ones. This discrepancy gradually fades as the discharge continues, until reaching a global SoL = 0.76, where the plots for D8 and D12 are identical in the vicinity of the separator, as a result of surface saturation of the D8 particles. Fig. 6d compares the effect of mixing ratio on the rated capacity. It displays a trivial difference between the electrodes with the D8 content from 33% to 100% when the current density is below 3 mA cm⁻², beyond which a drastic performance drop is observed. These electrodes provide much superior rated capacity than the pure D12 electrode, which only manages to match the others when the current density is below 1 mA cm⁻².

Fig. 6 Comparison of the 60 μm thick ε_L electrodes with distinct spatial distribution of active material particles. (a) An electrode consisting of randomly distributed bimodal particles; (b) the corresponding SoL distribution at 60% DoD discharged at 3C; (c) Differential SoL of individual particles across the electrode thickness at incremental lithiation timesteps; (d) comparing rated capacity of various electrodes with increasing volume fraction of small particles; (e)–(h) the corresponding results for the electrode with layered particle size.

Building on the insights of preferential lithiation in the vicinity of the separator in the electrodes with sluggish LST, as well as the Ds limiting region, a layered electrode with varying particle size could be a promising candidate for next-generation automotive batteries. Smaller particles at the separator are conducive to the mitigation of the polarization arising from SST, whereas larger particles at the deeper region of the electrode ensure the cycle lifetime and slow degradation of the cell. Fig. 6e shows the layered ε_L electrode with the same composition as the randomly mixed electrode (Fig. 6a). It is observed that lithiation primarily takes place in the D8 layer where the polarisation is low (Fig. 6f). The D12 particles are less active compared to those in the randomly arranged electrode and thereby exhibit less SST limitation. Fig. 6g shows a lower ΔSoL at SoL = 0.28 compared to Fig. 6c, suggesting a more uniform lithiation than the corresponding region in the randomly distributed bimodal electrode, which also explains a less saturated state at SoL = 0.6 so that the D8 particles are more active. Fig. 6h compares the rate capability of electrodes with incrementally layered microstructure, extending from the separator to 30 μm deep into the electrode. The performance generally increases as a function of the layer thickness of the fine particles, attributed to the mitigation of the SST polarization. In particular, when the layered thickness reaches 30 μm, the rated capacity shows negligible difference compared to the electrode with pure D8 (100%), until reaching 5 mA cm⁻². This is consistent with the quantitatively estimated SST limiting region (approx. 0.5 of the total thickness) in Fig. 4f. Further increase of the thickness of the fine-particle layer would not benefit the rate performance significantly, and would come at the expense of additional side reactions and faster degradation. Despite having the same composition (i.e., 50% D8), the 30 μm layered electrode exhibits noticeably improved rate performance compared to the bimodal design when the current density is larger than 3 mA cm⁻², which becomes even more significant at 5 mA cm⁻². This can be explained by the fact that the mixture of D12 and D8 leads to imbalanced SoL and lithiation rate between the small and large particles due to the different SST resistance, particularly at the initial discharge stage, as can be seen in Fig. 6c (SoL = 0.28 and 0.44), which causes an early saturation of the D8 particles in the vicinity of the separator, making them less reactive and driving the charge transfer to take place primarily deep in the electrode, where the electric potential and C_ey are much lower. The bimodal 50% D8 electrode still provides better rate capability than the layered electrode when the fine-particle layer thickness is less than 18 μm.

3.5 Single crystal vs. polycrystalline NMC electrodes

The insights of SST and LST competition and spatial dynamics of lithiation are conducive to an improved understanding of the discharge rate performance of commercial batteries. In this section, we examine and compare the rate performance of commercially available SC and PC NMC811 electrodes due to their distinct difference in PSD, morphology and transport dynamics. The former has received broad attention in recent years due to its advantage in eliminating inter-granular crack/fracture, which is the major degradation mechanism in Li-rich PC NMC electrodes undergoing fast/over-charge or long-term cycling.^15,27,43Fig. 7a and b are cross-sectional views displaying the microstructure of the SC and PC NMC811 electrodes, respectively, obtained by X-ray nano-CT. Both electrodes had been pre-calendered to a target density of 3.3 g cm⁻³, and the resultant NMC volume fraction is measured to be 60.5% and 62.1% for SC and PC electrodes, respectively. The SC particles are evenly distributed across the electrode thickness, whereas the PC electrode is more heterogeneous with larger and more spherical secondary particles. Cracked secondary particles due to heavy calendering are observed in Fig. 7b but not in Fig. 7a, which is a combined effect of the particle size and primary particle boundaries. This is the reason why SC electrodes are advantageous to improve the packing density.

Fig. 7 (a) and (b) Cross-sectional view of the SC and PC electrodes obtained by X-ray nano-CT; (c) and (d) PSD for the two electrodes; (e) and (f) graphical visualization of the PSD colour-coded by the maximum C-rate based on the diffusion time constant as a function of the particle diameter. Ds at 50% SoL is used. (g) OCV measurements of the two electrodes and (h) solid-state diffusion coefficient as a function of DoD obtained from GITT experiment.

The PSD of each electrode is compared in Fig. 7c (SC) and Fig. 7d (PC). The SC particles have a much smaller mean diameter (D_mean = 2.38 μm) and narrower PSD than the PC electrode. Calendering a high mass loading PC electrode (96.4 wt%) introduces a large number of fragmented particles that reduce the average diameter of the particles. Thus, the PSD in Fig. 7d arises from a mixture of primary and secondary particles. Fig. 7e and f visualize the PSD, with the colour code representing the solid diffusion-controlled maximum C-rate (C_t), which is related to the SST time constant (t_d = r²/Ds, r is the particle radius) and is calculated as C_t = 3600/t_d. The open circuit voltage (OCV) measured by the GITT method (Fig. S10, ESI†) for the two types of electrodes is observed to be globally identical except for a subtle mismatch towards the end of the curve (Fig. 7g). The upper cut-off voltage was set to 4.2 V to avoid phase transition from H2 to H3 that is accompanied by a drastic contraction of c-axis and would initiate structural and chemical degradations.¹⁴ Ds as a function of SoL for the SC and PC electrodes is shown in Fig. 7h, where the PC electrode has a Ds approximately 1.3 times higher than that of the SC. This is surprising because SC particles are expected to have faster SST than PC particles due to the absence of grain boundaries and aligned crystal orientations; however, this result is also reasonable as, like graphite particles, the SC particles suffer from anisotropic lithiation (i.e., along the planar direction), which is exacerbated by calendering. As was shown in Fig. 1g, the SoL gradient in the horizontal direction is smaller than that for the PC electrode (Fig. 1f), but is larger in the vertical direction. Overall, the benefit of aligned crystals is compromised by unidirectional transport. Although the SC and PC particles seem to have identical Ds based on the 2D SoL distribution in Fig. 1, the experimentally measured Ds for the PC electrode is 30% larger than for the SC electrode (Fig. 7h), suggesting that transport in the third dimension contributes a 30% increase of SST for the PC particles. Thus, the actual tortuosity of the SST associated with crystal orientation and cracking is corrected to 2.35 and 1.27, respectively, in comparison to 3.05 and 1.65 based on 2D measurements.

The two types of electrodes were assembled into coin cells (half-cell vs. lithium) and cycled at different C-rates to compare the discharge rate performance, as shown by the colour-coded solid curves in Fig. 8a (SC) and b (PC). It is found that the SC electrode demonstrates a significantly superior rated capacity to the PC one, particularly at high C-rates. The SC electrode exhibits a capacity fade of 18% at 2C in contrast to 30% for the PC electrode. This is speculated to be due to the smaller particle size of the SC electrode; nonetheless this is worth further investigation via modelling. The dashed lines in Fig. 8a and b represent the predicted performance at 0.2C, 0.5C, 1C, 2C, 3C and 5C using microstructure-resolved modelling based on the X-ray nano-CT scans, in which the predicted performance is in good agreement with the experimental results. The porosity and tortuosity as model parameters defining the LST in the hybrid carbon-binder/pore domain are 0.203 and 5.1, respectively, for the SC electrode and 0.218 and 8.4, respectively, for the PC electrode, obtained by image analysis and CFD simulation⁵¹ on the reconstructed 3D data with the real CBD superimposed using the previously developed technique⁹ (Fig. S11, ESI†). The PC electrode has a larger tortuosity given the similar porosity with the SC electrode is attributed to the less percolated pore network. A complete list of the modelling parameters can be found in Table S3 (ESI†).

Fig. 8 Comparing the discharge rate performance of the SC and PC NMC811 electrodes by a combined analysis of experiment and modelling. (a) and (b) Discharge curves at incremental C-rates using coin cell (half-cell vs. lithium) for the SC and PC electrode, respectively, with the dashed black lines indicating the predicted performance by microstructure-resolved modelling; (c) and (d) SoL (e) and (f) C_ey (g) and (h) J_ct distribution at 65% DoD, 3C discharge for SC and PC electrode respectively; (i) and (j) actual C-rate of individual particles (C_p, symbols) shown alongside the volume fraction of the NMC particles (lines) across the electrode thickness. The symbol size is proportional to the actual particle size and the colour map represents the difference of the C_p with the maximum C-rate calculated without LST limitation (C_t). Grey symbols represent those particles with C_t larger than C_p; (k) simulated performance of the PC electrode with reversed current flow direction (RPC), with the black dashed line showing the performance of the original electrode for comparison; (i) and (n) SoL, C_ey and J_ct of the RPC electrode; (o) the C_p and particle volume fraction distribution of the RPC electrode.

The microstructure-resolved model is a valuable tool in the interpretation of the experimental results by resolving the distribution of the electrochemical state variables. Fig. 8c and d graphically compare the SoL of the SC and PC electrodes at 65% DoD at a discharge rate of 3C. As expected, the SC electrode exhibits a higher degree of lithiation in the small particles in contrast to the PC electrode, in which large particles are underutilized. The cracked secondary particles are treated as electrically connected to the composite matrix, whereas a fraction of those isolated fragmented primary particles (not connected to any neighbours) arising from the calendering, whose sizes are smaller than 1.5 μm, are treated as ‘dead’ particles. The cracked secondary particles are observed to have improved rate capability (indicated by the black arrow in Fig. 8d) compared to neighbouring intact particles of the same size. Similar to the results for monodisperse electrodes (see Section 3.3), a more remarkable SoL gradient along the electrode thickness is observed in the SC electrode due to the dominant role of LST, whereas PC particles display SoL saturation at the outer surface of the particle, extending from the separator to approx. 50% of the electrode thickness. Fig. 8e and f compare the C_ey distribution. Both electrodes show an evident C_ey gradient at 3C. Particularly, a significant drop in concentration is observed at the bottom region of the PC electrode, consistent with the less lithiated particles at the bottom in Fig. 8d. This drastic drop is related to the high local volume fraction of the particles that hinder the LST (evidence is shown later).

Fig. 8g and h compare the charge transfer current density J_ct at the electrode/electrolyte interface. It is seen that the SC electrode has a much more uniform J_ct distribution than the PC electrode as a consequence of the narrow PSD, which results in an extended surface area. In fact, small-sized SCs yield a specific surface area of 1.23 × 10³ mm⁻¹ in contrast to 0.56 × 10³ mm⁻¹ for the PC electrode, therefore the average J_ct per particle is significantly lower in the SC electrode. Note that J_ct in the upper half of the electrode is higher than at the bottom of the SC electrode, which is consistent with the observation in Fig. 5b due to the enhancement of reaction kinetics by C_ey. However, in Fig. 8h the highest J_ct is predominantly at the surface of large particles in the PC electrode where the surface concentration of lithium is less saturated compared to the small particles, as can be correlated with Fig. 8d. Fig. 8i and j show the effective C-rate of individual particles (C_p), calculated by dividing the mean J_ct of each particle by the reference J_ct value (total current at 1C divided by the total surface area) according to their J_ct across the entire thickness of the electrode. The sizes of the symbols are proportional to the particle diameter. The grey symbols represent the particles with C_p smaller than C_t, meaning a thorough lithiation of the particle without polarization from SST, whereas the colour-coded particles stand for the condition where C_p is larger than C_t, with the colour legend indicating the difference of the two C-rates (C_diff). It is convenient to identify the distinct spatial reaction kinetics between the two electrodes: the smallest particles in the PC electrode are preferentially lithiated until saturation, as evidenced by the grey symbols at the C_p level of 0 (inactive), whereas almost none of the particles in the SC electrode is fully lithiated. This is because the reactivity difference between the particles in the SC electrode is much smaller than those in the PC electrode due to the distinct difference of the particle size and thus the SST limits; larger particles have higher C_p than smaller ones at each depth of the electrode for both cases. This mechanism was also well explained in the context of Fig. 6c. Moreover, a gradient of C_diff is noticed from the separator to the current collector in the SC electrode, whereas it is flat for most of the particles in the PC electrode. This substantiates the fact that the rate performance of the SC electrode is mainly determined by reaction kinetics, which heavily relies on LST (C_ey). In contrast, despite a broad PSD, the high rate performance of the PC electrode is predominantly governed by SST, as is evident due to a much larger C_diff compared to the SC electrode. This implies that from the perspective of material design, high porosity and low thickness should be targeted only for the SC electrode. These are not conducive to the rate performance of the PC electrode, but will significantly undermine the areal and volumetric energy density.

The volume fraction of NMC particles at each depth is plotted above the symbols. The SC electrode displays a plateau at approx. 62.5% within the first 60% of the electrode thickness, then drops by 5% towards the current collector. However, this trend is reversed in the PC electrode, in which the NMC content macroscopically increases with depth despite the local fluctuations. Moreover, larger particles (>10 μm) are found to locate preferentially at the bottom half of the PC electrode (Fig. S12, ESI†). This microstructure inhomogeneity is speculated to arise from either the slurry mixing step or the drying speed of the electrode coating, both of which may lead to uneven distribution of the binder^17,52,53 and thereby the particles. The SC electrode is less susceptible to this process due to the more uniform PSD and less gravimetric force.

To investigate the effect of uneven distribution of NMC volume fraction and particle size, electrochemical simulation is conducted on the PC electrode with a reversed current flow direction (i.e., reversed PC electrode, RPC) and the discharge rate performance is shown in Fig. 8k by colour-coded dashed lines, with the performance of the original electrode added for comparison from 1C to 3C (black dashed lines). It is found that the rate performance of the two electrodes is identical until 2C, where inferior performance of the RPC electrode is noticeable and becomes significant at 3C. This proves that advanced design approaches could provide extra improvement of the rate performance particularly at high C-rates, given the same mass loading. The SoL distribution (Fig. 8l) shows that the RPC electrode is less lithiated in the central one-third region of the electrode, which can be explained by the approx. 20% difference of particle volume fraction between the two electrodes in the vicinity of the separator, i.e., the charge transfer is more localized in the RPC electrode. Moreover, such high particle localization yields a large LST resistance, evidenced by a sharp drop of the C_ey from 1500 mol m⁻³ to 750 mol m⁻³ (indicated by the black arrow in Fig. 8m), while it is much smoother at the corresponding depth in the PC electrode in Fig. 8f. It is noted that C_ey in the final one-third region of the RPC electrode is higher than that in the PC electrode, which is also due to the 20% lower NMC volume fraction and thus improved LST. However, the rate performance of the RPC electrode benefits little from the particles in the lower part of the electrode; Fig. 8n spatially visualizes the J_ct distribution of the RPC electrode and Fig. 8o quantitatively manifests that the charge transfer mainly takes place in the vicinity of the separator, where a high density of large particles locate and consequently the electrode experiences large polarization owing to the C_diff in this area. Compared to the RPC electrode, the large particles at the bottom of the PC electrode are more active (black dashed circle in Fig. 8j). Considering the better rate performance in the PC electrode, this proves that SST outweighs the reaction kinetics in determining the rate performance as it is more beneficial to have the same number of large particles intercalated in a low C_ey environment at the current collector rather than to place them in the vicinity of the separator where they cannot fully utilize the fast reaction kinetics. However, it will significantly enhance the rate performance if a high volume fraction of small NMC particles is distributed close to the separator.

As a closing remark, the authors believe hierarchical microstructural design from single particle to electrode scale can substantially improve the discharge rate performance in high energy density automotive batteries. SC NMC particle shows low SST resistance due to size effect which however inevitably leads to severe parasitic side reactions and safety concerns. Its high structural integrity is favourable for extended cycle life. In contrast, the PC NMC particle suffers from a decay of SST capability over long-term cycling or high voltage application due to the formation of intra-particle cracks, particularly for Ni-rich NMC particles. The design of double-layer particle with gradient transition metal concentration is one of the promising candidates for the next-generation automotive battery as the radial primary particles not only minimize the internal stress/strain mismatch but also suppress lithium saturation at particle surface, which is conducive to faster reaction kinetics. It can be regarded as a design hybridizing the advantage of SC and PC particle respectively. A secondary particle with pure radially-aligned primary particles improves the rate performance and structure integrity further compared to the double-layer design at the cost of energy density due to the absence of a Ni-rich core.⁵⁴ At the electrode level, porosity and thickness are more influential for electrodes with small particles as only a fraction of the electrode close to the separator is affected by the SST, in contrast to that with large particles. Building on this knowledge, an electrode with layered particle size distribution is proved to further enhance the rate performance without sacrificing the gravimetric energy density. For stationary energy storage, a mixture of small and large particles based on the layered structure would be beneficial for packing density and thus the volumetric energy density. The observed spatial dynamics of self-balancing mechanism informs that smart drive cycles such as multistage constant current discharge can be implemented via BMS control. It is also necessary to point out that the insights and design strategy obtained from this study, particularly the SST and LST-dominance, can be easily transferred to other battery chemistries such as sodium-ion batteries (NaBs)⁵⁵ and all solid-state batteries (ASSBs).⁵⁶ The former is regarded as an important alternative to LiB due to the low cost and element abundancy.⁵⁷ It is similar to LiB in the electrode structure (layered metal oxide cathode and hard carbon anode, although other options are available too), separator and electrolyte, and the multiscale microstructural design is also crucial due to the large diameter of sodium ion. For the ASSBs, the transport percolation in the ion and electron-conducting phases can be significantly improved via architecture tuning and volume fraction refinement between the active material, conductive carbon and solid electrolyte. Moreover, the morphological evolution both at the electrode/electrolyte interface⁵⁸ (e.g., wetting, voids, etc.) and within the solid state electrolyte⁵⁹ (cracks) under high rate operating conditions can be captured in operando and modelled to assist the material optimization.

4. Conclusions

This study has elucidated a microstructural design and optimization strategy to improve the discharge rate performance of lithium-ion battery electrodes across multiple length scales, ranging from the arrangement of primary particles, the role of internal/surface cracks and surface roughness, to the competing transport properties in the particles and electrolyte at the electrode level. It is found that the random orientation of the primary particles in a PC NMC electrode not only incurs heterogeneous lithiation but also leads to an increased tortuosity for solid-state diffusion (2.35 measured at 5C). Independent of particle size, SC particles do not show improved diffusivity compared to PC particles due to the planar intercalation propensity. Double-layered secondary particles manifest a significant advantage in rate performance, implying that the outer layer of the secondary particle plays a dominant role in determining the SST resistance, which also explains why secondary particles with surface cracks show superior rated capacity. However, internal cracks increase the SST resistance (by a factor of 1.27). Surface roughness is found to have little impact on the rate performance at the particle level.

At the electrode level, the SST-controlling depth is quantified and it suggests that the porosity and thickness are more influential for an electrode with small particles as only a fraction of the electrode close to the separator is affected by the SST, in contrast to that with large particles, which is governed by SST throughout the thickness. Rational operating windows are proposed to maximize the power and energy performance for different electrode geometries. By investigating the spatial dynamics of the electrochemical reaction, a self-balancing mechanism by means of shuffling of the reaction front in the electrode is observed, which could provide valuable insights into the development of fast discharging protocols and BMS control to suppress polarization and degradation for electrodes with different geometries. Building on this knowledge, an electrode with layered particle size distribution is proved to further enhance the rate performance without sacrificing the gravimetric energy density. For stationary energy storage, a mixture of small and large particles based on the layered structure would be beneficial for packing density and thus the volumetric energy density.

The commercial SC NMC811 electrode studied in this work is superior to the PC counterpart in rate performance due to the smaller particle size. The SC electrode shows 18% capacity decay at 2C discharge, in contrast to 30% for the PC electrode, even though the intrinsic solid-state diffusivity of the SC electrode is lower. Microstructure-resolved modelling reveals significant heterogeneities in lithiation, reactivity and polarization in the PC electrode, in which large particles are overloaded after the saturation of small particles. It is proved that the thickness and porosity should be the design parameters for the SC electrode rather than the PC, in which a gradient particle fraction and size distribution are recommended so that the fast reaction kinetics can be fully utilized in the vicinity of the separator (with small-sized particles) in order to ameliorate polarization arising from particle surface saturation.

Author contributions

X. L. and P. R. S. conceived the study. X. L., S. R. D., C. T., K. B. O. and E. K. conducted the electrochemical cycling and GITT test. X. Z. wrote the python code and helped the image analysis. X. L., M. L. and A. B. conducted the modelling. X. L. and T. MM. H conducted the X-ray CT scans. H. G. J. helped with the FIB-SEM data acquisition. X. L. drafted the manuscript. X. L., X. Z., S. R. D., C. T., K. B. O., A. B., M. L., T. MM. H., H. G. J., G. H., J. P., E. K., D. JR. B. and P. R. S. reviewed the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the Engineering and Physical Sciences Research Council [EP/R020973/1, EP/M028100/1]; and the Faraday Institution (Faraday.ac.uk; EP/S003053/1, grant numbers FIRG003, FIRG001 and FIRG015). P. R. S. acknowledges funding from the Royal Academy of Engineering (CiET1718\59). X. L., J. P. and G. H. acknowledge support from the National Measurement System of the UK Department of Business, Energy and Industrial Strategy. A. B. and M. L. acknowledge support from the Università di Pisa under the “PRA–Progetti di Ricerca di Ateneo” (Institutional Research Grants)–Project no. PRA_2020-2021_48.

References

1. Y. Hua, S. Zhou, H. Cui, X. Liu, C. Zhang, X. Xu, H. Ling and S. Yang, Int. J. Energy Res., 2020, 44, 11059–11087.
2. B. Y. Liaw and M. Dubarry, J. Power Sources, 2007, 174, 76–88.
3. M. N. Ates, S. Mukerjee and K. M. Abraham, RSC Adv., 2015, 5, 27375–27386.
4. Y. Su, G. Chen, L. Chen, Y. Lu, Q. Zhang, Z. Lv, C. Li, L. Li, N. Liu, G. Tan, L. Bao, S. Chen and F. Wu, ACS Appl. Mater. Interfaces, 2019, 11, 36697–36704.
5. X.-G. Yang, G. Zhang, S. Ge and C.-Y. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7266.
6. P. Arora, M. Doyle and R. E. White, J. Electrochem. Soc., 1999, 146, 3543–3553.
7. K. G. Gallagher, S. E. Trask, C. Bauer, T. Woehrle, S. F. Lux, M. Tschech, P. Lamp, B. J. Polzin, S. Ha, B. Long, Q. Wu, W. Lu, D. W. Dees and A. N. Jansen, J. Electrochem. Soc., 2015, 163, A138–A149.
8. D. P. Finegan, A. Quinn, D. S. Wragg, A. M. Colclasure, X. Lu, C. Tan, T. M. M. Heenan, R. Jervis, D. J. L. Brett, S. Das, T. Gao, D. A. Cogswell, M. Z. Bazant, M. Di Michiel, S. Checchia, P. R. Shearing and K. Smith, Energy Environ. Sci., 2020, 13, 2570–2584.
9. X. Lu, A. Bertei, D. P. Finegan, C. Tan, S. R. Daemi, J. S. Weaving, K. B. O’Regan, T. M. M. Heenan, G. Hinds, E. Kendrick, D. J. L. Brett and P. R. Shearing, Nat. Commun., 2020, 11, 2079.
10. W. Deng, W. Shi, Q. Liu, J. Jiang, X. Li and X. Feng, ACS Sustainable Chem. Eng., 2020, 8, 17062–17068.
11. C. Huang and P. S. Grant, J. Mater. Chem. A, 2018, 6, 14689–14699.
12. Y.-H. Zhu, X.-Y. Yang, T. Liu and X.-B. Zhang, Adv. Mater., 2020, 32, 1901961.
13. W. Li, S. Lee and A. Manthiram, Adv. Mater., 2020, 32, 2002718.
14. C. Xu, K. Märker, J. Lee, A. Mahadevegowda, P. J. Reeves, S. J. Day, M. F. Groh, S. P. Emge, C. Ducati, B. Layla Mehdi, C. C. Tang and C. P. Grey, Nat. Mater., 2021, 20, 84–92.
15. T. M. M. Heenan, A. Wade, C. Tan, J. E. Parker, D. Matras, A. S. Leach, J. B. Robinson, A. Llewellyn, A. Dimitrijevic, R. Jervis, P. D. Quinn, D. J. L. Brett and P. R. Shearing, Adv. Energy Mater., 2020, 10, 2002655.
16. K. Smith and C.-Y. Wang, J. Power Sources, 2006, 161, 628–639.
17. X. Lu, S. R. Daemi, A. Bertei, M. D. R. Kok, K. B. O’Regan, L. Rasha, J. Park, G. Hinds, E. Kendrick, D. J. L. Brett and P. R. Shearing, Joule, 2020, 4, 2746–2768.
18. Y. Wang and G. Cao, Adv. Mater., 2008, 20, 2251–2269.
19. J. Hassoun, G. Derrien, S. Panero and B. Scrosati, Adv. Mater., 2008, 20, 3169–3175.
20. D. Liu and G. Cao, Energy Environ. Sci., 2010, 3, 1218–1237.
21. S. Nowak and M. Winter, J. Electrochem. Soc., 2015, 162, A2500–A2508.
22. G. Sikha, B. N. Popov and R. E. White, J. Electrochem. Soc., 2004, 151, A1104.
23. M. M. Forouzan, B. A. Mazzeo and D. R. Wheeler, J. Electrochem. Soc., 2018, 165, A2127–A2144.
24. D. P. Finegan, E. Darcy, M. Keyser, B. Tjaden, T. M. M. Heenan, R. Jervis, J. J. Bailey, N. T. Vo, O. V. Magdysyuk, M. Drakopoulos, M. Di Michiel, A. Rack, G. Hinds, D. J. L. Brett and P. R. Shearing, Adv. Sci., 2018, 5, 1700369.
25. S. He, J. Zeng, B. T. Habte and F. Jiang, Sci. Bull., 2016, 61, 656–664.
26. R. Chowdhury, A. Banerjee, Y. Zhao, X. Liu and N. Brandon, Sustainable Energy Fuels, 2021, 5, 1103–1119.
27. U.-H. Kim, E.-J. Lee, C. S. Yoon, S.-T. Myung and Y.-K. Sun, Adv. Energy Mater., 2016, 6, 1601417.
28. D.-W. Chung, P. R. Shearing, N. P. Brandon, S. J. Harris and R. E. García, J. Electrochem. Soc., 2014, 161, A422–A430.
29. W. Weppner and R. A. Huggins, J. Electrochem. Soc., 1977, 124, 1569–1578.
30. C.-H. Chen, F. Brosa Planella, K. O’Regan, D. Gastol, W. D. Widanage and E. Kendrick, J. Electrochem. Soc., 2020, 167, 080534.
31. J. J. Bailey, T. M. M. Heenan, D. P. Finegan, X. Lu, S. R. Daemi, F. Iacoviello, N. R. Backeberg, O. O. Taiwo, D. J. L. Brett, A. Atkinson and P. R. Shearing, J. Microsc., 2017, 267, 384–396.
32. R. Schurch, S. M. Rowland, R. S. Bradley and P. J. Withers, IEEE Trans. Dielectr. Electr. Insul., 2014, 21, 53–63.
33. S. Singh, M. K. Kalra, J. Hsieh, P. E. Licato, S. Do, H. H. Pien and M. A. Blake, Radiology, 2010, 257, 373–383.
34. K. H. Höhne and W. A. Hanson, J. Comput. Assist. Tomogr., 1992, 16, 285–294.
35. J. T. Gostick, Z. A. Khan, T. G. Tranter, M. D. Kok, M. Agnaou, M. Sadeghi and R. J. J. O. O. S. S. Jervis, J. Open Source Softw., 2019, 4, 1296.
36. J. T. J. P. R. E. Gostick, Phys. Rev. E, 2017, 96, 023307.
37. L. Cai and R. E. White, J. Power Sources, 2011, 196, 5985–5989.
38. M. Doyle, T. F. Fuller and J. J. J. O. T. E. S. Newman, J. Electrochem. Soc., 1993, 140, 1526.
39. W. Lai and F. Ciucci, Electrochim. Acta, 2011, 56, 4369–4377.
40. Y.-c. K. Chen-Wiegart, Z. Liu, K. T. Faber, S. A. Barnett and J. Wang, Electrochem. Commun., 2013, 28, 127–130.
41. S. R. Daemi, C. Tan, A. Vamvakeros, T. M. M. Heenan, D. P. Finegan, M. Di Michiel, A. M. Beale, J. Cookson, E. Petrucco, J. S. Weaving, S. Jacques, R. Jervis, D. J. L. Brett and P. R. Shearing, Phys. Chem. Chem. Phys., 2020, 22, 17814–17823.
42. P. Yan, J. Zheng, M. Gu, J. Xiao, J.-G. Zhang and C.-M. Wang, Nat. Commun., 2017, 8, 14101.
43. Y.-K. Sun, S.-T. Myung, B.-C. Park, J. Prakash, I. Belharouak and K. Amine, Nat. Mater., 2009, 8, 320–324.
44. S. Yuan, Y.-H. Zhu, W. Li, S. Wang, D. Xu, L. Li, Y. Zhang and X.-B. Zhang, Adv. Mater., 2017, 29, 1602469.
45. M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533.
46. S.-K. Jung, H. Gwon, J. Hong, K.-Y. Park, D.-H. Seo, H. Kim, J. Hyun, W. Yang and K. Kang, Adv. Energy Mater., 2014, 4, 1300787.
47. X. Han, L. Lu, Y. Zheng, X. Feng, Z. Li, J. Li and M. Ouyang, eTransportation, 2019, 1, 100005.
48. M. M. Kabir and D. E. Demirocak, Int. J. Energy Res., 2017, 41, 1963–1986.
49. C. Liu and L. Liu, ECS Trans., 2015, 69, 5–15.
50. Z. An, L. Jia, Y. Ding, C. Dang and X. Li, J. Therm. Sci., 2017, 26, 391–412.
51. S. J. Cooper, A. Bertei, P. R. Shearing, J. A. Kilner and N. P. Brandon, SoftwareX, 2016, 5, 203–210.
52. M. Müller, L. Pfaffmann, S. Jaiser, M. Baunach, V. Trouillet, F. Scheiba, P. Scharfer, W. Schabel and W. J. J. O. P. S. Bauer, J. Power Sources, 2017, 340, 1–5.
53. C.-C. Li and Y.-W. Wang, J. Power Sources, 2013, 227, 204–210.
54. G.-T. Park, N.-Y. Park, T.-C. Noh, B. Namkoong, H.-H. Ryu, J.-Y. Shin, T. Beierling, C. S. Yoon and Y.-K. Sun, Energy Environ. Sci., 2021, 14, 5084–5095.
55. S. Yuan, Y.-B. Liu, D. Xu, D.-L. Ma, S. Wang, X.-H. Yang, Z.-Y. Cao and X.-B. Zhang, Adv. Sci., 2015, 2, 1400018.
56. A. Bielefeld, D. A. Weber and J. Janek, J. Phys. Chem. C, 2019, 123, 1626–1634.
57. S. Wang and X.-B. Zhang, Adv. Mater., 2019, 31, 1805432.
58. J. Wang, G. Huang and X.-B. Zhang, Batteries Supercaps, 2020, 3, 1006–1015.
59. Z. Ning, D. S. Jolly, G. Li, R. De Meyere, S. D. Pu, Y. Chen, J. Kasemchainan, J. Ihli, C. Gong, B. Liu, D. L. R. Melvin, A. Bonnin, O. Magdysyuk, P. Adamson, G. O. Hartley, C. W. Monroe, T. J. Marrow and P. G. Bruce, Nat. Mater., 2021, 20, 1121–1129.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee01388b

---