Organic solar cells with near-unity charge generation yield

Abstract

The subtle link between photogenerated charge generation yield (CGY) and bimolecular recombination in organic semiconductor-based photovoltaics is relatively well established as a concept but has proven extremely challenging to demonstrate and probe especially under operational conditions. Received wisdom also teaches that charge generation in excitonic systems will always be lower than non-excitonic semiconductors such as GaAs – but this view is being challenged with the advent of organic semiconductor blends based upon non-fullerene acceptors (NFAs) with power conversion efficiencies exceeding 18%. Using a newly developed approach based upon temperature dependent ultra-sensitive external quantum efficiency measurements, we observe near unity CGY in several model NFA-based systems measured with unprecedented accuracy. We find that a relatively small increase in yield from 0.984 to 0.993 leads to a reduction in bimolecular recombination from 400 times to 1000 times relative to the Langevin limit. In turn, this dramatic reduction delivers the best thick junction performance to date in any binary organic solar cell – notably 16.2% at 300 nm. The combination of high efficiency and thick junction is the key for industrial fabrication of these devices via high-throughput deposition processing such as roll-to-roll, and thus central to a viable solar cell technology. These results also clearly reveal and elucidate the relationship between photo-generation and recombination in excitonic semiconductor photovoltaics thus providing an important bridge between basic device physics and practical cell engineering.

---

Broader context

Organic solar cells (OSCs) hold the promise of low-cost, lightweight, flexible solar energy conversion technology, and in which have been attracting considerable research interest in the last 20 years. They are excitonic devices and as such photons absorbed result in strongly bound hole–electron pairs, which need to be separated into free carriers in order to produce power. Consequently, the charge generation process in OSCs is a multi-step process and the associated charge generation yield (CGY) has been historically considered to be low and inferior to inorganic photovoltaic semiconductors such as silicon. In this work, by utilizing ultra-sensitive, temperature dependent external quantum efficiency measurements, we advance a novel approach to accurately study the CGY in OSCs. We reveal that it is possible to achieve near-unity CGY in solar cells based on organic semiconductors. Specifically, the state-of-art polymer: non-fullerene-blend system, based on PM6:Y6, achieves a near-unity CGY of 98.4%. This value can be further increased to 99.3% by changing the non-fullerene acceptor to the Y6 derivate BTP-eC9. We also found that this small difference in CGY has a major impact on free carrier recombination which in turn has a big impact on performance in industrially relevant thick junction cells. Our observations are further validated using device simulations, validating the underlying mechanism and demonstrating a landmark >16% power conversion efficiency achieved in a 300 nm junction binary organic solar cell.

Introduction

The performance of organic solar cells (OSCs) has steadily improved in the past two decades but very recently there has been a sharp increase in power conversion efficiencies (PCE). This has been driven by radical improvements in the constituent materials properties via the development of new non-fullerene electron acceptors (NFAs) – the n-type component.¹ Throughout the history of OSCs, one of the most significant factors limiting the PCE of bulk heterojunction cells (BHJs – the dominant and highest performing architecture) has been large photocurrent and photovoltage losses. These losses are associated with incomplete charge generation and the excitonic nature of organic semiconductors, compared to other semiconductors used in photovoltaics such as perovskites, GaAs and silicon in which charges can be generated with near-unity probability once a photon is absorbed.² Due to the low dielectric constant in organic semiconductors, photogenerated electron–hole pairs (excitons) remain strongly Coulombically bound at room temperature. For excitons to efficiently dissociate, electron donor:acceptor interfaces are required in a BHJ interconnected network. Free charge carriers can be subsequently generated at the interfaces and collected at the corresponding electrodes generating a photocurrent.³ According to a former and rather historic picture driven by the use of fullerene-based electron acceptors, efficient charge generation requires a driving force for exciton dissociation, which is generally believed to be provided by the energy difference between the charge transfer (CT) state and the photoexcited exciton (S1) state: ΔE_CT = E_S1 − E_CT1.^4,5 Consequently, the prevailing wisdom is that an energy offset of about 0.3 eV is required to drive the charge generation process.⁶ However, the existence of this driving force also creates a problematic trade-off between the short-circuit current (J_sc) and open-circuit voltage (V_oc), which inevitably reduces the maximum PCE for OSCs.^7,8

In several recent high-efficiency organic solar cells based on NFAs, in particular the new “Y6” series, efficient charge generation at low energy offsets has been reported.⁹ This means that even though the energetic offset between the donor and acceptor is smaller than 0.3 eV (but still larger than 0.1 eV^10,11), highly efficient solar cells can be created. Combined with the complementary light absorption of donor and NFA semiconductor materials, the smaller energetic offset allows for an increase of J_sc and V_oc simultaneously^12,13 which ultimately provides for PCEs exceeding 18%.^14–16 These new findings are extremely promising for OSCs technologically and have also encouraged further fundamental work on the dynamics of charge generation.^17–19 This new insight into NFA-based OSCs^20–22 has raised important, and potentially field re-defining questions such as: what is the maximum charge generation yield that can be realized in organic semiconductor photovoltaics; is a driving force for efficient charge generation always required; and what role do charge generation kinetics play in determining the charge carrier recombination and device performance?

Even though PCEs as high as 18% have been realized, 20% in sight, and a benchmark 25% optimistically predicted,¹ several limitations still hold back OSCs from industrial-scale production with one important limitation being intolerance of the PCE to increasing the thickness of the active layer. As a general rule OSC performance in most systems is optimized at active layer thicknesses of around 100 nm – increasing the thickness of the active layer predominantly results in a dramatic loss of fill factor (FFs) and PCE due to relatively poor free carrier transport. However, thin active layer thicknesses are challenging for large-scale production (via high throughput, low-cost methods such as roll-to-roll) and generally also suffer from photocurrent losses due to incomplete above-gap absorption. As such, significant recent efforts have been expended to identify high performance OSC systems that can tolerate thick active layers (300 nm and above).^23,24 Several such systems have been identified, all of which exhibit a common feature of strongly reduced second order (bimolecular) recombination relative to the Langevin limit.^25–27 In this regard, reduction factors as large as 2000 times have been reported for fullerene-based systems,²³ but they unfortunately suffer from large photovoltage losses and relatively low short-circuit currents. The obvious question arises as to whether any low-offset, low-loss NFA-based systems exhibit similarly high reduction factors. To address this question, one must appreciate the subtle relationship between the efficiency of charge photo-generation and bimolecular recombination – as the former approaches unity, the latter should in principle reduce considerably. This important link, although historically appreciated, has been difficult to probe and fully understand, especially under operationally relevant, steady state conditions.

Motivated by these considerations and challenges, in this work we investigate the charge generation quantum yield (CGY) of several NFA-based organic solar cells using a new approach involving a kinetic model applied to temperature-dependent, ultra-sensitive external quantum efficiency measurements. The results reveal for the first time, that it is possible to achieve near-unity charge generation quantum yields and realize fully Shockley-type solar cells with organic semiconductors by utilizing state-of-the-art NFA materials. In particular, we show that for PM6:BTP-eC9 (see ESI† for molecular definitions), the charge generation efficiency can be as high as 99.3%. In addition to the energetics, which have been the subject of several recent and important studies,^17–22 we also show the central role of kinetics in charge generation. Our results reveal that charge generation in this system involves an energetic barrier which is several times larger than the thermal energy at room temperature (in accordance with previous reports on similar systems²⁸) yet is extremely efficient due to the faster dissociation rate of bound states to free charges compared with their decay rate. This means that even though the charge generation mechanism is energetically disadvantaged, it is kinetically driven.²⁹ The near-unity CGY of PM6:BTP-eC9 results in a reduction of the bimolecular recombination rate constant by more than 1000 times (relative to the Langevin limit) ultimately enabling organic solar cells with active thicknesses of approximately 300 nm to be realized with a maximum PCE of 16.2% and FF greater than 71%. Our control systems exhibit (considerably) smaller charge generation yields and hence are unable to achieve high efficiencies in the thick junction limit. The results for PM6:BTP-eC9 solar cells indicate that this system is suitable for lab-to-fab scaling and additionally, the presented approach provides a route for recognizing and developing other systems with similar potential. It is also a means to probe in accurate detail the link between generation and recombination in excitonic semiconductors.

Results and discussion

Four different polymeric donor:NFA systems PM6:Y6, PM6:BTP-eC9, PM6:ITIC, and PBDB-T:EH-IDTBR were employed to study their charge generation yields (see ESI† for molecular definitions). Fig. 1a shows the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy levels of the four blend systems PM6:Y6, PM6:BTP-eC9, PM6:ITIC and PBDB-T:EH-IDTBR obtained previously.^9,15,30,31 While the former three systems possess rather small HOMO–HOMO energy offsets of roughly ΔE_HOMO–HOMO = 0.1 eV, PBDB-T:EH-IDTBR has a relatively large offset of ΔE_HOMO–HOMO ≈ 0.3 eV. The current density versus voltage (J–V) characteristics along with the photovoltaic external quantum efficiency (EQE_PV) spectra of the corresponding optimized OSC BHJ devices are shown in Fig. 1b and c. Experimental details of device fabrication and measurements are provided in the ESI.† Despite the low energy offset, PM6:ITIC provides for a respectable photovoltaic performance of PCE = 9.2% (9.0 ± 0.2%) and maximum EQE_PV (66% at 680 nm), while superior PCEs of 15.7% (15.3 ± 0.4%) and 17.1% (16.7 ± 0.2%) were obtained for PM6:Y6 and PM6:BTP-eC9, respectively, both accompanied by EQE_PV of over 80% at around 780 nm, consistent with values published recently.^9,15 In contrast, PBDB-T:EH-IDBTR achieved a lower PCE of 5.9% (5.6 ± 0.3%) and maximum EQE_PV of 54% at 570 nm. The above results highlight the significance of both energetics (i.e., the energy offset ΔE_CT = E_S1 − E_CT1) and kinetics (the CT dissociation and decay rates) in the charge generation mechanism in light harvesting devices. Clearly there is not just a simple correlation between energetic offset and efficiency and so one is led to question as to what drives the relative performance in this small but diverse set of models.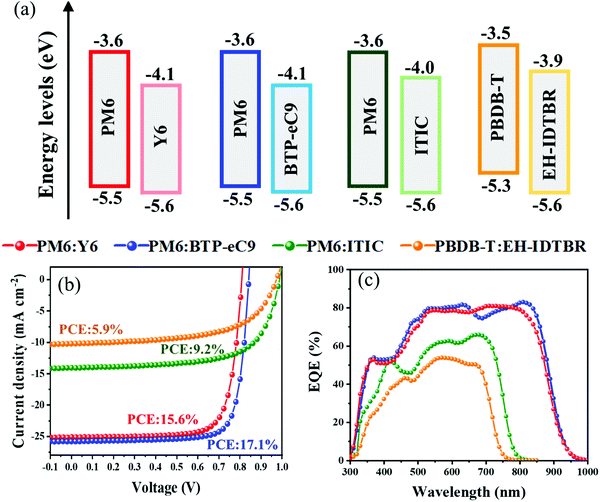

Fig. 1 Basic device characteristics of four different NFA-based organic solar cells. (a) Energy levels of polymer donors and non-fullerene acceptors reported from previous work,^9,15,30,31 (b) current density versus voltage (J–V) characteristics under artificial 1 sun AM 1.5G conditions, and (c) external quantum efficiency (EQE) of ∼100 nm PM6:Y6, PM6:BTP-eC9, PM6:ITIC, and PBDB-T:EH-IDTBR solar cells. Both panels (b) and (c) are for hero devices and full statistics on multiple devices are provided in the ESI.†

To clarify the charge generation quantum yield in the above four systems, we employed a new approach based upon temperature (T) dependent, ultra-sensitive EQE_PV measurements (Fig. S2, ESI†). In general, we have EQE_PV(T) = η_abs(T) × IQE(T), noting that the absorption probability of the active layer η_abs is temperature dependent. Here, IQE(T) denotes the internal quantum efficiency and is related to the charge generation yield via IQE(T) = η_CC × CGY(T) where η_CC is the charge collection efficiency. Since charge carrier recombination is expected to be small due to the low light intensities (at which the EQEs were probed), changes in η_CC with temperature are assumed to be negligible. Hence, to probe charge generation, we use a normalized IQE(T) given by Herein, as PM6, Y6, BTP-eC9, ITIC, PBDB-T, and EH-IDTBR exhibit appreciable absorption at a wavelength of 650 nm, the logarithm of IQE* of the four NFA-based systems (optimized full devices) at an excitation wavelength of λ_exc = 650 nm are shown in Fig. 2a, as a function of the inverse thermal energy (with k_B being the Boltzmann constant). The experimental data (symbols) are fitted to a kinetic model (solid lines) which accounts for the competition between thermally-activated dissociation [of rate constant k_d(T)] and recombination (with rate constant k_f) of bound electron–hole pairs: 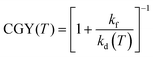.³² Here, , where k₀ corresponds to the rate k_d at infinite temperature and E_a is the activation energy of the charge dissociation. The uncertainties of our CGY calculations are shown in the ESI.†

Fig. 2 Temperature dependent ultra-sensitive measurements for probing charge generation in organic solar cells. (a) Logarithm of the normalized internal quantum efficiency (IQE*) of ∼100 nm thick PM6:BTP-eC9, PM6:Y6, PM6:ITIC and PBDB-T:EH-IDTBR solar cells. The experimental data are indicated by the symbols, while solid lines show the corresponding fit to the kinetic model of the charge generation yield (CGY). The excitation wavelength was set to 650 nm and no bias voltage was applied. (b) The extracted activation energies (E_a), (c) CGY (filled symbols), and (d) CT recombination probability (γ_CT) for PM6:BTP-eC9, PM6:Y6, PBDB-T:EH-IDTBR and PM6:ITIC based on the fits. For comparison, the corresponding EQE_PV (open symbols) at RT and 650 nm are included in (c).

From the fits, the activation energies of PM6:BTP-eC9 (E_a = 118 ± 10 meV), PM6:Y6 (E_a = 103 ± 6 meV), PBDB-T:EH-IDTBR (E_a = 45 ± 2 meV) and PM6:ITIC (E_a = 53 ± 4 meV) were determined (see Fig. 2b). Based on our analysis, all four BHJ systems exhibit a small, yet non-negligible energy barrier for charge generation, strongly suggesting these systems possess a kinetically driven CT state dissociation and thermally activated k_d rate at room temperature (RT) (i.e., E_a > 25 meV). The corresponding CGYs of the four OSCs at RT are shown in Fig. 2c. Relatively low CGYs of CGY = 0.633 ± 0.026 for PBDB-T:EH-IDTBR, and CGY = 0.857 ± 0.019 for PM6:ITIC were obtained, consistent with their modest EQE_PV of approximately 50% and 64% at 650 nm, respectively. Interestingly, while PM6:Y6 shows a very high charge generation yield of CGY = 0.984 ± 0.003 close to unity, this value increases even further to CGY = 0.993 ± 0.003 for the PM6:Y6 derivative PM6:BTP-eC9. Our new approach combining ultra-sensitive, temperature dependent and absorptance-corrected EQE measurements with a kinetic rate model, allows one to not only evaluate the CGY with very high accuracy, but also proves that near-unity charge generation quantum yields in excitonic organic solar cells are indeed possible.

Although all four OSC systems exhibit similar activation energies, a near-unity CGY was only obtained in PM6:Y6 and PM6:BTP-eC9 suggesting different CT state recombination kinetics. The corresponding recombination probability for CT states γ_CT = 1 − CGY, critically determined by the rate constant ratio k_f/k_d, is shown in Fig. 2d at RT. Indeed, while the PBDB-T:EH-IDTBR and PM6:ITIC devices showed a relatively high γ_CT of 0.37 ± 0.03 and 0.14 ± 0.02, we find γ_CT = 0.016 ± 0.03 for PM6:Y6 and an approximately two times smaller γ_CT = 0.007 ± 0.003 for PM6:BTP-eC9. The above findings demonstrate that both energetics and kinetics determine the CGY with the latter being the key factor underpinning the better device performance in PM6:BTP-eC9 and PM6:Y6. The low CT state recombination probabilities have direct implications for the bimolecular recombination coefficient β in PM6:Y6 and PM6:BTP-eC9. In this regard, the important figure-of-merit is the Langevin reduction factor γ = β/β_L, where β_L is the Langevin recombination coefficient given by β_L = q[μ_n + μ_p]/εε₀, with q being the elementary charge, μ_n (μ_p) the electron (hole) mobility and εε₀ the permittivity of the active layer. However, γ_CT is related to the Langevin-reduction factor via γ = γ_CT × γ_geo, where γ_geo = β_enc/β_L is the geometrical reduction factor with β_enc being the encounter rate coefficient for charge carriers to form CT states.³³ Therefore, we expect significantly reduced Langevin reduction factors in these two systems.

To verify this, we conducted charge transport and recombination measurements to estimate γ. Firstly, we applied resistance-dependent photovoltage (RPV) measurements at zero applied bias voltage to obtain the mobilities in PM6:Y6 and PM6:BTP-eC9 operational devices (Fig. S3 in the ESI†). For PM6:Y6, slower and faster charge carrier mobilities of μ_slow ≈ 2 × 10⁻⁴ cm² V⁻¹ s⁻¹ and μ_fast ≈ 1.2 × 10⁻³ cm² V⁻¹ s^-1 were extracted, respectively, whereas μ_slow ≈ 4 × 10⁻⁴ cm² V⁻¹ s⁻¹ and μ_fast ≈ 1.5 × 10⁻³ were found in PM6:BTP-eC9. We note that the mobility values obtained for PM6:Y6 are close to the ones estimated via space-charge-limited-current (SCLC) measurements by Shoaee and co-workers.^34,35 Subsequently, we assigned the faster carriers to electrons and the slower carriers to holes. Next, we quantified the corresponding β from steady-state double injection (DoI) currents. Based on the DoI measurements, we find γ ≈ 2.5 × 10⁻³ for PM6:Y6 and γ ≈ 10⁻³ for PM6:BTP-eC9, respectively, corresponding to 400 times and 1000 times reduced recombination relative to the Langevin limit. This confirms the presence of strongly reduced recombination coefficients in PM6:Y6 and PM6:BTP-eC9, as expected from the near-unity CGY. From γ and γ_CT, we further estimate geometrical Langevin-reduction factors of γ_geo ≈ 0.16 and γ_geo ≈ 0.13 for PM6:Y6 and PM6:BTP-eC9, respectively. These values are consistent with theoretically expected values for γ_geo,³⁶ verifying the accuracy of the obtained CGY values.

The strongly suppressed recombination (low γ), being a direct consequence of the near-unity CGY, is expected to translate into improved device performance in thick junctions. Concomitantly, PM6:Y6, PM6:BTP-eC9, PM6:ITIC and PBDB-T:EH-IDTBR devices were fabricated with different active layer thickness from 30 to 470 nm. The J–V curves and full statistics of photovoltaic parameters on multiple devices (minimum of 15) are shown in Fig. S4 and Tables S1–S4 in the ESI.†Fig. 3a and b show the corresponding FFs and PCEs at different active layer thicknesses. The PCE of PBDB-T:EH-IDTBR and PM6:ITIC systems drop off rapidly with increasing active layer thickness due to a significant reduction of both J_sc and FF, suggesting that enhanced carrier recombination (due to the increased thickness) severely limits the charge collection efficiency in these thick-junction devices. In contrast, PM6:Y6 shows a much less severe thickness dependency, with FF = 61.4%, J_sc = 26.8 mA cm⁻² and PCE = 13.1% for the hero device at a thickness of 300 ± 10 nm. However, although PM6:Y6 exhibits respectable device performance in thick junctions, a substantial degradation in efficiency is still observed when compared with the 100 nm thick junction. Finally, the best thickness dependent device performance is obtained for PM6:BTP-eC9 showing a hero PCE of 16.2%, together with an FF of 71.3%, in a 300 ± 10 nm thick junction. To the best of our knowledge, this ∼300 nm thick PM6:BTP-eC9 BHJ is the most efficient binary OSC at this active layer thickness, leaving PM6:BTP-eC9 as a promising candidate for lab-to-fab up-scaling. Importantly, since PM6:Y6 and PM6:BTP-eC9 systems have similar optical constants, energy levels, and energy losses (see Fig. S5 and S6 in the ESI†), their contrasting thick-junction performance further confirms the relation between CGY and efficiency of thick-junction OSCs. The thicknesses dependent EQE_PV of PM6:Y6 and PM6:BTP-eC9 (see Fig. S7 and S8 in the ESI†) reveal EQE_PV responses over 75% in the main absorption region (500 to 850 nm), with the integrated J_sc obtained from the EQE_PV being consistent with the measured J_sc under artificial 1 sun AM 1.5G conditions (less than 5% difference). This confirms the accuracy of calibration and measurement robustness.

Fig. 3 Thickness dependent device performance. (a) Fill factors (FFs) and (b) power conversion efficiencies (PCEs) of PM6:Y6, PM6:BTP-eC9, PM6:ITIC, and PBDB-T:EH-IDTBR OSCs plotted as a function of active layer thickness (average values for multiple devices with error bars representing standard deviations). FFs and PCEs were determined from current density versus voltage curves measured under artificial 1 sun AM 1.5G conditions.

To further confirm that the thickness dependent device performance is related to the suppressed recombination (and thus the near-unity CGY), we performed electro-optical device simulations for PM6:Y6 and PM6:BTP-eC9 devices, based on a drift-diffusion (DD) model.^37,38 An optical transfer-matrix model which accounts for optical interference effects in the device stack was used to calculate the generation profile within the active layer.^39,40 The measured refractive indices of PM6:Y6 and PM6:BTP-eC9 were used as input for the optical model (Fig. S5 in the ESI†). The resultant “charge generation” profiles under AM 1.5G were then imported to the DD simulations to calculate the corresponding J–V parameters. In Fig. 4, the experimentally measured (symbols) and simulated (solid lines) PV parameters are plotted as a function of active layer thickness. A good overall agreement between simulations and experimental data is obtained, validating the measured transport and recombination parameters. We note that a considerable deviation between experimental data and DD simulations is only seen for the thickest PM6:Y6 device (see Fig. 4a and b). A possible explanation for this deviation could be the presence of traps,⁴¹ which are expected to become increasingly important at larger thicknesses,⁴² or morphological non-uniformities due to different active layer drying rates after deposition.

Fig. 4 Electro-optical simulations of PM6:Y6 and PM6:BTP-eC9 solar cells. (a) Short-circuit current density (J_sc) and (b) power conversion efficiency (PCE) of PM6:Y6 and PM6:BTP-eC9 as a function of active layer thickness. The symbols are experimental data (averages with standard deviations as error bars), solid (dashed) lines correspond to drift-diffusion (optical transfer-matrix model) simulations. (c) Experimentally obtained Fill Factors (FFs) (symbols) of PM6:Y6 plotted as a function of active layer thickness and compared with DD simulations (solid lines) assuming different Langevin reduction factors. (d) Repetition of panel (c) but for PM6:BTP-eC9 OSCs. The input parameters for the simulations are provided in the ESI.†

Importantly, the enhanced performance of PM6:BTP-eC9, relative to PM6:Y6, is well-reproduced by the DD model confirming the lower recombination coefficient in PM6:BTP-eC9 to be the primary underlying reason for the relative improvement. Since γ ∝ 1 − CGY, the value of the Langevin reduction factor is very sensitive to small changes of CGY in systems where CGY ≈ 1. This also explains why the modest increase of only 0.9% in the CGY in PM6:BTP-eC9, relative to PM6:Y6, can result in noticeably smaller γ and subsequently considerably improved device performance in thicker junctions. For reference, the FF of PM6:Y6 and PM6:BTP-eC9 devices with different γ (and mobilities) were also simulated and are shown in Fig. 4c and d (and Fig. S10 in the ESI†). It is clear that both systems benefit more from reduced recombination enabling high efficiencies in thick junctions, whereas the degradation of the FF in thicker junctions is much more pronounced for larger recombination coefficients. It should be noted, however, that a high enough electron mobility is also vital to ensure balanced charge extraction in conventional thick OSC junctions (where charge carriers are predominantly generated near the transparent anode), as discussed in previous works.^43,44

Finally, we quantified the competition between charge extraction and recombination in PM6:Y6 and PM6:BTP-eC9 devices at different thicknesses using the modified Shockley model proposed by Neher et al.⁴⁵ The associated figure-of-merit α is given by:

where J_G is the photogeneration current density and d is the active layer thickness. In this context, if α < 1, the device is not limited by transport and referred to as Shockley-type. In Fig. 5a, the FFs of PM6:Y6 and PM6:BTP-eC9 at different thicknesses are shown as a function of α estimated from the measured charge transport and recombination parameters. Both systems exhibit with increasing active layer thickness a regime of Shockley-type behavior. This behavior is maintained up to active layer thicknesses of 109 nm and 200 nm for PM6:Y6 and PM6:BTP-eC9, respectively. For comparison, in Fig. 5a we have also included the analytical approximation for the FF as per the modified Shockley model (dashed line).⁴⁵ To further support the presence of Shockley-type behavior, we calculated the effective series resistance R_S,eff from the inverse slope of the J–V curve at V = V_oc, for cells of different junction thicknesses. 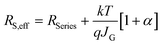Based on the modified Shockley equation,⁴⁵ we find , where R_series is the combined series resistance from the contacts, the electrodes, and the external wires. As shown in Fig. 5b, upon comparing R_S,eff from experimental data (symbols) with the analytical R_S,eff using the estimated α (solid lines), a good overall agreement is indeed obtained.

Fig. 5 Modified Shockley model for describing thickness dependence of FF. (a) Estimated Fill Factors (FFs) of PM6:Y6 and PM6:BTP-eC9 with different active layer thicknesses (symbols) plotted as a function of the figure-of-merit α. For comparison, an analytical approximation for the Fill Factor based on the modified Shockley model⁴⁵ is also shown as indicated by the dashed line. The vertical green line marks the transition from Shockley type (α < 1) to transport-limited (α > 1) solar cells. (b) Effective series resistances R_S,eff = [dJ(V_oc)/dV]⁻¹ extracted from the experimental J–V curves at different active layer thicknesses are shown (symbols). The corresponding analytical approximation based on the modified Shockley equation 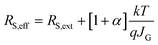is indicated by the solid lines; for comparison, the cases when α = 0 and α = 1 corresponding to the dashed and dotted lines, respectively, have been included for PM6:BTP-eC9.

From the above combined experimental and simulation results it is clear that the CGY of a thin film OSC is linked to both donor:acceptor interfacial energetics (energy offset and activation energy) and kinetics, inevitably reflected in the efficiency of the corresponding thick junction BHJ. Based on this framework it becomes clear that a 0.9% higher, near-unity CGY, translating into a ∼2.5 stronger suppressed recombination, leads to a drastic improvement in PM6:BTP-eC9 relative to PM6:Y6 not only in thin junction BHJs, but more importantly in the thick-junction limit. This subtle link between photo-generation and charge recombination provides a powerful tool to merge basic device physics and practical solar cell engineering, allowing for promising candidates for industrial large-area solar cell fabrication to be identified.

Conclusions

The charge generation dynamics of several state-of-art organic solar cells were investigated via a kinetic model based upon temperature dependent ultra-sensitive external quantum efficiency measurements. Near-unity charge generation quantum yields (0.993) were found in a recently reported high efficiency PM6:BTP-eC9 system, outperforming its PM6:Y6 (CGY = 0.984) counterpart and other non-fullerene solar cell models. This apparently small difference in the CGY makes these two systems very different in how they perform in the industrially-relevant thick junction limit. The presented results not only confirm it is possible to achieve near-unity charge generation quantum yields using organic semiconductors and to realize Shockley-type solar cells (i.e., not limited by charge transport), but also shows the importance of kinetics in charge generation in addition to the energetics. More significantly, PM6:BTP-eC9 was found to exhibit a faster dissociation of bound states to free charges compared to PM6:Y6, enabling a reduction of bimolecular recombination rate constant by more than 1000 times. As a result, an unprecedented power conversion efficiency over 16% with an FF greater than 71% was achieved in PM6:BTP-eC9 solar cells with an active layer thicknesses of approximately 300 nm. The above results not only reveal the interplay between charge generation, recombination, and device efficiency in novel state-of-art non-fullerene solar cells, but also present a route for recognizing and developing other systems with similar potential.

Experimental sections

Light and dark current density versus voltage (J–V) measurement

The current density versus voltage (J–V) curves of the devices (pixel area: 0.04 cm²) were measured through a shadow mask using an Ossila Solar Cell I–V Test System. The simulator was calibrated by a standard silicon reference cell certified by the National Renewable Energy Laboratory. Dark J–V curves were measured by a Keithley source-measure unit (model 2400). The values of the effective series resistances of devices were obtained from the Ossila Solar Cell I–V Test System which were calculated from the inverse of the gradient at the appropriate points of the J–V curve.

Electroluminescent external quantum efficiency (EQE_EL)

The electro-luminescent external quantum efficiency (EQE_EL) was measured using a HAMAMATSU EQE measurement system (C9920-12). An integrating sphere was used as the sample chamber to account for different radiation angles and absorption by the sample. A Keithley source-measure unit (model 2400) was used to drive the electroluminescence of the samples. A photonic multichannel analyzer was used to measure the spectral luminescence. The software (U6039-06 Version 4.0.1) for the spectral measurement and EQE_EL calculation was provided by HAMAMATSU.

Photovoltaic external quantum efficiency (EQE_PV)

The photovoltaic external quantum efficiency (EQE_PV) was measured between 300 nm and 1100 nm using a home-build EQE setup. Details of the EQE setup are provided elsewhere.^41,46 A liquid nitrogen-based, temperature-controlled sample holder (Linkam) was used for temperature dependent EQE_PV measurements.

Steady-state double-injection (DoI) currents

The Langevin reduction factor γ = β/β_L was quantified by steady-state double-injection (DoI) on operational PM6:Y6 and PM6:BTP-eC9 devices.³³ Here, β is the bimolecular recombination coefficient and is the Langevin coefficient, where ε is the dielectric constant of the active layer, ε₀ is the vacuum permittivity, and μ_n (μ_p) denotes the electron (hole) mobility. According to the theory of double injection in insulators, the space-charge-limited current (of electrons and holes) in forward-bias (V ≫ V_bi) is limited by the recombination of electrons and holes injected from the contacts (here, V is the applied voltage and V_bi the built-in voltage). For β ≫ β_L, the injected electrons and holes from the electrodes recombine as soon as they encounter each other in the active layer. In this limit, the total current J is given by the combined space charge limited currents from the separate electron- and hole-dominated regions:
where, V_dev is the applied voltage across the device and d is the thickness of the active layer. For β ≪ β_L, corresponding to the case when the recombination is reduced with respect to the Langevin rate, the electron and hole currents do not immediately annihilate each other upon meeting in space, resulting in the establishment of an injected electron–hole plasma in the bulk. In this case, the total current J is given by:
where
Finally, the externally applied voltage V is related to the device voltage via

V_dev = V − JR_seriesA

where R_series is the external series resistance and A is the device area. Neglecting the presence of an external series resistance (especially in thin devices) generally results in an underestimation of γ. Note that the DoI theory is only valid for V ≫ V_bi; therefore, to account for the presence of a built-in voltage, V is usually replaced by V − V_bi in the above relations for J_SCL and J_DI.

Resistance dependent photovoltage

For resistance dependent photovoltage measurements, the device under test (DUT) was in series with a variable load resistance. A diode pumped, Q-switched Nd:YAG laser (Viron, Quantel Laser) was used to create a short laser pulse, thus photo-generating charge carriers in the active layer of the DUT. An oscilloscope (Rhode & Schwarz, RTM 3004), in parallel to the DUT, was used to measure the photo-pulse induced photovoltage of the DUT. The load resistance was stepwise increased from 50 Ω to 1 MΩ. From the RPV transients and the corresponding transit times (t_tr) the charge carrier mobility was calculated via, where V_bi denotes the built-in voltage, V corresponds to the applied bias voltage and d is the thickness of the active layer.

Temperature dependent absorbance

A liquid nitrogen-based, temperature-controlled sample holder (Linkam) and a high-performance spectrophotometer Lambda 950 (PerkinElmer) in combination with an integrating sphere module were used to measure temperature dependent absorbance of films of interest on glass.

Electro-optical device simulations

For the simulations, a numerical drift-diffusion (DD) model was used to describe the electrical behavior of the device. The DD model solves the Poisson equation for the electrical potential and the continuity equations for electrons and holes inside the active layer. Furthermore, the electron and hole current densities are assumed to be given by the drift-diffusion (Nernst–Planck) relations. These equations are discretized using the Scharfetter–Gummel discretization scheme and solved iteratively using Gummel's method, allowing for the current density to be evaluated. The default input parameters for the simulations in Fig. 4 and Fig. S9 and S10 (ESI†) are listed in Table S6 (ESI†). The active layer is treated as an effective medium with the transport level of holes in donor and of electrons in the acceptor act as effective valence and conduction levels, respectively. These energy levels are separated by the (effective) electrical bandgap E_g,DA. Unless otherwise stated, the active layer is assumed trap-free and undoped, with the recombination within the bulk being bimolecular. The associated bimolecular recombination coefficient is given by β = γβ_L, where γ is the Langevin reduction factor and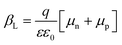 . Thermal equilibrium is assumed to prevail at the contacts. Further details about the model are provided in ref. 37. The photogeneration profile, used as input for the DD simulations, was obtained from an optical transfer-matrix (TMM) model which accounts for interference effects and reflection.⁴⁰ For the TMM model, a device stack consisting of glass/ITO(110 nm)/PEDOT:PSS(10 nm)/active layer/PDINO(10 nm)/Ag(100 nm) was used, where glass is treated as an incoherent layer in accordance with ref. 40. Based on the refractive indices and extinction coefficients of the different layers, the TMM model then evaluates the absorption profile inside the active layer, for incident photons described by the AM 1.5G solar spectrum.

Uncertainty calculations for charge generation quantum yield (CGY) and charge transfer (CT) recombination probability (γ_CT)

The uncertainty of the calculated parameters CGY and γ_CT were determined based upon error propagation. For the fittings, we take the logarithm of the normalized IQE(T) [IQE*(T) = CGY(T)/CGY(T_max)] and fit the data to the function , where A = −ln[CGY(T_max)] and B = k_f/k₀. From the fit function we obtain the parameters [errors] E_a [d(E_a)], B [d(B)] and A [d(A)]. At T = T_max, γ_CT = 1 − CGY; the corresponding uncertainties d(CGY(T_max)) and d(γ_CT) are then calculated via d(γ_CT) = |−d(CGY(T_max))| = d(CGY(T_max)) = CGY(T_max) × d(A).

The details of device fabrication can be found in the ESI.†

Author contributions

AA and PM provided the overall leadership of the project. WL fabricated the devices. WL and SZ performed most measurements. DBR performed electroluminescence measurements. OJS performed numerical simulations. WL and SZ analysed the data. WL, SZ, AA, and OSJ interpreted the results. All authors contributed to the interpretation of the data and preparation of the manuscript which was initially drafted by WL.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the Sêr Cymru II Program through the European Regional Development Fund, Welsh European Funding Office, and Swansea University strategic initiative in Sustainable Advanced Materials. A. A. is a Sêr Cymru II Rising Star Fellow and P. M. is a Sêr Cymru II National Research Chair. S. Z. is the recipient of an EPSRC Doctoral Training Partnership studentship. D.B.R. acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), [PGSD3-545694-2020]. This work was also funded by UKRI through the EPSRC Program Grant EP/T028511/1 Application Targeted Integrated Photovoltaics (ATIP).

References

1. A. Armin, W. Li, O. J. Sandberg, Z. Xiao, L. Ding, J. Nelson, D. Neher, K. Vandewal, S. Shoaee, T. Wang, H. Ade, T. Heumüler, C. Brabec and P. Meredith, Adv. Energy. Mater., 2021, 2003570.
2. Y. Xu, H. Yao, L. Ma, J. Wang and J. Hou, Rep. Prog. Phys., 2020, 83, 082601.
3. P. Meredith, W. Li and A. Armin, Adv. Energy Mater., 2020, 10, 2001788.
4. J. Benduhn, K. Tvingstedt, F. Piersimoni, S. Ullbrich, Y. Fan, M. Tropiano, K. A. Mcgarry, O. Zeika, M. K. Riede, C. J. Douglas, S. Barlow, S. R. Marder, D. Neher, D. Spoltore and K. Vandewal, Nat. Energy, 2017, 2, 1–6.
5. T. M. Burke, S. Sweetnam, K. Vandewal and M. D. McGehee, Adv. Energy Mater., 2015, 5, 1500123.
6. M. C. Scharber, D. Mülbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. J. Brabec, Adv. Mater., 2006, 18, 789–794.
7. M. Azzouzi, T. Kirchartz and J. Nelson, Trends Chem., 2019, 1, 49–62.
8. D. Qian, Z. Zeng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Ingan, V. Coropceanu, J. L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709.
9. J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H. L. Yip, T. K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Joule, 2019, 3, 1140–1151.
10. L. Perdig-Toro, L. Q. Phuong, S. Zeiske, K. Vandewal, A. Armin, S. Shoaee and D. Neher, ACS Energy Lett., 2021, 6, 557–564.
11. Y. Xie, W. Wang, W. Huang, F. Lin, T. Li, S. Liu, X. Zhan, Y. Liang, C. Gao, H. Wu and Y. Cao, Energy Environ. Sci., 2019, 12, 3556–3566.
12. J. Liu, S. Chen, D. Qian, B. Gautam, G. Yang, J. Zhao, J. Bergqvist, F. Zhang, W. Ma, H. Ade, O. Ingan, K. Gundogdu, F. Gao and H. Yan, Nat. Energy, 2016, 1, 1–7.
13. H. Fu, Y. Wang, D. meng, Z. Ma, Y. Li, F. Gao, Z. Wang and Y. Sun, ACS Energy Lett., 2018, 3, 2729–2735.
14. Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275.
15. Y. Cui, H. Yao, J. Zhang, K. Xian, T. Zhang, L. Hong, Y. Wang, Y. Xu, K. Ma, C. An, C. He, Z. Wei, F. Gao and J. Hou, Adv. Mater., 2020, 32, 1908205.
16. Y. Lin, M. I. Nugraha, Y. Firdaus, A. D. Scaccabarozzi, F. Ani, A. H. Emwas, E. Yengel, X. Zheng, J. Liu, W. Wahyudi, E. Yarali, H. Faber, O. M. Bakr, L. Tsetseris, M. Heeney and T. D. Anthopoulos, ACS Energy Lett., 2020, 5, 3663–3671.
17. A. Karki, J. Vollbrecht, A. J. Gillett, S. S. Xiao, Y. Yang, Z. Peng, N. Schopp, A. L. Dixon, S. Yoon, M. Schrock, H. Ade, G. N. M. Reddy, R. H. Friend and T. Q. Nguyen, Energy Environ. Sci., 2020, 13, 3679–3692.
18. H. Zhong, M. G. Asl, K. H. Ly, J. Zhang, J. Ge, M. Wang, Z. Liao, D. Makarov, E. Zschech, E. Brunner, I. M. Weidinger, J. Zhang, A. V. Krasheninnikov, S. Kaskel, R. Dong and X. Feng, Nat. Commun., 2020, 11, 1409.
19. G. Zhang, X. K. Chen, J. Xiao, P. C. Y. Chow, M. Ren, G. Kupgan, X. Jiao, C. C. S. Chan, X. Du, R. Xia, Z. Chen, J. Yuan, Y. Zhang, S. Zhang, Y. Liu, Y. Zou, H. Yan, K. S. Wong, V. Coropceanu, N. Li, C. J. Brabec, J. L. Bredas, H. Yip and Y. Cao, Nat. Commun., 2020, 11, 3943.
20. L. Perdig-Toro, H. Zhang, A. Markina, J. Yuan, S. M. Hosseini, C. M. Wolff, G. Zuo, M. Stolterfoht, Y. Zou, F. Gao, D. Andrienko, S. Shoaee and D. Neher, Adv. Mater., 2020, 32, 1906763.
21. X. Zhu, G. Zhang, J. Zhang, H. L. Yip and B. Hu, Joule, 2020, 4, 2443–2457.
22. T. F. Hinrichsen, C. C. S. Chan, C. Ma, D. Paleček, A. Gillett, S. Chen, X. Zou, G. Zhang, H. L. Yip, K. S. Wong, R. H. Friend, H. Yan, A. Rao and P. C. Y. Chow, Nat. Commun., 2020, 11, 5617.
23. K. N. Schwarz, P. B. Geraghty, V. D. Mitchell, S. U. Z. Khan, O. J. Sandberg, N. Zarrabi, B. Kudisch, J. Subbiah, T. A. Smith, B. P. Rand, A. Armin, G. D. Scholes, D. J. Jones and K. P. Ghiggino, J. Am. Chem. Soc., 2020, 142, 2562–2571.
24. Y. Liu, J. Zhao, Z. Li, C. Mu, W. Ma, H. Hu, K. Jiang, H. Lin, H. Ade and H. Yan, Nat. Commun., 2014, 5, 5293.
25. J. Gao, W. Gao, X. Ma, Z. Hu, C. Xu, X. Wang, Q. An, C. Yang, X. Zhang and F. Zhang, Energy Environ. Sci., 2020, 13, 958–967.
26. J. Qin, L. Zhang, Z. Xiao, S. Chen, K. Sun, Z. Zang, C. Yi, Y. Yuan, Z. Jin, F. Hao, Y. Cheng, Q. Bao and L. Ding, Sci. Bull., 2020, 2095–9273.
27. L. Ma, S. Zhang, H. Yao, Y. Xu, J. Wang, Y. Zu and J. Hou, ACS Appl. Mater. Interfaces, 2020, 12, 18777–18784.
28. A. J. Gillett, A. Privitera, R. Dilmurat, A. Karki, D. Qian, A. Pershin, G. Londi, W. K. Myers, J. Lee, J. Yuan, S. J. Ko, M. K. Riede, F. Gao, G. C. Bazan, A. Rao, T. Q. Nguyen, D. Beljonne and R. H. Friend, 2020, arXiv preprint arXiv:2010.10978.
29. A. Classen, C. L. Chochos, L. Lüer, V. G. Gregorious, J. Wortmann, A. Osvet, K. Forberich, I. McCulloch, T. Heumüller and C. J. Brabec, Nat. Energy, 2020, 5, 711–719.
30. H. Cha, J. Wu, A. Madsworth, J. Nagitta, S. Limbu, S. Pont, Z. Li, J. Searle, M. F. Wyatt, D. Baran, J. S. Kim, I. McCulloch and J. R. Durrant, Adv. Mater., 2017, 29, 1701156.
31. S. Li, L. Ye, W. Zhao, S. Zhang, S. Mukherjee, H. Ade and J. Hou, Adv. Mater., 2016, 28, 9423–9429.
32. C. L. Braun, J. Chem. Phys., 1984, 80, 4157–4161.
33. A. Armin, J. Subbiah, M. Stolterfoht, S. Shoaee, Z. Xiao, S. Lu, D. J. Jones and P. Meredith, Adv. Energy Mater., 2016, 6, 1600939.
34. N. Tokmoldin, S. M. Hosseini, M. Raoufi, L. Q. Phuong, O. J. Sandberg, H. Guan, Y. Zou, D. Neher and S. Shoaee, J. Mater. Chem., 2020, 8, 7854–7860.
35. S. M. Hosseini, N. Tokmoldin, Y. W. Lee, Y. Zou, H. Y. Woo, D. Neher and S. Shoaee, Sol. RRL, 2020, 4, 2000498.
36. M. C. Heiber, C. Baumbach, V. Dyakonov and C. Deibel, Phys. Rev. Lett., 2015, 114, 136602.
37. O. J. Sandberg, M. Nyman and R. Österbacka, Phys. Rev. Appl., 2014, 1, 024003.
38. O. J. Sandberg, A. Sundqvist, M. Nyman and R. Österbacka, Phys. Rev. Appl., 2016, 5, 044005.
39. L. A. Pettersson, L. S. Roman and O. Ingan, J. Appl. Phys., 1999, 86, 487–496.
40. G. F. Burkhard, E. T. Hoke and M. D. McGehee, Adv. Mater., 2010, 22, 3293–3297.
41. N. Zarrabi, O. J. Sandberg, S. Zeiske, W. Li, D. B. Riley, P. Meredith and A. Armin, Nat. Commun., 2020, 11, 5567.
42. J. Wu, J. Luke, H. K. H. Lee, P. S. Tuladhar, H. Cha, S. Y. Jang, W. C. Tsoi, M. Heeney, H. Kang, K. Lee, T. Kirchartz, J. S. Kim and J. R. Durrant, Nat. Commun., 2019, 10, 5159.
43. M. Nyman, O. J. Sandberg, W. Li, S. Zeiske, R. Kerremans, P. Meredith and A. Armin, Sol. RRL, 2021, 2100018.
44. A. Armin, A. Yazmaciyan, M. Hambsch, J. Li, P. L. Burn and P. Meredith, ACS Photonics, 2015, 2, 1745–1754.
45. D. Neher, J. Kniepert, A. Elimelech and L. J. A. Koster, Sci. Rep., 2016, 6, 1–9.
46. S. Zeiske, C. Kaiser, P. Meredith and A. Armin, ACS Photonics, 2019, 7, 256–264.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee01367j

---