Open Access Article
Open Access ArticleIntegrated mechanistic engineering models and macroeconomic input–output approach to model physical economy for evaluating the impact of transition to a circular economy†
Venkata Sai Gargeya
Vunnava
 a and
Shweta
Singh
a and
Shweta
Singh
 *ab
*ab
aAgricultural & Biological Engineering, Purdue University, West Lafayette, IN, USA
bEnvironmental & Ecological Engineering, Purdue University, West Lafayette, IN, USA. E-mail: singh294@purdue.edu; Tel: +01 765-496-1390
First published on 26th July 2021
Abstract
Sustainable transition to low carbon and zero waste economy requires a macroscopic evaluation of opportunities and impact of adopting emerging technologies in a region. However, a full assessment of current physical flow and waste is a tedious task, thus leading to a lack of comprehensive assessment before scale up and adoption of emerging technologies. Utilizing the mechanistic models developed for engineering and biological systems with the macroeconomic framework of Input–Output models, we propose a novel integrated approach to fully map the physical economy, that automates the process of mapping industrial flows and wastes in a region. The approach is demonstrated by mapping the agro-based physical economy of the state of Illinois, USA by using mechanistic models for 10 agro-based sectors, which have a high impact on waste generation. Each model mechanistically simulates the material transformation processes in the economic sector and provides the necessary material flow information for physical economy mapping. The model for physical economy developed in the form of a Physical Input–Output Table (PIOT) captures the interindustry physical interactions in the region and waste flows, thus providing insight into the opportunities to implement circular economy strategies i.e., adoption of recycling technologies on a large scale. In Illinois, adoption of technologies for industrial waste-water and hog manure recycling will have the highest impact by reducing >62% of hog industry waste outputs, >99% of soybean hull waste, and >96% of dry corn milling (corn ethanol production) waste reduction. A small % reduction in nitrogen fertilizer manufacturing waste was also observed. The physical economy model revealed that the urea sector had the highest material use of 5.52 × 108 tons and green bean farming with the lowest material use of 1.30 × 105 tons for the year modeled (2018). The mechanistic modeling also allowed elemental flows across the physical economy to be captured, with the urea sector using 8.25 × 107 tons of elemental carbon per operation-year (highest) and green bean farming using 3.90 × 104 tons of elemental carbon per operation-year (least). The approach proposed here establishes a connection between engineering and physical economy modeling community for standardizing the mapping of physical economy that can provide insights for successfully transitioning to a low carbon and zero waste circular economy.
Broader contextTransitioning current economic systems towards zero waste and low carbon systems will require synergistic efforts among various industrial systems and adoption of appropriate technologies at scale in a region for recycling or decarbonization. However, selection of sustainable technologies for this transition requires a macroscopic view of physical flows (wastes, emissions, resources) in the economy along with evaluating the impact of adopting potential emerging technologies on economy wide physical flows. The work here proposes an approach to create this macroscopic view of physical flows (interindustry flows, wastes, emissions) in an economy through integration of mechanistic engineering models and macroeconomic framework of Input–Output (IO) models. Furthermore, the work demonstrates the advantage of this approach in evaluating the opportunity for reducing waste and the impact of adopting a new technology in a region on economy wide waste/material flows for transition towards a circular economy. In summary, this work establishes an approach that connects mechanistic engineering simulations with macroeconomic framework for identifying potential transition opportunities and evaluating the impact of adopting any emerging technology on economy wide material flows. This approach will facilitate micro to macro scale integration for sustainable transition to a low carbon and circular economy. |
1 Introduction
Earth has entered a phase of Anthropocene where anthropogenic mass is larger compared to the overall living mass.1 A large portion of this anthropogenic mass is discarded as waste that affects the environment negatively. Waste and emissions generated by human activities are projected to increase by 60% for solid waste and 52% for GHG emissions by 2050,2 from the already high values of 49.2 Giga metric tons (GT) of waste and emissions (approx. 49% of total material use in 2017). Hence, it is crucial to identify pathways for sustainable transition to low carbon and zero waste or a circular economy. While significant advancements are being made in renewable energy and recycling technologies, identifying the most suitable technology based on an existing industrial set up of a regional economy is not obvious. Furthermore, evaluating the impact in terms of reducing waste and emissions while maintaining the same level of production in a region is also important to inform adoption of proposed technological solutions. In order to gain insights into these open questions, a full-scale physical map of the whole economic region in terms of material flows among industries, waste generation and associated emissions is necessary. Material Flow Analysis (MFA) is one such approach that enables comprehensive flow accounting, thus helping to better understand how materials flow from one industrial/human activity to another, and eventually back into nature as emission or waste flows.3 Apart from quantifying flows, MFAs need to be designed to make crucial connections between economics and other engineering or social science fields.4 Economy Wide Material Flow Analysis (EW-MFA),5 such as shown in Fig. 1, on a global scale have been performed in recent years.2 Such analyses provide a clear insight into the relationship between consumption or production activities in the economy and associated waste or emissions. This understanding of flow mobility enables development of sustainable resource use strategies ranging from identifying hot-spots for increasing production efficiencies at a single process or an industry level to economy-wide circular economy implementations that will reduce impacts on the environment. Furthermore, it can inform development of policies or technologies to reduce waste and emissions.6 While EW-MFAs have been performed at national7 and multi-national levels,2 there are very few studies that perform EW-MFA at regional levels with high sectoral level resolution.8 One key reason behind lack of mapping regional physical economies is unavailability of data at finer spatial resolution (Fig. 1). Another reason is that the current approach to create these MFAs is tedious and slow due to manual collection of data and mapping to different industrial sectors. Furthermore, reliance on empirical data in creating these MFAs poses additional challenges of continuity, reproducibility, validation, and increased efforts for collecting data on a sub-regional scale. As decisions are made at a local scale for implementing technologies for transitioning to lower waste/emissions or meeting environmental regulations, lack of MFAs at a regional scale lead to sub-optimal decisions or adoption of technologies that may have unintended long term consequences.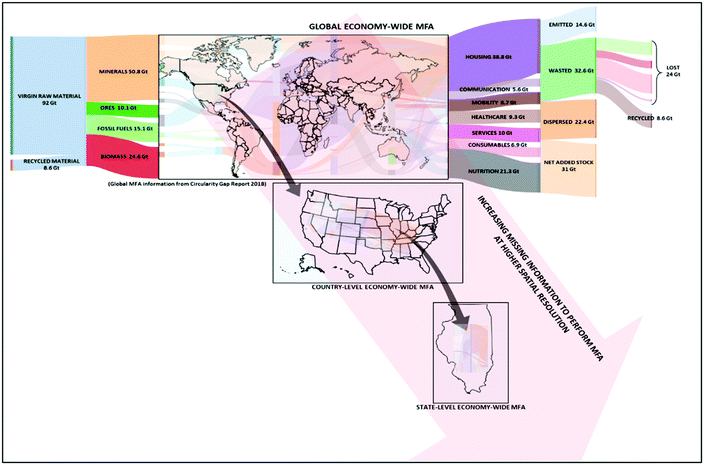 | ||
| Fig. 1 Economy wide material flow analysis at different spatial resolution (Global EW-MFA numbers taken from the circularity gap report2). | ||
In this work, we address these challenges by proposing a novel integrated mechanistic–macroscopic approach. The proposed approach uses computational mechanistic Engineering Models (EMs) to simulate material flows at high regional and sectoral level resolutions and connect these flows to the macroeconomic framework of input–output (IO) models to generate detailed material flow maps of a regional economy. Although IO models were predominantly used by economists in the past, these are now actively being used to quantify environmental flows and assessing environmental impact of economic activities both at national9 and multi-national levels.10 This use was originally envisioned by Wassily Leontief who won the Nobel prize for proposing the IO model.11 As envisioned originally, IO models are now increasingly being used for performing EW-MFAs at national levels.12 However, these studies were performed over large spatial scales as empirical data that feed into these studies are often only available at a country or multi-national level.13,14 On the other hand, engineers, chemists, physicists and other physical scientists have been using mechanistic models for a long time to simulate the physical flows of any system as governed by first principles. We utilize the strength of such computational models and build scaled mechanistic models that mimic the material transformation processes in various economic sectors of a given region.15 The rationale behind this approach is that physical economy is a manifestation of production processes, consumption of goods and waste generation, with circular economy bringing these back into the production cycle. Hence, the models based on fundamental mass balance and physics-based equations that mechanistically simulate production of various commodities and wastes can provide necessary physical data without only relying on empirical data related to outputs of an economic sector. This mechanistic approach greatly reduces allocation challenges as material flow information can be simulated at an individual sector level of a given region. Next, we establish an approach that integrates the sectoral EMs with the standard IO methods to generate Physical Supply Tables (PSTs), Physical Use Tables (PUTs) and Physical Input Output Tables (PIOT) that captures the material flow interactions between industries. This enables us to develop a physical economy model at regional levels that can be used to perform EW-MFAs and evaluate the impact of implementing circular economy (CE) strategies on waste and emissions reduction in a region at a macroscopic scale using PIOTs. We first provide an overview of the proposed methodology for PIOT generation and the methodology to evaluate the impact of CE strategies in Section 2. In Section 3, we demonstrate the application of the approach to map the physical economy of Illinois in the year 2018 and also show the potential impact of adopting recycling technologies for CE on overall economy-wide waste reduction. In Section 4, we discuss the strengths, limitations and potential for wide scale adoption of the proposed approach as a critical bridge between engineering, physical sciences and economics research communities for sustaining production while minimizing waste and environmental impacts.
2 Methodology
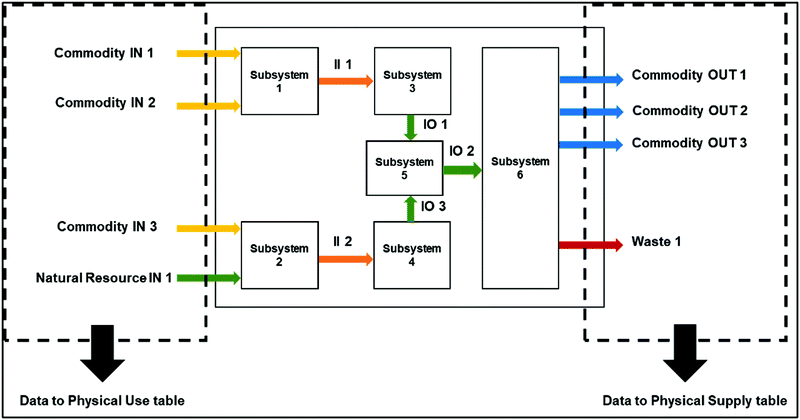
The methodology developed in this work integrates mechanistic EMs with the Input–Output (IO) macroeconomic framework. The method proposed will facilitate automating and standardizing the process of mapping physical flows among industries and waste generation in a regional economy. As shown in Fig. 2, EMs form the core of the methodology that can allow for automation while integrating the EMs to the macroeconomic framework of Physical Supply Tables (PSTs), Physical Use Tables (PUTs) and Physical Input–Output Tables (PIOTs) allows for standardization.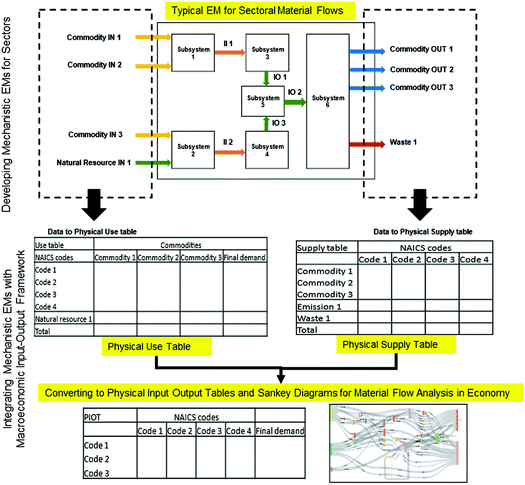 | ||
| Fig. 2 Proposed integration of mechanistic EMs with a macroeconomic Input–Output framework for modeling physical economies and EW-MFAs. | ||
There are two key steps in the method: EM development for sectors in a region, and mapping the simulation results from EMs to build standardized PSTs, PUTs and PIOTs. The first step of the EM development process consists of three stages (Section 2.1): (i) identifying the economic sectors to be modeled and mapping to economic sector codes used in a region, (ii) using physical, chemical or physiological based mechanistic approaches to model material transformation processes in the identified economic sector, and (iii) scaling the developed EM to represent material flows of the region being studied. Once the EMs are developed and scaled to represent various industries/sectors of a region, in the second step, the material flow information is organized to quantify the physical economy model using PSTs, PUTs and PIOTs which provide the physical model of the economy (Section 2.2). This model can then be used to study the impact of any technology introduction/changes in a region or strategies for transition to a circular economy as described in Section 2.3.
2.1 EM development for sectors to map regional physical flows
| Model material flow feature | Type |
|---|---|
| Raw material | Input |
| Intermediate input | Input |
| Intermediate output | Output |
| Commodity production | Output |
| Waste and emissions | Output |
In Table 1, we propose “Input side” or “Output side” scaling. Whenever input scaling data in the form of commodity consumption (as raw material or intermediate input) is available, the material flow input data for all possible input commodities can be used to scale EMs. Since EMs are based on underlying production or operation methodology, it will scale the rest of the physical flows as defined by the mechanistic rules. When only “Output side” information is available, scaling EMs to represent the sector in an economy is not straightforward. This is because most mechanistic EMs are built as “input” driven models. In this case, we have proposed using a stochastic approach. A range of input flows can be used to simulate the EMs and the resulting output can be compared with available “output flow” data. This is an iterative approach; however, a reasonable level of accuracy can be obtained. Automation of simulation allows for testing a vast range of input flows, which is not a challenge due to increasing computation power availability. An example of the output side scaling is shown in the ESI† (SI-2, Table S2).
Validation of scaled Ems. While scaling the EMs, care has to be taken to make sure that each material flow (input or output) associated with an EM should be a realistic representation of the material flows in the region in order to model the true size of the physical economy. Hence, it is recommended to cross validate the flows against empirical data as per the availability. If input side scaling was used and there is data on one of the “output” flows, the model simulation can be cross checked to ensure that EMs have been developed correctly. In the case of output side scaling, the validation is harder. If additional “output” flows such as a co-product or emissions data is reported by sectors, that can be used for validation. If both inputs and outputs are not available, then a decision must be made about how to use the only available input/output data, however such cases are rare as all industrial sectors collect some information on input or output side flows. Since the EMs are mechanistic in nature, if they are correctly modeled and scaled, their outputs should be close to the “validating” stream material flow information, which is calculated as % error. Once validated, the confidence of using the EMs for modeling physical economy at scale and reusing the EMs for different operating scales in the economy is established.
2.2 Transforming material flow information from EMs to PSUTs and PIOTs
In order to standardize models for mapping physical economy and use the model for evaluating the impact of technology interventions at an economy scale, the input and output material flow information from scaled EMs are transformed into PSTs, PUTs and PIOTs. PIOTs allow for standardization of depicting physical interconnections among sectors (industries) in an economy. IO models allow for analyzing macro-scale economic and environmental impacts of production changes or technology interventions.17 The data from EM provides information about use and supply of different “commodities” along with “natural resource” use and “waste” generation in the region for the modeled industrial sector (Fig. 3). The information from EMs is then organized into Physical Supply Table (PST) and Physical Use Table (PUT) as shown in Tables 2 and 3. The tables PST and PUT are “commodity × industry” with dimensions m × n (m is no of commodities and n is no of industries). RoE is the supply and use of commodities by industries in the rest of the economy, i.e. the sectors which are not being modeled or are out of scope for analysis. Since, these industrial sectors are not modeled there is not a straightforward way to fill this data at this stage and it is proposed to be used as the balancing column in our approach.| Commodities | Industry 1 | “””” | Industry N | ROE | Exports | FC | Total commodity used |
|---|---|---|---|---|---|---|---|
| (EM_IN: material input data from EMs, EM_NAT_IN: natural resource input data from EMs, ROE_IN: material inputs from ROE, FC: commodity final demand, EX: commodity exports, S_IN: balancing slack variable in PST, TCU: total commodity used, TII: total industry input.). | |||||||
| Commodity 1 | |||||||
| “ | EM_IN | ROE_IN | EX | FC | TCU | ||
| ” | |||||||
| Commodity M | |||||||
| Natural resources | |||||||
| Natural resource 1 | |||||||
| “ | EM_NAT_IN | ||||||
| ” | |||||||
| Natural resource P | |||||||
| Stocks (balancing slack) | S_IN | ||||||
| Total industry IN | TII | ||||||
| Commodities | Industry 1 | “”“” | Industry N | ROE | Imports | Total commodity supplied |
|---|---|---|---|---|---|---|
| (EM_OUT: material output data from EMs, EM_W_OUT: waste output data from EMs, ROE_OUT: material outputs from ROE, IM: commodity imports, S_OUT: balancing slack variable in PST, TCS: total commodity supplied, TIO: total industry output.). | ||||||
| Commodity 1 | ||||||
| “ | EM_OUT | ROE_OUT | IM | TCS | ||
| ” | ||||||
| Commodity N | ||||||
| Waste flows | ||||||
| Waste flow 1 | ||||||
| “ | EM_W_OUT | |||||
| ” | ||||||
| Waste flow P | ||||||
| Stocks (balancing slack) | S_OUT | |||||
| Total industry IN | TIO | |||||
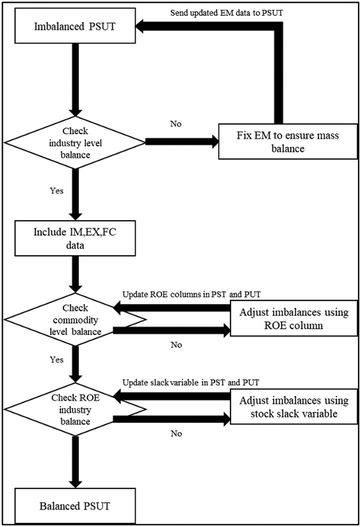
In Tables 2 and 3, the data in matrices EM_IN, EM_NAT_IN, EM_OUT, and EM_W_OUT are obtained directly from the material flow information provided by the EMs. Additional information about exports (EX), imports (IM), and final consumption (FC) of each commodity can be obtained from empirical data sources such as survey data or consumption statistics.19 The imports and exports can also be filled in using interregional trade models.20 Once these tables are populated using data from EM simulation and empirical data for EX, IM and FC, the tables are checked for imbalances and balanced to satisfy the IO framework requirement, as discussed below.
As shown in Fig. 4, industry level mass balances are checked first. If imbalanced, EMs are modified to ensure that the inherent mechanistic equations used ensure mass balance. In the next stage, all available empirical data on EX, IM and FC is appended to the PST and PUT containing data from EMs. This is then followed by a commodity level balance check for the region. Since imports, exports and final demand of commodities are already taken care of in the empirical data addition stage, the remaining commodity imbalances are assigned to the RoE (Rest of the Economy, i.e. industries not modeled) industry that either supplies or uses any deficit or excess in commodities. Since the ROE commodity adjustment may create an imbalance in the ROE industry level balances, a slack stock variable is used (S-IN and S-OUT in Tables 2 and 3) to account for the imbalances in industries included in RoE. As detailed information about stocks of commodities are not available, at this stage a simple deficit balance is assumed.
| T = V·diag(TCS)−1 | (1) |
| Z = T·U | (2) |
| FD = T·FC | (3) |
| EX_D = T·EX | (4) |
Finally, the imports data available at a commodity level are redistributed and allocated to sectors, final consumption and exports (cross-hauling). The allocation was done by weighting a sector's or final consumption or export column's usage of commodity imported. For example, if a commodity “A” is used 20% by sector 1, 50% by sector 2, 25% by final consumption and 5% by exports based on PUT data, then any imported commodity “A” was allocated 20%, 50%, 25%, and 5% to sector 1, sector 2, final consumption and exports respectively. At the end, these inter-industry flows, Z, and industry level FD, EX_D and IM_D are used to construct a PIOT as shown in Table 4.
| Industry 1 | “”“” | Industry N | ROE | Exports | Final demand | Waste | Total output | |
|---|---|---|---|---|---|---|---|---|
| Industry 1 | ||||||||
| “ | EM_Z | ROE_Z | EX_D | FD | W | TIO | ||
| ” | ||||||||
| Industry N | ||||||||
| Natural resources | ||||||||
| Natural resource 1 | ||||||||
| “ | N | |||||||
| ” | ||||||||
| Natural resource P | ||||||||
| Stocks (balancing slack) | S | |||||||
| Imports | IM_D | |||||||
| Total industry IN | TII |
2.3 Simulating impact of technology adoption for a circular economy
The symmetric PIOTs developed can be used to perform standard Environmentally Extended Input–Output (EEIO) analysis to study the impact of novel technology adoption or implementing new recycling technology on the inter-industry dependence and waste/emissions generation for the region. EEIO models provide a systematic way to assess environmental impacts based on dollar based (ex: impact per USD) emission factors24 and recently, in the work by Donati et al.25 further expanded on the EEIO approach to study global material flows. While EEIO models were conventionally employed using monetary IO tables (MIOTs) as their primary source to quantify inter-industry dependencies, we use the proposed PIOTs to quantify the dependencies.8 The flows represented by MIOTs are prone to variability in the prices assigned to different materials26 (purchaser's price, producer's price, margins, etc.) and create further uncertainty in quantifying material flows in an economy. Hence, to overcome such challenges, PIOTs are used to ensure the correct representation of material flows.27 For example, all material flows that do not have an economic value are not accounted for in MIOTs. Whereas in PIOTs, all flows, irrespective of their economic value are included in the table and it removes the variability associated with pricing of materials (e.g., a ton of steel is always a ton of steel irrespective of the region/industry/sector using it). Finally, since the underlying mathematical framework behind IO methodology remains the same, we can use similar equations used in conventional EEIO studies to simulate the impacts of final demand in the economy on material flows. Eqn (5) shows the change in total physical through flows for a change in Final Demand (FD) of the specific industries in the economy. To calculate overall impact using eqn (5), we calculate L as (I −A)−1 which is called the Leontiefs inverse (L). L quantifies the changes in total material throughput including direct and indirect impacts for industries (sectors) in response to per unit change in final demand.17 A is called the technical coefficient matrix which is derived using information from the Z matrix and the X column vector (eqn (6)). X is the matrix of total useful output from each sector, calculated as [TIO-W]. TIO and W are from PIOT in Table 4. In eqn (6), zi,j represents each element of the Z matrix and Xj represents each element of the column sum vector of matrix X. It has to be noted that waste flows were not included in calculating the A matrix since waste flows are not primary or co-products that are used by other industries and not driving the production process as discussed in detail in the IO literature.28 Furthermore, the coefficients A calculated here are Regional Input Coefficients (RICs), which capture the industrial interaction within the region. As import data were used to separate industrial uses of commodities between regional input and import use, it was feasible to calculate RICs.| ΔX = L·ΔFD | (5) |
| ai,j = zi,j/Xj | (6) |
Two types of structural changes can be observed as a result of emerging technology adoption or implementation of CE strategies. Since the A matrix quantifies the material requirements of an industry per unit output produced (technical coefficients), owing to the economies of scale, the A matrix may change as a result of introducing structural changes in the economy due to adoption of new technologies. If Ab and Aa represent the A matrices before and after implementing CE, then the changes in material requirements of industries to produce unit outputs can be quantified by:
| ΔA = Aa −Ab | (7) |
Since each element in the A matrix represents the requirement of inputs per unit output, the difference between the two A matrices will quantify by how much the input requirements change to produce the same unit output. The other type of change can be observed in the Leontief matrix. The L matrix before (Lb) and after (La) technology adoption for CE implementation can provide insights into how industrial interactions change in response to new technology adoption for the same per unit changes in final demands of industries. If changes in industry outputs before are represented by ΔXb and after CE implementation are represented by ΔXa and if the change in final demand is ΔFD then the difference in change of outputs can be calculated using eqn (8). In eqn (8), subscript ΔL refers to the fact that the physical changes throughout are due to the changes in direct and indirect impact coefficients after implementing the CE strategy.
| ΔXΔL = (La·ΔFD) − (Lb·ΔFD) | (8) |
This analysis allows evaluation of the impact of adopting new recycling technology in any region by improving overall material efficiency and reduction of waste in the economy.
Apart from studying the impact of structural changes, the waste intensities of each sector can also be quantified. If W represents the waste flow matrix, the waste intensity w (tons of waste/ton) can be calculated by dividing each sector's waste with the sector's output. The difference in waste intensities before and after CE is calculated as wb − wa.
3 Results
We present a detailed mapping of the physical economy for the major economic sectors that constitute the agro-based economy in Illinois to establish the standardization process using the proposed approach in Sections 3.1 and 3.2. Illinois was selected based on prior studies8,29 where PIOTs for Illinois existed that provided a benchmark for selection of sectors to model. Furthermore, in Section 3.3, we demonstrate how the approach developed in this work can be used to select recycling strategies and evaluate the impact of adoption of recycling technology on the Illinois agro-based sectors.3.1 EMs for agro-based physical economy of Illinois
The major agro-based sectors in Illinois, USA were first identified and tagged with a 6-digit NAICS code as shown in Table 5 and the EM type was given to each sector based on the type of material transformation processes. The EMs developed capture all the material processing-related flows for waste and emissions quantification in this case study, emissions and upstream wastes related to energy consumption in sectors are not included.| EM no. | Sector name | NAICS code | EM type |
|---|---|---|---|
| 1 | Soybean farming | 111110 | Plant growth model – Python |
| 2 | Bean farming | 111130 | Plant growth model – Python |
| 3 | Wheat farming | 111140 | Plant growth model – Python |
| 4 | Corn farming | 111150 | Plant growth model – Python |
| 5 | Potato farming | 111211 | Plant growth model – Python |
| 6 | Hog farming | 112210 | Animal growth model – Python |
| 7 | Urea manufacturing | 325311 | Chemical process model – Aspen plus |
| 8 | Soybean crushing | 311224 | Chemical process model – Aspen plus |
| 9 | Soybean biodiesel | 324199 | Chemical process model – Aspen plus |
| 10 | Corn ethanol manufacturing | 325193 | Chemical process model – Aspen plus |
| NAICS Code | Sector name | Scaling variables | Output variables | Model value | Unit | Validation source | Error (%) |
|---|---|---|---|---|---|---|---|
| Soybean crushing, bio-diesel and ethyl alcohol were scaled from the output side. Since the only available output data was used for scaling, it was not used to measure the error percentages. | |||||||
| 111110 | Soybean farming | Fertilizers used | Soybean yield | 5.74 × 101 | bu per ac | 30 | 10 |
| 111130 | Bean farming | Fertilizers used | Bean yield | 1.18 × 108 | kg | 30 | 5 |
| 111140 | Wheat farming | Fertilizers used | Wheat yield | 8.03 × 101 | bu per ac | 30 | −18 |
| 111150 | Corn farming | Fertilizers used | Corn yield | 1.72 × 102 | bu per ac | 30 | −18 |
| 111211 | Potato farming | Fertilizers used | Potato yield | 9.12 × 103 | kg ha−1 | NA | |
| 112210 | Hog farming | Hogs produced | Hog mass | 1.23 × 106 | ton | 30 | −26 |
| 325311 | Urea manufacturing | Ammonia used | Urea produced | 5.36 × 108 | ton | Industry is very small in Illinois (only used for EM representation) | NA |
| 311224 | Soybean crushing | Soybeans crushed | Soybean oil | 1.36 × 106 | ton | 31 | 0.07 |
| — | — | — | Soybean meal | 3.15 × 106 | ton | 7 | |
| 324199 | Soybean biodiesel | Soybean biodiesel | Soybean biodiesel | 1.53 × 102 | Mgal | 32 | — |
| 325193 | Corn ethanol manufacturing | Ethanol produced | Ethanol produced | 1.75 × 103 | Mgal | 32 | — |
3.2 Physical model for the agro-based economy in Illinois
After validating all the EMs developed for the agro-based sectors, the material flow information was extracted from these scaled models to construct PUT and PST using the proposed approach in Section 2.2. The various material inputs and outputs of each EM provided commodity data for each industry which were tabulated as individual columns following the structure shown for PUT (Table 2) and PST (Table 3). The PST and PUT constructed for the agro-based economy of Illinois are shown in SI-1 (ESI†), Tabs-“PST” and “PUT” which provide detailed commodity use and supply in the region. The corresponding Sankey diagrams for both the tables are shown in Fig. 5 and 6. The PST and PUT were converted to PIOT following the approach in Section 2.2. The PIOT captures the inter-industry dependence for materials in Illinois (see SI-1, Tab-PIOT, ESI†). Since the EMs developed are bottom-up and mechanistic in nature, information such as any available elemental chemical composition of different flows is also retained throughout the process.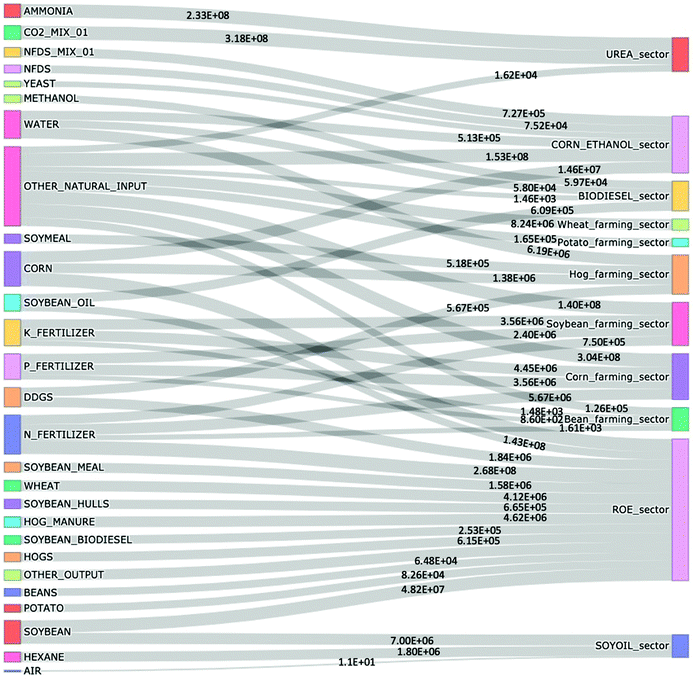 | ||
| Fig. 5 Detailed commodity use by sectors in Illinois, USA in 2018, based on the physical use table (PUT) developed (tons). | ||
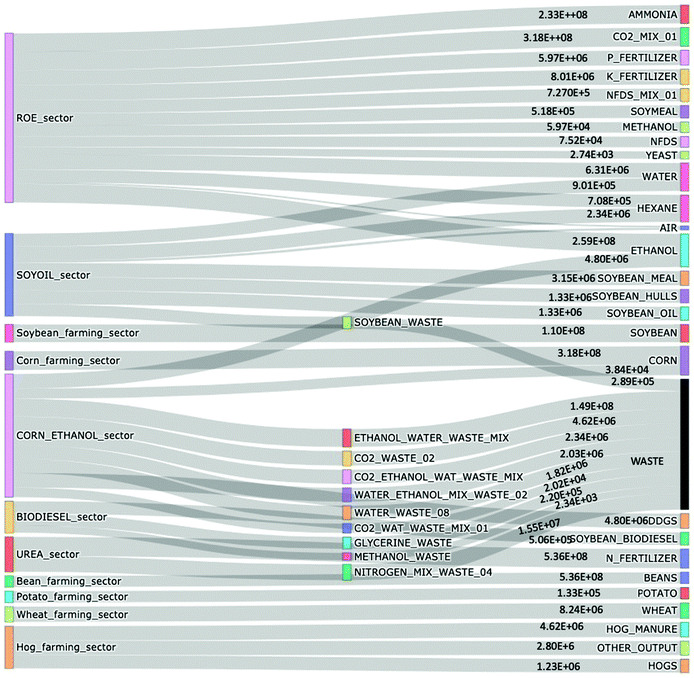 | ||
| Fig. 6 Detailed commodity supply by sectors in Illinois, USA in 2018, based on the physical supply table (PST) developed (tons). | ||
All the tables, Sankey diagrams and heatmaps presented here provide a highly detailed physical map of materials flowing from one agro-based industry to another in Illinois. Such physical economy models can be critically useful to better manage regional resource usage and to track elemental use efficiencies of different industries. The two Sankey diagrams comprehensively show how different commodities are moving from one industry to another and all the while interacting with nature by using raw materials and emitting waste flows. One important and easy to see observation is that water accounts for a significant amount of the total flows, and the corn-ethanol and hog farming sectors had the highest amount of waste being produced in 2018. Exact tracking of the waste flows through modeling at an economy scale provides an approach to automate projection of these flows in the future as well. Another important observation is that dry corn milling (or bioethanol/corn ethanol manufacturing) has the maximum number of input flows and also has the highest number of output waste flows. Using these quantitative observations about the type and amount of waste flows, we develop a CE strategy in next section. The detailed information on commodity flows can also be utilized to perform sensitivity analysis of the dry corn milling industry supply chains to study how the industry behaves if one of the many input requirements is low in supply. The two Sankey diagrams and the PST/PUT provides highly disaggregate material flow information at detailed economic sector and commodity levels with exact composition of material flows as well. Furthermore, using the aggregate information from the PST, PUT, PIOT and Sankey diagrams developed, key material flow characteristics of the physical economy of Illinois has been identified as shown in Table 7. The highest material inputs are for the urea manufacturing sector consuming high volumes of ammonia and CO2, this also makes urea manufacturing a key sector for carbon and nitrogen flows and potentially a target for carbon capture technologies to integrate with fertilizer manufacturing. The sector with the least material flow intensity was the bean farming sector. This is due to the low nutrient input requirement (as N fixation happens), thus beans could be a target for sustainable food production. Lastly, corn-ethanol manufacturing was the sector with highest number of waste flows including water mixture with organic content (2.34 × 106 tons) and water with CO2 and ethanol mixing (1.49 × 108 tons). Given the organic content of these water mixtures, these form targets for further treatment and recycling of both water and any organic waste content.
| Physical characteristics | Industry name | Value | Units |
|---|---|---|---|
| Highest mass output | Urea sector | 5.52 × 108 | tons per oper-yr |
| Least mass output | Bean farming | 1.30 × 105 | tons per oper-yr |
| Highest known elemental C output | Urea sector | 1.07 × 108 | tons per oper-yr |
| Least known elemental C output | Bean farming | 3.90 × 104 | tons per oper-yr |
| Highest known elemental C input | Urea sector | 8.25 × 107 | tons per oper-yr |
| Least commodity use intensity | Bean farming | 3.00 × 10−2 | tons per ton |
| Highest waste flows | Corn ethanol manufacturing | 1.60 × 108 | tons per oper-yr |
The second source of uncertainty can arise from the input/output scaling data provided to all the developed EMs. While information such as coefficient of variation (CV) was provided in some model output sources in USDA census data,30 the required uncertainty parameters for all the input data was unavailable to fit a probability distribution and perform detailed uncertainty analysis such as Monte Carlo.22 Hence, we did not quantify uncertainty propagation due to uncertainty in scaling data. However, if such detailed uncertainty information is available for all scaling variables, it then becomes possible to quantify how uncertainty can propagate throughout the material flow modeling framework to the estimation in PSTs/PUTs/PIOTs.
3.3 Identifying and quantifying the impact of circular economy strategies
Since it was possible to capture highly detailed chemical characteristic information of individual material flows across the physical economy model, we used the compositions and stream flow information to determine the recycling potential and appropriate technologies for various waste flows. The identified waste flows can then be recycled to implement a circular economy strategy by selecting appropriate recycling technology. It has to be noted that some waste flows may have very high concentrations of a valuable chemical, but the required recycling/extraction technology may not be available. Hence, the available recycling technologies could constrain the real potential of recycling and proper techno-economic assessment (TEA) of the recycling technologies must be done for selection of appropriate technology to be adopted at scale. However, TEA is not the focus of our work and we assume that the technology selected is economically viable for adoption at the required scale. If the technology is available and viable, the waste flows can be supplied as an input to the recycling industry where it transforms them into valuable commodities. To study the impact of this strategy, new EMs can be developed for the new recycling technology and included in the PST, PUT and PIOT construction to reflect the recycling of materials in a physical model of the economy. We utilize this approach for transitioning the Illinois economy towards a CE by adopting technologies for recycling industrial waste water and hog manure, and evaluating their impact on physical material flows in the economy along with inter-industry dependence changes. However, we acknowledge the lack of uncertainty quantification on material flows and waste flows that can affect the actual impact of implementation of the CE strategies described in this work. Therefore, the results presented only pertain to the waste quantities (see SI-1, ESI†) modeled with particular EM models (see SI-2, ESI†) and scaling values used.Based on the waste data obtained from the PST (see SI-1, ESI†), the manure flow from hog farming and industrial waste from corn-ethanol manufacturing and soybean crushing were identified as flows which can be potentially recyclable. A manure recycling industry and water recycling industry was introduced in the economy to process these streams and the entire process of constructing PST, PUT and PIOT was repeated as in the previous section. Each recycling sector was represented as an EM. One EM was developed using Aspen Plus to recycle waste-water flows coming from different sectors. The EM was based on the work by Rajendran et al.36 where a modified Anaerobic Digestion Model 1 (ADM 1) was used to simulate the biochemical reactions of treating wastewater under anaerobic conditions. The wastewater recycling EM divides the digestion or fermentation reactions into two groups of reaction-sets: (a) the reactions of hydrolysis operating based on the extent of the reaction, and (b) reactions of other phases (acidogenic, acetogenic, and methanogenic reactions) in AD functioning on a kinetic basis. Hydrolysis is one of the rate-limiting steps in AD, and henceforth a separate reaction-set was added. The second EM was an operations model that empirically converted hog manure into fertilizer, developed using a manure composting technology assumption. Details on both the recycling EMs are provided in the ESI† (SI-2, Tabs-“Water Recycling”, “Manure Recycling”). Both the EMs were scaled from the input side with each EM taking in the waste flows it can process, data for which was available from PST developed for mapping the waste in the Illinois economy. This scaling was chosen as no empirical data was available to scale the introduced recycling EMs with CE implementation scenario. Since water is a natural resource, no industry had to be scaled down to ensure water final demand. The major changes observed were the reduced dependence on water as a natural resource by industries and the availability of recycled fertilizer commodity that can be used by farming sectors.
During CE implementation, it was assumed that the final demand of commodities will remain the same. This was done to specifically understand the role of the recycling sector in changing the material exchanges between industries in the simulated CE physical model while meeting the same level of production demand from the economy. Since the recycling industry is now supplying water and fertilizer to the economy, interaction with other industries that provide water and fertilizer changes in the economy while ensuring that the economy meets the same final demand even after implementing a CE. Since water is a natural resource, using recycled water implies lower water withdrawal from nature to meet the demand of water requirements to the same production level in all sectors in the economy. As seen in Fig. 8, the input requirements of all the sectors change as a result of introducing new technologies in the economy. This increase or decrease in input requirements can depend on the inherent mechanistic methods used to model and also the economies of scale. The PIOT heatmap for the newly created recycling economy is shown in Fig. 7 and captures these nonlinear changes in industrial exchanges under CE implementation. The heatmap also shows how the sectors are interacting with each other and the newly introduced recycling sector.
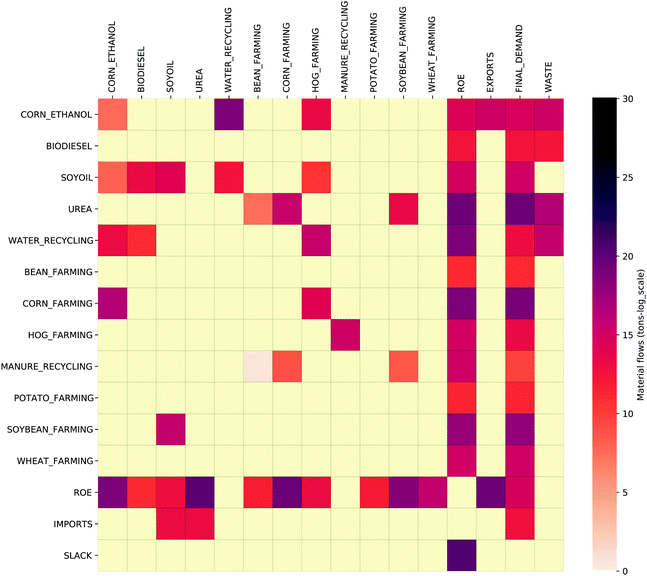 | ||
| Fig. 7 The heatmap of PIOT after implementing CE (numerical table in SI-2, ESI†). | ||
It can be observed from the heatmap (Fig. 7) that the recycling sectors, water recycling and manure recycling, is taking inputs from corn-ethanol manufacturing, soybean oil manufacturing and hog farming sectors. The recycling sector is also supplying recycled materials such as water and fertilizer to other sectors such as corn-ethanol manufacturing, soybean biodiesel, bean farming, corn farming, pea farming, soybean farming, and hog farming. Additionally, the recycling sector provides biogas as a new commodity to the economy. Fig. 8 shows how the material requirements of industries to produce a unit output changed as a result of introducing the recycling sector. It can be observed that the farming industries (bean, corn, peas, soybean, and hog) are now requiring fewer materials from the remaining agro-based industries in the region and the rest of the economy. This deficit is now being contributed by the recycling industry. The recycling industry is also supplying recycled water to sectors such as corn-ethanol, soybean processing and hog farming, which reduces water withdrawal from natural systems.
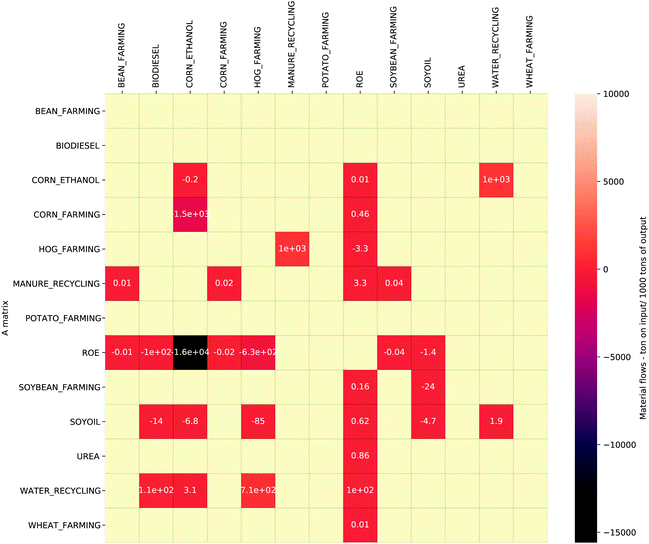 | ||
| Fig. 8 Difference in input material requirements per 1000 tons of output before and after CE implementation. | ||
Furthermore, to study the impact of restructuring the economy on total material requirements for meeting the final demand changes (FD), artificial demand pulls were simulated using eqn (1)–(8). The marginal increase was simulated using a vector of all ones (1 ton of products from sectors). Note that the final demand changes for both the newly introduced recycling sectors (water recycling and manure recycling) was assumed to be 0, to only simulate the material requirement to meet the demand of the original economy. This implies that these recycling sectors are only recycling wastes and providing commodities back to industries in the economy but not providing outputs to consumers. Since these industries did not exist in original economy, this assumption provides a fair comparison of physical flows required to meet the original demands in economy. The Leontief inverses (L) were calculated for both the baseline scenario (Lb) and after implementing a circular economy (La). Then changes in the physical throughput of all the industries were calculated based on the simulated demand pull. The difference in throughputs (ΔX) is shown in Table 8.
| Sector | ΔXbeforeCE | ΔXafterCE | Change | % Change |
|---|---|---|---|---|
| Corn_ethanol | 1.23 | 4.27 | 3.12 | 248 |
| Soybean Biodiesel | 1.01 | 1.00 | 0.00 | −1 |
| Soy_oil | 2.99 | 2.66 | −0.20 | −11 |
| Urea Manufacturing | 10.65 | 5.00 | −4.93 | −53 |
| Bean_farming | 1.00 | 1.00 | 0.00 | 0 |
| Corn_farming | 8.45 | 3.69 | −4.08 | −56 |
| Hog_farming | 1.12 | 1.12 | −0.15 | 0 |
| Soybean_farming | 5.05 | 3.71 | −1.11 | −27 |
| Potato_farming | 1.00 | 1.00 | 0.00 | 0 |
| Wheat_farming | 1.15 | 1.06 | −0.08 | −8 |
| ROE | 50.66 | 20.81 | −26.10 | −59 |
| Water_Recycling | 0.00 | 3.03 | 3.03 | 100 |
| Manure_Recycling | 0.00 | 0.07 | 0.07 | 100 |
Overall, there was significant reduction in total material throughflows for all but one sectors to meet the final demand of 1 tons of products in the restructured economy. Sectors showing reduction of material throughflow are soy-oil manufacturing (−11%), urea manufacturing (−53%), corn farming (−56%), soybean farming (−27%), wheat farming (−8%) and other sectors in ROE (−59%). These decreases are due to reduced extraction of new materials and increased recycling rate which can allow meeting the demand at a lower level of external resource inputs. The significant reduction in throughflow of urea manufacturing is because of the manure recycling industry which is transforming hog manure into N fertilizer, which reduces the dependency of other sectors on the urea manufacturing sector, hence lower throughflow in this sector. However, reliance on the urea manufacturing industry to also supply N fertilizer increases the physical economies resilience to fluctuations in the final demand of N fertilizer as there are now two industries (urea manufacturing and the manure recycling sector) in the economy supplying the same commodity. Since the urea production industry has the capacity to produce more as originally in the baseline scenario, it can ramp up its production to pre-CE physical economy levels in case demand arises. This makes the economy less prone to fluctuations in fertilizer demand as compared to the baseline scenario. However, it has to be noted it may be economically beneficial for the urea production industry to produce at original capacity, however the trade-off on environmental impact needs to be considered in cases when extra production from virgin materials is not needed and regional economy can meet demands by re-utilizing wastes. Alternatively, this industry can utilize the extra production capacity to provide fertilizers to “nitrogen/phosphorus” poor regions by exporting, which can help in the imbalances of resource availability in different parts of the world. Thus, a CE strategy in one region can eventually help in equitable distribution of important resources such as nitrogen/phosphorus for food production in areas challenged with food poverty, while overcoming the environmental challenges arising due to run-off of nutrient wastes.37 The corn-ethanol sector shows an increase in throughflow because of the increased indirect dependence of this sector on other sectors through re-using water from the recycling sector and corn-farming dependence on recycled manure. However, overall, these recycling strategies reduced the total throughflows for the economy as shown in the high reduction of throughflows in other sectors.
Lastly, to understand the impact of adopting these recycling technologies on overall waste reduction in Illinois, we show the sector-wise reduction of waste flows after implementing a CE strategy. In Table 9, one of the main differences we observe is that the number of waste flows has decreased in the economy as the recycling industry is consuming them to produce useful commodities, which is an intuitive result. However, there is a new waste flow in the system coming out of the recycling industry which was not present in the baseline scenario, this can be systematically quantified using generated PIOTs. Although the recycling industry has its own waste, it is producing far more quantities of useful commodities from the waste compared to its own waste flows. There was a reduction of total 1.48 × 108 tons of waste flows in the economy as a result of recycling while meeting the same demand from the economic sectors in the region (waste before CE was 1.76 × 108 tons and mass of waste after CE was 2.75 × 107 tons; the percentage reductions in waste flows are shown in Table 9). Water recycling used 1.55 × 108 tons of waste from corn-ethanol and 2.89 × 105 tons of waste from soy-oil while manure recycling used 4.62 × 106 tons of hog manure. After recycling, 3.07 × 104 tons of nitrogen fertilizer and 1.17 × 104 tons of phosphorus fertilizer were supplied by the recycling sector. Overall, the introduction of the recycling sector reduced >96% of waste from the corn-ethanol sector, >99% of soybean oil sector waste, and >62% hog farming waste outputs. All this waste was despite a total of 7.14 × 106 tons of waste being generated from the water recycling system. It has to be noted that, while it is true the quality of the recycled material flows may be inferior to virgin material flows, the scope of the current work assumes that the recycled water is primarily used by industries and is not potable. The EM model used in water recycling ensured that the water output meets standard requirements (all organic contaminants, particulate matter, and volatile solids removed) to be reused by industries. In the case of recycled hog manure as fertilizer, elemental nutrient mass requirements were considered when using the recycled manure as fertilizer. For example, 1 kg of nitrogen from urea being used by crop farming sectors was replaced by 1 kg of nitrogen from recycled hog manure, hence the equivalent functional substitution was ensured.
| INDUSTRY | GLYCERINE_WASTE | METHANOL_WASTE | WATER_RECYCLING_WASTE | CO2_WASTE_02 | NITROGEN_MIX_WASTE_04 | WATER_RECYL_08 | OTHER_OUTPUT_WASTE | WASTE_REDUCTION (%) |
|---|---|---|---|---|---|---|---|---|
| CORN_ETHANOL | 4.6 × 106 | 1.8 × 106 | 96 | |||||
| BIODIESEL | 2.2 × 105 | 2.2 × 103 | 0 | |||||
| SOYOIL | 100 | |||||||
| UREA | 1.6 × 107 | 0 | ||||||
| WATER_RECYCLING | 7.1 × 106 | 5.1 × 104 | 0 | |||||
| BEAN_FARMING | 0 | |||||||
| CORN_FARMING | 0 | |||||||
| HOG_FARMING | 2.8 × 106 | 62 | ||||||
| MANURE_RECYCLING | 4.6 × 106 | 0 | ||||||
| POTATO_FARMING | 0 | |||||||
| SOYBEAN_FARMING | 0 | |||||||
| WHEAT_FARMING | 0 | |||||||
| ROE | 0 |
4 Conclusion
The integrated bottom-up approach developed in this work by utilizing mechanistic EMs to simulate material transformations and using the extracted data in a standardized IO framework to create PSTs, PUTs and PIOTs proved to be a comprehensive technique to account for economy-wide material flows without overly relying on empirical data. The only empirical data used was in validating and scaling the models. Once validated, the same EMs can now be used for other regions or to find material flows in consequential scenario assessments, thus making this approach highly reproducible. Hence, this approach solves a long-lasting issue of lack of standardized techniques for mapping material flow in the economy. In previous work, to build a regional physical economy model as PIOTs, an empirical approach was taken by Singh et al.8 for nitrogen flows and only process models with manual mapping was used in Wachs & Singh.29 Both these earlier approaches prove to be tedious in mapping the data and were limited in scope such as lacking standardization/reproducibility for modeling the physical economy. Hence, this work provides a novel and significant advancement to previous approaches to build PIOTs by establishing an approach that allows automation and standardization of integrating mechanistic models for all type of sectors that was not feasible in tedious empirical and manual mapping work. Here, we have shown how mechanistic physics-based modeling approaches can be effectively used to simulate material flows across different industries in a region and map the physical economy in a standardized framework. Thus, this work also fills a critical gap of lack of computational approaches for evaluating the economy wide impact of emerging technologies or adoption of a new technology in a region on overall material changes and waste flows.Since the final output of the approach is in the form of PSTs, PUTs and PIOTs, the approach is also compatible with other existing top-down and hybrid flow accounting techniques widely used in industrial ecology for assessing the economic and environmental impact of demand changes.38,39 Finally, as demonstrated in the case study, the established approach can have wide ranging applications such as: providing detailed insights into sectoral dependence on different material flows, and sectors with the highest waste flows and streams with the potential for recycling technologies adoption that can be simulated to evaluate the overall impact on reducing environmental impacts of the regional production system.
Thus, our approach can feed into the growing emphasis on using regional material flow data to perform circular economy implementations.25,40–42 In the work by Donati et al.,41 the authors use a framework of supply using tables to account for waste supplies from different sectors at a city level relying on empirical data for highly aggregate sectors. The approach presented in this work can supplement the data needs of the framework of using supply use tables used in the work by Donati et al. as well as to make the approach reproducible for other sectors and regions, thus reducing the time effort for building PST and PUTs. There is also work on the use of an IO supply use table approach to model material flows and circular economies,25 however reliance on monetary EEIO tables to map global material flows may provide biased results as monetary tables are generally not an accurate description of physical economies. The work presented here overcomes this challenge by generating the physical A matrix as explained in the method section. Thus, our approach can also overcome a significant challenge for data generation over time to map physical economies reliably. In the future, the approach on reuse, recycling and refurbishing presented in Donati et al.25 can be combined with our work using physical A matrices. Overall, the approach presented in this work addresses the challenge of physical models for the economy in the current literature by both making the approach highly reproducible and relying on a technical coefficient matrix derived from purely physical flows based on mechanistic models for material conversion in sectors. Sharing of EMs will allow fast generation of physical economy models for other regions as well. Since, the EMs can be validated, errors on modeling a region can be easily checked and iteratively improved for accuracy which is not feasible in current empirical approaches. Furthermore, these EMs should be simulated with a range of values to capture the uncertainty in material flows in the economy that can provide insights into variations in the impact of recycling strategies. Updating the EMs to reflect changes in technologies will also allow the study of scenarios of adoption of emerging technologies in various sectors.
Apart from addressing the challenges in the literature, the authors believe that the work presented here pushes the boundary of material flow accounting methods by inviting mechanistic modeling researchers using physics, chemistry, and biological models along with process systems engineering community to integrate their work with a macroeconomic framework to account for large scale economy-wide impact of emerging technologies. With growing computational power and increasing use of machine learning to develop process/materials/physical models,43,44 the approach presented here can act as a blueprint for automation of mapping materials flows in the economy from any computational model derived data. For example, once a large number of models are developed using different techniques to represent all sectors in the economy, all the material flows can be mapped at a global/country/state level, providing a truly collaborative effort to solve the challenge of environmental impact of waste generation and design of sustainable technologies.
We discuss more about this idea of collaborative and automated effort of simulating large scale economy-wide material flow data in another work focused on cloud-based PIOT-Hub. The PIOT-Hub45 uses a Python based automated tool called Material Flow Data Extractor and Simulator (MFDES) at the backend46 to implement the proposed approach. This cloud-based platform at scale will provide the computational tool for a global effort to map physical economy using the approach presented in this work, similar to large scale efforts of mapping the human genome. This tool will be available to researchers for non-commercial use via Purdue's MyGeoHub platform to comply with license restriction (https://mygeohub.org/piot). Recently, an effort to map global physical flows in a virtual laboratory has been made using a top down approach,47 which can be complemented with the approach presented in this work. We envision that these physical maps of the local/global economy will enable us to function within the constraints of planetary limits48 by connecting anthropogenic material flows with ecological and planetary mass flows.
Conflicts of interest
There are no conflicts to declare. A US Patent is pending on the cloud platform implementing the methodology for automation, with potential for commercialization as technology.Acknowledgements
Authors are grateful for support from the U.S. National Science Foundation CBET-1805741. We also thank the anonymous reviewers for their feedback that has further improved this manuscript.Notes and references
- E. Elhacham, L. Ben-Uri, J. Grozovski, Y. M. Bar-On and R. Milo, Nature, 2020, 588, 442–444 CrossRef CAS PubMed
.
- The Circularity Gap Report 2020, Circle economy technical report, 2020.
-
Y. Moriguchi and S. Hashimoto, in Material Flow Analysis and Waste Management, ed. R. Clift and A. Druckman, Springer International Publishing, Cham, 2016, pp. 247–262 Search PubMed
.
- T. E. Graedel, Environ. Sci. Technol., 2019, 53, 12188–12196 CrossRef CAS PubMed
.
- M. Fischer-Kowalski, F. Krausmann, S. Giljum, S. Lutter, A. Mayer, S. Bringezu, Y. Moriguchi, H. Schütz, H. Schandl and H. Weisz, J. Ind. Ecol., 2011, 15, 855–876 CrossRef
.
- Circularity Economy Action Plan, European union technical report, 2020.
- A. Schaffartzik, N. Eisenmenger, F. Krausmann and H. Weisz, J. Ind. Ecol., 2014, 18, 102–112 CrossRef
.
- S. Singh, J. E. Compton, T. R. Hawkins, D. J. Sobota and E. J. Cooter, Ecological modelling, 2017, 360, 194–203 CrossRef CAS PubMed
.
- B. Reutter, P. Lant, C. Reynolds and J. Lane, J. Cleaner Prod., 2017, 153, 506–514 CrossRef
.
- A. Tukker, E. Poliakov, R. Heijungs, T. Hawkins, F. Neuwahl, J. M. Rueda-Cantuche, S. Giljum, S. Moll, J. Oosterhaven and M. Bouwmeester, Ecological Economics, 2009, 68, 1928–1937 CrossRef
.
- W. Leontief, The Review of Economics and Statistics, 1970, 52, 262–271 CrossRef
.
- J. Kovanda, J. Ind. Ecol., 2019, 23, 893–905 CrossRef
.
- United Nations, Food and Agriculture Organization, 2020, http://www.fao.org/faostat/en.
- United Nations, UN Comtrade, International Trade Statistics Database, 2019, https://comtrade.un.org/.
- T. E. Casavant and R. P. Coˆté, J. Cleaner Prod., 2004, 12, 901–908 CrossRef
.
- North American Industry Classification System - NAICS, https://www.census.gov/naics/.
-
R. E. Miller and P. D. Blair, Input–output analysis: foundations and extensions, Cambridge university press, 2009 Search PubMed
.
- Y. Yang, The International Journal of Life Cycle Assessment, 2019, 24, 620–626 CrossRef
.
- Commodity Flow Survey (CFS), https://www.census.gov/programs-surveys/cfs.html.
- R. Boero, B. K. Edwards and M. K. Rivera, Regional Studies, 2017, 52, 225–238 CrossRef
.
-
Eurostat, Eurostat Manual of Supply, Use and Input–Output Tables, 2008, ch. 8, pp. 1–592 Search PubMed
.
- Y. Wang and H.-w. Ma, J. Cleaner Prod., 2018, 170, 1017–1028 CrossRef
.
- D. Laner, H. Rechberger and T. Astrup, J. Ind. Ecol., 2014, 18, 859–870 CrossRef CAS
.
- Y. Yang, W. W. Ingwersen, T. R. Hawkins, M. Srocka and D. E. Meyer, J. Cleaner Prod., 2017, 158, 308–318 CrossRef PubMed
.
- F. Donati, G. A. Aguilar-Hernandez, C. P. Sigüenza-Sánchez, A. de Koning, J. F. Rodrigues and A. Tukker, Resour., Conserv. Recycl., 2020, 152, 104508 CrossRef
.
- S. Merciai and R. Heijungs, Ecological Economics, 2014, 102, 69–74 CrossRef
.
- S. Nakamura, K. Nakajima, Y. Kondo and T. Nagasaka, J. Ind. Ecol., 2007, 11, 50–63 CrossRef CAS
.
- S. Suh, Ecological Economics, 2004, 48, 9–17 CrossRef
.
- L. Wachs and S. Singh, Economic Structures, 2018, 7, 1–24 CrossRef
.
- United States Department of Agriculture, USDA - National Agricultural Statistics Service - Statistics by State, 2018, https://www.nass.usda.gov/Statistics_by_State/.
- US Department of Agriculture, Agricultural Marketing Service, US Department of Agriculture, 2020, https://mymarketnews.ams.usda.gov/viewReport/3191.
- US Department of Energy, Energy Information Administration (EIA), 2020, https://www.eia.gov/.
- A. J. de Wit, PCSE: The Python Crop Simulation Environment, 2018, https://pcse.readthedocs.io/en/stable/index.html.
- N. Power, API Documentation | NASA POWER, https://power.larc.nasa.gov/docs/v1/.
-
A. Giwa and K. S. Umanah, International Journal of Engineering Research in Africa, 2019, pp. 38–48 Search PubMed
.
- K. Rajendran, H. R. Kankanala, M. Lundin and M. J. Taherzadeh, Bioresour. Technol., 2014, 168, 7–13 CrossRef CAS
.
- D. Cordell, J.-O. Drangert and S. White, Global Environmental Change, 2009, 19, 292–305 CrossRef
.
- S. Merciai and J. Schmidt, J. Ind. Ecol., 2018, 22, 516–531 CrossRef
.
- M. K. Heun, A. Owen and P. E. Brockway, Appl. Energy, 2018, 226, 1134–1162 CrossRef
.
- M. Virtanen, K. Manskinen, V. Uusitalo, J. Syvänne and K. Cura, J. Cleaner Prod., 2019, 235, 1020–1025 CrossRef
.
- V. Zeller, E. Towa, M. Degrez and W. M. Achten, Waste Manage., 2019, 83, 83–94 CrossRef PubMed
.
- I. Plastinina, L. Teslyuk, N. Dukmasova and E. Pikalova, Resources, 2019, 8, 90 CrossRef
.
- T. Bikmukhametov and J. Jäschke, Comput. Chem. Eng., 2020, 138, 106834 CrossRef CAS
.
- S. Stocker, G. Csányi, K. Reuter and J. T. Margraf, Nat. Commun., 2020, 11, 1–11 Search PubMed
.
- PIOT Hub: Cloud Infrastructure for Automated Generation of PIOTs, https://mygeohub.org/piot, Accessed: 2021-02-19.
- G. Vunnava, J. Shin, L. Zhao and S. Singh, J. Ind. Ecol., 2021 Search PubMed
, accepted.
- H. Wieland, M. Lenzen, A. Geschke, J. Fry, D. Wiedenhofer, N. Eisenmenger, J. Schenk and S. Giljum, Ecological Economic Papers, 2020, 36, https://epub.wu.ac.at/7949/1/WP_36.pdf Search PubMed.
- W. Steffen, K. Richardson, J. Rockström, S. E. Cornell1, I. Fetzer, E. M. Bennett, B. Reinette, C. R. Stephen, D. V. Wim, A. D. W. Cynthia, F. Carl, G. Dieter, H. Jens, M. M. Georgina, P. M. Linn, R. Veerabhadran, R. Belinda and S. Sverker, Science, 2015, 347, 6223 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee00544h |
| This journal is © The Royal Society of Chemistry 2021 |