Tuning metal single atoms embedded in NxCy moieties toward high-performance electrocatalysis†
Received
15th January 2021
, Accepted 4th May 2021
First published on 7th May 2021
Abstract
Noble nanoparticle (NP)-sized electrocatalysts have been exploited for diverse electrochemical reactions, in particular, for an eco-friendly hydrogen economy such as water splitting. Recently, minimal amounts of single atoms (SAs) are exploited to maximize the active surface area and to tune the catalytic activity by coordinating the SAs in defect sites of N-doped graphene (GN). For the hydrogen evolution reaction (HER) and oxygen evolution/reduction reactions (OER/ORR), we show high-performance 3d–5d transition metal (TM) SA catalysts using density functional theory (DFT) along with machine learning (ML)-based descriptors. We explore the stability and activity of TM–GN from the view of structure/coordination, formation energy, structural/electrochemical stability, electronic properties, electrical conductivity, and reaction mechanism, which have not been seriously explored yet. Among various –NnCm moieties, the –N2C2 moieties tend to be more easily formed and show higher electrochemical catalytic performance and longer durability (without aggregation/dissolution) compared with the widely studied pure –C4/C3 and –N4/N3 moieties. We found that some TM(SA)s favor a new OER/ORR mechanism, completely different from any known mechanism. The ML-based descriptors showing super HER/OER/ORR performances better than those of bench-mark noble metal catalysts are assessed. In the N2C2 templates, Ni/Ru/Rh/Pt show low HER overpotentials. Here, the H adsorption sites are shared by both the metal and C (not N), which was undiscussed in most of the previous literature where the H is attached on top of a metal atom. Low OER overpotentials are found for Pt/Ni–N2C2, Ni/Pd–C4, and Rh–N4, while low ORR overpotentials are found for Ir/Rh-N4, Pd–C4, Ru–N3C1 and Ni/Pd/Pt–N1C3. The present findings should help in designing high-performance SA catalysts for other various electrocatalytic reactions such as the ammonia evolution reaction.
Broader context
A high catalytic performance in water splitting for hydrogen fuel is essential for an ever-clean hydrogen economy including hydrogen vehicles and hydrogen power generation. Transition metal d-orbitals can be modified to be highly active for specific electrochemical reactions by altering the coordination environment, for which we could utilize high-throughput computational screening. However, the complicated electrochemical reactions have shown wide-ranging different activities depending on the chemical environment and calculation methods, which has caused a lack of reliable clear-cut reference data. Thus, here we report the electrocatalytic properties of thirty 3d–5d transition-metal single-atoms [(TM)SAs] ligated by –NnCm, using density functional theory along with machine learning-based descriptors. High-performance (TM)SA catalysts in hydrogen evolution and oxygen evolution/reduction reactions are assessed. The –N2C2 moiety tends to show higher catalytic performance than those of the widely studied pure –C4/C3 and –N4/N3 moieties. A vast amount of information for electrochemical reactions including new reaction mechanisms will provide impacts on high-performance single-atom catalytic tuning. In addition to the data for electronic/geometric structures and electrocatalytic activities, their XANES spectra and conductivities, which are not available in the literature but are critically important for material characterization and faster reaction kinetics, will be a useful guide for developing new catalysts towards diverse electrocatalytic reactions.
|
Introduction
Recently, it has been of utmost importance to develop high-performance, energy-efficient and eco-friendly electrocatalysts. These can be utilized for various types of electrochemical reactions1,2 such as the HER,3 OER/ORR,4–7 water oxidation/splitting,8 fuel cell reactions,9 carbon-oxidation/CO-reduction–oxidation/CO2-reduction reactions,10,11 MeOH/EtOH oxidation reactions,12 nitrogen-reduction/ammonia-oxidation reactions,13 peroxide/chlorine evolution reactions,14 acid oxidation reaction,15etc. Until recently, most of these catalysts were usually made of highly expensive and scarce novel metals (Pt/Ir/Ru).16 Hence, tremendous efforts have been paid to using a tiny amount of novel metal SAs/NPs17,18 or replacing them with inexpensive alternatives.19 In this regard, minimal amounts of metal (M) SAs20–26 are exploited to maximize the active surface area and to tune the catalytic activity by coordinating the SAs to glue atoms in defect sites of graphene (Gr) or other 2D materials.17,27–36 However, while most metal NPs behave like conducting metals, metal SAs embedded in supports often lose some of the electric conductivity (σ), because once embedded metal SAs are ligated by C/N atoms in vacant sites, the π-conjugation through C/N atoms in the 2D sheet can be lost.17,27,28,31 This would cause a reduction in the kinetic reaction rate of SA electrocatalysts.31,37,38 To maximize the catalytic performance, (TM)SA-embedded electrocatalysts need to be optimized in view of coordination-structure, stability, conductivity, and catalytic activity. To this end, high-throughput computer screening is a powerful approach.39–46
(TM)SA catalysts embedded in M–N4/C4 and M–N3/C3 moieties of GN/Gr have been reported to be promising as HER/OER/ORR electrocatalysts.31,34 The localized d orbital energy levels in (TM)SAs are modified by the coordination environments.47 Thus, they dictate the stability and activity of SAs. Also, they dictate the σ when the (TM)SAs are embedded in π-conjugated GN, which enables fast transport of charges (i.e., electrons) in electrochemical reactions.17 In this regard, we have considered 3d (Sc–Zn), 4d (Y–Cd), and 5d (La, and Hf–Hg) TMs in the mono/di-vacancy defect sites of GN. GN is particularly considered here because of its high σ compared with that of Gr and its high tunability towards better electrochemical activity by a variety of coordination environments around a (TM)SA with tetra-coordination (–Nn=0–4C4−n) in di-vacancy sites or tri-coordination (–Nn=0–3C3−n) in mono-vacancy sites. We thus studied 11 different pyridinic/graphitic-type defect configurations for each (TM)SA embedded in GN. For high-throughput computational screening towards high-performance electrocatalysts of (TM)SAs embedded in GN [M–NnCm–GN], we have performed DFT calculations (see Method & Tables S1 and S2, ESI†).
Here we investigate the stability of each embedded (TM)SA, the X-ray absorption near-edge structure (XANES) (which helps in characterization of the coordination environment of SAs onto the GN template), the electronic properties including σ, the reaction mechanisms and the HER/OER/ORR activities of M–NnCm–GN. We find that the (TM)SAs, in particular, in the –N2C2 moiety, display superior durability and high σ in favour of fast HER reaction kinetics. These complicated electrochemical reactions have shown very different activities depending on different chemical environments and calculation methods, causing a lack of reliable clear-cut reference data. Thus, we report the lucid understanding of TM(SA) catalysts, in particular, for HER/OER/ORR towards water splitting and hydrogen fuel, which are vital for clean green energy environments such as hydrogen cars and electric power. We assess highly effective (TM)SAs ligated by various –NnCm, in particular, by –N2C2 for superb electrochemical performance. The machine learning-based descriptors describing high-performance HER/OER/ORR catalysts are also assessed.
Results and discussion
Formation and stability of M–NnCm–GN
To analyse the degree of formation and stability of various –NnCm moieties in GN/Gr defects, we study the representative pyridinic/graphitic-type defects and (TM)SA-embedded configurations and these formation energies including metal-embedding energies, based on the refined DFT method (Tables S1–S6, ESI†). Here we show that the (TM)SAs embedded in the –N2C2 vacant sites are consistently the most stable among possible conformations of M–NnCm–GN.
SA-catalysts templated in GN are often synthesized using Gr, GN, N-containing carbon compounds (such as melamine) and other materials.34,48–50 In the absence of metals, it is not energetically easy to form significant vacancy sites in GN/Gr (based on Table S3, ESI†). M–NnCm–GN is often formed in the presence of (TM)SAs and N sources (NH3, N2H4, etc.) or N-containing carbon materials.17,27,34,48–50 According to our DFT-predicted formation energies of 11 different pyridinic/graphitic-type defect configurations (Fig. 1 and Fig. S1, ESI†) with optimal H atoms attached on edge C/N atoms (Fig. 2a and Table S3, ESI†), the –NnCm defect sites in GN can be formed easily in the presence of H atoms (which is naturally present even in moderately high vacuum) with the formation energies of ∼2 eV. The formation of pyrrolic defect sites is less favoured due to their higher formation energies (∼5 eV) (Fig. S2 and Table S4, ESI†). We investigate the formation energies and metal embedding stabilities on the mono/di-vacancy pyridinic defect sites with tri/tetra-coordination (Nn=0–3C3−n)/(Nn=0–4C4−n) (Table S5, ESI†).
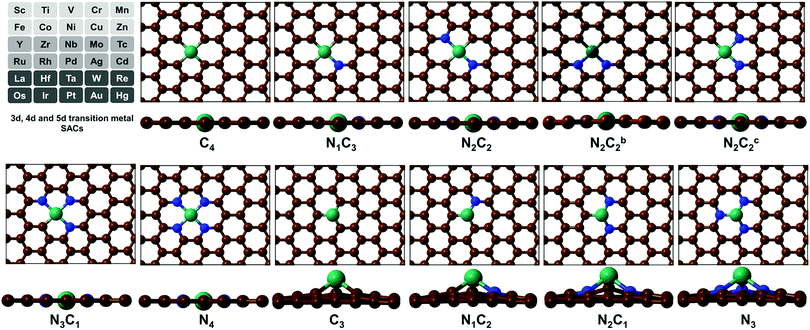 |
| | Fig. 1 Configurations of a (TM)SA embedded in M–NnCm–GN [n + m = 4 (a di-vacancy site) or 3 (a mono-vacancy site)]. The superscripts “b” and “c” in N2C2b and N2C2c denote two different cis forms of two N atoms with respect to the central TM, which is Ni here [C: brown, N: blue, and Ni: dark green]. (cf. Fig. S1, ESI† where the TM is Zr located above the graphene sheet due to its slightly larger radius; Fig. S2 and Tables S8 and S9 (ESI†) which show the off-plane distances for various (TM)SA moieties before and after H-adsorption; Table S10, ESI† after O-adsorption.) | |
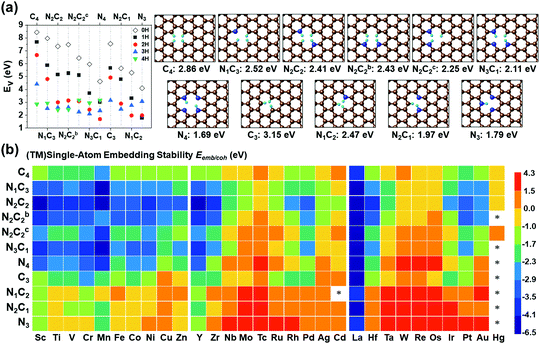 |
| | Fig. 2 Vacancy forming energies (Ev in eV) in –NnCmHh moieties of GN. (a) Ev in –NnCmHh moieties of GN in the presence of H (in atmosphere or acid medium) but in the absence of metal and their representative structures with the optimal H atoms attached on the edge C/N atoms at the RPBE(U) + TS level of theory. (Ev = Etotal − mμC − nμN − hμH, where μC = energy of a C atom in graphene, μN = energy of a N atom in N2, and μH = energy of a H atom in H2), and [C: brown, N: blue, and H: cyan] (cf. Table S4, ESI† for Ev). (b) (TM)SA embedding stability (Eemb/coh ≡ Eemb − E−coh; Ecoh = −E−coh in eV) color map of (TM)SAs in GN over the TM cohesion. Bluish colors strongly favor SA-embedding over TM-cohesion, while reddish colors favour the opposite. “*” denotes unstable systems. The –NnC4−n (particularly –N2C2) divacancy sites tend to be more bluish, while the –NnC3−n (particularly M–N3) mono-vacancy sites tend to be more reddish (cf. Table S6 for Eemb, Table S7 for Eemb/coh, ESI†). In –NnC3−n mono-vacancy sites, all (TM)SAs are off the GN plane by >1.5 Å. | |
The stability criterion of “metal embedding (embedding a metal atom into/onto the support)” over “metal cohesion (adding a metal atom to the bulk)” is defined as the difference (Eemb/coh = Eemb − E−coh) of the (TM)SA-embedding energy (Eemb) on GN (Fig. 2b and Tables S6, S7, ESI†) from the bulk cohesive energy (Ecoh= −E-coh; Table S1, ESI†). Here, embedding energy is defined in a negative value. A more negative embedding energy means stronger embedding, while cohesion is generally defined by a positive value. If Eemb/coh < 0, the embedding into graphene is preferred over metal clustering. However, even for small positive Eemb/coh, the embedding into graphene can still be transiently stable unless the concentration of metal is significantly present to be able to form clusters.
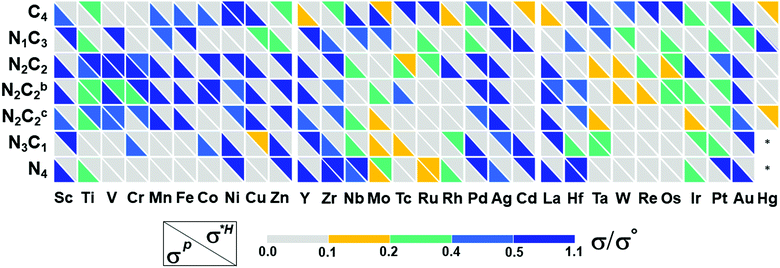
Embedding energy shows that the N2C2 moiety is the most favorable for the M–NnCm–GN formation with the trend of embedding strength (−Eemb) in the order of N2C2 > (N3C1, N2C2b, and N1C3) > (N2C2c) > (C4, N4, C3) > (N2C1, N1C2) > N3 (where N2C2b and N2C2c are the cis forms, while N2C2 is the trans form; Fig. 1 and Fig. S1, ESI†). The N2C2 case shows high embedding stability of (TM)SA over TM-cohesion, and thus their SAs can be easily formed (shown in blue-to-yellow color in Fig. 2b). In contrast, the cases of N1C2, N2C1 and N3 are less stable than the (TM)-cohesion (shown in orange/red color). Thus, these SAs are not so stable that their clusters/NPs are formed. Most (TM)SAs are slightly large to fit into the di-vacant site of GN, but several of the (TM)SAs (such as (Mn/Fe), Co/Ni/Cu/Zn/Pt) just fit into that site (Fig. S3 and Table S8, ESI†). The planar embedding structures are highly stable. However, in all –NnC3−n mono-vacancy moieties, all (TM)SAs are off the plane by more than 1.5 Å. Upon *H/*O adsorption, a slight/small structural change can be noted (Fig. S4 and Tables S9, S10, ESI†).
To understand the aggregation of SAs by clustering, we report the 2nd (TM)SA's clinging energy (E2M) and the (TM)SA-stability over TM-cohesion (E2M/coh) (Tables S11 and S12, ESI†). A few M–Nn=0–3C3−n–GN systems have smaller E2M/coh (or even negative values) than M–Nn=0–4C4−n–GN due to their weak metal–ligand interaction. Then, in some cases 2nd (TM)SAs bind the C atoms in the cases of –N1C3–GN and –C4–Gr sites, showing small E2M/coh. The Hg/Cd/Zn/Ag/Au/Pd TMs have rather small E2M/coh, and Mn/Cu have moderate values, while other (TM)SAs show large stability (>3eV) over TM-cohesion. Since d-orbitals of (TM)SAs split due to the metal–ligand interaction by C/N atoms in GN, the 1st (TM)SAs hardly interact with the 2nd (TM)SAs.
Electrochemical stability
To analyse the electrochemical stability of a (TM)SA embedded in a –NnCm moiety, we investigate its stability over metal-aggregation and metal-dissolution. We find that the –N2C2 moiety generally shows the highest durability against aggregation and dissolution.
The electrochemical stability is governed by dissolution potential 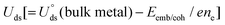 ,51 where
,51 where 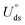 is the standard dissolution potential (pH = 0) of bulk metal in aqueous solution, e is the electron charge, and ne is the number of electrons involved in dissolution. A more positive Uds relative to the equilibrium potential indicates that the metal atoms bind the M–NnCm–GN support more strongly and the dissolution of metal atoms can be better avoided under electrochemical reactions, which enhances the durability of (TM)SA in a harsh electrochemical environment. While there can be a different number of electron transfers in the dissolution process, we here use a broad range of Uds (>0 V) based on the reported experimental studies on most of the synthesized (TM)SA-catalysts.52
is the standard dissolution potential (pH = 0) of bulk metal in aqueous solution, e is the electron charge, and ne is the number of electrons involved in dissolution. A more positive Uds relative to the equilibrium potential indicates that the metal atoms bind the M–NnCm–GN support more strongly and the dissolution of metal atoms can be better avoided under electrochemical reactions, which enhances the durability of (TM)SA in a harsh electrochemical environment. While there can be a different number of electron transfers in the dissolution process, we here use a broad range of Uds (>0 V) based on the reported experimental studies on most of the synthesized (TM)SA-catalysts.52
The stability against metal-aggregation and metal-dissolution in the M–NnCm–GN system is plotted in the Eemb/cohvs. Uds plot (Fig. 3). Negative Eemb/coh indicates the thermodynamical stability against clustering, while positive Uds reflects the electrochemical stability against dissolution. Following these two stability criteria, the whole figure is divided into four quadrants, depicted by blue, green, yellow, and pink. We set the stability criteria as the unaggregatable and indissoluble system with Eemb/coh < 0 eV and Uds > 0 V. It can be noted that most of the double vacancy systems are stable, and the –N2C2 moiety is particularly stable among –NmCn moieties (Tables S13 and S14, ESI†). In contrast, most TM elements (except for La and Y) in mono-vacancy site of –Nn=1–3C3−n–GN (excluding –C3–Gr having weak stability) show poor stability over metal cohesion, and so these SAs tend to aggregate as clusters. This is a salient finding in that most studies for TM(SA) electrocatalysts in Gr/GN have focused on pure C(C4/C3) or N(N4/N3) coordination except for very recent studies showing remarkable electrocatalytic performance in both activity and durability by using the –N2C2 moiety.17,27–29 Among all the M–NnCm–GN, we find that the –N2C2 moieties show favorable Eemb/coh and Uds values for promising hosts, which provide high durability for metal atoms. This finding would help in accelerating various SA-driven electrochemical reactions.
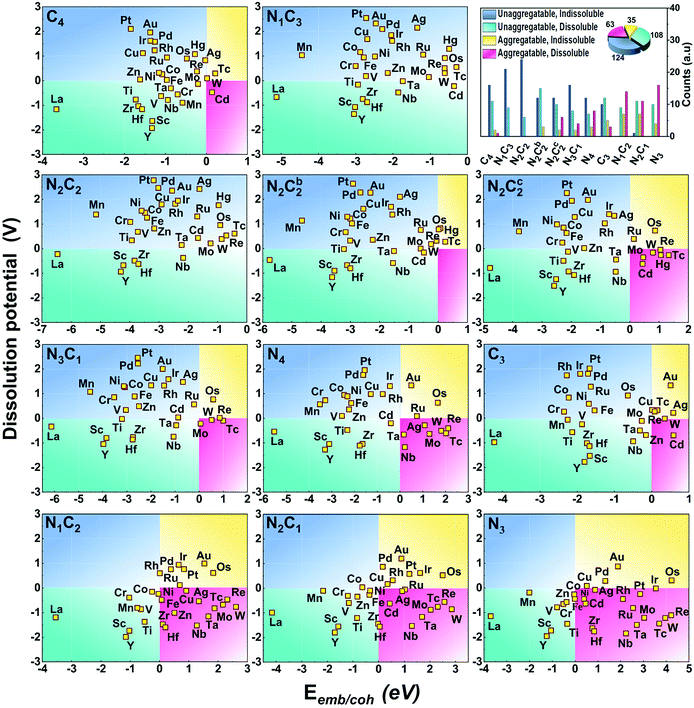 |
| | Fig. 3 Stability of (TM)SAs in M–NnCm–GN against metal aggregation and electrochemical dissolution in terms of (TM)SA-embedding over metal-cohesion (Eemb/coh) and dissolution potential (Uds) of metal atoms for M–NnCm–GN (cf. Tables S13 and S14, ESI†). The more negative Eemb/coh and the more positive Uds indicate the better stability. | |
Generally, the early (TM)SAs (Sc/Ti/Y/Zr/La/Hf) are more likely to be stabilized on the defective sites of the substrates, as indicated by the more negative Eemb/coh values, while the late (TM)SAs (Co–Zn, Rh–Cd, and Ir–Hg) tend to be stabilized against electrolytic dissolution. Overall, (TM)SAs including Pt/Pd/Au/Ag/Cu/Ir/Rh/Ni in the –N2C2 moiety display superior durability.
Electronic structure and XANES
The band structure is reflected in the X-ray absorption near edge structure (XANES), conductivity, catalytic activity, etc. The coordination environments of defect sites in GN affect the electronic properties of (TM)SAs and hence the thermodynamic adsorption/desorption strength of intermediates in electrochemical redox reactions. Here, we study the electronic properties of TM(SA) in M–NnCm–GN and XANES showing the coordination environments of a (TM)SA to aid experimental characterization.
Fig. 4a–f show the projected density of states (PDOS) for (V/Ni/Zn)–N2C2–GN and (V/Ni/Zn)–N3–GN defect sites. Square planar complexes are stable as 16-electron species.47 The Ni on a Ni–N2C2–GN (as Ni2+ ion) has eight d electrons after forming four bonds with four C/N atoms, resulting in a 16-electron d4 + dsp2 electron configuration in the square-planar like structure (Fig. 4a). Early TM elements like V on di-vacancy sites cannot fill the 16-electron configuration, and so the orbitals are not occupied evenly, showing a magnetic property (Fig. 4b, Fig. S5, S6, Table S15, ESI†). Group 12 elements like Zn have fully occupied 10 d electrons in +2 oxidized states along with 8 electrons from –N2C2, resulting in 18 electrons in total (Fig. 4c). Meanwhile, (TM)SAs on mono-vacancy sites have tetrahedral like structures. As an example, in Ni–N3–GN, the Ni atom (3d84s2) is tri-coordinated to N atoms, resulting in 16 electrons in total around the Ni atom. The calculation shows d9 electrons with one unoccupied minor spin state in the d-orbital (dxz) due to the electron transfer to the N atoms, showing a magnetic moment (Fig. 4d). The magnetic properties can change upon *H/*O-adsorption (Fig. S7, S8 and Tables S16, S17, ESI†). The less oxidized metal atom can be found in early TM elements as in V–N3–GN (Fig. 4e) and group 12 elements as in Zn–N3–GN (Fig. 4f).
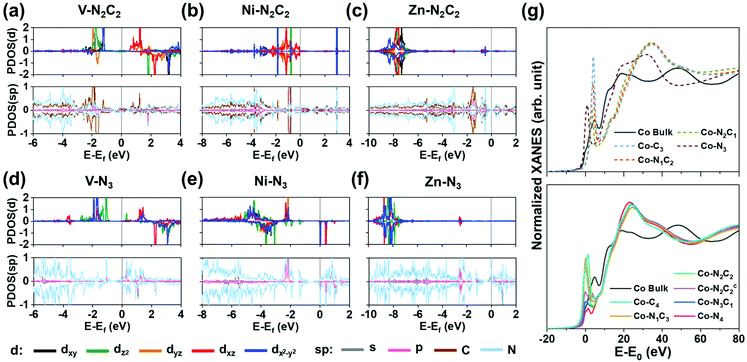 |
| | Fig. 4 Projected density of states (PDOS) of pristine M–N2C2–GN (a–c) and M–N3–GN systems (d–f) and (g) XANES of Co–N2C2–GN. (a and d) Case for M = V [early transition metal d3]. (b and e) Case for M = Ni [square planar d8; 16 electron rule]. (c and f) Case for M = Zn [group 12; fully occupied d orbital d10]. The major-spin (positive) and minor-spin (negative) PDOS of M (d orbitals) are plotted in each upper box, and those of M (s, p orbitals) and C, N and H are plotted in each lower box. Charge densities related to H-adsorption on each system are shown on top of PDOS plots. (Ni,Zn)–N2C2–GN have planar structures, while V–N2C2–GN has a non-planar structure. See the text for the planar d4 + dsp2 electron configuration favoring 16-electron rule and the octahedral sp3d2 electron configuration favoring 18-electron rule in the Ni case. (g) Co K-edge XANES of Co–NnCm–GN showing edge shifts to a higher energy than that of Co bulk, while giving a rising pre-edge (an exemplary case to show the difference between various Co–NnCm–GN coordination environments). See Fig. S9 (ESI†). | |
From these differences, XANES of M–NnCm–GN systems show each characteristic peak. For example, the edge energy of XANES shifts according to the oxidization state of (TM)SAs. Also, the symmetry of the structure and p–d orbital hybridization increase the intensity of pre-edge peaks. The group of TM is another factor affecting XANES associated with the number of empty orbitals for electron excitation. The calculated K-edge XANES data of all 3d and 4d (TM)SAs are in Fig. S9 (ESI†), which are essential for analyzing the SA-coordination analysis but not available in the literature. In Fig. 4g, the Co K-edge XANES is provided as an exemplary case to show the difference between various Co–NnCm–GN coordination environments. Co–N2C2–GN and Co–N2C2c–GN show distinguishable pre-edge structures from each other (Supplementary Note, ESI†). The pre-edge peaks are usually broader and less intense in 4d (TM)SAs, and additional effects like symmetry and distortion of the structure affect XANES, which helps in characterizing the coordination environments for each (TM)SA. In-situ XANES analysis upon *H/*O–adsorption during the HER/OER can also be made, as seen from the PDOS (Fig. S8, ESI†).
Electrical conductivity
A good electrical conductivity is vital for high-performance electrocatalysts. This issue was not important in the past because the catalysts on electrodes were made with conductive metals or carbon materials, but nowadays the SA-embedded supports are not necessarily good conductors. Hence, σ is an important issue in determining the kinetic reaction rate, in particular, in fast reactions such as the HER. However, there is no serious study on this issue except for our recent work.17,27,28
In the HER, the reaction rates in (TM)SAs are often very fast by the Tafel mechanism where H2 gas is released by combining two neighboring adsorbed H atoms on catalytic sites; thus, fast charge transfer plays a critical role.31 This charge transfer effect is rather less important in the OER, which shows a rather sluggish reaction rate. Thus, we consider the fast H-adsorption in the HER. Here, the σ for M–NnCm–GN before/after H-adsorption is calculated at 300 K and compared with the σ of 2.1% N-doped GN [σo ≈ 7 × 102σ(Gr)] (Fig. S10 and Tables S18, S19, ESI†). Overall, M–N2C2 tends to show higher σ than any other double vacancy M–NnCm–GN system (Fig. 5). The change in electronic structure by coordination environment affects the σ significantly. The covalent bonding of Gr is disrupted by (TM)SA-doping and N-adsorption; hence, the σ of metal-doped GN tends to be much reduced, showing poor conductivity. Among the (TM)SAs, early TM elements [group-3(Sc/Y/La), and group-4(Ti/Zr/Hf)] show moderately high σ (>0.2σo) regardless of NnCm-coordination/H-adsorption environments, while other (TM)SAs doped on –NnCm–GN introduce band gaps, resulting in rather poor σ. As examples, we analysed the band structure of Ni/Pd/Pt–N2C2–GN as a candidate for HER catalysts (Fig. S11, ESI†). Their pristine structures show poor conductivity with small band gaps near the Fermi energy level (EF), while the electrons fill the valence band fully up to the Dirac-like point in the band structure. Upon adsorbing H*, the conduction band gets filled and the σ increases with one conducting channel at EF = 0. Highly conductive systems have conducting channels at EF and accelerate electrocatalytic reactions with fast charge transfer.
 |
| | Fig. 5 Color code map for the electrical conductivity (σ) of M–NnCm–GN with respect to that of GN before and after H-adsorption. Each σ is calculated from the band structure. Assuming similar scattering rates (τ) for M–NnCm–GN and GN from the experimental value of ∼100 fs,62 the [σ(M–NnCm–GN)/σo] values are reported in Tables S18 and S19 (ESI†) [σo/σ(Gr) = ∼7 × 102]. “*” denotes an unstable state. Overall, among the divalent NnC4−n moities, the N2C2 moiety tends to show high σ for most of the TM(SA)s embedded in GN. For example, Co, Ni, Pd and Pt show enhanced σ upon H-adsorption, which accelerates the HER rate towards the Tafel mechanism, which readily combines two neighboring adsorbed H atoms into H2 gas. Since the OER/ORR rates are sluggish, the large overpotential is much more critical than the high σ. Thus, this high σ is particularly investigated for fast HER. | |
We also study the σ when O*, HO*, and HOO* are adsorbed on the active sites of M–NnCm–GN, where the σ tends to decrease compared to the pristine case (Fig, S12 and Table S19b, ESI†). However, in the cases of OER/ORR, the overpotentials are large, and so lowering their high barriers, which exponentially forbid the charge transfer, is the critical issue, while the conductivity is not a significant issue unless it becomes very small.
Electrochemical activity: reaction mechanism
For the adsorption of intermediates (O*/HO*/HOO*-adsorption) in the OER/ORR, the well-known mechanism (path-I) for M–N/C prevails. However, we note a new mechanism (path-II) in the OER/ORR for certain (TM)SA cases of M–NnCm–GN. Here, we discuss both mechanisms.
Based on the structural/electronic stability of M–NnCm–GN, the candidates for HER/OER/ORR active catalysts are considered particularly among double vacancy systems. The schematics of HER/OER/ORR mechanisms are shown in Fig. 6. The H*/O*/HO*/HOO*-adsorption free energies (ΔGH*/HO*/O*/HOO*) are investigated (Methods). For the HER, the reaction rate in Volmer–Tafel mechanism is fast by combining neighboring adsorbed H atoms on active sites into H2, while that in the Volmer–Heyrovsky mechanism is slow because an additional H* should be near the H* adsorbed on the neighboring active site. In OER and ORR cases, path-I where each O*/HO*/HOO* is adsorbed on a metal SA site has generally been considered. However, we find a new path (path-II), which has OH− on the metal–SA and beside O* (rather than on the O* attached to the metal-SA because of the difficulty in adsorbing OH− on O*). Thus, the O-poisoned site (M–O*) works as a new active site, and each O*/HO*/HOO* is attached on the metal-SA site. The reverse steps of these two mechanisms are also applied to the ORR. Though path-I is generally preferred in most (TM)SAs, in some metals path-II is preferred. For example, V–N4 follows path-II for the OER. The preferred mechanism depends on TM and the coordination environment.
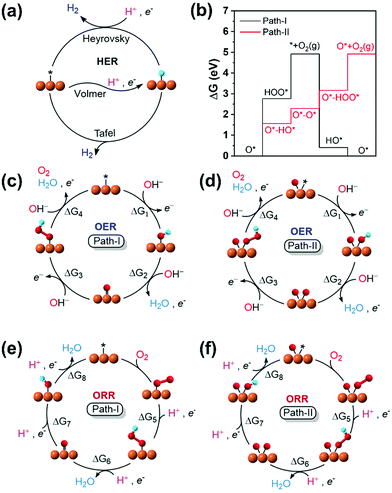 |
| | Fig. 6 Schematic representation for the mechanisms and reaction pathways of electrocatalytic reaction cycles on a metal binding site. (a) HER. (b) Free energy profiles of V–N4 for OER path-I and path-II. (c) OER: path-I. (d) OER: path-II. (e) ORR: path-I. (f) ORR: path-II. On most systems, the OER/ORR follows the conventional mechanism with the metal as the active site (path-I). On a few systems, surface poisoning by oxygen inhibits direct *OOH formation. They follow a different pathway with an O-poisoned metal site (O*–M) as the active site, while other intermediates are adsorbed on O*-M site [path-II: Re/Os for C4; (Ta,Re)/(Mo,Tc,Ru,W,Os) for N2C2; (Nb,Mo,Tc,Ta,W)/(V,Ru,Re,Os) for N4]. The direct O2 OER mechanism (or dissociative ORR mechanism) is not preferable (see Tables S26 and S27, Supplementary Note, ESI†). See the equation for ΔG1–8 in Methods. | |
HER activity
The HER of M–NnCm–GN is achieved through their active sites such as metal atom M, and bridge sites between M and C, or C/N atoms. One should also consider if the Kubas active site54 can help in accelerating H2 desorption by combining both H atoms, leading to a Tafel-like reaction. Here we assess high-performance HER SA catalysts.
The catalytic activity is investigated in terms of H-adsorption binding/free energies (ΔEH*/ΔGH* in Tables S20 and S21, ESI†) for the intermediates during the HER. The solvent effect on the HER is rather insignificant within 0.03 eV for ΔEH*/ΔGH* (see Table S22, ESI†). The zero-point energy and entropy contributions to ΔGH* when H is on a metal atom show an almost constant shift by 0.24 eV (for H2),53 but this shift changes significantly when H is on a C/N atom or a bridging bond between metal and C/N atoms, and thus such a correction is made by phonon calculations. Then, the refined HER overpotential (ηHER, Tables S30a and S31, ESI†) is calculated based on the ΔGH*, which is used to find outstanding HER catalysts. Mo/Rh/La/Os/Pt in C4–Gr, Ti/Zr/Ag/Cd in N1C3–GN, Co/Ni/Ag in N2C2b–GN, Cr/Cu/Cd in N3C1–GN, Rh/Cd in N4–GN, and Ni/Ru/Rh/Pt in –N2C2-GN templates show −ηHER < 0.1 V (red colored in Fig. 7a and in filled red triangle in Fig. 7b) and are likely to be super-performing HER catalysts, given that the Pt(111) surface shows −ηHER = 0.2 V on the fcc-hollow site. Indeed, Pt–N2C2 (−ηexpt/calc= 0.01–0.02/0.03 V),17 Ru–N2C2 (−ηexpt/calc= 0.01–0.04/0.06 V)27–29 and Rh–N2C2 (−ηexpt/calc = 0.04/0.06 V)55 are reported as remarkably active HER (TM)SA catalysts. In these cases, the H adsorption sites are shared by both the metal and C (not N) except for Ru (Fig. 7a).
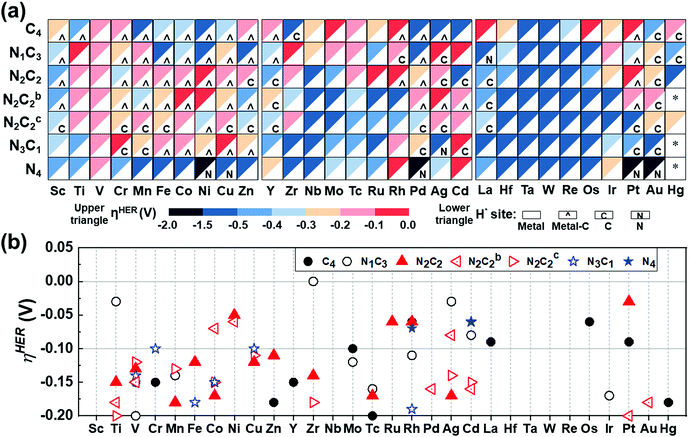 |
| | Fig. 7 HER overpotentials (ηHER) of M–NnCm–GN based on the refined values (Table S30 based on Tables S20, S21, ESI†). (a) Color code map for ηHER (upper triangle) and most stable H-adsorption sites (H*) (lower triangle), which are denoted by metal site (in white blank), metal-C bridge site (by a hat symbol “^”), C site (by “C”) or N site (by “N”). The solvent effect for ΔEH*/ΔGH* is generally very small (Table S22, ESI†). Also, it is worthwhile to consider the Volmer–Kubas reaction free energies (Table S23, ESI†). “*” denotes unstable systems. The reddish colors represent near-zero free energies (responsible for near-zero overpotential). Zr/Ti/Ag/Cd–N1C3, Pt/Ni/Ru/Rh–N2C2, Cd/Rh–N4, and Rh/Os/Pt–C4 would be high-performance HER catalysts (−0.1 V < ηHER < 0 in red color) and those within (−0.2 V < ηHER < −0.1 V in pink color) are likely to perform well in the HER, as compared with a Pt(111) surface (ηHER = −0.2 V). (b) Cases for −0.2 V < ηHER < 0, many of which belong to the –N2C2 type (denoted by filled red triangle) and the –N2C2b/N2C2c types (in open red triangles). | |
It is generally expected that the strongest H-adsorption site for M–NnCm–GN is just metal-SA M, as noted in most of the previous literature, which did not consider other options. However, in certain cases it is a C or N site, while often sharing the metal site. The H adsorption sites can be shared by both metal and C (not N) (i.e., the bridge site denoted by a hat symbol in Fig. 7). The metal-adjacent C sites (but not N sites) are the most active in some cases of –N3C1, –N2C2, –N2C2b, –N2C2c, –N1C3, and –C4, while the N sites can be the most active in certain cases of –N3C1 and –N4. In certain cases where a C or N site is the most active, the metal site can be a coactive site. Among the active C/N atoms, the metals in Zr–C4 and Pt–N4 are nearly compatible in activity to the C and N atoms, respectively. In particular, when a H atom is adsorbed on 3d (Sc/Cr/Mn/Fe/Co/Ni/Cu/Zn), 4d (Y/Rh/Pd), and 5d (Pt) TM–GN systems, the H tends to share a C site, while a H adsorbed on the (Ag/La/Pt)–GN system tends to be on C/N sites instead of metal sites (Fig. 7a).
When a 2nd H atom is attached to the same TM atom embedded in GN, the Kubas active site54 can help in accelerating H2 desorption by combining both H atoms, leading to a Tafel-like reaction, but its role is not dominating in the HER reaction. The Volmer–Kubas structures and free energy changes for selected (TM)SAs in (N2C2) systems are shown along with the PDOS of Ru upon H/2H-adsorption in Fig. S13, 14 and Table S23 (ESI†).
OER/ORR activity
We note that the (TM)SA–NnCm–GN catalysts show good performance in the OER/ORR, based on their overpotentials. Here, their OER/ORR performance and their preferred pathways among two different paths (I and II) are investigated and the predicted high-performance OER/ORR materials are assessed.
We consider the catalytic activity in terms of the overpotential of the OER/ORR (ηOER/ηORR). The HO*/O*/HOO*-adsorption free energies (ΔGHO*/O*/HOO*) are calculated by adding zero-point energy and entropic contributions to binding energies of each intermediate for path-I and path-II (Tables S24–S27, Methods, ESI†). Then, ηOER/ηORR values are obtained from the free energies of intermediates during OER/ORR (Methods). The lowest ηOER/ηORR values between path-I and path-II are reported. The solvent effect is important in particular for d1 or d2 SAs, while it is much less in other cases (Table S28 and S29, ESI†). Here we discuss the activities by taking into account the solvent effect.
In the OER/ORR cases, only several TM(SA)s show good activity regardless of coordination environments (Fig. 8a). Among thermodynamically/electrochemically stable systems, the low ηOER/V values (compared with 0.43 ± 0.09 (upper limit: 0.52) for Pt(111)) are shown for Pt/Ni–N2C2 (0.27/0.40), Ni/Pd–C4 (0.31/0.36), and Rh–N4 (0.31) (Tables S30b and S31, ESI†). The low ηORR/V values (compared with 0.47 ± 0.21 (upper limit 0.68) for Pt(111)) are shown for Ir/Rh–N4 (0.31/0.36), Pd/Ni/Pt/Cd–C4 (0.34/0.43/0.46/0.48), Ru–N3C1 (0.36), Ni/Pd/Pt/Hg/Zn–N1C3 (0.36/0.36/0.37/0.48/0.50), Zn–N2C2b (0.48), Cd–C4 (0.48), Rh–N3C1 (0.49), Cd–N2C2 (0.55), Mo/Tc/Co–N4 (0.55/0.55/0.58), Co/Ni–N2C2b (0.60/0.66), Ni/Ir/Ru–N2C2c (0.64/0.64/0.68), and Zn/Pt/Ni/Co–N2C2 (0.65/0.65/0.66/0.67) (Tables S30c and S31, ESI†). Our predicted ηORR[Pt–N1C3] = 0.37 V is in agreement with an experimental value (ηORR = ∼0.3 V) of Pt in GN as one of possible structures of Pt–NnCm.56 Fe and Co atoms embedded in N-doped carbon templates were reported to be better in performance than those in pure carbon templates, respectively,57–60 while Co behaves better than Fe in both N-doped and un-doped carbon templates, respectively,57 the results of which are consistent with our predicted values. Co–N4 is predicted to be the most active for the ORR among Co–NnCm–GN, in agreement with experiments.60
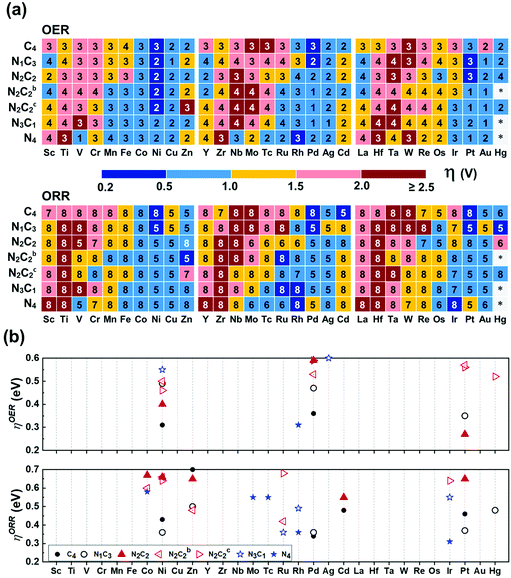 |
| | Fig. 8 OER/ORR overpotentials (ηOER/ORR) based on the refined values (Table S30 based on Tables S24–S29, ESI†). (a) Color code map for ηOER/ORR and their corresponding potential determining step (“1–8“ in each small box denotes ΔG1–8, respectively; Fig. 6 & Methods). The lowest ηOER/ORR is reported among path-I and path-II. (b) Color code maps for ηOER < 0.6 V and ηORR < 0.7 V (Table S30, ESI†). High-performance SA catalysts for the OER are predicted to be Pt–N2C2 (ηOER = 0.27 V), Ni–C4 (0.31 V), Rh–N4 (0.31 V), Pd–C4 (0.36 V), and Ni–N2C2 (0.40 V), while those for ORR are Ir/Rh–N4 (ηORR =0.31/0.36 V), Pd–C4 (0.34 V), Ru–N3C1 (0.36 V), Ni/Pd/Pt–N1C3 (0.36/0.36/0.37 V), Pt/Cd–C4 (0.46/0.48 V), and Zn–N2C2b (0.48 V) and Hg–N1C3 (0.48 V). | |
The HO* and HOO* are adsorbed on metal atoms much more strongly than on the surrounding C/N atoms. Although O* forms a bond with both M and C in certain cases, the active sites for the OER/ORR are metal sites in all investigated systems in contrast to those for the HER, which vary from metal to C/N or metal-C bridging site depending on the metal and ligands. As a result, the ηOER/ηORR values of each (TM)SA are affected by the coordination environment.
In general, OH− tends to be on top of O* to form HOO* (path I), known as the well-known OER/ORR mechanism. However, we find that in some systems the HO* adsorbs on the O-poisoned metal site (M–O*), which needs to be considered as the active site (path-II). Re/Os prefers path-II in all templates, while V/Nb follows path-II only in –N4–GN. Tc/Ru/Ta/W/Mo follows path-II only in –N4–GN and –N2C2c–GN. Also, the Cr/Fe follows path-II only in –N2C2c–GN. Tc/Ru/Ta/W/Mo follows path-II on most of the double vacancy –NnCm–GN except –C4–Gr. When O* tends to adsorb strongly on a metal atom, it tends to follow path-II. If the metal atom is more positively charged due to a higher coordination by N atoms, two O atoms can be further coordinated. For example, ΔGO* on V–N4 (−1.17 eV) is much stronger than those on V–N2C2 (−0.01 eV) and V–C4 (0.26 eV). The adsorption of OH− on top of O* makes the M–O* bonding weaker (i.e., ΔGHOO* > ΔGO*); then, the HOO* formation step along path-I tends to be less favoured. In contrast, the OH− adsorption (beside O*) on the metal atom creates an additional M–O* bond [HO*–(M–O*)]; nevertheless, the repulsion between two O atoms around the metal atom arises. If this repulsion is not large enough, path-II would be favoured, and vice versa. The O* adsorption energy gets affected by the coordination environment around the metal atom. However, the optimal overpotential is governed by the balance among the four e− reaction steps in the OER/ORR, and thus, the delicate preference between paths I and II is not easily describable. The stability of the M–O* site is confirmed by Pourbaix diagrams (Fig. S15–S17, ESI†).
Descriptors for HER/OER/ORR activity
As a supervised machine learning approach to the classification of di-vacancy configurations into good and bad catalysts, we searched for a descriptor taking the properties of atomic elements constituting the configuration, which works universally for all M–NnCm–GN systems.
We considered the following machine learning algorithms: Gaussian naïve Bayes, logistic regression, k-nearest neighbors, radius neighbor classifier, support vector classifier, neural network, and decision trees as well as the following ensemble methods: random forest, extremely randomized trees, and gradient boosting. The best hyper-parameters were found using an exhaustive search implemented in GridSearchCV.61
We constructed the descriptors as Coulomb matrix elements (CM = Z1Z2/r12 where Z = atomic number and r12 = the distance from each other)62 between M and neighbouring C/N atoms, between M and adsorbent atoms (H/O), and between adsorbents and the closest non-metal surface atom (C/N), along with atomic numbers, atomic first ionization energy etc. (see Supplementary Note, ESI†). The classified activity data of M–NnCm–GN systems at given criteria (|ηHER| < 0.2 V for HER and ηOER/ORR < 1 V for OER/ORR) are used for training and test. The Coulomb matrix for the distances from the TM to the coordinating C/N atoms and the first ionization potential of TM are found to describe high-performance HER/OER/ORR catalysts with ROC AUC63 of 0.79–0.89 (Fig. S18–S21 and Tables S32–S34, ESI†). The importance of engineering coordination environments of (TM)SA–GN catalysts is noticed based on the correlation between activity and coordination environment, which is described as a combination of the ionization energy of the metal atom and the Coulomb matrix elements with the ligating atoms.
Conclusion
TM(SA) electrocatalysts of M–NnCm–GN are analyzed to characterize their stability/durability, activity, active sites, electronic properties, σ, and XANES depending on the coordination environment. This diverse coordination-driven information essential for the design of highly efficient SA-driven electrocatalysts is rather barely available in previous studies despite the development of diverse SA-driven electrochemical catalysts. The early (TM)SAs are more likely to be stabilized on the defective site of substrates, while the late (TM)SAs tend to be stabilized against electrolytic dissolution. The (TM)SAs in –N2C2 moiety display superior durability and high σ in favor of fast Tafel reaction kinetics. The present results show most suitable coordination environments for stability and activity towards the design of high-performance (TM)SA electrocatalysts. Overall, (TM)SAs including Pt/Pd/Au/Ag/Cu/Ir/Rh/Ni in the –N2C2 moiety display superior durability. Thus, instead of –N4 or –C4 moieties that have been well studied, the –N2C2 moiety is suggested to be highly useful. As for catalytic activity, the –N2C2 moiety performs very well in the HER and reasonably well in the OER, while –N4, –C4, –N3C1 and –N1C3 moieties perform well in the ORR. Ti/Zr/Ag/Cd–N1C3, Pt/Ni/Ru/Rh–N2C2, Cd/Rh–N4, and Mo/Rh/La/Os/Pt–C4 are likely to perform well in the HER (−ηHER/V < 0.1). The low ηOER/V values are shown for Pt/Ni–N2C2 (0.27/0.40), Ni/Pd-C4 (0.31/0.36), and Rh–N4 (0.31). The low ηORR/V values are found for Ir/Rh–N4 (0.31/0.36), Pd/Ni/Pt/Cd–C4 (0.34/0.43/0.46/0.48), Ru–N3C1 (0.36), Ni/Pd/Pt/Hg/Zn–N1C3 (0.36/0.36/0.37/0.48/0.50), Zn–N2C2b (0.48), Cd–C4 (0.48), Rh–N3C1 (0.49), and Cd–N2C2 (0.50). Consequently, the diversity of –NnCm moieties can be exploited to achieve better performance for diverse types of electrocatlytic reactions. The calculated K-edge XANES of systems for (TM)SAs and conductivity would be beneficial in experimental characterization of their coordination environments and fast reaction kinetics of TM(SA). The present findings should be vital for the design of new (TM)SA catalysts for various electrocatalytic reactions.
Computational methods
Theoretical calculations
Spin-polarized DFT calculations using the Vienna ab initio simulation package (VASP)64 are performed to optimize structures and to obtain electronic properties. Instead of the Perdew–Burke–Ernzerhof (PBE)65 exchange–correlation functional (which is commonly used for bulk systems), the revised PBE (RPBE) type66 (which was optimized for surface states) is used for these 2-dimensional (2D) systems with Tkatchenko–Scheffler (TS)67 dispersion correction. For 3d metals, the Hubbard Ueff correction68 (with the values of 2.11, 2.58, 2.72, 2.79, 3.06, 3.29, 3.42, 3.40, 3.87, and 4.12 eV in the order of Sc through Zn) is included based on the literature.39 Given that our focus is more on the surface phenomena, the RBPE(U)+TS method is employed here. The RPBE+TS results without U are also provided for a guide even for 3d elements because the experimental cohesive energies and interatomic distances of TMs tend to be between RPBE(U)+TS and RPBE+TS values (Tables S1 and S2, ESI†). Thus, in the evaluation of η, we may consider both U=0 and U values as the upper/lower limits, or simply consider their mid value with the error bar (ε) as the half of their difference (see the legend of Table S30, ESI†).
Bulk transition metals are optimized with the conjugated gradient algorithm using a Monkhorst–Pack grid of 11 × 11 × 11 special k points and 700 eV cutoff for the kinetic energy and the Gaussian smearing method with an energy width of 0.02 eV. Crystal structures for all bulk transition metals are used for their primitive unit cells and their lattice vectors. Despite the fact that the dispersion correction (which is not present in PBE results) is essential, the TS dispersion correction (PBE+TS) tends to overestimate the experimental TM cohesive energies probably because the parameters of the PBE functional (without considering dispersion correction) were optimized directly for the experimental data. The Hubbard U correction is also necessary for self-energy correction in order to obtain more reliable electronic structure such as a band gap, but it tends to underestimate cohesive energies. Since the parameters of PBE were optimized for bulk materials, RPBE was introduced to give better surface energies.69 In this regard, RPBE(U)+TS is expected to better describe the 2D systems including both 3d TMs and π systems (such as Gr and GN). Thus, we have chosen the RPBE(U) + TS method to study free energies of (TM)SAs embedded in 2D GN, while taking into account spin polarization. For the study of the catalytic phenomena, the projector augmented wave (PAW)70 pseudopotentials are employed and the kinetic energy cutoff for plane-wave expansions is set to 500 eV with Gaussian broadening by 0.05 eV. Each energy of (TM)SA is optimized in the asymmetric supercell (19 Å × 20 Å × 21 Å) for a better description of their degeneracy states using the Γ point. Each isolated (TM)SA is embedded in a Gr supercell composed of 48 C atoms, and 7 × 7 × 1 k-point sampling is used. Geometric relaxations are done until the Hellman–Feynman forces converge to 0.01 eV Å.
Solvent effect
The solvation effect is considered using the pure implicit model implemented in VASPsol71 and the explicit model (which uses an implicit model in the presence of one water molecule added explicitly to the system). For the HER overpotentials, the solvent effect is found to be insignificant (no more than 0.03 eV for ΔGH*) (Table S22, ESI†), so it was not necessary to include the solvent effect in HER analysis. In the case of the Mn system, the magnetic moment of the metal atom changes in the implicit solvation model, resulting in 0.09 eV in free energy change, but it does not change in the explicit model, which is more reliable, resulting in an insignificant solvent effect on the ΔGH*. However, the solvent effect is somewhat significant in the OER/ORR, and so it is included in our results and discussion (Tables S27–S29, ESI†). In a bulk dielectric medium the implicit solvent model would be reliable, while in ~1 nm-sized confined medium the Debye screening is far from complete, and so the dielectric constant is much reduced due to the limited polarization arising from the rotationally forbidden surface water molecules at catalytic sites. Owing to the much reduced dielectric effect of interfacial water, the implicit solvent effect could overestimate the solvent effects on η of (TM)SA catalysts embedded on GN/Gr. In this regard, we consider both vacuum and implicit solvent models as the upper/lower limits, namely the mid value with the error bar as the half of their difference (see the legend of Table 30, ESI†).
Reaction mechanism and Gibbs free energy calculation
While the HER is a fast reaction, the OER is a sluggish reaction, which generates oxygen gas through several electron/proton complex reaction pathways. The OER consists of four elementary steps, which strongly depend on the pH of the reaction medium. In acidic pH, the reaction operates via oxidation of two water molecules to form one oxygen molecule with four proton-coupled electron transfer steps, while in basic pH, the four hydroxyl groups are converted into O2 and two water molecules with four electron transfer steps. ORR kinetics is also generally slow. In acidic conditions, O2 reduces to H2O with four proton-coupled electron transfer steps, while in basic conditions, O2 reduces to OH− with four electron transfer steps. The reactions for the HER, OER and ORR in acidic and basic pH are summarized as follows.31,72,73 The detailed mechanisms we considered are described below.
HER mechanism
HER in acidic conditions with free energy equations:53| | | * + H+ + e− → H* → * + 0.5H2 | (1) |
| | | ΔGH* = (EH* − E* − 0.5EH2) − (ZPEH* − ZPE* − 0.5ZPEH2) − T(SH* − S* − 0.5SH2) | (2) |
HER in basic conditions is the same as below with the same free energy equation as eqn (2):
| | | * + H2O + e− → H* + OH− → * + 0.5H2 | (3) |
OER and ORR mechanisms
We have considered various OER and ORR mechanisms, as shown below. The overpotential of each mechanism is calculated from the maximum difference between the Gibbs free energies in each step, as provided for path-I in (37) and (38). The lowest overpotential values for the best pathway are reported in Tables S28–S29 (ESI†).
(ii) ORR mechanism in basic conditions.
d. Conventional (associative) mechanism on M (path-I):| | | * + O2 + H2O + e− ⇌ HOO* + OH− | (21) |
| | 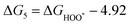 | (22) |
| | 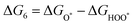 | (24) |
| | | O* + H2O + e− ⇌ HO* + OH− | (25) |
| | 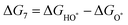 | (26) |
| | 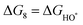 | (28) |
e. Conventional (associative) mechanism on O*–M (path-II):
| | | O*–M + O2 + H2O + e− ⇌ O*–HOO* + OH− | (29) |
| | | O*–HOO* + e− ⇌ O*–O* + OH− | (30) |
| | | O*–O* + H2O + e− ⇌ O*–HO* + OH− | (31) |
| | | O*–HO* + e− ⇌ O*–M + OH− | (32) |
f. Dissociative mechanism:
| | | O*–O* + H2O + e− ⇌ O*–HO* + OH− | (34) |
| | | O*–HO* + H2O + e− ⇌ HO*–HO* + OH− | (35) |
| | | HO*–HO* + 2e− ⇌ * + 2OH− | (36) |
Then, the overpotential (η) of OER, and ORR for path-I are calculated as follows:31,72,73
| | | ηOER = max(ΔG1, ΔG2, ΔG3, ΔG4)/e − 1.23 V | (37) |
| | | ηORR = max(ΔG5, ΔG6, ΔG7, ΔG8)/e + 1.23 V | (38) |
The intermediates of the OER and ORR are the same in both acidic and basic conditions and the Gibbs free energies of adsorbates are calculated by adding zero-point energies (ZPEs) and entropic contributions (S) to the adsorption energies. 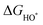 ,
,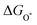 , and
, and 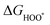 equations are given for path-I and
equations are given for path-I and 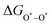 ,
, 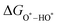 , and
, and 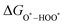 can be calculated by changing G* to GO*–M in each equation, where the TS value of H2 is 0.41 eV and that of H2O is 0.67 eV.53 For the active site and adsorbates, their TS values are 0 eV.
can be calculated by changing G* to GO*–M in each equation, where the TS value of H2 is 0.41 eV and that of H2O is 0.67 eV.53 For the active site and adsorbates, their TS values are 0 eV.
| | 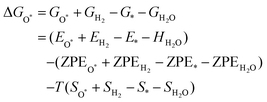 | (39) |
| | 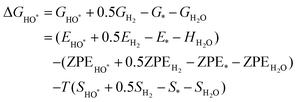 | (40) |
| | 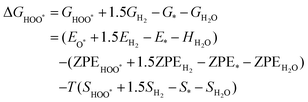 | (41) |
where the
TS value of H
2 is 0.41 eV and that of H
2O is 0.67 eV.
52 For active sites and adsorbates, their
TS values are 0 eV.
Electrical conductivity and XANES calculation
Electrical conductivities (σ) are calculated using the Boltzmann transport theory74 and the scattering rates τ are assumed to be the same as ≈100 fs for GN.75 X-ray absorption near edge structures for all optimized structures are calculated by using the FDMNES code.76 Muffin-tin approximation and the Hedin–Lundqvist functional are used to conduct full multiple scattering calculations. The spectra are convoluted using the Lorentzian function.
Author contributions
M.H., D.Y.K. and C.W.M. initiated the project. M.H., D.Y.K., M.U., and C.W.M. performed DFT calculations and analyzed the results. V.G. and M.U. investigated machine learning-based descriptors. M.H., C.W.M. and K.S.K. wrote the manuscript. K.S.K. supervised the project.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by NRF (National Honor Scientist Program: 2010-0020414), A.I. Incubation Project Fund (1.210091.01) of UNIST, and KISTI (KSC-2018-CHA-0057, KSC-2019-CRE-0103, KSC-2019-CRE-0253, KSC-2020-CRE-0049, KSC-2020-CRE-0146 and KSC-2020-CRE-0185). C. W. M., M. H. and D. Y. K. acknowledge the support from KISTI (KSC-2019-CRE-0139, KSC-2020-CRE-0081, and KSC-2021-CRE-0009, respectively). D. Y. K. also acknowledges the NRF grant funded by the Korean Government (2018H1A2A1062086).
References
- J. Zhu, L. Hu, P. Zhao, L. Y. S. Lee and K. Y. Wong, Chem. Rev., 2019, 120, 851–918 CrossRef PubMed
 .
.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed
 .
.
- J. Mahmood, F. Li, S. M. Jung, M. S. Okyay, I. Ahmad, S. J. Kim, N. Park, H. Y. Jeong and J. B. Baek, Nat. Nanotechnol., 2017, 12, 441–446 CrossRef CAS PubMed
 .
.
- V. Vij, S. Sultan, A. M. Harzandi, A. Meena, J. N. Tiwari, W. G. Lee, T. Yoon and K. S. Kim, ACS Catal., 2017, 7, 7196–7225 CrossRef CAS
 .
.
- M. Lefèvre, E. Proietti, F. Jaouen and J. P. Dodelet, Science, 2009, 324, 71–74 CrossRef PubMed
 .
.
- H. W. Kim, M. B. Ross, N. Kornienko, L. Zhang, J. Guo, P. Yang and B. D. McCloskey, Nat. Catal., 2018, 1, 282–290 CrossRef
 .
.
- E. Jung, H. Shin, B. H. Lee, V. Efremov, S. Lee, H. S. Lee, J. Kim, W. Hooch Antink, S. Park, K. S. Lee, S. P. Cho, J. S. Yoo, Y. E. Sung and T. Hyeon, Nat. Mater., 2020, 19, 436–442 CrossRef CAS PubMed
 .
.
- S. Sultan, M. Ha, D. Y. Kim, J. N. Tiwari, C. W. Myung, A. Meena, T. J. Shin, K. H. Chae and K. S. Kim, Nat. Commun., 2019, 10, 5195 CrossRef PubMed
 .
.
- M. K. Debe, Nature, 2012, 486, 43–51 CrossRef CAS PubMed
 .
.
- Y. Y. Birdja, E. Pérez-Gallent, M. C. Figueiredo, A. J. Göttle, F. Calle-Vallejo and M. T. M. Koper, Nat. Energy, 2019, 4, 732–745 CrossRef CAS
 .
.
- Y. Wu, Z. Jiang, X. Lu, Y. Liang and H. Wang, Nature, 2019, 575, 639–642 CrossRef CAS PubMed
 .
.
- J. N. Tiwari, W. G. Lee, S. Sultan, M. Yousuf, A. M. Harzandi, V. Vij and K. S. Kim, ACS Nano, 2017, 11, 7729–7735 CrossRef CAS PubMed
 .
.
- B. H. R. Suryanto, H. L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Nat. Catal., 2019, 2, 290–296 CrossRef CAS
 .
.
- T. Lim, G. Y. Jung, J. H. Kim, S. O. Park, J. Park, Y. T. Kim, S. J. Kang, H. Y. Jeong, S. K. Kwak and S. H. Joo, Nat. Commun., 2020, 11, 412 CrossRef PubMed
 .
.
- Z. Li, Y. Chen, S. Ji, Y. Tang, W. Chen, A. Li, J. Zhao, Y. Xiong, Y. Wu, Y. Gong, T. Yao, W. Liu, L. Zheng, J. Dong, Y. Wang, Z. Zhuang, W. Xing, C. T. He, C. Peng, W. C. Cheong, Q. Li, M. Zhang, Z. Chen, N. Fu, X. Gao, W. Zhu, J. Wan, J. Zhang, L. Gu, S. Wei, P. Hu, J. Luo, J. Li, C. Chen, Q. Peng, X. Duan, Y. Huang, X. M. Chen, D. Wang and Y. Li, Nat. Chem., 2020, 12, 764–772 CrossRef CAS PubMed
 .
.
- L. Zhang, K. Doyle-Davis and X. Sun, Energy Environ. Sci., 2018, 12, 492–517 RSC
 .
.
- J. N. Tiwari, S. Sultan, C. W. Myung, T. Yoon, N. Li, M. Ha, A. M. Harzandi, H. J. Park, D. Y. Kim, S. S. Chandrasekaran, W. G. Lee, V. Vij, H. Kang, T. J. Shin, H. S. Shin, G. Lee, Z. Lee and K. S. Kim, Nat. Energy, 2018, 3, 773–782 CrossRef CAS
 .
.
- D. Liu, X. Li, S. Chen, H. Yan, C. Wang, C. Wu, Y. A. Haleem, S. Duan, J. Lu, B. Ge, P. M. Ajayan, Y. Luo, J. Jiang and L. Song, Nat. Energy, 2019, 4, 512–518 CrossRef CAS
 .
.
- I. Roger, M. A. Shipman and M. D. Symes, Nat. Rev. Chem., 2017, 1, 0003 CrossRef CAS
 .
.
- A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81 CrossRef CAS
 .
.
- J. Li, M. Chen, D. A. Cullen, S. Hwang, M. Wang, B. Li, K. Liu, S. Karakalos, M. Lucero, H. Zhang, C. Lei, H. Xu, G. E. Sterbinsky, Z. Feng, D. Su, K. L. More, G. Wang, Z. Wang and G. Wu, Nat. Catal., 2018, 1, 935–945 CrossRef CAS
 .
.
- X. Wan, X. Liu, Y. Li, R. Yu, L. Zheng, W. Yan, H. Wang, M. Xu and J. Shui, Nat. Catal., 2019, 2, 259–268 CrossRef CAS
 .
.
- H. Xu, D. Rebollar, H. He, L. Chong, Y. Liu, C. Liu, C. J. Sun, T. Li, J. V. Muntean, R. E. Winans, D. J. Liu and T. Xu, Nat. Energy, 2020, 5, 623–632 CrossRef CAS
 .
.
- X. Cui, W. Li, P. Ryabchuk, K. Junge and M. Beller, Nat. Catal., 2018, 1, 385–397 CrossRef CAS
 .
.
- E. D. Goodman, A. C. Johnston-Peck, E. M. Dietze, C. J. Wrasman, A. S. Hoffman, F. Abild-Pedersen, S. R. Bare, P. N. Plessow and M. Cargnello, Nat. Catal., 2019, 2, 748–755 CrossRef CAS PubMed
 .
.
- Y. Xiong, J. Dong, Z. Q. Huang, P. Xin, W. Chen, Y. Wang, Z. Li, Z. Jin, W. Xing, Z. Zhuang, J. Ye, X. Wei, R. Cao, L. Gu, S. Sun, L. Zhuang, X. Chen, H. Yang, C. Chen, Q. Peng, C. R. Chang, D. Wang and Y. Li, Nat. Nanotechnol., 2020, 15, 390–397 CrossRef CAS PubMed
 .
.
- J. N. Tiwari, A. M. Harzandi, M. Ha, S. Sultan, C. W. Myung, H. J. Park, D. Y. Kim, P. Thangavel, A. N. Singh, P. Sharma, S. S. Chandrasekaran, F. Salehnia, J. W. Jang, H. S. Shin, Z. Lee and K. S. Kim, Adv. Energy Mater., 2019, 9, 1900931 CrossRef
 .
.
- A. M. Harzandi, S. Shadman, M. Ha, C. W. Myung, D. Y. Kim, H. J. Park, S. Sultan, W. S. Noh, W. Lee, P. Thangavel, W. J. Byun, S. Lee, J. N. Tiwari, T. J. Shin, J. H. Park, Z. Lee, J. S. Lee and K. S. Kim, Appl. Catal., B, 2020, 270, 118896 CrossRef CAS
 .
.
- J. N. Tiwari, N. K. Dang, S. Sultan, P. Thangavel, H. Y. Jeong and K. S. Kim, Nat. Sustainable, 2020, 3, 556–563 CrossRef
 .
.
- K. Jiang, S. Siahrostami, T. Zheng, Y. Hu, S. Hwang, E. Stavitski, Y. Peng, J. Dynes, M. Gangisetty, D. Su, K. Attenkofer and H. Wang, Energy Environ. Sci., 2018, 11, 893–903 RSC
 .
.
- S. Sultan, J. N. Tiwari, A. N. Singh, S. Zhumagali, M. Ha, C. W. Myung, P. Thangavel and K. S. Kim, Adv. Energy Mater., 2019, 9, 1900624 CrossRef
 .
.
- J. N. Tiwari, A. N. Singh, S. Sultan and K. S. Kim, Adv. Energy Mater., 2020, 10, 2000280 CrossRef CAS
 .
.
- M. D. Hossain, Z. Liu, M. Zhuang, X. Yan, G. L. Xu, C. A. Gadre, A. Tyagi, I. H. Abidi, C. J. Sun, H. Wong, A. Guda, Y. Hao, X. Pan, K. Amine and Z. Luo, Adv. Energy Mater., 2019, 9, 1803689 CrossRef
 .
.
- H. Fei, J. Dong, Y. Feng, C. S. Allen, C. Wan, B. Volosskiy, M. Li, Z. Zhao, Y. Wang, H. Sun, P. An, W. Chen, Z. Guo, C. Lee, D. Chen, I. Shakir, M. Liu, T. Hu, Y. Li, A. I. Kirkland, X. Duan and Y. Huang, Nat. Catal., 2017, 1, 63–72 CrossRef
 .
.
- Y. Zhang, Nat. Rev. Chem., 2018, 2, 0151 CrossRef
 .
.
- Y. Wang, J. Mao, X. Meng, L. Yu, D. Deng and X. Bao, Chem. Rev., 2018, 119, 1806–1854 CrossRef PubMed
 .
.
- H. Wang, S. Min, Q. Wang, D. Li, G. Casillas, C. Ma, Y. Li, Z. Liu, L.-J. Li, J. Yuan, M. Antonietti and T. Wu, ACS Nano, 2017, 11, 4358 CrossRef CAS PubMed
 .
.
- S. Wang, D. Z. B. Li, C. Zhang, Z. Du, H. Yu, X. Bi and S. Yang, Adv. Energy Mater., 2018, 8, 1801345 CrossRef
 .
.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348 CrossRef CAS
 .
.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed
 .
.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed
 .
.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed
 .
.
- H. Shin, H. Xiao and W. A. Goddard, J. Am. Chem. Soc., 2018, 140, 6745–6748 CrossRef CAS PubMed
 .
.
- C. Choi, S. Back, N. Y. Kim, J. Lim, Y. H. Kim and Y. Jung, ACS Catal., 2018, 8, 7517–7525 CrossRef CAS
 .
.
- M. Zafari, D. Kumar, M. Umer and K. S. Kim, J. Mater. Chem. A, 2020, 8, 5209–5216 RSC
 .
.
- D. Y. Kim, M. Ha and K. S. Kim, J. Mater. Chem. A, 2021, 9, 3511–3519 RSC
 .
.
- C. A. Tolman, Chem. Soc. Rev., 2004, 1, 337 RSC
 .
.
- D. Deng, X. Pan, L. Yu, Y. Cui, Y. Jiang, J. Qi, W.-X. Li, Q. Fu, X. Ma, Q. Xue, G. Sun and X. Bao, Chem. Mater., 2011, 23, 1188 CrossRef CAS
 .
.
- D. Wei, Y. Liu, Y. Wang, H. Zhang, L. Huang and G. Yu, Nano Lett., 2009, 9, 1752 CrossRef CAS PubMed
 .
.
- J. N. Tiwari, Y. K. Seo, T. Yoon, W. G. Lee, W. J. Cho, M. Yousuf, A. M. Harzandi, D. S. Kang, K. Y. Kim, P. G. Suh and K. S. Kim, ACS Nano, 2016, 11, 742–751 CrossRef PubMed
 .
.
- J. Greeley and J. K. Nørskov, Electrochim. Acta, 2007, 52, 5829–5836 CrossRef CAS
 .
.
-
P. Vanýsek, in CRC Handbook of Chemistry and Physics 87th, ed. D. R. Lide, Taylor & Francis, Boca Raton, 2007, ch. 8, pp. 20–29 Search PubMed
 .
.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef
 .
.
- G. J. Kubas, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6901–6907 CrossRef CAS PubMed
 .
.
- H. Jin, S. Sultan, M. Ha, J. N. Tiwari, M. G. Kim and K. S. Kim, Adv. Funct. Mater., 2020, 30, 2000531 CrossRef CAS
 .
.
- J. Liu, M. Jiao, L. Lu, H. M. Barkholtz, Y. Li, Y. Wang, L. Jiang, Z. Wu, D.-J. Liu, L. Zhuang, C. Ma, J. Zeng, B. Zhang, D. Su, P. Song, W. Xing, W. Xu, Y. Wang, Z. Jiang and G. Sun, Nat. Commun., 2017, 8, 15938 CrossRef CAS PubMed
 .
.
- Y. Zhao, K. Watanabe and K. Hashimoto, J. Am. Chem. Soc., 2012, 134, 19528–19531 CrossRef CAS PubMed
 .
.
- W.-J. Jiang, L. Gu, L. Li, Y. Zhang, X. Zhang, L.-J. Zhang, J.-Q. Wang, J.-S. Hu, Z. Wei and L.-J. Wan, J. Am. Chem. Soc., 2016, 138, 3570–3578 CrossRef CAS PubMed
 .
.
- P. Yin, T. Yao, Y. Wu, L. Zheng, Y. Lin, W. Liu, H. Ju, J. Zhu, X. Hong, Z. Deng, G. Zhou, S. Wei and Y. Li, Angew. Chem., Int. Ed., 2016, 55, 10800–10805 CrossRef CAS PubMed
 .
.
- Q. Yang, Y. Jia, F. Wei, L. Zhuang, D. Yang, J. Liu, X. Wang, S. Lin, P. Yuan and X. Yao, Angew. Chem., Int. Ed., 2020, 59, 6122–6127 CrossRef CAS PubMed
 .
.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
 .
.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed
 .
.
- D. K. McClish, Med. Decis. Making., 1989, 9, 190 CrossRef CAS PubMed
 .
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 2002, 6, 15–50 CrossRef
 .
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 2002, 77, 3865–3868 CrossRef PubMed
 .
.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 59, 7413–7421 CrossRef
 .
.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed
 .
.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 57, 1505–1509 CrossRef
 .
.
- J. Wellendorff and T. Bligaard, Top. Catal., 2011, 54, 1143–1150 CrossRef CAS
 .
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 50, 17953–17979 CrossRef PubMed
 .
.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed
 .
.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS
 .
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef
 .
.
- G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS
 .
.
- Y. W. Tan, Y. Zhang, K. Bolotin, Y. Zhao, S. Adam, E. H. Hwang, S. Das Sarma, H. L. Stormer and P. Kim, Phys. Rev. Lett., 2007, 99, 246803 CrossRef PubMed
 .
.
- O. Bunău and Y. Joly, J. Phys.: Condens. Matter, 2009, 21, 345501 CrossRef PubMed
 .
.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary note, Fig. S1–S21 and Tables S1–S34 as described in the main text. See DOI: 10.1039/d1ee00154j |
| ‡ These authors contributed equally. |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Dong Yeon
Kim‡
ab,
Dong Yeon
Kim‡
 a,
Muhammad
Umer‡
a,
Vladislav
Gladkikh
a,
Chang Woo
Myung
a,
Muhammad
Umer‡
a,
Vladislav
Gladkikh
a,
Chang Woo
Myung
 *ac and
Kwang S.
Kim
*ac and
Kwang S.
Kim
 *a
*a


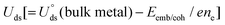 ,51 where
,51 where 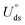 is the standard dissolution potential (pH = 0) of bulk metal in aqueous solution, e is the electron charge, and ne is the number of electrons involved in dissolution. A more positive Uds relative to the equilibrium potential indicates that the metal atoms bind the M–NnCm–GN support more strongly and the dissolution of metal atoms can be better avoided under electrochemical reactions, which enhances the durability of (TM)SA in a harsh electrochemical environment. While there can be a different number of electron transfers in the dissolution process, we here use a broad range of Uds (>0 V) based on the reported experimental studies on most of the synthesized (TM)SA-catalysts.52
is the standard dissolution potential (pH = 0) of bulk metal in aqueous solution, e is the electron charge, and ne is the number of electrons involved in dissolution. A more positive Uds relative to the equilibrium potential indicates that the metal atoms bind the M–NnCm–GN support more strongly and the dissolution of metal atoms can be better avoided under electrochemical reactions, which enhances the durability of (TM)SA in a harsh electrochemical environment. While there can be a different number of electron transfers in the dissolution process, we here use a broad range of Uds (>0 V) based on the reported experimental studies on most of the synthesized (TM)SA-catalysts.52





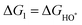
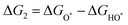
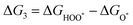
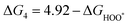
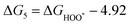
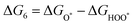
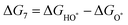
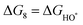
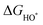 ,
,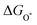 , and
, and 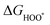 equations are given for path-I and
equations are given for path-I and 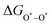 ,
, 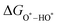 , and
, and 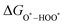 can be calculated by changing G* to GO*–M in each equation, where the TS value of H2 is 0.41 eV and that of H2O is 0.67 eV.53 For the active site and adsorbates, their TS values are 0 eV.
can be calculated by changing G* to GO*–M in each equation, where the TS value of H2 is 0.41 eV and that of H2O is 0.67 eV.53 For the active site and adsorbates, their TS values are 0 eV.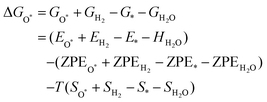
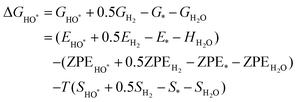
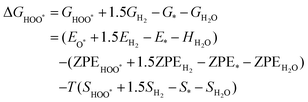
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
