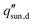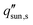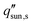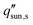Open Access Article
Open Access ArticlePassive, high-efficiency thermally-localized solar desalination
Lenan
Zhang
 a,
Zhenyuan
Xu†
a,
Zhenyuan
Xu†
 ab,
Lin
Zhao†
ab,
Lin
Zhao†
 a,
Bikram
Bhatia†
c,
Yang
Zhong
a,
Bikram
Bhatia†
c,
Yang
Zhong
 a,
Shuai
Gong
a and
Evelyn N.
Wang
*a
a,
Shuai
Gong
a and
Evelyn N.
Wang
*a
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: enwang@mit.edu
bInstitute of Refrigeration and Cryogenics, Shanghai Jiao Tong University, Shanghai 200240, China
cDepartment of Mechanical Engineering, University of Louisville, Louisville, KY 40292, USA
First published on 19th March 2021
Abstract
Solar desalination holds significant promise for the water-energy nexus. Recent advances in passive solar desalination using thermal localization show great potential for high-efficiency freshwater production, which is particularly beneficial for areas without well-established water and energy infrastructure. However, there is a significant knowledge gap between laboratory scale innovation and commercial adoption. In this review, we discuss two critical factors – water production and reliability – which, if addressed systematically, could enable high-performance thermally-localized solar desalination systems. We show that optimizing heat and mass transfer of the entire device and recycling the latent heat of condensation are important to enhance total water production. Meanwhile, we discuss the potential of novel system architectures and fluid flow engineering to enable anti-fouling and robust desalination devices. In addition, we present techno-economic analysis that highlights the balance between water production, reliability, and cost. A criterion for economic feasibility is provided by comparing the price of desalinated water with commercially available bottle and tap water, which provides a roadmap for future development of solar desalination technologies.
Broader contextMore than one half of the global population is experiencing water scarcity. Desalinating seawater using natural sunlight takes advantage of two abundant resources, and could provide a sustainable solution to water shortage. However, conventional solar desalination systems either require well-established infrastructure or suffer from low energy efficiency, which has thus far limited their widespread adoption. The recent development of thermally-localized solar desalination enables passive and high-efficiency water production, providing a promising approach to address water shortages in underdeveloped regions. Although tremendous efforts have led to significant innovations in materials and evaporator designs for thermally-localized solar desalination, a device-level perspective considering both water production and reliability is limited, which is crucial for commercially competitive water production. In this review, we discuss the recent progress of thermally-localized solar desalination, with a focus on operating configurations, optimizing water production, and enhancing anti-fouling property. This article also provides a perspective on future opportunities, which could enable next-generation solar desalination technologies. |
1. Introduction
During the last few decades, it has become evident that freshwater scarcity is becoming a threat to sustainable development of human society due to a steadily increasing demand.1,2 In its most recent annual risk report, the World Economic Forum listed water crises as the largest global risk in terms of potential impact.3 The increasing world population, improving living standards, changing consumption patterns, and expansion of irrigated agriculture are the main driving forces for the rising global demand for water. As a consequence, a significant fraction of the world population faces water scarcity (Fig. 1a) – 17 countries classified as extremely high water stressed and another 27 high stressed countries, particularly concentrated around the Middle East, North Africa and Sub-Saharan Africa. Several of these countries are also resource-constrained and cannot afford expensive large-scale energy-intensive desalination technologies to meet their freshwater needs.4,5 Fortunately, many of the water-stressed countries have access to ample solar radiation resource which can enable low-cost distributed renewable water desalination technologies.6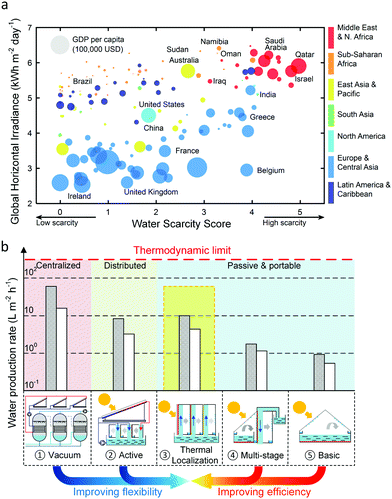 | ||
| Fig. 1 Water and solar resource distribution in the world, and comparison of desalination technologies. (a) Plot showing the availability of water,3 average daily solar irradiation,6 and per capita gross domestic product (GDP) of countries belonging to different regions of the world.5 Solar thermal desalination offers a promising solution for low-income water-scarce countries with high solar resource availability (smaller circles in the upper-right corner), particularly in the Middle East, North Africa and Sub-Saharan Africa. (b) Water production rate achieved by different solar thermal desalination technologies. The red dashed line represents the thermodynamic limit of solar thermal desalination, and the white and gray bars represent the operational10,17,18,21,23,25,34 and theoretical16,19,20,22,24,36 water production rates, respectively. | ||
Solar thermal desalination offers a path towards low-cost, modular and high-efficiency desalination systems that are powered by renewable energy and are ideally suited for resource-constrained environments.7–9 Solar thermal desalination relies on the conversion of solar radiation to heat, which is then used for vapor generation, and consequently condensed to produce clean water. These systems can be passive, portable and economical because they can be fabricated with readily available low-cost materials and do not require electricity. While reverse osmosis is the dominant technology for large-scale systems, thermal desalination systems offer a modular approach that can fulfill the water needs of a household.2,7
Significant research has focused on improving the performance of solar thermal desalination systems. Specifically, the focus has been to maximize the solar-to-vapor conversion efficiency, defined as,8–11
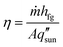 | (1) |
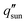 is the incident solar flux. The solar-to-vapor conversion efficiency accounts for the effectiveness of solar-thermal energy conversion, the rate of thermal energy conversion used for evaporation, and the degree to which the latent heat of condensation is reused for further distillation (often quantified as the gain output ratio, GOR).7,12 Another key metric that incorporates both the solar-to-vapor and vapor-to-water generation processes is the water production rate, which quantifies the water produced per unit absorber area per unit time (units: L m−2 h−1).7–14 However, water production rate of a desalination device depends on the incident solar flux. To quantify the intrinsic capability of water production, the water productivity is also commonly used, which is defined as the ratio of water production rate to incident solar flux (units: L kWh−1) and scaled with η by the proportional constant hfg.15
is the incident solar flux. The solar-to-vapor conversion efficiency accounts for the effectiveness of solar-thermal energy conversion, the rate of thermal energy conversion used for evaporation, and the degree to which the latent heat of condensation is reused for further distillation (often quantified as the gain output ratio, GOR).7,12 Another key metric that incorporates both the solar-to-vapor and vapor-to-water generation processes is the water production rate, which quantifies the water produced per unit absorber area per unit time (units: L m−2 h−1).7–14 However, water production rate of a desalination device depends on the incident solar flux. To quantify the intrinsic capability of water production, the water productivity is also commonly used, which is defined as the ratio of water production rate to incident solar flux (units: L kWh−1) and scaled with η by the proportional constant hfg.15
Solar desalination technologies span a wide range of complexity and performance levels – depicted in Fig. 1b. Solar still – the earliest and most basic solar desalination technology is simple, cheap and passive.16 However, the operational and theoretical efficiencies are typically less than 45%10,17,18 and 70%,19,20 respectively, due to the poor thermal management and loss of vaporization enthalpy. Slightly more complex multi-stage or multi-effect solar stills with condensation heat recovery enable improved performance. These multi-stage devices achieve operational and theoretical efficiencies up to 90%21 and 160%,22 respectively, while maintaining passive operation. Despite passive operation and low cost of solar stills, their low efficiency and productivity make the produced water expensive. To achieve high-efficiency solar desalination, passive operability is sacrificed to improve heat and mass transfer – implemented in active solar stills and solar humidification-dehumidification systems that are typically powered by solar collectors and photovoltaics. The active control of heat and mass transport pushes the operational and theoretical efficiencies to 320%23 and 650%,24 respectively. Even greater performance enhancement can be achieved by large-scale multi-effect distillation and multi-stage flash systems, which can reach operational and ideal efficiencies up to 1100%25 and 5000%,16 respectively. However, these systems require a vacuum and significant power resources – possible only in centralized solar desalination facilities. Thus, there exists a clear trade-off between flexibility and performance of conventional solar desalination technologies.
Recent developments, particularly those relying on thermal localization26–33 and latent heat reutilization,15,34,35 have demonstrated the potential for high-performance, passive, and portable solar desalination, which enables the simultaneous improvement of flexibility and efficiency (yellow-shaded area in Fig. 1b). Experimentally demonstrated efficiency as high as 385% – comparable to that of active solar desalination systems – have already been demonstrated.34 With design optimization, even higher efficiencies – as high as 750% – could be possible.36 However, while these significant advances in performance have been realized through the development of novel materials and configurations for solar thermal desalination, a quantitative understanding of heat and mass transport that has enabled these performance enhancements is lacking. In addition, the vast majority of reported studies have focused on vapor generation, while the other half of the desalination process – efficient condensation and effective recovery of the latent heat of condensation have received relatively less attention. Therefore, a systematic framework is needed that evaluates performance contribution of each process and helps identify the most effective strategies to achieve high-performance solar thermal desalination. Such a framework is also necessary to compare the performance of devices with different designs, tested under varied experimental conditions. Furthermore, practical challenges such as fouling due to salt accumulation that affect the reliability need to be addressed. We believe, a quantitative understanding of transport within each component of a solar desalination system will help identify the key bottlenecks and provide design solutions to maximize performance, improve reliability, and reduce cost.
The goal of this paper is to analyze past works on thermally-localized solar desalination, identify critical gaps in knowledge, and use a quantitative approach to determine areas that could improve performance. Specifically, we focus on the following key aspects. (1) Develop a general framework to identify different configurations, heat loss mechanisms, fundamental limits of performance, and bottlenecks for evaporator design. (2) Evaluate heat and mass transport within different configurations of high-performance solar desalination devices based on thermal localization, and provide a roadmap from the current demonstrated device-level performance to efficiencies and water production rates achievable in the future. (3) Examine salt accumulation in desalination devices and its effect on device performance, and recommend design strategies to balance water production and reliability. (4) Analyze the economics of passive solar-driven desalination systems, and determine the key metrics required to ensure scalability and cost-competitiveness. Addressing the above elements could help realize the full potential of passive solar desalination and provide a sustainable pathway to meet our freshwater needs.
2. Design of a high-performance evaporator for solar desalination systems
The evaporator constitutes a key component in a solar thermal desalination device that transforms input thermal energy into water vapor. Conventional evaporators are typically comprised of designs where the absorber is far from the evaporating surface.16–25 In contrast, recent works have focused on evaporator designs that localize the solar-thermal conversion process that reduces heat loss and therefore improves the solar-vapor conversion efficiency.7,8,10,13 In this section, we review the recent progress in the design of thermally-localized evaporator enabled by material-level innovations and optimized thermal management. In addition to presenting different evaporator configurations and materials, we quantitatively analyze the heat and mass transport characteristics and associated bottlenecks that have received relatively less attention. We provide a general modeling framework for the heat and mass transport which could guide the design of the evaporator and optimization of the vapor generation process.2.1. Evaporator configurations using thermal localization
In this article, unlike previous reviews that typically categorized evaporator designs based on their material composition and morphology,8–10,13,14,37–43 we focus on analyzing recent high-efficiency evaporator designs based on their operating configurations. We classify different evaporator configurations based on the relative orientation of the evaporation and the solar absorption processes. In most common evaporators, classified as “front-side” evaporators, the two processes occur on the same side (Fig. 2a). More recently, few works have demonstrated “back-side” evaporator configurations where evaporation occurs on the opposite side of the solar absorber (Fig. 2b).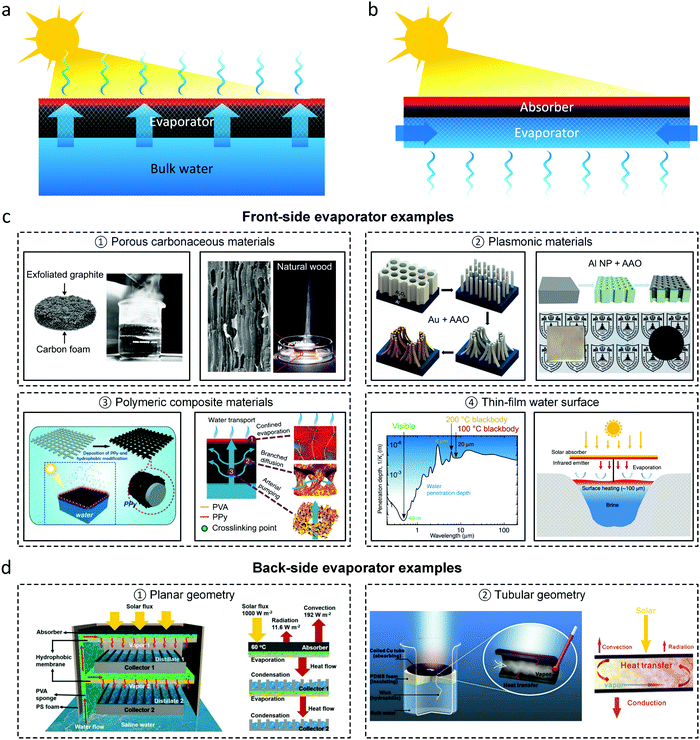 | ||
| Fig. 2 Evaporator configurations utilizing thermal localization. (a) Schematic representing the front-side configuration where evaporation and solar absorption occur on the same side. (b) Schematic representing the back-side configuration where evaporation and solar absorption occur on opposite sides. (c) Representative front-side evaporators based on different materials. State-of-the-art front-side evaporators commonly employ porous carbonaceous (①),26,49 plasmonic (②),29,30 or polymeric (③) materials.31,58 Reproduced with permissions from Springer Nature,26,29–31 Elsevier,49 and John Wiley and Sons.58 Contactless solar vapor generation (④) uses the water surface, with its small penetration depth (∼10 μm) in the infrared, as a thin-film absorber.63,64 Reproduced with permissions from Springer Nature.63,64 (d) Representative back-side evaporator designs based on planar (①)65 and tubular geometries (②).66 Reproduced with permissions from John Wiley and Sons65 and Elsevier.66 | ||
In front-side designs, the evaporator achieves four main functionalities: (1) solar absorption and conversion to heat, (2) evaporation via localized heating, (3) supply water passively using capillary pressure to enable continuous evaporation, and (4) thermally insulate bulk water. To efficiently capture sunlight, a broadband solar absorber is ideal and can be realized using carbonaceous materials,26,44–52 plasmonic structures,29,30,53–57 and polymeric materials31–33,58,59 as shown in Fig. 2c. To enable localized heating, efficient water transport, and thermal insulation, front-side evaporators often comprise porous materials with connected pores to allow a continuous water path. For example, the carbon foam developed by Ghasemi et al.26 and the hierarchical gel developed by Zhao et al.31 have a randomly connected porous structure to achieve interfacial heating, capillary pumping, and heat loss suppression. To further optimize water transport, directional water pathways have also been investigated in natural wood,49 anodic aluminum oxide (AAO),29 and three-dimensional structures.60–62 A fundamentally different front-side design is the contactless configuration,63,64 where a solar absorber converts sunlight into infrared (IR) thermal radiation. As water is a strong IR absorber, with a penetration depth ∼10 μm in IR, most of the thermal radiation is absorbed within a thin water layer – enabling interfacial heating. As the water body itself serves as the absorber and evaporator, external water supply is no longer needed. One drawback of the current contactless evaporator designs is the lack of thermal insulation which results in significant heat loss through the bulk water body.
Several recent studies have optimized front-side evaporators and achieved exceptionally high solar-to-vapor conversion efficiency.7,10,26,31 However, there are a few inherent limitations associated with front-side design. Firstly, because front-side evaporators combine four functionalities, it poses stringent material property requirements that are difficult to meet. Moreover, vapor collection and condensation are challenging since water vapor escapes from the front surface and can interfere with the solar absorption process – discussed in Section 3.1. Lastly, it is difficult to suppress heat loss from the absorber surface, e.g., by applying thermal insulation such as a convection cover, without affecting vapor transport since solar absorption and evaporation occur on the same side.
The alternative back-side configuration, where the front surface is only used for solar absorption, decouples the competing demands of multiple functionalities in the front-side configuration and therefore allows a greater choice of absorber and evaporator materials, and geometries (Fig. 2d).15,34,35,65–68 For instance, the absorber could simply comprise commercially available spectrally selective surfaces,15,28,34 low-cost black paints,69 and even photovoltaic (PV) cells.35 Meanwhile, the evaporators could utilize conventional low-cost wicking materials without specific optical properties such as fabric70 and paper.34,69,71 In addition to the material choice flexibility, the back-side configuration offers two additional benefits for desalination applications – (1) it is easier to integrate with a vapor condenser or collector on the evaporator side since it does not interfere with solar absorption, and (2) it allows better heat loss suppression since it is easier to apply a convection cover or an optically selective shield to reduce the convective and radiative heat loss from the absorber surface without affecting the evaporation process. We discuss the application of back-side evaporator in high-performance desalination devices in Sections 3.2 and 3.3.
2.2. Factors limiting evaporator performance
The design of high-efficiency evaporators warrants a clear understanding of the solar-vapor conversion process and identification of factors limiting its performance. In this section, we analyze the three key aspects of evaporator operation – heat loss, coupling of heat and mass transport, and water transport – which leads to the discussion of evaporator design bottlenecks and corresponding optimization strategies in Section 2.3.In addition to the conventional definition given by eqn (1), the solar-vapor conversion efficiency can also be defined based on the total heat loss 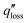 using an energy balance,
using an energy balance,
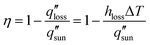 | (2) |
Another key factor limiting the vapor generation performance is the coupling of heat and mass transport. Similar to most studies on evaporator design, we consider an evaporator as an open system, i.e., vapor transport is from the evaporator to the far-field air ambient.72–76 According to the energy balance, the total input solar energy Qsun (units: W) is converted into thermal energy driving evaporation Qevap and heat loss Qloss,
| Qsun = Qevap + Qloss = SevapDahfg(csat(Ts) − ϕ∞csat(T∞)) + AhlossΔT | (3) |
The ability of the evaporator to transport water is another factor limiting evaporator performance, particularly because capillary driven flow enables passive solar thermal desalination. When the maximum liquid water supply rate of the capillary wick is less than the required evaporation rate, dryout occurs and the evaporator cannot generate more vapor. Liquid transport in the capillary wick can be described by Darcy's law and capillary pressure can be evaluated using the Young–Laplace equation.73 Substituting the Young–Laplace equation into Darcy's law and considering one-dimensional (1D) liquid transport in the front-side configuration, the critical solar flux 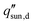 inducing evaporator dryout can be estimated as,
inducing evaporator dryout can be estimated as,
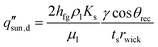 | (4) |
2.3. Thermal management strategies for optimizing evaporator performance
Since heat loss and vapor transport are two dominant factors affecting solar-vapor conversion efficiency, here we discuss specific thermal management strategies used to optimize coupled heat and mass transport. Fig. 4a shows a schematic of the heat and mass transport for a front-side evaporator. The total heat loss is mainly attributed to thermal radiation (Qrad), convection (Qconv) from the top of the evaporator and heat conduction (Qcond) to the bulk water. Accordingly, there are three thermal management strategies applied to reduce heat loss in practice. Spectrally selective solar absorbers, which have high absorptance in the solar spectrum (wavelength ≈ 0.3–3 μm) but low emissivity in the infrared (wavelength > 3 μm), are used in high-performance evaporators to reduce radiative losses. Fig. 4b shows a representative spectrum for a selective absorber which significantly reduces thermal radiation losses in the infrared (the shaded dark-red area) compared with a blackbody absorber at 50 °C (the shaded grey area) due to its low emissivity (= 0.05).28Fig. 4c and d show examples of front-side and back-side evaporators that used commercially available spectrally selective absorbers to minimize radiative losses.28,34 Convective heat losses from the absorber surface are typically suppressed using a convection cover, which is a highly solar-transparent material with low thermal conductivity, such as glass, air gap, bubble wrap, and silica aerogel.15,28,34,77–79 The high-performance convection cover can also be opaque to infrared radiation (e.g., silica aerogel), which further reduces the radiative loss from the absorber.78 In the examples shown in Fig. 4c and d, low-cost bubble wrap and silica aerogel constituted the convection covers.28,34 Note that for solar absorbers operating at high temperatures (≈ 100 °C or even higher) under solar concentration,29,30,80,81 thermal concentration,28,82 or contactless heating,63,64 it is particularly important to use spectrally selective solar absorbers and convection covers to maximize the solar-vapor conversion efficiency.78 To minimize heat loss from the evaporator to bulk water, it is also necessary to reduce conduction heat transfer. For the front-side configuration, the conduction barrier is typically a low-thermal conductivity wick or foam (Fig. 4c).26,28,70 Whereas for the back-side configuration, the conduction barrier is realized by reducing the contact area between the evaporator and bulk water, e.g., by converting surface contact (Fig. 4c) to a line contact (Fig. 4d).15,34,35,67,68,83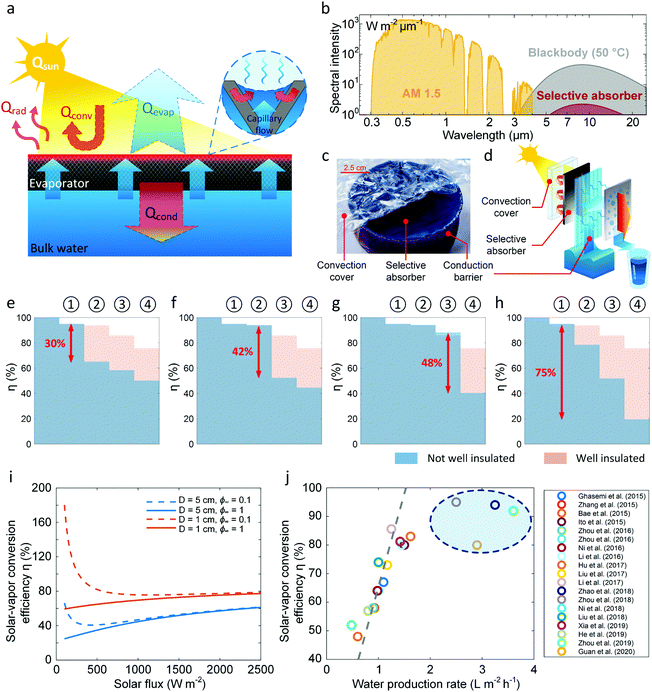 | ||
| Fig. 4 Thermal management strategies for optimizing the evaporator performance. (a) Schematic showing heat and mass transport contributions for a front-side evaporator. The input solar energy Qsun is converted into evaporative heat flow Qevap, radiative heat loss Qrad, convective heat loss Qconv, and conductive heat loss Qcond. Inset: Passive liquid transport driven by capillary pressure of the liquid–vapor interface in the porous structure of the evaporator. Solar energy is absorbed and converted into heat by the solid part of the wick. Heat is transferred from the solid structure to the liquid inside the pore through the solid–liquid interface to drive evaporation. (b) AM 1.5 standard solar spectrum and blackbody spectrum at 50 °C. The dark-red area represents the thermal radiation spectrum of a modeled spectrally selective absorber with infrared emissivity of 0.05 at 50 °C. (c) and (d) Representative thermally-localized (c) front-side and (d) back-side evaporators using spectrally selective absorber, convection cover and conduction barrier as thermal insulation.28,34 Reproduced with permissions from Springer Nature (c)28 and Royal Society of Chemistry (d).34 In the design shown in (c), a bubble wrap and a low thermal conductivity foam are used as the convection cover and conduction barrier, respectively. In the design shown in (d), a transparent silica aerogel is used as the convection cover and reduced contact between the bulk water and the evaporator minimizes conduction. (e)–(h) Reduction of solar-vapor conversion efficiency η due to ① imperfect absorption, ② radiative heat loss, ③ convective heat loss, and ④ conductive heat loss. Comparison between a well-insulated evaporator (pink background in (e)–(h)) and a not well-insulated evaporator (blue area in (e)–(h)) by removing (e) spectrally selectivity of the absorber, (f) convection cover, (g) conduction barrier and (h) all thermal insulation. Significant loss in solar-vapor efficiency is observed when thermal insulation is removed. The evaporator is modeled as a circular disk with diameter D = 5 cm, thickness ts = 3 cm and solar absorptance α = 0.95. The ambient temperature T∞ = 20 °C. For the well-insulated case, the infrared emissivity of solar absorber, total convective loss coefficient, and effective thermal conductivity of the capillary wick are ε = 0.03, hconv = 1.5 W m−2 K−1, and kwick = 0.06 W m−1 K−1, respectively. ε = 0.95, hconv = 10 W m−2 K−1, and kwick = 0.6 W m−1 K−1 are used to represent the conditions without a spectrally selective absorber, convection cover, and conduction barrier, respectively. (i) Effect of mass transport on the solar-vapor conversion efficiency η as a function of solar flux, modeled using representative circular disk evaporators with diameters D = 1 cm and D = 5 cm under low relative humidity ϕ = 0.1 and saturated conditions ϕ = 1. The convective loss coefficient is hconv = 10 W m−2 K−1. Smaller size evaporator has better performance due to the reduced vapor transport resistance. The dashed and solid lines show the solar-vapor conversion efficiency with/without the contribution of dark evaporation. Dark evaporation contributes significantly to the total vapor generation at the low solar flux regime (< 200 W m−2) whereas it becomes negligible when the solar flux is larger than 1500 W m−2. (j) A compilation of solar-vapor conversion efficiencies η and corresponding water production rates reported by recent studies using the thermal localization approach.26,28–32,46,48,51,53,55,58,59,70,80,84–87 Solar-vapor conversion efficiency is usually proportional to water production rate as indicated by the grey-dashed line, since latent heat of water is nearly constant. The results highlighted in the blue-dashed area represent recent studies using hydrogel31,32,59 and bacterial cellulose nanocomposites87 which report higher water production rates due to a reduction in latent heat of water. | ||
To quantitatively compare the impact of each thermal management strategy on solar-vapor conversion efficiency, we refined the heat and mass transport analysis in eqn (3) by including the radiative, convective, and conductive heat loss contributions for a front-side evaporator configuration,
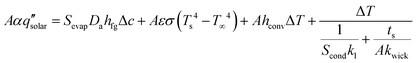 | (5) |
We use the heat and mass transfer framework given by eqn (5) to analyze the relationship between different loss mechanisms and resulting solar-vapor conversion efficiency. In the results presented in Fig. 4e–h, four loss mechanisms are considered for an evaporator with D = 5 cm and ts = 3 cm under one sun illumination with imperfect solar absorption (α = 0.95, ① in Fig. 4e–h), radiative loss (② in Fig. 4e–h), convective loss (③ in Fig. 4e–h), and conductive loss (④ in Fig. 4e–h). Fig. 4e–h show how the solar-vapor conversion efficiency decreases due to each loss mechanism. The pink background indicates a reference condition with relatively good thermal insulation (ε = 0.03, hconv = 1.5 W m−2 K−1, and kwick = 0.06 W m−1 K−1) while the blue regions represent cases without spectrally selectivity (ε = α = 0.95, Fig. 4e), without convection cover (hconv = ha = 10 W m−2 K−1, Fig. 4f), without conduction barrier (kwick = kl = 0.6 W m−1 K−1, Fig. 4g), and without any thermal insulation (ε = 0.95, hconv = 10 W m−2 K−1, and kwick = 0.6 W m−1 K−1, Fig. 4h). Imperfect solar absorption (α = 0.95) leads to a 5% reduction in solar-vapor conversion efficiency (① in Fig. 4e–h). The results of this analysis show that spectrally selective absorber, convection cover and conduction barrier are all essential to achieve a high efficiency. Specifically, in comparison with the well-insulated case, the absence of absorber spectral selectivity reduces η by 30% (② in Fig. 4e). Directly exposing the evaporator to the air ambient without a convection cover could reduce η by more than 40% due to convection (③ in Fig. 4f). Suppressing conductive loss through bulk water is comparatively more important and could cause η to reduce by 50% if the conduction barrier is removed (④ in Fig. 4g). If no thermal insulation is applied, more than 75% of the incident solar energy would be lost to the environment which leads to η less than 20% (Fig. 4h). This analysis highlights the significance of optimizing thermal transport to reduce hloss and increase η.
In addition to thermal transport, mass transport can also have a significant impact on solar-vapor conversion efficiency. For evaporation to the far-field air ambient under the diffusion limit, vapor transport is governed by two parameters according to eqn (3) and (5) – the evaporator geometry (diameter D) and the far-field condition (relative humidity ϕ∞). A smaller evaporator results in a smaller effective boundary layer thickness δ, leading to a smaller vapor transport resistance. When the vapor in the far-field is not saturated (i.e., ϕ∞ < 1), evaporation can still occur even in the absence of a temperature difference between the evaporator and air ambient (i.e., ΔT = Ts − T∞ = 0 °C) because the concentration gradient Δc = csat(Ts) − ϕ∞csat(T∞) = (1 − ϕ∞)csat(T∞) is greater than zero. This evaporation phenomenon without any input solar flux is known as dark evaporation11,73 or evaporation harnessing environmental energy.61 Dark evaporation increases the total vapor production but is typically removed from calculations of solar-vapor conversion efficiency by careful experimental calibration, since it is not a solar-induced process and is highly dependent on far-field weather conditions.73 The total measured vapor generation rate under a non-saturated far-field condition is the sum of the evaporation rate under a saturated condition and the dark evaporation rate, because Qevap ∼ csat(Ts) − ϕ∞csat(T∞) = [csat(Ts) − csat(T∞)] + [(1 − ϕ∞)csat(T∞)]. Fig. 4i shows the solar-vapor conversion efficiency as a function of solar flux for different evaporator diameters and far-field conditions. As expected, a smaller evaporator performs better due to smaller vapor transport resistance. The solid line in Fig. 4i is the solar-vapor conversion efficiency without dark evaporation. If we include the dark evaporation contribution (the dashed lines in Fig. 4i), it significantly increases the solar-vapor conversion efficiency at a low solar flux (< 200 W m−2) but has a negligible effect when the solar flux is greater than 1500 W m−2. Since typical solar evaporators are operated under a low solar flux condition (< 1000 W m−2), the contribution of dark evaporation should be carefully calibrated and can be used to increase the overall evaporation rate. As shown in Fig. 4i, careless calibration could lead to a solar-vapor conversion efficiency greater than 100% since dark evaporation is not driven by solar energy. To accurately calibrate dark evaporation, the evaporator shape factor (including the configuration of the evaporator relative to the water surface and reservoir) and the far-field conditions (including the far-field temperature and relative humidity) should be the same for both experiments – with and without solar illumination. Note that although evaporation to air ambient can take advantage of dark evaporation to drive more vapor generation, it has no effect on evaporation in a closed system which is commonly used for desalination devices – discussed further in Section 3.
Advances in thermal management approaches have led to improvements in solar-vapor conversion efficiency and water production rates reported by recent studies (Fig. 4j).26,28–32,46,48,51,53,55,58,59,70,80,84–87 The reported studies used thermal localization to achieve solar-vapor conversion efficiencies greater than 50%. By incorporating thermal management strategies discussed above, the demonstrated η can be as high as 90% with more than 1.5 L m−2 h−1 water production rate under the one sun illumination. The solar-vapor conversion efficiency is typically linearly related to the water production rate (the dashed-grey line in Fig. 4j) since the latent heat of water is almost a constant (≈ 2400 kJ kg−1). However, several recent studies show that it is possible to produce more than 2.5 L m−2 h−1 of water using hydrogel31,32,59 and bacterial cellulose nanocomposites,87 which indicates a reduction of water latent heat during evaporation (the blue-dashed circle in Fig. 4j). These novel materials offer a new pathway for efficient vapor and water generation; more theoretical and experimental evidence is, however, required to explain the underlying mechanism for the reduction of latent heat. In particular, according to eqn (5), the high evaporation rate with reduced latent heat also indicates an increased vapor pressure or a reduced mass transport resistance. Therefore, it is of great interest to understand the underlying physics of the hydrogel evaporator from the perspective of mass transport in future works.
Using our analysis in this section, we show that optimizing heat and mass transport at the device level is crucial for high-performance evaporator design. On the other hand, further research on advanced materials has relatively limited impact on enhancing the energy efficiency unless those materials fundamentally change the thermodynamic properties (such as latent heat) of water.7,12,13 Diverse thermal management strategies such as spectrally selective absorber, convection cover and conduction barrier have already led to significant reductions in heat loss. Future advances could be enabled by optimizing vapor transport by engineering the geometry of the evaporator or the external flow field. In addition, modeling tools that account for the complex coupling of heat and mass transport with fluid flow could facilitate optimization and quantify the performance of laboratory scale prototypes as well as large-scale industrial setups.
3. Design of high-performance solar desalination devices using thermal localization
A passive solar desalination device can be constructed by integrating an evaporator with a condenser in a closed system. In this section, we highlight the recent progress in solar desalination device designs based on thermally-localized evaporators. We analyze different configurations and underlying heat and mass transport characteristics, which have led to significant improvements in the performance of solar desalination devices. In particular, we show that the efficiency of a desalination device is not strongly correlated with the performance of the evaporator in an open system due to the significantly different heat and mass transport mechanisms. Furthermore, we discuss the extension of desalination device designs from single-stage to multistage devices, which have shown multifold enhancement in water production rates through latent heat recycling during vapor condensation.3.1. Single-stage solar desalination device configurations
Single-stage desalination devices can be characterized based on the configuration of their evaporators – front-side or back-side. Fig. 5a shows the schematic of a desalination device with a front-side evaporator, where the condenser is placed between the evaporator and incident sunlight due to the vapor flow direction. The condenser should be solar transparent to ensure the sunlight reaches the absorber. Alternatively, the desalination device can be also constructed using a back-side evaporator, where the condenser is placed on the opposite side of incident sunlight, behind the evaporator (Fig. 5b). Fig. 5c–f show a few examples of single-stage desalination devices from literature.31,69,70 These demonstrations primarily used front-side evaporators where a transparent cover (acrylic – Fig. 5c or polyester film – Fig. 5e) serves as the condenser and the condensed droplets are removed by gravity. In addition to the advantages discussed in Section 2.1, desalination devices using back-side evaporators offer three additional benefits. First, in comparison with front-side devices which severely restrict the choice of condenser materials due to the requirements of solar transparency and relatively high thermal conductivity, back-side devices allow the use of a wide range of materials for condensation including common low-cost metals such as copper and aluminum.34,77 Moreover, additional cooling, e.g., through direct contact of the condenser back-side with water, can be easily implemented to further enhance vapor condensation.15,34 Second, the back-side design eliminates the loss of input solar energy due to the condenser positioned in front of the evaporator in front-side devices (Fig. 5g), where the incident sunlight can be further reduced due to backscattering by the condensed droplets.88 Third, the single-stage desalination device based on the back-side evaporator can be easily upgraded to a multistage device using a modular design (discussed in Section 3.3). On the other hand, as mentioned in Section 2.1, a potential drawback of the back-side design is the limited water transport capability due to the water supply from the side of the evaporator. Although it has been experimentally demonstrated that the water transport capability of the back-side desalination device is sufficient under dilute solar flux (≈ 1000 W m−2),15,34,35,67,68 additional design constraints need to be considered for the back-side device operation under concentrated solar/thermal fluxes.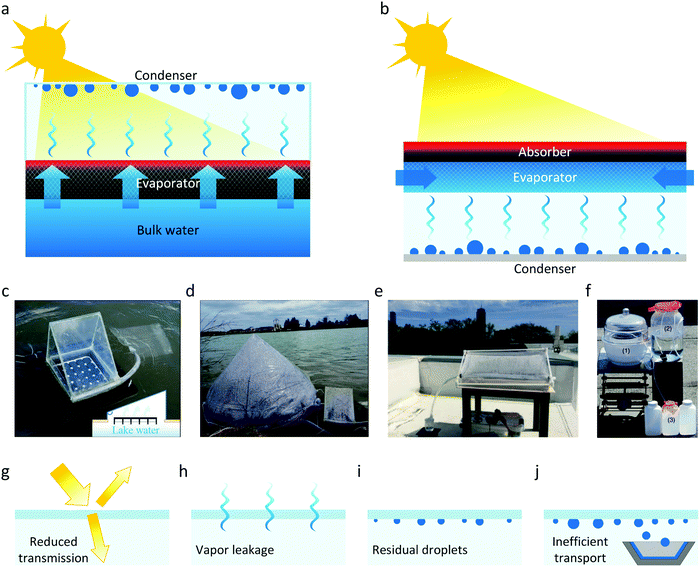 | ||
| Fig. 5 Single-stage desalination device configurations based on thermally-localized evaporators. (a) and (b) Schematics of single-stage desalination device based on (a) front-side and (b) back-side evaporators. In the front-side device, a solar-transparent condenser is placed in front of the evaporator, allowing sunlight to reach the absorber. In the back-side device, the solar absorber directly faces the incident sunlight while the condenser is behind the evaporator. (c)–(f) Representative single-stage desalination devices using the front-side configuration shown in literature.31,69,70 Reproduced with permissions from John Wiley and Sons (c and d),69 Royal Society of Chemistry (e),70 and Springer Nature (f).31 (g)–(j) Additional loss mechanisms during water desalination due to (g) reduced transmission through the condenser, (h) vapor leaking from the device, (i) droplets pinning on the condenser, and (j) inefficient water transport and collection. | ||
The vapor condensation and water collection processes in desalination devices introduce additional losses, when compared with evaporation only. In addition to the optical loss due to the condenser and droplets in the front-side device (Fig. 5g), vapor leakage (Fig. 5h), residual droplets (Fig. 5i), and inefficient water transport and collection (Fig. 5j) in both the front-side and back-side devices due to imperfect sealing, droplet pinning,89–91 and liquid film wetting,92,93 respectively, could reduce the amount of collected fresh water.34 Therefore, an airtight system with high droplet mobility, e.g., using hydrophobic coatings94–97 and efficient water transport98–102 are critical to achieving high water production rates.
Losses in water collection also require more thoughts and considerations during experimental characterization. In studies measuring evaporator performance in an open system, the production rate is usually measured from the mass loss rate of the bulk water in a reservoir. However, since there are additional losses associated with desalination devices, the production rate given by the mass loss rate of the reservoir is higher than the actual desalinated water collection rate. Therefore, a more accurate measure of the desalination device performance would involve characterization of both the mass loss rate of the reservoir and the collection rate of desalinated water. The mass loss rate is a more fundamental property that shows the effect of heat and mass transport on vapor generation, whereas the actual water collection is a more practical standard to quantify the ultimate performance with all losses. The ratio of the water collection and reservoir mass loss shows the relative significance of imperfect water transport and collection for the overall desalination device design.
3.2. Heat and mass transport in a single-stage solar desalination device
This section focuses on the heat and mass transport characteristics and the resulting optimization strategy for a single-stage desalination device. We consider the back-side device as an example. Fig. 6a shows the heat and mass transport processes where the incident solar energy (Qsun) is balanced by radiative heat loss (Qrad) and convective heat loss (Qconv) from the absorber, and conductive heat loss (Qcond) and evaporative heat flow (Qevap) through the air gap between the evaporator and condenser. Heat loss from sidewalls (Qside) due to convection can reduce the energy reaching the condenser. Vapor condenses on the condenser and releases latent heat (Qlat), which is then lost to the environment. Although the vapor transport resistance can be reduced by creating a vacuum or pure vapor environment with pumping or evacuated tube, to ensure the passive operation and simple architecture, the vacuum or pure vapor environment is not commonly used in current small-scale solar desalination devices. Therefore, vapor transport within the air gap, driven by a concentration gradient between the hot evaporator and cold condenser, is described by the Fick's law. In a 1D condition, the evaporative heat flow rate is given by,72,73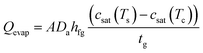 | (6) |
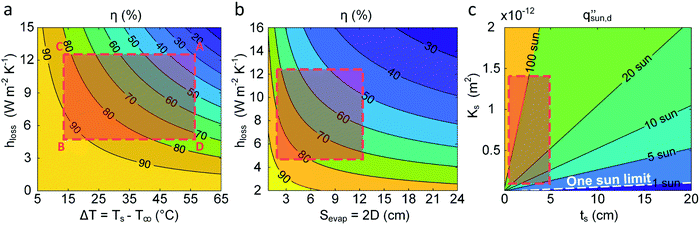
Fig. 6b shows the solar-vapor conversion efficiency as a function of air gap thickness for the modeled single-stage device. The modeled device area is 5 cm × 5 cm and ambient temperature is 20 °C. We assumed that the condenser is inserted in bulk liquid and therefore, the condenser temperature is maintained at Tc = 20 °C. The absorber temperature, and heat and mass flow rates are solved by substituting eqn (6) into the overall energy balance. Detailed modeling procedures and simulation parameters can be found in our recent work.36 With increasing tg, η first increases and then decreases, leading to an optimal gap thickness tg = 0.3 cm (Fig. 6b). This optimal solar-vapor efficiency arises from the simultaneous increase of the vapor diffusion and heat conduction resistance with tg. When the air gap is small (tg < 0.7 cm), conduction through the air gap is the dominant heat loss. Therefore, even though reducing tg below 0.3 cm decreases the vapor diffusion resistance, the resulting increase in conductive heat loss leads to a reduction in η for tg < 0.3 cm. When 0.7 cm < tg < 3 cm, the device transitions to a regime dominated by front-side heat loss Qfront (Qfront = Qrad + Qconv) due to the elevated temperature of the solar absorber. When tg > 3 cm, heat loss from the sidewall becomes dominant mainly because of the large sidewall area. Significant increase in total heat loss leads to a rapid decay of η at large air gap thicknesses (tg > 0.7 cm). The heat and mass transport for the front-side configuration follow principles similar to those described above, but require consideration of extra loss mechanisms discussed in Section 3.1.
3.3. Improving water production using latent heat recycling by a multistage design
Although heat and mass transport optimization and heat loss reduction during water collection significantly improve device performance, water production by a single-stage desalination device is inherently limited by the latent heat Qlat lost to the ambient environment after vapor condensation (Fig. 6a). Therefore, the solar-vapor conversion efficiency of a single-stage device cannot exceed 100% (GOR = 1). Recently, multifold enhancement of solar-vapor conversion efficiency beyond 100% was demonstrated by recycling the latent heat using multistage device designs.15,34,35,68,103,104Fig. 7a shows a schematic of the multistage solar desalination device. This multistage design comprises a closely packed layered structure with several stages aligned with the incident sunlight (Fig. 7a). Liquid is supplied passively from the side of the device driven by capillary pressure. The evaporator in each stage is separated from the condenser by a hydrophobic membrane or an air gap.15,34,35,68,103,104 During operation, the latent heat released from the previous stage is used to drive evaporation in the next stage, leading to more vapor and water production.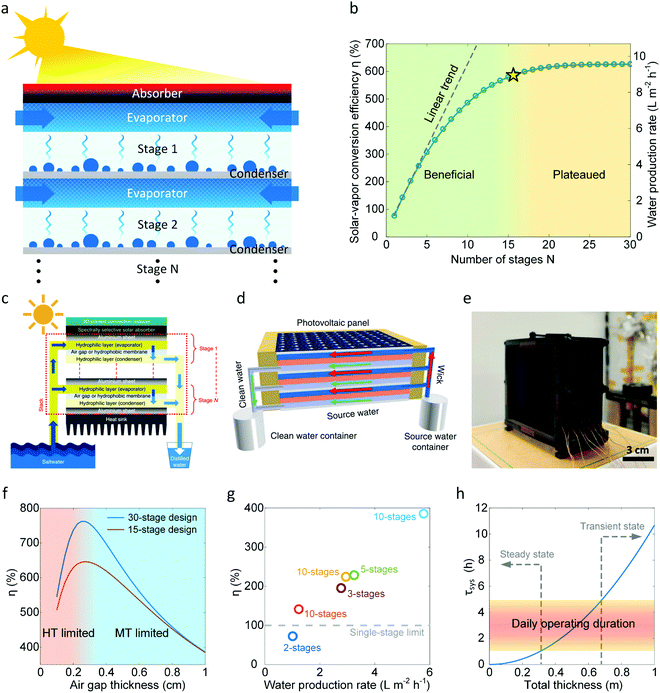 | ||
| Fig. 7 Improving water production by recycling latent heat with a multistage design. (a) Schematic of a thermally-localized multistage solar desalination device showing the use of latent heat released in one stage to drive evaporation in the next stage. (b) Increase in solar-vapor conversion efficiency η and water production rate with the number of stages N. The water production rate and GOR in the modeled multistage device are predicted to increase by more than six times than that of a single-state device. The relative benefit of adding each additional stage diminishes with increasing N, leading to beneficial (green area in (b)) and plateaued (yellow area in (b)) regimes. The yellow star indicates the transition point beyond which the improvement of water production by increasing N becomes negligible. (c)–(e) Three representative demonstrations of the multistage design in recent studies.15,34,35 Reproduced with permissions from Springer Nature (c and d)15,35 and Royal Society of Chemistry (e).34 Devices reported in (c) and (d) used hydrophilic membranes to evaporate water and hydrophobic membranes to transport vapor.15,35 The device reported in (d) included a PV panel as the solar absorber and demonstrated simultaneous electricity and water production.35 A record-high water production rate of 5.78 L m−2 h−1 was demonstrated in (e) by optimizing the heat and mass transport through the multistage structure.34 (f) Solar-vapor conversion efficiency η as a function of single-stage air gap thickness for a 15-stage and a 30-stage device. As the air gap thickness increases, the device transitions from a heat transfer limited regime (red region in (f)) to a mass transport limited regime (blue region in (f)), leading to an optimal air gap thickness of about 0.3 cm. Note that this optimal air gap thickness is for the modeled device and conditions – 15 cm × 15 cm area device operated under one sun illumination and 20 °C ambient temperature. The general optimization procedures can be found in ref. 36. (g) Solar-vapor conversion efficiencies (η) and corresponding water production rates for various multistage devices reported by recent studies.15,34,35,65 The grey-dashed line indicates the 100% efficiency limit for the single-stage device. (h) Thermal response time of the desalination device τsys as a function of the total thickness. τsys is estimated using ttot2/αa, where ttot is the combined thickness of all the layers and αa is the thermal diffusivity of air.72 The orange band ranging from 1 h to 5 h indicates the typical daily operation duration of the device based on the availability of solar radiation. When τsys is smaller than the lower bound of the daily operation duration, the device can reach steady state operation as indicated by the left-grey arrow. When τsys is larger than the upper bound of the daily operation duration, the device can never reach steady state as indicated by the right-grey arrow. | ||
The concept of recycling latent heat is not new – it is a mature technology widely used in conventional large-scale and centralized thermal desalination systems such as multistage flash and multiple-effect distillation.22,105–110 However, the successful implementation of latent heat recycling in small-scale passive desalination devices was only demonstrated recently.15,34,35 Since the motivation and potential benefits of recycling latent heat have been carefully reviewed by Wang et al.,7 we will focus on the design principle and opportunity space for high-performance multistage desalination devices. Fig. 7b shows the predicted solar-vapor conversion efficiency and water production rate as a function of the number of device stages N. The modeled multistage device with a 15 cm × 15 cm area and a 0.5 cm air gap thickness is operated at 20 °C ambient temperature and one sun illumination. The details of the modeling procedures can be seen in ref. 36. In this example, a greater than six-fold enhancement in solar-vapor conversion efficiency (i.e., GOR > 6) over a single-stage device is predicted when N > 20 (Fig. 7b), which corresponds to a water production rate of about 10 L m−2 h−1. Interestingly, η does not follow a linear trend (the grey-dashed line in Fig. 7b) with increasing N due to the accumulated sidewall heat loss from each stage. As a result, the benefit of adding one more stage keeps diminishing, leading to a plateauing of the achievable solar-vapor conversion efficiency (yellow regime in Fig. 7b). The yellow star at about N = 15 marks the approximate position where the plateauing occurs (less than 5% difference compared with the maximum solar-vapor conversion efficiency); the region before (green regime in Fig. 7b) represents the regime where increasing N is beneficial. Therefore, for a practical multistage design, the number of stages should be carefully chosen to balance the performance enhancement and material cost.
Fig. 7c–e show recent representative studies using the multistage approach to enhance solar desalination performance. Chiavazzo et al. developed a multistage device (Fig. 7c) with two hydrophilic layers separated by a hydrophobic microporous membrane as a single stage.15 The two hydrophilic layers serve as the evaporator and condenser, respectively. The vapor-permeable hydrophobic layer separates the evaporator and the condenser and only allows vapor to transport through. They demonstrated a water production rate of 3 L m−2 h−1 using a ten-stage device.15 Wang et al. designed and demonstrated a hybrid photovoltaic (PV) solar desalination device with multiple evaporation and condensation stages (Fig. 7d).35 A commercial polycrystalline silicon solar cell is used as the solar absorber to convert short-wavelength photons to electricity and long-wavelength photons to heat. On the back of the solar cell, a three-stage evaporator–condenser unit is attached. The single-stage design is similar to Chiavazzo et al.'s work with a hydrophobic membrane separating two hydrophilic layers.15,35 The hybrid device can generate electricity at 11% efficiency while producing portable water at 1.64 kg m−2 h−1 production rate.35 Unlike previous works by Chiavazzo et al. and Wang et al.,15,35 Xu et al. developed a simpler multistage device with higher water productivity (Fig. 7e).34 In Xu et al.'s device, each single stage consists of a capillary wick (evaporator), an air gap, and a thin metal condenser. Instead of using a hydrophobic porous membrane, the air gap separates the evaporator and condenser while allowing water vapor to pass through. By optimizing the heat and mass transport processes, they demonstrated a record-high water production rate of 5.78 L m−2 h−1 with a ten-stage device.34
Similar to the single-stage device, heat and mass transport plays a critical role in the design of a multistage device. Our discussion in Section 3.2 is also valid for the multistage device, which should incorporate coupling between stages – outlined in the detailed modeling approach developed recently by Zhang et al.36Fig. 7f shows the effect of air gap thickness on the overall solar-vapor conversion efficiency of 15-stage and 30-stage modeled devices. Both devices have 15 cm × 15 cm area and are operated under one sun illumination. As the air gap thickness tg increases, the solar-vapor conversion efficiency first increases and then decreases, passing through an optimal point at tg = 0.3 cm. This optimal solar-vapor conversion efficiency is attributed to the transition from a heat transport (HT) limited regime (red region in Fig. 7f) to a mass transport (MT) limited regime (blue region in Fig. 7f). Specifically, when tg is small (< 0.3 cm), heat conduction between the evaporator and condenser in each stage is significant, which leads to the heat transport limited regime. When tg is large (> 0.3 cm), the mass transport resistance between the evaporator and condenser becomes the dominant resistance and the device transitions to the mass transport limited regime. The above analysis highlights the importance of in-depth modeling and quantitative optimization of the multistage device design.
We summarize the reported solar-vapor conversion efficiency of the state-of-the-art multistage designs in Fig. 7g.15,34,35,65 Most designs with more than two stages can easily break the 100% efficiency limit of the single-stage design and therefore produce water at a rate over 2 L m−2 h−1.15,34,35 A comparison with the best performance predicted by modeling36 indicates there exists significant room for improving the multistage design, which requires optimization of the heat and mass transport. In terms of water production, pursuing the multistage design is a more rewarding direction compared with its single-stage counterpart. However, the device cost per unit area of the multistage device could be much higher than that of the single-stage device due to the large number of stages, which might offset the performance benefits of the multistage design. Therefore, in addition to improving the water production, reducing the total cost with commercially available materials and simpler structures is of equal importance. We discuss the trade-off between the water production rate and device cost in Section 5.
Current theoretical and experimental investigations of multistage devices mainly focus on steady-state operation. However, the solar desalination device operation is inherently transient, because of the continuously changing solar flux from sunrise to sunset and the random fluctuations in solar flux and ambient temperature. When the response time of a desalination device is comparable to the characteristic timescale of the above-mentioned transient factors, the dynamics of the device become important. Fig. 7h shows that the thermal response time τsys quadratically increases with the total thickness of a desalination device.72 The daily operating duration of the device is typically one to five hours around the solar noon (the orange band in Fig. 7h). For a single-stage device which is thin (total thickness ∼ cm), τsys is much smaller than the daily operating duration and the device can rapidly reach steady state. However, for a full-scale multistage device, the total thickness could be large (e.g., ∼ 10 cm to ∼ 1 m), which leads to a time constant comparable to the daily operating duration (∼ h). Such a multistage device responds slowly and might never reach steady state during the period of operation. Since the slow thermal response will lead to both slow warm-up and cool-down processes of the desalination device, its impact on the overall water production compared to the steady state operation needs to be well-understood. In addition, large τsys also indicates a longer recovery time under the external perturbation of solar flux and ambient temperature due to the weather conditions. Therefore, an in-depth understanding of the transient behavior and dynamic response for the multistage device could be valuable for future high-performance solar desalination systems.
4. Designing anti-fouling, salt-rejecting and robust desalination devices
In addition to achieving a high production rate, a practical solar desalination device also needs to be reliable to ensure a long lifetime and reduce cost of maintenance. Fouling due to salt accumulation is one of the most common degradation mechanisms which blocks water transport and reduces the solar absorption area. In this section, we analyze salt transport during solar evaporation which helps identify the mechanisms causing salt accumulation and potential opportunities for effective salt removal. We also review state-of-the-art strategies for avoiding salt accumulation and accelerating salt rejection, which could enable desalination device designs with strong resistance to fouling.4.1. Salt transport in thermally-localized solar desalination devices
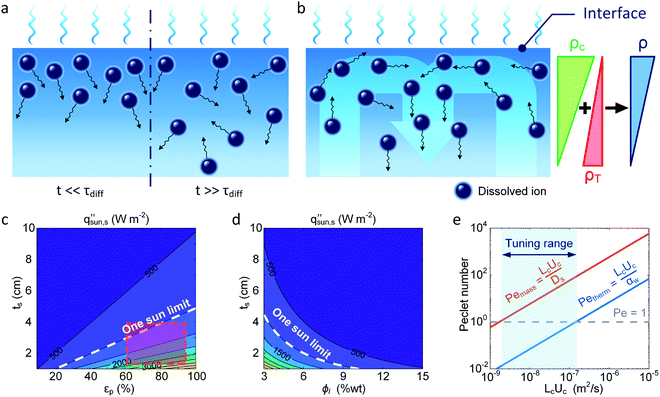
Salt transport in the evaporator determines the salt accumulation and rejection rates. A clear understanding of salt migration dynamics during solar desalination is missing in the literature. In this section, we elucidate the physical mechanisms responsible for salt migration which show the complexity due to its transient, diffusive, and convective nature and its coupling with the temperature and flow field. Our analysis also illustrates why salt accumulation is a significant challenge for solar thermal desalination and highlights potential solutions to improve salt rejection by thermofluidic engineering.The transport of salt ions is governed by the time-dependent convection–diffusion equation,72,111
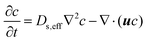 | (7) |
Here, we provide a simplified analysis of salt transport in 1D assuming steady-state diffusion. Fig. 8c shows the critical solar flux for salt separation 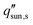 as a function of evaporator thickness and porosity. The critical solar flux for salt separation is defined as the absorbed solar flux corresponding to saturation salt concentration at the liquid-air interface, beyond which salt crystallization will occur in the evaporator. The salinity of bulk water is assumed to be 35 g L−1 (3.4 wt%) – same as that of typical seawater.
as a function of evaporator thickness and porosity. The critical solar flux for salt separation is defined as the absorbed solar flux corresponding to saturation salt concentration at the liquid-air interface, beyond which salt crystallization will occur in the evaporator. The salinity of bulk water is assumed to be 35 g L−1 (3.4 wt%) – same as that of typical seawater. 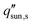 decreases rapidly with increasing ts and decreasing εp due to the resulting increase in diffusion resistance. The line representing the one sun limit (
decreases rapidly with increasing ts and decreasing εp due to the resulting increase in diffusion resistance. The line representing the one sun limit (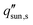 = 1000 W m−2, white-dashed line in Fig. 8c) crosses the typical operation regime (red-dashed box in Fig. 8c), indicating that salt accumulation is relatively common and can be a severe problem for solar thermal desalination. Salt accumulation can be even more problematic for applications dealing with high-concentration salt water such as wastewater treatment. Fig. 8d shows the critical solar flux for salt separation as a function of evaporator thickness and bulk water concentration ϕl, when the evaporator porosity is 80%.
= 1000 W m−2, white-dashed line in Fig. 8c) crosses the typical operation regime (red-dashed box in Fig. 8c), indicating that salt accumulation is relatively common and can be a severe problem for solar thermal desalination. Salt accumulation can be even more problematic for applications dealing with high-concentration salt water such as wastewater treatment. Fig. 8d shows the critical solar flux for salt separation as a function of evaporator thickness and bulk water concentration ϕl, when the evaporator porosity is 80%. 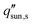 decreases with increasing ϕl due to a decrease of concentration gradient between the liquid–air interface and bulk water. When ts > 1 cm and ϕl > 10 wt%, it is almost impossible to completely reject salt only relying on diffusion under one sun illumination (the white-dashed line in Fig. 8d).
decreases with increasing ϕl due to a decrease of concentration gradient between the liquid–air interface and bulk water. When ts > 1 cm and ϕl > 10 wt%, it is almost impossible to completely reject salt only relying on diffusion under one sun illumination (the white-dashed line in Fig. 8d).
Since salt rejection through diffusion alone is relatively inefficient, it is desirable to enhance salt transport using natural convection which can be triggered by concentration as well as temperature gradients. It is also possible to introduce forced convection to further accelerate the salt rejection, which can be driven by gravity or additional mechanical parts. However, since convective flow will also increase heat loss, the trade-off between enhancing salt rejection and reducing heat loss needs to be carefully considered. Fig. 8e shows the potential opportunity to accelerate salt rejection by engineering the fluid flow. The contribution of convection relative to diffusion is quantified by the Peclet number. The Peclet numbers for heat and mass transport are given by Petherm = LcUc/αw and Pemass = LcUc/Ds, respectively, where Uc is the characteristic flow velocity and αw is the thermal diffusivity of water. When the Peclet number is significantly smaller than one, diffusion is the dominant transport mechanism. When the Peclet number is significantly larger than one, convection becomes more important. Fig. 8e shows Petherm and Pemass as a function of LcUc. For efficient salt rejection via convection, it is desirable to have a large enough flow velocity Uc such that Pemass > 1. Meanwhile, Uc should be small enough such that, Petherm < 1, which ensures that the additional heat loss due to convection is negligible. Since αw (∼10−7 m2 s−1) and Ds (∼10−9 m2 s−1) typically differ by two orders of magnitude, there exists a tuning range (blue band in Fig. 8e) where Pemass > 1 and Petherm < 1 hold simultaneously – achievable through evaporator geometry and fluid flow engineering. Specific strategies enabling optimization of mass and thermal transport and its impact on the overall salt rejection and water production need to be investigated in future studies.
4.2. Strategies for avoiding salt accumulation and accelerating salt rejection
In this section, we summarize several practical strategies for avoiding salt accumulation and accelerating salt rejection based on a fundamental understanding of salt transport discussed above. In general, these strategies can be classified into four categories, i.e., (1) separation by function, (2) enhanced salt diffusion/convection, (3) water confinement without porous media, and (4) contactless heating. The separation by function strategy focuses on reducing the side effects of salt accumulation.85,115–118 Xu et al. developed a Janus absorber using a double-layer structure, which decouples the solar absorbing and capillary wicking functionalities (top panel of Fig. 9a).115 The upper layer is hydrophobic, acting as the solar absorber whereas the bottom layer is hydrophilic, creating capillary pressure for water supply. Since salt can only accumulate in the bottom layer, it no longer affects solar absorption. Xia et al. demonstrated a spatially isolating strategy to preserve the evaporation area, while salt crystallization is confined to the edge of the circular disk evaporator due to the large transport resistance from the edge to the center (bottom panel of Fig. 9a).85 Although the separation by function strategy is capable of reducing the side effects of salt accumulation, it cannot enhance salt rejection which is particularly important for desalinating high-concentration salt water. Improved salt rejecting performance can be achieved by engineering diffusion/convection resistance.70,86,119 Kuang et al. created more salt diffusion pathways by drilling vertical channels on a carbonized natural wood evaporator, which shortens the distance between the evaporating interface and bulk water (left panel of Fig. 9b) – demonstrating enhanced salt rejection during a six-hour continuous test using 20 wt% NaCl solution.119 Ni et al. designed similar vertical channels using hydrophilic cellulose fabric, which enables both water transport and salt rejection (right panel of Fig. 9b).70 More interestingly, in addition to concentration gradient-driven salt diffusion, natural convection was observed in the experiment and confirmed as the major driving force of salt rejection using numerical simulations.70 Similarly, Morciano et al.68 and Zhang et al.67 also demonstrated enhanced salt rejection by engineering Marangoni and unidirectional flow, respectively. However, to fully take advantage of the enhanced salt diffusion/convection strategy, quantitative optimization of the geometry, number, size, and spacing of salt rejection channels is required.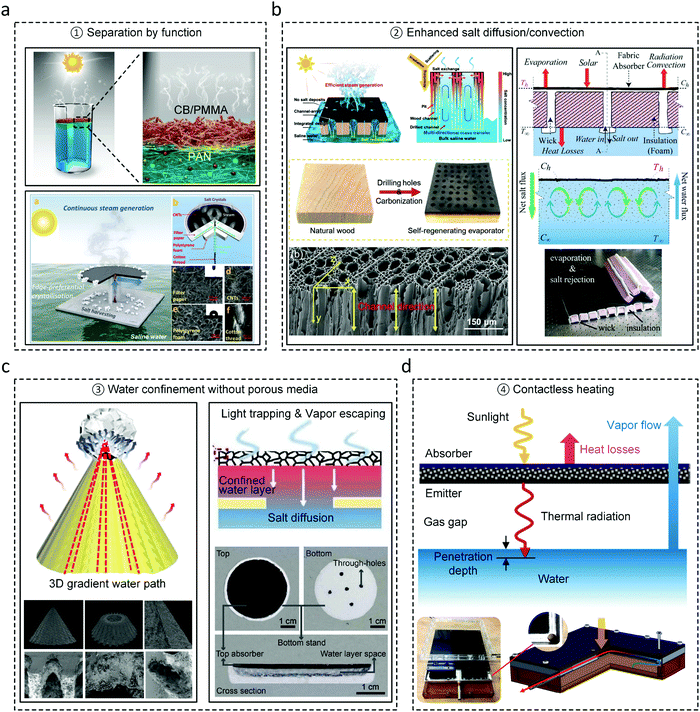 | ||
| Fig. 9 Strategies for avoiding salt accumulation and accelerating salt rejection. (a) Representative examples of the separation by function strategy85,115 which focuses on eliminating side-effects due to salt accumulation. Reproduced with permissions from John Wiley and Sons115 and Royal Society of Chemistry.85 (b) Representative examples of the enhanced salt diffusion/convection strategy70,119 which accelerates salt rejection by reducing the salt transport resistance. Reproduced with permissions from John Wiley and Sons119 and Royal Society of Chemistry.70 (c) Representative examples of the water confinement strategy44,120 which removes the porous evaporator that induces salt accumulation and localizes heat in the confined water layer. Reproduced with permissions from Springer Nature120 and American Association for the Advancement of Science.44 (d) Representative example of the contactless heating strategy63 which addresses the fouling and inefficient salt rejection due to the contact between the absorber and water surface. Reproduced with permissions from Springer Nature.63 | ||
Since the increase in salt transport resistance due to the porous evaporator is one of the main reasons for salt accumulation, the water confinement approach achieved thermal localization without a porous evaporator.44,120 Wu et al. designed a conical solar evaporator with asymmetric ratchets and microcavity arrays on the surface, which creates a capillary pressure gradient for water confinement and unidirectional water transport (left panel in Fig. 9c).120 Salt crystallization is localized at the apex of the conical evaporator due to the Marangoni effect, which has negligible effect on the evaporation process. High solar-to-vapor conversion efficiency of 96% was demonstrated in desalinating 25 wt% NaCl solution under one sun illumination.120 Xu et al. developed a waterlily-inspired solar evaporator where water layer is confined between a hydrophobic porous solar absorber and a thermal insulating layer (right panel in Fig. 9c).44 Heat is localized into this confined water layer due to heat transfer from the absorber and thermal insulation from the bulk water at the bottom. Salt rejection from the confined water layer to the bulk water is achieved through the macroscopic holes in the thermal insulating layer (right panel in Fig. 9c). This design achieved about 80% solar-to-vapor conversion efficiency for a 10 wt% NaCl solution under one sun illumination.44 The water confinement strategy has inspired a new pathway for the thermally-localized evaporator design, however, its integration with desalination devices requires further investigation.
Contactless heating is another effective approach to avoid fouling due to the complete separation between the absorber and water surface and removal of the evaporator (Fig. 9d), where desalinating 25 wt% NaCl solution has been demonstrated under one sun illumination.63,64 Although superior anti-fouling performance has been shown, the demonstrated solar-vapor conversion efficiency for the contactless configuration is still relatively low (about 25% for superheated vapor generation63 and 43% for wastewater treatment64), indicating a potential opportunity to significantly improve performance through a better understanding of the heat and mass transport. In addition to the above strategies, salt rejections using ion exchange by adding chemicals,117,121 directional solvent extraction,122 selective ion penetration materials,123 and self-rotating evaporator124 are also promising for integration with solar desalination devices.
Our discussion in this section mainly focused on NaCl-accumulation induced fouling and reliability. Although dissolved salt (NaCl) is one of the major species causing fouling and has attracted most attention, other salts like sulfates and carbonates, organic compounds like hydrocarbons, and biological organisms might lead to significant fouling during operation. For example, the crystallization of species with very low solubility in water (e.g., Ca2+ and CaSO4·2H2O) can be even more challenging in real practice and typical salt rejection tests using NaCl solution can be inadequate. Therefore, in-depth analysis of other fouling mechanisms, anti-fouling strategies, and long-term robustness tests in realistic environments also need to be performed in future studies.
5. Techno-economic analysis of thermally-localized solar desalination
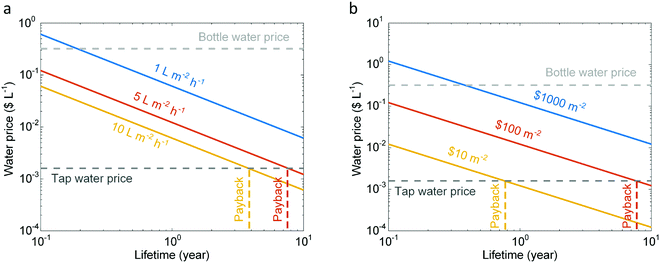
The primary driving force behind the significant interest in thermally-localized solar desalination in recent years is its potential economic-feasibility and scalability which can enable widespread adoption. In this section, we highlight the interplay between different device designs and efforts to achieve high water production, long-lasting reliability, and low material cost. Using a simple techno-economic analysis, we evaluate the cost competitiveness of desalination devices with varying target production rates and device costs.The aggregate cost of materials, manufacturing, labor, and maintenance represent the total device cost since solar desalination does not consume electricity. The unit price for purified water Pw (units: $ L−1) is thus given by,36
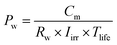 | (8) |
6. Conclusions and perspectives
This review highlights the significant potential of solar desalination in addressing the global water shortage. Specifically, this paper focused on thermally-localized solar desalination systems which can simultaneously achieve flexibility and high energy efficiency. Instead of focusing on the material composition and morphology, we classified the evaporators and desalination devices reported in the literature based on their configurations – front-side and back-side. Although most of the current designs use the front-side configuration, we show that the back-side evaporator is advantageous since it offers greater flexibility in the choice of materials, integration with condenser, and heat loss suppression. Back-side desalination devices are also more desirable because they allow a wide range of materials for condenser, enhance condensation heat transfer, and avoid reduction of incident solar flux due to interfering condensed droplets.We analyzed different strategies to improve water production and presented a theoretical framework which can be used to quantitatively guide the design for both the evaporator and desalination device. Specifically, we focused on three factors limiting the evaporator performance – heat loss, coupling of heat and mass transport, and water transport. We show that heat loss and coupling of heat and mass transport are critical in determining solar-vapor conversion efficiency, while the water transport capability is usually not a bottleneck due to the dilute solar flux. Using a theoretical framework, we analyzed the effectiveness of three thermal management strategies employing a spectrally selective absorber, convection cover, and conduction barrier; indicating that improper thermal insulation accounts for more than 75% reduction in solar-vapor conversion efficiency.
An important point that is often overlooked is that the water productivity of a desalination device is largely independent of its evaporator performance in an open system because the heat and mass transfer mechanisms are different. An important design parameter – the air gap thickness between the evaporator and condenser – governs the solar-to-vapor conversion efficiency of the desalination device. An optimal air gap thickness exists due to the transition from a heat transfer limited to a mass transfer limited regime. The insights gained from modeling and experiments indicate that device-level heat and mass transport optimization is as important as advancements in evaporator materials. In addition, we show that the efficient recycling of latent heat using a multistage design is critical to achieving a multifold enhancement in desalination performance, where more than 600% solar-vapor conversion efficiency and about 10 L m−2 h−1 water production rate are predicted. Quantitative optimization of the number of stages, device size, and air gap thickness is important to approach the theoretical limit. Similar to the single-stage design, an optimal air gap thickness also exists for the multistage desalination device.
In addition to increasing the water production, enhancing reliability is equally important for a high-performance desalination device. We analyzed the salt transport due to diffusion and convection using a theoretical framework and show that salt accumulation can be significant even under natural sunlight due to the low diffusivity of ions in water. We also show the complex salt transport processes due to the coupling of temperature- and concentration-induced fluid flow, which could inform future research opportunities to accelerate salt rejection. In addition, we reviewed different strategies for avoiding salt accumulation and accelerating salt rejection including separation by function, enhanced salt diffusion/convection, water confinement without porous media, and contactless heating.
Finally, in order to evaluate the real-world feasibility of thermally-localized solar desalination, we performed a techno-economic analysis that took into account the efficacy of water production and reliability. Three parameters determine the commercial feasibility of a device – water production rate, lifetime, and device cost. Compared with bottled water, solar desalination is generally more cost-effective. However, to be comparable with the price of tap water, solar desalination is expected to have a water production rate greater than 5 L m−2 h−1, device cost less than $100 m−2, and lifetime longer than a few years.
In summary, this review provides a comprehensive analysis of the recent progress and future opportunities of thermally-localized solar desalination, which could enable its transition from laboratory prototypes to industrial applications. With efforts that increase water production, enhance anti-fouling capability, and reduce device cost, we believe efficient, robust, and thermally-localized solar desalination will become economically feasible and play an important role in addressing the global water crisis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. Zhang gratefully acknowledges funding support from MIT Martin Family Society of Fellows for Sustainability, Abdul Latif Jameel Water and Food Systems Lab (J-WAFS), and Singapore-MIT Alliance for Research and Technology (SMART) LEES Program. Z. Xu acknowledges funding supports from the National Natural Science Foundation of China (Grant No. 51976123) and Shanghai Pujiang Program (Grant No. 2019PJD022).References
- M. M. Mekonnen and A. Y. Hoekstra, Sci. Adv., 2016, 2, e1500323 CrossRef PubMed.
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Mariñas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed.
- R. W. Hofste, S. Kuzma, S. Walker, E. H. Sutanudjaja, M. F. P. Bierkens, M. J. M. Kuijper, M. F. Sanchez, R. V. Beek, Y. Wada, S. G. Rodriguez and P. Reig, Aqueduct 3.0: Updated Decision-Relevant Global Water Risk Indicators, https://www.wri.org/publication/aqueduct-30, (accessed 11 November 2020).
- M. S. Mauter and P. S. Fiske, Energy Environ. Sci., 2020, 13, 3180–3184 RSC.
- GDP per capita (current US$), https://data.worldbank.org/indicator/NY.GDP.PCAP.CD?end=2019&start=1960&view=chart, (accessed 11 November 2020).
- Solar irradiance data, https://solargis.com/, (accessed 11 November 2020).
- Z. Wang, T. Horseman, A. P. Straub, N. Y. Yip, D. Li, M. Elimelech and S. Lin, Sci. Adv., 2019, 5, eaax0763 CrossRef CAS PubMed.
- Y. Zhang, T. Xiong, D. K. Nandakumar and S. C. Tan, Adv. Sci., 2020, 7, 1903478 CrossRef CAS PubMed.
- Y. Pang, J. Zhang, R. Ma, Z. Qu, E. Lee and T. Luo, ACS Energy Lett., 2020, 5, 437–456 CrossRef CAS.
- P. Tao, G. Ni, C. Song, W. Shang, J. Wu, J. Zhu, G. Chen and T. Deng, Nat. Energy, 2018, 3, 1031–1041 CrossRef.
- X. Li, G. Ni, T. Cooper, N. Xu, J. Li, L. Zhou, X. Hu, B. Zhu, P. Yao and J. Zhu, Joule, 2019, 3, 1798–1803 CrossRef.
- S. K. Patel, S. K. Patel, C. L. Ritt, A. Deshmukh, Z. Wang, M. Qin, M. Qin, R. Epsztein, M. Elimelech and M. Elimelech, Energy Environ. Sci., 2020, 13, 1694–1710 RSC.
- F. Zhao, Y. Guo, X. Zhou, W. Shi and G. Yu, Nat. Rev. Mater., 2020, 5, 388–401 CrossRef.
- X. Zhou, Y. Guo, F. Zhao and G. Yu, Acc. Chem. Res., 2019, 52, 3244–3253 CrossRef CAS PubMed.
- E. Chiavazzo, M. Morciano, F. Viglino, M. Fasano and P. Asinari, Nat. Sustain., 2018, 1, 763–772 CrossRef.
- J. Lienhard, M. Antar, A. Bilton, J. Blanco and G. Zaragoza, Annu. Rev. Heat Transfer, 2012, 15, 267–347 Search PubMed.
- A. E. Kabeel and S. A. El-Agouz, Desalination, 2011, 276, 1–12 CrossRef CAS.
- A. E. Kabeel, Energy, 2009, 34, 1504–1509 CrossRef.
- A. El-Bahi and D. Inan, Renewable Energy, 1999, 17, 509–521 CrossRef.
- P. I. Cooper, Sol. Energy, 1973, 15, 205–217 CrossRef.
- J. Xiong, G. Xie and H. Zheng, Energy Convers. Manage., 2013, 73, 176–185 CrossRef.
- H. Tanaka, T. Nosoko and T. Nagata, Desalination, 2000, 130, 279–293 CrossRef CAS.
- G. Prakash Narayan, M. G. St. John, S. M. Zubair and J. H. Lienhard, Int. J. Heat Mass Transfer, 2013, 58, 740–748 CrossRef CAS.
- G. P. Narayan, K. M. Chehayeb, R. K. McGovern, G. P. Thiel, S. M. Zubair and J. H. Lienhard, Int. J. Heat Mass Transfer, 2013, 57, 756–770 CrossRef.
- M. W. Shahzad, M. Burhan, L. Ang and K. C. Ng, Desalination, 2017, 413, 52–64 CrossRef CAS.
- H. Ghasemi, G. Ni, A. M. Marconnet, J. Loomis, S. Yerci, N. Miljkovic and G. Chen, Nat. Commun., 2014, 5, 4449 CrossRef CAS PubMed.
- Z. Wang, Y. Liu, P. Tao, Q. Shen, N. Yi, F. Zhang, Q. Liu, C. Song, D. Zhang, W. Shang and T. Deng, Small, 2014, 10, 3234–3239 CrossRef CAS PubMed.
- G. Ni, G. Li, S. V. Boriskina, H. Li, W. Yang, T. Zhang and G. Chen, Nat. Energy, 2016, 1, 16126 CrossRef CAS.
- L. Zhou, Y. Tan, J. Wang, W. Xu, Y. Yuan, W. Cai, S. Zhu and J. Zhu, Nat. Photonics, 2016, 10, 393–398 CrossRef CAS.
- K. Bae, G. Kang, S. K. Cho, W. Park, K. Kim and W. J. Padilla, Nat. Commun., 2015, 6, 10103 CrossRef CAS PubMed.
- F. Zhao, X. Zhou, Y. Shi, X. Qian, M. Alexander, X. Zhao, S. Mendez, R. Yang, L. Qu and G. Yu, Nat. Nanotechnol., 2018, 13, 489–495 CrossRef CAS PubMed.
- X. Zhou, F. Zhao, Y. Guo, Y. Zhang and G. Yu, Energy Environ. Sci., 2018, 11, 1985–1992 RSC.
- Y. Guo, X. Zhao, F. Zhao, Z. Jiao, X. Zhou and G. Yu, Energy Environ. Sci., 2020, 13, 2087–2095 RSC.
- Z. Xu, L. Zhang, L. Zhao, B. Li, B. Bhatia, C. Wang, K. L. Wilke, Y. Song, O. Labban, J. H. Lienhard, R. Wang and E. N. Wang, Energy Environ. Sci., 2020, 13, 830–839 RSC.
- W. Wang, Y. Shi, C. Zhang, S. Hong, L. Shi, J. Chang, R. Li, Y. Jin, C. Ong, S. Zhuo and P. Wang, Nat. Commun., 2019, 10, 3012 CrossRef PubMed.
- L. Zhang, Z. Xu, B. Bhatia, B. Li, L. Zhao and E. N. Wang, Appl. Energy, 2020, 266, 114864 CrossRef.
- L. Zhu, M. Gao, C. K. N. Peh and G. W. Ho, Nano Energy, 2019, 57, 507–518 CrossRef CAS.
- V.-D. Dao, N. H. Vu and S. Yun, Nano Energy, 2020, 68, 104324 CrossRef CAS.
- P. Wang, Environ. Sci.: Nano, 2018, 5, 1078–1089 RSC.
- H. Liu, Z. Huang, K. Liu, X. Hu and J. Zhou, Adv. Energy Mater., 2019, 9, 1900310 CrossRef.
- C. Zhang, H. Liang, Z. Xu and Z. Wang, Adv. Sci., 2019, 6, 1900883 CrossRef CAS PubMed.
- M. Gao, L. Zhu, C. K. Peh and G. W. Ho, Energy Environ. Sci., 2019, 12, 841–864 RSC.
- C. Chen, Y. Kuang and L. Hu, Joule, 2019, 3, 683–718 CrossRef CAS.
- N. Xu, J. Li, Y. Wang, C. Fang, X. Li, Y. Wang, L. Zhou, B. Zhu, Z. Wu, S. Zhu and J. Zhu, Sci. Adv., 2019, 5, eaaw7013 CrossRef CAS PubMed.
- J. Yang, Y. Pang, W. Huang, S. K. Shaw, J. Schiffbauer, M. A. Pillers, X. Mu, S. Luo, T. Zhang, Y. Huang, G. Li, S. Ptasinska, M. Lieberman and T. Luo, ACS Nano, 2017, 11, 5510–5518 CrossRef CAS PubMed.
- X. Li, W. Xu, M. Tang, L. Zhou, B. Zhu, S. Zhu and J. Zhu, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13953–13958 CrossRef CAS PubMed.
- F. Jiang, H. Liu, Y. Li, Y. Kuang, X. Xu, C. Chen, H. Huang, C. Jia, X. Zhao, E. Hitz, Y. Zhou, R. Yang, L. Cui and L. Hu, ACS Appl. Mater. Interfaces, 2018, 10, 1104–1112 CrossRef CAS PubMed.
- Y. Ito, Y. Tanabe, J. Han, T. Fujita, K. Tanigaki and M. Chen, Adv. Mater., 2015, 27, 4302–4307 CrossRef CAS PubMed.
- C. Jia, Y. Li, Z. Yang, G. Chen, Y. Yao, F. Jiang, Y. Kuang, G. Pastel, H. Xie, B. Yang, S. Das and L. Hu, Joule, 2017, 1, 588–599 CrossRef.
- P. Mu, Z. Zhang, W. Bai, J. He, H. Sun, Z. Zhu, W. Liang and A. Li, Adv. Energy Mater., 2019, 9, 1802158 CrossRef.
- X. Hu, W. Xu, L. Zhou, Y. Tan, Y. Wang, S. Zhu and J. Zhu, Adv. Mater., 2017, 29, 1604031 CrossRef PubMed.
- P. Zhang, J. Li, L. Lv, Y. Zhao and L. Qu, ACS Nano, 2017, 11, 5087–5093 CrossRef CAS PubMed.
- H. Liu, X. Zhang, Z. Hong, Z. Pu, Q. Yao, J. Shi, G. Yang, B. Mi, B. Yang, X. Liu, H. Jiang and X. Hu, Nano Energy, 2017, 42, 115–121 CrossRef CAS.
- Q. Ma, P. Yin, M. Zhao, Z. Luo, Y. Huang, Q. He, Y. Yu, Z. Liu, Z. Hu, B. Chen and H. Zhang, Adv. Mater., 2019, 31, 1808249 CrossRef PubMed.
- L. Zhou, Y. Tan, D. Ji, B. Zhu, P. Zhang, J. Xu, Q. Gan, Z. Yu and J. Zhu, Sci. Adv., 2016, 2, e1501227 CrossRef PubMed.
- O. Neumann, A. S. Urban, J. Day, S. Lal, P. Nordlander and N. J. Halas, ACS Nano, 2013, 7, 42–49 CrossRef CAS PubMed.
- G. Ni, N. Miljkovic, H. Ghasemi, X. Huang, S. V. Boriskina, C.-T. Lin, J. Wang, Y. Xu, M. M. Rahman, T. Zhang and G. Chen, Nano Energy, 2015, 17, 290–301 CrossRef CAS.
- L. Zhang, B. Tang, J. Wu, R. Li and P. Wang, Adv. Mater., 2015, 27, 4889–4894 CrossRef CAS PubMed.
- X. Zhou, F. Zhao, Y. Guo, B. Rosenberger and G. Yu, Sci. Adv., 2019, 5, 1–8 Search PubMed.
- J. Li, X. Wang, Z. Lin, N. Xu, X. Li, J. Liang, W. Zhao, R. Lin, B. Zhu, G. Liu, L. Zhou, S. Zhu and J. Zhu, Joule, 2020, 4, 928–937 CrossRef CAS.
- X. Li, J. Li, J. Lu, N. Xu, C. Chen, X. Min, B. Zhu, H. Li, L. Zhou, S. Zhu, T. Zhang and J. Zhu, Joule, 2018, 2, 1331–1338 CrossRef CAS.
- Y. Shi, R. Li, Y. Jin, S. Zhuo, L. Shi, J. Chang, S. Hong, K.-C. Ng and P. Wang, Joule, 2018, 2, 1171–1186 CrossRef CAS.
- T. A. Cooper, S. H. Zandavi, G. W. Ni, Y. Tsurimaki, Y. Huang, S. V. Boriskina and G. Chen, Nat. Commun., 2018, 9, 5086 CrossRef CAS PubMed.
- A. K. Menon, I. Haechler, S. Kaur, S. Lubner and R. S. Prasher, Nat. Sustain., 2020, 3, 144–151 CrossRef.
- G. Xue, Q. Chen, S. Lin, J. Duan, P. Yang, K. Liu, J. Li and J. Zhou, Glob. Challenges, 2018, 2, 1800001 CrossRef PubMed.
- X. Wang, Y. Liu, R. Feng, Y. Zhang, C. Chang, B. Fu, T. Luan, P. Tao, W. Shang, J. Wu, C. Song and T. Deng, Prog. Nat. Sci.: Mater. Int., 2019, 29, 10–15 CrossRef CAS.
- Y. Zhang, H. Zhang, T. Xiong, H. Qu, J. J. Koh, D. K. Nandakumar, J. Wang and S. C. Tan, Energy Environ. Sci., 2020, 13, 4891–4902 RSC.
- M. Morciano, M. Fasano, S. V. Boriskina, E. Chiavazzo and P. Asinari, Energy Environ. Sci., 2020, 13, 3646–3655 RSC.
- Z. Liu, H. Song, D. Ji, C. Li, A. Cheney, Y. Liu, N. Zhang, X. Zeng, B. Chen, J. Gao, Y. Li, X. Liu, D. Aga, S. Jiang, Z. Yu and Q. Gan, Glob. Challenges, 2017, 1, 1600003 CrossRef.
- G. Ni, S. H. Zandavi, S. M. Javid, S. V. Boriskina, T. A. Cooper and G. Chen, Energy Environ. Sci., 2018, 11, 1510–1519 RSC.
- Y. Liu, S. Yu, R. Feng, A. Bernard, Y. Liu, Y. Zhang, H. Duan, W. Shang, P. Tao, C. Song and T. Deng, Adv. Mater., 2015, 27, 2768–2774 CrossRef CAS PubMed.
- A. F. Mills, Heat Transfer, Pearson Education, 1999 Search PubMed.
- G. Vaartstra, L. Zhang, Z. Lu, C. D. Díaz-Marín, J. C. Grossman and E. N. Wang, J. Appl. Phys., 2020, 128, 130901 CrossRef CAS.
- L. Zhang, L. Zhao and E. N. Wang, Int. Commun. Heat Mass Transfer, 2020, 110, 104255 CrossRef.
- Z. Lu, I. Kinefuchi, K. L. Wilke, G. Vaartstra and E. N. Wang, Nat. Commun., 2019, 10, 2368 CrossRef PubMed.
- L. Zhang, Y. Zhu, Z. Lu, L. Zhao, K. R. Bagnall, S. R. Rao and E. N. Wang, Appl. Phys. Lett., 2018, 113, 163701 CrossRef.
- A. LaPotin, Y. Zhong, L. Zhang, L. Zhao, A. Leroy, H. Kim, S. R. Rao and E. N. Wang, Joule, 2021, 5, 166–182 CrossRef CAS.
- L. Zhao, B. Bhatia, S. Yang, E. Strobach, L. A. Weinstein, T. A. Cooper, G. Chen and E. N. Wang, ACS Nano, 2019, 13, 7508–7516 CrossRef CAS.
- L. Zhao, E. Strobach, B. Bhatia, S. Yang, A. Leroy, L. Zhang and E. N. Wang, Opt. Express, 2019, 27, A39 CrossRef CAS PubMed.
- H. Liu, C. Chen, G. Chen, Y. Kuang, X. Zhao, J. Song, C. Jia, X. Xu, E. Hitz, H. Xie, S. Wang, F. Jiang, T. Li, Y. Li, A. Gong, R. Yang, S. Das and L. Hu, Adv. Energy Mater., 2018, 8, 1701616 CrossRef.
- L. A. Weinstein, J. Loomis, B. Bhatia, D. M. Bierman, E. N. Wang and G. Chen, Chem. Rev., 2015, 115, 12797–12838 CrossRef CAS PubMed.
- L. Zhao, B. Bhatia, L. Zhang, E. Strobach, A. Leroy, M. K. Yadav, S. Yang, T. A. Cooper, L. A. Weinstein, A. Modi, S. B. Kedare, G. Chen and E. N. Wang, Joule, 2020, 4, 1–13 CrossRef.
- S. C. Singh, M. ElKabbash, Z. Li, X. Li, B. Regmi, M. Madsen, S. A. Jalil, Z. Zhan, J. Zhang and C. Guo, Nat. Sustain., 2020, 3, 938–946 CrossRef.
- X. Li, X. Min, J. Li, N. Xu, P. Zhu, B. Zhu, S. Zhu and J. Zhu, Joule, 2018, 2, 2477–2484 CrossRef.
- Y. Xia, Q. Hou, H. Jubaer, Y. Li, Y. Kang, S. Yuan, H. Liu, M. W. Woo, L. Zhang, L. Gao, H. Wang and X. Zhang, Energy Environ. Sci., 2019, 12, 1840–1847 RSC.
- S. He, C. Chen, Y. Kuang, R. Mi, Y. Liu, Y. Pei, W. Kong, W. Gan, H. Xie, E. Hitz, C. Jia, X. Chen, A. Gong, J. Liao, J. Li, Z. J. Ren, B. Yang, S. Das and L. Hu, Energy Environ. Sci., 2019, 12, 1558–1567 RSC.
- Q.-F. Guan, Z.-M. Han, Z.-C. Ling, H.-B. Yang and S.-H. Yu, Nano Lett., 2020, 20, 5699–5704 CrossRef CAS PubMed.
- Y. Huang, C. Feng, J. Hoeniges, K. Zhu and L. Pilon, J. Quant. Spectrosc. Radiat. Transfer, 2020, 251, 107039 CrossRef CAS.
- J. W. Rose and L. R. Glicksman, Int. J. Heat Mass Transfer, 1973, 16, 411–425 CrossRef CAS.
- S. Kim and K. J. Kim, J. Heat Transfer, 2011, 133, 1–8 CrossRef.
- L. Zhang, Z. Xu, Z. Lu, J. Du and E. N. Wang, Appl. Phys. Lett., 2019, 114, 163701 CrossRef.
- R. Tadmor, Soft Matter, 2011, 7, 1577–1580 RSC.
- S. Goh, J. Zhang, Y. Liu and A. G. Fane, Desalination, 2013, 323, 39–47 CrossRef CAS.
- N. Miljkovic, R. Enright, Y. Nam, K. Lopez, N. Dou, J. Sack and E. N. Wang, Nano Lett., 2013, 13, 179–187 CrossRef CAS PubMed.
- R. Enright, N. Miljkovic, N. Dou, Y. Nam and E. N. Wang, J. Heat Transfer, 2013, 135, 091304 CrossRef.
- Z. Xu, L. Zhang, K. Wilke and E. N. Wang, Langmuir, 2018, 34, 9085–9095 CrossRef CAS.
- L. Zhang, J. Zhu, K. L. Wilke, Z. Xu, L. Zhao, Z. Lu, L. L. Goddard and E. N. Wang, ACS Nano, 2019, 13, 1953–1960 CAS.
- K.-H. Chu, R. Xiao and E. N. Wang, Nat. Mater., 2010, 9, 413–417 CrossRef CAS.
- T. “Leo” Liu and C.-J. “CJ” Kim, Science, 2014, 346, 1096–1100 CrossRef PubMed.
- K.-C. Park, P. Kim, A. Grinthal, N. He, D. Fox, J. C. Weaver and J. Aizenberg, Nature, 2016, 531, 78–82 CrossRef CAS PubMed.
- Y. Hou, Y. Shang, M. Yu, C. Feng, H. Yu and S. Yao, ACS Nano, 2018, 12, 11022–11030 CrossRef CAS PubMed.
- H. Chen, T. Ran, Y. Gan, J. Zhou, Y. Zhang, L. Zhang, D. Zhang and L. Jiang, Nat. Mater., 2018, 17, 935–942 CrossRef CAS PubMed.
- L. Huang, H. Jiang, Y. Wang, Z. Ouyang, W. Wang, B. Yang, H. Liu and X. Hu, Desalination, 2020, 477, 114260 CrossRef CAS.
- D. Ghim, X. Wu, M. Suazo and Y.-S. Jun, Nano Energy, 2020, 105444 Search PubMed.
- H. T. El-Dessouky, H. M. Ettouney and Y. Al-Roumi, Chem. Eng. J., 1999, 73, 173–190 CrossRef CAS.
- H. El-Dessouky, H. I. Shaban and H. Al-Ramadan, Desalination, 1995, 103, 271–287 CrossRef CAS.
- H. T. El-Dessouky, H. M. Ettouney and F. Mandani, Appl. Therm. Eng., 2000, 20, 1679–1706 CrossRef CAS.
- M. Rosso, A. Beltramini, M. Mazzotti and M. Morbidelli, Desalination, 1997, 108, 365–374 CrossRef CAS.
- H. Tanaka, T. Nosoko and T. Nagata, Desalination, 2002, 150, 131–144 CrossRef CAS.
- A. D. Khawaji, I. K. Kutubkhanah and J.-M. Wie, Desalination, 2008, 221, 47–69 CrossRef CAS.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena, Wiley, 1960 Search PubMed.
- H. Kim, S. Yang, S. R. Rao, S. Narayanan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Science, 2017, 356, 430–434 CrossRef CAS PubMed.
- S. Narayanan, H. Kim, A. Umans, S. Yang, X. Li, S. N. Schiffres, S. R. Rao, I. S. McKay, C. A. Rios Perez, C. H. Hidrovo and E. N. Wang, Appl. Energy, 2017, 189, 31–43 CrossRef CAS.
- S. Narayanan, S. Yang, H. Kim and E. N. Wang, Int. J. Heat Mass Transfer, 2014, 77, 288–300 CrossRef CAS.
- W. Xu, X. Hu, S. Zhuang, Y. Wang, X. Li, L. Zhou, S. Zhu and J. Zhu, Adv. Energy Mater., 2018, 8, 1702884 CrossRef.
- Y. Yang, H. Zhao, Z. Yin, J. Zhao, X. Yin, N. Li, D. Yin, Y. Li, B. Lei, Y. Du and W. Que, Mater. Horiz., 2018, 5, 1143–1150 RSC.
- J. Zeng, Q. Wang, Y. Shi, P. Liu and R. Chen, Adv. Energy Mater., 2019, 9, 1900552 CrossRef CAS.
- Z. Liu, B. Wu, B. Zhu, Z. Chen, M. Zhu and X. Liu, Adv. Funct. Mater., 2019, 29, 1905485 CrossRef CAS.
- Y. Kuang, C. Chen, S. He, E. M. Hitz, Y. Wang, W. Gan, R. Mi and L. Hu, Adv. Mater., 2019, 31, 1900498 CrossRef PubMed.
- L. Wu, Z. Dong, Z. Cai, T. Ganapathy, N. X. Fang, C. Li, C. Yu, Y. Zhang and Y. Song, Nat. Commun., 2020, 11, 521 CrossRef CAS PubMed.
- C. Zhang, Y. Shi, L. Shi, H. Li, R. Li, S. Hong, S. Zhuo, T. Zhang and P. Wang, Nat. Commun., 2021, 12, 998 CrossRef CAS PubMed.
- J. Guo, Z. D. Tucker, Y. Wang, B. L. Ashfeld and T. Luo, Nat. Commun., 2021, 12, 437 CrossRef CAS PubMed.
- H. Geng, Q. Xu, M. Wu, H. Ma, P. Zhang, T. Gao, L. Qu, T. Ma and C. Li, Nat. Commun., 2019, 10, 1512 CrossRef PubMed.
- Y. Xia, Y. Li, S. Yuan, Y. Kang, M. Jian, Q. Hou, L. Gao, H. Wang and X. Zhang, J. Mater. Chem. A, 2020, 8, 16212–16217 RSC.
- U.S. Annual Solar GHI, https://www.nrel.gov/gis/solar.html, (accessed 11 November 2020).
- Tap Water vs. Bottled Water, https://www.foodandwaterwatch.org/about/live-healthy/tap-water-vs-bottled-water, (accessed 11 November 2020).
- A. Livingston, Bottled Water vs. Tap Water – Facts & 4 Reasons to Drink Tap, https://www.moneycrashers.com/bottled-water-vs-tap-water-facts/#:~:text = According to the IBWA%2C, the Environmental Protection Agency (EPA), (accessed 11 November 2020).
- Average monthly residential cost of water in the U.S. from 2010 to 2019 (in U.S. dollars), https://www.statista.com/statistics/720418/average-monthly-cost-of-water-in-the-us/, (accessed 11 November 2020).
Footnote |
| † Equal contribution to this work. |
| This journal is © The Royal Society of Chemistry 2021 |