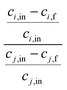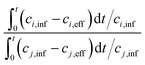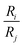Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Recent advances in ion selectivity with capacitive deionization
J. G.
Gamaethiralalage
 a,
K.
Singh
a,
K.
Singh
 ab,
S.
Sahin
ab,
S.
Sahin
 a,
J.
Yoon
a,
J.
Yoon
 c,
M.
Elimelech
c,
M.
Elimelech
 d,
M. E.
Suss
e,
P.
Liang
d,
M. E.
Suss
e,
P.
Liang
 f,
P. M.
Biesheuvel
f,
P. M.
Biesheuvel
 *b,
R. L.
Zornitta
*b,
R. L.
Zornitta
 a and
L. C. P. M.
de Smet
a and
L. C. P. M.
de Smet
 *ab
*ab
aLaboratory of Organic Chemistry, Wageningen University & Research, Stippeneng 4, 6708 WE Wageningen, The Netherlands. E-mail: louis.desmet@wur.nl
bWetsus – European Centre of Excellence for Sustainable Water Yechnology, Oostergoweg 9, 8911 MA Leeuwarden, The Netherlands. E-mail: maarten.biesheuvel@wetsus.nl
cSchool of Chemical and Biological Engineering, Institute of Chemical Processes, Seoul National University, Daehak-dong, Gwanak-gu, Seoul 151-742, Republic of Korea
dDepartment of Chemical and Environmental Engineering, Yale University, New Haven, CT 06520-8286, USA
eFaculty of Mechanical Engineering, Technion – Israel Institute of Technology, Haifa, 32000, Israel
fState Key Joint Laboratory of Environment Simulation and Pollution Control, School of Environment, Tsinghua University, Beijing 100084, P. R. China
First published on 6th January 2021
Abstract
Within the last decade, in addition to water desalination, capacitive deionization (CDI) has been used for resource recovery and selective separation of target ions in multicomponent solutions. In this review, we summarize the mechanisms of selective ion removal utilizing different electrode materials, carbon and non-carbon together with or without membranes, from a mixture of salt solutions, by a detailed review of the literature from the beginning until the state-of-the-art. In this venture, we review the advances made in the preparation, theoretical understanding, and the role of electrodes and membranes. We also describe how ion selectivity has been defined and used in literature. Finally, we present a theory of selective ion removal for intercalation materials that, for the first time, considers mixtures of different cations, evidencing the time-dependent selectivity of these electrodes.
Broader contextIncreasing demand of non-renewables and dwindling resources require robust solutions to establish secure supply lines in the immediate future. The ability of capacitive deionization (CDI) to tune the system selectivity towards a particular ion of interest reveals tremendous potential in this endeavor. CDI has exhibited promising and exponential growth in the last two decades. This progress has been inspired by a multitude of motives including new electrodes, membranes, and their surface functionalization, CDI cell architectures, novel applications, and a better understanding of theory and practice. Particularly considering novel applications, CDI has recently deepened its roots in the field of selective ion separation. Ion selectivity is a crucial component in resource recovery, wastewater treatment, as well as ion sensing. Therefore, this work is intended to thoroughly examine the rapid growth of CDI in the field of ion selectivity until the state-of-the-art, and consequently, initiate new research dimensions by bringing forth a new theory of selective ion separation with intercalation materials. |
1. Introduction
Fresh water scarcity and rapidly increasing global demand for clean water have stimulated scientists to seek out innovative methods of securing potable water supplies. Even though water desalination is deeply rooted within the human history, spanning across centuries,1 it was not until the latter half of 20th century that desalination techniques became commercialized.2 Conventional desalination methods, such as reverse osmosis (RO), electrodialysis (ED), multi-stage-flash (MSF), and multi-effect desalination (MED), are commonly used, but in some cases require significant energy input to produce fresh water. Furthermore, the majority of these systems often desalinate ‘to completion’, or do not preferentially remove the ions that are desired to be removed or even harvested. Ion selectivity is of key importance because it is often not necessary, and perhaps even detrimental, to remove the vast majority or entirety of ions from water. There are ample examples where one specific ion is to be removed because of its toxicity (arsenic, boron, heavy metals, ions leading to fouling, and sodium in irrigation water) or value (lithium, gold). In this review we focus on the ion selectivity (i.e. preferential removal of a particular ion of interest within a mixture of ions) aspect of water desalination via capacitive deionization (CDI).CDI was conceived as a concept in 1960 by Blair and Murphy using porous electrodes.3 The term “capacitive deionization” was later coined by Farmer et al. in 1995.4 CDI has attracted attention as a technique that could compete with existing desalination technologies, especially for applications with a salt concentration <≈10 g L−1, for households or small businesses not requiring trained operators, because it does not operate with high pressure or temperature. Instead the system operates on low voltages (≈1 V) in a way commensurate with common consumer electrical equipment, thus can be run without operator supervision. As a result, within the last few decades, CDI has emerged out as a promising technology in the field of desalination. More and more attention has recently developed to address the potential of CDI to be used as a technique for selective ion removal and harvest. Here, CDI offers tremendous potential because of the enormous, and still expanding library of capacitive materials that can be used and further modified. In addition, CDI can be operated in combination with (ion-selective) membranes, in which case selectivity becomes membrane dominant.
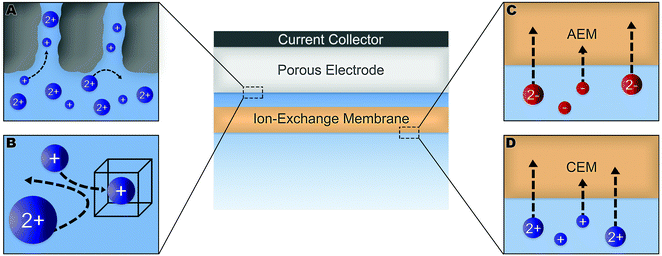
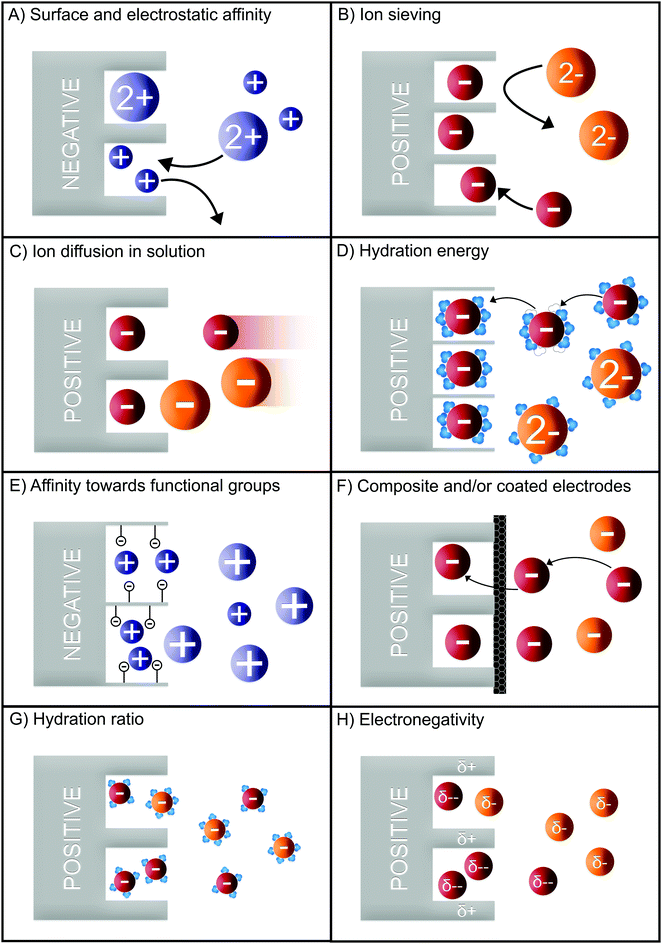
Numerous methods have been suggested to improve or introduce the selectivity of pristine CDI electrodes. These include the use of electrode materials with different pore sizes and compositions, functional groups, introduction of standard or special-grade ion-selective membranes, optimized operational parameters or combinations of them. Electrodes in CDI can induce ion selectivity, and a general mechanism of size-based selective ion separation is presented in Fig. 1A and B. Ion selectivity based on the valence of the adsorbing counter-ions, which also occurs in CDI electrodes, is not shown in the figure. On the other hand, in membrane- and flow-based CDI (see Box: General aspects of CDI for the cell geometries), the membranes induce ion selectivity. The separation of the ions based on their valence is shown in Fig. 1C and D. An anion-exchange membrane (AEM), while differentiating between cation and anions, can also differentiate among anions. The same is applicable for a cation-exchange membrane (CEM) and cations. It must be noted, however, that the mechanisms depicted in Fig. 1 are generalized, and exceptions are not uncommon. These behaviors will be discussed in detail in Section 2 (electrodes) and Section 3 (membranes).
A graphical timeline, as depicted in Fig. 2, shows how the state-of-the-art evolved over the last two decades including selective cation as well as anion separation in both CDI and MCDI.
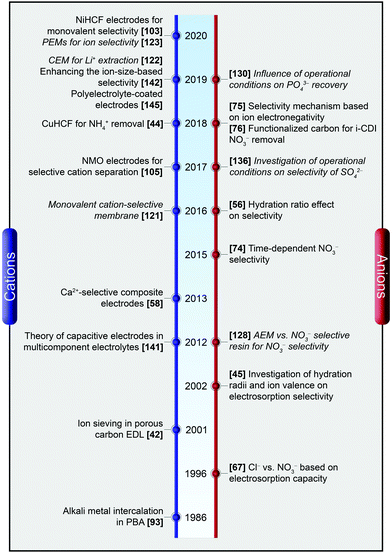 | ||
| Fig. 2 A graphical timeline depicting the evolution of ion selectivity in CDI and MCDI. The works employing membranes are denoted in italics. | ||
Recovering high-value nutrients, especially phosphates and nitrates, or metals, such as lithium, copper, silver, gold, is crucial. For instance, phosphate, a highly essential nutrient in sustaining all life, is expected to reach its global peak production in the next decade and the remaining world reserves are predicted to be depleted within 50–100 years.5 While the exact figures are still debated, it is ill-advised to overlook this issue. Lithium, on the other hand, has become a strategic natural resource with the ever-growing electronics market, which currently depends on lithium-ion batteries.6 While the need for efficient ion-recovery methods is evident from the scarcity point of view, the selective removal of ions is beneficial in many other aspects, including environmental- and health-related issues. Numerous regulatory authorities around the world, such as the Environmental Protection Agency (EPA) in the United States or the European Union (EU), have set restrictions on contaminant concentrations in both drinking water and in discharged wastewater (council directive 91/271/EEC). Substances that are detrimental to human health, for example heavy metals (e.g., lead, cadmium, arsenic) need to be eliminated from water. Thus, it is desirable to selectively remove the contaminants, since the complete removal of ions is not needed and may even be not desirable, because it enhances costs and energy usage. In this regard, CDI is an attractive technology because it has the potential to specifically (partially) remove certain ions, and not others.
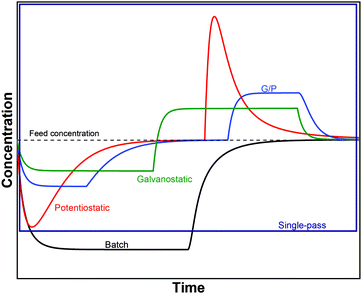
One of the challenging aspects in reviewing literature on ion selectivity in CDI stems from the many different approaches utilized by different research groups. Therefore, a direct comparison between literature may not be fully justified and great care must be taken. Some of the widely used selectivity definitions are provided in Table 1. These definitions are based on taking solutions with two competing ions (of the same polarity), i and j, into account. In some literature, the two components are referred to as target (t) and competing (c) ions. It is evident that ρ and Si/j are similar in nature. Both parameters calculate the selectivity based on the amount of ions removed by the electrodes. However, R reflects the amount of ions left in the effluent. Therefore, taking i to be the ion of interest, a ρ or Si/j value above one indicates that the system is selective towards the ion of interest, while in the R-definition a value less than one indicates the same.
Various aspects of CDI, such as the theory,7–9 applications,10–13 electrode materials,14–19 energy efficiency,20–23 and operational conditions,24,25 have already been thoroughly studied. Yet there is still lack of a comprehensive review including a discussion of storage mechanisms, electrode materials, selectivity definitions, and theoretical modelling that specifically addresses the challenges related to the topic of ion selectivity in CDI. In this review, we summarize how ion selectivity has been achieved in literature, address the commonly targeted ions, main challenges, relevant terminologies, and discuss future prospects in this field. The review will first present the fundamental concepts in CDI (see Box: General aspects of CDI), then we present the state-of-the-art literature which is classified in terms of the main element employed for achieving ion selectivity, i.e., electrodes (Section 2. Electrodes for ion selectivity) and membranes (Section 3. Membranes for ion selectivity). Finally, we introduce a new theoretical model for CDI with porous electrodes made out of intercalation material.
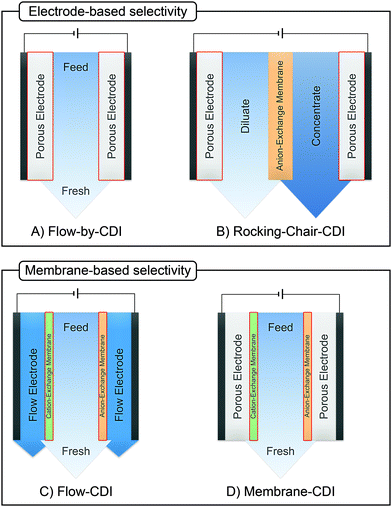
Box: General aspects of CDIA standard CDI cell, depicted in Fig. 3A, consists of two parallel electrodes (the anode and the cathode), made of a porous material that conducts electronic charge, allows access for ions and has an ion storage capacity, and a non-conductive “spacer” channel where the water flows through. A potential bias or a constant current is applied to the electrodes. Then, as the saltwater flows through the spacer channel, the ions migrate towards the electrode of opposite polarity, reducing the salt concentration. Following the desalination step, the electrodes can be short-circuited, the polarity can be inverted, or the current direction is reversed, to release the ions captured by the electrodes.Membrane capacitive deionization (MCDI), shown in Fig. 3D,26 utilizes ion-exchange membranes (IEMs) to enhance the desalination efficiency. The IEMs act as barriers in front of the electrodes preventing the co-ions from being expelled from the electrodes to the treated water.21 This also enables the use of inverted polarities during the desorption stage, similar to electrodes with functionalized micropore surfaces.27 They can also be used to enhance ion selectivity. The IEMs can be either freestanding or directly coated onto the solid-phase electrodes.28–30 In flow-electrode capacitive deionization (FCDI) (Fig. 3C),31 on the other hand, the electrode material is dispersed in a suspension, which circulates a pre-determined path over a current collector. The spacer channel and the electrode material are separated by IEMs. The ions permeate through the membrane and get electrosorbed into the electrodes. Finally, a design, often termed rocking-chair-CDI, with a single membrane and two flow channels is also possible (Fig. 3B).9,32–34 This works particularly well when the electrode is highly selective for anions or cations. In contrast to the other three configurations, the symmetric cell contains two chambers separated by an IEM and is capable of treating water uninterrupted by regeneration steps. In Fig. 3, we in particular highlight the key element that is fundamental to achieving a desired ion selectivity in a CDI cell, which is denoted by a red box in the sub-panels in the figure. Formation of an electrical double-layer (EDL) is a fundamental feature of many topics in physics and chemistry, and is also exploited in CDI. The first EDL model, the Helmholtz model, was proposed by Hermann Helmholtz in 1879. This model was later revised by Louis Gouy and David Chapman in 1910 and in 1913, respectively. The Helmholtz model and the Gouy–Chapman model were combined into the widely utilized Gouy–Chapman–Stern (GCS) model by Otto Stern in 1924.35 Graphical representations of common EDL models are depicted in Fig. 4, taking a positively charged electrode as an example. In the presence of an electrical driving force, the ions migrate towards electrodes of opposite polarities, and form EDLs across the accessible surfaces. Thus, materials with high surface area available for electrosorption are usually of importance in CDI.36 Since the formation of EDL is intrinsically a physical process, the regeneration of the electrodes only based on the EDL formation does not require the use of any chemicals, which is one of the primary advantages of CDI.
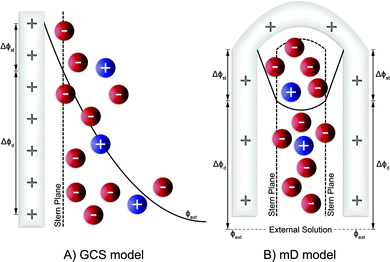
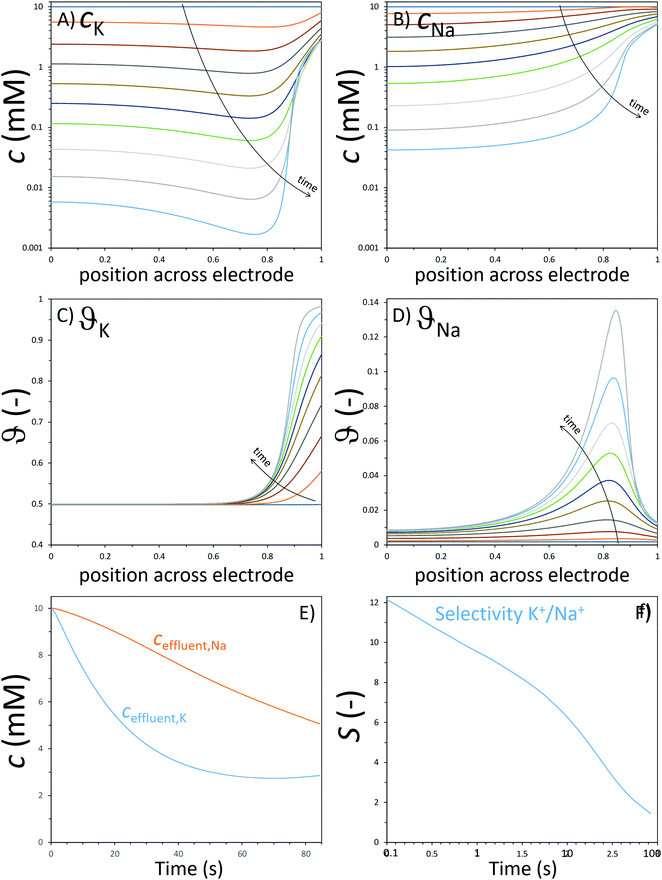
The GCS model, depicted in Fig. 4A, describes the distribution of charges across a charged solid/electrolyte interface. Thus, this can be used to understand the fundamentals of EDLs. While this would suffice for applications in which non-micropore material are considered, the GCS model approaches its limitations when the Debye length (a measure of the distance where notable charge separation can occur) is comparable to the finite micropore sizes of porous electrodes. In CDI, where microporous electrodes are prominent, the GCS model may deviate from real-life cases. In contrast, the modified Donnan (mD) model (Fig. 4B) accounts for the possibility that within a finite pore structure, the EDLs may overlap, considering that the Debye length is larger than that of the average pore size. In such cases where the EDLs overlap significantly, it can be assumed that the potential inside the pore to be constant.37 In order to realize ion selectivity with CDI, many aspects, including electrode characteristics, surface functional groups, operational parameters, ion size, valence, and hydrated radius can be exploited and/or optimized. Understanding the differences in behavior of ions under constant voltage (potentiostatic) and constant current (galvanostatic) is also crucial. Under potentiostatic conditions (at t → 0 s), the rate at which the charge is accumulated on electrodes is at maximum, and accordingly, after some time we find in the effluent a minimum concentration, as illustrated in Fig. 5. As the electrodes become saturated over time, the current flowing through the cell goes to zero, and no variation in concentration is observed. In contrast, under galvanostatic conditions, the charge accumulation rate remains constant, and consequently the potential between the two electrodes increases steadily over time until it reaches a cut-off potential. It is often the case that a cut-off potential is set in galvanostatic mode, such that the cell voltage does not exceed a limiting value, such as carbon electrooxidation and/or oxygen reduction voltage. One can also continue to hold the system at this potential for a certain period, in case the electrodes were not yet saturated sufficiently by the time the system reaches the cut-off potential. In this case, the system would temporarily switch from galvanostatic to potentiostatic mode (G/P), and now the current starts to gradually decrease. By making use of the differences between these operational modes, the selectivity of a system can be tuned by using an appropriate mode or a combination of them. Apart from potentiostatic and galvanostatic modes, CDI can also be divided into batch mode or single-pass mode (Fig. 5). In batch-mode operation, the effluent from the cell circulates back into the feed reservoir, creating a closed system. Therefore, it is crucial that the volume (consequently the total amount of ions available) of the feed solution is kept small, such that an appreciable concentration difference is detectable at equilibrium. The concentration is monitored in the reservoir itself during adsorption, desorption, and at equilibrium. In single-pass mode, the feed solution passes through the cell once and goes into a separate container. Thus, the concentration of the effluent decreases in the beginning, and then reverts to the original feed concentration once the electrodes are saturated, as also shown in Fig. 5. Alternatively, the effluent can circulate back to the feed reservoir similar to batch mode, provided that the volume of the feed stock is large enough. In this case, the concentration variation of the feed during the adsorption step should be typically less than 1%.8 Thus, this method still simulates a single-pass system since the decrease in total concentration during adsorption is negligible, and the concentration of the feed remains virtually constant. The concentration variation in single-pass mode under different conditions is shown in Fig. 5. In potentiostatic mode and single-pass, a sharp decrease in concentration is observed. This could translate selectivity into a time-dependent quantity.24 In galvanostatic and G/P modes, a constant desalination performance is observed, i.e., the ion transport towards electrodes remains constant. Therefore, if the selectivity is potential independent, then it can be maintained for longer, increasing the productivity towards the target ion. The duration, of course, is dependent on the capacity of the electrodes, and the cut-off potential. For CDI, the capacity to store ions is of paramount importance, and is important to study by electrosorption experiments at different values of the charging and discharging voltages that define a CDI cycle. In addition, we can use methods to measure the charge stored in the EDLs in the CDI electrodes, using the GITT method (galvanostatic intermittent titration technique). The charge that can be stored is often formulated as a capacity in C per gram electrode material which is typically defined by total mass of both electrodes38 (also reported as mA h g−1 in some literature) while the change of capacity with voltage is the capacitance, expressed in F g−1. Additional information can possibly be inferred from electrochemical methods such as cyclic voltammetry (CV) and electrochemical impedance spectroscopy (EIS). Data for charge (capacity) provide valuable information for electrodes used for desalination since it can indicate whether an electrode is feasible as a CDI electrode. Although the storage capacity cannot be directly translated into desalination capacity, good correlations between capacitance and salt adsorption capacity have been reported.39 In terms of selectivity, the storage capacity values in different single-salt solutions is a simple and fast way to compare whether an electrode has preference for a target ion or not. Comparisons between capacitance values were used by different research groups to explore the preference of one ion over another.40–42 In case of intercalation materials, CV can provide information about the preference of the active materials towards different ions. Higher cathodic peak potential associated with intercalation of an ion indicate a higher preference for intercalation of the electrode towards that ion. This technique of determination has been used in CDI literature for selective separation from cationic mixtures.43,44 | ||||||
2. Electrodes for ion selectivity
In this section, we explore and present the manner in which electrodes are utilized to achieve ion selectivity in CDI. The following sub-sections discuss electrode materials used for selective separation of cations as well as anions. Moreover, additional ion-selectivity techniques which includes redox couples are briefly addressed.2.1 Cation selectivity
In CDI, porous carbon is the most commonly used electrode material for desalination and selective ion separation. One of the most-studied parameters for ion selectivity is the pore characteristics of the electrode material. In 2001, Eliad et al. demonstrated the relationship between ion selectivity and the size of the hydrated ion, concluding that the monovalent ions were preferred over divalent ions. It was attributed to the smaller hydrated size of the studied monovalent ions compared to the average pore size of the electrode, i.e. carbon.42 Similarly, Gabelich et al. also studied the effect of the micropore size of carbon aerogel electrodes and reported selectivity towards monovalent over divalent cations.45 This claim was later confirmed by Avraham et al.46 They studied the same effect by using carbon fiber as the electrode material. Moreover, Han et al. studied the dependence of selectivity on pore size distribution using three different types of activated carbon cloth.47 Depending on the mesoporosity/microporosity ratio, the electrodes revealed distinct trends for ions with different hydrated radii. A larger hydrated radius caused a reduction in electrosorption of the ion with increased microporosity of the electrode whereas smaller ions were better accommodated on the surface of the electrode. These results indicate that micropores adsorb more ions with smaller hydrated radius when the hydrated size of ion is comparable to pore size.47 This ion-sieving effect is illustrated in Fig. 6B. Hou and Huang studied this phenomenon for multicomponent mixtures concluding that the affinity among the monovalent cations is affected by their hydrated radii. This trend was also confirmed by other studies.48–50 Furthermore, they also observed divalent over monovalent cation selectivity from a mixture containing two competing ions.51 Mossad et al. also observed that Ca2+ and Mg2+ were preferentially electrosorped compared to Na+ in line with Hou and Huang.52 Between Ca2+ and Mg2+, a higher Ca2+ removal efficiency was observed, which again was attributed to the smaller hydrated radii of calcium ions. Furthermore, Hassanvand et al. reported that normalized electrosorption capacities of Ca2+, Na+, and K+ are comparable when the ions have equivalent ratios in the feed solution. However, Ca2+ adsorbed and then desorbed slower than Na+ and K+ due to its larger size (Fig. 6B) and therefore slower diffusion rate.53 Seo et al. investigated the effect of morphological characteristics of carbon aerogel electrodes on the electrosorption rates of different cations and – contrary to previous series of observations on size-based selectivity – observed a higher selectivity for Ca2+ and Mg2+ over the monovalent ions. The authors rationalized their results in terms of the pore structure (branched micropores and highly accessible mesopores) and wettability of the electrodes.54In addition to the pore size and morphological characteristics of the electrodes, the valence of the adsorbing ion has an influence on its selectivity. Studies have reported that ions with a higher valence are more effectively adsorbed in the EDL due to their stronger interactions with the electrodes.25,52,54,55 In a mixture of mono- and divalent ions, at equilibrium the divalent ions were preferably electrosorbed as a result of the higher electrostatic attraction (Fig. 6A).56 Gao et al. obtained a higher divalent ion selectivity using carbon nanotube and carbon nanofiber electrodes due to charge-exclusion effect as depicted in (Fig. 6B).50 They also stated that ions with smaller hydrated radii were preferred if they have the same valence. Ions with identical valence are electrosorbed according to their hydration energy (Fig. 6D). Thus, ions with lower hydration energy are preferred as their hydration shell can be readily rearranged inside the pores.57
In addition to the properties of the electrode and the adsorbing ion, the operational parameters in CDI can affect the ion selectivity. Zhao et al. proposed and validated a theory of selectivity for a solution with 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Na+ and Ca2+ feed ratio.24 The authors reported a time-dependent selectivity as Na+ was electrosorbed 5 times more than Ca2+ at the early stage of desalination cycle. The higher electrosorption of sodium ions is explained by the higher concentration, causing higher diffusion to the pores of the electrode (Fig. 6C). However, with time, the preference switches to Ca2+ due to the stronger interaction between the divalent ion and the electrode surface, causing a ion-swapping effect, shown in Fig. 6A. Hou and Huang also studied the effect of feed concentration on ion selectivity.51 By varying the concentrations of K+, Na+, Ca2+, and Mg2+, the authors observed that an increase in Na+ concentration over other cations yielded preferential electrosorption of Na+, which was attributed to the higher availability of sodium ions. Apart from varying the feed concentration, they also studied the effect of applied potential on the electrosorption capacities of different ions, and concluded that increasing the voltage increased the preferential removal of K+ over Na+ and Na+ over Ca2+.
1 Na+ and Ca2+ feed ratio.24 The authors reported a time-dependent selectivity as Na+ was electrosorbed 5 times more than Ca2+ at the early stage of desalination cycle. The higher electrosorption of sodium ions is explained by the higher concentration, causing higher diffusion to the pores of the electrode (Fig. 6C). However, with time, the preference switches to Ca2+ due to the stronger interaction between the divalent ion and the electrode surface, causing a ion-swapping effect, shown in Fig. 6A. Hou and Huang also studied the effect of feed concentration on ion selectivity.51 By varying the concentrations of K+, Na+, Ca2+, and Mg2+, the authors observed that an increase in Na+ concentration over other cations yielded preferential electrosorption of Na+, which was attributed to the higher availability of sodium ions. Apart from varying the feed concentration, they also studied the effect of applied potential on the electrosorption capacities of different ions, and concluded that increasing the voltage increased the preferential removal of K+ over Na+ and Na+ over Ca2+.
The use of modified electrodes and/or composite electrodes is also a common method of enhancing ion selectivity (Fig. 6F). In one study that employed carbon nanotube (CNT)/zeolite composite electrodes, Ca2+ and Mg2+ adsorption increased in single-salt batch experiments, with increasing zeolite to CNT ratio.58 However, the performance of the zeolite–CNT electrodes deteriorated within a few cycles, suggesting that it was either degraded or not fully regenerated. Yoon et al. used a calcium-alginate coated carbon electrode in CDI.59 The coated cathode adsorbed more Ca2+ over Na+. While no selectivity coefficients were presented, we estimated a selectivity (ρ) of 2.5 for calcium ions over sodium ions using the provided graphs. The selectivity was attributed to the strong affinity of Ca2+ towards alginate. Similarly, Kim et al. reached Ca2+ over Na+ selectivity of 3.5–5.5 (Si/j, Table 1) with a calcium-selective nanocomposite layer (Fig. 6F).60
Apart from more commonly targeted alkali and alkaline-earth metals, selective removal of heavy metals has also been of interest in CDI. In 2010, Li et al. utilized electrodes made of graphene nanoflakes to remove Fe3+ and compared the electrosorption capacity with Mg2+, Ca2+, and Na+ in single-salt experiments.61 The Fe3+ were preferred over the others, which was attributed to its higher valence (Fig. 6A). Between Ca2+ and Mg2+, Ca2+ were preferred due to their smaller hydrated radii (Fig. 6B), as described before, whereas Na+ exhibited the lowest electrosorption among all. In another study, Huang et al. employed activated carbon electrodes to remove Cu2+ from aqueous solutions.62 They also compared the Cu2+ electrosorption in the presence of NaCl, natural organic matter (NOM), and dissolved reactive silica in binary salt solutions, and reported that Cu2+ removal decreases with an increasing amount of the competitive species. However, no significant decrease in Cu2+ electrosorption was observed in the presence of dissolved reactive silica.
A heavy metal (Pb2+) and salt (Na+) recovery method from wastewater using 3D graphene-based electrodes was proposed by Liu et al.63 They used 3D graphene electrodes modified with ethylenediamine triacetic acid (EDTA) and 3-aminopropyltriethoxysilane (APTES) as the cathode and the anode, respectively. Two different mechanisms were presented for Pb2+ and Na+ removal. Pb2+ is adsorbed via a chelation reaction with EDTA (Fig. 6E), whereas Na+ is adsorbed via electrosorption in the pores. Based on these mechanisms, the separation of ions was achieved during the desorption stage. First, Na+ was desorbed by applying an inverse potential, followed by a short circuit potential. Afterwards Pb2+ was desorbed in a separate step using nitric acid as an eluent.
Selective removal of Pb2+ over Ca2+ and Mg2+ was studied by Dong et al. by using activated carbon electrodes in an asymmetric CDI setup. This setup only contained an AEM (hence asymmetric), as the Pb2+ desorption was reported inefficient when a CEM was used as well, thus hindering its selectivity.64 The asymmetric system was selective towards Pb2+ over Ca2+ and Mg2+. The selectivity mechanism was hypothesized to be a swapping process where Ca2+ and Mg2+ are initially adsorbed due to their higher mobilities, but later replaced by Pb2+ owing to its higher affinity towards the native functional groups (e.g., carboxyl groups) present on the electrode.
Recently, Zhang et al. used activated carbon in flow CDI to selectively remove Cu2+ from a solution which also contained Na+.65 A higher affinity towards Cu2+ was obtained in the system. This was attributed to the preferential adsorption of Cu2+ on the carbon particles and was also reduced to Cu. The preference of carbon towards divalent over monovalent cations, as shown in Fig. 6A was also reported here. The Na+ removed from the feed remained in the electrolyte of the flow electrode.
The removal of an unconventional ion, uranium(VI), using phosphate-functionalized graphene hydrogel electrodes was studied by Liao et al.66 The electrodes were tested in equimolar solutions (0.3 mM) containing uranium(VI) and a series of interfering metals ions (Cs+, Co2+, Ni2+, Sr2+, and Eu3+). The authors reported that the electrodes preferred uranium(VI) over all the other metals that were tested. Furthermore, they observed that the uranium(VI) is more selective against monovalent metal ions compared to that of divalent or trivalent ions. This phenomenon was attributed to the stronger electrostatic interaction between trivalent ions and the electrode surface, thus adsorbing more trivalent ions resulting in reduced selectivity of uranium(VI). Apart from ion valence, the selectivity of the electrode is also attributed to the formation of strong acid–base complexes with the phosphate groups attached to the electrode (Fig. 6E).
2.2 Anion selectivity
The mechanisms used to achieve cation selectivity may be extrapolated, and used to achieve anion selectivity in CDI. One of the pioneering studies in CDI anion selectivity is the one of Farmer et al., reported in 1996, which showed a difference in electrosorption capacity of different anions.67 In their work, the authors employed 192 pairs of carbon aerogel electrodes to investigate the desalination of NaCl and NaNO3 in single-salt experiments. Although this work was not intended to investigate ion selectivity, the difference in electrosorption observed by the authors was the first clue that CDI could be a valuable technology for selective anion adsorption.Years later, Eliad et al. investigated the sieving effect of carbon electrodes based on the pore size distribution of different carbon electrodes.42 It was shown that SO42− ions were not able to penetrate the carbon pores with an average pore size of 0.36 nm due its large hydrated radius (Fig. 6B). The electrosorption capacity for this carbon electrode was NO3− > Cl− ≫ ClO4− ⋙ SO42−. The higher electrosorption capacity of NO3− compared to Cl− was attributed to a combination of the slit-shaped pores of the carbon electrode and the planar shape of hydrated NO3−, facilitating its storage in the micropores. The use of a larger average carbon pore size (0.58 nm) resulted in the electrosorption of all anions and no sieving effect was observed.
The selectivity of anions was further investigated by Gabelich et al. taking into account ionic properties such as the ionic mass, radius, and valence.45 Compared to the work of Eliad et al., the authors used an electrode with pore size distribution large enough to prevent ion sieving by the electrode (lowest average pore size of 4 nm). A strong correlation was observed between the valence of the ionic species, and its preferential electrosorption into the carbon micropores using single-salt solutions. No statistical difference was observed for the electrosorption of anions of different radii and mass.
The works of Eliad et al, Gabelich et al., and later of Huang et al., provided evidence on electrosorption behavior of different anions on porous carbon electrodes. They demonstrated that CDI could be used to selectively remove different species of ions from aqueous solutions. However, at this early stage of ion selectivity with CDI, some questions regarding the parameters involved and the accurate mechanisms behind the selectivity, still remained unanswered.68
In 2013, Zafra et al. evaluated the electrosorption capacity of high surface area electrodes using single-salt solutions consisting of nutrients (Cl−, NO3−, and H2PO4−/HPO42−).40 The authors found a lower phosphate electrosorption compared to nitrate or chloride. It was suggested that this reduced capacity was caused by the sieving effect of the prepared activated carbon (average pore size of 0.855 nm) towards to the smaller ions (Cl− and NO3−) compared to the large phosphate species (H2PO4−/HPO42−). This investigation agrees well with the report about the sieving effect of the porous carbon described by former authors (Fig. 6B). In the same line of nutrient recovery, Ge et al. investigated the competition between physical adsorption and electrosorption of phosphate anions.69 The authors suggested that electrosorption could only overcome the effect of physical adsorption at very high cell voltages. Therefore, to improve phosphate electrosorption the authors applied a cell voltage as high as 3.0 V, which also cause faradaic reactions. Although the authors suggest that some species formed during the faradaic reactions could also promote a disinfection of the treated water, there is an expressive reduction of the charge efficiency. Nevertheless, this work is important in understanding the lower electrosorption capacity of phosphate at neutral pH compared to other ions.
More recently, high phosphate selectivity was achieved by using a layered double hydroxide/reduced graphene oxide composite electrode (LDH/rGO).70 The preference of the LDH/rGO electrode towards phosphate anions was explained by the inner-sphere complexation via a ligand-exchange process of phosphate with the transition metal sites on the surface of the electrode (selectivity based on surface affinity, Fig. 6F), with further intercalation of the anions into the electrode interlayer. The electrode showed selectivity towards phosphate regardless the pH of the solution, achieving the highest value of Si/j around 24 at a pH of 6 with a chloride concentration 10 times higher than phosphate.
The rationalization of the anion selectivity was also investigated by adapting and fitting some CDI models to the experimental data. Tang et al.71 adapted the one-dimensional dynamic model for batch CDI desalination proposed by Porada et al.8 to account for ion mixtures, and for the different diffusion constants of the anions. The authors showed that the model fitted well the dynamic variation of the anions in solutions. Nevertheless, small selectivity values were observed between chloride, fluoride, and nitrate, agreeing well with the selectivity values measured by Pugazhenthiran et al., a study in which the authors used microporous cellulose derived graphitic fibers as CDI electrodes.72 Pugazhenthiran et al. obtained a selectivity (ρ) of ≈1.2, 1.3, and 1.4 for Cl−/NO3−, Cl−/F−, and Cl−/SO42−, respectively, attributing the modest selectivity to the hydrated radii of the ions (SO42− > F− > NO3− ≈ Cl−) (Fig. 6B).
Similar to the work of Tang et al., Xing et al. investigated the selectivity towards ClO4− over Cl− by adapting the one-dimensional EDL model for carbon electrodes.73 The authors showed that bare carbon electrodes prefer ClO4− over Cl− reaching a selectivity (ρ) of about 11 even for lower concentrations of ClO4−. Based on the model, the authors ascribed this high selectivity value to the higher diffusivity of ClO4− (9 × 10−10 m2 s−1) compared to Cl− (1 × 10−10 m2 s−1) inside the pores of the carbon (Fig. 6C).
Further hypotheses were explored in order to unravel the mechanism of anion selectivity for carbon electrodes. Li et al. proposed a hypothesis explaining the manner in which the ions are selectively removed in carbon electrodes based on ion size.56 Instead of considering the hydrated radius, the authors introduced a new parameter called hydration ratio. This constant indirectly indicates the extent of ion-solvation in water and is calculated by dividing the hydrated radius by the ion radius. The authors suggest that for a high hydration ratio the charge on the adsorbing ion would be better screened. This weakens the driving force experienced by the ions during electrode polarization (Fig. 6G). The hypothesis proposed by the authors was confirmed through selectivity experiments, and the selectivity order matched well with the hydration ratio of the analyzed anions (NO3− > Br− > Cl− > F−). However, the experiments also demonstrated that the selectivity towards sulfate was higher than that of nitrate, contrary to the trend dictated by the hydration ratio. In agreement with former works, the authors reported that divalent species are preferred over monovalent, when no sieving effect is observed. The theory presented by Li et al. provided a viable explanation for the selectivity among monovalent ions. However, the results conflict with those previously obtained by Zafra et al. and Pugazhenthiran et al. showing equal or lower selectivity of nitrate over chloride. A possible explanation for such discrepancy can arise from the dependence of ion selectivity on the type and pore size of the electrode material and operational parameters such as cell voltage, time dependency, and initial feed ratio and concentration.24,74 Since there was no selectivity value provided by the authors, we calculated the selectivity towards chloride based on the removal efficiencies (R, Table 1) (Table 3 of Li et al.); Cl−/NO3− ≈ 0.7, Cl−/F− ≈ 2.3, Cl−/Br− ≈ 0.45, NO3−/F− ≈ 3.6, NO3−/Br− ≈ 2.5, Br−/F− ≈ 2.5, and NO3−/SO42− ≈ 0.5 for solutions with two competing ions.
Sun et al.75 proposed another mechanism of ion adsorption in carbon electrodes based on electronegativity. Instead of ionic size, the authors proposed that ion selectivity was a result of the differences in the electronegativity of adsorbing ions. The authors suggest that an electrode may form hydrogen bonds with the anions from solution, and therefore, the electronegativity of the anions would play a major role on its affinity towards the electrode surface. For the same feed concentration, the following order of selectivity was found: ReO4− > NO3− > Cl− > SO42−. It is worth noting that this mechanism relies on specific conditions, such as the presence of functional surface groups (e.g. carboxyl), and acidic pH (pH = 2). Therefore, it is not straightforward to compare the preferential removal obtained by the authors with other selectivity works from literature. Although no selectivity values were provided, it is possible to back calculate the selectivity coefficient for all the anions over ReO4− based on their electrosorption experiment (Fig. 5, Sun et al.). This results in ρ (Table 1) of ReO4−/Cl− = 13.6, ReO4−/SO42− = 13.6, ReO4−/NO3− = 2.3.
Modification of the electrode surface by adding functional surface groups is another approach to enhance the anion selectivity, as similarly observed in terms of cations (Fig. 6E). Oyarzun et al. modified the carbon electrode surface with cetyltrimethylammonium bromide (CTAB) and sodium dodecylbenzenesulfonate (SDBS) to obtain a higher selectivity towards nitrate via inverse CDI (i-CDI).76 The process of i-CDI can occur when the surface of the electrode is covered with functional surface groups. Therefore, during charging at high voltages, there is discharge of ions, while at lower voltages, there is adsorption of ions. The surface modification preferentially adsorbed nitrate by a factor of ≈7.7 over chloride. However, when using the i-CDI process, the selectivity was reduced to 6.5 at low cell voltages, 16% lower than the value observed for adsorption. Interestingly, the authors did not observe strong differences in the selectivity by varying the chloride ion concentration while keeping the nitrate ion concentration constant.
A recent study by Hawks et al. showed a high selectivity for nitrate over chloride and sulfate by using ultra-microporous (pore diameter < 1 nm) carbon electrodes.41 The idea is similar to the one already explored by Eliad et al. (2001), in which selectivity is achieved due to sieving effect of very small carbon pores. The authors explored the effect of the solvation shell of the ion in aqueous media on their selective adsorption (Fig. 6D). While chloride and sulfate ions are nearly homogeneously surrounded by water molecules, the solvation shell of a nitrate ion is mostly located at the edge of the ion and is not strongly bound to the molecule. As such, the authors suggested that the position of the solvation shell and the hydration energy instead of the average hydrated radius should be a more accurate parameter to be used in the investigation of ions selectivity based on ion size. The selectivity of nitrate over sulfate was also investigated. In this case, only a small amount of sulfate was electrosorbed inside the miniscule pores of the carbon electrode, which is explained by the higher solvation energy of sulfate compared to nitrate or chloride. In the electrosorption experiments, different cell potentials were applied to achieve the maximum selectivity (ρ, Table 1) of NO3−/Cl− ≈ 6 and NO3−/SO42− ≈ 18 at 0.6 V. At a cell voltage of 1.0 V, the NO3−/Cl− and NO3−/SO42− selectivities were found to be ≈3 and ≈9, respectively. The observed reduction in selectivity with increasing cell voltage is explained by the solvation energy. At higher cell voltages, more energy is available to rearrange the solvation shell, and the ions be stored in the electrode. Consequently, the removal efficiencies of chloride and sulfate increase, reducing nitrate selectivity. In contrast, lower cell voltages limit the ion removal capacity due to co-ion repulsion, reducing the charge efficiency of the electrodes. Therefore, there is an optimum voltage that should be considered to maximize both energy efficiency and nitrate selectivity.
Akin to the work of Hawks et al., Mubita et al. investigated the selectivity of nitrate over chloride for carbon electrodes, analyzing pure carbon adsorption, ion concentration, and cell voltage.77 In addition, a model was proposed for ion electrosorption which was validated by the experimental results. Compared to the work of Hawks et al., the activated carbon used by Mubita et al. has larger pore sizes than the radii of hydrated nitrate and chloride. Therefore, no sieving effect was considered. The authors observed that by increasing the cell voltage from 0 V (short-circuit) to 1.2 V, the selectivity (ρ) towards nitrate reduced from ≈10 to ≈6. It is also shown in this work that nitrate ions have stronger affinity towards the carbon electrode surface, since chloride ions are replaced by nitrate ions similarly to the time-dependent effect described by Zhao et al for a mixture of mono/divalent ions, and well aligned with the work of Lin et al.24,56 In this case, time-dependent selectivity is observed due to higher diffusion of chloride ions in the early stage of electrosorption (Fig. 6C), later replaced by nitrate ions during the electrosorption process due to the better affinity of nitrate with the carbon surface (Fig. 6A).
2.3 Intercalation materials
Application of intercalation materials in desalination via CDI has been reported with an increasing interest in the past years.10 High SACs have been reported for CDI cells with electrodes fabricated from various intercalation materials including Prussian blue (PB) and its analogues (PBAs),34,78,79 NaMnO2 (NMO),80–82 NaFe2P2O7,83 and NaTi2(PO4)384 among others.85,86 The mechanism of charge storage in these materials involves intercalation of cations (of multiple valences87) in a lattice or between layers. As a result, they do not require high surface areas to achieve high storage capacity. In some materials like the PBAs,88 this insertion is accompanied by a redox change in the lattice. Interestingly, this mechanism results in the absence of co-ion repulsion,89 enhancing the charge efficiency of electrosorption of intercalation materials without the use of membranes, as reported in literature.78,80,90Research into intercalation materials has also been catalyzed by their inherent selectivity towards ions, usually by size.98 This is especially true for PB and PBAs, that have a cubic lattice structure and store cations in their interstitial sites.88 These lattices can differentiate cations based on their size/hydration energy in a trend summarized in Fig. 7A. The reversible (de)insertion of cations in the lattice of PB(A) is made possible by a simultaneous oxidation or reduction of a redox-active element, generally a Fe2+/Fe3+ redox couple, in the lattice.99 High coulombic efficiencies for the (de)insertion processes indicate a facile regeneration of these materials. The intercalation (reduction) and deintercalation (oxidation) potential associated with the redox reaction differs with the intercalating ion.100 The intercalation of the incoming ion under the influence of an applied current or voltage is associated with a specific electrode potential which forms the basis for the preferential electrosorption of ions that have higher intercalation potentials,101 as presented in Fig. 7B. It is clear that the ions with smaller hydration energy readily insert into the lattice of the two most commonly used PBAs, namely nickel and copper hexacyanoferrate, NiHCF and CuHCF. Comparing the potentials also reveals that the insertion of hydrated alkali metal ions is easier in CuHCF over NiHCF.
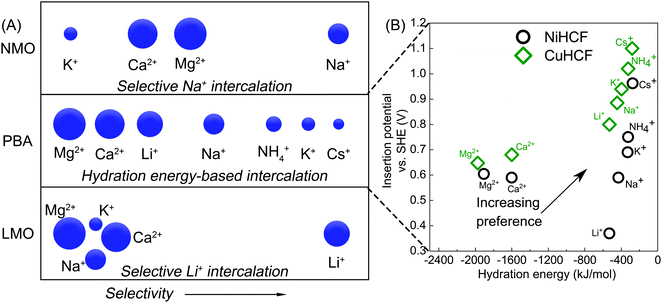 | ||
| Fig. 7 (A) Ion intercalation preference of three intercalation materials, namely lithium manganese oxide (LMO), Prussian blue analogues (PBA), and sodium manganese oxide (NMO), towards different hydrated, monovalent and divalent cations from an aqueous mixture in CDI. Cations on the right are the most preferred while those on the left are the least preferred by the electrode. Data adopted from ref. 91–93. (B) Insertion potential of various hydrated cations in the lattice of two most commonly used PBAs, nickel and copper hexacyanoferrate, NiHCF and CuHCF, as a function of their hydrated radii. Data adopted from ref. 94–97. | ||
One of the earliest intercalation studies in ion selectivity,93 performed in 1986 by Ikeshoji, used a thin film PB electrode to observe selective electrosorption of cations from a mixture of alkali metal ions. A clear size-based preference of the electrode was established for the first time for the hydrated alkali metal ions, with Cs+ as the most preferred and Li+ as the least preferred ion for intercalation into the lattice. Lower hydration energy of Cs+ makes its insertion in the lattice easier. PBAs, that have been extensively used as electrode material for desalination via CDI,10 have also found application in selective ion separation.44,78,91,97 Lilga et al. used NiHCF for selective adsorption of alkali metal ions and reported a preference towards Cs+ from a mixture of Cs+ and Na+ in which the latter was in excess.102 A facile electrosorption of smaller alkali metal ions was also observed by Porada et al., where NiHCF electrodes were used in a symmetric CDI configuration.78 A ρ ≈ 3 was reported for K+ over Na+ from an equimolar feed solution. Singh et al. also used NiHCF in a symmetric cell to study the preferential adsorption of monovalent Na+ over divalent Ca2+ and Mg2+ ions from a mixture containing all three ions.103 The authors reported a ρ of 20 and 25 for Na+ over Ca2+ and Mg2+, respectively and claimed that the selectivity towards Na+ remained largely independent of its concentration in the mixture. These ρ values are especially remarkable since the intercalation potential of Na+ is very close to that of Ca2+ and Mg2+, as shown in Fig. 7B. Therefore, the competition between ions during adsorption from a mixture must also plays a role in high selectivity observed towards monovalent Na ions. Kim et al.,44 used CuHCF in a symmetric CDI cell configuration, as presented in Fig. 1B, to study the selective removal of NH4+ from an aqueous mixture containing NH4+ and Na+, based on the different intercalation potentials of NH4+ and Na+ in the CuHCF lattice (Fig. 7B). The cathode and anode were identical CuHCF-based electrodes. A ρ ≈ 3 was reported for NH4+ over Na+ from a feed with 5 mM NH4+ and 20 mM Na+. It was observed that increasing the cell voltage increased the total amount of ions removed but decreased the preferential adsorption of NH4+ over Na+ due to the increased adsorption of both ions, bringing the ρ down to 2. The cell voltage values reported in the study would, however, differ with every CDI setup as it is a system-dependent parameter and can change with its components including volume of the feed channel and electrode thickness.104 Choi et al. used CuHCF as a cathode in an asymmetric CDI cell with activated carbon anode, for deionization of water containing multiple ions.97 The feed solution comprised of Na+, K+, Mg2+, and Ca2+ ions. The intercalation potential of these ions was inversely proportional to their hydration energy, as shown in Fig. 7B. Consequently, the CuHCF lattice showed highest affinity towards K+ and the lowest towards Mg2+, which can be expected from Fig. 7B. Adsorption of K+ and Na+ was ≈70 and 25% higher than that of Mg2+ ions. The selectivity performance was not evaluated in terms of the definitions described in Table 1. The affinity towards monovalent ions was attributed to their smaller hydration energies in comparison to the divalent ions. Fig. 7B suggests that the intercalation of monovalent cations in the CuHCF lattices should be easier in comparison to NiHCF due to higher intercalation potentials, indicating a more facile intercalation in the crystal lattices.
Apart from PB and its analogues, other intercalation materials like NMO, LMO and TiS2 have been used in CDI for selective removal of ions from an ionic mixture. Yoon et al. used NaMnO2 (NMO) as a Na+ selective electrode along with PB as a K+ selective electrode in a non-symmetric CDI setup for purification of a KCl feed solution contaminated with sodium ions.91 The authors reported that 36% of Na+ impurity was removed from the feed solution by the NMO electrode while the PB intercalated potassium ions. The preference of NMO electrodes towards different ions is summarized in Fig. 7A. Kim et al.92 also used a λ-MnO2/AC system for recovery of Li+ from brine containing Na+, K+, Ca2+, and Mg2+. From the data reported by the authors, a ρ ≈ 12 towards Li+ was calculated over all the other ions in the brine. This selectivity Li+ was attributed to its facile intercalation into the spinel structure of λ-MnO2. Unlike the PBAs, the λ-MnO2 primarily intercalated Li+ over any other cation. This selectivity was attributed to the smallest ionic size of the Li+ due to which it fit the tetrahedral sites of the λ-MnO2 electrode. Kim et al.105 explored the Na+ selective property of NMO in CDI configuration with a Ag/AgCl anode. The ρ values of 13, 7 and 8 were observed for Na+ over K+, Mg2+, and Ca2+ respectively, from a mixture of these ions. Unlike PBAs, the intercalation of cations in NMO or LMO does not adhere to a hydration energy trend, as depicted in Fig. 7A, as they specifically interact with Na and Li ions. Srimuk et al. paired a TiS2 intercalation electrodes43 with an AC anode in a CDI setup to study selective removal of Mg2+vs. Cs+. The TiS2 electrodes were found to be more selective towards Mg2+ (ρ ≈ 30) in a specific applied electrode potential range (vs. Ag/AgCl). This selectivity could also be reversed by changing the electrode potential window such that the TiS2 electrodes prefer Cs+ over Mg2+ (ρ ≈ 2). Such behavior was attributed to different potential windows (vs. Ag/AgCl) where Cs+ and Mg2+ were preferably adsorbed. Therefore, by controlling the cell voltage, the affinity of the electrode towards the ions could be controlled. A similar reversal of selectivity with change in applied voltage has not been reported in literature with electrodes fabricated from PB(A)s.
Layered intercalation electrode materials have received limited attention so far in selectivity studies as they seem to lack specific filters to differentiate between intercalating ions. However, selectivity can be induced in layered electrodes by tailoring their structure to act as a sieve/filter or by fabricating active materials with adsorption centers that have affinity towards a desired type of ion, as reported by Hong et al. for double layered hydroxides.70 On the morphological aspect, the structure of layered electrode materials, such as MXene,106 can be modified by inducing variable inter-layer spacings or different stacking of the layers itself, resulting in different diffusion paths for the inserting ions.107 It would be interesting to investigate whether these different structures would then lead to a preference towards certain ions. Byles et al.81 reported the use of layered MnO2 electrodes for hybrid CDI. The layers in the electrode material were stabilized by Na and Mg ions. The presence of these cations influenced the ion uptake capacity of the electrode in NaCl and MgCl2 solutions by modifying the interlayer spacing of the material, resulting in higher adsorption of Na+ over Mg2+ from single-salt solutions. Further investigation into the presence of ion selectivity in layered MnO2 electrodes and its correlation with the stabilizing ions can support inducing selectivity in other layered intercalation materials.
2.4 Additional techniques and electrodes in ion-selective CDI
In addition to the above-mentioned and clearly defined methods of ion-separation via electrodes in CDI, there are a few more alternatives that have been explored in literature.108 Electrodes decorated with redox-active species are one such example. Su et al.109 prepared anion-selective redox electrodes by functionalizing carbon nanotubes with poly(vinyl)ferrocene (PVF), due to which, highly selective adsorption of organic anions such as carboxylates, sulfonates, and phosphonates was obtained over ClO4−, present in excess in the aqueous medium. The authors claimed a separation factor of 140 for carboxylate over ClO4− from an aqueous medium. The calculation method to obtain the separation factor was not mentioned. This selectivity was further enhanced in an organic medium as the authors reported a high separation factor (3000) for carboxylates over PF6−, the competing anion. The electrodes were regenerated by the application of a more negative potential in comparison to the one used for adsorption. In another study, the same research group fabricated an asymmetric system with the cathode and anode with different redox functionalities.110 The anode had the same PVF while the cathode in the cell was functionalized with (cyclopentadienyl)-cobalt(tetraphenyl-cyclobutadiene) (CpCoCb) to induce a selectivity towards cations due to a strong chemical interactions with them, and compliment the anionic selectivity obtained by the PVF-functionalized anode. The adsorption experiments demonstrated a high selectivity towards organic cations such as butyl-pyridinium and methyl viologen from an aqueous mixture containing an excess of NaClO4. The functionalized cathodes were selective towards organic cations from an ionic mixture in which the competing cation was 300-fold in excess.Another technique reported in literature is the use of faradaic reactions at the electrodes for ion-separation.111 Cohen et al. used activated carbon electrodes in an asymmetric CDI cell with an oversized counter electrode to selectively remove Br− present in a mixture with Cl−. The potential of the working electrode was controlled, and the cell voltage was monitored. When the working electrode was polarized to 1 V vs. Ag/AgCl, the bromide ions were selectively electro-oxidized to Br2 which was physically adsorbed on the surface of the carbon. Following the oxidation step, the electrodes were regenerated by setting the potential of working electrode at 0.5 V, vs. Ag/AgCl. This led to reduction of Br2 in the pores back to Br−. In comparison to Cl−, Br− was preferred with a ρ value of ≈175.
Along the same lines, Chang et al.112 reported the use of a bismuth based electrode which can selectively remove chloride. The authors reported the oxidation of the Bi electrode to BiOCl at +0.28 V vs. Ag/AgCl, and the reduction back to Bi at −0.85 V vs. Ag/AgCl in a 1 M NaCl solution. The peaks disappeared in a 1 M Na2SO4 solution. On the other hand, in an equimolar mixture of NaCl and Na2SO4 the presence of sulfate suppressed the ability of Bi capturing chloride, reducing both the total ion adsorption capacity, and negligible selectivity was observed. The authors suggest that the suppression caused by the presence of sulfate is due to the screening of the electrode surface with SO42−, which hinders the access of chloride to the Bi electrode. By reducing the concentration of sulfate, higher removal of chloride was observed, and a selectivity achieved a value of 4.5 at 1.6 V for a concentration of chloride 8 times higher than sulfate.
Recently, Hu et al. proposed a new electrode based on layered metal oxide with Pd to remove nitrate using an approach similar to CDI.113 However, the main difference was the reduction of NO3− to N2 in the cathode of the cell by faradaic reactions. Although the authors did not provide a selectivity value, the electrodes are expected to exhibit high selectivity towards NO3− since its concentration in the electrode did not reach saturation.
In summary, the use of various electrode material, operational conditions, and surface modifications for selective ion separation was reviewed in this section. Thus, it is evident that electrodes can act as selective elements in CDI processes. In the following section, we will review the use of membranes for selective ion separation in CDI.
3. Membranes for ion selectivity
In the previous section, ion selectivity in terms of electrodes was discussed. The use of membranes also plays a vital role in CDI. This section is dedicated for exploring the studies which rely on membranes for achieving ion selectivity.3.1 Cation selectivity
Several different studies have demonstrated the advantages of using IEMs to prevent co-ion repulsion, reduce anode oxidation, and to boost the salt removal by employing gradient of solutions in multi-chamber cells.7,114 An IEM can also be used as a barrier for specific ions, and therefore, improve the ion selectivity.Commercially available cation-exchange membranes (CEMs) like Neosepta CMX typically have negatively charged functional groups (e.g., carboxylate, sulfonate, and phenolate) in the membrane backbone, which only allow cations to migrate through the membrane.115 On the other hand there are CEMs that exhibit affinities towards certain monovalent ions, such as monovalent cation-selective membranes CSO (e.g., Selemion) and CIMS, (e.g., Neosepta). CIMS membranes have a highly cross-linked (bulk) structure which allows monovalent cations with smaller hydration shells to pass through while rejecting divalent cations with larger hydration shells, while CSO membranes are coated with a thin positively charged layer which rejects divalent over monovalent cations due to the charge exclusion effect (Fig. 8B).116–118
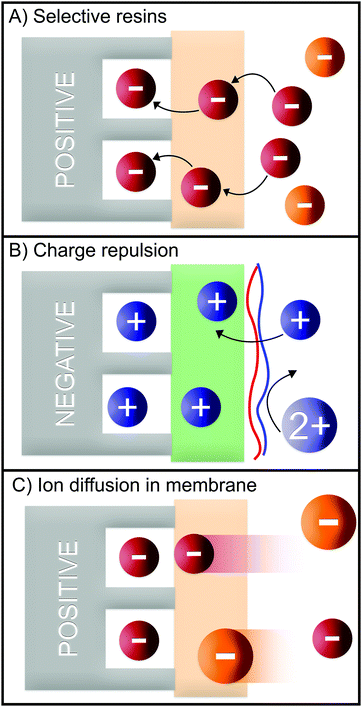 | ||
| Fig. 8 Generalized selectivity mechanisms in MCDI based on (A) selective resins, (B) charge repulsion, and (C) ion diffusion in membranes. | ||
In CDI experiments using a CMX membrane, selectivity towards divalent over monovalent cations was reported.119,120 Although the CMX membrane was not designed to differentiate between different cations, its negatively charged outermost layer attracts divalent more than the monovalent cations.121 Hassanvand et al. stated that the implementation of CMX in CDI leads to sharper desorption peaks of divalent cations since larger amounts of di-over monovalent cations are temporarily stored within the CMX membrane.53 On the other hand, the CIMS membrane resulted in preferential transport of monovalent over divalent cations.122 Similarly, Choi et al. used a CIMS membrane and obtained monovalent cation selectivity (R) of 1.8 for sodium over calcium ions.121 By selectively removing Na+, a Ca2+-rich solution was obtained. In addition, the selectivity attained its maximum value at higher cell voltages, pH, and lower TDS (total dissolved solids) concentration.
Similar to Choi et al., Shi et al. also used an MCDI system equipped with a CIMS membrane to recover Li+ in the presence of Mg2+, and obtained a selectivity (ρ) of 3.122 They observed a decrease in the selectivity from ≈3 to 2 upon increasing voltage. We assume that the increase in driving force reduced the blocking effect of the membrane as there are more charge interactions between divalent cations and the electrodes compared to monovalent cations. An increase in flow rate also increased the selectivity until a certain flow rate after which, the selectivity decreased. Furthermore, they studied the effect of operation time, and found that the adsorption was found to be slower for Mg2+ compared to Li+. Sahin et al. implemented a layer-by-layer polyelectrolyte multilayer (PEM) on a CMX membrane in order to tune the monovalent cation selectivity in MCDI (Fig. 8B).123 While the bare CMX membrane had a ρ of ≈0.5 for Na+ over Mg2+, the selectivity of the PEM-coated membrane was found to be ≈3. This switch in selectivity was attributed to the charge rejection experienced by ions with higher valence (Fig. 6B) due to the presence of the PEM.
He et al. performed FCDI experiments with a CMX and AEM (both Fujifilm Type-1). They varied the current density and the hydraulic retention time (HRT) in a single pass, galvanostatic mode and reached a maximum selectivity (ρ) of ≈6 for Ca2+ over Na+, for the lowest current density and HRT.124 They hypothesized that Ca2+ transport is favored due to the passive adsorption of Ca2+ on the membrane surface. Similarly, Wang et al. focused on the effect of current density, HRT, and ratio of different ions in the feed solution.119 They observed a selectivity (ρ) of ≈3 for calcium ions over sodium ions. Higher current density and HRT produced higher the selectivity, which agrees well with He et al. Moreover, increase in Ca2+ over Na+ in the feed caused an increase in Ca2+ selectivity.
3.2 Anion selectivity
Similar to the use for cation selectivity, MCDI has been vastly employed for anion selectivity investigations as well, typically by employing an AEM or anion-selective resins. In the context of nutrient recovery, several studies addressed the selective removal of nitrate among competing anions. Yeo et al. investigated nitrate selectivity by coating nitrate-selective resins over the anode and compared it with the selectivity obtained from a standard-grade AEM.125 Typically, nitrate-selective resins are strong base anion exchangers with long carbon chains which are highly selective towards nitrate compared to other monovalent anions.126 The MCDI system used for comparison presented a nitrate over chloride selectivity (ρ) of ≈2 and a sulfate over chloride selectivity of ≈1.3, following the same trend of other studies in MCDI literature.127 The selectivities of NO3−/Cl− and NO3−/SO42− were enhanced to ≈3.7 and 1.3, respectively after replacing the AEM with the resin-coated electrode. A similar result was obtained by Kim and Choi (NO3−/Cl− ≈ 3.2) using a nitrate-selective resin.128 Although good nitrate selectivity values were consistently achieved in MCDI literature using nitrate-selective resins, recent studies have identified some operational issues regarding the discharge of nitrate, especially for solutions containing low nitrate concentration compared to the competing anions.129,130Akin to the work of Yeo et al., Zuo et al. investigated the viability of a resin to selectively remove sulfate from a mixture with chloride.131 An experiment with the pristine high surface area carbon electrode demonstrated a higher selectivity towards chloride than sulfate (Si/j = 2.2), in agreement with the work of Sun et al.75 The authors were able to reverse the selectivity (SO42−/Cl− of 2.4) by coating the activated carbon electrode with the selective resin. The resin-coated carbon was able to maintain the selectivity of 1.9 towards sulfate even upon increasing the chloride concentration by a factor of 100. In contrast to some of the studies using nitrate-selective resins,129,130 the authors did not report any issue during the desorption of the electrosorbed sulfate anions.
Phosphate recovery was also explored using MCDI. Jiang et al. investigated the removal of phosphate over sulfate and chloride using MCDI and analyzed the effect of the cell voltage, ion concentration, and pH.132 The authors observed small differences in electrosorption kinetics and capacity at different pH values. While at a pH of 7.8 the SAC was 7 mg g−1, it dropped to 6 mg g−1 at a pH of 6.6. Using a mixture of a high concentration of chloride, in an equimolar mixture of sulfate, and phosphate, the following order of selectivity was observed: Cl− > SO42− > H2PO4−/HPO42−. In this case, the higher selectivity for Cl−/SO42− was possibly caused by its higher concentration in solution (Fig. 8C). The higher selectivity for SO42− over H2PO4−/HPO42−, however, was likely caused by a better screening of the electrode charge by the divalent species, therefore, dependent on the electrode, rather than the membrane (Fig. 6A). Regardless of the adsorption time, cell voltage, or flow rate used, chloride was preferred over phosphate. However, at lower cell voltages, and lower flow rates, a preference for phosphate over sulfate (R = 1.6) was observed. It is important to note that, in this case, selectivity values seemed not to be majorly influenced by the AEM, and therefore, selectivity was mostly governed by the CDI electrode.
Ren et al. employed a flow MCDI (FCDI) cell to remove phosphate and ammonium from an aqueous solution.133 Although it was found to be possible to remove large amounts of phosphate, the selectivity using this cell design was not explored. Further insight about selectivity using FCDI was reported by Bian et al. who studied the best operational conditions for the removal of phosphate and nitrate.134 They observed a strong increase in the phosphate removal by increasing the carbon loading of the anode. This increase was steeper than that for nitrate (and ammonia), and was ascribed to the physical adsorption of phosphate in addition to electrosorption (Fig. 6E), similar to the results obtained by Ge et al. On the other hand, for low carbon loadings, FCDI was found to be much more selective towards nitrate (1.1 at 15 wt% carbon loading to 1.7 at 5 wt%).
The effect of operational conditions on anion selectivity was explored in MCDI processes. Hassanvand et al. compared the electrosorption performance of MCDI with CDI using multicomponent solutions.53 Compared to MCDI, CDI showed a lower nitrate removal than chloride, and a lower charge efficiency. Simultaneously, the presence of inverse peaks, which is caused by co-ion repulsion, was also observed during nitrate removal. Since nitrate has a high affinity to the carbon surface (both hydrophobic), nitrate accumulates on its surface being then repelled during the cathodic polarization, which was also reported by Mubita et al. The inversion peak disappeared by using an AEM, as already reported in literature,7,135 and the removal of nitrate and chloride as well as their charge efficiencies became similar. At the same time, the removal of sulfate was lower than that of chloride and nitrate in CDI as well as MCDI. The use of an AEM resulted in a faster sulfate desorption even though the monovalent ions were preferred during the adsorption. A possible explanation of this observation provided by the authors is that a part of the sulfate ions were retained in the membrane surface, and therefore, the path length during the desorption was much shorter compared to that of monovalent ions.
Tang et al. investigated the effect of different operational parameters on the selective removal of sulfate over chloride.136 One of the most important features of this research is the use of the constant current method in MCDI instead of the constant voltage used in most CDI processes. A constant current provides a suitable way to control the electrosorption kinetics, and therefore, makes it possible to obtain a constant change in effluent concentration, dependent on the applied current (Box: General aspects of CDI). In solutions containing the same initial concentration of sulfate and chloride, Tang et al. observed a higher selectivity of sulfate over chloride. This high selectivity towards the divalent species is in good agreement with earlier works, and can be explained by the Nernst–Planck equation (Section 4. Theory), in which both show a strong effect of the valence on the transport and on the concentration of ions on the electrode (Fig. 8C).24 At low currents and high flow rate, the authors achieved a selectivity (ρ) of ≈1.4 for sulfate ions over chloride ions.
Another recent approach that has provided viable results for selectivity between mono/divalent ions is the use of monovalent ion-selective membranes. Pan et al. investigated the use of such membranes to separate fluoride and nitrite from sulfate.137 Using an equimolar solution, the authors observed a selectivity (ρ) of ≈1.4 for fluoride ions over sulfate ions. Furthermore, it was found that the pH of the feed solution was an important parameter to control and improve the ion selectivity. Higher pH values increased the selectivity towards fluoride, while for acidic solutions the selectivity was lost due to an interaction between protons and the surface of the membrane. The effect of the feed concentration was also explored, keeping the concentration ratio between the two anions constant. An increasing fluoride selectivity was observed upon increasing the concentration of both F− and SO42−. When the cell voltage was increased, the selectivity was reduced towards F− demonstrating that high cell voltages cannot attain high selectivity. This result is in line with other works that show lower selectivity at higher cell voltages.41,77
In a study similar to Pan et al., Mao et al. employed nanofiltration monovalent-selective membranes to increase the selectivity of chloride over sulfate.138 The authors adapted an EDL model that shows a higher diffusion of chloride through the membrane than sulfate (Fig. 8C). This facilitates the ion separation, especially during the desorption step, in which a selectivity (ρ) of ≈3 towards chloride over sulfate was observed.
The use of membranes and resins for anion selectivity in CDI shows promising results. The mechanism for the ion selectivity varies similarly to the ones used for cation selectivity. Most AEMs have higher affinity towards the targeted ion, and therefore, the transport of the competing ions through the selective membrane is reduced. Considering the state-of-art of MCDI for ion selectivity, future work will probably focus on investigating (functionalized) ion-selective membranes which completely hinder the transport of competing ions, providing ideal selectivity towards the target ion. High selectivity towards the target ion with high charge efficiency should provide a promising low-cost technology for ions recovery.
4. Theory
This subsection on modelling and theory of CDI processes with focus on ion selectivity is divided into two parts, preceded by a state-of-the-art review of the models (Section 4.1) developed in literature to explain ion selectivity in CDI. Following this short review, we discuss equilibrium models that describe ion adsorption in the micropores in two types of electrodes, i.e. carbon and intercalation electrodes, as well as in ion-exchange membranes. We will make use of extended Donnan models for the structure of the EDL, which quantifies the extent of ion adsorption and selectivity. This will conclude part I (Section 4.1.1) of this subsection. In part II (Section 4.1.2), we discuss a novel theory for the dynamics of ion transport and adsorption in intercalation materials that, for the first time, considers mixtures of different cations. We also discuss how the selectivity between cations is time dependent in this case, and can be less than an equilibrium model (Section 4.1.1) might predict, if the system lacks optimal design.4.1 State-of-the-art review of models in CDI
Ion selectivity in CDI has been investigated by theoretical methods in a limited number of papers. Models that discuss ion selectivity because of different transport rates through IEMs, commonly applied in MCDI, are not addressed in this section. Equilibrium studies of ion adsorption in porous carbon electrodes were first presented by Zhao et al.24 where monovalent/divalent (henceforth mono/di, mono/mono, and di/di) mixtures of cations were considered (Ca2+ and Na+), while Suss et al.49 described an equilibrium theory and data for various mixtures of different mono/mono anions and cations of the same valency. In both papers the mD model was used while in Suss et al., the mD model was extended to include ion volume effects, which led to a moderate preference towards smaller ions, in line with experimental observations. Mubita et al.77 used the amphoteric Donnan (amph-D) model to describe the selectivity between different anions in porous carbon electrodes extending the use of the amph-D model in Biesheuvel et al. where it was successfully used to describe equilibrium adsorption in carbon electrodes for mixtures of Ca2+ over Na+ as function of cell voltage and mixing ratio.139 Measured equilibrium selectivities for NO3− over Cl− of a factor of 6 to 9 in Mubita et al., could be successfully reproduced by the amph-D model.The most accurate approach in describing the ion transport in combination with adsorption has been the porous electrode theory, put forward in 2010.140 It was further developed by Biesheuvel and co-workers when they used this framework in a model that combined faradaic reactions and capacitive electrode charging for a mixture of a monovalent anion, a monovalent cation, and divalent cations, making use of the mD model to describe ion adsorption (μatt = 0).141 The same porous electrode theory was also used by Zhao et al. for a purely capacitive electrode, and extended by Dykstra et al.48 for a solution with two types of monovalent cations and a monovalent anion. Here for the first time, a full cell with two electrodes is considered. Furthermore, the simple mD model with μatt = 0 is replaced by the improved mD model which considers a salt-concentration dependent ion adsorption energy. In Dykstra et al., the only mechanism causing a difference in adsorption between different monovalent cations was the diffusion coefficient of the ions leading to a selectivity for K+ over Na+ of up to S ≈ 1.4, in close agreement with detailed experiments. Theoretical calculations predict this selectivity to be at a maximum at intermediate cycle times, a result that was not fully corroborated by the experiments. Recently, Guyes et al. presented a theory which predicted an enhancement of size-based selectivity towards K+ over Li+ and Na+, with increasing chemical charges in the micropore added by surface modification.142
Dynamic calculations by Zhao et al. using porous electrode theory for mono/di cation mixtures, with monovalent anions, showed that an electrode that initially selectively adsorbed monovalent cations, switched to the adsorption of divalent cations and desorption of the adsorbed monovalent cations later in the process, in line with experimental observations. Also, in Zhao et al., Gouy–Chapman–Stern (GCS) theory was used for mono/di cation mixtures containing the same monovalent anion, and combined with a model that describes ion transport to a planar charged wall. This model qualitatively showed the same phenomenon of replacement of monovalent cations by divalent cations during prolonged charging of the electrode. Finally, Zhao et al. summarized relevant equations for the GCS model for the excess ion adsorption in an EDL in mono/di cation mixtures (or, equivalently, for mono/di anion mixtures containing the same monovalent cation). For the GCS model, these equations did not yet exist for a three-ion mixture, and therefore they extended the existing classical expressions for binary ion mixtures, such as mono/di cation mixtures with the same monovalent anion.143,144 Iglesias et al.145 combined a simple transport model for mono/di cation mixtures with an mD model, and also combined it with a model based on the Poisson–Boltzmann equation including the permanent fixed charges (their Fig. 4B) to describe ion adsorption. A similar Poisson–Boltzmann calculation including salt mixtures was developed for the reverse of CDI, the controlled mixing of salt and fresh water, by Fernandez et al.146 and by Jimenez et al.147 who included ion-volume effects as well.
The theory for CDI with multiple ions (i.e., selectivity effects) was also included in the work by Dykstra et al.148 with an important extension. Here, MCDI was described by combining a detailed membrane transport model and porous electrode theory. A monovalent salt solution was considered but in addition, two extra ions, namely OH− and H+, were included in the theory. These extra ions are different from the common salt ions, because they are reactive. The reaction between these ions (the water self-dissociation reaction) was included in the theory in a way that the water equilibrium was attained at all times, i.e. the product of the concentrations of H+ and OH− was always at the same value. Like in Biesheuvel et al.,141 faradaic reactions were included in Dykstra et al. but now they involve H+ and OH− ions. Suss et al.49 used a mD model to describe equilibrium data for ion adsorption from mixtures, where ion size effects were included. This was achieved by modifying the Carnahan–Starling (CS) equation-of-state to include the impact of ion size on its adsorption, with the smaller ion being preferentially adsorbed. The theory was compared with data for Cl−/F− separation as well as for Na+/K+ separation. The selectivity in all cases levelled off at values of ≈1.5, which implies a 50% higher adsorption of one ion over another ion. The same modified CS equation was used in combination with GCS theory to describe data of ion adsorption near a highly charged interface for mono/mono and di/di cationic mixtures in Soestbergen et al.,149 achieving results very close to experimental observations of ion adsorption in EDLs.
To describe ion adsorption from feeds containing many types of salt ions into membranes or electrodes, we set up a Donnan model. The underlying approximation invoked in the Donnan model is that the geometry of the membrane or electrode pores is highly confined (with characteristic length scale on the order of 1 nm), so that we only need to consider a single potential, ϕD, within these pores.141 The potential ϕD is referred to as the Donnan potential and is defined as a difference in potential inside the pore relative to the potential outside the pore in the bulk electrolyte. Generally, for such systems (provided surface charge is not extreme), changes in ϕD across the pore width (i.e., differences between the center of the pore and the pore wall) are small. Given the confined geometry inside intercalation materials (such as PBA as an example), activated carbon micropores, and in chemically charged membranes, the Donnan model can be applied to describe ion adsorption in all these, seemingly disparate, systems. For simplicity, we will neglect a Stern layer capacitance, although this layer is known to play an important role in microporous carbon electrodes.154,155 An ion–ion attraction term is often considered for cations in intercalation materials (extended Frumkin isotherm), and this term will be left out as well in this part.156 With these two modifications, we will here demonstrate that we arrive at the same equations governing ion adsorption for all three systems just mentioned (intercalation materials, microporous carbons, and IEMs).
In an electrode, the Donnan potential can be modulated by changing the cell voltage between two electrodes, or by changing the bulk electrolyte composition. By contrast, for a given IEM, the Donnan potential depends solely on electrolyte composition.157 Both for electrodes and membranes, the charge density in the confined pore geometry is of importance, and in the Donnan approach this is defined per volume of micropores, thus has unit C m−3 or mol m−3 = mM. We will denote micropore charge with the symbol σ0 with unit mol m−3. It can be multiplied by Faraday's number, F, and the microporosity to obtain the charge per volume of total electrode. This electronic charge σ0 can be changed from negative to positive in carbon micropores, to adsorb either cations or anions, respectively. Meanwhile, in some other materials, such as PBA, an intercalation material, the charge is very negative and so, this material only absorbs cations.78 On this count it resembles a subset of IEMs containing negatively charged groups, such as sulfonic groups, known as CEMs. Unlike in CEMs, in PBA the negative charge can be modulated up or down via injection or removal of electronic charge.
For an ionic mixture with ions of all possible valencies z, typically ranging between −2 and +2, an overall micropore charge balance is
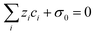 | (1) |
μi = μref,i + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ci,j + ziϕj + μexc,i,j + μaff,i,j ci,j + ziϕj + μexc,i,j + μaff,i,j | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ci,j, and the electrostatic field, given by ziϕj. Potential ϕj refers to the electric potential of phase j, and ϕ − ϕ∞ is the dimensionless Donnan potential, ϕD. This potential can be multiplied by VT = RT/F to obtain a voltage with unit volt. At phase equilibrium, the chemical potential of ion i is balanced between the micropore and bulk electrolyte, yielding
ci,j, and the electrostatic field, given by ziϕj. Potential ϕj refers to the electric potential of phase j, and ϕ − ϕ∞ is the dimensionless Donnan potential, ϕD. This potential can be multiplied by VT = RT/F to obtain a voltage with unit volt. At phase equilibrium, the chemical potential of ion i is balanced between the micropore and bulk electrolyte, yieldingln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ci + ziϕD + μaff,i + μexc,i = ln ci + ziϕD + μaff,i + μexc,i = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ci,∞ + μexc,i,∞ + μaff,i,∞. ci,∞ + μexc,i,∞ + μaff,i,∞. | (3) |
We introduce the volumetric partitioning function Φexc,i = exp(μexc,i,∞ − μexc,i), and a similar term for affinity-based effects, Φaff,i = exp(μaff,i,∞ − μaff,i), which lumps together all effects acting on the ion that are not ideal (entropy), volumetric, or charge-related. These factors Φexc,i and Φaff,i will be between 0 and 1 when such effects act to repel the ion from the micropore environment but will be >1 when they act to adsorb the ion into the micropore. We use Φi = Φexc,i·Φaff,i. We obtain from eqn (3) a modified Boltzmann relation
| ci = ci,∞·Φi·exp(−ziϕD). | (4) |
Taking Φi = 1 for the moment, we can insert eqn (4) in eqn (1) and obtain the result
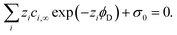 | (5) |
For the case where all ions are monovalent, or all ions are divalent, the resulting equation for σ0versus ϕD has been often presented, see ref. 156.
Here we develop eqn (5) for another situation, that when we have a mixture of cations with varying valence. If cations were to have the same valence and Φi, eqn (5) shows that the ratio of cation concentrations in the micropore is the same as that in solution: c1/c2 = c1,∞/c2,∞. However, for a mixture of divalent and monovalent cations, the ratio of concentrations in the micropore is strongly favoured towards the divalent ion. To demonstrate this result, we evaluate eqn (5) neglecting the anions, as micropore anion concentration approaches zero for the case where the dilution, β = |σ0|/c∞ ≫ 1, where c∞ is the total concentration of the anions in the bulk solution. For charge versus potential, we then arrive at
c+,∞![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ϕD) + 2c++,∞ exp(−ϕD) + 2c++,∞![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2ϕD) + σ0 = 0 exp(−2ϕD) + σ0 = 0 | (6) |
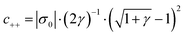 | (7) |
This short analysis illustrates the intricacies of what can happen with mixtures of monovalent and divalent (cat-)ions. From this point onward we consider mixtures of cations where all ions have the same valence, namely z = +1. Selective separation from a mixture of only monovalent ions has been a point of focus in CDI, as reviewed previously. In this case, selectivity can be based on an affinity to one monovalent cation over another, as described by the factor Φaff,i in eqn (4). [Volume effects are similar in many respects, but we focus now on chemical affinity effects, and discuss volume effects further on, thus for now Φexc,i = 1.] If one ion has a higher value for this partitioning function, it will be selectively absorbed. If ion type 1 has no affinity to being in the micropores, the value of μaff,i is the same inside and outside the pore. If for ion 2 inside the pore μaff is lower by a value of 1 kT, μaff, we have more adsorption of ion 2 relative to ion 1, and its partitioning function Φaff,i will be higher by a value of e (≈2.72). Thus, this small difference in energy of only 1 kT per ion has a large effect on selectivity. Note that also ion dehydration when entering the pore can be described as an affinity effect. Some types of ions are assumed to dehydrate upon entering micropores, especially those under 1 nm in characteristic size.158 This dehydration translates into an energy penalty, and thus a lower Φaff,i, and a reduction in that ion's concentration in the pore relative to the ideal case.
We finally discuss the effect of ion volume on the partitioning function, now described by an excluded volume-based effect, Φexc,i. And now we set Φaff,i = 1 in eqn (4). The volume effect is due to the size of the (hydrated) ion, and volume exclusion interactions between ion i and other ions taking up volume in the phase, also modulated by volumetric interactions with the porous medium.149,159 The interaction can be understood in the context of hard sphere models, where such spheres repel each other strongly as they come into direct contact. In a mixture of ions of varying sizes, the excluded volume effect can result in a selectivity towards the smaller ion, captured by a difference in Φexc,i between ions. We make use here of a very useful expression for the contribution to the chemical potential of a volume/excess term, μexc,i in the pore, which results in a contribution Φexc,i = exp(−μexc,i) where we assume that this excess term is zero in bulk solution, which is approximately valid for a low salt concentration (order 10 mM).142 For an ion inside a pore, μexc,i was derived to be155,156
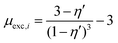 | (8) |
For the term, γα′, γ is a constant, namely γ = 0.0725, while α′ = di/hp. Here, di is the (hydrated) ion size and hp is the ratio of pore volume over pore wall area. For a slit-shaped pore, hp is equal to the pore width divided by 2, and for a cylindrical pore it is equal to pore size (i.e., pore diameter) divided by 4. Thus hp is a characteristic pore size, but because we typically do not know these values exactly, neither the ion size in the pore, nor the factor hp, α′ is typically an empirical factor.
In the limit of a relatively low concentration of ions in the pore (η → 0) and small ion size (α′ → 0), we arrive at μexc,i = 8γα′, and thus for the selectivity S between an ion 1 and ion 2 (ratio of ion concentrations in the pore, relative to that outside the pore) with different ion sizes di we arrive at
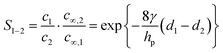 | (9) |
To conclude, in this section we briefly addressed three reasons why there can be an ion selectivity in microporous materials, be they capacitive electrodes such as an intercalation material, as well as in ion-exchange membranes. As outlined above these three effects are: ion charge, ion affinity (a chemical interaction with the pore environment), and ion volume effects.
In CDI with NiHCF intercalation materials78 in a salt mixture with K+ and Na+, it is known that NiHCF is highly selective for K+versus Na+, with a separation factor that can be as high as 160 (calculated from the extended Frumkin isotherm in Section 7 in ESI of Porada et al.78). Thus, of all the interstitial sites inside the intercalation material (IHC, for intercalation host compound), NiHCF here, more than 99% is occupied by K+, with less than 1% occupied by the Na+ cation. This conclusion can be based on the measured difference in the charge–voltage curves for NiHCF in concentrated solutions of K2SO4 and Na2SO4 (Fig. S5, ESI in Porada et al. (2017)). The calculation of which the results are presented below, is in accordance with this high intrinsic selectivity of the IHC particles for K+vs. Na+ adsorption, of a factor significantly beyond 100. However, the calculation example shows that the actual selectivity obtained in a realistic cell is still high, but due to transport and mixing, it is lower than the maximum calculated value by a factor of ≈10, as noted in Section 2.3. Intercalation materials.
The calculation is based on a description of a single porous electrode consisting of IHC particles, using the porous electrode theory presented in Singh et al.,9 based on West et al.,161 developed for a simple solution with the cations (mono) and anions (mono) having the same diffusion coefficient in solution as well as in the macropores of the electrode. We now extend the theory of Singh et al. to a mixture of two cations (K+ and Na+) and one anion, Cl−, with the two cations having a different diffusion coefficient. In the modelled cell, the planar porous intercalation electrode is in contact with a flow (spacer) channel. Beyond this channel is a membrane that only allows anions to pass, and no cations. We only model this single electrode, to which constant current is applied, and one flow channel, to which fresh solution is continuously added. Like Singh et al., we model transport in the electrode only in one spatial direction, namely the direction away from the spacer channel, while assuming that the entire spacer volume is well-mixed. This is referred to as the “stirred tank” approach. The resulting “one-slice” calculation approach has also been successfully used in models for electrodialysis.162 The calculation includes a mass transfer resistance to ion transport in the macropores of the electrode, described by the Nernst–Planck equation, with no mass transport limitation in the spacer channel and neither inside the IHC particles.
For each of the three ions, an ion mass balance inside the electrode is given by
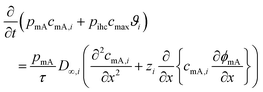 | (10) |
Eqn (10) is solved together with local electroneutrality at each position in the macropores,
| cmA,Na+ + cmA,K+ − cmA,Cl− = 0 | (11) |
At each x-coordinate, the relationship between electrode potential ϕe, solution potential ϕmA and occupancy of a cation in the IHC, ϑi, is implemented. This is given by the extended Frumkin equation eqn (12) for binary mixtures,78
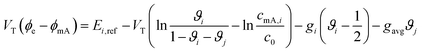 | (12) |
The ion mass balance in the spacer is given by
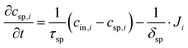 | (13) |
At the spacer-electrode edge, the flux by diffusion and electro-migration of the two cations is continuous, i.e., the same on each side of this edge, and ion concentrations are also continuous. Finally, the charge balance is given by
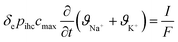 | (14) |
Results of this calculation are presented in Fig. 9 and show profiles in macropore ion concentration across the electrode in panels A and B, as well as profiles in IHC cation occupancy, ϑi, at the same moments in time (panels C and D). These profiles develop from moment zero when the cell is still uncharged and the salt concentrations in the macropores of the electrode are the same as in the spacer channel. This is same as the 10 mM K+ and 10 mM Na+ feed solution flowing into the spacer channel. From time zero onwards a fixed current of 28 A m−2 is applied to the cell. In panel E the concentration of the two cations in the effluent water leaving the cell is presented as a function of time. Finally, panel F gives the ratio of these two effluent concentrations minus the inflow concentration, which is the K+/Na+ selectivity. After the current is applied, the electrode begins to adsorb cations from solution, storing them in the IHC particles, whose occupancy ϑi for both the ions starts to increase, mainly in the region near the flow channel. At the same time, the macropore concentration for both ions in the electrodes drops precipitously, going down to values of one-tenth to one-hundredth of 1 mM (Fig. 9A and B). This low macropore concentration hinders a fast diffusion of cations across the electrode, which are mainly adsorbed in the IHC particles near the spacer channel. To make more of the electrode accessible with more ease, a larger macroporosity would help in this regard, but even better will be a cell design with some degree of advection of the solution through the macropores, as realized in flow-through CDI.154
After the current is applied, the effluent concentrations of Na+ and K+ decrease rather slowly because in the calculation, the flow channel residence time is relatively large, at τ ≈ 30 s. After ≈40 s, the effluent concentration for K+ reaches a more constant value, while that of Na+ still decreases. Therefore, the K+/Na+ selectivity, SK+/Na+ (Table 1 for definition) starts off at an appreciable value of ≈12 at the start of charging, but subsequently drops to values below ≈2 after 80 s. Thus, two general conclusions can be drawn about the selectivity of electrodes for cation adsorption, by NiHCF intercalation materials. The first is that the selectivity changes strongly during a CDI cycle, i.e., it depends on the moment within a cycle, and likely also on the durations of the charge and discharge steps in a full cycle.123 The second conclusion is that the actual realized selectivity can be much lower than the maximum calculated selectivity, which in this case is a value significantly above 100. This is in line with the conclusion presented by Porada et al.78 Careful design of the electrodes and the cell will be essential in obtaining selectivity values that in practice come closer to the ideal value. Only in this way can the significant potential of intercalation materials to achieve very high mono/mono cation selectivity be realized. Note that we here only presented a calculation of a single charging step, of a pre-equilibrated electrode. Calculations for full cycles (with current directions reversed again and again) are of interest to show the behavior of this cell in a complete desalination + release cycle.
5. Outlook
It becomes evident upon reviewing the literature that the interest in ion-selective CDI is growing swiftly. This has led to significant advances, especially in the use of different electrode materials for cation as well as anion selectivity, when compared to membranes in CDI. Furthermore, the theory of ion selectivity has been developed and validated with experiments. However, due to diverse methods, techniques, and materials employed in achieving ion selectivity, a direct comparison of these studies is difficult. Furthermore, ion selectivity studies carried out in single-salt solutions, comparing individual electrosorption rates to calculate selectivity, provide little information on electrosorption behavior in competitive environments that resemble real-life cases. While it is challenging to introduce a standardized procedure to report ion selectivity, due to countless different ion combinations, it may be sensible to provide a selectivity coefficient for one ion in a mixture over the others, an approach commonly used in sensor studies.163,164Moving forward, research into new electrode materials and chemistries, modification and optimization of existing materials, investigation of parameters in selectivity operation, modeling of selectivity at the system and molecular level, and finally, techno-economic analysis into the viability of selective ion separation via CDI will be crucial for fully realizing the potential of ion-selectivity via CDI.
As reviewed here, new alternatives to carbon such as PBAs, TiS2, NMO and layered hydroxides show remarkable inherent selectivity towards certain cations. A better understanding of the preference of these materials, like the presence of different intercalation sites in PBAs165 or the complexation of ions with transition metal at the adsorption site of a double layered hydroxide,70 would help to further tune – or even switch – the preference of the materials, leading to a higher adaptability of selective CDI systems. Molecular dynamics (MD) simulations, providing insight into the adsorption (and a follow-up reaction, if applicable) will further prove useful in understanding the mechanism of selectivity and aid in fabricating materials with inherent selectivity towards desired ions. Inspiration for the development of new electrode materials for CDI can be drawn from the more mature field of energy storage.
Electrode modifications will be the key for inducing selectivity in materials that lack an inherent and strong preference towards ions. Since the modifications can be controlled and fine-tuned, this line of investigation can lead to highly application-specific CDI systems. The modification of the electrode may be as simple as changing the activation conditions of a carbon electrode to obtain very narrow micropores,41,42 by adding functional groups or resins with affinity towards specific species,128,166 or even by modifying carbon electrodes with redox active organometallic polymers to remove organic ions.109 In MCDI cells, selectivity may be also achieved by using or modifying ion-exchange membranes, e.g. adding polyelectrolyte multilayers to achieve monovalent selectivity.123
On a system level, dependence of cell selectivity on operation parameters such as applied current, cell voltage, ion concentration, and pH among others will have to be systematically studied to find optimum conditions that enhance selectivity for the CDI cell. Intercalation electrodes such as TiS2 show switchable preference depending on the potential of the electrode, as shown by Srimuk et al.43 Such insights will be useful in realizing the full potential of existing (and the search for new) electrode materials.
A standard set of operational parameters, similar to those proposed to objectively assess CDI systems,38 would further enable a better comparison between results in the ion-selective literature. For example, it would be beneficial to provide at least one set of experiments using single-pass mode under constant current, with the values of feed and outlet concentration of each ion clearly defined. As discussed in Box: General aspects of CDI, constant current enables continuous transport of ions to the electrodes (through the membrane, if applicable), making it easier to evaluate the selectivity of the system. Furthermore, this will also closely resemble real-life cases when scaling-up a system. An operational parameter to address selectivity that is often provided in literature is the cell voltage. However, voltage values can significantly differ between cell assemblies. A way around this problem would be to report individual electrode potentials, which would be nearly independent of cell architecture and a useful parameter in comparison between different studies.
An ability to predict ion-selectivity will help streamline the efforts being made in this field of CDI, enhancing the strength of the technology to remove ions selectively. Our work takes a step in this direction by putting forward a theory, at the system level, for prediction of ion-selectivity of a class of intercalation electrodes. A logical next step is the investigation of the molecular origins for the preference of electrode materials towards different ions. Further insight into the mechanism of preferential electrosorption of ions can help to tune the selectivity-inducing properties of the electrode material. Hawks et al.41 carried out molecular dynamics (MD) simulations to elucidate the selective adsorption of NO3− over Cl− and SO42− in carbon electrodes. This simulation assisted the authors to understand how hydration of the ions influenced the anion selectivity in very narrow micropores. According to the MD simulations, nitrate and chloride have similar hydration energies, much lower than sulfate, which suggests that sulfate is less prone to rearrange its solvation shell to fit inside of the micropores. At the same time, the higher selectivity of nitrate over chloride is explained by the higher distribution of the water molecules on the equatorial region rather than the perpendicular region of nitrate, suggesting that water molecules are weakly bound on the axial region of nitrate. Since NO3− has a delocalized water shell,41 as predicted by MD simulations, the ion is more prone to fit inside of the slit micropores of the investigated activated carbon. For porous carbon materials, the use of MD simulations can be extended to several other ions, which allows one to predict the ion selectivity based on the surface characteristics of the electrode material.
For intercalation materials such as PBA, density functional theory simulations, as performed by Jiang et al.,165 are useful to understand the preference of the electrode for a certain ion. In this study, binding energy and volume of a CuHCF lattice was calculated after intercalation of Li+, Na+, and K+. The results showed that cations, based on their size, preferred intercalating at different sites within the lattice. The preference of the lattice towards a cation was reflected by the reduced binding energy post-intercalation of that ion into the intercalation electrode. In addition, the calculated change in the volume was also found to be the smallest for the most preferred cation, K+ in this case, which has been confirmed experimentally as well.165 Such modeling exercises can help in fabrication of new intercalation materials with properties that suit selective removal of a desired ion.
One of the final yet critical aspects that needs to be elucidated is the feasibility of moving from the laboratory bench to an industrial scale selective ion separation process via CDI. This shift requires a thorough cost-benefit analysis, which is yet to be published. Despite the rapid growth of CDI in terms of selective ion separation, the field itself is not mature enough for a complete economic analysis. Nevertheless, a recent study by Hand et al.167 suggested CDI can be cost-competitive in selective ion separation, provided that significant selectivity values are achieved using CDI. Therefore, it is critical that future research directions focus on improving the degree of ion selectivity of CDI-based technologies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Union Horizon 2020 research and innovation program (ERC Consolidator Grant to LdS, Agreement No. 682444) and was performed in the cooperation framework of Wetsus, European Centre of Excellence for Sustainable Water Technology. Wetsus is co-funded by the Dutch Ministry of Economic Affairs and Ministry of Infrastructure and Environment, the European Union Regional Development Fund, the Province of Fryslân, and the Northern Netherlands Provinces.References
- J. D. Birkett, Desalination, 1984, 50, 17–52 CrossRef CAS.
- M. Kumar, T. Culp and Y. Shen, Winter Bridg. Front. Eng., 2016, 46, 21–29 Search PubMed.
- J. W. Blair and G. W. Murphy, Saline Water Conversion, Washington, DC, 1960, pp. 206–223 Search PubMed.
- J. C. Farmer, D. V. Fix, G. V. Mack, R. W. Pekala and J. F. Poco, Low Level Waste Conference, Orlando, FL, 1995 Search PubMed.
- D. Cordell, J. O. Drangert and S. White, Global Environ. Change, 2009, 19, 292–305 CrossRef.
- G. Liu, Z. Zhao and A. Ghahreman, Hydrometallurgy, 2019, 187, 81–100 CrossRef CAS.
- P. M. Biesheuvel, R. Zhao, S. Porada and A. van der Wal, J. Colloid Interface Sci., 2011, 360, 239–248 CrossRef CAS.
- S. Porada, R. Zhao, A. van der Wal, V. Presser and P. M. Biesheuvel, Prog. Mater. Sci., 2013, 58, 1388–1442 CrossRef CAS.
- K. Singh, H. J. M. Bouwmeester, L. C. P. M. De Smet, M. Z. Bazant and P. M. Biesheuvel, Phys. Rev. Appl., 2018, 9, 064036 CrossRef CAS.
- K. Singh, S. Porada, H. D. de Gier, P. M. Biesheuvel and L. C. P. M. de Smet, Desalination, 2019, 455, 115–134 CrossRef CAS.
- J. Choi, P. Dorji, H. K. Shon and S. Hong, Desalination, 2019, 449, 118–130 CrossRef CAS.
- R. Chen, T. Sheehan, J. L. Ng, M. Brucks and X. Su, Environ. Sci.: Water Res. Technol., 2020, 6, 258–282 RSC.
- X. Zhang, K. Zuo, X. Zhang, C. Zhang and P. Liang, Environ. Sci.: Water Res. Technol., 2020, 6, 243–257 RSC.
- Y. Liu, C. Nie, X. Liu, X. Xu, Z. Sun and L. Pan, RSC Adv., 2015, 5, 15205–15225 RSC.
- B. Jia and W. Zhang, Nanoscale Res. Lett., 2016, 11, 1–25 CrossRef CAS.
- Z. H. Huang, Z. Yang, F. Kang and M. Inagaki, J. Mater. Chem. A, 2017, 5, 470–496 RSC.
- K. Zaid and A. B. Suriani, Sci. Int., 2017, 29, 285–289 CAS.
- M. A. Ahmed and S. Tewari, Capacitive deionization: Processes, materials and state of the technology, Elsevier B.V., 2018, vol. 813 Search PubMed.
- P. Ratajczak, M. E. Suss, F. Kaasik and F. Béguin, Energy Storage Mater., 2019, 16, 126–145 CrossRef.
- R. Zhao, S. Porada, P. M. Biesheuvel and A. van der Wal, Desalination, 2013, 330, 35–41 CrossRef CAS.
- R. Zhao, P. M. Biesheuvel and A. van der Wal, Energy Environ. Sci., 2012, 5, 9520–9527 RSC.
- A. Hemmatifar, J. W. Palko, M. Stadermann and J. G. Santiago, Water Res., 2016, 104, 303–311 CrossRef CAS.
- M. A. Anderson, A. L. Cudero and J. Palma, Electrochim. Acta, 2010, 55, 3845–3856 CrossRef CAS.
- R. Zhao, M. van Soestbergen, H. H. M. Rijnaarts, A. van der Wal, M. Z. Bazant and P. M. Biesheuvel, J. Colloid Interface Sci., 2012, 384, 38–44 CrossRef CAS.
- M. Mossad and L. Zou, J. Hazard. Mater., 2012, 213–214, 491–497 CrossRef CAS.
- J. B. Lee, K. K. Park, H. M. Eum and C. W. Lee, Desalination, 2006, 196, 125–134 CrossRef CAS.
- P. M. Biesheuvel, H. V. M. Hamelers and M. E. Suss, Colloid Interface Sci. Commun., 2015, 9, 1–5 CrossRef CAS.
- Y.-J. Kim and J.-H. Choi, Water Res., 2009, 44, 990–996 CrossRef.
- J.-Y. Lee, S.-J. Seo, S.-H. Yun and S.-H. Moon, Water Res., 2011, 45, 5375–5380 CrossRef CAS.
- X. Gao, A. Omosebi, N. Holubowitch, A. Liu, K. Ruh, J. Landon and K. Liu, Desalination, 2016, 399, 16–20 CrossRef CAS.
- S. Jeon, H. Park, J. Yeo, S. Yang, C. H. Cho, M. H. Han and D. K. Kim, Energy Environ. Sci., 2013, 6, 1471–1475 RSC.
- K. C. Smith, Electrochim. Acta, 2017, 230, 333–341 CrossRef CAS.
- K. Singh, L. Zhang, H. Zuilhof and L. C. P. M. de Smet, Desalination, 2020, 496, 114647 CrossRef CAS.
- J. Lee, S. Kim and J. Yoon, ACS Omega, 2017, 2, 1653–1659 CrossRef CAS.
- O. Stern, Z. Elektrochem., 1924, 30, 508–516 CAS.
- R. L. Zornitta, K. M. Barcelos, F. G. E. Nogueira and L. A. M. Ruotolo, Carbon, 2020, 156, 346–358 CrossRef CAS.
- P. M. Biesheuvel, Y. Fu and M. Z. Bazant, Phys. Rev. E, 2011, 83, 61507 CrossRef CAS.
- S. A. Hawks, A. Ramachandran, S. Porada, P. G. Campbell, M. E. Suss, P. M. Biesheuvel, J. G. Santiago and M. Stadermann, Water Res., 2019, 152, 126–137 CrossRef CAS.
- T. Kim and J. Yoon, J. Electroanal. Chem., 2013, 704, 169–174 CrossRef CAS.
- M. C. Zafra, P. Lavela, C. Macías, G. Rasines and J. L. Tirado, J. Electroanal. Chem., 2013, 708, 80–86 CrossRef CAS.
- S. A. Hawks, et al. , Environ. Sci. Technol., 2019, 53, 10863–10870 CrossRef CAS.
- L. Eliad, G. Salitra, A. Soffer and D. Aurbach, J. Phys. Chem. B, 2001, 105, 6880–6887 CrossRef CAS.
- P. Srimuk, J. Lee, S. Fleischmann, M. Aslan, C. Kim and V. Presser, ChemSusChem, 2018, 11, 2091–2100 CrossRef CAS.
- T. Kim, C. A. Gorski and B. E. Logan, Environ. Sci. Technol. Lett., 2018, 5, 578–583 CrossRef CAS.
- C. J. Gabelich, T. D. Tran and I. H. Suffet, Environ. Sci. Technol., 2002, 36, 3010–3019 CrossRef CAS.
- E. Avraham, B. Yaniv, A. Soffer and D. Aurbach, J. Phys. Chem. C, 2008, 112, 7385–7389 CrossRef CAS.
- L. Han, K. G. Karthikeyan, M. A. Anderson and K. B. Gregory, J. Colloid Interface Sci., 2014, 430, 93–99 CrossRef CAS.
- J. E. Dykstra, J. Dijkstra, A. Van der Wal, H. V. M. Hamelers and S. Porada, Desalination, 2016, 390, 47–52 CrossRef CAS.
- M. E. Suss, J. Electrochem. Soc., 2017, 164, E270–E275 CrossRef CAS.
- Y. Gao, L. Pan, H. B. Li, Y. Zhang, Z. Zhang, Y. Chen and Z. Sun, Thin Solid Films, 2009, 517, 1616–1619 CrossRef CAS.
- C. H. Hou and C. Y. Huang, Desalination, 2013, 314, 124–129 CrossRef CAS.
- M. Mossad, W. Zhang and L. Zou, Desalination, 2013, 308, 154–160 CrossRef CAS.
- A. Hassanvand, G. Q. Chen, P. A. Webley and S. E. Kentish, Water Res., 2018, 131, 100–109 CrossRef CAS.
- S. J. Seo, H. Jeon, J. K. Lee, G. Y. Kim, D. Park, H. Nojima, J. Lee and S. H. Moon, Water Res., 2010, 44, 2267–2275 CrossRef CAS.
- P. Xu, J. E. Drewes, D. Heil and G. Wang, Water Res., 2008, 42, 2605–2617 CrossRef CAS.
- Y. Li, C. Zhang, Y. Jiang, T. J. Wang and H. Wang, Desalination, 2016, 399, 171–177 CrossRef CAS.
- R. K. Kalluri, M. M. Biener, M. E. Suss, M. D. Merrill, M. Stadermann, J. G. Santiago, T. F. Baumann, J. Biener and A. Striolo, Phys. Chem. Chem. Phys., 2013, 15, 2320 RSC.
- Y. Liu, W. Ma, Z. Cheng, J. Xu, R. Wang and X. Gang, Desalination, 2013, 326, 109–114 CrossRef CAS.
- H. Yoon, J. Lee, S. R. Kim, J. Kang, S. Kim, C. Kim and J. Yoon, Desalination, 2016, 392, 46–53 CrossRef CAS.
- J. Kim, A. Jain, K. Zuo, R. Verduzco, S. Walker, M. Elimelech, Z. Zhang, X. Zhang and Q. Li, Water Res., 2019, 160, 445–453 CrossRef CAS.
- H. Li, L. Zou, L. Pan and Z. Sun, Sep. Purif. Technol., 2010, 75, 8–14 CrossRef CAS.
- S.-Y. Huang, C.-S. Fan and C.-H. Hou, J. Hazard. Mater., 2014, 278, 8–15 CrossRef CAS.
- P. Liu, T. Yan, J. Zhang, L. Shi and D. Zhang, J. Mater. Chem. A, 2017, 5, 14748–14757 RSC.
- Q. Dong, X. Guo, X. Huang, L. Liu, R. Tallon, B. Taylor and J. Chen, Chem. Eng. J., 2019, 361, 1535–1542 CrossRef CAS.
- X. Zhang, F. Yang, J. Ma and P. Liang, Environ. Sci.: Water Res. Technol., 2020, 6, 341–350 RSC.
- Y. Liao, M. Wang and D. Chen, Appl. Surf. Sci., 2019, 484, 83–96 CrossRef CAS.
- J. Farmer, D. Fix, G. Mack, R. Pekala and F. Poco, J. Electrochem. Soc., 1996, 143, 159–169 CrossRef CAS.
- C.-C. Huang and Y.-J. Su, J. Hazard. Mater., 2010, 175, 477–483 CrossRef CAS.
- Z. Ge, X. Chen, X. Huang and Z. J. Ren, Environ. Sci.: Water Res. Technol., 2018, 4, 33–39 RSC.
- S. P. Hong, H. Yoon, J. Lee, C. Kim, S. Kim, J. Lee, C. Lee and J. Yoon, J. Colloid Interface Sci., 2020, 564, 1–7 CrossRef CAS.
- W. Tang, P. Kovalsky, D. He and T. D. Waite, Water Res., 2015, 84, 342–349 CrossRef CAS.
- N. Pugazhenthiran, S. Sen Gupta, A. Prabhath, M. Manikandan, J. R. Swathy, V. K. Raman and T. Pradeep, ACS Appl. Mater. Interfaces, 2015, 7, 20156–20163 CrossRef CAS.
- W. Xing, J. Liang, W. Tang, G. Zeng, X. Wang, X. Li, L. Jiang, Y. Luo, X. Li, N. Tang and M. Huang, Chem. Eng. J., 2019, 361, 209–218 CrossRef CAS.
- Z. Chen, H. Zhang, C. Wu, Y. Wang and W. Li, Desalination, 2015, 369, 46–50 CrossRef CAS.
- Z. Sun, L. Chai, M. Liu, Y. Shu, Q. Li, Y. Wang and D. Qiu, Chemosphere, 2018, 195, 282–290 CrossRef CAS.
- D. I. Oyarzun, A. Hemmatifar, J. W. Palko, M. Stadermann and J. G. Santiago, Water Res.: X, 2018, 1, 100008 Search PubMed.
- T. M. Mubita, J. E. Dykstra, P. M. Biesheuvel, A. van der Wal and S. Porada, Water Res., 2019, 164, 114885 CrossRef CAS.
- S. Porada, A. Shrivastava, P. Bukowska, P. M. Biesheuvel and K. C. Smith, Electrochim. Acta, 2017, 255, 369–378 CrossRef CAS.
- T. Kim, C. A. Gorski and B. E. Logan, Environ. Sci. Technol. Lett., 2017, 4, 444–449 CrossRef CAS.
- J. Lee, S. Kim, C. Kim and J. Yoon, Energy Environ. Sci., 2014, 7, 3683–3689 RSC.
- B. W. Byles, B. Hayes-Oberst and E. Pomerantseva, ACS Appl. Mater. Interfaces, 2018, 10, 32313–32322 CrossRef CAS.
- W. Shi, X. Zhou, J. Li, E. R. Meshot, A. D. Taylor, S. Hu, J. H. Kim, M. Elimelech and D. L. Plata, Environ. Sci. Technol. Lett., 2018, 5, 692–700 CrossRef CAS.
- S. Kim, J. Lee, C. Kim and J. Yoon, Electrochim. Acta, 2016, 203, 265–271 CrossRef CAS.
- K. Wang, Y. Liu, Z. Ding, Y. Li, T. Lu and L. Pan, J. Mater. Chem. A, 2019, 7, 12126–12133 RSC.
- P. Srimuk, F. Kaasik, B. Krüner, A. Tolosa, S. Fleischmann, N. Jäckel, M. C. Tekeli, M. Aslan, M. E. Suss and V. Presser, J. Mater. Chem. A, 2016, 4, 18265–18271 RSC.
- P. Srimuk, J. Lee, A. Tolosa, C. Kim, M. Aslan and V. Presser, Chem. Mater., 2017, 29, 9964–9973 CrossRef CAS.
- R. Y. Wang, B. Shyam, K. H. Stone, J. N. Weker, M. Pasta, H. W. Lee, M. F. Toney and Y. Cui, Adv. Energy Mater., 2015, 5, 1–10 Search PubMed.
- A. A. Karyakin, Electroanalysis, 2001, 13, 813–819 CrossRef CAS.
- X. Gao, A. Omosebi, J. Landon and K. Liu, Energy Environ. Sci., 2015, 8, 897–909 RSC.
- T. Wu, G. Wang, S. Wang, F. Zhan, Y. Fu, H. Qiao and J. Qiu, Environ. Sci. Technol. Lett., 2018, 5, 98–102 CrossRef CAS.
- H. Yoon, J. Lee, S. Kim and J. Yoon, Hydrometallurgy, 2018, 175, 354–358 CrossRef CAS.
- S. Kim, J. Lee, J. S. Kang, K. Jo, S. Kim, Y. E. Sung and J. Yoon, Chemosphere, 2015, 125, 50–56 CrossRef CAS.
- T. Ikeshoji, J. Electrochem. Soc., 1986, 133, 2108–2109 CrossRef CAS.
- Y. Marcus, Biophys. Chem., 1994, 51, 111–127 CrossRef CAS.
- C. D. Wessells, S. V. Peddada, M. T. McDowell, R. A. Huggins and Y. Cui, J. Electrochem. Soc., 2011, 159, A98–A103 CrossRef.
- R. Chen, H. Tanaka, T. Kawamoto, M. Asai, C. Fukushima, H. Na, M. Kurihara, M. Watanabe, M. Arisaka and T. Nankawa, Electrochim. Acta, 2013, 87, 119–125 CrossRef CAS.
- S. Choi, B. Chang, S. Kim, J. Lee, J. Yoon and J. W. Choi, Adv. Funct. Mater., 2018, 28, 1–9 Search PubMed.
- M. Giorgetti, E. Scavetta, M. Berrettoni and D. Tonelli, Analyst, 2001, 126, 2168–2171 RSC.
- V. D. Neff, J. Electrochem. Soc., 1978, 125, 886–887 CrossRef CAS.
- C. Erinmwingbovo, M. S. Palagonia, D. Brogioli and F. La Mantia, ChemPhysChem, 2017, 18, 917–925 CrossRef CAS.
- M. Asai, A. Takahashi, K. Tajima, H. Tanaka, M. Ishizaki, M. Kurihara and T. Kawamoto, RSC Adv., 2018, 8, 37356–37364 RSC.
- M. A. Lilga, R. J. Orth, J. P. H. Sukamto, S. M. Haight and D. T. Schwartz, Sep. Purif. Technol., 1997, 11, 147–158 CrossRef CAS.
- K. Singh, Z. Qian, P. M. Biesheuvel, H. Zuilhof, S. Porada and L. C. P. M. de Smet, Desalination, 2020, 481, 114346 CrossRef CAS.
- J. E. Dykstra, R. Zhao, P. M. Biesheuvel and A. Van der Wal, Water Res., 2016, 88, 358–370 CrossRef CAS.
- S. Kim, H. Yoon, D. Shin, J. Lee and J. Yoon, J. Colloid Interface Sci., 2017, 506, 644–648 CrossRef CAS.
- W. Bao, X. Tang, X. Guo, S. Choi, C. Wang, Y. Gogotsi and G. Wang, Joule, 2018, 2, 778–787 CrossRef CAS.
- S. Buczek, M. L. Barsoum, S. Uzun, N. Kurra, R. Andris, E. Pomerantseva, K. A. Mahmoud and Y. Gogotsi, Energy Environ. Mater., 2020, 3, 398–404 CrossRef CAS.
- X. Su and T. A. Hatton, Adv. Colloid Interface Sci., 2017, 244, 6–20 CrossRef CAS.
- X. Su, H. J. Kulik, T. F. Jamison and T. A. Hatton, Adv. Funct. Mater., 2016, 26, 3394–3404 CrossRef CAS.
- X. Su, K. J. Tan, J. Elbert, C. Rüttiger, M. Gallei, T. F. Jamison and T. A. Hatton, Energy Environ. Sci., 2017, 10, 1272–1283 RSC.
- I. Cohen, B. Shapira, E. Avraham, A. Soffer and D. Aurbach, Environ. Sci. Technol., 2018, 52, 6275–6281 CrossRef CAS.
- J. Chang, Y. Li, F. Duan, C. Su, Y. Li and H. Cao, Sep. Purif. Technol., 2020, 240, 116600 CrossRef CAS.
- C. Hu, J. Dong, T. Wang, R. Liu, H. Liu and J. Qu, Chem. Eng. J., 2018, 335, 475–482 CrossRef CAS.
- R. L. Zornitta and L. A. M. Ruotolo, Chem. Eng. J., 2018, 332, 33–41 CrossRef CAS.
- A. Hassanvand, K. Wei, S. Talebi, G. Q. Chen and S. E. Kentish, Membranes, 2017, 7 Search PubMed.
- J. Moreno, V. Díez, M. Saakes and K. Nijmeijer, J. Membr. Sci., 2018, 550, 155–162 CrossRef CAS.
- T. Rijnaarts, D. M. Reurink, F. Radmanesh, W. M. de Vos and K. Nijmeijer, J. Membr. Sci., 2019, 570–571, 513–521 CrossRef CAS.
- T. Luo, S. Abdu and M. Wessling, J. Membr. Sci., 2018, 555, 429–454 CrossRef CAS.
- L. Wang and S. Lin, Environ. Sci. Technol., 2019, 53, 5797–5804 CrossRef CAS.
- T. Sata, T. Sata and W. Yang, J. Membr. Sci., 2002, 206, 31–60 CrossRef CAS.
- J. Choi, H. Lee and S. Hong, Desalination, 2016, 400, 38–46 CrossRef CAS.
- W. Shi, X. Liu, C. Ye, X. Cao, C. Gao and J. Shen, Sep. Purif. Technol., 2019, 210, 885–890 CrossRef CAS.
- S. Sahin, J. E. Dykstra, H. Zuilhof, R. L. Zornitta and L. C. P. M. de Smet, ACS Appl. Mater. Interfaces, 2020, 12, 34746–34754 CrossRef CAS.
- C. He, J. Ma, C. Zhang, J. Song and T. D. Waite, Environ. Sci. Technol., 2018, 52, 9350–9360 CrossRef CAS.
- J. H. Yeo and J. H. Choi, Desalination, 2013, 320, 10–16 CrossRef CAS.
- S. Samatya, N. Kabay, Ü. Yüksel, M. Arda and M. Yüksel, React. Funct. Polym., 2006, 66, 1206–1214 CrossRef CAS.
- H. I. Uzun and E. Debik, Sep. Purif. Technol., 2019, 209, 776–781 CrossRef CAS.
- Y.-J. Kim and J.-H. Choi, Water Res., 2012, 46, 6033–6039 CrossRef CAS.
- L. Gan, Y. Wu, H. Song, S. Zhang, C. Lu, S. Yang, Z. Wang, B. Jiang, C. Wang and A. Li, Sep. Purif. Technol., 2019, 212, 728–736 CrossRef CAS.
- D. I. Kim, R. R. Gonzales, P. Dorji, G. Gwak, S. Phuntsho, S. Hong and H. Shon, Desalination, 2020, 484, 114425 CrossRef CAS.
- K. Zuo, J. Kim, A. Jain, T. Wang, R. Verduzco, M. Long and Q. Li, Environ. Sci. Technol., 2018, 52, 9486–9494 CrossRef CAS.
- J. Jiang, D. I. Kim, P. Dorji, S. Phuntsho, S. Hong and H. K. Shon, Process Saf. Environ. Prot., 2019, 126, 44–52 CrossRef CAS.
- S. Ren, M. Li, J. Sun, Y. Bian, K. Zuo, X. Zhang, P. Liang and X. Huang, Front. Environ. Sci. Eng., 2017, 11, 17 CrossRef.
- Y. Bian, X. Chen, L. Lu, P. Liang and Z. J. Ren, ACS Sustainable Chem. Eng., 2019, 7, 7844–7850 CrossRef CAS.
- A. Omosebi, X. Gao, J. Landon and K. Liu, ACS Appl. Mater. Interfaces, 2014, 6, 12640–12649 CrossRef CAS.
- W. Tang, D. He, C. Zhang and T. D. Waite, Water Res., 2017, 121, 302–310 CrossRef CAS.
- J. Pan, Y. Zheng, J. Ding, C. Gao, B. van der Bruggen and J. Shen, Ind. Eng. Chem. Res., 2018, 57, 7048–7053 CrossRef CAS.
- S. Mao, L. Chen, Y. Zhang, Z. Li, Z. Ni, Z. Sun and R. Zhao, J. Colloid Interface Sci., 2019, 544, 321–328 CrossRef CAS.
- P. M. Biesheuvel, 2015, arXiv, preprint, arXiv: 1509.06354, http://arxiv.org/abs/1509.06354.
- P. M. Biesheuvel and M. Z. Bazant, Phys. Rev. E, 2010, 81, 031502 CrossRef CAS.
- P. M. Biesheuvel, Y. Fu and M. Z. Bazant, Russ. J. Electrochem., 2012, 48, 580–592 CrossRef CAS.
- E. N. Guyes, T. Malka and M. E. M. Suss, Environ. Sci. Technol., 2019, 53, 8447–8454 CrossRef CAS.
- D. C. Grahame, J. Chem. Phys., 1953, 21, 1054–1060 CrossRef CAS.
- D. M. Mohilner, in Electroanalytical Chemistry, ed. A. J. Bard, Marcel Dekker, New York, 1966, pp. 241–409 Search PubMed.
- G. R. Iglesias, S. Ahualli, M. M. Fernández, M. L. Jiménez and A. V. Delgado, Environ. Sci.: Water Res. Technol., 2019, 5, 873–883 CAS.
- M. M. Fernández, S. Ahualli, G. R. Iglesias, F. González-Caballero, Á. V. Delgado and M. L. Jiménez, J. Colloid Interface Sci., 2015, 446, 307–316 CrossRef.
- M. L. Jiménez, S. Ahualli, P. Arenas-Guerrero, M. M. Fernández, G. Iglesias and A. V. Delgado, Phys. Chem. Chem. Phys., 2018, 20, 5012–5020 RSC.
- J. E. Dykstra, K. J. Keesman, P. M. Biesheuvel and A. van der Wal, Water Res., 2017, 119, 178–186 CrossRef CAS.
- P. M. Biesheuvel and M. van Soestbergen, J. Colloid Interface Sci., 2007, 316, 490–499 CrossRef CAS.
- C. Hou, P. Taboada-serrano, S. Yiacoumi and C. Tsouris, J. Chem. Phys., 2008, 129, 224703 CrossRef.
- W. Tang, P. Kovalsky, B. Cao and T. D. Waite, Water Res., 2016, 99, 112–121 CrossRef CAS.
- P. Nativ, O. Lahav and Y. Gendel, Desalination, 2018, 425, 123–129 CrossRef CAS.
- S. Porada, L. Borchardt, M. Oschatz, M. Bryjak, J. S. Atchison, K. J. Keesman, S. Kaskel, P. M. Biesheuvel and V. Presser, Energy Environ. Sci., 2013, 6, 3700–3712 RSC.
- E. N. Guyes, A. N. Shocron, A. Simanovski, P. M. Biesheuvel and M. E. Suss, Desalination, 2017, 415, 8–13 CAS.
- P. M. Biesheuvel, S. Porada, M. Levi and M. Z. Bazant, J. Solid State Electrochem., 2014, 18, 1365–1376 CrossRef CAS.
- P. M. Biesheuvel and J. E. Dykstra, Physics of Electrochemical Processes, 2020 Search PubMed.
- M. Tedesco, H. V. M. Hamelers and P. M. Biesheuvel, J. Membr. Sci., 2016, 510, 370–381 CrossRef CAS.
- P. Srimuk, J. Lee, Ö. Budak, J. Choi, M. Chen, G. Feng, C. Prehal and V. Presser, Langmuir, 2018, 34, 13132–13143 CrossRef CAS.
- B. Giera, N. Henson, E. M. Kober, M. S. Shell and T. M. Squires, Langmuir, 2015, 31, 3553–3562 CrossRef CAS.
- N. F. Carnahan and K. E. Starling, J. Chem. Phys., 1969, 51, 635–636 CrossRef CAS.
- K. West, T. Jacobsen and S. Atlung, J. Electrochem. Soc., 1982, 129, 1480–1485 CrossRef CAS.
- M. Tedesco, H. V. M. Hamelers and P. M. Biesheuvel, J. Membr. Sci., 2018, 565, 480–487 CrossRef CAS.
- E. Bakker, E. Pretsch and P. Bühlmann, Anal. Chem., 2000, 72, 1127–1133 CrossRef CAS.
- W. J. Peveler, M. Yazdani and V. M. Rotello, ACS Sens., 2016, 1, 1282–1285 CrossRef CAS.
- P. Jiang, H. Shao, L. Chen, J. Feng and Z. Liu, J. Mater. Chem. A, 2017, 5, 16740–16747 RSC.
- R. Epsztein, R. M. DuChanois, C. L. Ritt, A. Noy and M. Elimelech, Nat. Nanotechnol., 2020, 15, 426–436 CrossRef CAS.
- S. Hand and R. D. Cusick, Environ. Sci.: Water Res. Technol., 2020, 6, 925–934 CAS.
| This journal is © The Royal Society of Chemistry 2021 |