Open Access Article
Open Access ArticleMeasurements of the partitioning of nitric acid and sulfuric acid in aqueous/organic phase-separated systems†
Benjamin L.
Deming
 ab and
Paul J.
Ziemann
ab and
Paul J.
Ziemann
 *ab
*ab
aDepartment of Chemistry, University of Colorado, Boulder, Colorado 80309, USA. E-mail: paul.ziemann@colorado.edu; Fax: +1-303-492-1149
bCooperative Institute for Research in Environmental Sciences (CIRES), Boulder, Colorado 80309, USA
First published on 20th January 2021
Abstract
Partitioning of nitric acid and sulfuric acid between aqueous and organic phases may play a role in the chemistry of aqueous/organic phase-separated atmospheric aerosol particles, as well as other environmental systems. To assess the extent to which these acids partition to organic phases, organic compounds with O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios ranging from 0 to 0.75 were mixed with acidified aqueous phases. The organic phase was removed and its acid content quantified with a mass-based measurement. Up to 60% of the acid was observed to partition to the organic phase, present either entirely in the dissociated form, the undissociated form, or both depending on the organic phase. Values of partitioning coefficients, Ddiss and Dun, corresponding to partitioning of the dissociated and undissociated acid, were determined by fitting a simple partitioning model to the data. Values of Dun correlated well with the O
C ratios ranging from 0 to 0.75 were mixed with acidified aqueous phases. The organic phase was removed and its acid content quantified with a mass-based measurement. Up to 60% of the acid was observed to partition to the organic phase, present either entirely in the dissociated form, the undissociated form, or both depending on the organic phase. Values of partitioning coefficients, Ddiss and Dun, corresponding to partitioning of the dissociated and undissociated acid, were determined by fitting a simple partitioning model to the data. Values of Dun correlated well with the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of the organic component and to a lesser extent with the water content of the organic phase. The addition of ammonium sulfate led to an increase or decrease in partitioning of sulfuric acid to the organic phase, apparently depending on the balance between the resulting enhancement in the HSO4− concentration and the reduction in the water content of the organic phase. These results demonstrate that significant fractions of sulfuric and nitric acid can partition to the organic phase in phase-separated systems in undissociated and dissociated forms, and thus potentially participate in specific or general acid catalysis of organic reactions.
C ratio of the organic component and to a lesser extent with the water content of the organic phase. The addition of ammonium sulfate led to an increase or decrease in partitioning of sulfuric acid to the organic phase, apparently depending on the balance between the resulting enhancement in the HSO4− concentration and the reduction in the water content of the organic phase. These results demonstrate that significant fractions of sulfuric and nitric acid can partition to the organic phase in phase-separated systems in undissociated and dissociated forms, and thus potentially participate in specific or general acid catalysis of organic reactions.
Environmental significanceAqueous/organic phase-separated systems are common to the atmosphere in the form of aerosols, but are also found in other environments such as soils and the surface microlayer of oceans and lakes. In many of these systems inorganic acids are presumed to reside predominantly in the aqueous phase, but data on this partitioning are relatively rare. Measurements of the partitioning of nitric acid and sulfuric acid between an aqueous phase and a number of model organic phases covering a range of polarity demonstrate that significant quantities of acid can partition to the organic phase, to an extent that depends on the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of the organic phase, as well as other factors. These acids can then participate in organic reactions. C ratio of the organic phase, as well as other factors. These acids can then participate in organic reactions.
|
1. Introduction
Liquid–liquid phase-separated systems are prevalent in the environment, particularly in the atmosphere.1,2 Depending on their composition and the surrounding conditions, homogenous aerosol particles can undergo phase separation, typically forming a phase dominated by water, inorganic species, and water-soluble organic compounds and a relatively non-polar, organic-rich phase.3 This is not a rare occurrence; recent modeling work suggests that in the southeastern United States approximately 65% of the aerosol is phase separated.4 Whether aerosols are phase-separated can have dramatic impacts on properties such as cloud condensation nuclei activity,5 particle mass and growth,6,7 particle reactivity,8 and optical properties.9 Because phase-separation can so strongly influence aerosol properties, much effort has been dedicated to determining the factors that control or predict its occurrence.10–12 Compositionally, one of the best predictors of whether an aerosol will undergo liquid–liquid phase-separation is the ratio of oxygen to carbon atoms of the organic material (O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio).13 This value serves as a surrogate for polarity or oxidation state, as it is readily determined by mass spectrometry in laboratory and field measurements.14
C ratio).13 This value serves as a surrogate for polarity or oxidation state, as it is readily determined by mass spectrometry in laboratory and field measurements.14
In addition to having important physical properties, atmospheric aerosols also serve as sites for condensed-phase chemical reactions, essentially acting as suspended micro-reactors. Particle-phase reactions of organic compounds can be initiated by OH radicals, NO3 radicals, and O3, similar to atmospheric gas-phase oxidation, and they can occur via the coupling of functional groups (such as carbonyl, hydroxyl, hydroperoxy, and carboxyl) to form oligomers.15,16 These oligomerization reactions can modify particle chemical and physical properties and also contribute to particle growth by reducing effective compound vapor pressures, thus drawing more mass into the particle through subsequent gas-to-particle partitioning. Like many condensed-phase reactions, a number of those that can occur in aerosol particles are catalyzed by strong acids. For example, the dehydration of alcohols, the formation of hemiacetals and hemiketals, the formation of acetals and ketals, the conversion of hydroperoxides to carbonyls, and ester formation can be significantly faster in the presence of strong acid.16 Notably, many of these reactions produce water as a product, so that in an aqueous environment there will be a strong driving force against their occurrence. But in a phase-separated system, one in which organic reactants are concentrated in an organic phase where the water content is much reduced, such reactions may be highly favorable as long as sufficient acid partitions to the organic phase to drive catalysis.
The most common inorganic acids in the atmosphere are sulfuric acid, predominantly formed from oxidation of SO2, and nitric acid, formed from various reactions of nitrogen oxides.17 Though strong acids in aqueous solution, they may exist in either their dissociated or undissociated form in predominantly organic phases. This distinction is especially important for the catalysis of particle-phase reactions. When the solvent mixture is sufficiently polar to allow significant dissociation, the rate is likely controlled by the H+ concentration (referred to as specific acid catalysis). On the other hand, if the undissociated form of the acid dominates in the solution, the rate can instead be determined by the molecular form (general acid catalysis).18 Depending on the reaction and conditions, one pathway may be significantly faster than the other. It is therefore important to have some understanding of the extent to which sulfuric and nitric acid partition to organic phases, as well as the forms in which they reside.
The purpose of this study was to investigate the partitioning of sulfuric and nitric acid in model organic/aqueous phase-separated systems that were chosen to act as proxies for phase-separated aerosol. Understanding the partitioning behavior of these acids in these simple model systems can help determine the extent to which the processes discussed above are relevant to real environmental systems.
2. Materials and methods
2.1 Materials
Chemicals with purities/grade and suppliers were as follows: HPLC grade water, ACS grade nitric acid (69 ± 1 w/w% in water, <5 ppm impurities), and ACS grade hexane (a mixture of isomers, 98.5%) from Macron Fine Chemicals; ACS Plus grade sulfuric acid (96.5 ± 1.5 w/w% in water, <3 ppm impurities), ACS grade ethyl acetate (99.9%), and ammonium sulfate (99.5%) from Fisher Scientific; 2-hexanone (98%) from J&K Scientific; ACS reagent grade 2-butanone (>99.0%) and anhydrous propylene carbonate (99.7%) from Sigma-Aldrich; ammonium bisulfate (99.9%) from Alfa Aesar; and anhydrous ammonia and ultra-high purity (UHP) nitrogen from Airgas. Chemicals were used as received, with no further purification.2.2 Acid partitioning measurements
The partitioning of nitric acid and sulfuric acid in organic/aqueous phase-separated systems was investigated using the shake-flask method.19,20 The procedures used in this work were validated in a number of experiments noted below and described in detail in the ESI along with Fig. S1–S4.† Aqueous phases consisted of either pure water or 30 w/w% = 2.27 M (mol L−1) ammonium sulfate solutions that are typical for the atmosphere.21 Organic phases were chosen to act as proxies for organic aerosol, covering a range of O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios and therefore polarities. To be compatible with the partitioning measurements they also needed to be non-reactive towards both strong acid and ammonia for the concentrations and exposure times used here. Hexane, 2-hexanone, 2-butanone, ethyl acetate, and propylene carbonate were thus used as organic phases. Other relevant organic compounds tested, notably carboxylic acids, alcohols, and aldehydes, were found to react with the ammonia and/or strong acid, and therefore could not be used. The phases and relevant properties are listed in Table 1, and the structures of the organic components are given in ESI.†
C ratios and therefore polarities. To be compatible with the partitioning measurements they also needed to be non-reactive towards both strong acid and ammonia for the concentrations and exposure times used here. Hexane, 2-hexanone, 2-butanone, ethyl acetate, and propylene carbonate were thus used as organic phases. Other relevant organic compounds tested, notably carboxylic acids, alcohols, and aldehydes, were found to react with the ammonia and/or strong acid, and therefore could not be used. The phases and relevant properties are listed in Table 1, and the structures of the organic components are given in ESI.†
| Organic or aqueous phase | O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio C ratio |
Molecular weight (g mol−1) | Organic phase water (vol%) | Density (g mL−1) |
|---|---|---|---|---|
| Hexane | 0.00 | 86.2 | 0.01 | 0.66 |
| 2-Hexanone | 0.17 | 100.2 | 2 | 0.81 |
| 2-Butanone | 0.25 | 72.1 | 1 | 0.81 |
| Ethyl acetate | 0.50 | 88.1 | 3 | 0.90 |
| Propylene carbonate | 0.75 | 102.1 | 8 | 1.21 |
| Water | — | 18.0 | — | 1.00 |
| Aqueous ammonium sulfate (30%, w/w) | — | — | — | 1.17 |
The aqueous phases were acidified to create solutions between approximately 0 and 1 M, not considering any reaction with ammonium sulfate. Aliquots (typically 1.5 mL each) of organic phase and acidified aqueous phase were added to test tubes and then mixed by vortexing for approximately 30 s, a time that is shown in the ESI† to be sufficient to establish partitioning equilibrium. The test tubes were then centrifuged and 1 mL of organic phase was transferred to a vial pre-weighed on a Mettler Toledo XS3DU Microbalance. Because the addition of acid or ammonium sulfate could change the overall volume of each phase, the total aqueous and organic volumes after mixing were measured using a syringe that is accurate to approximately 0.05 mL. The sampled organic solution was exposed to a slow stream of ammonia (∼600 cm3 min−1) for ∼15 s, which is shown in ESI† to be sufficient to convert any nitric or sulfuric acid to the corresponding ammonium salt. This was often accompanied by the visible crystallization of these salts. Since strong acids were used, experiments were performed wearing gloves, a lab coat, and goggles. Samples were exposed to ammonia in a fume hood and remained within one for at least 10 min to allow for any residual vapor to dissipate.
With the exception of propylene carbonate, the organic phases were all sufficiently volatile to be removed via evaporation in a hood under a steady stream of nitrogen. Since ammonium nitrate might also evaporate during this process (it is much more volatile than ammonium sulfate), experiments described in ESI† were conducted to verify that under the conditions used here no ammonium nitrate was lost by evaporation. The vials, then containing only ammonium salt, assumed to be either ammonium sulfate or ammonium nitrate, were again weighed on the microbalance. The balance is accurate to ±0.5 μg, corresponding to minimum detectable organic-phase concentrations of 6.3 μM for nitric acid and 3.8 μM for sulfuric acid. Blanks were measured for all systems by conducting identical experiments but without adding acid, and in all cases yielded negligible mass after the organic phase was dried. Samples containing propylene carbonate were dried to a constant mass with nitrogen in a hood in an attempt to remove any organic-phase water, and then weighed. The mass of propylene carbonate was corrected for by treating the samples containing no added acid as a blank. This approach worked well for nitric acid but resulted in nonphysical results (blank mass higher than sample mass) for sulfuric acid, apparently because some residual water could not be fully removed by drying when ammonium sulfate was present. The results for experiments with propylene carbonate have larger uncertainties due to these additional complications.
We note that although the assumption that the mass of salt measured in all these experiments corresponded to either ammonium nitrate (NH4NO3) or ammonium sulfate ((NH4)2SO4) is valid for the nitric acid experiments, since ammonium nitrate is the only possible salt, in the sulfuric acid experiments ammonium bisulfate (NH4HSO4), letovicite ((NH4)3H(SO4)2), or ammonium sulfate hydrate ((NH4)2SO4·H2O) might also have formed. If the salt was one of these three instead of ammonium sulfate, then the reported concentration of sulfuric acid would be in error by −15%, −7%, and 12%, respectively. Considering the other sources of uncertainty in these measurements, these alternate forms could be present without significantly affecting the results presented here. Nonetheless, in an attempt to verify that the salt formed was ammonium sulfate, the behavior of a phase-separated salt sample and ammonium sulfate and ammonium bisulfate standards were compared when heated in an oven at 230 °C. Although the thermal decomposition of ammonium sulfate salts is complicated,22 it is expected that ammonium sulfate would be stable at this temperature while ammonium bisulfate, letovicite, and ammonium sulfate hydrate would not. Based on the results of these experiments, which are described in ESI,† it appears that the phase-separated salt sample was ammonium sulfate.
The acidity of the organic phases in these systems was also measured over a larger concentration range using pH strips (Sigma Chemical Company). Aqueous phases containing between 10−6 and 10 M of either HNO3 or H2SO4 were prepared and then 2 mL of each aqueous phase and 2 mL of either hexane, 2-butanone, ethyl acetate, and propylene carbonate were added to a test tube and mixed by vortexing for 30 s. The organic layer was then removed using a syringe and a pH strip was submerged in the solvent. The four dye squares were compared visually to the provided key and matched to the closest pH value.
2.3 Data analysis
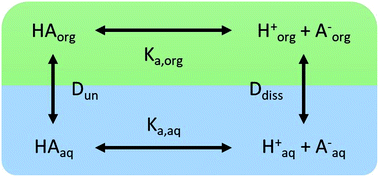
We consider four potential states of the strong acids, as shown in Fig. 1: undissociated acid (HA = HNO3 or H2SO4) and dissociated acid (H+ and A− = NO3− or HSO4−) in both the aqueous and organic phases. In the figure and throughout the text, the subscript “org” refers to a species in the organic phase, while the subscript “aq” refers to one in the aqueous phase. Note that this framework only considers the first dissociation of sulfuric acid, and that the consequences of this assumption will be discussed in detail below.The dissociation of these acids in the aqueous phase is well understood and the corresponding values of the acid dissociation constants for the aqueous and organic phases, Ka,aq and Ka,org, are defined using the species concentrations as
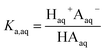 | (1) |
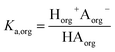 | (2) |
Concentrations are designated in units of moles of species per liter of the noted phase (either organic or aqueous). The partitioning of undissociated and dissociated acid between the organic and aqueous phases is quantified by the distribution coefficients, Dun and Ddiss, defined as
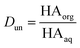 | (3) |
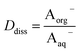 | (4) |
Small distribution coefficients indicate that acid (in either the dissociated or undissociated form) prefers the aqueous phase over the organic phase. Eqn (1)–(4) and the equations Haq+ = Aaq− and Horg+ = Aorg− can also be combined to obtain
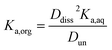 | (5) |
| Torg = HAorg + Aorg− | (6) |
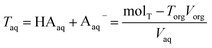 | (7) |
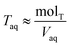 . Lastly, we define the ratio of total acid in the organic phase to the total in the aqueous phase, R, as
. Lastly, we define the ratio of total acid in the organic phase to the total in the aqueous phase, R, as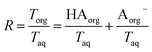 | (8) |
Because nitric and sulfuric acid are strong acids, they are almost entirely dissociated in the aqueous phase. Using values of Ka,aq of 40 M for nitric acid and 104 M (a lower limit) for sulfuric acid,23 at most 3% and 0.01% of each should be in the undissociated form in the aqueous phase in these experiments. Assuming that Taq ≈ Aaq− = Haq+ and that 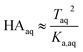 , eqn (8) becomes
, eqn (8) becomes
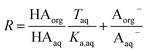 | (9) |
Substituting in the equations defining Dun and Ddiss, this becomes
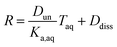 | (10) |
Plotting values of R as a function of Taq should therefore result in straight lines. The slope of the line corresponds to 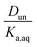 and the y-intercept is equal to Ddiss.
and the y-intercept is equal to Ddiss.
It is worth considering some limiting cases of this relationship in order to orient one to the figures that follow. As noted above, the values of Ka,aq for nitric and sulfuric acid are 40 and >104, so that these acids are predominantly dissociated in water. If Dun is on the order of 1 or less, indicating that undissociated nitric and sulfuric favor the aqueous phase over the organic phase, then 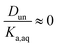 . Eqn (10) will therefore reduce to R = Ddiss and the plots will appear as flat, straight lines with y-intercepts equal to Ddiss. In this case, the fraction of total acid in the organic phase is constant and does not depend on how much acid is present. Furthermore, since
. Eqn (10) will therefore reduce to R = Ddiss and the plots will appear as flat, straight lines with y-intercepts equal to Ddiss. In this case, the fraction of total acid in the organic phase is constant and does not depend on how much acid is present. Furthermore, since
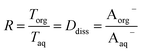 | (11) |
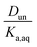 and a y-intercept ≈ 0. In cases when significant fractions of the acid in the organic phase are present in the undissociated and dissociated forms, then the plot will have a non-zero slope and y-intercept. We note here that the inclusion of the second dissociation of sulfuric acid has a slight effect on this framework, as shown by derivations in the ESI† that take this dissociation into account. Under the assumption that SO42− does not significantly partition to the organic phase (discussed in more detail in Section 3.4 and the ESI†), these considerations result in correction factors of 1.11 and 1.46 applied to the derived values of Dun and Ddiss, respectively.
and a y-intercept ≈ 0. In cases when significant fractions of the acid in the organic phase are present in the undissociated and dissociated forms, then the plot will have a non-zero slope and y-intercept. We note here that the inclusion of the second dissociation of sulfuric acid has a slight effect on this framework, as shown by derivations in the ESI† that take this dissociation into account. Under the assumption that SO42− does not significantly partition to the organic phase (discussed in more detail in Section 3.4 and the ESI†), these considerations result in correction factors of 1.11 and 1.46 applied to the derived values of Dun and Ddiss, respectively.
2.4 Liquid–liquid equilibrium model of acid partitioning
A number of thermodynamic models can be used to predict the partitioning of inorganic acids in liquid–liquid phase-separated systems. In this work, the algorithm described in Zuend and Seinfeld (2013)24 was used to predict the composition of each phase given the composition of the system as a whole. Briefly, the algorithm generates a series of initial guesses based on the idea that one phase will contain mostly water and inorganic species, while the other will consist mostly of organic compounds. The activity coefficients for all species are then calculated using the group-contribution model AIOMFAC (Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients) described in Zuend et al. (2008, 2011).25,26 At equilibrium, the activity of each species should be the same in each phase, so the activity coefficients can be used to adjust the modeled phase-separation. Activity coefficients are then calculated for the adjusted system, allowing the initial guesses to be iteratively improved. Importantly, the model allows for inorganic species to exist in the predominantly organic phase, although it considers them to be totally dissociated (with the exception of the bisulfate ion, for which the partial dissociation is solved explicitly using ion activities and known equilibrium constants).AIOMFAC is available for download (https://github.com/andizuend/AIOMFAC), and here the liquid–liquid equilibrium model was built on top of it using Zuend and Seinfeld (2013)24 as a guide. To ensure that this version of the model performs as expected, Fig. 5d in Zuend and Seinfeld (2013)24 was captured using the “IgorThief” tool in Igor Pro and compared with the corresponding model outputs. This figure was chosen because it most closely resembles the kinds of systems and results the model was used for in this work. The comparison, shown in Fig. S5,† indicates that this version of the model adequately reproduces those results. In addition to using AIOMFAC for the partitioning modeling, it also was used to calculate the equilibrium concentrations of species in aqueous sulfuric acid and sulfuric acid/ammonium sulfate solutions.
3. Results & discussion
3.1 Partitioning of acid between aqueous and organic phases
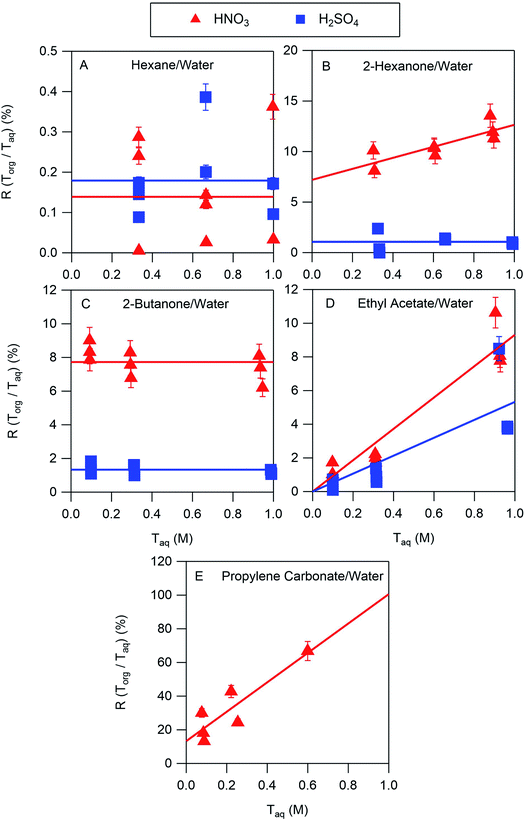
The results of the nitric and sulfuric acid partitioning measurements are shown in Fig. 2 for phase-separated aqueous/organic systems containing water and either hexane, 2-hexanone, 2-butanone, ethyl acetate, or propylene carbonate. From Table 1, the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios of these organic components are 0.0, 0.17, 0.25, 0.50, and 0.75, respectively, indicating that the polarity increases in the order shown. This trend is also roughly reflected in the vol% water in these components of 0.01, 2, 1, 3, and 8, respectively. One can expect that the addition of water to the organic phase will increase the polarity of the resulting solution, thus enhancing the extent to which both the undissociated and dissociated forms of the acid can be solvated and increasing partitioning of both species to the organic phase. In the figures, values of R(Torg/Taq) are plotted against Taq, as suggested by the discussion above and eqn (10). Least-squares lines were first fit to the data, and then because of the significant scatter, in cases where the uncertainty in the slope was greater than the value the slope was set to zero. And in one case where the y-intercept was slightly negative, and thus nonphysical, that value was also set to zero. Visual inspection of the resulting lines indicates that this approach is reasonable, and it allows the profiles to be classified according to zero or positive slope and zero or positive y-intercept, thus simplifying the data interpretation and comparisons between systems.
C ratios of these organic components are 0.0, 0.17, 0.25, 0.50, and 0.75, respectively, indicating that the polarity increases in the order shown. This trend is also roughly reflected in the vol% water in these components of 0.01, 2, 1, 3, and 8, respectively. One can expect that the addition of water to the organic phase will increase the polarity of the resulting solution, thus enhancing the extent to which both the undissociated and dissociated forms of the acid can be solvated and increasing partitioning of both species to the organic phase. In the figures, values of R(Torg/Taq) are plotted against Taq, as suggested by the discussion above and eqn (10). Least-squares lines were first fit to the data, and then because of the significant scatter, in cases where the uncertainty in the slope was greater than the value the slope was set to zero. And in one case where the y-intercept was slightly negative, and thus nonphysical, that value was also set to zero. Visual inspection of the resulting lines indicates that this approach is reasonable, and it allows the profiles to be classified according to zero or positive slope and zero or positive y-intercept, thus simplifying the data interpretation and comparisons between systems.
The ratio Torg/Taq is approximately 0.001 for hexane; 0.01–0.1 for 2-hexanone, 2-butanone, and ethyl acetate; and 0.1–1 for propylene carbonate. These values correlate better with the vol% water for each group of 0.01, 1–3, and 8 than with the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios of 0.0, 0.17–0.5, and 0.75, although in either case there is clear evidence that partitioning increases with increasing polarity of the organic phase. The results also indicate that nitric acid partitions more strongly to the organic phase than sulfuric acid. As discussed in Section 2.3, the presence of three types of lines: (1) zero slope and positive y-intercept, (2) positive slope and zero y-intercept, and (3) positive slope and positive y-intercept are indicative of acids being fully dissociated, undissociated, and partially dissociated, respectively, in the organic phase. In addition, the y-intercept gives the value of the Ddiss, the distribution coefficient for NO3− or HSO4−, and the slope gives the value of
C ratios of 0.0, 0.17–0.5, and 0.75, although in either case there is clear evidence that partitioning increases with increasing polarity of the organic phase. The results also indicate that nitric acid partitions more strongly to the organic phase than sulfuric acid. As discussed in Section 2.3, the presence of three types of lines: (1) zero slope and positive y-intercept, (2) positive slope and zero y-intercept, and (3) positive slope and positive y-intercept are indicative of acids being fully dissociated, undissociated, and partially dissociated, respectively, in the organic phase. In addition, the y-intercept gives the value of the Ddiss, the distribution coefficient for NO3− or HSO4−, and the slope gives the value of 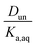 , the ratio of the distribution coefficient for HNO3 or H2SO4 divided by its acid dissociation constant in water. Values of Ddiss and Dun determined from the lines are given in Table 2, although for lines with zero slope the value of Dun cannot be determined. The uncertainties were taken from the fits to the data as output by Igor Pro. Values of Ddiss and Dun range from approximately 0.001–0.1 and 2–60, respectively, indicating that larger fractions of undissociated acid partition to the organic phase than dissociated acid. It should be remembered, however, that for values of Ka,aq of 40 M for nitric acid and 104 M for sulfuric acid (Levanov et al., 2018)23 at most about 3% and 0.01% of these acids should be undissociated in the aqueous phase. As a result, except in the case of ethyl acetate, a significant fraction of the acid present in the organic phase is always dissociated. When both Ddiss and Dun are known, Ka,org can be calculated using eqn (5). This is only possible with this data set for nitric acid in 2-hexanone and propylene carbonate, resulting in values of 0.11 M and 0.022 M, respectively. Unsurprisingly, the dissociation of nitric acid is therefore significantly reduced in predominantly organic phases as compared to the aqueous phase. Although the values of Ddiss and Dun indicate that in some systems the undissociated form of the acid dominates, in others the dissociated form does, and in still others both forms are significantly present in the organic phase, one could expect that for the complex mixture of oxidized organic compounds present in SOA, that significant amounts of both undissociated and dissociated forms of nitric and sulfuric acid should be present. This should allow for the occurrence of both specific and general acid catalysis in the organic phase, even though reactions in the aqueous phase are probably limited to specific acid catalysis.
, the ratio of the distribution coefficient for HNO3 or H2SO4 divided by its acid dissociation constant in water. Values of Ddiss and Dun determined from the lines are given in Table 2, although for lines with zero slope the value of Dun cannot be determined. The uncertainties were taken from the fits to the data as output by Igor Pro. Values of Ddiss and Dun range from approximately 0.001–0.1 and 2–60, respectively, indicating that larger fractions of undissociated acid partition to the organic phase than dissociated acid. It should be remembered, however, that for values of Ka,aq of 40 M for nitric acid and 104 M for sulfuric acid (Levanov et al., 2018)23 at most about 3% and 0.01% of these acids should be undissociated in the aqueous phase. As a result, except in the case of ethyl acetate, a significant fraction of the acid present in the organic phase is always dissociated. When both Ddiss and Dun are known, Ka,org can be calculated using eqn (5). This is only possible with this data set for nitric acid in 2-hexanone and propylene carbonate, resulting in values of 0.11 M and 0.022 M, respectively. Unsurprisingly, the dissociation of nitric acid is therefore significantly reduced in predominantly organic phases as compared to the aqueous phase. Although the values of Ddiss and Dun indicate that in some systems the undissociated form of the acid dominates, in others the dissociated form does, and in still others both forms are significantly present in the organic phase, one could expect that for the complex mixture of oxidized organic compounds present in SOA, that significant amounts of both undissociated and dissociated forms of nitric and sulfuric acid should be present. This should allow for the occurrence of both specific and general acid catalysis in the organic phase, even though reactions in the aqueous phase are probably limited to specific acid catalysis.
| Organic phase | HNO3 | H2SO4 | ||
|---|---|---|---|---|
| D diss | D un | D diss | D un | |
| Hexane | 0.0014 ± 0.0004 | — | 0.0026 ± 0.0004 | — |
| 2-Hexanone | 0.072 ± 0.01 | 1.9 ± 0.6 | 0.016 ± 0.003 | — |
| 2-Butanone | 0.077 ± 0.003 | — | 0.019 ± 0.001 | — |
| Ethyl acetate | 0 | 3.3 ± 0.2 | 0 | 59 ± 10 |
| Propylene carbonate | 0.13 ± 0.06 | 31 ± 8 | — | — |
The pH of the organic phases measured after equilibration with a series of aqueous HNO3 or H2SO4 solutions ranging in concentration from 10−6 M to 10 M are shown in Fig. 3. It was assumed that the H+ activity measured by the pH strips was equal to the H+ concentration. This assumption ignores any activity effects, which are likely negligible compared to the uncertainty of the pH measurement (roughly one or two pH units), but may be important in extreme cases. These organic phase H+ concentrations are compared with those estimated using Ddiss values derived above and shown by the lines in Fig. 3. Note that not all systems had measurable Ddiss values and so there is not a line for each solvent. Although there is a fair amount of scatter, the H+ concentrations obtained from pH measurements largely line up with those obtained using Ddiss values. These results suggest that the mass-based measurements discussed above extend over a wider concentration range than measured. The notable exception is hexane, which is either overestimated by the mass-based measurements (probably because of the small amount of acid that partitioned to the organic phase) or underestimated by the pH measurements (perhaps due to activity effects or a relative lack of water in the organic phase).
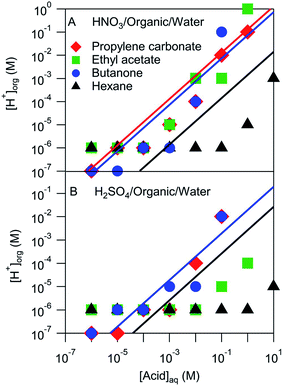 | ||
| Fig. 3 Measured and modeled organic phase H+ concentrations. Markers represent pH strip measurements and lines correspond to values derived from measured Ddiss values. | ||
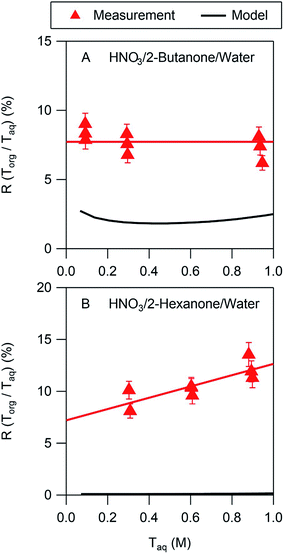
3.2 Comparison of acid partitioning measurements and liquid–liquid equilibrium model results
In all cases the liquid–liquid equilibrium model underpredicts the amount of acid partitioning to the organic phase. This is perhaps not surprising, however, since the model does not consider undissociated acid, which is a significant fraction of the organic phase acid in many of the systems studied here. The model performs best for nitric acid in 2-butanone/water, as shown in Fig. 4A. The measurements indicate that the acid in the organic phase is fully dissociated, with a value of Ddiss of 0.077 (Table 2). The model, on the other hand, predicts a value of Ddiss ≈ 0.02, about a factor of 4 lower than measured. As noted above, the model assumes that the acid is fully dissociated in the organic phase, leading to a relatively flat curve that for this case is consistent with the measurements. In contrast, whereas the measured value of Ddiss is 0.072 for nitric acid in 2-hexanone/water, the model predicts a value of 0.001. Furthermore, the measurements show a significant slope for the line of 5.4, indicative of undissociated acid, which the model cannot capture since it assumes nitric acid is always fully dissociated. The model predictions for all the other systems are similar to those shown in Fig. 4B, thus always underpredicting values of Ddiss. Because undissociated acid is not considered, organic-phase acid in the ethyl acetate/water and propylene carbonate/water systems are similarly underpredicted. These results suggest that the presence of undissociated acid in predominantly organic phases should be included in models to more accurately describe the partitioning, although more partitioning measurements are likely needed before such inclusion is possible.3.3 Correlation of partitioning parameters with organic phase properties
Environmental phase-separated systems are highly complex and can contain hundreds of individual components. Furthermore, they also typically contain many more (and more exotic) functional groups than the alkyl, carbonyl, and ester groups studied in this work. Relationships between general organic phase properties and partitioning parameters like the ones derived here are therefore highly desirable. The measured values of Dun for HNO3 are plotted in Fig. 5 as a function of the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of the organic phase. To supplement the measurements made here, relevant data sets from Stephen and Stephen (1963)27 were also fit to eqn (10) (Fig. S6†). The values of Dun (including measured and literature-derived values) were found to be approximately linear with respect to the O
C ratio of the organic phase. To supplement the measurements made here, relevant data sets from Stephen and Stephen (1963)27 were also fit to eqn (10) (Fig. S6†). The values of Dun (including measured and literature-derived values) were found to be approximately linear with respect to the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of the organic phase, following the equation
C ratio of the organic phase, following the equationDun = 42 × (O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C) − 6 C) − 6 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C value. Also included in the plot is a value of 8.2 calculated from the Henry's law coefficients of 1.6 × 105 M atm−1 for partitioning of gaseous HNO3 to water28 and 3.7 × 104 M atm−1 for partitioning to SOA formed from the oxidation of n-pentadecane by OH radicals.29 This SOA contained carbonyl, hydroxyl, carboxyl, ester, hydroperoxy, and peroxide groups and had an average molecular weight of 260 g mol−1 and an O
C value. Also included in the plot is a value of 8.2 calculated from the Henry's law coefficients of 1.6 × 105 M atm−1 for partitioning of gaseous HNO3 to water28 and 3.7 × 104 M atm−1 for partitioning to SOA formed from the oxidation of n-pentadecane by OH radicals.29 This SOA contained carbonyl, hydroxyl, carboxyl, ester, hydroperoxy, and peroxide groups and had an average molecular weight of 260 g mol−1 and an O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of 0.19.30 This data point, shown as a green diamond, lies slightly above the fitted line in Fig. 5, but still suggests that the values derived in this work are relevant to real aerosol systems despite the differences in functionality and molecular weight. Unlike the case for Dun, values of Ddiss do not correlate with O
C ratio of 0.19.30 This data point, shown as a green diamond, lies slightly above the fitted line in Fig. 5, but still suggests that the values derived in this work are relevant to real aerosol systems despite the differences in functionality and molecular weight. Unlike the case for Dun, values of Ddiss do not correlate with O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios, and although there is a general increase with increasing vol% water, there is too much scatter for this value to be a reliable predictor of this parameter (plots not shown).
C ratios, and although there is a general increase with increasing vol% water, there is too much scatter for this value to be a reliable predictor of this parameter (plots not shown).
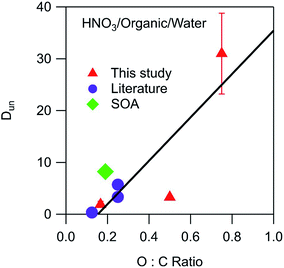 | ||
Fig. 5 Relationship between Dun and the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of the organic phase for partitioning of HNO3. Values correspond to the following organic phase and O C ratio of the organic phase for partitioning of HNO3. Values correspond to the following organic phase and O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios: dibutyl ether (0.13),27 2-hexanone (0.17), SOA (0.19),29,30 ethyl ether (0.25),27 diethylene glycol dibutyl ether (0.25),27 ethyl acetate (0.50), and propylene carbonate (0.75). The error bars correspond to ± one standard deviation as determined from the linear fits used to calculate Dun, and in most cases fall within the symbol. The line is a linear least-squares fit to the data. C ratios: dibutyl ether (0.13),27 2-hexanone (0.17), SOA (0.19),29,30 ethyl ether (0.25),27 diethylene glycol dibutyl ether (0.25),27 ethyl acetate (0.50), and propylene carbonate (0.75). The error bars correspond to ± one standard deviation as determined from the linear fits used to calculate Dun, and in most cases fall within the symbol. The line is a linear least-squares fit to the data. | ||
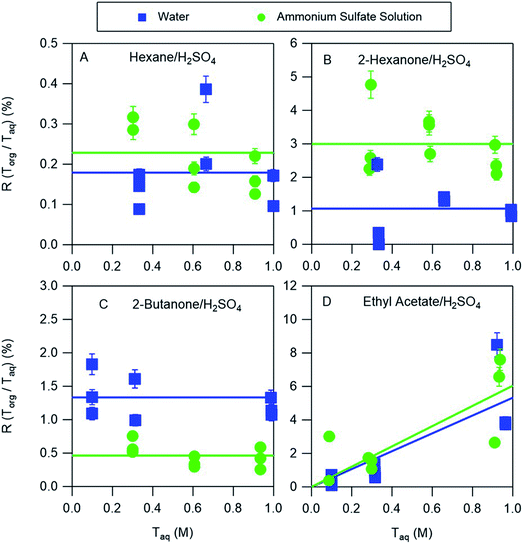
3.4 Influence of ammonium sulfate on acid partitioning
The partitioning of nitric acid and sulfuric acid is likely to be perturbed by the presence of salts. Ammonium sulfate is prevalent in atmospheric aerosol and so experiments were also conducted to investigate the potential effects of this salt on acid partitioning. In the aqueous phase, the combination of ammonium sulfate and sulfuric acid produces H+, HSO4−, SO42−, and NH4+. Similarly, ammonium sulfate and nitric acid produce H+, HSO4−, SO42−, NH4+, and NO3−. In the nitric acid systems, it is therefore possible for both ammonium nitrate and ammonium sulfate to precipitate when ammonia is bubbled in the organic phase, complicating the interpretation of those measurements. We therefore discuss only the partitioning of sulfuric acid between organic phases and either water or ammonium sulfate aqueous phases. The equilibria between these species in aqueous solutions is well understood and may be accurately predicted using thermodynamic models such as AIOMFAC. For example, AIOMFAC calculations indicate that in a solution of ammonium sulfate in water >99% of the sulfate is present as SO42−. Because of the difficulty of solvating this divalent ion in the organic phase little partitioning is expected, consistent with aqueous ammonium sulfate partitioning measurements that showed no measurable salt in any of the organic phases. When ammonium sulfate is added to an aqueous sulfuric acid solution the reaction of SO42− with H+ should increase the concentration of HSO4−, with AIOMFAC calculations indicating that the concentrations of HSO4− in 0.3 M and 1.0 M aqueous solutions of sulfuric acid (the approximate range covered in these experiments) increase from 0.23 and 0.75 to 0.43 and 1.36, respectively, when 30 w/w% = 2.27 M ammonium sulfate is added, typical of the concentration in atmospheric aerosol particles.21 As a result, additional HSO4− would be expected to partition to the organic phase. The results of the partitioning measurements shown in Fig. 6, and the distribution coefficients obtained from the fitted lines are given in Table 3. For hexane, ethyl acetate, and 2-hexanone there are enhancements in partitioning of sulfuric acid to the organic phase compared to the ammonium sulfate-free measurements. They are relatively small for hexane and ethyl acetate but about a factor of three for 2-hexanone, and might be explained by the increase in the aqueous phase concentration of HSO4−. Conversely, partitioning decreases for 2-butanone, and might be attributed to reductions in the vol% water in the organic phases when ammonium sulfate is added, which was shown above to generally correlate with partitioning. In particular, as the aqueous phase becomes saturated with ammonium sulfate less water will partition to the organic phase, and so less HSO4− will partition. This effect can thus compensate for or even overcome the enhanced partitioning due to the increase in the aqueous phase concentration of HSO4−. Notably, the only organic phase for which acid partitioning decreases with the addition of ammonium sulfate is 2-butanone, which has the highest vol% water. Despite some differences, it is notable that distribution coefficients derived from systems using pure water are within a factor of three of those obtained for nearly saturated ammonium sulfate solutions. By using a thermodynamic model like AIOMFAC to understand the aqueous phase equilibria, the values derived in this work may therefore be used to predict the amount and forms of acids in the organic phases of even relatively salty aerosols.| Organic phase | Water | Ammonium sulfate solution | ||
|---|---|---|---|---|
| D diss | D un | D diss | D un | |
| Hexane | 0.0026 ± 0.0004 | — | 0.0034 ± 0.0004 | — |
| 2-Hexanone | 0.016 ± 0.003 | — | 0.0439 ± 0.0044 | — |
| 2-Butanone | 0.019 ± 0.001 | — | 0.0067 ± 0.0007 | — |
| Ethyl acetate | 0 | 59 ± 10 | — | 68 ± 11 |
4. Conclusions
This study sought to determine the extent to which strong acids might be present in the organic phase of environmentally important aqueous/organic phase-separated systems, and thus potentially participate in organic chemical reactions. By using a series of model organic phases with a range of polarity and a simple gravimetric analytical method it was shown that nitric and sulfuric acid, the dominant strong acids in atmospheric aerosol particles, can undergo significant partitioning to an organic phase. The extent of this partitioning tends to be greater for nitric than sulfuric acid, to increase with increasing O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio and vol% water of the organic phase, and to be influenced positively or negatively by the presence of ammonium sulfate, a dominant salt in atmospheric aerosol. Since studies were conducted with organic components having O
C ratio and vol% water of the organic phase, and to be influenced positively or negatively by the presence of ammonium sulfate, a dominant salt in atmospheric aerosol. Since studies were conducted with organic components having O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios ranging from 0 to 0.75, the results should be applicable to the atmosphere, where the O
C ratios ranging from 0 to 0.75, the results should be applicable to the atmosphere, where the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of organic aerosol typically ranges from 0.2 to 0.8.14 By fitting the data to a simple partitioning model, values of distribution coefficients, Ddiss and Dun, for partitioning of dissociated and undissociated acid to the organic phase were obtained, providing quantitative information on the amounts and form of partitioned acids. The results of this study suggest that partitioning of inorganic acids to predominantly organic phases can be significant and warrants further study. It would therefore be useful if future studies could expand on the limited selection of single organic phases employed here to include more complex mixtures and compounds with other functional groups, which might be possible by using more dilute acid solutions (which would be less likely to catalyze reactions of functional groups) and more sensitive acid detection methods such as ion chromatography or electrochemical measurements. Furthermore, it is an open question how well investigations of acidity and partitioning of the bulk solutions studied here apply to aerosol particles. For example, studies by Wei et al.31 suggest that pH gradients exist within particles, with protons accumulating at the surface and correspondingly more basic conditions towards the center of the particle. But on the other hand, studies by Dallemagne et al.32 showed that the pH of an organic shell in a phase-separated particle essentially matches that in the corresponding bulk solution. Comparison of the measurements made here with predictions of a liquid–liquid equilibrium model showed that the model seriously underpredicted the extent of acid partitioning to the organic phase, which was due at least in part because the model only considers the dissociated acid. The inclusion of undissociated acid should improve predictions, though more partitioning measurements are likely needed before this can be implemented. Depending on the acid and the particular model organic phase, these acids can exist primarily in either the dissociated or undissociated form, or both. One could then expect that for the complex mixture of oxidized organic compounds present in atmospheric aerosol that significant amounts of both forms of nitric and sulfuric acid should be present, allowing for the occurrence of both specific (H+) and general (HA) acid catalysis in the organic phase, even though reactions in the aqueous phase are probably limited to specific acid catalysis.
C ratio of organic aerosol typically ranges from 0.2 to 0.8.14 By fitting the data to a simple partitioning model, values of distribution coefficients, Ddiss and Dun, for partitioning of dissociated and undissociated acid to the organic phase were obtained, providing quantitative information on the amounts and form of partitioned acids. The results of this study suggest that partitioning of inorganic acids to predominantly organic phases can be significant and warrants further study. It would therefore be useful if future studies could expand on the limited selection of single organic phases employed here to include more complex mixtures and compounds with other functional groups, which might be possible by using more dilute acid solutions (which would be less likely to catalyze reactions of functional groups) and more sensitive acid detection methods such as ion chromatography or electrochemical measurements. Furthermore, it is an open question how well investigations of acidity and partitioning of the bulk solutions studied here apply to aerosol particles. For example, studies by Wei et al.31 suggest that pH gradients exist within particles, with protons accumulating at the surface and correspondingly more basic conditions towards the center of the particle. But on the other hand, studies by Dallemagne et al.32 showed that the pH of an organic shell in a phase-separated particle essentially matches that in the corresponding bulk solution. Comparison of the measurements made here with predictions of a liquid–liquid equilibrium model showed that the model seriously underpredicted the extent of acid partitioning to the organic phase, which was due at least in part because the model only considers the dissociated acid. The inclusion of undissociated acid should improve predictions, though more partitioning measurements are likely needed before this can be implemented. Depending on the acid and the particular model organic phase, these acids can exist primarily in either the dissociated or undissociated form, or both. One could then expect that for the complex mixture of oxidized organic compounds present in atmospheric aerosol that significant amounts of both forms of nitric and sulfuric acid should be present, allowing for the occurrence of both specific (H+) and general (HA) acid catalysis in the organic phase, even though reactions in the aqueous phase are probably limited to specific acid catalysis.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This material is based on work supported by the Army Research Office under Grant W911NF-17-1-0607. We also thank Andreas Zuend for helpful comments.References
- M. A. Freedman, Liquid-Liquid Phase Separation in Supermicrometer and Submicrometer Aerosol Particles, Acc. Chem. Res., 2020, 53, 1102–1110 CrossRef CAS.
- Y. Zhang, Y. Chen, Z. Lei, N. E. Olson, M. Riva, A. R. Koss, Z. Zhang, A. Gold, J. T. Jayne, D. R. Worsnop, T. B. Onasch, J. H. Kroll, B. J. Turpin, A. P. Ault and J. D. Surratt, Joint Impacts of Acidity and Viscosity on the Formation of Secondary Organic Aerosol from Isoprene Epoxydiols (IEPOX) in Phase Separated Particles, ACS Earth Space Chem., 2019, 3, 2646–2658 CrossRef CAS.
- Y. You, M. L. Smith, M. Song, S. T. Martin and A. K. Bertram, Liquid-liquid phase separation in atmospherically relevant particles consisting of organic species and inorganic salts, Int. Rev. Phys. Chem., 2014, 33, 43–77 Search PubMed.
- R. Schmedding, Q. Z. Rasool, Y. Zhang, H. O. T. Pye, H. Zhang, Y. Chen, J. D. Surratt, F. D. Lopez-Hilfiker, J. A. Thornton, A. H. Goldstein and W. Vizuete, Predicting secondary organic aerosol phase state and viscosity and its effect on multiphase chemistry in a regional-scale air quality model, Atmos. Chem. Phys., 2020, 20, 8201–8225 CrossRef CAS.
- M. Bilde and B. Svenningsson, CCN activation of slightly soluble organics: the importance of small amounts of inorganic salt and particle phase, Tellus B, 2004, 56, 128–134 CrossRef.
- A. Zuend, C. Marcolli, T. Peter and J. H. Seinfeld, Computation of liquid-liquid equilibria and phase stabilities: implications for RH-dependent gas/particle partitioning of organic-inorganic aerosols, Atmos. Chem. Phys., 2010, 10, 7795–7820 CrossRef CAS.
- A. Zuend and J. H. Seinfeld, Modeling the gas-particle partitioning of secondary organic aerosol: the importance of liquid-liquid phase separation, Atmos. Chem. Phys., 2012, 12, 3857–3882 CrossRef CAS.
- M. Kuwata and S. T. Martin, Phase of atmospheric secondary organic material affects its reactivity, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17354–17359 CrossRef CAS.
- M. A. Freedman, Phase separation in organic aerosol, Chem. Soc. Rev., 2017, 46, 7694–7705 RSC.
- V. G. Ciobanu, C. Marcolli, U. K. Krieger, U. Weers and T. Peter, Liquid-Liquid Phase Separation in Mixed Organic/Inorganic Aerosol Particles, J. Phys. Chem. A, 2009, 41, 10966–10978 CrossRef.
- M. Song, C. Marcolli, U. K. Krieger, A. Zuend and T. Peter, Liquid-liquid phase separation in aerosol particles: dependence on O:C, organic functionalities, and compositional complexity, Geophys. Res. Lett., 2012, 39, L19801 Search PubMed.
- D. J. Losey, R. G. Parker and M. A. Freedman, pH Dependence of Liquid-Liquid Phase Separation in Organic Aerosol, J. Phys. Chem. Lett., 2016, 7, 3861–3865 CrossRef CAS.
- A. K. Bertram, S. T. Martin, S. J. Hanna, M. L. Smith, A. Bodsworth, Q. Chen, M. Kuwata, A. Liu, Y. You and S. R. Zorn, Predicting the relative humidities of liquid-liquid phase separation, efflorescence, and deliquescence of mixed particles of ammonium sulfate, organic material, and water using the organic-to-sulfate mass ratio of the particle and the oxygen-to-carbon elemental ratio of the organic component, Atmos. Chem. Phys., 2011, 11, 10995–11006 CrossRef CAS.
- A. C. Aiken, P. F. DeCarlo, J. H. Kroll, D. R. Worsnop, J. A. Huffman, K. S. Docherty, I. M. Ulbrich, C. Mohr, J. R. Kimmel, D. Sueper, Y. Sun, Q. Zhang, A. Trimborn, M. Northway, P. J. Ziemann, M. R. Canagaratna, T. B. Onasch, M. R. Alfarra, A. S. H. Prevot, J. Dommen, J. Duplissy, A. Metzger, R. Baltensperger and J. L. Jimenez, O/C and OM/OC ratios of primary, secondary, and ambient organic aerosols with high-resolution time-of-flight aerosol mass spectrometry, Environ. Sci. Technol., 2008, 42, 4478–4485 CrossRef CAS.
- J. H. Kroll and J. H. Seinfeld, Chemistry of secondary organic aerosol: formation and evolution of low-volatility organics in the atmosphere, Atmos. Environ., 2008, 42, 3593–3624 CrossRef CAS.
- P. J. Ziemann and R. Atkinson, Kinetics, products, and mechanisms of secondary organic aerosol formation, Chem. Soc. Rev., 2012, 41, 6582–6605 RSC.
- M. I. Khoder, Atmospheric conversion of sulfur dioxide to particulate sulfate and nitrogen dioxide to particulate nitrate and gaseous nitric acid in an urban area, Chemosphere, 2002, 49, 675–684 CrossRef CAS.
- A. Ault, General Acid and General Base Catalysis, J. Chem. Educ., 2007, 84, 38–39 CrossRef CAS.
- K. Takács-Novák and A. Avdeef, Interlaboratory study of log P determination by shake-flask and potentiometric methods, J. Pharm. Biomed. Anal., 1996, 14, 1405–1413 CrossRef.
- A. Paschke, P. L. Neitzel, W. Walther and G. Schüürmann, Octanol/Water Partition Coefficient of Selected Herbicides: determination Using Shake-Flask Method and Reversed-Phase High-Performance Liquid Chromatography, J. Chem. Eng. Data, 2004, 49, 1639–1642 CrossRef CAS.
- Y. P. Kim, B. K.-L. Pum, C. K. Chan, R. C. Flagan and J. H. Seinfeld, Determination of water activity in ammonium sulfate and sulfuric acid mixtures using levitated single particles, Aerosol Sci. Technol., 1994, 20, 275–284 CrossRef CAS.
- M. Jariwala, J. Crawford and D. J. LeCaptain, In situ Raman spectroscopy analysis of the regeneration of ammonium hydrogen sulfate from ammonium sulfate, Ind. Eng. Chem. Res., 2007, 46, 4900–4905 CrossRef CAS.
- A. V. Levanov, O. Y. Isaikina, U. D. Gurbanova and V. V. Lunin, Dissociation Constants of Perchloric and Sulfuric Acids in Aqueous Solution, J. Phys. Chem. B, 2018, 122, 6277–6286 CrossRef CAS.
- A. Zuend and J. H. Seinfeld, A practical method for the calculation of liquid-liquid equilibria in multicomponent organic-water-electrolyte systems using physicochemical constraints, Fluid Phase Equilib., 2013, 337, 201–213 CrossRef CAS.
- A. Zuend, C. Marcolli, B. P. Luo and T. Peter, A thermodynamic model of mixed organic-inorganic aerosols to predict activity coefficients, Atmos. Chem. Phys., 2008, 8, 6069–6151 CrossRef.
- A. Zuend, C. Marcolli, A. M. Booth, D. M. Lienhard, V. Soonsin, U. K. Krieger, D. O. Topping, G. McFiggans, T. Peter and J. H. Seinfeld, New and extended parameterization of the thermodynamic model AIOMFAC: calculation of activity coefficients for organic-inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups, Atmos. Chem. Phys., 2011, 11, 9155–9206 CrossRef CAS.
- H. Stephen and T. Stephen, Solubilities of inorganic and organic compounds, Oxford Pergamon Press, 1963 Search PubMed.
- S. E. Schwartz and W. H. White, Solubility equilibria of the nitrogen oxides and oxyacids in dilute aqueous solution, Adv. Environ. Sci. Eng., 1981, 4, 1–45 CAS.
- A. P. Ranney and P. J. Ziemann, Kinetics of Acid-Catalyzed Dehydration of Cyclic Hemiacetals in Organic Aerosol Particles in Equilibrium with Nitric Acid Vapor, J. Phys. Chem. A, 2016, 120, 2561–2568 CrossRef CAS.
- S. Aimanant, Development and Application of Functional Group Analysis for Secondary Organic Aerosol Studies, Ph.D. thesis, University of California Riverside, 2012.
- H. Wei, E. P. Vejerano, W. Leng, Q. Huang, M. R. Willner, L. C. Marr and P. J. Vikesland, Aerosol microdroplets exhibit a stable pH gradient, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7272–7277 CrossRef CAS.
- M. A. Dallemagne, X. Y. Huang and N. C. Eddingsaas, Variation in pH of Model Secondary Organic Aerosol during Liquid-Liquid Phase Separation, J. Phys. Chem. A, 2016, 120, 2868–2876 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ea00003e |
| This journal is © The Royal Society of Chemistry 2021 |