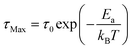Multiple rotor modes and how to trigger them: complex cation ordering in the family of relaxing hybrid formates

Abstract

A combination of structural, dielectric and calorimetric studies is used to describe a highly atypical behaviour of novel hybrid formate [NH₃(CH₂)₃NH₂(CH₂)₃NH₃][Mn(HCOO)₃]₃, incorporating large triprotonated molecular cations. Two successive phase transitions, switching between fast multiple rotor modes, and the surprising probable coexistence of static and dynamic disorder are discussed for this compound.

---

Hybrid organic–inorganic formates constitute one of the most intensely studied classes of chemical compounds. The massive interest in these coordination polymers has been aroused by their unique magnetic, dielectric, ferroelastic, ferroelectric and multiferroic properties, as well as their phase transitions with related dielectric anomalies.^1–7 Consequently, numerous structures have been designed, containing primarily small organic cations.^6,8–10 A step forward in terms of sophistication and complexity was the incorporation of long overgauge polyammonium molecular ions into the metal–formate framework, such as [CH₃NH₂(CH₂)₂NH₂CH₃]²⁺, [CH₃NH₂(CH₂)₃NH₂CH₃]²⁺,¹¹ [NH₃(CH₂)₄NH₃]²⁺, [NH₃(CH₂)₃NH₂(CH₂)₃NH₃]³⁺ and [NH₃(CH₂)₃NH₂(CH₂)₃NH₂(CH₂)₃NH₃]⁴⁺.^12–15 These cations misfit the free spaces of the organic–inorganic skeleton, which results in highly unique features. As a result, particular attention has been directed towards the search for general structure–property relations in this class of chemical compounds.^11,16–18 In this current of research, it was found that metal–formate frameworks containing polyammonium cations crystallize in niccolite-like systems.^8,12 Their topology is bimodal and hierarchical, evolving from (4¹²·6³)(4⁹·6⁶) to (4¹²·6³)(4⁹·6⁶)₃ in a series of hybrid formates with di-, tri- and tetraammonium cations.¹⁹ All polyammonium-templated formates become antiferro- or ferromagnets at low temperatures, i.e. around 9, 10–13, 20 and 28 K for Mn, Co, Fe and Ni analogues, respectively.^18,19 Their magnetization declines with the increasing charge and length of the organic molecular cation. Finally, these compounds are characterized by rich dielectric features, such as relaxation phenomena. Their occurrence constitutes a dielectric reflection of the dynamic disorder related to the loose binding of the polyprotonated ions in the crystal lattice. Different from their monoprotonated analogues, these ions possess multiple anchorage points (terminal and inner). Therefore, it was suggested that various rotor modes could be activated depending on the thermodynamic conditions. However, only two slow relaxation processes with different underlying molecular mechanisms have been registered for [NH₃(CH₂)₃NH₂(CH₂)₃NH₃][Co(HCOO)₃]₃ (dptaCo).¹⁵ Moreover, switching between different rotor modes, as for various classical amphidynamic crystals,²⁰ has never been observed in the case of hybrid organic–inorganic formates. In addition, only a few hybrid formates templated by polyammonium cations are known. This situation raises numerous questions, such as whether the segmental dynamics of the rotating moiety is possible at all.

Considering the shortcomings, we decided to use long triprotonated bis(3-ammoniumpropyl)ammonium (dpta³⁺) as the template cation to synthesize a novel hybrid organic–inorganic formate: [NH₃(CH₂)₃NH₂(CH₂)₃NH₃][Mn(HCOO)₃]₃ (dptaMn). Based on calorimetric, structural and dielectric studies, we have determined its physicochemical properties and discuss how to trigger effectively different rotor modes of the misfitting dpta³⁺ ions. Finally, we show that, contrary to popular belief, there is no simple relationship between the charge of the polyammoniums and the speed and energy barriers to their dynamic movements.

MnCl₂ (99%, Sigma-Aldrich), methanol (99.8%, Sigma-Aldrich), bis(3-aminopropyl)amine (98%, Sigma-Aldrich) and formic acid (98%, Fluka) were commercially available and used without further purification. To grow single crystals of dptaMn, a 10 mL methanol solution containing 2 mmol (0.28 mL) of bis(3-aminopropyl)amine and 20 mmol (0.75 mL) of HCOOH was placed at the bottom of a glass tube (9 mm inner diameter). A 20 mL aliquot of a methanol solution containing 2 mmol of MnCl₂ was gently added to this solution. The tube was sealed and kept undisturbed. Pale pink crystals were harvested after 3 days, washed with methanol and dried at room temperature.

In order to characterize the compound in question, first, its thermal properties were determined based on calorimetric DSC and adiabatic studies. Two thermal effects are detectable in the temperature dependence of the excess heat capacity. The first one takes place at 9 K (see lower inset in Fig. 1). As reported previously for the dptaCo analogue and other Mn²⁺-containing inorganic–organic formates, the anomaly around this temperature is strictly connected to the onset of magnetic order.^6,15 Therefore, one can assume that dptaMn orders magnetically at 9 K. The second heat anomaly occurs at T₀ = 337/347 K during cooling/heating cycles (Fig. S2†). Its symmetrical shape, considerable temperature hysteresis and sharp change of entropy, ΔS, indicate that the phase transition is close to the first-order type. As shown in the upper inset in Fig. 1, the ΔS value is roughly 9 J mol⁻¹ K⁻¹. Assuming the order–disorder mechanism of the phase transition that is typical for hybrid formates, one can determine the ratio of the number of possible configurations in the disordered and ordered systems, N, using the formula: ΔS = R ln(N), where R is the gas constant. For dptaMn, the value of N ≈ 3 was calculated. This result suggests a 3-fold order–disorder model for the bis(3-ammoniumpropyl)ammonium cation. To confirm this hypothesis, further XRD studies were performed. In addition, the thermogravimetric data indicate that dptaMn starts to decompose near 485 K (see Fig. S3†). The weight loss between 485 and 650 K is about 68% and corresponds well to complete decomposition into amine, CO₂ and MnO.

Fig. 1 The change in heat capacity of dptaMn for the cooling run. The bottom inset shows the change in entropy related to the phase transition. The upper inset depicts the change in heat capacity at low temperatures related to the magnetic phase transition.

According to structural studies performed at 360, 300 and 120 K, dptaMn crystallizes in the monoclinic system (centrosymmetric space group I2/a) and above T₀ the structure transforms to trigonal with R3̄c symmetry (Table S1).† This transformation is fully reversible, as revealed by the reproductivity of the monoclinic phase after re-cooling of the sample to 295 K during powder diffraction studies (see Fig. S4 and S5 in ESI†). The high temperature (HT) phase, presented in Fig. 2a, is isomorphic to the recently published cobalt analogue dptaCo.¹⁵ Both high- and low-temperature structures possess a binodal 3D metal–formate framework comprising two metal nodes, octahedral (4¹²·6³) and trigonal prismatic (4⁹·6⁶), connected by anti–anti formate ligands. The ratio of the two nodes (4¹²·6³) to (4⁹·6⁶) is 1 : 2, which gives a unique (4¹²·6³) (4⁹·6⁶)₂ topology. The formate ligands form distorted octahedral coordination around both metal centres. At 360 K, The Mn–O distances in the octahedral node of −3. symmetry are equal to 2.167 Å, whereas Mn–O distances in the trigonal prismatic node of 3. symmetry are longer and vary between 2.178 and 2.182 Å. The respective cis O–Mn–O angles range between 85.44–94.57° and 86.68–93.22°. The Mn⋯Mn distances via the formate bridge are 6.07–6.08 Å.

Fig. 2 (a) Crystal structure of dptaMn in HT R3̄c phase. (b) Side view of the cavity with disordered dpta˙³⁺. (c) A view of the cavity along the c-axis.

The framework is built from extended cavities accommodating long dpta³⁺ cations (see Fig. 2b and c). In the HT phase, all organic cations are trigonally disordered. Only two –CH₂– groups (both symmetry related) lie on the threefold axis while the remaining atoms are arranged around the three-fold axis and may adopt three equivalent placements of 1/3 occupancy. The disorder related to the presence of the trigonal axis is present in numerous metal–organic frameworks accommodating trigonal or hexagonal symmetries owing to the impossibility of symmetry of the amines with the aforementioned crystal systems.²¹

The pronounced dynamics of dpta³⁺ cations become significantly suppressed after transformation to the low-temperature (LT) phase, the structure of which is presented in Fig. 3a. Additionally, the cation ordering disturbs Mn⋯Mn distances that vary between 5.90 and 6.16 Å. The symmetry of the octahedral environment around metal centers decreases to C₁ and C_i. Hence, the mechanism of the phase transition can be classified as order–disorder, accompanied by framework distortion. In the LT phase, all dpta³⁺ are anchored in the framework by N–H⋯O hydrogen bond (HB) interactions. However, symmetry lowering introduces two kinds of cavities that accommodate two independent dpta³⁺ cations, A and B, with a ratio of 1 : 2 (Fig. 3b and c). Cation A adopts C₂ symmetry (.2.) and possesses a disordered middle-chain –NH₂⁺– group. The NH₂ group is split through the .2. (2-fold) axis. Thus, it accommodates two very close symmetry equivalent positions of equal occupancy (0.5). The distance between the two split sites is equal to 0.86 Å at 120 K and 0.81 Å at 300 K. As the disorder is symmetry restricted, the occupancy does not change with temperature within the monoclinic phase. Both disordered nitrogen positions possess two identical oxygen neighbours at distances of 3.08 and 3.06 Å that may serve as acceptors in N–H⋯O HB, and hence the middle-chain NH₂ group may be prone to temperature-induced motion between these two positions. Cation B of C₁ (.1.) symmetry is almost totally ordered. The small positive electron density, found near the terminal –NH₃⁺ indicates a possible alternative arrangement of this group. Interestingly, the occupancy of this position (equal to 0.2 at 300 and 120 K) does not change with a decrease in temperature. Additionally, the ratio of this disorder does not vary much for different samples. We investigated three single crystals from three separate syntheses (K1, K2, K3) and the occupancy ratios around room temperature were equal to 0.8/0.2 (K1), 0.8/0.2 (K2) and 0.72/0.27 (K3) and did not change with temperature lowering. Possibly, the growing conditions have a decisive influence on the ratio of occupancies of the disordered terminal NH₃ group in cation B, as all samples were grown under similar temperature and humidity conditions.

Fig. 3 (a) Crystal structure of dptaMn in the monoclinic LT phase. (b and c) dpta³⁺ cations A and B interacting with manganese(II)-formate scaffolded by N–H⋯O hydrogen bond interactions (blue dot lines).

To investigate the potentially dynamic nature of A- and B-type dpta³⁺ cations, broadband dielectric measurements between 30 and 380 K were performed. Fig. 4a depicts the temperature dependence of the real part, ε′, of the complex dielectric permittivity for several frequencies. On cooling, the ε′ values at all frequencies demonstrate a step-like decrease between 360 and 330 K. This change occurs around T₀. Therefore, it reflects the structural transformation between HT and LT phases of dptaMn. Further cooling leads to another step-like anomaly, moving progressively towards lower temperatures with decreasing frequency. For the probing frequency 10⁶ Hz, this can be detected around 180–200 K. The anomaly is accompanied by well-resolved bell-shaped peaks in the imaginary part, ε′′, of the complex dielectric permittivity. Both features, even more visible in the frequency domain (see Fig. 4b and c), show that a relaxation process takes place in the LT phase of dptaMn. The occurrence of this phenomenon confirms the dynamic disorder of the dpta³⁺ cations in the crystal lattice, in agreement with the crystallographic data. Surprisingly, the Cole–Cole diagrams exhibit a single, slightly distorted semicircle at each temperature, which is typical of a single dielectric relaxation (Fig. 4d). Moreover, further cooling to 30 K does not make any additional, faster process appear at 10⁶ Hz (see inset in Fig. 4a). Consequently, one can speculate that there is only one mechanism underlying the relaxation phenomenon in the LT phase. This hypothesis seems to be supported by another dielectric anomaly around 200 K (as marked Fig. 4a). Here, the ε′ values also decrease in a step-like manner on cooling, but independently of frequency. This feature is particularly visible for lower frequencies, for which the anomaly is not superimposed on the relaxation process. Considering that the lattice parameters change monotonically around this temperature (i.e. no discontinuity can be observed, as presented in Fig. S6†) and the crystal symmetry remains the same, one can speculate that the step-like frequency-independent decrease in ε′ values results from a gradual freezing of some cage cations. Freezing of the A-type dpta³⁺ cations would lead to a break in symmetry. Hence, the most probable scenario is gradual freezing of the B-type dpta³⁺ cations without change in the occupancy ratio (as indicated by crystallography). It is thus highly likely that dptaMn possesses two types of disorder in the LT phase below 150 K: static and dynamic. However, further studies are required to confirm this hypothesis.

Fig. 4 (a) Temperature dependence of ε′ at several frequencies between 10⁰ and 10⁶ Hz. The inset shows ε′ at 10⁶ Hz measured down to 30 K. (b) Frequency-dependent ε′(f) spectra between 130 and 180 K. (c) Dielectric losses at several temperatures plotted versus frequency. (d) The Cole–Cole diagrams for 130–180 K. (e) Relaxation map for dptaMn in the LT phase. (f) Temperature dependence of ε′′ at several frequencies with superimposed Havriliak–Negami fitting function transformed to the temperature domain. (g) Temperature dependence of ε′ between 10² and 10³ Hz for cooling and heating scans. The inset shows the static value of ε′ plotted versus temperature.

To shed more light on the dynamic nature of dpta³⁺ cations in the LT phase, more precise analysis of the relaxation process is proposed based on general Havriliak–Negami (HN) formalism. Such an approach assumes parametrization of the relaxation anomalies in the frequency domain by the following equation:

where ε* is the complex dielectric permittivity, ε_∞ is the high-frequency contribution, α and β are the shape parameters of the relaxation peak and τ_HN and Δε are the most probable relaxation time and dielectric increment, respectively.^22–24 The relaxation times, τ_Max, are then calculated according to the formula:²⁵

As presented in Fig. S7,† a single HN function is sufficient for the description of the relaxation peaks of dptaMn, which fits the hypothesis of there being only one mechanism underlying the relaxation. The shape parameters α, β deviate from 1 to a small extent (α·β ≈ 0.75). Finally, the logarithm of τ_Max depends linearly on temperature inverse for dptaMn (Fig. 4e), indicating that the relaxation process obeys the Arrhenius law and the motion of dpta³⁺ cations is thermally activated. From the equation

with k_B ≈ 1.38 J K⁻¹, the following values of the activation energy E_a and pre-exponential factor τ₀ were determined: 0.29 ± 0.01 eV and (1.3 ± 0.1) × 10⁻¹⁴ s. Surprisingly, the energy barrier for the motion of dpta³⁺ is relatively low. It is comparable with the E_a of hybrid formates occupied by small flexible monoprotonated molecular cations, the motion of which requires the breaking of HBs around one ammonium group (see Fig. S8†). For example, the energy barrier for reorientation of dimethylammonium cation (DMA⁺) takes the value of 0.28 eV.^26–28 The E_a is much lower for dptaMn in comparison with systems containing disordered diprotonated cations (e.g. 1,4-butanediammonium DAB²⁺, for which E_a = 0.49 eV).²⁹ Therefore, the obtained value of E_a suggests reorientation of only one protonated amine group in dpta³⁺. Such a partial motion of molecular cations is highly atypical and has never been observed in hybrid organic–inorganic formates before. However, such a conception is well supported by structural studies.

Apart from the low activation energy, there are even more surprising signs of atypical behavior of dpta³⁺ cations. Although the relaxation peaks are located at the same frequencies at given temperatures, their amplitudes vary between cooling and heating (Fig. 4f). This peculiarity is also reflected in the static values of ε′, which are different for heating and cooling cycles between 130 and 220 K (see insert in Fig. 4g). As a consequence, a hysteresis is formed. The hysteresis is also clearly visible on the ε′(T) dependences (Fig. 4g). Such a behavior was observed independently of the investigated sample (see Fig. S9†). Therefore, one can speculate that such a feature originates from the differences in pace of freezing and defreezing of some cage cations. However, additional studies are required to confirm this hypothesis.

In summary, we have successfully designed exceptional hybrid formate [NH₃(CH₂)₃NH₂(CH₂)₃NH₃][Mn(HCOO)₃]₃ (dptaMn), in which various rotor modes of the overgauge dpta³⁺ cation are triggered during the phase transition. This compound crystallizes in the LT monoclinic I2/a system, which above 347 K transforms to the fully disordered HT phase of trigonal R3̄c symmetry. Different from all previously reported hybrid formates, dptaMn possesses two types of disorder in the LT phase: static and dynamic. Surprisingly, the dynamically disordered cations preserve only segmental motional freedom, connected with the rearrangement possibilities of a single ammonium group. Such an atypical rotational mode, which has not previously been observed in hybrid formates, is reflected dielectrically as an extremely fast relaxation process of low activation energy. Consequently, the results show that, contrary to popular belief, there is no direct relationship between the number of accepted protons in polyammoniums and the speed and energy barrier of their dynamic movements between energetically degenerate locations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr Daria Szewczyk for adiabatic calorimetric studies. We are deeply grateful for financial support by the National Science Centre within the framework of the Opus13 project (grant no. DEC-2017/25/B/ST3/02321).

References

1. Y. Tian, A. Stroppa, Y. Chai, L. Yan, S. Wang, P. Barone, S. Picozzi and Y. Sun, Sci. Rep., 2014, 4, 1–5.
2. W. Zhang, Y. Cai, R.-G. Xiong, H. Yoshikawa and K. Awaga, Angew. Chem., Int. Ed., 2010, 49, 6608–6610.
3. E. Pardo, C. Train, H. Liu, L. M. Chamoreau, B. Dkhil, K. Boubekeur, F. Lloret, K. Nakatani, H. Tokoro, S. I. Ohkoshi and M. Verdaguer, Angew. Chem., Int. Ed., 2012, 51, 8356–8360.
4. H. C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674.
5. K. S. Asha, N. Ahmed, R. Nath, D. Kuznetsov and S. Mandal, Inorg. Chem., 2017, 56, 7316–7319.
6. W. J. Xu, Z. Y. Du, W. X. Zhang and X. M. Chen, CrystEngComm, 2016, 18, 7915–7928.
7. S. Burger, M. G. Ehrenreich and G. Kieslich, J. Mater. Chem. A, 2018, 6, 21785–21793.
8. R. Shang, S. Chen, Z.-M. Wang and S. Gao, Chem. – Eur. J., 2014, 20, 15872–15883.
9. G. C. Xu, W. Zhang, X. M. Ma, Y. H. Chen, L. Zhang, H. L. Cai, Z. M. Wang, R. G. Xiong and S. Gao, J. Am. Chem. Soc., 2011, 133, 14948–14951.
10. M. Mączka, A. Ciupa, A. Gągor, A. Sieradzki, A. Pikul, B. Macalik and M. Drozd, Inorg. Chem., 2014, 53, 5260–5268.
11. Y. H. Zhao, S. Liu, B. W. Wang, Z. M. Wang and S. Gao, Chem. – Eur. J., 2019, 25, 9303–9314.
12. M. Y. Li, M. Kurmoo, Z. M. Wang and S. Gao, Chem. – Asian J., 2011, 6, 3084–3096.
13. Z. Wang, X. Zhang, S. R. Batten, M. Kurmoo and S. Gao, Inorg. Chem., 2007, 46, 8439–8441.
14. Z. Wang, K. Hu, S. Gao and H. Kobayashi, Adv. Mater., 2010, 22, 1526–1533.
15. R. Shang, S. Chen, K. L. Hu, Z. C. Jiang, B. W. Wang, M. Kurmoo, Z. M. Wang and S. Gao, APL Mater., 2014, 2, 124104.
16. M. Mączka, A. Gągor, N. L. M. Costa, W. Paraguassu, A. Sieradzki and A. Pikul, J. Mater. Chem. C, 2016, 4, 3185–3194.
17. M. Y. Li, M. Kurmoo, Z. M. Wang and S. Gao, Chem. – Asian J., 2011, 6, 3084–3096.
18. Z. Wang, X. Zhang, S. R. Batten, M. Kurmoo and S. Gao, Inorg. Chem., 2007, 46, 8439–8441.
19. Y.-H. Zhao, S. Liu, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. – Eur. J., 2019, 25, 9303–9314.
20. Z. X. Zhang, T. Zhang, P. P. Shi, W. Y. Zhang, Q. Ye and D. W. Fu, J. Phys. Chem. Lett., 2019, 10, 4237–4244.
21. M. Mączka, A. Gągor, M. Ptak, W. Paraguassu, T. A. Da Silva, A. Sieradzki and A. Pikul, Chem. Mater., 2017, 29, 2264–2275.
22. S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210.
23. A. K. Jonscher, J. Mol. Liq., 2000, 86, 259–268.
24. A. K. Jonscher, J. Phys. D: Appl. Phys., 1999, 32, R57.
25. A. Schönhals and F. Kremer, in Broadband Dielectric Spectroscopy, Springer, 2003, pp. 35–57.
26. N. Abhyankar, J. J. Kweon, M. Orio, S. Bertaina, M. Lee, E. S. Choi, R. Fu and N. S. Dalal, J. Phys. Chem. C, 2017, 121, 6314–6322.
27. P. Peksa, J. Trzmiel, K. Fedoruk, A. Gagor, M. Šimenas, A. Ciupa, S. Pawlus, J. Banys, M. MacZka and A. Sieradzki, J. Phys. Chem. C, 2019, 123, 23594–23603.
28. T. Asaji and K. Ashitomi, J. Phys. Chem. C, 2013, 117, 10185–10190.
29. M. Mączka, M. Ptak, S. Pawlus, W. Paraguassu, A. Sieradzki, S. Balciunas, M. Simenas and J. Banys, Phys. Chem. Chem. Phys., 2016, 18, 27613–27622.

---

Footnote

† Electronic supplementary information (ESI) available: Full experimental procedures and results. See DOI: 10.1039/d1dt03333f

---