Rich redox-activity and solvatochromism in a family of heteroleptic cobalt complexes

Abstract

The combination of redox-active metals with redox-active ligands can lead to interesting charge transfer behaviours, including valence tautomerism and solvatochromism. With the aim of investigating a relatively underexplored redox-active metal/redox-active ligand combination, complexes [Co^II(acac)₂(X-BIAN)] (acac⁻ = acetylacetonate; X-BIAN = bis(4-X-phenyl)iminoacenaphthene; 1: X = –CF₃, 2: X = –Cl, 3: X = –H, 4: X = –Me) and [Co^III(acac)₂(Me-BIAN)]⁺ (5⁺) have been synthesised and characterised. At all temperatures investigated, and in both the solid and solution state, complexes 1–4 exist in a Co^II-BIAN⁰ charge distribution, while 5⁺ adopts a Co^III-BIAN⁰ charge distribution. In the case of 1–4, the potential Co^III-BIAN˙⁻ valence tautomer is inaccesible; the energy ordering between the ground Co^II-BIAN⁰ state and the excited Co^III-BIAN˙⁻ state must be reversed in order for an entropically driven interconversion to be possible. The energy gap between the states can be monitored via metal-to-ligand charge transfer bands in the visible region. We demonstrate tuning of this energy gap by varying the electronic properties of the BIAN ligand, as well as by controlling the molecular environment through solvent choice. Solvatochromic analysis, in combination with crystallographic evidence, allows elucidation of the specific solvent–solute interactions that govern the molecular behaviour of 1–4, affording insights that can inform potential future applications in sensing and switching.

---

Introduction

In the pursuit of new molecule-based materials, redox-active ligands have proven useful in a variety of wide-ranging applications.^1–3 The inherent ease with which redox-active ligands accept and/or donate electrons often leads to interesting charge transfer activity,^4,5 and the ability to access two or more stable redox states can be used to modulate molecule-based properties, for example, by turning on or off spin crossover (SCO) or other magnetic behaviour.^6–8 In particular, systems combining a redox-active ligand with a redox-active metal have the potential to exhibit valence tautomerism (VT): a stimulated, reversible, intramolecular electron transfer between a metal and a ligand.^9–12 As with any switchable system, valence tautomeric compounds may ultimately be utilised as components of molecular memory.^13–15 However, due to the dramatic colour changes that often accompany the switching, as well as the wide variety of stimuli that can induce the transition, the possible application of valence tautomeric molecules in colour-based displays, sensors, and “smart materials” is equally, if not more promising.^16–18

One obstacle hampering the use of switchable molecules in devices is the potential loss of useful properties upon a change in environment.^19–22 The switching process can be altered, or even turned off entirely, by subtle changes in crystal packing,^23,24 deposition onto surfaces,^25–27 and changes in solvent environment.^28–30 The latter case is often accompanied by the phenomenon of solvatochromism, the solvent dependence of a compound's electronic spectrum. Solvatochromism is a valuable property that can lead to applications in colorimetric sensing.^31–33 A compound that dramatically changes colour in response to a certain stimulus can be exploited in a device that detects that stimulus: for example, the solvent polarity dependence of a cyanostilbene derivative was used to develop a detection system for trace water in organic solvents.³⁴

A variety of sensing applications are possible, depending on the specific solvent–solute interactions experienced by a particular solvatochromic molecule. Solvatochromic theory can be used to describe and quantify these interactions.^35,36 The use of solvatochromic parameters to model solvent-dependent excitation energies is a well-established procedure, and has been used to elucidate the environmental interactions relevant to a wide range of inorganic and organic molecules.^31,34,37,38 Solvatochromic analysis is a particularly valuable tool for understanding environmental effects on valence tautomeric systems, as the combination of a redox-active ligand and redox-active metal often leads to solvatochromic charge transfer bands.^39,40

In previous studies, we have focussed on variation of the ancillary ligand in cobalt–dioxolene systems as a way of tuning valence tautomerism.^{20,28,29,41,42} In this work, we have instead sought to combine a cobalt metal centre with a family of redox-active ligands that has been relatively underutilised in this context: bis(aryl)iminoacenaphthene (BIAN). The BIAN ligand family is attractive due to its ability to access multiple oxidation states: most commonly, neutral, monoanionic radical, and dianionic.^43–45 The redox lability of the Co-BIAN moiety, in particular, has led to its use in numerous catalytic applications.^46–50 While VT has not been observed experimentally in Co-BIAN systems,^24,51 its occurrence in three complexes with the general formula [Co(L^NO)₂(BIAN)] (L^NO = a Schiff base ligand, Chart S1†) has been computationally predicted, involving an interconversion between low-spin (LS) Co^III-BIAN˙⁻ and high-spin (HS) Co^II-BIAN⁰ forms.⁵² However, the calculated [Co(L^NO)₂(BIAN)] complexes are difficult to access experimentally as they each contain either an ancillary ligand that cannot be isolated because it self-reacts and/or a BIAN ligand that has never been reported.

Hence, for ease of synthesis, we decided to target the family of complexes [Co(acac)₂(X-BIAN)] (acac⁻ = acetylacetonate; X-BIAN = bis(4-X-phenyl)iminoacenaphthene; 1: X = –CF₃, 2: X = –Cl, 3: X = –H, 4: X = –Me, Scheme 1), which employ the ubiquitous acetylacetonate ligand instead of the calculated Schiff base ligands.⁵² To assist the characterisation of 1–4, the complex 5⁺ was synthesised from the oxidation of complex 4. Our initial aim was simply to investigate the effects of redox tuning on complexes 1–4 through a combined electrochemical, spectroscopic, and crystallographic study. Upon the emergence of dramatic solvatochromic effects exhibited by 1–4, we then sought to understand the mechanisms underlying this behaviour. This was achieved by using solvatochromic analysis to identify and quantify the solvent–solute interactions governing the energy difference between ground and excited states. In the case of 1–4, the excited state of the solvatochromic transition is similar to a valence tautomer of the ground state, thus the solvatochromic insights obtained pertain directly to the VT transition we are targeting. Moreover, due to the distinct green-to-red colour change that toluene solutions of 1–4 undergo on exposure to strongly hydrogen-bond-donating species, the complexes are potential colorimetric indicators for the presence of alcohols.

Scheme 1 Synthetic targets of this work: [Co(acac)₂(X-BIAN)]^0/+ complexes.

Experimental section

Synthesis

All chemicals purchased were of reagent grade or higher and used as received. All procedures were undertaken under ambient conditions, except for the syntheses of 2 and 5(PF₆)⋅0.5THF, which were performed under an atmosphere of N₂ using standard Schlenk techniques. Solvents were dried over 3 Å molecular sieves and de-gassed with a minimum of three freeze-pump-thaw cycles prior to use. The X-BIAN ligands were synthesised according to literature procedures,^53–57 as was the precursor compound [Co(acac)₂(OH₂)₂].⁵⁸

A note on the naming of samples of [Co ^II (acac) ₂ (Cl-BIAN)]: The compound [Co^II(acac)₂(Cl-BIAN)] crystallises in two distinct phases, denoted 2H and 2, with the key difference being that 2H exhibits a hydrogen bonding interaction between solvent and acac⁻ oxygen atoms, while 2 does not. This distinction is important for our interpretation of the solvatochromic behaviour of 1–4. For each of the phases, the bulk sample solvation differs from that of the fresh crystals. Namely, the bulk sample 2H·0.2H₂O and the crystal 2H·H₂O are of the same phase and are crystallographically distinct from the bulk sample 2 and the crystal 2·0.1H₂O, which are of the same phase as each other.

[Co^II(acac)₂(CF₃-BIAN)] (1). An orange-red solution of CF₃-BIAN (141 mg, 0.300 mmol) in tetrahydrofuran (THF) (15 mL) was added dropwise to a rapidly stirring lilac solution of [Co(acac)₂(OH₂)₂] (88.0 mg, 0.300 mmol) in THF (8 mL). After two hours, the resulting deep green solution was dried over MgSO₄ and filtered, before all solvent was removed under vacuum. The residue was dissolved in a minimum of toluene (3.1 mL). The solution was filtered and divided into six equal portions. Each of these was layered with hexane (7.5 mL) to afford a crystalline product after a week, which was collected by vacuum filtration, washed with cold hexane, and air dried (149 mg, 65%). The product (77.4 mg, 0.101 mmol) was dissolved in toluene (2.05 mL). The emerald-green solution was divided into two equal portions, which were each layered with hexane (7 mL) to afford dark red block crystals of 1 after a week, which were collected by vacuum filtration, washed with cold hexane, and air dried (58 mg, 79%). Anal. calcd for C₃₆H₂₈N₂O₄F₆Co: C, 59.60; H, 3.89; N, 3.86. Found: C, 60.14; H, 4.04; N, 3.83. ESI-MS (TOF) m/z [M]⁺ calcd for C₃₆H₂₈N₂O₄F₆Co: 725.1285. Found: 725.1283. Absorption spectrum (toluene): λ_max/nm (ε/M⁻¹ cm⁻¹) = 644 (1.1 × 10³). Selected FT-IR data (ATR, cm⁻¹): ν_CN 1665 (w), ν_CN 1630 (w), ν_CO 1583 (s), 1515 (s), 1321 (s), 1160 (s), 1111 (s), 1063 (s), 1012 (m), 919 (w), 828 (m), 777 (m), 558 (m). The lack of solvation in 1 was confirmed via TGA (Fig. S1†) and elemental analysis. The measured powder X-ray diffraction pattern of bulk 1 matched that calculated from the single crystal structure (Fig. S2†).

[Co^II(acac)₂(Cl-BIAN)] (2H·0.2H₂O). An orange-red solution of Cl-BIAN (120 mg, 0.300 mmol) in THF (15 mL) was added dropwise to a rapidly stirring lilac solution of [Co(acac)₂(OH₂)₂] (88.0 mg, 0.300 mmol) in THF (8 mL). After two hours, the resulting deep green solution was dried over MgSO₄ and filtered, before all solvent was removed under vacuum. The residue was dissolved in a minimum of toluene (1.2 mL). The solution was filtered and divided into three equal portions. Each of these was layered with hexane (7.5 mL), to afford dark red block crystals after a week, which were collected by vacuum filtration, washed with cold hexane, and air dried (147 mg, 72%). Analysis of the freshly mounted crystal is consistent with one H₂O molecule per asymmetric unit, giving the formula 2H·H₂O, while elemental and TGA measurements (Fig. S1†) on the bulk sample are consistent with partial desolvation to the formula 2H·0.2H₂O. The PXRD pattern of bulk 2H·0.2H₂O matches that calculated from the structure of 2H·H₂O (Fig. S2†), indicating that the crystal structure of 2H·H₂O is minimally disrupted upon partial desolvation to 2H·0.2H₂O. Anal. calcd for C₃₄H_28.4N₂O_4.2Cl₂Co: C, 61.68; H, 4.32; N, 4.23. Found: C, 61.23; H, 4.33; N, 4.23. Selected FT-IR data (ATR, cm⁻¹): ν_CN 1665 (w), ν_CN 1628 (w), ν_CO 1585 (s), 1510 (s), 1480 (m), 1253 (m), 1010 (m), 913 (m), 828 (m), 820 (m), 777 (s), 762 (s), 651 (m), 542 (m).

[Co^II(acac)₂(Cl-BIAN)] (2). Under an inert atmosphere, compound 2H·0.2H₂O (86.1 mg, 0.130 mmol) was dissolved in toluene (1.6 mL) and then layered with hexane (30 mL). The layering was left at room temperature for 10 days to afford dark red crystals, which were collected by vacuum filtration, washed with cold hexane, and air dried (60 mg, 70%). Analysis of the freshly mounted crystal is consistent with approximately 0.1 H₂O molecules per asymmetric unit, giving the formula 2·0.1H₂O, while elemental and TGA measurements (Fig. S1†) on the bulk sample are consistent with full dehydration to 2. The PXRD pattern of bulk 2 matches that calculated from the structure of 2·0.1H₂O (Fig. S2†), indicating that the crystal structure of 2·0.1H₂O is minimally disrupted upon dehydration to 2. Anal. calcd for C₃₄H₂₈N₂O₄Cl₂Co: C, 62.02; H, 4.29; N, 4.25. Found: C, 61.75; H, 4.24; N, 4.26. ESI-MS (TOF) m/z [M]⁺ calcd for C₃₄H₂₈N₂O₄Cl₂Co: 657.0758. Found: 657.0754. Absorption spectrum (toluene): λ_max/nm (ε/M⁻¹ cm⁻¹) = 638 (1.3 × 10³). Selected FT-IR data (ATR, cm⁻¹): ν_CN 1665 (w), ν_CN 1626 (w), ν_CO 1585 (s), 1513 (s), 1482 (m), 1255 (m), 1014 (m), 915 (m), 830 (s), 779 (m), 765 (s), 649 (m), 542 (m).

[Co^II(acac)₂(H-BIAN)] (3). An orange-red solution of H-BIAN (99.6 mg, 0.300 mmol) in THF (15 mL) was added dropwise to a rapidly stirring lilac solution of [Co(acac)₂(H-BIAN)] (88.0 mg, 0.300 mmol). After two hours, the resulting deep green solution was dried over MgSO₄ and filtered, before all solvent was removed under vacuum. The residue was dissolved in a minimum of toluene (2 mL). The solution was filtered and divided into 4 equal portions. Each of these was layered with hexane (7.5 mL) to afford dark red plates of 3 after a week, which were collected by vacuum filtration, washed with cold hexane, and air dried (94.1 mg, 53%). Anal. calcd for C₃₄H₃₀N₂O₄Co: C, 69.09; H, 5.13; N, 4.83. Found: C, 69.27; H, 5.13; N, 4.75. ESI-MS (TOF) m/z [M]⁺ calcd for C₃₄H₃₀N₂O₄Co: 589.1538. Found: 589.1534. Absorption spectrum (toluene): λ_max/nm (ε/M⁻¹ cm⁻¹) = 624 (1.7 × 10³). Selected FT-IR data (ATR, cm⁻¹): ν_CN 1667 (w), ν_CN 1631 (w), ν_CO 1585 (s), 1510 (s), 1399 (s), 1251 (m), 1012 (m), 917 (m), 828 (m), 754 (s), 694 (s), 538 (m). The lack of solvation in 3 was confirmed via TGA measurements (Fig. S1†) and elemental analysis. The measured powder X-ray diffraction pattern of bulk 3 matched that calculated from the single crystal structure (Fig. S2†).

[Co^II(acac)₂(Me-BIAN)] (4). An orange-red solution of Me-BIAN (108 mg, 0.300 mmol) in THF (15 mL) was added dropwise to a rapidly stirring lilac solution of [Co(acac)₂(OH₂)₂] (88.0 mg, 0.300 mmol) in THF (8 mL). After two hours, the resulting deep green solution was dried over MgSO₄ and filtered, before all solvent was removed under vacuum. The residue was dissolved in a minimum of toluene (2 mL). The solution was filtered and divided into four equal portions. Each of these was layered with hexane (7.5 mL) to afford dark red-green crystalline plates of 4 after a week, which were collected by vacuum filtration, washed with cold hexane, and air dried (143 mg, 77%). Anal. calcd for C₃₆H₃₄N₂O₄Co: C, 70.01; H, 5.55; N, 4.54. Found: C, 70.12; H, 5.81; N, 4.72. ESI-MS (TOF) m/z [M]⁺ calcd for C₃₆H₃₄N₂O₄Co: 617.1851. Found: 617.1848. Absorption spectrum (toluene): λ_max/nm (ε/M⁻¹ cm⁻¹) = 621 (1.2 × 10³). Selected FT-IR data (ATR, cm⁻¹): ν_CN 1663 (w), ν_CO 1587 (s), 1513 (s), 1253 (m), 1193 (w), 1119 (w), 1010 (m), 915 (m), 816 (m), 781 (m), 653 (w), 550 (m), 511 (w). The lack of solvation in 4 was confirmed via TGA (Fig. S1†) and elemental analysis. The measured powder X-ray diffraction pattern of bulk 4 matched that calculated from the single crystal structure (Fig. S2†).

[Co^III(acac)₂(Me-BIAN)](PF₆) (5(PF₆)·0.5THF). Under an inert atmosphere, solid Fc(PF₆) (49.7 mg, 0.150 mmol, Fc⁺ = ferrocenium) was added to a stirred solution of 4 (92.6 mg, 0.150 mmol) in THF (15 mL). The resulting mixture was sonicated for three hours, over the course of which the colour changed from deep green to deep red-brown. The volume was reduced to about 2 mL, upon which a brown precipitate formed. The solution was filtered, and the residual solid was washed with THF (6 × 0.5 mL). The combined filtrates were layered with Et₂O (30 mL) to afford red-orange crystalline plates of 5(PF₆)·THF after a week, which were collected by vacuum filtration, washed with cold Et₂O, and air dried (54.2 mg, 43%). Analysis of the freshly mounted crystal is consistent with one THF molecule per asymmetric unit, however, elemental and TGA measurements (Fig. S1†) are consistent with 0.5 THF molecules per complex in the bulk sample. Anal. calcd for C₃₈H₃₈N₂O_4.5CoPF₆: C, 57.15; H, 4.80; N, 3.51. Found: C, 57.03; H, 4.70; N, 3.57. ESI-MS (TOF) m/z [M]⁺ calcd for C₃₆H₃₄N₂O₄Co: 617.1851. Found: 617.1849. Absorption spectrum (MeCN): λ_shoulder/nm (ε/M⁻¹ cm⁻¹) = 590 (2.6 × 10²). Selected FT-IR data (ATR, cm⁻¹): ν_CN 1667 (w), ν_CN 1631 (w), ν_CO 1585 (s), 1517 (s), 1372 (s), 1280 (m), 1069 (m), 1016 (m), 933 (w), ν_PF6 830 (s), 781 (s), 665 (m), 626 (m), δ_PF6 556 (s), 495 (m), 466 (m). The measured powder X-ray diffraction pattern of bulk 5(PF₆)⋅0.5THF matches that calculated from the single crystal structure of 5(PF₆)·THF, indicating that the two exhibit the same structural phase (Fig. S2†).

X-ray data collection, structure solution, and refinement details

The crystallographic data are presented in Table 1. For all compounds except 3, crystallographic data were obtained using a Rigaku XtaLAB Synergy-S diffractometer equipped with a Cu-Kα (λ = 1.54148 Å) microfocus source, graphite monochromator, HyPix-6000 E detector, and an Oxford Diffraction Cryostream 800. Crystals were transferred directly from the mother liquor to crystallographic oil to prevent solvent loss, and then immediately mounted on the diffractometer at the data collection temperature. Data reduction was performed using the program CrysAlis PRO (version 40_64.67a),⁵⁹ employing a numerical absorption correction based on Gaussian integration over a multifaceted crystal. The crystallographic data for 3 were collected at the Australian Synchrotron on the MX2 beamline,⁶⁰ equipped with a silicon double crystal monochromator and an Oxford Instruments Cryojet 5, and tuned to approximately Mo-Kα radiation (λ = 0.7108 Å). Data reduction was performed using XDS, using moderate multi-scan absorption correction in SADABS.⁶¹ All structures were solved using the SHELXT routine and refined using a full matrix least squares procedure based on F² using SHELXL within OLEX2.⁶² All non-hydrogen atoms were refined using anisotropic displacement factors. Hydrogen atoms were placed and constrained using a riding model.

Table 1 Crystallographic data for compounds 1, 2·0.1H₂O, 2H·H₂O, 3, 4 and 5(PF₆)⋅THF

	1	2·0.1H2O	2H·H2O	3	4	5(PF6)⋅THF
Empirical formula	C36H28CoF6N2O4	C34H28.23Cl2CoN2O4.12	C34H30Cl2CoN2O5	C51H45Co1.5N3O6	C36H34CoN2O4	C40H42CoF6N2O5P
Formula weight	725.53	660.53	676.43	884.29	617.58	834.66
Temperature/K	100	100	100	293(2)	100	175
Crystal system	Monoclinic	Monoclinic	Monoclinic	Monoclinic	Monoclinic	Triclinic
Space group	P21/n	P21/n	P21/n	C2/c	P21/n	P1̄
a/Å	14.3831(2)	12.32350(10)	13.19180(10)	30.221(6)	11.63630(10)	12.2535(4)
b/Å	16.40050(10)	20.2915(2)	19.02700(10)	19.317(4)	20.4317(2)	12.3381(4)
c/Å	15.1624(2)	12.52390(10)	13.23210(10)	21.459(4)	12.93790(10)	14.8997(4)
α/°	90	90	90	90	90	84.468(2)
β/°	114.3810(10)	100.6520(10)	107.2720(10)	133.02(3)	93.6250(10)	75.530(3)
γ/°	90	90	90	90	90	61.275(3)
Volume/Å^3	3257.69(7)	3077.79(5)	3171.49(4)	9159(5)	3069.82(5)	1911.99(12)
Z	4	4	4	8	4	2
ρ calc/g cm^−3	1.479	1.425	1.417	1.283	1.336	1.450
μ/mm^−1	4.814	6.310	6.158	0.601	4.720	4.507
F(000)	1484.0	1361.0	1396.0	3684.0	1292.0	784.0
Crystal size/mm^3	0.235 × 0.141 × 0.112	0.265 × 0.191 × 0.142	0.151 × 0.109 × 0.085	0.03 × 0.03 × 0.03	0.155 × 0.112 × 0.076	0.164 × 0.137 × 0.075
Radiation	CuKα (λ = 1.54184)	CuKα (λ = 1.54184)	CuKα (λ = 1.54184)	MoKα (λ = 0.71073)	CuKα (λ = 1.54184)	CuKα (λ = 1.54184)
2Θ range for data collection/°	7.13 to 153.142	8.402 to 153.1	8.31 to 153.358	4.596 to 64.538	8.1 to 153.192	6.128 to 155.316
Index ranges	−17 ≤ h ≤ 18, −15 ≤ k ≤ 20, −19 ≤ l ≤ 18	−14 ≤ h ≤ 15, −12 ≤ k ≤ 25, −15 ≤ l ≤ 14	−16 ≤ h ≤ 16, −18 ≤ k ≤ 23, −16 ≤ l ≤ 16	−44 ≤ h ≤ 44, −26 ≤ k ≤ 26, −26 ≤ l ≤ 26	−14 ≤ h ≤ 14, −24 ≤ k ≤ 25, −15 ≤ l ≤ 9	−15 ≤ h ≤ 13, −15 ≤ k ≤ 15, −18 ≤ l ≤ 17
Reflections collected	24 516	22 985	43 278	78 316	23 065	26 610
Independent reflections	6622 [Rint = 0.0309, Rsigma = 0.0290]	6207 [Rint = 0.0312, Rsigma = 0.0295]	6576 [Rint = 0.0343, Rsigma = 0.0213]	13 257 [Rint = 0.0487, Rsigma = 0.0381]	6195 [Rint = 0.0324, Rsigma = 0.0302]	7860 [Rint = 0.0342, Rsigma = 0.0319]
Data/restraints/parameters	6622/0/444	6207/379/400	6576/437/471	13 257/1003/652	6195/385/404	7860/354/458
Goodness-of-fit on F^2	1.052	1.045	1.061	1.081	1.042	1.094
Final R indexes [I ≥ 2σ(I)]	R 1 = 0.0358, wR2 = 0.0898	R 1 = 0.0313, wR2 = 0.0796	R 1 = 0.0319, wR2 = 0.0834	R 1 = 0.0469, wR2 = 0.1317	R 1 = 0.0309, wR2 = 0.0766	R 1 = 0.0791, wR2 = 0.2378
Final R indexes [all data]	R 1 = 0.0395, wR2 = 0.0918	R 1 = 0.0351, wR2 = 0.0821	R 1 = 0.0346, wR2 = 0.0851	R 1 = 0.0568, wR2 = 0.1426	R 1 = 0.0353, wR2 = 0.0791	R 1 = 0.0837, wR2 = 0.2434
Largest diff. peak/hole/e Å^−3	0.49/−0.51	0.26/−0.34	0.42/−0.36	0.32/−0.48	0.27/−0.36	1.05/−0.91

---

Co-crystallised water molecules were evident for 2·0.1H₂O and 2H·H₂O. For crystals of 2·0.1H₂O, the occupancy was refined freely. For 2H·H₂O, one molecule of H₂O was found disordered over two positions and refined freely to give an approximate 50 : 50 occupancy of each part. Crystals of 5(PF₆)⋅THF displayed highly disordered solvent that could not be readily modelled, and accordingly, refinement was carried out using the OLEX2 solvent mask routine.⁶³ One void per unit cell was found, with 80 electrons in a volume of 339 ų. This is consistent with the presence of one molecule of THF per formula unit.

For 1, one CF₃ group was disordered over two orientations with the fluorine atoms of both components refined to have similar anisotropic displacement parameters. For crystals of 2H·H₂O, disorder over two positions was modelled for both a methyl group of one acetylacetonate ligand, and one of the aryl groups of the bis(4-chlorophenyl)iminoacenaphthene ligand. Each component was refined freely to give the relative occupancies. For crystals of 3, both a coordinated acetylacetonate ligand and the phenyl group of the coordinated bis(phenylimino)acenaphthene ligand were found to be disordered over two positions. In both cases, the disordered atoms associated with each part were restrained to have similar anisotropic displacement parameters. Where necessary for the phenyl group, displacement parameters of equivalent atoms were constrained to be equal. The PF₆⁻ anion in crystals of 5(PF₆)⋅THF was disordered over two orientations with both components set to an ideal geometry, however, it was necessary to constrain the displacement parameters of equivalent atoms to be equal. Attempts to model the anion over more than two positions were unsuccessful and didn't allow for convergence.

Powder X-ray diffraction measurements were performed on a Rigaku XtaLAB Synergy-S diffractometer using Cu-Kα radiation (λ = 1.54148 Å). Samples were prepared by grinding the solids and loading them into borosilicate glass capillaries for measurement. The data were collected up to 2θ = 80° with an exposure time of 60 seconds per frame, and processed using CrysAlis PRO (version 40_64.67a).⁵⁹

Spectroscopic, elemental, and thermogravimetric analysis

Elemental analyses (C, H, N) were performed at the Campbell Microanalytical Laboratory, University of Otago. Thermogravimetric analyses were performed on a Mettler Toledo TGA/SDTA851e using a ramp rate of 5 °C per minute up to a maximum temperature of 500 °C in a flow of N₂. Attenuated total reflectance infrared (ATR-IR) spectra were measured on a Bruker Alpha II FT-IR spectrometer. Solid-state diffuse reflectance UV-vis spectra were measured on samples diluted ∼1% in KBr on a Thermo Scientific Evolution 220 UV-vis spectrophotometer. Electrospray ionisation mass spectrometry was performed on an Agilent 6220 Series TOF on samples in dichloromethane solution. Solution-state ultraviolet-visible (UV-vis) absorption spectra were measured on an Agilent Cary 60 UV-vis spectrophotometer. Ultraviolet-visible-near-infrared (UV-vis-NIR) absorption spectra were measured on a PerkinElmer UV-vis-NIR Lambda 1050 spectrophotometer. For the solvatochromic analysis of the electronic absorption spectra, the peak positions were extracted from maxima in the negative of the second derivative spectrum.⁶⁴

Electrochemistry

Cyclic voltammetry (CV) and rotating disk electrode (RDE) voltammetry were conducted using a standard three-electrode cell configuration under an N₂ atmosphere, using a Pt-wire auxiliary electrode, a leak-free Ag/AgCl reference electrode calibrated via an internal standard against the ferrocene/ferrocenium (Fc/Fc⁺) couple, and, respectively, a 1 mm and 3 mm diameter glassy carbon working electrode. All measurements were performed with an analyte concentration of 1 mM in 5 mL of spectroscopic grade MeCN or THF, with 0.25 M Bu₄NPF₆ as the supporting electrolyte.

Results and discussion

Synthesis

Compounds 1–4 are accessed via the precursor [Co(acac)₂(OH₂)₂], which was prepared according to literature procedures.⁵⁸ In THF, an equimolar amount of the appropriate X-BIAN ligand was added to the precursor. After evaporation of the reaction solvent, the residue was purified by dissolution in toluene and then layering with hexane, which yielded crystalline product in good yield after seven days. In the case of 3 and 4, these crystals are phase pure, while for 1, a recrystallisation using an increased toluene-to-hexane ratio is necessary to access a phase pure sample.

The compound [Co(acac)₂(Cl-BIAN)] crystallises in two crystallographically unique phases, denoted 2H and 2. When the compound is recrystallised in air, analysis of the freshly mounted crystal yields the formula 2H·H₂O, whereas isolation of the bulk solid results in partial desolvation to 2H·0.2H₂O. When 2H·0.2H₂O is recrystallised under inert conditions, analysis of the freshly mounted crystals affords a crystallographically distinct structure with the formula 2·0.1H₂O, and isolation of the bulk solid results in desolvation to 2. PXRD measurements (Fig. S2†) confirm that the crystal 2H·H₂O and the bulk sample 2H·0.2H₂O are both of one phase, and that the crystal 2·0.1H₂O and the bulk sample 2 are both of a second phase, crystallographically unique from the first.

To assist in the assignment of the electrochemical processes, we opted to chemically oxidise 4, which exhibits the most accessible oxidation process in the series (the electrochemical data are discussed below). Compound 4 was reacted with one equivalent of Fc(PF₆). Due to the sparing solubility of Fc(PF₆) in THF, sonication was employed to increase the rate of the reaction, as previously demonstrated in similar reactions.^28,29 Recrystallisation of the crude product afforded single crystals of 5(PF₆)⋅THF, which contains the oxidised complex, [Co^III(acac)₂(Me-BIAN)]⁺.

The purity of the bulk samples of all compounds is evident from elemental and thermogravimetric analysis (Fig. S1†), while powder X-ray diffraction indicates that the bulk samples are consistent with the single crystal structures (Fig. S2†). The crystals of compounds of 1–4 are red, and upon crushing, the resulting powders are green, while the crystals of 5(PF₆)⋅THF are red-orange, and remain the same colour upon crushing.

Structure descriptions

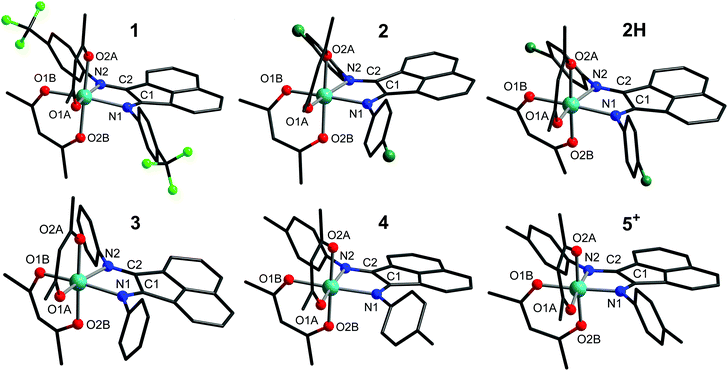
The structures of the cobalt complexes in 1, 2·0.1H₂O, 2H·H₂O, 3, 4 and 5(PF₆)⋅THF are presented in Fig. 1. All single crystal X-ray diffraction data were collected at 100 K, except for data for 3 and for 5(PF₆)⋅THF, which were collected at 300 K and 175 K, respectively. For 3 and 5(PF₆)⋅THF, at lower temperatures, the peaks in the diffraction pattern smear out due to a loss in crystallinity. Compounds 1, 2·0.1H₂O, and 2H·H₂O crystallise as dark red blocks. All three structures belong to the monoclinic P2₁/n space group, with one complex per asymmetric unit. Compound 3 crystallises as dark red needles. The structure belongs to the monoclinic C2/c space group, with two crystallographically unique molecules in the structure, 3a and 3b. The asymmetric unit contains one molecule of 3a, and one half of a molecule of 3b (the other half is generated via rotation about a C₂ axis). Compound 4 crystallises as dark red plates. The structure belongs to the monoclinic P2₁/n space group, with one complex per asymmetric unit. Finally, compound 5(PF₆)⋅THF crystallises as red-orange plates, with the structure belonging to the P1̄ space group and one complex per asymmetric unit. Details of the solvation in the structures of 2·0.1H₂O, 2H·H₂O, and 5(PF₆)⋅THF, and disorder in the structures of 1, 2H·H₂O, 3, and 5(PF₆)⋅THF are discussed in the Experimental section.

Fig. 1 Molecular structures of 1, 2 in 2·0.1H₂O, 2H in 2H·H₂O, 3a in 3, 4 and 5⁺ in 5(PF₆)⋅THF. Colour code: C (grey), N (blue), O (red), Co (aqua), F (light green), Cl (dark green). Hydrogen atoms omitted for clarity.

Complexes 1–4 and 5⁺ all exhibit a pseudo-octahedral geometry around the cobalt centre, with an N₂O₄ coordination sphere. The oxidation states of the metal centres can be assigned by examination of the Co–N/O bond lengths (Table 2). For 1–4, all Co–N bond lengths are over 2.15 Å, and all Co–O bond lengths are greater than 2.0 Å. In general, Co–N/O bonds follow the trend: LS-Co(III) < LS-Co(II) < HS-Co(II), with six-coordinate pseudo-octahedral low-spin cobalt(II) also characterised by an axial Jahn-Teller distortion. At the temperature of data collection, the Co–O/N distances measured for the structures of 1–4 are consistent with high-spin cobalt(II). However, for 5⁺, the bond lengths are significantly shortened, with an average Co–O bond length of 1.89 Å and an average Co–N bond length of 1.95 Å. These data suggest a low-spin cobalt(III) centre, and hence confirm that the 1e⁻ oxidation of 4 is metal-centred.

Table 2 Selected interatomic distances (Å) and structural parameters for compounds 1, 2·0.1H₂O, 2H·H₂O, 3a, 3b, 4, and 5(PF₆)⋅THF

Bond/parameter	1	2·0.1H2O	2H·H2O	3a	3b	4	5(PF6)⋅THF
a In 3a, atoms O1B and O2B are disordered over two positions, hence the data reported above are an average of the two disordered data points.
Co–O1A	2.033(1)	2.045(1)	2.027(1)	2.036(1)	2.019(2)	2.047(1)	1.885(3)
Co–O2A	2.049(1)	2.047(1)	2.074(1)	2.055(2)	2.053(1)	2.044(1)	1.885(3)
Co–O1B	2.028(2)	2.023(1)	2.063(1)	2.008^a	2.019(2)	2.028(1)	1.883(3)
Co–O2B	2.057(1)	2.066(1)	2.052(1)	2.047^a	2.053(1)	2.059(1)	1.889(4)
Co–N1	2.159(2)	2.164(1)	2.162(1)	2.178(2)	2.176(2)	2.158(1)	1.945(4)
Co–N2	2.214(1)	2.167(1)	2.195(1)	2.207(2)	2.176(2)	2.172(1)	1.954(3)
C1–C2	1.519(2)	1.513(2)	1.515(2)	1.510(3)	1.511(3)	1.516(2)	1.492(5)
C1–N1	1.284(3)	1.279(2)	1.281(2)	1.271(2)	1.274(2)	1.279(2)	1.287(4)
C2–N2	1.279(2)	1.281(2)	1.284(2)	1.279(3)	1.274(2)	1.282(2)	1.294(6)
O1–H1A⋯O1B (2 − x, 1 − y, 2 − z)	—	—	1.991(1)	—	—	—	—
O2–H2A⋯O1B (2 − x, 1 − y, 2 − z)	—	—	1.982(1)	—	—	—	—
O1–H1B⋯Cl1B (−½ + x, ½ – y, −½ + z)	—	2.203(1)	—	—	—	—	—
S(Oh)^65	0.772	0.649	0.695	0.854^a	0.442	0.406	0.221
Σ ^67	55°	53°	57°	56°^a	29°	39°	39°
Θ ^67	173°	157°	181°	195°^a	134°	118°	106°

---

The degree of distortion around the cobalt centre can be quantified for each complex using the value of the octahedral continuous symmetry measure, S(O_h), with zero indicating a fully symmetric octahedron. These values range from 0.406 to 0.854 for 1–4 (Table 2), and exhibit no clear correlation with the nature of the BIAN substituent. The discrepancy of over 0.4 between the S(O_h) values of 3a and 3b suggests that crystal packing effects play a large role in S(O_h) variation across the series. The S(O_h) value of 0.221 for 5⁺ is consistent with the preference of low-spin cobalt(III) centres for higher symmetry environments.^42,65,66 Comparison of the Σ and Θ octahedral distortion parameters of the complexes is also consistent with a higher symmetry around the metal centre of 5⁺ compared to that of 1–4 (Table 2).⁶⁷

The X-BIAN bond lengths for 1–4 and 5⁺ (Table 2) are consistent with a neutral BIAN ligand in each case (Fig. S3†).^43,68 However, comparing 4 to its oxidised product 5⁺, the C₁–C₂ bond is around 0.02 Å shorter in the latter, while the C₁–N₁ and C₁–N₂ bonds are around 0.01 Å longer. These changes are identical to those expected to arise from an increased population of the low-lying 5b₂ BIAN molecular orbital, which is localised to the α-diimine moiety and features C–C bonding and C–N antibonding character.^45,69 Notably, the addition of an electron to the 5b₂ orbital via reduction to the monoanionic radical typically results in a shortening of the C–C bond by around 0.05 Å and an elongation of the C–N bonds by around 0.05 Å (Fig. S3†).^6,68 While the bond length changes observed moving from 4 to 5⁺ are much smaller than this, they still indicate an increased population of the 5b₂ orbital in 5⁺. This is most likely due to increased π-back bonding, which arises from the increase in the number of electrons in the π-symmetric t_2g orbitals as the high-spin cobalt(II) centre is oxidised to low-spin cobalt(III). The analysis of the infrared spectra in the next section is consistent with this conclusion.

In the crystal structures of 1, 2·0.1H₂O, 2H·H₂O, 4 and 5(PF₆)⋅THF, the cobalt complexes pack in pairs, with a π–π stacking interaction between the naphthalene moieties of the BIAN ligands (shown for 2·0.1H₂O in Fig. S4,† left). For compound 3, the molecules pack in groups of three, with the naphthalene moieties again involved in π–π stacking (Fig. S4,† right). A molecule of 3b lies in the middle of each of these stacks of three, with molecules of 3a lying above and below it. Each molecule is rotated approximately 120° in the naphthalene plane relative to the molecule above or below it. It is notable that the intermolecular plane–plane distances (Table S1†) increase with the electron-donating strength of the 4-substituent on the X-BIAN phenyl rings increases. This trend is in accordance with the Hunter-Sanders model of π–π interactions, which describes π-systems as being composed of a positively charged σ-framework sandwiched between two negatively charged π-clouds.⁷⁰ According to this model, electron-donating groups should increase the negative charge of the naphthalene π-clouds, resulting in increased repulsion and a lengthening in the plane–plane distance, as is observed in the series from 1 to 4.⁷¹ Moving from 4 to 5(PF₆)⋅THF, the plane–plane distance reduces from 3.539 Å to 3.416 Å. This is seemingly inconsistent with the increase in π-back bonding to the 5b₂ orbital mentioned above. However, the π-back bonding orbital is localised to the α-diimine moiety, and so, minimally affects the charge of the π-clouds on the naphthalene unit. Rather, the dominant effect involves the comparatively electron-deficient cobalt(III) centre in 5(PF₆)⋅THF, which reduces the negative charge of the naphthalene π-clouds through inductive effects, thereby decreasing the electrostatic repulsion between the naphthalene planes.^70,71

Intermolecular hydrogen bonding is evident from the crystal structure of 2H·H₂O. This hydrogen bonding interaction is key to our interpretation of the solvatochromic behaviour of [Co^II(acac)₂(Cl-BIAN)] discussed below. Moving from 2·0.1H₂O to 2H·H₂O, the slight expansion in the a- and c-axes and slight contraction in the b-axis results in an overall increase in the unit cell volume. This is associated with the addition of approximately one H₂O molecule per asymmetric unit, which is disordered over two positions. Both are hydrogen-bonded to an oxygen atom of one of the acac⁻ ligands (Fig. 2), with O_1/2–H_1A/2A⋯O_1B (2 − x, 1 − y, 2 − z) distances of 1.982(1) and 1.991(1) Å, respectively (Table 2). The significant asymmetry in the C–O bond lengths of the hydrogen-bonded acac⁻ ligand (1.390(6) Å for the hydrogen-bonded oxygen atom, and 1.269(2) Å for the non-hydrogen-bonded oxygen atom, Fig. 2) provides further crystallographic evidence for the interaction and is consistent with both parts of the disordered water molecule hydrogen-bonding to the same oxygen atom. In contrast, the crystal structure of 2·0.1H₂O does not display any similar O–H⋯O interactions (Table 2).

Fig. 2 Hydrogen bonding between H₂O and [Co^II(acac)₂(Cl-BIAN)] molecules in the crystal structure of 2H·H₂O. Only one position of the disordered H₂O molecule is shown; the hydrogen bond and relevant bond lengths on the acac⁻ ligands are labelled in Å. Hydrogen atoms, except for those on the H₂O molecule, omitted for clarity. Colour code: C (grey), N (blue), O (red), Co (aqua), Cl (dark green).

Infrared spectroscopy

The ATR-IR spectra of compounds 1–4 and 5(PF₆)⋅0.5THF are shown in Fig. S5,† together with the spectrum of free H-BIAN for comparison. Free H-BIAN exhibits three weak C=N bands at 1657, 1636, and 1622 cm⁻¹, and a strong C=N signal at 1589 cm⁻¹. This general pattern (a group of weak peaks in the 1620–1670 cm⁻¹ region and a strong peak in the 1580–1590 cm⁻¹ region) may be observed in the spectra of each of the cobalt complexes. Across the series 1–4, varying the 4-substituent on the X-BIAN ligand has a minimal effect on the position of the C=N signals. In all cases, the C=N modes of the complexes all lie at similar energies to those of the corresponding free ligands, which is consistent with the neutral oxidation state of the BIAN ligands. Upon oxidation of 4 to 5(PF₆)⋅0.5THF, the C=N signals at 1663 cm⁻¹ and 1583 cm⁻¹ redshift to 1630 cm⁻¹ and 1572 cm⁻¹ (Fig. S5†), consistent with an increase in π-back bonding to the 5b₂ molecular orbital.^45,69 As discussed above, this arises due to an increase in the number of electrons in the π-symmetric t_2g orbitals upon moving from 4 to 5(PF₆)⋅0.5THF. In the spectrum of 5(PF₆)⋅0.5THF, the strong signals at 830 and 556 cm⁻¹ arise from an asymmetric stretch and a deformation mode of the PF₆⁻ anion, respectively.⁷²

Electronic spectroscopy

Following confirmation of the presence of complexes 1–4 and 5⁺ in dichloromethane (DCM) solutions of compounds 1–4 and 5(PF₆)⋅0.5THF by mass spectrometry studies, room temperature electronic absorption spectra in the UV-vis-NIR range (280–1400 nm) were measured in DCM (Fig. 3, S6 and S7†). Upon the emergence of solvent-dependent colour changes of solutions of 1–4, room temperature electronic absorption spectra of 1–4 and 5⁺ were measured in five other solvents: methanol (MeOH), n-butanol (n-BuOH), acetonitrile (MeCN), tetrahydrofuran (THF), and toluene (Fig. S8†). To assist in the interpretation of the solvatochromic behaviour, solid-state diffuse reflectance spectra (∼1% in KBr) were measured for 1–4 and 5(PF₆)⋅0.5THF in the UV-vis region (Fig. S9 and S10†). These spectra lie in best agreement with the solution-state spectra measured in toluene (as depicted for 1 in Fig. S11†). The solvatochromic and diffuse reflectance data are presented and discussed in detail in the Solvatochromic Analysis section. For all compounds, the solution spectra remained unchanged over a period of at least several hours under ambient conditions, consistent with solution stability and insensitivity to oxygen and moisture.

Fig. 3 UV-vis-NIR absorbance spectrum of 1 in dichloromethane.

The UV-vis-NIR spectrum of 1 in dichloromethane is shown in Fig. 3. It is representative of the spectra of 2, 3, and 4, which all exhibit analogous features with the wavelengths slightly shifted (equivalent plots for 2–4 and 5⁺ are presented in Fig. S6†). The highly absorbing bands in the 240–450 nm region are assigned to ligand π–π* or n–π* transitions. The spectra of the complexes in this region display excellent agreement with the spectrum of the free H-BIAN ligand (Fig. S7†), except for a peak at around 290 nm, which may be assigned to an acac⁻ π–π* transition by comparison with spectra of metal acetylacetonates.⁷³ In the visible region, two bands are evident, the higher energy band denoted by λ₁ and the lower energy band by λ₂. The peak positions are tabulated in Table 3. The bands are assigned as metal-to-ligand charge transfer (MLCT) excitations, due to the molar extinction coefficients (Table 3) being too high for d–d transitions, and by analogy to other transition metal BIAN complexes.^48,74,75 The only band observed in the 800–2200 nm region is assigned to a Co(II)-centred ⁴T₁(F) → ⁴T₂ transition. For 1, this band appears at λ_max = 1032 nm (ε_max = 17 cm⁻¹ M⁻¹) in DCM, which is close to where the same band is reported in other octahedral Co^II complexes.^76,77 The remaining spin-allowed d–d transitions of 1–4 (namely, ⁴T₁(F) → ⁴T₁(P) and ⁴T₁(F) → ⁴A₂) presumably lie beneath the MLCT bands in the visible region, or the ligand-centred bands in the UV region.

Table 3 Positions of the λ₁ and λ₂ MLCT excitations of 1–4 in various solvents. The peak positions tabled below are taken from the peak maxima in the negative of the second derivative spectrum, while the molar extinction coefficients are the ε values at these peak positions

λ/nm (ε/M^−1 cm^−1 × 10^2)
Solvent		Toluene	THF	DCM	MeCN	n-BuOH	MeOH
λ 1	1	538 (7.5)	546 (3.6)	515 (7.8)	512 (7.1)	509 (7.3)	507 (4.3)
	2	534 (9.6)	519 (6.6)	515 (9.2)	511 (9.7)	506 (9.7)	501 (9.1)
	3	529 (13)	530 (8.1)	512 (11)	509 (12)	501 (11)	501 (9.3)
	4	531 (9.9)	541 (3.9)	511 (11)	512 (7.4)	507 (11)	507 (9.6)
λ 2	1	669 (10)	656 (3.8)	631 (8.0)	625 (6.0)	593 (5.8)	593 (2.7)
	2	667 (12)	649 (5.5)	627 (8.4)	618 (7.5)	593 (6.8)	580 (5.4)
	3	651 (16)	631 (7.6)	623 (8.5)	603 (9.1)	577 (7.3)	573 (4.3)
	4	653 (11)	655 (4.2)	623 (8.1)	626 (6.3)	594 (6.5)	593 (3.5)

---

Moving along the series from 4 to 1, the MLCT transitions generally shift to lower energies, while the NIR transition shifts monotonically to higher energies. For the MLCT transitions, the trend is most apparent in toluene, the only solvent for which a λ_max value is defined for λ₂ in the spectra of each of 1–4. Toluene data for the λ₂ transition and dichloromethane data for the ⁴T₁(F) → ⁴T₂ transition are shown in Fig. 4, while the solid-state data are shown in Fig. S9.† The λ_max value of the λ₂ transition monotonically increases moving from 4 to 1 in toluene (Fig. 4, left), indicating that as the electron-withdrawing strength of the 4-substituent is increased, the MLCT energy decreases. The same trend is observed in the diffuse reflectance spectra (Fig. S9,† right).

Fig. 4 Selected regions of UV-vis-NIR absorbance spectra of 1–4. Data are normalised to the λ₁ (left) and ⁴T₁(F) → ⁴T₂ (right) peaks. The black arrow illustrates the peak shift moving from 4 to 1.

The effect of the 4-substituent of the BIAN ligand is twofold: increasing the electron-withdrawing strength destabilises the excited cobalt(III) state as a result of reduced σ-donation, and stabilises the ground cobalt(II) state due to increased π-acceptance, effects which alone would increase the MLCT energy. At the same time, increasing the electron-withdrawing strength stabilises the excited state BIAN radical, which alone would decrease the MLCT energy. From the observed trend, the MLCT energy decreasing with increasing electron-withdrawing strength, we may conclude that the dominant effect is stabilisation of the excited state BIAN radical, rather than destabilisation of the excited state cobalt(III) centre.

Unlike the MLCT transitions, the λ_max values for the near-infrared band decrease as the BIAN ligand becomes more electron-withdrawing (Table S2†). The dominant effect on the energy of the ⁴T₁(F) → ⁴T₂ transition is the field strength of the ligand, which in turn is primarily affected by π-interactions rather than σ-interactions: as the electron-withdrawing strength of the 4-substituent increases, the π-acceptor strength of the BIAN ligand increases, resulting in an increase of the ligand field strength and a subsequent increase in the ⁴T₁(F) → ⁴T₂ transition energy.

Similarly to compounds 1–4, the UV region of the spectra of 5⁺ is dominated by highly absorbing bands assigned to ligand-centred transitions (Fig. S6†). In the NIR region (800–2200 nm), no absorption bands are observed. This is consistent with the assignment of the metal centre in 5⁺ as LS-Co(III), as typically the lowest energy d–d transition (namely, ¹A₁ → ¹T₁) of octahedral LS-Co(III) complexes appears at wavelengths of around 600 nm or lower.^78,79

In the visible region, the bands present in 1–4 are largely quenched in the spectra of 5⁺, however, a weak absorption band (ε ≈ 2 × 10² M⁻¹ cm⁻¹) persists as a shoulder at around 600 nm (Fig. S6†). This excitation does not exhibit any significant solvatochromic effects (Fig. S8†) and appears at the same position in the diffuse reflectance spectrum (Fig. S10†). Assignment of the band to a t_2g → π*(acac⁻) ligand-to-metal charge transfer can most likely be ruled out, as in other heteroleptic Co^III-acac⁻ complexes, this excitation appears at much higher energies (<350 nm).^80,81 Furthermore, the 600 nm shoulder of 5⁺ lies somewhat out of the typical range of MLCT transitions of octahedral cobalt(III) complexes (<450 nm),^82–84 and so, is unlikely to be a MLCT transition. Hence, the band most likely arises from a Co(III)-centred d–d transition (¹A₁ → ¹T₁). The weak nature of the absorption and the lack of significant solvatochromic effects are consistent with this assignment. In the compound [Co^III(acac₂)(bipy)]⁺ (bipy = 2,2′-bipyridine), the ¹A₁ → ¹T₁ transition is found at 553 nm,⁸⁰ suggesting that the ligand field of 5⁺ is weaker than that of [Co^III(acac)₂(bipy)]⁺. The ¹A₁ → ¹T₂ transition of 5⁺ is presumably obscured by the ligand-centred transitions below 450 nm.

Electrochemistry

Having confirmed solution stability via electronic absorption spectroscopy, electrochemical measurements were performed on compounds 1–4 and 5(PF₆)⋅0.5THF in order to gain further insight into the effects of tuning the BIAN ligand's electronic properties. Cyclic and rotating disk electrode voltammograms were measured for 1 mM solutions of 1–4 and 5⁺ in THF (Fig. 5) and MeCN (Fig. S13†), with 0.25 M Bu₄NPF₆ support electrolyte and using a glassy carbon electrode. All potentials are referenced to the Fc/Fc⁺ couple using Fc as an internal standard.

Fig. 5 Cyclic voltammograms of 1–4 and 5⁺ in THF (1.0 mM with 0.25 M Bu₄NPF₆) at a scan rate of 100 mV s⁻¹, and RDE voltammograms of 1–4 and 5⁺ (50 mV s⁻¹ scan rate, 500 rpm rotation rate).

While in all cases the voltammetry measured in THF and MeCN are similar, the processes are generally better resolved in THF, so the following discussion will only focus on the THF data. Complexes 1–4 each exhibit three reduction processes and one oxidation process, while complex 5⁺ exhibits four reduction processes. The anodic peak (E_pa), cathodic peak (E_pc), or half-wave (E_1/2) potentials for each process in THF are tabulated in Table 4, while the MeCN data are tabulated in Table S3.† The oxidation and reduction processes are easily distinguished based on the position of zero current in the RDE voltammograms.

Table 4 Cyclic and RDE voltammetry data for compounds 1–4 and 5⁺ in THF (1.0 mM analyte with 0.25 M Bu₄NPF₆)

	Cyclic voltammetry data in V (ΔE in mV)				Rotating disk electrode voltammetry E1/2 in V (iL in μA)
	I, Epc	II, E1/2 (ΔE)	III, E1/2 (ΔE)	IV, Epa	I	II	III	IV^d
a E pc or E1/2 of the overlapped process combining I and II. b E pc rather than E1/2. c E pc rather than Epa. d Value undefined for all compounds except 5^+ due to severe broadening of the oxidation process.
1	−1.405^a	—	−1.540^b	0.340	−1.368 (15.6)^a	—	−1.630 (11.8)	—
2	−1.468^a	—	−1.708 (60)	0.127	−1.442 (22.7)^a	—	−1.762 (10.1)	—
3	−1.538	−1.628^b	−1.866 (65)	−0.078	−1.540 (29.9)^a	—	−1.908 (7.9)	—
4	−1.513	−1.646 (65)	−1.906 (65)	−0.118	−1.489 (27.6)	−1.670 (11.4)	−1.942 (9.4)	—
5^+	−1.588	−1.728^b	−1.931 (105)	−0.538^c	−1.614 (23.9)^a	—	−1.967 (12.5)	0.516 (12.9)

---

It is easiest to begin the discussion with 4, which exhibits the best resolved processes among the compounds in the series. The first reduction, process I, is irreversible, while processes II and III are chemically reversible, both with peak-to-peak separations (ΔE) comparable to that of the Fc/Fc⁺ process under the same conditions. The relative limiting currents from the RDE voltammogram suggest that process I is a two-electron process, while processes II and III are one-electron processes. Based on this, and by comparison to similar complexes,^85,86 process I may be assigned to a concerted reduction of each of the acac⁻ ligands to an acac˙²⁻ radical. Process II may then be assigned to the first BIAN reduction, and process III to the second BIAN reduction (Scheme 2). The potentials for processes II and III are similar to those reported for the first and second BIAN reductions in a series of tetrahedral complexes [CoCl₂(X-BIAN)] (X = a range of electron-withdrawing and electron-donating substituents).⁸⁷ In BIAN complexes with other metals (for example, Fe and Ir), the ligand reductions also appear at similar potentials.^6,88,89 Moving along the series from 4 to 1, the two BIAN reduction processes shift to less reducing potentials as the electron-withdrawing strength of the X-BIAN ligand increases, consistent with the trend observed in the series of tetrahedral complexes [CoCl₂(X-BIAN)].⁸⁷

Scheme 2 Assigned redox processes for 1–4 and 5⁺.

The oxidation process exhibited by each of 1–4 (process IV) shows some chemical reversibility, but a large separation between anodic and cathodic peaks is consistent with slow electron transfer. The RDE profile does not show a well-defined plateau, and so an accurate value of the limiting current cannot be determined. Moving along the series from 4 to 1, the separation between anodic and cathodic peaks increases as the electron-withdrawing strength of the X-BIAN ligand increases, with the anodic peak potential showing the larger shift.

The assignment of process IV may be clarified by considering the electrochemistry of 5⁺, the product of chemical oxidation of 4. Among the compounds in the series, 4 was selected for chemical oxidation because it exhibited the most accessible oxidation process. The voltammetry of 4 and 5⁺ are nearly identical, except for the CV rest potential and RDE position of zero current. The first reduction of 5⁺ therefore corresponds to process IV. In the RDE voltammetry, the limiting current of this process is well-defined, and is consistent with the assignment of the process to the one-electron reduction of cobalt(III) to cobalt(II). The oxidation process exhibited by each of 1–4 is therefore assigned to the one-electron oxidation of cobalt(II) to cobalt(III) (Scheme 2). Finally, the three remaining reduction processes exhibited by 5⁺ (processes I, II, III) have identical assignments to the equivalent processes exhibited by 1–4.

These voltammetric measurements clearly highlight trends in the redox behaviour of the system: as the electron-withdrawing strength of the 4-substituent is increased, the first and second reduction processes of the BIAN ligand shift to less reducing potentials, while the cobalt(II) to cobalt(III) oxidation shifts to more oxidising potentials. This provides electrochemical evidence for the two concurrent effects on the MLCT transition discussed in the previous section: as the BIAN ligand becomes more electron-deficient, reduced BIAN forms become more accessible, stabilising the Co^III-BIAN˙⁻ state, but at the same time, oxidation of the metal centre becomes more inaccessible due to decreased σ-donation, destabilising the Co^II-BIAN⁰ state.

In previous work, some of us have reported an empirical rule that for valence tautomerism to be observed around room temperature or below, the separation between frontier metal and ligand redox processes must be less than approximately 740 mV.²⁹ This criterion is far from being met by any of the present complexes 1–4, with a separation of over 1 V for all complexes. Moreover, unexpectedly, the acetylacetonate ligands are more readily reduced than the BIAN ligands, precluding any Co-BIAN valence tautomerism in these complexes. Valence tautomerism between Co and acac⁻ also does not occur, consistent with the large separation between the Co(II) oxidation and acac⁻ reduction processes.

Solvatochromic analysis

Complexes 1–4 exhibit solvatochromism, appearing deep green-blue in toluene, deep green in THF, yellow-green in DCM, and red in MeOH (Fig. 6). Underlying these effects is a shift in both wavelength and intensity of both MLCT bands in the visible region, as the polarity of the solvent changes. Moving from toluene to methanol, the wavelength and intensity both decrease, as shown for 1 in Fig. 6, and for 2–4 in Fig. S8.† The solvatochromic data are summarised in Table 3 (above). Decomposition of the complexes in more polar solvents can be ruled out, since a toluene solution of 3 can be evaporated to dryness, redissolved in MeOH, evaporated to dryness again, and redissolved in toluene with no changes between the initial and the final spectrum.

Fig. 6 Visible spectra and photographs of 1 in various solvents.

Solvatochromic analysis may be applied to model the solvent-dependent behaviour. A number of physical constants and empirical parameters have been used to model solvent properties, each reflecting a different mechanism by which the solvent can interact with the solute.^32,35,36 When multiple interactions are relevant, a linear combination of parameters can be used to fit the experimental excitation energies.

Dipole stabilising interactions are particularly relevant to charge transfer excitations; the large change in dipole moment that typically accompanies charge transfer can often lead to solvatochromism.^4,39,90 The stabilisation of a dipole in a dielectric medium is proportional to the magnitude of the dipole, and hence, if the magnitude of the excited state dipole differs from that of the ground state, a change in solvent dielectric properties will change the relative energies between the ground and excited state, thereby altering the excitation energy. To capture these purely electrostatic effects, the Onsager function, f_O(ε) = (ε − 1)/(2ε + 1), which is proportional to the energetic stabilisation of a dipole in a dielectric medium, is often applied.^31,37

In the case of 1–4, it is not possible to obtain a good correlation between the measured excitation energies and f_O(ε) alone: the experimental energies increase in the order toluene < THF < DCM < MeCN < n-BuOH < MeOH, whereas f_O(ε) increases in the order toluene < THF < DCM < n-BuOH < MeOH < MeCN. The discrepancies lie in the latter half of the series, with n-BuOH and MeOH affecting the excitation energies more than would be expected based purely on electrostatics. Hence, there must be at least one other interaction contributing to the solvatochromic behaviour. Based on the strong hydrogen bonding abilities of n-BuOH and MeOH, a plausible hypothesis would be the involvement of hydrogen bonding interactions between solvent and solute. The complexes can potentially accept hydrogen bonds either via the nitrogen atoms of the BIAN ligand or via the oxygen atoms of the acac⁻ ligands. The latter option is more likely, as a space-filling diagram of the complex illustrates that the oxygen atoms are more sterically accessible. A hydrogen bonding interaction at this site would cause a decrease in the σ-donating strength of the acac⁻ ligand, destabilising the cobalt(III) centre in the MLCT excited state, and thereby increasing the MLCT energy, as experimentally observed. Hydrogen bonding between solvent and catecholate oxygen atoms has previously been found responsible for solvatochromism in a cobalt complex,³¹ while in another cobalt complex, intramolecular hydrogen bonding involving acac⁻ oxygen atoms even triggered an intramolecular electron transfer.⁹¹

Spectroscopic evidence for hydrogen bonding between solvent and acac⁻ oxygen atoms is apparent from a comparison of the diffuse reflectance spectra of the hydrogen-bonded (2H) and non-hydrogen-bonded (2) phases of [Co^II(acac)₂(Cl-BIAN)]. As discussed above, the 2H phase exhibits hydrogen bonding between the water molecule and the oxygen atom of one of the acac⁻ ligands (Fig. 2). As a result, the bulk samples 2H·0.2H₂O and 2 exhibit marked differences between their diffuse reflectance spectra, as shown in Fig. 7, left. The λ₂ band for 2H·0.2H₂O is blue-shifted compared to 2, and is less intense relative to the λ₁ band, despite the relative intensities being reversed in 2. Hence, the changes moving from 2 to 2H·0.2H₂O are similar to the spectral changes observed upon moving from toluene to hydrogen bonding solvents (Fig. 7). This observation is consistent with hydrogen bonding between solvent and acac⁻ oxygen atoms contributing to the measured solvatochromic shifts of the visible bands for solutions of 1–4.

Fig. 7 Left: Diffuse reflectance UV-vis spectra of 2 and 2H·0.2H₂O (∼1% in KBr), normalised to the highest absorbing peak. Right: Absorption spectra of 2 in toluene and n-BuOH.

A solvent's hydrogen bond donation strength can be described with the empirically derived Kamlet-Taft α-parameter.³⁵ To incorporate both the electrostatic and hydrogen bonding effects, an appropriate solvatochromic model should involve a linear combination of f_O(ε) and α. Hence, we fit our experimental data to the linear equation:

E_fit = c₁ + c₂·f_O(ε) + c₃·α (1)

where c₁, c₂, and c₃ are constants. The results of the fitting are summarised in Table S4,† where c₁, c₂, and c₃ are the constants from eqn (1), and R² is the coefficient of determination. Apart from two cases (the fit of the lower wavelength visible band for 1 and for 4), the linear models capture the solvatochromic trends well. For both visible bands of 1, plots of the experimental excitation energies, E_exp, vs. the fitted model are shown in Fig. 8 (equivalent plots for 2–4 available in Fig. S14†).

Fig. 8 Experimental excitation energies of the lower energy (top) and higher energy (bottom) visible excitations of 1, plotted against the model presented in eqn (1). The fitted equation for λ₁ is E_fit = 2.236 + 0.246·f_O(ε) + 0.116·α, and for λ₂ is E_fit = 1.785 + 0.293·f_O(ε) + 0.197·α.

The y-axis intercept, c₁, may be interpreted as the predicted excitation energy in the absence of any solvent interactions. Though a consistent trend between 1–4 is not observed, a comparison of the c₁ values of 1 and 4 shows that for both MLCT excitations, the energy in the absence of solvent interactions is lower for 1 than for 4, again consistent with the stabilisation of the BIAN radical being the dominant effect of increasing the electron-withdrawing strength of the BIAN ligand. The c₂ and c₃ values reflect the contributions of the two solvent–solute interactions to the observed solvatochromism. Being the coefficient of f_O(ε) in eqn (1), c₂ reflects the contribution of the dipole interaction, while c₃, being the coefficient of α, reflects the contribution of hydrogen bonding. The c₂ value varies between 0.1 and 0.4 for both λ₁ and λ₂ bands, while c₃ is consistently around 0.20 for λ₂, and consistently around 0.11 for λ₁, except in the case of 2, for which c₃ = 0.062. The inconsistencies in c₂ likely arise from limitations in the procedure used to determine the peak positions. However, despite the variance in the c₂ and c₃ values, they are, in each case, within an order of magnitude of each other.

Including both f_O(ε) and α in the model reproduces the solvatochromic trend with greater accuracy than modelling using only one of the two, and so, altogether, it may be concluded that both dipole interactions and hydrogen bonding play key roles in the solvatochromism observed for 1–4. A study on the solvatochromic ligand-to-metal charge transfer (LMCT) excitation of [Co(5,5′-dimethyl-2,2′-bipyridine)₂(o-catechol)]⁺ reached a similar conclusion, in which case the linear fit had values of c₂ = 0.695 and c₃ = 0.109. These values are similar to those calculated for the complexes in this work, indicating a comparable sensitivity to solvent.³¹

Concluding remarks

The heteroleptic compounds [Co(acac)₂(X-BIAN)] (X = –CF₃, –Cl, –H, –Me) adopt a Co^II-BIAN⁰ charge distribution at all temperatures investigated, both in the solid and solution states. In the solution state, the separation of over 1 V between the Co^II/Co^III and BIAN⁰/BIAN˙⁻ electrochemical processes is consistent with the absence of a thermally-induced VT interconversion to a Co^III-BIAN˙⁻ tautomer upon cooling. However, electrochemical and spectroscopic investigations indicate that the gap between Co^II-BIAN⁰ and Co^III-BIAN˙⁻ states is reduced as the BIAN ligand is made more electron withdrawing, suggesting that the BIAN˙⁻ stabilisation dominates over the concurrent cobalt(III) destabilisation. Any future efforts targeting VT in Co-BIAN complexes based on the BIAN⁰/BIAN˙⁻ redox couple will require complexes with a LS-Co^III-BIAN˙⁻ ground state and close lying HS-Co^II-BIAN⁰ excited state to allow an entropy driven interconversion, rather than the HS-Co^II-BIAN⁰ ground state that is exhibited by the present complexes. This energy ordering has indeed been calculated for hypothetical heteroleptic Co-BIAN complexes with Schiff base rather than β-diketonate ancillary ligands.⁵² The present work suggests that achievement of valence tautomeric heteroleptic Co-BIAN complexes may be facilitated by utilising BIAN ligands functionalised by electron withdrawing substituents, in combination with highly electron donating ancillary ligands. If the Co^III-BIAN˙⁻ state is sufficiently stabilised by these effects, it should become the ground state, thereby achieving the correct energy ordering for an entropy driven VT interconversion.

The solvent–solute interactions governing the solvatochromic behaviour of 1–4 were elucidated following an investigation in six solvents. Increasing either the solvent dielectric constant or hydrogen bond donating strength causes a decrease in intensity and an increase in energy of the two MLCT transitions, indicating that electrostatic and hydrogen bonding interactions destabilise the Co^III-BIAN˙⁻ excited state relative to the Co^II-BIAN⁰ ground state. The electrostatic effects operate via dipole–dipole interactions, while the hydrogen bonding effects operate via hydrogen bonding between solvent and acac⁻ oxygen atoms, as evidenced in the solid state by the comparison of the diffuse reflectance spectra of 2 and 2H·0.2H₂O.

The solvatochromic insights outlined above could be of critical importance for the incorporation of switchable molecules into devices. Using our model, we are able to predict the shift in the energy gap between Co^II-BIAN⁰ and Co^III-BIAN˙⁻ states caused by a change in the solvent properties. In the same way, the solvatochromic analysis of a switchable molecule could be used to predict modulation of its switchable behaviour caused by a change in environment, such as incorporation into a polymer film of known polarity or hydrogen bonding ability. While multi-parameter analyses have been commonly employed to model solvatochromic bands, such approaches have not yet been used to model the solvent dependence of the transition temperature in VT systems. Hence, we also note the importance of considering multiple environmental effects in combination, which, in the case of 1–4, led to a more complete picture of the interactions governing the observed properties.

Finally, the distinct green-to-red colour change exhibited by 1–4, observed when moving from a non-hydrogen-bonding to a hydrogen-bonding environment, affords the compounds potential for use in colorimetric sensing. Given an appropriate non-hydrogen-bonding substrate, a thin film of any of 1–4 could in principle act as an alcohol indicating device, turning from green to red in the presence of alcohols.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Australian Research Council for funding (DP190100854). This research was undertaken in part using the MX2 beamlines at the Australian Synchrotron (using the Australian Cancer Research Foundation (ACRF) detector).

References

1. M. A. Hay and C. Boskovic, Chem. – Eur. J., 2021, 27, 3608–3637.
2. W. Kaim, Dalton Trans., 2019, 48, 8521–8529.
3. O. R. Luca and R. H. Crabtree, Chem. Soc. Rev., 2013, 42, 1440–1459.
4. J. Burgess, J. G. Chambers and R. I. Haines, Transition Met. Chem., 1981, 6, 145–151.
5. C. Förster and K. Heinze, Chem. Soc. Rev., 2020, 49, 1057–1070.
6. M. Schmitz, M. Seibel, H. Kelm, S. Demeshko, F. Meyer and H. J. Krüger, Angew. Chem., Int. Ed., 2014, 53, 5988–5992.
7. J. A. Degayner, I. R. Jeon and T. D. Harris, Chem. Sci., 2015, 6, 6639–6648.
8. P. Perlepe, I. Oyarzabal, A. Mailman, M. Yquel, M. Platunov, I. Dovgaliuk, M. Rouzières, P. Négrier, D. Mondieig, E. A. Suturina, M.-A. Dourges, S. Bonhommeau, R. A. Musgrave, K. S. Pedersen, D. Chernyshov, F. Wilhelm, A. Rogalev, C. Mathonière and R. Clérac, Science, 2020, 370, 587–592.
9. T. Tezgerevska, K. G. Alley and C. Boskovic, Coord. Chem. Rev., 2014, 268, 23–40.
10. E. Evangelio and D. Ruiz-Molina, Eur. J. Inorg. Chem., 2005, 2957–2971.
11. E. Evangelio and D. Ruiz-Molina, C. R. Chim., 2008, 11, 1137–1154.
12. G. K. Gransbury and C. Boskovic, Valence Tautomerism in d-block complexes, in Encyclopedia of Inorganic and Bioinorganic Chemistry (online), Wiley, 2021.
13. M. Mörtel, M. Seller, F. W. Heinemann and M. M. Khusniyarov, Dalton Trans., 2020, 49, 17532–17536.
14. H. B. Li, B. E. Tebikachew, C. Wiberg, K. Moth-Poulsen and J. Hihath, Angew. Chem., Int. Ed., 2020, 59, 2–8.
15. O. Kahn, Science, 1998, 279, 44–48.
16. M. Mörtel, J. Oschwald, A. Scheurer, T. Drewello and M. M. Khusniyarov, Inorg. Chem., 2021, 60, 14230–14237.
17. M. M. Paquette, D. Plaul, A. Kurimoto, B. O. Patrick and N. L. Frank, J. Am. Chem. Soc., 2018, 140, 14990–15000.
18. N. A. Vázquez-Mera, F. Novio, C. Roscini, C. Bellacanzone, M. Guardingo, J. Hernando and D. Ruiz-Molina, J. Mater. Chem. C, 2016, 4, 5879–5889.
19. C. Cervetti, E. Heintze and L. Bogani, Dalton Trans., 2014, 43, 4220–4232.
20. Y. Mulyana, G. Poneti, B. Moubaraki, K. S. Murray, B. F. Abrahams, L. Sorace and C. Boskovic, Dalton Trans., 2010, 39, 4757–4767.
21. N. A. Vázquez-Mera, C. Roscini, J. Hernando and D. Ruiz-Molina, Adv. Funct. Mater., 2015, 25, 4129–4134.
22. S. Beniwal, X. Zhang, S. Mu, A. Naim, P. Rosa, G. Chastanet, J.-F. Létard, J. Liu, G. E. Sterbinsky, D. A. Arena, P. A. Dowben and A. Enders, J. Phys.: Condens. Matter, 2016, 28, 206002.
23. A. Caneschi, A. Dei, F. Fabrizi de Biani, P. Gütlich, V. Ksenofontov, G. Levchenko, A. Hoefer and F. Renz, Chem. – Eur. J., 2001, 7, 3926–3930.
24. I. L. Fedushkin, O. V. Maslova, A. G. Morozov, S. Dechert, S. Demeshko and F. Meyer, Angew. Chem., Int. Ed., 2012, 51, 10584–10587.
25. R. Ash, K. Zhang and J. Vura-Weis, J. Chem. Phys., 2019, 151, 104201.
26. N. G. R. Hearns, J. L. Korčok, M. M. Paquette and K. E. Preuss, Inorg. Chem., 2006, 45, 8817–8819.
27. L. Kipgen, M. Bernien, F. Tuczek and W. Kuch, Adv. Mater., 2021, 33, 2008141.
28. T. Tezgerevska, E. Rousset, R. W. Gable, G. N. L. Jameson, E. C. Sañudo, A. Starikova and C. Boskovic, Dalton Trans., 2019, 48, 11674–11689.
29. G. K. Gransbury, M. E. Boulon, S. Petrie, R. W. Gable, R. J. Mulder, L. Sorace, R. Stranger and C. Boskovic, Inorg. Chem., 2019, 58, 4230–4243.
30. S. Rodríguez-Jiménez, A. S. Barltrop, N. G. White, H. L. C. Feltham and S. Brooker, Inorg. Chem., 2018, 57, 6266–6282.
31. G. Cioncoloni, H. M. Senn, S. Sproules, C. Wilson and M. D. Symes, Dalton Trans., 2016, 45, 15575–15585.
32. C. Reichardt, Chem. Rev., 1994, 94, 2319–2358.
33. B. Qin, S. Wu, G. Gahungu, H. Li, Y. Zhao, X. Zhang and J. Zhang, Chem. – Eur. J., 2020, 26, 14187–14193.
34. Y. Zhang, C. Liang and S. Jiang, New J. Chem., 2017, 41, 8644–8649.
35. M. J. Kamlet, J. L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887.
36. V. Gutmann, Electrochim. Acta, 1976, 21, 661–670.
37. I. Ratera, C. Sporer, D. Ruiz-Molina, N. Ventosa, J. Baggerman, A. M. Brouwer, C. Rovira and J. Veciana, J. Am. Chem. Soc., 2007, 129, 6117–6129.
38. A. S. I. Amer, A. M. M. Alazaly and A. A. Abdel-Shafi, J. Photochem. Photobiol., A, 2019, 369, 202–211.
39. V. L. Nadurata and C. Boskovic, Inorg. Chem. Front., 2021, 8, 1840–1864.
40. J. Guasch, L. Grisanti, S. Jung, D. Morales, G. D'Avino, M. Souto, X. Fontrodona, A. Painelli, F. Renz, I. Ratera and J. Veciana, Chem. Mater., 2013, 25, 808–814.
41. J. T. Janetzki, F. Z. M. Zahir, R. W. Gable, W. Phonsri, K. S. Murray, L. Goerigk and C. Boskovic, Inorg. Chem., 2021, 60, 14475–14487.
42. G. K. Gransbury, B. N. Livesay, J. T. Janetzki, M. A. Hay, R. W. Gable, M. P. Shores, A. Starikova and C. Boskovic, J. Am. Chem. Soc., 2020, 142, 10692–10704.
43. S. Pelties, T. Maier, D. Herrmann, B. de Bruin, C. Rebreyend, S. Gärtner, I. G. Shenderovich and R. Wolf, Chem. – Eur. J., 2017, 23, 6094–6102.
44. J. Wang, H. Sen Soo and F. Garcia, Commun. Chem., 2020, 3, 1–13.
45. P. Mondal, H. Agarwala, R. D. Jana, S. Plebst, A. Grupp, F. Ehret, S. M. Mobin, W. Kaim and G. K. Lahiri, Inorg. Chem., 2014, 53, 7389–7403.
46. O. M. Williams, A. H. Cowley and M. J. Rose, Dalton Trans., 2015, 44, 13017–13029.
47. C. G. P. Ziegler, T. M. Maier, S. Pelties, C. Taube, F. Hennersdorf, A. W. Ehlers, J. J. Weigand and R. Wolf, Chem. Sci., 2019, 10, 1302–1308.
48. T. M. Maier, P. Coburger, N. P. van Leest, E. Hey-Hawkins and R. Wolf, Dalton Trans., 2019, 15772–15777.
49. S. Sandl, T. M. Maier, N. P. van Leest, S. Kröncke, U. Chakraborty, S. Demeshko, K. Koszinowski, B. de Bruin, F. Meyer, M. Bodensteiner, C. Herrmann, R. Wolf and A. Jacobi von Wangelin, ACS Catal., 2019, 9, 7596–7606.
50. V. Rosa, S. A. Carabineiro, T. Avilés, P. T. Gomes, R. Welter, J. M. Campos and M. R. Ribeiro, J. Organomet. Chem., 2008, 693, 769–775.
51. J. Bendix and K. M. Clark, Angew. Chem., Int. Ed., 2016, 55, 2748–2752.
52. A. G. Starikov, A. A. Starikova and V. I. Minkin, Russ. J. Gen. Chem., 2017, 87, 98–106.
53. Y. L. Wong, Y. Yan, E. S. H. Chan, Q. Yang, T. C. W. Mak and D. K. P. Ng, Dalton Trans., 1998, 3057–3064.
54. U. Mazzi, F. Tisato, G. Bandoli and M. Nicolini, Dalton Trans., 1986, 1623–1628.
55. P. Papanikolaou, P. D. Akrivos, A. Czapik, B. Wicher, M. Gdaniec and N. Tkachenko, Eur. J. Inorg. Chem., 2013, 2418–2431.
56. M. Gasperini, F. Ragaini and S. Cenini, Organometallics, 2002, 21, 2950–2957.
57. A. Cimino, F. Moscatelli, F. Ferretti, F. Ragaini, S. Germain, J. Hannedouche, E. Schulz, L. Luconi, A. Rossin and G. Giambastiani, New J. Chem., 2016, 40, 10285–10293.
58. M. Shahid, Anjuli, S. Tasneem, I. Mantasha, M. N. Ahamad, F. Sama, K. Fatma and Z. A. Siddiqi, J. Mol. Struct., 2017, 1146, 424–431.
59. CrysAlisPRO, Oxford Diffraction/Agilent Technologies UK Ltd, Yarnton, England.
60. D. Aragão, J. Aishima, H. Cherukuvada, R. Clarken, M. Clift, N. P. Cowieson, D. J. Ericsson, C. L. Gee, S. Macedo, N. Mudie, S. Panjikar, J. R. Price, A. Riboldi-Tunnicliffe, R. Rostan, R. Williamson and T. T. Caradoc-Davies, J. Synchrotron Radiat., 2018, 25, 885–891.
61. G. M. Sheldrick, SADABS, University of Göttingen, Germany, 1996.
62. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
63. P. van der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 194–201.
64. B. J. G. de Aragão and Y. Messaddeq, J. Braz. Chem. Soc., 2008, 19, 1582–1594.
65. M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE 2.1, 2013.
66. S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, New J. Chem., 2002, 26, 996–1009.
67. R. Ketkaew, Y. Tantirungrotechai, P. Harding, G. Chastanet, P. Guionneau, M. Marchivie and D. J. Harding, Dalton Trans., 2021, 50, 1086–1096.
68. M. M. Khusniyarov, K. Harms, O. Burghaus and J. Sundermeyer, Eur. J. Inorg. Chem., 2006, 2985–2996.
69. N. J. Hill, I. Vargas-Baca and A. H. Cowley, Dalton Trans., 2009, 9226, 240–253.
70. C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534.
71. M. O. Sinnokrot and C. D. Sherrill, J. Am. Chem. Soc., 2004, 126, 7690–7697.
72. X. Xuan, J. Wang and H. Wang, Electrochim. Acta, 2005, 50, 4196–4201.
73. R. H. Holm and F. A. Cotton, J. Am. Chem. Soc., 1958, 80, 5658–5663.
74. P. A. Papanikolaou and N. V. Tkachenko, Phys. Chem. Chem. Phys., 2013, 15, 13128–13136.
75. J. Wang, R. Ganguly, L. Yongxin, J. Díaz, H. Sen Soo and F. García, Inorg. Chem., 2017, 56, 7811–7820.
76. R. W. Kiser and T. W. Lapp, Inorg. Chem., 1962, 1, 401–404.
77. I. S. Y. Louise, S. Nabila and K. H. Sugiyarto, Orient. J. Chem., 2019, 35, 1500–1507.
78. E. Kai, T. Arakawa and K. Nishimoto, Inorg. Chim. Acta, 1983, 76, L287–L289.
79. F. E. Jorge, J. Autschbach and T. Ziegler, Inorg. Chem., 2003, 42, 8902–8910.
80. R. D. Archer and B. P. Cotsoradis, Inorg. Chem., 1965, 4, 1584–1589.
81. T. Unruh, L. I. Domenianni and P. Vöhringer, Mol. Phys., 2021, 1–14.
82. B. Li, W. Liu, J. Shao, C.-L. Xue, C.-Z. Xie, Y. Ouyang and J.-Y. Xu, J. Coord. Chem., 2013, 66, 2465–2476.
83. S. Srinivasan, J. Annaraj and P. Athappan, J. Inorg. Biochem., 2005, 99, 876–882.
84. M. Lalia-Kantouri, C. D. Papadopoulos, M. Quirós and A. G. Hatzidimitriou, Polyhedron, 2007, 26, 1292–1302.
85. M. G. Vinum, L. Voigt, C. Bell, D. Mihrin, R. W. Larsen, K. M. Clark and K. S. Pedersen, Chem. – Eur. J., 2020, 26, 2143–2147.
86. M. G. Vinum, L. Voigt, S. H. Hansen, C. Bell, K. M. Clark, R. W. Larsen and K. S. Pedersen, Chem. Sci., 2020, 11, 8267–8272.
87. M. Zhou, X. Li, D. Bu and H. Lei, Polyhedron, 2018, 148, 88–99.
88. K. Hasan, J. Wang, A. K. Pal, C. Hierlinger, V. Guerchais, H. Sen Soo, F. García and E. Zysman-Colman, Sci. Rep., 2017, 7, 2–12.
89. K. Hasan and E. Zysman-Colman, Inorg. Chem., 2012, 51, 12560–12564.
90. W. Kaim, S. Kohlmann, S. Ernst, B. Olbrich-Deussner, C. Bessenbacher and A. Schulz, J. Organomet. Chem., 1987, 321, 215–226.
91. L. Lohmeyer, F. Schön, E. Kaifer and H. J. Himmel, Angew. Chem., Int. Ed., 2021, 10415–10422.

---

Footnote

† Electronic supplementary information (ESI) available: Thermogravimetric analysis, PXRD, additional crystallographic figures, additional electronic spectroscopy, complete solvatochromic fitting, electrochemical data in MeCN. CCDC 2112796–2112801. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1dt03327a.

---