Insights on the coupling between vibronically active molecular vibrations and lattice phonons in molecular nanomagnets

Abstract

Spin–lattice relaxation is a key open problem to understand the spin dynamics of single-molecule magnets and molecular spin qubits. While modelling the coupling between spin states and local vibrations allows to determine the more relevant molecular vibrations for spin relaxation, this is not sufficient to explain how energy is dissipated towards the thermal bath. Herein, we employ a simple and efficient model to examine the coupling of local vibrational modes with long-wavelength longitudinal and transverse phonons in the clock-like spin qubit [Ho(W₅O₁₈)₂]⁹⁻. We find that in crystals of this polyoxometalate the vibrational mode previously found to be vibronically active at low temperature does not couple significantly to lattice phonons. This means that further intramolecular energy transfer via anharmonic vibrations is necessary for spin relaxation in this system. Finally, we discuss implications for the spin–phonon coupling of [Ho(W₅O₁₈)₂]⁹⁻ deposited on a MgO (001) substrate, offering a simple methodology that can be extrapolated to estimate the effects on spin relaxation of different surfaces, including 2D materials.

---

Introduction

Molecular magnetism is a field that has seen remarkable progress over the last three decades. This has resulted in a rich bibliography that covers hundreds of coordination complexes and requires specialized data science tools to properly visualize the experimental results.^1–4 Starting from single-molecule magnets (SMMs) based on transition metal clusters,⁵ the discovery of the so-called single-ion magnets (SIMs), mainly based on lanthanides, allowed the obtention of improved magnetic properties, which stem from the intrinsically large magnetic moment and spin–orbit coupling of rare earth ions.^6,7 Eventually, the SIM strategy lead to the design of coordination spheres resulting in record potential energy barriers and hysteresis temperatures above liquid nitrogen.^8–10 This was possible, at least in part, because this path provides a more intuitive picture to model and rationalize the magnetic anisotropy of a single magnetic ion and its coordination environment.^11–13 While new avenues are still being explored to design and achieve higher potential energy barriers, most theoretical research now focuses on decoupling spin states from molecular vibrations using first principles calculations.^14,15 Indeed, the step that allowed rising the hysteresis temperature from 60 K to 80 K involved precisely a judicious modification of the ligands, not to rise the barrier but to eliminate a vibronically active vibrational mode, i.e. a mode that coupled significantly to spin states.^9,16,17 It has been shown in different ways that spin states in magnetic molecules couple most strongly with local vibrations,^16,18,19 rather than with lattice phonons as is the case for other magnetic solids.²⁰ Moreover, the details of the spin relaxation mechanism in systems with the highest hysteresis temperatures are being actively investigated, in terms of whether Orbach or Raman are the dominant processes.^21,22 However, there is still an open question in determining how local vibrations couple with lattice phonons to allow for the energy to flow from the spins of the molecule to the thermal bath of the solid. More generally, understanding the coupling between spin states, molecular vibrations and lattice phonons will also help to understand the dynamics of molecular ferroelectrics²³ and hybrid molecular solid-state materials.

A recent work combining 4D Inelastic Neutron Scattering (4D-INS) with DFT calculations has demonstrated that explicit analysis of phonon eigenvectors is necessary to properly estimate spin–phonon coupling. This involves not only localized molecular vibrations, related to optical phonon, but also extended lattice vibrations, also known as acoustic phonons.²⁴ The participation of low-lying optical phonons, i.e. molecular vibrations, in spin relaxation is more obvious, since the distortions couple strongly with the spin Hamiltonian. Less obvious, but also crucial, is the consideration of anticrossings between low-lying optical branches and acoustic phonons. These can be experimentally detected only by measuring phonon dispersions and it is well-known that can cause a decrease on the phonon lifetimes.^25–27 The mixing of optical and acoustic phonon eigenvectors due to these anticrossings results in an effective communication of the spin states with the thermal bath, thus enhancing magnetic relaxation in molecular nanomagnets and reducing T₁ in molecular spin qubits.²⁸

In order to advance towards a solution, it seems adequate to start from a model molecular nanomagnet that has been extensively studied in the past few years. For that, we focus our attention on [Ho(W₅O₁₈)₂]⁹⁻, a polyoxometalate system that displays so-called Atomic Clock Transitions, which protect qubit states from magnetic noise. This allows for coherent operation at high concentrations.²⁹ Over the years, the spin energy level structure of this system has been widely characterized, both from the experimental and theoretical points of view.^30–34 In particular, recent studies have been able to determine the couplings between spin states and molecular vibrations or distortions. In particular, a theoretical characterization at CASSCF level has been employed to rationalize experiments of quantum coherent electrical control of spins³⁵ and magneto-infrared spectroscopy.³⁶ In Liu et al.,³⁵ the molecular structure was distorted by applying an external electric field, and the coupling of this distortion with the Crystal Field Hamiltonian was modeled by expanding it in the basis of normal modes of vibration. A first principles model was able to reproduce the experimentally determined effect of the electric field on the tunneling gap. In Blockmon et al.,³⁶ modelling of vibronic coupling allowed us to reproduce the observed dependence of the infrared spectra atrising magnetic fields. Starting from these successful schemes for the vibronic coupling in Na₉[Ho(W₅O₁₈)₂]·35H₂O, herein we develop a theoretical model to explore the missing link between local vibrations and the thermal bath, namely vibronic–phonon coupling.

Results and discussion

Modelling vibronic–phonon coupling

Previous analyses in [Ho(W₅O₁₈)₂]⁹⁻ have identified the more crucial vibronically active vibrations.³⁶ Specific M_J spin energy levels couple to various HoO₈ rocking and stretching modes. This includes asymmetric HoO₈ stretching with cage tilting, and, in particular, the vibrational mode n = 1, presenting the lowest vibrational frequency ν = 8.6 cm⁻¹ (Fig. 1). This mode can be approximated as a torsion along the near-C₄ molecular axis, where the upper moiety rotates clockwise while the lower one rotates anti-clockwise. At the low temperature range, relevant for the clock transition experiments, this vibration is involved in the thermal dependence of the spin–lattice relaxation rate T₁.³⁶ The vibronic coupling S_n for a dense spectrum of vibronically active vibrations, as calculated in that work, is represented in Fig. 1. The key question is therefore whether all these vibrational modes, and in particular n = 1, couple directly to phonons.

Fig. 1 (a) Structure of the molecular anion [Ho(W₅O₁₈)₂]⁹⁻, superimposed with vectors indicating the atomic displacements for normal mode n = 1 and the (x,y,z) reference frame. (b) Vibronic coupling S_nvs. vibrational frequency for molecular normal modes in [Ho(W₅O₁₈)₂]⁹⁻.

A conceptual cornerstone of the model employed in the present work is the fact that we deal with phonons of long-wavelength, which we assume to (i) not depend on the molecular details and (ii) couple only weakly to spin states. To model this kind of phonons one can employ the same approach described previously in the context of strong and weak interacting two level systems in disordered solids.³⁷ This is based on the generally accepted idea that it is often a convenient approximation to distinguish between “longitudinal” and “transverse” acoustic phonons, although in practice they are not pure.²⁴

Let us say we want to model the effect on a local excitation of a phonon field μ_αβ, where α = x is the unit vector of the phonon amplitude and β = x is the unit vector of the phonon propagation direction. For simplicity we can take as an example the longitudinal phonon μ_xx along x. Assuming that the phonon has a long-wavelength compared with our local excitation, we can just employ a homogeneous lattice contraction by a fraction b along crystallographic direction x tomimic the effect of a longitudinal phonon along the same coordinate. The distorted molecular coordinates d_α can be defined by considering, for each atom, the equilibrium coordinates e_α and the distortion b, which is proportional to the position e_β along the propagation vector β:

d_α = e_α + b·e_β (1)

The application of a longitudinal phonon μ_xx to an atom with equilibrium coordinates (e_x,e_y,e_z) results in the distorted coordinates (e_x + b·e_x,e_y,e_z). As an example for transverse phonon let us take μ_xz, which results in the distorted coordinates (e_x + b·e_z,e_y,e_z) (see Fig. 2). Three longitudinal phonons μ_xx,μ_yy,μ_zz and six transverse phonons μ_xy,μ_xz,μ_yx,μ_yz,μ_zx,μ_zy can be constructed in this way. Locally, each of the three longitudinal phonons acts like a uniaxial strain, while each of the six transverse ones acts as a shear strain. This permits an exploration of the long-wavelength part of the phonon spectrum employing just 9 model phonons. Fig. 2 illustrates the relation between phonon amplitude and atomic position for the example of a transverse phonon μ_zx, as well as the qualitative effect of such a phonon on the molecular anion [Ho(W₅O₁₈)₂]⁹⁻, where we take as a criterion that the long axis of the molecule defines the x axis.

Fig. 2 Left: Long-wavelength transverse phonon μ_zx, with phonon amplitude along z and propagating along x (phonon amplitude greatly exagerated to facilitate visualization). Assuming the molecule fits in the width of the red line, each atom suffers a strain b_z along the phonon amplitude direction z that is directly proportional to its position u_x along the propagation direction x. Right: Relative effect of transverse phonon μ_zx on [Ho(W₅O₁₈)₂]⁹⁻ with respect to the central Ho³⁺ ion. Color code: Ho (green), W (gray) and O (red).

To facilitate comparisons one can impose a normalizing condition to the phonon displacements so that the product for any α,β. The vibronic–phonon coupling S(μ_n,αβ) is simply calculated as the scalar product between the normalized displacement vectors defining each normal mode 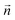and each of the idealized phonons 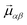, in absolute value:

In practice, we are estimating the intensity of anticrossings between optical and acoustic phonon branches. This could be experimentally characterized using 4D-INS as previously shown.²⁴

Application to [Ho(W₅O₁₈)₂]⁹⁻

Fig. 3 shows the coupling of each molecular normal mode of vibration to our 9 model phonons (for full details, see ESI†). Since S(μ_n,αβ) = 1 is the theoretical maximum for a normal mode that has the exact displacement vector as one of the idealized phonons we defined, it is immediate to see that many vibrations couple significantly to at least a type of phonon, with values 0.1 < S(μ_n,αβ) < 0.2. Additionally, vibrations n = 4, 5, 6 (24, 30, 43 cm⁻¹) couple strongly with the three phonons propagating along the molecular axis μ_xx,μ_yx,μ_zx. At the same time one can notice that the spectrum is much more sparse compared to the one depicting vibronic coupling strength in Fig. 1. Note that the values are influenced by the reference frame choice defining the phonons, but that for symmetry reasons all qualitative conclusions are independent of that choice. In particular, vibrations that are orthogonal to all 9 phonons in a given reference frame will consistently be orthogonal for any other reference frame.

Fig. 3 Plots of vibronic–phonon coupling vs. normal mode energy, overlayed with vibronic coupling of each mode. Rows correspond to the direction of the phonon amplitude of the distortion, columns correspond to the direction of the phonon propagation. The long axis of the molecule defines the x axis. Longitudinal phonons μ_xx,μ_yy,μ_zz are thus in the diagonal, and transverse phonons μ_xy,μ_xz,μ_yx,μ_yz,μ_zx,μ_zy in their corresponding extradiagonal locations.

Inspecting the numbers in some detail (see ESI†) we find that for mode n = 1 all vibronic–phonon couplings S(μ_1,αβ) are of the order of 0.01 or smaller. This means that, even if at low temperature the lowest frequency vibrational mode was found in a previous work to be the one that couples with the spin subsystem and governs the relaxation,³⁶ it cannot communicate directly with the phonon bath. Thus, an extra step is required to complete the relaxation pathway, probably via the anharmonicity of the molecular vibrations which breaks their exact orthogonality and allows energy transfer between them.

In the original ac susceptometry experimental measurements on [Ho(W₅O₁₈)₂]⁹⁻, a strongly frequency-dependent shoulder was observed in χ″, situated at ca. 5 K (for a frequency of 10.000 Hz), which tended to disappear when the frequency was reduced, and a divergence at lower temperatures.³¹ This behavior closely resembled that of the SMM Er derivative when studied at low frequencies. This relatively poor but non-negligible SMM behavior, gradually lost above 5 K due to processes that start to dominate around 3 K, is consistent with our present theoretical findings.

In the calculations, it is also noticeable that there is a window between 220 and 320 cm⁻¹ with practically no coupling between local vibrations and phonons. The molecular design of systems where this window is at low energies would be a novel way of forcing a phonon bottleneck that would facilitate long relaxation times. This idea of minimizing vibronic–phonon coupling for vibrations accessible at low temperature is of course complementary to the well-known strategy of avoiding vibronic coupling for the same energy range.

It would now be possible to map known phonon spectra of relevant surfaces onto our 9 phonon scheme and obtain useful insights. In particular, for illustration purposes let us focus on MgO(001), which was employed to decouple Ho atoms from the underlying Ag substrate in the first single atom magnet experiments.³⁸ Recent studies in this system have already elucidated the role of localized vibrational modes in its spin relaxation.³⁹ Calculations on a thin slab model⁴⁰ identified surface phonons in the region of 150 cm⁻¹, corresponding to out-of plane and in-plane shear vibrations. If we define x as the vector normal to the MgO surface, these out-of plane and in-plane shear vibrations would correspond to phonons of the kind μ_xz,μ_xy and μ_yz,μ_zy respectively. Our analysis evidences that it would be an advantageous environment for [Ho(W₅O₁₈)₂]⁹⁻ anions, since the first molecular vibrations which are significantly coupled to this kind of phonons would be n = 5 at 25–30 cm⁻¹. Regarding the orientation of the molecule on the surface, due to the stronger coupling of molecular normal modes with the three phonons propagating along the molecular axis, it would be desirable to orient the molecular axis perpendicular to the surface. A possible approach for this purpose is the covalent functionalization of the molecular nanomagnet using a grafting functional group. Indeed, it has been reported that in [Ho{Mo₅O₁₃(OMe)₄NNC₆H₄-p-NO₂}₂]³⁻,⁴¹ the molybdenum analogue to [Ho(W₅O₁₈)₂]⁹⁻, the magnetic ion presents an equivalent coordination sphere in a chemically identical structure, except for the presence of two apical –NO₂⁻ grafting groups that can be chemically tuned to control the orientation of the molecule in different substrates. Although challenging, alternative chemical strategies such as the use of α-cyclodextrins rings, which have been experimentally combined with polyoxopalladates,⁴² or rotaxanes that can form surface-attached rotaxanes on gold substrates,⁴³ can be proposed in order to stabilize an off-plane orientation of the molecular axis, which would minimize vibronic–phonon coupling in this molecule, as we have estimated in this work. More generally, this kind of efficient calculation could offer a set of preliminary guidelines in order to reduce the coupling between vibronically active molecular vibrations and surface phonons when the magnetic molecules are deposited onto bidimensional substrates, such as graphene⁴⁴ or transition metal dichalcogenides in which charge density waves are also present.⁴⁵

Conclusions

Considerable progress has been made in the modelling of spin–lattice relaxation in molecular spin qubits and molecular nanomagnets. However, most of the state-of-the-art models are still essentially zero-dimensional and thus fundamentally unable of describing the energy dissipation to the thermal bath, and only extremelly challenging combinations of state of the art experiments and theory can explicitly unveil these mechanisms.²⁴ We have employed a model to offer an estimate of the coupling between local vibrational modes and long-wavelength phonons to the clock-like spin qubit Na₉HoW₁₀O₃₆·xH₂O. We found that the first vibrational mode, which presents significant vibronic coupling and had been attributed to play a crucial role in spin–lattice relaxation does not couple significantly to long-wavelength lattice phonons, neither longitudinal nor transverse, thus revealing that further intramolecular energy transfer via anharmonic vibrations is involved in the spin relaxation process. As a more general insight, this simple model provides information on the relation of molecular vibrations vis-à-vis long-wave phonons. This can be obtained from a very efficient calculation and even in some cases from visual inspection and can be of interest in the design of more robust molecular nanomagnets and spin qubits. This can be especially valuable for the case of single molecules deposited on well-known surfaces, where experiments are challenging and can benefit from theoretical insights.

Author contributions

Conceptualization and methodology: A. G. A. Investigation, software and formal analysis: A. U. Supervision: J. J. B. and A. G. A. Original draft: A. G. A. Reviewing and editing: E. C. and J. J. B.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge funding by the EU (ERC-2014-CoG-647301 DECRESIM, ERC-2018-AdG-788222 MOL-2D, the SUMO QUANTERA Project and FET-OPEN grant 862893 FATMOLS); the Spanish MCIU (grant MAT2017-89993-R and CTQ2017-89528-P cofinanced by FEDER; the Unit of excellence ‘María de Maeztu’ CEX2019-000919-M); the Generalitat Valenciana (PROMETEO/2019/066 and PROMETEO/2017/066, SEJI/2018/035 and grant CDEIGENT/2019/022).

References

1. G. Aromí and O. Roubeau, Handbook on the Physics and Chemistry of Rare Earths, Elsevier, 2019, vol. 56, pp. 1–54.
2. J. Long, Y. Guari, R. A. Ferreira, L. D. Carlos and J. Larionova, Coord. Chem. Rev., 2018, 363, 57–70.
3. E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104.
4. Y. Duan, J. T. Coutinho, L. E. Rosaleny, S. Cardona-Serra, J. J. Baldoví and A. Gaita-Ariño, 2021, arXiv, 2103.03199.
5. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
6. N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
7. S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733.
8. K. L. Harriman, J. L. Brosmer, L. Ungur, P. L. Diaconescu and M. Murugesu, J. Am. Chem. Soc., 2017, 139, 1420–1423.
9. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
10. Z.-H. Li, Y.-Q. Zhai, W.-P. Chen, Y.-S. Ding and Y.-Z. Zheng, Chem. – Eur. J., 2019, 25, 16219–16224.
11. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
12. L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043–10056.
13. S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. Walsh and F. Tuna, Coord. Chem. Rev., 2017, 346, 216–239.
14. A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620.
15. A. Ullah, J. Cerdá, J. J. Baldoví, S. A. Varganov, J. Aragó and A. Gaita-Ariño, J. Phys. Chem. Lett., 2019, 10, 7678–7683.
16. C. A. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
17. K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503.
18. M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244.
19. L. E. Rosaleny, K. Zinovjev, I. Tuñón and A. Gaita-Ariño, Phys. Chem. Chem. Phys., 2017, 548, 439–442.
20. K. R. O'Neal, A. Paul, A. Al-Wahish, K. D. Hughey, A. L. Blockmon, X. Luo, S.-W. Cheong, V. S. Zapf, C. V. Topping and J. Singleton, et al. , npj Quantum Mater., 2019, 4, 1–6.
21. M. J. Giansiracusa, A. K. Kostopoulos, D. Collison, R. E. P. Winpenny and N. F. Chilton, Chem. Commun., 2019, 55, 7025–7028.
22. A. Castro-Alvarez, Y. Gil Sanchez, L. C. Llanos and D. Aravena, Inorg. Chem. Front., 2020, 7, 2478–2486.
23. J. Long, M. S. Ivanov, V. A. Khomchenko, E. Mamontova, J.-M. Thibaud, J. Rouquette, M. Beaudhuin, D. Granier, R. A. Ferreira and L. D. Carlos, et al. , Science, 2020, 367, 671–676.
24. E. Garlatti, L. Tesi, A. Lunghi, M. Atzori, D. Voneshen, P. Santini, S. Sanvito, T. Guidi, R. Sessoli and S. Carretta, Nat. Commun., 2020, 11, 1–10.
25. C. H. Lee, I. Hase, H. Sugawara, H. Yoshizawa and H. J. Sato, Phys. Soc. Jpn., 2006, 75, 123602.
26. M. Christensen, A. B. Abrahamsen, N. B. Christensen, F. Juranyi, N. H. Andersen, K. Lefmann, J. Andreasson, C. R. H. Bahl and B. B. Iversen, Nat. Mater., 2008, 7, 811–815.
27. E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843–15852.
28. A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051–6059.
29. M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351.
30. R. Shiozaki, A. Inagaki, A. Nishino, E. Nishio, M. Maekawa, H. Kominami and Y. Kera, J. Alloys Compd., 1996, 234, 193–198.
31. M. A. AlDamen, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467–3479.
32. S. Ghosh, S. Datta, L. Friend, S. Cardona-Serra, A. Gaita-Ariño, E. Coronado and S. Hill, Dalton Trans., 2012, 41, 13697–13704.
33. M. Vonci, M. J. Giansiracusa, W. Van den Heuvel, R. W. Gable, B. Moubaraki, K. S. Murray, D. Yu, R. A. Mole, A. Soncini and C. Boskovic, Inorg. Chem., 2017, 56, 378–394.
34. L. Escalera-Moreno and J. J. Baldoví, Front. Chem., 2019, 7, 662.
35. J. Liu, J. Mrozek, Y. Duan, A. Ullah, J. J. Baldoví, E. Coronado, A. Gaita-Ariño and A. Ardavan, 2021, arXiv, 2005.01029.
36. A. L. Blockmon, A. Ullah, K. D. Hughey, Y. Duan, K. R. O'Neal, M. Ozerov, J. J. Baldoví, J. Aragó, A. Gaita-Ariño, E. Coronado and J. L. Musfeldt, 2021, arXiv, 2102.08713.
37. A. Gaita-Ariño and M. Schechter, Phys. Rev. Lett., 2011, 107, 105504.
38. F. B. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Nature, 2017, 543, 226–228.
39. F. Donati, S. Rusponi, S. Stepanow, L. Persichetti, A. Singha, D. M. Juraschek, C. Wäckerlin, R. Baltic, M. Pivetta, K. Diller, C. Nistor, J. Dreiser, K. Kummer, E. Velez-Fort, N. A. Spaldin, H. Brune and P. Gambardella, Phys. Rev. Lett., 2020, 124, 077224.
40. V. Shpakov, A. Gotte, M. Baudin, T. Woo and K. Hermansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 195427.
41. J. J. Baldoví, Y. Duan, C. Bustos, S. Cardona-Serra, P. Gouzerh, R. Villanneau, G. Gontard, J. M. Clemente-Juan, A. Gaita-Ariño and C. Giménez-Saiz, et al. , Dalton Trans., 2016, 45, 16653–16660.
42. M. Stuckart, N. V. Izarova, J. van Leusen, A. Smekhova, C. Schmitz-Antoniak, H. Bamberger, J. van Slageren, B. Santiago-Schübel and P. Kögerler, Chem. – Eur. J., 2018, 24, 17767–17778.
43. A. L. Vance, T. M. Willey, T. van Buuren, A. Nelson, C. Bostedt, G. A. Fox and L. J. Terminello, Nano Lett., 2003, 3, 81–84.
44. N. Konstantinov, A. Tauzin, U. N. Noumbé, D. Dragoe, B. Kundys, H. Majjad, A. Brosseau, M. Lenertz, A. Singh and S. Berciaud, et al. , J. Mater. Chem. C, 2021, 9, 2712–2720.
45. C. Boix-Constant, S. Mañas-Valero, R. Córdoba, J. J. Baldoví, A. Rubio and E. Coronado, ACS Nano, 2021 DOI:10.1021/acsnano.1c03012.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary tables including vibronic and vibronic-phonon coupling for 110 normal modes. See DOI: 10.1039/D1DT01832A

---