Open Access Article
Open Access Article1st row transition metal aluminylene complexes: preparation, properties and bonding analysis†‡
Richard Y.
Kong
 and
Mark R.
Crimmin
and
Mark R.
Crimmin
 *
*
Molecular Science Research Hub, Imperial College London, 82 Wood Lane, White City, London, W12 0BZ, UK. E-mail: m.crimmin@imperial.ac.uk
First published on 30th April 2021
Abstract
The synthesis and spectroscopic characterisation of eight new first-row transition metal (M = Cr, Mn, Fe, Co, Cu) aluminylene complexes is reported. DFT and ab initio calculations have been used to provide detailed insight into the metal–metal bond. The σ-donation and π-backdonation properties of the aluminylene ligand are evaluated via NBO and ETS-NOCV calculations. These calculations reveal that these ligands are strong σ-donors but also competent π-acceptors. These properties are not fixed but vary in response to the nature of the transition metal centre, suggesting that aluminylene fragments can modulate their bonding to accommodate both electron-rich and electron-poor transition metals. Ab initio DLPNO-CCSD(T) calculations show that dispersion plays an important role in stabilising these complexes. Both short-range and long-range dispersion interactions are identified. These results will likely inform the design of next-generation catalysts based on aluminium metalloligands.
Introduction
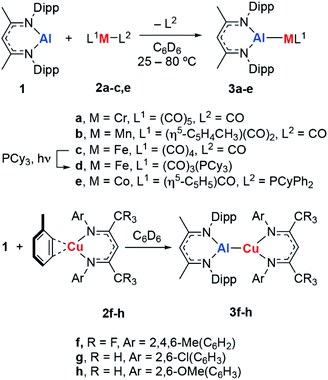
Metalloligands can engage in bonding with transition metals through the formation of direct and unsupported metal–metal bonds. These ligand types can result in significant modification of the electronics of transition metal complexes and even provide an additional reaction site which can engage in cooperative substrate activation.1 The use of aluminium-based metalloligands in catalysis is becoming increasingly popular, in part due to the abundance and low cost of this element.2–5For example, the inclusion of aluminium sites in pincer complexes of group 9 or 10 metals has led to new catalysts based on X-type aluminyl§ metalloligands for alkane dehydrogenation,6 the hydroarylation of alkenes with pyridine,7 the magnesiation of aryl fluorides,8 and the activation of CO2.9–11 Related Z-type aluminium ligands have been shown to influence the catalytic competency of nickel metal-centres for alkene hydrogenation.12 For our part, we have been interested in the development of L-type aluminylene¶ ligands derived from low-valent aluminium(I) compounds and their role in the catalytic functionalisation of C–H, C–O and C–F bonds (Fig. 1a).13–15
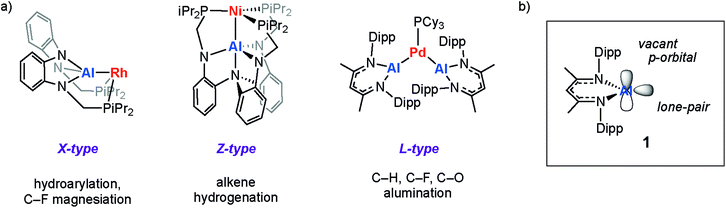 | ||
| Fig. 1 (a) Pre-catalysts with X-type, Z-type, and L-type aluminium metalloligands. (b) The aluminylene ligand, 1. Dipp = 2,6-diisopropylphenyl. | ||
Despite rapid progress in this area, the fundamental properties of aluminium-based metalloligands remains poorly understood. A deeper, understanding of this interaction could improve insight into the existing catalytic processes, inspire new approaches to catalyst design and ultimately allow development of more sustainable catalysts based on 1st row transition metals. Herein we focus on the aluminylene ligand 1 (Fig. 1b) which is a neutral aluminium(I) species and isoelectronic with widely applied carbene based ligands (NHCs, cAACs). The electronic structure of 1 has been studied in detail. The aluminium centre is proposed to be close to sp-hybridised with low-lying acceptor p-orbitals orthogonal to and in-plane with the β-diketiminate ligand.16
The coordination of aluminylene metalloligands to transition metals can be traced back to a pioneering study by Fischer, Frenking, and co-workers from 1998.17 A series of group 6 complexes of the form [M(CO)5{AlR(κ2-TMEDA)}] were isolated and characterised (M = Cr, Mo, W; TMEDA = tetramethylenediamine; R = Cl, Me, Et). Calculations on the analogous amine-free complexes showed some degree of tungsten to aluminium π-backdonation. The π-acceptor character of aluminylene ligands has been further highlighted by Aldridge, Willock, and co-workers using DFT calculations.18
Following this breakthrough, the coordination of [AlCp*] to Fe,19,20 Cr,21 Ru,20 Pt,22 and Ni23 centres was reported. Coordination complexes of 1 were also been documented,24,25 along with related species containing a base-stabilised borylaluminylene ligand.26 Analysis of the bonding in these complexes is complicated by the propensity for the electron-deficient metalloligand to promote dimer formation by either directly bridging metal⋯metal centres or forming bridging interactions with secondary ligands (e.g. isocarbonyl bridges).
Only in a handful of cases have coordination complexes with unsupported aluminium to transition metal bonds been isolated and characterised. For [AlCp*], heterobimetallic complexes possessing terminal Al–M (M = Fe, Ru, Ni, and Cr) have been prepared, and analysis has shown that the metal–metal bond is highly ionic, with the [AlCp*] metalloligand acting as a pure σ-donor.19–21,23 In 2014, Tokitoh and co-workers synthesized a platinum complex with a terminal arylaluminylene ligand. The π-acceptor character of the aluminylene ligand was shown to be significant; the metal–metal bond was estimated to be 55.8% in σ-character and 44.2% in π-character through NBO analysis.27 In 2020, Power and co-workers reported the synthesis of an Al–Cu heterobimetallic complex of 1.28 In addition to the strong σ-donor and π-acceptor properties of 1, examination of these complexes using energy decomposition analysis and D3-corrected density functional theory (DFT) led to the identification of a key role of dispersion interactions involving the β-diketiminate ligand.29 Related complexes involving terminal Al–Pd bonds have also been reported.13,24,25 We have championed the catalytic applications of these types of complexes and suggested that dispersion interactions between the metalloligand and substrate can influence selectivity.4,13–15
In this paper, we report the synthesis of a series of eight new aluminylene complexes of 1 with first-row transition metals. These complexes have been characterised in the solid state and solution. Detailed calculations were performed to understand the nature of the metal–metal bond through both ab initio and DFT studies. Specifically, we show that the σ-donation properties of the aluminium(I) ligand are dependent on the transition metal identity, while the π-acceptor characteristics are predominantly affected by the ligands bound to the transition-metal. Dispersion is surprisingly uniform across the diverse ligand set: both short-range and long-range interactions are key contributors to the stabilisation of these complexes.
Results and discussion
Synthesis and characterisation
Reaction of 1 with a series of transition metal complexes (2) in C6D6 solution furnished the corresponding heterobimetallic aluminylene complexes (3a–h). These reactions occurred at 25 °C, with the exception of the formation of 3b which required heating at 80 °C over 18 h to reach completion (Scheme 1). Photolysis of 3c in the presence of PCy3 results in substitution of the trans CO ligand by PCy3. This reaction could be followed by 31P NMR spectroscopy and occurs with consumption of PCy3 (δ = 9.8 ppm) and formation of 3d (δ = 84.5 ppm). In all cases, coordination of the aluminylene ligand to the transition metal occurred with displacement of a weakly bound ligand (toluene, CO, PCyPh2); a process that likely proceeds by a dissociative mechanism for the 18-electron transition metal fragments. Consumption of 1 was evidenced by the bleaching of the orange-red colour during the synthesis. 3a–h can be assigned with formal d6, d8 or d10 electron-counts and are expected to be low-spin and diamagnetic.30,31 Characterisation of 3a–h by 1H and 19F NMR spectroscopy shows that coordination occurs with preservation of the Cs symmetry element of 1.The infrared data for complexes 3a–d showed that the ν(CO) absorption is red-shifted relative to the parent metal carbonyl 2a–d. This observation is consistent with increased electron density at the transition metal centre and both superior σ-donor and inferior π-acceptor properties of the aluminylene ligand relative to CO. The ν(CO) absorption in 3a–d is similarly red-shifted compared to their analogous NHC-complexes supported by IPr ligands (IPr = 1,3-bis(2,6-diisopropylphenyl)imidazol-2-ylidene). In the case of 3e, the highly red-shifted carbonyl stretch of ν(CO) = 1640 cm−1 is characteristic of a bridging isocarbonyl ligand (Table 1).26
Solid-state data
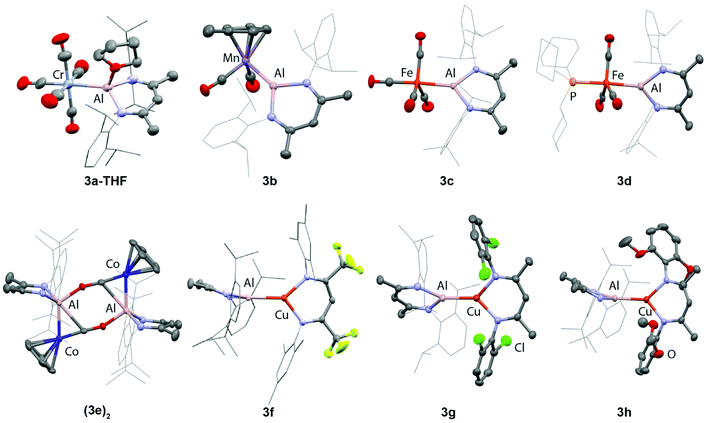
3a–h have been characterised in the solid state by single crystal X-ray diffraction (Fig. 2, Table 2). These complexes all feature unsupported Al–M bonds in which M is a first-row transition metal (Cr–Co, Cu). 3a crystallises as the THF adduct 3a·THF, while 3e dimerises in the solid state to form an isocarbonyl bridged dimer (3e)2. The complete insolubility of (3e)2 in common NMR solvents precluded the solution characterisation of this species and as such it is unclear if the dimeric form of 3e persists in solution. DFT calculations suggest the dimerisation is an exergonic process and (3e)2 is calculated to be 29.9 kcal mol−1 more stable than 2 equiv. of 3e. For 3d, the single crystal X-ray diffraction data confirm that ligand exchange occurs to form an isomer in which 1 is coordinated at the apical position of a five-coordinate trigonal bipyramidal iron complex. In all other cases, there are no issues of selectivity on substitution.| Al–M (Å) | FSR | Al–N (Å) | N–Al–N (°) | |
|---|---|---|---|---|
| 1 | — | — | 1.957(2) | 89.86(8) |
| 1.958(2) | ||||
| 3a·THF | 2.557(2) | 1.03 | 1.952(2) | 93.9(2) |
| 1.934(2) | ||||
| 3b | 2.3094(7) | 0.94 | 1.9177(18) | 93.46(8) |
| 1.9075(18) | ||||
| 3c | 2.2762(10) | 0.94 | 1.8663(18) | 97.80(11) |
| 1.8663(18) | ||||
| 3d | 2.2547(9) | 0.93 | 1.895(2) | 95.27(10) |
| 1.888(2) | ||||
| (3e)2 | 2.3152(7) | 0.98 | 1.924(2) | 97.75(9) |
| 1.9128(19) | ||||
| 3f | 2.3021(7) | 0.97 | 1.9183(19) | 94.01(8) |
| 1.9090(19) | ||||
| 3g | 2.3132(7) | 0.97 | 1.920(2) | 92.21(9) |
| 1.922(2) | ||||
| 3h | 2.2670(9) | 0.95 | 1.922(3) | 93.25(12) |
| 1.915(3) |
The metal–metal bond lengths can be compared across the series 3a–h through considering the formal shortness ratio (fsr) of these bonds. In essence, the fsr provides a normalised metal–metal bond length that factors in the changes in radii of the transition metal.37,38 Fsr's which are much lower than 1 are a potential indicator of multiple bond character. The fsr's of 3a–h support the assignment of the Al–M bond as a single bond and vary little across the series. Notably, however, in complexes where the p-orbital of aluminium is occupied by an oxygen donor, e.g.3a·THF and (3e)2, larger fsr's (>0.97) are observed. This effect could in part be explained by the increased coordination number at Al causing a lengthening of the metal–metal bond.
The aluminylene ligands of 3a–h retain a Cs symmetry element, as expected based on the multinuclear NMR data. Structural metrics can be used as an indicator of the formal oxidation state of the aluminium centre in derivatives of 1. Longer Al–N bond lengths and more acute N–Al–N bond angles are indicative of a lower formal oxidation state (+1 vs. +3). Within the series 3a–h, a range of Al–N (1.8663 A to 1.952(2) A) bond distances and N–Al–N angles (92.21(9)° to 97.80(11)°) are observed. While in all complexes the aluminium fragment can be assigned a formal +1 oxidation state, the broad range of these metrics suggests considerable variation of the electronic environment of aluminium occurs in response to changes in the transition metal fragment.
Consideration of the impact of aluminylene coordination on auxiliary ligands in the cis and trans position the transition metal in 3a–h provides some further insight into the properties of this ligand class. The electropositive aluminium site in 1 drives the formation of semi-bridging carbonyl interactions in 3c and 3d, with the asymmetry parameter (α) taking values of 0.47 and 0.49 respectively for these complexes.39 The structure of (3e)2 contains a rare example of an isocarbonyl bridged aluminylene ligand. The isocarbonyl ligand is characterised by a short Co–C bond length of 1.624(3) Å and elongated C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O bond of 1.240(3) Å. The isocarbonyl ligand is also semi-bridging between Co and Al in each monomeric unit (α = 0.49). Further, the trans-influence of 1 can considered by inspecting the data for 3a·THF and 3c. In the case of 3c, the M–C bond length trans carbonyl ligand to the aluminylene ligand is statistically identical to the cis carbonyl ligands. In contrast, for 3a·THF, the M–C bond length of the trans CO is slight shorter than those of the cis CO. Population of the partially vacant p-orbital of 1 appears to impact the properties of this ligand weakening its trans-influence.
O bond of 1.240(3) Å. The isocarbonyl ligand is also semi-bridging between Co and Al in each monomeric unit (α = 0.49). Further, the trans-influence of 1 can considered by inspecting the data for 3a·THF and 3c. In the case of 3c, the M–C bond length trans carbonyl ligand to the aluminylene ligand is statistically identical to the cis carbonyl ligands. In contrast, for 3a·THF, the M–C bond length of the trans CO is slight shorter than those of the cis CO. Population of the partially vacant p-orbital of 1 appears to impact the properties of this ligand weakening its trans-influence.
Bonding analysis
In order to further interrogate the nature of metal–metal bonding, we turned to density functional theory (DFT) and ab initio calculations. Calculations were performed in Gaussian 09 and Orca 4.2.1, and a range of computational techniques were used (NBO, ETS-NOCV, LED) in order to interrogate the metal–metal bond. 3a·THF and (3e)2 were modelled without coordinated solvent and as the monomer, respectively. For completeness, we also investigated a model complex, [Ni(CO)3(1)]. Structures were optimised using density functional theory (DFT) with the M06l functional and a hybrid basis set of 6-31-G** (C, H, N, O, P) and SDDAll (Al, M).The Wiberg bond indices (WBI) for the aluminium-metal bond in the series range from 0.43 to 0.79 (Table 3). The Wiberg bond index is a measure of covalency within a chemical bond with values close to 1 indicating a highly covalent single bond. Based on the calculations, the metal–metal bonds in these complexes can be assigned as single bonds in which the covalent contribution varies in response to the nature of the transition metal fragment. When the transition-metal fragment is coordinated by strong π-acceptor ligands, e.g.3a, 3c, 3d, and [Ni(CO)3(1)], WBIs and the covalent character of the bond are low. When the transition metal is bound by σ-donor and π-donor ligands, e.g.3b, 3e–h, WBIs increase. The trend is further exemplified by the series of copper complexes with the most electron-rich ligand system in 3h resulting in the highest calculated WBI for the Al–Cu bond. These data suggest the covalency of the metal–metal bond is highly correlated to the electron density at the transition-metal centre.
| Wiberg bond index | NPA charge | ||
|---|---|---|---|
| Al–M | Al | M | |
| 1 | — | 0.78 | — |
| 3a | 0.46 | 1.50 | −1.40 |
| 3b | 0.64 | 1.57 | −0.75 |
| 3c | 0.42 | 1.51 | −0.58 |
| 3d | 0.43 | 1.54 | −0.66 |
| 3e | 0.73 | 1.37 | −0.15 |
| [Ni(CO)3(1)] | 0.39 | 1.12 | 0.22 |
| 3f | 0.76 | 1.09 | 0.51 |
| 3g | 0.72 | 1.00 | 0.57 |
| 3h | 0.79 | 1.05 | 0.50 |
Analysis of the natural population analysis (NPA) charges on the family of compounds shows that the charge of the aluminium centre is further dependent on the transition metal identity and ligand set. In the complexes of the earlier transition metals (Cr, Fe, Co), aluminium has a larger NPA charge (>1.25) than those of the later transition metals (Ni, Cu), where aluminium is calculated to have a smaller NPA charge (<1.15). This implies that the extent of the σ-donation is modulated by transition metal identity, and likely reflects diminished electron-transfer from 1 to d10 metal complexes. The poorer σ-donation properties of 1 to later transition metals is supported by ETS-NOCV calculations.
ETS-NOCV calculations on the complexes were performed to obtain deeper insight into the bonding interactions (Table 4). The principal contribution (Δρ1) in all complexes to the orbital interaction, ΔEorb, is the donation of the aluminium based lone-pair to the transition-metal fragment. The σ-donation of the aluminium lone pair varies with the transition metal fragment. A broad trend emerges that σ-donation is stronger for the earlier first row transition metals (Cr, Mn, Fe), than for the later transition metals (Co, Ni, Cu). Inspection of the deformation density plots allows visualisation of this donor–acceptor interaction. In the case of 3a–e the acceptor orbital is comprised of a linear combination of a dz2 orbital with the anti-bonding (π*) orbitals of the CO ligands (Fig. 3a). In the case of [Ni(CO)3(1)], the acceptor orbital is comprised almost entirely of the π* manifold of the three CO ligands. This interaction is reminiscent of the bonding between alkali metals with the {Ni(CO)3} fragment (Fig. 3b).40 For the series 3f–h, Δρ1 depicts contribution of the aluminium lone-pair into the copper 4s-orbital (Fig. 3c). Hence, the extent of σ-contribution to the transition metal fragment is governed by the 3d occupancy of the transition-metal, as well as the acceptor character of ligands on the transition metal.
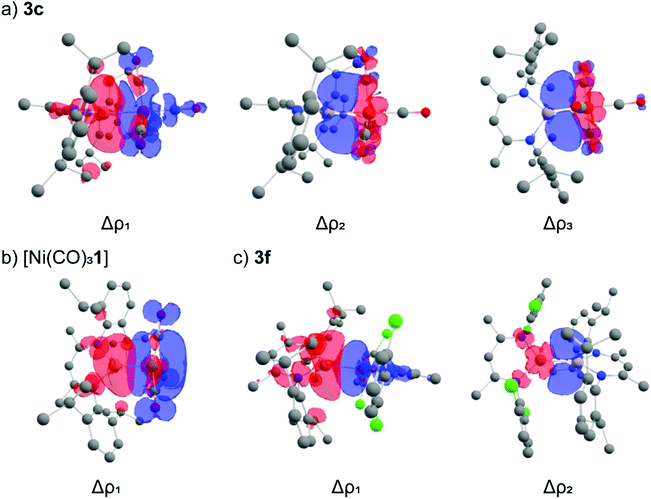 | ||
| Fig. 3 Selected deformation density plots for (a) 3c (b) [Ni(CO)3(1)] and (c) 3f. Charge flow is from red to blue. | ||
| ΔEorb | Δρ1 (%) | Δρ2 | Δρ3 | Σπ(Δρ2 + Δρ3) (%) | |
|---|---|---|---|---|---|
| 3a | −84.4 | −64.6 (77%) | −7.1 | −5.9 | −13.0 (15%) |
| 3b | −93.3 | −64.2 (65%) | −13.0 | −8.5 | −21.5 (23%) |
| 3c | −128.1 | −103.0 (80%) | −9.7 | −7.8 | −17.5 (14%) |
| 3d | −129.7 | −102.1 (79%) | −10.9 | −8.8 | −19.7 (15%) |
| 3e | −86.1 | −55.3 (64%) | −16.4 | −7.1 | −23.5 (27%) |
| [Ni(CO)3(1)] | −65.5 | −46.1 (70%) | −7.2 | −5.7 | −12.9 (20%) |
| 3f | −47.5 | −22.5 (47%) | −8.0 | −4.1 | −12.1 (25%) |
| 3g | −43.4 | −21.3 (49%) | −7.0 | −4.1 | −11.1 (26%) |
| 3h | −47.4 | −18.6 (39%) | −9.9 | −4.9 | −14.8 (31%) |
π-Backdonation comprises the second and third most significant contributions to ΔEorb in the ETS-NOCV analysis. In all cases, π-backdonation is a smaller component of the interaction that σ-donation. Donation from metal-based d-orbitals can occur to two aluminium vacant p-orbitals. These acceptor orbitals on Al are orthogonal and coplanar to the plane created by the N–C–C–C–N atoms of the β-diketiminate ligand and contribute to Δρ2 and Δρ3 respectively. The magnitude of π-backdonation varies across the series, ranging from 11.1 kcal mol−1 to 23.5 kcal mol−1. Transition-metal centres which are more electron-rich have relatively strong π-backdonation (3b, 3e; >20 kcal mol−1) compared to the rest of the series (<20 kcal mol−1). Similarly, the backdonation in 3d is calculated to be stronger than in 3c, due to the trans coordinated phosphine ΔE = 2.2 kcal mol−1. For 3g–h, the complex with most electron rich β-diketiminate ligand (3h) has the largest back-donation contribution to bonding. The ratio of σ-donation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) π-backdonation components in 3a–h varies from ∼5
π-backdonation components in 3a–h varies from ∼5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 across the series. Those complexes with the smallest σ-donation component also have the highest comparative contribution of the π-backdonation energy to ΔEorb stabilisation energy.
1 across the series. Those complexes with the smallest σ-donation component also have the highest comparative contribution of the π-backdonation energy to ΔEorb stabilisation energy.
The bonding in 3a–h was also analysed by local energy decomposition analysis at the DLPNO-CCSD(T) level of theory.41–43 This method decomposes the interaction energy (ΔEint) at the DLPNO-CCSD(T) level between fragments into Hartree–Fock components (electrostatic, electronic-preparation, and exchange) and correlated components (dispersive, and non-dispersive). The data suggest that, in all cases the correlated contribution to the interaction energy exceeds the Hartree–Fock interaction energy for 3a–h (Table 5).
| ΔEint | ΔEHFint | ΔECint | ΔEC-CCSD(T)disp | ||
|---|---|---|---|---|---|
| 3a | −77.2 | −27.4 | −49.7 | −38.5 | 64% |
| 3b | −78.5 | −5.5 | −73.0 | −42.7 | 54% |
| 3c | −95.7 | −20.0 | −75.6 | −42.1 | 44% |
| 3d | −95.5 | −12.3 | −83.3 | −44.8 | 47% |
| 3e | −78.6 | −5.5 | −73.1 | −40.5 | 52% |
| [Ni(CO)3(1)] | −54.1 | −18.3 | −35.8 | −27.5 | 51% |
| 3f | −62.3 | −8.7 | −53.6 | −42.3 | 68% |
| 3g | −61.6 | −8.1 | −53.5 | −42.5 | 69% |
| 3h | −63.0 | −0.2 | −62.8 | −50.3 | 80% |
The stabilising electrostatic and exchange components of the Hartree–Fock interaction energy is offset by a destabilising electronic-preparation energy (see ESI‡ for further details). This results in a modestly stabilising Hartree–Fock interaction energy (ΔEHFint), ranging from −0.2 kcal mol−1 to −27.4 kcal mol−1. Compounds where the metal–metal bond has significant ionic character, as determined by NBO calculations (vide supra), are calculated to have some of the largest Hartree–Fock interaction energies (3a, 3c, 3d, [Ni(CO)3(1)] > 10 kcal mol−1). In all cases, however, the correlated component of the interaction energy is greater than the Hartree–Fock interaction energy.
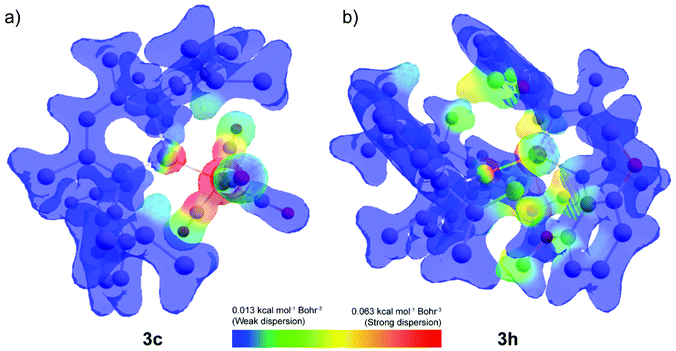
The dispersion contribution EC-CCSD(T)disp ranges between 44% and 80% of the total interaction energy. While this is somewhat expected due to the large β-diketiminate ligand, it is surprising to find that comparatively small transition-metal fragments such as 3c have similar values of dispersion stabilisation to their larger counterparts such as 3f–h. Dispersion is uniformly more stabilising than the interaction of the two fragments calculated at the Hartree–Fock level (ΔEHFint). At the extreme, in the case of 3g this comprises 80% of the interaction energy.
Dispersion interaction density (DID) plots were used to elucidate the origin of this stabilisation. Inspection of the plots show that in the case of 3c strong short-range dispersion interactions between the aluminium centre and iron carbonyl ligands are the origin for the dispersive stabilisation (Fig. 4a). Only weak dispersion interactions can be identified between the β-diketiminate ligand and the iron fragment. Accordingly, installation of a trans ligand to the aluminylene does not significantly impact the dispersion interaction between the two fragments. In the case of [Ni(CO)3(1)], the tetrahedral geometry results in a weaker dispersion contribution (−27.5 kcal mol−1) as the carbonyl ligands are now angled away from the aluminium centre. In the case of 3h, medium-strength long-range dispersion interactions between the two β-diketiminate ligands are the dominant non-covalent interactions (Fig. 4b).
Conclusions
In summary, we have prepared a series of 1st row transition metal complexes supported by aluminylene ligands and undertaken a detailed analysis of the bonding in these complexes. It is worth concluding on some of the properties of these ligands.σ-Donating properties
Commensurate with previous reports, 1 is an extremely strong σ-donor ligand. The ν(CO) absorption data evidence a dramatic redshift of the ν(CO) absorptions on coordination. While in 3a–3h, the aluminium atom in 1 is formally in +1 oxidation state, variation β-diketiminate bite angle (N–Al–N) and Al–N bond lengths across the series suggest that the electronic environment of the Al centre varies with transition-metal identity. ETS-NOCV and NBO calculations support a clear trend in the σ-donation component of the orbital interaction; donation is strongest for the earlier first-row transition metals, and weaker for the later first row transition metals. In the case of [Ni(CO)3(1)] and 3f–h, the weaker donation likely reflects the difficulty in reducing d10 metal complexes.π-Accepting properties
1 has been shown to be a competent π-acceptor. The nature of the transition metal again influences the degree of π-backdonation to 1. Greater electron density on the transition-metal results in stronger π-backdonation, as demonstrated by ETS-NOCV calculations. Notably, as the σ-donation aspect of bonding becomes weaker, π-backdonation becomes a greater component of the orbital bonding interaction. At the extreme, in 3h, the two are of a similar magnitude (σ: −18.6 kcal mol−1, π: −14.8 kcal mol−1). Furthermore, coordinated 1 can bind external Lewis bases as in the formation of 3a·THF, providing a potential reaction site for substrate coordination and activation. This binding event is expected to disrupt π-backdonation from the transition metal. Structural metrics support this hypothesis as the trans-influence of 1 is smaller upon occupation of the vacant p-orbital by a donor ligand.Dispersion
Dispersion plays a large role in stabilising these complexes. Remarkably, calculations suggest that the magnitude of the dispersion interaction between 1 and the transition-metal fragment is largely independent of transition-metal fragment size. For smaller fragments, short-range dispersion interactions between cis-carbonyl ligands and the aluminium site of 1 are a key contributor. For larger fragments, long-range dispersion interactions occur between the flanking aryl groups of β-diketiminate ligand of 1 and similar groups on the transition metal.In the context of developing new reagents and catalysts based on aluminium-ligands these findings are revealing. They suggest that 1 can be used as a strong σ-donor to generate electron-rich transition metal sites, but also that it is not a passive ligand. It can play a role as a π-acceptor either through coordination of external substrates or accepting electron-density from the transition metal. It can also stabilise both small and large ligands, or potentially bound substrates, in adjacent coordination sites through dispersion interactions. In particularly, the responsiveness of the electronic properties of 1 to changes at the transition metal centre bodes well for the development of inexpensive 1st row catalysts supported by this ligand type.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Imperial College London for provision of a President's PhD Scholarship (RYK), and to the EPSRC (EP/S036628/1) for provision of generous funding.References
- I. G. Powers and C. Uyeda, ACS Catal., 2017, 7, 936–958 CrossRef CAS.
- R. J. Baker and C. Jones, Coord. Chem. Rev., 2005, 249, 1857–1869 CrossRef CAS.
- R. C. Cammarota, L. J. Clouston and C. C. Lu, Coord. Chem. Rev., 2017, 334, 100–111 CrossRef CAS.
- M. Batuecas, N. Gorgas and M. R. Crimmin, Chem. Sci., 2021, 12, 1993–2000 RSC.
- J. Takaya, Chem. Sci., 2021, 12, 1964–1981 RSC.
- S. Morisako, S. Watanabe, S. Ikemoto, S. Muratsugu, M. Tada and M. Yamashita, Angew. Chem., Int. Ed., 2019, 58, 15031–15035 CrossRef CAS PubMed.
- N. Hara, T. Saito, K. Semba, N. Kuriakose, H. Zheng, S. Sakaki and Y. Nakao, J. Am. Chem. Soc., 2018, 140, 7070–7073 CrossRef CAS PubMed.
- I. Fujii, K. Semba, Q.-Z. Li, S. Sakaki and Y. Nakao, J. Am. Chem. Soc., 2020, 142, 11647–11652 CrossRef CAS PubMed.
- J. Takaya and N. Iwasawa, J. Am. Chem. Soc., 2017, 139, 6074–6077 CrossRef CAS PubMed.
- J. Hicks, A. Mansikkamäki, P. Vasko, J. M. Goicoechea and S. Aldridge, Nat. Chem., 2019, 11, 237–241 CrossRef CAS PubMed.
- L. Escomel, I. Del Rosal, L. Maron, E. Jeanneau, L. Veyre, C. Thieuleux and C. Camp, J. Am. Chem. Soc., 2021, 143, 4844–4856 CrossRef CAS PubMed.
- R. C. Cammarota and C. C. Lu, J. Am. Chem. Soc., 2015, 137, 12486–12489 CrossRef CAS PubMed.
- T. N. Hooper, M. Garçon, A. J. P. White and M. R. Crimmin, Chem. Sci., 2018, 9, 5435–5440 RSC.
- T. N. Hooper, R. K. Brown, F. Rekhroukh, M. Garçon, A. J. P. White, P. J. Costa and M. R. Crimmin, Chem. Sci., 2020, 11, 7850–7857 RSC.
- F. Rekhroukh, W. Chen, R. K. Brown, A. J. P. White and M. R. Crimmin, Chem. Sci., 2020, 11, 7842–7849 RSC.
- A. B. Altman, C. D. Pemmaraju, C. Camp, J. Arnold, S. G. Minasian, D. Prendergast, D. K. Shuh and T. Tyliszczak, J. Am. Chem. Soc., 2015, 137, 10304–10316 CrossRef CAS PubMed.
- R. A. Fischer, M. M. Schulte, J. Weiss, L. Zsolnai, A. Jacobi, G. Huttner, G. Frenking, C. Boehme and S. F. Vyboishchikov, J. Am. Chem. Soc., 1998, 120, 1237–1248 CrossRef CAS.
- S. Aldridge, A. Rossin, D. L. Coombs and D. J. Willock, Dalton Trans., 2004, 2649–2654 RSC.
- J. Weiss, D. Stetzkamp, B. Nuber, R. A. Fischer, C. Boehme and G. Frenking, Angew. Chem., Int. Ed., 1997, 36, 70–72 CrossRef CAS.
- T. Steinke, M. Cokoja, C. Gemel, A. Kempter, A. Krapp, G. Frenking, U. Zenneck and R. A. Fischer, Angew. Chem., Int. Ed., 2005, 44, 2943–2946 CrossRef CAS PubMed.
- Q. Yu, A. Purath, A. Donchev and H. Schnöckel, J. Organomet. Chem., 1999, 584, 94–97 CrossRef CAS.
- D. Weiss, T. Steinke, M. Winter, R. A. Fischer, N. Fröhlich, J. Uddin and G. Frenking, Organometallics, 2000, 19, 4583–4588 CrossRef CAS.
- T. Steinke, C. Gemel, M. Cokoja, M. Winter and R. A. Fischer, Angew. Chem., Int. Ed., 2004, 43, 2299–2302 CrossRef CAS PubMed.
- A. Kempter, C. Gemel and R. A. Fischer, Chem. Commun., 2006, 1551–1553 RSC.
- A. Kempter, C. Gemel and R. A. Fischer, Chem. – Eur. J., 2007, 13, 2990–3000 CrossRef CAS PubMed.
- D. Dange, C. P. Sindlinger, S. Aldridge and C. Jones, Chem. Commun., 2017, 53, 149–152 RSC.
- K. Nagata, T. Agou and N. Tokitoh, Angew. Chem., Int. Ed., 2014, 53, 3881–3884 CrossRef CAS PubMed.
- K. L. Mears, C. R. Stennett, E. K. Taskinen, C. E. Knapp, C. J. Carmalt, H. M. Tuononen and P. P. Power, J. Am. Chem. Soc., 2020, 142, 19874–19878 CrossRef CAS PubMed.
- D. J. Liptrot and P. P. Power, Nat. Rev. Chem., 2017, 1, 1–12 CrossRef.
- A. E. Nako, Q. W. Tan, A. J. P. White and M. R. Crimmin, Organometallics, 2014, 33, 2685–2688 CrossRef CAS.
- A. Hicken, A. J. P. White and M. R. Crimmin, Inorg. Chem., 2017, 56, 8669–8682 CrossRef CAS PubMed.
- F. A. Cotton and C. S. Kraihanzel, J. Am. Chem. Soc., 1962, 84, 4432–4438 CrossRef CAS.
- S. Kim, S. Y. Choi, Y. T. Lee, K. H. Park, H. Sitzmann and Y. K. Chung, J. Organomet. Chem., 2007, 692, 5390–5394 CrossRef CAS.
- M. Batool, T. A. Martin, A. G. Algarra, M. W. George, S. A. Macgregor, M. F. Mahon and M. K. Whittlesey, Organometallics, 2012, 31, 4971–4979 CrossRef CAS.
- S. Warratz, L. Postigo and B. Royo, Organometallics, 2013, 32, 893–897 CrossRef CAS.
- R. W. Simms, M. J. Drewitt and M. C. Baird, Organometallics, 2002, 21, 2958–2963 CrossRef CAS.
- Multiple Bonds between Metal Atoms, ed. F. A. Cotton, C. A. Murillo and R. A. Walton, Springer-Verlag, New York, 3rd edn, 2005 Search PubMed.
- P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2008, 15, 186–197 CrossRef PubMed.
- S. R. Parmelee and N. P. Mankad, Dalton Trans., 2015, 44, 17007–17014 RSC.
- C. Chi, S. Pan, L. Meng, M. Luo, L. Zhao, M. Zhou and G. Frenking, Angew. Chem., Int. Ed., 2019, 58, 1732–1738 CrossRef CAS PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
Footnotes |
| † Raw data from NMR and IR spectroscopy, along with xyz coordinates from calculations can be downloaded from DOI: 10.14469/hpc/8012. |
| ‡ Electronic supplementary information (ESI) available: Crystallographic data for 3a–h. CCDC 2071011–2071018. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1dt01415c |
| § Also referred to as alumanyl, known aluminyl ligands are defined here as X-type ligands and generate complexes of the form M-AlX2 or M-AlX2L. |
| ¶ Contains aluminium in the formal +1 oxidation state and generates complexes of the form, M-AlX, M-AlLX or M-AlXL2. |
| This journal is © The Royal Society of Chemistry 2021 |