Open Access Article
Open Access ArticleThird time's the charm: intricate non-centrosymmetric polymorphism in LnSiP3 (Ln = La and Ce) induced by distortions of phosphorus square layers†
Georgiy
Akopov‡
 ab,
Justin
Mark‡
ab,
Justin
Mark‡
 ab,
Gayatri
Viswanathan‡
ab,
Gayatri
Viswanathan‡
 ab,
Shannon J.
Lee
ab,
Shannon J.
Lee
 ab,
Brennan C.
McBride
ab,
Brennan C.
McBride
 b,
Juyeon
Won
ab,
Frédéric A.
Perras
b,
Juyeon
Won
ab,
Frédéric A.
Perras
 a,
Alexander L.
Paterson
a,
Alexander L.
Paterson
 a,
Bing
Yuan
c,
Sabyasachi
Sen
a,
Bing
Yuan
c,
Sabyasachi
Sen
 c,
Adedoyin N.
Adeyemi
b,
Feng
Zhang
ad,
Cai-Zhuang
Wang
c,
Adedoyin N.
Adeyemi
b,
Feng
Zhang
ad,
Cai-Zhuang
Wang
 ad,
Kai-Ming
Ho
d,
Gordon J.
Miller
b and
Kirill
Kovnir
ad,
Kai-Ming
Ho
d,
Gordon J.
Miller
b and
Kirill
Kovnir
 *ab
*ab
aAmes Laboratory, U.S. Department of Energy, Ames, IA 50011, USA. E-mail: kovnir@iastate.edu
bDepartment of Chemistry, Iowa State University, Ames, IA 50011, USA
cDepartment of Materials Science and Engineering, University of California, Davis, Davis, CA 95616, USA
dDepartment of Physics and Astronomy, Iowa State University, Ames, IA 50011, USA
First published on 31st March 2021
Abstract
Complex polymorphic relationships in the LnSiP3 (Ln = La and Ce) family of compounds are reported. An innovative synthetic method was developed to overcome differences in the reactivities of the rare-earth metal and refractory silicon with phosphorus. Reactions of atomically mixed Ln + Si with P allowed for selective control over the reaction outcomes resulting in targeted isolation of three new polymorphs of LaSiP3 and two polymorphs of CeSiP3. In situ X-ray diffraction studies revealed that the developed method bypasses formation of the thermodynamic dead-end, the binary SiP. Careful re-determination of the crystal structure ruled out the previously reported ordered centrosymmetric structure of CeSiP3 and showed that the main LnSiP3 polymorphs crystallize in the non-centrosymmetric Pna21 and Aea2 space groups featuring distinct distortions of the regular P square net to yield either cis–trans 1D phosphorus chains (Pna21) or disordered-2D phosphorus layers (Aea2). The disordered 2D nature of the P layers in the Aea2 LaSiP3 polymorph was confirmed by Raman spectroscopy. A unique centrosymmetric P21/c polymorph was observed for LaSiP3 and has a completely different crystal structure lacking P layers. Consecutive polymorphic transformations at increasing temperatures for LaSiP3(Pna21 → P21/c → Aea2) were derived from optimized synthetic profiles and confirmed by a combination of phonon computations and experimental in situ and ex situ annealings. Crystal structures of the LaSiP3 polymorphs were verified via advanced solid state NMR analysis using 31P MAS and 31P{139La} double resonance techniques. A combination of phonon and electronic structure calculations, NMR T1 relaxation times, UV/Vis/NIR spectroscopy, and resistivity measurements revealed that all the reported polymorphs are semiconductors with resistivities and thermal conductivities strongly dependent on the degree of distortion of P square layers in the crystal structure. Reported here, non-centrosymmetric LnSiP3 polymorphs with tunable resistivity and thermal conductivity provide a platform for the development of novel functional materials with a wide range of applications.
Introduction
Various materials, including many main group elements, exhibit polymorphism: the ability of a substance to crystallize in different structures while having the same chemical composition. The most famous example of elemental polymorphism is that of carbon. Graphite, a relatively soft allotrope of carbon, crystallizes in a layered structure with good thermal and electrical conductivities while diamond, the hardest naturally occurring material, adopts a structure with a 3D tetrahedral net of carbon atoms and is a wide bandgap insulator. Besides carbon, examples of polymorphism are known for many elements such as phosphorus (white, red, violet and black forms) and boron (α-, β-, and high pressure γ- and δ-forms).Selective control in the synthesis of specific polymorphs is extremely important in chemistry, materials science, mineralogy, and pharmaceutics as the underlying differences in the crystal structures of polymorphs result in vastly different physical and electronic properties. In addition to elements, polymorphism is observed in simple binary compounds like boron nitride (BN) which can exist in the cubic and hexagonal form.1–3 Hexagonal BN, the more stable form, is an interesting 2D material with a structure similar to that of graphite. It can be used as a lubricant and is studied for its optical properties.1,4 Cubic BN, the high-pressure and high-temperature form, however is second only to diamond in hardness with a Vickers Hardness of 60–75 GPa.2,5,6 Another recently studied polymorphic binary is NiP2, in which the metallic cubic form exhibits superior electrocatalytic properties for the water splitting reaction than its semiconducting monoclinic counterpart.7
Polymorphism is also present in ternary and multinary phases; however, properties characterization is scarce because the synthesis of single-phase samples becomes increasingly challenging.8–12 One such example is a family of ternary metal-silicon-phosphides CeSiP3. There are several reports regarding the crystal structures of these phases, but there are significant disagreements on the exact symmetry of the various polymorphs.13–15 Employing an innovative synthetic technique, we have been able to overcome solid–solid diffusion barriers and achieve high selectivity in the bulk synthesis of desired polymorphs for CeSiP3 and the growth of its single crystals for redetermination of crystal structures. Applying this technique to the less-studied La–Si–P phase space resulted in the discovery of three novel polymorphs. In the LaSiP3 system, the high- and low-temperature polymorphs are non-centrosymmetric and structurally related while the intermediate-temperature polymorph has a completely different centrosymmetric crystal structure. The non-centrosymmetric polymorphs of LaSiP3 and CeSiP3 reported here crystallize in similar structures which differ in the degree of distortion of their planar square nets of P atoms. Structures containing such square nets are of significance due to their potential for topological properties. Unlike the title compounds, a vast majority of materials containing topological square nets are centrosymmetric.16,17 Breaking of the inversion symmetry results in spin–orbit coupling which splits the Fermi surface by removing the spin degeneracy of electrons and potentially changes the band structure topology.
In this work, we report an innovative synthetic method, followed by detailed in situ X-ray diffraction studies of the synthetic mechanism of LnSiP3 which culminated in a high degree of selective control in polymorphic transformations. The structures of the P fragments were confirmed by advanced 31P/139La solid state NMR spectroscopy. Detailed electronic and phonon computations, heat and charge transport measurements, and optical spectroscopy illuminated the semiconducting nature of the five new LnSiP3 (Ln = La, Ce) compounds which exhibit ultra-low thermal conductivities which depend on the degree of the distortion of their P square nets.
Experimental methods
A detailed description of synthetic, characterization, and analysis methods are provided in ESI.† Bulk powders of the different polymorphs of LnSiP3 (Ln = La and Ce) were prepared using pre-arc-melted LaSi or CeSi precursors and phosphorus, while crystal growth was achieved using a Sn flux synthesis from either the elements or a pre-arc-melted precursor, as well as a flux-free synthesis from a pre-arc-melted precursor.HAZARD: The amount of P in any reaction container should be kept to a minimum because at relatively high temperatures during synthesis the resulting vapor pressure of P may be sufficient to cause the sealed ampoule to shatter or explode!
Synthesized phases were analyzed by laboratory powder and single crystal X-ray diffraction (PXRD and SCXRD); synchrotron high-resolution and in situ PXRD at the 11-BM and 17-BM beamlines at the Advanced Photon Source at Argonne National Lab (APS ANL); 31P and 139La solid state nuclear magnetic resonance (NMR) spectroscopy; Raman spectroscopy; scanning electron microscopy/energy dispersive spectroscopy (SEM/EDS); and differential scanning calorimetry (DSC). Electronic structure calculations using density functional theory (DFT) were employed to examine the electronic properties and dynamic stability of the synthesized phases. Transport properties were measured using a physical property measurement system (PPMS) on high density pellets that were pressed using spark plasma sintering (SPS). Optical bandgaps were measured using a UV/Vis/NIR spectrophotometer.
Results and discussion
Crystal structure
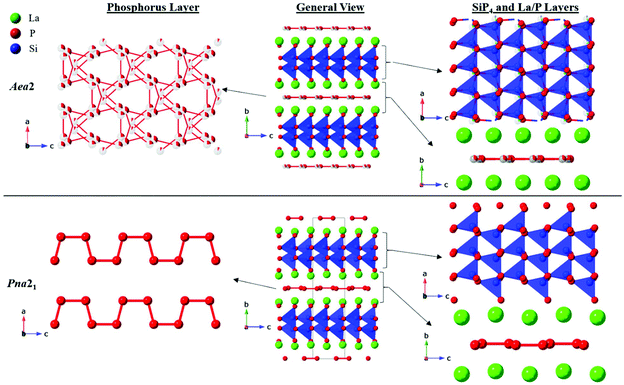
CeSiP3 was first reported in 1975 to crystallize in the Cm2a or Cmma space groups.14 In 1976, it was reported to have Pn21a (a nonstandard setting of Pna21) or Pnma space group symmetry, and then redetermined several years later to crystallize in the Pn21a space group.13,15 No crystal structures were reported for the La and Pr analogues, but formation of phases similar to CeSiP3 was identified by powder XRD.13 The crystal structure of a single ternary phase was already reported in the La–Si–P phase space, LaSi2P6.18 Here we report three new polymorphs in this system. Two of the LaSiP3 polymorphs exhibit related non-centrosymmetric structures and crystallize in the primitive and base-centered orthorhombic space groups Pna21 (No. 33) and Aea2 (No. 41), respectively, while the third polymorph of LaSiP3 crystallizes in the distinctly different centrosymmetric primitive monoclinic space group P21/c (No. 14) (Fig. 1 and 2).The non-centrosymmetric Pna21 and Aea2 polymorphs have related structures with the primary difference being in their planar phosphorus layers as well as the significant degree of disorder in the Aea2 structure. Both crystal structures are composed of the following layers stacked along the [010] direction: La, double-tetrahedral [SiP2], La, and flat P layers. The double-tetrahedral layers are composed of corner-sharing SiP4 tetrahedra and are surrounded above and below by nearly planar square nets of La atoms. Within the La layers, the La–La distances exceed 4.00 Å. Adjacent lanthanum layers are separated by planar P nets, which can be considered distortions from an ideal square net of P atoms.
In the Pna21 polymorph, the planar P layers contain 1D cis–trans chains of P atoms along the [001] direction. P–P distances within the chains are 2.26–2.30 Å which are comparable to the single covalent inter-phosphorus bonds found in many phosphides, while inter-phosphorus distances between neighboring chains in the structure exceed 3.7 Å, indicating no covalent interactions.8,9,19–22 Similar distortions of square nets with hypervalent pnictides and chalcogenides into cis–trans 1D chains have been predicted and experimentally observed, primarily for heavier main group elements such as Sb and Te.16,23–26
The Aea2 structure of LaSiP3 differs from the Pna21 version in the apparent distortion of the P layer. Instead of ordered cis–trans chains, the P layers in the Aea2 polymorph form disordered square nets which can be considered as superposition of several possible distortions from the ideal square net (Fig. 1). An ideal square net of P atoms would result in unreasonably long P–P distances of approximately 3 Å, while the longest reported P–P distances in regular, undistorted P square nets are 2.7 Å.27,28 The P sites within this layer are split into four different crystallographic positions with occupancies ranging from 8% to 38%. The observed P layer site splitting in the Aea2 structure results in a wide distribution of shorter interatomic P–P distances ranging 2.0–2.9 Å. While a single covalent P–P bond is close to 2.2 Å, significantly longer P–P distances have been reported in metal phosphides.21,27,28 The P net shown in Fig. 1 was plotted with reasonable P–P covalent distances of 2.1–2.5 Å. The view of this net may be altered if longer P–P separation (2.5 Å and 2.7 Å) are included (Fig. S19†). This disordered P layer may seem like a superposition of several cis–trans P chain running in different directions, but spectroscopic Raman and NMR studies do not support such a simplified description. The Aea2 phase also displays disorder in the [SiP2] double-tetrahedral layer in which, in addition to the sites found in Pna21, the layer contains additional split Si and P positions that account for approximately 5% of the atoms in the double-tetrahedral layer.
Layers of La atoms in these two non-centrosymmetric polymorphs are staggered along the [010] direction of the unit cell in an …ABBA… arrangement and are ‘held-in-place’ by the rigid [SiP2] double-tetrahedral layers. The La layers in the two polymorphs distinctly differ when looking along the [100] direction: La atoms are flat in the Aea2 structure, but there is mild corrugation in the Pna21 structure (Fig. S11a and b†). In the Pna21 polymorph, the corner-connected tetrahedra of the [SiP2] double-tetrahedral layers allow for little flexibility within the La layers. To compensate for this rigidity and the ordered P layer, the La atoms displace slightly above or below the plane. However, in the Aea2 polymorph, the disordered P layers and mildly disordered double-tetrahedral layers provide enough degrees of freedom for the La atoms to sit completely within the plane.
In both of these structures La is surrounded by 9 P atoms (assuming the idealized P sites are used for the disordered planar P nets in the Aea2 polymorph), but the local environments of La atoms differ slightly due to small displacements of the La atoms in the Pna21 polymorph. The subscripts dtet and plane are used to distinguish P atoms of the double tetrahedral layer and planar phosphorus layer, respectively. La–Pplane distances range from 2.983(3)–3.299(3) Å in the Pna21 structure and 2.87(1)–3.50(1) Å in the Aea2 phase. The somewhat wider range of distances observed in the Aea2 polymorph can be attributed to the disorder within the P layers. However, when La–Pdtet distances from the [SiP2] double-tetrahedral layer are considered, the distribution of interatomic distances is inversed: La–Pdtet distances are 3.004(4)–3.120(1) Å in the Aea2 polymorph, but range from 2.955(4)–3.148(1) Å in Pna21 structure.
The structure of the P layer in the Aea2 case could be assumed to be an averaged superposition of several P-layers, composed of P chains going in two orthogonal directions instead of the disordered square net layer. If this assumption is correct, the spectroscopic signatures of P–P layers are expected to be similar for Pna21 and Aea2 polymorphs. However, the Raman spectra of these two polymorphs of LaSiP3 show a significant difference in the P–P stretching band (Fig. S18†). For the Pna21 LaSiP3 polymorph, the band at ∼320 cm−1 corresponding to the P–P stretching in the 1D P chains is broader than the bands below 200 cm−1 corresponding to vibrational modes associated with Si–P and La–P bonds. The corresponding P–P stretching band for the Aea2 polymorph centered at ∼323 cm−1 is three times wider (full-width-at-half-maximum FWHM ∼50 cm−1) than that in the spectrum of the Pna21 polymorph (FWHM ∼17 cm−1). Such substantial broadening of this band for the Aea2 polymorph rules out a simple picture of the P layer as a superposition of locally ordered 1D P chains running in two orthogonal directions. The 31P solid state NMR spectra discussed below also indicate significant differences between the structures of the Pna21 and the Aea2 polymorphs.
The Pna21 structure of LaSiP3 can be derived from the Aea2 structure by a klassengleiche transformation of index 2 that splits the 8b Wyckoff positions in Aea2 into two distinct sets of 4a sites. In LnSiP3 (Ln = La, Ce), this results in twice as many sites for Ln, Si, and P in the lower symmetry Pna21 structure as the Aea2 polymorph (Fig. S12†).
Single crystals acquired from the initial synthesis of the CeSiP3 sample confirmed the previously reported structural model with space group Pna21,15 but the powder diffraction pattern of this phase contained several unassigned peaks. This result, in combination with the discovery of the three new LaSiP3 polymorphs, led to a more detailed synthetic investigation resulting in the discovery of a new polymorph of CeSiP3 crystallizing in the Aea2 space group. The crystal structures of the CeSiP3 polymorphs are analogous to LaSiP3 apart from the P21/c polymorph, which exists for LaSiP3 only. The Pna21 phase of CeSiP3 is completely ordered while the Aea2 phase exhibits a higher degree of disorder in SiP2 double tetrahedral layer then the La analogue due to overall contraction of the unit cell arising from the smaller size of the Ce cation, although the P layer in Aea2 CeSiP3 polymorph can be described with only three split P sites.
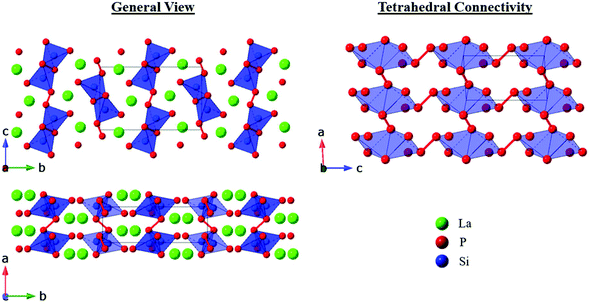
The P21/c polymorph was only observed for LaSiP3 and all attempts to synthesize this polymorph for Ce resulted in formation of either the Pna21 or Aea2 phases. The crystal structure of P21/c LaSiP3 is composed of only two types of layers – alternating La and [Si2P6] double tetrahedral layers (with differing inter-connectivity from the other polymorphs) in which the shortest La–P distances are 2.9892(8) Å. SiP4 tetrahedra share edges to form Si2P6 units with Si–P distances of 2.186(1)–2.321(1) Å. These units are interconnected via P–P bonds of 2.197(2) Å and 2.217(2) Å propagating along the [100] and [001] directions, respectively, to form the [Si2P6] layers. Inter-phosphorus bonds that connect neighboring tetrahedra have also been observed in the polymorphs of Ba2SiP4 and La2SiP4.8,9,20,29 In particular, tetragonal AE2SiP4 (AE = Sr, Eu, Ba) involves single tetrahedra bonded by P–P bonds to form a 3D framework,8,9,20 while orthorhombic Ba2SiP4 and La2SiP4 contain chains of single SiP4 tetrahedra bonded through P–P bonds to neighboring tetrahedra.9,29 With the compounds reported here, as well as LaSi2P6 and La2SiP4,29 3 out of 5 compounds in the La–Si–P phase space are non-centrosymmetric (NCS). This high abundance of NCS structures in a single system is not observed in binary metal pnictides or silicides, where the amount of NCS compounds is less than 10%. However, silicide-pnictides of alkaline-earth metals exhibit similar high abundance of NCS structures such as Mg–Si–As (2 out of 3 are NCS)22,30 and Ba–Si–P (3 out of 5 are NCS).8,9,19,20,31,32 We hypothesize that the ability of Si–P and Si–As substructures to provide flexible coordination environments to electropositive metals, due to multiple binding modes and localized electron lone-pairs on pnictogen atoms, is crucial for generation of such NCS structures in metal–tetrel–pnictide systems.
Synthesis
Bulk powder samples of LnSiP3 were prepared using precursor metal silicides (Fig. S1†) and stoichiometric molar quantities of phosphorus, LnSi:3P, with no flux and with the dwell times and temperature profiles summarized in Table 1. The main synthetic challenge comes from the high difference in reactivities between Ln, Si, and P due to high melting point of silicon (1410 °C) compared to the melting point of the lanthanides (La: 920 °C; Ce: 800 °C) and phosphorus sublimation temperature (400–600 °C). Traditional solid-state reactions of the elements, Ln + Si + 3P, at elevated temperatures did not yield ternary phases but, instead, resulted in preferential formation of LnP and SiP binaries, which do not react with one another due to slow solid–solid diffusion.| Polymorph | LaSiP3 | CeSiP3 |
|---|---|---|
| Aea2 | 1050 °C/0 h | 1050 °C/0 h |
| P21/c | 900 °C/240 h | N/A |
| Pna21 | 750 °C/240 h | 900 °C/240 h |
To make silicon more reactive, it was first arc melted with Ln to form the binary compound LnSi. Arc-melted precursors chosen in this study, have higher temperature stability than Si with melting points of 1620–1630 °C. Nevertheless, such precursors react with P at temperatures as low as 650 °C (Fig. 3). We hypothesize that the main advantage of the LnSi precursors is the spatial proximity of Ln and Si atoms which may facilitate formation of ternary phase rather than a mixture of two separate binaries due to minimized diffusion limitations. As shown below by in situ studies a reaction of LnSi with phosphorus vapor directly forms a ternary phase and bypass formation of SiP.
In situ synchrotron PXRD experiments shed light on the formation mechanism of LnSiP3. Fig. 3 shows the results of an in situ study of LaSiP3 formation from the LaSi precursor and phosphorus in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 molar ratio. The LaSi precursor (Fig. S1†) was prepared by arc-melting La and Si in a 1
3 molar ratio. The LaSi precursor (Fig. S1†) was prepared by arc-melting La and Si in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
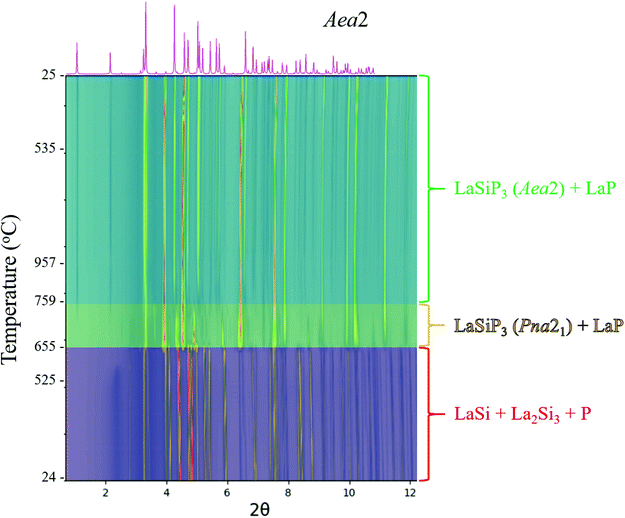
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.05 molar ratio, and the excess of Si accounts for the minor presence of La2Si3 in the starting materials. The low temperature polymorph (Pna21) together with LaP forms above 650 °C via direct conversion of lanthanum silicide into a lanthanum silicon phosphide, no intermediate silicon-containing phases were detected with temperature resolution of ∼1 °C. This is contrast with reaction of elements (La + Si + 3P) where SiP binary is observed in reaction products of all reactions carried at different temperatures, 750–1100 °C.
1.05 molar ratio, and the excess of Si accounts for the minor presence of La2Si3 in the starting materials. The low temperature polymorph (Pna21) together with LaP forms above 650 °C via direct conversion of lanthanum silicide into a lanthanum silicon phosphide, no intermediate silicon-containing phases were detected with temperature resolution of ∼1 °C. This is contrast with reaction of elements (La + Si + 3P) where SiP binary is observed in reaction products of all reactions carried at different temperatures, 750–1100 °C.
As the temperature increases further, a transformation to the high temperature polymorph (Aea2) can be observed above 760 °C. No further transformations upon cooling were observed and, as a result, the cooling rate for this non-flux reaction is not crucial for synthesis. The P21/c LaSiP3 polymorph is not observed during this short ∼2 h synchrotron experiment, which is in line with ex situ experiments that suggest optimal synthesis of this phase requires long annealing times. The CeSiP3 system behaves in a similar manner to LaSiP3, as shown in Fig. S2,† whereby a CeSi precursor reacts with phosphorus to form the ternary polymorphs at temperatures above 730 °C. In situ experiments resulted in the formation of LaP and CeP in addition to the ternary phases due to the fast rate of these reactions compared to bulk synthesis and the possibility of being off-stoichiometry due to sample loading in a capillary. In the laboratory ex situ syntheses where proper mixing of correct ratio of LaSi precursor and P was achieved the LaP admixture was minimized (Fig. 4).
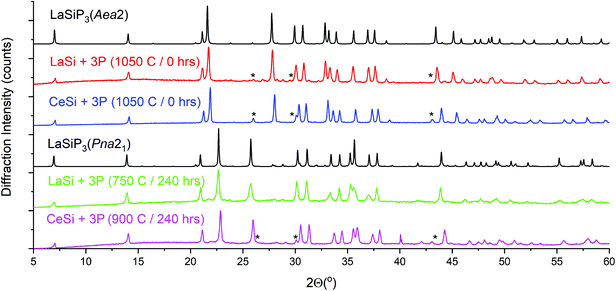
Selective ex situ synthesis of clean bulk powders requires that the appropriate temperature and dwell time profiles be followed (Fig. 4 and Table 1). The high-temperature Aea2 polymorph readily forms above 1000 °C and requires no dwell time. High resolution synchrotron powder data for LaSiP3 clearly shows that despite similarities between the crystal structures of the Aea2 and Pna21 polymorphs, the phases possess clearly distinguishable powder patterns (Fig. S3A and B†). The low-temperature Pna21 polymorphs for both rare earth metals require significantly longer synthesis time due to a lower temperature of formation (Fig. 4). The third polymorph, monoclinic P21/c, can be prepared by annealing LaSi and phosphorus at 900 °C over 240 hours (Fig. S4†). Further annealing of P21/c product at a higher temperature resulted in formation of mainly the Aea2 polymorph. Long time annealing of the Aea2 polymorph at temperatures above 1000 °C resulted in the decomposition of LaSiP3 and formation of yet another ternary compound, La2SiP4.29 This indicated metastable nature of the Aea2 LaSiP3 polymorph.
CeSiP3 polymorphs can be prepared in a similar manner starting from CeSi, although CeP becomes a prominent secondary phase (Fig. 4). Our screening of the other rare-earth elements shows that the LnSiP3 ternary phase forms for Pr and Nd, although LnP binary become major phase, while the formation of LnSiP3 was not observed for Sm and Gd with the synthesis resulting in a mixture of binary phosphides (Fig. S5†).
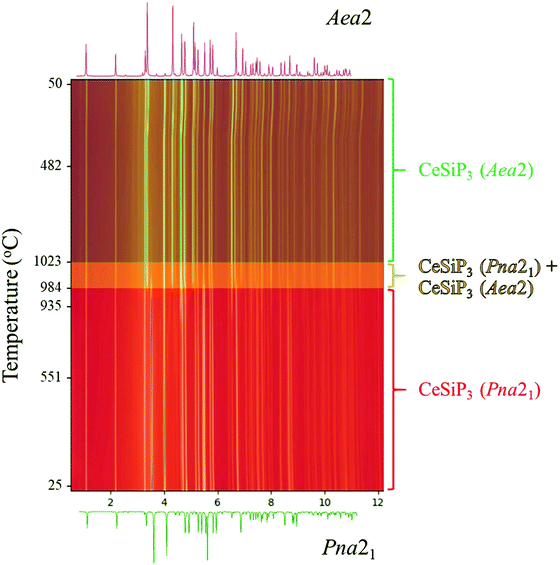
Both in situ and ex situ annealing experiments show that the low temperature polymorphs of LnSiP3 can be transformed into the high temperature ones by reannealing the samples at a higher temperature. Fig. 5 shows the 17-BM diffraction experiment for a transformation of CeSiP3 from Pna21 to Aea2 at temperatures above 980 °C. Similar experiments can be conducted on a larger scale; for example, the ex situ reannealing of a Pna21 LaSiP3 sample at 1000 °C transforms it to the high temperature Aea2 polymorph (Fig. S6†).
DSC
Differential scanning calorimetry experiments were hampered by the reaction of the LaSiP3 melt with the silica DSC ampoule, resulting in the formation of La2Si2O7 (Fig. S7†). An endothermic event, which may correspond to melting of LaSiP3, was observed at 1035 °C. For the CeSiP3 sample, which contained a mixture of the Pna21 and Aea2 polymorphs, events corresponding to typical congruently melting and crystallization were observed at 1033 °C and 1011 °C, correspondingly. PXRD confirms the presence of only the high-temperature Aea2 polymorph after the DSC experiment (Fig. S7† bottom). This agrees with synthetic results in which long time annealing at low temperatures were required to stabilize the Pna21 polymorph.SEM/EDS
Backscattered electron images (Fig. S8†) for all three polymorphs of LaSiP3 confirm the samples to be majority ternary metal silicon phosphide. Further EDS analysis gave average compositions (normalized to 1 La atom) of La1.00Si1.11(3)P2.95(6) (Aea2), La1.00Si1.02(2)P2.87(9) for (Pna21), and La1.00Si1.04(7)P2.71(9) (P21/c) which are in good agreement with the nominal composition, LaSiP3.Electronic structure calculations
Vienna Ab initio Simulation Package (VASP) was used to calculate energy-optimized structures of the various LaSiP3 polymorphs. Complete relaxation of the unit cell and atomic positions of the P21/c and Pna21 polymorphs did not result in any significant distortions or changes to the crystal structure. Both polymorphs are predicted to be semiconductors with bandgaps of 0.7 eV (P21/c) and 0.5 eV (Pna21) (Fig. 6). Near the Fermi level, P states contribute most to the valence band with a visible contribution from La states. The contribution from Si states is similar to that of La states in the valence band at 2–3 eV below the Fermi level but tapers off when approaching the top of the valence band. La states dominate the lower regions of the conduction band with minor Si and P contributions.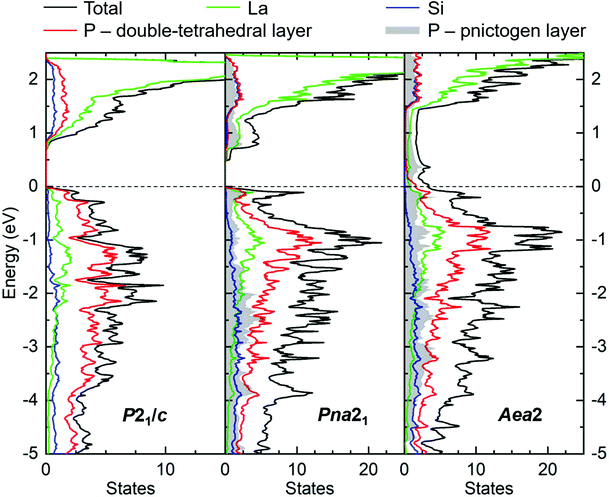 | ||
| Fig. 6 Calculated DOS for three polymorphs of LaSiP3 after complete structure relaxation using VASP: P21/c (left), Pna21 (middle), Aea2 (right). For the latter polymorph, the fully relaxed P layer model shown in Fig. S13c† was used. The total DOS is shown by the black line and partial DOS curves are shown for La (green), Si (blue), and P (red and gray filled). The P states are divided into contributions from the [SiP2] double-tetrahedral layer (red) and the P layer (gray filled) for the Pna21 and Aea2 polymorphs. The Fermi level, indicated by the dashed black line, is the reference energy. | ||
The overall shape of the DOS for monoclinic LaSiP3 resembles that of La2SiP4.29 La–P orbital mixing in the upper region of the valence band is notable and is expected to strongly influence charge transport properties. For example, replacement of Ba with La in the clathrate La2Ba6Cu16P30 with similar La/P orbital mixing resulted in a an order of magnitude increase in hole mobility.33 Unfortunately, attempts to study the transport properties of monoclinic LaSiP3 were hampered by the inability to sinter a dense sample. Based on the computational results, a Zintl-type formulation can be proposed for this semiconducting phase. La adopts a formal charge of +3 and Si is assigned 0 because it is four-bonded to P atoms. The two types of P atoms are each assigned as −1 because they are two-bonded. One type of P bridges two Si atoms while the other type bonds to Si and another P atom. An alternative, completely ionic formulation La3+Si4+(P2−)2(P3−), differentiates these two P sites from those that form P–P bonds (2−) and those that bond only to Si (3−).
In the relaxed structure of Pna21 LaSiP3 the cis–trans P chains are preserved with reasonable interatomic distances (blue and black lines in Fig. S13a†). However, unlike the P21/c structure, Pna21 LaSiP3 has P atoms in two distinct types of layers, i.e., [SiP2] double-tetrahedral and planar pnictogen layers. The partial DOS curves reveal that P states in the double-tetrahedral layer primarily contribute to the valence band, especially intensifying at 0.5–3.0 eV below the Fermi level, while P states in the pnictogen layer contribute almost consistently throughout the valence and conduction bands. This broad dispersion of pnictogen states has been observed in the partial DOS for ZrSiS-type YbPS which also features a pnictogen layer of P atoms.34 Again, Zintl-type and purely ionic formulations can be constructed for Pna21 LaSiP3:La3+Si0(Pdtet2−Pdtet0)(Pplane1−) or La3+Si4+(Pdtet3−)2(Pplane1−). Here, the P atoms of the double tetrahedral layer (Pdtet) are bonded to either a single Si or used to corner-connect three SiP4 tetrahedra. The semiconducting nature of this phase is supported by resistivity and diffuse reflectance measurements (vide infra).
Both the P21/c and Pna21 polymorphs of LaSiP3 show no computed imaginary phonon modes (Fig. S15†) indicating these two structures are dynamically stable. Fig. S16† gives the free energy difference between these two polymorphs as a function of the temperature. At T = 0, the free energy of the P21/c polymorph is only 2.5 meV per atom higher than that of the Pna21 polymorph, with the zero-point energy 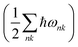 included. Calculations predict a phase transformation from the Pna21 to the P21/c polymorph at T = 374 K. This transition temperature is lower than that observed experimentally suggesting a high kinetic barrier could exist between these two polymorphs.
included. Calculations predict a phase transformation from the Pna21 to the P21/c polymorph at T = 374 K. This transition temperature is lower than that observed experimentally suggesting a high kinetic barrier could exist between these two polymorphs.
The crystallographic disorder in the phosphorus layer of the Aea2 polymorph poses significant challenges from a computational perspective. Several ordered models constrained under the space group Aea2 were constructed to examine the possible electronic behavior of this phase as described in the ESI.† The fully relaxed model retains the Aea2 symmetry with reasonable unit cell lattice parameters (a = 5.9046 Å, b = 25.5768 Å, c = 5.7885 Å). However, a significant distortion of the flat pnictogen layer results in the formation of isolated P2 dumbbells along the a-direction in a ladder-type substructure; this substructure is known to form as a result of a Peierls distortion in 2D square pnictogen sheets.26 Phonon calculations show instability of this fully relaxed model of the Aea2 polymorph because of imaginary modes (Fig. S15†). The total energy at T = 0 for this model (−6.000 eV per atom) is significantly higher than that of the P21/c (−6.042 eV per atom) and Pna21 (−6.045 eV per atom) polymorphs. These results demonstrate that Aea2 model with dumbbell-like P2 dimers is an unrealistic oversimplification of the observed crystal structure, in agreement with the diffraction and spectroscopic experimental observations that P atoms form a more complex network in the Aea2 polymorph. The DOS for the fully relaxed Aea2 model (Fig. 6) does not yield a bandgap which opposes the semiconducting behavior of this polymorph indicated by NMR T1 relaxation times, as well as resistivity and diffuse reflectance measurements. All other considered Aea2 models also resulted in a metallic DOS (Fig. S14†). To fully explore the crystal structure of the Aea2 polymorph, further studies such as molecular dynamics simulations and high-resolution electron microscopy are required. The latter has been crucial in identifying the superstructure of complex polytellurides such as K0.33Ba0.67AsTe2, AMRETe4, ALn3Te8, and RETe3 which were initially assumed to have much smaller unit cells.35–38 These systems have been shown to undergo lattice distortions driven by electronic structure instead of maintaining a perfect square net of tellurium atoms; the result is the formation and unique sequencing of various oligomeric units that can be identified using electron microscopy techniques.39
Assuming the same ionic electron-counting scheme used for the other LaSiP3 polymorphs, we can devise an electron-balanced Zintl formalism for the Aea2 polymorph of LaSiP3. The assignments for La, Si, and P atoms of the double-tetrahedral layer are identical to the Pna21 polymorph. To maintain the electron-balanced composition, the disordered pnictogen layer must have an oxidation state of −1 yielding a Zintl composition of La3+Si4+(Pdtet3−)2Pplane1− or La3+(SiP2)dtet2−Pplane1− as described for the Pna21 polymorph. However, if we assume the formation of P2 dumbbells as predicted in calculations, we arrive at oxidation states of −2 for the P atoms in the pnictogen layer.
Summarizing the results of phonon calculations, optimized synthetic profiles, as well as ex situ and in situ annealings, the following thermal stability of the three polymorphs of LaSiP3 can be deduced: Pna21 → P21/c → Aea2. It is peculiar that the low-temperature and high-temperature polymorphs in this sequence are closely related in structure, while the intermediate polymorph has a completely different arrangement of chemical bonds. While the intermediate polymorph can be bypassed in fast in situ experiments (going directly from Pna21 to Aea2), ex situ annealings performed for several days clearly show formation of the P21/c polymorph at 900 °C. For CeSiP3, the polymorphic relations are simplified by absence of the P21/c polymorph: Pna21 → Aea2.
31P and 31P{139La} solid state NMR
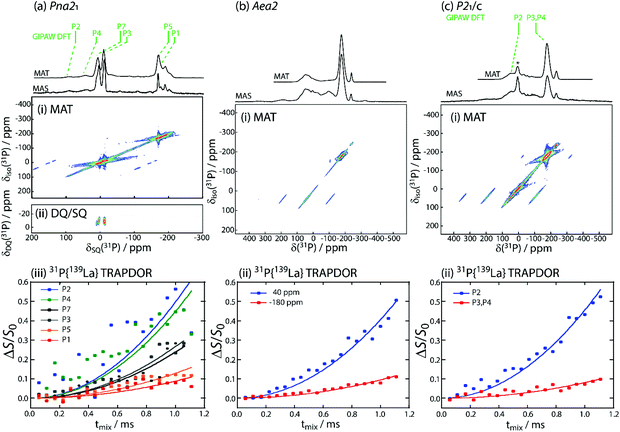
Solid-state 31P NMR spectroscopy was applied to distinguish the different phosphorus environments present in the different LaSiP3 polymoprhs. Despite the use of fast-magic-angle-spinning (fast-MAS, νr = 36 kHz), sideband overlap was a challenge due to the wide spectral bandwidths and large chemical shift anisotropy found in these samples. As such, magic-angle-turning (MAT),40,41 using the 5π sequence,42 was applied to separate the anisotropic and isotropic components of the chemical shift tensors and obtain purely isotropic 31P NMR spectra.We first describe the results obtained for the Pna21 polymorph (structure with labeled P atoms is given in Fig. S9†). In the 31P MAS spectrum of LaSiP3Pna21, there are a large number of resonances, in agreement with the six sites found in its crystal structure (Fig. 7a(i)). The spectrum is somewhat simplified with the use of MAT where we are able to further identify the six isotropic resonances (see Table S2†). To assign them, we performed gauge-including projector augmented-wave (GIPAW) density functional theory (DFT) calculations of the 31P magnetic shielding tensors which were later converted to chemical shifts using the shielding calculated for GaP as a secondary reference (see ESI† for details). Notably, these calculations predicted that the P2 and P4 sites, which terminate the SiP4 tetrahedral layers and are coordinated by La atoms, would have the greatest chemical shift anisotropy (Table S2†) which is in agreement with their assignment to the higher frequency resonances that have the most intense spinning sidebands.
The general placement of the resonances is only in moderate agreement with the experimental chemical shifts. There are three most likely causes for the disagreement: the relatively simple consideration of relativistic effects in our calculations, the known deficiency of PBE in describing empty La 4f orbitals,43,44 and the sensitivity to slight changes in the energy levels of the conduction bands, which shares the same root cause as the band gap problem, vide supra.45 The first two causes, in particular, are expected to significantly affect the calculated shieldings of phosphorus atoms surrounded by lanthanum. As such, we turned to the measurement of internuclear proximities to verify these assignments. Using the back-to-back (BaBa)46 homonuclear double-quantum dipolar recoupling sequence, we were able to obtain a 31P double-quantum-single-quantum (DQ/SQ) correlation spectrum, Fig. 7a(ii), which showed only a single correlation between the sites at −12 and 5 ppm. Based on the DFT results, these sites would correspond to the P3 and P7 sites, respectively, which are found in the phosphorus chains originating from Peierls distortion of the square P layer. As these sites form the only direct P–P bonds, the DQ/SQ spectrum confirms their assignments.
We then probed 31P–139La proximities using a transfer of population double-resonance (TRAPDOR)47,48 experiment to differentiate the sites from the La-rich and Si-rich layers. This experiment requires the acquisition of echo datasets as a function of the echo delay both with and without the inclusion of 139La irradiation. Irradiation at the 139La Larmor frequency led to the recoupling of 31P–139La dipolar interactions and an attenuation of the echo signal. Data are commonly shown with the difference in intensity between these two experiments normalized to the regular echo intensity (ΔS/S0), Fig. 7a(iii). The initial dephasing is well described by a parabola, with the second-order rate constant being proportional to the sum-squared dipolar couplings (∑RDD2) between the two nuclides.49–54 We observed that the higher frequency resonances dephased significantly faster (0.497 ms−2 and 0.449 ms−2) than the lower frequency resonances (0.129 ms−2 and 0.089 ms−2), with the P3 and P7 sites dephasing at intermediate rates of 0.239 ms−2 and 0.267 ms−2. This is in good agreement with the ∑RDD2 values for the three environments (250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 973 s−2, 56
973 s−2, 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 s−2, and 186
950 s−2, and 186![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 449 s−2), confirming the GIPAW-DFT assignments of the phosphorus sites from the La-rich layer (P2 and P4) to the higher frequency resonances and those from the Si-rich layer (P5 and P1) to the lower frequency resonances.
449 s−2), confirming the GIPAW-DFT assignments of the phosphorus sites from the La-rich layer (P2 and P4) to the higher frequency resonances and those from the Si-rich layer (P5 and P1) to the lower frequency resonances.
The 31P MAS and MAT spectra for the Aea2 polymorph (Fig. 7b) featured considerable overlap and far greater chemical shift anisotropy, in agreement with this polymorph's highly disordered structure (structure with labeled P atoms is given in Fig. S9†). Only two environments are resolved in the MAT projection, centered around −175 and 46 ppm. The peak at 46 ppm, however, does have an uneven line-shape suggesting the presence of multiple resonances. Unfortunately, the 31P signals dephased too rapidly to enable acquisition of a 31P DQ/SQ correlation spectrum, which would have confirmed the location of the terminal site in SiP4 layer, P2. The 31P{139La} TRAPDOR experiment was nevertheless successful and showed the two resonances dephasing at rates of 0.405 ms−2 and 0.094 ms−2, Fig. 7b(ii), thus identifying the resonance at the higher chemical shift to the La-rich layer, in agreement with that observed in the Pna21 polymorph. A closer inspection of the TRAPDOR spectra revealed that the higher frequency maximum, centered at 46 ppm, dephased significantly faster than the shoulder around −17 ppm (most clearly seen in the echo spectrum, Fig. 7b), suggesting that this shoulder belongs to the phosphorus layer sites, P2, in good agreement with their chemical shift in the Pna21 polymorph. Note that the similarity of the 31P chemical shifts from the phosphorus layers in both the Pna21 and Aea2 polymorphs strongly suggests that the Aea2 polymorph also features infinite P fragments as opposed to the isolated P2 dumbbells resulting from the DFT optimizations.
We lastly studied the monoclinic polymorph that crystalizes in the P21/c space group (structure with labeled P atoms is given in Fig. S10†). This polymorph featured two main resonances, namely a sharp resonance at −172 ppm and a broader one at 42 ppm (Fig. 7c). Additional resonances correspond to impurities present in the sample. GIPAW DFT calculations predicted that the P2 site from the La-rich layer would again resonate at the higher chemical shift while the P3 and P4 sites would have nearly identical lower frequency chemical shifts. These assignments were confirmed by the 31P{139La} TRAPDOR measurement which showed the fastest dephasing for the 42 ppm resonance (Fig. 7c(iii)). The room-temperature spin–lattice-T1 relaxation times for the three polymorphs were of 2.2 s for all sites in Aea2, 4.1 and 3.4 s for high and low frequency signals in P21/c; and 26.5, 11.1 and 39.2 s for the three regions from high to low frequency in Pna21 (Table S2 and Fig. S9, 10†). The magnitude of T1 relaxation times suggest all three polymorphs are semiconductors.
Transport properties
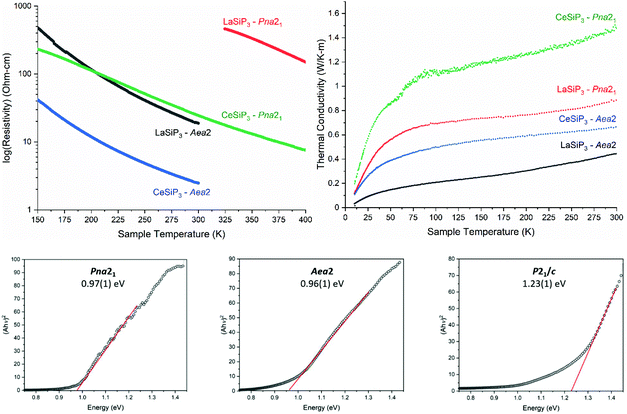
Measurements of the resistivities and thermal conductivities of the LnSiP3 (Ln = La and Ce) phases were performed on highly compacted polycrystalline sintered samples (Fig. 8). All four phases exhibit a semiconducting behavior with resistivity increasing with decreasing temperature. This agrees with T1 relaxation times from solid-state NMR studies of LaSiP3 polymorphs (Table S2†), thus disproving the computational prediction of metallic behavior in Aea2. Diffuse reflectance measurements further support the semiconducting nature of the LaSiP3 polymorphs with both non-centrosymmetric polymorphs having similar direct bandgaps of 0.97(1) eV (Pna21) and 0.96(1) eV (Aea2), while the significantly different crystal structure of the monoclinic polymorph (P21/c) results in larger bandgap of 1.23(1) eV (Fig. 8). Below 150 K for LaSiP3 (Aea2) and both CeSiP3 samples, and below 325 K for LaSiP3 (Pna21) sample, resistivity measurements become unreliable (cross-section and cooling/heating rate dependent) and such data are not shown. Based on computations and the smaller NMR relaxation times for the LaSiP3Aea2 polymorph as compared to Pna21 polymorph, one can expect that the Aea2 phases have higher carrier concentrations. Indeed, for both rare-earth metals studied, either La or Ce, the resistivity of the completely ordered Pna21 polymorph is higher than that for the disordered Aea2 forms (Fig. 8).For the thermal conductivities, we expect the disordered nature of P layers coupled with additional minor disorder in the Si–P layer to reduce the thermal conductivity for Aea2 polymorphs. This was indeed observed with both Pna21 polymorphs having higher thermal conductivities than the Aea2 polymorphs (Fig. 8). Moreover, the disorder present in the P layers in Aea2 polymorphs resulted in glass-like behavior of the thermal conductivity with gradual increase of the thermal conductivity over a wide temperature range. Overall, the studied phases exhibit quite low thermal conductivity for the crystalline samples in the range of 0.4–1.6 W m−1 K−1 at room temperature. Complex non-centrosymmetric semiconductors with high thermal stability and low thermal conductivity might be a useful platform for the development of thermoelectric materials assuming the carrier concentration is tunable. Studies of various aliovalent substitutions to modify the carrier concentrations of these phases are currently underway.
Conclusions
The synthesis and characterization of five LnSiP3 compounds (Ln = La and Ce) are presented: Pna21, Aea2, and P21/c polymorphs for LaSiP3; and Pna21 and Aea2 polymorphs for CeSiP3. The synthesis of these phases involved a novel method of atomically mixing the refractory components (Ln + Si) via arc-melting and then reacting the precursor with elemental P. In situ studies reveal that the main advantage of this method is direct conversion of LnSi to ternary LnSiP3 phase, bypassing the formation of SiP – a common by-product of the reaction from the elements. This study emphasizes the value of the proposed synthetic method as it allows to overcome solid–solid diffusion and reactivity limitations. The developed synthetic method is widely applicable for systems with conflicting reactivities of the components.The structures of the Pna21 and Aea2 polymorphs are similar with alternating layers of lanthanide, [SiP2] double tetrahedral, and phosphorus layers (2D distorted square nets of P for Aea2 and 1D cis–trans chains of P for Pna21). The P local environments were confirmed using Raman spectroscopy and advanced solid-state NMR methods, including the measurement of 31P–31P and 31P–139La proximities. Electronic DOS calculations predicted semiconducting behavior for the P21/c and Pna21 polymorphs, and phonon DOS calculations supported that these two polymorphs are dynamically stable with a predicted and experimentally-verified phase transformation from the Pna21 to the P21/c polymorph. Several computational models were constructed to study the disordered Aea2 polymorph but did not accurately depict the semiconducting behavior observed from properties. Transport properties measurements and diffuse reflectance spectroscopy showed the Pna21 and Aea2 polymorphs for both La and Ce are semiconductors with bandgaps of less than 1 eV. Ultra-low thermal conductivities at room temperature were observed for the Aea2 polymorphs which feature highly disordered P layers. Studies of the tunability of non-centrosymmetric P layers for further studies of the topological and electronic properties of these complex materials is currently underway.
Author contributions
The manuscript was written through contributions of all authors.Funding sources
G. A. is grateful to the Ames Laboratory Spedding Postdoctoral Fellowship for financial support. B. C. M. is thankful to the Jonathan and Susan Rich Undergraduate Research Scholarship and ISU LAS Dean's High Impact Undergraduate Research Award for financial support. This work was supported by the Ames Laboratory's Laboratory Directed Research and Development (LDRD) program (G. A., J. M., G. V, J. W., S. J. L., K. K.). F. Z., C.-Z. W., and K.-M. H. were supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Division of Materials Science and Engineering, including computer time support on National Energy Research Scientific Computing Center (NERSC) in Berkeley, CA. Solid-state NMR work (F. A. P. and A. P.) was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. The Ames Laboratory is operated for the U.S. DOE by Iowa State University under contract #DE-AC02-07CH11358. Use of the Advanced Photon Source at Argonne National Laboratory was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357.Conflicts of interest
Authors declare no conflict of interests.Acknowledgements
We thank Prof. J. V. Zaikina (ISU) for access to the SPS and UV/Vis/NIR spectrophotometer, and Prof. V. Pecharsky (ISU and Ames Laboratory) for access to the arc-melting setup. We thank the beamline scientists Dr S. Lapidus, Dr A. Yakovenko, and Dr W. Xu for the help in data collection at the 11-BM and 17-BM beamlines at the Advanced Photon Source at Argonne National Laboratory.References
- K. Watanabe, T. Taniguchi and H. Kanda, Direct-Bandgap Properties and Evidence for Ultraviolet Lasing of Hexagonal Boron Nitride Single Crystal, Nat. Mater., 2004, 3(6), 404–409, DOI:10.1038/nmat1134.
- Y. Tian, B. Xu, D. Yu, Y. Ma, Y. Wang, Y. Jiang, W. Hu, C. Tang, Y. Gao, K. Luo, Z. Zhao, L.-M. Wang, B. Wen, J. He and Z. Liu, Ultrahard Nanotwinned Cubic Boron Nitride, Nature, 2013, 493(7432), 385–388, DOI:10.1038/nature11728.
- R. T. Paine and C. K. Narula, Synthetic Routes to Boron Nitride, Chem. Rev., 1990, 90(1), 73–91, DOI:10.1021/cr00099a004.
- Y. Kubota, K. Watanabe, O. Tsuda and T. Taniguchi, Deep Ultraviolet Light-Emitting Hexagonal Boron Nitride Synthesized at Atmospheric Pressure, Science, 2007, 317(5840), 932–934, DOI:10.1126/science.1144216.
- V. L. Solozhenko, O. O. Kurakevych and Y. Le Godec, Creation, of Nanostuctures by Extreme Conditions: High-Pressure Synthesis of Ultrahard Nanocrystalline Cubic Boron Nitride, Adv. Mater., 2012, 24(12), 1540–1544, DOI:10.1002/adma.201104361.
- N. Dubrovinskaia, V. L. Solozhenko, N. Miyajima, V. Dmitriev, O. O. Kurakevych and L. Dubrovinsky, Superhard Nanocomposite of Dense Polymorphs of Boron Nitride: Noncarbon Material Has Reached Diamond Hardness, Appl. Phys. Lett., 2007, 90(10), 101912, DOI:10.1063/1.2711277.
- B. Owens-Baird, J. Xu, D. Y. Petrovykh, O. Bondarchuk, Y. Ziouani, N. González-Ballesteros, P. Yox, F. M. Sapountzi, H. Niemantsverdriet, Y. V. Kolen'ko and K. Kovnir, NiP2: A Story of Two Divergent Polymorphic Multifunctional Materials, Chem. Mater., 2019, 31(9), 3407–3418, DOI:10.1021/acs.chemmater.9b00565.
- A. Haffner and D. Johrendt, Synthesis, Crystal Structure, and, Chemical Bonding of Ba2SiP4: Synthesis, Crystal Structure, and Chemical Bonding of Ba2SiP4, Z. Anorg. Allg. Chem., 2017, 643(21), 1717–1720, DOI:10.1002/zaac.201700320.
- A. Haffner, V. Weippert and D. Johrendt, Polymorphism of Ba 2 SiP 4: Polymorphism of Ba 2 SiP 4, Z. Anorg. Allg. Chem., 2020, 646(3), 120–124, DOI:10.1002/zaac.201900188.
- V. Sousa, B. F. Gonçalves, M. Franco, Y. Ziouani, N. González-Ballesteros, M. Fátima Cerqueira, V. Yannello, K. Kovnir, O. I. Lebedev and Y. V. Kolen'ko, Superstructural Ordering in Hexagonal CuInSe 2 Nanoparticles, Chem. Mater., 2019, 31(1), 260–267, DOI:10.1021/acs.chemmater.8b04368.
- A. F. Moodie and H. J. Whitfield, Determination of the Structure of Cu 2 ZnGeS 4 Polymorphs by Lattice Imaging and Convergent-Beam Electron Diffraction, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42(3), 236–247, DOI:10.1107/S0108768186098282.
- A. S. R. Chesman, J. van Embden, E. Della Gaspera, N. W. Duffy, N. A. S. Webster and J. J. Jasieniak, Cu 2 ZnGeS 4 Nanocrystals from Air-Stable Precursors for Sintered Thin Film Alloys, Chem. Mater., 2014, 26(19), 5482–5491, DOI:10.1021/cm501393h.
- S. Ono, H. Hayakawa and K. Nomura, Synthesis of Ln-Si-P (Ln=La, Ce, Pr) Ternary Compounds, J. Chem. Soc. Jpn., 1976, 11, 1700–1709 CrossRef.
- H. Hayakawa, T. Sekine and S. Ono, Chemical Transport Reactions of Some Rare Earth Phosphides: Syntheses of New Rare Earth-Silicon-Phosphorus Ternary Compounds, J. Less-Common Met., 1975, 41(2), 197–210, DOI:10.1016/0022-5088(75)90028-4.
- H. Hayakawa, S. Ono and A. Kobayashi, The Crystal Structure of Cerium Silicon Triphosphide (CeSiP3), J. Chem. Soc. Jpn., 1978, 9, 1214–1220 CrossRef.
- S. Klemenz, S. Lei and L. M. Schoop, Topological Semimetals in Square-Net Materials, Annu. Rev. Mater. Res., 2019, 49(1), 185–206, DOI:10.1146/annurev-matsci-070218-010114.
- S. Klemenz, A. K. Hay, S. M. L. Teicher, A. Topp, J. Cano and L. M. Schoop, The Role of Delocalized Chemical Bonding in Square-Net-Based Topological Semimetals, J. Am. Chem. Soc., 2020, 142(13), 6350–6359, DOI:10.1021/jacs.0c01227.
- P. Kaiser and W. Jeitschko, The Rare Earth Silicon Phosphides LnSi2P6(Ln = La, Ce, Pr, and Nd), J. Solid State Chem., 1996, 124(2), 346–352, DOI:10.1006/jssc.1996.0248.
- J. Mark, J. Wang, K. Wu, J. G. Lo, S. Lee and K. Kovnir, Ba2Si3P6: 1D Nonlinear Optical Material with Thermal Barrier Chains, J. Am. Chem. Soc., 2019, 141(30), 11976–11983, DOI:10.1021/jacs.9b04653.
- J. Mark, J.-A. Dolyniuk, N. Tran and K. Kovnir, Crystal and Electronic Structure and Optical Properties of AE2 SiP 4 (AE = Sr, Eu, Ba) and Ba4Si3P8: Crystal and Electronic Structure and Optical Properties of AE2 SiP4 (AE = Sr, Eu, Ba) and Ba4Si3P8, Z. Anorg. Allg. Chem., 2019, 645(3), 242–247, DOI:10.1002/zaac.201800430.
- J.-A. Dolyniuk, D. C. Kaseman, S. Sen, J. Zhao, F. E. Osterloh and K. Kovnir, MP-BaP3: A New Phase from an Old Binary System, Chem. – Eur. J., 2014, 20(34), 10829–10837, DOI:10.1002/chem.201305078.
- K. E. Woo, J. Wang, K. Wu, K. Lee, J.-A. Dolyniuk, S. Pan and K. Kovnir, Mg-Si-As: An Unexplored System with Promising Nonlinear Optical Properties, Adv. Funct. Mater., 2018, 28(30), 1801589, DOI:10.1002/adfm.201801589.
- D. Rutzinger, C. Bartsch, M. Doerr, H. Rosner, V. Neu, T. Doert and M. Ruck, Lattice Distortions in Layered Type Arsenides LnTAs2 (Ln=La–Nd, Sm, Gd, Tb; T=Ag, Au): Crystal Structures, Electronic and Magnetic Properties, J. Solid State Chem., 2010, 183(3), 510–520, DOI:10.1016/j.jssc.2009.12.021.
- X. Lin, S. S. Stoyko and A. Mar, Ternary Rare-Earth Zinc Arsenides REZn2As3 (RE=La–Pr) Containing Defect Fluorite-Type Slabs, J. Solid State Chem., 2013, 199, 189–195, DOI:10.1016/j.jssc.2012.12.026.
- A. Mills, Chains, Planes, and Antimonides, Coord. Chem. Rev., 2002, 233–234, 207–222, DOI:10.1016/S0010-8545(02)00097-8.
- G. A. Papoian and R. Hoffmann, Hypervalent Bonding in One, Two, and Three Dimensions: Extending the Zintl-Klemm Concept to Nonclassical Electron-Rich Networks, Angew. Chem., Int. Ed., 2000, 39, 2408–2448, DOI:10.1002/1521-3773(20000717)39:14<2408::aid-anie2408>3.0.co;2-u.
- R. Troc, J. Leciejewicz and R. Ciezewski, Antiferromagnetic Structure of Uranium Diphosphide, Phys. Status Solidi, 1966, 15, 515–519 CrossRef CAS.
- S. I. Chihrii, Synthesis and Crystal Structure of SmCuP2 Compound, Zh. Neorg. Khim., 1990, 35, 1656–1658 Search PubMed.
- G. Akopov, G. Viswanathan and K. Kovnir, Synthesis, Crystal and Electronic Structure of La2SiP4, Z. Anorg. Allg. Chem., 2020, 647, 91, DOI:10.1002/zaac.202000378.
- J. Wang, J. Mark, K. E. Woo, J. Voyles and K. Kovnir, Chemical Flexibility of Mg in Pnictide Materials: Structure and Properties Diversity, Chem. Mater., 2019, 31(20), 8286–8300, DOI:10.1021/acs.chemmater.9b03740.
- B. Eisenmann, H. Jordan and H. Schäfer, Ba3Si4P6, Eine Neue Zintlphase Mit Vernetzten Si4P5-Käfigen/On Ba3Si4P6, a New Zintl Phase with Connected Si4P5 Cages, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1984, 39(7), 864–867, DOI:10.1515/znb-1984-0705.
- B. Eisenmann, H. Jordan and H. Schäfer, Zintl-phasen mit komplexen anionen: Darstellung und struktur der o-phosphosilikate und -germanate EII4EIVP4 (MIT EII = Ca, Sr, Ba und EIV = Si, Ge), Mater. Res. Bull., 1982, 17(1), 95–99, DOI:10.1016/0025-5408(82)90188-X.
- J. Wang, Y. He, N. E. Mordvinova, O. I. Lebedev and K. Kovnir, The Smaller the Better: Hosting Trivalent Rare-Earth Guests in Cu–P Clathrate Cages, Chem, 2018, 4(6), 1465–1475, DOI:10.1016/j.chempr.2018.04.001.
- W. Tremel and R. Hoffmann, Square Nets of Main-Group Elements in Solid-State Materials, J. Am. Chem. Soc., 1987, 109(1), 124–140, DOI:10.1021/ja00235a021.
- X. Zhang, J. Li, B. Foran, S. Lee, H.-Y. Guo, T. Hogan, C. R. Kannewurf and M. G. Kanatzidis, Distorted Square Nets of Tellurium in the Novel Quaternary Polytelluride K0.33Ba0.67AgTe2, J. Am. Chem. Soc., 1995, 117(42), 10513–10520, DOI:10.1021/ja00147a012.
- R. Patschke, J. Heising, J. Schindler, C. R. Kannewurf and M. Kanatzidis, Site Occupancy Wave and Unprecedented Infinite Zigzag (Te2–2)NChains in the Flat Te Nets of the New Ternary Rare Earth Telluride FamilyALn3Te8, J. Solid State Chem., 1998, 135(1), 111–115, DOI:10.1006/jssc.1997.7606.
- C. D. Malliakas and M. G. Kanatzidis, Charge Density Waves in the Square Nets of Tellurium of AMRE Te 4 (A = K, Na; M = Cu, Ag; RE = La, Ce), J. Am. Chem. Soc., 2007, 129(35), 10675–10677, DOI:10.1021/ja073986m.
- C. Malliakas, S. J. L. Billinge, H. J. Kim and M. G. Kanatzidis, Square Nets of Tellurium: Rare-Earth Dependent Variation in the Charge-Density Wave of RETe 3 (RE = Rare-Earth Element), J. Am. Chem. Soc., 2005, 127(18), 6510–6511, DOI:10.1021/ja0505292.
- R. Patschke and M. G. Kanatzidis, Polytelluride Compounds Containing Distorted Nets of Tellurium, Phys. Chem. Chem. Phys., 2002, 4(14), 3266–3281, 10.1039/b201162j.
- N. M. Szeverenyi, A. Bax and G. E. Maciel, Magic-Angle Hopping as an Alternative to Magic-Angle Spinning for Solid State NMR, J. Magn. Reson. (1969), 1985, 61(3), 440–447, DOI:10.1016/0022-2364(85)90184-2.
- Z. Gan, High-Resolution Chemical Shift and Chemical Shift Anisotropy Correlation in Solids Using Slow Magic Angle Spinning, J. Am. Chem. Soc., 1992, 114(21), 8307–8309, DOI:10.1021/ja00047a062.
- J. Z. Hu, D. W. Alderman, C. Ye, R. J. Pugmire and D. M. Grant, An Isotropic Chemical Shift-Chemical Shift Anisotropy Magic-Angle Slow-Spinning 2D NMR Experiment, J. Magn. Reson., 1993, 105, 82–87 CrossRef CAS.
- M. Profeta, M. Benoit, F. Mauri and C. J. Pickard, First-Principles Calculation of the 17 O NMR Parameters in Ca Oxide and Ca Aluminosilicates: The Partially Covalent Nature of the Ca–O Bond, a Challenge for Density Functional Theory, J. Am. Chem. Soc., 2004, 126(39), 12628–12635, DOI:10.1021/ja0490830.
- A. Sadoc, M. Body, C. Legein, M. Biswal, F. Fayon, X. Rocquefelte and F. Boucher, NMR Parameters in Alkali, Alkaline Earth and Rare Earth Fluorides from First Principle Calculations, Phys. Chem. Chem. Phys., 2011, 13(41), 18539, 10.1039/c1cp21253b.
- R. Laskowski, P. Blaha and F. Tran, Assessment of DFT Functionals with NMR Chemical Shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(19), 195130, DOI:10.1103/PhysRevB.87.195130.
- M. Feike, D. E. Demco, R. Graf, J. Gottwald, S. Hafner and H. W. Spiess, Broadband Multiple-Quantum NMR Spectroscopy, J. Magn. Reson., Ser. A, 1996, 122(2), 214–221, DOI:10.1006/jmra.1996.0197.
- C. P. Grey and W. S. Veeman, The Detection of Weak Heteronuclear Coupling between Spin 1 and Spin l/2 Nuclei in MAS NMR; 14N/’ 3C/‘H Triple Resonance Experiments, Chem. Phys. Lett., 1992, 192(4), 7 CrossRef.
- C. P. Grey and J. Vega, Determination of the Quadrupole Coupling Constant of the Invisible Aluminum Spins in Zeolite HY with 1H/27Al TRAPDOR NMR, J. Am. Chem. Soc., 1995, 117, 8232–8242 CrossRef CAS.
- J. C. C. Chan and H. Eckert, Dipolar Coupling Information in Multispin Systems: Application of a Compensated REDOR NMR Approach to Inorganic Phosphates, J. Magn. Reson., 2000, 147(2), 170–178, DOI:10.1006/jmre.2000.2191.
- M. Bertmer and H. Eckert, Dephasing of Spin Echoes by Multiple Heteronuclear Dipolar Interactions in Rotational Echo Double Resonance NMR Experiments, Solid State Nucl. Magn. Reson., 1999, 15(3), 139–152, DOI:10.1016/S0926-2040(99)00050-8.
- M. Bertmer, L. Züchner, J. C. C. Chan and H. Eckert, Short and Medium Range Order in Sodium Aluminoborate Glasses. 2. Site Connectivities and Cation Distributions Studied by Rotational Echo Double Resonance NMR Spectroscopy, J. Phys. Chem. B, 2000, 104(28), 6541–6553, DOI:10.1021/jp9941918.
- W. Strojek, M. Kalwei and H. Eckert, Dipolar NMR Strategies for Multispin Systems Involving Quadrupolar Nuclei: 31P{ 23 Na} Rotational Echo Double Resonance (REDOR) of Crystalline Sodium Phosphates and Phosphate Glasses, J. Phys. Chem. B, 2004, 108(22), 7061–7073, DOI:10.1021/jp037041c.
- W. Strojek and H. Eckert, Medium-Range Order in Sodium Phosphate Glasses: A Quantitative Rotational Echo Double Resonance Solid State NMR Study, Phys. Chem. Chem. Phys., 2006, 8(19), 2276, 10.1039/b518080e.
- S.-J. Huang, S.-B. Liu and J. C. C. Chan, Heteronuclear Dipolar Recoupling of Half-Integer Quadrupole Nuclei under Fast Magic Angle Spinning, Solid State Nucl. Magn. Reson., 2009, 36(2), 110–117, DOI:10.1016/j.ssnmr.2009.07.002.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details including synthesis descriptions as well as methods, figures, and tables pertinent to characterization techniques used: powder and single crystal X-ray diffraction, 11-BM synchrotron powder XRD, 17-BM in situ powder XRD, scanning electron microscopy, energy dispersive X-ray spectroscopy, Raman spectroscopy, differential scanning calorimetry, DFT calculations, solid-state diffuse reflectance spectroscopy, transport property measurements. CCDC 2051281 (LaSiP3-Aea2), 2051282 (LaSiP3-P21/c), 2051283 (LaSiP3-Pna21), 2051284 (CeSiP3-Aea2) and 2051285 (CeSiP3-Pna21). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1dt00845e |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |