Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
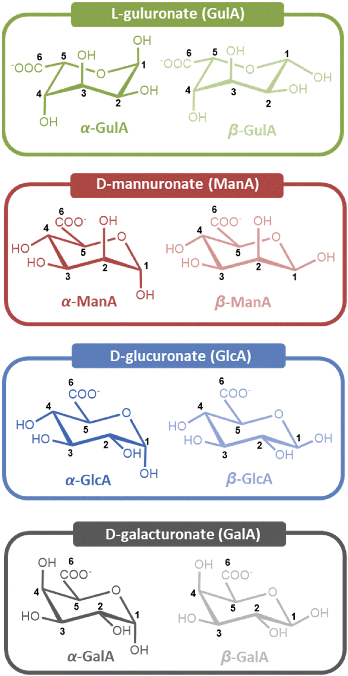
Opening the Egg Box: NMR spectroscopic analysis of the interactions between s-block cations and kelp monosaccharides†
Jack S.
Rowbotham
 *ab,
H.
Christopher Greenwell
*ab,
H.
Christopher Greenwell
 ac and
Philip W.
Dyer
ac and
Philip W.
Dyer
 *a
*a
aDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: p.w.dyer@durham.ac.uk
bCurrent address: Department of Chemistry, Inorganic Chemistry Laboratory, University of Oxford, South Parks Road, Oxford, OX1 3QR, UK
cDepartment of Earth Sciences, Durham University, South Road, Durham, DH1 3LE, UK
First published on 6th September 2021
Abstract
The best-known theory accounting for metal-alginate complexation is the so-called “Egg Box” model. In order to gain greater insight into the metal-saccharide interactions that underpin this model, the coordination chemistry of the corresponding monomeric units of alginate, L-guluronate (GulA) and D-mannuronate (ManA) have been studied herein. GulA and ManA were exposed to solutions of different s-block cations and then analysed by 1H and 13C NMR spectroscopy. It was found that the α/β ratio of the pyranose anomeric equilibria of GulA showed large pertubations from the starting value (α/β = 0.21 ± 0.01) upon contact with 1.0 M Ca2+, Sr2+, and Ba2+ (α/β = 1.50 ± 0.03, 1.20 ± 0.02, and 0.58 ± 0.02, respectively) at pD 7.9, but remained almost constant in the presence of Na+, K+, and Mg2+ (α/β = 0.24 ± 0.01, 0.19 ± 0.01, and 0.26 ± 0.01, respectively). By comparison, no significant changes were observed in the α/β ratios of ManA and related mono-uronates D-glucuronate (GlcA) and D-galacturonate (GalA) in the presence of all of the metal ions surveyed. Analysis of the 1H and 13C coordination chemical shift patterns indicate that the affinity of α-GulA for larger divalent cations is a consequence of the unique ax–eq–ax arrangement of hydroxyl groups found for this uronate anomer.
Introduction
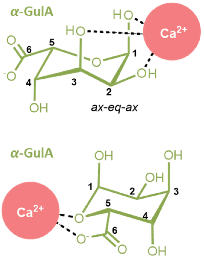
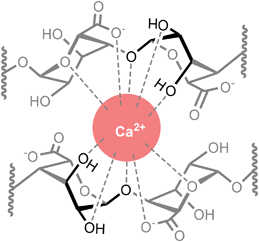
Kelps are large brown seaweeds that are found commonly across the shores of Northern Europe and contain the biopolymer alginate at high levels (up to 40% of the dry weight).1 Alginates are a class of anionic polysaccharide comprised of linear chains of (1 → 4)-linked (1C4)-α-L-gulopyranuronate and (4C1)-β-D-mannopyranuronate units,2,3 and are well-known for their metal-binding properties.4,5 Notably, in the presence of divalent metal cations alginates form gels,6 which are used extensively in food preparation,7 cosmetics,8 and biomedical applications.9–12 Of particular importance are the high affinities of alginates for specific metal ions (such as Pb2+, Cu2+, and Cd2+),13,14 which enables use of kelp biomass for the bioremediation of contaminated water.4 This technological importance of metal-alginate coordination interactions has driven considerable research interest.15–17The most well-known theory for the nature of metal-alginate binding is the so-called Egg Box model, originally formulated by Morris, Rees, and co-workers,18 and independently by Angyal19 and Smidsrød et al.20 This model remains the subject of much research interest even after almost 50 years of its original proposal. The premise of the model is that the buckled structure of poly-α-L-guluronate chains give rise to anionic cavities, in which divalent metal ions can nestle like eggs in an egg box. Key to the Egg Box binding motif is the axial–equatorial–axial (ax–eq–ax) arrangement of oxygen atoms on the α-L-gulopyranuronate units, which enables a di-pentadentate coordination of a metal ion (Fig. 1). The model successfully explains why some metals (such as Ca2+) readily form gels, whilst others (such as Mg2+) do not, as a result of the size match/mis-match of the pseudo 3D metal ion cavity.21,22 This Egg Box model also offers an explanation for why the flatter, ribbon-like poly-β-D-mannuronate chains do not show the same gelation behaviour as their guluronate counterparts.14,18,23,24
 | ||
| Fig. 1 Ca2+ coordinated within an Egg Box site formed by two buckled, parallel poly-α-L-guluronate chains of an alginate. The ax–eq–ax arrangements of hydroxyl groups are highlighted (bold). | ||
Nevertheless, since its initial suggestion, many authors have questioned the validity of the Egg Box binding model, particularly the high-coordination numbers of the central metal ion that have been proposed.25 Consequently, a number of alternative models have been put forward supported by computational studies.26–33 However, experimental validation of these models remains a challenge, as techniques such as NMR spectroscopy and X-ray diffraction are not easily applied and interpreted for disordered metal-alginate gels.34–37 To circumvent these problems Plazinski and Drach have sought recently to refine computational investigations of metal alginate systems by first modelling the interactions of the mono- and oligo-saccharide units involved.28,38 Again, however, supporting experimental data for such endeavours is scarce owing to the, often prohibitively, expensive nature of the requisite isolated sugars.39–44
In this present manuscript, we provide detailed experimental data on metal-uronate interactions. This has been achieved by contacting aqueous solutions of various s-block metal cations with the monomeric units of which alginate is comprised, namely L-guluronate (GulA) and D-mannuronate (ManA) (Fig. 2), which we have recently prepared and characterised.45 By studying the resulting solutions by NMR spectroscopy, changes to the anomeric equilibria and chemical shifts of the sugars upon metal coordination can be determined, which are indicative of the different metal-saccharide binding interactions established.25 In addition, parallel experiments were also carried out with commercially available D-galacturonate (GalA) and D-glucuronate (GlcA) (Fig. 2). Both GalA and GlcA are found abundantly in nature (in pectins and hemicelluloses, respectively), and their metal-binding properties have been much more widely investigated than that of the algal uronates, hence providing a useful comparison.42–44,46–63
To our knowledge, the work presented herein represents the most extensive investigation of the complexation of metal ions to mono-uronates to-date, and will help to inform future studies of the behaviour and applications of their parent polysaccharides.
Results
Changes in mono-pyranuronate anomeric equilibria in the presence of s-block metal ions
Initially, the interactions of the four mono-uronates (GulA, ManA, GlcA, and GalA) with different s-block cations were probed. In each case, the changes to the pyranose anomeric equilibria (expressed as the ratio of α-anomer to β-anomer, α/β) on addition of the metal ions was determined. Perturbations of the α/β ratio are indicative of preferential complexation of the metal by one of the two anomers. To this end, the 1H NMR spectra (295 K, 400 MHz) of the sodium salts of GulA, ManA, GlcA, and GalA were recorded in D2O solutions (42 mM, pD 7.9) containing the desired metal chloride salt (1.0 M). A control experiment in which no additional metal salt was added was run in parallel, (referred to as the “no metal” case). Following the acquisition of the NMR spectra at pD 7.9, the pD was lowered to 1.4 (well below the pKa values of the uronates),45 and the spectra re-recorded. In addition to the influence of pD, the impact of other variables (ionic strength and metal counter-anion) were also evaluated (ESI sections 3.1 and 3.2†). The measured α/β ratios are summarised in Fig. 3. Changes to the pyranose/furanose equilibria were generally small and are disregarded for this analysis, but are reported in full in ESI section 3.4.†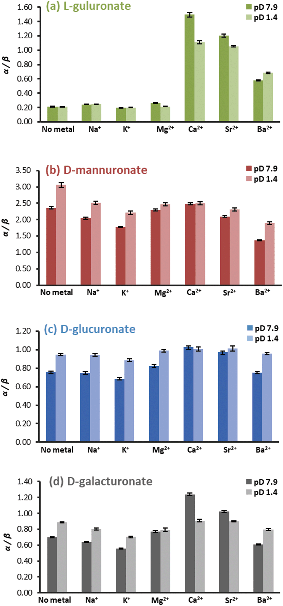 | ||
| Fig. 3 The α/β ratios of (a) L-guluronate, (b) D-mannuronate, (c) D-glucuronate, and (d) D-galacturonate in 1.0 M aqueous solutions of different metal chloride salts at 295 K and pD 7.9 or 1.4. | ||
GulA was found to exhibit the lowest α/β ratio of all of the four uronates studied (α/β = 0.21 ± 0.01 when measured at pD 7.9 in the metal-free case). It was found that addition of Na+, K+, or Mg2+ had virtually no effect, with α/β ratios all staying within ± 0.05 of the metal-free value (Fig. 3(a)). However, addition of the ions Ca2+, Sr2+ and (to a lesser extent) Ba2+ all perturbed the anomeric equilibrium strongly in favour of the α-pyranose configuration, yielding α/β values of 1.50 ± 0.03, 1.20 ± 0.02, and 0.58 ± 0.02, respectively.
In contrast to the effects determined for GulA, changes to the α/β ratios for the other mono-uronates on addition of metal ions were much smaller. For ManA, the only mono-uronate to have an inherent energetic preference for the α-anomer over the β-configuration under the metal-free conditions (α/β = 2.36 ± 0.04), addition of Na+, Ca2+, Sr2+, or Mg2+ had little impact on the α/β ratio (Fig. 3(b)). However, ions with larger radii than that of Sr2+ did promote a slight increase in the proportion of the β-ManA (with Ba2+ and K+, giving rise to α/β values of 1.36 ± 0.02 and 1.77 ± 0.02, respectively). The observation of a small increase in the proportion of mannofuranuronate upon the addition of Ca2+ is also noteworthy (ESI Table S.13†) as the formation of Ca2+-mannofuranose adducts has been identified previously.64
Irrespective of the metal ions added GlcA showed no significant deviation from the α/β value of the free uronate (metal-free α/β ratio of 0.75 ± 0.01 at pD 7.9) (Fig. 3(c)). Similarly, GalA (metal-free α/β ratio of 0.70 ± 0.01 at pD 7.9) was not affected significantly by the presence of excess Na+, K+, Mg2+ or, Ba2+ ions (Fig. 3(d)). However, a stabilisation of α-GalA was detected upon addition of Ca2+ (α/β = 1.24 ± 0.01) and Sr2+ (α/β = 1.02 ± 0.01), albeit much smaller effects than those for α-GulA discussed above.
The trends in α/β ratios of the four mono-uronates remained the same upon changing the pD from 7.9 to 1.4. However, one point of difference was seen for GulA and GalA in the presence of Ca2+. At the lower pD, the stabilisation of α-GalA is virtually lost (with the pD 1.4 metal-free solution exhibiting an α/β ratio of 0.89 ± 0.01 compared to 0.91 ± 0.01 with Ca2+), in contrast to α-GulA (pD 1.4 metal-free α/β = 0.21 ± 0.01, compared to 1.11 ± 0.02 with Ca2+). These results indicated a notable degree of complexation between α-GulA and Ca2+, which persisted even upon protonation of the carboxylate moiety, something that is explored further in the following sections.
Notably, the lower pD conditions employed herein also allowed for analysis of the behaviour of the uronates in the presence of Zn2+. To keep it in solution to prevent Zn hydroxide. Here, the results were found to be almost exactly analogous to those of Mg2+, with only very minor changes detected in the α/β anomeric equilibria upon addition of Zn2+ relative to the no metal case (see ESI section 3.4†).
Changes to mono-uronate 1H NMR chemical shift values in the presence of s-block metal ions
Having established the metals for which the α- and β-mono-pyranuronates show affinities (summarised in Fig. 3), the nature of the corresponding coordination modes were analysed by studying changes to 1H chemical shifts (δ1H) of the respective 1H NMR signals of the uronates. In order to interpret the chemical shift data, changes in δ1H of the uronate protons in the metal-containing solutions relative to the metal-free and (i.e. coordination chemical shifts, Δδobs) were first recorded. As large values for Δδobs were found for all uronate signals in the metal chloride solutions, it was convenient to define a second parameter, Δδrel, determined by subtracting the value of Δδobs of H4 of the particular anomer under investigation. The H4 signal was chosen arbitrarily as it was often the resonance most shifted following addition of the metal salts; see Fig. 2 for numbering schemes.The metric Δδrel is helpful because it is close to zero in most cases, enabling rapid analysis of the large data sets (tables of all Δδobs and Δδrel values are provided for each experiment in the ESI section 3.3†). Where Δδrel is non-zero, it implies that the protons around the saccharide ring are affected differently by the presence of the metal ion, indicative of binding with different hydroxyl groups. Notably in this regard, the values of Δδrel at pD 7.9 for the protons of α-GulA, which were very small in the presence of Na+, K+, and Mg2+, were up to 10-fold larger when Ca2+, Sr2+, and Ba2+ ions were present (Table 1). These results therefore provide further evidence of a mode of complexation between α-GulA and larger divalent cations that is not accessible for other smaller metals. In contrast, the Δδrel values for β-Gul (Table 1), α- and β- ManA (ESI Tables S.6–7†), GlcA (ESI Tables S.8–9†) and GalA (ESI Tables S.8–9†), are all much smaller for all of the metals studied. The closest comparison to α-GulA is α-GalA, but even then, the differences are significant. For example, whilst α-GulA showed large Δδrel values in the presence of Ca2+ at pD 7.9 for H1 (0.27 ppm), H2 (0.19 ppm), H3 (0.13 ppm), and H5 (0.20 ppm), α-GalA only displayed significant Δδrel values for H1 (0.18 ppm) and H5 (0.13 ppm). Taken as a whole, these results indicate binding mode(s) for Ca2+, Sr2+, and Ba2+ in α-GulA, that are not operative for other metals or uronates.
| Solution | pD | Alpha pyranose | Beta pyranose | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Change in chemical shift (ppm) compared to metal-free solution relative to H4 (Δδrel) | |||||||||||
| αH1 | αH2 | αH3 | αH4 | αH5 | βH1 | βH2 | βH3 | βH4 | βH5 | ||
| No metal | 7.9 | 0.00 | 0.00 | 0.00 | — | 0.00 | 0.00 | 0.00 | 0.00 | — | 0.00 |
| NaCl | 7.9 | 0.04 | 0.03 | 0.04 | — | 0.04 | 0.01 | 0.01 | 0.02 | — | 0.02 |
| KCl | 7.9 | 0.03 | 0.02 | 0.03 | — | 0.01 | 0.01 | 0.01 | 0.01 | — | 0.01 |
| CaCl2 | 7.9 | 0.27 | 0.19 | 0.13 | — | 0.2 | 0.05 | 0.04 | 0.01 | — | 0.07 |
| SrCl2 | 7.9 | 0.28 | 0.20 | 0.14 | — | 0.22 | 0.07 | 0.06 | 0.03 | — | 0.08 |
| BaCl2 | 7.9 | 0.28 | 0.20 | 0.14 | — | 0.22 | 0.12 | 0.07 | 0.03 | — | 0.11 |
| MgCl2 | 7.9 | 0.06 | 0.00 | 0.02 | — | 0.04 | 0.01 | 0.00 | 0.01 | — | 0.02 |
| Ca(NO3)2 | 7.9 | 0.24 | 0.15 | 0.09 | — | 0.19 | 0.05 | 0.04 | 0.02 | — | 0.06 |
| Cal2 | 7.9 | 0.28 | 0.21 | 0.15 | — | 0.21 | 0.09 | 0.06 | 0.05 | — | 0.10 |
| Solution | pD | Alpha pyranose | Beta pyranose | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Change in chemical shift (ppm) compared to metal-free solution relative to H4 (Δδrel) | |||||||||||
| αH1 | αH2 | αH3 | αH4 | αH5 | βH1 | βH2 | βH3 | βH4 | βH5 | ||
| No metal | 1.4 | 0.00 | 0.00 | 0.00 | — | 0.00 | 0.00 | 0.00 | 0.00 | — | 0.00 |
| NaCl | 1.4 | 0.02 | 0.02 | 0.02 | — | 0.02 | 0.00 | −0.01 | 0.00 | — | 0.01 |
| KCl | 1.4 | 0.02 | 0.01 | 0.01 | — | 0.01 | 0.00 | 0.00 | 0.00 | — | 0.01 |
| CaCl2 | 1.4 | 0.13 | 0.15 | 0.10 | — | 0.11 | 0.01 | 0.00 | 0.02 | — | 0.01 |
| SrCl2 | 1.4 | 0.14 | 0.16 | 0.10 | — | 0.12 | 0.01 | 0.00 | 0.02 | — | 0.01 |
| BaCl2 | 1.4 | 0.15 | 0.15 | 0.10 | — | 0.14 | 0.04 | 0.01 | 0.01 | — | 0.04 |
| MgCl2 | 1.4 | 0.00 | 0.00 | 0.01 | — | −0.02 | −0.01 | −0.01 | −0.01 | — | 0.00 |
Upon lowering the pD from 7.9 to 1.4, a decrease in the magnitude of the Δδrel values for α-GulA was observed in all cases, though not uniformly for all protons. Notably, in the presence of Ca2+, Δδrel(α-GulA-H1) and Δδrel(α-GulA-H5) were lowered by 0.14 and 0.09 ppm, respectively, on decreasing the pD from 7.9 to 1.4, whilst Δδrel(α-GulA-H2) and Δδrel(α-GulA-H3) were only reduced by 0.04 and 0.03 ppm, respectively. Again, this is evidence for a coordination mode of α-GulA that persists even after protonation. In contrast, the Δδrel values for β-GulA, α- and β-ManA, GlcA, and, GalA were all reduced to near zero at pD 1.4, demonstrating the importance of the carboxylate anion in the main binding modes of all of these saccharides.
1H and 13C NMR spectroscopic titrations of mono-uronates with Ca2+
From the initial screening of the behaviour of mono-uronates in the presence of different metal ions, the interaction between α-GulA and Ca2+ was found to be unique. Consequently, a more in-depth series of experiments was carried out, whereby solutions of sodium mono-uronates (0.26 M, pD 7.9) were titrated with increasing amounts of calcium chloride (0.0–1.3 M) and studied by both 1H and 13C NMR spectroscopy (295 K). As previously, the analysis was restricted to the α- and β-pyranose forms of the GulA and ManA uronates, as the furanose isomers are not present in sufficiently high concentrations. Although GlcA was again studied for comparison, GalA was excluded since precipitation occurs during the titration sequence (the reader is instead referred to the work of Jacques et al. for a similar study of GlcA and GalA together).57The values of Δδobs(13C) and Δδobs(1H) of the 13C/1H signals from the α- and β-anomers of GulA, ManA, and GlcA were plotted against the number of equivalents of Ca2+ added (Fig. 4 and Fig. 5, respectively). Representative spectra for GulA are provided in ESI section 3.5,† and show no line broadening across the range of the titration. Full data-sets for the titrations (including the corrected anomer concentrations at each value of [Ca2+]) are also provided in ESI section 3.6.†
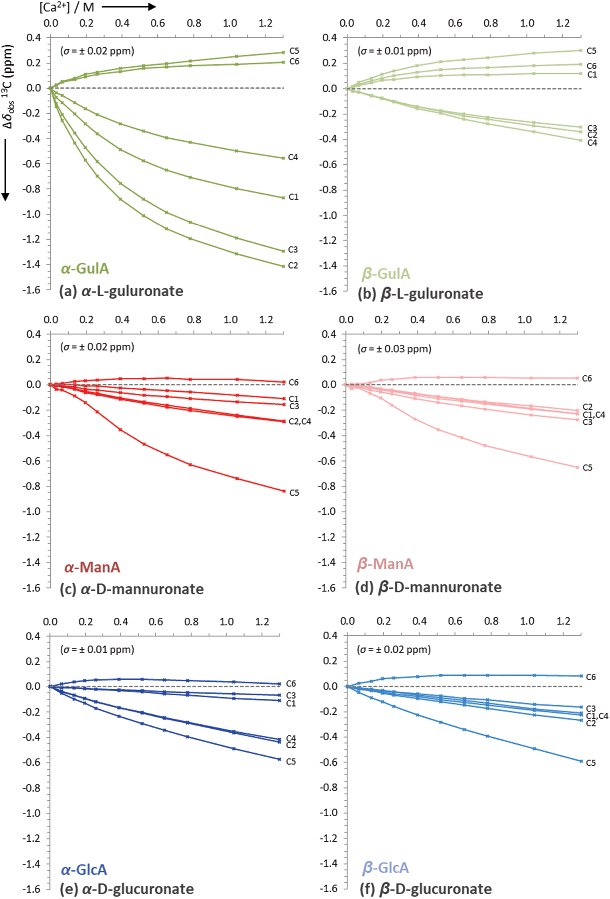 | ||
| Fig. 4 Uncorrected changes in chemical shifts, Δδobs (ppm), of carbon signals in the 13C NMR spectra of sodium mono-uronates upon the addition of aliquots of CaCl2. The nominal concentration of uronate is 0.26 M in each case (though the individual concentration of each anomer must be calculated separately for every value of [Ca2+], see ESI section 2.6†). Spectra recorded in D2O at pD 7.9, 295 K, 100 MHz. Each plot represents the average of two independent runs. Individual error bars are omitted for clarity, but an average error, σ, is stated in parentheses for each plot. | ||
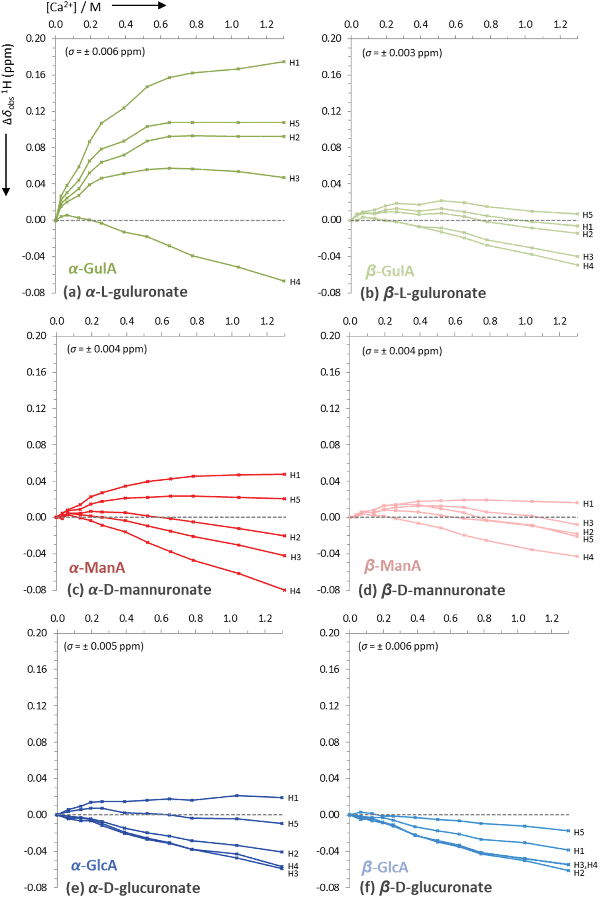 | ||
| Fig. 5 Uncorrected changes in chemical shifts, Δδobs (ppm), of proton signals in the 1H NMR spectra of sodium mono-uronates upon the addition of aliquots of CaCl2. The nominal concentration of uronate is 0.26 M in each case (though the individual concentration of each anomer must be calculated separately for every value of [Ca2+], see ESI section 2.6†). Spectra recorded in D2O at pD 7.9, 295 K, 400 MHz. Each plot represents the average of two independent runs. Individual error bars are omitted for clarity, but an average error, σ, is stated in parentheses for each plot. | ||
The data presented in Fig. 4(a) show that the Δδobs(13C) values for α-GulA at 5.0 eq. Ca2+ span 1.71 ppm, whilst those of β-GulA vary by only 0.71 ppm (Fig. 4(b)). Similarly, the range of Δδobs(1H) values for α-GulA at 5.0 eq. Ca2+ spans 0.24 ppm (Fig. 5(a)), compared to only 0.06 ppm for β-GulA (Fig. 5(b)). Whilst C4, C5, C6, and H4 all display similar Δδ values upon the addition of Ca2+ in both α- and β-GulA anomers, the large negative shift changes for αC1 (−0.87 ppm), αC3 (–1.30 ppm) and αC2 (–1.42 ppm) and positive shift changes for αH3 (0.05 ppm), αH2 (0.09 ppm), αH5 (0.11 ppm), and αH1 (0.17 ppm) contrast strongly with the equivalent β-shifts and, indeed, with all shifts determined in the experiments employing ManA and GlcA. In the cases of ManA and GlcA, Δδobs(13C) for C1, C2, C3, C4, and C6 and Δδobs(1H) for H1-H5 all remain small and tightly clustered with increasing Ca2+ concentration, relative to those from α-GulA. In the case of C5, both α- and β-GulA show a positive Δδobs(13C) value (both + 0.30 ppm) corresponding to a deshielding of the C5 nucleus, whilst α- and β-ManA and α- and β-GlcA show negative shifts (−0.57 to −0.84 ppm) for the same carbon atom. These distinct patterns of chemical shift changes can be used to discern the nature of the binding modes between Ca2+ and the various uronates, which are evaluated synoptically in the discussion section.
Finally, the Ca2+/uronate NMR titrations also enabled the calculation of tentative stability constants for the metal-carbohydrate complexes, using the open source Bindfit model developed by Thordarson et al. (see ESI section 2.6†).65–67 Using the data for C2-C4 for each anomer, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Ca2+:uronate stability constants (K1,1) were calculated: α-GulA 2.20 M−1, β-GulA 0.61 M−1, α-GlcA 0.38 M−1, β-GlcA 0.25 M−1, α-ManA 0.30 M−1, β-ManA 0.26 M−1, all with errors < ± 5%. Attempting to fit the data arising from carbons close to the carboxylate and ring oxygens (C1, C5, C6) to the same model as C2–C4 was unsuccessful, indicating that additional binding modes utilising the carboxylate moiety were also present.
1 Ca2+:uronate stability constants (K1,1) were calculated: α-GulA 2.20 M−1, β-GulA 0.61 M−1, α-GlcA 0.38 M−1, β-GlcA 0.25 M−1, α-ManA 0.30 M−1, β-ManA 0.26 M−1, all with errors < ± 5%. Attempting to fit the data arising from carbons close to the carboxylate and ring oxygens (C1, C5, C6) to the same model as C2–C4 was unsuccessful, indicating that additional binding modes utilising the carboxylate moiety were also present.
Discussion
Coordination of α-GulA to Ca2+ and similar dications
From the preceding NMR spectroscopic experiments, it is clear that α-GulA shows a preferential affinity for the larger divalent cations (Ca2+r+ = 114 pm, Sr2+r+ = 132 pm, Ba2+r+ = 149 pm) as evidenced by the significant changes in anomeric equilibria (α/β ratio) upon coordination of these ions compared to the monovalent (Na+r+ = 113 pm, K+r+ = 151 pm) and smaller divalent ions (Mg2+r+ = 71 pm, Zn2+r+ = 74 pm).68 In contrast to GulA, the α/β ratio for ManA, GlcA, and GalA show minimal perturbations upon contact with all of the cations studied (Fig. 3). Together these observations suggest that α-GulA adopts a binding mode with Ca2+ (and similar dications) that lowers the free energy of the molecule relative to the β-form, which is unique amongst the eight uronate anomers studied.It is proposed that the ax–eq–ax arrangement of hydroxyl groups found for C1, C2, and C3 of α-GulA is responsible for the Ca2+ coordination. It has previously been established that the 1,3-di-axial clash of hydroxyl oxygen atoms renders the ax–eq–ax motif particularly unstable,69,70 yet here we observe that the dipolar charges are screened by the presence of a suitable cation, which stabilises the structure significantly. The identification of ax–eq–ax binding by α-GulA is consistent with the stability trends elucidated by Angyal, for metal ion coordination to different arrangements of hydroxyl groups in cyclic polyols.19,25,71–75
If the change in α/β ratio is used as the metric to determine the favourability of coordination between divalent cations and a monopyranuronate then a metal ion affinity series can be established, which for α-GulA is Ca2+ > Sr2+ > Ba2+ ≫ Mg2+ ≈ Zn2+. Thus, whilst Ca2+ may be regarded as being well suited to binding to the ax–eq–ax arrangement, Mg2+ and Zn2+ are either too small or too strongly solvated by H2O to be able to coordinate. In this context, it is tempting to suggest that the notably lower affinity for Ba2+ of α-GulA is a result of a combination of its large ionic radius and low charge density, which minimise the strength of its binding to the ax–eq–ax arrangement of hydroxyl groups. However, from the NMR spectroscopic experiments described herein alone, it is not possible to rule out that the smaller perturbation of the equilibrium towards the α-anomer of GulA by Ba2+ may simply arise because this metal ion can also coordinate to the β-anomer in a favourable manner (discussed further below).
Further proof of the Ca2+ coordination to the ax–eq–ax arrangement of hydroxyl groups on α-GulA is given by the coordination chemical shift data Δδobs(13C) and Δδobs(1H). Shielding of carbons C1, C2, and C3 and deshielding of protons H1, H2, and H3 can be considered to be diagnostic of ax–eq–ax binding, owing to the polarisation of the respective C–H bonds by the electric field of the cation.57,72 Whilst qualitatively this trend is observed for α-GulA in the presence of Ca2+ (Fig. 4(a) and 5(a)), the numerical results do not match perfectly with those observed by Angyal for other Ca2+/ax–eq–ax complexes, such as epi-inositol.72 Furthermore, the large deshielding of the αH5 signal observed here for α-GulA would not be predicted by a pure ax–eq–ax binding arrangement. Together these anomalies indicate the presence of a second coordination mode in the α-GulA system.
It seems likely that such a secondary mode would be similar to that previously found in α-GalA, as the two anomers possess the same relative orientation of functional groups on C1, C2, C4, and C5. α-GalA is believed to bind Ca2+ through the carboxylate moiety and ring oxygen.43,49 Comparison of the Δδobs(1H) values of α-GalA in the presence of Ca2+ (see ESI Table S.10†) show a deshielding of H1 and H5, which is also be observed in the α-GulA system. Hence, it can be concluded that Ca2+ binding to α-GulA can occur through both (i) the ax–eq–ax hydroxyl groups and (ii) the carboxylate plus ring oxygen (Fig. 6). It was calculated that the tentative stability constant of Ca2+ binding through the first mode K1,1(α-GulA, ax–eq–ax) = 2.20 M−1, which is roughly similar to K1,1(ax–eq–ax) determined for the analogous saccharides α-L-gulose (K1,1 ≈ 3.7 M−1)25,76 and epi-inositol (K1,1 ≈ 3.0 M−1).72 The stability constant for Ca2+ binding to the second site, K1,1(α-GulA, carboxylate), could not be calculated here in this qualitive study as the data in the early stages of the titration are insufficiently granular, but is likely to be higher than K1,1(α-GulA, ax–eq–ax) based on literature values for K1,1(GlcA) and K1,1(GalA) at pD = 7–8.44,55–59 At low pD however, the magnitude of K1,1(carboxylate) is heavily reduced due to protonation, as evidenced by the loss of affinity of α-GalA for Ca2+ observed here, and also by other authors.54 In contrast, the extent of binding of Ca2+ by α-GulA is only slightly diminished by acidifying the solution, as the ax–eq–ax coordination mode remains operative.
Whilst the coordination behaviour of the monomeric form of α-L-guluronate does not necessarily translate to that of its polymeric alginate analogue, it is nevertheless interesting to note that both binding modes detected here (ax–eq–ax and carboxylate) are featured in the Egg Box model as it is classically depicted (Fig. 3).18–20 This affinity of α-GulA for larger divalent metal ions may also influence the interactions of oligo-uronides with enzymes such as bacterial alginate lyases, which are believed to employ Ca2+ for catalysis.77
Coordination of other uronate anomers to Ca2+
Compared to the effects of Ca2+ ions on α-GulA (discussed above), the influence of this dication on the other uronates is more subtle. The non-carboxylate K1,1 values calculated for Ca2+ with β-GulA, α-GlcA, β-GlcA, α-ManA, and β-ManA were around 3–7 times smaller than K1,1(α-GulA, ax–eq–ax). The small K1,1 values (≪1.0 M−1) for all anomers except α-GulA are consistent with the much weaker coordination by less distinct mono-/bi-dentante arrangements of hydroxyl groups on those saccharides,25,55,78 which are not unambiguously identifiable from the chemical shift data.With the exception of α-GulA therefore, it can be concluded that Ca2+ binding occurs predominantly through the carboxylate moiety of most uronates. This is something that is in line with previous reports of Ca2+ coordinating preferentially to the α-anomers of GlcA and GalA through the carboxylate and ring oxygens, and less favourably to their β-anomers through just the carboxylate moiety.43,44,49,57,58 These literature results are further supported by the results presented here. For example, the α/β ratio measurements are consistent with slightly higher affinities of α-GlcA and α-GalA for Ca2+ than the affinities of their β-anomers (Fig. 3a). Similarly, Δδrel for H1 and H5 were greater than those of H2 and H3 for α-GlcA and α-GalA, but in the β-anomers, these values were more similar (see ESI†). The same Δδrel patterns were also shown by α- and β-ManA, and β-GulA. From this, we conclude that α-ManA predominantly binds to Ca2+via the carboxylate and ring oxygens (like α-GalA and α-GlcA), whilst β-ManA and β-GulA predominantly bind through just the carboxylate group (like β-GalA and β-GlcA). From this qualitative study we have not been able to provide K1,1 values for these carboxylate binding modes, but note that they are likely to be much higher than the K1,1 values for the hydroxyl-binding modes reported above, based on previous literature reports.
Other notable metal/uronate interactions
A final observation that is worthy of note relates to the coordination of cations larger than Sr2+ to GulA and ManA. Despite the affinity of α-GulA for Ca2+ and Sr2+, changes to the α/β ratio in the presence of Ba2+ do not appear to be as large, possibly indicating a more favourable interaction of β-GulA with this larger ionic radii dication compared to that of α-GulA as a result of unfavourable binding of the latter. Additionally, ManA, which showed minimal response to the addition of metal ions, tended towards the formation of the β-anomer in the presence of Ba2+ and K+. Hence, it can be concluded that larger ions such as Ba2+ or K+ are able to coordinate to the wide, open faces of the pyranose rings of β-ManA and β-GulA, specifically giving rise to interactions with β-GulA-O2 and β-GulA-O3, and β-ManA-O1, β-ManA-O2, and β-ManA-Oring (Fig. 7). Indeed, cis-hydroxyl groups (as found on β-ManA and β-GulA) were identified by Angyal as being favourable binding sites for metal ions in carbohydrates, although less so than the ax–eq–ax arrangement.25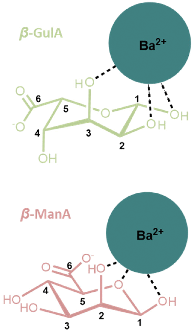 | ||
| Fig. 7 Possible coordination modes between β-anomers of (upper) GulA and (lower) ManA and the large Ba2+ ion. Both complexes involve a cis arrangement of hydroxyl oxygen atoms. | ||
Conclusions
The interactions of the two monomeric units of alginate, GulA and ManA, and two related biomass-derived monosaccharides (GlcA and GalA) with environmentally abundant s-block metal cations have been investigated. Particular focus centred on the interaction of the α-pyranose anomer of GulA, which is of relevance to the metal coordination proposed by the long-standing Egg Box model of metal-alginate binding.18–20Here, we have shown that one of the monomeric units of alginate, α-GulA, shows a preferential affinity for the coordination of larger divalent cations (Ca2+, Sr2+, and Ba2+). This is attributed to the greater stabilisation conferred to this anomer over that achieved with its lower energy β-GulA counterpart as a result of the coordination of these dications. The origin of this stabilisation is ascribed predominantly to be the result of an interaction between the divalent cation and the ax–eq–ax arrangement of hydroxyl atoms that is unique to α-GulA. The ax–eq–ax binding mode of α-GulA has a value of K1,1 of 2.20 M−1 with Ca2+, which is around 3-times higher than any such hydroxyl-binding mode on the β-GulA counterpart. Furthermore, this coordination motif remains operative even at low pH. A second binding mode of Ca2+ with α-GulA was also detected, which is generic to all α-mono-uronates, and involves the carboxylate moiety and ring oxygen. In contrast, the β-anomers principally coordinate to metal ions through just their carboxylate groups. Additionally, we report evidence for weak complexation of very large cations by the cis hydoxyl groups of β-ManA and β-GulA.
Together, this study represents the most comprehensive comparative analysis to-date of the coordination of metal ions to mono-uronates. Whilst the results presented for metal binding to GulA, ManA, GalA, and GlcA do not necessarily reflect the coordination environment present in the parent biopolymers, the results provide valuable data for the benchmarking of computational models. Such models will ultimately facilitate a fuller understanding of metal coordination by alginates and related polyuronides, both in their natural environments and in their important technological applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The staff of the Durham University NMR service, Drs Alan Kenwright and Juan Aguilar, are thanked for their assistance in the running of experiments for this work. Funding: This work was supported by the Centre for Process Innovation (CPI), Durham University, and the Engineering and Physical Sciences Research Council (EPSRC).Notes and references
- I. Donati and S. Paoletti, in Microbiology Monographs, 2009, vol. 13, pp. 1–53 Search PubMed.
- E. D. T. Atkins, I. A. Nieduszynski, W. Mackie, K. D. Parker and E. E. Smolko, Biopolymers, 1973, 12, 1879–1887 CrossRef CAS PubMed.
- E. D. T. Atkins, I. A. Nieduszynski, W. Mackie, K. D. Parker and E. E. Smolko, Biopolymers, 1973, 12, 1865–1878 CrossRef CAS PubMed.
- T. A. Davis, B. Volesky and A. Mucci, Water Res., 2003, 37, 4311–4330 CrossRef CAS PubMed.
- B. Gyurcsik and L. Nagy, Coord. Chem. Rev., 2000, 203, 81–149 CrossRef CAS.
- P. Gacesa, Carbohydr. Polym., 1988, 8, 161–182 CrossRef CAS.
- W. J. S. Peschardt, US2403547A, 1946, 1–2.
- M. Wilkinson, Aquat. Conserv. Mar. Freshw. Ecosyst., 1992, 2, 209–210 CrossRef.
- K. Y. Lee and D. J. Mooney, Prog. Polym. Sci., 2012, 37, 106–126 CrossRef CAS PubMed.
- K. I. D. Skja, in Renewable Resources for Functional Polymers and Biomaterials : Polysaccharides, Proteins and Polyesters, 2011, pp. 186–209 Search PubMed.
- K. G. Mandel, B. P. Daggy, D. A. Brodie and H. I. Jacoby, Aliment. Pharmacol. Ther., 2000, 14, 669–690 CrossRef CAS PubMed.
- S. S. Pedersen, A. Kharazmi, F. Espersen and N. Høiby, Infect. Immun., 1990, 58, 3363–3368 CrossRef CAS PubMed.
- A. Haug, J. Bjerrum, O. Buchardt, G. E. Olsen, C. Pedersen and J. Toft, Acta Chem. Scand., 1961, 15, 1794–1795 CrossRef CAS.
- R. Kohn, Pure Appl. Chem., 1975, 42, 371–397 CAS.
- Q. Yu, J. T. Matheickal, P. Yin and P. Kaewsarn, Water Res., 1999, 33, 1534–1537 CrossRef CAS.
- W. M. Antunes, A. S. Luna, C. a. Henriques and A. C. A. Da Costa, Electron. J. Biotechnol., 2003, 6, 174–184 Search PubMed.
- P. Lodeiro, B. Cordero, J. Barriada, R. Herrero and M. Sastredevicente, Bioresour. Technol., 2005, 96, 1796–1803 CrossRef CAS PubMed.
- G. T. Grant, E. R. Morris, D. A. Rees, P. J. C. Smith and D. Thom, FEBS Lett., 1973, 32, 195–198 CrossRef CAS.
- S. J. Angyal, Pure Appl. Chem., 1973, 35, 131–146 CAS.
- O. Smidsrød, A. Haug, S. G. Whittington, E. Sjöstrand and S. Svensson, Acta Chem. Scand., 1972, 26, 2563–2566 CrossRef.
- F. Topuz, A. Henke, W. Richtering and J. Groll, Soft Matter, 2012, 8, 4877 RSC.
- A. Haug, O. Smidsrød, B. Högdahl, H. A. Øye, S. E. Rasmussen, E. Sunde and N. A. Sørensen, Acta Chem. Scand., 1970, 24, 843–854 CrossRef CAS.
- A. Penman and G. R. Sanderson, Carbohydr. Res., 1972, 25, 273–282 CrossRef CAS PubMed.
- R. Kohn, B. Larsen, L. J. Sæthre, E. Sjöstrand and S. Svensson, Acta Chem. Scand., 1972, 26, 2455–2468 CrossRef CAS PubMed.
- S. J. Angyal, Adv. Carbohydr. Chem. Biochem., 1989, 47, 1–43 CrossRef CAS.
- C. DeRamos, A. Irwin, J. Nauss and B. Stout, Inorg. Chim. Acta, 1997, 256, 69–75 CrossRef CAS.
- I. Braccini and S. Pérez, Biomacromolecules, 2001, 2, 1089–1096 CrossRef CAS PubMed.
- W. Plazinski and M. Drach, J. Phys. Chem. B, 2013, 117, 12105–12112 CrossRef CAS PubMed.
- W. Plazinski and M. Drach, Appl. Surf. Sci., 2012, 262, 153–155 CrossRef CAS.
- M. B. Stewart, S. R. Gray, T. Vasiljevic and J. D. Orbell, Carbohydr. Polym., 2014, 102, 246–253 CrossRef CAS PubMed.
- P. Agulhon, V. Markova, M. Robitzer, F. Quignard and T. Mineva, Biomacromolecules, 2012, 13, 1899–1907 CrossRef CAS PubMed.
- K. Panczyk, K. Gaweda, M. Drach and W. Plazinski, J. Phys. Chem. B, 2018, 122, 3696–3710 CrossRef CAS PubMed.
- L. Bekri, M. Zouaoui-Rabah, M. Springborg and M. S. Rahal, J. Mol. Model., 2018, 24, 312 CrossRef PubMed.
- C. A. Steginsky, J. M. Beale, H. G. Floss and R. M. Mayer, Carbohydr. Res., 1992, 225, 11–26 CrossRef CAS PubMed.
- Z.-Y. Wang, Q.-Z. Zhang, M. Konno and S. Saito, Biopolymers, 1993, 33, 703–711 CrossRef CAS.
- L. Li, Y. Fang, R. Vreeker, I. Appelqvist and E. Mendes, Biomacromolecules, 2007, 8, 464–468 CrossRef CAS PubMed.
- P. Sikorski, F. Mo, G. Skjåk-Braek and B. T. Stokke, Biomacromolecules, 2007, 8, 2098–2103 CrossRef CAS PubMed.
- W. Plazinski and M. Drach, New J. Chem., 2015, 39, 3987–3994 RSC.
- F. Mo, T. J. Brobak and I. R. Siddiqui, Carbohydr. Res., 1985, 145, 13–24 CrossRef CAS.
- R. Kohn, I. Furda, A. Haug and O. Smidsrød, Acta Chem. Scand., 1968, 22, 3098–3102 CrossRef CAS.
- J. T. Triffitt, Nature, 1968, 217, 457–458 CrossRef CAS PubMed.
- T. Anthonsen, B. Larsen, O. Smidsrød, Å. Pilotti, S. Svensson and C.-G. Swahn, Acta Chem. Scand., 1973, 27, 2671–2673 CrossRef CAS PubMed.
- S. J. Angyal, D. Greeves and L. Littlemore, Carbohydr. Res., 1988, 174, 121–131 CrossRef CAS.
- J. W. Haas, Mar. Chem., 1986, 19, 299–304 CrossRef CAS.
- J. S. Rowbotham, J. A. Aguilar, A. M. Kenwright, H. C. Greenwell and P. W. Dyer, Carbohydr. Res., 2020, 495, 108087 CrossRef CAS PubMed.
- S. Thanomkul, J. A. Hjortås and H. Sørum, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 920–922 CrossRef.
- S. E. B. Gould, R. O. Gould, D. A. Rees and W. E. Scott, J. Chem. Soc., Perkin Trans. 2, 1975, 237 RSC.
- H. S. Isbell and H. L. Frush, J. Res. Natl. Inst. Stand. Technol., 1944, 32, 77–94 CAS.
- K. Izumi, Agric. Biol. Chem., 1980, 44, 1623–1631 CAS.
- B. J. Kvam, H. Grasdalen, O. Smidsrød, T. Anthonsen and R. Kivekäs, Acta Chem. Scand., 1986, 40b, 735–739 CrossRef.
- H. Grasdalen, T. Anthonsen, B. Larsen, O. Smidsrød, O. Dahl, O. Buchardt and G. Schroll, Acta Chem. Scand., 1975, 29b, 99–108 CrossRef PubMed.
- L. Fuks, D. Filipiuk and W. Lewandowski, J. Mol. Struct., 2001, 563–564, 587–593 CrossRef CAS.
- H. Grasdalen, T. Anthonsen, O. Harbitz, B. Larsen, O. Smidsrød, C.-O. Pontchour, P. Phavanantha, S. Pramatus, B. N. Cyvin and S. J. Cyvin, Acta Chem. Scand., 1978, 32a, 31–39 CrossRef.
- T. Anthonsen, B. Larsen, O. Smidsrød, M. J. Tricker and S. Svensson, Acta Chem. Scand., 1972, 26, 2988–2989 CrossRef CAS.
- B. Kutus, X. Gaona, A. Pallagi, I. Pálinkó, M. Altmaier and P. Sipos, Coord. Chem. Rev., 2020, 417, 213337 CrossRef CAS.
- A. Pallagi, C. Dudás, Z. Csendes, P. Forgó, I. Pálinkó and P. Sipos, J. Mol. Struct., 2011, 993, 336–340 CrossRef CAS.
- L. W. Jaques, J. B. Macaskill and W. Weltner, J. Phys. Chem., 1979, 83, 1412–1421 CrossRef CAS.
- R. O. Gould and A. F. Rankin, J. Chem. Soc. D, 1970, 489–490 RSC.
- D. M. Whitfield, S. Stojkovski and B. Sarkar, Coord. Chem. Rev., 1993, 122, 171–225 CrossRef CAS.
- J. A. Rendleman, Food Chem., 1978, 3, 47–79 CrossRef CAS.
- L. Fuks and J.-C. G. Bünzli, Helv. Chim. Acta, 1993, 76, 2992–3000 CrossRef CAS.
- L. DeLucas, C. E. Bugg, A. Terzis and R. Rivest, Carbohydr. Res., 1975, 41, 19–29 CrossRef CAS.
- J. Hjortås, B. Larsen, S. Thanomkul, I. Szabo-Lin, C. Guthenberg and B. Mannervik, Acta Chem. Scand., 1974, 28b, 689–689 CrossRef.
- D. C. Craig, N. C. Stephenson and J. D. Stevens, Carbohydr. Res., 1972, 22, 494–495 CrossRef CAS.
- http://supramolecular.org .
- D. B. Hibbert and P. Thordarson, Chem. Commun., 2016, 52, 12792–12805 RSC.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- R. D. Shannon, Acta Crystallogr. Sect. A, 1976, 32, 751–767 CrossRef.
- A. E. Vickman, D. C. Ashley, M.-H. Baik and N. L. B. Pohl, J. Mol. Model., 2017, 23, 214 CrossRef PubMed.
- S. J. Angyal, in Advances in Carbohydrate Chemistry and Biochemistry, 1984, pp. 15–68 Search PubMed.
- S. J. Angyal, Chem. Soc. Rev., 1980, 9, 415–428 RSC.
- S. J. Angyal and K. P. Davies, J. Chem. Soc. D, 1971, 500–501 RSC.
- S. J. Angyal, Aust. J. Chem., 1972, 25, 1957 CrossRef CAS.
- M. E. Evans and S. J. Angyal, Carbohydr. Res., 1972, 25, 43–48 CrossRef CAS.
- S. J. Angyal, Tetrahedron, 1974, 30, 1695–1702 CrossRef CAS.
- H. S. Isbell, Bur. Stand. J. Res., 1930, 5, 741–755 CrossRef CAS.
- F. Xu, F. Dong, P. Wang, H.-Y. Cao, C.-Y. Li, P.-Y. Li, X.-H. Pang, Y.-Z. Zhang and X.-L. Chen, J. Biol. Chem., 2017, 292, 4457–4468 CrossRef CAS PubMed.
- B. Kutus, D. Ozsvár, N. Varga, I. Pálinkó and P. Sipos, Dalton Trans., 2017, 46, 1065–1074 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details and NMR parameters, full datasets for chemical shift changes, observed equilibrium populations, and titration measurements. See DOI: 10.1039/d0dt04375c |
| This journal is © The Royal Society of Chemistry 2021 |