Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Outside the box: quantifying interactions of anions with the exterior surface of a cationic coordination cage
Michael D.
Ludden
and
Michael D.
Ward
 *
*
Department of Chemistry, University of Warwick, Coventry CV4 7AL, UK. E-mail: m.d.ward@warwick.ac.uk
First published on 3rd February 2021
Abstract
We describe a study of the binding of anions to the surface of an octanuclear coordination cage HW, which carries a 16+ charge, in aqueous solution. Anionic aromatic fluorophores such as fluorescein (and derivatives) and hydroxypyrene tris-sulfonate (HPTS) bind strongly to an extent depending on their charge and hydrophobicity. Job plots indicated binding of up to six such fluorescent anions to HW, implying that one anion can bind to each face of the cubic cage, as previously demonstrated crystallographically with small anions such as halides. The quenching of these fluorophores on association with the cage provides the basis of a fluorescence displacement assay to investigate binding of other anions: addition of analyte (organic or inorganic) anions in titration experiments to an HW/fluorescein combination results in displacement and restoration of the fluorescence from the bound fluorescein, allowing calculation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding constants for the HW/anion combinations. Relative binding affinities of simple anions for the cage surface can be approximately rationalised on the basis of ease of desolvation (e.g. F− < Cl− < Br−), electrostatic factors given the 16+ charge on the cage (monoanions < dianions), and extent of hydrophobic surface. The interaction of a di-anionic pH indicator (bromocresol purple) with HW results in a pKa shift, with the surface-bound di-anionic form stabilised by approximately 1 pKa unit compared to the non-bound neutral form due to the charge on the cage.
1 binding constants for the HW/anion combinations. Relative binding affinities of simple anions for the cage surface can be approximately rationalised on the basis of ease of desolvation (e.g. F− < Cl− < Br−), electrostatic factors given the 16+ charge on the cage (monoanions < dianions), and extent of hydrophobic surface. The interaction of a di-anionic pH indicator (bromocresol purple) with HW results in a pKa shift, with the surface-bound di-anionic form stabilised by approximately 1 pKa unit compared to the non-bound neutral form due to the charge on the cage.
1. Introduction
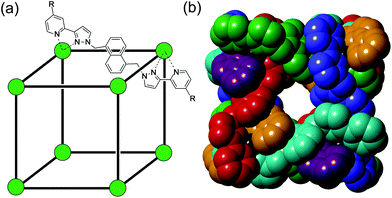
Much of the interest in the chemistry of coordination cages arises from their host guest chemistry, i.e. the ability of hollow cages to act as hosts which can bind guest molecules which occupy the central cavity.1–4 Such binding of guests inside cage cavities is responsible for multiple applications in supramolecular chemistry including catalysis,2 sensing,3 and externally-triggered uptake/release for transport purposes.4 As a result, the metaphorical spotlight has been largely focussed on guest binding inside the central cavities of the host cages, with all that this implies for design of host cages with suitable cavity properties for specific guests, measurement of and understanding of the various interactions responsible for guest binding, and structural characterisation of cage/guest complexes.More recently, attention has turned to the interactions between guests and the exterior surfaces of coordination cages as not all interactions of host cages with small molecules need to occur inside the cavity. In our cage family,5 in particular the M8L12 octanuclear cages which are the basis for this work (Fig. 1),6 we have found that the windows in the face centres provide sites where counter-ions X− can bind via an array of multiple C–H⋯X− hydrogen bonds, aided by the high positive (16+) charge of the cage:7 this calls to mind the seminal example from Lehn and co-workers in 1996 of a chloride ion binding tightly in the central cavity of a cyclic pentanuclear double helicate,8 and other related examples of anion binding in cyclic cavities defined by predominantly hydrocarbon-based ligand fragments.9
In our M8L12 cages, binding of anions in surface portals in this way means that a cavity-bound guest may be surrounded by an octahedral array of six anions around the cage surface (Fig. 2).7a This provides the basis for very effective catalysis of some reactions of cavity-bound guests with surface-bound anions as the two reaction partners are co-located via orthogonal interactions: a neutral guest binds inside the cage cavity in water using the hydrophobic effect, but desolvation of anions and binding to the cage surface is driven by electrostatic factors, with the cavity-bound guest and surface-bound anions being independently changeable.7a,10
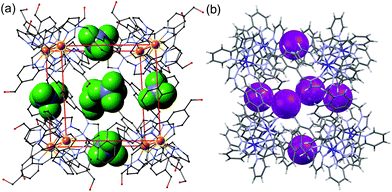 | ||
| Fig. 2 Crystal structures of different salts of the host system showing the location of anions in the windows in the centre of each face, giving an octahedral array of surface-bound anions surrounding the central cavity: (a) the tetrafluoroborate salt (from ref. 6b); (b) the iodide salt (from ref. 7a). | ||
Several other groups have noted the importance of interactions between small molecule guests (particularly counter-ions) and the cage surface. Nitschke and co-workers have shown how tetraphenylborate anions on the exterior of a cage surface – with one phenyl ring pointing into the central cavity – templated formation of an M6L4 capsule that more usually required a cavity-based templating agent.11 In a similar vein the same group reported how surface-binding perchlorate anions template formation of an unusual pentagonal bipyramidal cage that also tightly binds chloride.12 Nitschke and co-workers have also incorporated specific fluoride-binding sites (Lewis-acidic boron centres) into the exterior surface of an M4L4 tetrahedral cage to allow exterior binding of fluoride, which modulates the cage charge and hence its affinity for different solvent phases.13 Raymond and co-workers have shown how the interaction of tetraphenyborate with a cage exterior surface was driven by quite different thermodynamic effects than binding in the central cavity;14 and Wu's group have shown how hydrogen-bonded cages, formed using urea/phosphate interactions instead of metal/ligand dative bonds, can be switched between different structural types based on interaction of the cage surfaces with counter-ions of different size and shape.15 Interaction of solvent molecules and counter-ions with the exterior surfaces of a pair of isostructural tetrahehedral cages bearing different charges has recently been studied in detail by Stelson and co-workers.16 Overall, the importance of interactions of the exterior surface of cages with species in the surrounding medium is becoming more appreciated as being as important as the more obvious interactions associated with cavity-bound guests – a particular focus of host–guest chemistry that has been with us since the first complexes of crown ethers with alkali metal ions.
In our recent work on cage-based catalysis of the Kemp elimination (reaction of cavity-bound benzisoxazole with the shell of ions surrounding it, either hydroxide or phenolates, due to interactions with the cage surface),7a,10 it became apparent that the tendency of an anion to bind to the highly cationic M8L12 cage surface in aqueous solution is related to the ease with which it can be desolvated (thus, the binding affinity order with the cage was phenolate > chloride > hydroxide):7a in retrospect a fairly unsurprising conclusion, but one which implies that we should be able to control which type of anionic reaction partner binds to the cage surface and surrounds a cavity-bound guest for catalysed reactions. Accordingly, we felt that it would be of interest to undertake a systematic, quantitative study of the affinity of different anions for the M8L12 cage. To do this we have developed a fluorescence displacement assay,17 utilising our M8L12 cage in combination with an anionic surface-bound fluorophore (fluorescein), which is capable of allowing determination of the association strengths of both organic and inorganic anionic species through a displacement process that leads to an easily-observable change in fluorescence of the fluorophore. In this way we have built up a very clear picture of the interactions of different anions with the surface binding sites of the M8L12 cubic cage.
2. Materials and methods
The studies conducted within this paper use the water-soluble cubic Co8 cage HW which was prepared as previously described.6b The fluorescent species fluorescein, hydroxypyrene tris-sulfonate (trisodium salt), 6-carboxyfluorescein and Eosin Y were purchased from Acros Organics or Merck Life Sciences and used as received. Inorganic salts used to evaluate anion binding affinities were purchased from Sigma-Aldrich and used as delivered. Fluorescence measurements were carried out using either a BMG ClarioStar plate reader with 96-well plates, or an Agilent Cary Eclipse fluorimeter. UV/Vis spectra were obtained using an Implen C40 Nanophotometer.Fluorescence titrations were performed by preparing a solution of fluorescein (FLU; 10 μM) and cage (HW; 100 μM) in deionised water, which was then used to prepare two solutions at 5/50 μM FLU/HW through addition of either deionised water or a premade sodium salt solution of the anion under investigation. Samples for titrations were dissolved in 50 mM borate buffer at pH 8.5 to ensure a constant pH. (It follows that there is a high concentration of borate anions always present which may affect binding of other anions under investigation. However, this is fixed for all titration experiments in sections 3.2 and 3.4 and represents part of the standard baseline set of conditions (like the nature of the solvent) common to all experiments. Although absolute values of binding constants would probably be different with different buffers because different competing anions are present, comparisons within a guest series and – in particular – relative orderings of anion affinities measured under a fixed set of conditions, are legitimate).
Titrations were run using between 10 and 14 wells of a 96-well plate filled to 200 μL each with varying ratios of HW·FLU solution and the analyte under investigation. The instrument was equilibrated to 298 K for all measurements. Fluorescence spectra between 500 and 600 nm were recorded for each well using an excitation wavelength of 472 nm, and the intensity of emission peak of FLU at 515 nm was measured to determine binding constants for all analytes studied. Calculation of the binding constants for anions in the displacement assay used software written by Prof. Chris Hunter as described previously.18a
3. Results and discussion
3.1. General principles and background
The octanuclear, approximately cubic, coordination cage HW (formula [Co8L12][BF4]16, Fig. 1) possesses a cavity of volume of 409 Å3 which is slightly elongated with the approximate shape of a rugby ball. The cavity-based host–guest chemistry of this cage has been studied extensively, with small organic guests able to bind within the cavity, entering through small windows on each face of the cube which allow guest ingress/egress.4f,5,6b,18,19 Binding constants for organic guests within the cavity in aqueous solution have been reported up to 106 M−1 and correlate closely with hydrophobic surface area.6b,18aThe presence of Co(II) ions in the cage result in quenching of fluorescent organic guests when they bind, likely through energy transfer from the fluorophore's excited state to the low energy Co(II) d–d transitions. This quenching of fluorescent guests provided, in previous work, the basis for a fluorescence displacement assay using the organic fluorophore MAC (4-methyl-7-amino coumarin) which is quenched when bound: addition of a guest that could compete for binding within the cavity resulted in partial displacement of MAC and restoration of its fluorescence, to an extent depending on the binding strength of the new guest.18a This allowed binding constants for the added guests to be calculated. Based on this, we sought to develop a similar fluorescence displacement assay which would allow us to probe the strength of binding of different anions to the cage exterior surface, which requires a surface-binding, anionic fluorophore that could be displaced by other anions from the binding sites on the cage surfaces.
3.2. Binding of fluorescein and derivatives to Hw
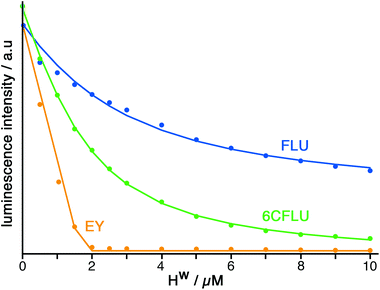
The well-known fluorophore fluorescein (denoted FLU, see Chart 1) is a green-emitting xanthene-type dye molecule containing both phenol and carboxyl moieties. When deprotonated, the emission intensity of the molecule increases dramatically. The pKa of these two groups is 6.3 and 3.4 respectively, meaning that at pH 8 the molecule will be dianionic and should associate with the exterior of HW (FLU being too large for cavity-binding). Sequential additions of a solution of HW to a solution of FLU (10 μM) resulted in a rapid decrease in the FLU luminescence intensity (Fig. 3) with quenching essentially complete after addition of only two equivalents of HW.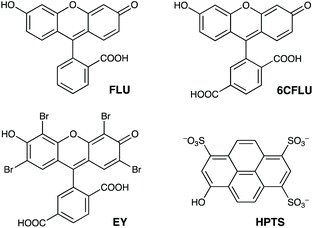 | ||
| Chart 1 The aromatic, anionic fluorophores used in this work (shown in the forms existing in weakly acidic solution). | ||
The fluorescence data could be fitted to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model, which afforded a binding constant of 1.0 × 105 M−1 for interaction of FLU with an individual cage face. Although each cage molecule has six equivalent potential anion binding sites, this titration is done under conditions where HW is in excess as the titration proceeds which means that a 1
1 binding model, which afforded a binding constant of 1.0 × 105 M−1 for interaction of FLU with an individual cage face. Although each cage molecule has six equivalent potential anion binding sites, this titration is done under conditions where HW is in excess as the titration proceeds which means that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 HW
1 HW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FLU complex will dominate: species in which multiple FLU units bind to one cage would require excess FLU (see later).
FLU complex will dominate: species in which multiple FLU units bind to one cage would require excess FLU (see later).
This means that these fluorescence data fit a simple 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding isotherm which corresponds to formation of the 1
1 binding isotherm which corresponds to formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 HW
1 HW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FLU complex with one FLU on one face of the cubic cage. The value of K so obtained was calculated using the concentration of potential binding sites available to account for the statistical effect of each host having six equivalent anion binding sites, and give a K value corresponding to the intrinsic binding constant of FLU with one face of HW.
FLU complex with one FLU on one face of the cubic cage. The value of K so obtained was calculated using the concentration of potential binding sites available to account for the statistical effect of each host having six equivalent anion binding sites, and give a K value corresponding to the intrinsic binding constant of FLU with one face of HW.
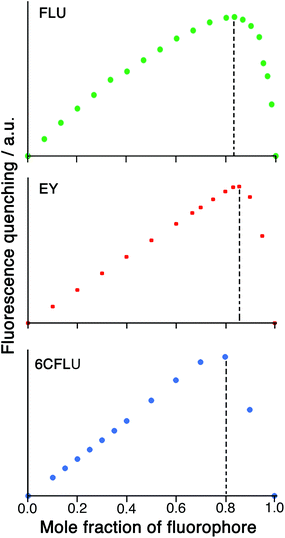
Given the possibility of each cage being able to quench multiple FLU units (potentially, up to six) by surface binding if excess FLU is present, and the likelihood that the second and subsequent binding events are still strong, we looked further into the HW/FLU stoichiometry using a Job plot to observe how many faces of the cube could be occupied by guest molecules under what amount to forcing conditions (large excess of FLU compared to HW at the appropriate point in the Job plot). When HW and FLU were combined in different mole fractions, the maximum decrease in FLU-based fluorescence intensity (compared to unquenched FLU at the same concentration) was found at a mole fraction of 0.83 (Fig. 4a), equating to a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry of FLU
1 stoichiometry of FLU![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HW, strongly suggesting that the highly cationic cage HW can bind (and quench) several FLU units simultaneously, each at a different face. The dominance of five FLU units in the speciation rather than six is possibly ascribable to electrostatic factors: each FLU has a charge of 2−, so there comes a point where accumulation of several of these will hinder binding of subsequent guests, such that the sixth binding event may not be observed under the dilute conditions used, such that the 1
HW, strongly suggesting that the highly cationic cage HW can bind (and quench) several FLU units simultaneously, each at a different face. The dominance of five FLU units in the speciation rather than six is possibly ascribable to electrostatic factors: each FLU has a charge of 2−, so there comes a point where accumulation of several of these will hinder binding of subsequent guests, such that the sixth binding event may not be observed under the dilute conditions used, such that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 species HW·(FLU)5 dominates the speciation at this concentration.
5 species HW·(FLU)5 dominates the speciation at this concentration.
We emphasise that there is no contradiction in the observation of a HW·(FLU)5 complex in the Job plot under conditions when FLU is in excess, and the fitting of fluorescence titration data to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 model under conditions when HW is excess (resulting in measurement of a value for K1 only, with second and subsequent binding constants K2 up to K5 not being measurable). We note also that use of Job plots to delineate limiting stoichiometries of supramolecular complexes has serious limitations, as several authors have pointed out recently.19c,20 However, if we are using conditions under which the quantity being measured is additive (i.e. binding of two FLU units to a cage causes twice as much loss of luminescence as does binding of one FLU unit) then the main pitfall is avoided.
1 model under conditions when HW is excess (resulting in measurement of a value for K1 only, with second and subsequent binding constants K2 up to K5 not being measurable). We note also that use of Job plots to delineate limiting stoichiometries of supramolecular complexes has serious limitations, as several authors have pointed out recently.19c,20 However, if we are using conditions under which the quantity being measured is additive (i.e. binding of two FLU units to a cage causes twice as much loss of luminescence as does binding of one FLU unit) then the main pitfall is avoided.
Whilst we do not know the geometry of the HW/FLU interaction – there are two anionic sites on FLU under these conditions which could interact with the portals around the cage surface – the carboxylate site will be more hydrophilic than the phenolate site and so more likely to project into the aqueous solvent. We have been unable to obtain X-ray quality single crystals of this HW/FLU ensemble. Our previous work has clearly shown, however, that phenolate anions associate with the cage surface sufficiently strongly to displace chloride and hydroxide,7a and we suggest therefore that the HW/FLU interaction primarily involves the phenolate moiety of the FLU dianion. We tried to probe this by 1H NMR spectroscopy, looking to see if the protons close to the phenolate unit of FLU (and therefore closest to the cage surface) were paramagnetically shifted/broadened to a greater extent than the protons close to the carboxylate site, for example, which might be more remote from the paramagnetic cage surface. Effectively this would use the cage as a paramagnetic shift reagent to probe the geometry of the cage/FLU interaction. However the substantial broadening/overlap of FLU signals in the presence of cage, and their overlap with cage signals in the same spectra region, meant that this experiment did not yield clear-cut results.
Similar experiments on binding to HW were conducted using the related anionic fluorophores 6-carboxyfluorescein and Eosin-Y (abbreviated as 6CFLU and EY, respectively; see Chart 1). These have significant differences from FLU, as follows: (i) the additional carboxylate group of 6CFLU means that it has a charge of 3− compared to 2− for FLU under weakly basic conditions (pKa 3.4 for the carboxylates); (ii) eosin-Y is tetrabromofluorescein, with the same 2− charge as FLU but with higher hydrophobicity due to the additional Br substituents.21 Thus we can independently change the charge, or the hydrophobicity, of the fluorescein derivative to see how these two parameters affect binding of the fluorophores to the cationic but hydrophobic surface of HW.
Titration of HW into samples of EY and 6CFLU (at 10 μM of fluorophore) in water at pH 8, in the same way as with FLU, immediately reveals more rapid quenching of the fluorescence than was obtained with FLU (Fig. 3). From the rate at which fluorescence quenching occurs on addition of HW the affinity order of these fluorescein derivatives for HW is clearly FLU < 6CFLU < EY, implying that the additional hydrophobicity of EY compared to FLU is more significant than the additional negative charge of 6CFLU. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding constant for 6CFLU can be determined from this data with K = 3.8 × 105 M−1, however given the near-linearity of the fluorescence decrease of EY as HW is added we cannot get reliable binding constants with this fluorophore under these conditions: but the binding affinity order (FLU < 6CFLU < EY) is clear.
1 binding constant for 6CFLU can be determined from this data with K = 3.8 × 105 M−1, however given the near-linearity of the fluorescence decrease of EY as HW is added we cannot get reliable binding constants with this fluorophore under these conditions: but the binding affinity order (FLU < 6CFLU < EY) is clear.
A Job plot for the EY/HW system using a 50 μM total concentration clearly shows a sharp maximum corresponding to a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of fluorophore to cage for EY (Fig. 4b). In contrast, with the 6CFLU/HW system at 100 μM total concentration the maximum in the Job plot at a mole fraction of 0.8/0.2 implies a 4
1 ratio of fluorophore to cage for EY (Fig. 4b). In contrast, with the 6CFLU/HW system at 100 μM total concentration the maximum in the Job plot at a mole fraction of 0.8/0.2 implies a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry under these conditions (Fig. 4c) – fewer equivalents of the anionic fluorophore 6CFLU are bound to HW than was observed with FLU, likely due to the higher negative charge.
1 stoichiometry under these conditions (Fig. 4c) – fewer equivalents of the anionic fluorophore 6CFLU are bound to HW than was observed with FLU, likely due to the higher negative charge.
3.3. Binding of a different anionic fluorophore to HW: hydroxypyrene tris-sulfonate
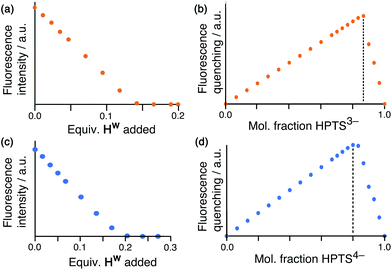
Having demonstrated the ability of FLU to bind to HW, we sought to extend this behaviour using other anionic fluorophores. The next choice was hydroxypyrene tris-sulfonate (HPTS), also known as pyranine – another well-known fluorophore with a charge of 3− or 4− depending on the pH and whether or not the hydroxy group is deprotonated (pKa 7.3) in addition to the three sulfonates.Titration of portions of cage HW into a solution of HPTS at pH 4, where the anion has a 3− charge, resulted in progressive quenching of the HPTS fluorescence, with complete quenching of the fluorophore occurring after addition of only 0.16 equivalents of cage (Fig. 5a). The linearity of the luminescence decrease as HW is added indicates that association is at the strong binding limit even under the dilute conditions used (20 μM HPTS). The number of equivalents of cage needed for total quenching of HPTS (0.16) is also significant and suggests that each cage HW is fully quenching six molecules of HPTS, with one HPTS binding to each face of the cubic host. To confirm this, a Job plot experiment was performed between HW and HPTS at pH 4 (total concentration of species 50 μM). The maximum for this plot was seen at a mole fraction of HPTS of 0.86, confirming the stoichiometry as being 6 fluorophores per cage (Fig. 5b), as also observed with EY. It is clear that HPTS binds more strongly to the surface of HW than does FLU, which may partly be ascribed to its greater charge (3− vs. 2−).
As HPTS is pH sensitive and can be deprotonated through its phenol group, we conducted the same experiments at pH 8 to observe any differences in binding associated with an even greater negative charge (−4 instead of −3). Again, addition of small portions of HW to a solution of HPTS at 20 μM under these basic conditions occurs with the same linear decrease in fluorescence intensity with added HW, indicative of binding at the strong limit at this concentration. However, the stoichiometry has changed with maximum quenching/minimum emission achieved after addition of 0.25 equivalents of cage as opposed to 0.16, implying that each cage HW can strongly bind only four HPTS units when they are in the 4− state (Fig. 5c). To confirm that this number correlates to the stoichiometry of binding, a Job plot was performed and shows maximum quenching at a mole fraction of HPTS of 0.80, indicative of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 cage
4 cage![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (HPTS)4− stoichiometry (Fig. 5d). We ascribe this difference in the binding of (HPTS)3− (six equivalents strongly bound) and (HPTS)4− (four equivalents strongly bound) to electrostatic factors: the cage cation carries a charge of 16+, hence it only needs four (HPTS)4− units to neutralise it. Addition of fifth and then a sixth fluorophore is presumably still possible for steric reasons [cf. binding of six (HPTS)3− units] but if these interactions are weaker for electrostatic reasons they will not contribute significantly to the speciation behaviour at the concentration used for these measurements.
(HPTS)4− stoichiometry (Fig. 5d). We ascribe this difference in the binding of (HPTS)3− (six equivalents strongly bound) and (HPTS)4− (four equivalents strongly bound) to electrostatic factors: the cage cation carries a charge of 16+, hence it only needs four (HPTS)4− units to neutralise it. Addition of fifth and then a sixth fluorophore is presumably still possible for steric reasons [cf. binding of six (HPTS)3− units] but if these interactions are weaker for electrostatic reasons they will not contribute significantly to the speciation behaviour at the concentration used for these measurements.
3.4. Displacement of fluorescein as the basis of an anion-binding assay
To be able to perform a displacement assay to allow us to quantify binding of anions to the surface of HW, we chose FLU as our indicator, as its binding constant to HW is known, which means that the extent of displacement of FLU by different anions can be used to evaluate their binding constants (as we have done for our previous displacement assay for cavity-binding guests).18a In contrast the stronger binding of the other fluorophores such as EY and HPTS, and in particular the absence of specific K values for binding to HW, is less desirable for this purpose as the bound fluorophore would be less susceptible to displacement by competing anions. Titration experiments with different anions were performed on a 96 well plate using a plate reader, by monitoring the restoration of FLU fluorescence as different anions were added during the titration (see Experimental section). Each titration experiment was repeated at least twice and with a minimum of 10 data points in each repeat experiment; the resulting 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding constants for a range of simple anions are given in Table 1, with representative titration results in Fig. 6.
1 binding constants for a range of simple anions are given in Table 1, with representative titration results in Fig. 6.
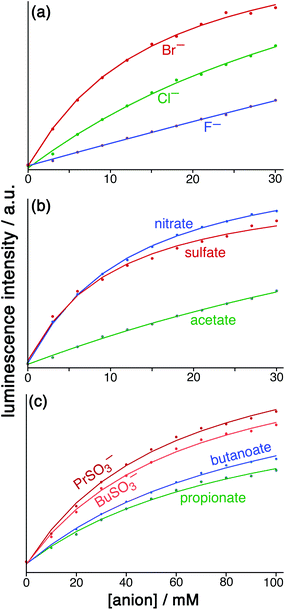 | ||
Fig. 6 Results from the displacement assay showing how addition of portions of sodium salts with various anions [(a) halides; (b) nitrate, sulfate and acetate; (c) other organic anions] to a solution containing HW (50 μM) and FLU (5 μM) in water (pH 8.5) results in a steady increase in the fluorescence from FLU as it is displaced from the cage surface by the added anions which compete for the same sites, restoring the FLU emission. The measured data (small circles) could in all cases be fit to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding isotherm (solid lines) which takes account of the known binding constant of FLU, affording the anion binding constants in Table 1. 1 binding isotherm (solid lines) which takes account of the known binding constant of FLU, affording the anion binding constants in Table 1. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding isotherms, repeated two or three times and averaged. Estimated uncertainty 20%
1 binding isotherms, repeated two or three times and averaged. Estimated uncertainty 20%
| Anion | K/M−1 | Anion | K/M−1 |
|---|---|---|---|
| F− | 350 | HCO2− | 840 |
| Cl− | 750 | CH3CO2− | 470 |
| Br− | 2900 | CH3CH2CO2− | 440 |
| IO3− | 470 | CH3CH2CH2CO2− | 390 |
| NO3− | 3100 | CH3CH2CH2SO3− | 530 |
| HPO42− | 2100 | CH3CH2CH2CH2SO3− | 500 |
| SO42− | 3600 | Gluconate (1−) | 2900 |
| S2O32− | 4000 | Succinate (2−) | 6500 |
| Malate (2−) | 7600 | ||
| Tartrate (2−) | 7200 |
For initial tests to quantify binding of other anions to HW, three anions were used: chloride, sulfate and nitrate (as their sodium salts). These were selected as they differ significantly in their position in the Hofmeister series – a ranking of anions based originally on the ability of anions to aggregate proteins in solution, but which is broadly a measure of hydration and hydrophilicity.22 Addition of salts of these anions to a solution of HW/FLU (typically a combination of 5 μM FLU and an excess – 50 μM – of HW to ensure essentially complete binding/quenching of FLU by the cage) resulted in an increase in the FLU-based emission in all three cases as the added anions occupied cage binding sites on the HW surface, resulting in displacement of FLU from the cage surface. This happened to different extents for a given concentration of different anion types.
The observed increase in fluorescence occurs because as the sites of HW are progressively saturated by the added anion, which is in a large excess as small anions are more hydrophilic than FLU and bind to the cage more weakly, the number of free cage surface sites available for FLU to bind steadily decreases and a higher proportion of FLU remains free in solution. Given the likely complexity of the speciation behaviour, with (i) potentially six different stepwise binding constants for analyte anions progressively occupying cage surface sites, and (ii) the effect of different numbers of bound anions on electrostatic repulsion of a FLU unit in the same cage which would modulate its K value during a titration, there is no reason to expect that the increase in FLU emission intensity with amount of added analyte anion would show simple behaviour.
However we observed, fortunately, that the steady increase of FLU emission intensity as analyte anions were added could be fit to a simple 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model and we have analysed the data accordingly, and the resulting K values for binding of the simple anions can be compared with each other. This afforded binding constants of 750 M−1 for chloride, 3100 M−1 for nitrate and 3600 M−1 for sulfate (Table 1). Stronger binding of nitrate than chloride is expected based on the basis of its weaker solvation enthalpy, however the even stronger binding of sulfate to the cage goes against this trend. It seems that the high cost of desolvating the very kosmotropic sulfate ion is more than compensated for by the 2− charge which will result in stronger electrostatic interaction with the 16+ cage than occurs with nitrate and chloride, and indeed we saw the effects of increasing anion charge in the comparison of FLU with 6CFLU.
1 binding model and we have analysed the data accordingly, and the resulting K values for binding of the simple anions can be compared with each other. This afforded binding constants of 750 M−1 for chloride, 3100 M−1 for nitrate and 3600 M−1 for sulfate (Table 1). Stronger binding of nitrate than chloride is expected based on the basis of its weaker solvation enthalpy, however the even stronger binding of sulfate to the cage goes against this trend. It seems that the high cost of desolvating the very kosmotropic sulfate ion is more than compensated for by the 2− charge which will result in stronger electrostatic interaction with the 16+ cage than occurs with nitrate and chloride, and indeed we saw the effects of increasing anion charge in the comparison of FLU with 6CFLU.
Following the success of these initial experiments, a wider range of additional anions was then tested in a similar manner, again using FLU as the indicator species being displaced. The anions studied include (i) common inorganic anions including halides, sulfate, thiosulfate and hydrogen phosphate; (ii) organic alkyl carboxylates and alkyl sulfonates of varying carbon chain length; and (iii) a broader range of organic anions such as tartrate, gluconate, and others. Results are in Table 1.
Amongst the inorganic anions, the singly-charged species largely follow the order of the Hofmeister series: for example fluoride, chloride and bromide show 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding constants of 350, 750 and 2900 M−1 respectively, in line with their respective ease of desolvation. In contrast the dianions sulfate, thiosulfate and hydrogen phosphate have significantly higher binding constants (2000–4000 M−1) for the electrostatic reasons described earlier which appear to outweigh the higher cost of desolvation for these anions.
1 binding constants of 350, 750 and 2900 M−1 respectively, in line with their respective ease of desolvation. In contrast the dianions sulfate, thiosulfate and hydrogen phosphate have significantly higher binding constants (2000–4000 M−1) for the electrostatic reasons described earlier which appear to outweigh the higher cost of desolvation for these anions.
The singly charged alkyl carboxylate and alkyl sulfonate anions all exhibit similar binding constants in the range 390–530 M−1, comparable to the inorganic mono-anions. Comparison between different alkyl carboxylate anions is interesting as there is essentially no difference between the binding constants with alkyl chain length: the hydrophobicity of the anion as a whole does not make a significant difference. The implication is that the desolvation of the carboxylate unit and its interaction with the cage surface is the same in each case, with the alkyl chain projecting outwards into the solvent and therefore not undergoing a change in environment when the polar carboxylate terminus binds to the cage surface. This contrasts markedly with what happens on binding of guests inside the cage cavity, when increasing the hydrophobic content of the guest increases its binding strength in the cavity as the whole guest is removed from the aqueous phase when it binds.6b,18a,19d Formate is an exception here (840 M−1) with a significantly higher binding constant than the alkyl carboxylates, which is consistent with a previous report that the formate ion is less well hydrated than alkyl carboxylates.23
We note a similar lack of sensitivity to the nature of the alkyl chain with propyl and butyl sulfonate anions whose binding constants to the cage are the same within experimental error despite the different hydrophobicities of the alkyl chains. The carboxylates however bind to HW slightly less well than the sulfonates, cf the pair C3H7SO3− and C3H7CO2− which have 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding constants of 530 and 440 M−1 respectively. This implies stronger hydration of the carboxylates that the sulfonates and is also consistent with the known relative behaviour of carboxylates and alkyl sulfates.24
1 binding constants of 530 and 440 M−1 respectively. This implies stronger hydration of the carboxylates that the sulfonates and is also consistent with the known relative behaviour of carboxylates and alkyl sulfates.24
More hydrophilic organic anions such as gluconate, malate, succinate, and tartrate were also tested (as their sodium salts) with the results in Table 1. The concentrations used for these needed to be typically an order of magnitude lower than in the previous experiments as higher concentrations showed a tendency to precipitate the cage out of solution. The sequence succinate, malate and tartrate are all linear C4 dicarboxylates but with 0, 1 and 2 additional OH groups on the carbon skeleton. All have higher binding constants (ca. 6500–7500 M−1) than we saw for any of the mono- or di-anions discussed above which suggests that, in addition to high electrostatic interaction between the 2− anion and the 16+ cage surface, the hydrophobicity associated with the central alkyl unit facilitates binding (cf. the stronger binding of EY compared to FLU based on its extra hydrophobicity). The presence or absence of the OH groups appears to make little difference, however. Compared to these the mono-anion gluconate has a slightly smaller binding constant of 2900 M−1, as expected, though it is substantially larger than for the simpler inorganic anions and alkyl mono-carboxylates reported in Table 1.
Given the complexity of the combination of factors underpinning the anion/cage interaction (not just electrostatics and hydrophobicity but possibly also changes of conformation associated with rigidification of flexible species;19d direct hydrogen-bonding interactions involving CH donors around the cage portals and different electron-rich H-bond acceptor atoms on the anions; and changes in bulk solvation associated with complex formation) we prefer not to speculate or over-analyse further. The key points from this section are that (i) this displacement assay provides a convenient and effective way to evaluate cage/anion interactions, which are of direct relevance to potential use of the cage as a vehicle for catalysis;5,7a,10 and (ii) within the range of inorganic anions of the same charge (−1) there is a clear relation of binding constant of anion with its position in the Hofmeister series, such that less well solvated anions (such as bromide) bind more strongly to HW than more highly solvated anions (such as fluoride).
3.5. Stabilisation of anionic species through association with the cage HW
Having investigated the interaction between a range of anionic species and the exterior surface of HW, we turned our attention to investigating any possible stabilisation of these anions imparted through the association with the cationic cage surface. Raymond et al. reported a stabilisation of ammonium cations by ca. 4 pH units inside a highly anionic cage: this ability of the anionic cage to stabilise protonated species could be used to facilitate acid-based catalysis of bound guests even under basic conditions.25 To see whether a similar pKa shift was observable between the cage HW and anionic species, we monitored the behaviour of the pH indicators phenolphthalein (PP) and bromocresol purple (BCP) as surface-bound guests during a pH titration.In the first experiment (in contrast to others reported in this paper) the concentration of both the host cage (40 μM) and PP (80 μM) remain constant; the ratio of cage![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PP and the concentration are sufficient to ensure near-complete binding of PP to the surface sites of HW. Starting at a pH of 4.22 (unbuffered), the pH was increased by sequential additions of 0.1 M NaOH solution. A UV/Vis spectrum was recorded after each addition and the absorbance at 560 nm plotted against the pH. This was repeated without cage present and the two resulting curves compared. For free PP the onset of the characteristic pink colour occurred at pH 8.7; in the presence of HW the same optical density was achieved by pH 8.0 indicating that the dianionic form of PP (containing a carboxylate and a phenolate, resulting from opening of the lactone ring) is being stabilised by its interaction with HW. However we could not get a complete pH titration curve for this experiment because as the pH was raised further precipitation occurred, probably because of formation of an insoluble HW/(phenolphthalein anion) complex or decomposition of HW under more strongly basic conditions.
PP and the concentration are sufficient to ensure near-complete binding of PP to the surface sites of HW. Starting at a pH of 4.22 (unbuffered), the pH was increased by sequential additions of 0.1 M NaOH solution. A UV/Vis spectrum was recorded after each addition and the absorbance at 560 nm plotted against the pH. This was repeated without cage present and the two resulting curves compared. For free PP the onset of the characteristic pink colour occurred at pH 8.7; in the presence of HW the same optical density was achieved by pH 8.0 indicating that the dianionic form of PP (containing a carboxylate and a phenolate, resulting from opening of the lactone ring) is being stabilised by its interaction with HW. However we could not get a complete pH titration curve for this experiment because as the pH was raised further precipitation occurred, probably because of formation of an insoluble HW/(phenolphthalein anion) complex or decomposition of HW under more strongly basic conditions.
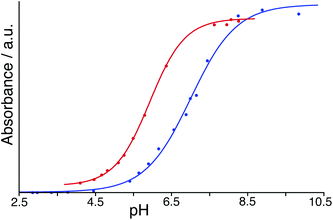
To avoid the problems associated with using high pH, a similar experiment was performed but using BCP which has a pKa of 6.3 compared to 9.4 for PP: in its dianionic form it contains both sulfonate and phenolate anionic centres. With both HW and BCP at a concentration of 50 μM, monitoring the absorbance during a steady increase in pH by addition of aqueous NaOH provided a full sigmoidal curve characteristic of an acid–base titration (Fig. 7) with the mid-points giving pKa values in our hands of 7.0 for BCP on its own but 5.9 in the presence of HW. Thus, the surface-bound dianion is stabilised by ≈1 pKa unit by its interaction with the 16+ exterior surface of HW. This is smaller than the effect than seen by Raymond and co-workers,25 but in their case the guest was fully encapsulated inside the cavity of a 12− cage and therefore was positioned much closer to a larger number of stabilising opposite charges. The effect of stabilisation of the surface-bound anion in this case however is clear.
4. Conclusions
In this work we have examined systematically the interaction of our cationic, cubic coordination cage HW with anions at the surface binding sites. This is a much less well trodden path (both for us with this particular cage host, and more broadly for the field of coordination cages in general) than the study of binding of small-molecule guests in the central cavity: although less obvious, it is however just as important for understanding the catalysed reactions of cavity-bound guests with surface-bound anions.7aAromatic organic fluorophores which are anionic (FLU and some derivatives; HPTS in its two different charge states) bind strongly to the surface of HW with quenching of fluorescence, with binding driven by a combination of electrostatic factors and hydrophobicity. These fluorophores are all too large to bind inside the cavity, but are proposed to interact with the cage exterior surface in the windows at the centre of each face where small inorganic anions have been shown to bind from X-ray crystallography experiments. Surface binding of these aromatic anions was further supported by Job plot experiments which showed fluorophore![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HW ratios of 4
HW ratios of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5
1, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 6
1 or 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (depending on charge and hydrophobicity of the fluorophore) with the maximum observed ratio of 6
1 (depending on charge and hydrophobicity of the fluorophore) with the maximum observed ratio of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, shown by both EY and (HPTS)3−, indicating that one anion interacts with every surface of the cubic cage HW. These interactions are strong with the weakest binder (FLU) having K ≈ 1 × 105 M−1, 6CFLU having K ≈ 4 × 105 M−1 (for binding of the fluorophore to one face of the cage), and EY being at the strong binding limit even at the dilute concentrations used.
1, shown by both EY and (HPTS)3−, indicating that one anion interacts with every surface of the cubic cage HW. These interactions are strong with the weakest binder (FLU) having K ≈ 1 × 105 M−1, 6CFLU having K ≈ 4 × 105 M−1 (for binding of the fluorophore to one face of the cage), and EY being at the strong binding limit even at the dilute concentrations used.
Using FLU as the indicator, a fluorescence displacement assay has been developed which allows us to determine the affinity of a range of other anions to the surface of HW according to how well increasing concentrations of the analyte anions displace FLU and restore its fluorescence. The affinity of a range of simple inorganic anions for HW broadly follows the Hofmeister series for 1− species with the most strongly solvated anions such as fluoride binding the most weakly. However the inorganic dianions SO42−, S2O32− and HPO42− do not follow the Hofmeister series, with the higher cost of desolvating them being more than compensated for by electrostatic factors given the 16+ charge on the cage, such that they bind more strongly to HW than do mono-anions such as halides. Organic dicarboxylates bind considerably more strongly, possibly due to the hydrophobicity of their alkyl skeleton, though these are still much weaker binders than the aromatic fluorophores such as (FLU)2− which have a much more substantial hydrophobic surface area.
Finally, a pH titration shows that the anionic form of bromocresol purple is stabilised by ≈1 pKa unit in the presence of HW due to its interaction with the cationic surface. This is similar in principle to, but smaller in magnitude than, the pKa shifts seen by Raymond and co-workers for guests that were fully encapsulated inside the cavity of a highly charged cage host.
In conclusion, the ability to measure the interaction of HW with anions at its exterior surface complements the well-understood host guest chemistry associated with the central cavity: and since both recognition components are required for the catalytic processes that we have seen, we will be able to build on this to develop more effective catalytic processes in which cavity-bound neutral molecules react with surface-bound anions.
Author contributions
MDL performed all experimental work and analysed the data. MDW conceived and supervised the project. MDL and MDW contributed equally to writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank EPSRC for a PhD studentship to MDL (grant number EP/N509796/1); the University of Warwick for additional financial support; and Prof. Chris Hunter (University of Cambridge) for valuable discussions and provision of the software used to determine binding constants (ref. 18a).Notes and references
- (a) T. R. Cook and P. J. Stang, Chem. Rev., 2015, 115, 7001 CrossRef CAS; (b) T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2013, 113, 734 CrossRef CAS; (c) R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810 CrossRef CAS; (d) M. M. J. Smulders, I. A. Riddell, C. Browne and J. R. Nitschke, Chem. Soc. Rev., 2013, 42, 1728 RSC; (e) D. Zhang, T. K. Ronson and J. R. Nitschke, Acc. Chem. Res., 2018, 51, 2423 CrossRef CAS; (f) H. Vardhan, M. Yusubov and F. Verpoort, Coord. Chem. Rev., 2016, 306, 171 CrossRef CAS.
- (a) Y. Fang, J. A. Powell, E. Li, Q. Wang, Z. Perry, A. Kirchon, X. Yang, Z. Xiao, C. Zhu, L. Zhang, F. Huang and H.-C. Zhou, Chem. Soc. Rev., 2019, 48, 4707 RSC; (b) C. J. Brown, F. D. Toste, R. G. Bergman and K. N. Raymond, Chem. Rev., 2015, 115, 3012 CrossRef CAS; (c) M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418 CrossRef CAS; (d) M. Otte, ACS Catal., 2016, 6, 6491 CrossRef CAS; (e) C. M. Hong, R. G. Bergman, K. N. Raymond and F. D. Toste, Acc. Chem. Res., 2018, 51, 2447 CrossRef CAS; (f) W.-X. Gao, H.-N. Zhang and G.-X. Jin, Coord. Chem. Rev., 2019, 386, 69 CrossRef CAS.
- (a) Y. Sun, C. Chen, J. Liu and P. J. Stang, Chem. Soc. Rev., 2020, 49, 3889 RSC; (b) M. Zhang, M. L. Saha, M. Wang, Z. Zhou, B. Song, C. Lu, X. Yan, X. Li, F. Huang, S. Yin and P. J. Stang, J. Am. Chem. Soc., 2017, 139, 5067 CrossRef CAS; (c) C.-L. Liu, R.-L. Zhang, C.-S. Lin, L.-P. Zhou, L.-X. Cai, J.-T. Kong, S.-Q. Yang, K.-L. Han and Q.-F. Sun, J. Am. Chem. Soc., 2017, 139, 12474 CrossRef CAS; (d) J. Wang, C. He, P. Wu, J. Wang and C. Duan, J. Am. Chem. Soc., 2011, 133, 12402 CrossRef CAS; (e) Y. Jiao, J. Wang, P. Wu, L. Zhao, C. He, J. Zhang and C. Duan, Chem. – Eur. J., 2014, 20, 2224 CrossRef CAS; (f) X.-Z. Li, L.-P. Zhou, L.-L. Yan, D.-Q. Yuan, C.-S. Lin and Q.-F. Sun, J. Am. Chem. Soc., 2017, 139, 8237 CrossRef CAS.
- (a) A. B. Grommett and J. R. Nitschke, J. Am. Chem. Soc., 2017, 139, 2176 CrossRef; (b) A. Garci, J.-P. Mbakidi, V. Chaleix, V. Sol, E. Orhan and B. Therrien, Organometallics, 2015, 34, 4138 CrossRef CAS; (c) T. Grancha, A. Carné-Sánchez, L. Hernández-López, J. Albalad, I. Imaz, J. Juanhuix and D. Maspoch, J. Am. Chem. Soc., 2019, 141, 18349 CrossRef CAS; (d) A. M. Castilla, T. K. Ronson and J. R. Nitschke, J. Am. Chem. Soc., 2016, 138, 2342 CrossRef CAS; (e) S. Löffler, J. Lübben, L. Krause, D. Stalke, B. Dittrich and G. H. Clever, J. Am. Chem. Soc., 2015, 137, 1060 CrossRef; (f) W. Cullen, S. Turega, C. A. Hunter and M. D. Ward, Chem. Sci., 2015, 6, 625 RSC.
- M. D. Ward, C. A. Hunter and N. H. Williams, Acc. Chem. Res., 2018, 51, 2073 CrossRef CAS.
- (a) I. S. Tidmarsh, T. B. Faust, H. Adams, L. P. Harding, L. Russo, W. Clegg and M. D. Ward, J. Am. Chem. Soc., 2008, 130, 15167 CrossRef CAS; (b) M. Whitehead, S. Turega, A. Stephenson, C. A. Hunter and M. D. Ward, Chem. Sci., 2013, 4, 2744 RSC; (c) M. D. Ward, C. A. Hunter and N. H. Williams, Chem. Lett., 2017, 46, 2 CrossRef CAS.
- (a) W. Cullen, A. J. Metherell, A. B. Wragg, C. G. P. Taylor, N. H. Williams and M. D. Ward, J. Am. Chem. Soc., 2018, 140, 2821 CrossRef CAS; (b) J. R. Piper, L. Cletheroe, C. G. P. Taylor, A. J. Metherell, J. A. Weinstein, I. V. Sazanovich and M. D. Ward, Chem. Commun., 2017, 53, 408 RSC.
- B. Hasenknopf, J.-M. Lehn, B. O. Kneisel, G. Baum and D. Fenske, Angew. Chem., Int. Ed. Engl., 1996, 35, 1838 CrossRef CAS.
- (a) B. L. Schottel, H. T. Chifotides and K. R. Dunbar, Chem. Soc. Rev., 2008, 37, 68 RSC; (b) J.-F. Ayme, J. E. Beves, D. A. Leigh, R. T. McBurney, K. Rissanen and D. Schultz, J. Am. Chem. Soc., 2012, 134, 9488 CrossRef CAS; (c) S. P. Argent, H. Adams, T. Riis-Johannessen, J. C. Jeffery, L. P. Harding, O. Mamula and M. D. Ward, Inorg. Chem., 2006, 45, 3905 CrossRef CAS.
- W. Cullen, M. C. Misuraca, C. A. Hunter, N. H. Williams and M. D. Ward, Nat. Chem., 2016, 8, 231 CrossRef CAS.
- F. J. Rizzuto, W. Y. Wu, T. K. Ronson and J. R. Nitschke, Angew. Chem., Int. Ed., 2016, 55, 7958 CrossRef CAS.
- I. A. Riddell, M. M. J. Smulders, J. K. Clegg, Y. R. Hristove, B. Breiner, J. D. Thoburn and J. R. Nitschke, Nat. Chem., 2012, 4, 751 CrossRef CAS.
- N. Mihara, T. K. Ronson and J. R. Nitschke, Angew. Chem., 2019, 58, 12497 CrossRef CAS.
- C. Sgarlata, J. S. Mugridge, M. D. Pluth, B. E. F. Tiedemann, V. Zito, G. Arena and K. N. Raymond, J. Am. Chem. Soc., 2010, 132, 1005 CrossRef CAS.
- B. Li, B. Zheng, W. Zhang, D. Zhang, X.-J. Yang and B. Wu, J. Am. Chem. Soc., 2020, 142, 6304 CrossRef CAS.
- A. C. Stelson, C. M. Hong, M. C. Groenenboom, C. A. E. Little, J. C. Booth, N. D. Orloff, R. G. Bergman, K. N. Raymond, K. A. Schwarz, F. D. Toste and C. J. Long, Commun. Chem., 2019, 2, 54 CrossRef.
- (a) B. T. Nguyen and E. V. Anslyn, Coord. Chem. Rev., 2006, 250, 3118 CrossRef CAS; (b) L. You, D. Zha and E. V. Anslyn, Chem. Rev., 2015, 115, 7840 CrossRef CAS.
- (a) S. Turega, W. Cullen, M. Whitehead, C. A. Hunter and M. D. Ward, J. Am. Chem. Soc., 2014, 136, 8475 CrossRef CAS; (b) J. S. Train, A. B. Wragg, A. Auty, A. J. Metherell, D. Chekulaev, C. G. P. Taylor, S. P. Argent, J. A. Weinstein and M. D. Ward, Inorg. Chem., 2019, 58, 2386 CrossRef CAS.
- (a) W. Cullen, S. Turega, C. A. Hunter and M. D. Ward, Chem. Sci., 2015, 6, 2790 RSC; (b) W. Cullen, K. A. Thomas, C. A. Hunter and M. D. Ward, Chem. Sci., 2015, 6, 4025 RSC; (c) C. G. P. Taylor, S. P. Argent, M. D. Ludden, J. R. Piper, C. Mozaceanu, S. A. Barnett and M. D. Ward, Chem. – Eur. J., 2020, 26, 3054 CrossRef CAS; (d) C. G. P. Taylor, W. Cullen, O. M. Collier and M. D. Ward, Chem. – Eur. J., 2017, 23, 206 CrossRef CAS; (e) A. J. Metherell, W. Cullen, N. H. Williams and M. D. Ward, Chem. – Eur. J., 2018, 24, 1554 CrossRef CAS.
- (a) P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305 RSC; (b) F. Ulatowski, K. Dabrowa, T. Balakier and J. Jurkzac, J. Org. Chem., 2016, 81, 1746 CrossRef CAS; (c) D. B. Hibbert and P. Thordarson, Chem. Commun., 2016, 52, 12792 RSC.
- A. Priimagi, G. Cavallo, P. Metrangelo and G. Resnati, Acc. Chem. Res., 2013, 46, 2686 CrossRef CAS.
- (a) K. D. Collins and M. W. Washabaugh, Q. Rev. Biophys., 1985, 18, 323 CrossRef CAS; (b) M. G. Cacace, E. M. Landau and J. J. Ramsden, Q. Rev. Biophys., 1997, 30, 241 CrossRef CAS; (c) R. J. Clarke and C. Lupfert, Biophys. J., 1999, 76, 2614 CrossRef CAS.
- Y. Koga, Phys. Chem. Chem. Phys., 2013, 15, 14548 RSC.
- N. Vlachy, B. Jagoda-Cwiklik, R. Vácha, D. Touraud, P. Jungwirth and W. Kunz, Adv. Colloid Interface Sci., 2009, 146, 42 CrossRef CAS.
- (a) M. D. Pluth, R. G. Bergman and K. H. Raymond, Science, 2007, 316, 85 CrossRef CAS; (b) M. D. Pluth, R. G. Bergman and K. N. Raymond, Acc. Chem. Res., 2009, 42, 1650 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |