On the support dependency of the CO₂ methanation – decoupling size and support effects

Abstract

The influence of the support basicity, according to the Lewis and Brønsted definition, was investigated for the Ru catalyzed CO₂ methanation in the temperature range from 200 °C to 400 °C. Due to the structure-sensitivity of the reaction, a novel building block approach was used to ensure a constant Ru particle size, while varying the support material. In this way, differences in the catalytic behaviour could be directly related to support effects. Eight oxides – the rare earth metal oxides Gd₂O₃, Sm₂O₃ and Y₂O₃ (REOs) as well as TiO₂, ZrO₂, Al₂O₃, MgO and SiO₂ as a non-basic oxide – were chosen to cover different types and combinations of basic surface sites on the support, such as Brønsted basic hydroxyl groups, Lewis basic oxygen atoms and oxygen vacancies. Above 310 °C, the REO supported catalysts showed the highest methane formation rates. The consumption of carbonate species formed upon CO₂ adsorption on all three types of basic sites indicated their catalytic involvement in the high temperature regime. Below 310 °C, TiO₂ and – to a lesser extent – ZrO₂ excelled the other supports. For ZrO₂ the enhanced performance could be related to the sole presence of Lewis basic oxygen vacancies, acting as additional CO₂ adsorption and activation sites on the support. On contrary, in case of TiO₂ they seemed not to be directly but only indirectly involved by facilitating the conversion on the Ru particles on the basis of a favourable electronic metal–support interaction. The inferior catalytic results obtained with the other supports were in accord with the absence of basic sites or a spectator role of the carbonates formed – except for Al₂O₃ which stood out probably due to Brønsted basic OH-groups formed under reaction conditions. Overall, the study reveals that basic supports can noticeably contribute to the catalytic turnover by opening new support-related pathways in addition to the Ru-related pathway evidenced in all cases and/or by promoting the latter. Their impact is dependent on the type, density and strength of basic sites available and varies with temperature.

---

1 Introduction

CO₂ methanation is often expected to play a prominent role in restructuring the energy sector. As part of the power-to-gas technology and in combination with electrolytically produced hydrogen, the reaction allows to chemically store excess wind or solar energy in form of methane that can be fed into the existing natural gas grid.^1,2 Concomitantly, climate harmful CO₂ is consumed and converted to an energy carrier. However, in addition to the desired reaction (eqn (1)), the reverse water-gas shift reaction (eqn (2)) may occur as an unwanted side reaction:³

CO₂ + 4H₂ ⇌ CH₄ + 2H₂O Δ_RH_298K = −165 kJ mol⁻¹ (1)

CO₂ + H₂ ⇌ CO + H₂O Δ_RH_298K = +41 kJ mol⁻¹ (2)

Most commonly applied for the methanation of CO₂ are supported Ni, Co and Ru catalysts, of which the latter are the most active ones. Still, Ru is seldom used and has not yet found its way into technical applications, because of its high prize and potential practical problems – Ru is, for instance, prone to form volatile oxides.^4–6

The CO₂ conversion as well as the CH₄ selectivity are primarily dependent on the Ru particle size,^7,8 but the catalytic performance was found to be influenced by the nature of the employed oxide support, too. Most studies trying to shed light on support effects have focused on standard materials so far, such as Al₂O₃, SiO₂, MgO and TiO₂. Only in recent years also support materials less often used, like Sm₂O₃ and CeO₂, have gained attention in the literature.^4,9,10 While it has become apparent that basic oxides have the most promising potential, fundamental understanding is still missing of how different types of surface basicity or basic adsorption sites, respectively, impact the catalytic conversion and how they mechanistically affect the surface reactions. One obstacle complicating systematic studies in this respect results from the particle size dependence, i.e. structure-sensitivity, of the reaction. To clearly identify and compare support effects, it is hence mandatory to deposit identical or at least very similar particle sizes of the active component (in this case Ru) on different support materials.¹¹ Conventional methods (such as wet impregnation, for instance) are based on in situ formation of the metallic nanoparticles on the support so that their size strongly depends on its surface chemistry – in addition to other factors, such as its crystallinity, porosity and also present impurities, to name just a few. For this reason, most studies conducted up to now, have not been able to avoid varying particle sizes of the deposits; e.g., Muroyama et al.¹² compared various supported Ni catalysts, but the authors had to deal with widely differing particle sizes obtained as a result of their catalyst preparation by impregnation. While on an Al₂O₃ support they ranged between 6–18 nm, they increased to 18–210 nm in case of ZrO₂. Therefore, approaches based on traditional preparation techniques have not been successful in identifying clear trends so far.

Clearly, in case of an inert support all necessary elementary steps – involving the competitive dissociative adsorption of H₂ and CO₂ – need to take place on Ru alone (“CO pathway”, Fig. 1). Since CO is formed as an intermediate of this pathway and stronger bound on the Ru nanoparticles than H₂, it can easily poison the metal surface and, depending on temperature, limit the catalytic turnover.^13–15 As a mild acid, CO₂ is able to also adsorb on the support if basic centers exist on the surface. If the resulting carbonates are accessible to further hydrogenation by reacting with hydrogen provided by spill-over from the metal deposits,^16–21 new reaction pathways are opened that can additionally contribute to the conversion and improve the catalytic activity. Naturally, neither carbonates that are bound too weakly nor carbonates being too stable in the temperature range where the methanation reaction is carried out are likely to get catalytically involved.²² In other words, basic sites of “intermediate” strength are required. Moreover, beneficial metal–support interactions promoting the Ru-related pathway itself are conceivable. Based on these considerations, the following three support effects could be envisioned:

Fig. 1 Conceptual depiction of the possible support effects and classification of the used support materials. No support effect (“CO pathway”), (1) CO₂ adsorption as monodentate or hydrogen carbonate, (2) CO₂ activation as bidentate carbonate and (3) beneficial influence of an electronic metal–support interaction; red squares indicate an oxygen vacancy, red arrows indicate electronic interactions. In all cases H₂ is expected to adsorb dissociatively on the metal (not shown here for the sake of simplicity).

1) CO₂ adsorption on the support (support effect 1, Fig. 1)

Brønsted basic OH groups exposed on the oxide support can bind CO₂ to form hydrogen carbonates, for instance. Also, surface oxygen atoms exhibiting sufficient Lewis basicity (e.g. at defects) may serve as adsorption sites. In this case, monodentate carbonates are formed.

2) CO₂ activation on oxygen vacancies (support effect 2, Fig. 1)

If in case of reducible oxides Lewis basic oxygen vacancies are available on their surface and CO₂ adsorbs there, one of the two oxygen atoms fills the vacancy so that bidentate carbonates are formed.^23–28 When the oxygen atom is left there in the course of subsequent hydrogenation steps, this type of binding represents an additional activation in form of a first reduction step of the molecule.^29,30 The loss of the vacancy can be compensated by the reaction of a lattice O with two H atoms spilled over from Ru, resulting in H₂O which eventually desorbs. Overall, such a scenario represents a Mars-van-Krevelen mechanism that contributes to the conversion acordingly. TiO₂ and ZrO₂ are chosen as representative oxides for this study,^27,31,32 but also the rare-earth metal oxides Sm₂O₃, Gd₂O₃ and Y₂O₃ are known for their ability to form sub-stoichiometric oxides so that they have the potential to show this support effect as well.³³

3) Facilitation of the CO₂ methanation on Ru (support effect 3, Fig. 1)

The support may not only directly but also indirectly enhance the catalytic performance by facilitating the conversion on the Ru nanoparticles themselves due to a metal–support interaction. A supportive effect of that kind can be expected if electron density is shifted from the metal to the oxide. In case of adsorbed CO, the reduced electron density leads to a weakening of the CO–metal bond and hence to a reduction of its surface coverage.^15,34–37 If another molecule needs to be competitively adsorbed for the catalytic reaction to run, as given for the Ru-related “CO pathway” of the CO₂ methanation reaction, a more favourable coverage ratio of the two reactants can be achieved. Since CO is usually the more strongly bound species, more free sites are available for the other reaction partner – in this case for the dissociative adsorption of H₂ on the Ru nanoparticles. Such an electronic influence that should accordingly result in more catalytic turnovers on the metal deposits has indeed been reported for sub-stoichiometric oxide phases, i.e. supports exhibiting oxygen vacancies as those coming into consideration for effect (2).

Aiming at a clarification to which extent the described possibilities of support effects can be exploited to increase the methane yield for the Ru catalyzed CO₂ methanation, we systematically investigated a variety of support materials with different acid–base properties. To rule out superimposed particle size effects on the catalytic performance, we used a novel building block approach by preparing uniform Ru nanoparticles independently from the support by a colloidal synthesis in a first step. Subsequently, these particles were deposited on eight different support materials, which can be grouped in four categories according to their possibility to contribute in form of one or more of the effects described above (see also Fig. 1): (A) Gd₂O₃, Sm₂O₃ and Y₂O₃ (REOs): support effect (1) + (2) + (3);^33,38 (B) ZrO₂ and TiO₂: (2) + (3);³³ (C) MgO and Al₂O₃: (1);^15,39 and (D) SiO₂ as an example of an inert oxide, showing neither Lewis nor Brønsted basicity.

All Ru loaded oxides were fully characterized by means of N₂ physisorption, powder X-ray diffraction (PXRD) and transmission electron microscopy (TEM); the results are presented in section 3.1. CO₂-temperature programmed desorption (CO₂-TPD) in combination with diffuse reflectance infrared Fourier-transformed spectroscopy (DRIFTS) measurements, discussed in section 3.2, were used to identify the types of carbonates formed on the various supports upon CO₂ exposure (at 50 °C) and to characterize their thermal stability. All catalysts were subsequently tested in a (lab) flow reactor under identical conditions to determine the (initial) methane formation rate after reaching steady state activity. In parallel, in situ DRIFTS was employed to identify the carbonates formed under reaction conditions. In this way, we were able to correlate the catalytic performance observed as a function of temperature with the support's basicity, i.e. the type, strength and density of Brønsted and Lewis basic sites available on the oxide surfaces (see section 3.3).

2 Experimental

2.1 Synthesis

Eight different catalyst systems were prepared by depositing colloidal Ru nanoparticles on various oxide supports. A Ru loading of 1 wt% was targeted in all cases.

Supports. Al₂O₃ (Sasol, Puralox SBa 200, 98%), MgO (Acros, 98%), SiO₂ (Sigma, Davisil 646, 99%), TiO₂ (Evonik, Aeroxide P25, 99.5%), ZrO₂ (Chempur, 99%) were purchased, whereas Sm₂O₃, Gd₂O₃ and Y₂O₃ were synthesized in-house by a sol–gel route.⁴⁰

First, the desired amount of the rare earth metal nitrates (Sm(NO₃)₃*xH₂O, Gd(NO₃)₃*xH₂O (Chempur, 99.9%) and Y(NO₃)₃*xH₂O (Alfa Aeser, 99.9%)) were dissolved in absolute ethanol (Merck, 1.7 g ethanol/1 mmol metal salt) under stirring in a polyethylene vial. Next, citric acid (CA, Roth, 99.5%, anhydrous) was added (1 mmol CA per 1 mmol metal salt). Upon complete dissolution, propylene oxide (Aldrich, 99.5%) was quickly added to the mixture (11 mmol of PO/1 mmol of metal salt). The resulting solution was stirred for a few seconds to ensure homogeneity and gelation occurred rapidly within a few seconds. The formed gel was aged undisturbed for 24 hours at room temperature. To remove any residues of the synthesis, a solvent exchange with pure ethanol was conducted after 24 h by decanting the old solvent. This procedure was repeated twice. Ambient drying for at least five days yielded xerogels, which were subsequently calcined in air at 600 °C (heating ramp: 1 °C min⁻¹) for 2 hours.

Ru nanoparticles. Ru nanoparticles with an average size of 1 nm were prepared by a colloidal synthesis route previously reported by Wang et al.⁴¹ In short, 0.223 g RuCl₃*xH₂O (Chempur, 41 wt% Ru content) were dissolved in 25 mL ethylene glycol (Merck) and further diluted with 25 mL 0.5 M NaOH (VWR, 99%) in ethylene glycol. The resulting solution was placed in an oil bath pre-heated to 150 °C for 90 min under stirring to ensure full reduction of Ru and nanoparticle formation. The particles were finally precipitated by adding 8 equivalents (vol./vol.) 1 M HCl to the solution. After centrifugation at 40 Hz, the Ru nanoparticles could be collected as solid particles by decanting the HCl.

To deposit the nanoparticles on the support, these were redispersed in four equivalents (vol./vol.) of acetone (p.a., Merck) and the required amount of the support material (particle size 75–150 μm) was added, before the solvent was removed by rotary evaporation under vacuum so that a dried powder was finally obtained.

2.2 Characterization

Atomic absorption spectroscopy (AAS). To determine the Ru loading, AAS measurements were conducted, using a flame atomic absorption spectrometer (Carl Zeiss Technology, AAS 5 FL). To this end, Ru was digested by a fusion method established by Taddia and Sternini,⁴² which was later confirmed to be the most efficient and reliable method to digest Ru⁰ as well as RuO_x.⁴³ In short, 150 mg of the supported catalysts were mixed with 0.38 g KOH and 0.65 g KNO₃, subsequently heated within 60 min to 450 °C in a muffle furnace and kept at this temperature for another 60 min. After cooling down, 50 mg of K₂S₂O₈ were added, before the melts were dissolved in Milli-Q water. Next, 10 mL of 1 M KOH were added and the resulting solution was further diluted with Milli-Q water to achieve a total volume of 50 mL. 10 mL of the solution were mixed with 5 mL of concentrated HCl and 10 mL Milli-Q water and then analyzed.

The following compositions were found and used for normalizing the reaction rates: 1.0 wt% Ru–Sm₂O₃, 0.9 wt% Ru–Y₂O₃, 1.0 wt% Ru–Gd₂O₃, 1.0 wt% Ru–TiO₂, 0.8 wt% Ru–ZrO₂, 1.0 wt% Ru–Al₂O₃, 1.2 wt% Ru–MgO and 1.0 wt% Ru–SiO₂. The differences in the loadings arose from different losses during precipitation and subsequent decanting of the residual HCl.

Powder XRD (PXRD). The catalysts were characterized by PXRD to identify the crystallographic phases of the used oxides. The samples were measured using a θ/2θ-Bragg–Brentano geometry on a X'Pert MPD powder diffractometer (Panalytical, Almelo, Netherlands). The instrument was equipped with a secondary Ni filter, Cu Kα_1,2 radiation (λ₁ = 154.05929(5) pm, λ₂ = 154.4414(2) pm) and an X'Celerator multi-strip detector. Data were collected at ambient condition in the 2θ range from 15° to 90° with a step width of 0.0167° per step and a collection time of 200 s per step.

N₂ physisorption. N₂ physisorption measurements were conducted in order to analyze the catalysts' porosity, using a NOVA 4000e (Quantachrome Instruments, USA) gas sorption system. Prior to data collection, the samples were outgassed at 200 °C for at least 2 hours under vacuum. Adsorption/desorption isotherms were collected in the pressure range 0.01–0.99 p/p₀. Using the desorption branches, the pore size distributions were calculated on the basis of the Barrett–Joyner–Halenda (BJH) model, whereas the pore volume was determined on the basis of the amount of adsorbed N₂ at p/p₀ = 0.99. The specific surface areas were calculated based on five-point Brunauer–Emmett–Teller (BET) measurements in the pressure range 0.1–0.3 p/p₀. All measurements were conducted at −196 °C.

Transmission electron microscopy (TEM). Transmission electron micrographs were acquired for all catalysts, using a Tecnai F20 S-TWIN (200 keV) microscope to gain insight into the catalyst microstructure and to determine the Ru particle size. To this end, the catalysts were ground to a fine powder, before being loaded onto a TEM grid (ultrathin carbon film, Quantifoil, Cu 200 mesh) by dragging the grid through the powder. The Ru mean particle size was determined by analysing the micrographs with the software ImageJ (version 1.48). For each sample, at least 250 particles were measured.

CO₂-Temperature programmed desorption (CO₂-TPD). To probe the basicity of the various systems, i.e. the strength of the basic sites, CO₂-TPD spectra were recorded. About 100 mg of the powder catalysts were placed in a stainless-steel reactor and pretreated at 400 °C for 60 min (3 °C min⁻¹) in 20 vol% H₂/Ar (V̇_tot = 50 mL_N min⁻¹), which corresponds to the activation of the catalysts in the catalytic experiments. After cooling down to 50 °C, the powders were saturated with CO₂ for 60 min, before flushing the set-up with pure Ar for 30 min to remove any remaining gaseous CO₂ from the system. Subsequently, the samples were heated to 950 °C with a linear heating rate of 5 °C min⁻¹ in Ar while desorbing CO₂ was detected, using a mass spectrometer (HPR20, Hiden Analytical). To enable a quantitative comparison, the mass spectrometer was calibrated for CO₂ (44 amu), CO (28 amu) and Ar (40 amu), of which Ar was used as internal standard. After subtraction of the CO₂ baseline (measured in pure Ar), the total amount of desorbing CO₂ was determined by integrating the desorption peaks, using the calibrated 44 amu/40 amu ratios.

DRIFTS. Diffuse reflectance infrared Fourier-transformed spectroscopy (DRIFTS) measurements were conducted, on the one hand, to characterize CO₂ adsorption on the catalysts and thus to complement the CO₂-TPD measurements. On the other hand, DRIFTS experiments were carried out under reaction conditions in an attempt to identify possible reaction intermediates (and spectator species) and thus get mechanistic indications. All measurements were conducted using a Varian-670 FT-IR spectrometer equipped with a liquid nitrogen cooled MCT detector and an IR cell in praying mantis geometry (VC-DRM-5, Harrick). All spectra were recorded with a resolution of 4 cm⁻¹ in absorbance mode and the average of 128 scans (acquisition time: 78 s) is reported here.

After placing the samples on the temperature-controlled sample holder in the IR cell, the sample compartment was flushed with He to remove any impurities prior to spectra collection. Subsequently, the samples were heated to 400 °C in 20 vol% H₂/He within 30 min. This temperature was then kept constant for another 60 min to activate the catalysts.

To characterize the CO₂ adsorption behaviour, the samples were cooled down to 50 °C in He after activation and background acquisition. Subsequently, the samples were saturated with CO₂ for 60 min. Next, the compartment was flushed with He (100 mL min⁻¹) for 30 min to remove any remaining gaseous CO₂ from the tubing and the sample stage. Afterwards, the spectra were collected.

For the reaction studies, the samples were cooled down to 100 °C in He atmosphere after activation and after the background was recorded. Subsequently, the catalysts were exposed to 5 vol% CO₂, 20 vol% H₂ and 75 vol% He at a total flow rate of 100 mL min⁻¹. The temperature was increased stepwise until 350 °C and a spectrum was recorded at each temperature after 5 min to ensure thermal equilibration.

In addition, isothermal studies were carried out. Again, the fresh catalysts were first activated and subsequently cooled down to 350 °C in He, where the background was recorded. Next, 5 vol% CO₂ were added for 15 min, while recording a spectrum every two minutes. Next, the CO₂ flow was stopped and the catalysts exposed to pure He (100 mL_N min⁻¹) for 20 min. Spectra were recorded after 1, 3, 5, 7, 9, 11, 15 and 20 min. Afterwards, the samples were exposed to a H₂/He mixture (20 vol% H₂) at a total flowrate of 100 mL_N min⁻¹ for another 20 min during which, again, spectra were collected in the same manner as before. Lastly, the samples were exposed to the reactant mixture (5 vol% CO₂, 20 vol% H₂ in He, total flowrate 100 mL_N min⁻¹) and a final spectrum was acquired after 1 min of exposure.

For the Ru–TiO₂ catalyst, a slightly different procedure was chosen (for reasons explained later). The fresh catalyst was first activated in H₂ at 400 °C and then cooled down to 350 °C in He, where a background spectrum was recorded. Subsequently, the sample was saturated with CO₂ for 15 min (5 vol% CO₂ in He, total flowrate 100 mL_N min⁻¹), in analogy to the other isothermal ad-/desorption experiments. In contrast to the other catalysts, however, the Ru–TiO₂ catalyst was then exposed to 5 vol% CO₂ and 20 vol% H₂ in He at a total flow rate of 100 mL_N min⁻¹. During the entire experiment, the temporal evolution of the adsorbed species was followed by collecting spectra every two minutes.

For the semi-quantitative evaluation of the detected surface species, a careful background correction of the spectra (in the corresponding wavenumber regime) was performed before the peaks were fitted with Gauss–Lorentzian profiles, using the LabSepc5 software (Horiba).

2.3 Catalytic set up and experiments

All measurements were conducted in a fixed-bed reactor, consisting of a quartz-glass tube (6 mm inner diameter) that was operated at atmospheric pressure. A metal block oven was used for reactor heating. The temperature was controlled by a thermocouple placed at the end of the catalyst bed inside the reactor. To preheat the gases and to prevent water condensation inside the set-up, all tubing was heated to at least 120 °C. The gas flow rates were controlled by mass-flow controllers (Bronkhorst Mättig).

The reactor was filled with 50 mg (75–150 μm) catalyst which was diluted in the ratio 1 : 10 with quartz particles in the same size fraction. Quartz wool was used to hold the mixed powder in place inside the reactor. Prior to the catalytic experiments, all catalysts were reduced in situ in flowing H₂ at 400 °C for 1 h (heating ramp: 3 °C min⁻¹). After this activation step, the reactor was cooled down to the starting temperature of 200 °C in inert gas atmosphere. The activity and selectivity of the catalysts for the CO₂ methanation reaction were determined in the temperature range between 200 to 400 °C, using a molar feed gas composition of 4/1/5 H₂/CO₂/Ar. The total flow rate was set to 50 mL_N min⁻¹, corresponding to a weight hourly space velocity (WHSV) of 60 L_N g_cat⁻¹ h⁻¹. Each temperature was kept constant for 42 min and conversion and selectivity were averaged over the last 24 min.

After passing a cold trap (operated at −1 °C) to remove water formed as reaction product, the effluent gases were analyzed with an on-line compact gas chromatograph (Global Analyser Solution), equipped with a thermal-conductivity sensor. A RT-Molsieve 5 Å column (15 m) was used to separate CO and CH₄, whereas CO₂ was separated on a RT-Porabond column (30 m). In pre-experiments, no C_2⁺ hydrocarbon formation was detected. Based on the inlet and outlet flow rates, the formation and consumption rates (referred to catalyst mass) of the involved compounds were calculated according to eqn (3),

3 Results and discussion

3.1 Structural characterization by PXRD, N₂ physisorption and TEM

Powder X-ray diffraction measurements were performed for all catalysts studied here. The X-ray diffraction patterns presented in Fig. S1 (ESI†) reveal that all supports were crystalline, except for SiO₂ which turned out to be X-ray amorphous. The rare-earth metal oxides prepared in house exhibited the expected crystal structures of cubic Sm₂O₃, Gd₂O₃ and Y₂O₃ (Ia3̄) – a result which is consistent with our previous findings.^40,44 The purchased TiO₂ employed in this study was comprised of a mixture of 91.5% anatase and 8.5% rutile, whereas all other purchased support materials consisted only of one phase, namely, monoclinic ZrO₂ (space group: P12₁/c1), cubic γ-Al₂O₃ (Fm3̄m) and cubic MgO (Fm3̄m). Diffraction peaks of Ru⁰ or RuO_x originating from the deposited Ru nanoparticles, were not detected in any of the diffractograms, as expected for the low loading and the small size of the particles (see below).

The specific surface areas, pore volumes as well as pore size distributions were determined for all catalysts, based on N₂ physisorption measurements (Table 1); the corresponding isotherms and pore size distributions are contained in the ESI† (Fig. S2 and S3, respectively).

Table 1 Specific surface areas, pore volumes as well as average pore sizes and maxima of the pore size distribution, as determined by N₂ physisorption measurements. The statistical error (standard deviation characterising the instrumental precision) was determined by measuring the Ru–Sm₂O₃ sample three times and can be considered to be representative also for the other samples

Sample	Specific surface area/m^2 g^−1	Pore volume/cm^3 g^−1	Average pore size/nm	Max. of pore size distribution/nm
Ru–Gd2O3	35	0.08	4.5	3.0
Ru–Sm2O3	36 ± 1	0.14 ± 0.01	7.5 ± 0.2	6.4 ± 0.1
Ru–Y2O3	61	0.13	4.4	3.0
Ru–Al2O3	195	0.46	4.7	3.2
Ru–MgO	12	0.03	—	—
Ru–TiO2	60	0.54	17.0	26.3
Ru–ZrO2	16	0.13	15	13
Ru–SiO2	224	0.84	7.5	5.0

---

First, transmission electron micrographs of the unsupported pristine Ru nanoparticles (deposited on a TEM grid) were acquired. To exclude agglomeration and ensure a fine dispersion of the deposited particles on the various supports, the catalysts were subsequently characterized by TEM as well. Unfortunately, in case of Ru–ZrO₂ the contrast between Ru and ZrO₂ was too low due to similar atomic masses of Ru and Zr, rendering it impossible to clearly identify the Ru deposits (in the TEM as well as STEM mode). For Ru–MgO, the particles could not be detected in the TEM mode either, but were observable by STEM. EDX measurements in selected areas of the samples confirmed the correct localization of the Ru deposits. To determine the particle size distribution and the average size, at least 150 Ru particles were evaluated for each sample. Representative images of all catalysts and the corresponding Ru size distributions are shown in Fig. 2.

Fig. 2 TEM images of the synthesized Ru nanoparticles and the supported catalysts. The insets show the respective Ru particle size distributions.

According to these results, the as-prepared Ru nanoparticles indeed exhibited an average diameter of 1.0 ± 0.2 nm and a comparatively narrow size distribution, as expected for the employed synthesis route.⁴¹ After deposition, they preserved their size within the respective standard deviations, proving that our synthetic approach indeed succeeded in preparing differently supported Ru catalysts with the same particle size. (It should be mentioned that in case of the REO supported catalysts, the size distributions appear somewhat broader as compared to those of the pristine and deposited Ru nanoparticles on the other supports. Most likely these differences are artefacts caused by the low contrast between Ru and the REOs, reducing the accuracy of the evaluation in these cases). Notably, in no case agglomerates of Ru particles were observed and a fine dispersion of the active component confirmed for all catalysts.

3.2 Determination of surface basicity

As discussed in the Introduction, the presence of different types of basic Brønsted and Lewis centers exposed on basic oxide supports can be expected, possibly amplifying the capabilities for CO₂ adsorption and its conversion on the catalyst so that an enhanced productivity (i.e. an increased rate of methane formation) is achieved. In order to characterize such sites, CO₂-TPD measurements were conducted for all catalysts studied here. While the thermal stabilities of the carbonates formed upon CO₂ adsorption are accessible via the temperature range of the observed desorption features, their density can be evaluated by integrating the peaks. To clarify which types of carbonates and thus basic sites are available on the various oxide supports, complementary DRIFT spectra were acquired. In both cases (TPD and DRIFTS), the same pre-treatment as applied prior to the catalytic tests was applied. In Fig. 3 all desorption profiles are presented and Table 2 summarizes the results of the quantitative evaluation in terms of the total amount of adsorbed CO₂ and the corresponding surface density of basic sites (calculated on the basis of the specific surface areas). Furthermore, Fig. 4 shows the DRIFT spectra.

Fig. 3 CO₂-TPD measurements of the catalysts. Conditions: ∼100 mg catalyst, temperature ramp 5 °C min⁻¹.

Table 2 Amount of CO₂ desorbed from the various catalysts and calculated surface densities of basic sites

Sample	Amount desorbed/μmol CO2 gcat^−1	Density of basic sites/μmol CO2 m^2cat^−1
Ru–Gd2O3	333	9.5
Ru–Sm2O3	644	17.9
Ru–Y2O3	759	12.4
Ru–Al2O3	198	1.0
Ru–MgO	319	26.6
Ru–TiO2	0	—
Ru–ZrO2	0	—
Ru–SiO2	77	0.3

---

Fig. 4 DRIFT spectra of the various catalysts after saturating them with CO₂ for 30 min at 50 °C; a) Ru–Sm₂O₃, b) Ru–Gd₂O₃, c) Ru–Y₂O₃, d) Ru–MgO, e) Ru–TiO₂ and f) Ru–ZrO₂.

For the rare earth metal oxides (Gd₂O₃, Sm₂O₃ and Y₂O₃), CO₂ desorption is observed between 200–400 °C, except for Sm₂O₃ where the desorption feature extends to ∼600 °C. This range of desorption temperatures, revealing medium basicity in good agreement with the literature, coincides well with the range of suitable reaction temperatures for the CO₂ methanation.⁴⁵ As far as the amount of adsorbed CO₂ is concerned, the rare earth metal oxides show the highest values of all investigated supports and the determined densities of basic sites correspond well with literature values.^15,45 The characterization by DRIFTS yielded similar spectra for all three REOs and revealed the presence of monodentate (m-CO₃²⁻, 1065 cm⁻¹), bidentate (b-CO₃²⁻, 1589 cm⁻¹ and 1296–1311 cm⁻¹) and hydrogen carbonates (HCO₃⁻, 1624–1639 cm⁻¹) on the surface (Fig. 4a–c).^16,46 These results confirm the assumption that all types of basic sites occur on the REO surfaces: monodentate carbonates corresponding to CO₂ adsorption on Lewis basic oxygen atoms, bidentate carbonates indicating Lewis basic oxygen vacancies and hydrogen carbonates Brønsted basic hydroxyl groups.^46,47

The TPD trace acquired for Ru–Al₂O₃ shows only a weakly pronounced CO₂ desorption peak, centered at around 500 °C. Consistently, the density of basic sites is low (see Table 2), evidencing a low initial surface basicity of the support after the pre-treatment and under the conditions of the characterization experiments. In accord, the complementary DRIFT spectra show no noticeable absorption bands due to carbonates on the surface (and are, therefore, not shown here). While such low abilities to bind CO₂ were also observed by other authors,^15,48 γ-Al₂O₃ is known to exhibit hydroxyl groups on the surface depending on the environmental conditions, i.e. the degree of hydroxylation. Since water is a side product of the methanation reaction, the presence of Brønsted basic centers under reaction conditions is not unlikely. As discussed in section 3.3, the catalytic results indeed provide evidence for that.

The TPD spectrum of Ru–MgO stands out by a narrow desorption feature between 300–400 °C in form of a double peak. Even though these temperatures are at the lower end of values reported in the literature, a similar behaviour was observed for other MgO materials as well.⁴⁹ The DRIFT spectra point to the presence of Lewis basic oxygen atoms on the surface, since the two features at 1508 cm⁻¹ and 1433 cm⁻¹ (Fig. 4d) indicate monodentate carbonates (m-CO₃²⁻), as expected in this case.^50,51 In fact, it was shown that such sites may indeed abundantly exist on MgO surfaces, provided that a sufficiently high density of under-coordinated oxygen atoms, i.e. surface defects, exists.^52,53

Unexpected at first glance, hardly any CO₂ desorption is observed for the TiO₂ and ZrO₂ support. The corresponding DRIFT spectra (Fig. 4e and f), even though revealing the formation of some carbonate species, corroborate very low abilities to bind CO₂ in both cases (note the different intensity scaling of the spectra as compared to the REO supports). In case of Ru–TiO₂, the small signal at 1554 cm⁻¹ including the weakly pronounced shoulder at around 1321 cm⁻¹ can be assigned to b-CO₃²⁻ carbonates, in actual agreement with the expected presence of Lewis basic oxygen vacancies.^46,54,55 A peak at 1410 cm⁻¹ attributable to HCO₃⁻ suggests that also some OH-groups must be exposed at the surface. But in any event, the density of all basic sites is negligible as inferred from the TPD data.

For Ru–ZrO₂ (Fig. 4f) slightly different DRIFT spectra were recorded. Here, monodentate carbonates (1363 cm⁻¹) and bidentate hydrogen carbonates (b-HCO₃⁻, 1435 and 1637 cm⁻¹) are detected.^56–59 While m-CO₃²⁻ species indicate the occurrence of some Lewis basic oxygen atoms at the surface, the b-HCO₃⁻ carbonates can be related to oxygen vacancies, when assuming that initially formed bidentate carbonates directly react further with remaining H_ad from the activation step. The facile conversion of b-CO₃²⁻ to b-HCO₃⁻ on this catalyst is in fact evidenced be the DRIFT spectra recorded under reaction conditions and will be discussed later (see section 3.3).

Although both oxides were chosen because of their Lewis basicity based on a sufficient concentration of oxygen vacancies at their surface, the above findings are in line with other reports in the literature.^12,60 It has to be taken into account that the TPD and DRIFT spectra were recorded in an inert gas atmosphere (after saturating the catalysts with CO₂ at 50 °C, see Experimental), while the methanation reaction is carried out at higher temperatures and in the presence of H₂ where a higher degree of reduction is expected. In agreement, the corresponding DRIFTS data (discussed in section 3.3) indeed reveal a significantly higher abundance of oxygen vacancies under these conditions.

The CO₂-TPD spectrum of Ru–SiO₂ consists of a broad but small desorption feature between 500–600 °C. Consistently, the DRIFTS data (not presented here) provided no evidence of carbonate formation, in accordance with literature.⁶¹ Thus, the results confirm the classification of SiO₂ as a non-basic support (exposing neither Lewis nor Brønsted basic sites).

3.3 Catalysis

The CH₄ formation rates achieved between 200 °C and 400 °C in the CO₂ methanation experiments are shown in Fig. 5 for the various catalysts (additional details, i.e. the CO₂ conversion rates, the CH₄ selectivities (Fig. S4) as well as the measured outlet concentrations (Table S1), can be found in the ESI†). The presented graphs are color-coded (in agreement with Fig. 1) to allow for an easy differentiation between the four categories of supports used in this study – green for TiO₂ and ZrO₂, red for the REOs, blue for Al₂O₃ and MgO and purple for SiO₂. Since the reaction rates are referred to the actual Ru loading as determined by AAS, the graphs quantitatively reflect differences in the catalytic performance of the catalysts and – because the same Ru particle size – can directly be attributed to support effects. The Weisz–Prater criterion was calculated for all data points – taking Knudsen diffusion (in agreement with the determined average pore sizes) into account – to verify the absence of internal mass transport limitations in the investigated temperature range (see Table S2 in the ESI†). Only at 400 °C, an influence of diffusion limitation on the observed rates cannot be fully excluded, as also indicated by the corresponding Arrhenius plots (Fig. S5†). Moreover, the stability of the catalysts was checked by prolonged catalytic runs at 400 °C over 10 h. In accordance with TEM images of selected spent catalysts showing no indications of sintering (Fig. S7†), stable methane formation rates were observed so that deactivation even at the highest investigated reaction temperature can be excluded (see Fig. S6†). The reproducibility of the catalytic results was furthermore checked by conducting several runs with different synthesis batches (see Fig. S8†).

Fig. 5 CH₄ formation rates for all catalysts in the investigated temperature range. Reaction conditions: pressure 1 bar, flow rate 50 mL min⁻¹, 4/1/5 H₂/CO₂/Ar, 50 mg catalyst. The vertical line at 310 °C indicates a change regarding the best performing catalysts. OV denotes Lewis basic oxygen vacancies, O²⁻ Lewis basic lattice oxygen ions and OH Brønsted basic hydroxyl groups.

Considering the temperature-dependent progression of the CH₄ formation rate, the results can be distinguished into two temperature regions – one below and one above 310 °C. Below 310 °C, the activity follows the order:

Ru–TiO₂ > Ru–ZrO₂ ≈ Ru–Gd₂O₃ > Ru–Sm₂O₃ > Ru–Y₂O₃ > Ru–Al₂O₃ > Ru–SiO₂ > Ru–MgO,

whereas above 310 °C the order is:

Ru–Gd₂O₃ > Ru–Sm₂O₃ > Ru–Y₂O₃ > Ru–ZrO₂ ≈ Ru–TiO₂ > Ru–Al₂O₃ > Ru–MgO > Ru–SiO₂.

Accordingly, in the high temperature regime the REO supported catalysts perform best and take the leading position while the titania supported catalyst is superior at lower temperatures followed by the ZrO₂ and Gd₂O₃ as supports. The SiO₂, MgO and Al₂O₃ supported catalysts are inferior in both regimes with the latter catalyst excelling the other two and showing intermediate methane yields.

To clarify whether and which support effects according to Fig. 1 are involved and contribute to the catalytic performance, we carried out temperature-dependent DRIFTS experiments under reaction conditions. In the following, the results for the most interesting supports TiO₂, ZrO₂ and Gd₂O₃ (the latter chosen as a representative for all REOs) are discussed, while the DRIFT spectra for the other catalysts can be found in the ESI.† In all cases, we focused on the question how the surface coverages of the carbonates detected change as a function of temperature in order to unravel their potential participation in the catalytic conversion. The identification of additionally observed hydrogenated species helped us to propose how involved carbonates react further, i.e. to make mechanistic proposals regarding support-related hydrogenation pathways. As the differentiation between spectator species and potential reaction intermediates was difficult in some instances, we additionally acquired DRIFT spectra under isothermal conditions at 350 °C. More elaborate experiments combining SSITKA and DRIFTS, however, will be necessary to elucidate the full mechanisms for the catalysts studied here.^13,62

Starting with Ru–Gd₂O₃, the results of the temperature-dependent measurements are presented in Fig. 6 (left). After reductive pre-treatment, we exposed the catalyst to the reaction gases at 100 °C and then stepwise increased the temperature to ultimately 350 °C. By starting well below the expected onset temperature for the reaction, we aimed at capturing adsorbed surface species possibly involved in the reaction, but not detectable at higher temperatures where they undergo fast turnover. Already at 100 °C, CO₂ dissociatively adsorbs on the Ru nanoparticles as indicated by the characteristic vibrations of bridge-bonded CO (Ru=CO, 1990 cm⁻¹) and linearly bound CO on Ru (Ru–CO, 2019 cm⁻¹).^13,15,63 In addition, a variety of bands is observed, which can be assigned to carbonates on the support: monodentate carbonates (m-CO₃²⁻, 1060 cm⁻¹ and 1508 cm⁻¹),^16,46,64 bidentate carbonates (b-CO₃²⁻, 1288 cm⁻¹ and 1583 cm⁻¹),⁴⁶ and hydrogen carbonates (HCO₃⁻, 1633 cm⁻¹, 1437 cm⁻¹ and 3626 cm⁻¹), in accord with the preliminary characterization (section 3.2).⁴⁶ An additional shoulder at around 1755 cm⁻¹ can furthermore be related to a formyl species (HCO⁻).^13,65 Furthermore, signals indicating first traces of gaseous CH₄ appear in the spectra for T > 140 °C (in form of the C–H stretch vibration at 3016 cm⁻¹ and with increasing temperature also in form of the bending vibrations at 1304 cm⁻¹).^66,67 Although these findings evidence first catalytic turnovers of CO₂ to CH₄ on the catalyst surface, the catalytic runs clearly show that temperatures above 200 °C are needed to achieve practically relevant conversions.

Fig. 6 (left) Temperature-dependent DRIFTS reaction study on Ru–Gd₂O₃; (right) normalized peak height for m-CO₃²⁻ (1061 cm⁻¹), b-CO₃²⁻ (1576 cm⁻¹), HCO₃⁻ (1633 cm⁻¹), bridge-bonded CO on Ru (Ru=CO, 1990 cm⁻¹) and top-bound CO on Ru (Ru–CO, 2019 cm⁻¹) as a function of reaction temperature; conditions: 5 vol% CO₂, 20 vol% H₂ in He, V̇_tot = 100 mL min⁻¹.

To analyze how the surface coverages of the species detected change as a function of temperature, we evaluated the intensities (peak heights) of the corresponding bands at each temperature. To this end, we first conducted a careful background correction and separated overlapping peaks by peak fitting (see Fig. S9 in the ESI† for an exemplary fit). The peak heights were then normalized to their maximum value and are plotted in Fig. 6 (right). The evolution of all carbonate species qualitatively follows the same trend. First, an accumulation on the surface is observed in all cases, before reaching a plateau at temperatures above 180 °C. In contrast, linearly and bridge-bonded CO on Ru increasingly form up to 200 °C and start vanishing at higher temperatures. Apparently, dissociative CO₂ adsorption takes place on the nanoparticles already at low temperatures leading to CO as an intermediate which, however, is only converted further at temperatures beyond 200 °C.

The additionally performed isothermal DRIFTS experiments turned out to be more suitable in elucidating a potential involvement of the carbonates in the reaction and are presented in Fig. 7 (left). In analogy to the experiments under reaction conditions, we performed here a quantitative evaluation of the signal intensities as well, which is contained in the figure (right). After activation at 400 °C and subsequent flushing with He to remove residual H₂ from the DRIFTS cell, the sample was exposed to 5 vol% CO₂ in He for 15 min at 350 °C and several spectra were recorded over time (step 1: red spectra). Overall, the same signals are observed as compared to the temperature-dependent measurements, including the characteristic signals for CO on Ru and all three types of carbonates (mono- and bidentate carbonates as well as hydrogen carbonates).^16,46,64 Considering that H₂ was not present in the feed, the formyl species detected here again supposedly originates from CO that spills over from Ru to the support and reacts with residual H that remained from the activation.^13,65 When stopping the CO₂ exposure and purging the cell with He for 20 min (step 2: green traces), CO adsorbed on Ru decreases rapidly (while the band for linearly bound CO vanishes completely after 11 min, a small peak for bridge-bonded CO remains). The features assigned to mono- and bidentate carbonates and hydrogen carbonates, as well as to formyl species also lose intensity over time, but much more slowly (see Fig. 7, right). If 20 vol% H₂ are eventually added to the feed (step 3: blue traces), methane can immediately be detected in the gas phase. Concomitantly, the coverages of all carbonates on the support surface drop significantly and then decrease further over time, suggesting that all three species are consumed by reacting with the supplied hydrogen. Upon exposure to the reactant mixture (step 4: yellow trace), basically the same spectrum as observed in the temperature-dependent measurements was recorded, proving that the catalyst surface was in the same condition than it was in the experiments under reaction conditions (Fig. 6).

Fig. 7 (left) Isothermal DRIFTS experiments carried out for Ru–Gd₂O₃ at 350 °C under different gas atmospheres. Red spectra: exposure to 5 vol% CO₂ in He for 15 min; green spectra: pure He for 20 min; blue spectra: subsequent exposure to 20 vol% H₂ in He; yellow trace: exposure to 5 vol% CO₂ and 20 vol% H₂ in He, V̇_tot = 100 mL min⁻¹. Temporal evolution of the spectra from lighter to darker colors (bottom to top); (right) temporal evolution of the peak heights for m-CO₃²⁻ (1061 cm⁻¹), b-CO₃²⁻ (1576 cm⁻¹) and HCO₃⁻ (1633 cm⁻¹). Normalized in respect to the peak heights after saturation with CO₂ for 15 min (last red spectrum).

In summary, the DRIFTS results provide an explanation of the superior catalytic performance of the REO supported catalysts, in particular above 310 °C (see Fig. 5). The fast consumption of CO on Ru occurring at low temperatures (below ∼300 °C) indicates that the Ru-based hydrogenation pathway is preferred in this temperature regime and the catalytic conversion of CO₂ to CH₄ predominantly takes place on Ru alone. On the contrary, the loss of mono- and bidentate carbonates as well as of hydrogen carbonates on the support surface in conjunction with the methane evolution observed in the isothermal DRIFTS experiments implies their consumption by hydrogenation at higher temperatures. According to the common notion,^13,15 the necessary hydrogen can be supplied by spill-over from the Ru deposits after dissociative adsorption of H₂ on the metal surface hence enabling further reaction of the carbonates on the support surface. The efficiency of such support-related pathways of course depends on the diffusion range of the hydrogen atoms on the oxide, which, in turn, is a function of the surface chemistry.^68–70 While for irreducible oxides this range was found to be comparatively small (0.5 nm on MgO at 75 °C, for instance),⁷¹ hydrogen spillover is significantly more facile in case of reducible and defect rich oxides, such as the REOs.^62,68 For instance, Wang et al.⁶² demonstrated by SSTIKA-DRIFTS that, in case of reduced CeO₂, the entire surface takes part in the CO₂ hydrogenation and not just on sites at or close to the metal–support perimeter. Due to the presence of all three kinds of basic sites on the REO surfaces – Lewis basic oxygen atoms and vacancies as well as Brønsted basic hydroxyl groups – and the susceptibility of the related carbonates to hydrogenation, these supports have the potential to catalytically contribute in all three ways described in the introduction and sketched in Fig. 1. The effects (1) and (2) apparently boost the activity above 310 °C. Notably, the detected formyl species (HCO) is a conceivable reaction intermediate and can be formed by H-assisted abstraction of oxygen from a hydrogen carbonate or by hydrogenation of a bidentate carbonate, for instance. At lower temperatures, where no indications for a direct involvement of the REO supports in form of secondary reaction pathways on their surfaces were found, the excellent catalytic activity also observed in this regime is probably due to effect (3), i.e. an indirect contribution.

At reaction temperatures below 310 °C, the TiO₂ and, to a lesser extent, the ZrO₂ supported catalyst take the lead and show the highest CH₄ yields. It is known that both oxides can exhibit oxygen vacancies which promote CO₂ adsorption and activation.^23–26,72 Although the CO₂-TPD and corresponding DRIFTS results (see section 3.2) provided no evidence of their presence, the temperature-dependent DRIFT spectra of Ru–ZrO₂, shown in Fig. 8, reveal their formation under reaction conditions. Already at 100 °C, bidentate hydrogen carbonates (b-HCO₃⁻, 1469 and 1628 cm⁻¹)^57,58 are detected which – as shown below – are related to b-CO₃²⁻ species, initially formed and directly hydrogenated to hydrogen carbonates by H_ad spilling over from the Ru nanoparticles. In addition, the characteristic bands of monodentate carbonates (1518 and 1488 cm⁻¹)^56,73 and formates (HCOO⁻, 1360, 1377 and 1383 cm⁻¹)^56,74 appear in the spectra. The features at 1979 cm⁻¹ and at 2063 cm⁻¹, corresponding to bridge bonded and linearly bonded CO on Ru, respectively (see Fig. 8 (left)), evidence parallel CO₂ adsorption and dissociation on the metal deposits, in analogy to the REOs. In contrast to them, however, the band of linearly bonded CO is blue-shifted suggesting the presence of some oxidized Ru species (Ru⁺–CO), probably formed at the metal/support interface. First bands of gaseous CH₄ (3016 cm⁻¹) appear at 230 °C, in good agreement with the onset of measurable catalytic activity in this case (see Fig. 5).⁷⁵

Fig. 8 (left) Temperature-dependent DRIFTS reaction study on Ru–ZrO₂, (right) normalized peak heights for m-CO₃²⁻ (1518 cm⁻¹), HCOO⁻ (1360 cm⁻¹), b-HCO₃⁻ (1469 cm⁻¹), Ru=CO (1979 cm⁻¹) and Ru⁺–CO (2063 cm⁻¹) as a function of reaction temperature; conditions: 5 vol% CO₂, 20 vol% H₂ in He, V̇_tot = 100 mL min⁻¹.

Again, the quantitative evaluation of the peak intensities allowed analyzing variations of the surface coverages in case of all relevant species as a function of temperature. The results presented in Fig. 8 (right) reveal that m-CO₃²⁻ species accumulate with increasing temperature, suggesting a role as spectator species here. In contrast, the concentrations of all other species on the surface increase first and then decrease again, reaching their maximum however at different temperatures. For b-HCO₃⁻ the maximum occurs at 180 °C, whereas the highest coverage of formate species (HCOO⁻) is found at 200 °C in form of a shallower maximum. This correlated progression of both species renders a mechanism probable where b-HCO₃⁻ is converted to HCOO⁻ as an intermediate through an unassisted C–O bond cleavage, i.e. by elimination of an O atom which eventually fills an oxygen vacancy on the ZrO₂ surface. Overall and in opposition to the Ru-REO catalysts, the DRIFTS results indicate the availability of a support-related pathway according to option (2) in Fig. 1 already below ∼300 °C. On the contrary, the Ru-based mechanism seems of minor importance in this temperature regime, as inferred from the coverage of Ru with CO showing a maximum at a by ∼100 °C higher temperature as compared to the hydrogen carbonate and formate species. So, in essence, the mechanistic scenario for the ZrO₂ supported catalyst seems inverted to the REOs. While for the latter a direct contribution of the support to the conversion seems to be limited to the second half of the temperature window studied, in the former case it is particularly pronounced in the low temperature regime.

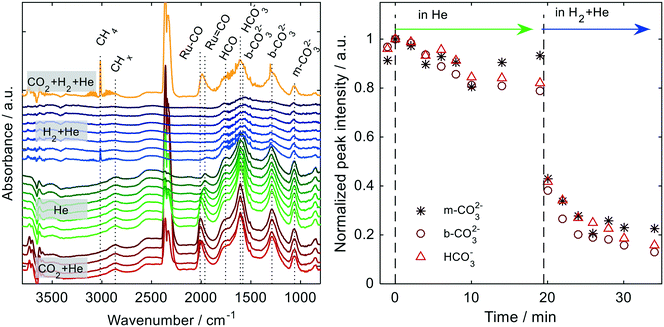
The isothermal DRIFTS measurements (Fig. 9) confirm the assumed genesis of the bidentate hydrogen carbonates as a first hydrogenation product of initially formed bidentate carbonates upon CO₂ adsorption on oxygen vacancies. The latter species directly appear in the spectra recorded in the first step (step 1, red traces) of the experiment, i.e. after exposing the catalyst to CO₂ (in He) at 350 °C, in form of a pronounced peak emerging at 1560 cm⁻¹.^58,76 Under these conditions, only minor amounts of b-HCO₃⁻ are formed as disclosed by the corresponding bands which are only weakly pronounced. (Bands associated with monodentate carbonates (1506 cm⁻¹) are present as well, but exhibit only minor intensities^56,58,73,76). Moreover, the spectra document the formation of CO on Ru. Upon purging with He (step 2, green traces), the coverage of the surface with bidentate carbonates remains fairly stable as deduced from the almost unchanged intensities of the IR signals, whereas the b-HCO₃⁻ species seem to fully desorb until the end of the purging step. However, after exposing the sample to H₂ (step 3, blue traces), the immediate reappearance of a much stronger b-HCO₃⁻ signal and the concurrent disappearance of the band associated with b-CO₃²⁻ indicate the direct conversion of the latter to the former species. As in case of the REO supports, a facile supply of the required hydrogen by spill-over from the Ru deposits is expected here as well. (Note that the negative peaks between 1900 and 2100 cm⁻¹ hint to the presence of minor amounts of adsorbed CO on Ru prior to the background collection, probably originating from the colloidal synthesis as residues⁷⁷). Upon subsequent exposure to the reaction gases (step 4: yellow trace), the bands of gaseous CH₄ reappear. In addition, the characteristic signal of formates (HCOO⁻) at 1360 cm⁻¹ emerges.

Fig. 9 Isothermal DRIFTS experiments carried out for Ru–ZrO₂ at 350 °C under different gas atmospheres. Red spectra: exposure to 5 vol% CO₂ in He for 15 min; green spectra: pure He for 20 min; blue spectra: subsequent exposure to 20 vol% H₂ in He; yellow trace: exposure to 5 vol% CO₂ and 20 vol% H₂ in He, V̇_tot = 100 mL min⁻¹. Temporal evolution of the spectra from lighter to darker colors (bottom to top).

Although TiO₂ is also capable of forming oxygen vacancies, this catalyst showed a distinctly different behavior than Ru–ZrO₂, indicating a different mechanistic scenario. The temperature-dependent DRIFT spectra acquired in this case (Fig. 10) exhibit only a few and very weakly pronounced features. A small but detectable band assignable to bridge bonded CO (1995 cm⁻¹) evidences that dissociative CO₂ on Ru occurs already at 100 °C. In analogy to ZrO₂, also a Ru⁺–CO species (due to partially oxidized Ru) is present on the surface, as can be concluded from the weak band at 2083 cm⁻¹.⁷⁵ Yet, no bands corresponding to carbonates on the titania surface are observed in the spectra, also ruling out any accumulation of such species on the catalyst surface with increasing temperature. Instead, the features of CO adsorbed on Ru completely disappear at around 230 °C, while bands of gaseous CH₄ already appear at 160 °C.

Fig. 10 Temperature-dependent DRIFT spectra for Ru–TiO₂; conditions: 5 vol% CO₂, 20 vol% H₂ in He, V̇_tot = 100 mL min⁻¹.

As in the case of the other catalysts, we additionally carried out isothermal experiments with a stepwise admission of the reactants (Fig. 11). On contrary to the other catalysts, these were conducted in a different way in an attempt to detect involved carbonates exhibiting such a low stability that they readily desorb during the purging step (step 2 in the other cases) but are detectable in the presence of hydrogen in form of more stable hydrogenation intermediates. Upon saturating the sample in a first step with CO₂ at 350 °C (in analogy to step 1 of the other experiments), the two already known peaks assignable to bridge bonded CO on Ru and CO on Ru⁺ evolve. As a new but only weakly pronounced feature, a peak at 1060 cm⁻¹ appears in the spectrum, revealing the formation of m-CO₃²⁻ in small amounts under these conditions. Upon additional admission of H₂ (step 4 otherwise), immediate and continuous formation of gaseous CH₄ is observed. Furthermore, a peak triplet at 2951, 2908 and 2864 cm⁻¹ points to the presence of CH_x species on the surface, not detected for the other catalysts. At the same time, the peaks of CO adsorbed on Ru disappear in spite of the constant CO₂ supply, indicating its rapid conversion on the metal surface. On the contrary, m-CO₃²⁻ apparently accumulates on the surface, as judged from the increasing intensities of the associated peaks (1060 and 1506 cm⁻¹) so that a role as spectator is probable.¹³

Fig. 11 Isothermal DRIFTS study for Ru–TiO₂ at 350 °C, red spectrum: after exposing the catalyst to 5 vol% CO₂ in He for 15 min; yellow spectra: subsequent exposure to 5 vol% CO₂, 20 vol% H₂ and 75 vol% He, V̇_tot = 100 mL min⁻¹. Temporal evolution of the spectra from lighter to darker colors (bottom to top).

In essence, the DRIFTS results for Ru–TiO₂ render the availability of a support-related hydrogenation pathway in analogy to ZrO₂ very unlikely. Rather, the data suggest that the reaction proceeds on the Ru particles alone – a finding that is in accord with other studies in the literature reporting that CO on Ru is the dominating reaction intermediate on this type of catalyst.⁷⁸ Since TiO₂ outperforms all other supports below 310 °C and even above yields similar CH₄ formation rates than ZrO₂, the question regarding the origin of the high activity arises. The appearance and fast conversion of CO on Ru already at low temperatures suggests that the hydrogenation reaction on the metal deposits runs more efficiently on this support than on others. As explained in the introduction and also proposed for the REOs, such an acceleration can result from an indirect support effect according to option (3) in Fig. 1. Apparently, the shift of electron density from the metal deposits to the oxide, being responsible for this beneficial interaction, is particularly pronounced for the Ru–TiO₂ system. The resulting decrease of electron density reduces the degree of electron back-donation from Ru to the antibonding π-orbital of CO and, as a result, the metal–carbon bond is weakened.^15,37,79 In this way, the coverage of the Ru nanoparticles with CO is lowered and, hence, a more favourable ratio of H/CO achieved on their surface.^15,35,79 Supposedly, for ZrO₂ such an electronic influence of the support also plays a role which, however, seems to be less pronounced.

To verify the presence of oxygen vacancies for TiO₂ under reaction conditions, we carried out in situ Raman measurements between 200–400 °C in a H₂ atmosphere, mimicking the reducing gas atmosphere of the methanation reaction (a detailed description of the experiments and the recorded spectra can be found in the ESI† (Fig. S15)). A characteristic temperature-dependent blue shift observed in the spectra indeed reveals that oxygen vacancies are increasingly formed in the temperature range of the catalytic conversion (Fig. S16†), in agreement with literature.⁸⁰

The results of the isothermal and temperature-dependent DRIFTS experiments for Ru–Al₂O₃ and Ru–MgO generally match the expectations and are in line with their lower catalytic activity. In contrast to MgO, in case of the Al₂O₃ support, HCO₃⁻ species are observed on the surface, indicating CO₂ adsorption on Brønsted basic OH groups (Fig. S11 and S12†). This finding confirms a partially hydroxylated surface under reaction conditions (see section 3.2). Formate species, also detected in the spectra with increasing temperature, fit to a support-related pathway according to support effect (1) as possible reaction intermediates. As in all other cases, conversion along the Ru-based pathway is evidenced by the bands of linearly and bridge bonded CO on Ru, which appear in the spectra above 140 °C. The additional contribution of the support suffices to achieve a better catalytic performance as compared to MgO and SiO₂. But overall only an intermediate position in the ranking of the catalysts is reached. For Ru–MgO (Fig. S13†), the DRIFT spectra indicate the formation of monodentate carbonates under reaction conditions, in agreement with the results of the surface characterization (section 3.2). Nevertheless, a relevant catalytic involvement of these carbonates (according to pathway (1)), i.e. a catalytic impact of the Lewis basic oxygen atoms obviously present on the MgO surface, can be ruled out, as judged from the activity of this catalyst which is similarly low as in case of the non-basic SiO₂ support.

As a final remark, we would like to mention that metal–support interactions seem to play a certain role for all supports studied here. When comparing the temperatures at which Ru–CO species are first detected and the temperature-dependent development of these species for the various catalysts (see Fig. S11–S14 in the ESI†), differences in the Ru–CO binding strength become obvious. For the REOs, TiO₂ and ZrO₂, the beneficial impact of a reduced binding strength on the Ru-related pathway according to support effect (3) has already been discussed. In contrast, for Al₂O₃ and MgO a progressive accumulation of CO on the Ru deposits is observed suggesting a contrary effect.

4 Conclusion

In this study, we investigated the influence of the support basicity on the performance of supported Ru catalysts for the CO₂ methanation reaction. In particular, we aimed at understanding the role of support-related reaction pathways, contributing to the conversion, and of beneficial electronic interactions, accelerating the conversion on Ru. To this end, we chose oxides with different Lewis and/or Brønsted basic surface properties. In contrast to previously published reports, we applied a building block approach, in which colloidally prepared Ru nanoparticles exhibiting the same average size (∼1 nm) and narrow size distribution were deposited on eight support materials. In this way, we were able to exclude differences in particle size for the catalysts studied which – due to the structure-sensitivity of the reaction – would otherwise obscure the identification of clear trends regarding the influence of the support basicity on the catalytic performance.

To cover different types and combinations of surface basicity, eight oxides were chosen for the study: Sm₂O₃, Gd₂O₃ and Y₂O₃, as rare earth metal oxides (REOs), TiO₂, ZrO₂, Al₂O₃, MgO as well as SiO₂ the latter as an example of a non-basic support. Our starting hypothesis was that the following three types of basic centers can act as additional CO₂ adsorption sites and possibly lead to higher formation rates of CH₄ as compared to non-basic supports: (a) Lewis basic oxygen vacancies enabling the formation of bidentate carbonates which, in addition to a fixation, correspond to a first reduction step of CO₂, (b) Brønsted basic hydroxyl groups that can bind CO₂ in form of hydrogen carbonates, and (c) sufficiently Lewis basic lattice oxygen atoms at the surface permitting CO₂ adsorption in form of monodentate carbonates. To verify the strength and density of these sites, the surface basicity of all supports was characterized by CO₂-TPD and DRIFTS in a first step.

In case the REO supported catalysts, the data revealed the presence of Lewis basic oxygen atoms and vacancies as well as hydroxyl groups on the surface. For TiO₂ and ZrO₂ neither CO₂-TPD nor DRIFTS provided indications of surface basicity, but Raman and DRIFTS experiments, respectively, carried out under reaction conditions, evidenced a significant and sufficient concentration of oxygen vacancies at temperatures typical for the methanation reaction and in the presence of H₂. While for MgO Lewis basic oxygen atoms were shown to be exposed at the surface – probably at surface defects –, the characterization of the Al₂O₃ support revealed a low basicity at first, but a partial hydroxylation of the surface, i.e. the formation of Brønsted basic OH-groups, was implied by DRIFTS under reaction conditions. In agreement with expectations, the SiO₂ support exhibited no basic adsorption sites.

All catalysts were tested with respect to their catalytic performance towards methanation of CO₂ by measuring the CH₄ formation rate in the temperature range between 200 °C and 400 °C. As expected, the results of supplementary DRIFTS experiments carried out under reaction conditions proved that in all cases a hydrogenation pathway on Ru alone exists. As known from literature, it is based on dissociative adsorption of H₂ and CO₂ on the metal nanoparticles, leading to H_ad and CO_ad as intermediates. Dependent on the type, density and strength of basic sites available on the various supports, clear indications of additionally contributing support-related pathways and electronic effects were found which could be correlated with increased CH₄ formation rates and the ranking of the catalysts observed.

In case of the REO supports, the presence of all three kinds of basic sites seems to play an enhancing role for the catalytic conversion in the upper half of reaction temperatures studied. Upon CO₂ exposure, an abundant formation of hydrogen, mono- and bidentate carbonates was observed on their surface. Their consumption at higher temperatures and the concomitant appearance of hydrogenated species, such as formyl species, point to hydrogenation pathways taking place on the support in parallel to the Ru-based pathway. Such pathways are apparently enabled by hydrogen spill-over from the Ru deposits and provide a conclusive explanation for the superior CH₄ formation rates we observed above 310 °C. In contrast, our results for ZrO₂, as a support exhibiting no Brønsted basicity and exposing no oxygen sites with sufficient Lewis basicity at the surface, revealed that the mere presence of oxygen vacancies can be sufficient to distinctly improve the catalytic performance. The temperature-dependent evolution of bidentate carbonates, formed by adsorption of CO₂ on these sites, and the appearance of a formate species indicate a support-related hydrogenation pathway that, in particular, contributes at lower temperatures to the conversion. In agreement with that, this catalyst performed better than most of the other ones below 310 °C.

At the example of TiO₂, we were able to show that oxygen vacancies not only can boost the activity by opening additional support-related pathways but also by accelerating the catalytic turnovers on Ru. By virtue of an electronic metal–support interaction, favourably influencing the strength of the Ru–CO bond, CH₄ formation rates even higher than those achieved with ZrO₂ were observed below 310 °C for this catalyst, although no evidence for the formation or participation of carbonates in the reaction was found. Yet not clearly delimitable from the direct support contributions, a beneficial electronic influence is likely for the REO supports and ZrO₂ as well.

In essence, the availability of additional support-related reaction pathways and favourable metal–support interactions in case of basic supports can obviously entail higher catalytic turnovers in the CO₂ methanation reaction. On these grounds, TiO₂ and ZrO₂ as well as the REOs yielded the best catalytic results, with the former being the better choice below 310 °C and the latter above 310 °C. On contrary, the Al₂O₃, MgO and SiO₂ supported catalysts showed distinctly lower CH₄ formation rates in the whole investigated temperature range. In this group, Al₂O₃ proved to be the best support and its intermediate position between the leading supports and SiO₂ and MgO (both behaving rather similarly) is probably caused by the formation of surface hydroxyl groups under reaction conditions where H₂O is formed as side product.

Summing up, our study reveals that CO₂ methanation catalysts can be optimized, when supports exhibiting a medium surface basicity are chosen. Lewis basic oxygen vacancies characteristic for reducible oxides as well as Brønsted basic hydroxyl groups turned out to be most influential. It has to be considered though that their surface density can change as a function of temperature and reaction conditions. Other Lewis basic sites, such as under-coordinated surface oxygen atoms, seem to play a minor or spectator role in most cases. Among the support materials studied, in particular, the REO supports, yet still less commonly employed, appear most promising for technical applications, where an optimization of CH₄ yields is sought. At high temperatures, where the thermodynamics of the exergonic reaction do not yet set boundaries, they allow a significant enhancement of the CH₄ formation rates.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JI and MB gratefully acknowledge funding through the DFG research training group 1860 MIMENIMA. The authors thank Petra Martinovic and Hesamodin Hosseini Ghahi for assistance with the experimental work.

References

1. A. Palzer and H.-M. Henning, Energy Technol., 2014, 2, 13–28.
2. A. Palzer and H.-M. Henning, Renewable Sustainable Energy Rev., 2014, 30, 1019–1034.
3. J. Gao, Y. Wang, Y. Ping, D. Hu, G. Xu, F. Gu and F. Su, RSC Adv., 2012, 2, 2358–2368.
4. S. Rönsch, J. Schneider, S. Matthischke, M. Schlüter, M. Götz, J. Lefebvre, P. Prabhakaran and S. Bajohr, Fuel, 2016, 166, 276–296.
5. G. A. Mills and F. W. Steffgen, Catal. Rev.: Sci. Eng., 1974, 8, 159–210.
6. P. Panagiotopoulou, D. I. Kondarides and X. E. Verykios, Appl. Catal., B, 2009, 88, 470–478.
7. X. Wang, Y. Hong, H. Shi and J. Szanyi, J. Catal., 2016, 343, 185–195.
8. J. H. Kwak, L. Kovarik and J. Szanyi, ACS Catal., 2013, 3, 2449–2455.
9. K. Ghaib and F.-Z. Ben-Fares, Renewable Sustainable Energy Rev., 2018, 81, 433–446.
10. J. Gao, Q. Liu, F. Gu, B. Liu, Z. Zhong and F. Su, RSC Adv., 2015, 5, 22759–22776.
11. S. Tada and R. Kikuchi, Catal. Sci. Technol., 2015, 5, 3061–3070.
12. H. Muroyama, Y. Tsuda, T. Asakoshi, H. Masitah, T. Okanishi, T. Matsui and K. Eguchi, J. Catal., 2016, 343, 178–184.
13. S. Eckle, H.-G. Anfang and R. J. Behm, J. Phys. Chem. C, 2011, 115, 1361–1367.
14. L. F. Liotta, G. A. Martin and G. Deganello, J. Catal., 1996, 164, 322–333.
15. J. A. H. Dreyer, P. Li, L. Zhang, G. K. Beh, R. Zhang, P. H. L. Sit and W. Y. Teoh, Appl. Catal., B, 2017, 219, 715–726.
16. P. A. U. Aldana, F. Ocampo, K. Kobl, B. Louis, F. Thibault-Starzyk, M. Daturi, P. Bazin, S. Thomas and A. C. Roger, Catal. Today, 2013, 215, 201–207.
17. J. J. Benitez, I. Carrizosa and J. A. Odriozola, Appl. Surf. Sci., 1993, 68, 565–573.
18. H. Muroyama, Y. Tsuda, T. Asakoshi, H. Masitah, T. Okanishi, T. Matsui and K. Eguchi, J. Catal., 2016, 343, 178–184.
19. L. Atzori, M. G. Cutrufello, D. Meloni, R. Monaci, C. Cannas, D. Gazzoli, M. F. Sini, P. Deiana and E. Rombi, Int. J. Hydrogen Energy, 2017, 42, 20689–20702.
20. S. Sharma, Z. Hu, P. Zhang, E. W. Mcfarland and H. Metiu, J. Catal., 2011, 278, 297–309.
21. S. Tada, T. Shimizu, H. Kameyama, T. Haneda and R. Kikuchi, Int. J. Hydrogen Energy, 2012, 37, 5527–5531.
22. Q. Pan, J. Peng, T. Sun, S. Wang and S. Wang, Catal. Commun., 2014, 45, 74–78.
23. C. Barzan, E. Groppo, S. Bordiga and A. Zecchina, ACS Catal., 2014, 4, 986–989.
24. L. Liu, Y. Jiang, H. Zhao, J. Chen, J. Cheng, K. Yang and Y. Li, ACS Catal., 2016, 6, 1097–1108.
25. C. Deleitenburg and A. Trovarelli, J. Catal., 1995, 156, 171–174.
26. A. Trovarelli, C. Deleitenburg, G. Dolcetti and J. L. Lorca, J. Catal., 1995, 151, 111–124.
27. S. Huygh, A. Bogaerts and E. C. Neyts, J. Phys. Chem. C, 2016, 120, 21659–21669.
28. H. Metiu, S. Chrétien, Z. Hu, B. Li and X. Sun, J. Phys. Chem. C, 2012, 116, 10439–10450.
29. R. Zhou, N. Rui, Z. Fan and C. J. Liu, Int. J. Hydrogen Energy, 2016, 41, 22017–22025.
30. W. Li, X. Nie, X. Jiang, A. Zhang, F. Ding, M. Liu, Z. Liu, X. Guo and C. Song, Appl. Catal., B, 2018, 220, 397–408.
31. M. Kogler, E. M. Köck, T. Bielz, K. Pfaller, B. Klötzer, D. Schmidmair, L. Perfler and S. Penner, J. Phys. Chem. C, 2014, 118, 8435–8444.
32. E. I. Kauppi, K. Honkala, A. O. I. Krause, J. M. Kanervo and L. Lefferts, Top. Catal., 2016, 59, 823–832.
33. V. M. Ganduglia-Pirovano, A. Hofmann and J. Sauer, Surf. Sci. Rep., 2007, 62, 219–270.
34. G. Pacchioni, ChemPhysChem, 2003, 4, 1041–1047.
35. S. Scirè, C. Crisafulli, R. Maggiore, S. Minicò and S. Galvagno, Catal. Lett., 1998, 51, 41–45.
36. S. Chen, A. M. Abdel-Mageed, C. Gauckler, S. E. Olesen, I. Chorkendorff and R. J. Behm, J. Catal., 2019, 373, 103–115.
37. S. Tada, T. Shimizu, H. Kameyama, T. Haneda and R. Kikuchi, Int. J. Hydrogen Energy, 2012, 37, 5527–5531.
38. S. Sato, R. Takahashi, M. Kobune and H. Gotoh, Appl. Catal., A, 2009, 356, 57–63.
39. G. Pacchioni, Numerical Simulations of Defective Structures: The Nature of Oxygen Vacancy in Non-reducible (MgO, SiO2, ZrO2) and Reducible (TiO2, NiO, WO3) Oxides, in Defects at Oxide Surfaces, ed. J. Jupille and G. Thornton, Springer International Publishing, Switzerland, 2015, ch. 1, pp. 1–29.
40. J. Ilsemann, A. Sonström, T. M. Gesing, R. Anwander and M. Bäumer, ChemCatChem, 2019, 11, 1732–1741.
41. Y. Wang, J. Ren, K. Deng, L. Gui and Y. Tang, Chem. Mater., 2000, 12, 1622–1627.
42. M. Taddia and P. Sternini, Ann. Chim., 2001, 91, 239–244.
43. T. Suoranta, M. Niemelä and P. Perämäki, Talanta, 2014, 119, 425–429.
44. M. A. Worsley, J. Ilsemann, T. M. Gesing, V. Zielasek, A. J. Nelson, R. A. S. Ferreira, L. D. Carlos, A. E. Gash and M. Bäumer, J. Sol-Gel Sci. Technol., 2019, 89, 176–188.
45. S. Sato, R. Takahashi, M. Kobune and H. Gotoh, Appl. Catal., A, 2009, 356, 57–63.
46. M. Daturi, C. Binet, J. C. Lavalley and G. Blanchard, Surf. Interface Anal., 2000, 30, 273–277.
47. M. Guo, J. Lu, Y. Wu, Y. Wang and M. Luo, Langmuir, 2011, 27, 3872–3877.
48. J. Liu, C. Liu, G. Zhou, S. Shen and L. Rong, Green Chem., 2012, 14, 2499–2505.
49. K. Sato, K. Imamura, Y. Kawano, S. I. Miyahara, T. Yamamoto, S. Matsumura and K. Nagaoka, Chem. Sci., 2016, 8, 674–679.
50. G. A. Mutch, S. Morandi, R. Walker, J. A. Anderson, D. Vega-Maza, L. Operti and G. Cerrato, J. Phys. Chem. C, 2016, 120, 17570–17578.
51. G. Busca and V. Lorenzelli, Mater. Chem., 1982, 7, 89–126.
52. M. L. Bailly, C. Chizallet, G. Costentin, J. M. Krafft, H. Lauron-Pernot and M. Che, J. Catal., 2005, 235, 413–422.
53. D. Cornu, H. Guesmi, J. M. Krafft and H. Lauron-Pernot, J. Phys. Chem. C, 2012, 116, 6645–6654.
54. M. Compagnoni, A. Villa, E. Bahdori, D. J. Morgan, L. Prati, N. Dimitratos, I. Rossetti and G. Ramis, Catalysts, 2018, 8, 623.
55. L. F. Liao, C. F. Lien, D. L. Shieh, M. T. Chen and J. L. Lin, J. Phys. Chem. B, 2002, 106, 11240–11245.
56. S. Kouva, J. Andersin, K. Honkala, J. Lehtonen, L. Lefferts and J. Kanervo, Phys. Chem. Chem. Phys., 2014, 16, 20650–20664.
57. K. Pokrovski, K. T. Jung and A. T. Bell, Langmuir, 2001, 17, 4297–4303.
58. T. Akune, Y. Morita, S. Shirakawa, K. Katagiri and K. Inumaru, Langmuir, 2018, 34, 23–29.
59. K. T. Jung and A. T. Bell, J. Catal., 2001, 204, 339–347.
60. E. Farfan-Arribas and R. J. Madix, J. Phys. Chem. B, 2003, 107, 3225–3233.
61. A. Ueno and C. O. Bennett, J. Catal., 1978, 54, 31–41.
62. F. Wang, S. He, H. Chen, B. Wang, L. Zheng, M. Wei, D. G. Evans and X. Duan, J. Am. Chem. Soc., 2016, 138, 6298–6305.
63. X. Wang, H. Shi, J. H. Kwak and J. Szanyi, ACS Catal., 2015, 5, 6337–6349.
64. T. Baidya and P. Bera, Catal., Struct. React., 2015, 1, 110–119.
65. W. J. Mitchell, Y. Wang, J. Xie and W. H. Weinberg, J. Am. Chem. Soc., 1993, 115, 4381–4382.
66. J. Wambach, J. Zarfl, A. Wokaun, T. J. Schildhauer and D. Ferri, Appl. Catal., A, 2015, 495, 104–114.
67. J. Guo, Z. Hou, J. Gao and X. Zheng, Chin. J. Catal., 2007, 28, 22–26.
68. W. Karim, C. Spreafico, A. Kleibert, J. Gobrecht, J. VandeVondele, Y. Ekinci and J. A. van Bokhoven, Nature, 2017, 541, 68–71.
69. R. Prins, Chem. Rev., 2012, 112, 2714–2738.
70. R. Prins, V. K. Palfi and M. Reiher, J. Phys. Chem. C, 2012, 116, 14274–14283.
71. P. G. Savva and A. M. Efstathiou, J. Catal., 2008, 257, 324–333.
72. S. Kattel, B. Yan, J. G. Chen and P. Liu, J. Catal., 2016, 343, 115–126.
73. W. Hertl, Langmuir, 1989, 5, 96–100.
74. M. Y. He and J. G. Ekerdt, J. Catal., 1984, 87, 381–388.
75. P. Panagiotopoulou, D. I. Kondarides and X. E. Verykios, J. Phys. Chem. C, 2011, 115, 1220–1230.
76. K. Pokrovski, K. T. Jung and A. T. Bell, Langmuir, 2001, 17, 4297–4303.
77. S. Neumann, S. Grotheer, J. Tielke, I. Schrader, J. Quinson, A. Zana, M. Oezaslan, M. Arenz and S. Kunz, J. Mater. Chem. A, 2017, 5, 6140–6145.
78. M. Marwood, R. Doepper and A. Renken, Appl. Catal., A, 1997, 151, 223–246.
79. C. Xiao, M. Liang, A. Gao, J. Xie, Y. Wang and H. Liu, J. Nanopart. Res., 2013, 15, 1822.
80. J. C. Parker and R. W. Siegel, Appl. Phys. Lett., 1990, 57, 943–945.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cy00399b

---