Early-stage formation of (hydr)oxo bridges in transition-metal catalysts for photosynthetic processes

Abstract

Water-oxidizing metal–(hydr)oxo catalyst films can be generally deposited and activated by applying a positive electrochemical potential to suitable starting aqueous solutions. Here, we used ab initio simulations based on density functional theory to investigate the initial formation process of hydroxo and oxo bridges between divalent transition metals [namely Co(II), Mn(II), and Ni(II)] in aqueous solution, leading to the growth of extended structures. Our simplified yet realistic model, rooted in the computational hydrogen electrode approximation, has been able to provide estimates in agreement with experimental measurements of the positive potential U required for deposition of the active amorphous metal–(hydr)oxo catalyst, taking into account variations in the solution composition. Our results reveal that: (i) Co, Mn, and Ni exposed to a positive potential form dinuclear building blocks through different reaction pathways, indicating structural features consistent with those previously reported for extended systems; (ii) key steps in the formation of stable hydroxo and oxo bonds are preceded by structural rearrangements of M(II)[H₂O]₆ complexes, which are stabilized by H-bond formation among the hydration shells upon the approach of two units. This arrangement yields suitable dinuclear precursors with one or two water molecules holding a bridging position between metals; (iii) anionic phosphate (for Co) and acetate (for Mn) ligands favor the formation of stable dinuclear structures, lowering the electrochemical potentials required to oxidize metals; (iv) in the case of manganese, acetate facilitates the formation of a Mn–(hydr)oxo dinuclear complex by lowering the required applied potential; this behavior parallels the initial stage in the formation of the Mn₄Ca cluster, the active site of the photosynthetic water-oxidizing catalyst in living organisms.

---

Introduction

In the long-lasting quest for the sustainable, direct conversion of solar energy into chemical fuels, a primary objective on the road toward a zero carbon footprint economy, first-row transition metals have always played two important roles. Nature converts solar energy by means of oxygenic photosynthesis. In the key step of this process, a small tetranuclear manganese–(hydr)oxo complex, contained in the photosystem II (PSII) protein complexes, oxidizes water molecules to molecular oxygen and protons.^1–3 This ability has motivated studies into the mechanisms of natural photosynthesis and the design of bio-inspired functional materials to mimic natural processes. The development of (photo)electrochemical devices assembled with man-made materials that have photosynthetic functions (e.g., artificial leaves) is considered as a major technological target for the 21st century. Such materials should be efficient, robust, inexpensive, and suitable for large scale production.^4–7 In this regard, amorphous transition-metal (hydr)oxides are considered to be promising catalyst materials for one of the most important steps in the synthesis of chemical fuels, namely the four-proton, four-electron reaction to release oxygen molecules from water. In particular, Mn-, Fe-, Co-, and Ni-based amorphous materials have received considerable attention since the first successful attempt to synthesize an efficient Co-based catalyst (CoCat) in 2008.^8–15 After more than ten years of intense research and development, promising results have been achieved, particularly by adding small or moderate quantities of iron to amorphous nickel or cobalt (hydr)oxo catalysts, namely Fe:NiCat and Fe:CoCat.^16–19 However, a striking lack of consensus must be registered when the investigation of such materials is focused at the atomic level or considers local structures. Reaction mechanisms are generally inferred by X-ray absorption spectroscopy and cyclic voltammetry measurements. However, some discrepancies exist between experimental results and their potential interpretations. Different techniques used to obtain active catalyst films give compounds nominally having the same stoichiometry and a similar structure but with very different local and atomic structures and distributions of active catalytic sites.^20–24

Notably, such catalytic films are generally formed from M(II) cations dissolved in a buffered water solution and exposed to a positive electrode potential. This situation is also true for the active site of PSII, if a more extensive definition of “positive electrode potential” is considered.^25–27 Hence, there is a need for an overview of the reaction mechanisms leading to the formation of oxo or hydroxo bridges between metal cations under such conditions. Such considerations should include different starting transition metals to shed light on the formation processes of the amorphous catalytic films and highlight basic differences among chemical species. To this end, we have developed a rigorous method based on ab initio calculations of free energies and electrode potentials, as detailed below. This approach has been tested on the early-stage formation of M–O(H)–M or M–[O(H)]₂–M bridges (M = Co, Ni, Mn) and on the role of buffer ions acting as ligands. Buffers are particularly relevant to the case of Mn because the participation of –COO⁻ terminal groups of protein residues stabilizes the Mn–(hydr)oxo active site of PSII. Our results highlight fundamental differences in the formation of metal–oxo connections. Co-based structures are oriented to the formation of hydroxo bridges, whereas Mn-based structures are oriented to the formation of mixed oxo/hydroxo bridges in neutral solution. Ni-Based structures require a basic starting solution for oxidation of Ni(II) to Ni(III) and the formation of the first bridge.

Theoretical and computational details

The formation of (hydr)oxo bridges between metal atoms has been investigated by a simple yet realistic computational protocol based on density functional theory (DFT) calculations performed using the ORCA program package version 4.2.^28,29 Geometry optimizations of metal atoms surrounded by a first coordination sphere of water molecules have been performed at the B3LYP level of theory^30,31 with the use of Grimme's atom-pairwise dispersion correction with Becke–Johnson damping (D3BJ).^32,33 The ZORA-recontracted def2-TZVPP Gaussian-type basis sets with the auxiliary SARC/J Coulomb fitting basis sets for resolution-of-identity/chain-of-spheres (RIJCOSX) technique³⁴ have been used for all atoms. The conductor-like polarizable continuum model (CPCM)³⁵ with the default parameters of water has been applied for all geometry optimization processes to enclose all systems in a suitable bulk solution environment. All calculations have been performed by maintaining the systems in their high-spin configuration and all oxidation states of relevant species have been checked with the use of Lowdin and Mulliken spin-polarizations as evaluation parameters. Zero-point energy calculations have been performed in the same framework after additional geometry optimization using Stuttgart/Dresden (SDD) effective core potentials (ECPs) instead of the all-electron ZORA method.

Free energies of the investigated species in aqueous solution have been estimated by the following equation:

G_aq = E^B3LYP_el + E^D3BJ_disp + (G⁰ − E_el)^B3LYP + ΔG^CPCM_hydr (1)

where E^B3LYP_el is the single-point B3LYP/def2-TZVPP electronic energy, E^D3BJ_disp is the D3BJ dispersion correction, and ΔG^CPCM_hydr is the free energy change due to hydration from the CPCM after correction for the solute charge density lying outside the cavity. The factor (G₀ − E_el)^B3LYP represents the thermochemical corrections at 1 atm and 298.15 K. The external potential, U, and ΔG values calculated for electrochemical processes in aqueous solution are connected with the use of the computational hydrogen electrode (CHE) equation, as discussed in more detail elsewhere.^36–41 In detail, the semireaction (HA → A + H⁺ + e⁻) indicating subtraction of one proton and one electron from the species HA is coupled with the standard hydrogen electrode (SHE) semireaction , yielding the equation:where G[A] and G[HA] are the free energies of the neutral species A and HA, calculated as specified by eqn (1), G⁰[H_2(g)] is the free energy of H₂ gas at 1 atm and 298.15 K, q is the electron charge, and k_B and T are the Boltzmann constant and the temperature, respectively. k_BT ln10 × pH = −0.059 pH is the free energy correction for the concentration of H⁺ ions.³⁹ If we apply an arbitrary value for the electrochemical potential U, then we can calculate thermodynamic profiles for a given multistep reaction. Conversely, if we impose an equilibrium condition (ΔG = 0), then U is the electrochemical potential calculated for the half-reaction (i.e., HA → A + H⁺ + e⁻), which allows theoretical estimation of its effective potential. Finally, all the results are conventionally referenced to the SHE at pH = 0, to provide a direct comparison between the different metals. We prefer this approach, irrespective of the fact that amorphous (hydr)oxo catalysts for oxygen evolution are generally synthesized from different starting solutions. Electrodeposition of MnCat and CoCat was performed at pH 6 in acetate buffer in the case of Mn,¹⁰ and at pH 7 in phosphate buffer in the case of Co.⁴² In particular, as a notable system, (Fe-doped) Ni was deposited at pH 9 in borate buffer, to prevent precipitation of Ni(OH)₂, and then activated by oxidation at pH 13.^22,23

Minimum energy path (MEP) analyses have been performed with the use of the nudged elastic band with climbing-image (NEB-CI) algorithm^43,44 at the same calculation level as the geometry optimizations. The MEP calculations have been performed with 10 replicas, fixing the coordination of the optimized geometries of reactants and products.

Results and discussion

Bridge formation and U calculation

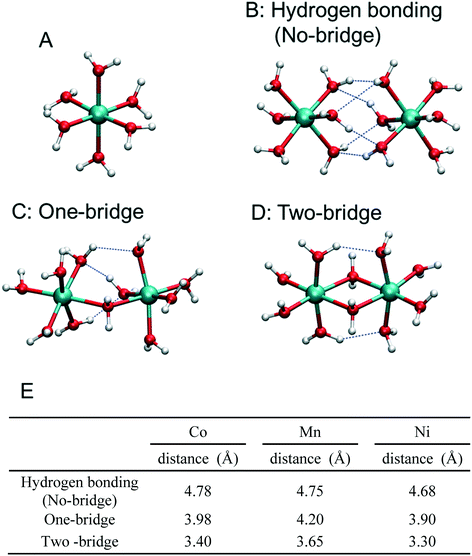
Divalent metal ions, especially Co, Mn, and Ni ions, are expected to be found as hexa-aqua complexes in aqueous solution.⁴⁵ Thus, we have prepared models of isolated or paired hydrated metals by geometry optimization, changing the protonation, and oxidation states and the number of –OH₂–, –OH– and –O– species holding a bridging position between metals. In comparing the properties of different metals, we define the S₀ state as the ground state of the hydrated, divalent metal before deprotonation and oxidation [i.e., Co(II) with six water molecules] and S_n as a state deprotonated and oxidized n times from the S₀ state. Different final high-valence states have been chosen for the three metal pairs, in agreement with X-ray absorption near-edge structure (XANES) measurements collected on amorphous structures, to avoid the simulation of unphysical regimes of applied potential where the OER rather than catalyst growth would occur. Maximum S_n with an average metal oxidation state of 3.0 in the case of Co and Ni and of 4.0 in the case of Mn have been considered.^10,46–48

Fig. 1 shows the stable structures of the hydrated Co models in the S₀ state with one (panel A) and two interacting Co(II) ions. In the latter case, three different structures with no, a single, and two water molecules in the bridging position between the cations have been considered, as shown in panels B, C, and D, respectively. Hereinafter, we call these kinds of links between metal ions as no-bridge, one-bridge and two-bridge structures, irrespective of the actual occurrence of –O–, –OH– or –OH₂– species as linking agents. We stress again that all models shown in Fig. 1 represent part of the investigated systems, actually treated at the DFT level of theory, surrounded by an implicit aqueous environment. In the S₀ state, as the number of water molecules holding the bridging position between the two-metal ions increases, the Co–Co distances is shortened from 4.78 Å in the no-bridge model to 3.40 Å in the two-bridge model, accompanied by a decrease in the number of H-bonds among water molecules. The Mn and Ni systems are also characterized by structures and relative energies similar to those of Co (Mn–Mn distances: 4.75 → 3.65 Å; and Ni–Ni distances: 4.68 → 3.30 Å upon the formation of two-bridge structures as shown in Fig. 1E).

Fig. 1 Optimized structures of hydrated Co ions in aqueous solution: (A) single metal form; (B) hydrogen bonding form; (C) one- and (D) two-bridge forms (red: oxygen, white: hydrogen, and cyan: Co atoms). (E) Metal–metal distances (Å) in the optimized structures for the two-Co, -Mn, and -Ni systems.

Table 1A shows the relative free energies for different configurations of S₀ alongside with the electrochemical potential U for both cases of isolated hydrated metals and hydrated two-metal systems, shown in Table 1B. As for the ground state, the no-bridge structure (Fig. 1) is the most stable in the S₀ state of the two-Co system. The other metals, Mn and Ni, also behave similarly to Co, with the no-bridge configurations as the lowest relative energy ones. Notably, in the case of Co(II), the no-bridge structure is also the most stable configuration with respect to separation of metal ions up to a distance of 8 Å. This suggests that, in the formation of weakly interacting Co(II)[H₂O]₆ pairs, first shell water molecules efficiently screen the repulsion between metal cations and allow for metal–metal approaching through the formation of strong H-bonds among water molecules.

Table 1 (A) Relative free energies (eV) for each oxidation state of bridged structures in two-Co, -Mn, and -Ni systems, and (B) calculated effective potentials for each oxidation step [U(S_i+1−S_i) (V)] at pH 0 for the isolated and two-metal systems of Co, Mn, and Ni

(A)
Oxidation state	Relative free energy G (eV)
	Co			Mn			Ni			Ni (less one H^+)
	No-bridge	One-bridge	Two-bridge	No-bridge	One-bridge	Two-bridge	No-bridge	One-bridge	Two-bridge	No-bridge	One-bridge	Two-bridge
S0	0.00	0.09	0.01	0.00	0.00	0.13	0.00	0.15	0.24	0.13	0.00	0.01
S1	0.34	0.00	0.48	0.20	0.00	0.03	0.06	0.00	0.10	0.25	0.18	0.00
S2	0.38	0.39	0.00	0.18	0.00	0.17	0.00	0.27	0.36	0.43	0.25	0.00
S3				0.14	0.01	0.00	0.00	0.08	0.15	0.53	0.35	0.00
S4				0.11	0.07	0.00	0.00	0.35	0.40

---

(B)
	Effective potential U (V)
	Co		Mn		Ni
Transition	Isolated	Two-metal	Isolated	Two-metal	Isolated	Two-metal	Isolated (less one H+)	Two-metal (less one H^+)
S0 → S1	2.02	1.70	1.47	1.16	2.56	2.59	1.80	2.04
S1 → S2	2.04	1.80	2.20	1.21	2.21	2.18		2.14
S2 → S3				1.87		2.74		2.41
S3 → S4				1.97		2.23

---

The U value represents the potential required to promote an S_n → S_n+1 transition when the corresponding semireaction HA → A + H⁺ + e⁻ is in equilibrium with the standard hydrogen electrode. In the case of isolated metals, our results for the Co(III) + e⁻ → Co(II) semireaction (+2.02 V) and for the Mn(III) + e⁻ → Mn(II) semireaction (+1.47 V) compare well with electrochemical measurements (+1.92 and +1.56 V, respectively).⁴⁹ Regarding Ni, no measurements can be performed in water in the case of Ni(III) + e⁻ → Ni(II). Our estimate of 2.56 V is in agreement with previous theoretical estimates (2.2–2.3 V)^49,50 and should be considered as the upper limit of transitions involving solid-state frameworks or organic ligands, falling between 1.0 and 1.7 V.⁵¹ Even in the case of hydrated metal pairs, the calculated U values for S₀ → S₁ transitions are 1.70, 1.16, and 2.59 V for the Co, Mn, and Ni systems, respectively. These values are comparable with the external potentials applied during electrodeposition of catalyst films.

A comparison between the free energies reported in Table 1 and the corresponding three two-metal configurations illustrated in Fig. 1B–D individuates the individual bridge formation pathways between metal pairs through lowest-energy intermediates. We note that in all the systems but Ni, at least one S₀ → S₁ transition occurred at a lower potential than the M(II) → M(III) transition for an isolated hydrated metal ion. In the case of Co and Mn, this result confirms that there is a pathway leading to the growth of catalytic films, which involves competitive reactions and direct oxidation of metals in water solution. However, considerable differences emerge from analyses of specific cases. In the case of Ni, the achieved result is compatible with non-redox formation of the catalyst film, followed by redox activation, as detailed below.

Cobalt

As discussed above, the no-bridge configuration is the most stable in the S₀ state, followed by the slightly less stable two-bridge (+0.01 eV) and one-bridge (+0.09 eV) configurations. In both cases, the formation of bridged configurations requires the climbing of a relatively low energy step when compared with the oxidized S₁ state, where the hydrated Co–Co complex strongly prefers (by 0.34 eV) the one-bridge structure with a single hydroxo bridge between the two Co upon the first Co oxidation. These energetic features suggest that a high energy barrier does not separate the no-bridge and one-bridge configurations in the S₀ state, which is consistent with the actual case, as detailed below. This transition of the equilibrium state between the no-bridge and one-bridge conformations promotes the formation of the most stable Co(II)–OH–Co(III) system upon the first Co oxidation. For example, at pH = 7, the same S₁ state can be formed by applying an external potential U = 1.29 V (Table S1†), compatible with the formation of CoCat in neutral solution and with an applied external potential of 1.4 V.⁴⁷ Similarly, for the S₁ → S₂ transition, the oxidation of the second Co(II) to Co(III) promotes the formation of a two-bridge Co(III)–(OH)₂–Co(III) system that is largely favored with respect to the oxidation of no-bridge or one-bridge systems. Such a two-ion S₂ state is consistent with the well characterized features of amorphous CoCat for oxygen evolution. As previously reported on the grounds of the fine comparison between measurements and simulations,^47,52 this system is actually characterized by a Co(III) resting state and by a stable protonation of all two-fold-coordinated oxo bridges.

Manganese

There is practically no energy difference between the no-bridge and one-bridge S₀ configurations for manganese. Hence, the formation of the first Mn(II)–OH–Mn(III) bridge, S₁, is therefore favored by the lowest U value of 1.16 V. As opposed to Co, the formation of a one-bridge Mn(III)–O–Mn(III) bridge in the S₂ state is favored with respect to the formation of a two-bridge (OH)₂ link. This result is particularly interesting because it reflects a tendency for the formation of unprotonated oxo bridges in low valence Mn compounds. The activation of a second hydroxo bridge is favored in the case of further oxidation of manganese to Mn(IV)–O (OH)–Mn(III) S₃. This behavior is compatible with the tendency of manganese to form amorphous structures in active catalyst films with Mn oxidation states ranging between Mn(III) and Mn(IV).^10,53 Our results also suggest that a steady oxidation of Mn (II) solutions can induce the formation of a Mn(IV)–(O)₂–Mn(IV) S₄ state, compatible with the formation of relatively inactive Mn(IV)-oxo catalyst films.^10,53

Nickel

In the case of Ni, our results suggest different behaviors that reflect the formation of extended NiCat films. In the S₀ state, one-bridge and two-bridge configurations are much less stable than the no-bridge configuration (+0.15 eV and +0.24 eV, respectively). Unlike Co and Mn, there is no notable advantage in terms of potential from bridged configurations for the S₀ → S₁ transition, because the U values calculated for all the two-metal configurations were higher than those calculated for isolated hydrated Ni. This result is consistent with the fact that a Ni(II)–(hydr)oxo film can be formed by precipitation of Ni(II) from the solution, without applying an external potential.^54–56 Further activation of the catalyst film is performed at pH = 13–14 by applying an external potential of 1.5–1.6 V, yielding a wide range of Ni oxidation states between 2 and 3.6, with higher values accessible by Fe-doped NiCat.^20,22,56 Electrodeposition of NiCat from Ni(II) solutions can be carried out under basic conditions.^9,57 We have tried to reproduce this complex electrochemical landscape leading to activation of Ni(II) films by considering the high-pH conditions by introducing a single OH⁻ species in the first coordination sphere of the two-metal Ni configurations. When the role of OH⁻ species is accounted for, the bridged structures became more stable than the no-bridge structure, even for the S₀ state, and all transitions are favored up to the formation of the two-bridge Ni(III)–(O)₂–Ni(IV) S₃ state, in which oxygen competes with nickel for the subtraction of the electron, trespassing the limit where oxidizing equivalents promote water oxidation rather than bridge formation. This behavior suggests compatibility with conditions involving an applied anodization potential at pH 13–14 (Table S1†). Destabilization of no-bridge structures has been also observed. Thus, the OH⁻ ligand facilitates the formation of bridges between the two metals by reversing the energy gap between the structures in the presence and absence of the bridges themselves.

We summarize in Fig. 2 the similarities and differences between Co, Mn and Ni in the formation of bridges discussed above. The corresponding formation pathways are effectively represented as a series of steps in which one electron is subtracted from one of the metals and one proton is subtracted from one of the ligands to form a (hydr)oxo bridge.

Fig. 2 Oxo-bridge formation processes of (A) Co, (B) Mn, and (C) Ni ions in an aqueous solution (red, oxygen; white, hydrogen; cyan, cobalt; pink, manganese; and blue, nickel).

MEP calculations

The S₀ → S₁ transition requires further investigation to elucidate the actual reaction process of (hydr)oxo-bridge formation. In particular, it is necessary to show that no high energy barrier prevents the transition from a no-bridge to a one-bridge configuration of the S₀ state, thus hindering the first metal oxidation and the subsequent release of a proton in solution. For this purpose, we have performed MEP calculations focusing on the formation of the one-bridge configuration in the Mn and Co systems, considering four different oxidation and protonation states, namely S₀, S₀⁻ (i.e., the S₀ state with one less proton), S₁, and S₁⁺ (i.e., the S₁ state with one more proton); the corresponding results are listed in Table 2. Very similar activation energies have been calculated in the case of the S₀ and S₁ states for both Co and Mn systems, with lower values in the case of S₀ (0.34 and 0.32 eV, respectively) and higher values for S₁ (0.51 and 0.48 eV, respectively). The calculated barriers are sufficiently low to permit structural changes at room temperature. Hence, the obtained energy barriers are generally compatible with the formation of bridges promoted by external potentials in the range of those actually applied for the electrodeposition of amorphous MCat films from M(II) starting solutions. The lowest barriers have been obtained for the S₀ (0.34 eV) and S₀⁻ (0.24 eV) states of the Co and Mn systems, respectively. We further note a tendency for lower energies in the S₀ and S₀⁻ states than in S₁ and S₁⁺ as a requirement for bridge formation. This result suggests that bridge formation might occur before oxidation in the S₀ → S₁ transition. In contrast, the activation energy of the S₁⁺ state in the Co system has a very high energy barrier of 1.44 eV, which suggests that early deprotonation might contribute to rapid bridge formation in the Co-based catalysts, as also explicitly shown in the case of Ni.

Table 2 Calculated activation energies (eV) for the first bridge formation of the Co and Mn systems

		Activation energy (eV)
Model	Total charge	Co	Mn
S0	+4	0.34	0.32
S0^−	+3	0.41	0.24
S1	+4	0.51	0.48
S1^+	+5	1.44	0.52

---

Deeper insight into the formation of bridges is obtained by analysis of the corresponding reaction coordinates obtained in the cases of Co and Mn by the aforementioned MEP calculations. In the case of Co, Fig. 3 shows the energy surfaces and relevant Co–Co and Co–O distances of the S₀ state, which lie along the formation pathway of the one-bridge structure with the lowest-barrier. The Co–Co and Co–O distances mark the formation of the Co–O–Co bridge and notably change around the TS. Conversely, conformational changes of the H-bond structure, particularly d₄ and d₅ in Fig. 3B, occur in the first part of the reaction pathway (i.e., before the bridge formation). In other words, H-bond rearrangements drive the W3 water molecule (as labeled in Fig. 3C) out of the first hydration shell and place W4 in a bridging position. Thus, it is highly likely that the H-bond rearrangement is the initial step of the bridge formation. Moreover, both d₁ and d₂ Co–O distances related to the same cobalt atom, which are for the water molecules forming the bridge and outgoing from the first solvation sphere (see Fig. 3C), respectively, exhibit relatively high values (3.27 and 3.21 Å, respectively) in the transition state. These lengths are notably longer than typical Co(II)–O distances of hydrated Co ions (∼2.2 Å). Hence, the first bridge formation is performed via attack of a regular six-coordinated Co(II)[H₂O]₆ on the five-coordinated structure of a neighboring hydrated Co ion.

Fig. 3 Calculated energy surface (A) and atomic distances (B) of the first bridge formation of two hydrated Co ions in the S₀ state. Assignments of Co–O and O–H distances are illustrated in C. (D) Reaction schemes of the first bridge formation of hydrated Co ions.

In the case of Mn, the energy surface has two peaks at 0.3 and 0.6 of the reaction pathway in the S₀⁻ state, enclosing a locally stable intermediate state, as shown in Fig. 4. The Mn–Mn and the d₁ and d₂ Mn–O distances (i.e., the distances of the formation of the bridge and the expulsion of a water molecule from the first coordination sphere, respectively) undergo notable changes around the latter peak in the energy profile, whereas the H-bond distance between W1 and W2 (d₃) starts shortening around the former peak. Thus, in the case of Mn, we can divide the reaction pathway in two steps, with the former corresponding to H-bond rearrangement and the latter to bridge formation, respectively. We consider the Mn–O distances corresponding to the incoming and outgoing water molecules in the solvation sphere of Mn(II) (d₁ and d₂, respectively; see Fig. 4C). These bond lengths are short enough around the TS (2.36 and 2.27 Å, respectively) to assume both O atoms as formally coordinated to Mn. Hence, the reaction intermediate has seven-fold coordination, which is unlike the Co system (Fig. 3D and 4D). This difference might originate from the different ionic radii of the metal ions; Co ions, having a smaller radius, prefer to break coordination bonds, whereas Mn ions, having a larger radius, are able to accommodate additional molecules within the first solvation sphere and accept a new coordination bond. Moreover, the five unpaired electrons of high-spin Mn(II) ions may promote sevenfold coordination as an advantageous transition state for the formation of bridged structures, hindered in the case of Co(II). In the latter case, the sharing of a bridging molecule between d₆ Co(II) ions may be favored instead by a Jahn–Teller mechanism, yielding longer distances along the Co–O–Co axis. Therefore, both ionic radius and electronic configuration may be critical factors affecting the bridge formation mechanism of transition-metal ions in aqueous solution.

Fig. 4 Calculated energy surface (A) and atomic distances (B) of the first bridge formation between two hydrated Mn ions in the S₀⁻ state. Assignments of Mn–O and O–H distances are illustrated in C. (D) Reaction schemes of the first bridge formation between hydrated Mn ions.

Anion effects

Although not strictly required, anions can act as ligands for hydrated M(II) species and strongly affect the formation of extended metal–(hydr)oxo structures.^58,59 For example, phosphate is a key anion that promotes rapid self-assembly of the amorphous CoCat, and an actual buffer used under experimental conditions.^60,61 Conversely, amino acid residues terminated with carboxylate groups function as ideal binding sites for the Mn₄Ca cluster in PSII,^25,26,62,63 and the acetate buffer has a similar role in the case of inorganic Mn and mixed MnCa catalyst films for oxygen evolution.^10,14 To elucidate the functional and electrochemical role of anions, we have estimated the effects of phosphate and acetate interacting with Co and Mn hydrated metals in aqueous solution, respectively, based on the calculated potentials along the steps of bridge formation. Specifically, we have used six simplified models for hydrated metals and metal pairs with phosphate and acetate, as illustrated in Fig. 5. In the case of Co systems, we have investigated two different interaction patterns with phosphate, i.e., H-bonded phosphate with the first Co hydration shell, without direct contact with metal ions and direct Co–O–P bonding of phosphate with metal ions. We have also considered two possible protonation states of phosphate because the pK_a between H₂PO₄⁻ and HPO₄²⁻ (7.2) is quite close to most typical experimental pH conditions (7.0–8.0).^8,60,64–66 Both protonation states were calculated separately.

Fig. 5 Optimized structures of hydrated metal ions: single Co ion with a phosphate ligand (a) hydrogen bonding with ligand water molecules and (b) directly coordinating with Co; (c) a single Mn ion with an acetate ligand; no bridge models of two Co ions with a phosphate ligand (d) hydrogen bonding with ligand water molecules and (e) directly coordinating with Co; and (f) no bridge models of two Mn ions with an acetate ligand. All models were calculated with the S₀ state as ground states (red: oxygen, white: hydrogen, yellow: phosphorus, gray: carbon, pink: Mn, and cyan: Co atoms).

The potential U values calculated in the case of the Co(II) → Co(III) transition of an isolated Co ion for H-bonding and ligand phosphates, respectively, are reported in Table 3. The H-bonded H₂PO₄⁻ induces no potential shift with respect to the phosphate-free system (Table 1), whereas the H-bonded HPO₄²⁻ markedly lowers U from 2.02 to 1.76 V. The H-bonded H₂PO₄⁻ and HPO₄²⁻ anions stabilize the two-cobalt bridged structure in the S₀ state, as shown in Table 3, but do not notably decrease U in the S₀ → S₁ transition compared with that of the phosphate-free system of 1.70 V. Hence, isolated phosphate in the aqueous solution likely first facilitates the association of two fully hydrated Co ions. When phosphate acts as a ligand, it affects the U values of the S₁ → S₂ transition, which are markedly lowered from 1.80 V for the phosphate-free system to 1.16 and 1.18 V for H₂PO₄⁻ and HPO₄²⁻, respectively. Thus, phosphate ligands likely play a key role in the second oxidation step.

Table 3 (A) Relative free energies (eV) for each oxidation state of bridged structures with phosphates and acetates in the two-Co and -Mn systems, respectively. Protonated and deprotonated phosphates interact with two Co ions as an H-bond acceptor of the hydration shell and a direct ligand of Co. An acetate interacts with two Mn ions as a direct ligand. (B) Calculated effective potentials for each oxidation step [U(S_i+1 − S_i) (V)] at pH 0 for the isolated and two-metal ion systems of Co and Mn with phosphate and acetate, respectively. Protonated and deprotonated phosphates interact with two Co ions as an H-bond acceptor of the hydration shell and a direct ligand of Co. Acetate interacts with two Mn ions as a direct ligand

(A)
Oxidation state	Relative free energy G (eV)
	2 Co + H-bonding phosphate						2 Co + ligand phosphate
	H2PO4^−			HPO4^2−			H2PO4^−			HPO4^2−			2 Mn + ligand acetate
	No-bridge	One-bridge	Two-bridge	No-bridge	One-bridge	Two-bridge	No-bridge	One-bridge	Two-bridge	No-bridge	One-bridge	Two-bridge	No-bridge	One-bridge	Two-bridge
S0	0.26	0.02	0.00	0.09	0.03	0.00	0.00	0.15	0.19	0.00	0.25	0.28	0.07	0.07	0.00
S1	1.51	0.00	0.24	1.55	0.18	0.00	0.26	0.00	0.00	0.33	0.00	0.07	0.44	0.00	0.10
S2	0.53	0.00	0.11	1.11	0.42	0.00	0.93	0.85	0.00	0.84	0.60	0.00	0.86	0.00	0.29
S3													0.83	0.00	0.15
S4													1.00	0.29	0.00

---

(B)
Transition	Effective potential U (V)
	Co + H-bonding phosphate				Co + ligand phosphate
	H2PO4^−		HPO4^2−		H2PO4^−		HPO4^2−		Mn + ligand acetate
	Isolated	Two-metal	Isolated	Two-metal	Isolated	Two-metal	Isolated	Two-metal	Isolated	Two-metal
S0 → S1	2.00	1.88	1.66	1.52	1.76	1.85	1.53	1.63	1.06	0.86
S1 → S2		1.90		1.62		1.16		1.18	1.71	0.92
S2 → S3										1.70
S3 → S4										1.64

---

Acetate has been used because it is not only a typical anion present in the starting solution for electrodeposition of MnCat and MnCaCat, but also a simplified model of aspartic acid and glutamic acid in protein environments. Recent studies have reported that such ligands are able to bond with Mn ions in the initial formation step of the MnCa cluster of PSII.^62,63,67 Insertion of acetate destabilizes the no-bridge structure in the S₁–S₄ states, showing a similar tendency to the effects of phosphate and OH⁻ ligands on Co and Ni, respectively. In addition, all the potentials U calculated along the same pathway discussed in the case of no-acetate systems are lowered in the case of a single acetate ligand (compare Tables 1 and 3). In the case of inorganic MnCat films electrodeposited from Mn(CH₃COO)₂ solutions, the fact that the S₂ → S₃ transition requires a potential (1.70 V) higher than that for the S₃ → S₄ transition (1.64 V) might explain the need to apply complex potential cycles to achieve the electrodeposition of a catalytically active, mixed valence [Mn(III)/Mn(IV)] MnCat film rather than an inactive Mn(IV) film.¹⁰ Conversely, the acetate binding with hydrated Mn ions requires a relatively low potential U for the S₀ → S₁ transition in both the single Mn system (1.06 V) and the two-Mn system (0.79 V). These potentials are compatible with the redox potential of D1-Tyr161, a direct electron acceptor of the MnCa cluster in the PSII active site, as the oxidizing agent of the first Mn ion in the photoactivation process. The redox potential of this tyrosine is considered to be in the range of 0.9–1.0 V.^68,69 Hence, our simple model based on the insertion of a single acetate ligand is able to shed light on the electrochemical roles of carboxylate ligands in the first oxidation step that builds the MnCa cluster of PSII.

Conclusions

We have used DFT simulations to investigate the early stages of the formation of –O– and –OH– bridges between divalent transition-metal atoms exposed to positive potentials in water. These calculations indicate that a simple model is flexible enough to account for different pH conditions and starting solutions and can describe most of the features observed during the electrodeposition of catalytically active amorphous metal–(hydr)oxo films. We applied our model to simulate the steps of oxidation/deprotonation redox processes applied to a single or two divalent metal (cobalt, manganese or nickel) ions, with the latter systems leading to the formation of –OH₂–, –OH–, or –O– bridges between the metal pairs.

Our results shed light on notably differences in the properties of the three investigated metals that emerge in these first stages, differences significant enough to promote the growth of different catalytic motifs in extended systems. In the case of Ni, no oxidation potential calculated for any oxidative step leading to the formation of Ni(III) was compatible with the applied potentials for the formation of NiCat films. This result is compatible with a two-step electrodeposition of Ni-based catalyst films. Precipitation of a Ni(II)–(hydr)oxo compound without application of a positive potential can be followed by further oxidation under basic conditions through oxidation/deprotonation steps. Our simulations also indicated that the calculated potentials U for the formation of a Ni(III)–(OH)₂–Ni(III) two-bridge system under basic conditions are compatible with applied potentials, when the presence of hydroxyl ligands is explicitly considered in the starting S₀ state. Co pairs easily form Co(III)–(OH)₂–Co(III) blocks at a potential consistent with experimental conditions. In line with experimental findings, the insertion of phosphate into the starting solution induces the formation of an advantageous equilibrium in which H-bonded phosphate favors the formation of bridged structures. Such an equilibrium is otherwise hindered by a moderate energy barrier, related to the formation of an under-coordinated transition state, compatible with the occurrence of a Jahn–Teller mechanism along the Co–O–Co axis. The ligated phosphate lowers the required potential for the redox conversion of the Co(II)–(OH₂)₂–Co(II) in Co(III)–(OH)₂–Co(III) bridges. As opposed to Co, Mn pairs tend to form single Mn(III)–O–Mn(III) rather than double Mn(III)–(OH)₂–Mn(III) bridges, through a more stable, fully coordinated reaction intermediate allowed by the longer ionic radius of Mn compared to that of Co. The calculated potentials are compatible with further oxidation of Mn to form Mn(III)–O(OH)–Mn(IV), representative blocks of active, mixed valence catalysts, and Mn(IV)–(O)₂–Mn(IV). These predictions are compatible with the formation of mostly inactive catalysts after prolonged exposure of Mn(II) to a steady positive potential. The addition of acetate to the starting solution lowers all the potentials required for Mn oxidation without altering the multistep pathway. This results suggest an interesting parallelism with the formation of the Mn₄Ca cluster in the biological environment of PSII. The potential applied for the first oxidative step of Mn ligated by acetate is indeed fully compatible with the redox potential of an electron-accepting tyrosine residue.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Computational resources to support this work have been provided by the PRACE consortium, project RA5393.

References

1. J. P. McEvoy and G. W. Brudvig, Water-splitting chemistry of photosystem II, Chem. Rev., 2006, 106, 4455–4483.
2. J. Barber, Photosynthetic energy conversion: natural and artificial, Chem. Soc. Rev., 2009, 38, 185–196.
3. H. Dau, I. Zaharieva and M. Haumann, Recent developments in research on water oxidation by photosystem II, Curr. Opin. Chem. Biol., 2012, 16, 3–10.
4. D. G. Nocera, The artificial leaf, Acc. Chem. Res., 2012, 45, 767–776.
5. J. R. McKone, N. S. Lewis and H. B. Gray, Will solar-driven water-splitting devices see the light of day?, Chem. Mater., 2013, 26, 407–414.
6. H. Dau, E. Fujita and L. Sun, Artificial photosynthesis: beyond mimicking nature, ChemSusChem, 2017, 10, 4228–4235.
7. D. K. Dogutan and D. G. Nocera, Artificial photosynthesis at efficiencies greatly exceeding that of natural photosynthesis, Acc. Chem. Res., 2019, 52, 3143–3148.
8. M. W. Kanan and D. G. Nocera, In situ formation of an oxygen-evolving catalyst in neutral water containing phosphate and Co²⁺, Science, 2008, 321, 1072–1075.
9. D. K. Bediako, B. Lassalle-Kaiser, Y. Surendranath, J. Yano, V. K. Yachandra and D. G. Nocera, Structure-activity correlations in a nickel-borate oxygen evolution catalyst, J. Am. Chem. Soc., 2012, 134, 6801–6809.
10. I. Zaharieva, P. Chernev, M. Risch, K. Klingan, M. Kohlhoff, A. Fischer and H. Dau, Electrosynthesis, functional, and structural characterization of a water-oxidizing manganese oxide, Energy Environ. Sci., 2012, 5, 7081–7089.
11. R. D. Smith, M. S. Prevot, R. D. Fagan, Z. Zhang, P. A. Sedach, M. K. Siu, S. Trudel and C. P. Berlinguette, Photochemical route for accessing amorphous metal oxide materials for water oxidation catalysis, Science, 2013, 340, 60–63.
12. M. Huynh, C. Shi, S. J. Billinge and D. G. Nocera, Nature of activated manganese oxide for oxygen evolution, J. Am. Chem. Soc., 2015, 137, 14887–14904.
13. C. Liu, B. C. Colon, M. Ziesack, P. A. Silver and D. G. Nocera, Water splitting-biosynthetic system with CO₂ reduction efficiencies exceeding photosynthesis, Science, 2016, 352, 1210–1213.
14. D. Gonzalez-Flores, I. Zaharieva, J. Heidkamp, P. Chernev, E. Martinez-Moreno, C. Pasquini, M. R. Mohammadi, K. Klingan, U. Gernet, A. Fischer and H. Dau, Electrosynthesis of biomimetic manganese-calcium oxides for water oxidation catalysis-atomic structure and functionality, ChemSusChem, 2016, 9, 379–387.
15. C. Pasquini, I. Zaharieva, D. Gonzalez-Flores, P. Chernev, M. R. Mohammadi, L. Guidoni, R. D. L. Smith and H. Dau, H/D isotope effects reveal factors controlling catalytic activity in Co-based oxides for water oxidation, J. Am. Chem. Soc., 2019, 141, 2938–2948.
16. M. Gong, Y. Li, H. Wang, Y. Liang, J. Z. Wu, J. Zhou, J. Wang, T. Regier, F. Wei and H. Dai, An advanced Ni-Fe layered double hydroxide electrocatalyst for water oxidation, J. Am. Chem. Soc., 2013, 135, 8452–8455.
17. R. D. Smith, M. S. Prevot, R. D. Fagan, S. Trudel and C. P. Berlinguette, Water oxidation catalysis: electrocatalytic response to metal stoichiometry in amorphous metal oxide films containing iron, cobalt, and nickel, J. Am. Chem. Soc., 2013, 135, 11580–11586.
18. J. Luo, J. H. Im, M. T. Mayer, M. Schreier, M. K. Nazeeruddin, N. G. Park, S. D. Tilley, H. J. Fan and M. Gratzel, Water photolysis at 12.3% efficiency via perovskite photovoltaics and Earth-abundant catalysts, Science, 2014, 345, 1593–1596.
19. R. D. L. Smith, C. Pasquini, S. Loos, P. Chernev, K. Klingan, P. Kubella, M. R. Mohammadi, D. Gonzalez-Flores and H. Dau, Spectroscopic identification of active sites for the oxygen evolution reaction on iron-cobalt oxides, Nat. Commun., 2017, 8, 2022.
20. D. Friebel, M. W. Louie, M. Bajdich, K. E. Sanwald, Y. Cai, A. M. Wise, M. J. Cheng, D. Sokaras, T. C. Weng, R. Alonso-Mori, R. C. Davis, J. R. Bargar, J. K. Norskov, A. Nilsson and A. T. Bell, Identification of highly active Fe sites in (Ni,Fe)OOH for electrocatalytic water splitting, J. Am. Chem. Soc., 2015, 137, 1305–1313.
21. M. B. Stevens, C. D. M. Trang, L. J. Enman, J. Deng and S. W. Boettcher, Reactive Fe-sites in Ni/Fe (oxy)hydroxide are responsible for exceptional oxygen electrocatalysis activity, J. Am. Chem. Soc., 2017, 139, 11361–11364.
22. N. Li, D. K. Bediako, R. G. Hadt, D. Hayes, T. J. Kempa, F. von Cube, D. C. Bell, L. X. Chen and D. G. Nocera, Influence of iron doping on tetravalent nickel content in catalytic oxygen evolving films, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1486–1491.
23. R. D. L. Smith, C. Pasquini, S. Loos, P. Chernev, K. Klingan, P. Kubella, M. R. Mohammadi, D. Gonzalez-Flores and H. Dau, Geometric distortions in nickel (oxy)hydroxide electrocatalysts by redox inactive iron ions, Energy Environ. Sci., 2018, 11, 2476–2485.
24. M. Gorlin, P. Chernev, P. Paciok, C. W. Tai, J. Ferreira de Araujo, T. Reier, M. Heggen, R. Dunin-Borkowski, P. Strasser and H. Dau, Formation of unexpectedly active Ni-Fe oxygen evolution electrocatalysts by physically mixing Ni and Fe oxyhydroxides, Chem. Commun., 2019, 55, 818–821.
25. H. Bao and R. L. Burnap, Photoactivation: the light-driven assembly of the water oxidation complex of photosystem II, Front. Plant Sci., 2016, 7, 578.
26. D. J. Vinyard, G. M. Ananyev and G. C. Dismukes, Photosystem II: the reaction center of oxygenic photosynthesis, Annu. Rev. Biochem., 2013, 82, 577–606.
27. K. Becker, K. U. Cormann and M. M. Nowaczyk, Assembly of the water-oxidizing complex in photosystem II, J. Photochem. Photobiol., B, 2011, 104, 204–211.
28. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
29. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
30. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
31. C. T. Lee, W. T. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
32. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
33. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, Empirical three-body dispersion correction from, J. Chem. Phys., 2010, 132, 154104.
34. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. a ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109.
35. V. Barone and M. Cossi, Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model, J. Phys. Chem. A, 1998, 102, 1995–2001.
36. M. Bajdich, M. Garcia-Mota, A. Vojvodic, J. K. Norskov and A. T. Bell, Theoretical investigation of the activity of cobalt oxides for the electrochemical oxidation of water, J. Am. Chem. Soc., 2013, 135, 13521–13530.
37. M. Garcia-Mota, A. Vojvodic, H. Metiu, I. C. Man, H. Y. Su, J. Rossmeisl and J. K. Norskov, Tailoring the activity for oxygen evolution electrocatalysis on rutile TiO₂(110) by transition-metal substitution, ChemCatChem, 2011, 3, 1607–1611.
38. Á. Valdés, Z. W. Qu, G. J. Kroes, J. Rossmeisl and J. K. Nørskov, Oxidation and photo-oxidation of water on TiO₂ surface, J. Phys. Chem. C, 2008, 112, 9872–9879.
39. Y. F. Li, First-principles simulations for morphology and structural evolutions of catalysts in oxygen evolution reaction, ChemSusChem, 2019, 12, 1846–1857.
40. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the overpotential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108, 17886–17892.
41. Á. Valdés, Z. W. Qu, G. J. Kroes, J. Rossmeisl and J. K. Nørskov, Oxidation and photo-oxidation of water on TiO₂ surface, J. Phys. Chem. C, 2008, 112, 9872–9879.
42. D. K. Zhong and D. R. Gamelin, Photoelectrochemical water oxidation by cobalt catalyst ("Co-Pi")/α-Fe₂O₃ composite photoanodes: oxygen evolution and resolution of a kinetic bottleneck, J. Am. Chem. Soc., 2010, 132, 4202–4207.
43. G. Henkelman and H. Jonsson, A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives, J. Chem. Phys., 1999, 111, 7010–7022.
44. E. Weinan, W. Q. Ren and E. Vanden-Eijnden, String method for the study of rare events, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 052301.
45. J. Burgess, Metal Ions in Solution, Ellis Horwood Limited, Chichester, England, 1978.
46. A. Bergmann, I. Zaharieva, H. Dau and P. Strasser, Electrochemical water splitting by layered and 3D cross-linked manganese oxides: correlating structural motifs and catalytic activity, Energy Environ. Sci., 2013, 6, 2745–2755.
47. M. Risch, V. Khare, I. Zaharieva, L. Gerencser, P. Chernev and H. Dau, Cobalt-oxo core of a water-oxidizing catalyst film, J. Am. Chem. Soc., 2009, 131, 6936–6937.
48. M. Gorlin, P. Chernev, J. Ferreira de Araujo, T. Reier, S. Dresp, B. Paul, R. Krahnert, H. Dau and P. Strasser, Oxygen evolution reaction dynamics, faradaic charge efficiency, and the active metal redox states of Ni-Fe oxide water splitting electrocatalysts, J. Am. Chem. Soc., 2016, 138, 5603–5614.
49. S. G. Bratsch, Standard electrode potentials and temperature coefficients in water at 298.15 K, J. Phys. Chem. Ref. Data, 1989, 18, 1–21.
50. M. Uudsemaa and T. Tamm, Density-functional theory calculations of aqueous redox potentials of fourth-period transition metals, J. Phys. Chem. A, 2003, 107, 9997–10003.
51. I. Zilbermann, E. Maimon, H. Cohen and D. Meyerstein, Redox chemistry of nickel complexes in aqueous solutions, Chem. Rev., 2005, 105, 2609–2625.
52. G. Mattioli, M. Risch, A. Amore Bonapasta, H. Dau and L. Guidoni, Protonation states in a cobalt-oxide catalyst for water oxidation: fine comparison of ab initio molecular dynamics and X-ray absorption spectroscopy results, Phys. Chem. Chem. Phys., 2011, 13, 15437–15441.
53. G. Mattioli, I. Zaharieva, H. Dau and L. Guidoni, Atomistic texture of amorphous manganese oxides for electrochemical water splitting revealed by ab Initio calculations combined with X-ray spectroscopy, J. Am. Chem. Soc., 2015, 137, 10254–10267.
54. N. Pinna and M. Niederberger, Surfactant-free nonaqueous synthesis of metal oxide nanostructures, Angew. Chem., Int. Ed., 2008, 47, 5292–5304.
55. M. Görlin, M. Gliech, J. F. de Araújo, S. Dresp, A. Bergmann and P. Strasser, Dynamical changes of a Ni-Fe oxide water splitting catalyst investigated at different pH, Catal. Today, 2016, 262, 65–73.
56. M. Gorlin, J. Ferreira de Araujo, H. Schmies, D. Bernsmeier, S. Dresp, M. Gliech, Z. Jusys, P. Chernev, R. Kraehnert, H. Dau and P. Strasser, Tracking catalyst redox states and reaction dynamics in Ni-Fe oxyhydroxide oxygen evolution reaction electrocatalysts: the role of catalyst support and electrolyte pH, J. Am. Chem. Soc., 2017, 139, 2070–2082.
57. M. Risch, K. Klingan, J. Heidkamp, D. Ehrenberg, P. Chernev, I. Zaharieva and H. Dau, Nickel-oxido structure of a water-oxidizing catalyst film, Chem. Commun., 2011, 47, 11912–11914.
58. M. Risch, K. Klingan, F. Ringleb, P. Chernev, I. Zaharieva, A. Fischer and H. Dau, Water oxidation by electrodeposited cobalt oxides--role of anions and redox-inert cations in structure and function of the amorphous catalyst, ChemSusChem, 2012, 5, 542–549.
59. J. Villalobos, D. Gonzalez-Flores, K. Klingan, P. Chernev, P. Kubella, R. Urcuyo, C. Pasquini, M. R. Mohammadi, R. D. L. Smith, M. L. Montero and H. Dau, Structural and functional role of anions in electrochemical water oxidation probed by arsenate incorporation into cobalt-oxide materials, Phys. Chem. Chem. Phys., 2019, 21, 12485–12493.
60. D. A. Lutterman, Y. Surendranath and D. G. Nocera, A self-healing oxygen-evolving catalyst, J. Am. Chem. Soc., 2009, 131, 3838–3839.
61. C. Costentin and D. G. Nocera, Self-healing catalysis in water, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13380–13384.
62. M. Zhang, M. Bommer, R. Chatterjee, R. Hussein, J. Yano, H. Dau, J. Kern, H. Dobbek and A. Zouni, Structural insights into the light-driven auto-assembly process of the water-oxidizing Mn₄CaO₅-cluster in photosystem II, eLife, 2017, 6, e26933.
63. M. Asada and H. Mino, Location of the high-affinity Mn²⁺ site in photosystem II detected by PELDOR, J. Phys. Chem. B, 2015, 119, 10139–10144.
64. M. W. Kanan, Y. Surendranath and D. G. Nocera, Cobalt-phosphate oxygen-evolving compound, Chem. Soc. Rev., 2009, 38, 109–114.
65. Y. Surendranath, D. A. Lutterman, Y. Liu and D. G. Nocera, Nucleation, growth, and repair of a cobalt-based oxygen evolving catalyst, J. Am. Chem. Soc., 2012, 134, 6326–6336.
66. Y. Surendranath, M. Dinca and D. G. Nocera, Electrolyte-dependent electrosynthesis and activity of cobalt-based water oxidation catalysts, J. Am. Chem. Soc., 2009, 131, 2615–2620.
67. S. Nakamura and T. Noguchi, Initial Mn²⁺ binding site in photoassembly of the water-oxidizing Mn₄CaO₅ cluster in photosystem II as studied by quantum mechanics/molecular mechanics calculations, Chem. Phys. Lett., 2019, 721, 62–67.
68. I. Vass and S. Styring, pH-Dependent charge equilibria between tyrosine-D and the S states in photosystem II. Estimation of relative midpoint redox potentials, Biochemistry, 1991, 30, 830–839.
69. J. G. Metz, P. J. Nixon, M. Rogner, G. W. Brudvig and B. A. Diner, Directed alteration of the D1 polypeptide of photosystem II: Evidence that tyrosine-161 is the redox component, Z, connecting the oxygen-evolving complex to the primary electron-donor, P680, Biochemistry, 1989, 28, 6960–6969.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cy02227f

‡ Present address: Institute for Materials Chemistry and Engineering and IRCCS, Kyushu University, Nishi-ku, Fukuoka 819-0395, Japan.

---