Open Access Article
Open Access ArticleRapid hybrid perovskite film crystallization from solution
Sandy
Sánchez
 *ab,
Lukas
Pfeifer
*ab,
Lukas
Pfeifer
 b,
Nikolaos
Vlachopoulos
b,
Nikolaos
Vlachopoulos
 a and
Anders
Hagfeldt
a and
Anders
Hagfeldt
 *a
*a
aLaboratory of Photomolecular Sciences, Institute of Chemistry and Chemical Engineering, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland. E-mail: sandy.sanchezalonso@epfl.ch; anders.hagfeldt@epfl.ch
bLaboratory of Photonics and Interfaces, Institute of Chemistry and Chemical Engineering, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
First published on 10th May 2021
Abstract
The use of a solution process to grow perovskite thin films allows to extend the material processability. It is known that the physicochemical properties of the perovskite material can be tuned by altering the solution precursors as well as by controlling the crystal growth of the film. This advancement necessarily implies the need for an understanding of the kinetic phenomena for the thin-film formation. Therefore, in this work we review the state of the art of perovskite hybrid crystal growth, starting from a comprehensive theoretical description towards broad experimental investigations. One part of the study focuses on rapid thermal annealing as a tool to control nucleation and crystal growth. We deduce that controlling crystal growth with high-precision photonic sintering simplifies the experimental framework required to understand perovskite crystallization. These types of synthesis methods open a new empirical parameter space. All this knowledge serves to improve the perovskite synthesis and the thin films' quality, which will result in higher device performances.
1. Introduction
Hybrid perovskite semiconductor materials have become of great interest in materials science, with an enormous potential to revolutionize the entire field and with promising applications such as thin film solar cells.1–3 However, scaling up perovskite solar cells (PSCs) for industrial production is a complex task for this young technology, mainly due to the poor stability of the material.4–8 All the perovskite chemical compositions are water soluble, which means that in normal environmental conditions (more than 25% of relative humidity), these lead-halide perovskites tend to degrade.9 Numerous approaches have been proposed to overcome this problem, and the different strategies can be divided into essentially three categories: 1 – chemical passivation; 2 – compositional engineering; and 3 – new synthesis methods.10–12The three mentioned strategies focus on removing crystal defects, either from the bulk or from the surface. The selecting layers and the final chosen architecture are as well part of the problem to be solved, however the perovskite itself not only attracts the most attention, it is also the fundamental component in the cell. This is the major reason why this review focuses on perovskite crystallization, in order to give a comprehensive overview of what has been accomplished that can provide paths to overcome the stability issues in PSCs. A defect-tolerant perovskite film has less chance to be degraded, since interstitial defects and deeps traps, among others, as non-radiative centres have a major cause in the crystallization mechanism.13,14 The change of microstrain in the perovskite lattice can be first determined by defects during crystal nucleation and growth, which can be further detrimental by external stress factors like humidity, photodegradation, and temperature.15,16 These defects will have direct consequences in ion migration, non-radiative recombination, and organic decomposition, being examples of mechanisms triggering irreversible degradation pathways.17–20
We believe that a new theoretical framework is needed to understand a complex phenomena of perovskite crystallization, which occurs far from thermodynamic equilibrium.21 Therefore, this review relates the perovskite kinetic phenomena with new fabrication procedures and different theoretical approaches as for example the dendrite growth, very known in the polymers field.22,23 Thus this review is compiled in three parts, the state of the art of perovskite nucleation and crystal growth, from a more theoretical approach, passing through rapid or controlled growth to phase evolution during crystal growth. The two last sections rely in a more experimental style, to review the structural evolution, the final crystal shape and its relationship with crystallization method, the latter more detailed in section two.
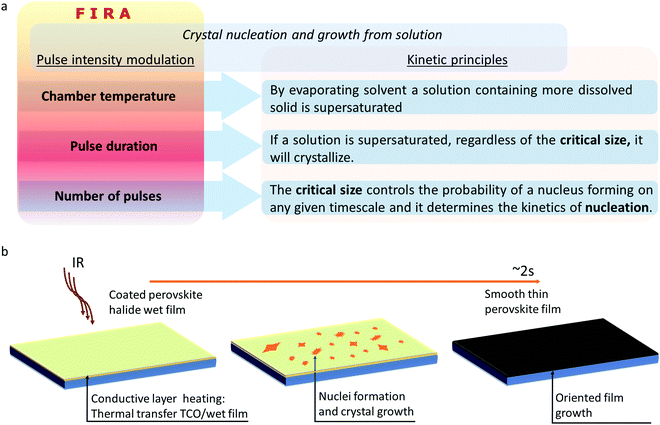
Looking for alternatives to deposit a defect-tolerant perovskite film, this review discusses in-depth a synthesis method called flash infrared annealing (FIRA).24–28 This method is based on thermal rapid processing, which has been widely employed to synthesize thin films for semiconductor applications.29–32 For deeply exploiting FIRA, an understanding of the thin-film crystallization phenomenon is needed. From FIRA optimization parameters to experimental approaches, this review addresses how to rapidly produce defect-tolerant perovskite thin films that enables the manufacturing of highly efficient solar cells. The kinetics of the nucleation and crystal growth process is also addressed, based on several fundamental studies of particular FIRA cases, disclosing the mechanism involved in driving film crystallization. These fundamental studies have the aim to use FIRA for manufacturing stable PSCs, increasing their power conversion efficiency (PCE), and enabling the scale-up to the industry of this technology.
2. Crystal nucleation and growth from solution
2.1. Thermodynamic of nucleation and crystal growth
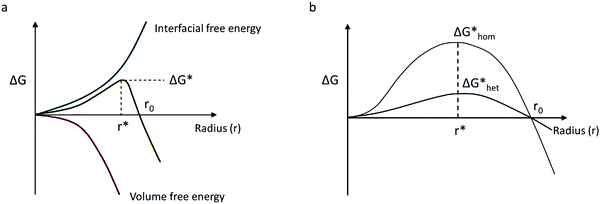
A nucleus can be defined as the minimum amount of a new phase, which can be a cluster of few atoms or molecules. A first-order phase transition mechanism is the formation of incipient crystallization nuclei in an initial metastable phase. The diffusion of particles rules the crystal growth step, which directly follows the nucleation. While, as growing clusters on the nuclei's surface follow later integration in the crystal lattice structure.33,34 In perovskite solutions, as the solvent evaporates, the precursor changes the chemical potential, eventually reaching supersaturation to allow a new phase through crystal growth. Nucleation is promoted by the supersaturation state, with the formation of nuclei-clusters that favored crystal growth. Nucleation processes have Gibbs energetic barriers that need to be surpassed. These barriers are a function of the critical nucleus size.35The relationship between supersaturation and the critical nucleus size inducing crystal growth can be described in terms of the Gibbs free energy of the system. Assume that a spherical nucleus cluster is formed on a substrate surface, with r as the nuclei radius, θ the contact angle which the nucleus forms with the substrate, ΔGv the Gibbs free energy per unit volume, γ0 the nucleus surface tension, γ1 the nucleus–substrate interfacial tension, and γ2 the substrate surface tension. In equilibrium, Young's equation is given by:
γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = γ2 − γ1. θ = γ2 − γ1. | (2.1) |
The change in surface and interfacial Gibbs free energy can be expressed as33
Gs2πr2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)π(r θ)π(r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2(γ1 − γ2) = πr2γ0(2 − 3 θ)2(γ1 − γ2) = πr2γ0(2 − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + cos3 θ + cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). θ). | (2.2) |
For the spherical cap nucleus, its volume V is
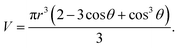 | (2.3) |
Therefore, the change of the volume free energy is
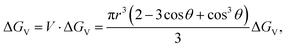 | (2.4) |
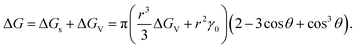 | (2.5) |
Setting:
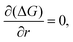 | (2.6) |
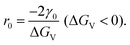 | (2.7) |
Since ΔGv is the energy needed from equilibrium state to supersaturation, it can be expressed as:
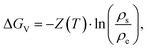 | (2.8) |
A significant empirical contribution was given by von Weimarn,37 where the size of the precipitated particle is inversely proportional to the relative supersaturation state. The von Weirmarn rules for solutions imply how the precursors can react with different solvents to decrease/increase the solubility and emphasizes the average crystal size dependence on the supersaturation state. However, for precursor solutions other phenomena influencing the solubility are present and can be described by theories such as that of Lewis acidity-base behavior, as we will discuss herein.38 Supersaturation can be defined by the relation of solution concentration with respect to the equilibrium concentration at the same temperature:
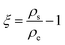 | (2.9) |
| ΔGV = Z(T)ln(ξ + 1). | (2.10) |
Based on the above relation, the critical nucleus radius can be expressed as
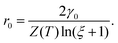 | (2.11) |
As supersaturation is reached, the balance of chemical potentials can result in the surpassing of the nucleation barrier for certain nuclei sizes. The free energy changes are associated with the formation of the nuclei and are a consequence of the formation of the new phase.39 On the surface, the interaction of molecules in solution with their neighbors differs from those in mass. Meanwhile, its contribution to the new stage's free energy varies and is usually more prominent in this manner. Therefore, the interfacial energy is given by the difference between the free energy per molecule in bulk and in the surface.40,41
A critical nucleus size is required for a nucleus to form from a supersaturated solution, which has a number of implications, as previously discussed. The critical size of the new phase is reached due to variations that add sufficient amounts of molecules. Therefore, the value of the critical size influences the nucleation probability.42 In parallel, nucleation is a function of interfacial energy, which has a direct relationship. Consequently, the interfacial energy or the probability of nucleation can be manipulated by modulating the nucleus's critical size.33
2.2. Crystal nucleation and growth
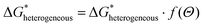 | (2.12) |
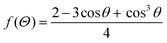 | (2.13) |
Fig. 1a shows the contribution of the interfacial energy and the volume for the total free energy needed to form a stable nucleus, as stated in eqn (2.5). Then, in Fig. 1b the two energy barriers related to the formation of a nucleus for homogeneous and heterogeneous nucleation can be seen as a function of the critical radius. The wetting effect determines the nucleation's feasibility by lowering the energy barrier.
For reaction rates treatment, the temperature is one of the most important variables due to its exponential dependence, as expressed in the Arrhenius equation proposed in 1889:50
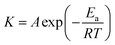 | (2.14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K versus 1/T. The empirical nature of the Arrhenius equation does not consider any mechanistic description of the intermediates species involved and only involves the macroscopic constant rate for a given reaction.51 The energy activation of an overall reaction is the composite of many activation energies from elementary reactions. Thus, the transition state theory based on statistical mechanics portrays a multidimensional potential surface related to the energy variation as a function of the atom positions for a given reaction.41 The size of the activation energy is a fundamental variable for controlling the rates in processes, and it can be derived from the maximum of the potential surface of the reaction corresponding to the variation of the Gibbs free energy vs. the generalized position coordinate of the reacting species. Therefore, the potential energy surface topology is an accurate description of the activated complex related to such intermediate reactive species.52
K versus 1/T. The empirical nature of the Arrhenius equation does not consider any mechanistic description of the intermediates species involved and only involves the macroscopic constant rate for a given reaction.51 The energy activation of an overall reaction is the composite of many activation energies from elementary reactions. Thus, the transition state theory based on statistical mechanics portrays a multidimensional potential surface related to the energy variation as a function of the atom positions for a given reaction.41 The size of the activation energy is a fundamental variable for controlling the rates in processes, and it can be derived from the maximum of the potential surface of the reaction corresponding to the variation of the Gibbs free energy vs. the generalized position coordinate of the reacting species. Therefore, the potential energy surface topology is an accurate description of the activated complex related to such intermediate reactive species.52
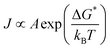 | (2.15) |
This means that the formation of a new phase contradicts the cluster separation assumption, which makes it impossible to analytically obtain the cluster distribution. The kinetic factor depends on the molecular mobility, being related to the attachment's rate of molecules to the nucleus. While the pre-exponential factor A is a remarkable assumption because of its dependence on temperature and its relationship to rapid molecular mobility changes.56
In a phase transformation process the energy of the atoms can follow the Maxwell–Boltzmann distribution. If n0 is the density of atoms in a liquid and nR is the density of cluster in equilibrium with the liquid, then:
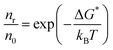 | (2.16) |
A cluster with a critical radius size r0 will grow when more atoms can be added and the rate of growing will be proportional to the atomic vibration frequency v0 and the probability of adding another atom to the surface σ. Then the homogeneous nucleation rate is given by:
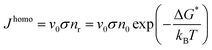 | (2.17) |
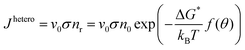 | (2.18) |
The nucleation rate for homogeneous nucleation strongly depends on temperature, but in the case of heterogeneous nucleation the factor f(θ) is also determining, which relates the contact angle and the radius of a spherical cluster. Therefore, the nucleation rate for heterogeneous nucleation also depends on the type of a foreign substrate.56
 | ||
| Fig. 2 Schematic representation of the crystallization of a system with three different polymorphs (reproduced with permission from ref. 58. ©2019 American Chemical Society). | ||
The growth stage, which follows nucleation, is produced by the diffusion of the particles to the surface of the existing nucleus and their integration into the crystal lattice structure. The initial stages of solution crystallization determine the crystal's properties, mainly the size distribution and the crystal structure.21 For crystal growth, the main assumption is that stable nuclei exist prior to growth, adding molecules to a stable cluster driven by the decrease of the Gibbs free energy of the phase, with the change kinetically limited. The crystal shape can be analyzed by the Johnson–Mehl–Avrami equation,34,60 where the volume transformation x as a function of time of a new β-phase is given by:
| x(t) = 1 − exp[−(β)N] | (2.19) |
The parameter N depends on the shape of β-phase particles. For example, as regards different dimensions it is N = 3, N = 2, and N = 1 for sphere-, disk-, and rod-shaped particles, respectively.
At the beginning and the end of the process, the transformation rates are low but fast in-between. The time required for a sufficient nuclei formation for the new phase is due to the early slow rate. The transformation accelerates in the intermediate stage when the nuclei begin to grow into new particles. The new nuclei continue to form in an initial phase while the rest are incorporated into the growth phase.34,35 When the transformation is almost complete, there is still an untransformed nuclei material that slows down new particles' production. Then the grown particles begin to form boundaries between them (where the particle ends its growth).
The Johnson–Mehl–Avrami equation can be applied to the crystallization process in a variety of amorphous solids under isothermal conditions. Thus, to support interpretations of physicochemical mechanisms derived from the obtained kinetic parameters.61 During continuous heating, an isothermal process cannot be efficiently separated from the grain growth and crystallization process because it results in nanometers grain size. Consequently, the kinetic parameters obtained from an isothermal process apply more to a crystallization process.
A population balance equation is commonly used to obtain the population density n for any given value of crystal size, r. Randolph and Larson,62 has defined n as:
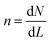 | (2.20) |
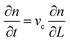 | (2.21) |
The population balance in a form of the continuity equation gives the time evolution of the crystal size distribution for a closed system.63,64 Constant rates of crystal nucleation and growth can be derived for reactions of chemical species involved.
2.3. Surface and crystallization
The driving force for the crystallization process depends on supersaturation, which is fundamental to the crystal growth rate.17,22,28 Crystal growth kinetics is a complex phenomenon, which usually takes place through an intermediate phase. Overall, fast nucleation can improve the extent of coverage of films, and the control of the crystal growth can contribute to form a highly crystalline material.29–32 To grow a crystal, a cluster has to be transported to the crystal surface and may have to rearrange to fit the lattice structure. The critical cluster is the equivalent of an activated complex in transition state theory. It can result in successive transport through solution and surface reaction processes. Both of these processes can be growth rate-controlling. The cluster transport can be controlled by diffusion, which is mass transport as a consequence of the thermal motion of the molecules, and by convection, which is mass movement due to an energy gradient in the system. Surface-controlled growth can be determined by nucleation and dislocation growth.25,33,34A major drawback of the Kossel–Stranski theory is that the accumulation of atoms in the kinked ledge to diffuse to the edge of the crystal would not correspond to a low energy nucleation site. Nevertheless, a continuous source of steps that can increase over to the crystal's surface can be provided by screw dislocations.67,68 The mechanism for step generation and transport was elucidated by Burton, Cabrera and Frank, in a crystal growth theory.69 An step on the crystal surface can be promoted by a screw dislocation with a size related to the lattice distortion vector's projection (Burgers vector) resulting from a dislocation.70,71 In this theory, additional growth can occur when there is a rotation of the step throughout the dislocation point.
Carl Steefel and Van Cappellen,73 have developed a new kinetic approach unveiling the role of nucleation, precursors and Oswalt ripening by using the balance population equation to calculate crystal size distribution. Assuming the conservation of mass and volume, they decouple the changes in population density due to the ripening of growth and dissolution, then the continuity equation is given by:
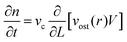 | (2.22) |
It has been reported that the Oswalt ripening effect can be used as a tool to suppress defects at the grain boundary during perovskite crystal growth,74,75 where the aging effect tends to remove defects in perovskite films. However, due to the complexity of the ripening ratio and coarsening, the above model has to be complemented with a better experimental framework description.
2.4. Dendrite growth
In general, short time annealing at high temperature can result in an energy process equivalent to the longer annealing at a lower temperature. However, different activation energies or driving forces are necessary to reach the supersaturated state in both cases; therefore, they depend differently on the temperature.22 For rapid thermal annealing at high temperatures, the controlled growth rate depends mainly on the thermal convection. The final crystalline morphology can be molded by the temperature gradient of the thermal process. The crystalline microarrangement will depend on the interfacial energy and the different chemical potential in the molecules (i.e., crystal growth from solution), where instabilities can provide a different directional growth, led by their anisotropy. This is the case of dendritic growth, where a metastable phase can grow in an energetically favorable direction, different from the final phase.61Therefore, it is of our interest to briefly introduce dendrite growth, which is the main morphological feature of the hybrid perovskites processed with the FIRA method.24 Rapid kinetic processes can result in dendrite growth, where diffusion processes can govern the phase transformation rate. Dendrites typically grow along energetically favorable crystallography directions. Dendrites require some anisotropy, usually of the interfacial energy between crystal and solution, but this could also be anisotropy of the attachment kinetics for non-metallic systems.76 Due to this anisotropy, dendrites can grow with different velocity, which causes the formation of stem and tips. This growth velocity mainly depends on the different diffusional processes converging, where thermal diffusivities involve faster growths.
| TRf = T∞f − 2Γslε | (2.23) |
Surface energy and atomic attachment kinetics can determine the extent to which the system is far from equilibrium with respect to the isotropic interfacial energy the conditions for equilibrium at the liquid/solid interface. Isotropicity in the systems means that the molar free Gibbs energy is constant everywhere; the crystal, therefore, is spherical. Following this, the equilibrium at the interface can be determined by the interfacial energy as a measure of the degree of anisotropy, which becomes a function of the surface normal η.77
The surface energy can be expressed in the form of:
γsl = γ0sl[1 + εη![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ηΘ)] cos(ηΘ)] | (2.24) |
Three dimensional Wulff constructions can be extrapolated in polar coordinates, as can be seen in Fig. 3a for different crystal shapes.80 The Wulff construction can determine the surface energy as a function of the growth orientation. Experimentally, surface energies are indirectly determined from surface tension measurements, which are made in the liquid phase and then extrapolated to zero temperature without relation to any particular orientation. However, computed methods can be used to simulate the growth and shape of the materials as a dimension of anisotropy, such as phase-field models.81–83 For instance, Y. Lu et al.,84 have simulated three-dimensional free dendritic growth of a pure material in the presence of fluid flow, as can be seen in Fig. 3b. In this study, the dendrite tip growth without domain boundary interfering on thermal and velocity boundary layers can reach a steady state. Hence, tips growing in different directions to the streamflow cannot reach a steady-state regime, allowing more realistic scenarios, where the parabolic dendrite tip radius can be insufficient as we will discuss in the next subsection.
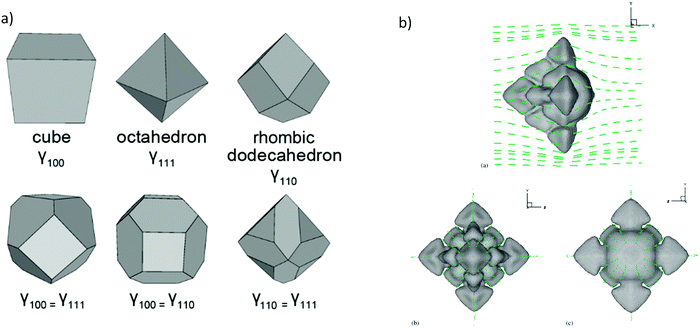 | ||
| Fig. 3 (a) Common Wulff constructions for materials with full cubic symmetry (reproduced with permission from ref. 79, Creative Commons License). (b) Computed dendrite morphology with directions heat flow, (a), (b) and (c) different views of the 3D construction (reproduced with permission from ref. 83, ©2005 Published by Elsevier B.V.). | ||
This topic can be summarized by following the “rules of thumb” for crystal growth. Firstly, the maximum surface energy is relevant to the case when the crystal seeks to minimize its total surface energy, which can be accomplished by the creation of a relatively higher curvature in the direction of the maximum energy. Secondly, the concept of minimum surface stiffness has to be considered in the particular case when the crystal prefers to grow in the direction where the surface has the smallest resistance to deformation.85 At the end, the dendritic growth direction depends strongly on the anisotropy of the solid–liquid interfacial energy. In this respect, the Wulff construction can determine the anisotropy of the surface energy from small solid/liquid particles in equilibrium.61
A steady state solution to the heat flow from a dendrite is provided by the Ivantsov equation for a paraboloid of revolution (3D):
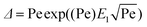 | (2.25) |
This solution uses a thermal diffusion equation as a boundary condition for the interface shape, expressing the thermal field in terms of Péclet Pe number:
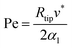 | (2.26) |
One of the limitations of Ivantsov relation is the surface energy, considering the surface isotropy, which does not satisfy the Gibbs–Thomson condition.91 Therefore, it indicates the steady-state in the form of parabolic dendritic crystals. However, it cannot determine Rtip and v uniquely, it only determines the product of both. The temperature remains constant across the surface, which is far from the anisotropic interfacial energy situation.77,92–94 Even the non-isothermal temperature boundary condition, for which the solution developed later by Horvay and Cahn95 is relevant, does not satisfy the energy conservation and the non-isothermal equilibrium temperature boundary condition. Other approximations have been developed to overcome this limitation, based on the choice of a predetermined interface shape.35,96 All these non-isothermal theories share the common feature that the values of ν* and Rtip can be determined independently, and they can be adapted to the determination of the dendritic shape for the solid transformation of perovskite films under rapid thermal growth.
3. Rapid perovskite crystallization
3.1. Crystallization kinetic
The crystallization kinetics for perovskite halide in a foreign substrate depend strongly on the interfacial energy of the solid/liquid interface. As well as to a lesser degree, the solid/gas interface, taking into account that most of the perovskite solidification processes are done in a controlled atmosphere.97,98 Moreover, the chemical bonding particularities between surface and liquid defines the strength of cohesive molecular forces, thus competing with thermal diffusion to shape the final crystal growth.99 Ayan A. Zhumekenov et al.100 have investigated the role of the surface tension on perovskite crystallization, elucidating that the increase of surface tension leads to preferential nucleation at the surface layer, as shown in Fig. 4a. They establish a relationship between intramolecular forces, interfacial energy and crystal preferential growth. These fundamental studies are crucial for obtaining highly uniform films and high-performance large-scale devices; for instance, Yehao Deng et al.101 have used amphoteric surfactants (L-α-phosphatidylcholine) to improve the adhesion of the perovskite to hydrophobic substrates, which allows them to scale-up the processes with fast blade-coating.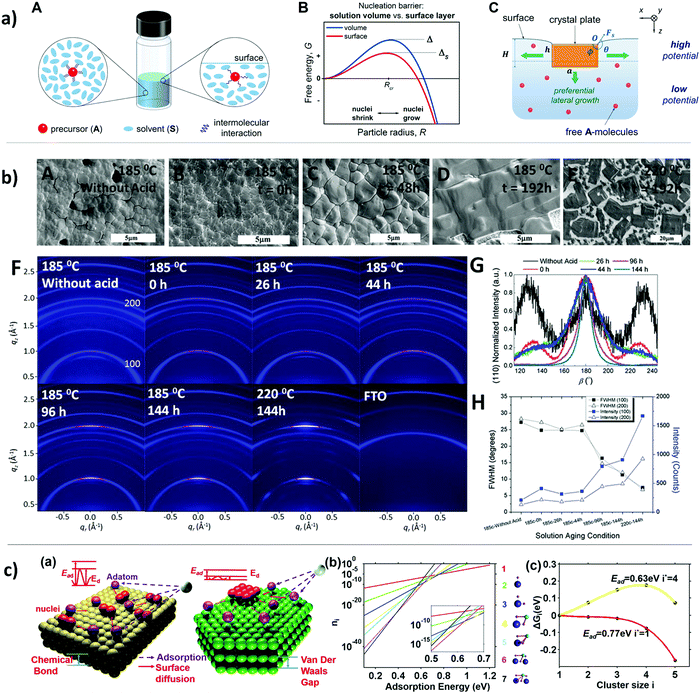 | ||
| Fig. 4 (a) (A) Schematic of change in molecular interaction energies, (B) graph illustrating nucleation barriers for the solution surface and in the volume and (C) schematic of crystal growth during inverse temperature crystallization (reproduced with permission from ref. 98, ©2017 American Chemical Society). (b) Impact of colloids in the precursor solution on morphology and crystal quality. (A–E) Top-view SEM images of perovskite thin film with and without hydrohalic acids. (F) A series of 2D X-ray diffraction patterns. (G) Diffraction peak of corresponding perovskite thin film. (H) Full-width half maximum (FWHM) of (100) and (200) orientation corresponding to the (100) and (200) diffraction peaks (reproduced with permission from ref. 14, ©2017 The Authors. Published by Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim). (c) (a) Schematic of different atomistic processes on substrate in terms of adsorption energy (Ead), diffusion barrier (Ed), and nuclei sizes. (b) Plot of cluster coverage with a size i changes with Ead (reproduced with permission from ref. 101, ©2015 American Chemical Society). | ||
David P. McMeekin et al.15 settled a relationship between the precursor solution's colloid concentration and the crystal morphology of the perovskite thin film by adding hydrohalic, initiating the lead polyhalide colloids and acting as nucleation sites for further crystal growth, as can be seen in Fig. 4b. Additionally, they applied a solution aging time to control the size and dispersion of colloids in solution, thus increasing the grain size, crystallinity, and texture. In the same line, Benjamin J. Foley et al.102 have demonstrated the use of additives for MAPbI3 precursor solutions to alter the nucleation and growth processes. They were able to lower the free energy of the precursor by incorporating a sulfoxide, which strongly interacts with MAPbI3 precursors, allowing a control over the nucleation density and growth rate. Yiping Wang et al.103 showed how the bonding nature of 3D materials affects the kinetics of crystallization for extremely thin film growth, as can be seen in Fig. 4c. They proposed that weak van der Waals film-substrate interaction and low cohesive energy of the perovskite halide lead to 2D growth.
3.2. Antisolvent crystallization
In antisolvent (AS) crystallization, the solute crystallizes due to reduced solubility. AS occurs when exposing a solution to another solvent in which the product is almost insoluble. Additionally, the reduction of solubility can be performed by the gas flow on the crystallization process.104–106 The way of reaching the supersaturation can determine several crystal features such as size, morphology, and coexisting atomic structures.107 Nevertheless, this review focuses on liquid room temperature solvent cases. Although, a complete description of the crystallization process requires mass and energy balances.108,109 In a continuous phase, the solute's mass balance contributes to the mass transfer into the growing crystal.110There are many advantages in AS crystallization, such as low operating temperature and solvent activities that can have a deep effect in the polymorphic form of the final crystal growth.111–113 Several models have been implemented for AS crystallization, in order to identify different patterns of behavior in terms of antisolvent addition rates, product average particle size and size distribution. Nowee et al.,114 found that a growth rate relation results in sharper mean size increases in the feeding's early stages. Therefore, the population balance model, previously discussed in Sections 2.2.3 and 2.3.3, and the solution approach has been used for many authors to combine a nucleation and growth rate description for the AS crystallization.115–117
3.3. The antisolvent method for perovskite halide crystallization
The solution processability of perovskite materials is one of the most important advantages of PSCs.118,119 The perovskite layer is typically deposited by a solution coating method.14 A one-step spin-coating method is most often used because of its simplicity and low cost.120–123 During the coating process, a so-called anti-solvent is dropped on top of the layer for the perovskite crystal growth. Additional thermal annealing is necessary to remove the remaining solvent and reach a purer perovskite phase.124–126 The solvent can be removed with AS and heat treatment, reaching the necessary driving force to induce crystallization on the perovskite films.10 In the solution preparation methods, the humidity plays a fundamental role. It is well-known that perovskite MAPbI3 films are sensitive to moisture, causing them to decompose into PbI2.11,12 Therefore, the manufacture of PSCs should be carried out under controlled atmosphere conditions with low humidity values.In 2014 Nam Joong Jeon et al.127 were the first to use the AS method for highly efficient perovskite solar cells. Starting from MAPbI2 precursors in a mixture of DMSO/GBL solvents they used toluene to supersaturate and crystallize the thin film during spinning by applying a relatively low-temperature thermal treatment. In the same year 2014, Xiao et al.128 used chlorobenzene as exhibiting a smooth and compact perovskite film surface, being composed of micron-sized grains as shown Fig. 5. In the Fig. 5, the transmission electron microscopy (TEM) image of the CH3NH3PbI3 is a corroboration of the formation of a crystalline structure of the tetragonal CH3NH3PbI3 phase, with the pattern of different thin film crystalline phases further confirmed by XRD analysis.
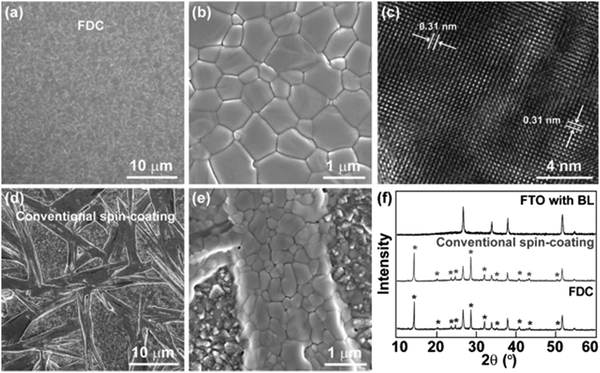 | ||
| Fig. 5 Morphological and structural characterization of MAPbI3 films prepared by fast crystallization-deposition (FDC) and a conventional spin-coating process (reproduced with permission from ref. 123, ©2014 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim). | ||
3.4. Acid–base reaction of perovskite halides
In 2016 Nayak et al.129 proposed one of the first approaches for understanding the mechanism of perovskite halide crystallization from solution, as can be seen in Fig. 6a. In their observations, increasing the solution acidity can surpass the supersaturation state of the solutes and in turn decrease the strength of the solvent. This results in the onset of crystallization, which in turn can be decoupled from the changes of temperature. Therefore, the crystallization can be initiated by the change of the solvent and the acid–base equilibria in the solution. In order to achieve high quality perovskite films, Fei Zhang et al.130 used a Lewis acid–base adduct approach as an effective way to control grain size, morphology and to suppress crystal defects.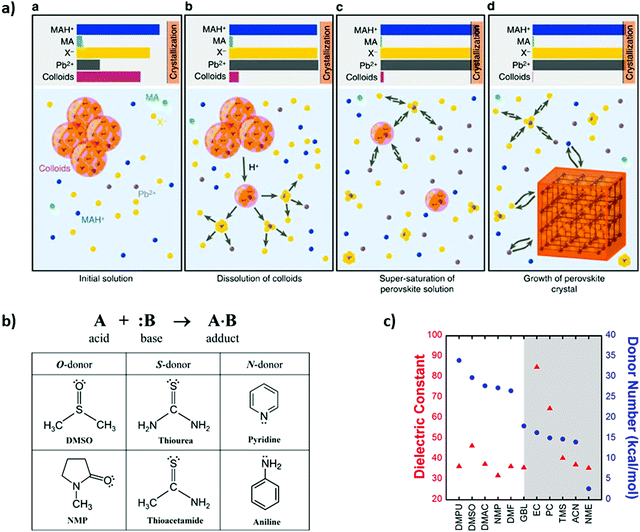 | ||
| Fig. 6 (a) Schematic of the mechanism for crystallization of perovskite solid phase, where it represents the state of the system at several key points (reproduced with permission from ref. 124, ©2016 Springer Nature). (b) Representation of the Lewis acid (A)–base (B) reaction to form an adduct (A·B) with a dative bond and Lewis bases with different molecule donors (reproduced with permission from ref. 126, ©2016 American Chemical Society). (c) Dielectric constant (red triangles) and Gutmann's donor number (DN, blue circles) of solvents used for perovskite processing (reproduced with permission from ref. 127, ©2017 American Chemical Society). | ||
Other approaches to control the rapid film growth have been carried out by Jin-Wook Lee et al.131 as shown in Fig. 6b, which presents the Lewis acid reaction forming an adduct. In this work, different iodide compounds were dissolved in polar aprotic solvents acting as Lewis basis. DMSO was proven as an intermediate solvent for controlling MAPbI3 morphology and grain size. FAPbI3 perovskite composition found that thiourea was a better solvent-complement than DMSO because of the chemical interaction differences. Hamill et al.132 demonstrated that solvent coordination with Pb2+ is correlated with Lewis basicity, which in turn influences solid-state perovskite formation, as shown in Fig. 6c. They focused on elucidating the role of Lewis basicity of the processing solvent, quantified by Gutmann's donor number, DN, as a strong predictor of a solvent's ability to solvate perovskite precursors.
3.5. Role of common solvents for perovskite crystallization
In the two-step approach for perovskite thin film preparation it is essential to ensure a complete reaction of the PbI2 film formed in the first step with the salt of the organic cation added in the second step as residual PbI2 has been demonstrated to have detrimental effects on efficiency, reproducibility133 and stability133–135 of PSCs. This can be facilitated if mesoporous films of PbI2 are formed in the first step allowing a more efficient conversion into the desired perovskite. Furthermore, this also prevents the formation of rough film surfaces otherwise caused by unit cell expansion upon intercalation of the organic halide.136 Formation of mesoporous films can, for example, be achieved by controlling the nucleation/growth process during crystallization of PbI2. To this end one can exploit the formation of PbI2·xSol (Sol = solvent) films during spin-coating of a solution of PbI2. Starting from a DMF solution of PbI2 a PbI2·xDMF film forms with x > 1 due to the presence of unbound solvent in the fresh films.136–139
Upon thermal annealing a solvent-mediated Ostwald ripening process takes place leading to the formation of cracks and voids resulting in a mesoporous film.140 However, due to the weak interaction of DMF with Pb2+ (DN(DMF) = 26.6 kcal mol−1) and its low boiling point (152 °C) DMF evaporates quickly not allowing enough time for this process. By keeping the PbI2·xDMF film in a closed Petri dish this time can be extended leading to the formation of larger voids and an increase in the fraction of voids in the whole film.141 Alternatively, fast removal of DMF by applying drops of IPA (anti-solvent) onto the as-prepared PbI2·xDMF films can be employed to prepare mesoporous PbI2.139,142 In addition to using pure DMF the introduction of co-solvents and additives (e.g. DMSO, NMP, HMPA) with higher boiling points and improved interaction with PbI2, as indicated by their higher DNs, has been used to improve the grain coarsening process during solvent annealing after spin-coating of PbI2.133,134,143–151 On the other hand, acetonitrile (DN(MeCN) = 14.1 kcal mol−1) as an example of a weakly Lewis basic solvent has also been used as an additive in PbI2/DMF to improve grain morphology and roughness of the final perovskite film.151,152
In other instances, the PbI2·xSol complexes formed before thermal annealing have been treated directly with the desired organic halide and shown to improve the final performance of PSCs.153–156 This approach uses the intercalation of solvent molecules such as DMF, DMSO or NMP into the PbI2 lattice to expand the PbI2 unit cell along the c-axis157 followed by an exchange with MAI or FAI to avoid unit cell expansion and therefore build-up of strain leading to rough surfaces during the perovskite formation step. The solvent molecules are removed during thermal annealing after the addition of the organic cation, inducing perovskite formation. More strongly coordinating solvents lead to larger grains in the final perovskite films.156,157 This was explained by their stronger interaction with Pb2+ slowing down iodide coordination.132,156,157
Finally, in a study by Etgar et al., the authors found that dropping toluene (AS) onto a perovskite precursor film prepared via the two-step method leads to a higher conductivity of the final film after subsequent thermal annealing. Furthermore, this treatment was found to efficiently suppress hysteresis. This demonstrates that the use of anti-solvents cannot only be used to control nucleation/growth kinetics and crystallinity of perovskite films but also to affect their electronic properties.
A further level of control was introduced into this process by Sang Il Seok et al. who employed a “solvent engineering” approach to control perovskite film formation.127 By spin-coating a solution of PbI2, PbBr2, MAI and MABr in a mixture of GBL and DMSO followed by toluene (anti-solvent) dripping they first obtained an intermediate phase film which was then converted into the final MAPb(I1−xBrx)3 (x = 0.1–0.15) perovskite structure by thermal annealing. This led to the formation of highly uniform films with 100% surface coverage which could not be achieved when either DMSO was excluded from the precursor solution or no anti-solvent was applied during spin-coating. The intermediate phase which only formed in the presence of DMSO was suggested to contain MAI, PbI2 and DMSO in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio following a series of experiments excluding MABr and PbBr2. Nam-Gyu Park and co-workers later prepared the clear intermediate phase from a precursor solution containing PbI2, MAI and DMSO in an exact 1
1 ratio following a series of experiments excluding MABr and PbBr2. Nam-Gyu Park and co-workers later prepared the clear intermediate phase from a precursor solution containing PbI2, MAI and DMSO in an exact 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio using diethyl ether as anti-solvent to avoid loss of DMSO due to their immiscibility.158 The exact structure of the intermediate film was revealed by Yao et al. to consist of ribbons with the formula [Pb3I8]2− with MA+ and DMSO molecules located in between to form a structure with the composition of MA2Pb3I8·2DMSO by using a 1
1 ratio using diethyl ether as anti-solvent to avoid loss of DMSO due to their immiscibility.158 The exact structure of the intermediate film was revealed by Yao et al. to consist of ribbons with the formula [Pb3I8]2− with MA+ and DMSO molecules located in between to form a structure with the composition of MA2Pb3I8·2DMSO by using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of DMF and DMSO and toluene as anti-solvent.158,159 The uncoordinated MAI was suggested to be either located on the surface of the intermediate phase crystals or homogeneously distributed around the intermediate phase domains.
3 mixture of DMF and DMSO and toluene as anti-solvent.158,159 The uncoordinated MAI was suggested to be either located on the surface of the intermediate phase crystals or homogeneously distributed around the intermediate phase domains.
The role of DMSO has been described as retarding the reaction between PbI2 and MAI during evaporation of the solvent thereby granting more control over the crystallization process allowing the production of higher quality perovskite films. Interestingly, in a follow-up study optimizing the annealing conditions for conversion of MA2Pb3I8·2DMSO into MAPbI3 perovskite the authors found that the devices demonstrating the highest PCEs of 15% still contained ca. 18% of the intermediate phase.160 They proposed that this prevented the formation of voids and cracks in the final perovskite film. Different ratios of PbI2, MAI and DMSO have been explored to prepare devices with high efficiency and reproducibility.160–162 Besides the commonly used anti-solvents toluene, diethyl ether and chlorobenzene also ethyl acetate,163 trifluorotoluene,163,164 hexane165 (39) and a mixture of 6% IPA in chlorobenzene165,166 have been shown to lead to high PCEs of final devices.
Using a mixture of NMP and DMA to dissolve PbI2 and MAI Ding et al. developed a thermal annealing-free method for the preparation of high quality perovskite films presenting a PCE of 17.09% compared to marginally higher 17.38% including thermal annealing.165–167 Padture et al. designed a solvent-solvent extraction method using diethyl ether to remove DMF after spin-coating their perovskite precursor solution in an effort to demonstrate a scalable way for the preparation of high-quality perovskite films.168 This process was carried out at room temperature and required no further thermal annealing due to the low boiling point of diethyl ether. To address the issue of a narrow time window for immersing the film in the washing solvent, Zhu et al. added MACl to the perovskite precursor solution of PbI2 and MAI in DMF/NMP to obtain a new ink which after blade coating gives a precursor film that remains stable for ca. 8 min during which it can be transferred into the diethyl ether bath.168,169
3.6. Perovskite film crystallization with IR pulses
The experimental investigation of crystal nucleation and growth is complex and still today a challenge for almost all systems. The classical nucleation theory stipulates that the critical nucleus is a sphere, where the important factor is how the total free energy associated with the formation of an average critical nucleus depends on its size, whatever the shape. However, this is a steady or quasi steady-state assumption. This analysis cannot be applicable to non-thermodynamic equilibrium as for example when the temperature changes too fast as in the case of the FIRA, which is still one of the main challenges for the rate calculations in these processes. Quasi-infinity steady-state numeric calculations corresponding to non-isothermal conditions, with a non-constant temperature rate, need to be performed.172–174 Particularly in perovskite film processing, the calculation of nucleation and growth rates needs to be adapted for specific cases.
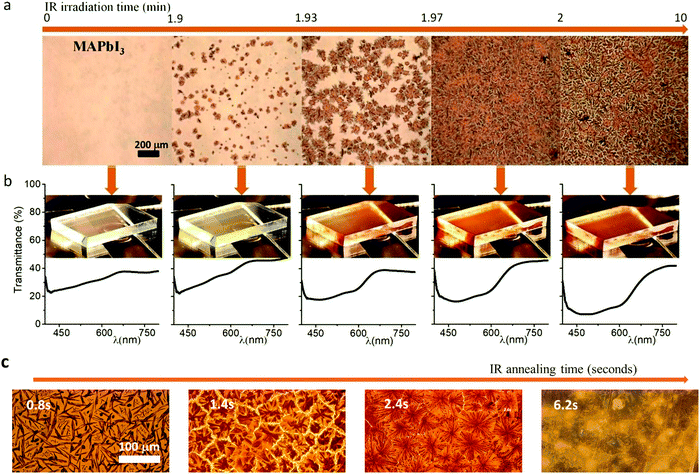 | ||
| Fig. 8 (a) Optical images in transmittance mode of in situ perovskite crystallization from solution. (b) Transmittance spectra and images of the sample measured in (a). (c) Optical images taken in transmission mode for different flash times. (Reproduced with permission from ref. 23, ©2020, American Chemical Society). | ||
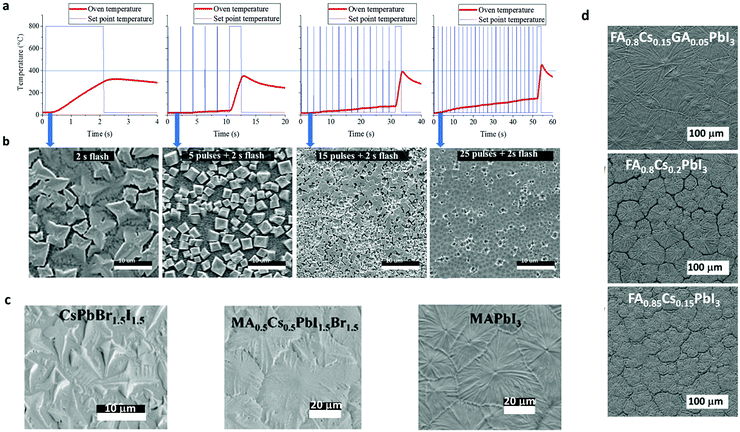 | ||
| Fig. 9 (a) Temperature profile of the IR photonic pulses for inorganic perovskite and (b) the SEM images resulting from the annealed samples (adapted with permission from ref. 26, ©2018 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim). Top view SEM images of (c) three different perovskite chemical compositions and (d) three different stoichiometry for triple and double cation halide perovskites, all synthesized by a single IR pulse (adapted with permission from ref. 136, ©2019 The Author(s). Published by Elsevier Ltd4). | ||
4. Crystal grow and phase evolution
4.1. Crystal growth
The perovskite crystallization dynamics will depend on the processing method to be used, such as the commonly so-called one- and two-step depositions (as previously discussed in Section 3.3). This kind of “step deposition” methods are based on a solution process, and the number of steps depends on the solution precursor to be deposited.122,179,180 All precursor can be contained in the same solutions, or different solutions with different solvents can be used, i.e. PbI2 in DMSO and MAI in IPA. Diffusion processes play a fundamental role in the reaction process and crystallization. For instance, Tetsuhiko Miyadera et al.,181 have observed anomalous diffusion, where the CH3NH3I diffuses into the PbI2 films with fractal morphology, as shown in Fig. 9a. They claim that two growth orientation modes are possible, one which during the initial stage of the crystal reaction maintains the orientation of the initial materials and another, which represents the ordinary crystal orientation in the vertical direction; finally, we have the random orientation in the final stage of the crystal growth.In terms of two steps deposition crystallization mechanism, Yongping Fu et al.182 have proposed two growth mechanisms: a solid–liquid interfacial conversion reaction (Fig. 10b-a) and a dissolution–recrystallization growth mechanism (Fig. 10b-b). They argue that at a low MAI precursor concentration the conversion occurs by a solid–liquid interfacial reaction, and the perovskite phase is obtained by MAI diffusion into the layered PbI2. Instead, Qiuju Liang et al.181,183 have used a selective solvent annealing, a similar procedure to the antisolvent method. Here, the chosen solvent IPA promotes the precipitation and crystallization of lead halide, as shown in Fig. 10c, thus promoting the intercalation of MA+ into an inorganic cage, resulting in a final perovskite phase. The Oswalt ripening process rearranges and coalesces during perovskite crystallization due to surface minimization, resulting in an increased crystal growth rate and optimized crystal orientation.
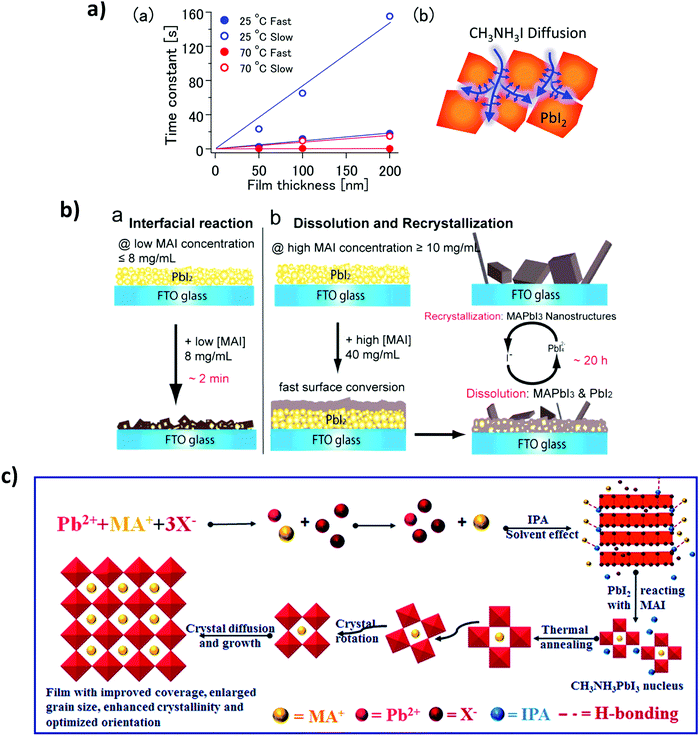 | ||
| Fig. 10 (a) (a) Time constant values (τ) were obtained under various conditions fitting. (b) Schematic illustration of the MAPbI3 diffusion with fractal peculiarities (Reproduced with permission from ref. 139, ©2015, American Chemical Society). (b) Schematic illustrations of the two growth mechanisms of MAPbI3 nanostructures, (a) interfacial reaction mechanism at lower MAI concentration and (b) dissolution–recrystallization growth mechanism at higher MAI concentration (reproduced with permission from ref. 140, ©2015, American Chemical Society). (c) The schematic diagram of the crystal nucleation during the selective solvent annealing and crystal growth during the thermal annealing processes (reproduced with permission of The Royal Society of Chemistry (RSC) on behalf of the Centre National de la Recherche Scientifique). | ||
4.2. Temperature phase transition
The phase transition as a function of temperature in perovskite halide has been widely investigated.7,184–186 However, there is still a lack of understanding how the temperature rate does affect the final perovskite grain shape and for instance the non-radiative defects on the solid films. In this effort, P. S. Whitfield et al.187 have examined the crystal structures and structural phase lattice parameters and phase transitions of a MAPbI3, Fig. 11a and b. They found that the cubic-tetragonal transition in MAPbI3 is driven by an out-phase rotation mode, while the tetragonal-orthorhombic transition is primarily driven by an in-phase in MAPbI3. They claimed that it is possible that the charge carrier scattering with these modes also contributes significantly to the electrical transport properties. Ilka M. Hermes et al,188 have resolved an anisotropic distribution of carrier diffusion times on isolated MAPbI3 grains correlated to the arrangement of ferroelastic twin domains, which reduces crystalline strain due to the cubic-tetragonal phase transition. Furthermore, Timothy W. Jones, et al.189 have suggested that non-radiative defects come from local strains (at different scales), associated with inhomogeneous nucleation and growth, where local differences or intermediate phases during solution deposition would lead to heterogeneous growth.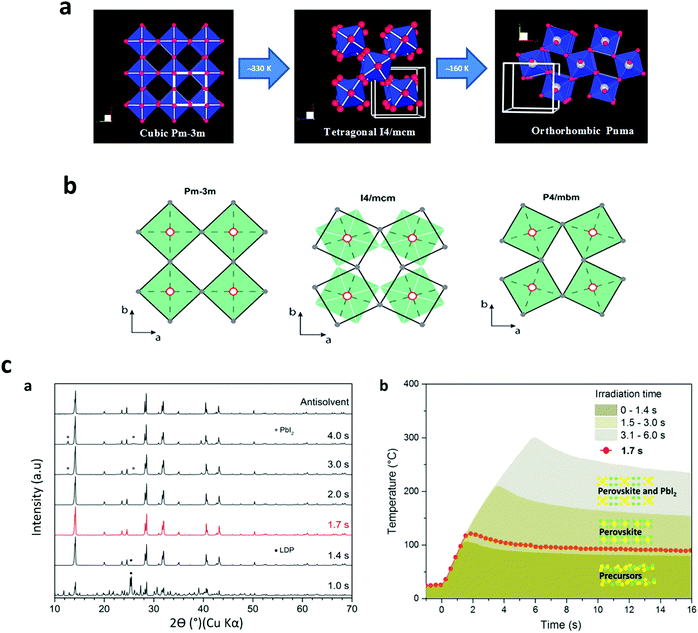 | ||
| Fig. 11 (a) Cubic to tetragonal transition-rotational distortion mode, and tetragonal to orthorhombic transition-a combination of two different distortion modes. (b) Filled green squares and unfilled black squares displays the relative rotations of neighboring layers of PbI6-octahedra along the c axis. (Reproduced with permission from ref. 145, ©2016, Springer Nature). (c) XRD patterns of MAPbI3 powders (scrapped from synthesized films) (a) on FTO and (b) temperature profile of the perovskite phases, extracted from (a) (reproduced with permission from ref. 25, ©2019 American Chemical Society). | ||
The phase transition can also be elucidated from the rapid temperature profile, which allows us to identify the annealing parameters. In the first published study on the FIRA method,26 the authors did comparative observations from a preliminary examination of the powder XRD data (Fig. 11c–a and b). While both perovskite films prepared, using the AS and FIRA-2.0 s methods exhibit similar XRD patterns, the 1.4 and 3.0 s FIRA annealed thin films show the boundary of the MAPbI3 black phase. FIRA can accurately determine phase evolution during annealing, as the short pulse duration allows screening of material properties at many different temperatures. Thus, making it possible to plot the temperature profile upon material degradation as a function of the annealing time, ∼16 s, representative of the phase transition obtained from the XRD data. This phase diagram shows a close phase transition as is widely reported in literature,190–192 and in turn is a useful tool for studying accurately the perovskite phase evolution under controlled and rapid thermal annealing.
4.3. Rapid thermal annealing
As well, it can be a consequence of the different interatomic distance in plane and the corresponding latent heat of phase transfer (and its relation with surface), where a complex interplay between geometric and electronic structure presents a challenge for theory.203 The crystal rapid growth kinetics for melt can be extrapolated for solutions precursor materials, with similar primary consequences mainly in morphology and crystal shape. However, other complex phenomena arise for solution processes due to the interaction of the solvents and precursors as reactant materials.204,205
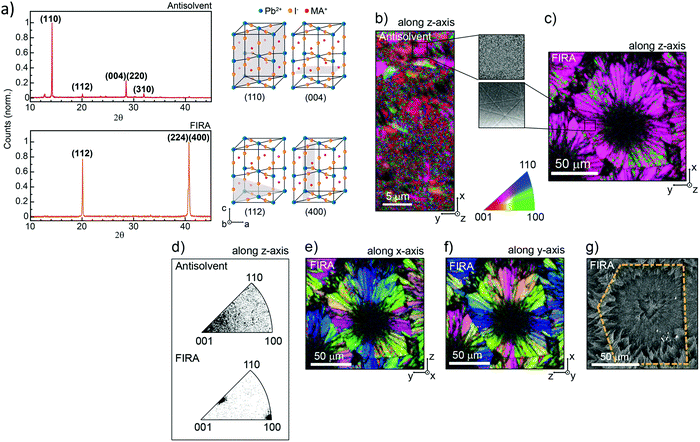 | ||
| Fig. 12 (a) XRD patterns of AS and FIRA perovskite films with the corresponding unit cell cut in different planes. (b) Crystallographic orientation along the z-direction of the EBDS figure map. (Inset) Magnification of the Kikuchi patterns of the sample. (c) Zoom-out of the image. (d) Distribution of orientation for the two samples along the z-direction. (e) EBDS image of the FIRA sample showing the crystallographic orientation along the x-direction and (f) y-direction. (g) Crystallographic orientation along the x-direction and (f) y-direction shown in the FIRA sample's EBDS image. (g) SEM image confirming the grain size of the sample. (Reproduced with permission from ref. 162, ©2019 American Chemical Society). | ||
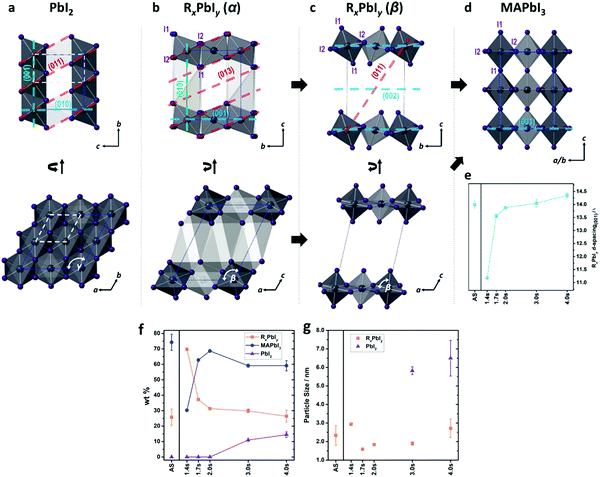 | ||
| Fig. 13 PbI6 structures of (a) PbI2, (b) RxPbIy (α), (c) RxPbIy (β), and (d) MAPbI3 viewed from different directions. (e) The evolution of the d-spacing between the (0 0 1) planes in RxPbIy. (f) Weight fraction evolution of each component and (g) particle sizes of PbI2 and RxPbIy derived from PDF refinement. (Reproduced with permission from ref. 163, ©2019 American Chemical Society). | ||
The phase fraction (wt%) evolution and particle size of the components derived from the PDF refinement as a function of annealing time can be seen in Fig. 13f and g. The incorporation of MA layer during annealing tilts the PbI6 octahedra leading to conversion from intermediates phases (alpha and beta), the 2D building blocks, to form the 3D perovskite phase. In this study, the 2.0 s of FIRA annealing give rise to 2D-to-3D structure transition reaching its maximum conversion rate. While intermediate phases contain around 30 wt%. The further increase of the temperature by continued exposure to IR (>2.0 s), results in a degradation of the thin film where both the intermediates and the perovskite decompose to PbI2. Finally, changing the interfacial energy anisotropy by a bottom layer of mesoporous TiO2 onto the FTO substrate does not significantly modify the perovskite phase evolution under the studied experimental conditions. However, there is a modification of the crystallization kinetics leading to different lateral domain sizes in the film, as predicted previously. Therefore, the thin film processing should avoid the formation of intermediate phases in order to enhance the stability and performance of PSCs.
5. Conclusions
In summary, the crystallization of perovskite films is one of the most important factors in order to manufacture highly efficient and stable devices. As discussed, there is a direct relationship between the quality of the solid film and efficiency losses and degradation. The target is to produce defect-tolerant thin films and low concentrations of non-radiant recombination centers and deep traps. Compositional engineering along with the deposition method are key instruments for perovskite crystal formation, which must be thoroughly understood before being chosen. The activation energy for the formation of perovskite crystals depends on the chemical reaction of the species involved and/or the temperature of the process. Together with the interfacial energy, specifically with the substrate to be used and the atmospheric conditions, it significantly influences crystal growth. Finally, in this review we reveal and relate the fundamentals of the FIRA manufacturing tool to be used as a reproducible method for highly crystalline perovskite thin film applications.Conflicts of interest
There are no conflicts to declare.References
- A. Rajagopal, K. Yao and A. K.-Y. Jen, Toward Perovskite Solar Cell Commercialization: A Perspective and Research Roadmap Based on Interfacial Engineering, Adv. Mater., 2018, 30, 1800455 CrossRef PubMed.
- Perovskite solar cells approaching commercialization, Phys. Today, 2014 DOI:10.1063/pt.5.028283.
- M. Jeong, et al., Stable perovskite solar cells with efficiency exceeding 24.8% and 0.3 V voltage loss, Science, 2020, 369, 1615–1620 CrossRef CAS PubMed.
- M. Pazoki, A. Hagfeldt and T. Edvinsson, Characterization Techniques for Perovskite Solar Cell Materials, Elsevier, 2019 Search PubMed.
- M. Graetzel, Molelcular Photovoltaics and Perovskite Solar Cells, Proceedings of the 10th International Conference on Hybrid and Organic Photovoltaics, 2018, DOI: 10.29363/nanoge.hopv.2018.205.
- J. L. Knutson, J. D. Martin and D. B. Mitzi, Tuning the band gap in hybrid tin iodide perovskite semiconductors using structural templating, Inorg. Chem., 2005, 44, 4699–4705 CrossRef CAS PubMed.
- N.-G. Park, M. Grätzel and T. Miyasaka, Organic-Inorganic Halide Perovskite Photovoltaics: From Fundamentals to Device Architectures, Springer, 2016 Search PubMed.
- N. S. Arul and V. D. Nithya, Revolution of Perovskite: Synthesis, Properties and Applications, Springer Nature, 2020 Search PubMed.
- K. Fu, A. W. Ho-Baillie, H. K. Mulmudi and P. T. T. Trang, Perovskite Solar Cells: Technology and Practices, CRC Press, 2019 Search PubMed.
- Electronic Traps and Their Correlations to Perovskite Solar Cell Performance via Compositional and Thermal Annealing Controls. 10.1021/acsami.8b17431.s001.
- T. Miyasaka, Compositional engineering of cost efficient durable perovskite solar cells. Proceedings of the 3rd International Conference on Perovskite and Organic Photovoltaics and Optoelectronics, 2018, DOI: 10.29363/nanoge.iperop.2019.016.
- W. Zhang, Metal Halide Perovskite Crystals: Growth, Techniques, Properties and Emerging Applications, MDPI, 2019 Search PubMed.
- Interface-Dependent Radiative and Nonradiative Recombination in Perovskite Solar Cells DOI:10.1021/acs.jpcc.8b00998.s001 .
- B. Chen, P. N. Rudd, S. Yang, Y. Yuan and J. Huang, Imperfections and their passivation in halide perovskite solar cells, Chem. Soc. Rev., 2019, 48, 3842–3867 RSC.
- D. P. McMeekin, et al., Crystallization Kinetics and Morphology Control of Formamidinium-Cesium Mixed-Cation Lead Mixed-Halide Perovskite via Tunability of the Colloidal Precursor Solution, Adv. Mater., 2017, 29, 1607039 CrossRef PubMed.
- S. Zhang, et al., Controlling Orientation Diversity of Mixed Ion Perovskites: Reduced Crystal Microstrain and Improved Structural Stability, J. Phys. Chem. Lett., 2019, 10, 2898–2903 CrossRef CAS PubMed.
- B. Chen, et al., Synergistic Effect of Elevated Device Temperature and Excess Charge Carriers on the Rapid Light-Induced Degradation of Perovskite Solar Cells, Adv. Mater., 2019, 31, e1902413 CrossRef PubMed.
- G. Tumen-Ulzii, et al., Detrimental Effect of Unreacted PbI on the Long-Term Stability of Perovskite Solar Cells, Adv. Mater., 2020, 32, e1905035 CrossRef PubMed.
- C. C. Boyd, R. Cheacharoen, T. Leijtens and M. D. McGehee, Understanding Degradation Mechanisms and Improving Stability of Perovskite Photovoltaics, Chem. Rev., 2019, 119, 3418–3451 CrossRef CAS PubMed.
- L. Liu, et al., Grain-Boundary ‘Patches’ by In Situ Conversion to Enhance Perovskite Solar Cells Stability, Adv. Mater., 2018, e1800544 CrossRef PubMed.
- H. Lorenz, Solubility and Solution Equilibria in Crystallization, Crystallization, 2013, 35–74, DOI:10.1002/9783527650323.ch3.
- H. Esaka and W. Kurz, Columnar dendrite growth: Experiments on tip growth, J. Cryst. Growth, 1985, 72, 578–584 CrossRef CAS.
- Lithium Dendrite Growth Through Polymer Electrolytes, ECS Meeting Abstracts (2013) DOI:10.1149/ma2013-02/14/1097.
- S. Sanchez, X. Hua and A. Guenzler, Flash infrared pulse time control of perovskite crystal nucleation and growth from solution, Cryst. Growth Des., 2020, 670–679 CrossRef CAS.
- S. Sánchez, M. Vallés-Pelarda and J. A. Alberola-Borràs, Flash infrared annealing as a cost-effective and low environmental impact processing method for planar perovskite solar cells, Mater. Today, 2019, 39–46 CrossRef.
- S. Sanchez, X. Hua, N. Phung and U. Steiner, Flash Infrared Annealing for Antisolvent-Free Highly Efficient Perovskite Solar Cells, Adv. Energy, 2018, 8, 1702915 CrossRef.
- S. Sanchez, N. Christoph and B. Grobety, Efficient and stable inorganic perovskite solar cells manufactured by pulsed flash infrared annealing, Adv. Energy, 2018, 1802060 CrossRef.
- P. S. V. Ling, A. Hagfeldt and S. Sanchez, Flash Infrared Annealing for Perovskite Solar Cell Processing, J. Vis. Exp., 2021, 168, e61730, DOI:10.3791/61730.
- R. B. Fair, Junction Formation in Silicon by Rapid Thermal Annealing, Rapid Therm. Process., 1993, 169–226, DOI:10.1016/b978-0-12-247690-7.50009-3.
- H. Gross, O. Khvostikova and U. Willkommen, Rapid Thermal Annealing for Large Area Applications. Society of Vacuum Coaters 57th (2014) Annual Technical Conference Proceedings (2015) DOI:10.14332/svc14.proc.1825.
- A. T. Fiory, Rapid Thermal Annealing, Encyclopedia of Materials: Science and Technology, 2001, pp. 8009–8017 DOI:10.1016/b0-08-043152-6/01440-6.
- C. Hill, S. Jones and D. Boys, Rapid Thermal Annealing - Theory and Practice, Reduced Thermal Processing for ULSI, 1989, 143–180, DOI:10.1007/978-1-4613-0541-5_4.
- H. L. Bhat, Introduction to Crystal Growth: Principles and Practice, CRC Press, 2014 Search PubMed.
- K. A. Jackson, Kinetic Processes: Crystal Growth, Diffusion, and Phase Transitions in Materials, John Wiley & Sons, 2010 Search PubMed.
- D. M. Herlach, Solidification and Crystallization, John Wiley & Sons, 2006 Search PubMed.
- K. Sangwal, Nucleation and Crystal Growth: Metastability of Solutions and Melts, John Wiley & Sons, 2018 Search PubMed.
- P. P. von Weimarn, 1879–1935. Kolloid-Zeitschrift74 1–10 (1936).
- M. R. Leach, Lewis Acid–base Reaction Chemistry, 1999.
- D. T. Haynie, Gibbs free energy – theory, Biol. Thermodyn., 2012, 85–133, DOI:10.1017/cbo9780511802690.005.
- W. C. M. Lewis, A System of Physical Chemistry: Kinetic theory, 1918.
- A. C. Lasaga, Kinetic Theory in the Earth Sciences, ( 2014) DOI:10.1515/9781400864874.
- A. E. S. Van Driessche, M. Kellermeier, L. G. Benning and D. Gebauer, New Perspectives on Mineral Nucleation and Growth: From Solution Precursors to Solid Materials, Springer, 2016 Search PubMed.
- Y. Shibuta, et al., Heterogeneity in homogeneous nucleation from billion-atom molecular dynamics simulation of solidification of pure metal, Nat. Commun., 2017, 8, 10 CrossRef PubMed.
- D. Bi, et al., Polymer-templated nucleation and crystal growth of perovskite films for solar cells with efficiency greater than 21%, Nat. Energy, 2016, 1, 16142 CrossRef CAS.
- F. L. Binsbergen, Natural and artificial heterogeneous nucleation in polymer crystallization, J. Polym. Sci., Polym. Symp., 1977, 59, 11–29 CrossRef CAS.
- M. K. Hoffmeyer, Heterogeneous Nucleation Catalysis and Grain Refinement, (1990).
- A. Hulanicki, Reactions of Acids and Bases in Analytical Chemistry, Ellis Horwood, 1987 Search PubMed.
- K. A. Connors, Chemical Kinetics: The Study of Reaction Rates in Solution, Wiley-VCH Verlag GmbH, 1990.
- A. C. Lasaga and D. M. Rye, Fluid flow and chemical reaction kinetics in metamorphic systems, Am. J. Sci., 1993, 293, 361–404 CrossRef CAS.
- S. Arrhenius, IV. Electrolytic dissociation versus hydration, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1889, 28, 30–38 CrossRef.
- J. W. Gooch, Arrhenius Equation. Encyclopedic Dictionary of Polymers, 2011, p. 48 DOI:10.1007/978-1-4419-6247-8_800.
- T. Turányi and A. S. Tomlin, Analysis of Kinetic Reaction Mechanisms, Springer, 2014 Search PubMed.
- J. W. P. Schmelzer, Nucleation Theory and Applications, John Wiley & Sons, 2006 Search PubMed.
- D. B. Abraham and C. M. Newman, Equilibrium Stranski–Krastanow and Volmer–Weber models, EPL, 2009, 86, 16002 CrossRef.
- M. Volmer, Thermodynamische Folgerungen ans der Zustandsgleichung für adsorbierte Stoffe, Z. Phys. Chem., 1925, 115U, 253–260 CrossRef.
- R. McGraw, Arrhenius Temperature Dependence of Homogeneous Nucleation Rates, Nucleation and Atmospheric Aerosols, 2007, 144–148, DOI:10.1007/978-1-4020-6475-3_29.
- P. J. Phillips, Polymer Crystallization: Growth by Secondary Nucleation, Encyclopedia of Materials: Science and Technology, pp. 7253–7255 ( 2001) DOI:10.1016/b0-08-043152-6/01290-0.
- G. D. Botsaris, Secondary Nucleation – A Review, Industrial Crystallization, 1976, 3–22, DOI:10.1007/978-1-4615-7258-9_1.
- G. M. Maggioni and M. Mazzotti, A Stochastic Population Balance Equation Model for Nucleation and Growth of Crystals with Multiple Polymorphs, Cryst. Growth Des., 2019, 19, 4698–4709 CrossRef CAS.
- W. Sha and S. Malinov, The Johnson–Mehl–Avrami method: isothermal transformation kinetics, Titanium Alloys, 2009, 117–164, DOI:10.1533/9781845695866.2.117.
- J. A. Dantzig and M. Rappaz, Solidification: 2nd Edition - Revised & Expanded, EPFL Press, 2016 Search PubMed.
- A. D. Randolph and M. A. Larson, The Population Balance. Theory of Particulate Processes, 1971, pp. 41–63 DOI:10.1016/b978-0-12-579650-7.50008-7.
- H. A. Jakobsen, The Population Balance Equation, Chemical Reactor Modeling, 2014, pp. 807–865 DOI:10.1007/978-3-540-68622-4_9.
- M. A. Henson, Distribution control of particulate systems based on population balance equation models. Proceedings of the 2003 American Control Conference, 2003 DOI:10.1109/acc.2003.1240456.
- A. W. Vere, Crystal Growth: Principles and Progress, Springer Science & Business Media, 1988 Search PubMed.
- W. W. Mullins, Macroscopic description of interface migration by ledge and kink motion controlled by volume diffusion, Metall. Trans. A, 1991, 22, 1225–1233 CrossRef.
- D. Kondrashova and R. Valiullin, Freezing and Melting Transitions under Mesoscalic Confinement: Application of the Kossel–Stranski Crystal-Growth Model, J. Phys. Chem. C, 2015, 119, 4312–4323 CrossRef CAS.
- C. Ratsch and A. Zangwill, Equilibrium theory of the Stranski–Krastanov epitaxial morphology, Surf. Sci. Lett., 1993, 293, A633 CrossRef.
- W. K. Burton, N. Cabrera and F. C. Frank, Role of Dislocations in Crystal Growth, Nature, 1949, 163, 398–399 CrossRef CAS.
- R. Bonnet, M. Loubradou and J. M. Pénisson, Burgers vector content of an interfacial ledge, Phys. Rev. Lett., 1992, 69, 104–107 CrossRef CAS PubMed.
- M. E. Gurtin, E. Fried and L. Anand, The Burgers vector and the flow of screw and edge dislocations in finite-deformation single-crystal plasticity, J. Mech. Phys. Solids, 2006, 588–592, DOI:10.1017/cbo9780511762956.118.
- V. A. Shneidman, Ostwald ripening with nucleation initial conditions, AIP Conf. Proc., 2013, 1527, 105–108, DOI:10.1063/1.4803214.
- C. I. Steefel and P. Van Cappellen, A new kinetic approach to modeling water-rock interaction: The role of nucleation, precursors, and Ostwald ripening, Geochim. Cosmochim. Acta, 1990, 54, 2657–2677 CrossRef CAS.
- M. Koolyk, D. Amgar, S. Aharon and L. Etgar, Kinetics of cesium lead halide perovskite nanoparticle growth; focusing and de-focusing of size distribution, Nanoscale, 2016, 8, 6403–6409 RSC.
- N. D. Pham, et al., Guanidinium thiocyanate selective Ostwald ripening induced large grain for high performance perovskite solar cells, Nano Energy, 2017, 41, 476–487 CrossRef CAS.
- I. Steinbach, Effect of interface anisotropy on spacing selection in constrained dendrite growth, Acta Mater., 2008, 56, 4965–4971 CrossRef CAS.
- B. J. Spencer and H. E. Huppert, The relationship between dendrite tip characteristics and dendrite spacings in alloy directional solidification, J. Cryst. Growth, 1999, 200, 287–296 CrossRef CAS.
- R. Dobrushin, R. Kotecký and S. Shlosman, Wulff Construction: A Global Shape from Local Interaction, Translations of Mathematical Monographs ( 1992) DOI:10.1090/mmono/104.
- E. Ringe, R. P. Van Duyne and L. D. Marks, Wulff Construction for Alloy Nanoparticles, Nano Lett., 2011, 11, 3399–3403 CrossRef CAS PubMed.
- G. D. Barmparis, Z. Lodziana, N. Lopez and I. N. Remediakis, Nanoparticle shapes by using Wulff constructions and first-principles calculations, Beilstein J. Nanotechnol., 2015, 6, 361–368 CrossRef PubMed.
- H. M. Ding and L. C. Pu, Thermal Kinetics Phase Field Model for the Metals’ Solidification - Mathematic Derivation of the Dendrite Growth Phase Field Variable Diffusion Model, Appl. Mech. Mater., 2013, 364, 614–618 Search PubMed.
- M. Hofacker and C. Miehe, A Phase Field Model for Three-Dimensional Dynamic Fracture and its Efficient Numerical Implementation, PAMM, 2011, 11, 153–154 CrossRef.
- M. Wouts, Surface Tension in the Dilute Ising Model. The Wulff Construction, Commun. Math. Phys., 2009, 289, 157–204 CrossRef.
- Y. Lu, C. Beckermann and J. C. Ramirez, Three-dimensional phase-field simulations of the effect of convection on free dendritic growth, J. Cryst. Growth, 2005, 280, 320–334 CrossRef CAS.
- J. P. van der Eerden, Relevance of surface roughening and surface melting for crystal growth, J. Cryst. Growth, 1993, 128, 62–68 CrossRef CAS.
- G. Ding, W. Huang, X. Lin and Y. Zhou, Prediction of average spacing for constrained cellular/dendritic growth, J. Cryst. Growth, 1997, 177, 281–288 CrossRef CAS.
- Z.-K. Liu and Y. Austin Chang, On the applicability of the Ivantsov growth equation, J. Appl. Phys., 1997, 82, 4838–4841 CrossRef CAS.
- T. Nishinaga, Handbook of Crystal Growth: Fundamentals, Elsevier, 2014 Search PubMed.
- G. Müller, J.-J. Métois and P. Rudolph, Crystal Growth - From Fundamentals to Technology, Elsevier, 2004 Search PubMed.
- B. C. Garrett and D. G. Truhlar, Transition State Theory, Encyclopedia of Computational Chemistry, 2002 DOI:10.1002/0470845015.cta014.
- A. Salhoumi and P. K. Galenko, Gibbs–Thomson condition for the rapidly moving interface in a binary system, Phys. A, 2016, 447, 161–171 CrossRef.
- W. Kurz and D. J. Fisher, Dendrite growth at the limit of stability: tip radius and spacing, Acta Metall., 1981, 29, 11–20 CrossRef CAS.
- S. Konstantinov, I. Smurov and G. Flamant, Influence of pulsed laser processing conditions on dendrite tip radius, Appl. Surf. Sci., 1997, 109-110, 113–123 CrossRef.
- R. González-Cinca and L. Ramírez-Piscina, Numerical study of the shape and integral parameters of a dendrite, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051612 CrossRef PubMed.
- G. Horvay and J. W. Cahn, Dendritic and spheroidal growth, Acta Metall., 1961, 9, 695–705 CrossRef CAS.
- S. G. R. Brown, T. Williams and J. A. Spittle, A cellular automaton model of the steady-state ‘free’ growth of a non-isothermal dendrite, Acta Metall. Mater., 1994, 42, 2893–2898 CrossRef CAS.
- Y. Sun, et al., Engineering the Phases and Heterostructures of Ultrathin Hybrid Perovskite Nanosheets, Adv. Mater., 2020, 32, e2002392 CrossRef PubMed.
- C. Bi, B. Chen, H. Wei, S. DeLuca and J. Huang, Efficient Flexible Solar Cell based on Composition-Tailored Hybrid Perovskite, Adv. Mater., 2017, 29, 1605900 CrossRef PubMed.
- S. Cui, et al., Rubidium Ions Enhanced Crystallinity for Ruddlesden-Popper Perovskites, Adv. Sci., 2020, 7, 2002445 CrossRef CAS PubMed.
- A. A. Zhumekenov, et al., The Role of Surface Tension in the Crystallization of Metal Halide Perovskites, ACS Energy Lett., 2017, 2, 1782–1788 CrossRef CAS.
- Y. Deng, et al., Surfactant-controlled ink drying enables high-speed deposition of perovskite films for efficient photovoltaic modules, Nat. Energy, 2018, 3, 560–566 CrossRef CAS.
- B. J. Foley, et al., Controlling nucleation, growth, and orientation of metal halide perovskite thin films with rationally selected additives, J. Mater. Chem. A, 2017, 5, 113–123 RSC.
- Y. Wang, Y. Shi, G. Xin, J. Lian and J. Shi, Two-Dimensional van der Waals Epitaxy Kinetics in a Three-Dimensional Perovskite Halide, Cryst. Growth Des., 2015, 15, 4741–4749 CrossRef CAS.
- D. J. Dixon and K. P. Johnston, Molecular thermodynamics of solubilities in gas antisolvent crystallization, AIChE J., 1991, 37, 1441–1449 CrossRef CAS.
- F. Kurniawansyah, L. Quachie, R. Mammucari and N. R. Foster, Improving the dissolution properties of curcumin using dense gas antisolvent technology, Int. J. Pharm., 2017, 521, 239–248 CrossRef CAS PubMed.
- R. Szostak, S. Sanchez and P. E. Marchezi, Revealing the Perovskite Film Formation Using the Gas Quenching Method by In Situ GIWAXS: Morphology, Properties, and Device Performance, Adv. Funct. Mater., 2021, 31, 2007473 CrossRef CAS.
- C. Zuo and L. Ding, An 80.11% FF record achieved for perovskite solar cells by using the NH4Cl additive, Nanoscale, 2014, 6, 9935–9938 RSC.
- J. Garside, Mass Crystallization, Number Balances and Size Distributions, Sci. Technol. Cryst. Growth, 1995, 209–220, DOI:10.1007/978-94-011-0137-0_16.
- M. Giulietti and A. Bernardo, Crystallization by Antisolvent Addition and Cooling, Cryst. Sci. Technol., 2012, 380–395, DOI:10.5772/50328.
- K. Fukui and K. Maeda, Effects of crystal growth rate and heat and mass transfer on solute distribution, Chem. Eng. Sci., 2002, 57, 3133–3140 CrossRef CAS.
- A. Vanhook, Kinetics of Crystallization Growth of Crystals, Crystallization, 2013, 149–187, DOI:10.1016/b978-1-4832-3051-1.50010-0.
- S. Ueno, Y. Hamada and K. Sato, Controlling Polymorphic Crystallization ofn-Alkane Crystals in Emulsion Droplets through Interfacial Heterogeneous Nucleation, Cryst. Growth Des., 2003, 3, 935–939 CrossRef CAS.
- K. Liao, et al., Aqueous solvent-regulated crystallization and interfacial modification in perovskite solar cells with enhanced stability and performance, J. Power Sources, 2020, 471, 228447 CrossRef CAS.
- S. M. Nowee, S. Mostafa Nowee, A. Abbas and J. A. Romagnoli, Antisolvent crystallization: Model identification, experimental validation and dynamic simulation, Chem. Eng. Sci., 2008, 63, 5457–5467 CrossRef.
- Z. K. Nagy, A population balance model approach for crystallization product engineering via distribution shaping control, Comput.-Aided Chem. Eng., 2008, 139–144, DOI:10.1016/s1570-7946(08)80028-4.
- C. Y. Ma and X. Z. Wang, Model identification of crystal facet growth kinetics in morphological population balance modeling of l-glutamic acid crystallization and experimental validation, Chem. Eng. Sci., 2012, 70, 22–30 CrossRef CAS.
- Y. D. Shu, J. J. Liu, Y. Zhang and X. Z. Wang, A multi-stage multi-component transfer rate morphological population balance model for crystallization processes, CrystEngComm, 2019, 21, 4212–4220 RSC.
- L. Yang, et al., Novel Insight into the Role of Chlorobenzene Antisolvent Engineering for Highly Efficient Perovskite Solar Cells: Gradient Diluted Chlorine Doping, ACS Appl. Mater. Interfaces, 2019, 11, 792–801 CrossRef CAS PubMed.
- M. M. Tavakoli, et al., Controllable Perovskite Crystallization via Antisolvent Technique Using Chloride Additives for Highly Efficient Planar Perovskite Solar Cells, Adv. Energy Mater., 2019, 9, 1803587 CrossRef.
- Unveiling the Concentration-Dependent Grain Growth of Perovskite Films from One- and Two-Step Deposition Methods: Implications for Photovoltaic Application DOI:10.1021/acsami.7b05892.s001 .
- C. Liu, et al., α-CsPbI Bilayers via One-Step Deposition for Efficient and Stable All-Inorganic Perovskite Solar Cells, Adv. Mater., 2020, 32, e2002632 CrossRef.
- J.-H. Im, H.-S. Kim and N.-G. Park, Morphology-photovoltaic property correlation in perovskite solar cells: One-step versus two-step deposition of CH3NH3PbI3, APL Mater., 2014, 2, 081510 CrossRef.
- F. Fang, J. Chen, G. Wu and H. Chen, Highly efficient perovskite solar cells fabricated by simplified one-step deposition method with non-halogenated anti-solvents, Org. Electron., 2018, 59, 330–336 CrossRef CAS.
- F. Yang, et al., Enhanced Crystallization by Methanol Additive in Antisolvent for Achieving High-Quality MAPbI3 Perovskite Films in Humid Atmosphere, ChemSusChem, 2018, 11, 2348–2357 CrossRef CAS PubMed.
- Y. Li, et al., Acetic Acid Assisted Crystallization Strategy for High Efficiency and Long-Term Stable Perovskite Solar Cell, Adv. Sci., 2020, 7, 1903368 CrossRef CAS PubMed.
- D. Angmo, et al., Controlling Homogenous Spherulitic Crystallization for High-Efficiency Planar Perovskite Solar Cells Fabricated under Ambient High-Humidity Conditions, Small, 2019, 15, e1904422 CrossRef PubMed.
- N. J. Jeon, et al., Solvent engineering for high-performance inorganic-organic hybrid perovskite solar cells, Nat. Mater., 2014, 13, 897–903 CrossRef CAS PubMed.
- M. Xiao, et al., A fast deposition-crystallization procedure for highly efficient lead iodide perovskite thin-film solar cells, Angew. Chem., Int. Ed., 2014, 53, 9898–9903 CrossRef CAS PubMed.
- P. K. Nayak, et al., Mechanism for rapid growth of organic–inorganic halide perovskite crystals, Nat. Commun., 2016, 7, 13303 CrossRef CAS PubMed.
- F. Zhang, et al., Suppressing defects through the synergistic effect of a Lewis base and a Lewis acid for highly efficient and stable perovskite solar cells, Energy Environ. Sci., 2018, 11, 3480–3490 RSC.
- J.-W. Lee, H.-S. Kim and N.-G. Park, Lewis Acid–Base Adduct Approach for High Efficiency Perovskite Solar Cells, Acc. Chem. Res., 2016, 49, 311–319 CrossRef CAS PubMed.
- J. C. Hamill, J. Schwartz and Y.-L. Loo, Influence of Solvent Coordination on Hybrid Organic–Inorganic Perovskite Formation, ACS Energy Lett., 2018, 3, 92–97 CrossRef CAS.
- C. Jiang, S. L. Lim, W. P. Goh, F. X. Wei and J. Zhang, Improvement of CH3NH3PbI3 Formation for Efficient and Better Reproducible Mesoscopic Perovskite Solar Cells, ACS Appl. Mater. Interfaces, 2015, 7, 24726–24732 CrossRef CAS PubMed.
- H. Zhang, et al., Nanostructures: A smooth CH3 NH3 PbI3 film via a new approach for forming the PbI2 nanostructure together with strategically high CH3 NH3 I concentration for high efficient planar-heterojunction solar cells, Adv. Energy mater. 23/2015, Adv. Energy Mater., 2015, 5, 1501354 CrossRef.
- J. Cao, et al., Porous PbI2 films for the fabrication of efficient, stable perovskite solar cells via sequential deposition, J. Mater. Chem. A, 2016, 4, 10223–10230 RSC.
- C.-H. Chiang and C.-G. Wu, Bulk heterojunction perovskite–PCBM solar cells with high fill factor, Nat. Photonics, 2016, 10, 196–200 CrossRef CAS.
- H. Zheng, W. Wang, S. Yang, Y. Liu and J. Sun, A facile way to prepare nanoporous PbI2 films and their application in fast conversion to CH3NH3PbI3, RSC Adv., 2016, 6, 1611–1617 RSC.
- X. B. Cao, et al., High quality perovskite films fabricated from Lewis acid–base adduct through molecular exchange, RSC Adv., 2016, 6, 70925–70931 RSC.
- A. Wakamiya, et al., Reproducible fabrication of efficient perovskite-based solar cells: X-ray crystallographic studies on the formation of CH3NH3PbI3 layers, Chem. Lett., 2014, 43, 711–713 CrossRef CAS.
- X. Cao, et al., Elucidating the Key Role of a Lewis Base Solvent in the Formation of Perovskite Films Fabricated from the Lewis Adduct Approach, ACS Appl. Mater. Interfaces, 2017, 9, 32868–32875 CrossRef CAS PubMed.
- T. Liu, et al., Mesoporous PbI2 Scaffold for High-Performance Planar Heterojunction Perovskite Solar Cells, Adv. Energy Mater., 2016, 6, 1501890 CrossRef.
- W.-T. Wang, S. K. Das and Y. Tai, Fully Ambient-Processed Perovskite Film for Perovskite Solar Cells: Effect of Solvent Polarity on Lead Iodide, ACS Appl. Mater. Interfaces, 2017, 9, 10743–10751 CrossRef CAS PubMed.
- J. Cao, et al., Identifying the Molecular Structures of Intermediates for Optimizing the Fabrication of High-Quality Perovskite Films, J. Am. Chem. Soc., 2016, 138, 9919–9926 CrossRef CAS.
- C. Yi, X. Li, J. Luo, S. M. Zakeeruddin and M. Grätzel, Perovskite Photovoltaics with Outstanding Performance Produced by Chemical Conversion of Bilayer Mesostructured Lead Halide/TiO2 Films, Adv. Mater., 2016, 28, 2964–2970 CrossRef CAS PubMed.
- W. Wu, et al., Tuning PbI2 layers by n-butanol additive for improving CH3NH3PbI3 light harvesters of perovskite solar cells, RSC Adv., 2016, 6, 89609–89613 RSC.
- X. Cao, et al., Control of the morphology of PbI2 films for efficient perovskite solar cells by strong Lewis base additives, J. Mater. Chem. C, 2017, 5, 7458–7464 RSC.
- Y. Shi, et al., Effects of 4-tert-butylpyridine on perovskite formation and performance of solution-processed perovskite solar cells, J. Mater. Chem. A, 2015, 3, 22191–22198 RSC.
- K. Sun, et al., Lewis acid–base interaction-induced porous PbI2 film for efficient planar perovskite solar cells, ACS Appl. Energy Mater, 2018, 1, 2114–2122 CrossRef CAS.
- B. Li, et al., Facile deposition of mesoporous PbI2 through DMF:DMSO solvent engineering for sequentially deposited metal Halide perovskites, ACS Appl. Energy Mater, 2020, 3, 3358–3368 CrossRef CAS.
- Z.-W. Kwang, C.-W. Chang, T.-Y. Hsieh, T.-C. Wei and S.-Y. Lu, Solvent-modulated reaction between mesoporous PbI2 film and CH3NH3I for enhancement of photovoltaic performances of perovskite solar cells, Electrochim. Acta, 2018, 266, 118–129 CrossRef CAS.
- P. M. Moreno-Romero, et al., Roughness and structural modification of PbI2 thin films by isopropanol treatment to improve methylammonium lead halide formation and solar cell efficiency, J. Mater. Sci.: Mater. Electron., 2019, 30, 17491–17503 CrossRef CAS.
- L. Li, et al., The Additive Coordination Effect on Hybrids Perovskite Crystallization and High-Performance Solar Cell, Adv. Mater., 2016, 28, 9862–9868 CrossRef CAS PubMed.
- W. S. Yang, et al., Solar Cells. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange, Science, 2015, 348, 1234–1237 CrossRef CAS PubMed.
- L. Zhi, et al., Perovskite Solar Cells Fabricated by Using an Environmental Friendly Aprotic Polar Additive of 1,3-Dimethyl-2-imidazolidinone, Nanoscale Res. Lett., 2017, 12, 632 CrossRef PubMed.
- Y. Jo, et al., High performance of planar perovskite solar cells produced from PbI2(DMSO) and PbI2(NMP) complexes by intramolecular exchange, Adv. Mater. Interfaces, 2016, 3, 1500768 CrossRef.
- X. B. Cao, et al., Fabrication of high quality perovskite films by modulating the Pb–O bonds in Lewis acid–base adducts, J. Mater. Chem. A, 2017, 5, 8416–8422 RSC.
- C. C. Coleman, H. Goldwhite and W. Tikkanen, A review of intercalation in heavy metal iodides, Chem. Mater., 1998, 10, 2794–2800 CrossRef CAS.
- N. Ahn, et al., Highly Reproducible Perovskite Solar Cells with Average Efficiency of 18.3% and Best Efficiency of 19.7% Fabricated via Lewis Base Adduct of Lead(II) Iodide, J. Am. Chem. Soc., 2015, 137, 8696–8699 CrossRef CAS PubMed.
- Y. Rong, et al., Solvent engineering towards controlled grain growth in perovskite planar heterojunction solar cells, Nanoscale, 2015, 7, 10595–10599 RSC.
- Y. Rong, et al., Critical kinetic control of non-stoichiometric intermediate phase transformation for efficient perovskite solar cells, Nanoscale, 2016, 8, 12892–12899 RSC.
- Y. Bai, et al., A pure and stable intermediate phase is key to growing aligned and vertically monolithic perovskite crystals for efficient PIN planar perovskite solar cells with high processibility and stability, Nano Energy, 2017, 34, 58–68 CrossRef CAS.
- Y. Wang, et al., Interfacial modification towards highly efficient and stable perovskite solar cells, Nanoscale, 2020, 12, 18563–18575 RSC.
- P. Zhou, et al., Efficient and stable mixed perovskite solar cells using P3HT as a hole transporting layer, J. Mater. Chem. C, 2018, 6, 5733–5737 RSC.
- S. Paek, et al., From nano- to micrometer scale: The role of antisolvent treatment on high performance perovskite solar cells, Chem. Mater., 2017, 29, 3490–3498 CrossRef CAS.
- Y. Yu, et al., Ultrasmooth Perovskite Film via Mixed Anti-Solvent Strategy with Improved Efficiency, ACS Appl. Mater. Interfaces, 2017, 9, 3667–3676 CrossRef CAS PubMed.
- Y. Wang, et al., Stitching triple cation perovskite by a mixed anti-solvent process for high performance perovskite solar cells, Nano Energy, 2017, 39, 616–625 CrossRef CAS.
- X. Fang, et al., Annealing-free perovskite films based on solvent engineering for efficient solar cells, J. Mater. Chem. C, 2017, 5, 842–847 RSC.
- Y. Zhou, et al., Room-temperature crystallization of hybrid-perovskite thin films via solvent–solvent extraction for high-performance solar cells, J. Mater. Chem. A, 2015, 3, 8178–8184 RSC.
- M. Yang, et al., Perovskite ink with wide processing window for scalable high-efficiency solar cells, Nat. Energy, 2017, 2, 17038 CrossRef CAS.
- High-Power and Flexible Indoor Solar Cells via Controlled Growth of Perovskite Using a Greener Antisolvent DOI:10.1021/acsaem.0c00997.s003.
- Y. Wang, T. Mahmoudi, W.-Y. Rho and Y.-B. Hahn, Fully-ambient-air and antisolvent-free-processed stable perovskite solar cells with perovskite-based composites and interface engineering, Nano Energy, 2019, 64, 103964 CrossRef CAS.
- R. J. Schaefer, The validity of steady-state dendrite growth models, J. Cryst. Growth, 1978, 43, 17–20 CrossRef CAS.
- D. A. Kessler and H. Levine, Computational approach to steady-state eutectic growth, J. Cryst. Growth, 1989, 94, 871–879 CrossRef CAS.
- S. Epure, T. Duffar and L. Braescu, Comparison between analytical and numeric determination of the interface curvature during dewetted Bridgman crystal growth, J. Cryst. Growth, 2008, 310, 1559–1563 CrossRef CAS.
- M. He, et al., Meniscus-assisted solution printing of large-grained perovskite films for high-efficiency solar cells, Nat. Commun., 2017, 8, 16045 CrossRef CAS PubMed.
- M. Rappaz and W. Kurz, Dendrites solidified by computer, Nature, 1995, 375, 103 CrossRef CAS.
- T. Haxhimali, A. Karma, F. Gonzales and M. Rappaz, Orientation selection in dendritic evolution, Nat. Mater., 2006, 5, 660–664 CrossRef CAS PubMed.
- S. Sánchez, J. Jerónimo-Rendon, M. Saliba and A. Hagfeldt, Highly efficient and rapid manufactured perovskite solar cells via Flash InfraRed Annealing, Mater. Today, 2020, 35, 9–15 CrossRef.
- G. Cotella, et al., One-step deposition by slot-die coating of mixed lead halide perovskite for photovoltaic applications, Sol. Energy Mater. Sol. Cells, 2017, 159, 362–369 CrossRef CAS.
- H.-S. Ko, J.-W. Lee and N.-G. Park, 15.76% efficiency perovskite solar cells prepared under high relative humidity: importance of PbI2 morphology in two-step deposition of CH3NH3PbI3, J. Mater. Chem. A, 2015, 3, 8808–8815 RSC.
- T. Miyadera, et al., Crystallization Dynamics of Organolead Halide Perovskite by Real-Time X-ray Diffraction, Nano Lett., 2015, 15, 5630–5634 CrossRef CAS PubMed.
- Y. Fu, et al., Solution growth of single crystal methylammonium lead halide perovskite nanostructures for optoelectronic and photovoltaic applications, J. Am. Chem. Soc., 2015, 137, 5810–5818 CrossRef CAS PubMed.
- Q. Liang, et al., Enhancing the crystallization and optimizing the orientation of perovskite films via controlling nucleation dynamics, J. Mater. Chem. A, 2016, 4, 223–232 RSC.
- A. Dobrovolsky, A. Merdasa, E. L. Unger, A. Yartsev and I. G. Scheblykin, Defect-induced local variation of crystal phase transition temperature in metal-halide perovskites, Nat. Commun., 2017, 8, 34 CrossRef PubMed.
- Local Rearrangement of the Iodide Defect Structure Determines the Phase Segregation Effect in Mixed-Halide Perovskites DOI:10.1021/acs.jpclett.0c01127.s001 .
- J. Lin, et al., Thermochromic halide perovskite solar cells, Nat. Mater., 2018, 17, 261–267 CrossRef CAS PubMed.
- P. S. Whitfield, et al., Corrigendum: Structures, Phase Transitions and Tricritical Behavior of the Hybrid Perovskite Methyl Ammonium Lead Iodide, Sci. Rep., 2017, 7, 42831 CrossRef CAS PubMed.
- I. M. Hermes, et al., Anisotropic carrier diffusion in single MAPbI3 grains correlates to their twin domains, Energy Environ. Sci., 2020, 13, 4168–4177, 10.1039/d0ee01016b.
- T. W. Jones, et al., Lattice strain causes non-radiative losses in halide perovskites, Energy Environ. Sci., 2019, 12, 596–606 RSC.
- A. Baumann, et al., Identification of Trap States in Perovskite Solar Cells, J. Phys. Chem. Lett., 2015, 6, 2350–2354 CrossRef CAS PubMed.
- T. Wang, et al., Indirect to direct bandgap transition in methylammonium lead halide perovskite, Energy Environ. Sci., 2017, 10, 509–515 RSC.
- J. M. Frost, K. T. Butler and A. Walsh, Molecular ferroelectric contributions to anomalous hysteresis in hybrid perovskite solar cells, APL Mater., 2014, 2, 081506 CrossRef.
- L. Pfeiffer, S. Paine, G. H. Gilmer, W. van Saarloos and K. W. West, Pattern Formation Resulting from Faceted Growth in Zone-Melted Thin Films, Phys. Rev. Lett., 1985, 54, 1944–1947 CrossRef CAS PubMed.
- J. Johansson, B. A. Wacaser, K. A. Dick and W. Seifert, Growth related aspects of epitaxial nanowires, Nanotechnology, 2006, 17, S355–S361 CrossRef CAS.
- D. P. Woodruff and D. P. Woodruff, The Solid–Liquid Interface, CUP Archive, 1973 Search PubMed.
- H. M. Anderson and P. J. Hargis, A Model for Silicon Dendrite Growth During Laser/Plasma Deposition from a Silane Discharge, MRS Proc., 1986, 75, 755–764 CrossRef.
- G. Y. Chen, H. K. Lin and C. W. Lan, Phase-field modeling of twin-related faceted dendrite growth of silicon, Acta Mater., 2016, 115, 324–332 CrossRef CAS.
- T. Aoyama, Y. Takamura and K. Kuribayashi, Dendrite growth processes of silicon and germanium from highly undercooled melts, Metall. Mater. Trans. A, 1999, 30, 1333–1339 CrossRef.
- B.-C. Sim, Y.-H. Jung, J.-E. Lee and H.-W. Lee, Effect of the crystal–melt interface on the grown-in defects in silicon CZ growth, J. Cryst. Growth, 2007, 299, 152–157 CrossRef CAS.
- T. Abe, T. Takahashi and K. Shirai, Steady distribution structure of point defects near crystal-melt interface under pulling stop of CZ Si crystal, J. Cryst. Growth, 2017, 459, 87–94 CrossRef CAS.
- Y. Yoshida and G. Langouche, Defects and Impurities in Silicon Materials: An Introduction to Atomic-Level Silicon Engineering, Springer, 2016 Search PubMed.
- D. W. Oxtoby and A. D. J. Haymet, A molecular theory of the solid–liquid interface. II. Study of bcc crystal–melt interfaces, J. Chem. Phys., 1982, 76, 6262–6272 CrossRef CAS.
- M. Schmidt, R. Kusche, B. von Issendorff and H. Haberland, Irregular variations in the melting point of size-selected atomic clusters, Nature, 1998, 393, 238–240 CrossRef CAS.
- G. Nasti, S. Sanchez, I. Gunkel, S. Balog and B. Roose, Patterning of perovskite–polymer films by wrinkling instabilities, Soft Matter, 2017, 13, 1654–1659 RSC.
- J. Wang, et al., Templated growth of oriented layered hybrid perovskites on 3D-like perovskites, Nat. Commun., 2020, 11, 582 CrossRef CAS PubMed.
- L. A. Muscarella, et al., Crystal Orientation and Grain Size: Do They Determine Optoelectronic Properties of MAPbI3 Perovskite?, J. Phys. Chem. Lett., 2019, 10, 6010–6018 CrossRef CAS PubMed.
- S. Sanchez, U. Steiner and X. Hua, Phase Evolution During Perovskite Formation—Insight from Pair Distribution Function Analysis, Chem. Mater., 2019, 9, 3498–3506 CrossRef.
- A Mechanistic Study of Phase Transformation in Perovskite Nanocrystals Driven by Ligand Passivation DOI:10.1021/acs.chemmater.7b02425.s001 .
- T. J. Jacobsson, L. J. Schwan, M. Ottosson, A. Hagfeldt and T. Edvinsson, Determination of Thermal Expansion Coefficients and Locating the Temperature-Induced Phase Transition in Methylammonium Lead Perovskites Using X-ray Diffraction, Inorg. Chem., 2015, 54, 10678–10685 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |