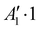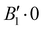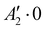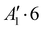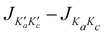Correction: Quantum tunneling dynamical behaviour on weakly bound complexes: the case of a CO₂–N₂ dimer

Abstract

Correction for ‘Quantum tunneling dynamical behaviour on weakly bound complexes: the case of a CO₂–N₂ dimer’ by Miguel Lara-Moreno et al., Phys. Chem. Chem. Phys., 2019, 21, 3550–3557, DOI: 10.1039/c8cp04465a.

---

About one year after the publication of our original article¹ reporting the first calculations of the rovibrational bound states of the van der Waals system CO₂–N₂, the lowest intermolecular bending frequency v₂ was measured by Barclay et al.² They found a large discrepancy between the calculated and measured frequencies, the calculated frequency being more than two times larger than the measured one. This discrepancy motivated Quintas-Sánchez et al.³ to perform new calculations, using a new accurate potential energy surface (PES). Conversely to the original article, their calculation of the lowest intermolecular bending frequency is in excellent agreement with the experimental one. This raised questions on the accuracy of our calculations. The PES we have used (PES-1) is expected to be slightly less accurate than the one (PES-2) used by Quintas-Sánchez et al. Both PESs have been generated by the explicitly-correlated coupled-cluster theory (CCSD(T)-F12), with a quadruple-zeta basis set for PES-1 and with an extrapolation based on triple- and quadruple-zeta basis sets for PES-2. The two PESs are quite similar. The comparison of the energies of the stationary points shows differences of a few cm⁻¹. Since it was difficult to attribute the large error on frequency to inaccuracies of PES-1, we turned our attention to the method used for the rovibrational states calculations. Quintas-Sánchez et al.'s and our methods are based on a Hamiltonian including all the allowed motions of two rigid rotors. Even if the technical details of the numerical methods used to solve the Hamiltonian equation are different, both methods are expected to produce accurate results as long as the rovibrational basis set used to represent the Hamiltonian is large enough. Therefore we could not identify a reasonable cause for the large error on the intermolecular bending frequency, leading us to consider the possibility of an error in the solving process of the Hamiltonian equation. After a meticulous screening of the source code, we found an error which is triggered when both monomers have a center of symmetry. This programming error suppresses part of the angular contributions of the PES. After rectifying this error, we have computed a new set of energy levels and wavefunctions, using exactly the same method and the same parameters as defined previously in the original article. Nevertheless, a supplementary check of the convergence with respect to the angular basis set has been done. We use 15 rotational functions for CO₂ and 8 for N₂. Since we build a Hamiltonian matrix for each irrep of the G₈ group, then only symmetric or antisymmetric angular functions are necessary in each Hamiltonian matrix representation. Thus the maximum values of the angular quantum numbers are 29 and 15 for CO₂ and N₂ respectively. However, Quintas-Sánchez et al. have used the maximum value of 37 in their calculations, suggesting that our angular basis set was too small. A new calculation with 19 angular functions both for CO₂ and N₂ has shown that the lowest rovibrational energies are changed by less than ∼0.01 cm⁻¹.

We report in Table 1 the new values of the energies which replace the values previously published in the original article. The energies of the ground state and the levels involving only excitation of the v₁ and v₃ modes are lowered by 2 or 3 cm⁻¹. The excited levels of the v₄ mode are lowered by ∼6 cm⁻¹ or more, and it is for the v₂ mode that the largest decrease is observed, about 24 cm⁻¹ per quantum. A high density of rovibrational levels is noticed. The number of levels for which we have been able to assign quantum numbers is much smaller than in the original work. Indeed, since there are now more coupling terms arising from PES-1, the nodal structures of highly excited states are much more intricate and therefore the contour plots of the wavefunctions allow us to assign quantum numbers only for a limited set of levels. The four van der Waals fundamental frequencies can be obtained from the rovibrational energies in Table 1. They are listed in Table 2, along with the calculated frequencies of Quintas-Sánchez et al. and the measured frequency.² Our new calculated frequencies are in good agreement with those of Quintas-Sánchez et al., except for the v₂ frequency where a significant difference of ∼4 cm⁻¹ is observed. In order to check this discrepancy, we have recalculated the rovibrational energies for PES-1 with the WAVR4 code⁴ and a convergence threshold of 0.1 cm⁻¹. As shown in Table 2, there is an excellent agreement between the results from our code and those of WAVR4. The difference found between our v₂ frequency and the one of Quintas-Sánchez et al. can then be attributed unequivocally to inaccuracies of PES-1.

Table 1 Lowest energy levels for J = 0 with their assigned vibrational quantum numbers v₁, v₂, v₃ and v₄, parity ε, irrep Γ_i of the group G₈ as well as the number of the level in a given irrep. Energies are given in cm⁻¹ with respect to the energy of separated monomers. For each set of quantum numbers, there is a pair of quasi-degenerate levels with the energy splitting |ΔE| due to tunneling. All the listed energy levels are localized in the global potential wells

v 1	v 2	v 3	v 4	ε	Energy	Γ i	|ΔE|
0	0	0	0	+	−227.389		<0.001
0	1	0	0	+	−202.343		<0.001
1	0	0	0	−	−195.032		0.006
					−195.026
0	2	0	0	+	−186.835		<0.001
0	0	1	0	+	−180.619		0.005
					−180.614
1	1	0	0	−	−170.900		0.003
					−170.897
0	3	0	0	+	−170.018		0.004
					−170.015
0	0	0	1	+	−167.701		<0.001
2	0	0	0	+	−165.583		0.132
					−165.451
0	1	1	0	+	−158.474		0.003
					−158.472
1	2	0	0	−	−155.267		0.019
					−155.249
1	0	1	0	−	−152.142		0.268
					−151.874
0	2	1	0	+	−151.558		0.008
					−151.550
0	0	0	2	+	−147.632		0.012
					−147.620
2	1	0	0	+	−142.852		0.102
					−142.751
1	0	0	1	−	−140.883		0.090
					−140.792
0	0	2	0	+	−140.203		0.013
					−140.191
3	0	0	0	−	−139.665		1.417
					−138.248

---

Table 2 Calculated and measured spectroscopic constants

Vibrational frequencies (cm^−1)	Original^1	Corrected	WAVR4	Quintas-Sánchez et al.^3	Exp.^2
ν 1	32.2	32.36	32.36	32.90	—
ν 2	45.9	25.05	25.06	21.07	21.38
ν 3	46.3	46.77	46.86	46.51	—
ν 4	51.2	59.69	59.74	59.46	—

---

Rotational constant (MHz)	Original^1	Corrected		Quintas-Sánchez et al.^3	Exp.^5
A 0	11861.37	11884.07	—	11881.46	11885.3
B 0	2087.97	2057.49	—	2062.18	2062.88
C 0	1780.38	1751.21	—	1744.39	1743.86

---

In Tables 2 and 3 we report the corrected values of the rotational constants and selected rotational transitions, respectively. As can be seen, the corrected calculated values are closer to the measured values than the previous calculated values. However, the agreement with the measured values is not as good as the one obtained by Quintas-Sánchez et al. This confirms the higher accuracy of PES-2 developed by the latter authors.

Table 3 Calculated and experimental frequencies (MHz) for the transitions . Relative errors with respect to experimental data are given in percent inside parentheses

	Exp.^5	Corrected	Original^1	Quintas-Sánchez et al.^3
101–000	—	3808.703	3880.484	3805.214
202–101	7608.377	7648.669 (0.53)	7527.429 (1.06)	7602.542 (0.08)
303–202	11388.436	11461.285 (0.64)	11277.417 (0.98)	11384.128 (0.04)
404–303	15148.195	15294.977 (0.97)	15003.717 (0.95)	15142.260 (0.04)
505–404	18877.125	18965.259 (0.47)	18698.230 (0.95)	18869.660 (0.04)

---

Rovibrational states localised in the region of the secondary minimum were identified and discussed in the original article. In the present correction, we re-investigate this issue. Selected plots of the rovibrational wavefunctions are presented in Fig. 1. The ground state and the first excited state are quasi-degenerate and arise from the symmetric and antisymmetric combinations of the wavefunctions localized in the two identical potential wells connected by the exchange of the N atoms. In contrast to what we found previously,¹ the state is now free of any nodal plane and the state has a single nodal plane.

Fig. 1 2D contour plots of the wavefunctions for selected states. For each point (θ₁, θ₂), the wavefunction has been calculated by taking ϕ = 90° and the value of R which maximizes the probability density.

A second difference with the original work is related to the localization of some wavefunctions in the region of the secondary minimum. PES-1 has a very shallow secondary minimum, located at θ₁ = 0° or 180° and θ₂ = 90°. This minimum does not exist in PES-2; instead there is a saddle point. Since the secondary minimum is very flat, with a well depth of only 0.78 cm⁻¹, it is not surprising that a change of basis set is sufficient to transform it into a saddle point. As PES-2 was developed on the basis of more accurate ab initio data than PES-1, we can assume that this stationary point is a saddle point and that the secondary minimum is an artifact of the ab initio model used for PES-1. Nevertheless, a systematic ab initio investigation with a series of growing basis sets could be necessary to determine with confidence the properties of this stationary point. Fig. 1 shows several examples of wavefunctions which have a significant probability density in the region of the secondary minimum, but in contrast with the wavefunctions presented in the original article, they have now also a significant probability density in the region of the global minimum. Fig. 1 replaces Fig. 5 of the original article. The other conclusions and findings of the original paper remain unchanged.

The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.

References

1. M. Lara-Moreno, T. Stoecklin, P. Halvick and M. Hochlaf, Quantum tunneling dynamical behaviour on weakly bound complexes: the case of a CO₂–N₂ dimer, Phys. Chem. Chem. Phys., 2019, 21, 3550–3557.
2. A. J. Barclay, A. R. W. McKellar and N. Moazzen-Ahmadi, Spectra of CO₂–N₂ dimer in the 4.2 μm region: Symmetry breaking of the intramolecular CO₂ bend, the intermolecular bend, and higher K-values for the fundamental, J. Chem. Phys., 2020, 153(1), 014303.
3. E. Quintas-Sánchez, R. Dawes, X.-G. Wang and T. Carrington, Computational study of the rovibrational spectrum of CO₂–N₂, Phys. Chem. Chem. Phys., 2020, 22(39), 22674–22683.
4. I. N. Kozin, M. M. Law, J. Tennyson and J. M. Hutson, New vibration–rotation code for tetraatomic molecules exhibiting wide-amplitude motion: WAVR4, Comput. Phys. Commun., 2004, 163(2), 117–131.
5. D. J. Frohman, E. S. Contreras, R. S. Firestone, S. E. Novick and W. Klemperer, Microwave spectra, structure, and dynamics of the weakly bound complex, N₂–CO₂, J. Chem. Phys., 2010, 133(24), 244303.

---