Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combined first-principles statistical mechanics approach to sulfur structure in organic cathode hosts for polymer based lithium–sulfur (Li–S) batteries†
Yannik
Schütze
 ab,
Ranielle
de Oliveira Silva
ab,
Ranielle
de Oliveira Silva
 cd,
Jiaoyi
Ning
ce,
Jörg
Rappich
cd,
Jiaoyi
Ning
ce,
Jörg
Rappich
 f,
Yan
Lu
f,
Yan
Lu
 cd,
Victor G.
Ruiz
cd,
Victor G.
Ruiz
 a,
Annika
Bande
a,
Annika
Bande
 g and
Joachim
Dzubiella
*ah
g and
Joachim
Dzubiella
*ah
aResearch Group for Simulations of Energy Materials, Helmholtz-Zentrum Berlin für Materialien und Energie GmbH, Hahn-Meitner-Platz 1, Berlin 14109, Germany. E-mail: yannik.schuetze@helmholtz-berlin.de
bInstitute of Chemistry and Biochemistry, Freie Universität Berlin, Arnimallee 22, Berlin 14195, Germany
cDepartment Electrochemical Energy Storage, Helmholtz-Zentrum für Materialien und Energie GmbH, Hahn-Meitner-Platz 1, Berlin 14109, Germany
dInstitute of Chemistry, University of Potsdam, Am Neuen Palais 10, Potsdam 14469, Germany
eSchool of Advanced Materials, Peking University Shenzhen Graduate School, Peking University, Shenzhen 518055, China
fInstitute Si-Photovoltaics, Helmholtz-Zentrum Berlin für Materialien und Energie GmbH, Kekuléstr. 5, Berlin 12489, Germany
gTheory of Electron Dynamics and Spectroscopy, Helmholtz-Zentrum Berlin für Materalien und Energie GmbH, Hahn-Meitner-Platz 1, Berlin 14109, Germany
hApplied Theoretical Physics – Computational Physics, Physikalisches Institut, Albert-Ludwigs-Universität Freiburg, Herrmann-Herder-Straße 3, Freiburg 79104, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
First published on 26th November 2021
Abstract
Polymer-based batteries that utilize organic electrode materials are considered viable candidates to overcome the common drawbacks of lithium–sulfur (Li–S) batteries. A promising cathode can be developed using a conductive, flexible, and free-standing polymer, poly(4-thiophen-3-yl)benzenethiol) (PTBT), as the sulfur host material. By a vulcanization process, sulfur is embedded into this polymer. Here, we present a combination of electronic structure theory and statistical mechanics to characterize the structure of the initial state of the charged cathode on an atomic level. We perform a stability analysis of differently sulfurized TBT dimers as the basic polymer unit calculated within density-functional theory (DFT) and combine this with a statistical binding model for the binding probability distributions of the vulcanization process. From this, we deduce sulfur chain length (“rank”) distributions and calculate the average sulfur rank depending on the sulfur concentration and temperature. This multi-scale approach allows us to bridge the gap between the local description of the covalent bonding process and the derivation of the macroscopic properties of the cathode. Our calculations show that the main reaction of the vulcanization process leads to high-probability states of sulfur chains cross-linking TBT units belonging to different polymer backbones, with a dominant rank around n = 5. In contrast, the connection of adjacent TBT units of the same polymer backbone by a sulfur chain is the side reaction. These results are experimentally supported by Raman spectroscopy.
1 Introduction
The continued dependency of modern society on fossil fuels is warming the world at an increasing pace while the energy demand is rising steadily at the same time. Hence, the utilization of renewable energies is gaining interest. Within this context, the storage of electrical power is one of the most critical aspects. Lithium–ion batteries have become prominent over the past three decades and are currently the leading practical battery type among other energy storage technologies. However, this technology is approaching its maximum theoretical limits.1,2 The theoretical gravimetric energy density limit (∼400 Wh kg−1) of a lithium–ion battery has already been reached by today's commercially available ones.3 Still, the demand for technologies such as high energy storage systems for renewable energy applications, electric vehicles, or devices increases the interest in batteries with high energy densities.Lithium–sulfur (Li–S) batteries are considered one of the most viable candidates for next-generation rechargeable batteries owing to their high theoretical specific energy of 2500 Wh kg−1.4 Furthermore, sulfur is a material that is naturally abundant, readily available, and comparably cheap. Despite its promising potential, several main challenges hinder its practical application so far: the insulation of elemental sulfur,5 the shuttle effect of dissolvable lithium polysulfides,6 and the volumetric change of sulfur during the charge/discharge processes.7,8 In recent years, enormous progress has been made in developing new sulfur host materials, efficient electrolytes, and novel cell configurations.9–16
One Li–S battery type that has gained significant attention is polymer-based batteries which utilize organic electrode materials.17 Numerous studies have been conducted on the usage of different organosulfur compounds as cathode materials.18–20 Here, conjugated polymers emerged as promising candidates due to their good conductivity,21,22 ability to suppress the shuttle effect by confining the sulfur content,23–26 and tolerance to large volume expansion during lithiation.27–29 Among them, thiol-containing polymers are one example where the –SH groups can be cross-linked with sulfur via covalent bonds.30–33
Yu et al. recently proposed a strategy to construct a free-standing cathode with the conductive and flexible polymer poly(4-thiophen-3-yl)benzenethiol) (PTBT) as the sulfur host material. Here, TBT monomers are first electro-polymerized onto the surface of nickel foam to form a porous PTBT network with the thiophene rings as the polymer backbone and benzenethiol as the side chains. In a second inverse vulcanization step,34 elemental sulfur S8 gets embedded into this framework. Therefore, it is heated up to 170 °C which causes ring-opening radical polymerization (ROP) of the sulfur with the thiol groups of PTBT. This S/PTBT@NF cathode can then be directly used to assemble Li–S batteries without any further modifications. This fabrication approach seems promising to overcome all typical drawbacks of Li–S batteries, but a detailed investigation of the structural aspects of the cathode is still missing.
Pyun et al. investigated the process of inverse vulcanization for the first time in an experimental study with an organic copolymer synthesized with 1,3-diisopropenylbenzene (DIB) monomers and elemental sulfur.34 Here, the authors analyzed the microstructure of the vulcanized polymer under different synthetic conditions. More precisely, they showed that, depending on the feed ratio of S8 and DIB monomers, the S-DIB copolymer exhibits varying structural features. The authors observed that, with increasing DIB content, the copolymer morphology changed from semi-crystalline to amorphous. At the same time, the sulfur rank (the number of sulfur units per DIB unit) decreased with increasing DIB content.
Guided by these findings, knowing the most likely outcome of the chemical binding process of sulfur in our PTBT polymer is highly desirable to characterize the initial stage of the charged cathode. In particular, electronic structure theory can give us insights into the structural features at an atomic level leading to a better understanding of the charged state of the cathode. In this work, we present the structural characterization of the charged cathode, that is, the sulfurized polymer, as it is prepared after the vulcanization process, using density functional theory (DFT). However, DFT is limited to minimum energy (0 K) states, and temperature effects (fluctuations and entropy) are not included. Therefore, we develop a statistical mechanics model that uses DFT energies as the input and calculate configurational distributions at operating temperatures. This novel combination of methods can be considered a multiscale approach and allows us to bridge the gap between the local description of the covalent bonding process and the derivation of the macroscopic properties of the polymer. We also compare our theoretical analysis to new experimental observations. Raman spectroscopy of the TBT monomer and the electro-polymerized PTBT motivates the reference states of our binding model and supports the results of our combined model approach.
This paper is organized as follows. In the subsequent Section 2, we first give a detailed description of how to derive a statistical binding model describing the vulcanized S/PTBT polymer. The basis of this model is the characterization of the molecular structure of S/PTBT by fragmenting it into different sulfurized TBT dimers. Here, we distinguish between two types of binding (intra and inter) and different sulfur chain lengths. Based on that, we describe the result of the vulcanization reaction as a thermodynamic equilibrium from which we can derive equilibrium constants. In Section 4, we first present the structural characterization and then the stability analysis of the polymer fragments identified in the theory part in terms of their electronic energy within DFT. For all configurations, we conduct a conformational space sampling to estimate their structure–stability relationship further. The following subsection compares these results with our experimental Raman spectroscopy of the TBT monomer and the electro-polymerized PTBT polymer. Ultimately, we combine the statistical model with the stability analysis results to derive binding probability distributions depending on the concentration of sulfur in the vulcanization process. Finally, we calculate the average sulfur rank and standard deviations for these distributions and look at their temperature dependency. The paper ends with some concluding remarks.
2 Statistical binding model
2.1 Modeling the initial state of the charged cathode
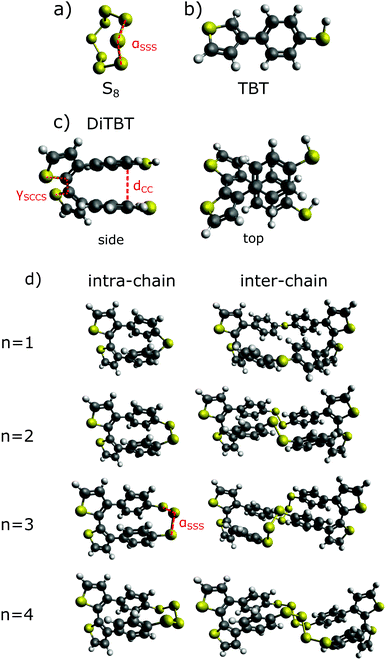
In Fig. 2 the schematic illustration of the preparation of the S/PTBT cathode is shown. In a first step, the TBT monomers are electro-polymerized to form a PTBT polymer. Polymerization of the five-membered heterocyclic thiophene ring can occur through bonding at the α- or β- (i.e. 2- or 3-) position (cf.Fig. 1). In the TBT monomer, the β-position is substituted by the benzenethiol group. It is well known that, in 3-substituted thiophene monomers, the α-position is most reactive in the polymerization, and therefore α,α-linkages will be dominant in the resulting polymer. It is most likely that the long PTBT polymer chains that form during polymerization will then have the thiophene rings as the main-chain backbones with the benzenethiol groups as the lateral chain.35–38During vulcanization, heating causes the ring-opening polymerization (ROP) of elemental S8 monomers into linear polysulfanes with diradical chain ends, which subsequently polymerize.11 Its diradical form is unstable and depolymerizes back into monomeric ring forms.34 Quenching of the diradical ends via polymerization with the thiol (–SH) groups of the lateral chain can stabilize sulfur in the PTBT polymer.
The difference between conventional and inverse vulcanization is that a small amount of sulfur is used in the former. In contrast, a large amount of sulfur is used together with a relatively modest amount of polymer in the latter. In the original sense, inverse vulcanization also means the copolymerization of elemental sulfur and small organic monomers as a bulk reaction.34 Here, we do not observe a copolymerization process since the PTBT polymer is electropolymerized in the first step before sulfur is embedded into this framework in a subsequent step. Therefore, in the following, we will describe the process of adding sulfur as vulcanization.
Furthermore, the sulfur deposition process in experiments occurs without the presence of any additional solvent. This work focuses on the initial state of the charged cathode, that is, the vulcanized polymer, before it gets assembled into a battery. Hence, we will study the outcome of the vulcanization in the framework of a gas phase model reaction.
Based on the structure of the main chains of the PTBT polymer, we generally distinguish two different ways in which the polysulfide chains can bind to the TBT units. On the one hand, a sulfur chain can connect two adjacent TBT units of the same polymer chain to form an intra-chain sulfur cross-link (bottom left picture of Fig. 2). On the other hand, as shown on the right, sulfur can form an inter-chain cross-link between TBT monomers that belong to different polymer chains. Here, we implicitly assume that the polymer chains are sufficiently close to each other. It should be noted that, in addition to the linkage of adjacent TBT units, intra-chain cross-links may in principle also occur between monomers that are further apart within the chain under real conditions. The linkage of remote monomers would then reflect a scenario similar to an inter-chain cross-linking of different polymer backbones. The limitation of considering only intra-chain connections of neighboring TBT units allows us to choose a well-defined reference state for the PTBT polymer chains within a different scenario from the inter-chain cross-links.
In the following, we derive a model that reflects the reaction type (intra- or inter-chain) and the sulfur rank n depending on the amount of sulfur that is embedded into the polymer. The sulfur rank n is defined as the total number of sulfur atoms in the chain that connects the two TBT units. We describe the PTBT polymer as a fixed configuration of binding sites (–SH groups) for the additional sulfur and the reactions of forming intra- or inter-chain sulfur links as two independent processes. Both reaction types include two –SH groups to be connected by a sulfur chain. Let us assume that the PTBT polymer consists of N thiol groups in total. Then the number of independent binding sites is nBS = N/2. After vulcanization, a binding site can have an intra- or inter-configuration or be still empty (the two –SH groups have not reacted). The binding polynomial Q, which describes all possible outcomes of the vulcanization, is then a sum of the statistical weights of these three scenarios:
| Q = 1 + Pintra + Pinter. | (1) |
Next, we distinguish between the number of sulfur atoms that can form an intra- or inter-chain (the sulfur rank n). Let us assume we have sulfur ranks ranging from n = 1 to m (n = 0 is the case of an ‘empty state’). We consider the binding of sulfur chains with different lengths again as independent processes (for both intra- and inter-reactions). Therefore, the statistical weights of intra- and inter-reactions are themselves sums over the weights of having n sulfur atoms bound:
 | (2) |
In general, we can describe the vulcanization process as bringing the two reference states ‘PTBT polymer’ and ‘elemental sulfur’ together to form a product state ‘vulcanized polymer’. We want to find out the most probable binding states in terms of intra- vs. inter-reaction, resolved by the sulfur rank n. To make computations feasible, we first have to reduce the complexity of the PTBT reference state, i.e. omit the long polymer chains. In our model, we have chosen a DiTBT molecule describing two neighboring, covalently bonded TBT monomers as the basic unit of a polymer chain. This DiTBT molecule represents one of many binding sites of the polymer. For the amount of sulfur embedded into the polymer, we take one-eighth of an S8 ring as the reference. In Fig. 3, we show a scheme for the two reaction types based on these new reference states.
 | ||
| Fig. 3 The schematic of vulcanization to form (a) an intra-chain sulfur link in one DiTBT unit or (b) an inter-chain cross-link between two DiTBT units. | ||
These reactions are explained in the following. The formation of an intra-chain is already realized by connecting the two thiol groups of a DiTBT. The smallest chain would consist of one S atom (n = 1). Since a DiTBT already has two S atoms as parts of the thiol groups, the second sulfur atom would react with the two hydrogen atoms to form the bi-product H2S. To create the next larger chain with n = 2, one additional sulfur atom is needed to react with the hydrogen atoms. In every case, we consider the loss of one S atom by the formation of H2S. The production of H2S gas during inverse vulcanization was already confirmed in experiments with similar thiol-group containing polymers.19,30,32 Therefore, the amount of sulfur atoms added is counted by the term (n − 1)/8 S8 giving
 | (3) |
For the inter-chain process, we have to make an additional assumption. Since a DiTBT molecule is a fragment of one polymer chain, we need to consider two DiTBT molecules in order to model the process of connecting two polymer chains by a sulfur link. The DiTBT molecules now represent two different binding sites, and therefore we must also double the amount of sulfur atoms compared to the intra-reaction. This product state describes a pair of sulfur cross-links between four TBT monomers (two DiTBT units on each polymer chain). For more than one DiTBT per chain, this would lead to an organized ladder-like structure. However, inter-chain cross-links may occur more randomly in a real system, such that neighboring TBT units of a given chain bind to monomers of two different polymer chains. In order to be consistent with the intra-chain binding process, however, we here take the same reference state of two DiTBTs. The corresponding reaction equation is then
 | (4) |
For both reactions, we define vulcanization energy33 as the electronic energy difference between the products and the reactants, i.e.
 | (5) |
 | (6) |
In eqn (6), we divide the energy difference of products and reactants by two in order to normalize the vulcanization energy to one unit of DiTBT and (n − 1)/8 S8. By doing this, we can compare the stability of different intra- and inter-reaction products in terms of their electronic energies.39
The next step in our model is to describe the final state after vulcanization as an equilibrium of intra- and inter-binding states resolved by the sulfur rank. We model the vulcanization as the binding process of a certain amount x = S8/8 of sulfur to a number of binding sites (BS). With these association reaction equilibria,
| BS + (n − 1) x ⇌ BS−xintran + H2S | (7) |
BS + (n − 1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x ⇌ BS−xintern + H2S, x ⇌ BS−xintern + H2S, | (8) |
we can formulate the equilibrium binding constants:
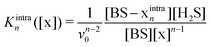 | (9) |
 | (10) |
| Pintra/intern([x]) = Kintra/intern(v0[x])n−1. | (11) |
At the same time, the binding constants can be associated with binding energies through
ΔGn = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln[Kn], ln[Kn], | (12) |
 | (13) |
It should be mentioned that, in general, the binding volumes for the intra- and inter-reactions will be different from each other. Since these quantities are computationally not accessible in our gas-phase calculations, we make a further approximation and assume an equal binding volume v0 for both processes. If we insert eqn (13) and (11) into eqn (1), we can finally write down the binding polynomial:
 | (14) |
2.2 Conformational space sampling and binding probabilities
With increasing sulfur chain length n, the number of degrees of freedom grows rapidly, and hence the search for a global minimum of the potential energy surface becomes a complex task itself. A typical strategy to solve this is a global conformational space search.46,47 In this study, however, we pursue an approach that not only looks for the global minimum structures but also considers a manifold of different conformations of the product states DiTBT-Sn and DiTBT-2Sn-DiTBT for each sulfur chain length. The aim of this conformational space sampling is not to find all possible conformations to get the global minimum, but rather to get an estimate of the structure–stability relationship of the products in the vulcanization process.First, a set of diverse low-energy conformers that cover different shapes of the sulfur chain are generated and then pre-relaxed, employing a force-field (FF) from classical molecular dynamics.48 These structures are then further optimized using density functional theory (DFT) to calculate their electronic energies. By making further distinction regarding the conformation of possible product states of the vulcanization, we have to adjust the binding polynomial according to
 | (15) |
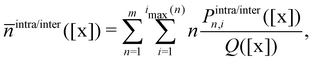 | (16) |
 | (17) |
3 Methods
3.1 Experimental methods
The previously synthesized monomer 4-(thiophen-3-yl)benzenethiol (TBT) was directly polymerized on a nickel foam (thickness: 0.5 mm). The electro-polymerization was carried out in acetonitrile solution to form PTBT (4 mg ml−1) using 0.1 M tetrabutylammonium hexafluorophosphate (TBAPF6) as the solution electrolyte. This process was conducted by CV in a three-electrode system at a potential between −1.8 and 1.8 V (100 mV s−1, 20 cycles) using an electrochemical workstation (GAMRY), Ag wire as the reference electrode, and platinum wire as the counter electrode. After electro-polymerization, the electrode was rinsed with ACN several times and then dried in a vacuum oven at 50 °C. Finally, a red-brown nickel foam electrode (PTBT@NF) was obtained and the mass loading of PTBT is ∼1 mg cm−2.Subsequently, the sulfur deposition was conducted through a vulcanization process: elemental sulfur dissolved in CS2 (mg ml−1) was first embedded into the porous PTBT framework at a low-temperature step, transferred under argon gas in a sealed vessel, and then heated up at 150 °C for one hour, followed by further heating at 170 °C for 8 hours, leading to ring-opening radical polymerization of elemental sulfur with the thiol groups of PTBT. Finally, the obtained S/PTBT@NF was rinsed with CS2 to wash away the physically adsorbed sulfur and dried at room temperature before being used. The loading amount of sulfur in S/PTBT@NF is ∼1.6 mg cm−2.
The Raman spectra were recorded using a micro-Raman setup with a confocal microscope (Dilor LabRAM) coupled to a CCD. The laser excitation was at 632.8 nm with a power density of about 2 W cm−2. The acquisition time was 300 s.
3.2 Computational details
For the generation of the possible conformations and their pre-relaxation, Avogadro software49 was used employing the MMFF94 force field50 using steepest descent minimization. All DFT calculations were performed using the all-electron, full-potential electronic-structure code FHI-aims.51–53 The exchange–correlation interactions were treated using the Perdew–Burke–Ernzerhof (PBE) functional54 together with the Tkatchenko–Scheffler method55,56 to include van der Waals (vdW) interactions. For comparison, we also used the hybrid PBE0 functional57 as well as the many-body dispersion (MBD) method58 to account for the long-range van der Waals interactions. FHI-aims-specific tier 2 basis sets and tight settings have been used. The convergence criterion for the total energy and the forces was set to 10−6 eV and 10−5 eV Å−1, respectively.4 Results and discussion
4.1 Structural characterization of product states
We first look at the structural characteristics of the reactants and the products of the vulcanization process. In Fig. 4, the DFT-relaxed structures of elemental sulfur (S8), TBT, and DiTBT are shown as well as those for the lowest energy conformations of the reaction products for sulfur ranks n = 1–4. First, we look at the most stable configuration of our reference state DiTBT (cf.Fig. 4c). As can be seen in the top view, the arrangement of the two neighboring benzenethiol groups is similar to the π–π stacked (parallel-displaced) conformation of benzene dimers.59 The distance of the two carbon atoms at the 9-position of TBT (the carbon atom binding to the thiol group, cf.Fig. 1) is dCC = 4.38 Å. The thiophene rings have a dihedral angle of γSCCS = 55.4° through the carbon atoms at the α-positions of the thiophene rings.We can now analyze the product states after DFT optimization with regard to these quantities to see how the structure of DiTBT gets altered by the insertion of sulfur chains. In Fig. 5, the C–C distance dCC, the dihedral angle γSCCS, and the sulfur bond angle αSSS among three neighboring sulfur chain atoms are shown for all intra-chain (red) and inter-chain (blue) products and compared against their reference values of isolated DiTBT and S8 (black dashed lines). For the products, we report the statistical mean and standard deviation of the conformational sample for the respective sulfur ranks. For all three quantities, we observe the largest deviations from the respective reference values for short chains (n = 1–4) and an approach towards them for increasing n. For the short-chain DiTBT-Sn (red solid line in a), dCC is shortened indicating that the benzenethioether rings are closer to each other than they are in DiTBT. This can be also clearly seen in Fig. 4d for n = 1, 2. At the same time, the dihedral angle between the thiophenes for short n is also smaller than the reference value. For the inter-chain DiTBT-2Sn-DiTBT products, we observe the opposite behavior that, for short chains, the values dCC and γSCCS are larger than the reference values.
 | ||
| Fig. 5 Structural analysis of the DFT-relaxed intra-chain (red) and inter-chain (blue) products depending on the sulfur rank n: (a) distance dCC between the terminating C9 (cf.Fig. 4) carbon atoms belonging to the benzenethioether; (b) dihedral angle γSCCS between neighboring thiophene rings; and (c) sulfur bond angle αSSS. The solid lines show the average overall conformations for the respective rank, and error bars represent the standard deviation of the sample. The black dashed lines indicate the values for the reference DiTBT in (a) and (b) and for S8 in (c). | ||
With increasing sulfur rank, both properties align with the reference values. This can be explained by the greater flexibility of the chains allowing the DiTBT in the product states to adopt conformations similar to the reference structure. Put another way, we can conclude that the insertion of short sulfur chains leads to modified conformations of the DiTBT. Due to the altered dihedral angle of the thiophenes, the resulting structures possess torsional strain.60 In addition to that, the variation in distance between the benzenethioethers changes their van der Waals interaction and thus leads to steric strain.60 In Fig. 5c, we can also see that the sulfur chains themselves possess angle strains compared with the crown conformation of an S8 ring.
What is noticeable is that, for longer chains, the curves of dCC and γSCCS show a similar zigzag behavior. This can also be explained by the greater flexibility of the long chains. With increasing n, the chains can adopt a variety of stable conformations (cf. Fig. S1, ESI†), which are probed with our sampling approach. For n = 1, there is only one stable configuration for the intra- and inter-chain products. With increasing n, the flexibility of the chain leads to a variety of stable configurations with a broad range of dihedral angles. Shown here are two extreme cases of the intra- and inter-chain processes, respectively. For the former, a wide range of dihedral angles is possible only for long chain lengths, while for the latter it can already be seen for short ranks. The jumps are probably due to the relatively small sample sizes (max. 10 conformations per sulfur rank). We also see that these fluctuations are less pronounced for the inter-chain configurations because the structures automatically lead to improved statistics (and hence smaller errors).
The S–S bond length for all products is in the interval of dSS = [2.07, 2.09] Å which matches the experimental value of S8 and is in good agreement with similar chain-like –R–Sn–R– polysulfanes.61,62
4.2 Stability analysis
Next, we proceed with the stability analysis of all reaction products according to eqn (5) and (6). Here, we mean the electronic stability of the products relative to our defined reference states. The vulcanization energies for the intra-chain process (red) and the inter-chain process (blue) are compared in Fig. 6. The colored areas represent the overall results for all sampled conformations, while the solid lines show the average trends. As it can be seen, the inter-chain cross-link reaction leads to negative vulcanization energies Eintervul throughout almost the whole range of sulfur chains showing that this process can chemically stabilize the sulfur content. Only the shortest chains (n = 1, 2) lead to a slightly positive energy. The intra-chain reaction on the other hand yields almost only positive values for Eintravul. Only for very long sulfur chains (n ≥ 11), we find some stable conformations, whereas particularly short sulfur chains (1 ≤ n ≤ 3) are very unlikely to form. | ||
| Fig. 6 The vulcanization energies Eintravul (eqn (5)) for intra-chain reactions (red) and Eintervul (eqn (6)) for inter-chain reactions (blue). The colored areas represent the results of all sampled conformations, and the solid lines show the averaged trends. In the inset, the vulcanization energies normalized by the sulfur rank Evul/n are shown. | ||
The fact that the short sulfur chains are less stable in both processes can be directly related to the structural features discussed above. The structural changes of the two reactants DiTBT and S8 which go along with their binding process lead to different kinds of strain. The additional strain energy of the binding products raises their internal energy and thus makes it unfavorable for them to form during the vulcanization process. We can also note that, although we made a rather small sampling of the conformational space, it can be seen that the stability of the reaction products is extremely sensitive to structural changes. Because of that we can also observe a similar zigzag behavior in the curves of Eintravul and Eintervul.
Besides the structure–stability relationship, the vulcanization energies show two additional features. Firstly, one can see a clear negative drift of the vulcanization energies with increasing sulfur rank. Even for the averaged curves, we observe a negative correlation on n. If we normalize the vulcanization energies by the sulfur rank (cf. the inset of Fig. 6), we can see that, for the inter-chain process, Eintervul/n, after reaching a minimum at n = 5, shows a plateau for n > 6. For the intra-chain process, Eintravul/n still goes down with increasing n but, for very long chains (n > 14), we start to see a saturation. The limit of constant normalized energies for large n indicates that the stability of the reaction products depends linearly on n after reaching a certain chain length. The drift in Evul suggests that wave-function hybridization of an S–S bond inside a polysulfide chain of the reaction products is energetically more favorable than that for the same bond inside an S8 ring given the formation of H2S. Indeed, the plateau of Eintervul/n for sulfur ranks higher than n = 5 shows that every additional S–S bond would yield a constant energy gain of about 20 meV, making the corresponding structure energetically more stable.
On the other hand, this energy gain per sulfur atom is in the order of the thermal energy kbT, showing that the energy differences between the structures of different chain lengths are sensitive to temperature and entropy effects. This should be put into the context of contributions that were not taken into account for this electronic stability analysis. If we refer back to eqn (12), we see that the actual chemical reaction is governed by the Gibbs free energy G = U + pV − TS. If we assume the contribution of the pV-term to be minor in our gas-phase reaction, the important correction comes with including the entropy S. Its inclusion would mean that the longer chains are entropically penalized over the shorter chains and thus cause a destabilization of the structures with higher sulfur ranks. While, for low sulfur ranks, the main driving force for the addition of sulfur atoms would be the electronic stability, with increasing n, the only driving force would be the entropy which should overcome the energy drift in Evul at a certain sulfur chain length. Indeed, experimental studies on the standard Gibbs free energy of equilibrium distributions of polysulfide chains have shown that pentasulfide chains (n = 5) represent the most stable configuration.63,64 This is in agreement with another DFT study of large sulfur rings (n = 8–20) which showed that considering only the electronic energy would allow rings with n = 12, 14, 18, but the inclusion of entropic effects leads to an S8 ring as the only stable allotrope.65
For the most stable inter-chain products with sulfur rank n = 1–8, we also calculated the electronic energies with PBE + MBD and PBE0 + vdW (cf. Fig. S2, ESI†) and compared them with the results for PBE + vdW from Fig. 6. The comparison shows that all three methods give relatively similar results for the stability analysis. Using the MBD method instead of the pairwise vdW correction to account for the dispersion interaction, we observe that as the sulfur rank n increases, the larger structures are less stable. This is a consequence of the inclusion of many-body interactions in the dispersion energy. Contrary to including only an attractive pairwise interaction via the vdW method, the inclusion of many-body effects becomes more relevant and less attractive when the chain consists of more sulfur atoms, yielding a less attractive long-range dispersion energy. This fact also points in the direction of an energy saturation in a real polymer chain where the many-body effects would become even larger. The comparison between PBE and PBE0 functionals shows that their curves are almost the same, but the PBE0 results decrease by about 0.03 eV.
4.3 Comparison to experimental Raman spectroscopy
The comparison of the stability of intra- and inter-reaction products shows that the latter process is more favorable in terms of electronic energies. The finding that inter-chain sulfur cross-links are dominant in the vulcanized polymer was also compared to the experimental Raman spectroscopy results of the monomer TBT and the electro-polymerized layer of TBT (PTBT) (cf.Fig. 7). Here, the spectrum of TBT (black line) shows a Raman signal around 2560 cm−1 due to the S–H stretching vibration of the thiol groups present at the benzene ring of the monomer.66 These groups vanish after electrochemical polymerization (red line of PTBT). The vibrational signatures between 600 and 1600 cm−1 are part of the benzene and thiophene ring structures, respectively.67,68 The Raman signature below 600 cm−1 is due to the formation of disulfide bonds, especially the signal around 480 cm−1.69 | ||
| Fig. 7 Raman spectra of the monomer TBT (black) and the electrochemically prepared polymer layer PTBT (red). The gray dashed lines indicate several distinct vibrational modes ν of the two samples. | ||
The absence of the S–H stretching mode coupled with the simultaneous occurrence of the S–S Raman modes between 300 and 480 cm−1 indicates the formation of disulfides as a side reaction during the anodic polymerization of TBT. It is well known in the literature that disulfide formation is an oxidative process driven by oxidizing agents.70 Hence, the thiol functional groups of TBT are activated to form disulfide bonds in the aqueous solution by the anodic oxidation process71 that is needed to drive the polymerization of the thiophene groups. From an experimental point of view, it is not possible to distinguish between intra- and inter-chain bonds (cf. Fig. S3, ESI†). However, if we compare these findings with the stability analysis, we can exclude that the disulfide bonds represent intra-chain compounds with sulfur rank n = 2 due to their high positive vulcanization energies. We can therefore say that S–S inter-chains are already present in the polymer before vulcanization. This result furthermore motivates the choice of reference states in our statistical binding model.
In summary, we see that the formation of inter-chain cross-links leads to more energetically stable structures than the intra-chain reaction. In the latter, we can already state that it would only lead to the formation of very long sulfur chains with rank n ≥ 11. For the inter-chain process, already short chains with n ≥ 2 are possible to form. So far, we have only looked at the energetic stability as a criterion for the formation of certain reaction products, but what will also determine the microscopic structure of the vulcanized polymer is the feed ratio of the reactants as it was already shown.34 Hence, we will now make use of our binding model derived in eqn (15) and vary the amount of sulfur to see how the binding probability distribution of sulfur chain lengths will change depending on the free sulfur concentration [x].
4.4 Binding probabilities
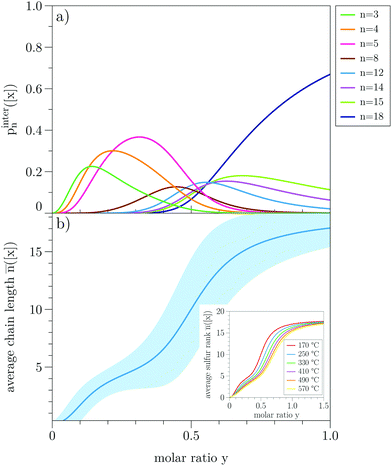
In Fig. 8a, the individual binding probabilities for the inter-chain process pintern([x]) are displayed versus the molar ratio of free sulfur and binding sites y = [x]/[BS]. We only show the binding curves for those sulfur ranks whose maximum probability is more than 10%. For the chosen range of y, we can qualitatively distinguish three different regions of short, medium-length, and long sulfur chains.For low sulfur concentrations, only the reactions for n = 3, 4, 5 have substantial contributions. These probabilities decrease with increasing y, and we observe the shift to longer sulfur ranks (n = 8, 12, 14, 15). In the limit of high concentrations, the probability of forming medium-length chains also vanishes, and only the longest chain we have considered (n = 18) contributes. It should also be noted that the binding probabilities for the intra-chain reaction are four orders of magnitude lower (cf. Fig. S4, ESI†) than those for the inter-chain process, which further corroborates that the latter one is the main reaction during vulcanization.
We can now relate these distributions to our previous stability analysis. The two smallest structures (n = 1, 2) do not contribute because they are unstable. If we increase the amount of free sulfur, the next longer chains with n = 3, 4, 5 will form. Interestingly, this behavior maximizes around n = 5 (the peak maximum of n = 6, 7 is less than 10%). Only if the sulfur concentration is substantially increased further, longer chains with n > 8 will then be present. The presence of the pinter5([x]) curve over a relatively long range of y seems to correspond with the minimum of Eintervul at n = 5 (cf. the inset of Fig. 6) indicating that a pentasulfide chain is the most probable outcome of the vulcanization for a certain range of free sulfur concentration. As discussed before, the temperature and (translational) entropy effects, included in the statistical mechanics model, lead to probable distributions of more but smaller ranks, especially the low energy state rank n = 5. Increasing the amount of sulfur then naturally pushes the system toward longer chains. The high stability of rank n = 5 is also reflected by the average sulfur rank ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ([x]) (eqn (16)) for the inter-chain reaction (solid blue line, Fig. 8, panel b). It shows that the transition from short to long chains cannot be described by a strictly monotonically increasing function. Instead, it shows a small plateau around
([x]) (eqn (16)) for the inter-chain reaction (solid blue line, Fig. 8, panel b). It shows that the transition from short to long chains cannot be described by a strictly monotonically increasing function. Instead, it shows a small plateau around ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ≈ 5 before saturating to
≈ 5 before saturating to ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ≈ 18 for high concentrations. This again corresponds to the upper limit we have calculated vulcanization energies for. The result that we would find more stable structures by extending the chain would mean that the average chain length would increase continuously. This is, of course, due to the shortcomings of the electronic stability analysis. Furthermore, one should keep in mind the limitations of this model, considering only small gas-phase molecules. Certainly, in a real polymer, there will be constraints for the growth of the sulfur chain, such as steric, excluded volume, and packing effects, which we cannot assess with our approach.
≈ 18 for high concentrations. This again corresponds to the upper limit we have calculated vulcanization energies for. The result that we would find more stable structures by extending the chain would mean that the average chain length would increase continuously. This is, of course, due to the shortcomings of the electronic stability analysis. Furthermore, one should keep in mind the limitations of this model, considering only small gas-phase molecules. Certainly, in a real polymer, there will be constraints for the growth of the sulfur chain, such as steric, excluded volume, and packing effects, which we cannot assess with our approach.
In the experimental process of vulcanization, there is no precise definition of the temperature given that it is above the ROP-temperature (floor temperature) of S8 for initiating the process (although there might be some reasons related to the setup or the used material to choose a specific temperature). We, therefore, analyzed the temperature dependency of the average sulfur rank for the inter-chain process. In the inset of Fig. 8b, we see that the change of the isotherm vanishes with higher temperatures indicating an upper limit. The lower limit is the floor temperature of S8 which has to be exceeded. In between these limits, we can partially enhance sulfur embedding with the temperature by choosing a value just above the floor temperature. The results show that an increase in the temperature would decrease the average sulfur rank.
5 Conclusions
In this study, we used a combination of first-principles computational methods and statistical mechanics to explore the structural characteristics of the initial state of a vulcanized organic polymer which serves as the cathode for a Li–S battery.We derived a statistical model to describe the outcome of the binding process of elemental sulfur to the thiol-containing PTBT polymer during vulcanization. The basis of this model is the fragmentation of the vulcanized S/PTBT polymer into small basic units for which simulations within electronic structure theory are feasible. By this, we can cover the essential features of the covalent binding process occurring on a local scale. The conformational space sampling, at the same time, allows us to study various structural configurations. The results of the DFT stability analysis are then fed back into our binding model. By calculating probability distributions and their quantitative measures, we can draw conclusions about the macroscopic features of the polymer. In that sense, our novel combination of methods can be described as a multi-scale approach to the structural characterization of the polymer.
Our results show that the main reaction of the vulcanization process leads to a sulfur chain cross-link between TBT units of different polymer backbones (inter-chain), whereas the binding of sulfur between adjacent TBT units of the same backbone is the side reaction (intra-chain). We could experimentally support this finding by Raman spectroscopy by identifying the S–S signal, which was detected already after electropolymerization, with our inter-chain structures. Based on our binding model, we calculated the average inter-chain sulfur rank for various sulfur concentrations and temperatures. Our results suggest that sulfur ranks around n = 5 are most likely for a wide range of sulfur concentrations and can then be continuously extended by increasing the sulfur concentration (while in reality, at some points, steric constraints may occur). Moreover, for a given concentration, the embedding of sulfur would be most effective for a temperature just above the floor temperature of elemental sulfur.
This study provides insights into the fundamental understanding of the microscopic structure of a vulcanized organic polymer. By combining electronic structure theory with a statistical mechanics model, we could draw more advanced conclusions than with pure DFT calculations. Hence, this approach seems beneficial when it comes to the structural characterization of novel cathode materials. Work to extend our model to describe the electronic properties of the polymer is in progress. An interesting aspect to investigate in future studies would be the comparison of the experimental Raman spectra to the calculated frequencies of the most representative structure.72,73 Furthermore, this study is the first step into a multi-scale approach bridging classical and ab initio molecular dynamics simulations that will focus on larger solvated polymer structures74,75 and spectroscopy calculations,76–78 respectively.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Pouya Partovi-Azar, Michael Walter, Sebastian Risse, Shilin Mei, Sebastien Groh, and Diptesh Gayen for helpful discussions. The authors thank the HPC Service of ZEDAT (Curta79), Freie Universität Berlin, for computing time. We acknowledge funding of the project through the DFG Priority Programme “Polymer-based batteries” (SPP 2248, project number: 441211139).References
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS
.
- A. Manthiram, Y. Fu and Y.-S. Su, J. Phys. Chem. Lett., 2013, 4, 1295–1297 CrossRef CAS PubMed
.
- X.-B. Cheng, R. Zhang, C.-Z. Zhao and Q. Zhang, Chem. Rev., 2017, 117, 10403–10473 CrossRef CAS PubMed
.
- A. Fotouhi, D. J. Auger, K. Propp, S. Longo and M. Wild, Renewable Sustainable Energy Rev., 2016, 56, 1008–1021 CrossRef CAS
.
-
J. A. Poulis, J. P. Frančlois, C. H. Massen and L. C. V. Poucke, Electrical Conductivity of Sulfur, John Wiley & Sons, Ltd, 1990, ch. 15.2.2.2.14, p. 53 Search PubMed
.
- Y. Diao, K. Xie, S. Xiong and X. Hong, J. Power Sources, 2013, 235, 181–186 CrossRef CAS
.
- X. He, J. Ren, L. Wang, W. Pu, C. Jiang and C. Wan, J. Power Sources, 2009, 190, 154–156 CrossRef CAS
.
- M. M. Islam, A. Ostadhossein, O. Borodin, A. T. Yeates, W. W. Tipton, R. G. Hennig, N. Kumar and A. C. Van Duin, Phys. Chem. Chem. Phys., 2015, 17, 3383–3393 RSC
.
- P. T. Dirlam, R. S. Glass, K. Char and J. Pyun, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 1635–1668 CrossRef CAS
.
- T. Danner, G. Zhu, A. F. Hofmann and A. Latz, Electrochim. Acta, 2015, 184, 124–133 CrossRef CAS
.
- F. Zhao, Y. Li and W. Feng, Small Methods, 2018, 2, 1800156 CrossRef
.
- Q. Pang, X. Liang, C. Y. Kwok and L. F. Nazar, Nat. Energy, 2016, 1, 1–11 Search PubMed
.
-
S. Walus, PhD thesis, Université Grenoble Alpes, 2015
.
- A. Manthiram, Y. Fu, S.-H. Chung, C. Zu and Y.-S. Su, Chem. Rev., 2014, 114, 11751–11787 CrossRef CAS PubMed
.
- A. Narayanan Kirshnamoorthy, K. Oldiges, M. Winter, A. Heuer, I. Cekic-Laskovic, C. Holm and J. Smiatek, Phys. Chem. Chem. Phys., 2018, 20, 25701–25715 RSC
.
- G. Bieker, D. Diddens, M. Kolek, O. Borodin, M. Winter, P. Bieker and K. Jalkanen, J. Phys. Chem. C, 2018, 122, 21770–21783 CrossRef CAS
.
- M. D. Hager, B. Esser, X. Feng, W. Schuhmann, P. Theato and U. S. Schubert, Adv. Mater., 2020, 32, 2000587 CrossRef CAS PubMed
.
- M. Wu, Y. Cui, A. Bhargav, Y. Losovyj, A. Siegel, M. Agarwal, Y. Ma and Y. Fu, Angew. Chem., Int. Ed., 2016, 55, 10027–10031 CrossRef CAS PubMed
.
- S. Zeng, L. Li, L. Xie, D. Zhao, N. Wang and S. Chen, ChemSusChem, 2017, 10, 3378–3386 CrossRef CAS PubMed
.
- D. Y. Wang, W. Guo and Y. Fu, Acc. Chem. Res., 2019, 52, 2290–2300 CrossRef CAS PubMed
.
- Y. Yang, G. Yu, J. J. Cha, H. Wu, M. Vosgueritchian, Y. Yao, Z. Bao and Y. Cui, ACS Nano, 2011, 5, 9187–9193 CrossRef CAS PubMed
.
- L. Xiao, Y. Cao, J. Xiao, B. Schwenzer, M. H. Engelhard, L. V. Saraf, Z. Nie, G. J. Exarhos and J. Liu, Adv. Mater., 2012, 24, 1176–1181 CrossRef CAS PubMed
.
- S.-E. Cheon, K.-S. Ko, J.-H. Cho, S.-W. Kim, E.-Y. Chin and H.-T. Kim, J. Electrochem. Soc., 2003, 150, A796 CrossRef CAS
.
- A. Manthiram, Y. Fu, S.-H. Chung, C. Zu and Y.-S. Su, Chem. Rev., 2014, 114, 11751–11787 CrossRef CAS PubMed
.
- J. Liu, M. Wang, N. Xu, T. Qian and C. Yan, Energy Storage Mater., 2018, 15, 53–64 CrossRef
.
- X. Liu, Y. Lu, Q. Zeng, P. Chen, Z. Li, X. Wen, W. Wen, Z. Li and L. Zhang, ChemSusChem, 2020, 13, 715–723 CrossRef CAS PubMed
.
- M. Rao, X. Song, H. Liao and E. J. Cairns, Electrochim. Acta, 2012, 65, 228–233 CrossRef CAS
.
- W. Li, G. Zheng, Y. Yang, Z. W. Seh, N. Liu and Y. Cui, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 7148–7153 CrossRef CAS PubMed
.
- W. Li, Q. Zhang, G. Zheng, Z. W. Seh, H. Yao and Y. Cui, Nano Lett., 2013, 13, 5534–5540 CrossRef CAS PubMed
.
- H. Kim, J. Lee, H. Ahn, O. Kim and M. J. Park, Nat. Commun., 2015, 6, 7278 CrossRef CAS PubMed
.
- A. Bhargav, M. E. Bell, Y. Cui and Y. Fu, ACS Appl. Energy Mater., 2018, 1, 5859–5864 CrossRef
.
- P. Sang, Y. Si and Y. Fu, Chem. Commun., 2019, 55, 4857–4860 RSC
.
- G. Gao, X. Sun and L.-W. Wang, J. Mater. Chem. A, 2020, 8, 21711–21720 RSC
.
- W. J. Chung, J. J. Griebel, E. T. Kim, H. Yoon, A. G. Simmonds, H. J. Ji, P. T. Dirlam, R. S. Glass, J. J. Wie, N. A. Nguyen, B. W. Guralnick, J. Park, Á. Somogyi, P. Theato, M. E. Mackay, Y.-E. Sung, K. Char and J. Pyun, Nat. Chem., 2013, 5, 518–524 CrossRef CAS PubMed
.
- R. M. S. Maior, K. Hinkelmann, H. Eckert and F. Wudl, Macromolecules, 1990, 23, 1268–1279 CrossRef CAS
.
- S. Hotta, S. D. Rughooputh, A. J. Heeger and F. Wudl, Macromolecules, 1987, 20, 212–215 CrossRef CAS
.
- S. Hotta, M. Soga and N. Sonoda, Synth. Met., 1988, 26, 267–279 CrossRef CAS
.
- E. W. Tsai, S. Basak, J. P. Ruiz, J. R. Reynolds and K. Rajeshwar, J. Electrochem. Soc., 1989, 136, 3683–3689 CrossRef CAS
.
- R. Kiani, D. Sebastiani and P. Partovi-Azar, ChemPhysChem, 2021, 1, 1–6 Search PubMed
.
-
K. Dill, S. Bromberg and D. Stigter, Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology, Garland Science, New York, NY, 2003 Search PubMed
.
- X. Xu and J. Dzubiella, Colloid Polym. Sci., 2020, 298, 747–759 CrossRef CAS
.
-
P. Atkins and J. Paula, Atkins' Physical Chemistry, Oxford University press, New York, NY, 2008 Search PubMed
.
- I. J. General, J. Chem. Theory Comput., 2010, 6, 2520–2524 CrossRef CAS PubMed
.
- Y. Deng and B. Roux, J. Phys. Chem. B, 2009, 113, 2234–2246 CrossRef CAS PubMed
.
-
D. McQuarrie and J. Simon, Molecular Thermodynamics, University Science Books, 1999 Search PubMed
.
- M. Rossi, S. Chutia, M. Scheffler and V. Blum, J. Phys. Chem. A, 2014, 118, 7349–7359 CrossRef CAS PubMed
.
- M. Schneider, C. Masellis, T. Rizzo and C. Baldauf, J. Phys. Chem. A, 2017, 121, 6838–6844 CrossRef CAS PubMed
.
- K. Vollmayr-Lee, Am. J. Phys., 2020, 88, 401–422 CrossRef CAS
.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS
.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS
.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS
.
- V. W.-Z. Yu, F. Corsetti, A. Garca, W. P. Huhn, M. Jacquelin, W. Jia, B. Lange, L. Lin, J. Lu, W. Mi, A. Seifitokaldani, Á. Vázquez-Mayagoitia, C. Yang, H. Yang and V. Blum, Comput. Phys. Commun., 2018, 222, 267–285 CrossRef CAS
.
- V. Havu, V. Blum, P. Havu and M. Scheffler, J. Comput. Phys., 2009, 228, 8367–8379 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 6–9 CrossRef PubMed
.
- V. G. Ruiz, W. Liu, E. Zojer, M. Scheffler and A. Tkatchenko, Phys. Rev. Lett., 2012, 108, 2–6 CrossRef PubMed
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed
.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 CrossRef CAS PubMed
.
-
R. T. Morrison and R. N. Boyd, Organic Chemistry, Allyn and Bacon, Boston, 2002, p. 1283 Search PubMed
.
-
B. Meyer, in The Structures of Elemental Sulfur, ed. H. Emeléus and A. Sharpe, Academic Press, 1976, vol. 18, of Advances in Inorganic Chemistry and Radiochemistry, pp. 287–317 Search PubMed
.
- R. Steudel, Chem. Rev., 2002, 102, 3905–3945 CrossRef CAS PubMed
.
- A. Kamyshny, A. Goifman, J. Gun, D. Rizkov and O. Lev, Environ. Sci. Technol., 2004, 38, 6633–6644 CrossRef CAS PubMed
.
- A. Kamyshny, J. Gun, D. Rizkov, T. Voitsekovski and O. Lev, Environ. Sci. Technol., 2007, 41, 2395–2400 CrossRef CAS PubMed
.
- R. Gleiter, G. Haberhauer and F. Rominger, Eur. J. Inorg. Chem., 2019, 3846–3853 CrossRef CAS
.
- D. M. Byler, H. Susi and H. M. J. Farrell, Biopolymers, 1983, 22, 2507–2511 CrossRef CAS PubMed
.
- K. B. Biggs, J. P. Camden, J. N. Anker and R. P. V. Duyne, J. Phys. Chem. A, 2009, 113, 4581–4586 CrossRef CAS PubMed
.
- X.-F. Wu, X. Zheng, H.-G. Wang, Y.-Y. Zhao, X. Guan, D. L. Phillips, X. Chen and W. Fang, J. Chem. Phys., 2010, 133, 134507 CrossRef PubMed
.
- H. E. Van Wart and H. A. Scheraga, J. Phys. Chem., 1976, 80, 1812–1823 CrossRef CAS
.
- B. Mandal and B. Basu, RSC Adv., 2014, 4, 13854–13881 RSC
.
- L. F. Sgobbi, C. A. Razzino, I. G. Rosset, A. C. Burtoloso and S. A. Machado, Electrochim. Acta, 2013, 112, 500–504 CrossRef CAS
.
- P. Partovi-Azar and T. D. Kühne, J. Comput. Chem., 2015, 36, 2188–2192 CrossRef CAS PubMed
.
- P. Partovi-Azar, T. D. Kühne and P. Kaghazchi, Phys. Chem. Chem. Phys., 2015, 17, 22009–22014 RSC
.
- C. Park, M. Kanduč, R. Chudoba, A. Ronneburg, S. Risse, M. Ballauff and J. Dzubiella, J. Power Sources, 2018, 373, 70–78 CrossRef CAS
.
- C. Park, A. Ronneburg, S. Risse, M. Ballauff, M. Kanduč and J. Dzubiella, J. Phys. Chem. C, 2019, 123, 10167–10177 CrossRef CAS
.
- M. Qureshi, S. H. Nowak, L. I. Vogt, J. J. Cotelesage, N. V. Dolgova, S. Sharifi, T. Kroll, D. Nordlund, R. Alonso-Mori, T. C. Weng, I. J. Pickering, G. N. George and D. Sokaras, Phys. Chem. Chem. Phys., 2021, 23, 4500–4508 RSC
.
- T. J. Zuehlsdorff and C. M. Isborn, Int. J. Quantum Chem., 2019, 119, 1–18 CrossRef
.
- K. H. Wujcik, T. A. Pascal, C. D. Pemmaraju, D. Devaux, W. C. Stolte, N. P. Balsara and D. Prendergast, Adv. Energy Mater., 2015, 5, 1500285 CrossRef
.
-
L. Bennett, B. Melchers and B. Proppe, Curta: A General-purpose High-Performance Computer at ZEDAT, Freie Universität Berlin, 2020 DOI:10.17169/refubium-26754
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04550d |
| This journal is © the Owner Societies 2021 |