Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mutual neutralisation of O+ with O−: investigation of the role of metastable ions in a combined experimental and theoretical study
Mathias
Poline
 *a,
Arnaud
Dochain
b,
Stefan
Rosén
a,
Jon
Grumer
*a,
Arnaud
Dochain
b,
Stefan
Rosén
a,
Jon
Grumer
 c,
MingChao
Ji
c,
MingChao
Ji
 a,
Gustav
Eklund
a,
Gustav
Eklund
 a,
Ansgar
Simonsson
a,
Peter
Reinhed
a,
Mikael
Blom
a,
Nicholas S.
Shuman
d,
Shaun G.
Ard
d,
Albert A.
Viggiano
d,
Mats
Larsson
a,
Henrik
Cederquist
a,
Henning T.
Schmidt
a,
Ansgar
Simonsson
a,
Peter
Reinhed
a,
Mikael
Blom
a,
Nicholas S.
Shuman
d,
Shaun G.
Ard
d,
Albert A.
Viggiano
d,
Mats
Larsson
a,
Henrik
Cederquist
a,
Henning T.
Schmidt
 a,
Henning
Zettergren
a,
Xavier
Urbain
a,
Henning
Zettergren
a,
Xavier
Urbain
 b,
Paul S.
Barklem
b,
Paul S.
Barklem
 c and
Richard D.
Thomas
c and
Richard D.
Thomas
 *a
*a
aDepartment of Physics, Stockholm University, AlbaNova, Stockholm, Sweden. E-mail: mathias.poline@fysik.su.se; rdt@fysik.su.se
bInstitute of condensed Matter and Nanosciences, Université catholique de Louvain, Louvain-la-Neuve, Belgium
cTheoretical Astrophysics, Department of Physics and Astronomy, Uppsala University, Box 516, S 75120, Uppsala, Sweden
dAir Force Research Laboratory, Space Vehicles Directorate, Kirtland Air Force Base, NM 87117, USA
First published on 25th October 2021
Abstract
The mutual neutralisation of O+ with O− has been studied in a double ion-beam storage ring with combined merged-beams, imaging and timing techniques. Branching ratios were measured at the collision energies of 55, 75 and 170 (± 15) meV, and found to be in good agreement with previous single-pass merged-beams experimental results at 7 meV collision energy. Several previously unidentified spectral features were found to correspond to mutual neutralisation channels of the first metastable state of the cation (O+(2Do), τ ≈ 3.6 hours), while no contributions from the second metastable state (O+(2Po), τ ≈ 5 seconds) were observed. Theoretical calculations were performed using the multi-channel Landau–Zener model combined with the anion centered asymptotic method, and gave good agreement with several experimentally observed channels, but could not describe well observed contributions from the O+(2Do) metastable state as well as channels involving the O(3s 5So) state.
1 Introduction
Mutual neutralisation (MN) is a reaction in which an electron is transferred between two oppositely charged ions, resulting in the formation of neutral products. For the interaction of two species, A and B, this can be written as| A+ + B− → A + B + EK, | (1) |
In addition to merged-beams experiments, other apparatuses are also used to study MN, e.g. Flowing Afterglow – Langmuir Probe (FALP).15–21 Data are obtained under thermal 300–600 K conditions, and report several interesting conclusions: systems of four or more atoms react with very similar rate constants and triatomic systems somewhat slower,16 while atom–atom systems proceed with widely varying rate constants. However, only under rare circumstances can the product distributions be measured and no information on the states of these products can be obtained.22 Merged-beams experiments are therefore usually more suitable for the study of MN reactions.
One limiting factor in merged-beams setups is that the initial state distributions of the colliding ions are generally unknown and are highly dependent on the methods of production and the time between ion creation and reaction. This can potentially affect the determination of the total cross section, and lead to additional features in the product-energy spectra as well as large spectral-broadening effects when dealing with molecular ions, making it difficult to resolve final quantum states. This issue can be partially resolved by allowing such ions to be stored for sufficiently long periods such that the species of interest have time to relax from their initially excited quantum-state distribution.
The double electrostatic ion ring facility DESIREE23,24 has been designed and constructed partly for this purpose. It consists of two race-track storage rings sharing a common straight section mounted in a double-walled vacuum vessel. The apparatus is cooled down to cryogenic temperatures in ultra high vacuum conditions, allowing for ion storage up to hours,25 and MN processes freely occur along the common straight section as the ions circulate. Rotational and vibrational cooling is only relevant to molecular species,26 nevertheless, many atomic ions can be formed in metastable electronically excited states. It is therefore of fundamental and applied interest to investigate atomic MN experiments where metastable ions are known to be present in order to determine the extent of this effect and the role such ions would have in the environments where they are present.
On the theoretical side, the MN of even the simplest systems is difficult to model accurately.12 The reaction is generally described as a non-adiabatic process in which electronic states interact at large internuclear distances. The semi-classical Landau Zener (LZ) model, dating back from 1932,27,28 gives the probability of a transition between the incident ion-pair state and the neutral-pair state. Recent ab initio treatments have been applied to systems with few electrons/few active electronic states9,12,29–31 though there is little high-quality experimental data to benchmark theory. Multichannel Landau–Zener models are therefore generally favored and provide results in good agreement with theory when the non-adiabatic couplings are properly described.1,14 Interestingly, in a recent study,32 the experimentally determined branching ratios were found to be in a better agreement with multichannel Landau–Zener models than with a full quantum mechanical treatment.
Mutual neutralisation of O+ with O−
The O+/O− system is of particular interest as it constitutes a charge removal process present in air-plasmas, and is highly relevant to the modelling of the ionosphere.33 At high altitudes, oxygen exists predominantly as atomic species as the solar UV radiation is sufficient to dissociate any molecular oxygen. This results in oxygen cations and free electrons which in turn form oxygen anions through radiative attachment. In charge-reducing reactions such as MN and the related dissociative recombination (DR) process, the oxygen fragments may either contribute to the heating of the geocorona, or escape this layer and move to higher altitudes.34 The excited neutrals formed in these reactions also emit photons through transitions to the ground states, leading to airglow in the ionosphere.35 Studies of the nightime spectrum suggest that MN could contribute up to 40% of the OI 135.6 nm emission arising from the O(3s 5So)→ O(3P) transition.36 Modelling of this reaction, i.e., determining reaction rate constants and product branching ratios as a function of collision energy is therefore of importance if such plasmas are to be fully understood.The O+/O− reaction was first investigated by Olson et al. in 1970,35 but these results were later found to disagree with experiments by Peart et al. in 1989,37 and in 1993.38 Possible explanations for this disagreement were suggested and are reviewed in those two latter papers. The first study at subthermal collision energy, only came much later, in 2018, by de Ruette et al.,1 who also measured the branching ratios of the neutral products into separate final quantum states for the first time. The following channels were then identified:
 | (2) |
Interestingly, the authors also reported an additional feature in their energy spectra which could only be attributed to the presence of metastable ions in the beams. These were, however, not clearly identified, which motivates further analysis and calculations. There are two known metastable states of the oxygen cation: The second excited state, O+(2Po) at 5.02 eV39 above the ground state, with a lifetime of about 5 seconds, and the first excited state O+(2Do) at 3.32 eV with a lifetime of about 3.6 hours.40 The latter can not be removed even through long-time storage but is still of particular interest when analyzing merged-beams experiments including those at DESIREE. Long lived metastable cations have been predicted to be produced in photon and electron ionization of atomic oxygen in the atmosphere,41 and are known to be produced under laboratory conditions.37,38 In the present study, we aim to combine experimental and theoretical methods in order to determine the branching ratios of the MN of O+ with O−, including metastable contributions.
2 Methods
Experimental setup
We combine storage ring, merged-beams, and imaging techniques to measure the kinetic energy released in the MN of oxygen ions over ion-beam storage time up to 30 seconds.The total kinetic energy after an MN reaction depends on the kinetic energy release EK and the collision energy Ec.m. in the center-of-mass frame. The latter is a function of the velocities of the two ion beams in the laboratory system of reference, vA and vB, and of the angle α between them.
 | (3) |
Thus in order to obtain the lowest collision energy, one must minimize α and adjust the ion beam energies accordingly. In DESIREE, this is done by adjusting the voltages on the ion-beam steerers and by biasing one or several of the drift tubes 1–7 of the merging section, as shown in Fig. 1.
In an MN event, the ions are neutralised and are then no longer affected by the electrostatic fields in the ion-optical elements. Consequently, they continue to move with the velocities obtained in the reaction. The neutral fragments then reach the imaging detector, which is located 1.40 m from the last drift tube. The detector consists of a microchannel-plate stack with a phosphor-screen anode,42 from which the light is guided to a complementary metal oxide semiconductor (CMOS) camera, which records the positions, and a 16 channel Photomultiplier Tube (PMT), which is used to measure the arrival time differences. A detailed description of the DESIREE storage ring facility can be found in Thomas et al.,23 while its first comissioning is described in Schmidt et al.24
For the present experiment, O+ is produced from an electron cyclotron resonance (ECR) ion source fed with molecular oxygen as a source gas. The O+ beam is extracted from the source and accelerated to 8.28 keV. The O− ions are produced from a TiO cathode using a Source of Negative Ions by Cesium Sputtering (SNICS), and accelerated to 7.16 keV. These are nominal beam energies based on measurements of the acceleration voltage on the ion source platforms.
At these energies, the MN events occurring in the interaction region yield products that arrive at the detector with a time difference between them of less than 200 ns. The overlap of the two ion beams was first optimised by monitoring their trajectories based on measurements of the beam positions at the pick-up electrodes, as indicated in Fig. 1. Different voltages were then applied to the drift tubes in order to find the minimum collision energy. As the cross section is inversely proportional to the collision energy at low energies,43 the maximum count rate corresponds to the lowest collision energy. This was obtained at a voltage of about 570 V on the middle drift tube (number 4 in Fig. 1), and this setting was used during the first part of the experiment. The biased region was then in the next step changed to the drift tube number 2, in order to increase the distance to the detector and thus the resolution in the products spectra. An additional measurement was performed at a voltage of 535 V, in order to measure at a higher collision energy.
Data evaluation
We define r as the separation between the two particles as the first particle reaches the detector, as illustrated in Fig. 2(a)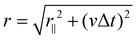 | (4) |
The quantity r is determined from coincidence measurements of r‖ and Δt, and is proportional to the square root of the center-of-mass kinetic energy release. This type of combined imaging technique has been extensively used in the past in dissociative recombination studies,44–47 and there exist analytical functions which approximate the distributions of these measured quantities. However, since here, the collision energy is adjusted through a bias voltage as described above, fringe field effects at the entrance and exit of the biased tube(s) must be taken into account. This is done by modelling the potential as a function of position along the merging section using the SIMION program,48 and determine the corresponding ion velocity vectors  and
and  . The r distributions are then simulated by calculating the recoil velocity components due to the excess energy of the reaction,
. The r distributions are then simulated by calculating the recoil velocity components due to the excess energy of the reaction,  and
and  , and determining the resulting vectors, as depicted in Fig. 2(a). In the region where the electric potential differs from the applied voltage, the collision energy is generally higher, resulting in higher r values. As larger collision energy implies smaller cross section in the present collision energy range, the events are not uniformly distributed along the interaction region, and a probability distribution proportional to
, and determining the resulting vectors, as depicted in Fig. 2(a). In the region where the electric potential differs from the applied voltage, the collision energy is generally higher, resulting in higher r values. As larger collision energy implies smaller cross section in the present collision energy range, the events are not uniformly distributed along the interaction region, and a probability distribution proportional to  is used to take this into account.
is used to take this into account.
Furthermore, the spread in the energies and velocity components of the ion beams results in broadening of the distributions. In recent MN studies at DESIREE by Eklund et al.,49,50 extensive Monte Carlo simulations were performed to take these effects into account. Given that these effects cannot be independently determined, here we instead chose to convolve the r distributions with Gaussians of adjustable width, in order to match the observed experimental broadening.
Correction for detection efficiency
The detectors have two limitations which must be taken into account. In order to measure the arrival time differences, the neutral particles must produce light that hit two different channels of the PMT, as illustrated in Fig. 2(b). The detector is thus less efficient in detecting pairs of particles in the horizontal plane or with small separations, as these are then likely to hit the same channel. Furthermore, light resulting from a single particle hitting the phosphor screen may trigger several adjacent PMT channels, resulting in false two particle events. This means that real MN events with small time differences Δt cannot be distinguished from false coincidences, and this constitutes another limiting factor of detection. Consequently, the probability of two neutrals being detected depends on the orientation of the products, that is, the angle between the beam axis and the line between the two products, θ, as well as the angle between the horizontal axis of the detector and the products, ϕ, as illustrated in Fig. 2(a) and (b). Neglecting the difference in arrival times of the two particles, the separation of the spots on the detector depends on the angle θ, through the relation23 | (5) |
The detection efficiency can then be related to this separation r‖ in the following ways: The minimum angle ϕ (see Fig. 2(b)) for which two events can be detected, depend on this quantity, and thus the detection efficiency ε1, due to the limitations of the PMTs is given by
 | (6) |
The second factor ε2, determines the loss of events due to the timing resolution. The cutoff in the time detection Δtcut, limits the separation of two fragments by
 | (7) |
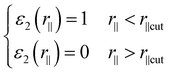 | (8) |
If the relative velocity between the ions is zero, then the angular distribution of the fragments is isotropic, i.e. cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is uniformly distributed between 0 and 1. The detection efficiency for a given kinetic energy release channel can then be evaluated analytically. At non-zero collision energies, the angular distribution is not necessarily isotropic. However, as these effects are not expected to be significant at the collision energies considered here, the detection efficiencies are calculated assuming isotropic distributions, and the branching ratios are corrected accordingly.
θ is uniformly distributed between 0 and 1. The detection efficiency for a given kinetic energy release channel can then be evaluated analytically. At non-zero collision energies, the angular distribution is not necessarily isotropic. However, as these effects are not expected to be significant at the collision energies considered here, the detection efficiencies are calculated assuming isotropic distributions, and the branching ratios are corrected accordingly.
Theoretical calculations
We follow largely the method presented by Zhou & Dickinson,51 which relies on the multi-channel Landau–Zener model, with an anion centered asymptotic method to determine the coupling matrix elements.The basis for this model is the introduction of a diabatic basis in which the ionic and covalent potential curves cross at some internuclear distance Rx (see Fig. 3). In the narrow region around these crossing points, the diabatic potentials are assumed to vary linearly with R, and the non diagonal elements Hif of the electronic Hamiltonian in this basis, determine the probability, p, to stay on the diabatic potential curve during a single passage of the crossing
 | (9) |
 | (10) |
 | ||
| Fig. 3 Landau Zener diabatic potentials of the ionic (black curves, eqn (10)) and covalent states (colored curves, eqn (2)). The O(np 3P) Rydberg series is shown as blue lines as an example. | ||
The dependence on the collision energy for the crossing probability (eqn (9)), is determined by the radial velocity vR, which classically is given by
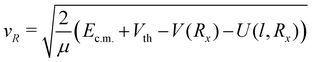 | (11) |
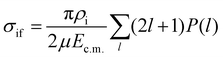 | (12) |
The main challenge in this model is the estimation of the coupling elements Hif for the different electronic states involved. Previous calculations of cross sections of MN reactions involving hydrogen have provided accurate results by using a linear combination of atomic orbitals (LCAO) method in order to solve the two electron Hamiltonian problem.54 This is, however, non trivial to calculate for the oxygen anion, and a more readily applicable approach is the asymptotic method developed by Landau & Herring,55 which was later formulated by Janev & Salin56 for the specific case of mutual neutralisation. The coupling elements are then derived from the surface integral method based on one-electron wavefunctions for the active electron centered on each atom, which results in an analytical expression in terms of parameters in these wavefunctions.57 The system is then considered as a quasimolecule, from which the allowed electronic states can be determined from the Wigner–Witmer rules.58
For the reactions involving the metastable cations, the number of output channels increases significantly as the additional energy allows more highly excited states to be populated. The potential curves of the first cationic metastable state and the O(np 3P) Rydberg series is shown in Fig. 3 to illustrate this (the full list of output states is later presented in the results section). However, the main configuration of most of these electronic states is an O+(4So) (ground state) core with a outer electron, which is not open to one-electron processes since this would require a spin flip transition in the core. It is therefore necessary to compute the mixing content of the O+(2Do) configuration in these particular states. In order to achieve this, multiconfigurational Dirac–Hartree–Fock (MCDHF) calculations were employed through the GRASP2018 atomic structure code.59
The MCDHF calculation is based on the Dirac–Coulomb Hamiltonian with corrections due to the frequency independent Breit interaction and leading quantum-electrodynamical effects included in a subsequent relativistic configuration interaction calculation. The mixing between different fine-structure (e.g. LSJ-coupled) states resulting from atomic structure calculations mainly depends on the definition of the basis space and the shape of the obtained electron orbitals. Core mixings in neutral oxygen were thus explored for a number of different electron correlation models. To best match the definition of the wavefunctions employed in the MN reaction calculations, i.e. pure LS coupled states augmented with an additional state differing only in its core-term coupling, the most appropriate definition for the core mixings is arguably that which results from an MCDHF model including a many-electron basis space spanned by only the fine-structure states of the target configuration. This is the approach adopted in the present analysis.
The coupling elements are then calculated using the obtained mixing coefficients, and the cross sections for these particular states are then computed using eqn (12).
3 Results and discussion
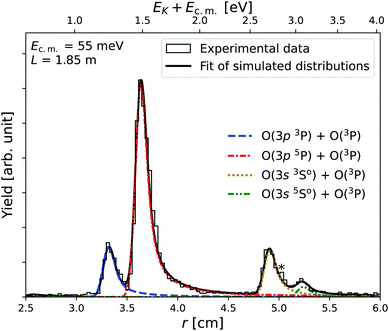
Our experimental r distribution for the O+ and O− MN at our lowest collision energy (Ec.m. = 55 ± 15 meV) is displayed in Fig. 4 as a histogram. The result from the fit of the simulated distributions of the channels in eqn (2) is shown as a full black line, with the individual distributions displayed in colored dashed lines. The four channels can clearly be identified, with the O(3p 5P) + O(3P) channel (red curve) as the dominating one, in agreement with previous results at 7 meV collision energy.1 Significant tails to larger distances (see for example at r = 4–4.5 cm) are observed, as expected from the fringe field effects. However, a small shoulder around 5.0 cm (marked here with an asterisk) cannot be accounted for solely by these effects and is believed to be due to a metastable state of O+. The corresponding energy (∼2.7 eV) also coincides with a similar shoulder in the kinetic energy release spectra of de Ruette et al.,1 which has not been marked as a metastable contribution in the original publication. We therefore perform further analysis of present and previous results, aided by our theoretical model.The high excess energy associated with the reaction involving the shorter lived (τ ≈ 5 s) O+(2Po) metastable state is likely to produce oxygen pairs with one atom in a highly excited auto-ionizing state, which would not contribute to the rate of neutral reaction pair products. Furthermore, no time dependence after ion injection was observed in the MN signal for storage times up to 30 seconds. We thus infer that the O+(2Po) has no significant contribution to the spectra. Therefore, only the longer lived, O+(2Do) metastable state, which has a lower excitation energy, is considered in the following. If one neglects two-electron processes, then spin and/or orbital angular momentum constraints limit the allowed transitions to the following channels upon neutralisation
 | (13) |
The 2.75 eV channel accounts well for the observed marked peak in present experimental results measured at DESIREE. On the other hand, angular momentum coupling allows for the O(3P) and O(3Do) states to be described as a linear combination of the cores of the two cationic states with an outer np/nd electron. Hence one-electron transfer to the following states is also allowed:
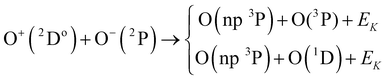 | (14) |
 | (15) |
In the present experiment at DESIREE, none of these states are clearly identified. However, in the experimental setup of de Ruette et al.,1 the ions were not stored, which allowed for small beam apertures and large beam currents, resulting in high count statistics. We therefore perform further analysis of their kinetic energy release spectrum, which is shown in Fig. 5 on an adjusted scale in order to reveal possible small scale contributions from metastables.
 | ||
| Fig. 5 Yield of neutral O pairs as function of the kinetic energy release, at collision energy Ec.m. = 7 meV. Spectrum is from the single-pass experiment performed by de Ruette et al.1 Predicted channel positions from the metastable state are shown as colored bars. The red dotted curve results from a fit of the individual simulated distributions. | ||
The presence of a broad feature around 4.5 eV is found to coincide with the n = 3 channel of the O(np 3P) series. Furthermore, small peaks at around 3.1 eV and 2.4 eV correspond to energy levels of that same series. Additionally, we observe some peaks from the O(nd 3Do) series, as highlighted in Fig. 5, as well as a plateau at lower energies corresponding to higher n values. We therefore interpret these small scale contributions as mainly resulting from the reaction of the O+(2Do) metastable cation neutralising to these two Rydberg series. Interestingly, we find that some of these coincide with the main peaks, and could therefore affect the deduced branching ratios for the dominating ground state ion beam component. Furthermore, the population of metastable states may differ between the two experiments due to different choice of parent gas (CO was used in the study by de Ruette et al.1). In order to elucidate this, a new fit of the experimental data was performed, including the channels from the metastable state of O+ (eqn (13)–(15)), using the method described in Section 2. The result of this fit for the experimental spectra of de Ruette et al.1 is shown in Fig. 5 as a red dotted curve and the obtained revised branching ratios are presented in Table 1, together with the present experimental and theoretical results.
| E K [eV] | R x [a0] | Exp. 7a meV [%] | Exp. 7b meV [%] | Exp. 55c meV [%] | Theoryd (<200 meV) | |
|---|---|---|---|---|---|---|
| a Results of de Ruette et al1. b Revised results of de Ruette et al. c Present results. d Present calculations. | ||||||
| O+(4So) + O−(2P)→ | ||||||
| O(3s 5So) + O(1D) | 1.05 | 25.86 | — | 0.52 ± 0.10 | — | 10−3 |
| O(3p 3P) + O(3P) | 1.17 | 23.32 | 14.06 ± 0.14 | 13.96 ± 0.17 | 15.8 ± 0.7 | 16.3 |
| O(3p 5P) + O(3P) | 1.42 | 19.25 | 67.63 ± 0.31 | 66.28 ± 0.32 | 67.0 ± 0.9 | 70.0 |
| O(3s 3So) + O(3P) | 2.64 | 10.44 | 14.61 ± 0.19 | 15.39 ± 0.26 | 14.1 ± 2.0 | 13.7 |
| O(3s 5So) + O(3P) | 3.01 | 9.18 | 3.71 ± 0.18 | 3.85 ± 0.21 | 3.1 ± 0.7 | 10−2 |
| O+(2Do) + O−(2P)→ | ||||||
| O(3s 3Do) + O(1D) | 0.98 | 27.44 | — | 1.95 ± 0.70 | — | 10−4 |
| O(n > 6) + O(3P) | 1.9–2.2 | 14.3–12.3 | — | 17.91 ± 4.46 | — | — |
| O(6d 3Do) + O(3P) | 2.24 | 12.16 | — | 6.44 ± 1.25 | — | 10−5 |
| O(6p 3P) + O(3P) | 2.35 | 11.63 | — | 3.37 ± 1.30 | — | 0.1 |
| O(5d 3Do) + O(3P) | 2.41 | 11.33 | — | 9.53 ± 1.38 | — | 10−5 |
| O(3p 3P) + O(1D) | 2.53 | 10.80 | — | 4.39 ± 4.39 | — | 0.2 |
| O(5p 3P) + O(3P) | 2.60 | 10.53 | — | 8.52 ± 1.00 | 30 ± 20 | 0.3 |
| O(4d 3Do) + O(3P) | 2.72 | 10.08 | — | {31.93 ± 2.66} | {70 ± 20} | 10−4 |
| O(3s 1Do) + O(3P) | 2.75 | 9.98 | — | 99.0 | ||
| O(3s 3Do) + O(3P) | 2.94 | 9.36 | — | 3.68 ± 1.61 | — | 0.5 |
| O(4p 3P) + O(3P) | 3.12 | 8.85 | — | 4.60 ± 3.11 | — | 10−6 |
| O(3d 3Do) + O(3P) | 3.39 | 8.18 | — | — | — | 10−7 |
| O(3p 3P) + O(3P) | 4.49 | 6.33 | — | 7.68 ± 3.78 | — | 10−3 |
For the reaction involving the ground state cation (first five rows), fair agreement between the results by de Ruette et al.1 (Exp. 7 meV) and present results at DESIREE (Exp. 55 meV) is obtained, though the present results have substantially larger uncertainties. These have several contributions: The uncertainty in the collision energy Ec.m., which is fitted to the spectra based on the simulations, the lower count statistics, and the uncertainty in the metastable contributions. Hence, the O(3s 3So) channel is associated with a large error given the possible presence of the O(5p 3P) channel, at only 0.04 eV from the O(3s 3So) channel. Theoretical calculations show good agreement with the experimental results involving the ground state cation, except for the channels involving the O(3s 5So) state, at 1.05 and 3.01 eV. This could indicate that the coupling element for that particular state is not well described by the model. Note that the contribution from the reaction involving the O(1D) product (EK = 1.05 eV) was previously not identified in the original publication of de Ruette et al.
For the reaction involving the metastable cation, contributions from most possible pathways (eqn (13)–(15)) are observed in the 7 meV collision energy measurement by de Ruette et al.,1 whereas only a few channels can be resolved in the present measurements at 55 meV, due to the lower resolution and the large contributions from fringe field effects. It is then no longer evident whether the O(3s 1Do) (2.75 eV) channel is the most populated as initially asserted. Another channel, very close in energy, namely the O(4d 3Do) at 2.72 eV is also present, and the two states can not be fully resolved in any of the two experiments. Theoretical calculations suggest that all production goes to the more energetic channel (2.75 eV), but ultimately fails to account for the observed production in the O(nd 3Do) series and yields smaller populations for the O(np 3P) series than the ones observed. This suggests that the theoretical model used is not sufficient in this case. A possible explanation for this is the following: Due to the mixing content of these states, significant overlap exists between the wavefunctions of the active electron when part of the negative ion, and the wavefunction, when in the Rydberg states of the neutral atom. The conditions of validity of the surface integrals used to calculate the coupling elements are then no longer fulfilled. Furthermore, at small crossing distances, the multichannel Landau–Zener model is generally less accurate, an issue previously discussed in the former paper,1 and may explain the theoretical model's failure to account for the observed contributions of the more energetic channels. These results show the limitations in the theoretical approach used, and suggest that more advanced models are required for the treatment of metastable states.
Our experimental results at the collision energy of 75 and 170 (± 15) meV are presented in Fig. 6(a). The increased relative velocity of the ions is found to correlate with a broadening of the r distributions. The same effect could be observed in other earlier experiments at DESIREE,49,50 and is mainly attributed to the spread in the energies of the ion beams and a decreased accuracy in the approximation made in eqn (4). The metastable contribution (marked with an asterisk) remains present in both measurements. The extracted branching ratios are shown in Fig. 6(b), in comparison with the results of de Ruette et al. at 7 meV collision energy and present theoretical calculations. A generally good agreement is found between present experimental results, previous experimental results of de Ruette et al.1 and theory, with no significant changes in populations observed, as expected by the calculations.
 | ||
| Fig. 6 Yield of neutral O pairs as a function of the separation r between the products, at collision energies of 75 and 170 meV (a). Branching ratios for the MN reaction of O+ with O− as a function of the collision energy. Present theoretical calculations are shown as lines. Error bars denote the present experimental results and crosses the revised results of de Ruette et al.1 (b). | ||
4 Conclusions
Using a combined merged-beams and storage ring apparatus, we have measured the kinetic energy release in the mutual neutralisation of O+ with O− at collision energies of 55, 75 and 170 (± 15) meV and determined the branching ratios. An additional feature in the spectra was found to correspond to one or two reaction channels involving the long lived (τ ≈ 3.6 hours) O+(2Do) metastable state. Further analysis of previous experimental results at 7 meV collision energy by de Ruette et al.1 additionally revealed several previously unidentified small scale contributions which were mainly found to correspond to neutralisation channels of that same metastable state to the O(np 3P) and O(nd 3Do) Rydberg series. These results were revised by taking into account these contributions and the fringe field effects in the fit.Multiconfigurational Dirac–Hartree–Fock calculations were employed to determine the ground/metastable core mixing in the available states, and estimate the branching ratios using the multi-channel Landau–Zener model combined with the anion centered asymptotic method. These theoretical results were found to be in good agreement with the experimental results for the reaction involving the ground state O+(4So) cation, except for the channels involving the O(3s 5So) state, which theory does not predict to contribute. For the reaction involving the O+(2Do) metastable state, the theoretical results were found to predict a large contribution where a noticeable feature is observed experimentally but failed to account for several other observed product states, indicating that the model might not be sufficient. Further improvements are therefore needed for accurate modelling of these more complex reactions.
The storage of the ions for up to 30 seconds did not reveal the presence of any contribution from the shorter lived (τ ≈ 5 s) metastable O+(2Po) in our spectra, suggesting that the latter does not contribute significantly or only populates auto-ionizing states which cannot be detected in current experimental setups.
The present results are mostly relevant to the modeling of the F region of the ionosphere, in which the observed OI 135.6 nm and 130.4 nm nighttime emissions correspond to the O(3s 5So)/O(3s 3So) → O(3P) (ground state) transitions, which either occur directly or through radiative cascades from higher excited states.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the Air Force Office of Scientific Research under Award No. FA9550-19-1-7012 and AFOSR-19RVCOR042. This work was performed at the Swedish National Infrastructure, DESIREE (Swedish Research Council Contract No. 2017-00621). The work is part of the project “Probing charge – and mass – transfer reactions on the atomic level”, supported by the Knut and Alice Wallenberg Foundation (2018.0028). HTS, HC, HZ and PSB thank the Swedish Research Council for individual project grants (contract No. 2018-04092, 2019-04379, 2020-03437, and 2020-03404). This article is based upon work from COST Action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology). AD and XU acknowledge support from the Fonds de la Recherche Scientifique-FNRS under grant No. 4.4504.10. XU is a Senior Research Associate of the Fonds de la Recherche Scientifique-FNRS.Notes and references
- N. de Ruette, A. Dochain, T. Launoy, R. F. Nascimento, M. Kaminska and M. H. Stockett, et al. , Phys. Rev. Lett., 2018, 121, 083401 CrossRef CAS PubMed.
- M. Larsson, W. D. Geppert and G. Nyman, Rep. Prog. Phys., 2012, 75, 066901 CrossRef CAS PubMed.
- W. D. Geppert and M. Larsson, Chem. Rev., 2013, 113, 8872 CrossRef CAS PubMed.
- S. C. Glover, D. W. Savin and A.-K. Jappsen, Astrophys. J., 2006, 640, 553 CrossRef CAS.
- S. F. Adams, J. A. Miles and A. C. Laber, 48th AIAA Aerospace Sciences Meeting, 2010.
- W. Aberth, J. R. Peterson, D. C. Lorents and C. J. Cook, Phys. Rev. Lett., 1968, 20, 979 CrossRef CAS.
- D. A. Hayton and B. Peart, J. Phys. B: At., Mol. Opt. Phys., 1993, 26, 2879 CrossRef.
- R. Padgett and B. Peart, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, L995 CrossRef CAS.
- M. Stenrup, Å. Larson and N. Elander, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 012713 CrossRef.
- B. Peart and D. A. Hayton, J. Phys. B: At., Mol. Opt. Phys., 1992, 25, 5109 CrossRef.
- J. Moseley, W. Aberth and J. R. Peterson, Phys. Rev. Lett., 1970, 24, 435 CrossRef CAS.
- S. M. Nkambule, N. Elander, Å. Larson, J. Lecointre and X. Urbain, Phys. Rev. A, 2016, 93, 032701 CrossRef.
- X. Urbain, J. Lecointre, F. Mezdari, K. A. Miller and D. W. Savin, J. Phys.: Conf. Ser., 2012, 388, 092004 CrossRef.
- T. Launoy, J. Loreau, A. Dochain, J. Liévin, N. Vaeck and X. Urbain, Astrophys. J., 2019, 883, 85 CrossRef CAS.
- T. M. Miller, J. F. Friedman and A. A. Viggiano, Int. J. Mass Spectrom., 2007, 267, 190 CrossRef CAS.
- T. M. Miller, N. S. Shuman and A. A. Viggiano, J. Chem. Phys., 2012, 136, 204306 CrossRef PubMed.
- N. S. Shuman, A. A. Viggiano and R. Johnsen, J. Chem. Phys., 2013, 138, 204302 CrossRef PubMed.
- N. S. Shuman, T. M. Miller, R. Johnsen and A. A. Viggiano, J. Chem. Phys., 2014, 140, 044304 CrossRef PubMed.
- N. S. Shuman, J. P. Wiens, T. M. Miller and A. A. Viggiano, J. Chem. Phys., 2014, 140, 224309 CrossRef PubMed.
- J. P. Wiens, N. S. Shuman and A. A. Viggiano, J. Chem. Phys., 2015, 142, 114304 CrossRef PubMed.
- J. P. Wiens, N. S. Shuman, T. M. Miller and A. A. Viggiano, J. Chem. Phys., 2016, 144, 204309 CrossRef PubMed.
- N. S. Shuman, T. M. Miller, N. Hazari, E. D. Luzik Jr. and A. A. Viggiano, J. Chem. Phys., 2010, 133, 234304 CrossRef PubMed.
- R. D. Thomas, H. T. Schmidt, G. Andler, M. Björkhage, M. Blom and L. Brännholm, et al. , Rev. Sci. Instrum., 2011, 82, 065112 CrossRef CAS PubMed.
- H. T. Schmidt, R. D. Thomas, M. Gatchell, S. Rosén, P. Reinhed and P. Löfgren, et al. , Rev. Sci. Instrum., 2013, 84, 055115 CrossRef CAS PubMed.
- E. Bäckström, D. Hanstorp, O. M. Hole, M. Kaminska, R. F. Nascimento and M. Blom, et al. , Phys. Rev. Lett., 2015, 114, 143003 CrossRef PubMed.
- H. T. Schmidt, G. Eklund, K. C. Chartkunchand, E. K. Anderson, M. Kamińska and N. de Ruette, et al. , Phys. Rev. Lett., 2017, 119, 073001 CrossRef CAS PubMed.
- L. D. Landau, Phys. Z. Sowietunion, 1932, 1, 88 CAS.
- L. D. Landau, Phys. Z. Sowietunion, 1932, 2, 46 CAS.
- S. M. Nkambule, P. Nurzia and Å. Larson, Chem. Phys., 2015, 462, 23 CrossRef CAS.
- J. Z. Mezei, J. B. Roos, K. Shilyaeva, N. Elander and Å. Larson, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 012703 CrossRef.
- Å. Larson, S. M. Nkambule and A. E. Orel, Phys. Rev. A, 2016, 94, 022709 CrossRef.
- J. Grumer, G. Eklund, A. M. Amarsi, P. S. Barklem, S. Rosén and M. C. Ji, et al. , Phys. Rev. Lett., 2021 Search PubMed , under review.
- P. D. Feldman, A. F. Davidsen, W. P. Blair, C. W. Bowers, S. T. Durrance and G. A. Kriss, et al. , Geophys. Res. Lett., 1992, 19, 453–456 CrossRef CAS.
- R. D. Thomas, Mass Spectrom. Rev., 2008, 77, 485 CrossRef PubMed.
- R. E. Olson, J. R. Peterson and J. Moseley, J. Chem. Phys., 1970, 53, 3391 CrossRef CAS.
- J. Qin, J. J. Makela, F. Kamalabadi and R. R. Meier, J. Geophys. Res.: Space Phys., 2015, 120, 10116 CAS.
- B. Peart, S. J. Foster and K. Dolder, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 1035 CrossRef CAS.
- D. A. Hayton and B. Peart, J. Phys. B: At., Mol. Opt. Phys., 1993, 26, 2879 CrossRef.
- W. C. Martin, V. Kaufman and A. Musgrove, J. Phys. Chem. Ref. Data, 1993, 22, 1179–1212 CrossRef CAS.
- E. C. Zipf, Can. J. Chem., 1969, 47, 1863 CrossRef CAS.
- D. G. Torr, Rev. Geophys. Space Phys., 1979, 17, 510 CrossRef CAS.
- S. Rosén, H. T. Schmidt, P. Reinhed, D. Fischer, R. D. Thomas and H. Cederquist, Rev. Sci. Instrum., 2007, 78, 113301 CrossRef PubMed.
- G. W. Drake, Springer Handbook of Atomic, Molecular, and Optical Physics, Springer, New York, 2006 Search PubMed.
- Z. Amitay, D. Zajfman, P. Forck, U. Hechtfischer, B. Seidel and M. Grieser, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 4032 CrossRef CAS PubMed.
- L. Vejby-Christensen, D. Kella, H. B. Pedersen and L. H. Andersen, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 3627 CrossRef CAS.
- J. R. Peterson, A. Le Padellec, H. Danared, G. H. Dunn, M. Larsson and A. Larson, et al. , J. Chem. Phys., 1998, 108, 1978 CrossRef CAS.
- D. Zajfman, Z. Amitay, C. Broude, P. Forck, B. Seidel and M. Grieser, et al. , Phys. Rev. Lett., 1995, 75, 814 CrossRef CAS PubMed.
- D. A. Dahl, Simion 3D version 6.0 User's Manual, 1995 Search PubMed.
- G. Eklund, J. Grumer, S. Rosén, M. C. Ji, N. Punnakayathil and A. Källberg, et al. , Phys. Rev. A, 2020, 102, 012823 CrossRef CAS.
- G. Eklund, J. Grumer, P. S. Barklem, S. Rosén, M. C. Ji and A. Simonsson, et al. , Phys. Rev. A, 2021, 103, 032814 CrossRef CAS.
- X. Zhou and A. Dickinson, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 124, 5 CrossRef CAS.
- A. Dalgarno, Adv. Phys., 1962, 11, 281–315 CrossRef CAS.
- A. Salop and R. E. Olson, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 1312 CrossRef CAS.
- P. S. Barklem, Phys. Rev. A, 2016, 93, 042705 CrossRef.
- C. Herring, Rev. Mod. Phys., 1962, 34, 631 CrossRef CAS.
- R. K. Janev and A. Salin, J. Phys. B, 1972, 5, 177 CrossRef CAS.
- R. K. Janev, Adv. At. Mol. Phys., 1976, 12, 1–37 CAS.
- E. Wigner and E. E. Witmer, Z. Phys., 1928, 51, 859 CrossRef CAS.
- C. Froese Fischer, G. Gaigalas, P. Jönsson and J. Bieroń, Comput. Phys. Commun., 2019, 237, 184 CrossRef CAS , https://github.com/compas/grasp, CompAS collaboration, https://compas.github.io.
| This journal is © the Owner Societies 2021 |