Open Access Article
Open Access ArticleWater/oil interfacial tension reduction – an interfacial entropy driven process†
Tai
Bui
 *abc,
Harry
Frampton
b,
Shanshan
Huang
b,
Ian R.
Collins
b,
Alberto
Striolo
*abc,
Harry
Frampton
b,
Shanshan
Huang
b,
Ian R.
Collins
b,
Alberto
Striolo
 de and
Angelos
Michaelides
de and
Angelos
Michaelides
 c
c
aThomas Young Centre and London Centre for Nanotechnology, and Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK. E-mail: tai.bui.14@ucl.ac.uk
bBP Exploration Operating Co. Ltd, Chertsey Road, Sunbury-on-Thames TW16 7LN, UK
cYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK
dDepartment of Chemical Engineering, University College London, Gower Street, London WC1E 6BT, UK
eSchool of Chemical, Biological and Materials Engineering, University of Oklahoma, Norman, OK 73019, USA
First published on 27th October 2021
Abstract
The interfacial tension (IFT) of a fluid–fluid interface plays an important role in a wide range of applications and processes. When low IFT is desired, surface active compounds (e.g. surfactants) can be added to the system. Numerous attempts have been made to relate changes in IFT arising from such compounds to the specific nature of the interface. However, the IFT is controlled by an interplay of factors such as temperature and molecular structure of surface-active compounds, which make it difficult to predict IFT as those conditions change. In this study, we present the results from molecular dynamics simulations revealing the specific role surfactants play in IFT. We find that, in addition to reducing direct contact between the two fluids, surfactants serve to increase the disorder at the interface (related to interfacial entropy) and consequently reduce the water/oil IFT, especially when surfactants are present at high surface density. Our results suggest that surfactants that yield more disordered interfacial films (e.g. with flexible and/or unsaturated tails) reduce the water/oil IFT more effectively than surfactants which yield highly ordered interfacial films. Our results shed light on some of the factors that control IFT and could have important practical implications in industrial applications such as the design of cosmetics, food products, and detergents.
1 Introduction
Surface and interfacial tension (IFT) are fundamental concepts, which affect our everyday life and play important roles in many chemical processes and industrial applications. For example, surface and interfacial tension determine the quality and the efficiency of detergent formulations. Usually, high performance formulations are those that can induce low surface/interfacial tension, which help in removing stains, fats, and oils from clothing.1 Many food products are emulsions and/or dispersions, for example milk, mayonnaise, and chocolate pastes and syrups. These products require emulsifiers (surface active agents) to reduce the IFT and assist emulsion formation and stabilization.2,3 In the oil and gas industry, controlling IFT is crucial in many areas.4 One of the most prominent applications is oil production,5–7 in which case low water/oil IFT is required to lower the capillary force, allowing oil to detach from the rock surfaces.8Due to scientific interest and industrial importance, many studies have been conducted to understand the relation between molecular structure and performance for various surfactants.9–19 However, to fully understand, predict, and manipulate IFT using surfactants more experimental and theoretical work needs to be conducted due to the complex interplay of many different factors e.g. temperature, nature and concentration of surface-active compounds. IFT is defined either as the energy required to create a unit of interfacial area or the interfacial free energy of two immiscible fluids. The energy term here is actually the interfacial free energy which is comprised of enthalpic and entropic contributions. Solely considering the difference in the interaction energy of atoms at the interface and that of atoms in the bulk due to the difference in the number and the types of neighbouring atoms is inadequate for complex systems with water, salts, and surfactants, because it neglects the degrees of freedom of molecules (vibrations, conformations and orientation), as well as the potential enrichment of some molecules at interfaces as respect as to the bulk. These terms are included in the entropy contribution, and are an important component of the interfacial energy. Indeed, previous studies have demonstrated that there is a strong correlation between surface tension and surface entropy. For example, Shah et al.20 studied the effect of different salts (NaCl, NaBr, NaNO3, KCl, KBr, KNO3) and temperature on water surface tension and found that the entropy of surface formation decreases as the salt concentration decreases, whereas the enthalpy of surface formation stays almost constant. Hu et al.21 measured surface tension of water in the presence of different surfactants at different temperatures. They found that surface entropy plays an important role in describing the surface tension of water, specifically the water surface tension is found to decrease as surfactants are added.
While most previous studies have focused on water/air systems, water/oil systems have received less attention. However, understanding the fundamental physics behind water/oil IFT is highly desirable because (a) water/oil systems are fundamentally different from water/air systems due to the different chemistry of the oil phase, and (b) controlling water/oil IFT is important in many industrial sectors especially cosmetics production and the petroleum industry.
With the rapid development of force fields, algorithms, and computer power, molecular simulations are increasingly proving useful in the study of interfacial problems.22–31 Simulations can also be used to understand interfacial tension at the molecular level.32–39 In this study molecular dynamics (MD) simulations are employed in an attempt to clarify connections between water/oil IFT and thermodynamic properties. The effect of temperature is firstly studied to disentangle the enthalpy and entropy contributions to the resultant IFT. By comparing the two contributions, interfacial entropy is identified among the controlling factors in reducing IFT when surfactants are added. We then systematically modify certain molecular features of the surfactants as a way to control interfacial entropy and investigate the influence this has on the water/oil IFT. Indeed, by adding a double bond in the surfactant alkyl tail or increasing the overall chain stiffness, the interfacial film becomes more disordered and consequently the water/oil IFT is reduced.
2 Theory and computational details
Atomistic molecular dynamics (MD) simulations were performed using the GROMACS package,40 version 2018.4. Fig. 1a shows a representative simulation box. The initial dimension of the simulation box was set to 5 × 5 × 20 nm3. Each simulated system contains a water slab, of approximate volume 5 × 5 × 4 nm3, located in the middle of the box. Two surfactant layers were placed on both sides of the water slab with the alkyl tails pointing outwards along the Z direction.In order to quantify the effect of surfactant concentration on the IFT, the number of surfactants at the interface was varied systematically from 0–5.2 × 10−6 mol m−2. Those values of SDS surface densities fall within the range of experimental observations varying from 1.1–8.0 × 10−6 mol m−2 from a variety of sources (please refer to Table S1 for more details, ESI†).41–45 The remainder of the simulation box was filled with n-alkane, representing the oil phase. It is worth noting that in this study, the adsorption and desorption of surfactant to/from interfacial films are not considered because they are slow processes (on the scale of a few microseconds to seconds)46 compared to the time accessible to molecular simulations when conducted at atomistic resolution. Indeed, we do not observe surfactant desorption from interfaces during our simulations, nor do we observe the formation of SDS micelles in the oil and water phases. As a result, the SDS surface density is effectively fixed in our simulations and calculated using the interface's planar average area (i.e., area = LX × LY, where LX, LY are the box lengths in the X and Y directions). By changing the number of surfactants in our initial configurations, we attempt to quantify the surface density effects on interfacial tension.
2.1 Force fields
The TIP4P-2005 model47 was used to simulate water. Due to the fact that crude oil contains a large portion of alkanes, in this study we chose n-dodecane, C12, to represent the equivalent carbon number for the alkane fraction. n-Dodecane was modeled using the united-atom version of the TraPPE-UA force field.48 The combination of these models yields good agreement with experimental data in terms of interfacial tension [see the study by Underwood and Greenwell49 as well as Fig. S1 of the ESI†]. sodium dodecyl sulfate (SDS) was chosen as the model surfactant for this study because it is used in a wide range of applications, and because it has been used in many academic studies, thereby providing ample sources to validate our results and corroborate our interpretations. The SDS alkyl tail was modelled using the TraPPE-UA force field48 with an exception that the torsional angle potential was refitted to ab initio data to correctly capture the melting point of long alkanes.50 The SDS headgroup was modelled explicitly using the parameters from Schweighofer et al.51 The counter ion, Na+, was modeled as a single charged Lennard-Jones (LJ) sphere with parameters taken from the study of Smith and Dang without polarizability.52 Non-bonded interactions were modeled by means of dispersive and electrostatic forces. The 12-6 LJ potentials were used to model dispersive interactions, using the Lorentz–Berthelot mixing rules to determine the parameters for non-like interactions.53,54 The electrostatic interactions were modeled by the Coulombic potential with long-range corrections treated using the particle mesh Ewald (PME) method. The distance cutoff for all non-bonded interactions was set to 1.4 nm with energy and pressure tail corrections for van der Waals interactions. Periodic boundary conditions were applied in three dimensions for all simulations.2.2 Simulation protocols
To relax the initial configurations and eliminate steric overlap of molecules, an energy minimization routine was conducted from the initial configurations using the steepest-descent method. Subsequently, NPnAT simulations (N = constant number of atoms, Pn = constant normal pressure, A = constant surface area, T = constant temperature) were conducted at the pressure of 1 bar. The NPnAT ensemble is a reliable ensemble for calculating the interfacial tension of gas/liquid systems55,56 (such as water/CH4, water/CO2, water/H2S systems), and liquid/liquid systems (including lipid bilayers, hydrocarbon/water), at conditions in which the surface area is constant.57–59 Simulations at constant surface area allow us to control the surface density of surfactants in different systems, simply by adding/removing the desired number of molecules at the relevant interfaces. The leapfrog algorithm with a 2 fs time step was employed to integrate the equations of motion. For the first 20 ns, velocity rescaling and the Berendsen barostat were used to efficiently re-scale the simulation temperature and box volume.60 After 20 ns, the thermostat and barostat were switched to Nosé–Hoover chain61 and the Parrinello–Rahman,62 respectively. Simulations were run for 100–150 ns, which was long enough to ensure stable interfaces, as shown in Fig. S2 of the ESI.†2.3 Entropy estimation
The entropy of surfactants adsorbed at the interface, water, and dodecane was estimated with the Quasi harmonic approach.63–65 In this method, the molar entropy, S, is calculated using: | (1) |
 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i − 〈
i − 〈![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i〉)(
i〉)(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j − 〈
j − 〈![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j〉)〉 where
j〉)〉 where ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i and
i and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j denote the position vectors of atoms i and j, the brackets denote average over the selected simulation time. By performing translational and rotational fitting of all frames to a reference (the average structure), one can separate the contribution of translational, rotational, and vibrational motions from the total entropy. In this study, non-weighted entropy was calculated using covariance analysis tools including gmx covar and gmx anaeig implemented in the GROMACS simulation package.
j denote the position vectors of atoms i and j, the brackets denote average over the selected simulation time. By performing translational and rotational fitting of all frames to a reference (the average structure), one can separate the contribution of translational, rotational, and vibrational motions from the total entropy. In this study, non-weighted entropy was calculated using covariance analysis tools including gmx covar and gmx anaeig implemented in the GROMACS simulation package.
2.4 Identification of interfacial molecules
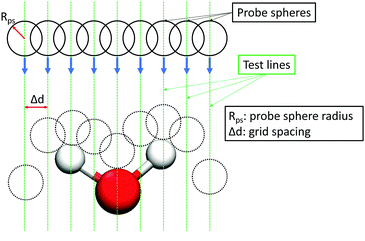
The interfacial water and dodecane molecules were determined by using the Identification of Truly Interfacial (ITIM) algorithm.66 An illustration of the method is shown in Fig. 2. In the ITIM algorithm, a fictitious probe sphere with a given radius is moved along straight test lines that are perpendicular to the plane of the interface (the Z direction). The test lines are generated from a grid in the XY plane with the distance between two adjacent grid points (grid spacing) considerably smaller than the radius of the probe sphere. Molecules first hit by the probe spheres are identified as the interfacial ones. For more details, please refer to the paper of Pártay et al.66 In this study, the probe sphere radius and the grid spacing were set to 1.5 Å and 0.2 Å, respectively, similar to those used in previous studies of interfacial water.67–693 Results and discussion
3.1 Temperature effects on interfacial tension
Fig. 1a shows a schematic of the simulated system, in which n-dodecane and sodium dodecyl sulfate (SDS) were chosen as the model oil and surfactant, respectively. In our study, to quantify the relation between IFT and temperature, we simulated each system at three different temperatures. The water/oil interfacial tension, γ, is calculated through the following relation:70,71 | (3) |
 are the normal and tangential components of the pressure tensor at position z along the Z direction of the simulation box. Lz is the box length along the Z direction.
are the normal and tangential components of the pressure tensor at position z along the Z direction of the simulation box. Lz is the box length along the Z direction. ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) N and
N and ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) T are the average normal and tangential pressure tensors calculated over the entire box length Lz. Note that in our simulations we maintain constant the size of the simulation box along the X and Y directions, while the Z dimension changes to maintain constant pressure in that direction using the NPnAT ensemble. Nevertheless, to probe the suitability of the algorithm for the systems studied, additional simulations were run using a constant volume ensemble (NVT) to calculate the n-dodecane/water IFT at three different temperatures and a surface density of 2.1 × 10−6 mol m−2 for SDS. Table S1 of the ESI† compares the results obtained from the two ensembles. As it can be seen, the results indicate that the IFT values obtained from the two ensembles are comparable, yielding values within statistical uncertainty of each other, implying the algorithm used to calculate the oil/water IFT in our simulations is reliable and appropriate for the issues addressed in this manuscript.
T are the average normal and tangential pressure tensors calculated over the entire box length Lz. Note that in our simulations we maintain constant the size of the simulation box along the X and Y directions, while the Z dimension changes to maintain constant pressure in that direction using the NPnAT ensemble. Nevertheless, to probe the suitability of the algorithm for the systems studied, additional simulations were run using a constant volume ensemble (NVT) to calculate the n-dodecane/water IFT at three different temperatures and a surface density of 2.1 × 10−6 mol m−2 for SDS. Table S1 of the ESI† compares the results obtained from the two ensembles. As it can be seen, the results indicate that the IFT values obtained from the two ensembles are comparable, yielding values within statistical uncertainty of each other, implying the algorithm used to calculate the oil/water IFT in our simulations is reliable and appropriate for the issues addressed in this manuscript.
In Fig. 3a we report the IFT results as a function of temperature at different SDS surface densities, and compare with the system without surfactant (black curve). The results indicate that the IFT decreases as the temperature increases, which is consistent with experimental data for SDS72–74 as well as for other surfactants75 and follows the Eotvos rule for surface tension of pure liquids.76 The effect of temperature is more noticeable when surfactants are added, which is indicated by the steeper slope of the IFT profiles at increasing surface densities. The results obtained are consistent with the experimental IFT values for the system of hexane/water,72 in which the magnitude of IFT reduction at increasing temperature is higher for the systems with SDS compared to that of the systems without SDS.
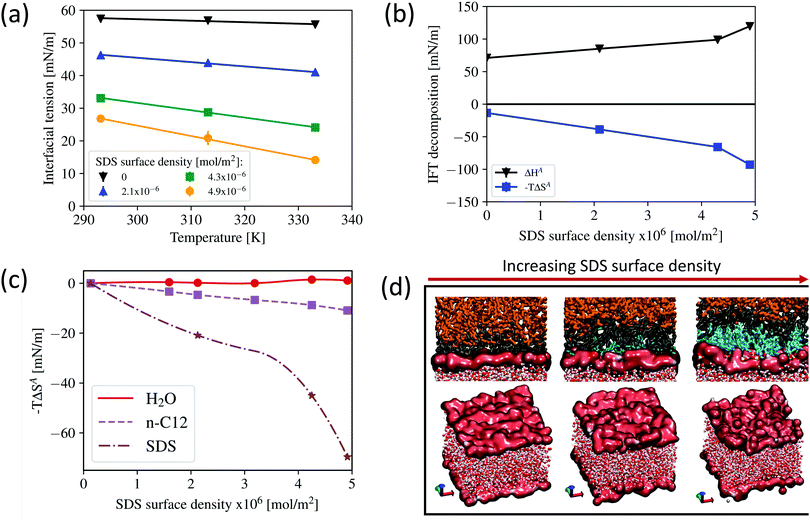 | ||
| Fig. 3 (a) Interfacial tension as a function of temperature calculated for systems at different SDS surface densities. (b) Decomposition of interfacial tension in terms of enthalpy and entropy contributions (with the same unit as IFT) calculated at 293.15 K at different SDS surface densities. Error bars are present but most are smaller than the symbols used to display the data. (c) Entropy change of water, dodecane, and SDS as a function of SDS surface density at 293.15 K with respect to the system without SDS. The entropy of water and dodecane is calculated using the Quasi harmonic approach, whereas the entropy of SDS is calculated by subtracting the system entropy from the contributions of water and dodecane. (d) Representative simulation snapshots illustrating the interfacial molecules identified using the ITIM algorithm with the recommended probe sphere of 1.5 Å and a grid spacing of 0.2 Å.66 Top panels: Interfacial dodecane molecules are shown in black, bulk dodecane in orange, SDS in cyan, and water oxygen and hydrogen in red and white, respectively. The bottom panels depict the interfacial water molecules. | ||
To understand why the IFT changes are more pronounced as temperature changes in the presence of SDS, in Fig. 3b we disentangle the contributions of interfacial entropy (ΔSA), and enthalpy (ΔHA) to the IFT as a function of SDS surface density at constant temperature of 293.15 K. Since the IFT is also defined as the change of Gibbs free energy needed to create a unit of interfacial area at constant pressure, temperature, and number of molecules:
 | (4) |
 | (5) |
 | (6) |
The results presented in Fig. 3b indicate that as SDS surface density increases both interfacial entropy and interfacial enthalpy increase. In our systems, it is worth noting that the entropy difference comes from the change in the entropy of water, oil, and surfactant molecules at the interface. To better understand the contributions of water, dodecane, and SDS on the system's interfacial entropy, the entropy changes experienced by water, dodecane, and SDS molecules at increasing SDS surface density were computed with respect to the system without SDS. The results are shown in Fig. 3c. In these calculations, the entropy of water and dodecane is calculated using the quasi harmonic approach,63–65 whereas the entropy of SDS is calculated by subtracting the system entropy from the contributions of water and dodecane. The system interfacial entropy is calculated as the partial derivative of the IFT with respect to temperature (with the opposite sign), following eqn (5). The results indicate that as the surface density of SDS increases, the entropy of water slightly decreases, resulting in a positive contribution to the IFT (thus increasing the IFT). This entropy loss occurs as a result of two diametrically opposed mechanisms: (1) a decrease in water entropy as a result of the strong interaction with surfactant headgroups; and (2) an increase in water entropy as a result of increased surface roughness. As illustrated in Fig. 4a, the strong interaction between water and SDS headgroups is demonstrated by an increased number of hydrogen bonds formed between water molecules and the oxygen atoms of the sulphate headgroups. This yields a small increase in the total number of hydrogen bonds in the system, despite the decrease in the number of hydrogen bonds formed between water molecules. Fig. 4b illustrates the relationship between surface roughness and SDS surface density. The interfacial roughness was defined as the full width at half maximum of the interfacial water distribution in the Z direction of the simulation box (see Fig. S3 of the ESI† for more details). The interfacial water molecules were identified using the ITIM algorithm66 with the recommended probe sphere of 1.5 Å and a grid spacing of 0.2 Å. The results indicate that as the surface density of SDS increases, so does the interfacial roughness, which is consistent with what has been observed with tri-n-butyl phosphate surfactants.67 Visual inspection of the interfacial film shown in the bottom panel of Fig. 3d confirms our observation. Increased surface roughness compensates for the loss of entropy caused by the strong interaction with the SDS headgroups.
 | ||
Fig. 4 (a) Number of hydrogen bonds as a function of SDS surface density calculated for all atoms, water–water, and water–SDS molecules. (b) The interfacial roughness based on the calculation of the width of the interfacial water film. The interfacial water film is identified using the ITIM algorithm.66 The inset plot depicts the distribution of interfacial water molecules along the Z axis of the simulation box used to determine the interfacial width/roughness. (c) Probability distribution of the angle formed by the end-to-end vector of the interfacial dodecane molecules and the Z direction at different surface densities of SDS. (d) Calculation of  (proportional to the rotational entropy) for the interfacial dodecane molecules based on the orientational probability distribution in panel (c). In this calculation, pi is the orientational probability of angle i ∈ [0; 180°]. (proportional to the rotational entropy) for the interfacial dodecane molecules based on the orientational probability distribution in panel (c). In this calculation, pi is the orientational probability of angle i ∈ [0; 180°]. | ||
The entropy of dodecane, on the other hand, increases linearly as the SDS surface density increases, thus contributing a non-negligible amount to the reduction of IFT. This is most likely because when no surfactant is present, the oil molecules at the interface lose some of their degrees of freedom as they align somewhat parallel to the interface (see the zoomed-in snapshot in Fig. 1b and the left panel of Fig. S5 of the ESI†). The parallel alignment of dodecane molecules along the interface is consistent with previous observations.80,81,82 This could be due to strong short-range van der Waals interactions at the interface between alkane and water molecules.80 However, when surfactants are added, dodecane molecules are pushed away from the water surface, making them more disordered and allowing them to rotate and translate more freely, as illustrated in the zoomed-in snapshot of Fig. 1a, the top panels of Fig. 3d, as well as the middle and right panels of Fig. S5 of the ESI.† The disordered structure of the oil molecules in the surfactant interfacial film is also indicated by the broader orientational distribution of the oil chain at increasing SDS surface density as presented in Fig. 4c. Similar calculations were performed to quantify the orientation of interfacial water molecules (see Fig. S6 of the ESI†). The results indicate that at low SDS surface densities, the water dipole moment is likely to align with the interface plane, resulting in a non-polarized interface that could facilitate/accommodate the dodecane molecules. This could be another reason explaining why dodecane molecules align parallel at the water-dodecane interface at low SDS surface densities (see above). However, as the SDS surface density increases, the dipole moment points away from the interface, allowing water O–H groups to form hydrogen bonds with oxygen atoms in the SDS sulphate headgroup. This is in agreement with findings from the study of Tummala et al.83 regarding the effect of SDS on the orientation of water near various solid-liquid interfaces. It is worth mentioning that the interfacial molecules are identified using the ITIM algorithm66 with the probe radius of 1.5 Å and a grid spacing of 0.2 Å (please refer to Fig. S4 of the ESI†). The oil molecules with broader orientational distribution indeed have higher rotational entropy  (see Fig. 4d), where pi is the orientational probability of angle i ∈ [0; 180°]. The effect of the oil molecules on the performance of SDS was also demonstrated by a greater degree of IFT reduction when water/dodecane/SDS was compared to water/air/SDS at the same SDS surface density (please refer to the results presented in Fig. S7 of the ESI†).
(see Fig. 4d), where pi is the orientational probability of angle i ∈ [0; 180°]. The effect of the oil molecules on the performance of SDS was also demonstrated by a greater degree of IFT reduction when water/dodecane/SDS was compared to water/air/SDS at the same SDS surface density (please refer to the results presented in Fig. S7 of the ESI†).
The contribution of SDS entropy was determined by subtracting the total interfacial entropy of the system from the contributions of water and dodecane. The results in Fig. 3c also indicate that SDS contributes significantly more to interfacial entropy than molecules from oil and/or water phase.
The results in Fig. 3 and 4 suggest that, in the presence of surfactants, increasing interfacial disorder is crucial in reducing the IFT especially at high surface density. This is usually the case in practical applications as surfactants accumulate significantly at the interface (with more than 80% saturated even at low bulk concentration).84 Because the increase in interfacial entropy is primarily due to an increase in the entropy of the oil and surfactant molecules, we believe that increasing the interfacial entropy could be accomplished by altering the molecular characteristics of the surfactant molecules. The following sections examine how altering the molecular structure with a particular emphasis on the surfactant tails, can affect the interfacial film properties, thereby affecting the water/oil IFT.
3.2 Surfactant tail structure effect: unsaturated vs. saturated
Experimental observations indicate that surfactants with unsaturated alkyl chains induce lower surface/interfacial tension than those with saturated alkyl chains of equivalent chain length.85,86 To provide a solid scientific basis for those observations, a double bond was added to the middle of the SDS alkyl tail (between carbon numbers 6 and 7), and then the IFT was calculated and correlated to the interfacial film's molecular properties. We expect that adding a double bond to the SDS surfactant tails will increase the disorder of the interfacial film, inspired by the fact that vegetable oils with double bonds in the hydrophobic tails have lower melting temperature than animal fat (with saturated tails) of the same length due to their low chain packing efficiency,87 thus further reducing the IFT. A schematic of the new surfactant is shown in Fig. 5a (and also in Fig. 1c), where we also present the IFT results obtained for the surfactant with and without the double bond in the tail. The simulations were conducted at 293.15 K. The results in Fig. 5a indicate that adding a double bond in the cis conformation to the alkyl tail has little effect at low surfactant surface density but noticeably reduces the IFT (up to 6 mN m−1) at high surface density (>4 × 10−6 mol m−2). These results are consistent with experimental data where water–air surface tension calculated for oleyl surfactant (unsaturated with cis conformation) is lower than that of stearyl surfactant.86 In that study, Bhadani et al.86 suggested that the decrease in the IFT of the oleyl surfactant is probably due to cation–π interactions between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond and the surfactant headgroup.
C double bond and the surfactant headgroup.
 | ||
Fig. 5 (a) Water/dodecane interfacial tension at 293.15 K as a function of SDS surface density. (b) Order parameter for the SDS tails. The results calculated for surfactants with a saturated tail (black curve) and an unsaturated tail with one double bond maintained in trans and cis conformations (blue and purple curves, respectively). The low-index carbon atoms (e.g. carbon number 1–3) are the ones close to the head groups, whereas the high-index carbon atoms represent the carbon atoms at the tail end near the dodecane phase. (c) Representative simulation snapshot and density profiles of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (solid purple curve), SDS (dashed cyan curve), and water (dash-dotted red curve) of the interfacial film with cis-unsaturated SDS at surface density of 4.9 × 10−6 mol m−2, the double bonds are highlighted in purple, color codes for other components are the same as those in Fig. 1. C (solid purple curve), SDS (dashed cyan curve), and water (dash-dotted red curve) of the interfacial film with cis-unsaturated SDS at surface density of 4.9 × 10−6 mol m−2, the double bonds are highlighted in purple, color codes for other components are the same as those in Fig. 1. | ||
This argument does not apply to our systems, where the double bonds are far from the surfactant headgroups (see Fig. 5c for a representative simulation snapshot and density profiles of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, water, SDS, showing that the double bonds in purple are far from the water phase where the surfactant headgroups reside). In fact, we found that the water/oil IFT is strongly correlated to the disorder of the surfactant interfacial film. To quantify the molecular order within the interfacial films, we calculated the order parameter Sorder [see eqn (7)] based on the so-called deuterium order parameter88–90 for the SDS alkyl tails. The order parameter describes the orientation of the C–H bond vector with respect to the Z direction and are calculated as a function of the carbon atom in the alkyl tails of the surfactants.
C, water, SDS, showing that the double bonds in purple are far from the water phase where the surfactant headgroups reside). In fact, we found that the water/oil IFT is strongly correlated to the disorder of the surfactant interfacial film. To quantify the molecular order within the interfacial films, we calculated the order parameter Sorder [see eqn (7)] based on the so-called deuterium order parameter88–90 for the SDS alkyl tails. The order parameter describes the orientation of the C–H bond vector with respect to the Z direction and are calculated as a function of the carbon atom in the alkyl tails of the surfactants.
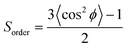 | (7) |
3.3 Surfactant molecular flexibility effect
In the previous section, we observed clearly the dependence of the water/oil IFT on the presence of a double bond in the surfactant tail. We now investigate the effect of another parameter that controls the architecture of the surfactant hydrophobic tail, namely, the degree of molecular flexibility or chain stiffness. Because the stiffness of the SDS alkyl chain is controlled by the C–C–C–C torsional angle terms, in our simulations we quantify two different sets of the torsional angle potentials, one from the original TraPPE-UA force field (denoted as TraPPE-UA) and another one from refitting to rotational energy profiles obtained from ab initio calculations in the study of Siu et al.,50 for long alkanes (denoted as refitted torsion). Noting that the refitted torsion potential is used throughout this study to model surfactant alkyl tails, as it was previously used to develop a force field for long alkanes (the L-OPLS force field) that accurately describes their physical properties such as diffusion coefficient, density, viscosity, and the melting point. It is worth mentioning that the main difference between the two potentials is the energy difference between gauche and trans configurations, which is higher in the TraPPE-UA force field than that observed from recent ab initio data (please refer to the left panel of Fig. S9 of the ESI†).In the left panel of Fig. 6, the simulated IFT results obtained by implementing the two sets of torsional angle potentials are shown and compared with experimental data from Llamas et al.41 The results show that the refitted torsional potential reproduces better the experimental data especially at high surface density of SDS. Upon visual inspection of simulation snapshots (see the middle panels of Fig. 6) we found that the original TraPPE-UA potential induces a more ordered interfacial film at high surface densities of SDS, whereas the refitted potential induces a much less ordered film. The order parameter obtained for the surfactant tails confirms this observation as shown in the right panel of Fig. S9 of the ESI.†
 | ||
| Fig. 6 Left: Water/oil interfacial tension as a function of SDS surface density. Experimental data are from literature41 (assuming the saturation surface density of SDS is 5.2 × 10−6 mol m−2). Two sets of simulation results are shown, the difference being in the description of the torsional angles within the SDS tail. In one force field, the original TraPPE-UA was implemented. In the other the torsional potential were fitted to reproduce ab initio simulation results, from literature.50 Middle: Representative simulation snapshots contrasting ordered (top) and disordered (bottom) surfactant interfacial films obtained when using the original TraPPE-UA and the refitted torsional potentials, respectively. Right: estimation of entropy applying the quasi harmonic approximation method for SDS modelled with the two different torsional potentials. Contributions of conformational, rotational, and translational components to the entropy are obtained by appropriately fitting these motions to the reference structure. Specifically, rot + trans fit represents the contribution of conformational entropy, trans fit represents the contribution of both conformational and rotational entropy, and no fit represents all three contributions. | ||
As discussed in previous sections, the reduction in the water/oil IFT is strongly correlated to the interfacial entropy or degree of disordering. To strengthen our conclusion, here we estimate the entropy values for SDS using the two sets of torsional angle potentials using the quasi harmonic approach.63–65 The results are shown in the right panel of Fig. 6. They reveal that indeed the entropy obtained for SDS with the refitted torsional potential is higher than that of the original TraPPE-UA one. It is important to point out that the conformational component (with rotational and translational fit) is the main contributor to the entropy difference obtained implementing the two set of torsional angle potentials. Whereas, rotational and translational components have minimal effect. The results presented above highlighted the effect of the chain stiffness of surfactant molecules on the behavior of the adsorbed surfactant layer at the water/oil interface. It has been shown that changing in the chain stiffness can alter the rigidity and packing efficiency of the interfacial film, which lead to a change in the water/oil IFT.93,94 In practice, the chain stiffness of the surfactants can be controlled by changing their chemical composition (e.g. fluorinated surfactants),95–98 the addition of functional groups, and branches.99
4 Conclusions
We have conducted equilibrium molecular dynamics simulations on systems containing n-dodecane, water, and SDS surfactant to identify molecular-level factors that control the water/oil interfacial tension. The simulations were conducted at different surfactant surface densities, molecular features (e.g. surfactant tail flexibility, adding a double bond), as well as temperatures. The results are in good agreement with experimental observations. The results of the water/oil IFT obtained at different temperatures indicate that the ability to reduce the IFT is strongly driven by the degree of disorder of the interfacial film, which is related to the interfacial entropy. We discovered that the increase in interfacial entropy in the presence of surfactant is primarily due to an increase in the entropy of the surfactant film and the interfacial oil molecules. By modifying the surfactant's molecular structure, we were able to further enhance its performance. Indeed, our simulation results show that adding a double bond to the surfactant alkyl tails reduces the surfactant film order, which in turn helps to reduce the IFT. More flexible surfactants with higher gauche/trans ratio within the alkyl tail also induce lower the IFT. The results reported here underline the importance of interfacial entropy in rationalising changes in surface structure and interfacial tension at oil/water interfaces in the presence of SDS, the most frequently used anionic surfactant. We hope that such insight can be exploited for designing new effective surface-active compounds for various applications.It is important to point out that in this study we mainly focused on the entropy effect of the interfacial layer, specifically on the contribution of the surfactant tails. However, the surfactant headgroups also play an equally important role. For example, experimental data shows that head group chemistry and interaction with water, salts impose strong influence on the water/oil IFT.100–102 Therefore, future studies (e.g. via molecular modelling) focusing on the fundamental physics behind those effects could further advance our understandings of how to control the water/oil IFT.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
T. B. would like to thank Andrea Zen, Michael Davies, Stephen Cox, Julia Schumann, Christoph Schran, Fabian Thiemann, and other members of the ICE group at the Yusuf Hamied Department of Chemistry, University of Cambridge for their thoughtful feedback to improve the quality of this manuscript. This work was supported by BP Exploration Operating Company Limited, University College London/The Thomas Young Centre, and Innovative UK under the Knowledge Transfer Partnership programme, number KTP011009. We acknowledge the use of the BP HPC facilities for conducting our simulations.Notes and references
- J. Isac-García, J. A. Dobado, F. G. Calvo-Flores and H. Martínez-García, in Experimental Organic Chemistry, ed. J. Isac-García, J. A. Dobado, F. G. Calvo-Flores and H. B. T. E. O. C. Martínez-García, Elsevier, 2016, pp. 239–289 Search PubMed.
- T. Kinyanjui, W. Artz and S. Mahungu, Encycl. Food Sci. Nutr., 2003, 2070–2077 CrossRef.
- V. Sattigeri, L. Gowda and P. Ramasarma, Encycl. Sep. Sci., 2000, 2829–2838 Search PubMed.
- W. Li, Y. Yu, M. Lamson, M. S. Silverstein, R. D. Tilton and K. Matyjaszewski, Macromolecules, 2012, 45, 9419–9426 CrossRef CAS.
- J. J. Sheng, Petroleum, 2015, 1, 97–105 CrossRef.
- V. Alvarado and E. Manrique, Enhanced Oil Recovery, Gulf Professional Publishing, 2010, pp. 477–565 Search PubMed.
- C. Negin, S. Ali and Q. Xie, Petroleum, 2017, 3, 197–211 CrossRef.
- A. Muggeridge, A. Cockin, K. Webb, H. Frampton, I. Collins, T. Moulds and P. Salino, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 2014, 372, 20120320 CrossRef PubMed.
- J. Eastoe, A. Paul, A. Downer, D. C. Steytler and E. Rumsey, Langmuir, 2002, 18, 3014–3017 CrossRef CAS.
- J. L. Salager, A. M. Forgiarini, L. Márquez, L. Manchego and J. Bullón, J. Surfact. Deterg., 2013, 16, 631–663 CrossRef CAS PubMed.
- J. L. Salager, A. M. Forgiarini and J. Bullón, J. Surfactants Deterg., 2013, 16, 449–472 CrossRef CAS.
- M. J. Schwuger, ACS Symp. Ser., 1984, 253, 3–26 CrossRef CAS.
- R. Catarino Centeno, R. A. Bustamante-Rendón, J. S. Hernández-Fragoso, I. Arroyo-Ordoñez, E. Pérez, S. J. Alas and A. Gama Goicochea, J. Mol. Model., 2017, 23, 306 CrossRef CAS PubMed.
- N. M. Kovalchuk, A. Trybala, V. Starov, O. Matar and N. Ivanova, Adv. Colloid Interface Sci., 2014, 210, 65–71 CrossRef CAS PubMed.
- J. Zhao, C. Dai, Q. Ding, M. Du, H. Feng, Z. Wei, A. Chen and M. Zhao, RSC Adv., 2015, 5, 13993–14001 RSC.
- B. E. Brycki, I. H. Kowalczyk, A. Szulc, O. Kaczerewska and M. Pakiet, Application and Characterization of Surfactants, InTech, 2017 Search PubMed.
- T. T. Phan, C. Attaphong and D. A. Sabatini, J. Am. Oil Chem. Soc., 2011, 88, 1223–1228 CrossRef CAS.
- M. Suttipong, N. R. Tummala, B. Kitiyanan and A. Striolo, J. Phys. Chem. C, 2011, 115, 17286–17296 CrossRef CAS.
- J. K. Ferri and K. J. Stebe, Adv. Colloid Interface Sci., 2000, 85, 61–97 CrossRef CAS PubMed.
- A. A. Shah, K. Ali and S. Bilal, Colloids Surf., A, 2013, 417, 183–190 CrossRef CAS.
- D. Hu, A. Mafi and K. C. Chou, J. Phys. Chem. B, 2016, 120, 2257–2261 CrossRef CAS PubMed.
- K. Esselink, P. A. J. Hilbers, N. M. van Os, B. Smit and S. Karaborni, Colloids Surf., A, 1994, 91, 155–167 CrossRef CAS.
- M. Ozboyaci, D. B. Kokh, S. Corni and R. C. Wade, Q. Rev. Biophys., 2016, 49, e4 CrossRef PubMed.
- J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674 CrossRef CAS PubMed.
- A. Striolo, A. Michaelides and L. Joly, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 533–556 CrossRef CAS PubMed.
- A. Striolo, Adsorpt. Sci. Technol., 2011, 29, 211–258 CrossRef CAS.
- W. F. van Gunsteren and H. J. C. Berendsen, Angew. Chem., Int. Ed. Engl., 1990, 29, 992–1023 CrossRef.
- S. A. Hollingsworth and R. O. Dror, Neuron, 2018, 99, 1129–1143 CrossRef CAS PubMed.
- T. Bui, F. Sicard, D. Monteiro, Q. Lan, M. Ceglio, C. Burress and A. Striolo, J. Phys. Chem. Lett., 2018, 9, 3491–3496 CrossRef CAS PubMed.
- S. J. Cox, S. M. Kathmann, B. Slater and A. Michaelides, J. Chem. Phys., 2015, 142, 184704 CrossRef PubMed.
- J. A. Greathouse, R. T. Cygan, J. T. Fredrich and G. R. Jerauld, J. Phys. Chem. C, 2017, 121, 22773–22786 CrossRef CAS.
- A. Ghoufi, P. Malfreyt and D. J. Tildesley, Chem. Soc. Rev., 2016, 45, 1387–1409 RSC.
- E. Deguillard, N. Pannacci, B. Creton and B. Rousseau, J. Chem. Phys., 2013, 138, 144102 CrossRef CAS PubMed.
- C. Herdes, Å. Ervik, A. Mejía and E. A. Müller, Fluid Phase Equilib., 2018, 476, 9–15 CrossRef CAS.
- B. Liu, J. Shi, M. Wang, J. Zhang, B. Sun, Y. Shen and X. Sun, J. Supercrit. Fluids, 2016, 111, 171–178 CrossRef CAS.
- F. Goodarzi and S. Zendehboudi, Ind. Eng. Chem. Res., 2019, 58, 8817–8834 CrossRef CAS.
- G. Alonso, P. Gamallo, A. Mejía and R. Sayós, J. Mol. Liq., 2020, 299, 112223 CrossRef CAS.
- S. S. Jang, L. Shiang-Tai, P. K. Maiti, M. Blanco, W. A. Goddard, P. Shuler and Y. Tang, J. Phys. Chem. B, 2004, 108, 12130–12140 CrossRef CAS.
- J. Zhao, G. Yao, S. B. Ramisetti, R. B. Hammond and D. Wen, Energy Fuels, 2018, 32, 11080–11092 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1-2, 19–25 CrossRef.
- S. Llamas, E. Santini, L. Liggieri, F. Salerni, D. Orsi, L. Cristofolini and F. Ravera, Langmuir, 2018, 34, 5978–5989 CrossRef CAS PubMed.
- N. R. Biswal, N. Rangera and J. K. Singh, J. Phys. Chem. B, 2016, 120, 7265–7274 CrossRef CAS PubMed.
- H. B. de Aguiar, A. G. F. de Beer, M. L. Strader and S. Roke, J. Am. Chem. Soc., 2010, 132, 2122–2123 CrossRef CAS PubMed.
- F. Hernáinz and A. Caro, Colloids Surf., A, 2002, 196, 19–24 CrossRef.
- S. J. Rehfeld, J. Phys. Chem., 1967, 71, 738–745 CrossRef CAS.
- J. Eastoe and J. S. Dalton, Adv. Colloid Interface Sci., 2000, 85, 103–144 CrossRef CAS PubMed.
- J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- T. R. Underwood and H. C. Greenwell, Sci. Rep., 2018, 8, 352 CrossRef PubMed.
- S. W. Siu, K. Pluhackova and R. A. Böckmann, J. Chem. Theory Comput., 2012, 8, 1459–1470 CrossRef CAS PubMed.
- K. J. Schweighofer, U. Essmann and M. Berkowitz, J. Phys. Chem. B, 1997, 19, 3793–3799 CrossRef.
- D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757–3766 CrossRef CAS.
- H. A. Lorentz, Ann. Phys., 1881, 248, 127–136 CrossRef.
- D. Berthelot, Compt. Rend., 1898, 126, 1703–1706 Search PubMed.
- F. Biscay, A. Ghoufi, V. Lachet and P. Malfreyt, J. Chem. Phys., 2009, 131, 124707 CrossRef CAS PubMed.
- F. Biscay, A. Ghoufi, V. Lachet and P. Malfreyt, J. Phys. Chem. B, 2009, 113, 14277–14290 CrossRef CAS PubMed.
- A. Skibinsky, R. M. Venable and R. W. Pastor, Biophys. J., 2005, 89, 4111–4121 CrossRef CAS PubMed.
- P. Linse, J. Chem. Phys., 1987, 86, 4177–4187 CrossRef CAS.
- M. Kunieda, K. Nakaoka, Y. Liang, C. R. Miranda, A. Ueda, S. Takahashi, H. Okabe and T. Matsuoka, J. Am. Chem. Soc., 2010, 132, 18281–18286 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. Van Der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- R. M. Levy, M. Karplus, J. Kushick and D. Perahia, Macromolecules, 1984, 17, 1370–1374 CrossRef CAS.
- I. Andricioaei and M. Karplus, J. Chem. Phys., 2001, 115, 6289–6292 CrossRef CAS.
- J. Carlsson and J. Åqvist, J. Phys. Chem. B, 2005, 109, 6448–6456 CrossRef CAS PubMed.
- L. B. Pártay, G. Hantal, P. Jedlovszky, R. Vincze and G. Horvai, J. Comput. Chem., 2008, 29, 945–956 CrossRef PubMed.
- M. J. Servis and A. E. Clark, Phys. Chem. Chem. Phys., 2019, 21, 2866–2874 RSC.
- M. J. Servis, A. McCue, A. J. Casella and A. E. Clark, Fluid Phase Equilib., 2020, 511, 112497 CrossRef CAS.
- N. Kumar, M. J. Servis, Z. Liu and A. E. Clark, J. Phys. Chem. C, 2020, 124, 10924–10934 CrossRef CAS.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1949, 17, 338–343 CrossRef CAS.
- A. Ghoufi, F. Goujon, V. Lachet and P. Malfreyt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031601 CrossRef CAS PubMed.
- J. Saien, A. Rezvani Pour and S. Asadabadi, J. Chem. Eng. Data, 2014, 59, 1835–1842 CrossRef CAS.
- J. Saien and S. Akbari, J. Chem. Eng. Data, 2006, 51, 1832–1835 CrossRef CAS.
- F. Hernáinz-Bermúdez de Castro, A. Gálvez-Borrego and M. Calero-de Hoces, J. Chem. Eng. Data, 1998, 43, 717–718 CrossRef.
- A. Mosayebi, M. T. Angaji and P. Khadiv-Parsi, Pet. Sci. Technol., 2016, 34, 1315–1322 CrossRef CAS.
- R. Eötvös, Ann. Phys., 1886, 263, 448–459 CrossRef.
- G. V. Lau, I. J. Ford, P. A. Hunt, E. A. Müller and G. Jackson, J. Chem. Phys., 2015, 142, 114701 CrossRef PubMed.
- E. Salomons and M. Mareschal, J. Phys.: Condens. Matter, 1991, 3, 3645–3661 CrossRef CAS.
- M. A. Floriano and C. A. Angell, J. Phys. Chem., 1990, 94, 4199–4202 CrossRef CAS.
- Y. Qiu and V. Molinero, Crystals, 2017, 7, 86 CrossRef.
- H. Fan, D. E. Resasco and A. Striolo, Langmuir, 2011, 27, 5264–5274 CrossRef CAS PubMed.
- P. Popov, L. Steinkerchner and E. K. Mann, Phys. Rev. E, 2015, 91, 5 CrossRef PubMed.
- N. R. Tummala, S. Liu, D. Argyris and A. Striolo, Langmuir, 2015, 31, 2084–2094 CrossRef CAS PubMed.
- S. Abbott, Surfactant Science: Principles and Practice, 2015, pp. 1–249 Search PubMed.
- M. El-Sukkary, N. Shaker, D. A. Ismail, S. M. Ahmed and A. I. Awad, Egypt. J. Pet., 2012, 21, 11–17 CrossRef CAS.
- A. Bhadani, K. Iwabata, K. Sakai, S. Koura, H. Sakai and M. Abe, RSC Adv., 2017, 7, 10433–10442 RSC.
- J. M. Berg, J. L. Tymoczko and L. Stryer, Biochemistry, WH Freeman, 2002 Search PubMed.
- J. Seelig, Q. Rev. Biophys., 1977, 10, 353–418 CrossRef CAS PubMed.
- H. Schindler and J. Seelig, Biochemistry, 1975, 14, 2283–2287 CrossRef CAS PubMed.
- L. S. Vermeer, B. L. De Groot, V. Réat, A. Milon and J. Czaplicki, Eur. Biophys. J., 2007, 36, 919–931 CrossRef CAS PubMed.
- J. Seelig and N. Waespe-Sarcevic, Biochemistry, 1978, 17, 3310–3315 CrossRef CAS PubMed.
- T. M. Ferreira, F. Coreta-Gomes, O. H. S. Ollila, M. J. Moreno, W. L. C. Vaz and D. Topgaard, Phys. Chem. Chem. Phys., 2013, 15, 1976–1989 RSC.
- J. Eastoe and D. Sharpe, Langmuir, 1997, 13, 3289–3294 CrossRef CAS.
- E. Acosta, E. Szekeres, D. A. Sabatini and J. H. Harwell, Langmuir, 2003, 19, 186–195 CrossRef CAS.
- P. Verdia, H. Q. Gunaratne, T. Y. Goh, J. Jacquemin and M. Blesic, Green Chem., 2016, 18, 1234–1239 RSC.
- Z. Zhang, D. M. Mitrinovic, S. M. Williams, Z. Huang and M. L. Schlossman, J. Chem. Phys., 1999, 110, 7421–7432 CrossRef CAS.
- A. M. Tikhonov, M. Li and M. L. Schlossman, J. Phys. Chem. B, 2001, 105, 8065–8068 CrossRef CAS.
- M. L. Schlossman and A. M. Tikhonov, Annu. Rev. Phys. Chem., 2008, 59, 153–177 CrossRef CAS PubMed.
- R. Varadaraj, J. Bock, P. Valint, S. Zushma and R. Thomas, J. Phys. Chem., 1991, 95, 1671–1676 CrossRef CAS.
- A. Bera, A. Mandal and B. B. Guha, J. Chem. Eng. Data, 2014, 59, 89–96 CrossRef CAS.
- Z. Ye, F. Zhang, L. Han, P. Luo, J. Yang and H. Chen, Colloids Surf., A, 2008, 322, 138–141 CrossRef CAS.
- R. Aveyard, B. P. Binks, S. Clark and J. Mead, J. Chem. Soc., Faraday Trans. 1, 1986, 125 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: A comparison of the water/dodecane/SDS IFT calculated using the NPnAT and NVT ensembles, maximum surface excess concentration of SDS gathered from multiple studies in the literature, results of the IFT of n-dodecane–water as a function of temperature, the evolution of the water/dodecane IFT and the system's potential energy, distribution of interfacial water, dodecane molecules using the ITIM algorithm, representative simulation snapshots showing the coexitence of dodecane and SDS at the interfacial film, a comparison between water/air/SDS and water/dodecane/SDS IFT, principal motions of saturated vs. unsaturated SDS molecules via PCA approach, C–C–C–C torsional potentials of SDS alkyl tail implementing the original TraPPE-UA force field and the refitted to the ab initio data, order parameter for SDS alkyl tail implementing two different sets of torsional angle potentials, simulation equilibration evaluation. See DOI: 10.1039/d1cp03971g |
| This journal is © the Owner Societies 2021 |