 Open Access Article
Open Access ArticleAb initio molecular dynamics simulations and experimental speciation study of levofloxacin under different pH conditions
Emanuele
Previti
a,
Claudia
Foti
 *a,
Ottavia
Giuffrè
*a,
Ottavia
Giuffrè
 a,
Franz
Saija
b,
Jiri
Sponer
c and
Giuseppe
Cassone
a,
Franz
Saija
b,
Jiri
Sponer
c and
Giuseppe
Cassone
 *b
*b
aDipartimento di Scienze Chimiche, Biologiche, Farmaceutiche ed Ambientali, Università degli Studi di Messina, Salita Sperone 31, 98166 Messina, Italy. E-mail: cfoti@unime.it
bInstitute for Chemical-Physical Processes, National Research Council of Italy (IPCF-CNR), Viale Stagno d’Alcontres 37, 98158 Messina, Italy. E-mail: cassone@ipcf.cnr.it
cInstitute of Biophysics of the Czech Academy of Sciences (IBP-CAS), Kràlovopolskà 135, 61265 Brno, Czechia
First published on 6th October 2021
Abstract
Levofloxacin is an extensively employed broad-spectrum antibiotic belonging to the fluoroquinolone class. Despite the extremely wide usage of levofloxacin for a plethora of diseases, the molecular characterization of this antibiotic appears quite poor in the literature. Moreover, the acid–base properties of levofloxacin – crucial for the design of efficient removal techniques from wastewaters – have never extensively been investigated so far. Here we report on a study on the behavior of levofloxacin under standard and diverse pH conditions in liquid water by synergistically employing static quantum-mechanical calculations along with experimental speciation studies. Furthermore, with the aim of characterizing the dynamics of the water solvation shells as well as the protonation and deprotonation mechanisms, here we present the unprecedented quantum-based simulation of levofloxacin in aqueous environments by means of state-of-the-art density-functional-theory-based molecular dynamics. This way, we prove the cooperative role played by the aqueous hydration shells in assisting the proton transfer events and, more importantly, the key place held by the nitrogen atom binding the methyl group of levofloxacin in accepting excess protons eventually present in water. Finally, we also quantify the energetic contribution associated with the presence of a H-bond internal to levofloxacin which, on the one hand, stabilizes the ground-state molecular structure of this antibiotic and, on the other, hinders the first deprotonation step of this fluoroquinolone. Among other things, the synergistic employment of quantum-based calculations and speciation experiments reported here paves the way toward the development of targeted removal approaches of drugs from wastewaters.
1. Introduction
Levofloxacin is an oral antibiotic mainly employed to counteract respiratory and genitourinary infections caused by bacteria. Its efficacy against a large variety of infections, including chronic respiratory diseases, tonsillitis, pharyngitis, pneumonias or acute bronchitis, has extensively been demonstrated.1–3 As far as genitourinary infections are concerned, levofloxacin has been proved to be effective in the treatment of pyelonephritis, uncomplicated cystitis and urethritis, and acute or chronic prostatitis and epididymitis. The incisiveness of levofloxacin has also been proven against illnesses like skin, soft tissue, gynecological, ocular, ear, nose, throat and odontogenic infections and bacterial enteritis.4–7Levofloxacin belongs to the family of fluoroquinolone antibiotics, a class of broad-spectrum antibacterial agents active against a wide range of Gram-positive and Gram-negative pathogenic bacteria. These properties led to a worldwide employment of fluoroquinolones contributing, among other things, to the development of antibiotic resistance.8–11 In addition, the continuous usage of these fluoroquinolones in everyday life, and of antibiotics in general, has led to their wide distribution and persistence in the environment, both in wastewaters and in natural water systems. Therefore, antibiotics have recently been recognized as an emerging class of contaminants and bio-accumulative compounds. As a result, an ever increasing number of studies on the presence, fate and effect of this class of medicines on aqueous environments appeared during the last decade. Nevertheless, little is known about their potential ecological and human toxicity via environmental exposure.12–14 For these reasons, a deep knowledge of the acid–base behavior of levofloxacin and, more generally, of antibiotics is crucial not only to evaluate the hazard of environmental pollution but also to develop appropriate removal techniques.
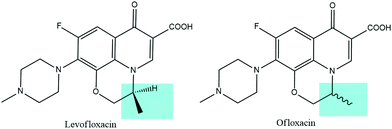
In contrast to earlier generations of quinolones, fluoroquinolones are characterized by the presence of a fluorine atom and a five- or six-membered heterocyclic ring, which are essential for improving the molecular activity, broadening the spectrum of action, and increasing the permeability through bacterial membranes. In fact, the fluorine atom is involved in the binding with the biological target together with the carboxylic group and the carbonyl group, while the 4-methyl-piperazin-1-yl substitution allows for a greater permeability through the bacterial cells and, therefore, for a significant broadening of the spectrum of action toward Gram-positive bacteria. In addition, levofloxacin holds an asymmetric carbon atom and it represents the optical S-(−) isomer of ofloxacin, as shown in Fig. 1. Levofloxacin is twice as active as ofloxacin and 8 to 128 times more powerful than the R-(+)-isomer due to the increased capability of binding to the DNA gyrase.3,15–18 DNA gyrase and topoisomerase IV are two related enzymes involved in the supercoiling process of DNA. They are also the biological targets of fluoroquinolones antibiotics. These enzymes are responsible for the cutting of the strands of the DNA double helix, passing the uncut portion of the molecule through the break and then resealing the strands previously separated. DNA gyrase is responsible for the introduction of negative supercoils into DNA and, generally, it is the primary target in Gram-negative bacteria. Topoisomerase IV, instead, provides a potent decatenation by means of the removal of the interlinking of daughter chromosomes and it is typically the primary target in Gram-positive organisms. Fluoroquinolones interact with the DNA–enzyme complex inhibiting the resealing of the strands, causing hence the block of the DNA synthesis and therefore the death of the bacterial cell.15,19–21
Some quantum-mechanical computational investigations reported on the molecular conformations of levofloxacin under standard conditions. In particular, a very recent study employing the B3LYP22–25 density functional theory (DFT) exchange and correlation functional elucidated on the stable structures and the Raman spectra of this fluoroquinolone and ciprofloxacin.26 Among other studies, the study by Sinha and Biswas26 concluded that the conformation and orientation of the piperazine ring and the orientation of the hydroxyl group play a key role in the stabilization process. At the same time, however, they observed that the experimental Raman spectrum is better reproduced when a larger number of H-bonds with the solvation water molecules are considered in the calculations.26 On the other hand, only a very exiguous number (i.e., 2) of solvating molecules was employed in that study and without any consideration of a priori relevant dynamical effects of the solvation shells stabilizing the levofloxacin structure. Although other computational studies reported some interesting data on the vibrational modes and on the electronic structure properties of levofloxacin from similar static quantum chemical simulations,27 the molecular structure employed in these calculations is in direct conflict with the most stable one recently determined in ref. 26.
The antibacterial action of fluoroquinolones is strongly influenced by their physicochemical properties stemming from the adopted fundamental molecular structures. In particular, the acid–base properties as well as the capability fluoroquinolones hold in forming complexes with metal ions strictly depend on their specific molecular arrangement and the available atomic sites.28–30 In this respect, quantum chemical calculations of boron complexes with levofloxacin have been reported.31 Furthermore, similar static DFT-based simulations have very recently been employed for investigating the capabilities hold by biochar-derived porous carbon sheets in removing levofloxacin.32 Also in this case, the peculiar structure exhibited by this fluoroquinolone is of fundamental relevance for designing efficient chemical approaches for removal. To understand the antimicrobial effect, the pharmacokinetic properties, or other relevant properties of levofloxacin, it is crucial to know, in depth, the form under which this molecule is present at different pH values and ionic strength found in biological fluids. Albeit the relevance of the existing computational investigations, all these properties can be carefully evaluated only by employing computational techniques explicitly taking into account the role of the water solvation shells. This way, here we report on not only an extensive investigation on the behavior of levofloxacin in water by employing quantum-mechanical calculations, but also the unprecedented simulation of levofloxacin in explicitly treated aqueous environments by means of state-of-the-art Car–Parrinello-like molecular dynamics33 under diverse pH conditions along with speciation experiments.
2. Methods
2.1 Static quantum-mechanical calculations
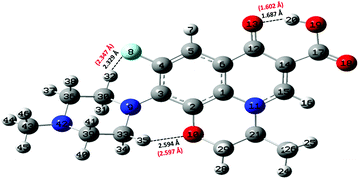
Static quantum-mechanical calculations were performed by means of Gaussian 09 software.34 This latter allowed us to identify the ground-state molecular structure of levofloxacin and to evaluate the energy difference of closely-related relevant structures. In this work, all calculations were performed using the B3LYP22–25 hybrid exchange and correlation functional, with 100% of exact exchange. Geometry optimization of the molecular structures was performed either in the gas phase (vacuum) or under implicit water solvation by employing the 6-311++G(d,p) atomic basis sets for all atoms. As far as the simulation of the solvent is concerned, the conductive polarizable continuum model (CPCM)35 was employed by setting parameters mimicking water electrostatics. After structural relaxation to the ground state, vibrational calculations were performed not only to establish the correctness of the previous calculations (i.e., absence of imaginary frequencies), but also to obtain the zero-point energy (ZPE) associated with each optimized molecular structure. Nuclear quantum effects have to be taken into account carefully in proton transfer phenomena in light of recent findings showing their relevance in water also under ambient conditions.36 Moreover, ZPE values are pivotal for determining the proton affinity (PA). With the aim of obtaining an as much as complete scenario on the capabilities that neutral levofloxacin holds in accepting protons, quantum-mechanical calculations were performed involving the most plausible molecular protonation sites, namely the nitrogen atom binding the methyl group and the other nitrogen atom of the piperazine ring, denoted as N42 and N9 in Fig. 2, respectively. This way, the PA values were obtained by calculating the energy difference between the optimized protonated and neutral molecules at the B3LYP/6-311++G(d,p) level of theory using the following equation:37,38| PA = −ΔH = −ΔE − ΔZPE + ΔEv(T) + C. | (1) |
2.2 Car–Parrinello-like molecular dynamics simulations
In this study, the software package CP2K39 was used to perform Car–Parrinello-like molecular dynamics (CPMD)33 simulations of levofloxacin solvated in aqueous solutions. In particular, a series of CPMD simulations were carried out within the classical nuclei approximation. A numerical sample composed of one levofloxacin and 253 water molecules (i.e., 814 atoms) was placed in a cubic simulation box with an edge equal to 20.21 Å under periodic boundary conditions. Such a molecular configuration was then equilibrated by means of first-principles molecular dynamics for 5 ps, after which an accumulation run 50 ps-long initiated. It is worth mentioning here that CPMD simulation boxes containing such a relatively large number of atoms represent a sort of computational upper-bound for most of the super-computing resources. Besides, also acidic and alkaline aqueous conditions were simulated in order to characterize, at the atomistic level, the speciation behavior of levofloxacin. To this aim, four additional samples were prepared. The more “acidic samples” were constituted of one levofloxacin, 3 (or 5) oxonium H3O+ cations and 250 (or 248) water molecules whereas the “basic samples” were composed of one levofloxacin molecule, 3 (or 5) hydroxide OH− anions and 250 (or 248) water molecules. In this way, simulation boxes having a global charge equal to ±3 (or ±5) e were investigated. In all cases, a compensating jellium background was included in order to avoid the divergences due to the infinite replica of the (charged) simulation boxes.40 Such a protocol has already been tested and appropriately works for charged boxes, as reported in the standard documentation of the used software package CP2K.39 Furthermore, comparisons with shorter CPMD trajectories (i.e., 10 ps each) gathered in the presence of either Na+ cations (in the basic samples) or Cl− anions (in the acidic samples) neutralizing the overall simulation box were performed; no discrepancies with respect to the results obtained in the charged boxes compensated with a jellium background were recorded. Trajectories of 50 ps each were accumulated in order to monitor the pH-induced levofloxacin (de)protonation mechanism(s) under acidic and basic conditions. Such a computational protocol has already been employed and validated by some of us for characterizing the behavior of hydrolytic arsenic species in aqueous solutions as a function of the pH.41Electronic wave-functions of each atomic species were expanded on triple zeta valence plus polarization (TZVP) basis sets. As for exchange and correlation effects, we adopted the gradient-corrected Becke–Lee–Yang–Parr (BLYP)23,24 functional in conjunction with D3(BJ) Grimme's dispersion corrections42,43 whereas Goedecker–Teter–Hutter44 pseudopotentials were chosen to mimic the core electronic interaction. As correctly argued by an anonymous reviewer, in modern theoretical chemistry it is by now widely accepted that due to the calibration procedure inherent to the vast majority of functionals used in density functional theory calculations, methods employing the (parametrized) BLYP functional along with D3 dispersion corrections are, in a strict sense, not compatible with the first-principles/ab initio concept. This way, the nomenclature “Car–Parrinello-like” instead of the “ab initio” one has been preferred throughout the text. A cut-off energy for the wave-function representation of 40 Rydberg (Ry) and a cut-off of 400 Ry for the charge density were employed whereas a timestep of 0.5 fs has been chosen for each of the trajectories. All the CPMD simulations were carried out at an average temperature of 300 K controlled by means of the canonical sampling through the velocity rescaling method.45 In this way, samples were simulated in an isothermal–isochoric (NVT) ensemble and the dynamics of the nuclei were classically propagated using the Verlet algorithm.
2.3 UV-Vis spectrophotometric measurements
Spectrophotometric measurements were carried out using a Varian Cary 50 UV-Vis spectrophotometer which allows for investigating the spectral region of visible and ultraviolet light. The system is equipped with an optical fiber probe and it is connected to a PC loaded with Varian Cary WinUV software to record the spectra. The titrant is delivered in the measurement cell by means of a 665 Metrohm automatic burette. Simultaneously, the pH of the solutions is measured using a combined glass electrode (Ross type 8102, from Thermo/Orion) connected to a Metrohm 713 potentiometer. The combined glass electrode is calibrated before each experiment in terms of pH = −log[H+]. Therefore, both data A vs. λ (nm) and pH vs. volume of titrant (mL) are simultaneously recorded. Measurements are recorded using thermostated glass jacket cells at T = 298.2 K ± 0.1 K and bubbling pure nitrogen in order to avoid O2 and CO2 inside the solution. Titrations were performed with 25 mL of solution containing levofloxacin (0.01 ≤ CL ≤ 0.04 mmol L−1), HCl (2 mmol L−1) to fully protonate the molecule, and NaCl (0.1 ≤ C ≤ 1 mol L−1) to fix the ionic strength. Standard NaOH solution was used as the titrant, and the pH was varied within the 3–10.5 range.2.4 Reagents
Solutions containing the ligand were obtained by weighing and dissolution of anhydrous levofloxacin (analytical standard, Sigma-Aldrich) and used without further purification. Fresh solutions of levofloxacin were habitually prepared. Sodium hydroxide and hydrochloric acid solutions were prepared from concentrated ampoules (Fluka, Munich, Germany) and titrated with potassium biphthalate (≥99.5%, Sigma-Aldrich) and sodium carbonate (≥99.5%, Sigma-Aldrich), respectively, previously dried in an oven at 383.2 K for at least one hour. NaOH solution was stored in dark bottles and preserved using CO2 by means of soda lime traps. Sodium chloride solution was prepared by weighing the corresponding salt (Sigma-Aldrich, puriss.) pre-dried in an oven at 383.2 K. All solutions were prepared using bidistilled water (conductivity <0.1 μS cm−1) and grade A glassware.3. Results and discussion
3.1 Computational results
As laid out in the Methods section, static quantum-mechanical simulations were executed at the B3LYP/6-311++G(d,p) density functional theory (DFT) level. In light of some data present in the literature,26,31 the employment of this DFT setup would ensure a quite robust description of the molecular structure of levofloxacin. In fact, simpler basis sets such as the 6-31+G(d,p) revealed to be sufficient for discerning among the most stable structures of levofloxacin.26 However, the presence of the fluorine atom would in principle require the employment of more diffuse basis functions. As a consequence, the ground-state structure of this antibiotic has been determined by means of a larger basis set (i.e., 6-311++G(d,p)) and it is here shown in Fig. 2. Interestingly, the H-bond length between the hydrogen atom H20 of the hydroxyl group (O19–H20) and the oxygen atom denoted as O13 in Fig. 2 is equal to 1.687 Å, a value only slightly different from that obtained with a 6-31+G(d,p) basis set (i.e., 1.671 Å).26 On the other hand, the H-bond formed by the fluorine atom (denoted as F8 in Fig. 2) and the closest hydrogen atom of the methylene group exhibits a ground-state length equal to 2.329 Å. This value is significantly smaller than that determined by employing the restricted 6-31+G(d,p) basis set (i.e., 2.511 Å)26 indicating, a posteriori, the importance of including in the basis set diffuse functions when dealing with fluorine atoms. Taking into account these important basis functions leads, indeed, to a ground-state levofloxacin structure which exhibits the piperazine ring slightly more tilted toward the fluorine atom. In fact, the other relevant internal H-bond present in this molecular structure – formed by the oxygen atom O10 and the hydrogen atom H35 in Fig. 2 – exhibits a length of 2.594 Å, a value in contraposition with that recorded by using less expanded basis sets (i.e., 2.318 Å).26 All these findings strongly indicate the need for employing sufficiently large basis sets for an adequate description of the ground-state molecular structure of levofloxacin.By means of a series of single-point calculations, the proton affinity (PA) of the nitrogen atom binding the methyl group (denoted as N42 in Fig. 2) and that of the other nitrogen atoms of the piperazine ring (denoted as N9 in Fig. 2) of the levofloxacin molecule has been determined. To this aim, as usual, the deformation energy (ΔE) between the protonated levofloxacin structures – one per protonation site – and that of the neutral molecule has been calculated. All the respective values, determined under implicit solvation, are listed in Table 1.
| Atom | PA (kcal mol−1) | ΔE (kcal mol−1) |
|---|---|---|
| N42 | 237.48 | +5.53 |
| N9 | 236.16 | +7.00 |
From the electronic standpoint, the N42 atom is manifested to be electron-rich due to the presence of the three substituted electron-donor alkyl groups, which increase the affinity of the nitrogen atom toward the acceptance of a proton. On the other hand, the nitrogen atom N9 of the piperazine ring exhibits a slightly lower PA value because of the binding with an aromatic system which, being a weaker electron-donor than the methyl group, gives rise to a lower PA associated with N9 with respect to that ascribed to N42. This way, notwithstanding the extra stabilization due to the formation of a new H-bond between the fluorine atom and the hydrogen atom of the protonated nitrogen N9 (not shown), quantum-mechanical calculations suggest that the most plausible site for the first protonation step offered by levofloxacin is represented by the nitrogen atom bound to the methyl group (N42). Nevertheless, the small quantitative difference between the PA values obtained (i.e., ≈ 1.5 kcal mol−1) does not allow for sharply discerning among the most effective proton acceptor sites of the levofloxacin molecule and an explicit treatment of the water environment is needed for investigating the behavior of the local aqueous environment assisting potential proton transfer events.
In parallel with traditional static quantum chemistry calculations, a series of Car–Parrinello-like molecular dynamics (CPMD) simulations have been performed in order to monitor not only the behavior of the water solvation shells in proximity to selected levofloxacin atomic sites, but also to directly track the protonation and deprotonation mechanisms of the neutral levofloxacin molecule under acidic and basic conditions, respectively. The first marked difference between quantum-mechanical calculations and CPMD techniques is related to the description of the solvent. In fact, in static quantum chemistry simulations an implicit solvent is – in the best scenario – used, where the solvation properties are approximated with respect to the dielectric constant of the solvent, whereas in CPMD methods the solvent is explicitly treated at the same level of theory of the solute, fully including its quantum nature. This way, the inclusion of entropic contributions stemming from a dynamical (quantum) aqueous environment allows for building up more realistic pictures of the interactions established by levofloxacin with the surrounding solvation shells, also including thermal fluctuations.
As shown by the radial distribution functions (RDFs) reported in Fig. 3a, the average water arrangement in proximity to the nitrogen atom binding the methyl group labeled as N42 exhibits highly structured hydration shells (black solid curve), whereas the aqueous environment around the N9 levofloxacin atom is only barely organized (red dotted-dashed curve). Moreover, the presence of a sharp first peak of the RDF located at 2.75 Å from the N42 atom reveals the existence of a directly H-bonded water molecule. On the other hand, the first maximum of the RDF between the N9 atom and the oxygen atoms of the hydrating local environment (Ow) falls at 4.70 Å, an evidence which suggests that some steric hindrance induced by levofloxacin prevents the sampling to the water molecules of shorter distances in this region of the fluoroquinolone structure. In fact, whilst the spatial distribution function (SDF) of the water oxygen atoms around the N9 levofloxacin atom is not visible for isovalues tracing the dynamical behavior of the local (within ≈ 4 Å) water molecules, the SDF of these solvating atoms in proximity to N42 is manifested, as shown in Fig. 3b. Interestingly, the horizontal confinement of this SDF indirectly reveals the directionality and the strength of the H-bond established between the nitrogen atom N42 binding the methyl group of the antibiotic and its first-neighbor water molecule. All these findings imply that the nitrogen atom N42 is sizably more prone to accept protons from the aqueous environment than the nitrogen N9 atom of the piperazine ring of levofloxacin.
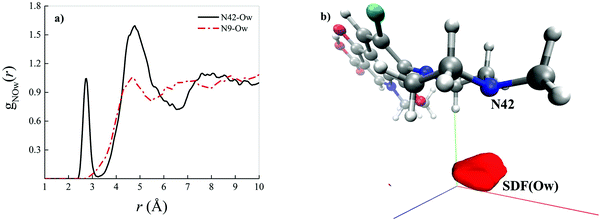 | ||
| Fig. 3 (a) Radial distribution function (RDF) between the nitrogen atom of levofloxacin labeled as N42 (see Fig. 2 for the atomic label definition) and the oxygen atoms of the solvating aqueous environment (black solid curve) and the RDF between the nitrogen atom of levofloxacin labeled as N9 and the oxygen atoms of the surrounding water molecules (red dashed-dotted curve) as determined from CPMD simulations. (b) Spatial distribution function (SDF) of the oxygen atoms (Ow) of the surrounding water molecules taking as a reference the levofloxacin nitrogen atom N42 (isovalue 7.99). | ||
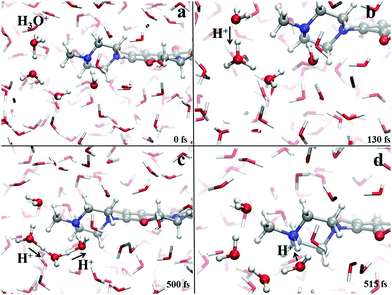
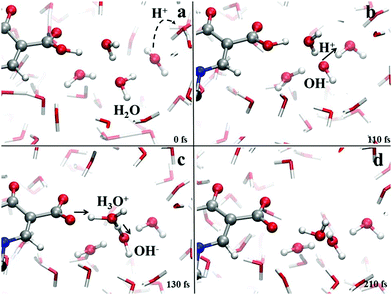
Crucially relevant proton transfer events ruling the behavior of levofloxacin under either acidic or alkaline conditions can only be caught by resorting an explicit treatment of the solvent, as typical in ab initio molecular dynamics and CPMD simulations.36,41,46–50 The spontaneous first protonation step of the levofloxacin molecule occurring under acidic conditions is atomistically traced in Fig. 4. As correctly forecasted by the previous analyses, it turns out that such a first protonation step takes place on the nitrogen atom binding to the methyl group (N42), a result which is also in line with the PA predictions of the piperazine ring nitrogen atoms obtained via static quantum-mechanical calculations. The protonation process depicted in Fig. 4 shows that, once released, the proton rapidly migrates across the H-bond network of the aqueous environment via the well-known Grotthuss mechanism. The release of the first proton from an already existing oxonium H3O+ cation occurs on timescales on the order of ≈100 fs (Fig. 4b) whereas, after ≈500 fs, cooperative mechanisms between the water molecules in the solvation shells lead to the transfer of the excess proton along H-bonded “water wires” (Fig. 4c). Once the proton reaches the water molecule first-neighbor to the nitrogen atom N42 binding the methyl group, an ultrafast proton transfer takes place and leads to the formation of the protonated HL form of the levofloxacin molecules (Fig. 4d).
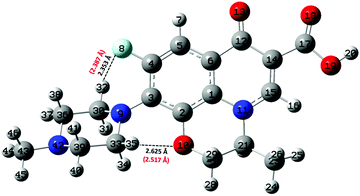
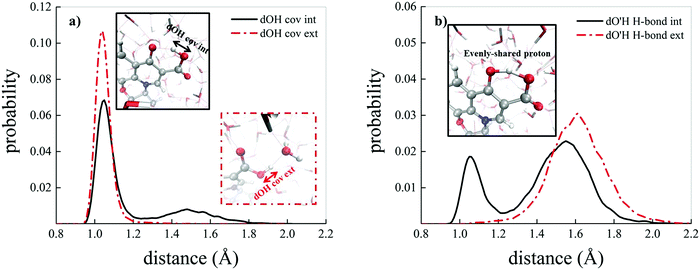
Albeit static quantum-mechanical calculations predict that the ground-state levofloxacin structure exhibits a (stabilizing) internal H-bond between the carboxylic and the carbonyl group, another higher-energy – but stable – conformer is indicated by the same calculations, whose molecular structure is shown in Fig. 5. In this structure, the hydrogen atom involved in the internal H-bond in the most stable configuration is now oriented toward the solvent. In fact, this carboxylic –OH group, rather than establishing an internal H-bond with other oxygen atoms of the fluoroquinolone structure, points outward of the antibiotic toward the external surrounding. When resorting to an explicit treatment of the aqueous environment through CPMD simulations, a deeply different behavior is recorded between the portion of the levofloxacin molecule hosting the carboxylic and carbonyl groups between the ground-state structure and the higher-energy conformer. As shown in Fig. 6a, the distribution of the carboxylic –OH covalent bond lengths in the two conformers exhibits, in the ground-state levofloxacin structure, a bimodal behavior, whereas in the higher-energy structure a unimodal profile. The same distribution modalities are also recorded by sampling the lengths of the H-bonds that the carboxylic –OH groups donate in the two fluoroquinolone structures, as depicted in Fig. 6b. By combining these information, it turns out that the higher-energy conformer establishes a strong and net H-bond with the nearest-neighbor water molecule of the solvating environment. On the other hand, fluctuations of thermal and entropic nature included in CPMD simulations render the ground-state structure of levofloxacin predicted by static quantum-mechanical calculations much more flexible than expected. In fact, frequent proton transfer events (namely, large amplitude motions) are recorded at room temperature between the carboxylic and the carbonyl group of the antibiotic, as atomistically shown in the inset of Fig. 6b, where a typical instantaneous structure exhibiting an evenly shared proton between these functional groups is reported. To the best of our knowledge, these internal proton transfer events in levofloxacin have never been reported before. The different interactions established by the oxygen atoms of the carboxylic –OH groups of the higher- and lower-energy levofloxacin structures with the local aqueous environment are also magnified by the respective RDFs shown in Fig. 7. The existence of an internal H-bond between the carboxylic and carbonyl groups prevents any structuring of the solvation shells, whereas a sharp first peak located at 2.66 Å is recorded in the RDF between the oxygen atom of the carboxylic –OH group of the higher-energy levofloxacin conformer and the oxygen atoms of the water environment, as visible from the red dashed-dotted curve in Fig. 7. This clearly implies that the higher-energy structure of levofloxacin could be a priori more prone to donate the proton from this portion of the molecule with respect to the same molecular region of the ground-state antibiotic structure. In fact, within the timescales afforded by the current CPMD investigations (i.e., 50 ps) and the alkaline regimes simulated, no proton releases were recorded from the ground-state structure, indicating a posteriori the strong stability conferred by the existence of the internal H-bond (and the internal proton transfer events) in the levofloxacin canonical structure.
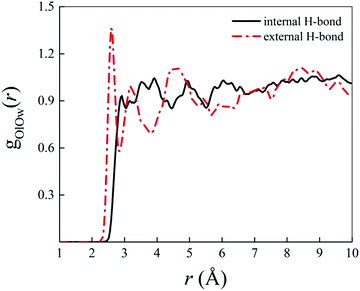 | ||
| Fig. 7 Radial distribution function (RDF) between the oxygen atoms of the carboxylic –OH group of the ground-state levofloxacin structure labeled as O19 (see Fig. 2) and the oxygen atoms of the solvating aqueous environment (black solid curve) and the RDF between the corresponding oxygen atom O19 of the higher-energy conformer of levofloxacin (see Fig. 5) pointing its covalently-bound proton toward the nearby solvent water molecules (red dashed-dotted curve). | ||
On the other hand, Fig. 8 shows the deprotonation mechanism of the neutral levofloxacin molecule in its higher-energy conformation (exhibiting the presence of a H-bond between the carboxylic group of the antibiotic and the solvent) under basic conditions. Such a process is triggered by the formation of a hydroxyl anion in one of the levofloxacin solvation shells (Fig. 8a). After ≈100 fs since this event, the protonation of this anion occurs and a nearby water molecule is consequently ionized (Fig. 8b). This way, after a series of concerted proton transfer events, the deprotonation of the carboxylic –OH and the consequent formation of the carboxylate anion have been observed (Fig. 8c). Water solvation shells play a crucial role in assisting the complex proton transfer network underlying each hydrolysis event. Moreover, the formation of a cluster of water molecules capable of solvating, via strong H-bonds, the carboxylate anion is observed ≈200 fs after the seminal formation of an OH− species in one of the levofloxacin hydration shells (Fig. 8d). It is worth stressing the fact that the presented mechanism has been monitored only for the higher-energy conformation of the levofloxacin molecule. In fact, the ground-state levofloxacin structure shown in Fig. 2, exhibiting a strong intramolecular H-bond between the carboxylic and the carbonyl group, does not show any deprotonation event, at least within the timescales afforded by CPMD simulations. The rate-limiting step characterizing the deprotonation process may therefore be ascribed to the presence of this internal H-bond, which remains stable (despite hosting frequent internal proton transfer events shown in Fig. 6) over the whole trajectories even making the aqueous solutions more alkaline.
To estimate the energy required to cleave the internal H-bond between the carboxylic and the carbonyl group, additional quantum-mechanical calculations have been performed. As previously discussed in Fig. 2, the minimum-energy conformation of the levofloxacin molecule is achieved when this H-bond is established. The situation can be better evaluated by considering the energy scan of the rotation of the dihedral angle between the O18–C17–O19–H20 atoms; in particular, these conformational studies were conducted by focusing on the rotation of the –OH group in water around the C17–O19 covalent bond. The scan was performed by sampling the relaxed total energy of every levofloxacin molecule with 10 degrees of rotation from the 180-degree conformation up to the zero-degree conformation. The most stable circumstance corresponds to the conformation in which the hydrogen H20 is oriented toward the carbonyl oxygen O13 forming a dihedral angle of 180 degrees, as denoted in Fig. 9. As this angle is rotated toward smaller values, a total energy increase occurs and, in order to reach another local energy minimum, a potential energy barrier of 21.28 kcal mol−1 has to be overcome. A metastable configuration is then reached when the considered dihedral angle is equal to 0 degrees, as shown in Fig. 9. The energy difference between such a structure and the ground-state one amounts to +9.80 kcal mol−1, a value indirectly magnifying the strength of the formed H-bond. Furthermore, in the conversion from the most stable structure toward the metastable one shown in Fig. 9, the length of the O19–H20 covalent bond – which varies from 0.995 Å to 0.968 Å – decreases, a circumstance marking once again the strength of the internal H-bond. In other words, the rate-limiting step of the deprotonation process of the carboxylic group is not only related to the formation of a hydroxide anion in one of the hydration shells but, mainly, to the cleavage of this strong intramolecular H-bond.
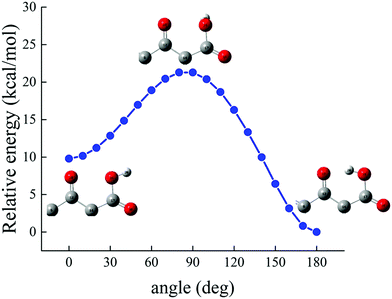 | ||
| Fig. 9 Relative energy, determined at the B3LYP/6-311++G(d,p) DFT level under implicit water solvation, of the levofloxacin molecule as a function of the rotation of the dihedral angle between the O18–C17–O19–H20 atoms considering the rotation of the –OH group around the C17–O19 bond (see Fig. 2 for the numbering scheme). | ||
3.2 Experimental results
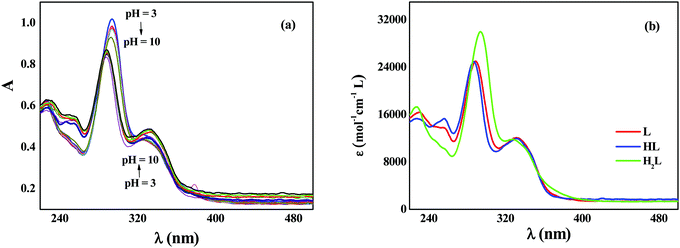
To experimentally evaluate the acid–base behavior of levofloxacin under different pH values, UV-spectrophotometric titrations have been performed, following procedures already reported.51–54 Measurements on solutions containing different concentrations of the ligand at different ionic strength values were carried out, varying the pH in the range 3 ≤ pH ≤ 10.5. Levofloxacin absorbs between 250 and 400 nm with two maxima at about 290 and 330 nm. As shown in Fig. 10a, as the pH increases, a decrease of the intensity of the main band (hypochromic effect) and a slight shift at wavelengths shorter than the maximum absorption (hypsochromic shift) are observed. Instead, the 330 nm band exhibits a small increase of the intensity (hyperchromic effect) and an equally slight shift to greater λ (bathochromic shift) in relation to the increase of the pH. This is strictly in accordance with the different forms (H2L, HL and L) under which levofloxacin can be present in solution as the pH varies.By processing the spectrophotometric data by using the HYSPEC program,55 the protonation constants at different ionic strengths have been obtained, together with the molar extinction coefficients of each species. These coefficients are shown in Fig. 10b: at λmax, the species most responsible for the absorption is the di-protonated H2L with a higher coefficient ε than HL and L forms. This explains the trend of the titration curves since, at lower pH, in which the molecule is mainly present in the protonated form, the absorbance is greater and tends to decrease as the pH increases (i.e., with the decrease in the percentage of formation of the H2L species). This effect is not found at 330 nm, as the protonated species has a slightly lower ε than that of HL and L, whose values are comparable.
Protonation constants at different ionic strengths (β) are reported in Table 2. In the same Table are listed values at infinite dilution (β0) calculated by the simple Debye–Hückel equation, as done for other systems:56–60
The knowledge of the protonation constants allows the prediction of the distribution of the species, as shown in Fig. 11, where the formation percentages are reported as a function of the pH. It turns out that levofloxacin is mainly found under the deprotonated form L for pH values greater than 8, whilst the HL species prevails in the range 6 < pH < 8, and the H2L for pH lower than 6. By taking into account the results emerging from quantum-based computations presented here and the identification of the protonation sites reported for other fluoroquinolones,61 the first protonation step (i.e., H+ + L− = HL0) can be attributed to the protonation of the nitrogen atom N42 binding the methyl group, whereas the second one (i.e., H+ + HL0 = H2L+) to the protonation of the carboxylic group.
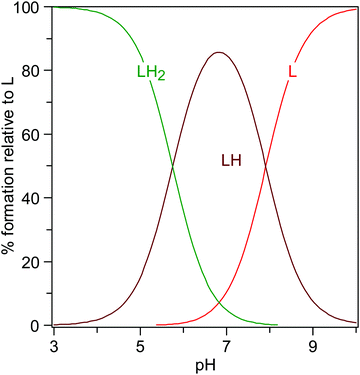 | ||
| Fig. 11 Distribution of the levofloxacin species as a function of the pH (CL = 0.01 mmol L−1, I = 0 mol L−1, T = 298.2 K). | ||
4. Conclusions
In this work, the standard and acid–base properties of levofloxacin have been studied by means of a series of computational and experimental investigations. With the aim of identifying a refined picture of the ground-state molecular structure of levofloxacin, static quantum-mechanical calculations at the B3LYP/6-311++G(d,p) density functional theory (DFT) level have been conducted. In contraposition with the results present in the literature, perhaps obtained with smaller basis sets (i.e., 6-31+G(d,p)), it turns out that the ground-state levofloxacin structure exhibits the piperazine ring more tilted toward the fluorine atom. Quantum-mechanical calculations allowed us to determine also the proton affinity (PA) of different atomic sites. From this analysis emerges that the nitrogen atom binding the methyl group of levofloxacin shows the highest PA value.Furthermore, for the first time, also a series of state-of-the-art Car–Parrinello-like molecular dynamics (CPMD) simulations of levofloxacin under standard, relatively acidic and basic conditions have been reported. These investigations, permitting a direct inspection of the behavior of the water solvation shells around selected atomic sites of this antibiotic, allowed us to predict the most likely atomic sites offered by levofloxacin in accepting/donating protons. This way, the dynamical aspects of the protonation and deprotonation mechanisms of levofloxacin in the presence of an explicit aqueous environment have been traced and depicted. All these findings are in line with speciation laboratory experiments which also suggest that the nitrogen atom binding the methyl group of levofloxacin could be the best candidate for accepting excess protons present in water. Finally, by means of quantum-based simulations we also quantify the energetic contribution associated with the presence of the internal H-bond between the carboxylic and the carbonyl group of levofloxacin which, on the one hand, stabilizes the ground-state molecular structure of this widely employed antibiotic – permitting inter alia internal proton exchanges between those functional groups – and, on the other, hinders the first deprotonation step of this fluoroquinolone under alkaline conditions.
The proposed approach, combining advanced computational techniques and experiments, allowed the successful characterization of – also at the atomistic level – the standard and acid–base behavior of levofloxacin and of the various chemical forms under which this molecule is present under different conditions of pH. This way, such a synergistic investigation paves the way toward the development of smart approaches for the removal of drugs from wastewaters on the basis of the knowledge of the specific molecular state under which the target antibiotics can be found.
Conflicts of interest
There are no conflicts of interest to declare.References
- A. Torres and A. Liapikou, Expert Opin. Pharmacother., 2012, 13, 1203–1212 CrossRef CAS PubMed.
- S. Ragnar Norrby, Expert Opin. Pharmacother., 1999, 1, 109–119 CrossRef.
- R. Davies and H. M. Bryson, Drugs, 1994, 47, 677–700 CrossRef PubMed.
- N. Wei, L. Jia, Z. Shang, J. Gong, S. Wu, J. Wang and W. Tang, CrystEngComm, 2019, 21, 6196–6207 RSC.
- V. R. Anderson and C. M. Perry, Drugs, 2008, 68, 535–565 CrossRef CAS PubMed.
- K. F. Croom and K. L. Goa, Drugs, 2003, 63, 2769–2802 CrossRef CAS PubMed.
- S. M. Wimer, L. Schoonover and M. W. Garrison, Clin. Ther., 1998, 20, 1049–1070 CrossRef CAS PubMed.
- L. S. Redgrave, S. B. Sutton, M. A. Webber and L. J. V. Piddock, Trends Microbiol., 2014, 22, 438–445 CrossRef CAS PubMed.
- N. L. Werner, M. T. Hecker, A. K. Sethi and C. J. Donskey, BMC Infect. Dis., 2011, 11, 187 CrossRef CAS PubMed.
- C. MacDougall, J. P. Powell, C. K. Johnson, M. B. Edmond and R. E. Polk, Clin. Infect. Dis., 2005, 41, 435–440 CrossRef CAS PubMed.
- R. E. Polk, C. K. Johnson, D. McClish, R. P. Wenzel and M. B. Edmond, Clin. Infect. Dis., 2004, 39, 497–503 CrossRef PubMed.
- I. T. Carvalho and L. Santos, Environ. Int., 2016, 94, 736–757 CrossRef PubMed.
- M. B. Ahmed, J. L. Zhou, H. H. Ngo and W. Guo, Sci. Total Environ, 2015, 532, 112–126 CrossRef CAS PubMed.
- X. Van Doorslaer, J. Dewulf, H. Van Langenhove and K. Demeestere, Sci. Total Environ, 2014, 500–501, 250–269 CrossRef CAS PubMed.
- T. L. Lemke, D. A. Williams, V. F. Roche and S. W. Zito, Foye's Principles of Medicinal Chemistry, VII ed., Lippincott Williams & Wilkins, 2012, 1083–1086 Search PubMed.
- C. Siporin, C. L. Heifetz and J. M. Domagala, The New Generation of Quinolones, Marcel Dekker, Inc., 1990 Search PubMed.
- A. Bryskier and J. F. Chantot, Drugs, 1995, 49, 16–28 CrossRef CAS PubMed.
- D. T. Chu and P. B. Fernandes, Antimicrob. Agents Chemother., 1989, 33, 131–135 CrossRef CAS PubMed.
- J. M. Blondeau, Surv. Ophthalmol., 2004, 49, S73–S78 CrossRef PubMed.
- K. Drlica, Curr. Opin. Microbiol., 1999, 2, 504–508 CrossRef CAS.
- J. S. Wolfson and D. C. Hooper, Antimicrob. Agents Chemother., 1985, 28, 581–586 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- R. K. Sinha and P. Biswas, J. Mol. Struct., 2020, 1222, 128946–128953 CrossRef CAS.
- S. Gunasekaran, K. Rajalakshmi and S. Kumaresan, Spectrochim. Acta, Part A, 2013, 112, 351–363 CrossRef CAS PubMed.
- A. I. Drakopoulos and P. C. Ioannou, Anal. Chim. Acta, 1997, 354, 197–204 CrossRef CAS.
- D. L. Ross and C. M. Riley, J. Pharm. Biomed. Anal., 1994, 12, 1325–1331 CrossRef CAS.
- S. Lecomte, M. H. Baron, M. T. Chenon, C. Coupry and N. J. Moreau, Antimicrob. Agents Chemother., 1994, 38, 2810–2816 CrossRef CAS PubMed.
- K. Sayin and D. Karakas, J. Mol. Struct., 2018, 1158, 57–65 CrossRef CAS.
- D. Yang, J. Li, L. Luo, R. Deng, Q. He and Y. Chen, Chem. Eng. J., 2020, 387, 124103 CrossRef CAS.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471 CrossRef CAS PubMed.
- M. J. Frisch et al. , Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- G. Cassone, J. Phys. Chem. Lett., 2020, 11, 8983–8988 CrossRef CAS PubMed.
- J. K. Wolken and F. Turecek, J. Am. Soc. Spectrom., 2000, 11, 1065–1071 CrossRef CAS.
- A. K. Chandra and A. Goursot, J. Phys. Chem., 1996, 100, 11596–11599 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- G. Galli and A. Pasquarello, Computer Simulation in Chemical Physics, ed. M. P. Allen and D. J. Tildesley, Kluwer Academic Publishers, Dordrecht, 1993, 261–313 Search PubMed.
- G. Cassone, D. Chillé, C. Foti, O. Giuffré, R. C. Ponterio, J. Sponer and F. Saija, Phys. Chem. Chem. Phys., 2018, 20, 23272–23280 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- P. L. Geissler, C. Dellago, D. Chandler, J. Hutter and M. Parrinello, Science, 2001, 291, 2121–2124 CrossRef CAS PubMed.
- A. M. Saitta, F. Saija and P. V. Giaquinta, Phys. Rev. Lett., 2012, 108, 207801 CrossRef PubMed.
- A. Hassanali, F. Giberti, J. Cuny, T. D. Kühne and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13723–13728 CrossRef CAS.
- M. Chen, et al. , Nat. Chem., 2018, 10, 413–419 CrossRef CAS PubMed.
- G. Cassone, J. Sponer and F. Saija, Top. Catal., 2021 DOI:10.1007/s11244-021-01487-0.
- C. De Stefano, C. Foti, O. Giuffrè and S. Sammartano, J. Mol. Liq., 2014, 195, 9–16 CrossRef CAS.
- O. Giuffré, S. Angowska, C. Foti and S. Sammartano, J. Chem. Eng. Data, 2019, 64, 800–809 CrossRef.
- D. Chillè, G. Cassone, F. Giacobello, O. Giuffrè, V. Mollica Nardo, R. C. Ponterio, F. Saija, J. Sponer, S. Trusso and C. Foti, J. Chem. Res. Toxicol., 2020, 33, 967–974 CrossRef PubMed.
- C. Foti and O. Giuffrè, Molecules, 2020, 25, 3110 CrossRef CAS.
- P. Gans, A. Sabatini and A. Vacca, Ann. Chim., 1999, 89, 45–49 CAS.
- P. Cardiano, C. Foti and O. Giuffrè, J. Mol. Liq., 2016, 223, 360–367 CrossRef CAS.
- D. Chillè, C. Foti and O. Giuffrè, J. Chem. Thermodyn., 2018, 121, 65–71 CrossRef.
- P. Cardiano, D. Chillè, C. Foti and O. Giuffrè, Fluid Phase Equilib., 2018, 458, 9–15 CrossRef CAS.
- D. Chillè, C. Foti and O. Giuffrè, Chemophere, 2018, 190, 72–79 CrossRef PubMed.
- D. Chillè, D. Aiello, G. I. Grasso, O. Giuffrè, A. Napoli, C. Sgarlata and C. Foti, J. Environ. Sci., 2020, 94, 100–111 CrossRef PubMed.
- A. Rusu, G. Tóth, L. Szőcs, J. Kökösi, M. Kraszni, Á. Gyéresi and B. Noszál, J. Pharm. Biomed. Anal., 2012, 66, 50–57 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2021 |

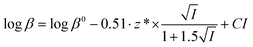
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)