Open Access Article
Open Access ArticleThe role of coordination strength in solid polymer electrolytes: compositional dependence of transference numbers in the poly(ε-caprolactone)–poly(trimethylene carbonate) system†
Therese
Eriksson
 ,
Amber
Mace
,
Amber
Mace
 ,
Jonas
Mindemark
,
Jonas
Mindemark
 and
Daniel
Brandell
and
Daniel
Brandell
 *
*
Department of Chemistry – Ångström Laboratory, Uppsala University, Box 538, SE-751 21 Uppsala, Sweden. E-mail: Daniel.Brandell@kemi.uu.se
First published on 8th November 2021
Abstract
Both polyesters and polycarbonates have been proposed as alternatives to polyethers as host materials for future polymer electrolytes for solid-state lithium-ion batteries. While being comparatively similar functional groups, the electron density on the coordinating carbonyl oxygen is different, thereby rendering different coordinating strength towards lithium ions. In this study, the transport properties of poly(ε-caprolactone) and poly(trimethylene carbonate) as well as random copolymers of systematically varied composition of the two have been investigated, in order to better elucidate the role of the coordination strength. The cationic transference number, a property well-connected with the complexing ability of the polymer, was shown to depend almost linearly on the ester content of the copolymer, increasing from 0.49 for the pure poly(ε-caprolactone) to 0.83 for pure poly(trimethylene carbonate). Contradictory to the transference number measurements that suggest a stronger lithium-to-ester coordination, DFT calculations showed that the carbonyl oxygen in the carbonate coordinates more strongly to the lithium ion than that of the ester. FT-IR measurements showed the coordination number to be higher in the polyester system, resulting in a higher total coordination strength and thereby resolving the paradox. This likely originates in properties that are specific of polymeric solvent systems, e.g. steric properties and chain dynamics, which influence the coordination chemistry. These results highlight the complexity in polymeric systems and their ion transport properties in comparison to low-molecular-weight analogues, and how polymer structure and steric effects together affect the coordination strength and transport properties.
Introduction
While solid polymer electrolytes (SPEs) have paved their way into several different solid-state Li-ion battery concepts in recent years,1,2 there still exist several gaps and inconsistencies regarding the fundamental understanding of the ion transport properties of these systems. Naturally, there has been a strive towards technological development in terms of reaching a high total ionic conductivity of the SPE materials – arguably the most problematic feature of SPEs for battery applications – but this has not truly been matched with in-depth investigations of the transport mechanisms. More knowledge in this respect is clearly desired.It is well established that the ions in a typical amorphous SPE, which by definition is free from liquid solvent components, are transported by means of the segmental motion of the polymer backbone.1 The cations are coordinated by the functional groups on the polymer and their movement is strongly correlated with the local motion of the polymer chain. Movement along or between polymer chains to new coordination environments requires the exchange of coordinating groups in the solvation shell of the cation. It is therefore obvious that the ion coordination properties of the polymer play a major role for the functionality of an SPE, in combination with the structure of the polymer host and its transport properties, and this interplay between coordination chemistry and ionic transport in SPEs has been researched for decades.3–13 It is generally acknowledged that the polymer needs to be able to coordinate the cations in order for them to dissociate from the anions and be transported through the matrix, but a too strong coordination will limit the mobility of the lithium ions and thereby generate a low cation transference number (T+).14 An example of this is the low transference number of polyethylene oxide (PEO; around 0.2), which is explained by the strong coordination and complexation of lithium ions.14,15 This means that most of the conductivity, or electrolyte current, instead originates from the anions and will not render the system an efficient SPE for application in Li-ion batteries. The role and determination of transference numbers in SPEs have in recent years been under intense debate,15–18 and recent data indicates that this property is directly correlated to the coordination strength between the cation and the coordinating groups of the polymer.1,19 The strength of the polymer–cation coordination is, in turn, dependent on the type of functional groups that the polymer possesses. Thus, depending on what coordinating functional group is active in coordination, the binding strength to the cation will change.
Here, we explore the properties of a well-known polyester–polycarbonate SPE system,20–23 but where novel aspects are investigated to shed new light on some of its fundamental properties. In general, both polycarbonates and polyesters have shown to work well as SPEs in solid-state battery setups,24–29 as well as poly(ε-caprolactone) (PCL) and poly(trimethylene carbonate) (PTMC) specifically.20–23 PCL possesses a comparatively high ionic conductivity, good mechanical properties, and is both easy to handle and to synthesise.30–32 Since it is a semi-crystalline polymer, some of these properties are highly influenced by the operating temperature. Below the melting point (around 60 °C), the mechanical properties are excellent, but at the cost of lowered ionic conductivity, and vice versa above the melting point. PTMC, on the other hand, is a fully amorphous polymer and therefore displays a more uniform dependence of ionic conductivity on temperature. The ionic conductivity follows a Vogel–Fulcher–Tammann (VFT) type of behaviour over a large temperature range, but in turn displays rather low ionic conductivity. This is correlated to the relatively high glass transition temperature of PTMC (−15 °C), resulting in limited chain dynamics.1,33,34
In a recent study, Rosenwinkel et al. studied the ion transport properties in SPEs based on PCL and PTMC, as well as in copolymers of the two with a CL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TMC molar ratio of 80
TMC molar ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20.14 The results were also compared to the well-known SPE host PEO. The molecular weight of the polymers was, however, kept to a maximum of 4000 g mol−1. Electrophoretic NMR has shown that PCL:LiTFSI has a transference number around 0.5, while PTMC:LiTFSI shows a value of almost 0.7 at the same salt concentration due to the stronger coordination in the polyester system than in the polycarbonate system, which was also indicated by NMR titrations.
20.14 The results were also compared to the well-known SPE host PEO. The molecular weight of the polymers was, however, kept to a maximum of 4000 g mol−1. Electrophoretic NMR has shown that PCL:LiTFSI has a transference number around 0.5, while PTMC:LiTFSI shows a value of almost 0.7 at the same salt concentration due to the stronger coordination in the polyester system than in the polycarbonate system, which was also indicated by NMR titrations.
In this present study, we investigate in greater depth the role of the coordination strength between the two extremes constituted by the PCL and PTMC homopolymers, and how the transference number depends on the polymer composition. To this end, we explore high-molecular-weight random PCL–PTMC copolymers of varied composition. It is seen that other factors than merely the coordinating group itself must play a major role for the coordination and transport properties in this system, which highlights the importance of taking more aspects of the SPE system into consideration in the design of novel materials and exploration of their properties. Compared to regular low-molecular-weight organic liquid electrolytes, the complexity increases as the coordinating groups in an SPE are chemically bonded to each other, which sterically limits the possible interactions between the coordinating groups and the cations. Thereby, it becomes important to consider several structural aspects of the polymer and its physical, sterical and chemical properties, beyond the simplistic direct coordination of the functional group.
Materials and methods
Materials
Homopolymers of distilled ε-caprolactone (CL) and trimethylene carbonate (TMC), as well as copolymers of varied molar ratio between CL and TMC (90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 80
10, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, 70
20, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, 40
30, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 30
60, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70, and 10
70, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90) were synthesised as described elsewhere.21 In short, a bulk ring-opening polymerisation was performed in argon atmosphere at 130 °C for 72 h using stannous 2-ethylhexanoate as a catalyst. As shown before,21,22 this synthesis method produces copolymers with a random monomer distribution and a molecular weight of around 200
90) were synthesised as described elsewhere.21 In short, a bulk ring-opening polymerisation was performed in argon atmosphere at 130 °C for 72 h using stannous 2-ethylhexanoate as a catalyst. As shown before,21,22 this synthesis method produces copolymers with a random monomer distribution and a molecular weight of around 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–500
000–500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1. Lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) was dried at 120 °C for 48 h before use. Solvent casting, sample preparation and cell assembly were all conducted in an argon-filled glovebox. Unless stated otherwise, all chemicals were received from commercial sources and used as received.
000 g mol−1. Lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) was dried at 120 °C for 48 h before use. Solvent casting, sample preparation and cell assembly were all conducted in an argon-filled glovebox. Unless stated otherwise, all chemicals were received from commercial sources and used as received.
Preparation of polymer electrolytes
Polymer electrolyte samples were prepared through a solvent casting method. The polymers with 30 wt% LiTFSI salt were dissolved in anhydrous acetonitrile and left with stirring overnight at 40 °C. The solutions were then poured into PTFE moulds and dried in a vacuum oven at 30 °C for 20 h while ramping down from 200 mbar to 1 mbar, followed by 60 °C for another 40 h at 1 mbar.Ionic conductivity
For ionic conductivity measurements, the cast samples with a known thickness and area were sandwiched between two stainless steel blocking electrodes and sealed in CR2025 coin cells. To ensure good contact, the cells were kept at 60 °C for 30 min and left to cool overnight to recrystallise. By measuring electrochemical impedance spectroscopy (EIS) with a Schlumberger SI 1260 Impedance/Gain-Phase Analyzer at a frequency range of 1 Hz–10 MHz and an amplitude of 10 mV, the ionic conductivity was determined for a range of temperatures, starting from 30 °C up to 90 °C.Transference number measurements
Transference numbers were determined through the Bruce–Vincent method.35 Using an Autolab PGSTAT30, the initial impedance was measured with EIS, followed by a polarization step at 10 mV and a final EIS measurement at 10 mV. The associated EIS measurements were done in a frequency range of 200 MHz to 1 MHz at an amplitude of 30 mV. The potential was applied until a stable current was measured. The interfacial resistances, bulk resistances and the steady-state current were extracted from the data, and the initial current was calculated using Ohms law and the total resistance in the cell.36 With these values, the transference numbers for the samples were calculated using eqn (1):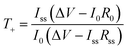 | (1) |
Density functional theory
DFT calculations were carried out to study the coordination of the respective monomers to the Li+ of LiTFSI. Subsequent geometry optimisation calculations were performed on the LiTFSI with the stepwise addition of 1–4 monomers. The calculations were performed with the Gaussian 16 software package37 at the B3LYP-D3/6-311++G level of theory, where the ground state molecular structures were fully optimised and verified by the absence of any imaginary frequencies.Infrared spectroscopy
Infrared spectroscopy (FT-IR) measurements were performed on polymers and monomers (with and without LiTFSI) using a PerkinElmer Spectrum One FT-IR spectrometer. Peaks corresponding to the coordinating and non-coordinating carbonyl groups were fitted using the Origin software, and were then used to calculate the coordination number from the Ocarbonyl:Li molar ratio of the sample.Results and discussion
A range of copolymers consisting of the same monomers, but at different ratios, were studied and used for SPE fabrication. The random copolymers were produced by ring-opening polymerisation of ε-caprolactone (CL) and trimethylene carbonate (TMC) with a varied CL content of 10–90 mol%. This system has been studied previously and has been shown to have a decent total ionic conductivity and battery performance, especially with a CL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TMC content of 80
TMC content of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20.21–23 It has, however, been observed that both the ionic conductivity as well as the thermal and physical properties varies significantly with the CL content.21,22 This is related to that pure PCL is a semi-crystalline polymer with a low glass transition temperature, but is limited by its crystallinity at room temperature.38,39 Pure PTMC, on the other hand, is fully amorphous but suffers from a relatively high glass transition temperature (limiting its total ionic conductivity) while it maintains a high transference number.23,33 This difference in transference numbers between the two is related to how the ester and carbonate groups that originate from the two monomers coordinate to the lithium ions. However, the importance of the coordination strength and its role for the overall transport properties in the context of other properties, have yet to be elucidated. The relationship between coordination properties and transference number is therefore systematically explored as the composition of the copolymers change.
20.21–23 It has, however, been observed that both the ionic conductivity as well as the thermal and physical properties varies significantly with the CL content.21,22 This is related to that pure PCL is a semi-crystalline polymer with a low glass transition temperature, but is limited by its crystallinity at room temperature.38,39 Pure PTMC, on the other hand, is fully amorphous but suffers from a relatively high glass transition temperature (limiting its total ionic conductivity) while it maintains a high transference number.23,33 This difference in transference numbers between the two is related to how the ester and carbonate groups that originate from the two monomers coordinate to the lithium ions. However, the importance of the coordination strength and its role for the overall transport properties in the context of other properties, have yet to be elucidated. The relationship between coordination properties and transference number is therefore systematically explored as the composition of the copolymers change.
The conduction and coordination properties in eight homopolymers and random copolymers were investigated. The polymers had compositions with CL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TMC molar ratios of 100
TMC molar ratios of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 90
0, 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 80
10, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, 70
20, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, 40
30, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 30
60, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70, 10
70, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 and 0
90 and 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100, while the salt content was kept constant at 30 wt% LiTFSI. The structure of the polymers is shown in Fig. 1.
100, while the salt content was kept constant at 30 wt% LiTFSI. The structure of the polymers is shown in Fig. 1.
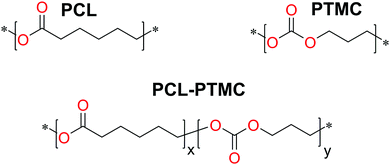 | ||
Fig. 1 Chemical composition of the synthesised polymers. The composition is denoted as the molar ratio x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y and the LiTFSI content was kept at 30 wt% (resulting in an O y and the LiTFSI content was kept at 30 wt% (resulting in an O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li ratio of 5.9–6.6). Li ratio of 5.9–6.6). | ||
The total ionic conductivity of the homo- and copolymers is shown in Fig. 2. The copolymers display an increasing conductivity with increased amount of CL as long as the polymer remains amorphous. With 30 wt% salt, even as little as 10% TMC monomer increases the ionic conductivity significantly at room temperature. This is due to that the crystallinity is significantly reduced at this relatively high salt content.38 Above the melting point of PCL (∼60 °C) though, the TMC addition has no positive influence on the ionic conductivity at this salt concentration. When the carbonate content is 30% or higher, the ionic conductivity decreases with increasing carbonate concentration over the entire temperature range and the lowest conductivity can be found in the pure carbonate polymer PTMC. This trend can be explained by an increasing glass transition temperature with increased TMC content, as has been shown previously.21 The ionic conductivity is therefore limited by the low degree of polymer segmental motion, as compared to PCL.
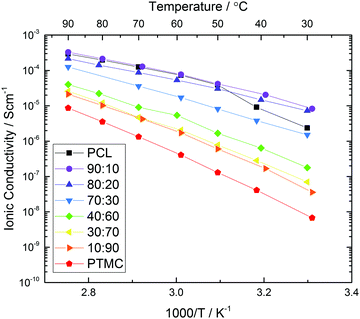 | ||
| Fig. 2 Total ionic conductivity measured while heating to 90 °C using impedance spectroscopy for copolymers with different CL:TMC ratio and 30 wt% LiTFSI. | ||
If judging the polymer electrolyte only on the metrics of ionic conductivity, it appears that PCL or copolymers thereof with 10–20% carbonate content would be the best choice depending on the operating temperature. The total ionic conductivity is, however, not the only property to consider for SPEs, not even regarding ionic transport. The total ionic conductivity says little about the efficiency of the ionic transport, i.e. how much of the conductivity that originate from cation or anion transport specifically. For that, the cation transference number (T+) is the key property. The transference number shows how mobile the respective cation and anion is in the polymer system, and indicates if the polymer–ion interactions are favourable, or perhaps too strong. A low transference number like in the case of PEO indicates a very strong coordination between the polymer and the cation, which prevents cationic mobility.1 It is therefore important to measure the lithium transference number (T+) to get a more complete view of the electrolyte transport properties.1
While the Bruce–Vincent method35,40 has grown to be standard for determining T+ in SPEs, it should be acknowledged that it is based on the Nernst–Einstein equation and therefore assumes that there ion–ion interactions are absent.1 While this is not the case in most SPEs, in a comparative study such as this, it can be assumed that the errors that occur will be comparable for all samples. A minimum of three samples were also measured for every sample to assure accuracy. The results are shown in Fig. 3.
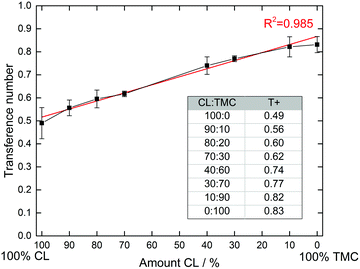 | ||
| Fig. 3 Measured transference numbers and standard errors for the CL:TMC copolymers. A minimum of three cells were measured for each sample. | ||
It is clear from Fig. 3 that the composition of the polymer greatly influences the transference number. The pure polyester electrolyte displays the lowest transference number, with an average of 0.49. When increasing the carbonate content, the transference number increases more or less linearly up to 0.83 for the pure polycarbonate. It therefore seems that the transference number is purely dependent on the CL:TMC ratio of the polymers, and does not follow the same trend as the total ionic conductivities in Fig. 2. This linearity is striking, and a regression line can be fitted with an R2 value of 0.985, with the primary deviations being for the extremes, i.e. the homopolymers. Few (or none) examples of similar trends between polymer composition and transference numbers have previously been shown in the literature for SPEs. That only minor deviations appear from the general linear trend strongly indicates that there indeed are fundamental differences in how strongly the different carbonyl groups bind to the Li+ cations, and that this is directly correlated to the transference number. The trend is also quite striking, considering that the chemical differences between the carbonate and ester functionalities are not particularly pronounced as compared to other cation coordinating functionalities (e.g. ethers, alcohols or nitriles),1 with the only extra oxygen in the carbonate group being non-coordinating to the cation.23
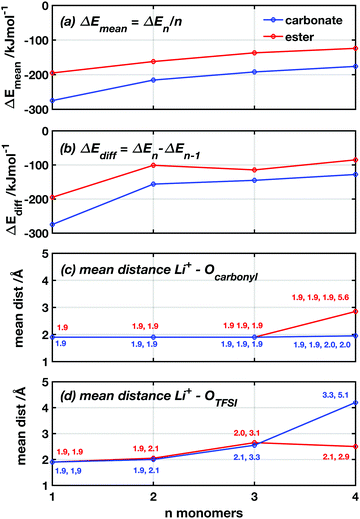
To examine the difference in coordination strength between the two functional groups more closely, DFT calculations were used to calculate the binding energies between the lithium ions and the carbonyl oxygens of the ester and carbonate groups. Since polymeric systems have too many degrees of freedom to reliably find the optimal conformation, a model system using CL and TMC monomers was used together with LiTFSI. Neither the monomeric form nor the ring shape of the monomers is expected to significantly affect the inherent binding properties of the functional groups, when comparing the ester and the carbonate systems. Subsequent additions were made of up to n = 4 monomers to form LiTFSI + n monomer complexes. When introducing one new monomer to the complex at each step, the monomer was placed so that the carbonyl oxygen is 2 Å away from Li+ with the ring pointing outwards. It was also given enough space from the atoms in the existing complex to avoid any strong repulsive interactions. In Fig. 4a and b, the binding energies are plotted as a function of the number of monomers in the complex in two different ways. First, the mean binding energy per monomer in the complex (ΔEmean) was computed by subtracting the molecular energies of LiTFSI and monomers from the total energy and dividing by n, ΔEmean = (Etot − ELiTFSI − nEmonomer)/n. Second, the binding energy for each addition of one monomer (ΔEdiff) was computed by subtracting ΔE of the previous complex of LiTFSI + n − 1 monomers and the molecular energy of a single monomer from the total energy of the new complex: ΔEdiff = Etot − En−1 − Emonomer. From these results, it appears that the TMC monomers consistently bind 30–50% stronger to the Li+ for all n values and with both metrics, compared to the CL monomers. This seems to contradict the trends in the transference numbers seen in Fig. 3.
To further understand the nature of the lithium coordination and how these differ between the TMC and the CL monomers, the bond lengths between Li+ and the carbonyl oxygen and the TFSI oxygen, respectively, were studied as a function of n (Fig. 4c and d). From these plots, it can be observed that the Li+ coordinates to both oxygen species in a similar manner and with similar bond lengths to both oxygen species for both TMC and CL complexes up to n = 3. Here, the bond distance between the Li+ and the carbonyl oxygen stays close to 2.0 (±0.1) Å. The two coordinated TFSI oxygens have similar bond lengths for n = 1 and 2, however, at n = 3 one of the coordinations are significantly weakened and the distance to the Li+ increases to 3.1 and 3.3 Å in the TMC and CL complexes, respectively. Then, when the fourth monomer is added, the coordination environment changes again and differences appear. In the CL complex, the double coordination of the Li+ to the TFSI oxygens is withheld, while the carbonyl oxygen of the fourth monomer does not coordinate to the Li+ and instead rotates to an outward-pointing position from the complex. In the TMC complex, on the other hand, a full coordination between all four carbonyl oxygens and the Li+ is withheld while the coordination to one of the TFSI oxygens is disrupted with a bond length of 5.1 Å and the second is further weakened with a bond length of 3.3 Å. Fig. S1 (ESI†) shows the coordination geometry around the Li+ in the LiTFSI + 4 monomer complexes.
Coordination in electrolyte systems fundamentally comes down to electrostatic interactions between the ions and the functional groups on the host material. The electrostatic potential (ESP) atomic charges computed by the Merz–Kollman scheme,41 indicate that the differing ΔE values can be explained by differences in charge distribution. Fig. 5 shows the contour surface of electrostatic potential of the monomers, and the same for the TFSI anion can be seen in Fig. S2 (ESI†). It can be seen from this that the TMC monomer is significantly more polar while the ESP partial charges show that the carbonyl oxygen is slightly more negative (−0.64e) than that of the CL (−0.59e), which would explain the stronger interaction with lithium ions. When coordinating to the Li+ the charges shift, but the same trend is still seen, and the coordinated carbonyl oxygen obtains lower ESP charge values −0.68e in the CL complex giving weaker electrostatic interactions as compared to the TMC complex −0.78e. If the charges of the carbon bonded to the carbonyl oxygen is also considered (being 0.79e for CL and 1.22e for TMC, when coordinated to Li+), the electrostatic force between the ion and the carbonyl group can be calculated straight-forwardly using Coulombs law (see eqn (S1) and Table S1, ESI†). The force was calculated to be 2.22 nN for CL and 1.77 nN for TMC when using values for charges and distances taken from calculations with 1 monomer and 1 LiTFSI. The electrostatic force therefore seems stronger for the ester system, due to the more positively charged carbon in TMC. In such a calculation, however, the interactions between monomers (or ligands) are not accounted for, in contrast to the DFT-computed coordination energies. If one only considers the Li+ and oxygen interaction, it can be seen that the carbonyl oxygen on the TMC is comparatively more negative in both the non-coordinated and coordinated state which would explain the more negative binding energies for this monomer.
 | ||
| Fig. 5 Charge distribution of electrostatic potential of TMC (top), CL (bottom). Blue colour indicates more positive charge and red more negative. | ||
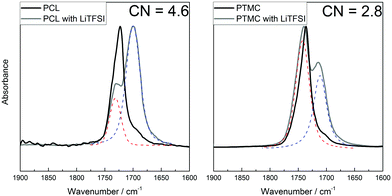
That the results from DFT calculations suggest that TMC would coordinate stronger to the lithium ion, which directly contradicts the measured transference numbers, indicates that it can be problematic to use the ΔE value directly. In the aforementioned study by Rosenwinkel et al., similar values for T+ for low-molecular-weight PCL and PTMC were found as in this work. The interactions between the polymer and lithium ion was then explored by NMR titration, in which a stronger interaction was seen between the PCL and Li+ as compared to PTMC and Li+, agreeing with the transference number trend. Thus, while the individual oxygens in the ester seem to have a weaker coordination to the lithium ion (as seen from the ΔE in the DFT results; Fig. 4a), the total interaction that appears in the full SPE matrix seems to be stronger in the ester than in the carbonate electrolytes according to the transference numbers and NMR studies.14 However, the reasoning so far has not considered the effect of the coordination number. Even if the coordination strength for the individual carbonyl oxygens in PCL have a lower binding strength, a higher coordination number may result in a higher total binding strength between the lithium ion and ester groups. To determine the coordination number, FT-IR spectroscopy was employed on PCL and PTMC with and without 30 wt% LiTFSI, as well as on the respective monomers. The coordination number was calculated using the Ocarbonyl:Li molar ratio and the area of the two relevant peaks (the coordinated and the uncoordinated carbonyl peak) at around 1700 and 1730 cm−1 for PCL and 1710 and 1740 cm−1 for PTMC.42 According to these measurements, the coordination number is significantly higher in PCL than in PTMC, as seen in Fig. 6, being around 4.6 for PCL while it is only 2.8 for the PTMC. The result from the measurements on the corresponding CL monomer is slightly lower (3.7) but still comparable to that of PCL, while the TMC shows multiple peaks which made the analysis uncertain and the results are therefore inconclusive (Fig. S3, ESI†). It was unfortunately not possible to determine a coordination number for the TFSI ion since signals from the polymers were overlapping with the TFSI peak, making the fitting too uncertain. As a comparison, an FT-IR spectrum of four monomer molecules together with one LiTFSI was determined using DFT calculations and is seen in Fig. S4 (ESI†). Multiple peaks are seen here as well, arising from the asymmetry of the coordinated monomers where the combinations of in- and out-of-phase C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching modes each result in slight shifts of the total dipole moment of the complex.
O stretching modes each result in slight shifts of the total dipole moment of the complex.
To summarise these results, the observation from the DFT calculations is that the carbonate has an inherently stronger bond to the lithium ion than does the ester. ΔE/n in Fig. 4a is always more negative for the carbonate than for the ester. In contrast, when considering not merely the carbonyl oxygen, but also the carbon atom of the functional group, it can be seen that the electrostatic force is actually stronger in the CL system. Furthermore, from the transference number and FT-IR measurements, in combination with previously published results,14 it appears that the polyester system should have a stronger overall coordination to the lithium ion (see Fig. 3 and 5). DFT does, however, only take enthalpy into consideration and not entropic effects. This in combination with inherent differences between a monomeric system and a polymeric system is something that needs to be considered in this context.
In a polymeric system, steric effects as well as chain flexibility need to be accounted for, since they affect the coordination chemistry and the possibility of exchanging coordination sites for the cations during ion transport. For example, Sai et al. showed that the addition of an ethyl side chain can sterically block certain coordination sites, forcing the Li+ to coordinate to a nitrile group instead of the more strongly binding ether groups, thereby achieving a lower transference number.43 Here, it seems that by moving from a low-molecular-weight system to a polymeric system, the importance of the electronic interactions and strength of a single bond between a carbonyl oxygen and a lithium ion is overpowered by steric effects and, as the functional groups are connected to each other, how many oxygens that can interact with the lithium ion. The coordination number to Li+ may thus to some extent be affected by the molecular weight of the solvent. This explains the deviations observed for low- and high-molecular-weight analogues in this particular ester/carbonate system, but likely also applies generally for many other SPEs as well. Yet another property that may affect the coordination structure and ion pairing in the polymer electrolyte system is the dielectric constant. Previously, a correlation between coordination strength and ion pairing has been observed,44 but its interrelation with the dielectric constant remains unclear. The resulting ion paring should, however, not significantly affect the transference number, unless the ion clustering results in an extensive formation of ion triplets. In a polymer system, steric effects may be more dominating than the electronic interactions and the total binding strength is dependent on the coordination number, while the coordination number in turn is indeed not only dependent on the strength of the individual ion–ligand bond but also other factors unique to polymeric solvents.
Conclusions
In PCL–PTMC random copolymers with LiTFSI salt, the cation transference number varies seemingly linearly from 0.49 for the pure PCL to 0.83 for pure PTMC as the TMC content is increased. While this implies stronger Li+ coordination with more ester groups in the electrolyte host material, DFT calculations suggest otherwise and instead indicate a stronger coordination strength between a carbonyl oxygen in the carbonate system and Li+ than in the ester system. The difference in binding strength for the polymeric systems, leading to the observed trend seen in the transference number measurements, instead lies in the coordination number being significantly higher in the ester system of the corresponding SPEs, rendering it possible for the total coordination between several carbonyl oxygens and a lithium cation to be stronger in the ester system. Thereby, it is seen that even if a system possesses a specific individual binding strength between a functional group and a lithium ion for low-molecular-weight analogues, the steric properties and coordination number in the resulting SPE must be considered in order to understand the structure–dynamic properties of the macroscopic SPE system, which may differ from the atomic-level picture.Author contributions
J. M., T. E. and D. B. conceptualised the project. T. E. performed the experimental work. A. M. performed DFT calculations. J. M. and D. B. supervised the project overall. T. E. and A. M. wrote first draft of the manuscript. All authors revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been financed through support from the ERC, grant no. 771777 FUN POLYSTORE and ECO2LIB (European Union H2020 research and innovation programme under grant agreement no. 875514). The authors would also like to acknowledge STandUP for Energy. A. M. is thankful for the support for Swedish National Strategic e-Science programme (eSSENCE) and Swedish Research Council (Registration No. 2019-05366) for funding. The DFT calculations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC.References
- J. Mindemark, M. J. Lacey, T. Bowden and D. Brandell, Prog. Polym. Sci., 2018, 81, 114–143 CrossRef CAS.
- Q. Zhang, K. Liu, F. Ding and X. Liu, Nano Res., 2017, 10, 4139–4174 CrossRef.
- R. Frech, S. Chintapalli, P. G. Bruce and C. A. Vincent, Macromolecules, 1999, 32, 808–813 CrossRef CAS.
- R. Frech, S. Chintapalli, P. G. Bruce and C. A. Vincent, Chem. Commun., 1997, 157–158 RSC.
- Y. G. Andreev and P. G. Bruce, Electrochim. Acta, 2000, 45, 1417–1423 CrossRef CAS.
- S. Suarez, J. Jayakody, S. Abbrent, S. G. Greenbaum, J. H. Shin and S. Passerini, Solid State Ionics, 2005, 176, 1113–1121 CrossRef CAS.
- D. Golodnitsky, E. Livshits, Y. Rosenberg, E. Peled, S. H. Chung, Y. Wang, S. Bajue and S. G. Greenbaum, J. Electroanal. Chem., 2000, 491, 203–210 CrossRef CAS.
- M. Marcinek, M. Ciosek, G. Żukowska, W. Wieczorek, K. R. Jeffrey and J. R. Stevens, Solid State Ionics, 2004, 171, 69–80 CrossRef CAS.
- W. Wieczorek, D. Raducha, A. Zalewska and J. R. Stevens, J. Phys. Chem. B, 1998, 102, 8725–8731 CrossRef CAS.
- S. Xue, Y. Liu, Y. Li, D. Teeters, D. W. Crunkleton and S. Wang, Electrochim. Acta, 2017, 235, 122–128 CrossRef CAS.
- S. Xue, D. Teeters, D. W. Crunkleton and S. Wang, Comput. Mater. Sci., 2019, 160, 173–179 CrossRef CAS.
- P. Johansson and P. Jacobsson, J. Phys. Chem. A, 2001, 105, 8504–8509 CrossRef CAS.
- P. Johansson, J. Tegenfeldt and J. Lindgren, J. Phys. Chem. A, 1998, 102, 4660–4665 CrossRef CAS.
- M. P. Rosenwinkel, R. Andersson, J. Mindemark and M. Schönhoff, J. Phys. Chem. C, 2020, 124, 23588–23596 CrossRef CAS.
- M. P. Rosenwinkel and M. Schönhoff, J. Electrochem. Soc., 2019, 166, A1977 CrossRef CAS.
- D. M. Pesko, S. Sawhney, J. Newman and N. P. Balsara, J. Electrochem. Soc., 2018, 165, A3014 CrossRef CAS.
- M. Gouverneur, F. Schmidt and M. Schönhoff, Phys. Chem. Chem. Phys., 2018, 20, 7470–7478 RSC.
- H.-K. Kim, N. P. Balsara and V. Srinivasan, J. Electrochem. Soc., 2020, 167, 110559 CrossRef CAS.
- N. S. Schauser, A. Nikolaev, P. M. Richardson, S. Xie, K. Johnson, E. M. Susca, H. Wang, R. Seshadri, R. J. Clément, J. Read de Alaniz and R. A. Segalman, ACS Macro Lett., 2021, 10, 104–109 CrossRef CAS.
- B. Sun, J. Mindemark, K. Edström and D. Brandell, Solid State Ionics, 2014, 262, 738–742 CrossRef CAS.
- J. Mindemark, E. Törmä, B. Sun and D. Brandell, Polymer, 2015, 63, 91–98 CrossRef CAS.
- J. Mindemark, B. Sun, E. Törmä and D. Brandell, J. Power Sources, 2015, 298, 166–170 CrossRef CAS.
- B. Sun, J. Mindemark, E. V. Morozov, L. T. Costa, M. Bergman, P. Johansson, Y. Fang, I. Furó and D. Brandell, Phys. Chem. Chem. Phys., 2016, 18, 9504–9513 RSC.
- Y. Tominaga and K. Yamazaki, Chem. Commun., 2014, 50, 4448–4450 RSC.
- K. Kimura, J. Motomatsu and Y. Tominaga, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 2442–2447 CrossRef CAS.
- J. Zhang, J. Yang, T. Dong, M. Zhang, J. Chai, S. Dong, T. Wu, X. Zhou and G. Cui, Small, 2018, 14, 1800821 CrossRef PubMed.
- J. Zhang, J. Zhao, L. Yue, Q. Wang, J. Chai, Z. Liu, X. Zhou, H. Li, Y. Guo, G. Cui and L. Chen, Adv. Energy Mater., 2015, 5, 1501082 CrossRef.
- D. M. Pesko, Y. Jung, A. L. Hasan, M. A. Webb, G. W. Coates, T. F. Miller and N. P. Balsara, Solid State Ionics, 2016, 289, 118–124 CrossRef CAS.
- M. Watanabe, M. Togo, K. Sanui, N. Ogata, T. Kobayashi and Z. Ohtaki, Macromolecules, 1984, 17, 2908–2912 CrossRef CAS.
- C. Polo Fonseca and S. Neves, J. Power Sources, 2006, 159, 712–716 CrossRef.
- C. P. Fonseca, D. S. Rosa, F. Gaboardi and S. Neves, J. Power Sources, 2006, 155, 381–384 CrossRef CAS.
- A. Bergfelt, M. J. Lacey, J. Hedman, C. Sångeland, D. Brandell and T. Bowden, RSC Adv., 2018, 8, 16716–16725 RSC.
- M. Ebadi, T. Eriksson, P. Mandal, L. T. Costa, C. M. Araujo, J. Mindemark and D. Brandell, Macromolecules, 2020, 53, 764–774 CrossRef CAS PubMed.
- J. Mindemark, L. Imholt and D. Brandell, Electrochim. Acta, 2015, 175, 247–253 CrossRef CAS.
- J. Evans, C. A. Vincent and P. G. Bruce, Polymer, 1987, 28, 2324–2328 CrossRef CAS.
- M. M. Hiller, M. Joost, H. J. Gores, S. Passerini and H.-D. Wiemhöfer, Electrochim. Acta, 2013, 114, 21–29 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- T. Eriksson, J. Mindemark, M. Yue and D. Brandell, Electrochim. Acta, 2019, 300, 489–496 CrossRef CAS.
- C. P. Fonseca, D. S. Rosa, F. Gaboardi and S. Neves, J. Power Sources, 2006, 155, 381–384 CrossRef CAS.
- P. G. Bruce and C. A. Vincent, J. Electroanal. Chem. Interfacial Electrochem., 1987, 225, 1–17 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- J. Mindemark, S. Tang, H. Li and L. Edman, Adv. Funct. Mater., 2018, 28, 1801295 CrossRef.
- R. Sai, K. Ueno, K. Fujii, Y. Nakano and H. Tsutsumi, RSC Adv., 2017, 7, 37975–37982 RSC.
- I. Gerz, E. M. Lindh, P. Thordarson, L. Edman, J. Kullgren and J. Mindemark, ACS Appl. Mater. Interfaces, 2019, 11, 40372–40381 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03929f |
| This journal is © the Owner Societies 2021 |