 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultrafast evolution of the complex dielectric function of monolayer WS2 after photoexcitation†
Stefano
Calati
 *ab,
Qiuyang
Li
c,
Xiaoyang
Zhu
c and
Julia
Stähler
*ab,
Qiuyang
Li
c,
Xiaoyang
Zhu
c and
Julia
Stähler
 ab
ab
aHumboldt-Universität zu Berlin, Institut für Chemie, Berlin, Germany
bFritz-Haber-Institut der Max-Planck-Gesellschaft, Abt. Physikalische Chemie, Berlin, Germany. E-mail: calatist@fhi-berlin.mpg.de
cDepartment of Chemistry, Columbia University, New York, USA
First published on 29th September 2021
Abstract
Transition metal dichalcogenides emerged as ideal materials for the investigation of exciton physics. Retrieving the excitonic signature in optical spectra, and tracking their time evolution upon photoexcitation requires appropriate analysis procedures, particularly when comparing different measurements, experimental techniques, samples, and substrates. In this work, we investigate the ultrafast time evolution of the exciton resonance of a monolayer of WS2 deposited on fused silica and Si/SiO2, and using two different measurement techniques: time-resolved reflectance and transmittance contrast. By modelling the dielectric function of the exciton with a Lorentz oscillator, using a Fresnell equations formalism, we derive analytical expressions of the exciton lineshape in both cases. The 2D linearized model introduced by Li et al. [Y. Li and T. F. Heinz, 2D Mater., 2018, 5, 025021] is used for the transmittance of the transparent substrate and a Fresnel transfer matrix method [O. Stenzel, The Physics of Thin Film Optical Spectra, Springer Series in Surface Science, 2016] is used to derive the reflectance in the case of the layered Si/SiO2 substrate. By fitting two models to the time-dependent optical spectra, we extract and quantify the time evolution of the parameter describing the excitonic resonance. We find a remarkable agreement between the extracted dynamics from both experiments despite the different side conditions, showing the equivalence and reliability of the two analysis methods in use. With this work, we pave the way to the resilient comparison of the exciton dynamics from different samples, measurements technique and substrates.
Transition metal dichalcogenides (TMDCs) attracted considerable interest in recent years due to their unique physical properties. Due to their two-dimensional nature, the resulting reduced screening makes these materials the ideal platform to investigate excitons.1 The physics of these Coulomb-bound quasi-particles is of interest from a fundamental point of view2 and potentially technologically relevant for optoelectronic applications in photonic devices.3 It is important that any device application includes transient regimes in which the system is driven out of its equilibrium state. In these transient regimes, shortly after a perturbation (such as photoexcitation for example), the properties of the system might not be the same as their steady state.4 Studying the response of materials when they are subject to photoexcitation, is a useful approach to understand the transient properties in the early stages after a perturbation and the recovery pathways to the equilibrium state. Time-resolved ultrafast spectroscopies are strong tools to access the non-equilibrium response of TMDCs.
While steady state experiments5–9 showed that the exciton resonance energy as well as the free particle band gap are influenced by the dielectric screening due to the environment of monolayer TMDCs, time-resolved10–13 and theoretical14–16 investigations find a pivotal contribution of photoexcited quasiparticles to resonance energy and broadening. The subtle interplay of these effects can contribute differently to the steady state spectra and non-equilibrium spectra. The different time-resolved optical experiments reported addressing the exciton dynamics upon photoexcitation, both on monolayer WS211–13 and MoS210,17 include reflection and transmission measurements, and use different models to isolate and describe the excitonic signature in the optical spectra and its photoresponse to an ultrafast excitation. Unfortunately, the consistency between these approaches is not examined broadly, rendering the comparison between different experiments difficult. Monolayer WS2 is one of the most extensively studied TMDC materials in the literature, together with MoS2. In particular its comparably large band gap, which is still accessible for common light (laser) sources, makes it an ideal candidate to study charge and energy transfer processes at potential optoelectronic interfaces.18–20
In this work, we make use of two models to isolate and track the excitonic signature in the transient optical response of monolayer WS2 deposited on different substrates and retrieved from different measurement techniques. We achieve this by extracting the dynamics of the complex dielectric function upon photoexcitation, assuming that the exciton's contribution to the permittivity can be modeled with a Lorentz oscillator. We first investigate the static and transient optical response of a monolayer WS2 deposited on a thick fused silica substrate. Employing the 2D linearized model, by Li et al.,21 and assuming a Lorentzian lineshape of the exciton resonance, we derive an analytical expression of the transmittance contrast (TC). By fitting the data with this model, we isolate the exciton's signature in the static spectrum. The dynamics of the exciton upon photoexcitation are then quantified by fitting the same model to the time-dependent TC spectra. An analogous approach is used to investigate the exciton dynamics in reflectance data of a different sample. The expression of the reflectance contrast (RC) spectrum of a WS2 monolayer deposited on a Si/SiO2 sample is derived utilizing the Fresnel transfer matrix formalism.22 The transient optical response of the exciton upon photoexcitation is then described by a time evolution of the complex dielectric function of the excitonic resonance. We finally compare the extracted dynamics of both cases under study. Remarkably, despite the fact that two different samples on two substrates were measured using complementary techniques, our quantitative analysis shows that the exciton dynamics coincide for the same excitation densities. This coincidence of the nonequilibrium response of different samples, retrieved with different experimental techniques, and analyzed with different models not only confirms the robustness of the previously reported formalisms, but demonstrates that results of different studies can be compared quantitatively within the accuracy of the excitation density determination.
1 Methods
The WS2 pristine monolayers are obtained by Au-assisted mechanical exfoliation of a CVD grown large area crystal, as described in detail in ref. 23 and 24. The monolayers are placed on a fused silica substrate (FS) and a silicon wafer covered with a 285 ± 15 nm layer of silicon oxide (Si/SiO2). Large monolayers areas of hundreds of micrometers are shown in the ESI.†For the sample deposited on FS and Si/SiO2 respectively, the transmittance contrast TC = (Tsub+WS2 − Tsub)/Tsub and the reflectance contrast RC = (Rsub − Rsub+WS2)/Rsub are measured. A pump and probe approach is employed to evaluate the time dependence of the TC and RC. For this, an optical pulse excites the system out of its equilibrium. After a variable time delay, a second pulse probes the reflectance or transmittance of the monolayer WS2. This process is iterated for different time delays. After every time-resolved scan, the transmittance/reflectance of the substrate is measured to calculate the TC or RC, respectively. All measurements were performed at room temperature and under ambient conditions. The laser pulses at 1.55 eV photon energy, at 200 kHz repetition rate and <40 fs time duration, are produced by a Ti:Sa laser system (Coherent RegA). Part of the laser system's output is used to drive an optical parametric amplifier (OPA) to generate the pump. The pump pulse is incident on the sample at a 45° angle in both measurements, tuned to 2.0 eV photon energy, with a time duration <100 fs. The white-light probe is generated by focusing the 1.55 eV light in a thin sapphire crystal, covering a spectral area ranging from 1.85 eV to 2.2 eV. It was compressed and characterized as described in ref. 25, to 16 fs duration. The probe pulse is aligned to normal incidence angle for the FS sample and to 45° incidence with s-polarization for the Si/SiO2 measurement. The spectrally resolved reflectance/transmittance on both substrate and sample were measured with a Shamrock 303i spectrometer obtaining, at each time delay, the entire transmittance/reflectance spectrum of the WS2 or substrate.
2 Results
2.1 Transmittance contrast using a fused silica substrate
First, we discuss the transmittance contrast spectra of a monolayer WS2 deposited on a fused silica substrate. In Fig. 1(a) we report the steady state transmittance contrast spectrum. It shows a Lorentzian-like peak at an energy of roughly 2 eV. A background signal also contributes to the total spectrum.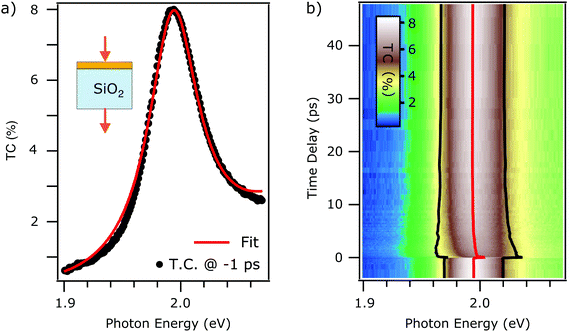 | ||
| Fig. 1 (a) Steady state TC contrast spectra of monolayer WS2 on thick FS substrate (black trace). Best fit using eqn (3) (red trace). (b) False color plot of the tr-TC as a function of probe photon energy (horizontal) and the pump–probe delay (vertical axis). The extracted fit parameter of exciton energy (red trace) and linewidth broadening (distance between black traces) obtained from fitting the time-dependent TC with eqn (4) are overlaid on the same axis. | ||
To model the exciton contribution to the reported spectrum, we use the 2D linearized model introduced by Li et al.21 This model allows the calculation of the transmittance contrast as a function of the dielectric function of the substrate, of the sample, and the thickness of the monolayer. The TC, in the approximation of low contrast (i.e. TC ≪ 1), is given by21
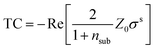 | (1) |
| Z0σs = −i2π(nWS22 − 1)(d/λ) | (2) |
We assume that the dielectric function of the exciton can be modelled with a Lorentz oscillator, as already reported in the literature,28,29 instead of a Gaussian or a Voigt lineshape.30 As will be shown below, the Lorentzian reproduces the experimental peak nearly perfectly. This is consistent with a high quality of the WS2 sample obtained by mechanical exfoliation, known to produce less defective samples,31 and with the fused silica substrate which, with respect to sapphire, leads to a more homogeneous response of the deposited TMDC.32
The corresponding permittivity is described as follows:
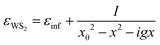 | (3) |
The TC background is attributed to the tail of higher energy electronic transitions.28,33 A rigorous description of this background can be achieved by adding more Lorentzian terms to the dielectric function to include higher energy transitions, as shown in ref. 28. The focus of this work, however, lies on the description of the dynamics of the A exciton upon photoexcitation and its comparison to different substrates and analysis procedures. It is, thus, sufficient to describe the background phenomenologically, because this is less computationally expensive. A polynomial function of second order gives very similar, if not coincident, parameters for the WS2 permittivity, as shown in the ESI.†
Based on this, we formulate the fit function of the TC spectra:
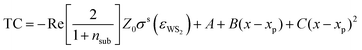 | (4) |
The fit result is shown in Fig. 1(a). The fit function reproduces the measured data and the extracted parameters are x0 = 1.994 ± 0.001 eV, g = 50 ± 3 meV, and I = 1.29 ± 0.06. The error estimation is discussed in the ESI.† The influence of the many-body excitonic state,34–36 which has traditionally been called trion, has been neglected as they are negligible at room temperature and intrinsic electron doping levels.37,38 In fact, one single Lorentzian reproduces the static spectrum accurately, without the need of including a second Lorentzian to model the trion which is observed in low temperature photoluminescence experiments.39
Having successfully modelled the steady state TC spectrum, we now focus on the nonequilibrium dynamics after photoexcitation. Fig. 1b shows the time-dependent TC in false colour scale, plotted as a function of probed photon energy and pump–probe delay. Every horizontal line corresponds to a TC spectrum for a specific time delay. We clearly observe pump-induced dynamics where the excitonic resonance maximum intensity decreases, as it undergoes a peak shift accompanied by a broadening. In order to quantify these effects, a fit using eqn (4) is then applied to every spectrum for different time delays, accessing position, width, and spectral weight of the resonance as a function of time delay. The polynomial background is kept constant for the different time delays. The extracted position of the resonance is reported by the red trace in Fig. 1(b), and the distance between the black traces represents the width g of the resonance as a function of time. Note that the spectral weight remains unchanged upon photoexcitation (see ESI†). This formalism allows to unveil the dynamics of the excitonic resonance precisely and the isolation from the background absorption that can be due to the inhomogeneous response of the sample,8 as discussed more in detail in the Discussion section.
2.2 Reflectance contrast using a Si/SiO2 substrate
We saw in the previous section that, when a monolayer WS2 is placed on a thick transparent substrate, as in the case of the fused silica, the transmittance contrast is mainly proportional to the absorptive part of the refractive index (i.e., imaginary part) of the WS2. This does not necessarily hold when measuring in reflection and when the substrate is layered with a thickness comparable to the laser wavelength, as sketched in the inset of Fig. 2(a). In fact, complex interference phenomena arise from the multiple reflections at the multiple interfaces between the constituent layers.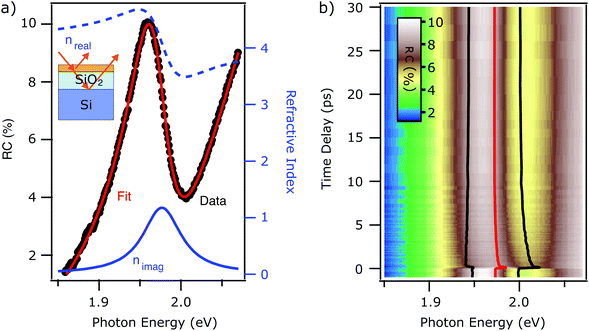 | ||
| Fig. 2 (a) Steady state RC contrast spectra of monolayer WS2 on Si/SiO2 substrate (black trace). Best fit using eqn (4) (red trace). The real (blue dashed) and imaginary (solid blue) parts of the refractive index are reported for comparison. (b) False color plot of the tr-RC as a function of probe photon energy (horizontal) and the pump–probe delay (vertical axis). The extracted fit parameters of exciton energy (red trace) and linewidth broadening (distance between black traces), obtained from fitting the time-dependent RC with eqn (8) are overlaid on the same axis. | ||
In Fig. 2(a), the black markers show the steady state RC spectrum of the Si/SiO2 sample. We observe an asymmetric and complicated line shape in the proximity of the exciton energy. To account for the multiple reflection problem and isolate the excitonic signature in the optical spectrum, we employ the Fresnel transfer matrix analysis (TMA)22 method to calculate the reflectance of what can be considered a heterostructure. The system in analysis is a monolayer of WS2 on a substrate, which consists of a silicon wafer covered with a 300 nm thick layer of silicon oxide.
We describe the dispersion and absorption of light in every layer employing the characteristic matrix.22 We will focus on the s-polarization case for an arbitrary incidence angle of the probe beam. More general cases for arbitrary polarization can be found in ref. 11.
The characteristic matrix of a film is given by the following expression:
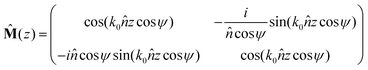 | (5) |
The characteristic matrix of a stack is then given by the multiplication of the characteristic matrices of all the constituent layers:22
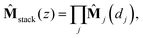 | (6) |
The reflected fraction from a stack of two layers in air is then given by:
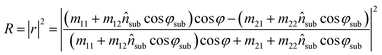 | (7) |
We can calculate the reflectance contrast by calculating the reflected fraction of the WS2 on the substrate and the reflectance of the bare substrate.
The expression of the formula for calculating the RC is a complicated function that depends on the thickness of the layers, dSiO2, dWS2, the incidence angle of the probe beam φ, and the refractive index of Si,27 SiO2,27 and WS2 respectively.
For the refractive index of the WS2, we assume that the dielectric constant can be modeled using a Lorenz oscillator, in analogy to the case of the FS substrate, according to eqn (3). Furthermore, a polynomial function is used again to reproduce the background in the RC data.
The resulting fit function is given by:
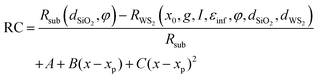 | (8) |
The fit function depends on seven parameters plus the four of the polynomial. In order to decrease the number of free parameters in the fitting as much as possible, the thickness of the WS2 monolayer is dWS2 = 0.7 nm.23,24 The incidence angle of the probe beam and the thickness of the SiO2 layer have been determined independently from a global fit of multiple static spectra, returning values of φ = 0.77 rad and dSiO2 = 305 ± 20 nm. Furthermore, εinf = 16.62 has been fixed to the value extracted from the fused silica case. The fit function then depends on the three parameters of the Lorentzian resonance: central energy, width, spectral weight, and the four parameters of the polynomial.
In Fig. 2(a), we report the best fit (red trace) to the steady state RC spectrum (black markers). The fit is in excellent agreement with the data. The extracted parameters for the exciton resonance are x0 = 1.973 ± 0.001 eV, g = 54 ± 2 meV and I = 1.05 ± 0.06. The errors are the same as the FS case, as discussed in the ESI.† The interference effect between multiple reflections at the interfaces provokes a mix of the dispersive and absorbing (i.e. real and imaginary) components of the refractive index. The resulting lineshape of the reflectance contrast is not centered at the same energy at which the peak of the imaginary part of the refractive index is (solid blue trace). The lineshape is mainly following the dispersive part of the refractive index (dashed blue trace).
In analogy to the case of the FS substrate, we proceed to the analysis of the time-dependent RC (tr-RC) reported in Fig. 2(b) In this figure, the tr-RC (false color scale) is reported as a function of probe photon energy (horizontal axis) and time delay (vertical axis). We clearly observe photoinduced dynamics in the proximity of the exciton energy. A qualitative description of these is non-trivial due to the mixing of the real and imaginary part of the refractive index that determine the RC lineshape. We proceed to the extraction of the dynamics of the refractive index by fitting the time-dependent RC with eqn (8). The polynomial background is again kept constant across the different time delays. The excitonic energy position x0, retrieved from the fitting, is highlighted by the red line shown in Fig. 2(b). In the same figure, the black traces provide a guide to the eye for the broadening of the resonance upon photoexcitation: the distance between the two black traces corresponds to the width g of the resonance. The spectral weight remains mainly unchanged. The accuracy of the fit for spectra at different time delays is reported in the ESI.†
This analysis allows to unravel the dynamics of the excitonic resonance upon photoexcitation precisely, as will be discussed in the following section.
3 Discussion
Above, we described the application of two different models that allow the quantitative extraction of linewidth broadening and peak shift of the excitonic resonance from tr-TC data in the case of a transparent substrate and from tr-RC data with an opaque layered substrate. Based on this, we now turn to a quantitative comparison of the transient response of the exciton resonance to photoexcitation of the two samples on different substrates. It is important to note that, although both, the TC and the RC experiment probe the non-equilibrium dynamics of the exciton in WS2, we do not necessarily expect the exact same results from the two different experiments, as – beyond the techniques – also analysis methods, samples, and substrates differ. In fact, both models used to calculate the TC and RC, derive from applying Fresnel equations to two different sets of boundary conditions and dealing with incoherent and coherent light–matter interaction for the FS and Si/SiO2 cases, respectively. Nevertheless, the different boundary conditions and limitations involved in the two models are not trivial. In addition, we can assume a similar, but not equal dielectric environment for the two substrates used in this work, affecting exciton binding energy and single particle band gap. Such effects have been reported in the literature and are, for instance, attributed to a local variation of the dielectric environment due to slightly different distances between the monolayer WS2 from the substrate or the presence of impurities or absorbates8 and to the impact of dielectric screening in the substrate.5In order to be able to quantitatively compare the exciton dynamics of both systems, it is necessary to calculate the initial photoexcitation density for both experiments. This quantity is fundamental for a correct analysis of the photoinduced dynamics since the exciton resonance is sensitive to the environment, screening, doping, and it can vary in peak position, broadening and spectral weight.8 A slight variation of any of these parameters can lead to a consistently different effective absorbance of the monolayer TMDC. The effective absorbance can be calculated starting from the complex dielectric function of the WS2 monolayer extracted from the fitting of the steady state spectra. The calculated absorbance of the monolayer WS2 deposited on the respective substrate is then compared to the pump lineshape to obtain an accurate value for the initial photoexcited particle density. The details of this calculation are reported in the ESI.† The initial photoexcited particle density for both experiments reported in Fig. 1 and 2, respectively, is 3.2 × 1012 cm−2 in both datasets and, therefore, below the Mott densities reported in the literature.2,12,16
Fig. 3 compares the relative exciton peak shift x0(t) − x0(eq) (top) and the photoinduced broadening g(t) − g(eq) (bottom) for the monolayer on the FS substrate (blue) and Si/SiO2 substrate (red), retrieved from Fig. 1 and 2 respectively. x0(eq) and g(eq) are the exciton energy and linewidth at equilibrium. Remarkably, both graphs show that the respective traces are coinciding with each other. Initially, right after photoexcitation, the exciton resonance is blue-shifted with respect to the steady state spectrum (Fig. 3, top). This shift relaxes within a few ps and turns into a red-shift with a decay time on the order of tens of ps. The exciton line broadens abruptly with photoexcitation and does not recover fully within 50 ps (Fig. 3, bottom).
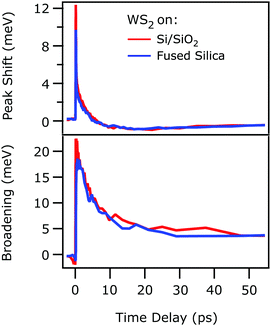 | ||
| Fig. 3 Time-dependent peak shift (top) and photoinduced linewidth broadening (bottom) of the excitonic resonance as a function of time delay, retrieved from a monolayer WS2 deposited on FS (blue traces) and Si/SiO2 (red traces) substrate, taken from Fig. 1 and 2 respectively. The initial photoexcited particle density is 3.2 × 1012 cm−2 in both cases. The two traces overlap across the whole range of delays. | ||
As outlined above, the observed perfect agreement of the exciton dynamics determined with different techniques, analysis methods, and samples was not to be expected prior to experiment. From this astounding observation, we draw the following conclusions: we assume that the coincidence of the exciton resonance energy shift and broadening is not accidental, but that the same excitation conditions actually cause the same exciton dynamics in the supported WS2 monolayer. Our finding, thus, implies that both, the 2D linearized model21 and the Fresnel transfer matrix formalism,22 used for extracting the exciton dynamics are accurate in tracking the evolution of the excitonic resonance upon photoexcitation and that the different boundary conditions and assumptions of the two analysis approaches are applicable to the systems investigated.
The above-described confidence in both models, secondly, allows the comparison of the absolute exciton resonance energy x0 for WS2 on both substrates, which is with 1.973 eV slightly red-shifted for the Si/SiO2 substrate compared to the fused silica case (x0 = 1.994 eV). As mentioned above, excitons in monolayers of TMDCs are highly sensitive to their dielectric environment,5,8 because of dielectric screening of the Coulomb interaction by the substrate. We therefore attribute the small variation of the steady state exciton resonance energy to slight differences in the dielectric environment for the FS and the Si/SiO2 substrate.
Thirdly, the coinciding photoinduced shift of the exciton resonance energy and broadening depicted in Fig. 3 clearly show that, beyond the dielectric screening, which differs for the two substrates, the exciton dynamics are dominated by the substrate-independent number of excited quasiparticles, as previously suggested for WSe214 and MoS2,10 respectively. These excited quasiparticles initially cause a blueshift of the exciton resonance that turns into a red shift within few ps (cf.Fig. 3). A slow recovery follows. It is known that, as for instance discussed by Ruppert et al.,40 changes of the exciton resonance energy depend on the fragile interplay of the photoinduced change of exciton binding energy and band gap renormalization. As both are determined by dynamic screening of the Coulomb interaction through excited quasiparticles, whose composition changes while the sample proceeds back to its equilibrium, complex changes of the exciton resonance energy can emerge. While at early times, right after photoexcitation, charge carriers and excitons dominate the dynamics, energy is transferred to the phonon system on a picosecond timescale, which then cools at even later times.40 The resonant excitation condition in our present experiment suggests that the observed initial blue shift is a result of dynamic screening by excitons as opposed to quasi-free electrons and holes that would be photoexcited by above-resonance pumping. Our study is, thus, complementary to ref. 40, in which a much weaker blue shift is observed, likely due to excitation with 2.4 eV photons that generate a larger portion of free carriers. Quantification of the dynamic screening of excitons and free carriers and its effect on exciton binding energy and free particle band gap, however, requires systematic experiments as a function of excitation energy and fluence, which will be subject of a forthcoming publication.41
4 Conclusions
The exciton dynamics in monolayer WS2, deposited on two different substrates (fused silica and Si/SiO2), were studied with time-resolved transmittance/reflectance contrast. The excitonic signature in the optical spectra (TC and RC) has been described by modeling the dielectric function with a Lorentz oscillator through the 2D linearized model21 and the Fresnel transfer matrix formalism22 for the monolayer on the two substrates, respectively. Using these models allows the isolation and quantitative description of the excitonic signature in the steady-state optical spectra.The dynamics of the complex dielectric function upon photoexcitation were also extracted by fitting the aforementioned models to the time-dependent optical spectra. This provides an accurate tracking of the photoresponse of the exciton to ultrafast excitation. By comparing the time evolution of the complex dielectric function extracted in the two experiments, we demonstrated the reliability of the models used for extracting the exciton non-equilibrium response for different samples, substrates, and measurement techniques.
Our results indicate that, while the steady-state exciton resonance energy is slightly influenced by the choice of substrate, the transient energy shift and broadening of the A exciton is clearly determined by the excited quasiparticles and independent of the substrate.
Based on these results, we conclude that exciton dynamics in TMDCs can be compared quantitatively even for different samples and optical sampling techniques, if the excited particle density is determined precisely. This finding may serve as the foundation for future studies and promises the reliable comparison of different experiments. These could lead to a univocal understanding of the non-equilibrium dynamics in TMDCs and other 2D materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 182087777—SFB 951. X. Y. Z. acknowledges support for sample preparation by the Materials Science and Engineering Research Center (MRSEC) through NSF grant DMR-2011738. S. C. and J. S. would like to thank Dr Samuel Palato and Dr Alexander Paarmann for the stimulating discussions.Notes and references
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- G. Wang, A. Chernikov, M. M. Glazov, T. F. Heinz, X. Marie, T. Amand and B. Urbaszek, Rev. Mod. Phys., 2018, 90, 021001 CrossRef CAS.
- D. Jariwala, V. K. Sangwan, L. J. Lauhon, T. J. Marks and M. C. Hersam, ACS Nano, 2014, 8, 1102–1120 CrossRef CAS PubMed.
- L. Gierster, S. Vempati and J. Stähler, Nat. Commun., 2021, 12, 978 CrossRef CAS PubMed.
- S. Park, N. Mutz, T. Schultz, S. Blumstengel, A. Han, A. Aljarb, L.-J. Li, E. J. W. List-Kratochvil, P. Amsalem and N. Koch, 2D Mater., 2018, 5, 025003 CrossRef.
- Y. Lin, X. Ling, L. Yu, S. Huang, A. L. Hsu, Y.-H. Lee, J. Kong, M. S. Dresselhaus and T. Palacios, Nano Lett., 2014, 14, 5569–5576 CrossRef CAS PubMed.
- M. L. Trolle, T. G. Pedersen and V. Véniard, Sci. Rep., 2017, 7, 39844 CrossRef CAS PubMed.
- A. Raja, L. Waldecker, J. Zipfel, Y. Cho, S. Brem, J. D. Ziegler, M. Kulig, T. Taniguchi, K. Watanabe, E. Malic, T. F. Heinz, T. C. Berkelbach and A. Chernikov, Nat. Nanotechnol., 2019, 14, 832–837 CrossRef CAS PubMed.
- S. Lippert, L. M. Schneider, D. Renaud, K. N. Kang, O. Ajayi, J. Kuhnert, M.-U. Halbich, O. M. Abdulmunem, X. Lin, K. Hassoon, S. Edalati-Boostan, Y. D. Kim, W. Heimbrodt, E.-H. Yang, J. C. Hone and A. Rahimi-Iman, 2D Mater., 2017, 4, 025045 CrossRef.
- E. A. A. Pogna, M. Marsili, D. De Fazio, S. Dal Conte, C. Manzoni, D. Sangalli, D. Yoon, A. Lombardo, A. C. Ferrari, A. Marini, G. Cerullo and D. Prezzi, ACS Nano, 2016, 10, 1182–1188 CrossRef CAS PubMed.
- E. J. Sie, A. Steinhoff, C. Gies, C. H. Lui, Q. Ma, M. Rösner, G. Schönhoff, F. Jahnke, T. O. Wehling, Y.-H. Lee, J. Kong, P. Jarillo-Herrero and N. Gedik, Nano Lett., 2017, 17, 4210–4216 CrossRef CAS PubMed.
- A. Chernikov, C. Ruppert, H. M. Hill, A. F. Rigosi and T. F. Heinz, Nat. Photonics, 2015, 9, 466–470 CrossRef CAS.
- P. D. Cunningham, A. T. Hanbicki, K. M. McCreary and B. T. Jonker, ACS Nano, 2017, 11, 12601–12608 CrossRef CAS PubMed.
- G. Moody, C. Kavir Dass, K. Hao, C.-H. Chen, L.-J. Li, A. Singh, K. Tran, G. Clark, X. Xu, G. Berghäuser, E. Malic, A. Knorr and X. Li, Nat. Commun., 2015, 6, 8315 CrossRef CAS PubMed.
- A. Steinhoff, M. Rösner, F. Jahnke, T. O. Wehling and C. Gies, Nano Lett., 2014, 14, 3743–3748 CrossRef CAS PubMed.
- A. Steinhoff, M. Florian, M. Rösner, G. Schönhoff, T. O. Wehling and F. Jahnke, Nat. Commun., 2017, 8, 1166 CrossRef CAS PubMed.
- S. Sim, J. Park, J.-G. Song, C. In, Y.-S. Lee, H. Kim and H. Choi, Phys. Rev. B, 2013, 88, 075434 CrossRef.
- X. Zhu, N. R. Monahan, Z. Gong, H. Zhu, K. W. Williams and C. A. Nelson, J. Am. Chem. Soc., 2015, 137, 8313–8320 CrossRef CAS PubMed.
- A. O. A. Tanoh, N. Gauriot, G. Delport, J. Xiao, R. Pandya, J. Sung, J. Allardice, Z. Li, C. A. Williams, A. Baldwin, S. D. Stranks and A. Rao, ACS Nano, 2020, 14, 15374–15384 CrossRef CAS PubMed.
- S. Fu, I. du Fossé, X. Jia, J. Xu, X. Yu, H. Zhang, W. Zheng, S. Krasel, Z. Chen, Z. M. Wang, K.-J. Tielrooij, M. Bonn, A. J. Houtepen and H. I. Wang, Sci. Adv., 2021, 7, eabd9061 CAS.
- Y. Li and T. F. Heinz, 2D Mater., 2018, 5, 025021 CrossRef.
- O. Stenzel, The Physics of Thin Film Optical Spectra, Springer Series in Surface Science, 2016 Search PubMed.
- F. Liu, M. E. Ziffer, K. R. Hansen, J. Wang and X. Zhu, Phys. Rev. Lett., 2019, 122, 246803 CrossRef CAS PubMed.
- S. B. Desai, S. R. Madhvapathy, M. Amani, D. Kiriya, M. Hettick, M. Tosun, Y. Zhou, M. Dubey, J. W. Ager III, D. Chrzan and A. Javey, Adv. Mater., 2016, 28, 4053–4058 CrossRef CAS PubMed.
- D. Wegkamp, D. Brida, S. Bonora, G. Cerullo, J. Stähler, M. Wolf and S. Wall, Appl. Phys. Lett., 2011, 99, 101101 CrossRef.
- Y. Huang, Y.-H. Pan, R. Yang, L.-H. Bao, L. Meng, H.-L. Luo, Y.-Q. Cai, G.-D. Liu, W.-J. Zhao, Z. Zhou, L.-M. Wu, Z.-L. Zhu, M. Huang, L.-W. Liu, L. Liu, P. Cheng, K.-H. Wu, S.-B. Tian, C.-Z. Gu, Y.-G. Shi, Y.-F. Guo, Z. G. Cheng, J.-P. Hu, L. Zhao, G.-H. Yang, E. Sutter, P. Sutter, Y.-L. Wang, W. Ji, X.-J. Zhou and H.-J. Gao, Nat. Commun., 2020, 11, 2453 CrossRef CAS PubMed.
- I. H. Malitson, J. Opt. Soc. Am., 1965, 55, 1205–1209 CrossRef CAS.
- N. Ansari and F. Ghorbani, J. Opt. Soc. Am. B, 2018, 35, 1179–1185 CrossRef CAS.
- M. Weismann and N. C. Panoiu, Phys. Rev. B, 2016, 94, 035435 CrossRef.
- L. Guo, C.-A. Chen, Z. Zhang, D. M. Monahan, Y.-H. Lee and G. R. Fleming, Nanoscale Adv., 2020, 2, 2333–2338 RSC.
- J. Liu, T. W. Lo, J. Sun, C. T. Yip, C. H. Lam and D. Y. Lei, J. Mater. Chem. C, 2017, 5, 11239–11245 RSC.
- K. M. McCreary, A. T. Hanbicki, S. Singh, R. K. Kawakami, G. G. Jernigan, M. Ishigami, A. Ng, T. H. Brintlinger, R. M. Stroud and B. T. Jonker, Sci. Rep., 2016, 6, 35154 CrossRef CAS PubMed.
- Y. Li, A. Chernikov, X. Zhang, A. Rigosi, H. M. Hill, A. M. van der Zande, D. A. Chenet, E.-M. Shih, J. Hone and T. F. Heinz, Phys. Rev. B, 2014, 90, 205422 CrossRef.
- M. Sidler, P. Back, O. Cotlet, A. Srivastava, T. Fink, M. Kroner, E. Demler and A. Imamoglu, Nat. Phys., 2017, 13, 255–261 Search PubMed.
- F. Rana, O. Koksal and C. Manolatou, Phys. Rev. B, 2020, 102, 085304 CrossRef CAS.
- D. K. Efimkin and A. H. MacDonald, Phys. Rev. B, 2017, 95, 035417 CrossRef.
- K. F. Mak, K. He, C. Lee, G. H. Lee, J. Hone, T. F. Heinz and J. Shan, Nat. Mater., 2013, 12, 207–211 CrossRef CAS PubMed.
- J. S. Ross, S. Wu, H. Yu, N. J. Ghimire, A. M. Jones, G. Aivazian, J. Yan, D. G. Mandrus, D. Xiao, W. Yao and X. Xu, Nat. Commun., 2013, 4, 1474 CrossRef PubMed.
- G. Wang, L. Bouet, D. Lagarde, M. Vidal, A. Balocchi, T. Amand, X. Marie and B. Urbaszek, Phys. Rev. B, 2014, 90, 075413 CrossRef CAS.
- C. Ruppert, A. Chernikov, H. M. Hill, A. F. Rigosi and T. F. Heinz, Nano Lett., 2017, 17, 644–651 CrossRef CAS PubMed.
- S. Calati, Q. Li, X. Zhu and J. Stähler, 2021, manuscript in preparation.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03437e |
| This journal is © the Owner Societies 2021 |
